| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117539 | |
| Published online | 09 February 2012 | |
The cosmic-ray and gas content of the Cygnus region as measured in γ-rays by the Fermi Large Area Telescope
1
W. W. Hansen Experimental Physics Laboratory, Kavli Institute for Particle
Astrophysics and Cosmology, Department of Physics and SLAC National Accelerator
Laboratory, Stanford University, Stanford, CA
94305, USA
2
Istituto Nazionale di Fisica Nucleare, Sezione di
Pisa, 56127
Pisa,
Italy
3
Laboratoire AIM, CEA-IRFU/CNRS/Université Paris Diderot, Service
d’Astrophysique, CEA Saclay, 91191
Gif-sur-Yvette,
France
e-mail: isabelle.grenier@cea.fr
4
Istituto Nazionale di Fisica Nucleare, Sezione di
Trieste, 34127
Trieste,
Italy
5
Dipartimento di Fisica, Università di Trieste,
34127
Trieste,
Italy
6
Istituto Nazionale di Fisica Nucleare, Sezione di
Padova, 35131
Padova,
Italy
e-mail: luigi.tibaldo@pd.infn.it
7
Dipartimento di Fisica “G. Galilei”, Università di
Padova, 35131
Padova,
Italy
8
INAF-Istituto di Astrofisica Spaziale e Fisica
Cosmica, 20133
Milano,
Italy
9
Istituto Nazionale di Fisica Nucleare, Sezione di
Perugia, 06123
Perugia,
Italy
10
Dipartimento di Fisica, Università degli Studi di
Perugia, 06123
Perugia,
Italy
11
Dipartimento di Fisica “M. Merlin” dell’Università e del
Politecnico di Bari, 70126
Bari,
Italy
12
Istituto Nazionale di Fisica Nucleare, Sezione di
Bari, 70126
Bari,
Italy
13
Laboratoire Leprince-Ringuet, École polytechnique,
CNRS/IN2P3, Palaiseau, France
14
Institut de Ciències de l’Espai (IEEE-CSIC),
Campus UAB, 08193
Barcelona,
Spain
15
Artep Inc., 2922 Excelsior Springs Court, Ellicott City, MD 21042,
resident at Naval Research Laboratory, Washington, DC
20375,
USA
16
ASI Science Data Center, 00044
Frascati, Roma, Italy
17
Laboratoire Univers et Particules de Montpellier, Université
Montpellier 2, CNRS/IN2P3, Montpellier, France
18
Dipartimento di Fisica, Università di Udine and Istituto Nazionale
di Fisica Nucleare, Sezione di
Trieste, Gruppo Collegato di Udine, 33100
Udine,
Italy
19
Space Science Division, Naval Research Laboratory,
Washington, DC
20375-5352,
USA
20
Université Bordeaux 1, CNRS/IN2p3, Centre d’Études Nucléaires de
Bordeaux Gradignan, 33175
Gradignan,
France
21
Department of Physical Sciences, Hiroshima
University, Higashi-Hiroshima, Hiroshima
739-8526,
Japan
22
INAF Istituto di Radioastronomia, 40129
Bologna,
Italy
23
Current address: Max-Planck-Institut für
Radioastronomie, Auf dem Hügel
69, 53121
Bonn,
Germany
24
Center for Space Plasma and Aeronomic Research (CSPAR), University
of Alabama in Huntsville, Huntsville, AL
35899,
USA
25
NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
26
Science Institute, University of Iceland,
IS-107
Reykjavik,
Iceland
27
College of Science, Ibaraki University,
2-1-1, Bunkyo, Mito
310-8512,
Japan
28
Research Institute for Science and Engineering, Waseda
University, 3-4-1, Okubo,
Shinjuku, Tokyo
169-8555,
Japan
29
CNRS, IRAP, 31028
Toulouse Cedex 4,
France
30
Université de Toulouse, UPS-OMP, IRAP,
Toulouse,
France
31
Yukawa Institute for Theoretical Physics, Kyoto
University, Kitashirakawa
Oiwake-cho, Sakyo-ku, Kyoto
606-8502,
Japan
32
Max-Planck Institut für extraterrestrische Physik,
85748
Garching,
Germany
33
Department of Physics and Department of Astronomy, University of
Maryland, College
Park, MD
20742,
USA
34
Istituto Nazionale di Fisica Nucleare, Sezione di Roma “Tor
Vergata”, 00133
Roma,
Italy
35
Department of Physics, Boise State University,
Boise, ID
83725,
USA
36
Hiroshima Astrophysical Science Center, Hiroshima
University, Higashi-Hiroshima, Hiroshima
739-8526,
Japan
37
Institute of Space and Astronautical Science,
JAXA, 3-1-1 Yoshinodai, Chuo-ku,
Sagamihara, Kanagawa
252-5210,
Japan
38
Department of Physics and Astronomy, University of
Denver, Denver,
CO
80208,
USA
39
Max-Planck-Institut für Physik, 80805
München,
Germany
40
Center for Earth Observing and Space Research, College of Science,
George Mason University, Fairfax, VA 22030, resident at Naval Research
Laboratory, Washington, DC
20375,
USA
41
Institut für Astro- und Teilchenphysik and Institut
fürTheoretische Physik, Leopold-Franzens-Universität Innsbruck,
6020
Innsbruck,
Austria
42
Santa Cruz Institute for Particle Physics, Department of Physics
and Department of Astronomy and Astrophysics, University of California at Santa
Cruz, Santa Cruz,
CA
95064,
USA
43
NYCB Real-Time Computing Inc., Lattingtown, NY
11560-1025,
USA
44
Department of Physics, Center for Cosmology and Astro-Particle
Physics, The Ohio State University, Columbus, OH
43210,
USA
45
Partially supported by the International Doctorate on
Astroparticle Physics (IDAPP) program
46
Institució Catalana de Recerca i Estudis Avançats
(ICREA), Barcelona,
Spain
47
Consorzio Interuniversitario per la Fisica Spaziale
(CIFS), 10133
Torino,
Italy
48
INTEGRAL Science Data Centre, 1290
Versoix,
Switzerland
49
NASA Postdoctoral Program Fellow,
USA
50
Dipartimento di Fisica, Università di Roma “Tor
Vergata”, 00133
Roma,
Italy
51
Department of Physics, Stockholm University,
AlbaNova, 106 91
Stockholm,
Sweden
52
The Oskar Klein Centre for Cosmoparticle Physics,
AlbaNova, 106 91
Stockholm,
Sweden
53
Laboratoire d’Astrophysique de Bordeaux, Université de Bordeaux,
CNRS/INSU, Floirac
Cedex, France
Received: 22 June 2011
Accepted: 29 October 2011
Context. The Cygnus region hosts a giant molecular-cloud complex that actively forms massive stars. Interactions of cosmic rays with interstellar gas and radiation fields make it shine at γ-ray energies. Several γ-ray pulsars and other energetic sources are seen in this direction.
Aims. In this paper we analyze the γ-ray emission measured by the Fermi Large Area Telescope (LAT) in the energy range from 100 MeV to 100 GeV in order to probe the gas and cosmic-ray content on the scale of the whole Cygnus complex. The γ-ray emission on the scale of the central massive stellar clusters and from individual sources is addressed elsewhere.
Methods. The signal from bright pulsars is greatly reduced by selecting photons in their off-pulse phase intervals. We compare the diffuse γ-ray emission with interstellar gas maps derived from radio/mm-wave lines and visual extinction data. A general model of the region, including other pulsars and γ-ray sources, is sought.
Results. The integral H i emissivity above 100 MeV averaged over the whole Cygnus complex amounts to [2.06 ± 0.11 (stat.) -0.84+0.15(syst.)] × 10-26 photons s-1 sr-1 H-atom-1, where the systematic error is dominated by the uncertainty on the H i opacity to calculate its column densities. The integral emissivity and its spectral energy distribution are both consistent within the systematics with LAT measurements in the interstellar space near the solar system. The average XCO = N(H2)/WCO ratio is found to be [1.68 ± 0.05 (stat.) -0.10+0.87(HI opacity)] × 1020 molecules cm-2 (K km s-1)-1, consistent with other LAT measurements in the Local Arm. We detect significant γ-ray emission from dark neutral gas for a mass corresponding to ~40% of what is traced by CO. The total interstellar mass in the Cygnus complex inferred from its γ-ray emission amounts to 8-1+5 × 106 M⊙ at a distance of 1.4 kpc.
Conclusions. Despite the conspicuous star formation activity and high masses of the interstellar clouds, the cosmic-ray population in the Cygnus complex averaged over a few hundred parsecs is similar to that of the local interstellar space.
Key words: ISM: abundances / ISM: clouds / cosmic rays / gamma rays: ISM
© ESO, 2012
1. Introduction
Regions with conspicuous star formation activity are of great interest for understanding the life cycle of interstellar matter and the properties of cosmic rays (CRs) in the Galaxy. Interstellar γ-ray emission produced by CR interactions with the interstellar gas via nucleon-nucleon inelastic collisions and electron Bremsstrahlung can be used to probe their CR and gas content.
High-energy γ-ray observations have entered a new era since the launch of the Fermi Gamma-ray Space Telescope in 2008. The Fermi Large Area Telescope (LAT; Atwood et al. 2009) has already measured strong γ-ray emission toward the 30 Doradus starburst region in the Large Magellanic Cloud (Abdo et al. 2010d), and it also pointed out a global correlation between the γ-ray luminosity and star-formation rate in a few normal galaxies (Abdo et al. 2010c).
A primary observational target for Fermi in our Galaxy is the Cygnus X star-forming region, owing to its proximity (~1.4 kpc; Hanson 2003; Negueruela et al. 2008) and the availability of numerous multiwavelength observations. Named after the strong emission at X-ray wavelengths (Cash et al. 1980), Cygnus X is located around the Galactic longitude l = 80°, tangent to the Local Spur. It contains numerous H ii regions and OB associations (Uyanıker et al. 2001; Le Duigou & Knödlseder 2002). It has long been debated whether it represents a coherent complex or the alignment of different structures along the line of sight. Recent high-resolution observations by Schneider et al. (2006) and Roy et al. (2011) have pointed out that most of the molecular clouds in the Cygnus X region are connected and partly show evidence of interactions with the massive stellar cluster Cygnus OB2 and other OB associations in the region. Foreground molecular clouds from the Great Cygnus Rift, at 0.6–0.8 kpc, contribute little to the high mass seen in interaction with the Cygnus X region itself, at 1.4 kpc. Therefore, the molecular cloud complex appears as one of the most massive in the Galaxy. Atomic gas seen in these directions is probably more widespread along the line of sight.
Abdo et al. (2007, 2008) analyzed Milagro measurements at energies >10 TeV and reports an excess of diffuse γ-ray emission with respect to predictions based on CR spectra equivalent to those near the Earth. They attribute the excess to the possible presence of freshly accelerated particles.
The escape of CRs from their sources and the early propagation in the surrounding medium have so far been poorly constrained by observations. In particular, particles accelerated in regions of massive star-formation are likely to be significantly influenced by the turbulent environment. It is therefore interesting to investigate how the CR populations on the scale of the massive stellar clusters and on the larger scale of the parent interstellar complex compare with each other and with the average CR population of the Local Spur.
This paper reports our analysis of the γ-ray emission measured by the LAT in the energy range between 100 MeV and 100 GeV across the entire Cygnus region. We focus on the large-scale properties of the interstellar emission to probe the CR population and to complement gas and dust observations at other wavelengths to constrain the amount of gas in different phases over the whole Cygnus complex. We also build an improved interstellar background framework for the study of individual γ-ray sources that will be treated in companion papers. We discuss interstellar emission in the star-forming region of Cygnus X in a dedicated paper (Ackermann et al. 2011a).
2. Data
In this section we describe the data used in the paper. First of all, we describe the γ-ray data sample (Sect. 2.1), including the selection criteria (Sect. 2.1.1) and the procedure to mitigate the signals from the brightest pulsars (Sect. 2.1.2). Then, we present an overview of the other data used to trace the distribution of the interstellar matter (Sect. 2.2), including radio and mm-wave lines (Sect. 2.2.1) to trace neutral gas, visual extinction (Sect. 2.2.2) to trace dark neutral gas, and the free-free emission intensities obtained from microwave observations (Sect. 2.2.3) to trace the ionized gas.
2.1. Gamma-ray data
2.1.1. Observations and data selection
The LAT is a pair-tracking telescope detecting photons from 20 MeV to more than 300 GeV. The instrument is described in Atwood et al. (2009) and its on-orbit calibration in Abdo et al. (2009a). The LAT operates most of the time in continuous sky-survey mode. We accumulated data for our region of interest from August 5, 2008 (MET1 239587201) to August 5, 2010 (MET 302659202).
We selected data according to the tightest available background rejection criteria, corresponding to the Pass 6 Dataclean event class (Abdo et al. 2010e)2. In order to limit the contamination from the Earth’s atmospheric γ-ray emission, we selected events with measured arrival directions within 100° of the local zenith and within 65° of the instrument boresight, taken during periods when the LAT rocking angle was less than 52°.
The angular resolution of the LAT strongly depends on the photon energy, improving as the energy increases (Atwood et al. 2009). Confusion at low energies is a problem since we aim to spatially separate the different components in the crowded Cygnus X region. We therefore accepted below 1 GeV only photons that produced electron-positron pairs in the thin converter planes of the front section of the tracker, which provides a higher angular resolution (Atwood et al. 2009). Above 1 GeV, we kept all events which converted either in the front or back section of the tracker.
We analysed data at Galactic longitudes 72° ≤ l ≤ 88° and latitudes −15° ≤ b ≤ + 15°. The longitude window contains the interstellar complexes associated with Cygnus X; the latitude window is large enough to allow a reliable separation of the large-scale emission from atomic gas, isotropic background and inverse-Compton (IC) scattering of low-energy radiation fields by CR electrons. We analysed the data in the 100 MeV–100 GeV energy band. Below 100 MeV the instrumental systematics are large (Rando et al. 2009) and the angular resolution is poor, whereas above 100 GeV we are limited by the low photon statistics.
2.1.2. Removal of bright pulsars
Three bright pulsars dominate the γ-ray emission from the region below a few GeV: the radio pulsar J2021 + 3651 (Abdo et al. 2009e) and the two LAT-discovered pulsars J2021 + 4026 and J2032 + 4127 (Abdo et al. 2009b). To increase the sensitivity to faint sources and to the spatial structure of the diffuse emission, we reduced their contribution by excluding the periodic time intervals when their pulsed emission is the most intense.Removing the intense pulsed flux helps to reduce the impact of any incorrect modeling of such bright sources on the results.
To assign pulse phases for each of the three pulsars, we produced timing models using Tempo2 (Hobbs et al. 2006) according to the method described in Ray et al. (2011)3. Figure 1 shows the three light curves and the phase intervals with bright pulsed emission. The phase boundaries are reported in Table 1, together with the fraction of time in the off-pulse interval suitable for our study. There is a considerable level of off-pulse emission toward PSR J2021 + 4026 that cannot be removed (Abdo et al. 2010b); however, given the brightness of the source, the removal of the on-pulse interval is useful for our aims.
 |
Fig. 1 Light curves and off-pulse phase intervals for the three bright pulsars. The light curves are constructed for illustration purposes with photons recorded in a circular region of radius 0.5° around the pulsar positions and energies >200 MeV. |
Off-pulse phase intervals and time fractions of the three bright pulsars.
A total count map in the off-pulse phase intervals of the three bright pulsars is provided for illustration in Fig. 2.
 |
Fig. 2 Total count map in the energy range 100 MeV–100 GeV, binned over a 0.125° × 0.125° grid in Galactic coordinates in Cartesian projection. Data were selected according to the criteria described in the text (Sect. 2.1.1) and in the off-pulse phase intervals of the three bright pulsars (Sect. 2.1.2), whose positions are marked by diamonds. Counts are saturated between 0 and 50, and smoothed for display with a Gaussian kernel of σ = 0.25°. |
To remove the pulsar signal without excessively sacrificing the photon statistics in
other directions, we restricted the timing selection to a circular region around the
pulsar position, namely to pixels in our angular grid (described later in Sect. 3.2) the centroids of which lie within the
energy-dependent radius ![\begin{equation} r_{{\rm cut}}(E)= 2 \times \left[0.8\degr \left(\frac{E}{1\:\mathrm{GeV}}\right)^{-0.8} \oplus 0.07\degr \right] \end{equation}](/articles/aa/full_html/2012/02/aa17539-11/aa17539-11-eq25.png) (1)where the symbol ⊕ indicates addition in
quadrature. This is an approximate representation of the LAT 95% containment angle as a
function of energy. We note that the accurate parametrization of the LAT point spread
function (PSF) depends on energy, pair-conversion point in the tracker and, to a lesser
extent, on the incidence angle. The PSF is best represented by the LAT instrument
response functions (IRFs), which are used later for the likelihood analysis. The above
acceptance-averaged approximation for the containment angle is only useful for
calculating the radius rcut, and we verified that the
results are insensitive to reasonable variations in this parameter.
(1)where the symbol ⊕ indicates addition in
quadrature. This is an approximate representation of the LAT 95% containment angle as a
function of energy. We note that the accurate parametrization of the LAT point spread
function (PSF) depends on energy, pair-conversion point in the tracker and, to a lesser
extent, on the incidence angle. The PSF is best represented by the LAT instrument
response functions (IRFs), which are used later for the likelihood analysis. The above
acceptance-averaged approximation for the containment angle is only useful for
calculating the radius rcut, and we verified that the
results are insensitive to reasonable variations in this parameter.
To take the cut on pulsar phases into account, for each direction in the sky and energy the exposure (see again Sect. 3.2) was multiplied by the remaining livetime fraction. The remainder of the pulsar emission was included in the model using
-
a point source to represent emission in the off-pulse interval;
-
a second point source, for which the number of expected counts is set to zero at r < rcut(E) from the pulsar position, to represent on-pulse γ-rays spilling over at r > rcut(E) in the tails of the PSF.
The two sources have free independent fluxes in each energy bin of the analysis. This is particularly important to account for the different spectra of the on-pulse and off-pulse γ-ray emission and also to compensate for any mismatch between the tails of the model PSF and the emission at large angles from the brightest sources in the region.
Since the three pulsars have exponential spectral cutoffs near 2−3 GeV (Abdo et al. 2010b) the phase selection was not applied above 10 GeV where the level of pulsed emission is low and each pulsar was accounted for by a single point source. On the other hand, given the abundant statistics but poor angular resolution at low energies (more than half of the region of interest would be subject to on-pulse event removal), we selected off-pulse photons for the whole region below 316 MeV4. In this case no “spill-over” source was necessary.
2.2. Ancillary data
2.2.1. Radio/mm-wave lines: neutral gas
Neutral atomic hydrogen, H i, was traced thanks to its 21-cm line. Where available5 we used data from the Canadian Galactic Plane Survey (CGPS; Taylor et al. 2003) rebinned onto the 0.125° × 0.125° grid used for the other maps. Elsewhere, we used data from the Leiden/Argentine/Bonn (LAB; Kalberla et al. 2005) survey, with a coarser binning of 0.5°. We checked the consistency of the two survey calibrations in the overlap region.
Molecular hydrogen cannot be observed directly in its most abundant cold phase. The velocity-integrated brightness temperature of the 12CO 2.6-mm line, WCO, is often assumed to linearly scale with the N(H2) column density. We used CO data from the composite survey by Dame et al. (2001), filtered with the moment-masking technique (Dame 2011) in order to reduce the noise while preserving the faint cloud edges and keeping the resolution of the original data.
The Doppler shift of radio/mm-wave lines can be used to kinematically separate the Cygnus complex from two faint segments of the Perseus and outer spiral arms seen beyond Cygnus in the same direction. We applied the kinematic separation procedure illustrated by Abdo et al. (2010f), starting from a preliminary boundary located at a Galactocentric radius6R = 9.4 kpc and then adapting the separation to the cloud structures and correcting for the spill-over due to the broad velocity dispersion of H i lines. The separation into two regions is accurate enough to model the interstellar γ-ray emission in Cygnus since Abdo et al. (2010f) and Ackermann et al. (2011b) did not find any significant gradients of the gas γ-ray emissivities in the outer region of the Milky Way. We applied the kinematic separation procedure to prepare maps of the column densities of atomic gas, N(H i), and of WCO. The maps are shown in Fig. 3 for H i and Fig. 4 for CO. All the gas maps mentioned in the paper have >10° borders around the analysis region used to properly convolve the model with the LAT PSF.
 |
Fig. 3 Maps of N(H i) column densities in the Cygnus complex in the Local Spur (left) and in the outer Galaxy (right), under the assumption of a uniform spin temperature of 250 K. The color scales with N(H i) in units of 1020 atoms cm-2. The maps were smoothed with a Gaussian kernel of σ = 0.25° for display. |
 |
Fig. 4 Maps of WCO intensities in the Cygnus complex in the Local Spur (left) and in the outer Galaxy (right). The color scales with WCO in units of K km s-1 above 1.5 K km s-1. The maps were smoothed with a Gaussian kernel of σ = 0.25° for display. |
Substantial uncertainties in the determination of N(H i) arise from the choice of spin temperature for the optical depth correction. We adopted a uniform TS = 250 K as baseline case, which is the average spin temperature that best reproduces the blending of cold and warm atomic gas according to observations of emission-absorption H i pairs in the region covered by the CGPS (Dickey et al. 2009). Other values 100 K ≤ TS < ∞ will be considered later to evaluate the related systematic uncertainties affecting the results of our analysis.
2.2.2. Visual extinction: dark neutral gas
Multiwavelength observations indicate that the combination of the H i and CO lines does not properly trace the total column densities of the neutral interstellar medium (ISM) (e.g. Magnani et al. 2003; Grenier et al. 2005; Abdo et al. 2010f; Langer et al. 2010; Ade et al. 2011). Since the work by Grenier et al. (2005), dust tracers have been used in γ-ray analyses to complement the H i and CO lines, under the assumption that dust grains are well mixed with gas in the warm and cold phases of the ISM and therefore provide an estimate of total gas column densities. Grenier et al. (2005) and Abdo et al. (2010f) adopted the E(B − V) color excess map by Schlegel et al. (1998) as a tracer of the total column densities, and used the E(B − V) residuals – i.e. E(B − V) minus the best-fit linear combination of N(H i) and WCO maps – as a tracer of the dark-gas column densities in nearby clouds of the Gould Belt.
The use of the E(B − V) map is problematic in the Cygnus X region for two reasons:
-
numerous infrared point sources contaminate the map;
-
the temperature correction used by Schlegel et al. (1998) to derive the dust column-density map from IRAS/ISSA measurements is highly uncertain in regions of massive star-formation because of the enhanced radiation fields.
We have therefore adopted the visual extinction AV as derived from the reddening of near-infrared sources in the 2MASS catalog (Skrutskie et al. 2006). The AV maps produced by Rowles & Froebrich (2009) and Froebrich & Rowles (2010) were used for AV < 5 mag. They exhibit saturation effects at higher extinction values, so we complemented them with an AV map obtained from 2MASS data using the code and method developed by Schneider et al. (2011). The latter use the Besançon stellar population model (Robin & Creze 1986; Robin et al. 2003) to filter out the contribution from the foreground bluest stars7. The second AV map was built in a 12° region centered on (l,b) = (80°,0°), and, compared with the first set of maps, it presented an offset of ~0.46 mag at low extinction. We constructed the final AV map from the direct Rowles & Froebrich (2009) data below 5 mag and from the second map, offset by 0.46 mag, at higher extinction.
The AV map was binned onto the same 0.125° × 0.125° grid in Cartesian projection as the other maps. The AV map was fitted with a linear combination of the N(H i) and WCO maps previously described. The input AV map minus the best-fit linear combination of the N(H i) and WCO maps yielded the AV excess map, AV,exc, which will be used to trace the dark neutral gas. Only residuals corresponding to input AV > 0.3 mag were kept to limit the noise off the plane. The AV excess map is shown in Fig. 5.
 |
Fig. 5 AV excess map (magnitudes) obtained from the optical extinction AV estimated from 2MASS data minus the best-fit linear combination of the N(H i) and WCO maps shown in Figs. 3 and 4, respectively. The map was smoothed using a Gaussian kernel of σ = 0.25° for display. |
2.2.3. Microwave emission: ionized gas
Away from H ii regions around massive stars and stellar clusters, the ionized gas constitutes a layer of characteristic height ≳1 kpc over the Galactic plane with little mass compared to the neutral phases (Cordes & Lazio 2002). Therefore, it has often been neglected in previous γ-ray studies. However, we find in the Cygnus X region many conspicuous H ii regions excited by the intense radiation fields of the numerous massive stars (Uyanıker et al. 2001; Paladini et al. 2003).
Ionized gas masses can be traced by free-free emission following the prescription by
Sodroski et al. (1989, 1997) to derive the N(H ii) column
densities: 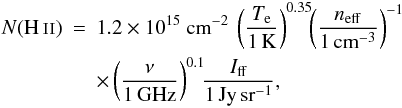 (2)where Iff is
the free-free emission intensity at the frequency ν,
Te is the electron temperature, and
neff the effective electron number density. We adopted a
free-free emission map derived from the seven-year WMAP data in the
Q band (40 GHz) by Gold et al.
(2011) using the maximum entropy method from the prior template given by the
extinction-corrected Hα map by Finkbeiner (2003). It was rebinned onto the 0.125° × 0.125° grid used for the
other maps, as shown in Fig. 6.
(2)where Iff is
the free-free emission intensity at the frequency ν,
Te is the electron temperature, and
neff the effective electron number density. We adopted a
free-free emission map derived from the seven-year WMAP data in the
Q band (40 GHz) by Gold et al.
(2011) using the maximum entropy method from the prior template given by the
extinction-corrected Hα map by Finkbeiner (2003). It was rebinned onto the 0.125° × 0.125° grid used for the
other maps, as shown in Fig. 6.
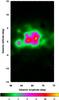 |
Fig. 6 Free-free emission intensities from WMAP data. The color scales with brightness temperature in mK. The map was smoothed using a Gaussian kernel of σ = 0.25° for display. |
3. Analysis
3.1. Analysis model
3.1.1. Diffuse emission
Since the bulk of Galactic CRs in the relevant energy ranges are expected to be smoothly distributed on scalesexceeding the typical dimensions of interstellar clouds and to penetrate all the phases of the ISM uniformly, the γ-ray emission produced by CR-gas interactions can be modeled to first order as a linear combination of the gas column densities summed for the different phases and different regions along the line of sight.
Ionized gas, with a total mass over the region of 0.4 × 106 (neff/1 cm-3)-1 M⊙ for Te = 104 K, represents less than 4% of the total atomic mass present in the Cygnus complex (assuming neff = 2−10 cm-3, Sodroski et al. 1997). The corresponding column densities are highest in the massive star-forming region of Cygnus X where we detected a bright and hard extended γ-ray source powered by freshly-accelerated particles, that will be called hereinafter “the cocoon” (Ackermann et al. 2011a). The free-free emission map was significantly detected in addition to the other interstellar components, but only at the expense of an unusually hard spectrum. To model the entire region, we introduced an extended source to account for the cocoon, as described in Sect. 3.1.2. The latter was found to provide the best fit to the LAT data, yielding a higher maximum-likelihood value than the free-free emission template. Since the cocoon source overlaps most of the ionized clouds, it absorbs their contribution to the γ-ray emission, so ionized gas was not included in the baseline model through the free-free emission template. The Cygnus X region is treated in detail in a companion paper (Ackermann et al. 2011a). The results presented in this paper were checked against the inclusion of the free-free emission template in the model.
The interstellar IC emission is produced by interactions of CR electrons and positrons with the low-energy interstellar radiation field (ISRF). To account for large-scale IC emission from the Milky Way we adopted a template calculated using the GALPROP CR propagation code8 (Strong & Moskalenko 1998; Strong et al. 2007), run 54_87Xexph7S. The IC emission was calculated on the basis of a CR electron spectrum consistent with recent measurements at the Earth (Abdo et al. 2009c) and the new calculation of the Galactic ISRF by Porter et al. (2008).
Local radiation fields could leave unmodeled structures in IC emission, notably in the massive star-forming region of Cygnus X (e.g. Orlando & Strong 2007). In the companion paper we show that an upper bound to the IC emission from the stellar and interstellar low-energy radiation fields upscattered by CR electrons with the local spectrum is two orders of magnitude fainter than the cocoon emission, which in turn is fainter than the emission from the neutral gas (Fig. 9). The CR electron sources within Cygnus X could further enhance the IC γ-ray yield. Any enhanced IC contribution from the inner region is accounted for in this analysis by the extended cocoon source, and it should not bias the determination of the gas emissivities we aim to study here.
The diffuse emission model is completed by the isotropic background which combines the residual backgrounds from misclassified CR interactions in the LAT and the isotropic, presumably extragalactic, γ-ray emission (studied in detail in Abdo et al. 2010e).
3.1.2. Sources
We included in the model the identified sources in the region of interest: Cygnus X-3 (Abdo et al. 2009f), PSR J1957 + 5033 (Saz Parkinson et al. 2010) and PSR J2030 + 3641 (Camilo et al. 2011), in addition to the three bright pulsars as discussed in Sect. 2.1.2.
We also iteratively included significant 1FGL point sources (Abdo et al. 2010a) either associated with active galactic nuclei (AGN) or characterized by variability or both. The sources were added with decreasing brightness: J2116.1 + 3338, J2001.1 + 4351, J2027.6 + 3335, J2115.5 + 2937, J2015.7 + 3708, J2029.2 + 4924, J2012.2 + 4629, and J2128.0 + 3623. The iterative procedure is useful for stabilizing the likelihood fitting procedure and assessing the significance of sources added at each step.
We detected extended γ-ray emission above the global interstellar emission model discussed here associated with the supernova remnants known as the Cygnus Loop (G74.0-8.5, e.g. Sun et al. 2006) and γ Cygni (G78.2+2.1, e.g. Ladouceur & Pineault 2008) and with the inner 100 pc of the Cygnus X complex. They are discussed in detail elsewhere. We briefly summarize here how these extended sources are modeled. For each of them we have tested different models and therefore verified that their presence does not bias the results concerning the properties of large-scale interstellar emission presented in the paper.
The Cygnus Loop was modeled using a ring centered at (l,b) = (74.1°,−8.5°) and with inner/outer radii of 0.7° and 1.6°, respectively, which best reproduces γ-ray emission from the Cygnus Loop (Katagiri et al. 2011).
We included two sources in the region of γ Cygni in addition to PSR J2021 + 4026:
-
a uniform disk centered at(l,b) = (78.2°, + 2.1°) and a radius of 0.5° (G78.2 + 2.1; Green 2009);
-
a 2D Gaussian corresponding to the moderately extended TeV source9 VER 2019 + 407 (Weinstein et al. 2009).
We detected extended γ-ray emission toward the inner ~100 pc of Cygnus X, which is effectively treated here as a source named “the cocoon”. We discuss the nature of the cocoon and its relation with CR acceleration in the massive star-forming region in a dedicated paper (Ackermann et al. 2011a), where we determine a Gaussian centered at (l,b) = (79.6° ± 0.3°,1.4° ± 0.4°) with a σ = 2.0° ± 0.2° width to be the model providing the best fit to the LAT data. As noted above, the cocoon source effectively accounts for the contribution from ionized gas and from enhanced IC emission in the Cygnus X massive star-forming region, as well as for locally-accelerated CRs. The spatial distribution of the sources included in the analysis model is summarized in Fig. 7.
 |
Fig. 7 Sources included in the analysis model. Diamonds mark the positions of the three bright pulsars that were dimmed by phase selection (Sect. 2.1.2). X points mark the positions of other identified sources. Crosses correspond to 1FGL sources either associated to AGN or variable, or both, confirmed by our analysis. The blue circles correspond to the rims of the templates adopted to model SNRs, the Cygnus Loop (G74.0−8.5) and γ Cygni (G78.2 + 2.1). The red circle marks the centroid of VER 2019 + 407 (whose extension is not appreciable in this large-scale view). The magenta circle represents the 1σ contour of the Gaussian used to model the cocoon. |
3.1.3. Summary of the analysis model
To summarize, the γ-ray intensities I (photons
cm-2 s-1 sr-1) are modeled in each energy bin by
![\begin{eqnarray} I(l,b) & = & \sum_{\imath=1}^2 \left[ \qhi{\imath} \nhi(l,b)_\mathrm{\imath}+ \qco{\imath} \wco(l,b)_\mathrm{\imath}\right] \nonumber\\ &&+ \qdust \avres (l,b) + \mathrm{IC}(l,b) + I_\mathrm{iso} \nonumber\\ &&+ \label{gasmodel} \sum_\jmath S_\jmath(l,b). \end{eqnarray}](/articles/aa/full_html/2012/02/aa17539-11/aa17539-11-eq77.png) (3)The sum over ı represents
the combination of the two regions: 1) Cygnus complex and 2) outer Galaxy. The free
parameters of the diffuse emission model are the emissivities per hydrogen atom,
qH I, ı (s-1 sr-1),
the emissivities per unit of WCO intensity,
qCO, ı (cm-2 s-1
sr-1 (K km s-1)-1), the emissivity per
AV excess unit
qAV (cm-2
s-1 sr-1 mag-1), and the isotropic intensity
Iiso (cm-2 s-1 sr-1). IC
stands for the IC emission model described above. The sum over
(3)The sum over ı represents
the combination of the two regions: 1) Cygnus complex and 2) outer Galaxy. The free
parameters of the diffuse emission model are the emissivities per hydrogen atom,
qH I, ı (s-1 sr-1),
the emissivities per unit of WCO intensity,
qCO, ı (cm-2 s-1
sr-1 (K km s-1)-1), the emissivity per
AV excess unit
qAV (cm-2
s-1 sr-1 mag-1), and the isotropic intensity
Iiso (cm-2 s-1 sr-1). IC
stands for the IC emission model described above. The sum over
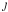 represents the combination of the sources, either point-like or extended, as described
in Sect. 3.1.2, including a free parameter (flux
normalization) independently for each of them.
represents the combination of the sources, either point-like or extended, as described
in Sect. 3.1.2, including a free parameter (flux
normalization) independently for each of them.
 |
Fig. 8 Residuals (data-model). Left: low energies (100 MeV–1 GeV); center: mid-energies (1 GeV–10 GeV); right: high energies (10 GeV–100 GeV). Units are approximate standard deviations (square root of model counts) saturated between ± 3 and smoothed for display with a Gaussian kernel of σ = 0.25°. In each panel the blue circle in the top left corner represents the effective LAT PSF 68% containment circle for the event selection used in the analysis (averaged over the corresponding energy range assuming a power-law spectrum with index 2.1). Diamonds mark the positions of bright pulsars for which phase selection was applied, as in Fig. 2. Crosses mark the positions of unassociated 1FGL sources coincident with positive residuals; the X point mark the position of 2FGL J2018.0 + 3626, coincident with a hot spot in the residual map 1 GeV–10 GeV. |
3.2. Analysis method
The model was fit to LAT data by using a binned maximum likelihood with Poisson statistics10 independently over several energy bins. We used a 0.125° × 0.125° binning in Cartesian projection, comparable to the LAT angular resolution at the highest energies. We considered three energy bands: low (100 MeV–1 GeV), mid (1 GeV–10 GeV) and high energies (10 GeV–100 GeV). The low and mid-energy bands were divided further into four logarithmic-spaced energy bins, the higher-energy band in two because of the limited statistics11. The analysis was based on the post-launch IRFs of the P6_V3 series, which consider efficiency losses due to pile-up and accidental coincidence effects in the detector (Rando et al. 2009).
To perform the convolution with the LAT PSF, a power-law spectrum with index 2.1 was assumed for the gas maps and other sources modeled by geometrical templates (the results do not significantly depend on this value). For all other sources we used power-law spectra with the spectral index reported in the 1FGL Catalog. For the pulsars included in the LAT pulsar catalog (Abdo et al. 2010b), we used the spectral functions described therein.
4. Results and discussion
4.1. Summary of the results and uncertainties
The γ-ray residuals corresponding to the best-fit model are shown in Fig. 8. They indicate that the model satisfactorily reproduces the morphology of the γ-ray emission on larger angular scales than the LAT PSF in all the energy bands. Localized positive residuals are still present. Some of them coincide with unassociated 1FGL sources and others are associated with sources of the 2FGL catalog12, notably 2FGL J2018.0 + 3626 also coincident with the TeV source MGRO J2019+27 (Abdo et al. 2007). We verified that including sources accounting for those residuals in the analysis model would not significantly affect the determination of γ-ray emissivities associated with the different gas components summarized in Table 2.
Figure 9 shows the γ-ray spectral energy distribution measured by the LAT over the whole region of interest. The LAT measurements are compared with the final model, and the different components are outlined. The data sample is dominated by emission from interstellar gas in the Cygnus complex. The largest contributor is H i. Emission associated with CO and AV excesses exceeds the signals from individual sources for the whole energy range considered. The cocoon has a very hard spectrum and becomes comparable to emission from CO-bright gas at energies >10 GeV.
 |
Fig. 9 Spectral energy distribution of γ-ray emission measured by the LAT compared with our best-fit model. The uncertainties shown are statistical only. We separately show the different components of the interstellar emission model, point sources and extended objects. The curve corresponding to γ Cygni combines the contributions of the off-pulse source, the disk associated with the remnant and the 2D Gaussian accounting for VER 2019 + 407. |
All the results presented so far have been based on the assumption of a uniform H i spin temperature of 250 K. To gauge the impact of the optical depth correction of H i data on the results, we repeated the analysis with other assumptions. TS = 400 K is considered since it is the value best reproducing pairs of emission/absorption H i spectra over most of the regions analyzed by Dickey et al. (2009), although they find that TS = 250 K is preferred in the region covered by CGPS data. TS = 125 K is considered because it has long been used for γ-ray studies (e.g. Bloemen et al. 1984; Hunter et al. 1997; Strong et al. 2004). We also considered two extreme assumptions: a low13TS = 100 K, and the optically thin approximation (equivalent to infinitely high spin temperature). Figure 10 shows the maximum likelihood profile obtained for the final model as a function of TS.
 |
Fig. 10 Maximum likelihood obtained as a function of the uniform spin temperature adopted for the optical depth correction of H i data. Values are offset so that log-likelihood is zero for a spin temperature of 100 K. |
The results support the average spin temperatures of a few hundred K deduced from radio absorption/emission measurements by Dickey et al. (2009), implying a mix of <25% cold and >75% warm H i.
To test the robustness of the results against the presence of ionized gas beyond the extended cocoon source, we replaced the latter in the baseline model with the free-free emission template. All the results for the gas emissivities were found to be consistent with the values listed in Table 2 within statistical errors.
The large-scale IC model introduced in Sect. 3.1.1 is affected by considerable uncertainties related to the distribution of CR densities and of the ISRF in the Galaxy. The intensity of IC emission expected over our region of interest is comparable to the one from interstellar gas. The latter, however, is highly structured and has a lower characteristic height above the Galactic plane, and can therefore be reliably determined in the likelihood fit. We verified that completely neglecting the large-scale IC emission leads to negligible variations in the emissivities of CO-bright gas and AV excesses, and to variations lower than or comparable to statistical uncertainties for the emissivities of the atomic hydrogen, which is less structured than the other ISM components and has a larger characteristic height.
Other systematic uncertainties are due to the LAT instrument response. The uncertainties in the γ-ray selection efficiency are estimated to be 10% at 100 MeV, 5% at 560 MeV, and 20% above 10 GeV for the IRFs we used here (Abdo et al. 2010e). The Monte Carlo-based PSF used for this study is known to not accurately reproduce in-flight data over the whole energy range considered. We verified by means of dedicated simulations that this does not significantly affect the determination of the gas emissivities considered for the discussion. The energy dispersion is routinely neglected in the likelihood fitting of LAT data for limitations in computing power: Monte Carlo simulations indicate that this approximation causes a bias on the order of 10% at 100 MeV decreasing to <5% above 200 MeV.
4.2. H I emissivity and CR densities
The H i emissivity per hydrogen atom relates to the average CR density in each of the regions considered. LAT measurements (Abdo et al. 2009d) show that the H i emissivity spectrum in the local ISM is consistent with production via electron Bremsstrahlung and nucleon-nucleon interactions by CRs with a spectrum consistent with that directly measured in the neighborhood of the Earth.
The integrated γ-ray emissivity >100 MeV we measure in the Cygnus
complex amounts to ![\hbox{$[2.06 \pm 0.11 \,(\mathrm{stat.})\; ^{+0.15} _{-0.84}\,(\mathrm{syst.})]\times 10^{-26}$}](/articles/aa/full_html/2012/02/aa17539-11/aa17539-11-eq3.png) s-1 sr-1.
Figure 11 shows the H i emissivity
spectrum obtained for the Cygnus complex and compares it with the expectations for the
local interstellar spectrum estimated in Abdo et al.
(2009d). The latter is compatible (within 10%) with LAT observations at mid
latitudes in the third Galactic quadrant in the energy range 100 MeV–10 GeV (Abdo et al. 2009d).
s-1 sr-1.
Figure 11 shows the H i emissivity
spectrum obtained for the Cygnus complex and compares it with the expectations for the
local interstellar spectrum estimated in Abdo et al.
(2009d). The latter is compatible (within 10%) with LAT observations at mid
latitudes in the third Galactic quadrant in the energy range 100 MeV–10 GeV (Abdo et al. 2009d).
 |
Fig. 11 H i emissivity spectrum in the Cygnus complex. Points: the best-fit estimate for the spin temperature TS = 250 K. Hatched rectangles: systematic uncertainties taking H i opacity and γ-ray selection efficiency into account. Line: model of the local interstellar spectrum by Abdo et al. (2009d) (with a nuclear enhancement factor of 1.84, Mori 2009). |
The spectrum is presented for a uniform spin temperature TS = 250 K; systematic uncertainties due to the H i opacity correction and to the γ-ray selection efficiency are added in quadrature for display. The latter give a non-negligible contribution only at energies larger than a few GeV.
The emissivity of atomic gas in the Cygnus region, averaged over ~400 pc, is consistent with the local emissivity in the 100 MeV–100 GeV energy range, except for the deviant point at 10−30 GeV. This can be explained by the difficulty distinguishing the H i and CO components at high energies, for which the γ-ray statistics are limited and the hard cocoon source is brighter (Fig. 9). The emissivity spectrum implies that the CR spectra in the relevant energy ranges (~1−100 GeV/n for nucleons) are similar to those measured in the vicinity of the Earth and inferred from γ-ray observations in the nearby interstellar space within 1 kpc.
The variations in average CR densities along the Local Spur between the dense Cygnus complex, two segments in the second and third quadrants that exhibit ~2 lower surface densities of gas (Abdo et al. 2010f; Ackermann et al. 2011b), and the mid-latitude diffuse medium with a factor ~5 lower surface density (Abdo et al. 2009d) are constrained to within 10% to 35%. This is difficult to reconcile with the idea of a dynamical coupling between gas and CR densities (e.g. Bertsch et al. 1993; Hunter et al. 1997). They are consistent, on the other hand, with the small arm-interarm emissivity contrast estimated from LAT data in the third Galactic quadrant (Ackermann et al. 2011b). In spite of the high column densities of gas, exceeding 1022 atoms cm-2 over many directions within the Cygnus complex, we find no hints of excluding CRs from the densest parts of the atomic clouds.
Owing to the bright foreground of the Cygnus complex and individual sources, studying the gas emissivity in the outer disk of the Milky Way in detail is beyond the scope of this study. However, the ratio of the integrated H i emissivity of the outer region over that in the Local Spur is (90 ± 7)%, in very good agreement with the results by Abdo et al. (2010f) and Ackermann et al. (2011b). It confirms in another direction the presence of high CR densities beyond the solar circle.
Located at a distance of ~1.4 kpc and l = 80°, the Cygnus complex lies at R ≃ 8.4 kpc from the Galactic center, at a slightly smaller radius than the solar system. We measure in this direction an emissivity that is consistent with other values found in the Local Spur and in three outer segments of the Milky Way with Galactocentric radii up to ~15 kpc. It yields a decrease in H i emissivity <60% over ~6 kpc in Galactocentric radius across and beyond the solar circle. Nevertheless, those measurements span a narrow range in azimuth around the Galactic center and may not be representative enough for comparison with axisymmetric propagation models in order to study the CR gradient across the solar circle.
4.3. CO-bright molecular gas
If molecular and atomic gas are illuminated by the same CR fluxes, we expect the
emissivity per hydrogen molecule to be twice the emissivity per hydrogen atom, so we can
calibrate the XCO ratio. We performed a linear fit,
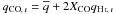 , taking the uncertainties on both
emissivities into account to derive the best linear relation shown in Fig. 12. We also give the residuals in units of standard
deviations.
, taking the uncertainties on both
emissivities into account to derive the best linear relation shown in Fig. 12. We also give the residuals in units of standard
deviations.
 |
Fig. 12 Top: emissivity per WCO intensity unit versus emissivity per hydrogen atom in the Cygnus complex (for TS = 250 K). The points correspond to the different energy bins; the emissivities decrease with increasing energy. The red line gives the best linear fit taking uncertainties on both axes into account. Bottom: residuals in units of standard deviations as a function of H i emissivity. |
A good linearity is found in the 0.1–10 GeV energy range. The highest energy (lowest emissivity) points show <3σ excess of emission associated with CO with respect to the XCO ratio determined at low energies. The high CO emissivity recorded at 10−30 GeV (second point) corresponds to a low emissivity in H i (Fig. 11) and may result from a fluctuation in the difficult spatial separation between the atomic and molecular components when photons are sparse given the hard 2° source that partially overlaps the CO peaks. Up to 10 GeV, the linearity is good, so there is no sign of CR exclusion from the dense cores of this giant molecular complex.
The slope of the best-fit linear relation provides a value of XCO = (1.68 ± 0.05) × 1020 cm-2 (K km s-1)-1 in the case of TS = 250 K. We obtain XCO = (1.58 ± 0.04) × 1020 cm-2 (K km s-1)-1 in the limit of small H i optical depth and XCO = (2.55 ± 0.08) × 1020 cm-2 (K km s-1)-1 in the case of TS = 100 K. The uncertainties in qH I associated with the H i spin temperature are particularly severe for the high-density clouds of the Cygnus complex. High optical depths (low spin temperatures) imply a large increase in N(H i), therefore substantially lower CR densities. Given the γ-ray luminosity of the molecular clouds, this subsequently implies a significant increase in their estimated masses14. The systematic errors on the γ-ray selection efficiency cancel out to the first order in the estimate of the XCO ratio.
The conversion factor
XCO = [1.68 ± 0.05(stat.)
![\hbox{$ _{-0.10}^{+0.87} \,(\hi\;\mathrm{opacity})] \times 10^{20}$}](/articles/aa/full_html/2012/02/aa17539-11/aa17539-11-eq131.png) cm-2 (K km
s-1)-1 is consistent with other LAT measurements in the Local
Spur, which range from 1.5 to 2 × 1020 cm-2 (K km
s-1)-1 (Abdo et al. 2010f;
Ackermann et al. 2011b). From the different
γ-ray measurements in the Galactic plane, the
XCO ratio at the solar circle appears well defined. It is,
however, significantly greater than in nearby well-resolved clouds off the plane in
Cassiopeia and Cepheus (Abdo et al. 2010f). Whether
the discrepancy is due to the sampling resolution or to an intrinsic
XCO variation on different scales inside a cloud will be
investigated in the future.
cm-2 (K km
s-1)-1 is consistent with other LAT measurements in the Local
Spur, which range from 1.5 to 2 × 1020 cm-2 (K km
s-1)-1 (Abdo et al. 2010f;
Ackermann et al. 2011b). From the different
γ-ray measurements in the Galactic plane, the
XCO ratio at the solar circle appears well defined. It is,
however, significantly greater than in nearby well-resolved clouds off the plane in
Cassiopeia and Cepheus (Abdo et al. 2010f). Whether
the discrepancy is due to the sampling resolution or to an intrinsic
XCO variation on different scales inside a cloud will be
investigated in the future.
Using the XCO ratio, we estimated the CO-bright molecular
mass in the complex. For this purpose we considered the region at
74° < l < 86°, −5° < b < 8°, where most of
the gas associated with the Cygnus complex is located. Assuming a distance of 1.4 kpc and
a mean atomic weight per hydrogen atom in the ISM of 1.36, we obtain a mass
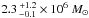 (where the uncertainties are dominated by
the H i opacity correction). This value (taking the different assumption on the
distance into account) is consistent with the results by Schneider et al. (2006) based on higher resolution, multi-isotopolog CO
observations, and it depicts Cygnus as a super-massive molecular complex.
(where the uncertainties are dominated by
the H i opacity correction). This value (taking the different assumption on the
distance into account) is consistent with the results by Schneider et al. (2006) based on higher resolution, multi-isotopolog CO
observations, and it depicts Cygnus as a super-massive molecular complex.
The small amount of CO-bright molecular gas in the outer region of the Milky Way in this longitude window (Fig. 4) makes determining its emissivities extremely sensitive to the details of the model (including point sources), so we do not consider it for scientific interpretation.
4.4. Dark neutral gas
Including the AV excess map in the model corresponds to an increase of 250.6 in the logarithm of the likelihood (for ten additional degrees of freedom). This corresponds to a significant detection of γ-ray emission associated with AV excesses, formally equivalent to a ~21σ confidence level. Figure 13 shows the emissivity per AV,exc unit, qAV, versus the emissivity per hydrogen atom, qH I, in the Cygnus complex. A good linear correlation is found between the two emissivities over three decades in energy, proving that γ-ray emission associated with AV excesses comes from the same physical processes as that associated with H i. AV residuals therefore trace interstellar gas.
 |
Fig. 13 Top: emissivity per AV,exc unit versus emissivity per hydrogen atom in the Cygnus complex (for TS = 250 K). The points correspond to the different energy bins; the emissivities decrease with increasing energy. The green line gives the best linear fit taking uncertainties on both axes into account. Bottom: residuals in units of standard deviations as a function of H i emissivity. |
With a procedure analogous to what is adopted to estimate
XCO, we can use the emissivity per hydrogen atom to calibrate
the dust-to-gas ratio in the dark neutral phase
XAV ≡ N(H)/AV,exc.
We obtain
XAV = (28 ± 2) × 1020 cm-2 mag-1
in the case of TS = 250 K,
XAV = (48 ± 3) × 1020 cm-2 mag-1
in the case of TS = 100 K and
XAV = (27 ± 2) × 1020 cm-2 mag-1
in the case of optically thin medium, so
XAV is
![\hbox{$[28 \pm 2\,(\mathrm{stat.})\; _{-1}^{+20} \,(\hi\;\mathrm{opacity})] \times 10^{20}$}](/articles/aa/full_html/2012/02/aa17539-11/aa17539-11-eq144.png) cm-2 mag-1.
cm-2 mag-1.
Assuming a standard total-to-selective extinction ratio RV = AV/E(B − V) = 3.10 (Wegner 2003), the dust-to-gas ratio just estimated appears to be ~50% higher than the average value in the diffuse ISM, N(H)/E(B − V) = 58 × 1020 cm-2 mag-1 (Bohlin et al. 1978), and a factor of three higher than what is inferred for the dark phase in local clouds from γ-ray measurements, N(H)/E(B − V) ≃ 30 × 1020 cm-2 mag-1 (Grenier et al. 2005; Abdo et al. 2010f). The discrepancy is confirmed by the extinction data. By fitting the latter with the H i and CO maps (Sect. 2.2.2), we obtained N(H i)/AV = 29.6 ± 0.1 × 1020 cm-2 mag-1 (statistical error only for TS = 250 K). A possible explanation is provided by an anomalous RV ratio driven by a peculiar distribution of dust grain sizes (Cardelli et al. 1989). Straižys et al. (1999) indeed report an anomalous extinction law in the Cygnus region, showing stronger extinction in the violet and near UV region.
The chemical state of the dark neutral gas cannot be deduced from γ-ray observations. Whereas there are compelling theoretical and observational reasons to believe that CO-quiet H2 is ubiquitous in the ISM (e.g. Wolfire et al. 2010; Magnani et al. 2003; Langer et al. 2010), we cannot exclude that part of the dark gas traced by AV excesses is missing cold atomic gas, especially since the dark neutral phase appears at the interface between the atomic and CO-bright phases in the nearby clouds (Grenier et al. 2005). Temperatures as low as 40−70 K were measured in cold H i clouds (Heiles & Troland 2003), and self absorption can be strong when cold clouds are seen against more diffuse warm H i. The AV excesses in Fig. 5 partially overlap an H i self-absorption feature associated with the Cygnus complex (Gibson et al. 2005, Fig. 1d). Nevertheless, the H i to H2 transition is very dynamical, both in space and time, and it is difficult at this stage to conclude anything about the exact mix of cold dense H i and diffuse CO-quiet H2 that forms the dark neutral phase in the outskirts of CO-bright molecular clouds.
Regardless of its nature, the mass of the dark neutral gas in the Cygnus complex at
1.4 kpc amounts to 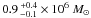 . Adding an atomic mass of
. Adding an atomic mass of
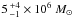 and including the CO-bright mass estimated
above the total interstellar mass of the Cygnus complex amounts to
and including the CO-bright mass estimated
above the total interstellar mass of the Cygnus complex amounts to
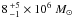 .
.
Assuming that all the dark neutral gas is molecular, we can calculate the molecular dark-gas fraction fDG = (Mmol − MCO)/Mmol, which amounts to15 0.27 ± 0.02, in excellent agreement with the model by Wolfire et al. (2010). The dark-gas fraction is also consistent with the one by Abdo et al. (2010f) for the nearby Cepheus and Cassiopeia clouds, which have a factor of two lower column densities and masses <2% of that contained in the Cygnus complex. This also agrees with the prediction by Wolfire et al. (2010) that the dark-gas fraction is fairly independent of the mean cloud column density and total mass for giant molecular clouds.
5. Conclusions
We performed an analysis of γ-ray emission across the entire Cygnus region measured by the Fermi LAT in the energy range 100 MeV–100 GeV. We built a general model for the region able to satisfactorily reproduce the LAT data. The model includes extended sources that have been detected over the interstellar emission model described here in association with the Cygnus Loop and γ Cygni supernova remnants and with a cocoon of freshly-accelerated CRs in the innermost part of the Cygnus X region. They are discussed in detail in companion papers.
We measured the average
XCO = N(H2)/WCO
factor for clouds in Cygnus, finding a value [1.68 ± 0.05(stat.)
![\hbox{$ _{-0.10}^{+0.87} (\hi\, \mathrm{opacity})] \times 10^{20}$}](/articles/aa/full_html/2012/02/aa17539-11/aa17539-11-eq160.png) cm-2
(K km s-1)-1 that is well consistent with other LAT measurements for
cloud complexes in the Local and Perseus spiral arms (Abdo
et al. 2010f; Ackermann et al. 2011b). These
XCO ratios, averaged over complexes, are, however,
significantly higher than the values found at higher sampling resolution in nearby clouds of
the Gould Belt (Abdo et al. 2010f). Thanks to the
correlation between dust and γ-ray emission excesses, we detected the
presence of conspicuous masses of dark neutral gas not traced by the combination of the
H i and CO lines, with total mass ~40% of the mass of the clouds traced by
CO. The good correlation over three decades in energy between the γ-ray
emissivity per AV excess unit and per H atom strengthens the
interpretation of such excesses as produced by dark neutral gas. The neutral gas in the
Cygnus complex, combining atomic, CO-bright, and dark masses, amounts to
cm-2
(K km s-1)-1 that is well consistent with other LAT measurements for
cloud complexes in the Local and Perseus spiral arms (Abdo
et al. 2010f; Ackermann et al. 2011b). These
XCO ratios, averaged over complexes, are, however,
significantly higher than the values found at higher sampling resolution in nearby clouds of
the Gould Belt (Abdo et al. 2010f). Thanks to the
correlation between dust and γ-ray emission excesses, we detected the
presence of conspicuous masses of dark neutral gas not traced by the combination of the
H i and CO lines, with total mass ~40% of the mass of the clouds traced by
CO. The good correlation over three decades in energy between the γ-ray
emissivity per AV excess unit and per H atom strengthens the
interpretation of such excesses as produced by dark neutral gas. The neutral gas in the
Cygnus complex, combining atomic, CO-bright, and dark masses, amounts to
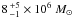 at a distance of 1.4 kpc.
at a distance of 1.4 kpc.
The emissivity of atomic gas measured over the whole Cygnus complex is consistent with other estimates in the local interstellar space. We do not find evidence of any possible exclusion of CRs by enhanced magnetic fields in the dense clouds. The emissivity per hydrogen atom compares with LAT estimates in other regions of the local and outer Galaxy, regardless of differences in gas surface density by about one order of magnitude and in Galactocentric radius by ~6 kpc. This uniformity does not support models based on the dynamical coupling of CRs with matter densities or predicting a strong emissivity gradient toward the outer Galaxy.
The CR population averaged over the whole Cygnus complex (~400 pc) is similar to the Local Spur average, in spite of the embedded regions of conspicuous massive star-formation and potential CR accelerators. Their impact on the CR population is only detected in the innermost region bounded by the ionization fronts from the massive stellar clusters on a scale <100 pc (Ackermann et al. 2011a). No counterpart to the broadly distributed excess of γ-ray emission seen at energies >10 TeV at 65° ≤ l ≤ 85° (Abdo et al. 2007, 2008) have been detected at GeV energies so far.
See Sect. 3.2 for the definition of the energy grid used in the analysis.
The 2D Gaussian fitted to TeV data by Weinstein et al. (2009) provides a better fit to LAT data with respect to the coincident point source 1FGL J2020 + 4049.
The bounds of the energy bins are reported in Table 2.
The preparation of the 2FGL catalog ran in parallel with the analysis reported in this paper. The source list is now available from http://fermi.gsfc.nasa.gov/ssc/data/access/lat/2yr_catalog/
Acknowledgments
The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT, as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the US, the Commissariat à l’Energie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council, and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. We made use of data from the Canadian Galactic Plane Survey (CGPS). CGPS is a Canadian project with international partners. The Dominion Radio Astrophysical Observatory is operated as a national facility by the National Research Council of Canada. The CGPS is supported by a grant from the Natural Sciences and Engineering Research Council of Canada. We thank T. M. Dame for providing the moment-masked CO data.
References
- Abdo, A. A., Allen, B., Berley, D., et al. 2007, ApJ, 658, L33 [Google Scholar]
- Abdo, A. A., Allen, B., Aune, T., et al. 2008, ApJ, 688, 1078 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, Astropart. Phys., 32, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, Science, 325, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009c, Phys. Rev. Lett., 102, 181101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009d, ApJ, 703, 1249 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009e, ApJ, 700, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009f, Science, 326, 1512 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJS, 187, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 709, L152 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, A&A, 512, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010e, Phys. Rev. Lett., 104, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010f, ApJ, 710, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011a, Science, 334, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2011b, ApJ, 726, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ade, P. A. R., Aghanim, N., Arnaud, M., et al. 2011, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Bertsch, D. L., Dame, T. M., Fichtel, C. E., et al. 1993, ApJ, 416, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Bloemen, J. B. G. M., Bennett, K., Bignami, G. F., et al. 1984, A&A, 135, 12 [NASA ADS] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Kerr, M., Ray, P. S., et al. 2011, ApJ, in press [arXiv:1111.4270] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W., Charles, P., Bowyer, S., et al. 1980, ApJ, 238, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astro-ph/0207156v3] [Google Scholar]
- Dame, T. M. 2011 [arXiv:1101.1499] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., Strasser, S., Gaensler, B. M., et al. 2009, ApJ, 693, 1250 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Froebrich, D., & Rowles, J. 2010, MNRAS, 406, 1350 [NASA ADS] [Google Scholar]
- Gibson, S. J., Taylor, A. R., Higgs, L. A., Brunt, C. M., & Dewdney, P. E. 2005, ApJ, 626, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Green, D. A. 2009, Bull. Astron. Soc. India, 37, 45 [Google Scholar]
- Grenier, I. A., Casandjian, J.-M., & Terrier, R. 2005, Science, 307, 1292 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hanson, M. M. 2003, ApJ, 597, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. H. 2003, ApJ, 586, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G. B., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, S. D., Bertsch, D. L., Catelli, J. R., et al. 1997, ApJ, 481, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katagiri, H., Tibaldo, L., Ballet, J., et al. 2011, ApJ, 741, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Ladouceur, Y., & Pineault, S. 2008, A&A, 490, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, W. D., Velusamy, T., Pineda, J. L., et al. 2010, A&A, 521, L17 [Google Scholar]
- LeDuigou, J., & Knödlseder, J. 2002, A&A, 392, 869 [Google Scholar]
- Magnani, L., Chastain, R. J., Kim, H. C., et al. 2003, ApJ, 586, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M. 2009, Astropart. Phys., 31, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Negueruela, I., Marco, A., Herrero, A., & Clark, J. S. 2008, A&A, 487, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orlando, E., & Strong, A. W. 2007, Ap&SS, 309, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Paladini, R., Burigana, C., Davies, R. D., et al. 2003, A&A, 397, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porter, T. A., Moskalenko, I. V., Strong, A. W., Orlando, E., & Bouchet, L. 2008, ApJ, 682, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Rando, R., et al. 2009 [arXiv:0907.0626] [Google Scholar]
- Ray, P. S., Kerr, M., Parent, D., et al. 2011, ApJS, 194, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A., & Creze, M. 1986, A&AS, 64, 53 [NASA ADS] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rowles, J., & Froebrich, D. 2009, MNRAS, 395, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., Ade, P. A. R., Bock, J. J., et al. 2011, ApJ, 727, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Saz Parkinson, P. M., Dormody, M., Ziegler, M., et al. 2010, ApJ, 725, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2006, A&A, 458, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2011, A&A, 529, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sodroski, T. J., Dwek, E., Hauser, M. G., & Kerr, F. J. 1989, ApJ, 336, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Sodroski, T. J., Odegard, N., Arendt, R. G., et al. 1997, ApJ, 480, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Straižys, V., Corbally, C. J., & Laugalys, V. 1999, Balt. Astron., 8, 355 [Google Scholar]
- Strong, A. W., & Moskalenko, I. V. 1998, ApJ, 509, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Reimer, O. 2004, ApJ, 613, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Ann. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X. H., Reich, W., Han, J. L., Reich, P., & Wielebinski, R. 2006, A&A, 447, 937 [Google Scholar]
- Taylor, A. R., Gibson, S. J., Peracaula, M., et al. 2003, AJ, 125, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Uyanıker, B., Fürst, E., Reich, W., Aschenbach, B., & Wielebinski, R. 2001, A&A, 371, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wegner, W. 2003, Astron. Nachr., 324, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Weinstein, A., et al. 2009 [arXiv:0912.4492] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Light curves and off-pulse phase intervals for the three bright pulsars. The light curves are constructed for illustration purposes with photons recorded in a circular region of radius 0.5° around the pulsar positions and energies >200 MeV. |
| In the text | |
 |
Fig. 2 Total count map in the energy range 100 MeV–100 GeV, binned over a 0.125° × 0.125° grid in Galactic coordinates in Cartesian projection. Data were selected according to the criteria described in the text (Sect. 2.1.1) and in the off-pulse phase intervals of the three bright pulsars (Sect. 2.1.2), whose positions are marked by diamonds. Counts are saturated between 0 and 50, and smoothed for display with a Gaussian kernel of σ = 0.25°. |
| In the text | |
 |
Fig. 3 Maps of N(H i) column densities in the Cygnus complex in the Local Spur (left) and in the outer Galaxy (right), under the assumption of a uniform spin temperature of 250 K. The color scales with N(H i) in units of 1020 atoms cm-2. The maps were smoothed with a Gaussian kernel of σ = 0.25° for display. |
| In the text | |
 |
Fig. 4 Maps of WCO intensities in the Cygnus complex in the Local Spur (left) and in the outer Galaxy (right). The color scales with WCO in units of K km s-1 above 1.5 K km s-1. The maps were smoothed with a Gaussian kernel of σ = 0.25° for display. |
| In the text | |
 |
Fig. 5 AV excess map (magnitudes) obtained from the optical extinction AV estimated from 2MASS data minus the best-fit linear combination of the N(H i) and WCO maps shown in Figs. 3 and 4, respectively. The map was smoothed using a Gaussian kernel of σ = 0.25° for display. |
| In the text | |
 |
Fig. 6 Free-free emission intensities from WMAP data. The color scales with brightness temperature in mK. The map was smoothed using a Gaussian kernel of σ = 0.25° for display. |
| In the text | |
 |
Fig. 7 Sources included in the analysis model. Diamonds mark the positions of the three bright pulsars that were dimmed by phase selection (Sect. 2.1.2). X points mark the positions of other identified sources. Crosses correspond to 1FGL sources either associated to AGN or variable, or both, confirmed by our analysis. The blue circles correspond to the rims of the templates adopted to model SNRs, the Cygnus Loop (G74.0−8.5) and γ Cygni (G78.2 + 2.1). The red circle marks the centroid of VER 2019 + 407 (whose extension is not appreciable in this large-scale view). The magenta circle represents the 1σ contour of the Gaussian used to model the cocoon. |
| In the text | |
 |
Fig. 8 Residuals (data-model). Left: low energies (100 MeV–1 GeV); center: mid-energies (1 GeV–10 GeV); right: high energies (10 GeV–100 GeV). Units are approximate standard deviations (square root of model counts) saturated between ± 3 and smoothed for display with a Gaussian kernel of σ = 0.25°. In each panel the blue circle in the top left corner represents the effective LAT PSF 68% containment circle for the event selection used in the analysis (averaged over the corresponding energy range assuming a power-law spectrum with index 2.1). Diamonds mark the positions of bright pulsars for which phase selection was applied, as in Fig. 2. Crosses mark the positions of unassociated 1FGL sources coincident with positive residuals; the X point mark the position of 2FGL J2018.0 + 3626, coincident with a hot spot in the residual map 1 GeV–10 GeV. |
| In the text | |
 |
Fig. 9 Spectral energy distribution of γ-ray emission measured by the LAT compared with our best-fit model. The uncertainties shown are statistical only. We separately show the different components of the interstellar emission model, point sources and extended objects. The curve corresponding to γ Cygni combines the contributions of the off-pulse source, the disk associated with the remnant and the 2D Gaussian accounting for VER 2019 + 407. |
| In the text | |
 |
Fig. 10 Maximum likelihood obtained as a function of the uniform spin temperature adopted for the optical depth correction of H i data. Values are offset so that log-likelihood is zero for a spin temperature of 100 K. |
| In the text | |
 |
Fig. 11 H i emissivity spectrum in the Cygnus complex. Points: the best-fit estimate for the spin temperature TS = 250 K. Hatched rectangles: systematic uncertainties taking H i opacity and γ-ray selection efficiency into account. Line: model of the local interstellar spectrum by Abdo et al. (2009d) (with a nuclear enhancement factor of 1.84, Mori 2009). |
| In the text | |
 |
Fig. 12 Top: emissivity per WCO intensity unit versus emissivity per hydrogen atom in the Cygnus complex (for TS = 250 K). The points correspond to the different energy bins; the emissivities decrease with increasing energy. The red line gives the best linear fit taking uncertainties on both axes into account. Bottom: residuals in units of standard deviations as a function of H i emissivity. |
| In the text | |
 |
Fig. 13 Top: emissivity per AV,exc unit versus emissivity per hydrogen atom in the Cygnus complex (for TS = 250 K). The points correspond to the different energy bins; the emissivities decrease with increasing energy. The green line gives the best linear fit taking uncertainties on both axes into account. Bottom: residuals in units of standard deviations as a function of H i emissivity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


