| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201117423 | |
| Published online | 13 February 2012 | |
Loops formed by tidal tails as fossil records of a major merger
1 Laboratoire GEPI, Observatoire de Paris, CNRS-UMR8111, Univ. Paris-Diderot, 5 place Jules Janssen, 92195 Meudon, France
e-mail: jianling.wang@obspm.fr; francois.hammer@obspm.fr
2 NAOC, Chinese Academy of Sciences, A20 Datun Road, 100012 Beijing, PR China
3 Laboratoire d’Astrophysique de Marseille, Observatoire Astronomique de Marseille Provence, Technopôle de l’Étoile, Site de Chateau-Gombert, 38 rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
Received: 6 June 2011
Accepted: 12 December 2011
Context. Many haloes of nearby disc galaxies contain faint and extended features, including loops, which are often interpreted as relics of satellite infall in the main galaxy’s potential well. In most cases, however, the residual nucleus of the satellite is not seen, although it is predicted by numerical simulations.
Aims. We test whether such faint and extended features can be associated to gas-rich, major mergers, which may also lead to disc rebuilding and thus be a corner stone for the formation of spiral galaxies. Our goal is to test whether the major merger scenario can provide a good model for a particularly difficult case, that of NGC 5907, and to compare to the scenario of a satellite infall.
Methods. Using the TreeSPH code GADGET-2, we model the formation of an almost bulge-less galaxy similar to NGC 5907 (B/T ≲ 0.2) after a gas-rich major merger. First, we trace tidal tail particles captured by the galaxy gravitational potential to verify whether they can form loops similar to those discovered in the galactic haloes.
Results. We indeed find that 3:1 major mergers can form features similar to the loops found in many galactic haloes, including in NGC 5907, and can reproduce an extended thin disc, a bulge, as well as the pronounced warp of the gaseous disc. Relatively small bulge fractions can be reproduced by a large gas fraction in the progenitors, as well as appropriate orbital parameters.
Conclusions. Even though it remains difficult to fully cover the large volume of free parameters, the present modelling of the loops in NGC 5907 proves that they could well be the result of a major merger. It has many advantages over the satellite infall scenario; e.g., it solves the problem of the visibility of the satellite remnant, and it may explain some additional features in the NGC 5907 halo, as well as some gas properties of this system. For orbital parameters derived from cosmological simulations, the loops in NGC 5907 can be reproduced by major mergers (3:1 to 5:1) and possibly by intermediate mergers (5:1 to 12:1). The major merger scenario thus challenges the minor merger one and could explain many properties that haloes of spiral galaxies have in common, including their red colours and the presence of faint extended features.
Key words: galaxies: evolution / galaxies: spiral / galaxies: individual: NGC 5907 / galaxies: interactions
© ESO, 2012
1. Introduction
The hierarchical galaxy formation theory assumes that galaxies have been assembled through mergers of smaller entities. The relative impact of both minor and major mergers is still being intensively debated (Fakhouri & Ma 2008; Lin et al. 2004, 2008; Hopkins et al. 2008, 2009; Bell et al. 2006; Lotz et al. 2008; Bridge et al. 2007). Peculiar galaxies are mostly related to merger or interaction events. For example, most luminous infrared galaxies (LIRGs; Sanders & Mirabel 1996) are merging or interacting galaxies, as revealed by their detailed substructures with multiple nuclei (see Haan et al. 2011). Toomre (1977) first pointed out that a major merger could result in the formation of elliptical galaxies. Later simulations showed that major mergers of gas-poor progenitors will destroy the disc and form a galaxy with a large spheroidal component.
Partly due to their frequency, even minor mergers challenge the survival of discs (Toth & Ostriker 1992; Stewart et al. 2009). Thus the number of unperturbed discs at low redshift argues that there should be some mechanisms that either preserve the disc from being destroyed or allow it to be rebuilt after the merger event. Analyses of merger remnants show that discs can survive from a merger. Simulations with low gas fractions (≤10%) also show that a significant fraction of the gas can survive a major merger and form a new disc (Barnes & Hernquist 1996; Barnes 2002). By observing and analysing the progenitors of local spirals at intermediate redshift, Hammer et al. (2005, 2007, 2009) suggest that many present-day discs could have been rebuilt after a major merger. Recent theoretical advances also support this scenario. Many hydrodynamical simulations indicate that new discs can be rebuilt after a major merger between disc galaxies (Robertson et al. 2006; Hopkins et al. 2009; Springel & Hernquist 2005), provided the initial gas fraction is sufficiently high. In this process gas plays the key role in the disc rebuilding process. High redshift galaxies have much higher gas fraction than local spirals, consistently with the above scenario.
It is expected that about half of the local disc galaxies have experienced a major merger in the past 9 Gyr (Puech et al. 2012), and it should thus be expected to find imprints of such events within the remnant halo. For example M31, the largest spiral of the Local Group, contains many faint structures in its halo. The Giant Stream (Ibata et al. 2001) is the most famous one, together with the large north-east loop with metal-poor stars recently discovered by the PANDA team (Richardson et al. 2011). Most of these faint features in the halo of M31 have often been thought to be caused by numerous minor merger events, as many as the stream number. Hammer et al. (2010), however, show that most of these faint features could, instead, be related to a single major merger event. In their models, most of the faint structures, including the Giant Stream, are due to stars coming back from tidal tails, a process that can be maintained for several Gyr.
If the disc of many spirals is indeed rebuilt after a major merger, it is expected that tidal tails can be a fossil record and that there should be many loops and streams in their haloes. Recently Martínez-Delgado et al. (2010) have conducted a pilot survey of isolated spiral galaxies in the Local Volume up to a low surface brightness sensitivity of ~28.5 mag/arcsec2 in V band. They find that many of these galaxies have loops or streams of various shapes and interpret these structures as evidence of minor merger or satellite infall. However, if these loops are caused by minor mergers, the residual of the satellite core should be detected according to numerical simulations. Why is it hardly ever detected?
The above question is the starting point for this paper, which intends to test whether a major merger scenario could, or could not, reproduce the observations of faint loops in nearby galaxy haloes better than the minor merger one. We choose to study here the NGC 5907 galaxy and its faint loop system observed by Martínez-Delgado et al. (2008, hereafter M08) because it is often regarded as the best evidence of a minor satellite interaction with a late-type spiral, i.e. not an easy configuration to be reproduced by a major merger.
The paper is organised as follows. In Sect. 2 we describe the properties of NGC 5907 and Sect. 3 summarises the peculiar features found in its halo. Simulation methods and initial conditions are described in Sect. 4, and in Sect. 5 we present the results of our simulations of both the galaxy and the associated loops. In Sect. 6 we discuss whether a major merger can reproduce a galaxy with similar properties to NGC 5907, and we then compare the relative merits of major and minor mergers. In the appendices, we present the implementation of star formation in the GADGET-2 code (Appendix A) and we give a general description of the loop properties formed during a major merger (Appendix B).
2. Properties of the NGC 5907 galaxy
NGC 5907 is a nearby Sc type spiral. There is a large uncertainty in the distance of NGC 5907 due to its peculiar motion. Zepf et al. (2000) got a distance 13.5 ± 2.1 Mpc from a combination of the Tully-Fisher relation in both optical and near infrared and a peculiar motion model, and they adopted a round value 14 Mpc, which is used by M08. For consistency, we use the same distance (14 Mpc) as M08. The measured disc scale-length of NGC 5907 is 6.1 kpc in R-band, while it is 3.82 kpc in H-band (Miller & Rubin 1995) when scaled to 14 Mpc. Saha et al. (2009) got 3.86 kpc by fitting Spitzer IRAC 4.5 μm data. Barnaby & Thronson (1992) obtained in H band a scale-height about 0.41 kpc and a bulge-to-disc luminosity ratio (B/D) of 0.05.
There are still considerable uncertainties in the stellar mass determination of NGC 5907. We need to re-estimate it carefully, accounting properly for the effects linked to the IMF (see Puech et al. 2008; Hammer et al. 2009) Our stellar mass determination follows the method of Bell et al. (2003) using the K-band observation from 2MASS and an optical colour, (B − V) from Just et al. (2006). The Ks apparent magnitude is 6.757, and the B − V colour is 0.86.
So the total stellar mass is 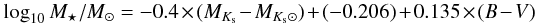 (1)where MKs⊙ is the solar absolute magnitude (Bell et al. 2003). Then the total stellar mass of NGC 5907 is 6.57 × 1010 M⊙ assuming a “diet” Salpeter IMF. The gas mass of NGC 5907 is about 1.94 × 1010 M⊙ including HI, H2 and He (Just et al. 2006). So the total baryonic mass is 8.51 × 1010 M⊙, and the gas fraction is 23%.
(1)where MKs⊙ is the solar absolute magnitude (Bell et al. 2003). Then the total stellar mass of NGC 5907 is 6.57 × 1010 M⊙ assuming a “diet” Salpeter IMF. The gas mass of NGC 5907 is about 1.94 × 1010 M⊙ including HI, H2 and He (Just et al. 2006). So the total baryonic mass is 8.51 × 1010 M⊙, and the gas fraction is 23%.
The large scatter of values found in the literature are mainly due to the different methods used to calculate the stellar mass. For example, methods assuming that NGC 5907 lies just on the baryonic Tully Fisher relation (e.g. McGaugh 2005; Stark et al. 2009) are not sufficiently accurate for an individual object. On the other hand, our estimate of the stellar mass may underestimate the contribution of the bulge because NGC 5907 is seen edge-on and even at near-IR wavelengths, dust lying in the disc may considerably affect its luminosity, and its precise contribution to the mass is still uncertain.
Comparing the number of constraints and parameters between minor and major mergers.
3. Peculiar properties of the NGC 5907 halo
Even though NGC 5907 is a member of the 396th Lyon Group of Galaxies (LGG 396), all of the identified group members are at very large separation and could not be interacting with NGC 5907 (Irwin & Madden 2006). This galaxy may be considered as a typical isolated and an almost bulge-less spiral in the local universe.
However, recent observations show that the NGC 5907 halo has many peculiar features.
-
There are two giant loops lying near the polar disc plane of NGC 5907. Shang et al. (1998) first discovered one half of one loop, and more deep observations by M08 confirmed this result, revealing two giant loops. The two loops extend up to 50 kpc from the galaxy centre. This strange structure indicates that NGC 5907 has experienced a former merger/interacting event, which could be relatively recent according to M08. The surface brightness of these loops is about 26.8 mag/arc-second2, corresponding to a stellar mass of approximately 3.5 × 108 M⊙ with a stellar mass surface density of 0.32 M⊙ pc-2.
-
The gaseous and the stellar discs are strongly warped. Previous observations have shown that the disc of NGC 5907 is sharply truncated at ~24 kpc. The radius profile clearly shows a break, which is common to many local spirals (van der Kruit 2007). The deep observations of M08 reveal that the star light extends out to the nominal cut-off radius. The stellar disc is also warped (see also Shang et al. 1998) in the same direction as the HI gas warp, suggesting a common origin for both the stellar and gas warps.
-
The halo of NGC 5907 is red according to Lequeux et al. (1998) with V − I = 1.4 and B − V = 1 at 5.6 kpc off the disc plane. According to Zibetti et al. (2004, see their Fig. 9) this is slightly redder than the stacked value of about a thousand SDSS galaxies. This implies that NGC 5907 shares the red halo properties of many nearby spiral galaxies, including M31 (see e.g. Mouhcine et al. 2005; Hammer et al. 2007), indicating that its halo includes a significant fraction of metal enriched stars.
-
Mid-infrared observations revealed the presence of considerable material on both sides of the disc, up to 10 kpc from the galaxy centre, including PAH emission (Irwin & Madden 2006) molecular gas (Laine et al. 2010) and diffuse dust emission (Burgdorf et al. 2009). This could indicate that the NGC 5907 disc is not completely relaxed.
There are a few existing models for NGC 5907, which have set up to explain the formation process of the red halo or of the loops. To keep the disc undisturbed, a minor merger with a high mass ratio has generally been proposed. Lequeux et al. (1998) model the red halo formation, assuming that it is from a merger with a red dwarf elliptical with mass of a few 109 M⊙. Reshetnikov & Sotnikova (2000) model the half ring discovered by Shang et al. (1998) by using a model with a 1000:1 mass ratio. A more recent model by M08 can reproduce both loop structures, assuming that they formed through a single merger event with a mass ratio of 4000:1. The small satellite, a spheroid, is assumed to fall into the potential well of NGC 5907, forming a tidal tail that literally draws out the two loops. Even though their model reproduces the geometry of the two loops well, it is unclear whether it can reproduce all the abnormal features of NGC 5907 described above. It is also confronted with the problem of the visibility of the progenitor residual.
We therefore investigate whether a gas-rich, major merger can reproduce most of the abnormal features observed in NGC 5907. Such an event may dramatically affect the whole structure of the main galaxy, and its modelling should also reproduce the massive, inner components (bulge, disc) of NGC 5907. To achieve this goal, we need to consider a much larger number of constraints than that for a very minor event. For comparison, we list in Table 1 the constraints and their possibly associated parameters in both major and minor merger cases. It naturally leads to a huge parameter space to be investigated for modelling NGC 5907 by a major merger, and a natural difficulty of getting an accurate model. Our goal is to show whether a single gas-rich merger event can reproduce the global structure of the NGC 5907 bulge-less galaxy, as well as its exceptional system of loops in its halo.
4. Simulations and initial conditions
We use the publicly available version of the GADGET-2 code (Springel 2005), which is a parallel TreeSPH code employing the fully conservative formulation (Springel & Hernquist 2002) of smoothed particle hydrodynamics (SPH). In this code both energy and entropy are conserved even when the smoothing lengths evolve adaptively (Springel & Hernquist 2003). Implementation of star formation, cooling, and feedback has been done following Cox et al. (2006), and our code is very similar to the one of Cox et al. (2006) (see Appendix A).
We begin our simulations with a total baryon mass equal to 9 × 1010 M⊙. This value is a few percent higher than the total baryonic mass of NGC 5907, to account for the mass loss during the merger (Hammer et al. 2010). The initial conditions are set up following Hammer et al. (2010). Each progenitor is composed of a stellar and a gas disc embedded in a dark matter halo. Both discs have an exponential distribution. The dark matter model is chosen following Barnes (2002). The density profiles of these two components are 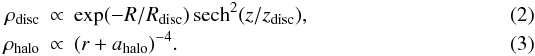 Following Cox et al. (2006), the gas-disc scalelength is set to three times that of stellar disc, since observations show that the gas disc has a more extended distribution than the stellar disc (van der Kruit 2007). The initial stellar disc scalelength is chosen following the scaling relation between rotation curve peak and disc scalelength (Hammer et al. 2007). We notice that fitting the rotation curve leaves a considerable degeneracy in the dark matter mass fraction in a galaxy such as NGC 5907. Here we adopt nine percent of the baryonic matter, which is slightly more than other adopted values (Hoekstra et al. 2005; Dutton et al. 2010) but less than those adopted in Barnes (2002), Cox et al. (2006), and Hammer et al. (2010). The final scale length of the dark matter profile is fixed using the baryonic Tully-Fisher relation (Puech et al. 2010). The disc scaleheight is set to be ten percent of the scalelength. We follow the method of Barnes (2002) to build the initial galaxy, which is stable enough for current work (see Appendix A). Parameters for each model are listed in Table 2.
Following Cox et al. (2006), the gas-disc scalelength is set to three times that of stellar disc, since observations show that the gas disc has a more extended distribution than the stellar disc (van der Kruit 2007). The initial stellar disc scalelength is chosen following the scaling relation between rotation curve peak and disc scalelength (Hammer et al. 2007). We notice that fitting the rotation curve leaves a considerable degeneracy in the dark matter mass fraction in a galaxy such as NGC 5907. Here we adopt nine percent of the baryonic matter, which is slightly more than other adopted values (Hoekstra et al. 2005; Dutton et al. 2010) but less than those adopted in Barnes (2002), Cox et al. (2006), and Hammer et al. (2010). The final scale length of the dark matter profile is fixed using the baryonic Tully-Fisher relation (Puech et al. 2010). The disc scaleheight is set to be ten percent of the scalelength. We follow the method of Barnes (2002) to build the initial galaxy, which is stable enough for current work (see Appendix A). Parameters for each model are listed in Table 2.
Eight models used in this study and their associated parameters.
The adopted mass distribution of halo is more susceptible to tidal tail formation (Dubinski et al. 1999; D’Onghia et al. 2009). To test the effect of the halo profile on the final result, we considered a Hernquist model (Hernquist 1990). This model is close to an NFW profile in the inner region (Springel et al. 2005) and we find that the results do not change significantly (M3L34H model in Table 2). The halo concentrations for the primary and secondary interlopers are found to be C = 11.48 and 15.6, respectively, the first value being very close to that of Cox et al. (2006), who model a gas-rich Sbc galaxy. We did not assume halo rotation since it is not expected (Springel & White 1999) to have a strong influence on tail formation. Simulations use between 180 000 and six million particles to test the effect of resolution.
The gas fraction is assumed to be quite high (from 60 to 80%), for progenitors that are intermediate mass galaxies at z > 1. For comparison gas fractions of 60% are found by Daddi et al. (2010) for z ~ 1.5 galaxies with stellar masses of 5 × 1010 M⊙ and similar values are found for massive galaxies at z ~ 2 (Erb et al. 2006; see also Rodrigues et al., in prep.). To evaluate the mass ratio between the two merging galaxies, we follow the Hopkins et al. (2010) zeroth order scaling relation between gas fraction, mass ratio, and bulge fraction. The small bulge component of NGC 5907 gives a constraint on the mass ratio, which cannot be too small and should be larger than or equal to 2.
 |
Fig. 1 Star and gas particles distributions for a merger with mass ration 3 (model M3L34A) at different epochs. Star particles are shown in the top two rows. The fit to best observations is at 8.6 Gyr, at which the structures of third and fourth loops can match the observations. The gas surface density is shown in the bottom two panels with gas density indicated by the colour bar. The size of each panel is 300 by 300 kpc and the arrows are explained in the text. |
By construction, the present simulations assume a single encounter of two galaxies, without accounting for other external supplies of gas such as cold flows. Not being able to extract a galaxy similar to NGC 5907 from cosmological simulations has several consequences. For example, the assumed gas fraction in the progenitors is certainly an upper limit, because some additional gas may be captured from the IGM before fusion. The stability of the gas-rich progenitors when they are isolated has been verified in Appendix A, and do not account for gas accretion and clumpy fragmentation as could be inevitable with sufficient levels of gas accretion. Besides this, our simulations of an isolated disc reproduce those of Cox et al. for all configuration of density and feedback. Possibly the absence of clump is related to ours and the Cox et al. recipes for SPH simulations; however, recent results from the AREPO code (Keres et al. 2011) show galaxies without numerous dense gaseous clumps, possibly contradicting with the numerous clumpy, intermediate-mass galaxies at z ~ 2 (Elmegreen et al. 2009). On the other hand, it is unclear whether clumpy disc progenitors would have changed our results after a major merger, which mostly destroy progenitor’s features, except possible bulge-like structures that could be enhanced in clumpy galaxies (Bournaud et al. 2011).
For some of our models, we assume a star formation history with a varying global efficiency in transforming gas to stars, in order to preserve enough gas from being consumed before fusion. Although this fine-tuned star formation history may have some physical motivations (see e.g. Hammer et al. 2010), its main role is also to ensure the formation of stars after the emergence of the gaseous disc just after fusion.
We adopt a retrograde-prograde merger, which is favourable for building a disc after the merger (Hopkins et al. 2009). The rotation direction for the secondary progenitor is set to be prograde and that of the massive progenitor, retrograde. This choice is because resonances have a strong effect on long tidal tail formation, which is enhanced in prograde and suppressed in retrograde encounters (Toomre & Toomre 1972; Barnes & Hernquist 1992). We also find that in order for the loop shapes to match the observations, the orbital eccentricities should not be as low as found by M08, who used an orbital eccentricity of 0.42. We find, however that an orbit eccentricity of 0.9 is enough to have loop shapes that match the observations.
Cosmological simulations (Khochfar & Burkert 2006) provide a relationship between the ratio of the pericentre to the virial radius and the orbit eccentricity. We carefully choose pericentre and eccentricity so that our orbital geometry fulfils this relation. For example, we estimate the virial radius of the primary galaxy halo at the beginning of the simulation (8–9 Gyr ago, z > 1) to be about 130 kpc from the relationship between virial radius and total mass derived from cosmological simulations (Springel & White 1999). Assuming a pericentre of 25 kpc implies eccentricity values of above 0.88 (see Fig. 6 of Khochfar & Burkert 2006).
5. Modelling NGC 5907 and its loop system
5.1. Formation of giant loops
5.1.1. Mechanisms of loop formation during the merger: setting the orbital parameters
Appendix B describes the basic properties of loops formed in a major merger from tidal tail particles, which later on are captured by the gravitational potential of the galaxy. Here we use these generic properties of tidal tails and loops to investigate different viewing angles and different forming epochs to reproduce the loops found by M08 in the NGC 5907 halo.
The assumption that the loops are well fitted by ellipses provides important constraints on the viewing angles. To form long-lived loops, their associated particles should not interact with the newly formed disc. We notice that one loop (noted as SW-SE-E1-W2 in M08) intersects the optical disc. Assuming it is a projection effect, this implies that the angle between the line of sight and the loop plane should be 60 degrees or larger. This is consistent with the M08 model, which assumed a loop rotation by 57 degrees. Moreover the inclination of the loop plane to the disc plane is constrained by the observed tip position of the ellipse. The observed angle between the tip of the SW-SE-E1-W2 and the direction perpendicular to the disc, is quite small (less than 15 degrees), indicating that the loop plane should be almost polar to the disc. The loop shape also depends on the precession, intrinsic eccentricity, and position.
Table 2 summarises the properties of the models that are used in this paper, including initial parameters, resolution, star formation, or feedback history, as well as the structural parameters of the remnant galaxy well after the merger. Feedback model 1 uses five times median feedback of Cox et al. (2006) used. Feedback model 2 (M3L34F) uses five times this median feedback before fusion,and changes to a low feedback after fusion. The bulge Sersic index n and disc scalelength are obtained by fitting the surface brightness density distribution with a Sersic profile, and two exponential functions. Model M3L34G6 changes gas fraction. Model M3L34H uses Hernquist model. Model M3L34A, M3L34B are similar to M3L34 after a fine tuning of galaxy inclinations. Figure 1 gives an example of a 3:1 merger and displays its evolution at different epochs. The first passage occurs at about 1.0 Gyr after the beginning of the simulation, and second at 2.7 Gyr. The first tidal tail is formed after the first passage, and expands at 2.7 Gyr, i.e. just before the second passage, as shown by a yellow arrow in the upper third panel. We found that by increasing the pericentre radius, this tidal tail becomes less prominent and provides fewer stellar particles falling back to the newly formed galaxy. After the second passage, a second tidal tail is formed, as shown by a black arrow in the upper right hand panel of Fig. 1 (3.5 Gyr). Particles in this second tidal tail may form loops, and at ~4.2 Gyr, the first loop begins to form (red arrow in the second left row panel). At this time the loop size is small. As time elapses an increasing number of high-elevation particles come back from the tail, and the first loop expands (see Appendix B). At ~5.6 Gyr, the new disc is well formed, and a second loop appears (pink arrow in the 2nd row 2nd column panel). As time evolves, more and more loops appear. At 8.6 Gyr, the third and fourth loops (green and blue arrows) are well formed, and their structures show some similarities with those of NGC 5907. At the same time, the first and the second loops have considerably expanded, which unavoidably leads to their dilution.
The two observed loops have approximately the same apparent size, which we interpret to be a projection effect. Indeed, the higher order loop should be smaller than the lower order one, as described in Appendix B. A colour bar in the top left hand panel of Fig. 1 indicates the stellar-mass surface density. The surface mass density of the loops is about ~0.1 to 1 M⊙ pc-2. M08 roughly estimate the loops’ surface brightness as ~0.32 M⊙ pc-2. Even though there is large uncertainty in the observed values, the model is able to reproduce the order of magnitude of the loop surface brightness.
 |
Fig. 2 Inclination angle between disc, loop, and orbital planes as a function of time. The lower solid lines show the angle between the loop and the orbital planes. Lines within shaded regions indicate the inclination angles of the disc plane relative to the orbital plane, while the line-shaded region around 90 degrees indicates the angles between disc and loop planes that are consistent with the observations. Different colour lines show the simulations with different initial disc inclinations to the orbital plane. All the models used here have a mass ratio of 3 (from bottom to top, models M3L12, M3L23, M3L34B). |
Figure 2 shows how the disc and loop inclinations evolve with time. The loops are formed by particles coming back from the tidal tail. We quantified the loop plane inclination relative to the orbital plane from the angular momentum of the tidal tail particles. Because the angular momentum of the tidal tails is dominated by the orbital angular momentum, tidal tail particles mostly lie on the orbital plane, and at most 20 degrees away from it. To quantify the disc plane, we use the angular momentum of the post-fusion stellar particles, following the procedure presented in Hammer et al. (2010). With evolving time, the disc plane systematically rotates so as to be aligned to the orbital plane. Using the inclinations of disc and tidal tail particles relative to the orbital plane, we can determine the inclination between the loops and the disc plane that is consistent with observations. The angle between loop and disc planes is about 80 degrees in M08, while Reshetnikov & Sotnikova (2000) use an angle of 90 degrees to fit one loop. We considered this ten degree difference as the uncertainty in the angle between the loop and disc planes, as well as the uncertainty in our models, so in Fig. 2 the acceptable angles are shown by the line-shaded region. Because higher order loops appear at later epochs, the initial disc inclination angle should be larger to make the disc and loop plane close to polar at later times.
 |
Fig. 3 Stellar mass surface density shown with different scales of stellar mass surface brightness at 8.6 Gyr for the model M3L34. Each panel size is 300 by 300 kpc. |
5.1.2. Comparison with observations: which loops matter?
As shown in the previous section, a major merger can generate loops with a geometry similar to the observed ones, at a time that depends on the initial orientation of the main progenitor disc plane. Because observations are surface brightness limited, we illustrate in Fig. 3 how the visual impression depends on the surface-brightness threshold. By varying the threshold, the thin disc, thick disc, and loop features are progressively revealed. Colour bars in Fig. 3 indicate that loop regions with surface brightness ranging from 0.1 to 1 M⊙ pc-2 coincide quite well with the observed loops. Since the loop surface brightness is 0.32 M⊙ pc-2, this argues that observations identify only the brightest part of the loop system, i.e. mostly above the galaxy in the panel corresponding to 8.6 Gyr.
After the merger, particles coming back from the tidal tail continuously form loops of increasing order as illustrated in Fig. 1. During this process, while higher order loops are forming and reach sizes comparable to the observed loops, lower order loops continuously expand and become more and more diluted with time. Another factor favouring the low-order loop dilution is related to the tidal tail surface brightness distribution, which is fainter farther from the galaxy. The low-order loops are formed at any time by particles coming back later, which results in lower surface brightness compared to high-order loops.
We also find that a more inclined initial disc can capture the material of the secondary interloper better by making it rotate closer to the disc plane. Thus, there is little residual signature when the disc is seen in an edge-on position and favours observed loops of a high-order type. This is illustrated well in Fig. 4, which compares the formation of different order loops at different epochs. Residuals from the secondary decrease dramatically with time, favouring high-order loops that match the observations. Figure 4 also illustrates that lower order loops almost vanish with time.
In our model, the left loop has a higher order than the right one. This is in good agreement with observations, since the left loop has been discovered first by Shang et al. (1998), and the discovery of the two loops by M08 has been done with much deeper observations, implying that the left loop is brighter than the right one and that surface brightness threshold has to be accounted for when modelling the loops.
Another strong argument favouring observed loops of the high-order kind is related to the nature of the progenitors, which are assumed to be gas-rich galaxies to allow the formation of a significant disc. Such gas-rich galaxies are common in the high-redshift universe, and far less common at intermediate redshifts. Using this argument, together with the absence of residuals, favours a scenario for which the observed loops coincide with a combination of at least third and fourth order loops, with a time after interaction longer than ~8.6 Gyr. Interestingly, this scenario can be falsified by further observations: deeper observations of a wider field of view should detect the fainter lower order loops.
 |
Fig. 4 Comparing loop structures formed by combining loops of different order for mass ratios of 3. The left panel shows the first and second loops (model M3L23), the second panel shows the third and fourth loops (model M3L34), while the first loop appears at the bottom of the galaxy and becomes diluted. The size of each panel is 300 by 300 kpc. The loop stellar surface mass densities are consistent with observations from M08. In all these images the threshold has been chosen slightly below the observed one from M08. |
5.2. The rebuilt central galaxy: disc and bulge
To test whether the final merger remnant is consistent with the disc of NGC 5907, we follow the decomposition method of Hammer et al. (2010). Each final remnant is decomposed into three-components, namely bulge, thick disc, and thin disc. This method is based on angular momentum distribution taking advantage of the full three dimensional information for each particle (see details in Hammer et al. 2010). Figure 5 gives an example for a 3:1 merger model. The top panels show the angular momentum distribution of young, intermediate age, and old stars, which are defined following Hammer et al. (2010). Most young and intermediate age stars have angular momentum along the disc polar axis (0.9 ≤ MAz/MA ≤ 1) or the thick disc (0.7 ≤ MAz/MA ≤ 0.9), with the rest of them mostly concentrated in the bulge. The top right hand panel shows the presence of many old stars at a large distance from the centre, with angular momentum very different from that of the disc. They are mostly particles of the loops, but not do rotate with the disc. The bottom panels of Fig. 5 show the projected mass distribution for different components, confirming the presence of a prominent thin disc including >70% of the baryonic mass after the merger event (left panel).
 |
Fig. 5 The top panel gives the distribution of z component of the angular momentum of stellar particles for model M3L34. The galaxy has been projected edge-on using the angular momentum of the baryons. From left to right, star of different age (from young, intermediate, and old) are shown. Old stars (red dots) already exist in the progenitors at the beginning of the simulation. Young stars (blue dots) are defined with ages over 3 Gyr after the beginning of the simulation. Ages between young and old are defined as intermediate stars (green dots), which are formed before the fusion. The bottom panel shows the projected mass distribution of the thin disc (left), and the bulge and thick disc (right). The thin disc is selected from its angular momentum ratio (MAz/MA ≥ 0.9, see Hammer et al. 2010), which cuts the warp off. Each panel has a size of 300 by 300 kpc. |
We also fitted the stellar surface brightness distribution similarly to what is usually done from observations. For each merger remnant, we fit the galaxy surface brightness with a bulge that has a free Sersic index and an exponential disc (Sersic n = 1). For each merger remnant, we define the disc plane using the three-dimensional information as defined after the galaxy decomposition using the angular momentum (see Fig. 5). The stellar surface density is then measured in logarithmically spaced annuli in the disc plane.
 |
Fig. 6 Stellar surface mass density distribution as a function of radius for model M3L34. Open circles show the total stellar density together with a fit by different components (solid line). Sersic bulge and exponential disc components (indicated by different colours) are used to fit the stellar mass surface brightness. The fitting process excludes an area with a radius equal to 2 times the softening length (labelled by arrows, see the text). |
Figure 6 shows one example of a fit for a model with a mass ratio of three. During the fit, we excluded the very central part because it could be affected by numerical softening. We note that an additional exponential component is necessary to fit the outskirts. This additional component presents a surface brightness similar to or fainter than that of the loops and corresponds to the inner halo of the simulated galaxy. The results of the different models are listed in Table 2. The disc scalelength of our models ranges from 3.9 to 4.5 kpc and is consistent with the observed scalelength value of 3.84 kpc. The bulge fraction ranges from 15 to 23%, and depends on both the model and the star formation history. We caution that this bulge fraction is derived from the stellar mass distribution, while in some models ~40% of baryons are still made of gas.
Observations show that NGC 5907 is relatively gas-rich (gas fraction of 23%), which can be compared to the final gas fractions of the different models listed in Table 2. Models with constant feedback result in excessive gas fraction in the final remnants. We verified that the final gas fraction may reach the observed value using a tuning of the feedback (or an increase in the star formation efficiency) just after the fusion (model M3L34F), as assumed by Hammer et al. (2010). This also leads to a lower bulge fraction, with B/T = 15%.
The surface-brightness fitting method also gives the bulge half light radius and the bulge sersic index. Most of our realisations of gas rich major mergers result in low Sersic index values (≲1.5), i.e. comparable to those of pseudo bulges (e.g., Kormendy & Kennicutt 2004).
 |
Fig. 7 Comparison of observed and simulated (model M3L34A) rotation curves. The blue points are from Sancisi & van Albada (1987) and are based on HI observations. Black solid points are from Hα and NII observations by Miller & Rubin (1995), including near the central regions. Solid line shows the prediction from the mass model |
5.3. Rotation curve
We also compared the model rotation curve with observations. We collected two observations for rotation curve of this galaxy as shown in Fig. 7. Even though the observations show some discrepancies between them, our model reproduces the observed rotation curve quite well.
5.4. Disc warp and disturbed material above the disc plane
The merger remnant is not very relaxed at the time of observation, which makes the disc dynamically hot. This violent process naturally results in a disc warp and disturbances. The bottom rows of Fig. 1 show the gas evolution after the merger and the presence of a warp at 8.6 Gyr. After the merger, gas is decoupled from stars owing to their different dissipational properties, which is consistent with the observational result that the loops only include stars. The merger process makes the gas warped at the edge of the disc, and this can be maintained for several Gyr. Shang et al. (1998) did a 6 h radio observation with the VLA. In their Fig. 2 of an integrated 21 cm intensity map, the gas distribution is very warped and extends above and below the plane of the disc.
The gas above the disc plane shows non-relaxed motions that are also expected with our modelling of a major merger. Irwin & Madden (2006) analysed the PAH distribution and found PAH emissions well above the disc, up to 8.3 kpc. CO observation of the central parts of the disc show a steeply rising rotation curve and non-circular molecular gas motions, presumably due to a bar (Garcia-Burillo et al. 1997). These observations could be consistent with a major merger origin of NGC 5907.
5.5. Effects related to resolution
To test the effect of resolution, we compared simulations with different numbers of particles, from 180 k particles to six million for model M3L23. This test is used to verify whether weighing dark matter particles and gas particles affects our final result differently. In this study, the mass of the individual particles for dark matter, gas, and stars has ratios from 10:1:2 to 4:1:1. By varying particles mass ratio and increasing total particles number up to six million, we find that our results, including the structure of the loops, are not significantly affected by resolution.
Comparing major and minor merger hypotheses, where “Y” means consistency with the observations.
6. Discussion and conclusions
6.1. Can the properties of NGC 5907 be reproduced by an ancient and gas-rich major merger?
We modelled NGC 5907 as the result of a gas-rich major merger, using progenitors with a mass ratio of three. With gas fractions in the progenitors ranging from 60 to 80% and a star formation history similar to the one in Hammer et al. (2010), our modelling is able to reproduce the main observed NGC 5907 structural parameters (the thin disc and its rotation curve, and the bulge). The exceptional features of NGC 5907 can be reproduced, together with the central galaxy properties, especially if we compare the observed loops to the high-order loops expected in a major merger model. Given the extremely large number of parameters, as well as the very numerous constraints provided by the observations, we cannot claim that we have already identified the exact and unique model of NGC 5907 and its halo properties. We nevertheless succeeded in reproducing the loop geometry, and a disc-dominated, almost bulge-less galaxy. The limitations of our modelling are two-fold, with one related to observational uncertainties, the other to our modelling procedure.
Distance uncertainties of ~30% translate into uncertainties in the total baryonic mass of the galaxy, which may affect the accuracy of our modelling. However, the main uncertainty when comparing observations to modelling is related to the striking difference of the NGC 5907 disc at visible and near-IR wavelengths as illustrated in Fig. 8. At visible wavelengths the thin disc axis ratio is almost eight, the bulge shows a negligible contribution, while this exposure is deep enough to detect the very low surface brightness loops. This is in sharp contrast to observations at near-IR wavelengths, which reveal a thicker disc, with an axis ratio of 4.2, and do not detect the loops.
 |
Fig. 8 Top: deep observations of NGC 5907 in the visible light showing the thin disc with the gigantic loops (from M08). Bottom: observations of NGC 5907 with IRAC at 3.6 μm revealing the whole extent of the disc that is twice thicker than in the visible light. |
Two effects can explain the above behaviour of the edge-on disc of NGC 5907. Firstly, it has been shown that thick discs are prominent at near-IR wavelengths (see e.g. Comeron et al. 2011), and secondly, the presence of diffuse interstellar dust up to 10 kpc above the disc has been identified in NGC 5907 (Burgdorf et al. 2009). At 5 kpc from the disc, we estimate the surface brightness of the disc to be 22.5 mag arcsec-2 at 3.6 μm, which translates into 25.3 mag arcsec-2 in the AB system. At this location, there is a very faint emission in the image by M08 with ~28.0 mag arcsec-2 in the R band, i.e. 28.3 mag arcsec-2 in the AB system. Such a huge gap of three magnitudes between near-IR and visible light is probably caused by a combination of both effects, very red stars in the extended thick disc, and dust attenuation in the visible. It translates to fν(V) ~ 0.06 × fν(3.6 μm). To estimate the impact of dust extinction at 5 kpc on both sides of the disc, we assume that the thick disc stars cannot be intrinsically redder than M stars. For a non-extincted M star with Te = 3500 K, Benjamin et al. (2007, see their Fig. 7) find fν(V) ~ 0.15 × fν(3.6 μm). Thus even if the thick disc was only populated by M stars, it should have been detected in the very deep exposure of M08, except if the visible light has been extincted by a factor 0.15/0.06 = 2.5, which corresponds to AV = 0.9 (galactic extinction law for R = 3.1). For illustration, by replacing M by K stars (with Te = 4500 K) would lead to an extinction factor of 12 instead of 2.5, emphasising the importance of dust extinction on both side of the edge-on disc. Ideally, only a very deep exposure at near-IR wavelength can provide an image that can be compared to the stellar mass distribution of a model.
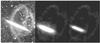 |
Fig. 9 Left: deep observations of NGC 5907 in the visible light showing the thin disc with the gigantic loops (from M08). Middle: one simulation of the loops at T = 8.0 Gyr with the M3L34G6 model, in which we assume a dust extinction screen affecting the stellar light density by a factor of 2.5 on both sides of the edge-on disc (see discussion in Sect. 6.1). Right: same model as middle panel shows all components with accounting for an extinction by a factor 12. The real extinction should be between the middle and right panel. |
Another substantial uncertainty from observations is related to the B/T estimate. Our model predicts B/T values around 20%, and a specific implementation of varying star formation history (or varying feedback history) reduces this value to 15%. The latter value is approximately twice the value we derive in fitting the luminosity profile of the 3.6 μm image (B/T ~ 0.08), which should be less affected by dust than at visible wavelengths. In fact our simulated B/T for the stellar mass may not coincide exactly with estimates from the luminosity. It has been argued, for example, that the IMF in elliptical galaxies is more dominated by low-mass stars than that of the Milky Way disc (van Dokkum & Conroy 2010). Given the similarities between ellipticals and bulges, one may speculate that the NGC 5907 bulge includes a larger fraction of low mass stars than the disc, leading to a B/T similar to the simulated one.
Limitations of our modelling are linked to the huge parameter space to be investigated. It leads to loops that behave like the observed ones, with some differences in the size and geometry. In Fig. 9 the modelled loops also show some differences with the observed ones when comparing their locations with respect to the disc. This indicates that, while we correctly identify the mechanism for loop formation, we do not yet recover the best solution for NGC 5907, which would require an enormous amount of time for fine tuning the models. Other limitations come from (1) the use of GADGET-2, which, for given resolution and star formation, feedback, and cooling recipes, provides less well defined discs (see Fig. 11 of Keres et al. 2011) with lower angular momentum than those predicted by the AREPO code; (2) the fact that our simulations are done in isolation, while other sources of gas supplies may be brought to the galaxy as done in cosmological simulations. Accounting for the above could have led to more realistic discs, and as it reduces the need for too high a gas fraction in the progenitors.
6.2. Comparing the relative merits of minor and major merger models
As mentioned above, the main drawback of the major merger scenario is caused by the enormous number of constraints to account for, leading to simulated configurations that still show some discrepancy with observations. This is in sharp contrast to a minor merger case for which the satellite orbit is only constrained by tracing the loops, without any influence on the main galaxy. This point, however, is mostly technical and should be discarded when discussing the relative relevance of both scenarios.
Table 3 summarises the exceptional features revealed by deep observations of NGC 5907 at visible, mid-IR, and radio wavelengths, and displays the merits of major, intermediate, and minor mergers, respectively, to reproduce them. To sample a wider range of mass ratios, we ran simulations of 10:1 and 15:1 mergers assuming a pericentre radius of 25 kpc and orbits consistent with the formation of loops similar to the observed ones. While the 10:1 merger occurs at T = 9 Gyr after the beginning of the simulation, the 15:1 merger would take more than a Hubble time to effectively merge. Thus we estimate that 12:1 is a limit for reproducing NGC 5907 with the orbital parameters expected from cosmological simulations.
A possible advantage of the major merger is linked to its being likely to predict all these features together, while the minor merger case can only reproduce the loops. Features like the warp or the gas and PAH emission above the disc can be explained well by other mechanisms, such as additional interactions or ejection of dust particles from the thin disc by galactic winds. The presence of considerable amounts of non-relaxed material (dust, gas including in molecular phase) in the disc outskirts, as well as the strong warp favours a scenario for which the NGC 5907 is not a relaxed disc, but this cannot lead to a decisive conclusion.
Possibly the absence of a remnant signature, together with loop colour, are more compelling for distinguing between the two scenarios. Using the IRAC 3.6 μm image (Ashby et al. 2004), we were able to model the light distribution with GALFIT (Peng et al. 2010) using a bulge, plus disc decomposition. After subtracting the model from the image, we examined the presence of a possible residual of the progenitor of a minor merger at the locations where the loops intersect the edge of the disc. At such a large distance (20 kpc) from the disc centre, it is unlikely that dust can affect the light that much, so we find no object that could be responsible of such an event. This is really problematic for a minor merger scenario, because with such an extended orbit, it is unlikely that tidal forces could destroy it. In the major merger case we have shown that the low surface-brightness features left by the secondary interloper gradually vanish with evolving time, because they are progressively captured by the disc (see Fig. 4).
The colour of the loops has been estimated by different groups and confirmed to be both red (Zheng et al. 1999; Lequeux et al. 1998) and comparable to that of elliptical galaxies (Zibetti et al. 2004). With the red colour R − I ~ 0.5 ± 0.3, Zheng et al. (1999) found it is consistent with Galactic globular clusters with [Fe/H] ~ −1. Following Hammer et al. (2007), we show in Fig. 10 the relation between rotational velocity and colour-inferred iron abundances of the stellar disc outskirts. NGC 5907 follows the same relation as defined by most spirals, which could be easily explained if stars in the inner halo are enriched by an ancient major merger (see Hammer et al. 2007). Given their location in the mass metallicity relation, a dwarf spheroid origin for the loop progenitor would generate a bluer colour than what is observed. For example, the colour of Sagittarius and its stream [Fe/H] = −1.2 (Sesar 2011) hardly matches the colour of the NGC 5907 halo.
 |
Fig. 10 Comparing iron abundances of outskirts of NGC 5907 with that of other galaxies from Hammer et al. (2007). The iron abundances of the NGC 5907 inner halo are from Zheng et al. (1999), who estimate them by comparing the loops colour with that of Galactic globular clusters. |
Assuming a cosmological origin for the encounter that is responsible for the loops has important consequences. In fact, this implies orbit eccentricities in excess of e = 0.85 (e.g. Khochfar & Burkert 2006) for a pericentre larger than 25 kpc. This would exclude the M08 model that assumes e = 0.42, as well as all models with mass ratio over 12:1, simply because the two galaxies would not have time to merge within a Hubble time, leading the problem of the absence of progenitor residual too critical.
Examination of Table 3 confirms the above: only mergers with mass ratios between 3:1 and 12:1 are consistent with most of the observations of the NGC 5907 halo. Given the observational constraints and our modelling, it is not possible to distinguish between the merits of intermediate mergers (5:1 to 12:1) and major mergers (3:1 to 5:1). In fact, we have failed to reproduce the observed loops with a 10:1 merger, although we certainly did not investigate the whole range of parameters to exclude this. On the other hand, with orbital eccentricities from 0.9 to 1, less dynamical friction is expected for a higher mass ratio, and it could be difficult to match the low loop eccentricity.
Possibly deeper exposures on larger scales of the NGC 5907 halo could reveal many very faint new structures that may help disentangle between these two alternatives. Using state-of-the-art AREPO code to reproduce the NGC 5907 loops would also be useful for providing a more realistic the disc and the distribution of matter in its surrounding.
6.3. Concluding remarks
This study shows that a major merger scenario for the formation of giant loops in NGC 5907 may explain the observations, as well as the infall of a minor merger with a mass ratio lower than 12:1. Together with the rebuilding of a thin disc in an almost bulge-less galaxy, a gas-rich major merger forms gigantic loops, within which stars may orbit in loops for several billion years. Low-mass ratios down to three are particularly efficient in removing the residuals of the secondary interloper, and are still consistent with the observational uncertainties on the bulge-to-total mass ratio. This is especially true when high order loops are considered, several billion years after the merger. This contrasts with minor mergers that are assumed to orbit at large distance from the galaxy centre, and should have left imprints of a residual core. This proposition of a major merger origin could apply as well to the faint tidal features found in many other spiral galaxies. Interestingly, our model of NGC 5907 can be falsified by new and extremely deep observations of a wider field surrounding this galaxy: if NGC 5907 has been formed by a major merger, there should be faint and extremely large structures at hundred kilo-parsecs or more, coinciding with lower order loops.
Future work will include modelling other nearby spiral galaxies with large and faint, extended features in their haloes. Most of them show no trace of a residual core of a minor merger residual. While it is accepted more and more that bulge-less galaxies could result from gas-rich major mergers (Guedes et al. 2011; Brook et al. 2011; Font et al. 2011), the consecutive modelling of faint features in their halo should put considerable constraints on the orbital parameters. A wide diversity of orbital parameters has been already found by Hammer et al. (2009) in modelling distant, unrelaxed galaxies by major mergers. These distant galaxies are likely similar to the progenitors, six billion years ago, of present-day spirals, and linking them together could provide another crucial test for the spiral rebuilding disc scenario.
Acknowledgments
This work has been supported by the “Laboratoire International Associé” Origins, and computations were done using the special supercomputer at the Center of Information and Computing at National Astronomical Observatories, Chinese Academy of Sciences, funded by Ministry of Finance under the grant ZDYZ2008-2, as well as at the Computing Center at the Paris Observatory. We are very grateful to Sylvestre Taburet and the GEPI software team for their precious help. The images in gas surface density of Figs. 1, 3, 4, and the bottom row of Fig. 5 were produced using SPLASH (Price 2007).
References
- Ashby, M. L. N., Pipher, J. L., Forrest, W. J., et al. 2004, BAAS, 36, 1444 [NASA ADS] [Google Scholar]
- Barnaby, D., & Thronson, H. A., Jr. 1992, AJ, 103, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E. 1992, ApJ, 393, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1992, ARA&A, 30, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1996, ApJ, 471, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Phleps, S., Somerville, R. S., et al. 2006, ApJ, 652, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Benjamin, R. A., Draine, B. T., Indebetouw, R., et al. 2007, The Science Opportunities of the Warm Spitzer Mission Workshop, 943, 101 [NASA ADS] [Google Scholar]
- Bessell, M. S. 2005, ARA&A, 43, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987 (Princeton, NJ: Princeton University Press) (BT87) [Google Scholar]
- Bizyaev, D., & Mitronova, S. 2002, A&A, 389, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Chapon, D., Teyssier, R., et al. 2011, ApJ, 730, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bridge, C. R., Appleton, P. N., Conselice, C. J., et al. 2007, ApJ, 659, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G., Gibson, B. K., et al. 2011 [arXiv:1105.2562] [Google Scholar]
- Burgdorf, M., Ashby, M. L. N., Pang, S., & Gilmore, G. F. 2009, The Evolving ISM in the Milky Way and Nearby Galaxies [Google Scholar]
- Choi, J.-H., Weinberg, M. D., & Katz, N. 2007, MNRAS, 381, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Comeron, S., Knapen, J. H., Sheth, K., et al. 2011, ApJ, 729, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, T. J., Jonsson, P., Primack, J. R., & Somerville, R. S. 2006, MNRAS, 373, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Besla, G., Cox, T. J., & Hernquist, L. 2009, Nature, 460, 605 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Vogelsberger, M., Faucher-Giguere, C.-A., & Hernquist, L. 2010, ApJ, 725, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., Mihos, J. C., & Hernquist, L. 1996, ApJ, 462, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., Mihos, J. C., & Hernquist, L. 1999, ApJ, 526, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., Conroy, C., van den Bosch, F. C., Prada, F., & More, S. 2010, MNRAS, 407, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., Fernandez, M. X., & Lemonias, J. J. 2009, ApJ, 692, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Fakhouri, O., & Ma, C.-P. 2008, MNRAS, 386, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmann, R., Mayer, L., & Carollo, C. M. 2008, ApJ, 684, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Font, A. S., Benson, A. J., Bower, R. G., et al. 2011, MNRAS, 417, 1260 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Burillo, S., Guelin, M., & Neininger, N. 1997, A&A, 319, 450 [NASA ADS] [Google Scholar]
- Guedes, J., Callegari, S., Madau, P., & Mayer, L. 2011, ApJ, 742, 76 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haan, S., Surace, J. A., Armus, L., et al. 2011, AJ, 141, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Flores, H., Elbaz, D., et al. 2005, A&A, 430, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, F., Puech, M., Chemin, L., Flores, H., & Lehnert, M. D. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Flores, H., Puech, M., et al. 2009, A&A, 507, 1313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, F., Yang, Y. B., Wang, J. L., et al. 2010, ApJ, 725, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbard, J. E., & Mihos, J. C. 1995, AJ, 110, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Hsieh, B. C., Yee, H. K. C., Lin, H., & Gladders, M. D. 2005, ApJ, 635, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Younger, J. D., & Besla, G. 2008, ApJ, 688, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Younger, J. D., & Hernquist, L. 2009, ApJ, 691, 1168 [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- House, E. L., Brook, C. B., Gibson, B. K., et al. 2011, MNRAS, 415, 2652 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R., Irwin, M., Lewis, G., Ferguson, A. M. N., & Tanvir, N. 2001, Nature, 412, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Irwin, J. A., & Madden, S. C. 2006, A&A, 445, 123 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Just, A., Möllenhoff, C., & Borch, A. 2006, A&A, 459, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, N., Weinberg, D. H., & Hernquist, L. 1996, ApJS, 105, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Keres, D., Vogelsberger, M., Sijacki, D., Springel, V., & Hernquist, L. 2011, MNRAS, submitted [arXiv:1109.4638] [Google Scholar]
- Khochfar, S., & Burkert, A. 2006, A&A, 445, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kormendy, J., & Kennicutt, R. C., Jr. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Laine, S., Appleton, P. N., Gottesman, S. T., Ashby, M. L. N., & Garland, C. A. 2010, AJ, 140, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Combes, F., Dantel-Fort, M., et al. 1998, A&A, 334, L9 [NASA ADS] [Google Scholar]
- Lin, L., Koo, D. C., Willmer, C. N. A., et al. 2004, ApJ, 617, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Davis, M., Faber, S. M., et al. 2008, ApJ, 672, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Peñarrubia, J., Gabany, R. J., et al. 2008, ApJ, 689, 184 (M08) [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Gabany, R. J., Crawford, K., et al. 2010, AJ, 140, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., & Bournaud, F. 2010, ApJ, 714, L275 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2005, ApJ, 632, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, B. W., & Rubin, V. C. 1995, AJ, 110, 2692 [NASA ADS] [CrossRef] [Google Scholar]
- Mouhcine, M., Ferguson, H. C., Rich, R. M., Brown, T. M., & Smith, T. E. 2005, ApJ, 633, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J. 2007, PASA, 24, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Puech, M., Flores, H., Hammer, F., et al. 2008, A&A, 484, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puech, M., Hammer, F., Flores, H., et al. 2010, A&A, 510, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puech, M., et al. 2012, ApJ, submitted [Google Scholar]
- Reshetnikov, V. P., & Sotnikova, N. Y. 2000, Astron. Lett., 26, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. C., Irwin, M. J., McConnachie, A. W., et al. 2011, ApJ, 732, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B., Bullock, J. S., Cox, T. J., et al. 2006, ApJ, 645, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., de Jong, R., & Holwerda, B. 2009, MNRAS, 396, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Sancisi, R., & van Albada, T. S. 1987, Dark matter in the universe, 117, 67 [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Sesar, B. 2011, RR Lyrae Stars, Metal-Poor Stars, and the Galaxy, ed. A. McWilliam, Pasadena, CA, 5, 135 [Google Scholar]
- Shang, Z., Zheng, Z., Brinks, E., et al. 1998, ApJ, 504, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2000, MNRAS, 312, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & Hernquist, L. 2003, MNRAS, 339, 289 [Google Scholar]
- Springel, V., & Hernquist, L. 2005, ApJ, 622, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., & White, S. D. M. 1999, MNRAS, 307, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New A, 6, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. V., McGaugh, S. S., & Swaters, R. A. 2009, AJ, 138, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, K. R., Bullock, J. S., Wechsler, R. H., & Maller, A. H. 2009, ApJ, 702, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1977, Evolution of Galaxies and Stellar Populations, 401 [Google Scholar]
- Toomre, A., & Toomre, J. 1972, ApJ, 178, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Toth, G., & Ostriker, J. P. 1992, ApJ, 389, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Shang, Z., Su, H., et al. 1999, AJ, 117, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., White, S. D. M., & Brinkmann, J. 2004, MNRAS, 347, 556 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 2007, A&A, 466, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Kruit, P. C., & Searle, L. 1982, A&A, 110, 61 [NASA ADS] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2010, Nature, 468, 940 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Implementation of cooling, feedback and star formation in GADGET-2
To account for cooling, star formation, and feedback processes of the ISM, we modified the publicly available version of the GADGET-2 code by adding these additional processes. We followed the method of Cox et al. (2006) and Springel (2000) to implement these physical processes. We give a brief description below and details are described in Cox et al. (2006).
Radiative cooling is important for gas to cool down to the central region of the dark halo and then form stars. The cooling rate is calculated following Katz et al. (1996), in which the primordial plasma of H and He and collisional ionisation equilibrium are assumed. Gas particles in these dense regions can form stars. The star formation rate is correlated to local gas density and anti-correlated to the local dynamic time: 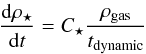 (A.1)where
(A.1)where 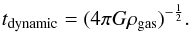 (A.2)The method of determining star formation rate relies on the Kennicutt-Schmidt law (Kennicutt 1998) according to which
(A.2)The method of determining star formation rate relies on the Kennicutt-Schmidt law (Kennicutt 1998) according to which 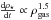 . Gas particles are converted into collisionless particles according to the above equation, using a stochastic technique.
. Gas particles are converted into collisionless particles according to the above equation, using a stochastic technique.
To regulate star formation, feedback is needed to prevent gas from being consumed by star formation. It assumes that the energy released by a supernova is first stored in a new reservoir of internal energy. The energy from this new reservoir will provide additional pressure to support the gas and prevent it from further collapsing to form stars. The feedback energy q can also be thermalised. Cox et al. (2006) introduced two free parameters to control this thermalisation process. One gives the time scale τfeedback of thermalisation process, the other controls the equation of state.
We verified that our implementation of additional routines that track the radiative cooling of gas and star formation.in the GADGET-2 code precisely follows that of Cox et al. (2006). We have indeed reproduced all the Cox et al. figures for all their adopted values of feedback (low, medium, and high) and for the density dependence of the feedback energy thermalisation timescale (n = 0, 1 and 2).
We also tested the stability of our model galaxies by running them in isolation as previously done by Cox et al. (2006). This is shown in Fig. A.1, which shows how the star and gas surface mass density have evolved after 3 Gyr. The gas and star components for both primary and secondary galaxies are stable during isolated evolution. This stability is also reflected by the evolution of the star formation rate as shown in Fig. A.2. During the 3 Gyr evolution, the star formation keeps a roughly constant value. The star formation rate of the secondary is about 0.18 M⊙ yr-1 and it is ~ 1.1 M⊙ yr-1 for the primary galaxy. It slowly decreases because the star formation affects the gas surface density. The star formation rate curve is not smooth because of the high feedback value (five times the median feedback of Cox et al. 2006) that is adopted to regulate the star formation. This test shows that the current feedback model can lead to a stable disc and preserve the gas before fusion, which is needed to form a disc after a merger.
 |
Fig. A.1 Projected mass density of the primary (left) and secondary (right) galaxies for model with mass ratio 3 (model M3L34) for which the galaxies are simulated in isolation for ~3 Gyr. The top row shows the stars and the bottom row show the gas distribution. A colour bar indicates the surface mass density scale shown in the top-left panel. The size of each panel is 160 by 160 kpc. |
 |
Fig. A.2 Star formation rates for isolated galaxy models of the primary (top curve) and the secondary (bottom curve) for a mass ratio 3 (model M3L34). Five times the median feedback of Cox et al. (2006) is used in these models. |
Appendix B: Properties of loops formed by particles coming back from tidal tails
Hammer et al. (2010) modelled the M31 galaxy with a 3:1, major merger event, which also reproduced the Giant Stream and, for some models, also the northwest big loop discovered by the PANDA team (Richardson et al. 2011). In these models, particles returning to the galaxy from the tidal tail can feed the loops for several Gyrs ( > 5 Gyr, see their Fig. 8). Here we explore the properties of such loops, and trace the motion of tidal tail particles. In this section, we take an overview of the loop properties as they result from our numerical computations.
 |
Fig. B.1 Loops formed by the particles falling back from second tidal tail. Each panel is centred on the centre of mass of the secondary galaxy, indicated by a cross. In this figure, the tidal tail is formed from a 3:1 merger (model M3L34, see Sect. 5). The size of each panel is 300 by 300 kpc. The stellar mass surface density of the loops at 8.6 Gyr is consistent with the estimation of Martínez-Delgado et al. (2008) for NGC 5907. The top row shows the loop formation process as seen from the observed viewing angle, while the bottom row gives a face-on view of the loops at the same times. The red arrows in the second column indicate the first loop, the pink arrows in the third column show the second loop, the blue and green arrows in the fourth column show the third and fourth loops, and the black arrow in the last column shows the fifth loop. In the bottom-left panel, solid and dotted circles indicate the radii of the original location of the particles which constitute the tidal tails at 5.6 Gyr and 8.6 Gyr, respectively. Particles with small elevations are selected from the region between the green and the black circles, and those with high elevation, from beyond the black circle. |
Particles stripped into a tidal tail are of two kinds: part of them have enough energy to escape the galaxy potential, while others reach a maximum distance and then fall back to the galaxy. We are mostly concerned by the orbital pattern shape of particles coming back from the tidal tail, because they can generate many faint features after the fusion. These features are very likely observable, because the process can be maintained for several Gyrs (see e.g. Hammer et al. 2010). These time estimates are considerably larger than those obtained for encounters of two ellipticals and in much better agreement with encounters of an elliptical and a spiral (Feldmann et al. 2008). This argues for the necessity of a cold component in order to produce strong and long-lived tidal features.
A tidal tail formed in a major merger is more complex than one formed in a minor merger. As shown by Choi et al. (2007), a massive satellite can change the morphology and radial velocity of a tidal tail by self-gravity. Meanwhile, the satellite will also feel the gravitational attraction from the tidal tail, affecting its energy and angular momentum. The resonance may affect the tail properties (D’Onghia et al. 2010). All these effects make tidal tail formation in major mergers more complex than in minor mergers and thus more difficult to reproduce. Important properties of the orbital pattern of tidal tails include the eccentricity of loops, which are approximated by ellipses, the width of the loops, and the precession rate of the particle orbits.
In the following we describe the interaction between the most massive (the primary) and the less massive (the secondary) galaxy in a major merger. To match the NGC 5907 loops better, we need to form two tidal tails. In the classic case of an encounter between two prograde discs, we witness the formation of two tidal tails, one from each galaxy. On the other hand, in our model one galaxy rotates prograde and the other retrograde so that both tails form from material stripped from the prograde companion, which in our model is the less massive one. The two tails form at different times, namely the times of the first and the second closest passages. The motion of all the particles that constitute the tidal tail is set before the interaction by the orbit of the secondary and its disc spin. After being stripped from the secondary by the gravitational interaction, these particles keep some orbital information from their initial orbits, i.e. from their progenitors. When the secondary is close to pericentre where the tidal perturbation is maximum, the tidal force will add energy to the particles of the secondary (Springel & White 1999), which makes its particles unbound and ejected (D’Onghia et al. 2010). Along the tidal tail, particle binding energy increases with radius (see Hibbard & Mihos 1995; Dubinski et al. 1996), i.e., particles ejected further from the centre have higher energy, leading to an increasing fallback time.
The motion of particles falling back from the tidal tail can be easily understood since the dynamical friction force can be neglected due to their low mass. If we also neglect the time evolution of the central potential, the motion is simply that of test particles in a static central potential, which is a rosette (Binney & Tremaine 1987, hereafter BT87). The angle between two consecutive apocentra depends on the potential, being 0 degrees in a Kepler potential and 180 degrees in a harmonic potential. Thus the orbit can be approximated by a precessing ellipse, while the precession angle can give information on the potential of the merger remnant.
 |
Fig. B.2 First and second loops for the same model as in Fig. B.1 are fitted by ellipses for simulation with mass ratio 3. The left panel is at 5.6 Gyr and the right panel shows loops at 8.6 Gyr. Particles belonging to different loops are naturally selected by their distance to the centre in the tail-forming epoch (3.5 Gyr). Green indicates particles with small elevations (see Fig. B.1, bottom-left panel), and black points indicate large elevation particles. Green points populate the second loop, while black points show particles of the first loop. Particles coming back from the tidal tail begin to outline the first loop and then enter in the second loop. The parameters of the fitted ellipses are given in the top left corner of each panel. They are the semi-major axis a, semi-minor axis b, focus distance, eccentricity, and position angle. |
 |
Fig. B.3 The left panel gives the distribution of loop phase angle differences between first and second loops. The right panel compares the loop and orbit eccentricities. Solid black line is the one-to-one relation. This statistics is coming from various models with different mass ratio (3, 4, and 5), orbital geometry and dark matter fraction. |
Figure B.1 shows an example of the particle locations at different epochs. The tidal tail particles have been tagged at 3.5 Gyr after the beginning of the simulation, i.e. after the fusion of the two galaxies (see Sect. 5), so that we can follow their individual motions. These particles continue to feed the loops as they return from the tidal tail. At 4.2 Gyr the first loop is already formed, and then at 5.6 Gyr a second loop is added. As time increases further, the third and fourth loops are formed, as shown by the 8.6 Gyr panel of Fig. B.1.
Particles are continuously feeding the loops following a similar track from the tidal tail. They first enter into the first loop and then continue by orbiting in higher order loops. Because particles falling back later have higher energies (or elevations relatively to the mass centre), the size of the first loop increases with time, as well as that of other loops after their formation (see Fig. B.1). We also fitted the first and second loops with ellipses at 5.6 Gyr and 8.6 Gyr as shown in Fig. B.2. Owing to the permanent motion of particles, it is not always simple to separate particles from different loops. We used the distance of particles from the centre at the tail-forming time (3.5 Gyr panel of Fig. B.1) to isolate particles for each loop. In Fig. B.2 different colours indicate different distances to the centre. The green particles are initially, at the time of forming the tail, closer to the centre and now form the second loop, while the black particles that are farther from the centre form the first loop. This shows that the particles forming the different loops come from different distances to the centre at the time the tidal tail is formed. In this simulation we notice that the first two loops formed by particles returning after reaching their apocentra are approximated well by two ellipses with a phase angle ~80 degree difference due to precession, as shown in the left hand panel of Fig. B.3.
The loop width depends on the orbital properties of the tidal tail. It has been shown that resonance is important for forming a long tidal tail for a spin system. Strong resonance occurs when rotation and orbital frequencies obey Ωdisc = Ωorbit (Toomre & Toomre 1972; Barnes & Hernquist 1992). As long as we can control the tidal tail length and width, we may control the shapes of the loops at some level. For various merger geometries, we can decrease the loop eccentricities by decreasing the orbital eccentricity of the secondary, because they are related. This is illustrated in the right hand panel of Fig. B.3, where we compare the loop eccentricity with the orbital eccentricity of the second-order loop. Loops used in this figure are coming from models with different mass ratio, pericentre, eccentricity, baryonic fraction (from 6% to 9%), and gas fraction. The arrow indicates the region for which orbital eccentricities provide loop eccentricities consistent with the observations.
All Tables
Comparing the number of constraints and parameters between minor and major mergers.
Comparing major and minor merger hypotheses, where “Y” means consistency with the observations.
All Figures
 |
Fig. 1 Star and gas particles distributions for a merger with mass ration 3 (model M3L34A) at different epochs. Star particles are shown in the top two rows. The fit to best observations is at 8.6 Gyr, at which the structures of third and fourth loops can match the observations. The gas surface density is shown in the bottom two panels with gas density indicated by the colour bar. The size of each panel is 300 by 300 kpc and the arrows are explained in the text. |
| In the text | |
 |
Fig. 2 Inclination angle between disc, loop, and orbital planes as a function of time. The lower solid lines show the angle between the loop and the orbital planes. Lines within shaded regions indicate the inclination angles of the disc plane relative to the orbital plane, while the line-shaded region around 90 degrees indicates the angles between disc and loop planes that are consistent with the observations. Different colour lines show the simulations with different initial disc inclinations to the orbital plane. All the models used here have a mass ratio of 3 (from bottom to top, models M3L12, M3L23, M3L34B). |
| In the text | |
 |
Fig. 3 Stellar mass surface density shown with different scales of stellar mass surface brightness at 8.6 Gyr for the model M3L34. Each panel size is 300 by 300 kpc. |
| In the text | |
 |
Fig. 4 Comparing loop structures formed by combining loops of different order for mass ratios of 3. The left panel shows the first and second loops (model M3L23), the second panel shows the third and fourth loops (model M3L34), while the first loop appears at the bottom of the galaxy and becomes diluted. The size of each panel is 300 by 300 kpc. The loop stellar surface mass densities are consistent with observations from M08. In all these images the threshold has been chosen slightly below the observed one from M08. |
| In the text | |
 |
Fig. 5 The top panel gives the distribution of z component of the angular momentum of stellar particles for model M3L34. The galaxy has been projected edge-on using the angular momentum of the baryons. From left to right, star of different age (from young, intermediate, and old) are shown. Old stars (red dots) already exist in the progenitors at the beginning of the simulation. Young stars (blue dots) are defined with ages over 3 Gyr after the beginning of the simulation. Ages between young and old are defined as intermediate stars (green dots), which are formed before the fusion. The bottom panel shows the projected mass distribution of the thin disc (left), and the bulge and thick disc (right). The thin disc is selected from its angular momentum ratio (MAz/MA ≥ 0.9, see Hammer et al. 2010), which cuts the warp off. Each panel has a size of 300 by 300 kpc. |
| In the text | |
 |
Fig. 6 Stellar surface mass density distribution as a function of radius for model M3L34. Open circles show the total stellar density together with a fit by different components (solid line). Sersic bulge and exponential disc components (indicated by different colours) are used to fit the stellar mass surface brightness. The fitting process excludes an area with a radius equal to 2 times the softening length (labelled by arrows, see the text). |
| In the text | |
 |
Fig. 7 Comparison of observed and simulated (model M3L34A) rotation curves. The blue points are from Sancisi & van Albada (1987) and are based on HI observations. Black solid points are from Hα and NII observations by Miller & Rubin (1995), including near the central regions. Solid line shows the prediction from the mass model |
| In the text | |
 |
Fig. 8 Top: deep observations of NGC 5907 in the visible light showing the thin disc with the gigantic loops (from M08). Bottom: observations of NGC 5907 with IRAC at 3.6 μm revealing the whole extent of the disc that is twice thicker than in the visible light. |
| In the text | |
 |
Fig. 9 Left: deep observations of NGC 5907 in the visible light showing the thin disc with the gigantic loops (from M08). Middle: one simulation of the loops at T = 8.0 Gyr with the M3L34G6 model, in which we assume a dust extinction screen affecting the stellar light density by a factor of 2.5 on both sides of the edge-on disc (see discussion in Sect. 6.1). Right: same model as middle panel shows all components with accounting for an extinction by a factor 12. The real extinction should be between the middle and right panel. |
| In the text | |
 |
Fig. 10 Comparing iron abundances of outskirts of NGC 5907 with that of other galaxies from Hammer et al. (2007). The iron abundances of the NGC 5907 inner halo are from Zheng et al. (1999), who estimate them by comparing the loops colour with that of Galactic globular clusters. |
| In the text | |
 |
Fig. A.1 Projected mass density of the primary (left) and secondary (right) galaxies for model with mass ratio 3 (model M3L34) for which the galaxies are simulated in isolation for ~3 Gyr. The top row shows the stars and the bottom row show the gas distribution. A colour bar indicates the surface mass density scale shown in the top-left panel. The size of each panel is 160 by 160 kpc. |
| In the text | |
 |
Fig. A.2 Star formation rates for isolated galaxy models of the primary (top curve) and the secondary (bottom curve) for a mass ratio 3 (model M3L34). Five times the median feedback of Cox et al. (2006) is used in these models. |
| In the text | |
 |
Fig. B.1 Loops formed by the particles falling back from second tidal tail. Each panel is centred on the centre of mass of the secondary galaxy, indicated by a cross. In this figure, the tidal tail is formed from a 3:1 merger (model M3L34, see Sect. 5). The size of each panel is 300 by 300 kpc. The stellar mass surface density of the loops at 8.6 Gyr is consistent with the estimation of Martínez-Delgado et al. (2008) for NGC 5907. The top row shows the loop formation process as seen from the observed viewing angle, while the bottom row gives a face-on view of the loops at the same times. The red arrows in the second column indicate the first loop, the pink arrows in the third column show the second loop, the blue and green arrows in the fourth column show the third and fourth loops, and the black arrow in the last column shows the fifth loop. In the bottom-left panel, solid and dotted circles indicate the radii of the original location of the particles which constitute the tidal tails at 5.6 Gyr and 8.6 Gyr, respectively. Particles with small elevations are selected from the region between the green and the black circles, and those with high elevation, from beyond the black circle. |
| In the text | |
 |
Fig. B.2 First and second loops for the same model as in Fig. B.1 are fitted by ellipses for simulation with mass ratio 3. The left panel is at 5.6 Gyr and the right panel shows loops at 8.6 Gyr. Particles belonging to different loops are naturally selected by their distance to the centre in the tail-forming epoch (3.5 Gyr). Green indicates particles with small elevations (see Fig. B.1, bottom-left panel), and black points indicate large elevation particles. Green points populate the second loop, while black points show particles of the first loop. Particles coming back from the tidal tail begin to outline the first loop and then enter in the second loop. The parameters of the fitted ellipses are given in the top left corner of each panel. They are the semi-major axis a, semi-minor axis b, focus distance, eccentricity, and position angle. |
| In the text | |
 |
Fig. B.3 The left panel gives the distribution of loop phase angle differences between first and second loops. The right panel compares the loop and orbit eccentricities. Solid black line is the one-to-one relation. This statistics is coming from various models with different mass ratio (3, 4, and 5), orbital geometry and dark matter fraction. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.