| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117312 | |
| Published online | 03 February 2012 | |
Evolution of the observed Lyα luminosity function from z = 6.5 to z = 7.7: evidence for the epoch of reionization?⋆
1
Laboratoire d’Astrophysique de Marseille, CNRS UMR 7326, Université
d’Aix-Marseille, 38 rue Frédéric
Joliot-Curie, 13388
Marseille Cedex 13,
France
2
Steward Observatory, University of Arizona,
933 N. Cherry Ave, Tucson, AZ
85721,
USA
3
Laboratoire d’astrophysique, École Polytechnique Fédérale de
Lausanne (EPFL), Observatoire de Sauverny, 1290
Versoix,
Switzerland
4
INAF Osservatorio Astronomico di Roma,
via Frascati 33, 00040
Monteporzio ( RM), Italy
5
European Southern Observatory, Karl-Schwarzschild Strasse, 85748
Garching bei München,
Germany
6
Dark Cosmology Centre, Niels Bohr Institute, Copenhagen
University, Juliane Maries Vej
30, 2100
Copenhagen Ø,
Denmark
7
Departamento de Astrofísica, Facultad de CC, Físicas, Universidad
Complutense de Madrid, 28040
Madrid,
Spain
8
School of Earth and Space Exploration, Arizona State University,
Tempe, AZ
85287,
USA
9
Australian Astronomical Observatory, Epping, NSW
1710,
Australia
10
Institute of Astronomy, Madingley Road, Cambridge
CB3 0HA,
UK
11
Department of Physics and Astronomy, University of
Victoria, Elliot Building, 3800
Finnerty Road, Victoria, BC,
V8P 1A1,
Canada
Received:
21
May
2011
Accepted:
19
September
2011
Aims. Lyα emitters (LAEs) can be detected out to very high redshifts during the epoch of reionization. The evolution of the LAE luminosity function with redshift is a direct probe of the Lyα transmission of the intergalactic medium (IGM), and therefore of the IGM neutral-hydrogen fraction. Measuring the Lyα luminosity function (LF) of Lyα emitters at redshift z = 7.7 therefore allows us to constrain the ionizing state of the Universe at this redshift.
Methods. We observed three 7'.5 × 7'.5 fields with the HAWK-I instrument at the VLT with a narrow band filter centred at 1.06 μm and targeting Lyα emitters at redshift z ~ 7.7. The fields were chosen for the availability of multiwavelength data. One field is a galaxy cluster, the Bullet Cluster, which allowed us to use gravitational amplification to probe luminosities that are fainter than in the field. The two other fields are subareas of the GOODS Chandra Deep Field South and CFHTLS-D4 deep field. We selected z = 7.7 LAE candidates from a variety of colour criteria, in particular from the absence of detection in the optical bands.
Results. We do not find any LAE candidates at z = 7.7 in ~2.4 × 104 Mpc3 down to a narrow band AB magnitude of ~26, which allows us to infer robust constraints on the Lyα LAE luminosity function at this redshift.
Conclusions. The predicted mean number of objects at z = 6.5, derived from somewhat different luminosity functions of Hu et al. (2010, ApJ, 725, 394), Ouchi et al. (2010, ApJ, 723, 869), and Kashikawa et al. (2011, ApJ, 734, 119) are 2.5, 13.7, and 11.6, respectively. Depending on which of these luminosity functions we refer to, we exclude a scenario with no evolution from z = 6.5 to z = 7.7 at 85% confidence without requiring a strong change in the IGM Lyα transmission, or at 99% confidence with a significant quenching of the IGM Lyα transmission, possibly from a strong increase in the high neutral-hydrogen fraction between these two redshifts.
Key words: methods: observational / early Universe / galaxies: high-redshift / techniques: image processing / galaxies: luminosity function, mass function / dark ages, reionization, first stars
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere (ESO), Chile, Prog-Id 181.A-0485, 181.A-0717, 60.A-9284, 084.A-0749. Based on observations obtained at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique of France (CNRS), and the University of Hawaii. This work is based in part on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA and in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. This paper includes data gathered with the 6.5 m Magellan Telescopes located at Las Campanas Observatory, Chile.
© ESO, 2012
1. Introduction
Observing high-z galaxies within the first billion years of the Universe is one of the main frontiers in extragalactic astronomy. Since the discovery, less than a decade ago, of the first astrophysical object at a redshift above 6, a Lyα emitter at redshift 6.56 (Hu et al. 2002), spectacular progress has been made in assembling large samples of high-redshift objects. The two main techniques for finding high-redshift galaxies is to look either for strong absorption breaks in the Lyα forest in broad band photometry (Lyman break galaxies – LBGs) or for a photometric excess in narrow band (NB) filters due to the Lyα line (Lyα emitters – LAEs). In the latter case, the NB filters are usually selected to coincide with regions of low OH emission of the night sky, leading to discrete redshift values. SuprimeCam on the Subaru Telescope has revolutionized the field by enabling large samples of LAEs to be furnished at z = 5.7 and z = 6.5 (Ouchi et al. 2010; Hu et al. 2010, and references therein). The largest samples of LBGs have been recently assembled (Bouwens et al. 2011) from HST observations after the successful installation of the Wide Field Camera3 (WFC3) in May 2009, but LBGs can also be found from the ground with 8–10 m telescopes equipped with efficient near infrared (NIR) cameras (Castellano et al. 2010). Quasars at high-redshift are also found using the Lyman break technique in multi-colour datasets over very wide fields. Most of the quasars at z > 6 have been discovered in the Sloan Digital Sky Survey (Fan et al. 2006) and from a targeted programme at CFHT (Willott et al. 2010). Finally, a few gamma ray bursts (GRBs) have been discovered at very high redshift (see e.g. Tanvir et al. 2009, for an example of a GRB at redshift 8.2), nicely complementing the other methods by probing the faint end of the luminosity function.
Combined with observations of the cosmic microwave background (CMB), the recent discovery of large samples of objects at high redshift allows astronomers to build a comprehensive picture of the Universe during the reionization epoch when it was 500 Myr to 1 Gyr old. Polarization measurements of the CMB from WMAP (Larson et al. 2011) show a large optical depth due to Thompson scattering of electrons in the early Universe, suggesting that the reionization started at z ~ 10.5 ± 1.2. Conversely, the strong increase of the optical depth in the Lyα forest of high-redshift quasars (Becker et al. 2001; Fan et al. 2006) above ~8500 Å is a likely indicator that reionization was mostly complete at a redshift of about 6. How and at what pace the reionization process has taken place in the [6–10] redshift range is more difficult to establish from observations, and is still a matter of debate. A compilation of the most recent results and constraints on the neutral-hydrogen fraction of the Universe between redshifts 5 and 11 from various probes is shown in Fig. 23 of Ouchi et al. (2010).
It has been proposed for a long time to use the Lyα transmission by the intergalactic medium (IGM) as a probe of its ionization state during the reionization epoch (see e.g. Santos 2004), hence the strong emphasis recently put on Lyα emission of LBGs and LAEs as more and more of these objects become available. Follow-up observations of high-z LBGs at z > 6 is now underway to detect the Lyα line in emission in spectroscopy. Stark et al. (2011) measure an increasing fraction of LBGs with strong Lyα emission from z ~ 3 to z ~ 6, and conjecture that Lyα emission should remain strong at higher redshifts unless the neutral-hydrogen fraction of the IGM suddently increases. Conversely, Fontana et al. (2010) report a low fraction of Lyα emitters in a sample of z > 6.5 LBGs. These are preliminary results based on still modest spectroscopic samples, and it is expected that ongoing and new observations will clarify the situation in a near future.
Another observational method of probing the Lyα IGM transmission is to study the evolution of the LAE luminosity function (LF) with redshift. Ouchi et al. (2010) and Kashikawa et al. (2006, 2011) infer from their observations that the evolution of the Lyα LAE LF between z = 5.7 and z = 6.5 can be attributed to a reduction of the IGM Lyα transmission of the order of 20%, which can in turn be attributed to a neutral-hydrogen fraction xHI of the order of 20% at z = 6.5 (see e.g. Ouchi et al. 2010). Various models are elaborated to reproduce this claim, which has generated considerable interest (see e.g. Kobayashi et al. 2010; Dayal et al. 2011; Laursen et al. 2011; Dijkstra & Wyithe 2010). However, the universality of the z = 6.5 LF from Kashikawa et al. (2006) and Ouchi et al. (2010) has recently been questioned. Hu et al. (2010) report significantly different LF parameters from the observations and analysis of a spectroscopically confirmed sample of NB selected LAEs. Similarly, Nakamura et al. (2011) report significantly lower number counts that they tentatively attribute to cosmic variance. Differences in the selection criteria and in extrapolations of the spectroscopic samples to photometric samples might partly explain the discrepancies between the various Lyα LAE LFs available in the literature: Kashikawa et al. (2011) have carried out extended spectroscopic confirmation of their earlier photometric sample, resulting in luminosity functions closer to the ones of Hu et al. (2010). Cassata et al. (2011) report the results from a pure spectroscopic sample of (mostly) serendipitous Lyα emitters found in deep spectroscopic samples with VIMOS at the VLT ; this sample is consistent with a constant LAE luminosity function from z ~ 2 to z ~ 6.6 as reported in the literature before the recent results from Hu et al. (2010).
 |
Fig. 1 Images of the CFHTLS-D4 (left), GOODS-South (centre), and Bullet Cluster (right) fields as in the final NB1060 image stacks. The inner and outer black contours on the Bullet Cluster image represent the regions where the gravitational amplification is respectively ≥ 2.5 (Δm ≤ −1) and ≥ 1.2 (Δm ≤ −0.2) for a source at redshift z = 7.7. |
The current situation at z ≳ 6 is therefore unclear, with somewhat contradictory observational results. This hampers the validation of the reionization models and of our understanding of this key epoch of the Universe. The discrepancy limits how well we can understand reionisation during this key epoch of the Universe. New data at z ~ 6 will help in resolving the current contention between observational results, while data at higher redshifts can bring new constraints at still poorly explored redshifts. In view of the strong interest in studying Lyα emission at high redshifts, searching LAEs at z > 7 is underway from various groups (Hibon et al. 2010; Tilvi et al. 2010; Nilsson et al. 2007). Finding z ~ 7 objects is not only interesting for probing the reionization epoch, but also for assessing the physical properties of these objects, which in turn allow constraining how and when they formed. Due to the extreme faintness of these very high-redshift objects, deriving their properties can only be done statistically over large samples (Bouwens et al. 2011) or on individual objects that are gravitationally amplified. For instance, Richard et al. (2011) infer a redshift of formation of 18 ± 4 for a gravitationally amplified object at z = 6.027.
This paper presents new results on the Lyα LAE LF at z = 7.7, from observations carried out at the VLT with the HAWK-I instrument. This paper is organized as follows. In Sect. 2 we describe the observations and the data reduction in Sect. 3. In Sect. 4 we describe our selection procedure of the z = 7.7 LAE candidates. In Sect. 5 we present the constraints that we infer from our results on the z = 7.7 Lyα LAE LF, before discussing our results in Sect. 6.
We use AB magnitudes throughout this paper. We assume a flat ΛCDM model with ΩM = 0.30 and H0 = 70 km s-1 Mpc-1.
2. Observations
This work is primarily based on extremely deep NIR imaging data obtained with HAWK-I at the
VLT, using an NB filter at 1.06 μm (hereafter referred to as
NB1060). Thanks to its wide field of view
(7 5 ×
7
5 ×
7 5), excellent
throughput and image quality, HAWK-I is ideally suited to searching for faint NIR objects
such as very high-redshift galaxies. The main data set was obtained through a dedicated ESO
large programme between September 2008 and April 2010. In addition, we include in our
analysis HAWK-I science verification NB data taken in 2007. We also make use of various
optical and NIR broad band data, publicly available and/or from our own large programme.
5), excellent
throughput and image quality, HAWK-I is ideally suited to searching for faint NIR objects
such as very high-redshift galaxies. The main data set was obtained through a dedicated ESO
large programme between September 2008 and April 2010. In addition, we include in our
analysis HAWK-I science verification NB data taken in 2007. We also make use of various
optical and NIR broad band data, publicly available and/or from our own large programme.
2.1. Fields
In preparing the proposal, we carefully balanced the relative merits of blank fields and cluster fields. While gravitational amplification of background sources by foreground massive galaxy clusters allows us to probe luminosities that are intrinsically fainter than in the field, this is at the expense of areal coverage due to space distortion. The relative merits of blank and cluster fields depend on the shape of the luminosity function (LF) of the objects that are being searched, and on the properties of the observations such as field of view, integation time and overheads (Maizy et al. 2010; Richard et al. 2008). From the Lyα LAE LF at z = 6.5 that was available at the time of proposal preparation, we computed that either type of fields should yield approximately the same number of targets, while probing different (unlensed) luminosity ranges. We also analysed the balance between wide-shallow and narrow-deep survey strategies. For a total time of about 100 h (in the NB filter only), it was deemed that observing four fields in total would be optimal in terms of high-z LAE yield, while mitigating the effects of cosmic variance. Operational constraints, such as the distribution of the fields in right ascension, were additionally taken into account when selecting the fields. Our selected fields were Abell 1689 (13h11m30s, –01°20′35′′, J2000) and 1E0657-56 (Bullet Cluster) (06h58m29s, –55°57′16′′, J2000) for the cluster fields, the northern half of the GOODS-S field (03h32m29s, –27°44′42′′, J2000) and a subarea of the one square degree CFHTLS-D4 field (22h16m38s, –17°35′41′′, J2000) for the two blank fields.
For Abell 1689, although an extensively studied field, it proved hard to assemble a
consistent multiwavelength dataset covering the full
7 5 ×
7
5 ×
7 5 HAWK-I field
of view. This field is therefore not included in the present analysis and it will be
analysed separetely. The Bullet Cluster is a massive merging cluster that allowed the
first direct empirical proof of the existence of dark matter by the combination of strong
and weak-lensing analyses (Clowe et al. 2006; Bradač et al. 2006). Both clusters have well-constrained
mass models and provide a lens magnification of at least a factor of 1.2 over 50% of the
HAWK-I field of view (see Fig. 1). The GOODS-S and
CFHTLS-D4 field were chosen for the wealth of multiwavelength data, in particular deep
optical data, publicly available. For the CFHTLS-D4 field, we chose the location of the
HAWK-I observations where NIR data were available1
(Bielby et al., in prep.), and paying attention to avoiding the brightest stars present in
this field. Figure 1 shows the finding charts
corresponding to our observations inside the CFHTLS-D4, GOODS-S and Bullet Cluster fields.
5 HAWK-I field
of view. This field is therefore not included in the present analysis and it will be
analysed separetely. The Bullet Cluster is a massive merging cluster that allowed the
first direct empirical proof of the existence of dark matter by the combination of strong
and weak-lensing analyses (Clowe et al. 2006; Bradač et al. 2006). Both clusters have well-constrained
mass models and provide a lens magnification of at least a factor of 1.2 over 50% of the
HAWK-I field of view (see Fig. 1). The GOODS-S and
CFHTLS-D4 field were chosen for the wealth of multiwavelength data, in particular deep
optical data, publicly available. For the CFHTLS-D4 field, we chose the location of the
HAWK-I observations where NIR data were available1
(Bielby et al., in prep.), and paying attention to avoiding the brightest stars present in
this field. Figure 1 shows the finding charts
corresponding to our observations inside the CFHTLS-D4, GOODS-S and Bullet Cluster fields.
Table 1 summarizes the various observations made as part of our large programme on each of the three fields considered in the present analysis. Figure 2 shows the overall transmission curves of the HAWK-I broad band and NB filters corresponding to these observations. Table 2 summarizes the main ancillary broad band data used in this work. Our large programme data consists of more than 110 h of on-sky integration time, of which ~80 h are NB1060 data.
HAWK-I narrow band and broad band observations from our large programme
Ancillary public and private data used in this paper.
2.2. The HAWK-I NB1060 data
HAWK-I is a 7 5 ×
7
5 ×
7 5 NIR (0.97–2.31
μm) imager installed on the ESO VLT UT4. It is equipped with four 2048
× 2048 pixels Hawaii-2RG detectors, separated by 15′′ wide gaps. The pixel
scale is 0
5 NIR (0.97–2.31
μm) imager installed on the ESO VLT UT4. It is equipped with four 2048
× 2048 pixels Hawaii-2RG detectors, separated by 15′′ wide gaps. The pixel
scale is 0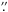 1065. The
NB1060 filter has a central wavelength of 1062 nm, a full width at half
maximum (FWHM) of Δλ ~ 100 Å, and is designed to match a
region of low OH emission from the night sky. The filter width samples
Lyα emission in the redshift range z = [7.70–7.78]. A
detector integration time of 300 s is used for all the NB1060 images,
ensuring background limited performance. Random telescope offsets within a box of
20′′ for the blank fields and 25′′ for the cluster fields is used
for dithering. For each field, the NB1060 data are acquired over two
epochs separated by one year, allowing us to discard transient objects that could be
detected in a one-epoch stack, and not in the other.
1065. The
NB1060 filter has a central wavelength of 1062 nm, a full width at half
maximum (FWHM) of Δλ ~ 100 Å, and is designed to match a
region of low OH emission from the night sky. The filter width samples
Lyα emission in the redshift range z = [7.70–7.78]. A
detector integration time of 300 s is used for all the NB1060 images,
ensuring background limited performance. Random telescope offsets within a box of
20′′ for the blank fields and 25′′ for the cluster fields is used
for dithering. For each field, the NB1060 data are acquired over two
epochs separated by one year, allowing us to discard transient objects that could be
detected in a one-epoch stack, and not in the other.
The instrument had a thermal leak at the beginning of the first semester, which approximately doubled the total background in the NB1060 filter. After a technical intervention on the instrument after a few months of operations, the background returned to its nominal value, and only the observations of the CFHTLS-D4 field were affected. We were granted compensatory time that allowed us to recover the expected limiting magnitude but at the expense of unbalanced limiting magnitudes (by ~0.5 mag) for the first and second epoch observations. For the two other fields the limiting magnitudes between the two epoch observations are within ~0.15 mag.
In total, after image selection discarding images with poor image quality or too high background, the final stacks used in this analysis total integration times in the NB1060 filter of 26.7 h for the CFHTLS-D4 field, 31.9 h for GOODS-S (including science verification data) and 24.8 h for the Bullet Cluster (see Table 1).
 |
Fig. 2 Transmission curves of the HAWK-I broad band and narrow band filters corresponding to the observations made as part of our large programme. The inset shows the profile of the NB1060 filter. |
2.3. Other imaging data
In addition to the NB1060 data, we performed dedicated broad band HAWK-I observations within our large programme to complement, on a case-by-case basis, the broad band data that were available elsewhere (see Table 1).
For the CFHTLS-D4 field, we had access to the very deep CFHTLS optical data and to the moderately deep NIR WIRDS data, but not as deep as our NB1060 data. We therefore took additional J and Ks data to improve the detection limit in these bands. For the Bullet Cluster, in the absence of well-established datasets in the optical and NIR bands, particularly over the full HAWK-I field of view, we devoted a significant fraction of the time on this field to get additional data in the Y, J, and Ks bands. We note that the HAWK-I Y filter bandpass includes, at its very red edge, the NB1060 filter bandpass. For this field we therefore secured a coherent and self-consistent dataset. We also used IMACS BVR images of the field obtained at the Magellan telescope (Clowe et al. 2006). For the GOODS-S field, we devoted a few hours of observations in the J band filter to reach a limiting magnitude fainter than that achieved with the public ISAAC images. We also used a very deep Y-band image of this field from a separate HAWK-I large programme (181.A-0717) led by one of us.
3. Data reduction
All reduced image stacks and ancillary data products (e.g. weight maps, etc.) from our large programme are currently available upon request and will be made public through the ESO archive, as part of the Phase 3 process2. We detail in this section the data reduction procedures that have been used to generate these high-level data products.
3.1. Overview
We use a mix of IRAF3 and AstrOmatic4 routines for the data reduction, allowing us to control the reduction process step by step. All single quadrant frames from the HAWK-I mosaic array are reduced similarly and independently until the very final steps. After a first pass at the sky subtraction, all images are characterized in terms of PSF and photometric quality, allowing us to identify and remove low-quality images that would degrade the final products. Depending on the field, between 3% and 13% of the NB1060 images are discarded, mostly when the image quality is worse than 1′′. This is the case for a fair fraction of the GOODS-S science verification images, for some of our large programme images that have been executed but not validated by the service observers, and, more rarely, for some fully validated images. A multi-pass sky subtraction is then performed, improving the quality of the masking of the objects at each pass. Images are then scaled to account for photometric variations and registered to a common reference frame. The final stacks are produced by averaging all images with a rejection algorithm using kappa-sigma clipping. The NB1060 photometric calibration is performed on unsaturated bright stars by interpolating their optical and 2MASS photometric data, following the approach described in Hibon et al. (2010). Finally, the final four stacks for each quadrant are aligned onto a common astrometric reference.
3.2. Data processing
-
1.
Pre-processing. Dark frames and twilight sky flats arecombined into master calibration frames on a nightly basis. Thereare typically eight dark frames and about 30 twilight sky flatfieldframes per night. No attempt is made to correct for the detector’snon-linearity, which, according to the HAWK-I users manual, isbelow the 1% level at 75% of the detector saturation level. Thiscould affect the accuracy of the photometric calibrationperformed on bright stars, and this is accounted for in thefollowing.
-
2.
Background subtraction. The most delicate step in the reduction of NIR data is the sky subtraction. With dithered images, the classical way of estimating the sky at any particular pixel is by building a running sky frame for each science frame. This running sky frame is usually computed as the median of Nsky frames around the central science frame to which it is subtracted. Some care is required, however, for this step to be optimally performed. First, the sky background varies, even in the NB1060 filter where the sky consists of a mixture of faint OH lines, sky continuum, and possibly faint thermal background leaking through the wings of the filter at wavelengths close to the detector cutoff. In addition, the background patterns have structures at low spatial frequencies that are changing with time, with the strongest changes occurring when the telescope crosses meridian. This is attributed to the rotation of the telescope pupil with time, with maximum velocity when passing the meridian. Therefore, the images used to generate a sky frame are carefully selected so as to have similar sky background patterns and to be close in time (within fewer than 15 days). The images thus selected are further zeroed to their median levels and normalized to their pixel to pixel standard deviation (with rejection of outliers). For each pixel, the median of its values in each running list of Nsky frames is computed, with kappa-sigma clipping for rejecting outliers. In this step, objects are masked (meaning that the values of the pixels where objects are detected are not included in the median determination) to avoid biasing the estimation of the sky toward high values. The masking process is initiated on individual sky-subtracted frames (where only the brightest objects are detected) and then repeated several times on combined stacks as described in step # 4.
-
3.
Bad pixels removal. Once the initial sky subtraction is performed on each science frame, bad pixel maps are generated on a nightly basis. Here again, we use the fact that with dithered data an object moves across the detector while bad pixels do not. Individual pixel values exceeding ±4σ of the local standard deviation over more than 70% of the frames in a given night are flagged as bad pixels and replaced by a linear interpolation of the surrounding pixel values along image lines.
-
4.
Object masking for sky subtraction. After the initial sky subtraction step and bad-pixel removal, the images are registered using a first-order astrometric solution and median-stacked with rejection of outliers. A mask is then generated from all objects detected in this image, together with detector regions of poor cosmetics. This mask is then used to reprocess the sky frames as described in step #2, after which a new image stack is produced. Steps #2 to #4 are typically repeated three to five times until the background around the objects in the final stack is flat. This iterative procedure improves the quality of the sky subtraction, which otherwise results in overestimated sky levels noticeable as dark regions around the bright objects and in larger photometric errors. As in step #2, the final sky frames are subtracted to the central science frames after zeroing to their median values and scaling to their standard deviations. Faint low-frequency sky subtraction residuals may still remain at this stage, which are removed with a bi-cubic-spline interpolation of a meshed background frame generated by SExtractor4 (Bertin & Arnouts 1996).
-
5.
Correction of photometric variations. Frame-to-frame scaling factors are derived from the number counts measured on bright and unsaturated stars detected in each individual sky-subtracted frame. These scaling factors account for variations of the atmosphere transparency and/or of the airmass. Between two to ten stars per quadrant frame are typically used and the fluxes derived from the SExtractor MAG_AUTO measurements. For all three fields, the variations of these frame-to-frame scaling factors are below 10% peak-to-peak, with a star-to-star variation within each frame of about 1.5%.
-
6.
Image registration. A relative astrometric solution is computed for each sky-subtracted frame using Scamp4 and a fourth-order polynomial fit of bright star positions across the detector plane. All the resulting images are then resampled to a common reference frame with Swarp (Bertin et al. 2002) using a LANCZOS4 interpolation kernel and a pixel scale of 0
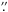 1065.
The interpolation introduces correlated noise between pixels, and this is accounted
for when computing the signal-to-noise ratio of the object as discussed in
Sect. 3.3.2. The accuracy of the image
registration is well within one pixel for the whole data set.
1065.
The interpolation introduces correlated noise between pixels, and this is accounted
for when computing the signal-to-noise ratio of the object as discussed in
Sect. 3.3.2. The accuracy of the image
registration is well within one pixel for the whole data set. -
7.
Final stacks and weight maps. The final stacks for each quadrant are finally produced by averaging with 4σ rejection the individual science frames processed as described. In this process, a map identifying the rejected pixels and a sigma map are produced. In the latter, sigma (σ) is the standard deviation of the N input pixel values, excluding the rejected ones, entering into the stacks. The weight maps are then derived by computing N/σ2.
-
8.
Absolute photometric calibration. The broad band J and Ks data taken as part of our main programme are photometrically matched to existing photometric catalogues and images of the fields in these filters. We carefully select stars in our HAWK-I images for the photometric match. For the CFHTLS-D4 field, the stellar samples consist of 67 and 58 stars in the J and Ks bands. The zeropoints of the HAWK-I images are adjusted to match the photometry of these samples to the photometry of the same stars in the WIRDS data (see Sect. 2.1). This process leaves residuals between 0.03 and 0.05 magnitude rms in the J and Ks bands, respectively. The corresponding magnitudes are found to be in very good agreement with the photometry of the 19 2MASS stars present in the field, which is no surprise considering that the WIRDS data were calibrated against 2MASS. We check that there are no systematic offsets in the colours of our stellar samples compared to the colours determined from the stellar library of Pickles (1998) and from a variety of stellar spectra models at various temperatures and metallicites (Marigo et al. 2008, and http://stev.oapd.inaf.it/cgi-bin/cmd). For the GOODS-S field, we use the publicly available ISAAC J/H/Ks catalogue (Retzlaff et al. 2010) to compute the zeropoint of our HAWK-I J-band image. For the Bullet Cluster field, the J-band and Ks-band images are calibrated from the 2MASS catalogue, leaving residual errors of 0.05 mag rms in both bands. For the calibration of the NB1060 data, because photometric standards in narrow band filters do not exist, we perform the calibration directly on the image stacks, following the approach detailed in Hibon et al. (2010). It consists in interpolating the NB1060 stellar photometry from the optical and NIR broad band data. This is justified by the large number of photometric datapoints available in at least two of our fields and by the absence of features at 1.06 μm in the infrared spectra of stars of spectral types earlier than M5 – the coldest stars in our samples as determined by fitting their spectral energy distribution with the stellar models mentioned above. In practice the procedure consists in performing an ad hoc cubic spline fitting, for each star, of their magnitudes in all available bands. The magnitudes in the NB1060 band are derived from this fit. The procedure is adjusted according to the broad band data available in each field. We use exactly the same approach for calibrating the Y image in the case of the Bullet Cluster. For the CFHTLS-D4 field we use the u∗, g′, r′, i′, z′ optical data from the T0006 CFHTLS release and the NIR J, H, and Ks WIRDS data mentioned above. The selection of stars that are neither too bright nor too faint in any of the available images leaves a sample of 23 objects. The residual error on the determination of the zeropoint from this sample is 0.05 mag rms after rejection of outliers. For the GOODS-S field, the optical F435W, F606W, F775W, and F850LP magnitudes are taken from the merged HST/ACS catalogue (version r2.0z) available on the GOODS website. In this field, there are 44 suitable stars, and the process leaves a residual error of 0.06 mag rms in determining the NB1060 zeropoint. For the Bullet Cluster we use a slightly modified procedure to calibrate the Y and NB1060 images. This is because of the lack of optical data for the entire field of view covered by HAWK-I, preventing us from performing a robust interpolation based on a large number of stars between the two wavelength ranges. Instead, we empirically determine the NB1060 zeropoints by matching the J vs. J − NB1060 (resp. Ks vs. NB1060 − Ks) colour-magnitude diagrams of the stars present in this field to the same diagrams produced on the GOODS-S and CFHTLS-D4 fields after calibration. The same procedure is used to calibrate the Y-band image by comparing it to the colours of the stars in the GOODS-S field for which Y band data are available. All the procedures described above are conducted quadrant by quadrant, with a further iteration on the full four quadrant images. In total, considering the consistency between the many checks that are performed, and despite the various methods used, we estimate that the final accuracy of the photometric calibration is of the order of 0.1 magnitude rms.
-
9.
Absolute astrometric registration and final image stitching. The last step in our reduction process consists in stitching and registering the four detector images to the reference images of each field. The final astrometric solution is computed by Scamp4 with a fourth-order polynomial fit of the star positions. The CFHTLS-D4 stacks are aligned to the archival CFHTLS images. The GOODS-S stacks are aligned to the optical HST/ACS images, and the Bullet Cluster stacks are aligned to the 2MASS catalogue in the absence of astrometrically calibrated data across the entire area. The final astrometric residuals are below the 0
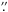 05 rms
level across the entire field of view for all images. Finally, the resampling and
final image stitching are performed using Swarp (Bertin et al. 2002). In addition, Swarp propagates the astrometric
solution to the weight maps and uses a weighted mean to compute pixel values in the
small overlap between quadrants due to the dithering pattern.
05 rms
level across the entire field of view for all images. Finally, the resampling and
final image stitching are performed using Swarp (Bertin et al. 2002). In addition, Swarp propagates the astrometric
solution to the weight maps and uses a weighted mean to compute pixel values in the
small overlap between quadrants due to the dithering pattern.
3.3. Final image properties
We now discuss the global properties of the final images: image quality (FWHM), noise, and detection limits. For consistency, the same procedure is applied to all the images used in this work, including archival data. The FWHM and the detection limits are listed in Table 1.
3.3.1. Image quality
The image quality is determined from a high signal-to-noise ratio point spread function
(PSF) generated by stacking unsaturated and isolated stellar images (range of 20–30) in
each field. After normalization, the stellar images are centred and median-stacked with
a 4σ outlier rejection. The rejection reduces the contribution from
faint neighbouring objects in the wings of the PSF but does not affect its profile. The
resulting NB1060 images are slightly elongated, for reasons that are
unknown to us, with a measured ellipticity from about 0.05 to 0.1 along a direction
≤10° away from the N-S axis. The FWHM values are derived
from a 2D-Gaussian fit to the median profile. The three NB1060 final
images have exquisite image qualities ranging from
0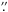 53 to
0
53 to
0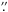 58 (see
Table 1).
58 (see
Table 1).
3.3.2. Photometric errors and correlated noise
Image resampling introduced by the distortion correction, shifting, stitching, and
registration processes introduces correlation in the noise of the images. This leads in
turn to underestimating the photometric errors when considering the pixel-to-pixel noise
properties, see e.g. Grazian et al. (2006),
Appendix A, or Casertano et al. (2000). To measure
and account for this well known effect, we carefully analyse the noise properties of the
images over apertures of varying sizes and derive correction factors that we can then
apply to the photometric data measured by SExtractor. Indeed, SExtractor derives the
photometric error for each object it finds by computing the local pixel-to-pixel noise
fluctuation in the vicinity of the object (in the faint-object, background-limited
regime). The SExtractor photometric errors are therefore affected by the correlation of
the noise. For each image, we select a thousand positions corresponding to source-free
background regions determined from the final SExtractor segmentation (object mask)
image. For each position, we measure the integrated flux in circular apertures of
diameters ranging from Nap = 1 to 25 pixels
(0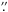 1065 to
2
1065 to
2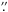 663). For a
given aperture size, the variance of these fluxes,
663). For a
given aperture size, the variance of these fluxes,
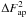 , differs, because
of the correlated noise, from the variance
, differs, because
of the correlated noise, from the variance 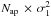 of the
errors computed from the pixel-to-pixel variance
of the
errors computed from the pixel-to-pixel variance 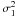 and the
number of pixels Nap in the aperture. The square root of the
ratio of these two quantities
and the
number of pixels Nap in the aperture. The square root of the
ratio of these two quantities 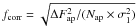 gives the noise-correction factor that can be used to correct the photometric errors
measured by SExtractor. The ratio fcorr clearly depends on
the aperture size: for apertures smaller than the correlation length of the noise, which
is related to the size of the resampling interpolation kernels,
fcorr ~ 1, whereas for large apertures
gives the noise-correction factor that can be used to correct the photometric errors
measured by SExtractor. The ratio fcorr clearly depends on
the aperture size: for apertures smaller than the correlation length of the noise, which
is related to the size of the resampling interpolation kernels,
fcorr ~ 1, whereas for large apertures
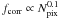 , ranging
from 1.11 for a three-pixel diameter aperture to 1.67 for a 25 pixel diameter aperture.
The procedure is repeated ten times for each field, and all three fields give similar
and consistent measurements.
, ranging
from 1.11 for a three-pixel diameter aperture to 1.67 for a 25 pixel diameter aperture.
The procedure is repeated ten times for each field, and all three fields give similar
and consistent measurements.
This analysis finally allows us to assign signal-to-noise ratios (SNR)
to the objects detected by SExtractor, in the sky background limited regime, using
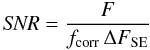 (1)where
ΔFSE is the photometric error measured by SExtractor. The
relation between SNR and the magnitude error Δm is
finally given by
(1)where
ΔFSE is the photometric error measured by SExtractor. The
relation between SNR and the magnitude error Δm is
finally given by 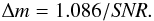 (2)
(2)
3.3.3. Aperture corrections and optimal apertures
We measured curves of growth on unsaturated stars for all image stacks used in this
work, using apertures between 1 and 150 pixels (0 1065 to
16′′) in diameter. Less than 1% of the flux resides in the wings of the PSF
beyond radii of 7′′, and we therefore safely use the 16′′aperture
correction to estimate the total flux of unresolved or moderately resolved objects. From
the curves of growth of both flux and noise, we derived the optimal diameter that
maximizes the signal-to-noise ratio for point-like objects. In practice, for all of our
NB1060 image stacks, a diameter of
1065 to
16′′) in diameter. Less than 1% of the flux resides in the wings of the PSF
beyond radii of 7′′, and we therefore safely use the 16′′aperture
correction to estimate the total flux of unresolved or moderately resolved objects. From
the curves of growth of both flux and noise, we derived the optimal diameter that
maximizes the signal-to-noise ratio for point-like objects. In practice, for all of our
NB1060 image stacks, a diameter of
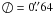 (6 pixels) is used. The
corresponding aperture corrections δmap for
the three NB1060 final images are
δmap = 0.90 ± 0.04 mag,
δmap = 0.82 ± 0.03 mag,
δmap = 0.85 ± 0.04 mag for the GOODS-S,
CFHTLS-D4, and Bullet Cluster fields, respectively. The corresponding noise correcting
factors are fcorr = 1.22, 1.14, and 1.14 for the GOODS-S,
CFHTLS-D4, and Bullet Cluster fields, respectively.
(6 pixels) is used. The
corresponding aperture corrections δmap for
the three NB1060 final images are
δmap = 0.90 ± 0.04 mag,
δmap = 0.82 ± 0.03 mag,
δmap = 0.85 ± 0.04 mag for the GOODS-S,
CFHTLS-D4, and Bullet Cluster fields, respectively. The corresponding noise correcting
factors are fcorr = 1.22, 1.14, and 1.14 for the GOODS-S,
CFHTLS-D4, and Bullet Cluster fields, respectively.
3.3.4. Detection limits
Finally, from the two parameters defined above, fcorr and
δmap, one can define the
1σ limiting magnitude
m1σ for point-like objects:
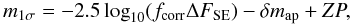 (3)where
fcorr, ΔFSE and
δmap correspond to apertures of
0
(3)where
fcorr, ΔFSE and
δmap correspond to apertures of
0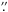 64 in
diameter. This leads to a 3σNB1060 point source
detection limit of m3σ = 26.65, 26.65, and
26.50 for the GOODS-S, CFHTLS-D4, and Bullet Cluster, respectively, as reported in
Table 1.
64 in
diameter. This leads to a 3σNB1060 point source
detection limit of m3σ = 26.65, 26.65, and
26.50 for the GOODS-S, CFHTLS-D4, and Bullet Cluster, respectively, as reported in
Table 1.
4. Candidate selection
4.1. Detection completeness
 |
Fig. 3 Completeness levels of the NB1060 images for the three observed fields. The coloured areas correspond to the Poissonian errors on the number counts in the corresponding magnitude bin. The triangles indicate the 5σ magnitude limits. |
We use SExtractor (Bertin & Arnouts 1996)
version 2.8.6 for source detection and photometric measurements. We fit the PSF median
profile discussed in Sect. 3.3.1 with a sum of three
2-dimensional Gaussians from which we derive the filter (9 × 9 pixels or
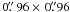 ) used by SExtractor for
spatial filtering during the detection process. We then use this point-source model to
generate mock sources injected into the image to estimate the image detection
completeness. We inject 500 mock sources per Δm = 0.1 mag bins in regions
of the images randomly distributed and free of objects. We perform a number of tests to
determine the optimum SExtractor detection parameters that maximize the number of detected
objects while minimizing the number of false alarms. Considering the absence of candidate
LAEs in our images, we choose to push to the faintest possible limits. False alarms are
investigated by running SExtractor on the negative images and are discussed in Sect. 4.3. We determine that an adequate set of SExtractor
parameters, for the purpose of our analysis, is to trigger a detection on one pixel
(DETECT_MINAREA) after spatial filtering at 0.7σ above the local
background (DETECT_THRESH). With these detection parameters, the average signal-to-noise
ratio of sources in the 50% completeness magnitude bin is of about 4, and a SNR
of 5 corresponds to a completeness rate of 70 to 80%. Figure 3 shows the completeness rates achieved in the three NB1060
images.
) used by SExtractor for
spatial filtering during the detection process. We then use this point-source model to
generate mock sources injected into the image to estimate the image detection
completeness. We inject 500 mock sources per Δm = 0.1 mag bins in regions
of the images randomly distributed and free of objects. We perform a number of tests to
determine the optimum SExtractor detection parameters that maximize the number of detected
objects while minimizing the number of false alarms. Considering the absence of candidate
LAEs in our images, we choose to push to the faintest possible limits. False alarms are
investigated by running SExtractor on the negative images and are discussed in Sect. 4.3. We determine that an adequate set of SExtractor
parameters, for the purpose of our analysis, is to trigger a detection on one pixel
(DETECT_MINAREA) after spatial filtering at 0.7σ above the local
background (DETECT_THRESH). With these detection parameters, the average signal-to-noise
ratio of sources in the 50% completeness magnitude bin is of about 4, and a SNR
of 5 corresponds to a completeness rate of 70 to 80%. Figure 3 shows the completeness rates achieved in the three NB1060
images.
4.2. Selection criteria
We do not expect z ~ 7.7 LAEs to be detected in any of the filters blueward of the Lyα line redshifted to 1.06 μm. First, negligible amounts of radiation are expected to escape the galaxy and to be transmitted by the IGM below the Lyman limit, which is redshifted to ~790 nm. In addition, all the radiation between the Lyα and Lyγ lines at z = 7.7 is entirely redshifted beyond the Gunn-Peterson trough at ~850 nm observed in the spectra of high-redshift quasars (Fan et al. 2006). Only in the blue part – the most depressed part – of the Lyα forest, just above the Lyman limit, can we therefore expect some flux from a z ~ 7.7 LAE to arrive on Earth, in the wavelength range [790–850] nm approximately. In practice, considering the limiting magnitudes of our optical and NB1060 images, an absorption of 2 mag or so will result in no detections in any of the optical bands.
For the purpose of the analysis described in this paper, we built a master catalogue of
all the NB1060 detected objects, measuring their magnitudes in each of
the optical and NIR broad band images by running SExtractor in double image mode. To do
so, we resample all images to the HAWK-I pixel scale
of 0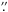 1065. We then
search objects in this master catalogue that are not detected in the optical images at an
initial SNR ≤ 3 level, reduced to SNR ≤ 2 after visual
inspection. In the case of the CFHTLS-D4 field, we request in addition that these objects
not be detected at a 2σ significance level in a
χ2 image of the field obtained by combining the
g′, r′, and
i′ images. In the case of the GOODS-S field, we use a
similar non-detection limit on a bviz
χ2 image obtained by combining the four broad band
HST/ACS images. Because the NB1060 bandpass is located within the
bandpass of the Y filter (at its red edge), the Lyα line
may be detected in the Y filter. To estimate the
Y − NB1060 colour as a function of redshift, we
generate simple synthetic models of LAE spectra, consisting of a narrow
Lyα line and a UV-continuum of energy distribution
fλ ∝ λβ.
We allow the UV slope β to vary from −3 to 0, and we set the flux
density below the Lyα line to zero. For objects with redshifts in the
interval [7.70−7.78] corresponding to the NB1060 filter, we find that
the Y − NB1060 colour is ~ 2.35 ± 0.35, with the
lowest values corresponding to situations where the Lyα line is
redshifted near the edges of the NB1060 filter transmission curve, and
therefore strongly attenuated. This corresponds to the case of high-redshift LBGs detected
through their continuum in the NB1060 filter. As we see in the next
section, the Y images (when available) are not deep enough, relative to
the NB1060 images, to measure such a colour on the faintest objects, but
they do allow us, conversely, to discard blue and moderately bright objects that pass the
other colour selection criteria. To secure the presence of an emission line in the
NB1060 filter, we further require a 1σ NB excess over
the flux measured in the J-band. From Eq. (6) in Hibon et al. (2010), NB1060 − J
≤ 0 corresponds to equivalent widths EWobs ≥ 50 Å or
EWrest ≥ 5.7 Å, assuming a flat continuum spectrum
(fν = const.). We note
that the NB1060 filter is placed approximately at the centre of the
bandpass covering the Y and J filters, allowing us to
further constrain the presence of an LAE from its colour between the NB1060
and Y+J bandpasses; however, in the absence of candidates from
the criteria used so far (see next section), this did not prove necessary to add to our
selection criteria. Finally, we restrict the analysis to sources having
SNR ≥ 5 in the NB1060 final images and
SNR ≥ 2 in partial or intermediate image stacks corresponding to
different observing epochs. In summary, our detection criteria are
1065. We then
search objects in this master catalogue that are not detected in the optical images at an
initial SNR ≤ 3 level, reduced to SNR ≤ 2 after visual
inspection. In the case of the CFHTLS-D4 field, we request in addition that these objects
not be detected at a 2σ significance level in a
χ2 image of the field obtained by combining the
g′, r′, and
i′ images. In the case of the GOODS-S field, we use a
similar non-detection limit on a bviz
χ2 image obtained by combining the four broad band
HST/ACS images. Because the NB1060 bandpass is located within the
bandpass of the Y filter (at its red edge), the Lyα line
may be detected in the Y filter. To estimate the
Y − NB1060 colour as a function of redshift, we
generate simple synthetic models of LAE spectra, consisting of a narrow
Lyα line and a UV-continuum of energy distribution
fλ ∝ λβ.
We allow the UV slope β to vary from −3 to 0, and we set the flux
density below the Lyα line to zero. For objects with redshifts in the
interval [7.70−7.78] corresponding to the NB1060 filter, we find that
the Y − NB1060 colour is ~ 2.35 ± 0.35, with the
lowest values corresponding to situations where the Lyα line is
redshifted near the edges of the NB1060 filter transmission curve, and
therefore strongly attenuated. This corresponds to the case of high-redshift LBGs detected
through their continuum in the NB1060 filter. As we see in the next
section, the Y images (when available) are not deep enough, relative to
the NB1060 images, to measure such a colour on the faintest objects, but
they do allow us, conversely, to discard blue and moderately bright objects that pass the
other colour selection criteria. To secure the presence of an emission line in the
NB1060 filter, we further require a 1σ NB excess over
the flux measured in the J-band. From Eq. (6) in Hibon et al. (2010), NB1060 − J
≤ 0 corresponds to equivalent widths EWobs ≥ 50 Å or
EWrest ≥ 5.7 Å, assuming a flat continuum spectrum
(fν = const.). We note
that the NB1060 filter is placed approximately at the centre of the
bandpass covering the Y and J filters, allowing us to
further constrain the presence of an LAE from its colour between the NB1060
and Y+J bandpasses; however, in the absence of candidates from
the criteria used so far (see next section), this did not prove necessary to add to our
selection criteria. Finally, we restrict the analysis to sources having
SNR ≥ 5 in the NB1060 final images and
SNR ≥ 2 in partial or intermediate image stacks corresponding to
different observing epochs. In summary, our detection criteria are
-
1.
NB1060 ≥ 5σ ∧ NB1060epoch1 ≥ 2σ ∧ NB1060epoch2 ≥ 2σ;
-
2.
no detection above the 2σ level in any of the visible broad band filters;
-
3.
2 ≤ Y − NB1060 ≤ 2.7 (when Y band data are available);
-
4.
NB1060 − J ≤ 0 with 1σ significance.
We finally note that astrophysical sources such as transients, extremely red objects (EROS), high-EW low-z line emitters or T-dwarfs can potentially satisfy the optical non-detection criteria defined here. Relatively deep NIR Y and/or J and/or Ks band data are therefore required for consolidating the selection (e.g. criteria #3 and #4) and reducing contamination from astrophysical sources. The J and Ks band data in particular are useful to identify T-dwarfs and EROs, even if the latter are often detected in deep optical images. In the absence of LAE candidate in our data, we are clearly not affected by contamination, thanks to the coherent datasets that we use. We refer the interested reader to Sect. 3.3 of Hibon et al. (2010) for a somewhat more detailed analysis of contamination effects in a similar z = 7.7 LAE search, in particular by Hα, [OIII], and [OII] line emitters.
4.3. Selection field by field
The 5σ detection limit in the NB1060 filter corresponds to magnitudes m5σ = 25.9 to m5σ = 26.1 depending on field (see Table 1), and to a completeness level of 70 to 80% (see Fig. 3). The corresponding colour criteria used for the selection of candidates differ among the three fields depending on the depth of the optical images available in each of them.
CFHTLS-D4. The selection criterion #2 in the previous section
corresponds to the following colour criteria:
![\begin{equation} \begin{array}{lcl} \textit{u*}_{2\sigma}-\textit{NB1060} & \ge & 1.7,\\[1mm] \textit{g\arcmin}_{2\sigma}-\textit{NB1060} & \ge & 2.5,\\[1mm] \textit{r\arcmin}_{2\sigma}-\textit{NB1060} & \ge & 2.3,\\[1mm] \textit{i\arcmin}_{2\sigma}-\textit{NB1060} & \ge & 1.8,\\[1mm] \textit{z\arcmin}_{2\sigma}-\textit{NB1060} & \ge & 0.9.\\ \end{array} \end{equation}](/articles/aa/full_html/2012/02/aa17312-11/aa17312-11-eq118.png) (4)There
are ~6500 NB1060 objects detected in this field. The application of
criteria #1 and #2 of Sect. 4.2 yields 20 objects.
Ten are visually identified as instrumental artefacts caused by electronic crosstalk (see
Sect. 4.4). Seven of the remaining objects are
detected and relatively bright in the J band and therefore rejected after
application of criterion #4. We note in passing that the brightest of these objects has
NB1060 = 24.15, J = 23.85 and
J − H2σ ≤ −0.85 and is
very likely a T-dwarf.
(4)There
are ~6500 NB1060 objects detected in this field. The application of
criteria #1 and #2 of Sect. 4.2 yields 20 objects.
Ten are visually identified as instrumental artefacts caused by electronic crosstalk (see
Sect. 4.4). Seven of the remaining objects are
detected and relatively bright in the J band and therefore rejected after
application of criterion #4. We note in passing that the brightest of these objects has
NB1060 = 24.15, J = 23.85 and
J − H2σ ≤ −0.85 and is
very likely a T-dwarf.
Amongst the three remaining objects, one is located near the edges of the image and appears sharper than the PSF. One is located in the wings (4′′) of a bright extended galaxy, therefore of suspicious photometry and therefore unusable. Finally, the last one appears to be a variable, extended object, with ≥ 1 magnitude difference between the first- and second-epoch observations. All three objects are therefore discarded.
To allow for possibly slightly extended LAE candidates and for consistency checks, we
carry out a second selection using larger apertures
(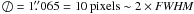 ), and applying the
appropriate aperture correction. Criteria #1 and #2 yielded 14 detections, out of which
nine are in common with the previous sample of 20 objects. Amongst the remaining five new
detections, one is an obvious artefact near a bright star, two are detected in the
J-band and are rejected due to the low significance of their NB excess.
The two last ones are low significance detections in the NB1060 image
(SNR ≤ 5.5) and both show extended and dubious morphologies.
), and applying the
appropriate aperture correction. Criteria #1 and #2 yielded 14 detections, out of which
nine are in common with the previous sample of 20 objects. Amongst the remaining five new
detections, one is an obvious artefact near a bright star, two are detected in the
J-band and are rejected due to the low significance of their NB excess.
The two last ones are low significance detections in the NB1060 image
(SNR ≤ 5.5) and both show extended and dubious morphologies.
Checking the robustness of the rejections further, we investigate the false alarms on the
negative image using the two aperture diameters mentioned above. After removing the
well-determined crosstalk features, which have a negative component, we are left with
eight objects using the 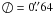 aperture and 2 using the
aperture and 2 using the
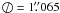 aperture, all of them at
the limit of our signal-to-noise ratio selection. These genuine noise artefacts have very
similar morphologies to those of the positive detections that were rejected on the science
image: either very sharp or extended and irregular with bright non-contiguous pixels. This
legitimizes our somewhat ad hoc, but pragmatic earlier selection based on the morphology
of the faintest positive candidates, and we therefore conclude that there are no
z = 7.7 LAE candidate in the CFHTLS-D4 field.
aperture, all of them at
the limit of our signal-to-noise ratio selection. These genuine noise artefacts have very
similar morphologies to those of the positive detections that were rejected on the science
image: either very sharp or extended and irregular with bright non-contiguous pixels. This
legitimizes our somewhat ad hoc, but pragmatic earlier selection based on the morphology
of the faintest positive candidates, and we therefore conclude that there are no
z = 7.7 LAE candidate in the CFHTLS-D4 field.
GOODS-S. Here the selection criterion #2 corresponds to the following
colour criteria: ![\begin{equation} \begin{array}{lcl} \textit{F435W}_{2\sigma}-\textit{NB1060} & \ge & 2.3,\\[1mm] \textit{F606W}_{2\sigma}-\textit{NB1060} & \ge & 2.5,\\[1mm] \textit{F775W}_{2\sigma}-\textit{NB1060} & \ge & 1.9,\\[1mm] \textit{F850LP}_{2\sigma}-\textit{NB1060} & \ge & 1.6.\\ \end{array} \end{equation}](/articles/aa/full_html/2012/02/aa17312-11/aa17312-11-eq125.png) (5)There
are ~5100 NB1060 detected objects. The application of criteria #1 and
#2 yields 16 objects, of which 12 are visually identified as instrumental artefacts caused
by electronic crosstalk. Amongst the four remaining objects, one is due to a mismatch on a
blended object, and two are marginally detected objects at the edges of the image. The
last object is detected in the Y-band but does not satisfy criterion #3
above; interestingly, it is identified with reference G2_1408 as a z ~ 7
object in Castellano et al. (2010, and references
therein). This object has been followed up in spectroscopy (Fontana et al. 2010), yielding a tentative detection of the
Lyα line at a redshift z = 6.97. This object therefore
appears to be an LBG, caught by its strong UV continuum emission detected in the
NB1060 filter.
(5)There
are ~5100 NB1060 detected objects. The application of criteria #1 and
#2 yields 16 objects, of which 12 are visually identified as instrumental artefacts caused
by electronic crosstalk. Amongst the four remaining objects, one is due to a mismatch on a
blended object, and two are marginally detected objects at the edges of the image. The
last object is detected in the Y-band but does not satisfy criterion #3
above; interestingly, it is identified with reference G2_1408 as a z ~ 7
object in Castellano et al. (2010, and references
therein). This object has been followed up in spectroscopy (Fontana et al. 2010), yielding a tentative detection of the
Lyα line at a redshift z = 6.97. This object therefore
appears to be an LBG, caught by its strong UV continuum emission detected in the
NB1060 filter.
Similar to what was done on the CFHTLS-D4 field, we then performed a second selection
using 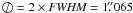 apertures. This yields two
new detections (beyond the obvious electronic artefacts): one is detected in the
Y-band and does not pass criterion #3, and is also marginally
noticeable in the optical bands. The other one has a dubious morphology and is close to a
bright object, and is therefore rejected. Finally, we carried out the false alarm analysis
on the negative image, and we detect a handful of events with dubious morphologies,
leading to the same conclusions as for the CFHTLS-D4 field.
apertures. This yields two
new detections (beyond the obvious electronic artefacts): one is detected in the
Y-band and does not pass criterion #3, and is also marginally
noticeable in the optical bands. The other one has a dubious morphology and is close to a
bright object, and is therefore rejected. Finally, we carried out the false alarm analysis
on the negative image, and we detect a handful of events with dubious morphologies,
leading to the same conclusions as for the CFHTLS-D4 field.
Bullet Cluster. The dataset for the Bullet Cluster field is somewhat different than for the other fields. As explained in Sect. 2.3, we accomodated a consistent set of HAWK-I data in the Y, NB1060, J and Ks bands within our large programme. In addition, we used HST/ACS images of the inner part of the field, as well as moderately deep IMACS images from the Magellan telescope (Clowe et al. 2006). There are ~7000 NB1060 objects satisfying criterion #1, the vast majority of which are detected in the Y filter and do not satisfy criterion #3. Only 127 objects are not detected in the Y image at 3σ, but because Y3σ − NB10605σ = 0.4, it is impossible to conclude whether they satisfy criterion #3 or not. After visual inspection and rejection of electronical ghosts and obvious artefacts, all but one object show a clear counterpart in either one of the HST/ACS images or in the IMACS images. This object shows no NB excess (NB1060 − J = 0.55 ± 0.25), and together with a marginal detection in the Y-band (SNR ~ 2.4, Y = 26.40 ± 0.45) and a non-detection in Ks (Ks ≤ 25.3, 3σ upper limit), we conjecture that this object is probably a T-dwarf. Finally, a selection based on larger apertures as for the two other fields yields no new candidates. We therefore conclude, again, that there are no z = 7.7 LAE candidates in the Bullet Cluster field.
4.4. Instrumental artefacts
Instrumental artefacts are a potentially important source of contamination. As explained in Sect. 4.3, candidates are found that are rejected as instrumental artefacts. We describe here some of the instrumental artefact sources that are observed in the HAWK-I data.
-
1.
Electronic crosstalk. The HAWK-I data suffer from inter-channel crosstalk from the readout electronics. This results indonut-shaped artefacts at regularly spaced intervals along de-tector lines where bright stars are present. These artefacts werelargely attenuated after a technical intervention in the instrumentthat took place in May 2009. The crosstalk pattern follows thedithering pattern and is therefore present on the final stackedimages. The crosstalk artefacts are easy to recognize from theirshapes and fixed distances from bright stars along detector rows.Because they do not have counterparts in optical images, theseartefacts are selected as candidates in our analysis, but are easilydealt with a posteriori. No attempt was made to remove theseartefacts during data processing.
-
2.
Optical ghosts. Reflections inside the instrument generate typical out-of-focus and decentred pupil images around bright stars. The surface brightness of these haloes was measured to be 10-4 of the peak intensity in the PSF profiles. Only focussed optical ghosts can be mistaken as candidates, and no such artefacts are observed on the HAWK-I images.
-
3.
Persistence. Persistence from previously observed bright stars is at a fixed detector position. The persistence features therefore do not follow the dithering pattern and are rejected when combining the images with sigma clipping in the final stacks. Considering the large number of frames used in the stacks (more than 200 frames), persistence effects are unlikely to leave residuals that can be mistaken as candidates.
-
4.
Radioactive events. One of the HAWK-I arrays (chip #2, Id: ESO-Hawaii2RG-chip78) suffers from a strong radioactive event rate, coming from the detector substrate (Finger et al. 2008). These radioactive events generate showers of variable intensity (typically thousands of electrons) and extent (typically a few tens of pixels on a side). Some events can be as bright as a few hundred thousand electrons and extend up to 400 pixels in one direction. Because of the long detector integration times (DIT) used for the NB1060 images (300 s), there are a few tens of such events in a single frame. This results in poor background subtraction and moderately high-frequency residuals (a few tens of pixels) in individual sky-subtracted frames. Although the global noise properties are not significantly different in this quadrant than in the others, the overall cosmetics are somewhat poorer. As a consequence, most of the low signal-to-noise ratio detections and with dubious morphologies reported in Sect. 4.3 appear to be in this quadrant and are therefore rejected as artefacts after visual inspection.
-
5.
Noise. As explained earlier, we chose a low detection threshold in order to push to the faintest detection limits, triggering a handful of low signal-to-noise ratio false alarms, particularly on the highly radioactive quadrant. We settle on a detection threshold that allows us to handle these false alarms.
5. Constraints on the z = 7.7 Lyα luminosity function
5.1. Comoving volume
The effective field of view in the transverse dimension of the NB1060 stacks is computed as a function of the detection limit for each field from the background noise maps generated by SExtractor, and accounting for the correlation of the noise as described in Sect. 3.3.2. The sensitivity is reduced at the edges of each quadrant image thanks to the dithering process and in regions close to bright objects. All objects are masked, reducing the total effective area by ~10% for the blank fields, and ~25% for the Bullet Cluster due to the large number of bright galaxy cluster members. For this field, we further use a map of the gravitational amplification and space distortion from a detailed model of the cluster (Richard et al., in prep.) to compute the effective, unlensed, comoving area corresponding to the image (see Willis et al. 2008, for a similar example). In the direction of the line of sight, we use the filter transmission curve to determine the effective width. We then approximate the NB1060 filter with a rectangular filter of width equal to this effective width. The effects of the filter transmission curve on LAE detection and comoving volumes are detailed in e.g. Willis & Courbin (2005) and Hu et al. (2010). Considering our null results, these effects will not affect our conclusions. We also assume that the filter transmission curve does not vary significantly over the instrument’s field of view, an assumption motivated by the relative uniformity of the sky background over the instrument’s field of view. We finally assume that the observed Lyα emission lines are significantly narrower than the filter width, as is the case for high-z LAEs, and we therefore ignore the effect of the line width on the line flux measured through the NB1060 filter. The effective width of the NB1060 (Δλeff ~ 100 Å) defines the [7.70−7.78] redshift interval probed by our observations.
Converting magnitudes to line luminosities requires assumptions on the equivalent width (EW) of the Lyα line. Distributions of observed Lyα lines in high-z LAEs vary from a few tens of Angstroms to lower limits of a few hundred Angstroms (see e.g. Taniguchi et al. 2005; Ouchi et al. 2010). The Taniguchi et al. (2005) distribution of Lyα line EWs is consistent with a conversion factor of 70%, as used in Hibon et al. (2010), when assuming that the EW lower limits are the real values. Conversely, Kobayashi et al. (2010) predict a distribution of Lyα EWs clearly peaked toward high values, hence favouring conversion factors closer to 100%. In the following, we therefore use these two values (70% and 100%) when converting NB1060 magnitudes to line luminosities.
In total, the comoving volume sampled by our images is 5.9 × 103 Mpc3 for the Bullet Cluster and 9 × 103 Mpc3 for each of the two blank fields, corresponding to a grand total of ~2.4 × 104 Mpc3 for the three fields. The volume-luminosity relation is shown in Fig. 4, and the effect of the gravitational amplification for the Bullet Cluster is clearly visible, where the gravitational amplification enables probing fainter luminosities, however over increasingly smaller volumes.
 |
Fig. 4 The comoving volume V(L) sampled by the NB1060 images as a function of Lyα luminosity. The two dashed curves correspond to the two blank fields (green – CFHTLS-D4; red – GOODS-S). The thin black curve corresponds to the Bullet Cluster. The thick black curve is the total comoving volume corresponding to the three fields. The Lyα luminosity corresponds to a 5σNB1060 limiting magnitude, assuming a 70% average conversion factor between the Lyα luminosities and NB1060 magnitudes (see text). |
5.2. Cosmic variance and Poisson noise
We do not detect any LAE candidates down to a NB1060 5σ
limiting magnitude of ~25.9 to ~26.1. To constrain the luminosity function of
z = 7.7 Lyα emitters and compare our results with
others, we make use of the Schechter formalism (Schechter
1976): 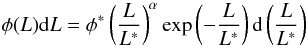 (6)where
L∗ is the characteristic luminosity defining the LF high
luminosity cutoff, φ∗ a volume density normalization factor,
and α the faint-end slope characterizing how steeply the LF increases at
low luminosities. Limited samples and large errors lead to degneracy between these three
LF parameters. Pending more observational data and more accurate determinations of the
high-z LAE LF parameters, most of the authors in the literature have
settled on a canonical faint end slope value of α = −1.5. Our
observations probe luminosities similar, or slightly fainter, than those observed by other
groups; therefore, we can compare our results to others, and to this aim we similarly
adopt, unless stated otherwise, a faint end slope of α = −1.5.
(6)where
L∗ is the characteristic luminosity defining the LF high
luminosity cutoff, φ∗ a volume density normalization factor,
and α the faint-end slope characterizing how steeply the LF increases at
low luminosities. Limited samples and large errors lead to degneracy between these three
LF parameters. Pending more observational data and more accurate determinations of the
high-z LAE LF parameters, most of the authors in the literature have
settled on a canonical faint end slope value of α = −1.5. Our
observations probe luminosities similar, or slightly fainter, than those observed by other
groups; therefore, we can compare our results to others, and to this aim we similarly
adopt, unless stated otherwise, a faint end slope of α = −1.5.
Denoting V(L) the comoving volume probed by our
observations as a function of the luminosity L, as described in
Sect. 5.1 and shown in Fig. 4, the total number of objects
N(L∗,φ∗,α)
is given by 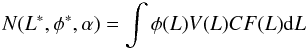 (7)where
CF(L) is the completeness function (see Sect. 4.1). The conversion of the completeness function as a
function of magnitude as shown in Fig. 3 to
CF(L) takes into account the conversion factor of 70%
and 100% mentioned above, and in the case of the Bullet Cluster further takes the
amplification map of the cluster into account.
(7)where
CF(L) is the completeness function (see Sect. 4.1). The conversion of the completeness function as a
function of magnitude as shown in Fig. 3 to
CF(L) takes into account the conversion factor of 70%
and 100% mentioned above, and in the case of the Bullet Cluster further takes the
amplification map of the cluster into account.
From a Poisson distribution, one can easily compute single-sided confidence levels (CL)
for the upper limits of the expected number of events Nu that
correspond to a measured number of events n, as (Gehrels 1986): 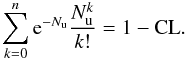 (8)In our situation
of zero detection (n = 0), the 84.13, 97.72, 99.87, and 99.99
percentiles5 confidence levels correspond to upper
limits of the mean number of events Nu of 1.84, 3.78, 6.61,
and 10.36, respectively. The situation Nu ≤ 1 corresponds to a
63% confidence level. Therefore, with zero detection and assuming pure Poisson statistics,
one can exclude, at a given confidence level CL, the luminosity function parameters that
would yield an expected number of objects Nu with our survey
parameters.
(8)In our situation
of zero detection (n = 0), the 84.13, 97.72, 99.87, and 99.99
percentiles5 confidence levels correspond to upper
limits of the mean number of events Nu of 1.84, 3.78, 6.61,
and 10.36, respectively. The situation Nu ≤ 1 corresponds to a
63% confidence level. Therefore, with zero detection and assuming pure Poisson statistics,
one can exclude, at a given confidence level CL, the luminosity function parameters that
would yield an expected number of objects Nu with our survey
parameters.
However, considering the somewhat limited area covered by our observations, we need to consider the effects of cosmic variance in our statistical analysis. Somerville et al. (2004) are among the first authors to derive quantitative estimates of the effects of cosmic variance from cold dark matter (CDM) models and observations of the two-point correlation functions of galaxy populations in the GOODS survey data. Trenti & Stiavelli (2008) expand on this work and propose a cosmic variance model, based on N-body simulations and halo occupation distribution models, and applied to a variety of high-z galaxy populations. We use below the on-line version of this model to estimate the effects of cosmic variance on our observations.
Various prescriptions have been proposed for the distribution function of galaxy number counts affected by cosmic variance, see Yang & Saslaw (2011) for a recent discussion and analysis of the galaxy counts-in-cells distribution functions in the SDSS data. Although not physically motivated, the negative binomial distribution (NBD) fits the SDSS data well at both low and high number counts and provides a convenient description for the distribution function of galaxies with positive number counts and overdispersion relative to a Poisson distribution. To prevent technical problems with the use of normal or lognormal distributions (e.g. truncation to positive numbers), we chose to adopt the NBD as an ad hoc representation of the probability density function of low galaxy number counts. The NBD can be conveniently expressed as a Poisson random variable whose mean population parameter is itself random and distributed as a Gamma distribution of variance equal to the relative cosmic variance.
By definition of the cosmic variance, the variance
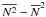 of the number of
galaxies of mean number
of the number of
galaxies of mean number 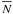 is in excess
of the Poisson variance
is in excess
of the Poisson variance 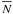 and is given
by
and is given
by 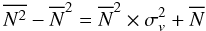 (9)where
(9)where
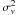 is the
relative cosmic variance. With the NBD prescription, one can derive the confidence level
CL corresponding to no detections in our observations, for a known
is the
relative cosmic variance. With the NBD prescription, one can derive the confidence level
CL corresponding to no detections in our observations, for a known
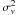 . To estimate
the cosmic variance, we run the on-line cosmic variance calculator6 (Trenti & Stiavelli
2008) and derive
. To estimate
the cosmic variance, we run the on-line cosmic variance calculator6 (Trenti & Stiavelli
2008) and derive 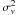 for low
number counts
for low
number counts 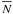 . We use the
parameters corresponding to our observations: the instrument’s field of view, a mean
redshift of 7.74, and a redshift interval of 0.08. We select the Sheth-Tormen bias
formalism, a value of 0.8 for σ8, and a value of 1.0 for the
user-selectable halo-filling factor. Although the filling factor of LAEs is likely to be
significantly lower than 1.0, see e.g. Ouchi et al.
(2010), adopting a value of 1.0 leads to overestimating the importance of cosmic
variance and therefore corresponds to a worst-case scenario in our analysis. Finally, we
define a completeness factor of 1.0 in the cosmic variance calculator since we use our
measured completeness function in Eq. (7)
to derive the number of galaxies that correspond to a given set of LF parameters. We then
fit the resulting relative cosmic variance
. We use the
parameters corresponding to our observations: the instrument’s field of view, a mean
redshift of 7.74, and a redshift interval of 0.08. We select the Sheth-Tormen bias
formalism, a value of 0.8 for σ8, and a value of 1.0 for the
user-selectable halo-filling factor. Although the filling factor of LAEs is likely to be
significantly lower than 1.0, see e.g. Ouchi et al.
(2010), adopting a value of 1.0 leads to overestimating the importance of cosmic
variance and therefore corresponds to a worst-case scenario in our analysis. Finally, we
define a completeness factor of 1.0 in the cosmic variance calculator since we use our
measured completeness function in Eq. (7)
to derive the number of galaxies that correspond to a given set of LF parameters. We then
fit the resulting relative cosmic variance 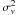 corresponding
to our survey parameters as a function of
corresponding
to our survey parameters as a function of 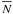 , and we plug
this cosmic variance into a gamma distribution. For each pair of
(L∗,φ∗)
parameters we thus derive a confidence level corresponding to no detections in our
observations.
, and we plug
this cosmic variance into a gamma distribution. For each pair of
(L∗,φ∗)
parameters we thus derive a confidence level corresponding to no detections in our
observations.
This is represented in Fig. 5 together with the best-fit parameters of the Lyα LAE luminosity functions at redshifts 5.7 and 6.5 from various sources. We report in this plot the range of (L∗,φ∗) parameters excluded at 85% and 99% confidence levels, for conversion factors between NB1060 magnitudes and Lyα luminosities varying from 70% and 100% (see discussion in Sect. 5.1). We report the upper (L∗,φ∗) exclusion zones derived from the absence of detections in the HAWK-I observations only (this work). Furthermore, we report the upper exclusion zones at the same confidence levels when adding to the null HAWK-I detections the null spectroscopic confirmation of the five brightest z = 7.7 LAE candidates7 presented in Hibon et al. (2010). Finally, for illustration, we also report the 85% confidence level derived from this work (HAWK-I observations only) for a faint end slope of the z = 7.7 Lyα LAE LF α = −1.7.
 |
Fig. 5 Parameters of the z = 7.7 luminosity function excluded at 85% and 99% confidence levels from our data, assuming the Schechter formalism and a fixed faint end slope α = −1.5 unless otherwise stated. Filled circles correspond to the best fit LF parameters at z = 5.7 (blue) and z = 6.5 (red) from Kashikawa et al. (2011). The ellipses correspond to the 3σ confidence levels for these datapoints. Open circles correspond to the best fit LF parameters of the photometric samples of Ouchi et al. (2008) at z = 3.1 (magenta) and z = 5.7 (blue) and of Ouchi et al. (2010) at z = 6.5 (red). The ellipses correspond to the 2σ confidence levels for these datapoints. The filled square symbols correspond to the best fit LAE LF parameters at z = 5.7 (blue) and z = 6.5 (red) from Hu et al. (2010). The plain (resp. dotted) black lines correspond to the 85% and 99% confidence levels corresponding to no detections in our HAWK-I data (this work), assuming a conversion factor of 70% (resp. 100%) between the NB1060 and Lyα fluxes. The dark (resp. light) grey zones correspond to the range of 85% (resp. 99%) confidence levels for conversion factors between 70% and 100%, as delimited by the plain and dotted lines. Similarly, the lines and hatched zones in magenta colour correspond to the 85% and 99% confidence levels when adding to our work the null spectroscopic confirmation of the five brightest z = 7.7 LAE candidates of Hibon et al. (2010). |
6. Discussion
The various LF parameters reported in the literature at redshifts 5.7 and 6.5 present some significant differences. We report in Fig. 5 some of the best-fit Schechter parameters at redshifts 3.1, 5.7 and 6.5. We report photometric samples partially confirmed in spectroscopy and purely spectroscopic samples. At the same redshift, the two series of datapoints clearly differ by significant amounts.
Ouchi et al. (2010), and previously Kashikawa et al. (2006) followed by Kashikawa et al. (2011), convincingly claim that the evolution, mostly in luminosity, of the z ~ 6.5 LF from the lower redshift LFs at z ~ 3.1 and z ~ 5.7 LFs is a signature of reionization, due to a neutral-hydrogen fraction xHI of the order of 20% at z = 6.5. Conversely, the Hu et al. (2010) evolution of the LF parameters between the two same redshifts is mostly in density; accordingly, they do not infer a signature of reionization, in agreement with an earlier claim by Malhotra & Rhoads (2004) that there was no evidence of reionization in the evolution of the LAE LF between these two redshifts.
In the light of the recent work from Hu et al. (2010), the question of the evolution of the Lyα LAE luminosity function beyond redshift 5.7 becomes more difficult to comprehend. If the z = 5.7 point of Hu et al. (2010) (and Malhotra & Rhoads 2004) is correct, the picture by which the LAE LF would be approximately constant between z = 3 and z = 5.7, and would evolve significantly beyond redshift ~6 as a consequence of an increasingly neutral intergalactic medium (IGM), might need to be revisited. How useful are our results in this context?
From Fig. 5, we infer that we can safely exclude a non evolution of the LF parameters at z = 7.7 at more than 99% confidence level from the Kashikawa et al. (2006, 2011), Ouchi et al. (2008) and Ouchi et al. (2010) values at z = 5.7 and 6.5. In that case, we should find ~13.7 and ~11.7 LAEs in the three HAWK-I fields based on the LF parameters estimated by Ouchi et al. (2010) and Kashikawa et al. (2011) at z = 6.5, respectively. The LF parameters of Hu et al. (2010) would predict ~2.5 LAEs at z = 6.5 and can be similarly excluded at an ~85% confidence level, or higher, when including the null spectroscopic confirmation of the brightest LAE candidates of Hibon et al. (2010) (see previous section and footnote 7). Our results therefore clearly show that the z = 7.7 Lyα LAE LF does evolve from lower redshifts, but in the absence of concordance between the data at lower redshifts, it is difficult to ascribe this evolution to the galaxy properties or to reionization.
To continue the discussion, we now consider two scenarios for the evolution of the LAE LF between z = 6.5 and z = 7.7, either in density or in luminosity. These scenarios are purely phenomenological and are not supported by theoretical considerations, only serving the purpose of assessing what the consequences of our results might be. This is illustrated in Fig. 6 in a cumulative luminosity function plot. For a luminosity function to be consistent with our null results, it should lie, ignoring statistical fluctuations, below the contours corresponding to the parameter space probed by our observations.
 |
Fig. 6 Cumulative Lyα luminosity functions. The blue (resp. red) lines show the cumulative luminosity functions at z = 5.7 (resp. z = 6.5) from Ouchi et al. (2008) (dotted-dashed lines), Hu et al. (2010) (plain lines) and Kashikawa et al. (2011) (dotted lines). The transitions to thin lines indicate the range of the luminosities probed by the observations. A fixed faint end slope of –1.5 is assumed. The parameter space probed by the HAWK-I observations is delimited by the black line, with the black dashed line corresponding to the HAWK-I observations and the null detection of the bright candidates of Hibon et al. (2010) mentioned in the text. The green dotted line corresponds to a 60% evolution in density of the Hu et al. (2010) LF, and the short-dashed-long-dashed line corresponds to a 60% evolution in luminosity of the Ouchi et al. (2010)z = 6.5 LF. The red filled diamond corresponds to the Iye et al. (2006) LAE detection at a redshift of 6.96. The black open diamonds correspond to the Vanzella et al. (2011) LAE detections at redshifts of 7.008 and 7.109. The magenta downward-pointing filled (resp. open) triangles are the photometric candidates at z = 7.7 from Tilvi et al. (2010) (resp. Krug et al. 2012). |
In the first scenario, we consider a ~60% evolution in density from the z = 6.5 datapoint of Hu et al. (2010). Such an evolution can be entirely ascribed, in principle, to an intrinsic evolution of the LAE LF between z = 6.5 and z = 7.7 as in the models of Kobayashi et al. (2007) where the z = 6.5 LF, multipling φ∗ by 0.4, almost perfectly coincides with the z = 7.7 LF. In practice, such an evolution could result from the combined evolution of the density of dark matter haloes and of the intrinsic galaxy properties. We also note that the UV LF of high-redshift galaxies between z ~ 4 and z ~ 8 evolves essentially in luminosity (Bouwens et al. 2011), so a pure evolution in density should be treated with caution. As can be seen in Figs. 5 and 6, such an evolution would fit most of the observational data, the shapes of the lower-redshift LFs, the datapoint from Iye et al. (2006) at z = 6.96, the datapoints from Vanzella et al. (2011) at z = 7.008 and z = 7.109, and our data. The mere existence of the Iye et al. (2006) and Vanzella et al. (2011) datapoints and of the Ota et al. (2010) LAE candidates at z ~ 7 provides interesting constraints at high luminosities that cannot be fully captured in the (L∗, φ∗) parameter space of Fig. 5 and are better seen in Fig. 6. The main conclusion to be drawn from this test case is that to be consistent with our results, it does not require invoking a change in the Lyα IGM transmission and therefore a change in the neutral-hydrogen fraction of the IGM.
In the second scenario, conversely, we consider a 60% change in luminosity from the z = 6.5 LF of Ouchi et al. (2010). This scenario clearly requires, by construction, a significant quenching of the IGM Lyα transmission. The present luminosity evolution scenario may be compatible with the claim by Fontana et al. (2010) of a significant quenching of Lyα emission among LBGs at z ~ 7. Although strongly model dependent, a high neutral-hydrogen fraction of the IGM due to a still incomplete reionization would then be required in this scenario, e.g. xHI ~ 60% according to the model of Santos (2004).
To conclude this discussion, we cannot safely decide on whether we are “seeing” signatures of reionization in our results, as this depends on which assumptions we use for the LFs at lower redshifts. We call for clarifications of the LAE luminosity functions at redshift 6.5 and below, a prerequisite to drawing firmer conclusions on reionization as inferred from LAE observations. We also note that our results are inconsistent with the photometric samples from Tilvi et al. (2010) and Krug et al. (2012) at z = 7.7, but spectroscopic confirmation is required before drawing firmer conclusions. In the meantime, observations at z = 7.7 continue. An ideal complement to the HAWK-I observations presented in this paper would be to probe higher luminosities (of the order of 1043 erg s-1) over significantly larger comoving volumes (a few times 106 Mpc3).
7. Conclusion
We searched for Lyα emitters in three fields, two blank fields and one cluster field with the HAWK-I instrument at the VLT, using a NB filter centred at 1.06 μm. Our data in this filter total 80 h of integration time. The total comoving volume is ~2.4 × 104 Mpc3. We reached a 5σ limiting magnitude that we use as detection threshold, of ~26.0 ± 0.1 AB magnitude. We selected the objects from various colour criteria, which depend on the auxiliary data available for each field. We did not detect any object matching our selection criteria that would correspond to z = 7.7 LAEs. We modelled the probability density function of high-z LAE populations including Poisson statistics and cosmic variance with a negative binomial distribution. From this statistical description and from the absence of LAE detections, we exclude a non-evolution scenario at ~85% (resp. 99%) confidence level from the z = 6.5 LF of Hu et al. (2010) (resp. Ouchi et al. 2010; Kashikawa et al. 2011). The large differences between the published LFs at z = 6.5 prevent us from inferring a robust estimate of the Lyα IGM transmission at z = 7.7, and therefore of the neutral-hydrogen fraction xHI at this redshift. However, in all cases but the Hu et al. (2010) LF, a significant quenching of the Lyα transmission by the IGM, probably due to reionization, is required.
From the CFHT WIRCam Deep Survey (WIRDS), see http://terapix.iap.fr/rubrique.php?id_rubrique=261
Acknowledgments
We acknowledge financial support from Agence Nationale de la Recherche (grant ANR-09-BLAN-0234-01). F.C. is supported by the Swiss National Science Foundation (SNSF). The Dark Cosmology Centre is funded by the Danish National Research Foundation.
References
- Becker, R. H., Fan, X., White, R. L., et al. 2001, AJ, 122, 2850 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, in Astronomical Data Analysis Software and Systems XI, ed. D. A. Bohlender, D. Durand, & T. H. Handley, ASP Conf. Ser., 281, 228 [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2011, ApJ, 737, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Clowe, D., Gonzalez, A. H., et al. 2006, ApJ, 652, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Casertano, S., de Mello, D., Dickinson, M., et al. 2000, AJ, 120, 2747 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Le Fèvre, O., Garilli, B., et al. 2011, A&A, 525, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castellano, M., Fontana, A., Boutsia, K., et al. 2010, A&A, 511, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clowe, D., Bradač, M., Gonzalez, A. H., et al. 2006, ApJ, 648, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Maselli, A., & Ferrara, A. 2011, MNRAS, 410, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., & Wyithe, J. S. B. 2010, MNRAS, 408, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Carilli, C. L., & Keating, B. 2006, ARA&A, 44, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Finger, G., Dorn, R. J., Eschbaumer, S., et al. 2008, in SPIE Conf. Ser., 7021 [Google Scholar]
- Fontana, A., Vanzella, E., Pentericci, L., et al. 2010, ApJ, 725, L205 [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Clowe, D., Bradač, M., et al. 2009, ApJ, 691, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Fontana, A., de Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hibon, P., Cuby, J., Willis, J., et al. 2010, A&A, 515, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, E. M., Cowie, L. L., McMahon, R. G., et al. 2002, ApJ, 568, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, E. M., Cowie, L. L., Barger, A. J., et al. 2010, ApJ, 725, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Iye, M., Ota, K., Kashikawa, N., et al. 2006, Nature, 443, 186 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kashikawa, N., Shimasaku, K., Malkan, M. A., et al. 2006, ApJ, 648, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kashikawa, N., Shimasaku, K., Matsuda, Y., et al. 2011, ApJ, 734, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, M. A. R., Totani, T., & Nagashima, M. 2007, ApJ, 670, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, M. A. R., Totani, T., & Nagashima, M. 2010, ApJ, 708, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Krug, H., Veilleux, S., Tilvi, V., et al. 2012, ApJ, 745, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Laursen, P., Sommer-Larsen, J., & Razoumov, A. O. 2011, ApJ, 728, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Maizy, A., Richard, J., de Leo, M. A., Pelló, R., & Kneib, J. P. 2010, A&A, 509, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malhotra, S., & Rhoads, J. E. 2004, ApJ, 617, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamura, E., Inoue, A. K., Hayashino, T., et al. 2011, MNRAS, 55 [Google Scholar]
- Nilsson, K. K., Orsi, A., Lacey, C. G., Baugh, C. M., & Thommes, E. 2007, A&A, 474, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ota, K., Iye, M., Kashikawa, N., et al. 2010, ApJ, 722, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Akiyama, M., et al. 2008, ApJS, 176, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Furusawa, H., et al. 2010, ApJ, 723, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Retzlaff, J., Rosati, P., Dickinson, M., et al. 2010, A&A, 511, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, J., Stark, D. P., Ellis, R. S., et al. 2008, ApJ, 685, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Kneib, J.-P., Ebeling, H., et al. 2011, MNRAS, L245 [Google Scholar]
- Santos, M. R. 2004, MNRAS, 349, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Somerville, R. S., Lee, K., Ferguson, H. C., et al. 2004, ApJ, 600, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., & Ouchi, M. 2011, ApJ, 728, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Taniguchi, Y., Ajiki, M., Nagao, T., et al. 2005, PASJ, 57, 165 [NASA ADS] [Google Scholar]
- Tanvir, N. R., Fox, D. B., Levan, A. J., et al. 2009, Nature, 461, 1254 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tilvi, V., Rhoads, J. E., Hibon, P., et al. 2010, ApJ, 721, 1853 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [Google Scholar]
- Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Willis, J. P., & Courbin, F. 2005, MNRAS, 357, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Willis, J. P., Courbin, F., Kneib, J.-P., & Minniti, D. 2008, MNRAS, 384, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Delorme, P., Reylé, C., et al. 2010, AJ, 139, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, A., & Saslaw, W. C. 2011, ApJ, 729, 123 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Images of the CFHTLS-D4 (left), GOODS-South (centre), and Bullet Cluster (right) fields as in the final NB1060 image stacks. The inner and outer black contours on the Bullet Cluster image represent the regions where the gravitational amplification is respectively ≥ 2.5 (Δm ≤ −1) and ≥ 1.2 (Δm ≤ −0.2) for a source at redshift z = 7.7. |
| In the text | |
 |
Fig. 2 Transmission curves of the HAWK-I broad band and narrow band filters corresponding to the observations made as part of our large programme. The inset shows the profile of the NB1060 filter. |
| In the text | |
 |
Fig. 3 Completeness levels of the NB1060 images for the three observed fields. The coloured areas correspond to the Poissonian errors on the number counts in the corresponding magnitude bin. The triangles indicate the 5σ magnitude limits. |
| In the text | |
 |
Fig. 4 The comoving volume V(L) sampled by the NB1060 images as a function of Lyα luminosity. The two dashed curves correspond to the two blank fields (green – CFHTLS-D4; red – GOODS-S). The thin black curve corresponds to the Bullet Cluster. The thick black curve is the total comoving volume corresponding to the three fields. The Lyα luminosity corresponds to a 5σNB1060 limiting magnitude, assuming a 70% average conversion factor between the Lyα luminosities and NB1060 magnitudes (see text). |
| In the text | |
 |
Fig. 5 Parameters of the z = 7.7 luminosity function excluded at 85% and 99% confidence levels from our data, assuming the Schechter formalism and a fixed faint end slope α = −1.5 unless otherwise stated. Filled circles correspond to the best fit LF parameters at z = 5.7 (blue) and z = 6.5 (red) from Kashikawa et al. (2011). The ellipses correspond to the 3σ confidence levels for these datapoints. Open circles correspond to the best fit LF parameters of the photometric samples of Ouchi et al. (2008) at z = 3.1 (magenta) and z = 5.7 (blue) and of Ouchi et al. (2010) at z = 6.5 (red). The ellipses correspond to the 2σ confidence levels for these datapoints. The filled square symbols correspond to the best fit LAE LF parameters at z = 5.7 (blue) and z = 6.5 (red) from Hu et al. (2010). The plain (resp. dotted) black lines correspond to the 85% and 99% confidence levels corresponding to no detections in our HAWK-I data (this work), assuming a conversion factor of 70% (resp. 100%) between the NB1060 and Lyα fluxes. The dark (resp. light) grey zones correspond to the range of 85% (resp. 99%) confidence levels for conversion factors between 70% and 100%, as delimited by the plain and dotted lines. Similarly, the lines and hatched zones in magenta colour correspond to the 85% and 99% confidence levels when adding to our work the null spectroscopic confirmation of the five brightest z = 7.7 LAE candidates of Hibon et al. (2010). |
| In the text | |
 |
Fig. 6 Cumulative Lyα luminosity functions. The blue (resp. red) lines show the cumulative luminosity functions at z = 5.7 (resp. z = 6.5) from Ouchi et al. (2008) (dotted-dashed lines), Hu et al. (2010) (plain lines) and Kashikawa et al. (2011) (dotted lines). The transitions to thin lines indicate the range of the luminosities probed by the observations. A fixed faint end slope of –1.5 is assumed. The parameter space probed by the HAWK-I observations is delimited by the black line, with the black dashed line corresponding to the HAWK-I observations and the null detection of the bright candidates of Hibon et al. (2010) mentioned in the text. The green dotted line corresponds to a 60% evolution in density of the Hu et al. (2010) LF, and the short-dashed-long-dashed line corresponds to a 60% evolution in luminosity of the Ouchi et al. (2010)z = 6.5 LF. The red filled diamond corresponds to the Iye et al. (2006) LAE detection at a redshift of 6.96. The black open diamonds correspond to the Vanzella et al. (2011) LAE detections at redshifts of 7.008 and 7.109. The magenta downward-pointing filled (resp. open) triangles are the photometric candidates at z = 7.7 from Tilvi et al. (2010) (resp. Krug et al. 2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


