| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201117034 | |
| Published online | 01 February 2012 | |
Spectral and spatial observations of microwave spikes and zebra structure in the short radio burst of May 29, 2003
1
Key Laboratory of Solar Activity, National Astronomical Observatories,
Chinese Academy of Sciences,
20A, Datun Road, 100012
Beijing
PR China
e-mail: gchernov@bao.ac.cn
2
N. V. Pushkov Institute of Terrestrial Magnetism,
Ionosphere and Radio Wave Propagation
Troitsk, Moscow
region
142190,
Russia
e-mail: gchernov@izmiran.rssi.ru
3
Institute of Solar-Terrestrial Physics of Siberian Branch of
Russian Academy of Sciences, 126a
Lermontov Street, 664033
Irkutsk,
Russia
e-mail: sych@iszf.irk.ru
Received: 6 April 2011
Accepted: 5 November 2011
Context. The unusual radio burst of May 29, 2003 connected with the M1.5 flare in AR 10368 has been analyzed. It was observed by the Solar Broadband Radio Spectrometer (SBRS/Huairou station, Beijing) in the 5.2–7.6 GHz range. It proved to be only the third case of a neat zebra structure appearing among all observations at such high frequencies. Despite the short duration of the burst (25 s), it provided a wealth of data for studying the superfine structure with millisecond resolution (5 ms).
Aims. We localize the site of emission sources in the flare region, estimate plasma parameters in the generation sites, and suggest applicable mechanisms for interpretating spikes and zebra-structure generation.
Methods. We analyze of flare area structures and spectral parameters of millisecond spikes and their radio sources. We then interpret the superfine structure in the framework of known models.
Results. Positions of radio bursts were obtained by the Siberian Solar Radio Telescope (SSRT) (5.7 GHz) and Nobeyama radioheliograph (NoRH) (17 GHz). The flare configuration includes two systems of loops with the common base near the N-spot. The loop bases coincide with polarized emission sources at 17 GHz. The sources in intensity gravitated to tops of short loops at 17 GHz, and to long loops at 5.7 GHz. Short pulses at 17 GHz (with a temporal resolution of 100 ms) are registered in the R-polarized source over the N-magnetic polarity (extraordinary mode). The positions of the subsecond pulse sources at 5.7 GHz change from pulse to pulse and are level with the tops of some loops over the magnetic field’s neutral line. Dynamic spectra show that all the emission comprised millisecond pulses (spikes) of 5–10 ms duration in the instantaneous band of 70 to 100 MHz, forming the superfine structure of different bursts, essentially in the form of fast or slow-drift fibers and various zebra-structure stripes. Five scales of zebra structures have been singled out. The occurrence of the spikes is associated with the formation of two new radio sources with different polarities, which appeared simultaneously on SSRT and NoRH maps. This took place after new magnetic fluxes of opposite polarity had emerged in the leading spot and a new magnetic “delta” configuration had been formed.
Conclusions. As the main mechanism for generating spikes (as the initial emission) we suggest the coalescence of plasma waves with whistlers in the pulse regime of interaction between whistlers and ion-sound waves. In this case one can explain the appearance of fibers and sporadic zebra-structure stripes exhibiting the frequency splitting.
Key words: Sun: flares / Sun: radio radiation / Sun: general
© ESO, 2012
1. Introduction
Fast solar radio bursts lasting a few milliseconds on the background of long-term continual radio emission in decimeter and microwave ranges have already been studied for more than twenty years (Benz 1986). They are considered to be tied to the elementary, primary energy release in a flare area (Benz & Güdel 1987). The report by Slottje (1978) of fully polarized spikes in a microwave event was generally considered evidence of species of spikes that are entirely different from fast bursts at lower frequencies. Subsequent observations by Stahli & Magun (1986) have confirmed the exceptionality of the phenomenon at microwaves. The typical duration of single spikes are 50–100 ms around 250 MHz, and it decreases to 10–50 ms at 460 MHz and up to 3–7 ms at 1420 MHz (Benz 1986). Rozhansky et al. (2008) have gathered all currently available measurements of spike duration and find a power law with exponent 1.29 for the spectral range 237–2695 MHz. This law predicts that the duration of spikes at f > 4.5 GHz should be less than 2 ms, which is well below the spectrometer temporal resolution.
Microwave spikes always have a duration <10 ms and usually appear in clusters where spikes are randomly distributed in the frequency-time plane. It is generally agreed that spikes are non-thermal, coherent emission that is closely connected with the particle acceleration and energy release in flares, and during subsequent years interest in researching spikes increased. Benz (1985; 1986) described spikes in the decimeter range at the base of observations with the digital spectrometer IKARUS (Zurich). In five events, clear time and frequency profiles were presented; a good correlation was found with type III bursts and hard X-ray bursts. From the flare configuration, a typical upper limit is found to the dimension of spike sources of 200 km. It was proposed that the observed fragmentation in the radio emission should already occur in the exciter thanks to the fragmentation of the primary energy release (Bastian et al. 1998).
With a diameter of 200 km and for a circular source, the brightness temperature of spikes is up to 1015 K. Only a coherent emission process can reach such intensity. Fleishman & Melnikov (1998) propose exhaustive review of all basic mechanisms of the excitation of spikes and their relevance to the observed parameters. Because it is based on the observations of spikes at the harmonic frequencies and the partial registrations of the radio emission of spikes in the extraordinary mode, they conclude that the spikes can only be excited by the cyclotron maser mechanism (the loss-cone instability of the first and second electromagnetic cyclotron harmonics). The electron cyclotron maser mechanism is examined in Fleishman & Melnikov (1998) in detail. The basic objection against this mechanism comes from many authors’ estimations of the absorption of radio emission at the third gyro-resonance level in the corona. Furthermore, this mechanism is only effective in those sources where the ratio of plasma and cyclotron frequencies is less than unity (ωpe/ωBe < 1), while practically all observational data provide evidence of the inverse relationship (ωpe/ωBe ≫ 1), not only in the meter but even in the microwave range.
Fleishman et al. (2003) only propose indirect evidence of the ratio ωpe/ωBe ≤ 1, related to the flat spectrum of gyrosynchrotron emission. This means that no indication of the Razin effect in the spike-producing bursts is present because the Razin effect begin to suppress the low-frequency part of the spectrum for the ratio ωpe/ωBe > 1. However a contribution into low-frequency part can give another radiation mechanism (for example, plasma emission). Besides this, some important properties of spikes have not been taken into account by Fleishman & Melnikov (1998), and Chernov et al. (2001) considered an alternative generation mechanism based on the interaction of Langmuir waves with ion-sound waves.
Analyzing the burst radio emission fine structure enables us to identify acceleration mechanisms of fast particles and their propagation in a flare area. Such investigations become effective if the positions and sizes of radio sources and radio emission polarization are measured concurrently with observations of the dynamic spectrum. Then we can estimate the radiating mode and generation mechanisms (Meshalkina et al. 2004). The sources of subsecond pulses can be localized, if they occur in the operating frequency bands of the Siberian Solar Radio Telescope (SSRT) at about 5.7 GHz. Such a set of observations was carried out on May 29, 2003 for a small microwave burst of only ~20 s duration, but enjoying more variety in the fine structures. The burst was remarkable for all its parameters: all emission comprised millisecond spikes, for ten seconds the spikes grouped in the form of fast-drift bursts, slow-drift fibers, and zebra-structure (ZS) stripes on five scales according to the frequency separation and stripe drift. The radio emission polarization was weak, but had different signs in different structures and changed with time. Such a combination of fine and superfine structures is of great interest to check known radio emission generation mechanisms.
 |
Fig. 1 The intensity profiles recorded by Nobeyama spectropolarimeters a)–c), f), g), SBRS d), SSRT e) (including the quiet Sun level) in the interval 02:12:55–02:13:25 UT. The vertical dashed lines mark the interval with the fine structure at 5.7 GHz.) |
We have previously described several phenomena in which millisecond spikes made up the superfine structure for other elements in the fine structure (e.g. ZS-stripes) (Chernov et al. 2003, 2006). But at that time, these were long-term events in which the conditions for forming such a superfine structure were being evolved over several hours, whereas this short-term phenomenon exhibited all the variety for 5 s, when it was immediately obvious that all the emission consisted of millisecond spikes. And, as opposed to many other events, here we can register the position of radio sources. Thus, in deciding on a model, it is necessary to consider this main circumstance. We should based it on the condition that the emission of millisecond spikes is primary, and in one source all the variety of fine structures in the form of fibers and zebra stripes develop over several seconds.
Spectral data and time intensity profiles from different observatories are discussed in Sect. 2. SSRT data on the positions of radio sources at 5.7 GHz are compared with the Nobeyama radioheliograph data at 17 GHz. Section 3 discusses observations and possible radio emission mechanisms.
2. Observations
2.1. Instruments
The extraordinary phenomenon of May 29, 2003 was discovered in the dynamic spectra of the Solar Broadband Radio Spectrometer (station Huairou) in the frequency band of 5.2 to 7.6 GHz. 120 frequency channels in this band (every 20 MHz) provide the 5 ms temporal resolution in the right (R) and left (L) circular polarization (Fu et al. 2004).
We used microwave total flux records from Nobeyama Radio Polarimeters NoRP, (Torii et al. 1979; Shibasaki et al. 1979; Nakajima et al. 1985) at 1, 2, 3.75, 9.4, and 17 GHz. The time resolution of routine NoRP data available at the NoRP Web site is 1 s, and for flares it is 0.1 s. We used the images obtained by Nobeyama Radioheliograph (Nakajima et al. 1994) at 17 (I,V) (temporal resolution is 0.1 s). The spatial resolution is 10″.
Positions and sizes of the radio sources were determined from observed data obtained at the SSRT, cross-shaped radiointerferometer operating in the 5.67–5.79 GHz frequency range (Smolkov et al. 1986; Grechnev et al. 2003). Two-dimensional solar disk maps are acquired every two to three minutes depending on the solar declination and the hour angle of observations. The full temporal resolution of one-dimensional scans is ~14 ms at the spatial resolution of ~15″. Time profiles of intensity (I = R + L) and polarization (V = R − L) of fast bursts are regularly put into the SSRT database on the website http://badary.iszf.irk.ru/Ftevents.php. Widths of one-dimensional SSRT diagrams, when the radio burst was recorded, were 16″ for the north–south antenna beam and 21″ for the east–west beam. Inclination angles to the central meridian of the Sun were –36° and 39°, respectively.
2.2. Observed data
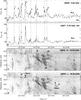 |
Fig. 2 Comparison of the time profiles recorded at SBRS a) and SSRT b) and the dynamic spectrum (c), (d) registered by the SBRS spectropolarimeter. The dark details correspond to the increased emission. The horizontal dashed line c) denotes the SSRT receiving frequency at 5.7 GHz. The calibration was performed using the SSRT-registered background burst. Arabic numerals (a), b), dashed vertical lines) mark the maximum moments of subsecond pulses recorded by the SSRT. |
The May 29, 2003 short radio burst of ~20 s duration in the main phase (02:13:00–02:13:20 UT) was related to the flare in the southen active region 10368 (S37E03), M1.5/1F in the GOES classification (02:09–02:24 UT). It occurred during the decay phase of a larger flare (X1.2) with a maximum at 01:05 UT, tied to another region 10365 (S06W37).
Figure 1 gives a general picture of this phenomenon at five frequencies of the Nobeyama spectropolarimeters and simultaneous observations at the SSRT and the SBRS spectropolarimeter at 5.7 GHz. The total duration of the radio burst was about 1.5 min. The maximum flux (~180 sfu) was registered at frequencies around 9.4 GHz (1 sfu = 10-22 Wm-2 Hz-1). It shows the interval with the fine structure at 5.7 GHz, located just between 3 and 9 GHz maxima (including all ZP stripes). It is seen that the maximum of background burst spectrum is located near 9 GHz, and it is late for three seconds relative to maximum on 3.75 GHz (the intensity scale for NoRP is in solar flux units (sfu)).
Figure 2 presents the intensity (Stokes parameter I) and polarization profiles (Stokes parameter V, lower curve) of the SBRS spectropolarimeter at 5.68 GHz (a) and the SSRT (Stokes parameter I, the NS line)(b) and the dynamic spectra in the left and right polarization of the SBRS spectrometer in the 5.2–7.6 GHz frequency band (c, d) in the interval marked off in Fig. 1. To remove the hardware interference we prepared a wavelet cleaning of the dynamic radio spectrum (Sych & Yan 2002) with deleted high-frequency noise around 13 Hz along the frequency channels. This technique allows the original solar signals from noise component to be separated.
The continual emission at 5.7 GHz was weakly polarized (the left sign within the limits of errors made up 5%). Nearly all the fast bursts were righthand circularly polarized (~20%). The amplitude of RCP and LCP at the dynamic spectra in Figs. 2c, d are identical, which points to a weak polarization degree, which is clearly visible on the ratio between polarization and intensity curves (Fig. 2a). This behavior of polarization is characteristic of the entire range of 5.2 to 7.6 GHz.
The emphasis will be on analyzing the fine structure in the interval 02:13:00–02:13:06 UT. The similarity between amplitudes and shapes of the subsecond pulses measured independently by two spaced instruments indicates that the observed fine time structure has a solar origin. The amplitude of the subsecond pulses is relatively high and reaches up to 60 sfu.
Various structures with relatively narrow instantaneous spectrum bands were observed in the background of the continuum emission (Figs. 2c, d). Among them are some fibers whose emission frequency varied with time. The spectrum also has several zebra structures separated into intervals.
It is worth noting that pulses 1 and 4 correspond to the intersection of the SSRT receiving band by bursts that drift to low frequencies in the dynamic spectra (and pulse 2 – to high frequencies); pulses 3 and 5 – to fibers, which drift in the opposite direction and look like fiber bursts. The sixth pulse is the superfine structure of the zebra-stripe, low-frequency edge. Pulses 7 and 8 are close to the horizontal zebra-structure stripe in episode IV; here, pulse 7 has inverse polarization.
Spectra in Figs. 2c, d demonstrate that all the emission comprises fine-structure details in the form of pulses (spikes). Their duration is limited to one pixel; i.e., it is at the limit of the 5 ms temporal resolution (rarely to two pixels, ~10 ms). They occupy the frequency band in the spectrum of ~70 to 100 MHz. Their band and duration might be below the resolution limit. The continual background burst also exhibits the spike structure. Groups of spikes create various fine-structure forms: fast and slow-drift fibers. The brightest (most intense) ones form different zebra-structure stripes.
 |
Fig. 3 The positions of radio sources at 5.7 GHz (SSRT) and 17 GHz (NoRH) superimposed on the MDI magnetogram. The orange dashed line indicates the position of the left polarized local source at 5.7 GHz at 02:17:54.8 UT. The dash-and-dot line shows the position of the left polarized background source of the burst at 17 GHz (extended southwestward) at 02:13:00 UT. The straight yellow crosses are the positions of spike sources 1–8 corresponding ones in Fig. 2. |
At 17 GHz, all subsecond pulses were only registered in the R-channel when the L-polarity emission background increased. The correlation curve of the burst in the polarization channel displays the origin of the fine temporal structures (pulses) with 300 ms periodicity. We can consider taking sensitivity curves into account for the appearance of fine spatial details about small angular size of pulse sources (<20″). To verify the parameters of observed R-polarity pulses during the maximum activity (02:13:00-02:13:06 UT), we synthesized the radio images at 17 GHz with 100 ms cadence, prepared the wavelet spectrum of amplitude profile for the new R-source, and constructed global wavelet spectrum (GWS-spectrum). This spectrum is shown for the SSP-related periods ≈300–400 ms. Comparing those values with the obtained periods of intensity oscillations in the SBRS dynamic spectrum (5.2–7.6 GHz) shows the presence of maxima oscillation in this period range. We can suppose that these periods can be considered as chains of the spikes in SBRS spectra.
2.3. Zebra structure
The zebra-structure fragments are shown in the lower panels (c, d) of Fig. 2. Drift ZS stripes of different frequency scales were observed for four seconds in a wide frequency range (5.8–7.2 GHz). All the stripes were made up of isolated pulses. The shortest ZS episode I (around 7 GHz) did not contain clear stripes. Such ZS behavior is known in the literature as braided ZS (Slottje 1981). In episode II, the frequency drift of stripes df/dt ≈ 1.3–1.5 GHz s-1 with a frequency separation between the stripes Δf ≈ 300–350 MHz. In episode III, df/dt ≈ 3.2–3.6 GHz s-1 with Δf ≈ 170–200 MHz. From approximately 02:13:03.3 UT, two neat almost stationary stripes (IV) with a frequency separation of 450 MHz appeared between 5.8 and 6.4 GHz. Fragments of slow-drift stripes are visible between them. After 02:13:03.8 UT they might have been taken for the frequency splitting of two main stripes. Nearly 1.5 s after this fragment, in the interval of 02:13:05.4 to 02:13:05.8 UT at 6.6–7.6 GHz, there were three more ZS stripes (V) with df/dt ≈ 1500 MHz/s and Δf ≈ 250 MHz. They were weak and diffuse, but had a spike structure and occurred with additional fragments between stripes (frequency splitting). There was also a very short fragment of small-scale ZS at 02:13:03.3 UT at ~7.150 GHz: the frequency separation was ~40 MHz; the width of these two stripes in the emission at the limit of the instrument resolution ~20 MHz.
At lower frequencies on SBRS spectra, 2.6–3.8 GHz, there was no ZS at that time (02:13:00–02:13:05 UT). Notable there are only several groups of drift spikes of ~20–30 ms duration each. The pattern of activity differed markedly from what is described in the range of 5.2 to 7.6 GHz. The main difference is associated with the lack of many pulses. Though the majority of bursts of 200–300 ms duration contain some inhomogeneity, they do not exhibit the superfine spike structure.
In the decimeter range (1–2 GHz), there were no spikes. The patch bursts were even more prolonged (>0.5 s) and, drifting gradually to high frequencies, formed a structure resembling a type II burst in its initial frequencies.
2.4. The flare area structure
The configuration of flare structures in the active region has been investigated using the time series of radio maps in intensity and polarization obtained at NoRH at 17 GHz. During the flare two sources of polarization were revealed: a compact source with righthand polarization in the west (R) (marked as B in Fig. 3) near the N-spot and a region in the east, extended from north to south with oppositely directed circular polarization (L). This region exhibited two centers of brightness, on the LN and LS edges (marked as A and C in Fig. 3). The LS source position corresponded to a small isolated N-polarity region; the north LN source appeared near the S-polarity spot. The combination of all the data on the positions of radio sources is presented in Fig. 3.
The flare configuration may be expected to be based on two loop systems R − LS (long) and R − LN (short). The presence of a shorter loop with bases in R and LS polarized emission centers is confirmed by the location of emission intensity center at 17 GHz between them. Between the bases of the second, longer, and higher loop system, there is a flare emission region at 5.7 GHz, extended along the photospheric field neutral line.
The background in Fig. 3 is the MDI magnetogram taken for the later period in order to show the evolution of the field “delta” – configuration (Kunzel et al. 1960; Bray & Loughhead 1964; Severny 1965). The thin black lines (dashed lines are the S-polarity, solid lines the N-polarity) indicate magnetic structures; the wide stripe is the neutral line. The coordinates of spike source centers were obtained using the projection method by comparing one-dimensional NS and EW scans (Fig. 4) with the maximum accuracy of 5 to 10″.
The spikes were weakly polarized for the most part, and so there is no point in determining the wave type. Even for spikes 3 and 4 with moderate polarization (20–30%), the wave type determination encounters difficulties in accurately assessing the magnetic field polarity.
Analysis has revealed that there were three emerging magnetic structures during the field “delta” – configuration evolution. They are lettered A, B, and C. The positions of SSRT spikes group together just in the place where structure A emerged. All fast bursts at 17 GHz are located at structure B. The large stripes (green and red) denote possible flare loops. In their common base, the highest magnetic field intensity near the photosphere was ~800 G. The main process associated with the occurrence of R-polarized pulses at 17 GHz is the appearance of a new R source.
The positions of the spike source centers at the SSRT receiving frequency were estimated from the projection profiles (scans) of sources shown in Fig. 4. The SSRT diagram did not exhibit broadening of the spike sources, therefore their sizes might be assessed as <15″.
The assumptions about the magnetic loop structure are confirmed by comparison of the time variation of emission fluxes (Fig. 5) from the sources marked as A, B, and C in Fig. 3. It is worth noting that the emission from the short loop exhibits a higher variability on time scales to 0.1 s – the temporal resolution of observations at 17 GHz (positions of short pulse sources). In integral spectra at low frequencies, the main contribution is made by long loops; at high frequencies, by short loops. Comparison of polarization signs with directions of the magnetic field in the sources points to the emission of an extraordinary wave in the background flare burst that conforms to the gyrosynchrotron emission mechanism (Fig. 3).
2.5. Brief conclusions from the observations
-
1.
The flare consists of two loop systems with close N-bases andspaced S-bases (flare of type Hanaoka 1999). The flare initiationis associated with the dynamics of the isolated S-region, theformation of which led to the “delta” – configuration of the flarearea.
-
2.
The microwave emission spectra in both loops suggest the gyrosynchrotron nature of the emission with frequencies of the spectra maxima as evidence that in short loops there is a larger magnetic field and a greater number of accelerated electrons.
-
3.
The sources of R-polarized pulses at 17 GHz were located in the N-base of the long flare loop, and narrow-band structures at 5–7 GHz at the tops of the long loops over the neutral line.
-
4.
Fast pulses (spikes) of 5–10 ms in the instantaneous frequency band 70–100 MHz are superfine structures of various drift bursts, fibers, and zebra-structure stripes.
-
5.
Most pulses (in the spectrum 5.2–7.6 GHz) are moderately R-polarized.
-
6.
The zebra structure appeared about 3 s after the first spikes in the form of five patterns of stripes on different scales (in the frequency drift, stripe separation). Some stripes bifurcate (exhibited the frequency splitting).
-
7.
The significant difference between parameters of each zebra-structure pattern suggests that their sources resided in different magnetic loops (different footpoints or tops of the loops).
3. Discussion of observations and possible mechanisms
On May 29, 2003, about six hours before the flare under study in AR 10368, the process began of long-term magnetic field reconfiguration and development of a potentially hazardous (in terms of flare initiation) “delta” – configuration of the magnetic field. New magnetic fields emerged from under the photosphere, and local neutral lines appeared.
The onset of the background burst must have been tied to the onset of new magnetic flux emergence. Two new flare loop complexes were formed from new emerging magnetic structures related with R and L radio sources at 17 GHz. The position of the centers of the sources of spikes 1–8 indicates the electron fluxes in long loops.
The dynamic spectrum in the 5.2–7.5 GHz frequency band attests to the presence of several sources with similar physical conditions, and the positions of their sources allow us to assert that they are located near the tops of long magnetic loops. The frequency drift is directed predominantly to high frequencies that might be connected with the gradual density increase in density of flare loops during the flare. The density increases at different rates in different loops. The emission of narrow structures is formed by pulses with a frequency band of about 100 MHz and a duration of 5–10 ms.
 |
Fig. 4 Left: the time intensity profiles obtained from one-dimensional scans. Right: the one-dimensional NS and EW scans during the pulse 8: positions of the spike sources in intensity distributions relative to the background burst source (dotted line). The background burst scan was approximated by the Gaussian distribution (dashed line) to determine accurately the position of the burst maximum. The horizontal bar at the top shows the size of the point source at the spatial half-width. Profile magnitudes are in arbitrary units. |
The frequency drift of burst maximum to the high frequencies (Fig. 1) is possibly related to the motion of the accelerated particles downward. The background continuum burst is similar to type III burst with the reverse drift, and we analyze fast millisecond fine structures against its background.
3.1. Generation mechanisms
It is natural to attribute the weak emission of the entire background burst of about 25 s to the gyrosynchrotron emission of nonthermal electron fluxes with a wide energy spectrum (100–200 keV) flowing from a reconnection region down toward a transition layer. The R-polarization subsecond pulses at 17 GHz may be induced by more energetic quasi-periodic particle beams (Altyntsev et al. 2000). The emission of fine structures in dynamic spectra is associated with coherent mechanisms.
The mazer mechanism (ECME, Fleishman & Melnikov 1998) drops out because of the low-intensity magnetic field under the region of the sources (<200 G). In this case, the cyclotron harmonics above the tenth one become ineffective.
The plasma mechanism (beam instability) is quite possible (Zaitsev et al. 1987). It provides the millisecond duration for radio brightness pulses in a microwave range. This mechanism may first be associated with the reverse drift bursts (at 02:13:02 UT).
The interaction between plasma waves and whistlers in a pulse regime and the interaction between whistlers and ion-sonic waves are also distinct possibilities (Chernov et al. 2003; Chernov et al. 2001). The presence of whistlers in flare loops is confirmed by the appearance of fibers and zebra-structure stripes. This mechanism may even be preferable because it can explain the observable chaotic distribution of structures in the wide frequency range (all the emission consisted of spikes).
In this case, one can naturally explain the appearance of fibers and zebra structure by the same superfine structure in the form of millisecond pulses (Chernov 2006). The whistlers were gradually captured into the flare loops, and different loops gave stripes on different scales. The instantaneous emission band of an isolated pulse is determined from linear sizes of particle beams with small velocity dispersion (beam instability) or from sizes of whistler wave packets (in a model with whistlers).
 |
Fig. 5 The comparison of the time profiles of the individual sources A, B, C at 17 GHz with integral spectra. It is obvious that the source A emission profile is close to the integral emission profile at 2 GHz; source C, to that at 17 GHz. The intensity scale is in solar flux units (SFU). |
3.2. ZS model at DPR
The widespread mechanism of zebra structure under double plasma resonance (DPR) conditions (Zheleznyakov & Zlotnik 1975a,b; Winglee & Dulk 1986) is engaged when, at discrete levels, in the magnetic trap the upper hybrid frequency equals to an integer of electron cyclotron harmonics. This phenomenon may be used as an example to demonstrate the possible difficulties that the mechanism at DPR faces for explaining the zebra structure with sporadic stripes. Originally, it was developed on the condition that there are always DPR levels in the source, and only the presence of fast particles with loss-cone or ring (DGH) velocity distribution provides the excitation of the regular zebra structure of different modulation depths (depending on the particle energy spectrum) (Kuznetsov & Tsap 2007). The presence of such particles may be considered obvious, so that the absence of zebra-structure at the beginning of the burst suggests there are no DPR levels.
DPR levels cannot quickly appear and disappear in the corona. Processes of emergence of new magnetic fluxes and formation of new loops are very slow. Changes in height scales of density and magnetic fields may be associated only with flare ejections and shocks. With the ejection velocity taken as Alfvén velocity (≈1000 km s-1), the DPR levels (in view of the magnetic field line freezing-in) may shift the flare loop by half (green in Fig. 3) with sizes of ~10″ for approximately 7 s. This time exceeds the lifetime of zebra-structure stripes by an order of magnitude. The sporadic nature of ZS stripes, the wave-like drift of two stripes, their splitting, and the presence of isolated fibers with forward and reverse drifts rule out the existence of any regular DPR levels. Moreover, the validity of the DPR conditions in fine flare loops along which density and magnetic field strength vary only slightly is in doubt (Aschwanden 2004). At the same time, all the effects can be naturally explained in the joint model of zebra structure and fibers when plasma waves interact with whistlers (Chernov 2006).
The unique data on the position of radio sources of certain ZS stripes in the dm-range was obtained the first time in the recent paper by Chen et al. (2011). The comparative analysis of DPR and whistler models made by the authors should be verified by new, more accurate estimations based on real plasma parameters.
3.3. The model with whistlers
All papers discussing the DPR mechanism (and its upgrading) omit a very important feature of the fast particle distribution function with loss cone: the particles excite whistlers simultaneously, and all the dynamics of the distribution function and emissions depend on the interaction of fast particles with whistlers (Chernov 1996). Let us note first of all that whistler excitation growth rates in the microwave range exceed their value in the meter range (Yasnov et al. 2002). According to the model described in Chernov (2006) (Sect. 3.6), zebra-structure stripes are associated with the whistler excitation by the anomalous Doppler effect at the top of the magnetic particle trap. Whistler wave packets fill the magnetic trap and propagate downward (at a significant angle to the magnetic field) at a group velocity of ~109 cm s-1. The wave packet size in the corona is determined by the linear size of relaxation of the whistler-exciting fast particle beam (Formula (13.4) in Breizman 1987), see also the discussion of Formula (29) in Chernov (2006, 2010).
In the recent short critical review by Zlotnik (2010), the advantages of the DPR model and the main failures of the model with whistlers are refined. The author asserts that the theory based on the DPR effect is the best-developed theory for a zebra pattern origin at meter-decimeter wavelengths at the present time. It explains the fundamental ZP feature in a natural way, namely, the harmonic structure (frequency spacing, numerous stripes, frequency drift, etc.) and gives a good fit for the observed radio spectrum peculiarities with quite reasonable parameters of the radiating electrons and coronal plasma. The statement that the theory based on whistlers is only able to explain a single stripe (e.g., a fiber burst) was made in Zlotnik (2010) without the correct ideas of whistler excitation and propagation in the solar corona.
Zlotnik uses the term “oscillation period” of whistlers connected with a bounce motion of fast particles in the magnetic trap. Actually, the loss-cone particle distribution is formed as a result of several passages of the particles in the magnetic trap. Kuijpers (1975) explained the periodicity of fiber burst using this bounce period (~1 s). And if we have one fast injection of fast particles, whistlers (excited at normal cyclotron resonance) are propagated towards the particles, they disperse in space. Quasilinear effects therefore do not operate in normal resonance. ZP is connected instead with whislers excited at anomalous resonance during long-lasting injection. In such a case, waves and particles propagate in one direction, quasilinear effects begin operating, and their role increases with an increasing duration for injections. ZP is excited because the magnetic trap should be divided into zones of maximum amplification of whislers, separated by intervals of whistler absorption (see more details Chernov 1990). The bounce period does not interfere with this process, but it can be superimposed on ZP.
However, the whistler amplification length is always small (on the order of ≤108 cm in comparison with the length of the magnetic trap being >109 cm) for any energy of fast particles (Breizman 1987; Stepanov & Tsap 1999). According to Gladd (1983), the growth rate of whistlers for relativistic energies of fast particles decreases slightly if the full relativistic dispersion is used. In this case, the whistlers are excited by anisotropic electron distributions due to anomalous Doppler cyclotron resonance.
Later, Tsang (1984) specified calculations of relativistic growth rates of whistlers with the loss-cone distribution function. It was shown that relativistic effects reduce growth rates slightly. According to Fig. 8 in Tsang (1984), the relativistic growth rate is roughly five times less than the nonrelativistic growth rate. However, the relativistic growth rates increase with the perpendicular temperature of hot electrons. According to Fig. 5 in Tsang (1984), the growth rate increases about two times when the electron energy is increased from 100 to 350 keV, if only to keep fixed other parameters of hot electrons: loss-cone angle, ratio of gyrofrequency to plasma frequency, temperature anisotropy (T⊥/T∥ = 3).
Thus, it was already known long ago that the whistlers can be excited by relativistic beam with loss-cone anisotropy. Formula 13.4 in Breizman (1987), used as formula (29) in Chernov (2006) for evaluating the smallest possible relaxation length of beam, has no limitations in the value of energy for fast particles. Critical comparison of models has been repeated in Zlotnik (2010), only with a new remark concerning the Manley-Rowe relation for the brightness temperature of electromagnetic radiation in result of coupling of Langmuir and whistler waves: 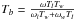 . She states that, since ωw ≪ ωl, in the denominator, only the first term remains and Tb depends only on Tl, and Tb ~ Tl; i.e., the process does not depend on the level of whistler energy1.
. She states that, since ωw ≪ ωl, in the denominator, only the first term remains and Tb depends only on Tl, and Tb ~ Tl; i.e., the process does not depend on the level of whistler energy1.
However, Kuijpers (1975) (formula (32) in p. 66) shows that the second term ωwTl should be ≫ ωlTw because Tl ≫ Tw. An analogous conclusion was made by Fomichev & Fainshtein (1988) with a more exact relation to three wave intensities (used by Chernov & Fomichev 1989, see also formula (11) in Chernov 2006). Therefore Tb in the process l + ω → t depends mainly on Tw. Our conclusion is that the entire magnetic trap can be divided into intermittent layers of whistler amplification and absorption remains valid for a broad energy range of fast particles. In Zlotnik (2010) the main matter that is ignored is that the model involves quasilinear interactions of whistlers with fast particles, allowing one to explain all the fine effects of the ZP dynamics, mainly the superfine structure of ZP stripes and the oscillating frequency drift of the stripes, which occurs synchronously with the spatial drift of radio sources.
For the central ZS frequency of 6.4 GHz, the ratio of the gyrofrequency to the plasma frequency 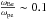 and the ratio of the cold plasma concentration to the hot particle one
and the ratio of the cold plasma concentration to the hot particle one 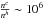 , we obtain the linear size of relaxation of ~2.8 × 106 cm. In the Avrett table model (Avrett 1981), this size corresponds to the change in the plasma frequency of ~350 MHz. This very frequency separation between ZS stripes was observed in Episode II (Fig. 2).
, we obtain the linear size of relaxation of ~2.8 × 106 cm. In the Avrett table model (Avrett 1981), this size corresponds to the change in the plasma frequency of ~350 MHz. This very frequency separation between ZS stripes was observed in Episode II (Fig. 2).
The large flare loop (green in Fig. 3) extends for about 20″. Whistlers should go from the top to the base at a group velocity of ~109 cm s-1 for ~0.7 s. It is the longest duration of stripes in ZS fragments II and IV. The shorter ZS episodes must have emanated from a smaller flare loop (red in Fig. 3). The Allen concentration model gives much the same plasma frequency gradient (for example, see Fig. IV.1 in Kruger 1979). It corresponds to the density height scale at these heights, about 107 cm.
We can determine the magnetic field strength from the frequency separation between stripes Δf ~ 350 MHz. The whistler group velocity peaks at the whistler frequency fω ~ 0.25fB. With the value of separation between emission and absorption taken as ~0.5 Δf and set equal to the whistler frequency, it is easy to obtain the electron gyrofrequency fB ~ 700 MHz (the magnetic field strength B ~ 250 G), which warrants our choice of the ratio 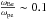 .
.
We consider ZS pattern IV: two stripes with slightly wave-like frequency drift (in zero value) and a large frequency separation, ~450 MHz. They are not identical, because the low-frequency stripe started 0.4 second early, and their intensity and frequency drift were not similar. Besides this the low-frequency stripe bifurcated two times, exhibiting the frequency splitting at 02:13:03.4 and 02:13:03.9 UT. The sources must have been located at the tops of different flare loops. Spike 6 (Fig. 2) is in the spectrum at the beginning of the low-frequency stripe, and according to the two-dimensional map, its source was at the top of the large flare loop (green in Fig. 3).
The absence of the frequency drift is likely to be tied to the propagation of whistler packets almost at the level of equal density at the top of the loop. In this case, whistlers may be excited by the normal Doppler effect, or more precisely, the scattering of fast particles by whistlers sets the distribution function into the oscillation regime when excitation by normal or anomalous Doppler effects is dominant. In a borderline case, both the effects work simultaneously, and at these moments, we can see the frequency splitting of ZS stripe because the excitation by different effects occurs with a frequency shift. This excitation may be referred to as the analog of the “fan” instability (for more detail, see Chernov 1996). In the meter range, this effect has been discussed twice to explain the frequency separation of ZS stripes and the wave-like frequency drift (Chernov et al. 1998; Chernov 2005). The change in the frequency drift of stripes at the “fan” instability is associated with the smooth change in the whistler group velocity direction. Episode III and the low-frequency ZS stripe from IV might be tied to the small flare loop (red in Fig. 3).
The ZS episode V at higher frequencies (6.7–7.6 GHz) with a frequency separation of ~300 MHz and the explicit stripe splitting occurred late in the phenomenon. It may be associated with a lower loop arcade. The same is true of the short fragment of ZS I, braided (in the terminology of Slottje 1981) and of the very short episode of the small-scale ZS at 02:13:03.3 UT at ~7.150 GHz: the frequency separation is ~40 MHz.
The sporadic nature of the fine structure suggests multiple pulsating acceleration of fast particles. However, the superfine spike structure is not necessarily determined by a pulsating acceleration as in Kuznetsov (2007). It is much more probable that the spike nature of the entire emission is formed by the pulsating mechanism of emission. ZS is generated by periodic whistler packets filling a magnetic trap. But whistlers should occupy the entire radio source and propagate in different directions. Spikes might therefore be related to the pulsating interaction of whistlers with ion-sound waves and subsequent coalescence with plasma waves. This mechanism is discussed in Chernov et al. (2001). In the microwave range it may be more effective because near the reconnection region the presence of nonisothermic plasma (Te ≫ Ti) is much more likely as a condition for ion sound excitation. ZS did not appear at lower frequencies (2.6–3.8 GHz), and there was no spike structure of the entire emission there. That is why we can say that the spike structure appeared only in regions of the source where whistlers existed.
However, at 5.2–7.6 GHz we could see many weak diffuse bursts with different frequency drifts, which did not exhibit this spike structure. Their polarization properties were similar to ZS ones. It can even be said that they were the extensions of ZS. They may therefore have been excited by the plasma mechanism at the upper hybrid frequency, when there were no conditions for DPR.
Kuznetsov (2008) proposes a new mechanism of superfine structure in which the emission modulation is associated with top-down propagation of MHD oscillations. But this mechanism only gives the superfine structure for ZS stripes, not for the whole emission, so the pulsating regime of whistlers remains preferable in our case.
3.4. New ZS models
Searching for solutions to difficulties in different models, recent papers have proposed several new mechanisms: the leakage of Z-mode trapped into regular inhomogeneities of plasma density (LaBelle et al. 2003), and various versions of the electromagnetic waves propagation through coronal inhomogeneities (Laptukhov & Chernov 2006; Barta & Karlicky 2006; Ledenev et al. 2006; Laptukhov & Chernov 2009). Two new exotic models have been proposed by Fomichev et al. (1988) (the explosive instability) and by Kovalev (2009) (periodic waves of electric charge). All these new mechanisms must be realized only in specific conditions. Their role in the ZS model hierarchy is still ill-defined (Chernov 2010).
4. Conclusion
We analyzed the unusual radio burst in the microwave range using spectral data from Chinese spectrographs in the 5.2–7.6 GHz frequency range and partially in the 2.6–3.8 GHz range and spatial data from SSRT and Nobeyama radioheliographs. It proved to be only the third case of a neat zebra structure appearing among all observations at such high frequencies. Despite the short duration of the burst (25 s), it provided a wealth of data for studying the superfine structure with millisecond resolution. The occurrence of the burst coincided with the formation of the magnetic field “delta” – configuration (for 3–5 h) as a precursor of the flare and with the appearance of local neutral lines.
All the emission in the spectrum in the 5.2–7.6 GHz frequency range consisted of spikes lasting 5–10 ms in the instantaneous frequency band of 70 to 100 MHz. These spikes make up the superfine structure of different drift bursts, fibers, and zebra-structure stripes. The zebra structure appeared about 3 s after the first spikes in the form of five patterns of stripes on different scales. The sources of some spikes were distributed along the flare loop.
The spikes were weakly polarized and had different signs. Their appearance concurred with the appearance of new strong R-polarized source at 17 GHz. The sizes of spike sources are estimated at <15″. Emission of spikes is generated during particle precipitation from the magnetic reconnection region down toward the footpoints of microloops. The spectral data point to an acceleration region height of ~15 000 km.
As the main mechanism for generating spikes (as initial emission) we suggest the coalescence of plasma waves with whistlers in a pulse regime of the interaction between whistlers and ion-sound waves. In this case, one can naturally explain the appearance of fibers and zebra structure with the same superfine structure in the form of millisecond pulses and the frequency splitting of zebra-structure stripes. Obviously some fast-drift bursts are excited by the beam instability in the pulse regime.
This approval was also used by Altyntsev et al. (2011), to reject the whistler model for ZS in this event
Acknowledgments
We are grateful to A. T. Altyntsev for his help in SSRT data processing and for the fruitful discussion of all results in this investigation. The authors thank B. L. Tan for valuable remarks on the manuscript. We also appreciate the Nobeyama observatory team for free access to the polarimeter and radioheliograph data. This work was supported by RFBR (grants 11-02-00757, 08-02-92204- GFNS, 09-02-92610-Ko, 09-02-00226, 10-02-00153-a) and by the Program of RAS No. 16. Y. Y. is supported by NSFC (10921303) and MOST (2011CB811401) grants. The research carried out by Dr. Robert Sych at National Astronomical Observatories (NAOC) was supported by the Chinese Academy of Sciences Visiting Professorship for Senior International Scientists, grant No. 2010T2J24. This research was supported by a Marie Curie International Research Staff Exchange Scheme Fellowship within the 7th European Community Framework Program.
References
- Altyntsev, A. T., Nakajima, H., Takano, T., & Rudenko, G. V. 2000, Sol. Phys., 195, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Altyntsev, A. T., Lesovoi, S. V., Meshalkina, N. S., Sych, R. A., & Yan, Y. 2011, Sol. Phys., 273, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J. 2004, Phys. Sol. Corona (Pruxis Publishing) [Google Scholar]
- Avrett, E. N. 1981, In The Physics of Sunspots, ed. By L. E. Cram, & J. N. Thomas, Sacramento Peak Obs., 235 [Google Scholar]
- Bárta, M., &Karlický, M. 2006, A&A, 450, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bastian, T. S., Benz, A. O., & Gary, D. E. 1998, ARA&A, 36, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, A. O. 1985, Sol. Phys., 96, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, A. O. 1986, Sol. Phys., 104, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, A. O., & Güdel, M. 1987, Sol. Phys., 111, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1964, Sunspots, Chapman and Hall, Ltd., London. [Google Scholar]
- Breizman, B. N. 1987, Voprosi teorii plazmi, ed. B. B. Kadomcev, Moscow Energoatomizdat, 15, 55 [Google Scholar]
- Chen, B., Bastian, T. S., Gary, D. E., & Jing, J. 2011, ApJ, 736, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P. 1990, Sol. Phys., 130, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P. 1996, Astron. Rep., 40, 561 [NASA ADS] [Google Scholar]
- Chernov, G. P. 2005, Plasma Phys. Rep., 31, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P. 2006, Space Sci. Rev., 127, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P. 2010, Res. Astron. Astrophys., 10, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P., & Fomichev, V. V. 1989, Soviet Astron. Lett., 15, 410 [NASA ADS] [Google Scholar]
- Chernov, G. P., Markeev, A. K., Poquerusse, M., et al. 1998, A&A, 334, 314 [NASA ADS] [Google Scholar]
- Chernov, G. P., Fu, Q. J., Lao, D. B., &Hanaoka, Y. 2001, Solar Phys., 201, 153 [Google Scholar]
- Chernov, G. P., Yan, Y. H., & Fu, Q. J. 2003, A&A, 406, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernov, G. P., Sych, R. A., Yan, Y., et al. 2006, Sol. Phys., 237, 2 [CrossRef] [Google Scholar]
- Fleishman, G. D., & Melnikov, V. F. 1998, Phys. Usp., 41, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Fleishman, G. D., Gary, D. E., & Nita, G. M. 2003, ApJ, 593, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Fomichev, V. V., Fainshtein, S. M. 1988, Sov. Astron., 32, 552 [NASA ADS] [Google Scholar]
- Fu, Q. J., Ji, H. R., Qin, Z. H., et al. 2004, Sol. Phys., 222, 167 [Google Scholar]
- Hanaoka, Y. 1999, PASJ, 51, 483 [NASA ADS] [Google Scholar]
- Gladd, N. T. 1983, Phys. Fluids., 26, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Grechnev, V. V., Lesovoi, S. V., Smolkov, G. Y., et al. 2003, Sol. Phys., 216, 239 [Google Scholar]
- Kovalev, V. A. 2009, Plasma Phys. Rep., 35, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, A. 1979, Introduction to Solar Radio Astronomy and Radio Physics (Dordrecht: Reidel), 162 [Google Scholar]
- Kuijpers, J. 1975, Collective wave-particle interactions in solar type IV radio source, Ph.D. Thesis, Utrecht University. [Google Scholar]
- Kunzel, H. 1960, Astron. Nachr., 285, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsov, A. A. 2007, Astron. Letters., 33, 319 [Google Scholar]
- Kuznetsov, A. A. 2008, Sol. Phys., 253, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsov, A. A., & Tsap, Yu. T. 2007, Sol. Phys., 241, 127 [NASA ADS] [CrossRef] [Google Scholar]
- LaBelle, J., Treumann, R. A., Yoon, P. H., & Karlicky, M. 2003, ApJ, 593, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Laptuhov, A. I., & Chernov, G. P. 2006, Plasma Phys., Rep., 32, 866 [Google Scholar]
- Laptuhov, A. I., & Chernov, G. P. 2009, Plasma Phys., Rep., 35, 160 [Google Scholar]
- Ledenev, V. G., Yan, Y., & Fu, Q. 2006, Sol. Phys., 233, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Meshalkina, N. S., Altyntsev, A. T., Sych, R. A., Chernov, G. P., &Yan, Yihua 2004, Sol. Phys., 221, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, H., Sekiguchi, H., Sawa, M., Kai, K., & Kawashima, S. 1985, PASJ, 37, 163 [NASA ADS] [Google Scholar]
- Nakajima, H., Nishio, M., Enome, S., et al. 1994, Proc. IEEE, 82, 705 [Google Scholar]
- Rozhansky, I. V., Fleishmann, G. D., & Huang, G.-L. 2008, ApJ, 681, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Severny, A. B. 1965, in Stellar and Solar Magnetic Fields, ed. R. Ltist, 238 [Google Scholar]
- Slottje, C. 1978, Nature., 275, 520 [CrossRef] [Google Scholar]
- Slottje, C. 1981, Atlas of fine structures of Dynamic Spectra of Solar Type IV-dm and Sme Type II Bursts, Utrecht Observatory. [Google Scholar]
- Stahli, M., & Magun, A. 1986, Sol. Phys., 104, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Smolkov, G. Ya., Pistolkors, A. A., Treskov, T. A., et al. 1986, Astrophys. Space Sci., 119, 1 [Google Scholar]
- Sych, R. A., & Yan, Y., 2002, ChJA& A, 2, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. V., & Tsap, Y. T., 1999, Astron. Rep., 43, 838 [NASA ADS] [Google Scholar]
- Shibasaki, K., Ishiguro, M., & Enome, S. 1979, Nagoya University, Research Institute of Atmospherics, Proceedings. 26, 117 [Google Scholar]
- Torii, C., Tsukiji, Y., Kobayashi, S., et al. 1979, Nagoya University, Research Institute of Atmospherics, Proceedings. 26, 129 [Google Scholar]
- Tsang, K. T. 1984, Phys. Fluids., 27, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Yasnov, L. V., Chernov, G. P., Yan, Y., & Fu, Q. 2002, Proc. 10th European SPM, Solar Variability: From Core to Outer Frontiers, Prague, (ESA SP 506), 791 [Google Scholar]
- Winglee, R. M., & Dulk, G. A. 1986, ApJ, 307, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitsev, V. V., Stepanov, A. V., & Sterlin, A. M. 1987, Sov. Astron. Lett., 11, 192 [NASA ADS] [Google Scholar]
- Zheleznykov, V. V., & Zlotnik, E. Ya. 1975a, Sol. Phys., 44, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznykov, V. V., & Zlotnik, E. Ya. 1975b, Sol. Phys., 44, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Zlotnik, E. Ya. 2009, Cent. Eur. Astrophys. Bull., 33, 281. [NASA ADS] [Google Scholar]
- Zlotnik, E. Ya. 2010, Solar-Terrestrial Physics, Collected articles, Sibirian Depatement of Russian Academy of Sciences Eds., (in Russian), 16, 49 [Google Scholar]
All Figures
 |
Fig. 1 The intensity profiles recorded by Nobeyama spectropolarimeters a)–c), f), g), SBRS d), SSRT e) (including the quiet Sun level) in the interval 02:12:55–02:13:25 UT. The vertical dashed lines mark the interval with the fine structure at 5.7 GHz.) |
| In the text | |
 |
Fig. 2 Comparison of the time profiles recorded at SBRS a) and SSRT b) and the dynamic spectrum (c), (d) registered by the SBRS spectropolarimeter. The dark details correspond to the increased emission. The horizontal dashed line c) denotes the SSRT receiving frequency at 5.7 GHz. The calibration was performed using the SSRT-registered background burst. Arabic numerals (a), b), dashed vertical lines) mark the maximum moments of subsecond pulses recorded by the SSRT. |
| In the text | |
 |
Fig. 3 The positions of radio sources at 5.7 GHz (SSRT) and 17 GHz (NoRH) superimposed on the MDI magnetogram. The orange dashed line indicates the position of the left polarized local source at 5.7 GHz at 02:17:54.8 UT. The dash-and-dot line shows the position of the left polarized background source of the burst at 17 GHz (extended southwestward) at 02:13:00 UT. The straight yellow crosses are the positions of spike sources 1–8 corresponding ones in Fig. 2. |
| In the text | |
 |
Fig. 4 Left: the time intensity profiles obtained from one-dimensional scans. Right: the one-dimensional NS and EW scans during the pulse 8: positions of the spike sources in intensity distributions relative to the background burst source (dotted line). The background burst scan was approximated by the Gaussian distribution (dashed line) to determine accurately the position of the burst maximum. The horizontal bar at the top shows the size of the point source at the spatial half-width. Profile magnitudes are in arbitrary units. |
| In the text | |
 |
Fig. 5 The comparison of the time profiles of the individual sources A, B, C at 17 GHz with integral spectra. It is obvious that the source A emission profile is close to the integral emission profile at 2 GHz; source C, to that at 17 GHz. The intensity scale is in solar flux units (SFU). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


