| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A79 | |
| Number of page(s) | 16 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201016083 | |
| Published online | 08 February 2012 | |
Modification of wave propagation and wave travel-time by the presence of magnetic fields in the solar network atmosphere⋆
1
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstrasse 6,
79104
Freiburg,
Germany
e-mail: nutto@kis.uni-freiburg.de
2
School of Physics University of Exeter,
Stocker Road,
Exeter, United
Kingdom, EX4
4QL, UK
Received: 5 November 2010
Accepted: 26 September 2011
Context. Observations of waves at frequencies above the acoustic cut-off frequency have revealed vanishing wave travel-times in the vicinity of strong magnetic fields. This detection of apparently evanescent waves, instead of the expected propagating waves, has remained a riddle.
Aims. We investigate the influence of a strong magnetic field on the propagation of magneto-acoustic waves in the atmosphere of the solar network. We test whether mode conversion effects can account for the shortening in wave travel-times between different heights in the solar atmosphere.
Methods. We carry out numerical simulations of the complex magneto-atmosphere representing the solar magnetic network. In the simulation domain, we artificially excite high frequency waves whose wave travel-times between different height levels we then analyze.
Results. The simulations demonstrate that the wave travel-time in the solar magneto-atmosphere is strongly influenced by mode conversion. In a layer enclosing the surface sheet defined by the set of points where the Alfvén speed and the sound speed are equal, called the equipartition level, energy is partially transferred from the fast acoustic mode to the fast magnetic mode. Above the equipartition level, the fast magnetic mode is refracted due to the large gradient of the Alfvén speed. The refractive wave path and the increasing phase speed of the fast mode inside the magnetic canopy significantly reduce the wave travel-time, provided that both observing levels are above the equipartition level.
Conclusions. Mode conversion and the resulting excitation and propagation of fast magneto-acoustic waves is responsible for the observation of vanishing wave travel-times in the vicinity of strong magnetic fields. In particular, the wave propagation behavior of the fast mode above the equipartition level may mimic evanescent behavior. The present wave propagation experiments provide an explanation of vanishing wave travel-times as observed with multi-line high-cadence instruments.
Key words: magnetohydrodynamics (MHD) / magnetic fields / Sun: chromosphere / Sun: magnetic topology / waves / Sun: helioseismology
Movies are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Classical helioseismology is the study of waves with frequencies below the acoustic cut-off frequency. These waves are trapped in the acoustic cavity of the Sun. In contrast, waves above the acoustic cut-off frequency, the so-called high frequency waves are able to travel freely into the solar atmosphere. Along their path through the atmosphere, these waves interact with the complex magnetic field that is present in the photosphere and the chromosphere. The detection of these running waves with instruments capable of recording several spectral lines at sufficiently high recording cadence, such as the Magneto-Optical filters at Two Heights (MOTH) instrument (Cacciani et al. 2003) or the Interferometric BIdimensional Spectrometer (IBIS) (Cavallini 2006), opened a new field in helioseismology, which can be broadly referred to as “seismology of the solar atmosphere” (Finsterle et al. 2004b). A Gabor wavelet analysis of Doppler time series stemming from high frequency waves observed with the MOTH instrument revealed an evanescent1 propagation behavior inside strong magnetic field concentrations, although propagating waves are expected (Finsterle et al. 2004c). Vecchio et al. (2007) probe atmospheric oscillations of a quiet Sun network region by simultaneously recording line-of-sight velocities of photospheric and chromospheric lines with the IBIS-spectrometer at the Dunn Solar Telescope on Sacramento Peak Observatory. A Fourier analysis, yielding phase differences and the coherence between the recorded time series, revealed evanescent behavior of the waves and vanishing phase shifts at the locations of the magnetic network.
The interpretation and the characterization of the interaction of the magneto-acoustic waves with the magnetic field from observational data is still difficult (Finsterle et al. 2004c; Haberreiter et al. 2007). For the interpretation of the observations, it is helpful to look at numerical simulations of wave propagation through a magnetically structured solar model atmosphere. In the past, these simulations have been carried out for rather idealized atmospheric models and magnetic configurations. Rosenthal et al. (2002) investigated numerically the interaction of waves with simple, exemplary magnetic field geometries to understand the variety of wavelike and oscillatory processes observed in the solar atmosphere. Bogdan et al. (2003) extended this work to focus on the coupling between fast and slow magneto-acoustic waves that takes place in a thin, quasi-one-dimensional layer, where the sound speed, cs, and the Alfvén speed, cA, are of comparable magnitude. Their numerical experiments demonstrate how the fast and slow magneto-acoustic waves emerge, interact, and propagate within a two-dimensional magneto-atmosphere. Khomenko & Collados (2006) consider the wave propagation through a thick, hydro-static flux-tube model representing a sunspot. They find that the fast magnetic mode, which propagates in the region where the magnetic field dominates (cA > cs), does not reach the chromospheric layer due to wave refraction, which is primarily caused by vertical and horizontal gradients in Alfvén speed. Only the slow acoustic mode can propagate upwards along the magnetic field into the chromosphere. Hasan & van Ballegooijen (2008) study short-period magneto-acoustic waves propagating through magneto-hydrostatic field concentrations in order to test whether slow acoustic modes provide enough energy to heat the magnetic network. They find that acoustic waves in the ambient medium convert into fast magnetic waves inside the field concentration, where they refract and travel rapidly across the flux-tube without forming any shock waves, hence do not contribute to the heating of the magnetic network. In contrast, Vigeesh et al. (2009) determine the acoustic emission from magnetic flux concentrations to the ambient medium. The emission stems from the conversion of fast magnetic modes inside the flux concentrations. The coupling between the different modes of magneto-acoustic waves at the layer where the sound speed and Alfvén speed are comparable, has been intensively studied analytically and numerically by Schunker & Cally (2006) and Cally (2007) for homogenous magnetic fields with a variety of field inclinations. They determine and discuss the principal parameters governing the process of mode conversion. By using ray theory, they are able to show the propagation path of the different modes with respect to regions where the Alfvén speed is either higher or lower than the speed of sound.
The aforementioned investigations exemplify the progress that has been made in understanding the behavior of magneto-acoustic waves in a two-dimensional magneto-atmosphere. To achieve a clearer understanding of observations, simulation data are analyzed using techniques similar to those applied to real observations. Thus, Cameron et al. (2008) and Shelyag et al. (2009) simulate the propagation of waves across a strong, static magnetic field concentration representing a sunspot, which is then analyzed by means of local time-distance helioseismology.
In the present paper, we report on two-dimensional simulations of magneto-acoustic wave propagation in a model of the solar atmosphere including granular velocity fields and complex magnetic fields. We understand this as a first attempt to increase the degree of physical realism in the underlying model – the treatment in three spatial dimensions is currently in progress. We use the same technique to determine wave travel-times as used in the analysis of observational data.
In Sect. 2, we give a short description of the setup of the initial atmospheric model and in Sect. 3 we discuss the wave propagation in the solar atmosphere. The wave travel-times are quantitatively analyzed in Sect. 4, while the power maps are studied in Sect. 5 The results are discussed in Sect. 6. Conclusions are drawn in Sect. 7.
1.1. Definitions
Speaking of modes, mode conversion, and mode transmission, the terminology can sometimes be confusing. In two spatial dimensions, we deal with only the slow and the fast magneto-acoustic mode but their physical nature depends on whether they propagate in a region where cA > cs or in a region where cA < cs, where cA is the local Alfvén speed and cs the local speed of sound. Wherever it is not obvious, we explicitly state whether the discussion concerns the region where cA < cs, which is generally below the equipartition level where cA = cs, or whether it concerns the region where cA > cs, which is generally above this level. For brevity, we call the waves in the following acoustic or magnetic depending on the predominance of the thermal or magnetic nature of their restoring forces, respectively. Thus, in the regime where cA < cs, we speak of the fast magneto-acoustic wave as the fast acoustic mode and of the slow magneto-acoustic wave as the slow magnetic mode. In the regime where cA > cs, the labels fast and slow apply to opposite modes – we speak of the fast magneto-acoustic wave as the fast magnetic mode and of the slow magneto-acoustic wave as the slow acoustic mode. In this way, we unambiguously indicate the physical nature of the wave as we speak of the different modes. When a wave travels across the level where cA = cs, it can change nature and label. Adhering to the terminology of Cally (2007), we call it mode conversion, when the physical nature of the wave changes from being acoustic to magnetic or vice versa. If the wave changes from slow to fast or vice versa without changing physical nature, we call this process wave transmission. We call the level or contour where cA = cs the equipartition level according to the terminology used by Cally (2007). We note, however, that this level does not exactly but approximately correspond to the equipartition between thermal and magnetic energy, namely, β = 1. We call β the ratio of the thermal to the magnetic energy density, β = pgas/(B2/8π).
2. Model and method
2.1. The code
The simulations are carried out in a dynamic solar background model using the CO5BOLD code (Freytag et al. 2002; Schaffenberger et al. 2005, 2006). The CO5BOLD code solves the magnetohydrodynamic equations for a fully compressible gas, taking heating and cooling by radiative transfer into account. It includes a realistic equation-of-state that accounts for the partial ionization of H, He, and a representative metal. The set of MHD-equations are solved using a Godunov type finite-volume scheme by applying the HLL-solver and the van-Leer reconstruction scheme (Toro 2009). The code replicates the granular structure at the solar surface to a high degree of realism including size, continuum contrast, velocity field, etc., as well as magnetic flux concentrations in intergranular lanes. Further details and references to the CO5BOLD code and the applied numerical techniques can be found in Freytag et al. (2011).
2.2. The background model
The computational domain covers 4920 km in the horizontal direction. In the vertical direction, it reaches from the upper convection zone to the middle layers of the chromosphere, corresponding to a height range from −1300 km to 1600 km. The point of reference for z = 0 km is given by the horizontal mean of the optical continuum depth τc = 1, corresponding to the bottom layer of the photosphere.
A non-equidistant grid consisting of 188 cells is used along the vertical direction. The respective vertical grid size is 46 km for the largest cells in the convection zone and 7 km for the cells in the photosphere and the chromosphere. Transmitting boundary conditions are applied at the upper boundary, allowing propagating waves to leave the box without significant reflection. More restrictive boundary conditions apply to the magnetic field: the magnetic field at either the upper and lower boundary is forced to have vanishing horizontal components. However, lines of force can move freely in the horizontal direction so that this constraint does not prevent the field from expanding freely with height in the atmosphere. The grid is equidistant in the horizontal direction, consisting of 123 cells of size 40 km. Periodic boundary conditions apply to each side of the box.
Since we are interested in the interaction of an artificially excited wave with the magnetic field, the presence of a strong magnetic field concentration in the simulation domain is necessary. Figure 1a shows the absolute magnetic field strength, log |B|, of the initial model.
 |
Fig. 1 a) Magnetic setup at the start of the simulation showing the logarithm of the magnetic field strength in gauss. The white contour displays the equipartition level, where cs = cA. The crosses indicate three different locations of local wave excitation, individually discussed in Sect. 3. b) Corresponding temperature in Kelvin (colors) and velocity (arrows). The longest arrows correspond to 10 km s-1. The dashed curve indicates optical depth τc = 1. |
On the right hand side of the simulation domain, a magnetic flux sheet with a maximum field strength of 2300 G has evolved in the course of a precursory simulation. This precursory simulation started from a model of relaxed thermal convection to which a homogenous vertical magnetic field of a strength of 100 G was superimposed. The left half of the simulation box contains a prevalently weak, horizontal magnetic field. The white contour represents the equipartition level for which the Alfvén speed, cA, equals the sound speed, cs. Energy can be transferred between the fast and slow magneto-acoustic wave to a zone around this level. The amount of energy that is transferred from one mode to the other depends on the angle between the wave vector and the magnetic field vector (the attack angle), the wave number k, and the width of the conversion zone (Schunker & Cally 2006; Cally 2007). Figure 1b shows the temperature field and the velocity of the initial model. Granules and intergranular lanes are visible beneath the τ = 1 level. Above z ≈ 500 km, high velocities and shock fronts occur.
In contrast to investigations of wave propagation in the presence of a strong, hydrostatic magnetic field (Rosenthal et al. 2002; Bogdan et al. 2003; Cameron et al. 2008; Khomenko & Collados 2006; Shelyag et al. 2009), we use a dynamically evolving model atmosphere. The amplitudes of the excited waves are kept small in order to avoid any non-linear change in the velocity field of the background model. As a consequence, the propagation of the wave is hidden in but influenced by the velocities of the background model. Thus, we need to carry out two simulation runs: one run including the artificial perturbation that excites the wave, which then travels through the regular background model, and another run without the perturbation. By subtracting the two runs, the residual then shows the artificially excited, propagating wave (Steiner et al. 2007). Tests of this approach and the mode conversion capabilities of the CO5BOLD code are presented in Nutto et al. (2010).
3. Simulations of wave propagation
3.1. Local wave sources
In the following, we discuss the propagation of waves originating from local sources placed at different locations. Our results are then used in Sect. 3.2 to interpret the interaction between a plane-parallel wave and the magnetic field.
3.1.1. Wave excitation
We apply local wave sources that temporarily excite spherical waves. The interaction of the spherical wave front with the magnetic field is spatially confined so that the effects of this local interaction can be easily identified.
Three different simulations are carried out, where the spherical waves are excited at three different lateral positions in the simulation domain (see Fig. 1a):
-
i)
outside the magnetic flux sheet, where the magneto-acousticwave interacts with the vertically expanding flux concentration,viz., the magnetic canopy of the flux sheet;
-
ii)
inside the flux sheet;
-
iii)
below the horizontally directed magnetic field in the left part of the simulation domain.
The vertical positions of the wave sources were chosen to be at −180 km.
 |
Fig. 2 Time sequences of the propagation of a wave launched at position (i) of Fig. 1a. The time increases from top to bottom. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the absolute magnetic field, δ|B|. The green contours (thin white in the print edition) display the equipartition level, where cs = cA. The white curves indicate the position of a single wave front during its evolution in time. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
It was numerically shown by Stein & Nordlund (2001) that the wave excitation in the convection zone is most likely to occur between the surface and 500 km in depth.
We follow the description given by Parchevsky & Kosovichev (2009) for the wave excitation. The spatial and temporal behavior of the wave source is modeled by the function ![\begin{eqnarray} f(r,t)\!=\!\left\{\begin{array}{lrl} A \left[\!1\!-\!\displaystyle\frac{r^2}{R^2_{{\text{src}}}}\!\right]^2\!\!\left(1-2\phi^2\right){\rm e}^{-\phi^2}& \mbox{for }\, r \le R_{{\text{src}}} , \\ 0& \mbox{for }\, r > R_{\text{src}} \end{array},\right.\label{Eq:rickerswavelet} \end{eqnarray}](/articles/aa/full_html/2012/02/aa16083-10/aa16083-10-eq29.png) (1)where
(1)where
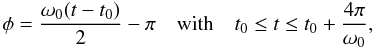 Rsrc is the radius of the source, A is the amplitude of the disturbance, and ω0 = 2πf0 determines the central frequency of the excited wave. The resulting source function, S = ∇f, is then added to the components of the pressure gradient in the momentum equation. Thus, S can be interpreted as a small perturbation to the pressure gradient, launching an acoustic wave with a central frequency of f0. In our simulations, the wave source has a radius of Rsrc = 150 km and a frequency of f0 = 20 mHz. Our reasons for choosing this relatively high frequency are given in Sect. 3.2.1. The simulations of the locally and temporally confined excitations are advanced for 250 s.
Rsrc is the radius of the source, A is the amplitude of the disturbance, and ω0 = 2πf0 determines the central frequency of the excited wave. The resulting source function, S = ∇f, is then added to the components of the pressure gradient in the momentum equation. Thus, S can be interpreted as a small perturbation to the pressure gradient, launching an acoustic wave with a central frequency of f0. In our simulations, the wave source has a radius of Rsrc = 150 km and a frequency of f0 = 20 mHz. Our reasons for choosing this relatively high frequency are given in Sect. 3.2.1. The simulations of the locally and temporally confined excitations are advanced for 250 s.
3.1.2. Wave interaction with the magnetic canopy
We now focus on the propagation of a spherical wave that is excited right beneath the magnetic canopy at location (i) in Fig. 1a. The canopy stems from the nearby, vertically expanding magnetic flux concentration. Figure 2 shows snapshots taken at three different times of the simulation from top to bottom. An mpeg animation of the simulation is available in the online edition of the article. The left column of Fig. 2 shows the perturbation of the absolute velocity, δ|v|, and the right column shows the perturbation of the absolute magnetic field, δ|B|. In velocity, both modes of the magneto-acoustic wave, the fast and the slow mode, can be followed at once because both modes introduce perturbations in the velocity. A characteristic criteria for the slow acoustic mode in the low β regime is that velocity and pressure perturbations propagate along the magnetic field lines. The fast magnetic mode in the low β regime is supported by magnetic forces, which causes significant perturbations of the magnetic field. Therefore, it can be followed individually by this quantity. Not only the slow acoustic but also the fast magnetic mode is compressible, causing additional small pressure perturbations.
Since the wave source is located in a region of high plasma-β, the excited waves are primarily acoustic in nature. Upon reaching the equipartition level, indicated by the solid green contour in Fig. 2, energy can be exchanged between the two modes of the magneto-acoustic waves (Cally 2007). Owing to the large attack angle of the local wave front with respect to the magnetic field at the location of the equipartition level, a large fraction of the acoustic wave energy is converted into the fast magnetic mode. The top row shows snapshots where a wave front, which is represented by the white curve, has just started to interact with the magnetic field. There, energy is transferred from the fast acoustic mode where cA/cs < 1 to the fast magnetic mode in the region where cA/cs > 1. Because of the large gradients in the Alfvén speed along the vertical and horizontal direction of the background model, the Alfvén speed gradually changes along the wave fronts of the fast magnetic mode, leading to strong refraction of the fast magnetic mode. Its wave travel-path gets curved to such a degree that it traces out an almost 180° turn so that the wave travels back again into the Sun.
 |
Fig. 3 Time sequences of the propagation of a wave launched at position (ii) of Fig. 1a. Time increases from top to bottom. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the absolute magnetic field, δ|B|. The green contours (thin white in the print edition) display the equipartition level, cs = cA. The white curves indicate the position of a single wave front of the fast magnetic mode and its evolution in time. In the last row, the fast magnetic mode (in the region where cA/cs > 1) has already been refracted and wave fronts of constant phase cannot be clearly identified. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
In the snapshots of the middle row, the wave front of the fast magnetic mode moves through the apex of the refracting wave path. Owing to the higher phase speed of the fast mode, the wavelength is significantly longer. In the apex of the refractive wave path, the wave front moves horizontally with the implication that over a wide height range of the upper atmosphere the velocity perturbations are in phase.
From the snapshots in the last row, it is obvious that the wave front has been refracted to such a degree that it travels back toward the lower atmosphere, where it gets converted back into a fast acoustic mode when crossing the equipartition level once again. From Fig. 2, it can also be seen that the fast magnetic mode is not restricted in its propagation path by the orientation of the magnetic field but rather by the sharp increase in the Alfvén speed with height in the solar atmosphere. Following the wave propagation of the perturbation of the magnetic field δ|B| (right column), one can see that the perturbation to the magnetic field is strongest in the vicinity of the equipartition level, where the conversion from the fast acoustic mode to the fast magnetic mode takes place.
 |
Fig. 4 Time sequences of the propagation of a wave launched at position iii) of Fig. 1. Time increases from top to bottom. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the pressure, δ|p|/p0. Note that different time steps apply to each column. The green contours (thin white in the print edition) display the equipartition level, cs = cA. The arrows in the right column indicate the direction of the magnetic field lines, along which the slow acoustic mode escapes the atmosphere. The black curves in the left column indicate the position of a single wave front and its evolution with time. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
The refractive wave path and the longer wavelength of the fast magnetic mode reduces the local wave energy density with height so that its amplitude decreases into the chromospheric layer.
3.1.3. Wave interaction inside the flux sheet
Next, we consider the scenario where the wave source is located inside the flux sheet at position (ii) in Fig. 1a, close to the equipartition level. Figure 3 again shows snapshots of the perturbation of the absolute velocity, δ|v|, in the left column and of the perturbation of the magnetic field, δ|B|, in the right column. An mpeg animation of the evolution of the absolute velocity perturbation, δ|v|, is available in the online edition of the article. This time, the wave source is located close to the equipartition level because the low plasma-β regime reaches deep into the magnetic funnel. Therefore, both the fast and the slow mode are excited at the same time. The fast magnetic mode is refracted to such a degree that it travels back towards the lower atmosphere. The slow acoustic mode emerging later from the excitation region, is guided along the field lines into the higher layers of the atmosphere. As the wave front travels upward, it steepens and eventually forms a shock front as is visible at (x,y) = (4250,700) km in the bottom left panel of Fig. 3. Both snapshots in the last row illustrate that there is no significant perturbation in the magnetic field that can be associated with the slow acoustic mode running along the field lines in the region where cA/cs > 1.
One can again see from the sequence of the perturbation in the magnetic field, δ|B|, that the strongest perturbation takes place at the equipartition level, where mode conversion occurs. However, in the present case, the perturbation is weaker than in the case of Sect. 3.1.2, because a large fraction of the energy remains in the acoustic branch of the magneto-acoustic wave.
3.1.4. Wave interaction with the horizontally directed magnetic field
We now study the propagation of waves that are excited below a horizontally oriented magnetic field at location (iii) in Fig. 1a. This case is special as the wave propagates through multiple equipartition levels, hence experiences multiple mode conversions. Figure 4 shows in the left column the perturbation of the absolute velocity, δ|v|, and in the right column the relative perturbation of the pressure, δ|p|/p0, where p0 is the local unperturbed pressure. An mpeg animation of the evolution of the absolute velocity perturbation, δ|v|, is available in the online edition of the article.
The wave excitation takes place well below the equipartition level. Thus, the wave starts primarily as an acoustic wave. At the first equipartition level, the local wave vector and the magnetic field vector are almost perpendicular to each other (large attack angle), which leads to most of the energy being converted from the fast acoustic mode in the region where cA/cs < 1 to the fast magnetic mode in the region where cA/cs > 1. There is no significant transmission of the acoustic mode into the region immediately above the first mode conversion zone. The fast magnetic mode is again refracted, although these multiple equipartition levels add to the complexity of the interpretation. In the right column of Fig. 4, it is evident that a strong pressure disturbance reemerges above the multiple conversion zones in the region of the elongated (filamentary) structure in the equipartition contour extending from (x,z) = (300,600) km to (x,z) = (1700,1400) km. This emerging slow acoustic mode is then guided along the field lines (indicated by the arrow in Fig. 4) and is able to escape the chromospheric layer.
 |
Fig. 5 Vertical section of the ratio of the Alfvén speed, cA, to the sound speed, cs, taken at x = 1300 km from the snapshot displayed in the bottom row of Fig. 4, corresponding to the time instance t = 200 s. The dashed horizontal line indicates the equipartition level. For each location where cA = cs, the transmission coefficient T is calculated for a range of most probable attack angles, α, for the studied wave propagation experiment. |
To clearly illustrate this behavior, Fig. 5 shows cA/cs as a function of height for a vertical section at x = 1300 km in the snapshot taken at t = 200 s. Three different locations can be identified in the atmosphere where the sound speed and the Alfvén speed are equal. For all three locations, the transmission coefficient, T, was calculated according to Eq. (2) of Cally (2007) for a range of attack angles specified further below. The transmission T is the fraction of the original wave energy that goes into the transmitted wave. The latter is driven by the same predominantly restoring force as the original wave but changes from either fast to slow or vice versa. The fraction of the wave energy that goes into the converted wave is C = 1 − T. In the case of mode conversion, the restoring force changes from acoustic to magnetic but the relative speed remains either fast or slow. The indicated range of attack angles is necessary, as the equipartition level is very dynamic itself in this region where shock waves propagate through the background atmosphere, constantly changing the orientation and location of the equipartition level, especially in the chromospheric layers. The first equipartition level, at z = 680 km, is rather steady and therefore, only a small range of attack angles, α = 80° to 90°, was chosen. The very low transmission of T = 0.098 to 0.092 at this location indicates that most of the energy is indeed converted into the fast magnetic mode, propagating above this first equipartition level. For the next equipartition level at z = 1200 km, the transmission coefficient is T = 0.53 to 0.49 for the range of attack angles of α = 70° to 90°. The width of this mode conversion zone, ![\hbox{$h_{\rm s}=[\mathrm d(c_{\rm A}^2/c_{\rm s}^2)\mathrm d s]^{-1}_{c_{\rm A}=c_{\rm s}}$}](/articles/aa/full_html/2012/02/aa16083-10/aa16083-10-eq63.png) , is smaller than for the other two mode-conversion widths, which increases the transmission. Thus, about half of the magnetic wave energy is converted back into the fast acoustic mode. The transmission coefficient of the next equipartition level, at z = 1380 km, refers to the transmission of this fast acoustic mode. Since the magnetic field orientation is more vertical in this specific region, we considered a wider range of attack angles of α = 45° to 90°, resulting in a range of transmission coefficients of T = 0.4 to 0.16, such that a significant fraction of the fast acoustic mode can be transmitted to the region above this last equipartition level where again cA > cs.
, is smaller than for the other two mode-conversion widths, which increases the transmission. Thus, about half of the magnetic wave energy is converted back into the fast acoustic mode. The transmission coefficient of the next equipartition level, at z = 1380 km, refers to the transmission of this fast acoustic mode. Since the magnetic field orientation is more vertical in this specific region, we considered a wider range of attack angles of α = 45° to 90°, resulting in a range of transmission coefficients of T = 0.4 to 0.16, such that a significant fraction of the fast acoustic mode can be transmitted to the region above this last equipartition level where again cA > cs.
In conclusion, despite a low transmission coefficient of 0.092 < T < 0.098 for the acoustic wave at the first equipartition level, a series of mode conversions can result in the transmission of an acoustic wave above the last equipartition level as observed in the simulation.
3.2. Extended plane-parallel wave source
3.2.1. Wave excitation
To investigate the wave travel-times under the influence of a strong magnetic field concentration in Sect. 4, we study the vertical propagation of a plane-parallel wave. We continuously excite a harmonic, sinusoidal wave with a frequency of f0 = 20 mHz at the lower boundary of the simulation domain.
 |
Fig. 6 Time sequences of a plane-parallel wave launched at the bottom of the computational domain travelling through the convection zone and the atmosphere. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the absolute magnetic field, δ|B|. The green contours represent the equipartition level, cs = cA. Time increases from top to bottom. The white curves indicate the position of a single wave front and its evolution in time. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
Although the use of lower frequencies would be more practical for a comparison of our results with observations, the choice of the relatively high frequency of f0 = 20 mHz is directly related to the analysis method. Since the simulation can only proceed for a certain amount of time, as explained in Sect. 4.1, the high frequency of f0 = 20 mHz increases the reliability of the analysis for the short time period and the relatively small height span that we consider. In any case, one can expect that the propagating waves behave similarly for all frequencies above the acoustic cut-off frequency, according to Khomenko & Collados (2006) and references therein, so that waves with f0 = 20 mHz should be a good representation of all waves above the acoustic cut-off frequency of the solar atmosphere of ≈ 5 mHz. We perform the wave propagation experiment for 1500 s in time.
3.2.2. Propagation of a plane-parallel wave
We now study the propagation of a plane-parallel wave based on the insights that we have gained in Sect. 3.1 from the local wave sources. Owing to the extended wave front, the interaction between the wave and the magnetic field is not confined and occurs everywhere along the equipartition level.
Figure 6 displays four snapshots of the wave propagation. The left column displays the results for δ|v|, the right column displays the perturbation of the magnetic field, δ|B|. An mpeg animation of the evolution of the absolute velocity perturbation, δ|v|, is available in the online edition of the article. In the first row, the wave front has not yet interacted with the magnetic field of the photosphere. The individual wave fronts can be distinguished and have not interfered. The distortions visible at x ≈ 1600 km, 2700 km, and 4000 km are due to downflows and lower temperatures in the intergranular lanes, causing the wave front to travel more slowly than within the granules (see also Fig. 1b). The snapshots of the second and third row are taken at time steps where the wave front has already interacted with the magnetic field of the flux sheet. At the location of the magnetic flux concentration, the interaction is similar to that described in Sect. 3.1.2, where the fast acoustic mode is converted into a fast magnetic mode. Owing to the large gradient in the Alfvén speed, the wave front gets refracted to such a degree that it travels back towards the solar interior as can be seen by following a single wave crest delineated by the white curve. The refraction of the wave causes the wave vector to be horizontal while passing through the apex of the refracting wave path. As is apparent from the second row in Fig. 6, the wave front extends in the vertical direction with velocities that are in phase over a large range of heights in the solar atmosphere. Thus, an observer looking vertically down into the atmosphere measures a very high phase speed similar to that of an evanescent wave, even though in reality it is a horizontally propagating wave. This point is addressed again when studying the wave travel-time between different heights in the atmosphere in Sects. 4.2 and 4.3. The third row shows how the wave front is refracted by the interaction with the magnetic flux sheet and travels back towards the lower layers of the atmosphere.
The fourth row displays snapshots taken well into the simulation. As for the situation described in Sect. 3.1.3, a slow magneto-acoustic wave is seen to emerge along the field lines of the magnetic flux concentration. Above the equipartition level, only the slow magneto-acoustic waves have the potential to escape the photosphere and the chromosphere in the upward direction without being refracted.
We next focus on the interaction of the plane-parallel wave with the horizontal magnetic field, in particular with the multiple equipartition levels that are present in the left half of the box. Figure 7 shows a time series of the perturbation of the magnetic field, δ|B|. The multiple equipartition levels form an elongated structure with isolated regions where cA/cs ≫ 1. Between these isolated regions, narrow channels are formed with cA/cs ≪ 1. This fibril-like structure as well as the narrow channels have their origins in the propagation of locally confined shock waves in the background model. The abrupt increase in temperature and density behind the shock front is responsible for the sudden rise in sound speed, cs, and the decrease in Alfvén speed, cA, respectively.
 |
Fig. 7 Time sequences of the magnetic field perturbation, δ|B|, resulting from the interaction of the plane-parallel wave with the horizontal magnetic field. Time increases from top to bottom. The green contours represent the equipartition level, cs = cA. The white arrow follows the propagation path of a single magnetic field perturbation. |
The time series indicates that magnetic perturbations are propagating along the elongated structure and the narrow channels. Here, the perturbations of the magnetic field are stronger than in the case of the interaction of the wave with the magnetic field of the flux sheet. These strong perturbations appear predominantly at the equipartition levels, where the fast magnetic wave is converted back into a fast acoustic wave when the wave propagates from a region with cA/cs > 1 to a region where cA/cs < 1. The existence of multiple equipartition layers and its consequences have not been discussed in the literature before and will be the subject of future investigations.
4. Travel-time analysis
With high-cadence, multi-line instruments such as the MOTH instrument (Cacciani et al. 2003; Finsterle et al. 2004b), it is possible to observe propagating high-frequency waves in the photosphere and the chromosphere of the Sun. With this instrument, Finsterle et al. (2004c) showed that the wave travel-time between the formation heights of different spectral lines can be directly connected to the presence of a magnetic field. Using our simulations, we have now a tool at our disposal to investigate the influence of the magnetic field on the wave travel-time between different heights in the solar atmosphere. At this stage we do not yet compute Doppler velocities from synthesized spectral lines but instead take the time series of the vertical velocity directly from the simulations. The analysis can be done for various levels of either constant geometrical heights in the atmosphere or constant optical depths. The wave travel-time is determined by calculating the phase shift between two velocity signals, v1(t) at the first height level and v2(t) at the second height level. According to Rajaguru et al. (2007), the phase shift is given by ![$$\phi_{1,2}(\omega)=\tan^{-1} \left(\frac{\text{Im}[v_1(\omega)v_2^*(\omega)]}{\text{Re}[v_1(\omega)v_2^*(\omega)]}\right),$$](/articles/aa/full_html/2012/02/aa16083-10/aa16083-10-eq80.png) where v1(ω) and v2(ω) are the Fourier transform of the two time series. A positive phase shift indicates a positive wave travel-time between both heights. Knowing the frequency of the wave, the phase shifts then yield the wave travel-time. After calculating the wave travel-time in the Fourier space, one can determine the coherence between both time series with
where v1(ω) and v2(ω) are the Fourier transform of the two time series. A positive phase shift indicates a positive wave travel-time between both heights. Knowing the frequency of the wave, the phase shifts then yield the wave travel-time. After calculating the wave travel-time in the Fourier space, one can determine the coherence between both time series with
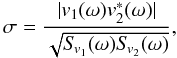 where S denotes the power spectrum of each time series. For two time series with a linear relationship, e.g., for unperturbed wave propagation, the coherence equals unity, while for two uncorrelated time series, the coherence vanishes identically. If the value for the coherence falls below the significance level of σcrit = 0.5, then the two time series show a lack of linearity, indicating that our result for the phase shift and the wave travel-time cannot be trusted (Priestley 1981).
where S denotes the power spectrum of each time series. For two time series with a linear relationship, e.g., for unperturbed wave propagation, the coherence equals unity, while for two uncorrelated time series, the coherence vanishes identically. If the value for the coherence falls below the significance level of σcrit = 0.5, then the two time series show a lack of linearity, indicating that our result for the phase shift and the wave travel-time cannot be trusted (Priestley 1981).
4.1. Properties of the time-averaged background model
For the analysis of the wave travel-time and the power spectra presented in subsequent sections, the entire time series of 1500 s is used. Therefore, the results refer to time-averaged properties of the background model. A time series longer than 1500 s cannot be considered for two reasons.
 |
Fig. 8 Top: magnetic field averaged over the entire time span of 1500 s. The solid curves represent magnetic field lines. The heavy white contour displays the time-averaged position of the equipartition level. Bottom: temporally and horizontally averaged temperature stratification of the background model. |
First, the two simulations (with and without perturbations) bifurcate because the small perturbation causes a steadily growing deviation from the model without the perturbation. After 1500 s, the differences between the original and the perturbed model exceed the signal from the wave, which then becomes swamped by the velocity field of the underlying convective motion. Second, the flux sheet gets pushed around in the computational domain by the ambient medium and changes its horizontal position slowly but continuously. Taking the time average for time series longer than 1500 s flattens the mean equipartition level without leaving any significant signature of the presence of the flux sheet. In the top panel of Fig. 8, we plot the temporally averaged magnetic field and the temporally averaged position of the equipartition level. This plot demonstrates the effect of the movement of the flux sheet, which causes the magnetic field to spread out and decrease in field strength compared to the initial model shown in Fig. 1. However, for the considered time series of 1500 s, the flux sheet is still confined to a small horizontal region. Comparing the equipartition level of the single snapshot of Fig. 1a with the mean equipartition level of Fig. 8, it becomes evident that the height variation in the mean equipartition level is smaller and shows less structure because of the horizontal movement of the flux sheet. Nonetheless, the time series is short enough to record a pronounced dip in the mean equipartition level at the location of the magnetic flux sheet. We also note that the timescale of a single fast wave front is much shorter than the evolutionary timescale of the magnetic field so that the magnetic field can be regarded as quasi static for a single fast wave front.
The bottom panel of Fig. 8 shows the horizontally and temporally averaged temperature stratification of the simulated model as a function of height. The occurrence of a multitude of shock waves propagating in the model atmosphere above z ≈ 500 km prevent a further decline in the temperature in the outward direction, so that the chromospheric layer of the mean background model can be treated as isothermal.
For the present two-dimensional simulation, we need to consider only the fast and the slow mode. The fast mode undergoes a significant increase in phase speed with height in the region where cA/cs > 1, because the gas pressure drops more quickly with height than the magnetic pressure does. Therefore, the increasing phase speed with height of the fast mode may result in shorter than expected measured wave travel-times between different heights in the upper layers of the model atmosphere. In contrast, the slow mode propagates at much lower and approximately constant speed because of the isothermal state of these layers (Fig. 8). The maximum phase speed of the fast mode is given by 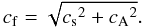 Figure 9 shows the temporally averaged phase speed of the fast mode as a function of horizontal position for different geometrical height levels (top panel) and different optical depth levels (bottom panel). The asterisks indicate where the mean equipartition level (cA = cs) crosses the height level to which the curve belongs. Bold lines refer to the regime where cA > cs. These plots demonstrate that the phase speed of the fast mode rapidly increases inside the magnetic flux sheet and its canopy. It can reach values of up to 150 km s-1 for the height level of 800 km. This increase is less pronounced when moving at a given optical depth level from locations with a weak to a location with a strong magnetic field. There, the optical depth levels drop to lower geometrical heights with lower Alfvén speeds.
Figure 9 shows the temporally averaged phase speed of the fast mode as a function of horizontal position for different geometrical height levels (top panel) and different optical depth levels (bottom panel). The asterisks indicate where the mean equipartition level (cA = cs) crosses the height level to which the curve belongs. Bold lines refer to the regime where cA > cs. These plots demonstrate that the phase speed of the fast mode rapidly increases inside the magnetic flux sheet and its canopy. It can reach values of up to 150 km s-1 for the height level of 800 km. This increase is less pronounced when moving at a given optical depth level from locations with a weak to a location with a strong magnetic field. There, the optical depth levels drop to lower geometrical heights with lower Alfvén speeds.
 |
Fig. 9 Time-averaged phase speed of the fast mode at selected fixed geometrical heights (top panel) and selected optical depth levels τ1 = 1, τ2 = 0.025, τ3 = 0.001, τ4 = 0.0001, and τ5 = 2.5 × 10-5 (bottom panel). The bold lines indicate the regime where cA/cs > 1, while the thin lines represent the regime where cA/cs < 1. The asterisks mark the locations where the respective height levels cross the equipartition level. |
Moreover, the vertical geometrical distances between the different optical levels is reduced in these locations so that the increase in phase speed from level to level is also less strong.
4.2. Wave travel-times between fixed geometrical heights
We now present our results for the vertical wave travel-times between fixed geometrical height levels in the model atmosphere. Assuming that the simulation represents a portion of the center of the solar disk, the vertical velocities, vz, correspond to line-of-sight velocities. Figure 10 shows the different heights to which the time series of the vertical velocities refer, where we overplotted the time-averaged position of the equipartition level for the whole time series of 1500 s. The vertical step size between the different heights is δz = 200 km, starting from z = 0 km in the photosphere and ending at z = 800 km in the chromosphere. Except for a narrow span in the center of the flux sheet, the two lower geometrical height levels do not cross but remain below the mean equipartition level, the upper three height levels crossing the equipartition level at different horizontal positions in the box. The uppermost level does stay above the mean equipartition level for most parts of the box.
The wave travel-times between neighboring height levels together with the coherences of the corresponding time series are plotted in Fig. 11. Panel (a) shows the travel time between z1 = 0 km and z2 = 200 km. The vertical travel time is almost constant with a horizontally averaged travel time of 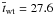 s. This is because the phase speed of the fast mode between these two levels does not vary much as a function of horizontal position, as can be seen from Fig. 9. The coherence is σ > 0.6 for all and σ > 0.8 for most horizontal positions, which implies that there is a good correlation between the vertical velocities of both time series. There are three regions in the box at x ≈ 700 km, x ≈ 1300 km, and x ≈ 4000 km, where the coherence drops to lower than average values. These positions correspond to downflows in the intergranular lanes. Since these evolve in the course of time, we may expect to find lower coherence. Within these downflows, the wave travel-time increases.
s. This is because the phase speed of the fast mode between these two levels does not vary much as a function of horizontal position, as can be seen from Fig. 9. The coherence is σ > 0.6 for all and σ > 0.8 for most horizontal positions, which implies that there is a good correlation between the vertical velocities of both time series. There are three regions in the box at x ≈ 700 km, x ≈ 1300 km, and x ≈ 4000 km, where the coherence drops to lower than average values. These positions correspond to downflows in the intergranular lanes. Since these evolve in the course of time, we may expect to find lower coherence. Within these downflows, the wave travel-time increases.
 |
Fig. 10 Computational domain with the solid contour displaying the mean equipartition level (cs = cA). The dashed horizontal lines indicate the different heights between which the wave travel-time is evaluated. The shaded boxes indicate the regions where the wave travel-time cannot be trusted because the coherence falls below the limit of σcrit = 0.5. |
Figure 11b shows the wave travel-time between z2 = 200 km and z3 = 400 km. For a large fraction of the horizontal distance, the travel time is again constant with a mean wave travel-time of 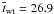 s. This result agrees well with the measured wave travel-time of
s. This result agrees well with the measured wave travel-time of 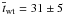 s between the Ni I (λ = 676.8 nm) and K I (λ = 769.9 nm) line-formation height in the quiet Sun atmosphere, corresponding to a height range from 200 km to 420 km (Finsterle et al. 2004a). Since both heights, z2 and z3, are mostly below the mean equipartition level, the wave travel-times remain similar to the quiet Sun value. However, between x ≈ 4000 kmandx ≈ 4920 km, the wave propagation is already influenced by the presence of the magnetic field, causing a reduction in the wave travel-time. This reduction is greatest at the position where both height levels are well within the region for which cA > cs. The wave travel-time is nearly constant for horizontal positions where the upper geometrical height, z3 = 400 km, remains below the mean equipartition level. The coherence is σ ≥ 0.5 for all horizontal positions. However, when the wave propagation is influenced by the magnetic field, the coherence drops close to σcrit. Possible reasons for this behavior are discussed in Sect. 6.
s between the Ni I (λ = 676.8 nm) and K I (λ = 769.9 nm) line-formation height in the quiet Sun atmosphere, corresponding to a height range from 200 km to 420 km (Finsterle et al. 2004a). Since both heights, z2 and z3, are mostly below the mean equipartition level, the wave travel-times remain similar to the quiet Sun value. However, between x ≈ 4000 kmandx ≈ 4920 km, the wave propagation is already influenced by the presence of the magnetic field, causing a reduction in the wave travel-time. This reduction is greatest at the position where both height levels are well within the region for which cA > cs. The wave travel-time is nearly constant for horizontal positions where the upper geometrical height, z3 = 400 km, remains below the mean equipartition level. The coherence is σ ≥ 0.5 for all horizontal positions. However, when the wave propagation is influenced by the magnetic field, the coherence drops close to σcrit. Possible reasons for this behavior are discussed in Sect. 6.
Figure 11c shows the wave travel-times between z3 = 400 km and z4 = 600 km. In regions where both heights are below the mean equipartition level, i.e., between x ≈ 900 kmandx ≈ 2800 km, the wave travel-times are similar to the previously obtained value, provided that σ ≥ 0.5. If the mean equipartition level is between or below both heights, i.e., between x ≈ 0 kmandx ≈ 900 km and between x ≈ 2800 kmandx ≈ 4920 km, the wave travel-time is considerably shorter. At x ≈ 4600 km, the wave travel-time increases, but the coherence remains below σcrit. This increase in travel time is due to the slow acoustic mode that travels along the magnetic field lines. The coherence of the time series is poorer in regions where either the mean equipartition level is close to one of each heights, or if both, the fast and slow mode, are mixed and of similar magnitude. Thus, the processes of mode conversion and mode mixing could explain the lack of coherence.
Figure 11d shows the wave travel-times between z4 = 600 km and z5 = 800 km. For the majority of the horizontal extent, both geometrical heights are above the mean equipartition level. In these regions, and where the coherence at the same time is good, the wave travel-time drops to twt ≈ 0 s. At around x ≈ 4700 km, there is again an increase in the wave travel-time owing to the detection of the slow magneto-acoustic wave that propagates along the magnetic field lines into the upper layers of the solar atmosphere. In the cases where the lower height is below the mean equipartition level, the wave travel-time again increases, but the coherence weakens and falls below σcrit.
 |
Fig. 11 Vertical wave travel-time, twt, (top plot in each panel) and coherence of the time series (bottom plot in each panel) between five different geometrical heights a)–d) in the atmosphere. The shaded intervals mark regions for which the coherence drops below σcrit = 0.5. |
Between x ≈ 1600 km and x ≈ 2200 km, both levels are below the equipartition level. In this region, the wave travel-time correspondingly approaches values that are similar to the undisturbed wave travel-times of the lower atmosphere.
4.3. Wave travel-times between different optical depths
Doppler shifts of absorption lines in the solar atmosphere do not refer to velocities at constant geometrical heights but rather to certain optical depths.
 |
Fig. 12 Computational domain, showing the different time-averaged optical depths τ that are used for the travel time analysis. The solid contour displays the mean equipartition level. The shaded boxes mark regions for which the coherence drops below σcrit = 0.5. |
However, we here neither use the detailed line opacities, nor do we compute synthetic line profiles, which would require non-LTE computations for chromospheric lines. We use instead a “gray” optical depth scale using Rosseland mean opacities as a first approximation to the line formation heights. Figure 12 shows the different mean optical depth levels considered in the analysis together with the mean equipartition level. The different levels were chosen in such a way that the temporally and spatially averaged position of the optical depth levels are comparable to the fixed geometrical heights considered in the previous section. This time, only the two lower levels can be considered as almost constant in geometrical height. The two upper levels show large height variations in the horizontal direction. While all optical depth levels approach each other within the flux sheet, there are large height variations outside the flux sheet, especially for the upper two levels. Thus, larger variations in the wave travel-times are to be expected.
The resulting wave travel-times of the phase shift analysis are shown in Fig. 13. The plots in the top of each panel again show the wave travel-time between neighbouring height levels, while the lower plots show the coherence between the respective time sequences. Figure 13a displays the wave travel-time between the optical depths τ1 = 1 and τ2 = 0.025. As expected, the travel time shows greater variations than in the corresponding case in Fig. 11a. Although the time-averaged optical depth levels are nearly constant in the horizontal direction in the photosphere, the time-dependent optical depth levels are strongly influenced by passing shock waves in the background model causing local height variations in the optical depth level. These variations are eventually leveled out by taking the time average of the optical depth levels. However, the variation in the travel time persists to some degree in the phase shift analysis, because the velocity perturbation at each optical depth level is recorded at each instant in time. Nonetheless, covering a similar height range as in panel (a) of Fig. 11 and despite the variation in the wave travel-time, the horizontally averaged wave travel-time of 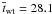 s is similar. In Fig. 13b, we plot the travel times between τ2 = 0.025 and τ3 = 0.001. The curve shows even stronger variations, although the peaks cannot be trusted because the coherence of the time series drops below σcrit at these locations. In the region of the flux sheet between x ≈ 4000 km and x ≈ 4700 km, the travel time starts to decrease to values below twt = 20 s. Here, both levels τ2 = 0.025 and τ3 = 0.001 lie above the mean equipartition level such that the conversion from the acoustic to the magnetic mode has fully taken place and the phase speed of the fast mode significantly increases, shortening the wave travel-time. Figure 13c displays the case for τ3 = 0.001 and τ4 = 0.0001. In the region where both levels are above or close to the mean equipartition level, viz., from x ≈ 320 kmtox ≈ 4920 km, the coherencies of the time series can be trusted and the wave travel-times show values in the range of twt = 0 to 20 s. The increase at around x ≈ 4500 km can be associated with the detection of the slow magneto-acoustic wave travelling along the magnetic field lines. For regions with multiple mean equipartition levels in the vertical direction, the coherence of the time series decreases below σcrit and cannot be trusted. Thus, the multiple mode conversions result in a degradation of the coherence. This situation changes again in Fig. 13d. Here both levels, τ4 = 0.0001 and τ5 = 0.000025, are mainly formed above the mean equipartition level and for most parts of the horizontal domain the coherence of the time series remains above σcrit. The regions, where the correlation of the time series can be trusted, show wave travel times between twt = 0 s and twt = 10 s. The peak at x ≈ 4500 km is again due to the slow acoustic mode, while the overall shorter travel times are caused by the fast magnetic mode, which is the dominant mode in the low-β regime.
s is similar. In Fig. 13b, we plot the travel times between τ2 = 0.025 and τ3 = 0.001. The curve shows even stronger variations, although the peaks cannot be trusted because the coherence of the time series drops below σcrit at these locations. In the region of the flux sheet between x ≈ 4000 km and x ≈ 4700 km, the travel time starts to decrease to values below twt = 20 s. Here, both levels τ2 = 0.025 and τ3 = 0.001 lie above the mean equipartition level such that the conversion from the acoustic to the magnetic mode has fully taken place and the phase speed of the fast mode significantly increases, shortening the wave travel-time. Figure 13c displays the case for τ3 = 0.001 and τ4 = 0.0001. In the region where both levels are above or close to the mean equipartition level, viz., from x ≈ 320 kmtox ≈ 4920 km, the coherencies of the time series can be trusted and the wave travel-times show values in the range of twt = 0 to 20 s. The increase at around x ≈ 4500 km can be associated with the detection of the slow magneto-acoustic wave travelling along the magnetic field lines. For regions with multiple mean equipartition levels in the vertical direction, the coherence of the time series decreases below σcrit and cannot be trusted. Thus, the multiple mode conversions result in a degradation of the coherence. This situation changes again in Fig. 13d. Here both levels, τ4 = 0.0001 and τ5 = 0.000025, are mainly formed above the mean equipartition level and for most parts of the horizontal domain the coherence of the time series remains above σcrit. The regions, where the correlation of the time series can be trusted, show wave travel times between twt = 0 s and twt = 10 s. The peak at x ≈ 4500 km is again due to the slow acoustic mode, while the overall shorter travel times are caused by the fast magnetic mode, which is the dominant mode in the low-β regime.
5. Power spectra
We study the power spectra of the velocity and the magnetic field fluctuations in the simulation of the plane-parallel wave source described in Sect. 3.2.
5.1. Power spectra of the velocity fluctuations
We consider both velocity components separately, the vertical velocity perturbation, δvz, and the horizontal velocity perturbation, δvx. The power spectra are calculated for each cell of the computational domain. Figure 14 shows the power map of (a) the vertical velocity perturbation and (b) the horizontal velocity perturbation of the frequency bin f0 = (20 ± 2.5) mHz. We overplot again the mean position of the equipartition level.
The power map of the vertical velocity perturbation, δvz, shows a conspicuous reduction in power at the center of the time-averaged flux sheet. The reduction in power can be explained in terms of the propagation path of the fast magnetic mode. Within the flux sheet, the fast mode travels across the magnetic field. In particular in the canopy region, the wave vector and the magnetic field vector are roughly perpendicular to each other. In this case, the fast mode possesses a longitudinal polarization with velocity perturbations parallel to the wave vector. Hence, it contributes mainly to the horizontal velocity perturbations.
Excited by a vertical driver, one does not expect to find significant power in the horizontal velocity component of the plane-parallel wave. This is indeed the case until the wave begins to interact with the magnetic field of the atmosphere. The power map of the horizontal velocity in Fig. 14b demonstrates that above the mean equipartition level, the power in horizontal velocities increases by several orders of magnitude.
 |
Fig. 13 Vertical wave travel-time, twt, (top plot of each panel) and coherence of the time series (bottom plot of each panel) between five different optical depths a)–d) in the atmosphere. The shaded intervals mark regions for which the coherence drops below σcrit = 0.5. |
This increase in power approximately aligns with the mean equipartition level. There, the conversion from the fast acoustic to the fast magnetic mode takes place, which then introduces horizontal velocities. In addition, acoustic waves that are transmitted to the region where cA > cs will travel along magnetic field lines, which are often horizontally oriented in the photosphere and the chromosphere and thus will also contribute to the power at horizontal velocities. Within the time-averaged flux sheet, the power of the horizontal velocity perturbation is rather homogenous and stronger than that of the vertical velocity perturbations. This is a consequence of the refracting fast magnetic waves, which travel transversely to the magnetic field within the flux sheet.
5.2. Power spectra of the magnetic field fluctuations
As previously discussed in Sect. 3.2, the waves in the convection zone are predominantly acoustic in nature. Upon reaching the photosphere and the chromosphere, the exchange of energy between the acoustic and magnetic mode results in strong magnetic field perturbations in the vicinity of the equipartition level. Figure 15 shows the power map for the magnetic field perturbations, δ|B|, for the binned frequency f0 = (20 ± 2.5) mHz. As expected, the power concentrates in the vicinity of the mean equipartition level. The strongest power can be found in the region with multiple equipartition levels, which could have been anticipated from the time series of Fig. 7 in Sect. 3.2, when we have discussed the propagation of strong magnetic field perturbations along the narrow channels of alternating equipartition levels.
Besides the strong power in the vicinity of the equipartition level, power is distributed over wide parts of the atmosphere and within the magnetic funnel of the flux sheet. The dotted contour in Fig. 15 discriminates the regions of the atmosphere where no equipartition level occurred in the course of the simulation from the rest where at least one occurrence of the equipartition level has taken place.
 |
Fig. 14 Power maps of the velocity perturbation of the simulation shown in Fig. 6. Top: power map of the vertical velocity perturbation, δvz. Bottom: power map of the horizontal velocity perturbation, δvx. Overplotted is the contour of the mean equipartition level. See the online edition for a color version of this plot. |
Power is mostly limited to the region where the equipartition level has occurred. This demonstrates again that the magnetic field perturbations of magneto-acoustic waves in the solar atmosphere are directly connected to the presence of the equipartition level.
Besides the distributed power in the atmosphere, there is also an elongated tail of power below the surface (z < 0 km) extending from x ≈ 1000 km to x ≈ 2000 km. This power enhancement occurs in a region of enhanced magnetic field strength but still with β > 1 (see Fig. 1). Owing to the inclination of the magnetic field, the fast, quasi plane-parallel acoustic wave that propagates from the bottom boundary in the upward direction excites transverse motions of this magnetic field concentration. The dominance of the thermal over magnetic pressure forces the magnetic field to follow the transverse plasma motion. Thus, the propagation of the fast acoustic mode across this magnetic field concentration introduces magnetic field fluctuations with the frequency of the passing wave.
6. Discussion
The lack of coherence in the vicinity of the equipartition level (Sects. 4.2 and 4.3) must be due to the conversion of the fast acoustic mode to the fast magnetic mode. Cally (2009) states that in a magnetized plasma this conversion comprises a phase jump in velocity. However, owing to the long wavelength and curved travel path in combination with the superposition of both modes in the conversion region, the slow and fast mode cannot be easily decoupled so that this phase jump cannot be directly demonstrated with our simulations. Higher up in the atmosphere, when both sensing heights are above the mean equipartition level, the coherence is again restored. According to Cally (2009), there is another phase jump at the apex of the refracting wave path of the fast magnetic mode in the region where cA/cs > 1. As the wave fronts extend vertically outwards at the turning point, the phase jump, which then occurs along the horizontal direction, should not significantly disturb the coherence, which is determined between the vertical velocities at two height levels separated in the vertical direction.
The drastic shortening of the wave travel-time between geometrical height levels that are located above the equipartition level is a consequence of the wave propagation path of the fast mode in the region where cA/cs > 1, and of its propagation speed. First, it is apparent from Fig. 9 that between the upper three levels, the maximum propagation speed of the fast mode drastically increases so that the fast mode can travel between individual levels within a few seconds.
 |
Fig. 15 Power map of the magnetic field fluctuations. The long dashed contour shows the mean equipartition level. The dotted contour separates the regions in the atmosphere where no equipartition level has occurred in the course of the simulation from the regions with at least one occurrence of the equipartition level. See the online edition for a color version of this plot. |
Second, because of the steep gradient in the Alfvén speed in the region where cA/cs > 1 inside the magnetic canopy, the fast mode undergoes refraction because the phase speed changes continuously along the wave fronts. In the apex of this refractive wave path, the wave fronts are vertically orientated and because of the long wavelength (high phase speed), wide regions of the atmosphere show velocity perturbations that are in phase along vertical lines of sight. This situation can lead to vanishing wave travel-times as measured with the phase shift analysis and is, in addition to the increase in Alfvén speed with height, another important cause of the measured reduction and fading of the wave travel-time. We note that this effect is a consequence of measuring phase shifts between vertically separated, horizontal sensing levels – it should not be misinterpreted as the evanescence of a reflecting wave. In terms of optical depth levels, another reason for the shorter wave travel-times is that inside the magnetic flux sheet and its canopy, the geometrical, vertical distances between the optical depth levels are shorter and the levels are depressed, forming at lower heights than outside the canopy. Although the phase speed of the fast magnetic mode decreases with depth, the optical depth levels are closer together, which again leads to shorter wave travel-times.
7. Summary and conclusions
We have carried out numerical experiments of wave propagation in a convectively unstable, time-dependent, magnetic solar model atmosphere. In particular, we have investigated the interaction of the magneto-acoustic waves with a strong magnetic field concentration representative of a network magnetic element. The experiments have been carried out for different cases of wave excitation.
We first investigated the propagation of spherical waves excited by local wave sources 180 km below τc = 1. The interaction between the propagating wave and the magnetic field is spatially confined and mode conversion occurs at the location of the equipartition level, where the sound speed, cs, equals the Alfvén speed, cA. The incident fast acoustic mode emerging there from the region where cA/cs < 1 is partially transmitted as a slow acoustic mode and partially converted into a fast magnetic mode when propagating into the region where cA/cs > 1. Thus, immediately above the equipartition level, both modes of the magneto-acoustic wave are present at the same time so that the velocity field includes the signature of both modes, which makes it difficult to observationally distinguish them. However, while the slow acoustic mode is guided along the field lines into the higher layers of the atmosphere, the fast magnetic mode is refracted because of the steep gradient in the Alfvén speed in the solar atmosphere. As a consequence, the two modes separate in the higher layers of the atmosphere. The equipartition level is very dynamic itself, showing excursions of several hundred kilometers. There are instants of time where multiple equipartition levels occur above each other, resulting in a series of mode conversions.
Second, we have investigated the propagation of a plane-parallel wave, which is excited at the lower boundary of the simulation domain. The resulting time series in vertical velocity, δvz(x,z,t), was used to determine the wave travel-time between different heights in the atmosphere. This was done for two different cases: first, for fixed geometrical heights, and second, for fixed optical depth levels. The vertical wave travel-time is determined by the phase shift analysis, which also yields the coherence of the considered time series for a confidence test.
In both cases, the wave travel-time is severely influenced by the presence of a strong magnetic field. If the wave travel-time is measured between two height levels, which are both located below the mean equipartition level, then the wave travel-times are about constant as a function of the horizontal distance and there exists a good degree of coherence. In this case, the wave travel-time corresponds to that of an acoustic wave in an unperturbed, quiet Sun atmosphere. If both height levels are above the mean equipartition level, the wave travel-time nearly vanishes and decreases to values twt < 5 s with a good degree of coherence. If the mean equipartition level is between, or close to one of the observing heights, then the coherence drops to insignificant values.
The influence of the mean equipartition level on the measured wave travel-time can be explained as follows. Below the mean equipartition level, the wave can freely propagate in the solar atmosphere and the time series are linearly related yielding a high degree of coherence. When the mean equipartition level is either close to or within the observing height levels, mode conversion effects become apparent.
The power maps of the vertical and horizontal velocity perturbations (Fig. 14) show that the power of the vertical velocities is suppressed at the center of the flux sheet. This is due to the propagation path of the refracted fast magneto-acoustic mode, which is expelled from the flux sheet interior. The power in the horizontal velocity perturbations increases above the mean equipartition level by several orders of magnitudes. Again, the refraction of the fast mode is responsible for this behavior. In the center of the flux sheet, the power of the horizontal velocity perturbations exceeds the power of the vertical velocities because of the transverse motion introduced by the fast magnetic mode. The power of the magnetic field fluctuations are confined to the equipartition level in the solar atmosphere and can therefore be used to reconstruct the topography of the equipartition surface as demonstrated by Finsterle et al. (2004a).
Finsterle et al. (2004a) offer different explanations of the observed vanishing wave travel-time with height and the evanescent behavior of the waves. They mention the possibility that the formation height of the observed spectral lines may converge inside strong magnetic elements, or that mode conversion could account for the vanishing wave travel-times. The present simulations now demonstrate that a combination of both processes plus the propagation path of the fast magnetic mode is responsible for the strongly decreasing or vanishing wave travel-times with height.
Mode conversion does influence the wave travel-time because of the excitation of the fast magnetic mode. Inside the magnetic flux sheet and its canopy, the phase speed of the fast mode strongly increases, which is one reason for the drastic reduction in wave travel-time. The strong gradient in phase velocity in the region where cA/cs > 1 causes the wave fronts of the fast magnetic mode to refract. In the apex of the resulting wave path, the wave fronts align with the vertical direction so that wide height ranges in the atmosphere contain velocities that are in phase. This causes vanishing phase travel-times, which mimics the behavior of an evanescent wave, although the waves in reality are propagating.
Although a proposal ruled out by Finsterle et al. (2004a), the simulations suggest that distances between the line-formation heights can be reduced within the magnetic flux concentrations. This would contribute to the reduction in the wave travel-times as measured from the Doppler shifts of the spectral lines. However, a detailed calculation of synthetic spectral-line profiles is necessary to confirm this finding.
Since mode conversion is responsible for the reduction in wave travel-times, it is important to consider the relative position of the conversion zone (i.e. the equipartition level) and the formation height of the spectral lines. In conclusion we can say that the apparent evanescence of waves in the vicinity of strong magnetic fields originates in reality from the propagating fast magnetic mode in the region where cA/cs > 1.
Online material
Movie of Figure 2 Access here
Movie of Figure 3 Access here
Movie of Figure 4 Access here
Movie of Figure 6 Access here
Acknowledgments
The authors acknowledge support from the European Helio- and Astroseismology Network (HELAS), which was funded as Coordination Action by the European Commission’s Sixth Framework Programme. We thank the referee for the thorough reading of the manuscript and for constructive remarks that helped to substantially improve the scientific perspective of the paper.
References
- Bogdan, T. J., Carlsson, M., Hansteen, V. H., et al. 2003, ApJ, 599, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Cacciani, A., Jefferies, S. M., Finsterle, W., et al. 2003, in GONG+ 2002, Local and Global Helioseismology: the Present and Future, ed. H. Sawaya-Lacoste, ESA SP, 517, 243 [Google Scholar]
- Cally, P. S. 2007, Astron. Nachr., 328, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Cally, P. S. 2009, Sol. Phys., 254, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. Gizon, L. & Duvall, Jr. T. L. 2008, Sol. Phys., 251, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Cavallini, F. 2006, Sol. Phys., 236, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Finsterle, W., Jefferies, S. M., Cacciani, A., & Rapex, P. 2004a, in SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, ed. D. Danesy, ESA SP, 559, 223 [Google Scholar]
- Finsterle, W., Jefferies, S. M., Cacciani, A., et al. 2004b, Sol. Phys., 220, 317 [Google Scholar]
- Finsterle, W., Jefferies, S. M., Cacciani, A., Rapex, P., & McIntosh, S. W. 2004c, ApJ, 613, L185 [Google Scholar]
- Freytag, B., Steffen, M., & Dorch, B. 2002, Astron. Nachr., 323, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2011, J. Comp. Phys., in press [Google Scholar]
- Haberreiter, M., Finsterle, W., & Jefferies, S. M. 2007, Astron. Nachr., 328, 211 [Google Scholar]
- Hasan, S. S., & van Ballegooijen, A. A. 2008, ApJ, 680, 1542 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E., & Collados, M. 2006, ApJ, 653, 739 [Google Scholar]
- Nutto, C., Steiner, O., & Roth, M. 2010, Astron. Nachr., 331, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Parchevsky, K. V., & Kosovichev, A. G. 2009, ApJ, 694, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Priestley, M. B. 1981, Spectral Analysis and Time Series (Elsevier Academic Press) [Google Scholar]
- Rajaguru, S. P., Sankarasubramanian, K., Wachter, R., & Scherrer, P. H. 2007, ApJ, 654, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, C. S., Bogdan, T. J., Carlsson, M., et al. 2002, ApJ, 564, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Schaffenberger, W., Wedemeyer-Böhm, S., Steiner, O., & Freytag, B. 2005, in Chromospheric and Coronal Magnetic Fields, ed. D. E. Innes, A. Lagg, & S. A. Solanki, ESA SP, 596, 65 [Google Scholar]
- Schaffenberger, W., Wedemeyer-Böhm, S., Steiner, O., & Freytag, B. 2006, in Solar MHD Theory and Observations: A High Spatial Resolution Perspective, ed. J. Leibacher, R. F. Stein, & H. Uitenbroek, ASP Conf. Ser., 354, 345 [Google Scholar]
- Schunker, H., & Cally, P. S. 2006, MNRAS, 372, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Shelyag, S., Zharkov, S., Fedun, V., Erdélyi, R., & Thompson, M. J. 2009, A&A, 501, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2001, ApJ, 546, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O., Vigeesh, G., Krieger, L., et al. 2007, Astron. Nachr., 328, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Toro, E. F. 2009, Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction, 3rd ed. (Berlin: Springer) [Google Scholar]
- Vecchio, A., Cauzzi, G., Reardon, K. P., Janssen, K., & Rimmele, T. 2007, A&A, 461, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigeesh, G., Hasan, S. S., & Steiner, O. 2009, A&A, 508, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 a) Magnetic setup at the start of the simulation showing the logarithm of the magnetic field strength in gauss. The white contour displays the equipartition level, where cs = cA. The crosses indicate three different locations of local wave excitation, individually discussed in Sect. 3. b) Corresponding temperature in Kelvin (colors) and velocity (arrows). The longest arrows correspond to 10 km s-1. The dashed curve indicates optical depth τc = 1. |
| In the text | |
 |
Fig. 2 Time sequences of the propagation of a wave launched at position (i) of Fig. 1a. The time increases from top to bottom. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the absolute magnetic field, δ|B|. The green contours (thin white in the print edition) display the equipartition level, where cs = cA. The white curves indicate the position of a single wave front during its evolution in time. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
| In the text | |
 |
Fig. 3 Time sequences of the propagation of a wave launched at position (ii) of Fig. 1a. Time increases from top to bottom. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the absolute magnetic field, δ|B|. The green contours (thin white in the print edition) display the equipartition level, cs = cA. The white curves indicate the position of a single wave front of the fast magnetic mode and its evolution in time. In the last row, the fast magnetic mode (in the region where cA/cs > 1) has already been refracted and wave fronts of constant phase cannot be clearly identified. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
| In the text | |
 |
Fig. 4 Time sequences of the propagation of a wave launched at position iii) of Fig. 1. Time increases from top to bottom. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the pressure, δ|p|/p0. Note that different time steps apply to each column. The green contours (thin white in the print edition) display the equipartition level, cs = cA. The arrows in the right column indicate the direction of the magnetic field lines, along which the slow acoustic mode escapes the atmosphere. The black curves in the left column indicate the position of a single wave front and its evolution with time. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
| In the text | |
 |
Fig. 5 Vertical section of the ratio of the Alfvén speed, cA, to the sound speed, cs, taken at x = 1300 km from the snapshot displayed in the bottom row of Fig. 4, corresponding to the time instance t = 200 s. The dashed horizontal line indicates the equipartition level. For each location where cA = cs, the transmission coefficient T is calculated for a range of most probable attack angles, α, for the studied wave propagation experiment. |
| In the text | |
 |
Fig. 6 Time sequences of a plane-parallel wave launched at the bottom of the computational domain travelling through the convection zone and the atmosphere. Left column: perturbation of the absolute velocity, δ|v|. Right column: perturbation of the absolute magnetic field, δ|B|. The green contours represent the equipartition level, cs = cA. Time increases from top to bottom. The white curves indicate the position of a single wave front and its evolution in time. δ|v|(t) is available as an mpeg animation in the online edition of the article. |
| In the text | |
 |
Fig. 7 Time sequences of the magnetic field perturbation, δ|B|, resulting from the interaction of the plane-parallel wave with the horizontal magnetic field. Time increases from top to bottom. The green contours represent the equipartition level, cs = cA. The white arrow follows the propagation path of a single magnetic field perturbation. |
| In the text | |
 |
Fig. 8 Top: magnetic field averaged over the entire time span of 1500 s. The solid curves represent magnetic field lines. The heavy white contour displays the time-averaged position of the equipartition level. Bottom: temporally and horizontally averaged temperature stratification of the background model. |
| In the text | |
 |
Fig. 9 Time-averaged phase speed of the fast mode at selected fixed geometrical heights (top panel) and selected optical depth levels τ1 = 1, τ2 = 0.025, τ3 = 0.001, τ4 = 0.0001, and τ5 = 2.5 × 10-5 (bottom panel). The bold lines indicate the regime where cA/cs > 1, while the thin lines represent the regime where cA/cs < 1. The asterisks mark the locations where the respective height levels cross the equipartition level. |
| In the text | |
 |
Fig. 10 Computational domain with the solid contour displaying the mean equipartition level (cs = cA). The dashed horizontal lines indicate the different heights between which the wave travel-time is evaluated. The shaded boxes indicate the regions where the wave travel-time cannot be trusted because the coherence falls below the limit of σcrit = 0.5. |
| In the text | |
 |
Fig. 11 Vertical wave travel-time, twt, (top plot in each panel) and coherence of the time series (bottom plot in each panel) between five different geometrical heights a)–d) in the atmosphere. The shaded intervals mark regions for which the coherence drops below σcrit = 0.5. |
| In the text | |
 |
Fig. 12 Computational domain, showing the different time-averaged optical depths τ that are used for the travel time analysis. The solid contour displays the mean equipartition level. The shaded boxes mark regions for which the coherence drops below σcrit = 0.5. |
| In the text | |
 |
Fig. 13 Vertical wave travel-time, twt, (top plot of each panel) and coherence of the time series (bottom plot of each panel) between five different optical depths a)–d) in the atmosphere. The shaded intervals mark regions for which the coherence drops below σcrit = 0.5. |
| In the text | |
 |
Fig. 14 Power maps of the velocity perturbation of the simulation shown in Fig. 6. Top: power map of the vertical velocity perturbation, δvz. Bottom: power map of the horizontal velocity perturbation, δvx. Overplotted is the contour of the mean equipartition level. See the online edition for a color version of this plot. |
| In the text | |
 |
Fig. 15 Power map of the magnetic field fluctuations. The long dashed contour shows the mean equipartition level. The dotted contour separates the regions in the atmosphere where no equipartition level has occurred in the course of the simulation from the regions with at least one occurrence of the equipartition level. See the online edition for a color version of this plot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


