| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201117609 | |
| Published online | 05 October 2011 | |
Letter to the Editor
The average optical spectra of intense starbursts at z ~ 2: outflows and the pressurization of the ISM⋆,⋆⋆
1
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
e-mail: matthew.lehnert@obspm.fr
2
Institut d’Astrophysique Spatiale, UMR 8617, CNRS, Université Paris-Sud, Bâtiment 121, 91405 Orsay Cedex, France
Received: 30 June 2011
Accepted: 7 September 2011
An important property of star-forming galaxies at z ~ 1−2 is the high local star-formation intensities they maintain over tens of kiloparsecs at levels that are only observed in the nearby Universe in the most powerful nuclear starbursts. To investigate how these high star-formation intensities affect the warm ionized medium, we present an analysis of the average spectra of about 50 such galaxies at z ≈ 1.2−2.6 and of subsamples selected according to their local and global star-formation intensity. Stacking allows us to probe relatively weak lines like [Sii]λλ6716,6731 and [Oi]λ6300, which are tracers of the conditions of the ISM and are undetectable in most individual targets. We find higher gas densities (hence pressures) in intensely star-forming regions compared to fainter diffuse gas and, overall, values that are comparable to starburst regions and the diffuse ISM in nearby galaxies. By modeling the Hα surface brightnesses and [Sii]/Hα line ratios with the Cloudy photoionization code, we find that our galaxies continue trends observed in local galaxies, where gas pressures scale with star-formation intensity. We discuss these results in the context of models of self-regulated star formation, where star formation determines the average thermal and turbulent pressure in the ISM, which in turn determines the rate at which stars can form, finding good agreement with our data. We also confirm the detection of broad, faint lines underlying Hα and [Nii], which have previously been considered evidence of either outflows or active galactic nuclei. Finding that the broad component is only significantly detected in stacks with the highest average local and global star-formation intensities strongly supports the outflow interpretation, and further emphasizes the importance of star-formation feedback and self-regulation in the early Universe.
Key words: galaxies: kinematics and dynamics / galaxies: evolution / galaxies: ISM / galaxies: high-redshift
Data obtained as part of Programs ID 074.A-9011, 075.A-0318, 075.A-0466, 076.A-0464, 076.A-0527, 076.B-0259, 077.B-0079, 077.B-0511, 078.A-0055, 078.A-0600, 079.A-0341, and 079.B-0430 at the ESO-VLT.
Figure 1 and Table 2 are available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
The nature and evolution of galaxies is a result of the complex interplay between heating, cooling and dynamical processes in the interstellar medium (ISM). The cyclic, or competitive, nature of these processes determines the rate at which stars form and creates a feedback loop that determines the chemistry and structure of galaxies, along with their ISM. This interplay ultimately results in galaxies as we observe them today.
In starburst galaxies, where the energy injection rate per unit volume from young stars is high, we may see the effects of the self-regulation of star formation, a process in which supernova feedback with its strong energy injection may well play an important role (Silk 2001) – and drive the cloud velocity dispersion (Joung & Mac Low 2006; Tasker & Bryan 2006) – as may turbulent pressure (Silk 2001; Blitz & Rosolowsky 2006). At low-energy injection rates into the ISM, global shear is likely to play the most significant role in determining the peculiar velocities in dense massive clouds (Gammie et al. 1991). The observed turbulence is dominated by nonaxisymmetric gravitational instabilities at low star-formation intensity levels, like the few to several tens of km s-1 seen in the Milky Way, but at high intensity levels mechanical energy from the stellar population may play the most significant role (Joung et al. 2009; Agertz et al. 2009).
Recently, we have proposed that the large Hα line widths observed in distant (z ~ 1−3) intensely star-forming galaxies are driven by the mechanical energy liberated by young stars, a relationship which can be understood within the context of self-regulated star formation (Lehnert et al. 2009; Le Tiran et al., in prep.). We hypothesized that mechanical energy is sufficient to keep the disk critically unstable against fragmentation and collapse, hence star formation (Toomre Q ~ 1). The intensity of the star formation in these distant galaxies is very high, similar to those in local starbursts but on a much larger physical scale, and it is maintained by large gas fractions and high mass-surface densities. These line widths do not appear to be driven by either cosmological accretion (Le Tiran et al. 2011) or gravitational instabilities.
In this manuscript, we develop these arguments further through a stacking analysis of rest-frame optical emission lines of about 50 galaxies with redshifts of 1.2 to 2.6 and high Hα surface brightnesses. Stacking allows us to analyze emission lines that are too faint to be observed in most individual galaxies such as [Sii]λλ6716,6731 or [Oi]λ6300, which are key indicators of the pressure and sources of ionization in the emission line gas. We analyze stacks of subsamples to investigate how the gas properties scale with star-formation intensity (rate per unit area). In a stacking analysis of a very similar sample, but focusing on trends with stellar mass and radius, Shapiro et al. (2009) identified a broad line underlying Hα and [Nii], but were unable to differentiate whether this broad line emission was from outflows or active galactic nuclei (AGN). We confirm the detection of a broad component and argue that its presence in our stacks, where the significance of the broad component increases with increasing star-formation intensity, can be interpreted as confirming the outflow hypothesis.
2. Data analysis
We use ESO archival data from a variety of programs with SINFONI on the ESO-VLT of a sample of more than fifty galaxies in the redshift range 1.2 − 2.6; see Le Tiran et al. (2011) for further details. We have excluded all galaxies with recognizable AGN features in their data cubes – especially broad lines and high ratios of [Nii]λ6583/Hα. We produce for each object an integrated spectrum using all the spectra in the data cube where Hα is detected above the 3-σ level, which are co-added after shifting Hα to its rest wavelength in order to remove any broadening due to the velocity field and weighted by the Hα signal-to-noise ratio (SNR) of each object in order to maximize the final SNR. Uncertainties were measured using a Monte-Carlo method fitting 1000 realizations of the spectrum (Fig. 1 inset).
To investigate whether the stacked emission line properties depend on the Hα surface brightness (and/or redshift) of the galaxies used, we also made comparative stacks of objects in three bins: (1) z < 1.8 and star-formation rate (SFR) < 100 M⊙ yr-1, (2) z > 1.8 and SFR < 100 M⊙ yr-1 and (3) z > 1.8 and SFR > 100 M⊙yr-1. All galaxies have similar isophotal sizes (Lehnert et al. 2009; Le Tiran et al. 2011). To investigate the role that star-formation intensity might play in determining the characteristics of the integrated spectrum, for each bin and for the entire sample we also made one sub stack using only the 18 brightest pixels in the Hα distribution of individual galaxies, and another using only the remaining, fainter pixels. Eighteen pixels correspond to approximately the FWHM of the PSF (~0′′ .6). Each brightest pixel stack contains about the same total fraction of the emission in its sample (~25%; Table 1). In Table 1, Ngals is the number of galaxies included in the stack; ⟨ ΣSFR ⟩ is the average SFR per unit area (M⊙ yr-1 kpc-2), calculated using the conversion factor for Hα luminosity to the SFR from Kennicutt (1998); and LHα,brightest/LHα,whole is the proportion of the Hα luminosity contained in the 18 brightest pixels stacks compared to the stacks of whole galaxies.
Properties of the different stacked spectra.
The galaxies generally have complex morphologies and the low spatial resolution of the data makes it difficult to accurately determine the relative centering and detailed morphology of the brightest pixels. They are usually within one resolution element but can have complex spatial distributions. High-resolution line imaging obtained using adaptive optics or HST continuum imaging show the morphologies of the highest surface brightness emission is frequently complex, clumpy, and often not at the dynamical or isophotal center (e.g., Lehnert et al. 2009; Genzel et al. 2011). Since all data sets reach roughly the same limiting observed Hα surface brightness level, over a wide range in redshift, we could not construct stacks at constant rest-frame surface brightness levels due to the strong impact of cosmological surface brightness dimming. The average rest-frame surface brightness of each stack is given in Table 2.
3. Emission line properties
We obtain log [Nii]λ6583/Hα = −0.75 to −0.55 in all four stacks, and log [Sii]λλ6716,6731 = −0.5 to −0.75. We did not detect [Oi]λ6300 in any of our stacks, with an upper limit of log [Oi]/Hα = −1.4 to −1.9 (1σ), similar to those in the integrated spectra of nearby star-forming galaxies (Lehnert & Heckman 1994) and Hii regions. The flux ratio of [Sii]λ6716/[Sii]λ6731 is about 1.2 to 1.4, near the low-density limit (1.45; Fig. 2), and the highest values are found in the stacks with the highest surface-brightness Hα emission. For most of the stacks the density must be very low (ne ~ 10−100 cm-2, see Fig. 2), whereas in the regions of the highest Hα surface brightnesses in each galaxy we find values of about 100 to 500 cm-3, with a mean of ~200 cm-3 (Table 2; Fig. 2). These values are similar to nearby starbursts, which show strong evidence of driving energetic outflows (Fig. 2; Lehnert & Heckman 1996). Finding that the full stacks and the stacks excluding the brightest pixels are at (or near) the low-density limit suggests that the most extended emission contributes most of the flux and indicates that these outer regions are more like the diffuse ISM in nearby disk galaxies (Lehnert & Heckman 1994; Wang et al. 1998).
We also find no significant differences in the widths of the various lines analyzed. Although there is a slight tendency for [Nii]λ6583 to be systematically broader than Hα in all stacks, all individual width measurements are the same within the uncertainties. We do find a trend for the narrow components of both lines to be broader for the stacks with high average surface brightnesses. This is related to the trend for the most intense star-forming regions to have the broadest lines (Lehnert et al. 2009).
 |
Fig. 2 [Sii]λ6716/[Sii]λ6731 line flux ratio as a function of electron density (cm-3), for a temperature of 104 K (blue line). Only results for the stacks of the brightest pixels of Hα emission are indicated (red crosses). The error bars indicate the 1σ uncertainties in the measurements. For clarity, stacks with [Sii] line ratios below the low-density limit are not shown. The inset at the lower left shows the distribution of electron densities ne in the nuclear region of nearby starburst galaxies (Lehnert & Heckman 1996), as well as the mean electron density for the stack, including only the brightest pixels of all our objects (solid blue line) and the corresponding ± 1σ uncertainties (dashed blue lines). |
Several of the spectral stacks have an apparent broad line component underlying the region around Hα (Fig. 3), as noted by Shapiro et al. (2009). It is not our intent to accurately constrain the properties of this component but to robustly demonstrate that some of the data are better fitted by including a broad line. To this purpose we adopted a Bayesian approach, as analysis of such data based on minimization is often not very constraining due to the difficulty of accurately estimating uncertainties (see Table 2). We computed the relative strength of evidence, Bayes factor B, for a model that includes a broad line versus one without. Generally speaking, ln(B) ≥ 5 is considered to be strong evidence in favor of the broad-line models (interpreted against the Jeffreys’ scale; see Trotta 2008, and references therein). We find strong evidence in favor of broad lines in the stacks with the highest average surface brightnesses (see B values listed in Table 2). In general, our fits (as derived from models with the highest values of B) agree with Shapiro et al. (2009). The stacks of the brightest 18 pixels have the lowest signal-to-noise as each is composed of only ~25% of the total flux and yet it is those stacks where the need for an additional broad component is the most robust. We also find that the best fits are broad (FWHM ~ 1500 km s-1) and that the total flux ratio of the broad to narrow Hα emission lines is about 30% for those stacks with a significant broad feature.
 |
Fig. 3 Zoom of the region of Hα and [Nii] for 12 different stacks (black lines). From left to right: the integrated spectrum of all the emission from each galaxy (whole), only the brightest 18 pixels in Hα (brightest), and all other pixels (faint); from top to bottom: all spectral bins, bins (1), (2), and (3). The dashed blue line is the best fit to the strongest component of each line, the green dashed line the fit to the weaker offset component, and the red line is the total of the fitted lines (see text for details). For each stack we show the residuals to the fit underneath each spectrum (in blue for stacks that do not require a broad component and in red for those that do). Velocity offsets range from ~ 100 − 500 km s-1 with the highest value seen in the stack with the highest average surface brightness. |
4. Discussion and conclusions
The results of the broad line analysis (Sect. 3) suggest a close relationship between the source of the broad emission and the star-formation intensity in these galaxies. Nearby galaxies whose starbursts are as intense as those observed in our distant sample show strong evidence of driving large-scale outflows (Lehnert & Heckman 1996). In fact, one can find close analogs between our spectra with or without a broad component and the low-redshift starburst galaxies in Lehnert & Heckman (1995), suggesting both samples must have similar phenomenology. Although Shapiro et al. (2009) have already suggested that broad lines in stacked spectra of z ~ 2 intensely star-forming galaxies may indicate outflows, since they stacked according to stellar mass and radius (comparing nuclear and off-nuclear stacks) they were unable to rule out that the broad lines were due to AGN. The trends we see with average star-formation intensity contradicts the AGN hypothesis, simply because many intensely star-forming regions in these galaxies are off-nucleus, whereas the nuclear regions often have very low surface brightness (e.g. Förster Schreiber et al. 2009).
In the outflow scenario we expect, in addition to single narrow components of Hα and [Nii]λλ6548,6583, three more lines of Hα and [Nii] that are offset and likely very broad (e.g., Lehnert & Heckman 1996). By making five physically motivated assumptions we avoid introducing nine additional free parameters: (1) all three additional lines have the same offset velocity; (2) velocity dispersions are the same for each Hα and [Nii] line component and are equal to the offset velocity; (3) the flux ratio of [Nii]/Hα is given by fast shock models (ratios ranging from ~0.2−1 for the velocities we considered in this modeling, see Allen et al. 2008); (4) the velocity offset and the shock speed are the same; and (5) the flux of the offset Hα component is 10% of that of the main Hα line. This last value provides a match to the estimated peak fluxes in the best-fit single broad component. This reduces the number of free parameters to only one, the offset velocity, while the other eight are constrained.
We find that these fits are as significant as assuming a single broad component for velocity offsets of a few 100 km s-1and narrow-to-broad Hα flux ratios of 10%. These values are similar to those in the extended (i.e., wind) emission in nearby starbursts (Lehnert & Heckman 1996). The derived pressures are also similar to those in nearby starbursts, which is a necessary condition for driving winds (Fig. 2). There is also enough mechanical energy in the shocks to power these flows. The mechanical energy output at a SFR of 150 M⊙ yr-1 (typical of our high surface brightness sample) is about 1044 erg s-1. The fraction of the total energy from shocks fast enough to explain the broad lines is about 1−2% (Allen et al. 2008). If we assume that the mechanical energy output from stars is efficiently thermalized, we only require around 1−10% of the mechanical energy to energize the broad, blueshifted line emission.
What do these results imply about the nature of the ISM in these high-redshift galaxies? We have already argued that the galaxies have high pressure. Figure 4 illustrates that the warm ionized medium in nearby star-forming and starburst galaxies and in our galaxies forms a continuity – a one-parameter family. Going from low to high Hα surface brightness we progress from diffuse ISM in nearby galaxies, through Hii regions (and their surroundings) to the nuclei of nearby starburst galaxies (e.g., Wang et al. 1998). On average our galaxies lie at the high surface-brightness, low [Sii]/Hα end of the relationship, similar to the positions of local powerful nuclear starbursts.
This continuity can be explained through a range of ISM pressures and radiation field intensities. We modeled the data as photoionized clouds (using the code Cloudy; Ferland et al. 1998), using the ionizing spectrum of a young (108 yrs) stellar population forming stars at a constant rate with a Salpeter IMF (Leitherer et al. 1999) and a range of column and volume densities. Our results suggest that the galaxies have high average gas densities (~10–few × 100 cm-3) and high ionization parameters (log U ~ −2 to 0, where U is proportional to the relative intensity of the photon field divided by the total gas density). This supports the hypothesis of Wang et al. (1998) that this relationship can be understood as an underlying proportionality between the thermal pressure and the mean star-formation intensity in a photoionized gas.
What is the source of this underlying proportionality? Star formation might be regulated by the average pressure in the ISM (Silk 1997), which Wang et al. (1998) suggested may itself be either regulated by the mechanical energy injection from star formation or related to the hydrostatic or turbulent pressure.
 |
Fig. 4 [Sii]λλ 6716,6731/Hα flux ratio versus average Hα surface brightness for our 12 different stacks (see Table 2) of galaxies (red circles, with 1-σ uncertainties) superimposed on data for the diffuse emission in nearby star-forming and starburst galaxies from Wang et al. (1998) (black dots). The lines represent Cloudy photoionization models (Ferland et al. 1998) with various column densities (1020, 1021 and 1022 cm-2 in green, red and purple, respectively), ionization parameters (U = 10-5 to 1 from left to right along each line) and densities (1, 10, 100, 1000 cm-3 as solid, dashed, dot-dash and dotted, respectively). The legend at the upper right indicates the colors of the lines for different column densities, while the legend at the lower left indicates the line styles for each volume density. |
If the mechanical energy from massive stars is controlling the over-pressure, we would expect the pressure to increase linearly with the star-formation intensity. This can be estimated as 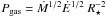 (where Pgas is the gas pressure, Ṁ the mass loss and entrainment rate, Ė the mechanical energy output, and R ⋆ the radius over which the energy and mass output occurs, e.g. Strickland & Heckman 2009). From Leitherer et al. (1999), we can estimate the mechanical energy and mass output rate from star formation. Adopting an equilibrium mass and energy output rate for continuous star-formation over 108 yrs, we estimate pressures of 1 × 10-10 dyne cm-2 (one-sided) for 0.5 M⊙ yr-1 kpc-2. If the mass entrainment rate is a factor of a few, this predicted pressure would be somewhat higher (consistent with that observed in M82 for example; Strickland & Heckman 2009). For our stacks, the results of the photoionization models suggest thermal pressures of 6 × 10-10 to 6 × 10-11 dyne cm-2.
(where Pgas is the gas pressure, Ṁ the mass loss and entrainment rate, Ė the mechanical energy output, and R ⋆ the radius over which the energy and mass output occurs, e.g. Strickland & Heckman 2009). From Leitherer et al. (1999), we can estimate the mechanical energy and mass output rate from star formation. Adopting an equilibrium mass and energy output rate for continuous star-formation over 108 yrs, we estimate pressures of 1 × 10-10 dyne cm-2 (one-sided) for 0.5 M⊙ yr-1 kpc-2. If the mass entrainment rate is a factor of a few, this predicted pressure would be somewhat higher (consistent with that observed in M82 for example; Strickland & Heckman 2009). For our stacks, the results of the photoionization models suggest thermal pressures of 6 × 10-10 to 6 × 10-11 dyne cm-2.
In an alternative interpretation (which may be particularly appropriate at low star-formation intensities), the pressures are set by gravitational processes. Star-formation intensity is related to a cloud-cloud collision model, which gives 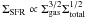 (Silk & Norman 2009). The pressure in the ISM can be related to gravity or turbulence through Pgas = ρgasσgas = πGΣgasΣtotal, where Pgas and ρgas are the gas pressure and density, respectively, and G is the gravitational constant. Combining them suggests that ΣSFR ∝ P(Σgas/Σtotal)1/2. We can normalize this relationship
(Silk & Norman 2009). The pressure in the ISM can be related to gravity or turbulence through Pgas = ρgasσgas = πGΣgasΣtotal, where Pgas and ρgas are the gas pressure and density, respectively, and G is the gravitational constant. Combining them suggests that ΣSFR ∝ P(Σgas/Σtotal)1/2. We can normalize this relationship
empirically with the appropriate values for the Milky Way – ISM pressure of ~3000 K cm-3, star-formation intensity ~2.5 × 10-3 M⊙ yr-1 kpc-2 and a gas fraction of about 10%. The gas fraction in distant galaxies is likely to be higher, a few 10s of percent (Daddi et al. 2010). Using the average pressure from our photoionization modeling and the relation between star-formation intensity and pressure based on the Milky Way scaling suggests that ΣSFR ~ 1 M⊙ yr-1 kpc-2.
If star formation is driving the gas pressure, then it is likely that turbulent pressure is similar or even higher than thermal pressure, especially at high star-formation intensities (Joung et al. 2009). In our stacking analysis, we find typical Hα line velocity dispersions of about 125 km s-1 and densities in the warm ionized gas of about 30 − 300 cm-3. If the clouds formed through turbulent compression, the pre-shocked material would have turbulent pressures: Pturb = ρgasσgas ~ 10-9 to 10-10 dyne cm-2. This is higher than the thermal pressures we observe in the emission line clouds of nearby galaxies, as suggested by models of ISM pressure regulated by feedback from star formation (e.g., Joung et al. 2009), but in the range of what we find at z ~ 1−2.
In summary we find that these distant galaxies have high ISM pressures and drive outflows, at least at the highest average Hα surface brightnesses. These are two characteristics similar to intense starbursts at low redshift. Overall, we favor a picture where the pressure in the ISM is determined by the intensity of the star formation and where feedback sets the scaling between them. Since the pressure is being regulated and it likely determines the nature of star formation, this suggests that the star formation is self-regulating in these high-redshift galaxies (Silk 1997). This extends our earlier conclusion that star formation is likely to regulate the pressure of the ISM based on spatially resolved properties of individual distant galaxies with high Hα surface brightness (Lehnert et al. 2009; Le Tiran et al. 2011).
Online material
 |
Fig. 1 Star-formation rate as a function of redshift for all galaxies used. Red dashed lines correspond to the boundaries between the 3 different bins used to make comparative stacks, which are labeled (1), (2), and (3). As an inset on the left, we show the stacked spectrum (signal-to-noise of Hα weighted average) of all the galaxies in the sample. The lines of Hα, [Nii]λλ6548,6583, and [Sii]λλ6716,6731 are all significantly detected, but we can only set an upper limit on the [Oi]λ6300 emission. |
Detailed properties of all the stacks.
Acknowledgments
The work of L.L.T., M.D.L., and P.D.M. was partially supported by a grant from the Agence Nationale de la Recherche (ANR). We thank the anonymous referee for helpful suggestions.
References
- Agertz, O., Lake, G., Teyssier, R., et al. 2009, MNRAS, 392, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Blitz, L., & Rosolowsky, E. 2006, ApJ, 650, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F., Ostriker, J. P., & Jog, C. J. 1991, ApJ, 378, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Newman, S., Jones, T., et al. 2011, ApJ, 733, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Joung, M. K. R., & Mac Low, M.-M. 2006, ApJ, 653, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Joung, M. R., Mac Low, M.-M., & Bryan, G. L. 2009, ApJ, 704, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Le Tiran, L., Lehnert, M. D., Di Matteo, P., Nesvadba, N. P. H., & van Driel, W. 2011, A&A, 530, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1994, ApJ, 426, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1995, ApJS, 97, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996, ApJ, 462, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Nesvadba, N. P. H., Le Tiran, L., et al. 2009, ApJ, 699, 1660 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, K. L., Genzel, R., Quataert, E., et al. 2009, ApJ, 701, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 1997, ApJ, 481, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2001, MNRAS, 324, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J., & Norman, C. 2009, ApJ, 700, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Heckman, T. M. 2009, ApJ, 697, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Tasker, E. J., & Bryan, G. L. 2006, ApJ, 641, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R. 2008, Contemp. Phys., 49, 71 [Google Scholar]
- Wang, J., Heckman, T. M., & Lehnert, M. D. 1998, ApJ, 509, 93 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 2 [Sii]λ6716/[Sii]λ6731 line flux ratio as a function of electron density (cm-3), for a temperature of 104 K (blue line). Only results for the stacks of the brightest pixels of Hα emission are indicated (red crosses). The error bars indicate the 1σ uncertainties in the measurements. For clarity, stacks with [Sii] line ratios below the low-density limit are not shown. The inset at the lower left shows the distribution of electron densities ne in the nuclear region of nearby starburst galaxies (Lehnert & Heckman 1996), as well as the mean electron density for the stack, including only the brightest pixels of all our objects (solid blue line) and the corresponding ± 1σ uncertainties (dashed blue lines). |
| In the text | |
 |
Fig. 3 Zoom of the region of Hα and [Nii] for 12 different stacks (black lines). From left to right: the integrated spectrum of all the emission from each galaxy (whole), only the brightest 18 pixels in Hα (brightest), and all other pixels (faint); from top to bottom: all spectral bins, bins (1), (2), and (3). The dashed blue line is the best fit to the strongest component of each line, the green dashed line the fit to the weaker offset component, and the red line is the total of the fitted lines (see text for details). For each stack we show the residuals to the fit underneath each spectrum (in blue for stacks that do not require a broad component and in red for those that do). Velocity offsets range from ~ 100 − 500 km s-1 with the highest value seen in the stack with the highest average surface brightness. |
| In the text | |
 |
Fig. 4 [Sii]λλ 6716,6731/Hα flux ratio versus average Hα surface brightness for our 12 different stacks (see Table 2) of galaxies (red circles, with 1-σ uncertainties) superimposed on data for the diffuse emission in nearby star-forming and starburst galaxies from Wang et al. (1998) (black dots). The lines represent Cloudy photoionization models (Ferland et al. 1998) with various column densities (1020, 1021 and 1022 cm-2 in green, red and purple, respectively), ionization parameters (U = 10-5 to 1 from left to right along each line) and densities (1, 10, 100, 1000 cm-3 as solid, dashed, dot-dash and dotted, respectively). The legend at the upper right indicates the colors of the lines for different column densities, while the legend at the lower left indicates the line styles for each volume density. |
| In the text | |
 |
Fig. 1 Star-formation rate as a function of redshift for all galaxies used. Red dashed lines correspond to the boundaries between the 3 different bins used to make comparative stacks, which are labeled (1), (2), and (3). As an inset on the left, we show the stacked spectrum (signal-to-noise of Hα weighted average) of all the galaxies in the sample. The lines of Hα, [Nii]λλ6548,6583, and [Sii]λλ6716,6731 are all significantly detected, but we can only set an upper limit on the [Oi]λ6300 emission. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


