| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201117525 | |
| Published online | 27 September 2011 | |
A new comprehensive 2D model of the point spread functions of the XMM-Newton EPIC telescopes: spurious source suppression and improved positional accuracy
1
Dept. of Physics and Astronomy, Leicester University,
Leicester
LE1 7RH,
UK
e-mail: amr30@star.le.ac.uk
2
XMM SOC, ESAC, Apartado 78, 28691 Villanueva de la
Cañada, Madrid,
Spain
3
Leibniz-Institut für Astrophysik Potsdam,
An der Sternwarte 16,
14482
Potsdam,
Germany
Received: 20 June 2011
Accepted: 23 August 2011
Aims. We describe here a new full 2D parameterization of the PSFs of the three XMM-Newton EPIC telescopes as a function of instrument, energy, off-axis angle and azimuthal angle, covering the whole field-of-view (FoV) of the three EPIC detectors. It models the general PSF envelopes, the primary and secondary spokes, their radial dependencies, and the large-scale azimuthal variations.
Methods. This PSF model has been constructed via the stacking and centering of a large number of bright, but not significantly piled-up point sources from the full FoV of each EPIC detector, and azimuthally filtering the resultant PSF envelopes to form the spoke structures and the gross azimuthal shapes observed.
Results. This PSF model is available for use within the XMM-Newton science analysis system via the usage of current calibration files XRTi_XPSF_0011.CCF and later versions. Initial source-searching tests showed substantial reductions in the numbers of spurious sources being detected in the wings of bright point sources. Furthermore, we have uncovered a systematic error in the previous PSF system, affecting the entire mission to date, whereby returned source RA and Dec values are seen to vary sinusoidally about the true position (amplitude ≈0.8″) with source azimuthal position.
Conclusions. The new PSF system is now available and is seen as a major improvement with regard to the detection of spurious sources. The new PSF also largely removes the discovered astrometry error and is seen to improve the positional accuracy of EPIC. The modular nature of the PSF system allows for further refinements in the future.
Key words: X-rays: general / instrumentation: miscellaneous / telescopes
© ESO, 2011
1. Introduction
XMM-Newton (Jansen et al. 2001), a cornerstone mission of ESA’s Horizon 2000 science program, was designed as an X-ray observatory able to study cosmic X-ray sources spectroscopically with the highest possible collecting area in the 0.2−10 keV band. This high throughput is achieved primarily through the use of 3 highly nested Wolter type I imaging telescopes. The design of the optics was driven by the need to have the highest possible effective area up to 10 keV, and in particular at ~7 keV, where the K lines of astrophysically significant iron appear. In grazing incidence optics, the effective area is generally increased by nesting many mirrors together and packing the front aperture as much as possible. In the case of the XMM-Newton mirrors, each of the three telescopes contains a mirror module of focal length 7.5 m, comprising 58 nested mirror shells, the axial length of the total mirror being 60 cm, this shared equally between the paraboloid and the hyperboloid halves of the Wolter I configuration. The maximum diameter mirror shell is 70 cm, and the outer and inner mirror shell thicknesses are 1.07 mm and 0.47 mm respectively (Aschenbach et al. 2000).
One of the three co-aligned XMM-Newton X-ray telescopes has an unimpeded light path to the primary focus, where the European Photon Imaging Camera (EPIC) pn camera (Strüder et al. 2001) is positioned. The two other telescopes have reflection grating assemblies (RGAs) in their light paths, diffracting part of the incoming radiation onto their secondary foci (where the reflection grating spectrometers, RGS; den Herder et al. 2001, are situated), leaving the remainder to travel straight through to the primary foci, where the two EPIC-MOS cameras (Turner et al. 2001) are positioned.
A critical parameter determining the quality of an X-ray mirror module is its ability to focus photons, i.e., its point spread function (PSF). Each of the three Wolter type I X-ray telescopes on board XMM-Newton has its own PSF. As an example, Fig. 1 shows the in orbit on-axis PSFs of the MOS1, MOS2 and pn X-ray telescopes, registered on the same on-axis non-piled-up source (specifically of 2XMM J130022.1+282402 from ObsID 0204040101 from orbital revolution 823). This figure shows the shape of the PSFs, with the characteristic radial spokes. Also note the coarser larger-scale shapes, in particular the strong triangular form of the MOS2 PSF, and the weaker pentagonal form of the MOS1 PSF. Note also that these coarse shapes are quite different in the 3 EPIC cameras.
 |
Fig. 1 PSFs of the 3 epic detectors (MOS1 left, MOS2 centre, pn right) for the same non-piled-up source from the same observation (2XMM J130022.1+282402, ObsID 0204040101, revolution 823). The images are 0.2−10 keV, are of binning 1.1″ × 1.1″, and are very lightly smoothed, to accentuate the features. |
 |
Fig. 2 (Left) a front-end view of one of the EPIC mirror modules containing the 58 co-axial mirrors shells, and the spider support structure used to hold the shells. (Right) the MOS2 PSF of the severely piled-up source GX 339-4 (ObsID 0204730301, revolution 783), showing the various PSF and other features (see text) − bad columns on the CCD are also visible as dark vertical lines. |
Any measurements of the PSF by the EPIC cameras may depend on the instrument readout mode, through combinations of out-of-time (OOT) event smearing and/or pile-up. The PSF can be severely affected by pile-up effects when the count rate exceeds a few counts per frame. Depending on the selection of event types in the EPIC event analysis process, a hole can even appear in the core of the PSF due to photon events undergoing severe pattern migration into unrecognized and rejected patterns, or yielding a reconstructed energy above the on-board high-energy rejection threshold. This is seen in Fig. 2 (right), where the PSF of a severely piled-up MOS2 on-axis source is shown (specifically of GX 339-4, ObsID 0204730301, revolution 783).
Much more outer detail can be seen in the piled-up PSF (see Fig. 2, right). Note for instance how the piled-up central hole follows the general MOS2 triangular structure. The 16 primary radial spokes are caused by the spider structure (see Fig. 2, left) supporting the mirror shells (the primary spokes in the image actually lie between the spider “legs”, i.e., were the spider absent, the PSF would be as bright as the primary spokes around the whole azimuth). Note that the spider support structure at the paraboloid front aperture is the only support structure for the entire module; there is no equivalent counterpart behind the hyperboloid rear aperture. Looking further, note the 16 lower-intensity secondary spokes lying between the primary spokes. These are thought to be due to low-level scattering from the sides of the spider legs. The dark lanes visible at larger radii from the secondary spokes are due to the electron deflector which is mounted after the rear aperture of the mirrors and whose legs are aligned with those of the front-end spider. The coarser (triangular and pentagonal) image structures are believed due to deformations in the mirror shells, certain sets of mirror shells, believed to be the outer shells (de Chambure et al. 1999), not being perfectly circular in the 3 EPIC mirror modules. Finally, though not formally due to the mirror system, note the diffuse streaks of OOTs to the top and bottom of the piled-up PSF. These various structures to the EPIC PSF are discussed throughout this paper.
1.1. PSF descriptions within the XMM-Newton SAS
Historically there have been a number of descriptions of the EPIC PSF that have been used as part of the XMM-Newton scientific analysis system (SAS)1. These include a number of two-dimensional (2D) and one-dimensional (1D) descriptions. The only previous 2D description is the “Medium” mode PSF − a set of simulated images in a matrix of 6 different off-axis angles and 11 different energies. This set of 66 images is identical for each EPIC instrument, and there is no azimuthal variation included. This PSF description is the one that has been used for source-searching throughout the XMM-Newton mission, and is referred to as the “default” PSF in this paper.
1D descriptions include (i) an “Extended” mode, incorporating a King profile (with core radius and slope), as a function of EPIC instrument, energy and off-axis angle; (ii) a “High” mode, incorporating a 3-Gaussian parametrization of the “Medium” mode images; and (iii) a “Low” mode, an early (and now unused) single-Gaussian approximation of the PSF. The 1D PSFs are often used within the SAS for spectral work. These PSFs can all be found within the particular XMM-Newton PSF current calibration files (CCFs). These are named as XRTi_XPSF_nnnn.CCF, where i refers to the instrument (1 = MOS1, 2 = MOS2, 3 = pn), and nnnn is the issue number of the file.
That the default (Medium) PSF is limited, in that it is the same for each EPIC instrument, and that no variation with source azimuth is included, is a drawback. This is the PSF that has been used for source-searching throughout the XMM-Newton mission, and it is likely that a number of these limitations may be responsible for many of the problems seen in the source-searching results and in constructing the XMM-Newton catalogues (e.g., 2XMM; Watson et al. 2008), the major problem being that a number of spurious sources are detected by the standard source-detection pipeline, especially close to bright point sources (note that post-pipeline visual screening does take place in the production of the XMM-Newton catalogues, and sources that lie in regions where spurious sources are considered likely to occur, are flagged). There is therefore the need for a full 2D energy- and off-axis angle-dependent PSF model that incorporates all aspects of the PSF structures, that is instrument-specific, and which accounts correctly for a source’s azimuthal position. This paper describes this new 2D PSF, and the structure of the paper is as follows: Sect. 2 describes the construction of the PSF − the data analysis and the modelling. Section 3 describes how the resultant new PSF model appears in the SAS. In Sect. 4 we discuss our testing of the PSF, and the major findings, and in Sect. 5 we present our conclusions.
2. Constructing the 2D PSF: data analysis and modelling
A standard method to obtain a fully 2D characterization of the PSF as a function of energy and off-axis angle across the entire field-of-view (FoV) of each of the three EPIC instruments would be to obtain a large number of images of appropriate point sources from the XMM-Newton archive, and stack these together in instrument/energy/off-axis angle groupings so that their shapes could be analysed and modelled.
It quickly became apparent however that such an approach was problematic. For a specific off-axis angle, the general tangentially-stretched profile of the PSF that is naturally due to the implementation of the Wolter I optic rotates naturally around the detector with source angle on the detector. The PSF details that are to do with the support structure and the mirror deformations however – i.e., the spokes and the triangles/pentagons – do not rotate with source angle. These − referred to collectively as the support structure features − remain fixed in detector angle as the source rotates around the detector. An immediate upshot of this is that the situation is very complex, with every single position on each of the three EPIC detectors having a single unique PSF. Even for such a high-throughput and long-term mission as XMM-Newton, nowhere near enough good quality data exists to perform this full stacking analysis at every detector position.
Consequently the new 2D PSF system, both the modelling described here and the incorporation of the PSF reconstruction into the SAS, has had to be re-designed in the following way: the stackings in the instrument/energy/off-axis angle groupings were used to construct general elliptical “envelopes” (due to the optic implementation) for that particular instrument, energy and off-axis angle, the support structure features (the spokes, triangles etc.) having been averaged and smeared out via the stacking procedure. 2D spatial models were then fit to these stacked envelopes to obtain general envelope spatial parameters. Then, for a particular source at a particular known azimuthal angle (whether on the detector, or on the sky), the particular azimuthal support structures required (the spokes, triangles etc.) were folded into the appropriate elliptical envelope to create the final 2D PSF appropriate for that particular instrument, energy, off-axis angle, and importantly, azimuthal angle. This is described in more detail in the following sections.
2.1. The elliptical envelope
A major driver for this new 2D description of the PSF was that it should cover the entire FoV, i.e., both on-axis and fully off-axis. It was necessary therefore to use data from those observing modes that cover the full FoV – i.e., the “full-frame” modes. Though smaller window modes can be useful in deriving some PSF parameters (see later), these modes only exist on-axis, and it was decided for the off-axis considerations, and for the sake of consistency and uniformity, to select all the data solely from the full-frame modes.
Sources were selected from the 2XMM catalogue (Watson et al. 2008) on the basis of them:
-
Being identified within 2XMM as point-like(i.e., no extension).
-
Having large numbers of (0.2−12 keV) counts (>5000 for MOS1 or MOS2 and >15 000 for pn).
-
Having a countrate below the appropriate pile-up limits2 (0.70 ct/s [MOS full-frame], 6 ct/s [pn full-frame], 2 ct/s [pn extended full-frame]).
-
Covering the full range in off-axis angle. (Note that the off-axis angle is just the “radial” angle relative to the optical axis, and any variation caused by mirror deformations (as opposed to support structure) with detector azimuth angle will be considered with the support structure features.)
The appropriate raw data – the observation data files (ODFs) – for each source were identified and obtained, and the standard SAS (v7.0) procedures (“epchain” for pn, “emchain” for MOS) were run on these to create the standard calibrated event lists. These were then filtered for periods of high background (solar proton flares) via standard good time interval (GTI) files created via analysis of high-energy off-source lightcurves. Files (and therefore candidate sources) where a large amount or long durations of high background flaring was observed were rejected from further analysis. Large-scale images around each source were created, and further rejections were made in cases of crowded fields or where chip gaps or bad CCD columns were seen to lie too close to the target source.
For the sources that passed through to this stage (>250 observations, mostly comprising useful exposures for all three EPICs, and several containing multiple valid sources), high-resolution images were constructed around each source position. These were constructed to be similar to the “Medium” PSF images (i.e., of 1.1″ resolution), and aligned such that the 2XMM source position lay at the centre of the image. These images were created for (where appropriate) each of the three EPIC cameras and in several different energy bands; 0.1−1.0 keV, 1.0−2.0 keV, 2.0−3.5 keV, 3.5−5.0 keV, 5.0−7.0 keV, 7.0−9.0 keV, 9.0−11.5 keV, 11.5−15.0 keV. All other sources (all of which were very faint and well separated from the target source) were excised from each image (using a circle of radius 35″), the holes filled with the average value in the surrounding (40″−70″) annulus. Each image was then rotated with respect to the source’s azimuthal angle on the sky (this angle is equivalent to a combination of the position angle of the observation and the source’s azimuthal angle on the particular detector). A Gaussian was fit to the rotated image to account for any tiny shifting in the procedure (always ≪ 1″), and a final rebinning of the rotated image about this fit centre was performed.
The final good images were collected together for each combination of EPIC instrument (3), energy band (8, linear fiducial midpoints: 0.55 keV, 1.5 keV, 2.75 keV, 4.25 keV, 6.0 keV, 8.0 keV, 10.25 keV, 13.25 keV) and off-axis angle band (6; 0−1.5′, 1.5−4.5′, 4.5−7.5′, 7.5−10.5′, 10.5−13.5′, & > 13.5′, these assigned to the fiducial values 0′, 3′, 6′, 9′, 12′, 15′). These sets of images were then stacked together, bringing them together to a common reference frame.
These stacked images were fit with a 2D King profile using the beta2d model in CIAO-Sherpa3: ![\begin{eqnarray*} B(r)=\frac{A}{[ 1+(r/r_0)^2]^{\alpha}} \end{eqnarray*}](/articles/aa/full_html/2011/10/aa17525-11/aa17525-11-eq9.png) where:
where: ![\begin{eqnarray*} r(x,y,\theta) \!=\! \sqrt{[(x \cos \theta + y \sin \theta)^2 ] \!+\! [(y \cos \theta - x \sin \theta)^2] / (1 - \epsilon)^2 } \end{eqnarray*}](/articles/aa/full_html/2011/10/aa17525-11/aa17525-11-eq10.png) and r0 (core radius), α (index), ϵ (ellipticity) and θ (angle of ellipticity) are the model parameters.
and r0 (core radius), α (index), ϵ (ellipticity) and θ (angle of ellipticity) are the model parameters.
To the parametrisation above, a further 2D Gaussian core has been added to model excess emission in the low- and medium-energy (E ≤ 6 keV) PSF at the very centre of the MOS cameras (no such core is observed to be necessary for pn). The model includes the same ellipticity term through the definition of the r variable as above. The 2D Gaussian function used (gaus2d model in CIAO-Sherpa) is: 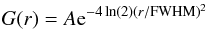 where FWHM is the full width at half maximum. All these parameters are contained within the PSF CCFs (issue numbers 0011 and after). Finally, a flat background level, fixed at the mean value beyond a 5′ radius was added to the model for each stacked image. For all instruments and off-axis angles, the two highest energy stacked images (at 10.25 keV and 13.25 keV) were seen to contain only very sparse data, and it proved impossible to obtain stable 2D fits with sensible error bounds in many of these cases. Consequently, the images in the two highest-energy bands have been combined together for all instruments and off-axis angles, and the resultant spatial fit parameters obtained have been applied to both energy bands in the resultant calibration files (at 10.25 keV and 13.25 keV). Future calibration, using more data, may be able to establish fit parameters for both energy bands separately. An example showing the results from a typical run of the 2D fitting (specifically for pn, 6′ off-axis angle, 1.5 keV) is shown in Fig. 3.
where FWHM is the full width at half maximum. All these parameters are contained within the PSF CCFs (issue numbers 0011 and after). Finally, a flat background level, fixed at the mean value beyond a 5′ radius was added to the model for each stacked image. For all instruments and off-axis angles, the two highest energy stacked images (at 10.25 keV and 13.25 keV) were seen to contain only very sparse data, and it proved impossible to obtain stable 2D fits with sensible error bounds in many of these cases. Consequently, the images in the two highest-energy bands have been combined together for all instruments and off-axis angles, and the resultant spatial fit parameters obtained have been applied to both energy bands in the resultant calibration files (at 10.25 keV and 13.25 keV). Future calibration, using more data, may be able to establish fit parameters for both energy bands separately. An example showing the results from a typical run of the 2D fitting (specifically for pn, 6′ off-axis angle, 1.5 keV) is shown in Fig. 3.
 |
Fig. 3 Results from a typical run of the 2D fitting (specifically for pn, 6′ off-axis angle, 1.5 keV). The top and middle panels show the data and final model respectively, at the same scaling. The bottom panel and colourbar (running from −0.2 to 0.2) show the residuals (data-model, the central peak of the data and model panels being ≈5 in the colourbar units). |
 |
Fig. 4 Schematic of the flat-topped triangular function used to parameterize the PSF spokes. The blue spoking function is constructed such that the red and the green areas exactly cancel out. The dashed line shows the unspoked function. The lengths 1.00, 0.165 (the half-width of the flat-top u) and 0.165 (the base to peak width v) are in units of half the inter-spoke distance, i.e., 11.25°. The figure is not to scale. |
The actual parameter values, which are contained within the PSF CCFs (described in more detail in Sect. 3.1), have evolved, and will continue to evolve, with iterations in the analysis and modelling. It is possible however to discuss some general trends in the current parameters (CCF issue number 0013). Dealing first with r0 (core radius) and α (index), note that there is some degeneracy between these two parameters; increasing (or decreasing) both parameters simultaneously can sometimes lead to only very small changes in the overall profile. The two MOS PSFs behave similarly; close to on-axis, r0 is seen to gently decrease with increasing energy, while α is seen to remain roughly constant with energy. The profile therefore is seen to get narrower at higher energies, as expected, as only a fraction of the mirror shells − the smaller, inner shells − contribute to the higher-energy PSF. At larger off-axis angles, the MOS r0 and α values are seen to decrease with increasing energy, but more steeply, starting from larger low-energy values than is seen on-axis. The pn PSF behaves slightly differently in that r0 decreases gently with increasing energy for all off-axis angles, but the average r0 value increases with off-axis angle (as expected, the PSF becoming wider off-axis). The pn α is seen to remain roughly constant for almost all energies and off-axis angles, hence, in conjunction with the gently decreasing r0 values with energy, the profile again gets narrower at higher energies. The ellipticity behaves as one would expect and very similarly for each instrument, getting larger with increasing off-axis angle, from ≈0 on-axis to ≈0.6 far off-axis. Also the ellipticity is seen (more prominently off-axis) to gently increase with increasing energy in each instrument. Finally, for the Gaussian component (which exists only for the MOS cameras at E ≤ 6 keV), both the FWHM and the relative normalization for both MOS PSFs are seen to fall from 0 to 6 keV, for all off-axis angles (i.e., to match there being no Gaussian at >6 keV).
2.2. The support structure features – The spokes
The radial spokes have been modelled with a flat-topped triangular function (Fig. 4), chosen after consultations with mirror experts (B. Aschenbach, priv. comm.; R. Willingale, priv. comm.). 16 equally-spaced spokes have been included in the model. The distance between two consecutive peaks of the spoke function is therefore 22.5°. The shape of this function has been tuned in such a way that it does not change the integral of the radial profile (i.e., the red and the green areas in Fig. 4 exactly cancel out). This filtering function is fixed in space with respect to the detector, such that any axis of the DETX/Y (or RAWX/Y) coordinate system lies exactly between two spokes, and is only applied to the elliptical envelope after the envelope has been rotated according to the azimuthal position of the source on the detector.
The current spoke dimensions have been obtained from measuring the azimuthal angles of the spoke troughs, peaks and flat-tops of a number of bright sources, including GX 339-4, using the full energy range (0.2−12 keV) and over a large radial range (20″−100″). The current dimensions are such that both the half-width of the flat-top (u), and the width from base to peak (v) equals 0.165 times half the width of the spoke-to-spoke distance (as indicated in Fig. 4). It can be shown that the height h of the spoke above the unspoked dashed line of Fig. 4 (if the spoke drops below the line by a depth of 1.0) is related to the half-width of the flat-top u and the base to peak width v via: 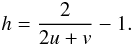 The strength (intensity) of the primary spokes is set such that the spoked PSF is made up of (at most) 42% of an image formed from the flat-topped triangular function depicted in Fig. 4, and the remainder is formed from an unspoked image. This is again based on the spatial analysis of a number of bright sources. The radial dependence of the intensity of the spoking is however not constant (see below), and this intensity value (42%) is the maximum value.
The strength (intensity) of the primary spokes is set such that the spoked PSF is made up of (at most) 42% of an image formed from the flat-topped triangular function depicted in Fig. 4, and the remainder is formed from an unspoked image. This is again based on the spatial analysis of a number of bright sources. The radial dependence of the intensity of the spoking is however not constant (see below), and this intensity value (42%) is the maximum value.
16 secondary spokes, observed in very bright sources (see Fig. 2), and situated half-way between the 16 main primary spokes, are modelled with the same spoke function, rotated by 11.25° with respect to the main spoke system, and with a (maximum) intensity factor of 3.5%.
The relative strength of the spokes is not constant with radius but appears to vary. Owen & Ballet (2011) were able to characterize the radial dependence of the spokes of the MOS1, MOS2 and pn PSFs to large radii (up to 2′) using bright, heavily piled-up sources, and using procedures developed to correct for the effects of pile-up. They found that the radial dependence of the spokes of the two MOS cameras and the pn camera appeared to be approximately the same. This is not surprising as the spokes and their radial dependencies are all due to the construction of the mirror modules, all of which were designed to be identical. Furthermore the spiders were constructed out of Inconel, a material chosen for its thermal expansion, which is close to that of the electrolytic nickel of the mirrors (de Chambure et al. 1999), thus keeping distortions to a minimum. This radial dependence has been modelled to match the Owen & Ballet (2011) on-spoke to off-spoke ratio results, and will be introduced into the PSF CCFs (for issue numbers 0014 and after) as follows: for each EPIC PSF, from the centre out to 10″, there is no spoking. From 10″to 110″ the spoke strength increases linearly from zero to the maximum (42%). From 110″ to 180″ the spoke strength decreases linearly from its maximum to zero, and there is no spoking beyond this radius.
Looking beyond the present model, when we compare in detail the azimuthal profile of good quality point source data with the current (CCF 0013) model (see Fig. 5), there are a number of points of interest: though there is significant statistical scatter, there may also be some true spoke-to-spoke variation. Further, it appears that there may be some variation of the spoke model width parameters u and v with radius − the spokes appearing to be narrower at larger radius. Interestingly it appears that there is a significant difference in the radial dependence of the secondary spoke strength, compared to that of the primary spokes − the secondary spokes falling off quicker (there also appears to be significant secondary spoke-to-spoke variation). None of these effects (nor their energy-dependencies) are yet contained within the current PSF model, but they impinge upon e.g., the on-spoke to off-spoke Owen & Ballet (2011) results, and on their interpretation and modelling − note that the on-spoke to off-spoke ratio is lower at smaller radius (44″−88″) than at larger radius (88″−132″), partly because the secondary spokes are relatively stronger at smaller radius than at larger radius. It is hoped that these issues can be revisited in future improvements in the modelling of the EPIC PSFs.
 |
Fig. 5 A section of the azimuthal profile (black line) from GX 339-4 (ObsID 0204730301) (MOS1, 0.2−12 keV) in annular extractions of (top) 44″−88″ and (bottom) 88″−132″. The current (CCF 0013) flat-topped triangular function for the primary spokes at maximum strength (i.e., at a radius of 110″) is shown in blue (see text). |
2.3. The support structure features – The large-scale azimuthal modulation
The apparent triangular shape of the MOS2 PSF can be modelled by a spatial low frequency overall modulation of the PSF shape. A pentagonal modulation is also present at a lower level in the MOS1 and also at a very low level in the pn PSF. These shapes are thought to be due to distortions and irregularities in certain sets of mirror shells within each of the telescopes – e.g., the outer shells not being perfectly circular (de Chambure et al. 1999). It is not surprising therefore that these deformities are different in the three EPIC PSFs.
This modulation M(φ) is modelled as a function of the azimuthal angle φ, with a multi-peaked cosine function in the PSFs of the cameras: 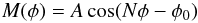 where A is the amplitude of the modulation, N is the number of peaks in the modulation in a full 360° revolution, and φ0 is the azimuthal offset of the cosine function. The current parameters of this function are shown in Table 1.
where A is the amplitude of the modulation, N is the number of peaks in the modulation in a full 360° revolution, and φ0 is the azimuthal offset of the cosine function. The current parameters of this function are shown in Table 1.
Current parameters of the large-scale azimuthal multi-peak modulation.
The radial dependence of these large-scale azimuthal modulations is also seen not to be constant with radius, and the maximum amplitude A is listed in Table 1. The dependence is only roughly similar to the radial dependence of the spokes, and there are variations between the EPIC detectors – the pn pentagon for example only appears to be visible over quite a narrow range in radius. This radial dependence of the large-scale azimuthal modulations (and the entire pn large-scale azimuthal modulation) has not been fully calibrated yet, but will appear in a future issue of the PSF CCFs.
 |
Fig. 6 The eight main steps in the formation of the full 2D PSF for a source in a given instrument, of a given energy and at a given off-axis and azimuthal angle: the King (beta2d) component [1] is constructed, then the Gaussian (gaus2d) core [2] is constructed, and these are added [3] in the correct ratio (the CCF parameters in steps 1−3 are all functions of instrument, energy and off-axis angle). Then this is rotated [4] according to the azimuthal position of the source on the detector, and only then are the radially-dependent primary [5] and secondary [6] spoke structures azimuthally filtered in, using a flat-topped triangular function. Finally, the large-scale azimuthal modulation (a function of EPIC instrument) is filtered in [7], and the very light radially-dependent smoothing applied [8]. The example shown is for MOS2, at an energy of 1.5 keV, an off-axis angle of 9′, and a source azimuthal position of 30°. |
As a final step in the construction of the 2D PSF, a radially-dependent very light smoothing is applied. A smoothed image of the PSF is constructed using a flat boxcar of halfwidth 1.65″. The final PSF is then a sum of f times this smoothed image plus (1 − f) times the original unsmoothed image, where f varies linearly from 0 at the source center to unity at 8.8″. Though this does not currently directly match the more elliptical nature of the PSF at larger off-axis angle, this will be investigated further, and the smoothing effect is very small, has been applied merely to de-pixelate the spoke structures at large radius, and does not have any significant large-scale effects (e.g., on radial profiles).
2.4. Additional features
The new 2D PSF system has been designed to be modular, and it is quite straightforward to add in further complexities. There are a number of additional features to the EPIC PSFs that will be added, it is intended, to future updates of the system (some may just require updates to the CCFs, others may require software and infrastructure changes). The radial dependencies of the large-scale azimuthal modulations, as discussed above, is one. It is very probable, as the large-scale azimuthal modulations are due to deformations only in certain mirror shells, that there are energy-dependencies to this effect, and these will also need to be incorporated. A further task is to include the effects of the dark lanes visible e.g., in Fig. 2, due to the electron deflector, mounted after the rear aperture of the mirrors and whose legs align with those of the front-end spider. It should be possible, once calibrated, to insert this effect into the system, via a similar azimuthal filtering technique as for the spokes. Features due to OOTs have not been considered to be part of the PSF. Though instrument-dependent, they are also mode-dependent, and in terms of the source-detection software, they are modelled via an alternative route (at least for the pn, where the OOT signal is much stronger). The OOT features here have, in a similar manner to the azimuthal structures (the spokes, triangles etc.), been diluted and smeared out via the stacking procedure prior to the envelope fitting. Furthermore there is set within the PSF system the possibility to allow for any azimuthal variations in the envelope 2D King and Gaussian parameters. Currently the CCFs are set such that these parameters do not vary with source azimuth, but future calibration may require changes, e.g., to account for variations due to the obscuring RGAs in the EPIC-MOS cameras.
3. Results: the 2D PSF in the XMM-Newton SAS
The new 2D PSF is contained within all XMM-Newton SAS PSF CCFs of the form XRTi_XPSF_nnnn.CCF, where nnnn, the issue number of the file, is 0011 or higher. The relevant parameters are contained within the ELLBETA_PARAMS extension.
A number of elements are used to describe the new 2D PSF in these CCFs, as summarized here:
-
A (currently) azimuthal-angle-independent parameterizationof the elliptical PSF envelope as a function ofinstrument, energy, and off-axis angle.An additional Gaussian “core” is added to thePSF envelope of the MOS camerasfor low and medium energies(E ≤ 6 keV) only.
-
An azimuthal filter of the elliptical envelope, which describes the effect of the spokes created by the spider supporting the 58 co-axial mirrors of each telescope. Primary and secondary spokes are included. The radial dependency of the strength of these spokes is to be included in version 0013 of the CCFs. The parameters of this filtering are currently hard-coded into the CAL software, but will appear as FITS keywords in version 0013 of the CCFs. The filtering to account for the dark lanes will appear in future CCF releases.
-
A further azimuthal dependency of the overall PSF envelope, which is responsible for the apparently triangular shape of the MOS2 PSF. Lower level similar effects are present in the PSFs of MOS1 and pn also. Currently, this correction is applied to the PSFs of MOS1 and MOS2 only. The parameters of this correction are currently hard-coded into the CAL package, but will appear as FITS keywords in version 0013 of the CCFs. The pn correction and the radial dependencies for all three will be included in future releases of the CCFs.
A scheme of the different physical ingredients of the 2D PSF parameterization and how they are combined to produce the final PSF is shown in Fig. 6. For a comparison with an actual EPIC off-axis source, Fig. 7 shows a very bright, ≈4′ off-axis angle MOS2 point source and the equivalent PSF model at a similar off-axis and the appropriate source azimuthal position.
Once the 2D PSF was incorporated into both the CCF system and the SAS, a next step was to compare it with the default PSF in terms of how well the SAS-constructed PSFs model the true source structures. To this end, full SAS calibrated event list creation, image formation and detection chain analysis (as per the standard pipeline) was performed on a large number of fields containing bright, non-piled-up point sources, detected by EPIC, and (where available and where observing mode constraints allowed) in all three EPIC cameras. The detection chain analysis was performed once using the default (MEDIUM) PSF and once using the 2D (ELLBETA) PSF. Next, taking great care to co-align each source image and each detection-chain-produced model PSF image, then for each source, both the source and the model counts within each of 30 radial bins (each 4″ wide) and 32 azimuthal bins (each 11.25° wide, arranged to be alternately fully on-spoke, then fully off-spoke) were computed. The co-alignment ensured that each azimuthal bin corresponded to the same azimuth on the PSF. This procedure was performed for 80 bright, non-piled up point sources, and the values were stacked together, in several energy bands and off-axis angle groupings. All this analysis was performed using both the 2D PSF and the default PSF.
Figure 8 shows the results of this analysis, for the example of MOS2, on-axis, 0.5−1 keV, arranged in the circular grid used of 30 radial bins combined with 32 azimuthal bins. The top row corresponds to the 2D PSF, and shows (left to right): (1) the stacked counts in the data; (2) the stacked counts in the model; (3) a χ2-like statistic, calculated from the stacked data counts and stacked model counts as:  and (4) r, a measure of whether the model consistently under- or overestimates the data, and calculated as the sum of the individual data – model “signs” via:
and (4) r, a measure of whether the model consistently under- or overestimates the data, and calculated as the sum of the individual data – model “signs” via: 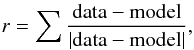 which ranges between +1 (white, always underestimates) and −1 (black, always overestimates). The bottom row of Fig. 8 shows the equivalent plots for the default PSF (and hence the two stacked data plots are identical). The colourbar (− 20 to +20) corresponds to the χ2 plot.
which ranges between +1 (white, always underestimates) and −1 (black, always overestimates). The bottom row of Fig. 8 shows the equivalent plots for the default PSF (and hence the two stacked data plots are identical). The colourbar (− 20 to +20) corresponds to the χ2 plot.
 |
Fig. 7 A very bright, slightly piled-up, ≈4′ off-axis angle MOS2 point source and the equivalent PSF model at a similar off-axis and the appropriate source azimuthal position. |
A number of conclusions can be drawn from this figure. Similar results are seen for MOS1 and pn, though some (e.g., to do with the large-scale azimuthal filtering) are harder to see. Very obvious is that the default PSF, due to its limitations discussed in Sect. 1.1, performs very poorly with regard to the spokes; the on-spoke regions are very underestimated by the default model, and the off-spoke regions are overestimated. Secondly, the default PSF performs extremely badly in modelling the large-scale azimuthal features − here, the MOS2 triangle (note the very large triple-peaked discrepancies in the χ2 and r plots for the default PSF). The 2D PSF however, performs very much better. Much less variation in χ2 and r is seen on- and off-spoke. The plot does suggest though that the 2D PSF relative spoke strength may be too strong. The most up-to-date SAS and the latest PSF CCF files that are available for this analysis (version 0012) however, do not yet include the radial dependency of the spoke strength, and the future inclusion of this will act to decrease this effect, and improve further the 2D PSF modelling. The 2D PSF modelling of the MOS2 triangle is also very much improved over the default PSF. Further refinements to this component include the modelling of both its radial-dependence and its energy-dependence.
3.1. Description of the PSF CCF parameters
The FITS extension ELLBETA_PARAMS in the PSF CCF XRTi_XPSF_0011.CCF (and later) files contains the parameters describing the elliptical envelope and the Gaussian core. This extension contains four columns:
-
ENERGY: the energy (in eV) to which the parameters refer;
-
THETA: the off-axis angle (in radians) to which the parameters refer;
-
PHI: the azimuthal angle (in radians) to which the parameters refer;
-
PARAMS: an array, containing the parameters of the 2D King (beta2d) plus Gaussian (gaus2d) function:
-
1: the King core radius (r0), in arcseconds;
-
2: the King power-law slope (α);
-
3: the ellipticity (ϵ) (of both the King and the Gaussian components);
-
4: the Gaussian Full Width Half Maximum (FWHM), in arcseconds;
-
5: the normalisation ratio of the Gaussian peak to the King peak (N).
-
 |
Fig. 8 Comparing the SAS-produced 2D PSFs and default PSFs with true source data. Left to right: (1) the stacked counts in the data; (2) the stacked counts in the model; (3) a χ2-like statistic; (4) r, a measure of whether the model consistently (white) under- or (black) overestimates the data (see text for all details), for (top) the 2D PSF and (bottom) the default PSF. The colourbar corresponds to the χ2 plot. The 30 radial bins are each 4″ wide, and the 32 azimuthal bins are each 11.25° wide, and arranged to be alternately fully on-spoke, then fully off-spoke. The example shown is for MOS2, on-axis, 0.5−1 keV. |
4. Discussion: testing of the PSF
Though this paper is primarily concerned with a description of the new 2D PSF and its construction etc., it is very useful here to discuss some of the testing, especially as regards the major reason why the new 2D PSF was originally desirable – i.e., to see if it could reduce the number of spurious sources detected by the standard source-detection pipeline, where the relatively poor description of the PSF can lead to large residuals in the constructed data-minus-model images, leading in turn to the detection of spurious sources. Also of major interest are the astrometry issues that have arisen as a consequence of these first tests. These issues are discussed in the following sections.
4.1. Source-searching and spurious sources
A comparison of the performance of the new 2D PSF (“Ellbeta”) with that of the current existing default PSF (“Medium”) has been performed, the primary objective being to establish whether the 2D PSF better suppresses the detection of spurious sources. The analysis first focussed on a set of 108 “problem” observations containing examples of various types of situations where spurious sources had previously been found to be present. These were mainly chosen to be around non-piled-up bright sources, but there were also several fields chosen involving bright piled-up sources, off-axis sources, extended sources, out-of-time (OOT) events from piled-up sources and single reflection arcs. A separate “random” set of 83 observations was also processed as a reference, as was a “clean” subset of 40 fields, free of any “problems”, extracted from the “random” subset.
Standard calibrated event file creation, and background cleaning was performed on the datasets, and standard images were extracted from the data in the 5 usual energy bands used for EPIC source-detection in the 2XMM catalogue (Watson et al. 2008). The main source-detection task emldetect (v5.15) was then used, once using the default PSF, and once using the 2D PSF. Importantly, exactly the same input files (specifically the source images, background images, exposure maps, detector masks and eboxdetect input lists) were used in the default and 2D runs, ensuring that no changes were introduced due to e.g., spatial randomization of the events, and that any changes seen would be due solely to the PSF usage.
The numbers of emldetect detections obtained using the default and the 2D PSFs for the “problem” fields (split into the various problem groups), and for the “random” fields and the “clean” fields are shown in Table 2.
Total numbers of emldetect detections with the 2D and default PSFs, and the percentage change in numbers, for various “problem” cases, and for the “random” and the “clean” samples (see text).
Overall for the problem cases, the number of detections with the 2D PSF is lower (by 2.9%) than for the default PSF. This is dominated by the large reductions in the on-axis non-piled-up and piled-up cases. The same analysis applied to the random cases (where many similar “problems” still exist) yields a smaller reduction than for the problem cases, while for the clean cases, there is almost no change. This all supports the idea that the 2D PSF performs better at avoiding likely spurious sources in problem fields. In fact, if one removes the clean subset from the random set, the excess of detections by the default PSF in the remaining “non-clean” cases is 3.1%, consistent with the “problem” 2.9% in Table 2. Two examples showing the improvement in the source detection around bright sources are shown in Fig. 9.
 |
Fig. 9 Example output from a full all-EPIC source-detection analysis of ObsIDs 0107660201 (left) and 0302850201 (right). The blue circles show the sources detected using the default PSF and the yellow circles show the sources detected using the 2D PSF. Many spurious sources previously detected by the default PSF in the spokes of the central bright source are now not detected by the 2D PSF. |
We then focussed on the detection statistics around the (typically brighter) objects that give rise to the excessive source detections. Using the set of problem fields, source counts were recorded for 3 circular apertures centred on the problem source of interest, with radii of 1′, 2′ and a radius determined by eye that enclosed the visible spoke structure. For insignificantly piled-up sources (examining 53 fields, with essentially one bright object per field) we find that use of the 2D PSF reduces the number of detections around bright sources by ≈23% on average, and is not noticably dependent on the aperture. Applying the same analysis to significantly piled up sources (14 sources) and to bright off-axis sources (21 sources) yields changes of between 26% and 31%.
 |
Fig. 10 Distributions of the (2D-default) change in returned (left) RA and (right) Dec of detected sources using the 2D (Ellbeta) and default (Medium) PSF for a sample of 70 clean observations. |
To examine more closely the distribution of sources around problem objects, a visual analysis was conducted on a subset of objects, counting sources that were either associated with the spoke features, or suspect objects found elsewhere in the 2′ aperture but generally close to the core of the source. The primary source detection itself was excluded. This is inevitably a subjective analysis and does not take account of the dependence on detection likelihood, but it provides a useful assessment of the impact of the 2D PSF. We find that for sources detected on spokes, overall the 2D PSF finds ≳ 42% fewer detections than the default PSF (or ≳ 92% fewer if we consider only detections on spokes that are not common to both PSFs). Likewise, for sources near the core of the primary source, the 2D PSF yields at least 22% fewer detections, or ≳ 69% fewer if we exclude the common detections.
Thus, we conclude that use of the 2D PSF substantially reduces the number of detections compared to the default PSF and that this reduction is primarily due to fewer detections on the spokes and in the core regions of bright sources. These are precisely the components of the PSF which are being better modelled by the 2D PSF. These model improvements suppress data-minus-model residuals that have hitherto given rise to spurious detections when using the default PSF.
4.2. Astrometry issues
A major outstanding concern in the comparison of the 2D PSF output with the default PSF output was that large and significant positional shifts are observed. Mean differences of ≈+0.8″ in RA and ≈-0.8″ in Dec (2D values minus default values) are observed between the 2D and default PSF results on any large set of observations. Figure 10 shows the distributions of the RA and Dec (2D-default) offsets for a sample of 70 observations (incorporating and extending on the clean sample of the previous section).
It was not known whether this shift was due to the 2D PSF or to the default PSF (or to both). One source of confusion and possible error is the fact that the default PSF (as described briefly in Sect. 1.1) consists of a set of images of dimensions 512 × 512 and pixel size 1.1″ × 1.1″. It was noted that the assumption of where the centre of one of these images is, and the propagation, correctly or incorrectly, of this assumption through the relevant SAS subsystems (PSF and image generation, PSF rotation, source-searching etc.) could lead to possible errors. This thinking also indicated that the rotation of the PSF could be vital in pinning down the root of the positional offset problem, and indeed, when the (2D-default) changes in RA and Dec are plotted against the source angle on the sky (Fig. 11), the +0.8″ and −0.8″ offsets are resolved into not only offset, but sinusoidal variations, indicating that (i) not only is there an offset problem between the two PSFs; but (ii) the rotation of one (or both) of the PSFs contains an additional systematic sinusoidal error.
 |
Fig. 11 (2D-default) offsets in (left) RA and (right) Dec of detected sources using the 2D (Ellbeta) and default (Medium) PSF plotted against the source angle on the sky (anti-clockwise from north) for the sample of 70 clean observations as in Fig. 10. |
In order to evaluate which of the PSFs is at fault, it is necessary to cross-correlate the X-ray positions obtained with the two PSFs with good-quality optical positions. Here we need to introduce the boresight matrix. This was calculated from fields of many bright sources, e.g., OMC2/3 (Kirsch 2004), and subsequently refined using 430 individual fields (Altieri 2004), cross-correlating the source X-ray positions (note, obtained using the default PSF) with their optical positions, and observing which particular offset in RA, Dec and position angle is seen to significantly optimize the correlation. This final calibrated boresight misalignment matrix has been applied to the determination of the X-ray sky position of every X-ray event in every calibrated event file.
It is therefore the case that any translation or offset problem that is due to the default (Medium) PSF is “corrected for” and calibrated out when implementing the current boresight misalignment matrix. As such, it is expected that the X-ray-optical source positional offsets for the default PSF will be centred around zero, and indeed, this is seen to be the case. The 2D PSF offsets are furthermore seen to be centred around the observed (Figs. 10 and 11) +0.8″ and −0.8″ offsets.
The clean samples of source detections (using both the 2D PSF and the default PSF) were cross-correlated with the Sloan Digital Sky Survey Quasar Catalog (Schneider et al. 2007) to a match radius of 10″. In almost every case where there was a match, it was the only match. We looked at the cross-correlations using the original (emldetect-obtained) X-ray positions and using the X-ray positions obtained by the SAS program eposcorr. This program, eposcorr, performs a similar task to the boresight misalignment matrix calculation in that, for each observation, it correlates the input (emldetect) source positions with the positions from optical source catalogues, and checks whether there are offsets in RA, Dec and position angle which optimize the correlation. If there are optimum offsets, these are then used to correct the input source positions which are then added as separate columns to the input X-ray source list.
When the (X − QSO) differences in RA and Dec between the X-ray positions and the optical quasar positions are plotted against source angle on the sky for both the default PSF (Fig. 12) and the 2D PSF (Fig. 13, both figures using the eposcorr-corrected output), several things are evident.
 |
Fig. 12 (Top) X-ray position − QSO optical position offsets (in arcseconds) in (left) RA and (right) Dec of default (medium) PSF-detected X-ray sources with a QSO match, plotted against the source angle on the sky (anti-clockwise from north). X-ray positions are after eposcorr (see text). (Bottom) The same data, binned into 25 equi-angular bins and averaged. |
 |
Fig. 13 (Top) X-ray position − QSO optical position offsets (in arcseconds) in (left) RA and (right) Dec of 2D (Ellbeta) PSF-detected X-ray sources with a QSO match, plotted against the source angle on the sky (anti-clockwise from north). X-ray positions are after eposcorr (see text). (Bottom) The same data, binned into 25 equi-angular bins and averaged. |
Firstly, regarding the offset problem, though the corresponding figures prior to eposcorr (not shown) do indeed show the default PSF distribution to be centred around zero offset, and the 2D PSF distribution to be centred around the +0.8″ and −0.8″ offsets, the 2D PSF eposcorr output (Fig. 13) is centred around zero − i.e., when it runs successfully, eposcorr is able to correct the offset problem. Secondly, regarding the sinusoidal problem, it is observed that it is for the default PSF case (Fig. 12) that the large sinusoidal variations are seen. For the 2D PSF (Fig. 13) the variations are very much smaller.
Looking in more detail, it was suggested earlier that the sinusoidal problem could be related to the default PSF CCF images, and the assumptions regarding where the centres of these images are, and how these assumptions are propagated through the entire PSF generation and source-searching system. This now does appear to be the case, and added to the lower panels of Fig. 12 are simple calculated cosine curves of what one would expect to see, given the simple offset of half the diagonal of a single default PSF image pixel, rotated around the 360 degrees of the detector. The data is seen to match this simple model extremely well. It is therefore undoubtedly the default PSF that is the cause of the sinusoid effect, and this problem has existed for the entirety of the XMM-Newton mission. The full positional capabilities of EPIC therefore have not been used to this date. The improvement here is such that, selecting the 67% of sources with a very good X-ray positional error (centroid error <1″), the mean X-ray-QSO positional offset is reduced from 1.13″ (default) to 0.94″ (2D), and the percentage of these sources with an X-ray-QSO positional offset less than 1″ increases from 52% (default) to 68% (2D). The percentage of cases where it is the 2D PSF X-ray position that is the closest to the QSO position is 70%.
Although the large sinusoids present in Fig. 12 have been largely removed in Fig. 13, they do not appear to have been completely removed (and are at the 0.2″−0.3″ level). One should bear in mind that, if there is any inaccuracy at all present in the true positioning of the PSF centre, and where it is assumed to be in the PSF system, then a very similar sinusoidal variation will be seen with source angle on the sky. The fact that some residual curvature possibly exists in Fig. 13 may indicate that the situation is not quite perfect, and there may still be a small residual misalignment of the centering of the PSF system and the true PSF system.
At present, the 2D PSF only returns the optimum positions when eposcorr is run. Eposcorr only provides gross field shifts and cannot correct for the residual sinusoidal effects. Also, the eposcorr task can not be run on every EPIC dataset, for instance in cases where there are very few (or very faint) X-ray sources in the field. In order for the full positional improvements of the 2D PSF to be usable therefore, a revised boresight misalignment matrix first needs to be calibrated, tested and incorporated correctly into the SAS (related SAS changes may also be required). This work, building on the above tests, is currently underway, and a future version of the SAS will include these improvements in the positional accuracy of EPIC.
5. Conclusions
A new and fully comprehensive full-FoV 2D model of the PSFs of the three XMM-Newton EPIC telescopes has been constructed. This has been performed via the stacking, and bringing-together to a common reference frame, of a large number of good quality, long-exposure, non piled-up, bright point sources from different positions within the full FoV of each EPIC detector. The resultant general PSF envelopes were then azimuthally filtered to construct the primary and secondary spoke structures (plus their radial dependencies) and the large-scale gross azimuthal PSF deformations that are observed. The PSF model also includes an additional Gaussian core, which accounts for (at most) 2% of the enclosed energy flux in the EPIC-MOS cameras.
This PSF model is available for use within the XMM-Newton SAS via the usage of CCFs XRTi_XPSF_0011.CCF and later versions. The modular nature of the new PSF system allows for further corrections and refinements in the future.
Initial EPIC source-searching tests using this new PSF model indicate that it performs significantly better with regard to the
major problem with the previous PSF; that of large numbers of spurious source being detected in the wings of, or close to bright point sources. The numbers of these spurious sources detected with the new PSF model are greatly reduced.
These tests also uncovered a systematic error in the previous PSF system, such that returned source RA and Dec values were seen to vary sinusoidally about the true position with source azimuthal position angle on the sky. This error in the previous PSF system (the amplitude of the sinusoid being ≈0.8″ in RA and in Dec) has existed since the beginning of the XMM-Newton mission, and affects all the EPIC positional determinations performed thus far. Usage of the new PSF results in a much smaller amplitude sinusoid, and therefore an improved positional accuracy. SAS changes, including a revised boresight misalignment matrix (presently under construction) are required to make full use of the improvements in the positional accuracy of EPIC introduced by the new PSF.
XMM-Newton Users Handbook: http://xmm.esac.esa.int/external/xmm_user_support/documentation/uhb/
Acknowledgments
The XMM-Newton project is an ESA Science Mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). We thank Matteo Guainazzi and Steve Sembay for careful readings of the paper, and the referee for useful comments which have improved the paper. A.M.R. and S.R.R. acknowledge the support of STFC/UKSA/ESA funding.
References
- Aschenbach, B., et al. 2000, ESA XMM-Newton Calibration Technical Note CAL-TN-0005 [Google Scholar]
- Altieri, B. 2004, XMM-Newton CCF Release Note XMM-CCF-REL-168 [Google Scholar]
- de Chambure, D., Lainé, R., van Katwijk, K., & Kletzkine, P. 1999, ESA Bull., 100, 30 [NASA ADS] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirsch, M. 2004, XMM-Newton CCF Release Note XMM-CCF-REL-156 [Google Scholar]
- Owen, R., & Ballet, J. 2011, XMM-SSC Technical Note SSC-CEA-TN-1001 [Google Scholar]
- Schneider, D. P., Hall, P. B., Richards, G. T., et al. 2007, AJ, 134, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, M., et al. 2008, A&A, 493, 339 [Google Scholar]
All Tables
Total numbers of emldetect detections with the 2D and default PSFs, and the percentage change in numbers, for various “problem” cases, and for the “random” and the “clean” samples (see text).
All Figures
 |
Fig. 1 PSFs of the 3 epic detectors (MOS1 left, MOS2 centre, pn right) for the same non-piled-up source from the same observation (2XMM J130022.1+282402, ObsID 0204040101, revolution 823). The images are 0.2−10 keV, are of binning 1.1″ × 1.1″, and are very lightly smoothed, to accentuate the features. |
| In the text | |
 |
Fig. 2 (Left) a front-end view of one of the EPIC mirror modules containing the 58 co-axial mirrors shells, and the spider support structure used to hold the shells. (Right) the MOS2 PSF of the severely piled-up source GX 339-4 (ObsID 0204730301, revolution 783), showing the various PSF and other features (see text) − bad columns on the CCD are also visible as dark vertical lines. |
| In the text | |
 |
Fig. 3 Results from a typical run of the 2D fitting (specifically for pn, 6′ off-axis angle, 1.5 keV). The top and middle panels show the data and final model respectively, at the same scaling. The bottom panel and colourbar (running from −0.2 to 0.2) show the residuals (data-model, the central peak of the data and model panels being ≈5 in the colourbar units). |
| In the text | |
 |
Fig. 4 Schematic of the flat-topped triangular function used to parameterize the PSF spokes. The blue spoking function is constructed such that the red and the green areas exactly cancel out. The dashed line shows the unspoked function. The lengths 1.00, 0.165 (the half-width of the flat-top u) and 0.165 (the base to peak width v) are in units of half the inter-spoke distance, i.e., 11.25°. The figure is not to scale. |
| In the text | |
 |
Fig. 5 A section of the azimuthal profile (black line) from GX 339-4 (ObsID 0204730301) (MOS1, 0.2−12 keV) in annular extractions of (top) 44″−88″ and (bottom) 88″−132″. The current (CCF 0013) flat-topped triangular function for the primary spokes at maximum strength (i.e., at a radius of 110″) is shown in blue (see text). |
| In the text | |
 |
Fig. 6 The eight main steps in the formation of the full 2D PSF for a source in a given instrument, of a given energy and at a given off-axis and azimuthal angle: the King (beta2d) component [1] is constructed, then the Gaussian (gaus2d) core [2] is constructed, and these are added [3] in the correct ratio (the CCF parameters in steps 1−3 are all functions of instrument, energy and off-axis angle). Then this is rotated [4] according to the azimuthal position of the source on the detector, and only then are the radially-dependent primary [5] and secondary [6] spoke structures azimuthally filtered in, using a flat-topped triangular function. Finally, the large-scale azimuthal modulation (a function of EPIC instrument) is filtered in [7], and the very light radially-dependent smoothing applied [8]. The example shown is for MOS2, at an energy of 1.5 keV, an off-axis angle of 9′, and a source azimuthal position of 30°. |
| In the text | |
 |
Fig. 7 A very bright, slightly piled-up, ≈4′ off-axis angle MOS2 point source and the equivalent PSF model at a similar off-axis and the appropriate source azimuthal position. |
| In the text | |
 |
Fig. 8 Comparing the SAS-produced 2D PSFs and default PSFs with true source data. Left to right: (1) the stacked counts in the data; (2) the stacked counts in the model; (3) a χ2-like statistic; (4) r, a measure of whether the model consistently (white) under- or (black) overestimates the data (see text for all details), for (top) the 2D PSF and (bottom) the default PSF. The colourbar corresponds to the χ2 plot. The 30 radial bins are each 4″ wide, and the 32 azimuthal bins are each 11.25° wide, and arranged to be alternately fully on-spoke, then fully off-spoke. The example shown is for MOS2, on-axis, 0.5−1 keV. |
| In the text | |
 |
Fig. 9 Example output from a full all-EPIC source-detection analysis of ObsIDs 0107660201 (left) and 0302850201 (right). The blue circles show the sources detected using the default PSF and the yellow circles show the sources detected using the 2D PSF. Many spurious sources previously detected by the default PSF in the spokes of the central bright source are now not detected by the 2D PSF. |
| In the text | |
 |
Fig. 10 Distributions of the (2D-default) change in returned (left) RA and (right) Dec of detected sources using the 2D (Ellbeta) and default (Medium) PSF for a sample of 70 clean observations. |
| In the text | |
 |
Fig. 11 (2D-default) offsets in (left) RA and (right) Dec of detected sources using the 2D (Ellbeta) and default (Medium) PSF plotted against the source angle on the sky (anti-clockwise from north) for the sample of 70 clean observations as in Fig. 10. |
| In the text | |
 |
Fig. 12 (Top) X-ray position − QSO optical position offsets (in arcseconds) in (left) RA and (right) Dec of default (medium) PSF-detected X-ray sources with a QSO match, plotted against the source angle on the sky (anti-clockwise from north). X-ray positions are after eposcorr (see text). (Bottom) The same data, binned into 25 equi-angular bins and averaged. |
| In the text | |
 |
Fig. 13 (Top) X-ray position − QSO optical position offsets (in arcseconds) in (left) RA and (right) Dec of 2D (Ellbeta) PSF-detected X-ray sources with a QSO match, plotted against the source angle on the sky (anti-clockwise from north). X-ray positions are after eposcorr (see text). (Bottom) The same data, binned into 25 equi-angular bins and averaged. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


