| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117248 | |
| Published online | 19 October 2011 | |
Towards understanding the structure of voids in the cosmic web
1
Tartu Observatory, 61602 Tõravere, Estonia
e-mail: einasto@aai.ee
2
Estonian Academy of Sciences, 10130 Tallinn, Estonia
3
ICRANet, Piazza della Repubblica 10, 65122 Pescara, Italy
4
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
5
Landau Institute for Theoretical Physics, RAS, 119334 Moscow, Russia
6
Research Center for the Early Universe (RESCEU), Graduate School of Science, The University of Tokyo, 113-0033 Tokyo, Japan
Received: 12 May 2011
Accepted: 20 August 2011
Context. According to the modern cosmological paradigm, cosmic voids form in low density regions between filaments of galaxies and superclusters.
Aims. Our goal is to see how density waves of different scale combine to form voids between galaxy systems of various scales.
Methods. We perform numerical simulations of structure formation in cubes of size 100, and 256 h-1Mpc, with resolutions 2563 and 5123 particles and cells. To understand the role of density perturbations of various scale, we cut power spectra on scales from 8 to 128 h-1Mpc, using otherwise in all cases identical initial random realisations.
Results. We find that small haloes and short filaments form all over the simulation box, if perturbations only on scales as large as 8 h-1Mpc are present. We define density waves of scale ≥ 64 h-1Mpc as large, waves of scale ≃ 32 h-1Mpc as medium scale, and waves of scale ≃ 8 h-1Mpc as small scale, within a factor of two. Voids form in regions where medium- and large-scale density perturbations combine in negative parts of the waves because of the synchronisation of phases of medium- and large-scale density perturbations. In voids, the growth of potential haloes (formed in the absence of large-scale perturbations) is suppressed by the combined negative sections of medium- and large-scale density perturbations, so that their densities are less than the mean density, and thus during the evolution their densities do not increase.
Conclusions. The phenomenon of large multi-scale voids in the cosmic web requires the presence of an extended spectrum of primordial density perturbations. The void phenomenon is due to the action of two processes: the synchronisation of density perturbations of medium and large scales, and the suppression of galaxy formation in low-density regions by the combined action of negative sections of medium- and large-scale density perturbations.
Key words: large-scale structure of Universe / early Universe / cosmology: theory
© ESO, 2011
1. Introduction
The goal of this series of papers is to study the role of perturbations on various scales in formation the cosmic web. Einasto et al. (2011) used wavelet techniques to understand the formation of rich systems of galaxies – clusters and superclusters. They conclude that superclusters are objects where density waves of medium and large scales combine in similar phases to generate high density peaks. Similarly, voids are regions in space where medium- and large-scale density perturbations combine in similar under-density phases of waves. Suhhonenko et al. (2011) demonstrated that the properties of the cosmic web depend essentially on density perturbations of small and medium scales, whereas perturbations of large scale ≥ 100 h-1Mpc modulate the richness of galaxy systems from clusters to superclusters, and make voids emptier. This paper is devoted to the study of the influence of medium- and large-scale density waves on the structure and evolution of voids in the cosmic web.
The cosmic web was first openly discussed at the IAU Symposium on Large Scale Structure of the Universe (Longair & Einasto 1978). At this symposium, four groups reported results of studies of the three-dimensional distribution of galaxies in space using available data for the redshifts of galaxies. The presence of voids in the distribution of galaxies was reported by Jõeveer & Einasto (1978), Tarenghi et al. (1978), Tifft & Gregory (1978), and Tully & Fisher (1978) in the Perseus-Pisces, Hercules, Coma, and Local superclusters, respectively.
The main results reported in this symposium were that: (1) galaxies, groups, and clusters of galaxies are not randomly distributed but form chains, converging in superclusters; (2) the space between galaxy chains contains almost no galaxies and forms voids of diameters 20...70 h-1Mpc; (3) superclusters are not isolated systems, but are connected by galaxy filaments to a connected network – the supercluster-void network (Jõeveer et al. 1978; Einasto et al. 1980; Zeldovich et al. 1982; Oort 1983) or the cosmic web (Bond et al. 1996). These early results were confirmed by the Second Harvard Sky Survey (de Lapparent et al. 1986; Geller & Huchra 1989) and the discovery of the very large Bootes void by Kirshner et al. (1981, 1987).
The presence of long essentially one-dimensional galaxy and group/cluster chains, and the elongated shape along the chain of the central cluster galaxies (often supergiant galaxies of type cD) suggests that galaxies and groups/clusters of the chain had formed within the chain simultaneously with the formation of the whole cosmic web. This occurred in the gaseous phase of the structure evolution, which allowed the dissipation and cancelling of velocities perpendicular to the chain axis. These data gave strong support to the Zeldovich (1970, 1978) pancake scenario of galaxy formation. The observed distribution of galaxies was quite similar to the distribution of simulation particles in a two-dimensional numerical simulation of the evolution of the structure of the Universe, prepared by Shandarin (1975, priv. comm.) and published by Doroshkevich et al. (1980). In this simulation a network of high- and low-density regions was seen: high-density regions form cells that surround large under-dense regions. Subsequent three-dimensional simulations confirmed this picture (Klypin & Shandarin 1983; Melott et al. 1983).
However, some important differences between the model and observations were evident. First of all, there exists a rarefied population of simulation particles in voids that is absent in real data. This was the first indication of physical biasing in galaxy formation (the term “biased galaxy formation” was introduced a few years later by Kaiser 1984; see also Bardeen et al. 1986). A theoretical explanation of the absence of galaxies in voids was given by Einasto et al. (1980, see also a more detailed discussion by Einasto et al. 1994a. A simple analytical solution of the cosmological evolution of the density of matter shows that in over-dense regions the density increases until the matter collapses to form compact objects (pancaking by Zeldovich 1970). In contrast, in under-dense regions the density decreases but never reaches a zero value – gravity cannot evacuate voids completely.
Even early studies proposed that the cosmic web has a hierarchical structure. The parts of the web formed by objects of different mass or luminosity have different characteristic sizes. As voids are defined by the web, the void assembly has several important properties: voids defined by more luminous (or massive) objects have larger diameters, and voids defined by clusters/galaxies of certain luminosity contain substructure formed by less luminous objects.
According to the present cosmological paradigm, all structural elements of the Universe were formed by the growth of initial small density perturbations created during the very early phase of the evolution of the Universe. To these elements belong galaxies, groups, clusters, and their systems, such as filaments and superclusters. Rich superclusters form a cellular distribution, with large voids surrounded by rich superclusters. The characteristic diameter of these supervoids is of the order of 100 h-1Mpc (Jõeveer et al. 1978; Kirshner et al. 1981; Einasto et al. 1994b, 1997b). Supervoids are not empty, but contain a hierarchy of voids (Einasto et al. 1989; Martel & Wasserman 1990; van de Weygaert & van Kampen 1993; Lindner et al. 1995; Müller et al. 2000; Gottlöber et al. 2003; Aragón-Calvo et al. 2007; von Benda-Beckmann & Müller 2008; van de Weygaert et al. 2009; van de Weygaert & Platen 2009; Aragon-Calvo et al. 2010a; Jones et al. 2010).
Among the early studies of the void evolution we mention Hoffman & Shaham (1982); Hoffman et al. (1983), Peebles (1982), Icke (1984), Fillmore & Goldreich (1984), Bertschinger (1987), among others. The study of the hierarchical evolution of voids was pioneered by Dubinski et al. (1993). Sahni et al. (1994) described the evolving void hierarchy within the context of the adhesion theory. Sheth & van de Weygaert (2004) developed the excursion set (extended Press-Schechter) description of a void hierarchy in the dark matter distribution, followed by Furlanetto & Piran (2006) comparing this with the void hierarchy in galaxy populations.
Superclusters are connected by filaments of galaxies, i.e voids have substructure. Observationally, this was already evident in early void studies (Jõeveer & Einasto 1978; de Lapparent et al. 1986). Theoretical discussion of the void substructure has been presented by Regos & Geller (1989), Martel & Wasserman (1990), van de Weygaert & van Kampen (1993), Goldberg & Vogeley (2004); Goldberg et al. (2005), and many others. The skeleton of the cosmic web was discussed by Hahn et al. (2007), Forero-Romero et al. (2009), Sousbie et al. (2008, 2009), Aragón-Calvo et al. (2010b), Bond et al. (2010a,b), Shandarin (2010), and Einasto et al. (2011).
It is generally accepted that the initial density perturbations had a smooth, extended power spectrum (quasi-flat in terms of metric perturbations ns ≈ 1) and a random (Gaussian) distribution of perturbation phases. The amplitude of perturbations (Δ ∝ k3P(k)) is larger at short wavelengths and per δlnk, where k is the wavenumber, and P(k) is the power spectrum of perturbations. For this reason, small objects (mini-haloes in numerical simulations and dwarf galaxies in the real Universe) should form first. The early formation of dwarf galaxies is confirmed by observation of very distant galaxies (Beckwith et al. 2006). These early galaxies grow by the attraction of more primordial matter and by clustering, as originally suggested by Peebles (1971).
Initial small-scale perturbations were present everywhere, and this raises the question: why do voids not contain galaxies, even dwarf galaxies? This question was asked more specifically by Peebles (2001). The deepest voids in the simulated dark matter distribution are never completely empty; they still contain low-mass condensations of primordial matter – mini-haloes. Therefore, voids could be the environment in which faint dwarf galaxies are most likely to reside. Why is this not the case?
This “Peebles question” has stimulated a number of studies, both observational and theoretical, to find dwarf void galaxies and to study either analytically or by numerical simulations void regions of the Universe. Studies of void galaxies were made by Szomoru et al. (1996), Grogin & Geller (1999), Gottlöber et al. (2003), Rojas et al. (2004), Hoeft et al. (2006), Stanonik et al. (2009), Kreckel et al. (2011b,a), and others. Among recent large-scale surveys, we mention here Hoyle & Vogeley (2004), Croton et al. (2004), Conroy et al. (2005), Patiri et al. (2006), and Tinker et al. (2007). Karachentsev et al. (2003, 2004, 2007) studied the Local Volume out to a distance 10 h-1Mpc, where they found about 550 mainly very faint galaxies. A void galaxy survey (VGS) was initiated by van de Weygaert and collaborators in our local neighbourhood out to redshift z = 0.02 (Stanonik et al. 2009; Kreckel et al. 2011a,b; van de Weygaert et al. 2011). These studies suggest that extremely faint galaxies do not fill voids, but are located in the vicinity of brighter galaxies.
To investigate the properties of galaxies in voids, the halo occupation distribution model is used to determine the relationship between galaxies and dark matter haloes (see Seljak 2000; Cooray & Sheth 2002; Berlind & Weinberg 2002; Zehavi et al. 2004, 2005; Zheng et al. 2007; van den Bosch et al. 2007; Tinker et al. 2006, 2007, 2008a,b; White et al. 2007; and Padmanabhan et al. 2009). The results obtained by analysing of observational data are in good agreement with the results of semi-analytic models, hydrodynamic cosmological simulations, and high-resolution collisionless simulations (Kravtsov et al. 2004; Zheng et al. 2005; Conroy et al. 2006; von Benda-Beckmann & Müller 2008; Tikhonov & Klypin 2009). In particular, the simulations of Tikhonov & Klypin (2009) and Ishiyama et al. (2011) show the presence of very low-mass haloes in voids, but their mass is probably too low for star formation to be possible. The comparison of the distribution of model haloes and dwarf galaxies shows that haloes should have a circular velocity of at least ~35 km s-1 in order to form a galaxy. Tinker et al. (2008b) showed that the smallest void haloes have so little mass that no galaxy formation is expected according to the model.
The absence of dwarf galaxies in voids can also be explained by gasodynamical processes. Using high-resolution hydrodynamical simulations, Hoeft et al. (2006), and Hoeft & Gottlöber (2010) showed that photoionisation by the UV radiation field is able to stop the cooling and collapse of gas in dwarf galaxy haloes. At the redshift z = 0, the characteristic mass scale of photo-evaporation corresponds to a circular velocity ~27 km s-1, in good agreement with other studies cited above.
All studies suggest that galaxy formation is a threshold phenomenon. In many of the studies cited above, it was demonstrated that galaxies do not form in voids, when the void haloes have very low masses. However, these studies did not explain what is the physical reason for the difference between the typical halo masses in the void and supercluster environments? In this paper, we try to find an explanation for the difference between the masses of haloes in various global environments.
In the case of the presence of an extended primordial perturbation spectrum, systems of galaxies are produced by an interplay of density perturbations on all scales. It is clear that the difference between the present distribution of galaxies and the very early distribution of protogalaxies must have something to do with perturbations of a typical scale-length that is larger than the scales responsible for the formation of primeval small protohaloes. This lead us to the study of the influence of perturbations of various scale-lengths on the evolution of the structure. Preliminary results of this study very interestingly demonstrated that the whole supercluster-void network is caused by the interplay of medium- and large-scale perturbations. These preliminary results were reported on several conferences and summer-schools (see the web-site of Tartu Observatory1).
In the present paper, we attempt to understand the influence of perturbations of various scale on the evolution and structure of voids in the cosmic web. As in Suhhonenko et al. (2011) and Einasto et al. (2011), we use numerical simulations in boxes of various scale-lengths from 100 to 256 h-1Mpc, calculated for power spectra cut off above different scales from 8 to 128 h-1Mpc, to determine the influence of perturbations of various scales on the formation and internal structure of voids. We employ a wavelet technique to follow the evolution of under-dense and over-dense regions in terms of density waves of various scales.
The paper is composed as follows. In the next section, we describe numerical models used in the study. In Sect. 3, we perform a wavelet analysis of our simulations. In Sect. 4, we describe our correlation analysis of wavelet-decomposed density fields. In Sect. 5, we investigate the structure of voids using haloes of various mass as objects which define voids. We discuss our results in Sect. 6, and in our last section we present our conclusions.
2. Modelling the evolution of voids in the cosmic web
Previous analyses of the observational galaxy samples and numerical simulations have shown that in the formation of superclusters and voids, large-scale perturbations play an important role. Thus, to understand the supercluster-void phenomenon correctly, we need to perform numerical simulation in a box containing large waves. On the other hand, most systems of galaxies in the Universe are groups of galaxies – there are almost no very isolated galaxies far away from groups. The characteristic scale of groups is 1 h-1Mpc, thus the simulation must have at least a resolution similar to this scale.
To have both a high spatial resolution and the presence of density perturbations in a larger scale interval, we performed simulations in boxes of sizes 100 h-1Mpc, and 256 h-1Mpc, and resolutions 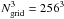 and
and 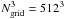 . The main parameters of our series of models are given in Table 1, where L is the cube size, Npart is the number of particles and cells used in simulations, and Mpart is the mass of a particle in units of 109 M⊙. We assumed the cosmological parameters (Seljak et al. 2005; Tegmark et al. 2004, 2006) Ωm = 0.28 for the matter density, ΩΛ = 0.72 for the dark energy density (in units of the critical cosmological density), and σ8 = 0.84 for the initial amplitude parameter. We use the notation h for the present-day dimensionless Hubble parameter in units of 100 km s-1 Mpc-1; in simulations, we used a value of h = 1.
. The main parameters of our series of models are given in Table 1, where L is the cube size, Npart is the number of particles and cells used in simulations, and Mpart is the mass of a particle in units of 109 M⊙. We assumed the cosmological parameters (Seljak et al. 2005; Tegmark et al. 2004, 2006) Ωm = 0.28 for the matter density, ΩΛ = 0.72 for the dark energy density (in units of the critical cosmological density), and σ8 = 0.84 for the initial amplitude parameter. We use the notation h for the present-day dimensionless Hubble parameter in units of 100 km s-1 Mpc-1; in simulations, we used a value of h = 1.
As we are interested in the study of the role of perturbations on different scales to the evolution of voids, we used simulations with the full power spectrum, as well as with a power spectrum truncated at wave-numbers kcut, so that the amplitude of the power spectrum on large scales is zero: P(k) = 0, if k < kcut, wavelength λcut = 2π/kcut. The cut scale in h-1Mpc, λcut = 2π/kcut, is given in Table 1. The amplitude of a spectrum was set to zero for k < kcut during the calculation of the initial density field, keeping all simulation parameters fixed across the full set of realisations.
Parameters of models.
As in Suhhonenko et al. (2011), we use the notations for our models whereby the first characters M and L designate models with resolutions of Ngrid = 256 and Ngrid = 512, respectively. The subsequent number gives the size of the simulation box, L, in h-1Mpc, and the next indicates the maximum wavelength used in the simulation in h-1Mpc. The locations of the cells inside the cubical density grid are marked by cell indices (i,j,k).
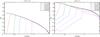 |
Fig. 1 The left and right panels show the power spectra for the models of the series L256 at the epochs z = 30 and z = 0, respectively. |
For the models of the M256 series, we used in simulations the AMIGA code (Knebe et al. 2001). This code uses an adaptive mesh technique in the regions where the density exceeds a fixed threshold. In this code, gravity is automatically softened adaptively, so that the softening length is near its optimum value in both high- and low-density regions. We chose a maximum level of eight refinements. For models with a 5123 resolution, we used the GADGET-2 code with a gravitational softening length of 10 h-1kpc (L100 models) and 20 h-1kps (L256 models) (Springel et al. 2001; Springel 2005). The simulation L100 was performed at the Leibniz-Institut für Astrophysik Potsdam, and simulations M256, and L256 at the High Performance Computing Centre of University of Tartu. The initial density fluctuation spectrum was generated using the COSMICS code by Bertschinger (1995)2; to generate the initial data, we assumed the baryonic matter density Ωb = 0.044. Calculations started at an early epoch, z = 100. For every particle, we calculated the local density in units of the mean density, using positions of 27 nearby particles. All models of the same series have the same realisation, so the role of different waves in models can be easily compared. To allow different models to be compared every particle has an identification number, the same for all models of a series. Particle positions and velocities were extracted for seven epochs in the redshifts range z = 30,...,0. Power spectra for the models of the L256 series are shown in Fig. 1 for an early epoch, z = 30, and for the present epoch z = 0.
For each particle, we also calculated the global density at the location of the particle (for details see Appendix A.1). To find the global density field, we used smoothing with the B3 spline kernel of scale ~8 h-1Mpc, which is rather close to smoothing with an Epanechnikov kernel of the same scale. Smoothing of density fields with different kernels is discussed by Martínez & Saar (2002). These local and global density fields were calculated for all models and all epochs, and were used in the subsequent analysis to select particles belonging to a population with given properties, and to follow the density evolution of the model. Hence, for each particle we stored coordinates, local, and global density values. Particles were sorted, thus their number in the file serves as an ID number.
To see the effects of density waves of different scale and to understand the evolution of the density field, we use the wavelet technique. We use the à trous wavelet transform (for details, see Martínez & Saar 2002; and Appendix A.2). The field is decomposed into several frequency bands as follows. The high-resolution (zero level) density field was calculated with the B3 spline kernel of width equal to the size of one cell of the field, where every next field was calculated with twice larger kernel. Wavelets were found by subtracting higher level density fields from the previous level fields. In such a way, each wavelet band contains waves twice the size of the previous band, in the range ± 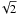 centered on the mean (central) wave. The sum of these bands restores the original density field. Using this technique, we calculated the density fields and wavelets up to index 5 (6 for models of the M256 series).
centered on the mean (central) wave. The sum of these bands restores the original density field. Using this technique, we calculated the density fields and wavelets up to index 5 (6 for models of the M256 series).
The high-resolution density fields of the model M256.256 for the epochs z = 0, 1, 5, 10 are shown in Fig. 2. The high-resolution density fields of models L100.100 and L100.016 for redshifts z = 0 and z = 2 are shown in Fig. 3. The scale of the cosmic web is rather different in models of different cutoff scale. The dependence of the scale of the web on the maximal wavelength of density perturbations was investigated in detail by Suhhonenko et al. (2011).
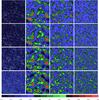 |
Fig. 2 The high-resolution density fields of the model M256.256 are shown in the left column, at the k = 140 coordinate. The second, third, and fourth columns show the wavelet w5, w4, and w3 decompositions at the same k, respectively. The upper row gives data for the present epoch, z = 0, the second row for the redshift z = 1, the third row for the redshift z = 5, and the last row for the redshift z = 10. Densities are expressed on a linear scale. In wavelet panels, green and red colours show the positive regions of wavelets, and the blue colour shows negative (under-density) wavelet regions. Colour codes are plotted at the bottom of the figure for wavelet w3 at epoch z = 10. |
To investigate the spatial structure of both the cosmic web and voids, we found haloes using the adaptive Amiga Halo Finder (AHF) code developed by Knollmann & Knebe (2009), with the number of particles in a halo Np ≥ 20. Haloes and their parameters (masses, virial radii, positions, velocities etc.) were found for all models and simulation epochs.
3. Analysis of models
To understand the evolution of the density field, and to see the effects of density waves of different scale, we analyse the density fields and their wavelet decompositions for various simulation epochs and cut off scales. We focus on the evolution of the following properties:
-
1.
the global patterns of the density field, using wavelets ofdifferent levels;
-
2.
the fine structure of the density field for perturbations of various scales;
-
3.
density perturbations of various scales;
-
4.
the density distribution in void regions.
3.1. The evolution of the global patterns of density fields
To compare the patterns of density fields and their wavelet decompositions for various cosmic epochs, we use the model M256.256.
In Fig. 2, we plot the high-resolution density field and wavelets of the model M256.256 at the four redshifts: z = 0, 1, 5, 10. In the second column of Fig. 2, the wavelets of order five are shown. The characteristic scale of density perturbations for this wavelet is 64 h-1Mpc. The upper density levels used in plotting for w5 are 1.2, 0.7, 0.2, and 0.1, for redshifts 0, 1, 5, and 10, respectively. Lower limits to these redshifts are −0.6, −0.35, −0.1, and −0.05. In wavelets of the order 4 and 3, a similar choice of colour limits is applied. This colour-coding of wavelets at different redshifts is chosen so that a certain colour corresponds approximately to the density level, corrected by the linear growth factor for that redshift. Wavelet blue colours correspond to under-dense regions of density waves, green colours to slightly over-density regions, and red colours to highly over-density regions.
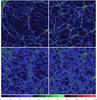 |
Fig. 3 Zoom-ins to the high-resolution density fields of the models L100.100 and L100.016, left and right columns, respectively. Zoom factor is 2, central 50 × 50 h-1Mpc (256 × 256 pixels) of all models are shown. Upper panels are for the present epoch z = 0, lower panels for the epoch z = 2. All panels are at the k = 51 coordinate. Cross sections (beams) at coordinates j = 222 and k = 51 for both models are shown in Fig. 5 for three redshifts to see the evolution of the density field and its wavelets. In the upper left corner of the figure there is a rich supercluster in the model L100.100, absent in the model L100.016. Both models have at the right edge of the figure a rich cluster. This cluster is well seen in Fig. 5 at i = 390 coordinate. Densities are expressed in the logarithmic scale, identical lower and upper limits for plotting with the SAO DS9 package are used. The border between the light blue and the dark green colours corresponds to the critical density Dloc = 1.6, which separates low-density haloes and haloes collapsed during the Hubble time (Kaiser 1984; Bardeen et al. 1986). Note that in both models and simulation epochs the majority of filaments in voids have densities below the critical density. |
 |
Fig. 4 Wavelets w1 of models L100.100 and L100.008 at redshift z = 10 are shown in the left and right panels, respectively, at coordinate k = 51. Densities are expressed on a linear scale, only over-density regions are shown. As in Fig. 3, the central 256 × 256 pixels of the full models are shown. The characteristic scale of density perturbations corresponding to this wavelet is 0.4 h-1Mpc. Note the weakening of peak densities of the model L100.100 in the region of future large under-dense region, seen in Fig. 3. |
Figure 2 shows that the pattern of the cosmic web on wavelet w5 is almost identical at all redshifts, only the amplitude of the density waves increasing approximately in proportion to the linear growth factor. This linear growth is expected for density waves of large scales, which are in the linear stage of growth. The pattern of the web of the wavelet w4 changes little, but the growth of the amplitude of density waves is more rapid. The pattern of the wavelet w3 changes much more during the evolution, and the amplitude of density waves increases more rapidly, but essential features remain unchanged, i.e. the locations of high-density peaks and low-density depressions are almost independent of the epoch.
Figure 2 shows that at all redshifts high-density peaks of wavelets of medium and large scales almost coincide. In other words, density perturbations of medium and large scales have a tendency of phase coupling or synchronisation at peak positions. Einasto et al. (2011) reached the same conclusion using models with a much broader scale interval. Figure 2 shows that the synchronisation of medium and large scales applies also to under-dense regions. The analysis below describes the differences between the synchronisation of over- and under-dense regions in quantitative terms.
3.2. The evolution of the fine structure in the density field
To follow the evolution of the fine structure in the density field, we compare high-resolution density fields of the models of L100 series (see Fig. 3). We show slices at the coordinate k = 51 of the full model L100.100, and of the strongly cut model L100.016, at epochs z = 0, and z = 2. The k coordinate is chosen so that the slice in the model L100.100 crosses a large under-dense region between a rich supercluster and several rich clusters. To see more clearly the differences between the density fields of models L100.100 and L100.016, we show in Fig. 3 only the zoom-in of the central 50 × 50 h-1Mpc (256 × 256 pixels) region. To compare the present field with the initial density field, we use the smallest scale wavelet w1 for both models at the redshift z = 10, shown as a zoom-in plot in Fig. 4, which is similar to the plot for the present epoch in Fig. 3.
The power spectrum of density perturbations has the highest power on small scales. Thus, the influence of small-scale perturbations relative to large-scale perturbations is strongest in the early period of evolution of structure. For this reason, density fields and wavelets w1 at early epochs are qualitatively rather similar for the full model L100.100, and for the model cut on small scales, λcut = 8 h-1Mpc, called L100.008 (see Fig. 4).
However, there are small but important differences in the patterns of small-scale structures in the models L100.100 and L100.008 at z = 10. The density peaks of the model L100.008 have more or less equal heights throughout the whole simulation box, whereas in the model L100.100 in regions of future voids the peak heights are lower than in the future supercluster regions. This shows that already at the epoch z = 10 large-scale perturbations started to influence the density field on small scales.
The colour coding is identical in all panels of Figs. 3. Codes are chosen so that the density level Dloc = 1.6 is clearly visible. Particle clouds of density above this limit can form collapsed haloes during the Hubble time, and below this limit they stay in pre-galactic more diffuse form. The actual collapse parameter is 1.69 (Kaiser 1984; Bardeen et al. 1986). In both models, there exists a network of filaments. We see that in all models shown in Fig. 3 the majority of filaments have densities below this limit, i.e. that filaments consist of strings of primordial matter that have not yet formed compact haloes.
At the epoch z = 2, there are already strong differences between the density fields of models L100.100 and L100.016. In the model L100.016, the high-density knots are distributed more uniformly, and the whole pattern of filaments has a smaller scale. We discuss the distribution of mean void sizes for both models below. In the full model L100.100, the fraction of particles above the critical density Dloc = 1.6 in regions of low global density (voids) is lower (see Fig. 7). Regions containing high-density knots (marked by green and red) start to form superclusters. In the model L100.016, these regions are more uniformly distributed.
The comparison of distributions for the epochs z = 2 and z = 0 shows that filaments contract with time, as known from many earlier studies cited above. In the model L100.016, the pattern of filaments changes very little between the epochs z = 2 and z = 0. In contrast, for the model L100.100 density evolution can be clearly seen. At z = 2, small-scale filaments fill almost the whole space of voids between rich systems. At z = 0, most of these small filaments have merged leaving more space for very low-density regions.
The differences between the models L100.100 and L100.016 at the present epoch z = 0 are very well seen in Fig. 3. In the model L100.100, between the supercluster at the left corner and the cluster at the right edge there is a large low-density region. This region is crossed near the center by a filament that has several knots in the green and red colour. In the model L100.016, there are no rich superclusters, the whole region being covered by a web of small-scale filaments. In other words, large-scale perturbations present in the model L100.100, have suppressed the growth of the density of filaments in void regions.
There exists a low-density smooth background, seen in Fig. 3 in deep dark-blue colour. The density of this background, D ≈ 0.1, is lower at the present epoch z = 0, i.e. the density of the smooth background decreases with time (see Fig. 7). Regions of very low density have much larger sizes in the model L100.100 than in the model L100.016.
3.3. The evolution of density perturbations of various scales
We now follow the evolution of density perturbations of various scales in the models of the series L100 and L256 in more detail. The evolution of density perturbations has several characteristics: the shapes of density perturbations of various scales and their change with time; synchronisation, amplification, and suppression of density perturbations of various scales; and the formation of regions of very low density.
 |
Fig. 5 The evolution of the local density and wavelets of the models L100.100 (left panels) and L100.016 (right panels) in beams along the i-coordinate at j = 220, k = 51. The same k-coordinate was used in plotting the density field in Fig. 3. Data are shown for epochs z = 0, 2, 5. To see better details only the region 144 ≤ i ≤ 400 of length 50 h-1Mpc is shown. The characteristic scale of the wavelet w5 is 12.5 h-1Mpc. Wavelets are divided by the factor f ∝ (1 + z)-1. |
 |
Fig. 6 The local density and wavelets of the models L256.256 (left panel) and L256.008 (right panel) in beams along the i − coordinate at j = 90, k = 105 at the early epoch, z = 30. To enhance details, only the region 100 ≤ i ≤ 250 of length 75 h-1Mpc is shown. The characteristic scale of the wavelet w5 is 32 h-1Mpc. |
 |
Fig. 7 Left panel: the distribution of void particle local densities of the model L100.100 as a function of redshift. Right panel: the distributions of void particle local densities at the present epoch of the models of the series L100 with different cutoff wavelengths. |
To see the evolution of the density field and its wavelets, we show in Fig. 5 one-dimensional density distributions (beams) along horizontal lines of the plane in Fig. 3. The distributions are generated along the axis j = 222, k = 51, for the models L100.100 and L100.016 at the redshifts 0, 2, 5. Beams are taken along the i-coordinate; at each i value, all cells in the j- and k-coordinate within ±5 from the centre of the beam are counted, i.e. beams have sizes 11 × 11 cells (about 2.15 × 2.15 h-1Mpc in the models of the L100 series). The average densities for a given i are found, and are given in the mean density units. We use overdensities D − 1 here, so the mean overdensity level is zero, which is similar to the mean value for wavelets. Wavelet amplitudes are divided by the linear growth factor, thus during linear growth their amplitudes should not change. The effective scale for the wavelet w5 of the model L100 is 12.5 h-1Mpc, as seen also from the separation between the high-density peaks in Figs. 5.
At high redshifts, perturbations of various scales have almost sinusoidal shapes, and the wave peaks have approximately equal heights. During the subsequent stages of evolution, Einasto et al. (2011) showed that perturbations of larger scales begin to affect the evolution. These perturbations amplify small-scale perturbations near maxima, and suppress small-scale perturbations near minima. Thereafter, still larger perturbations amplify smaller perturbations near their maxima, and suppress smaller perturbations near their minima, and so on.
For early stages, the density fields and wavelets are given for the models L256.256 and L256.008, for the epoch z = 30, in Fig. 6. This model also allows us to illustrate the influence of larger waves, because the characteristic scale for the wavelet w5 of the model L256 is 32 h-1Mpc.
We see that in the model L256.008 wavelets of different order have approximately sinusoidal shapes. The wavelet w5 of this model has zero amplitude, and the amplitude of the wavelet w4 is small, because in this model only waves of scale up to 8 h-1Mpc are present. The wavelet w3 of the effective scale, which is approximately equal to the cut scale of this model, has the highest amplitude. The maxima and minima of this wavelet are partly synchronised with the maxima and minima of the wavelets w2 and w1; synchronisation is better in the regions that happen to coincide with the maxima and minima of the wavelet w4.
In the model L256.256 at the early epoch z = 30, the wavelet w5 has the highest amplitude, the next highest being that of the wavelet w4. These two wavelets are only partly synchronised, i.e. the maxima of the wavelet w5 coincide in position only approximately with the maxima of the wavelet w4, and near the minima of the wavelet w5 there is a secondary maximum of the wavelet w4, i.e. the wavelet w4 behaves as the first overtone of the wavelet w5. The shape of small-scale wavelets is not sinusoidal. This is caused by large-scale waves that have started to change the shapes of small-scale waves.
Further evolution with time of the wavelets can be followed using the model L100 in Fig. 5. We discuss first the evolution of wavelets in the model L100.016 (see the right panels of the figure). The largest wavelet w5 has for all redshifts approximately the same amplitude and a sinusoidal shape, suggesting that density perturbations of this scale are in the linear growth regime. The shape of the next wavelet w4 is very different from sinusoidal. In some regions of maxima of the wavelet w5, the wavelet w4 has very strong maxima. An example is the region near i ≈ 370, where all wavelets of smaller scale also have strong maxima, and wavelets of all scales up to w4 are very well-synchronised. The overall shape of the density profile is determined by the wavelet w3 that has a characteristic scale 3.1 h-1Mpc. Most peaks seen in the density profile are due to the maxima of this wavelet. In most of these peaks, wavelets of smaller scale also have maxima, i.e. near the peaks small-scale wavelets are synchronised.
When we compare the density and wavelet distributions of this model at various epochs, we see little difference. This shows that in the model L100.016 the structure has rapidly evolved at early epochs and changes only a little later. The most important development is the decrease in the density in deep void regions, and the increase in the density in massive haloes.
We now consider the evolution of the full model L100.100, shown in the left columns of Fig. 5. We see that the evolution of the largest wavelet w5 is almost linear up to the epoch z ≥ 1 (the density and wavelet distributions for the epochs z = 1 and z = 2 are rather similar, only the amplitudes of wavelets up to w4 are smaller for z = 1). The shapes of the wavelet w5 for different epochs are almost sinusoidal and the heights of the maxima are approximately equal. The next wavelet w4 behaves as a first overtone of the wavelet w5 – near the minima of w5 there are maxima of w4, which have much lower heights than the maxima near the maxima of w5. Evidence of this phenomenon can also be clearly seen in the wavelet analysis of the Sloan Digital Sky Survey (see Fig. 6 of Einasto et al. 2011). Near the joint maxima of w5 and w4, there are very strong maxima of all wavelets of smaller order; this is very well seen at locations i ≈ 290 and i ≈ 380.
Near the minima of w5 and the maxima of w4, wavelets of smaller order also have maxima, but these maxima get weaker at lower redshifts, as in the region around i ≈ 220. Here, small-scale wavelets are partly synchronised, and small-scale peaks of the density field are related to maxima of the wavelets w2 and w3.
The density and wavelet distributions of the model L100.100 for the present epoch z = 0 are completely different from the distributions at higher redshifts. In the present epoch, the dominant feature is a large under-dense region in the interval 120 < i < 380. This large under-dense region is caused by large-scale density perturbations that are not shown as wavelets in the figure. In this region, these large-scale density waves have their minima and the amplitudes of density waves of smaller scales, including w4 and w5, are suppressed. The amplitudes of wavelets w3 and lower orders are almost zero. Near the density maxima seen at higher redshifts at i ≈ 210 and i ≈ 290, there are very weak density peaks with maxima below the mean density level. These maxima are seen in the density field as weak filaments (see Fig. 3).
The most remarkable feature of the density field in the model L100.100 at the present epoch is the presence of large under-dense regions of very low density D ≈ 0.1, which can be clearly seen in Fig. 3 in deep-blue colour. At earlier epochs, the density in these regions was higher and there were numerous low-density peaks within the regions, for the present epoch most of these peaks are gone. This is caused by density perturbations on larger scales.
When we compare the evolution of density distributions of models L100.100 and L100.016, we see remarkable differences. These differences are solely due to the presence of density perturbations of scales larger than λcut = 16 h-1Mpc in the model L100.100. We note that both models were generated with identical “random amplitudes”, i.e. the perturbations of scales λ ≤ λcut = 16 h-1Mpc are identical in both models.
The main result of the paper by Einasto et al. (2011) was that at all redshifts high-density peaks of wavelets of large and medium scales almost coincide. Figures 2, 3, and 5 show that the same conclusion is valid for positions of density depressions (deepest voids) of wavelets of large and medium scales. The other main conclusion of Einasto et al. (2011) was that positions of peaks of waves of different scale coincide, i.e. density waves of different scale are synchronised. A look at Figs. 2 and 5 shows that the synchronisation of density waves of different scales also concerns density depressions of large and medium scales. However, the synchronisation of the depressions of density waves, which is responsible for the formation of voids, is less pronounced than that of density peaks.
3.4. The evolution of density distributions in void regions
To investigate the evolution of the density distribution in void regions, we selected in all models void particles in the present epoch z = 0. We calculated the distributions of the global densities of full models (i.e. models with no cuts in the power spectra), and selected particles of the lowest global density values, about 10% of all particles (13.390.895 particles in the model L100.100). The corresponding value of the threshold global density is 0.565 for the model L100.100 (in units of the mean density).
The evolution of the distributions of local densities of void particles for the full model L100.100 is given in the left panel of Fig. 7. The distributions of void particle local densities for the models of the L100 series for the present epoch are shown in the right panel of Fig. 7.
Figure 7 shows that the initial distribution of particles at the redshift z = 10 is quite symmetrical in the log-log representation. The density distribution has a peak at D ≈ 0.8. As time goes on, the peak density decreases, and at the present epoch has a value D ≈ 0.2; the lowest density occurs close to D ≈ 0.1. Particles in overdense regions (D ≥ 1) form haloes; with decreasing redshift z, the peak densities increase, i.e. haloes in void regions become more massive and denser.
Density evolution depends strongly on the cutoff wavelength of the model. In the most strongly cut model L100.008 at the present epoch, the fraction of particles in very low-density regions (D ≈ 0.2) is about five times lower than in the full model L100.100. In the model L100.008, most particles in void regions form haloes of mean density D ≈ 100, and with the maximum density D ≈ 1000. With the increase in the cut wavelength λcut, the fraction of particles in very low-density regions increases. The maximal density of haloes in void regions reaches the highest value, D ≈ 2500, in the model L100.016. In this model, density waves between the scales 8 and 16 h-1Mpc amplify the density of haloes. If density perturbations of larger scale are included (models L100.032 and L100.100), then in the void regions still larger perturbations start to decrease the maximum masses of haloes. This depression is largest in the full model L100.100, where the maximum local densities in void haloes reach the values D ≈ 600.
4. Correlation analysis of wavelet-decomposed density fields
We now attempt to quantify some of the qualitative statements given earlier in the text. To this end, we perform the correlation analysis of wavelet-decomposed density fields. Our approach is analogous to the one presented in Einasto et al. (2011) with the exception that here instead of over-densities we focus on under-dense regions. In the following, we present our results only for the model M256 since the other ones lead to very similar results. We consider six wavelet levels: w1, w2, ..., w6 with the effective smoothing scales of 4, 8, ..., 128 h-1Mpc, respectively, and use the simulated density fields at five different redshifts z = 30, 10, 5, 1, 0.
Quite generally, one can choose two redshifts, zi and zj, along with two wavelet levels, wm and wn, and calculate the correlators 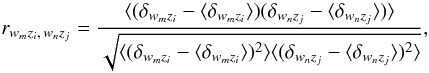 (1)where δwmzi corresponds to the wavelet-decomposed density field for level wm at redshift zi. The angle brackets represent an ensemble average, which under the ergodicity assumption is replaced by a simple spatial average. We note that we calculate the correlators for zero lag only, i.e. we do not shift one field with respect to the other.
(1)where δwmzi corresponds to the wavelet-decomposed density field for level wm at redshift zi. The angle brackets represent an ensemble average, which under the ergodicity assumption is replaced by a simple spatial average. We note that we calculate the correlators for zero lag only, i.e. we do not shift one field with respect to the other.
 |
Fig. 8 The behaviour of the correlation coefficient for different redshift pairs (zi,zj) ∈ { (30,10);(30,5);(30,1);(30,0) } for all the six wavelet levels. The solid and dashed lines correspond to the under- and overdensities, respectively (10% of the most under/over-dense cells). We see that for the largest smoothing scale, i.e. w6, all the correlators stay quite close to r = 1, while later on, as the other redshift decreases below z = 30, the lines start to deviate from r = 1. Thus, on the largest scales the information is approximately preserved, while on the smallest scales the information gets gradually erased. |
In what follows, the above correlators are not calculated for the full density fields, but instead masks are applied to separate under-dense void regions. If two wavelet fields δwmzi and δwnzj are correlated then the mask is always defined with the field that has larger smoothing scale, e.g., the field δwmzi if wm ≥ wn. The masking level is taken such that only 10% of the most under-dense cells end up inside the mask.
In the following, we use two types of correlators:
- 1.
fixed wavelet scale correlators, i.e. wm = wn, at different redshifts;
- 2.
correlators at fixed redshifts, i.e. zi = zj, for different wavelet levels.
In Fig. 9, we plot the correlators at fixed redshifts zi = zj = 30,10,5,1,0 from top to bottom (from light to dark blue). For m = 1, the curves are peaked at n = 1, while their amplitude decrease gradually as n increases to higher values. Similarly, the curves for m = 2 are peaked at n = 2, and decrease in amplitude as one moves to neighbouring wavelet levels. For the other n values, the behaviour is very similar. As long as the evolution proceeds in a linear manner, i.e. the growth depends only on redshift, but is independent of the wavelet scale, the coupling kernels plotted in Fig. 9 should stay exactly the same. However, we see that the lower the output redshift, the narrower the coupling kernels, i.e. a nonlinear evolution in under-dense regions leads to the additional decoupling of the nearby wavelet modes.
 |
Fig. 9 Correlators at fixed redshifts zi = zj = 30,10,5,1,0 from top to bottom (from light to dark blue) for the under-dense regions. For wm = 1, the curves are peaked at wn = 1, while they drop gradually as wn is increased to higher values. Similarly, the curves for wm = 2 are peaked at wn = 2, and get reduced as the distance increases from this point. For the other wm and wn values, the behaviour is very similar. We see that the lower the output redshift, the narrower the coupling kernels, i.e. a nonlinear evolution in under-dense regions leads to additional decoupling of nearby wavelet modes. |
The corresponding figure for the over-densities was given in Einasto et al. (2011, see Fig. 7 there). The main difference between Fig. 7 by Einasto et al. (2011) and Fig. 9 is that in the case of over-densities the coupling kernels become broader because of nonlinear evolution, i.e. instead of desynchronisation we have increasing synchronisation of over-densities of different wavelet levels.
 |
Fig. 10 The cumulative mass functions of the AHF haloes of models of the L100 series with various cutoff scales. The upper, middle, and lower panels are for the redshifts z = 0, 2, 5, respectively. |
It is important to realise that even with only the linear evolution of the Gaussian density field the nearby wavelet levels at fixed redshift get significantly coupled, since the neighbouring levels tend to contain some of the common Fourier space modes. However, assuming only linear evolution it is clear that the coupling does not change with redshift.
 |
Fig. 11 The left panels show the numbers of voids, defined by the AHF haloes for various threshold masses and models, as shown in Fig. 10. The right panels show the mean radii of voids, defined by the AHF haloes for different threshold masses, Mth, and for various cut-off scales. The upper, middle, and lower panels are for the redshifts z = 0, 2, 5, respectively. |
5. The structure of voids
Cosmic voids are defined by objects surrounding them – galaxies and clusters of galaxies of various luminosity (mass). In the case of models, it is customary to use dark matter haloes instead of galaxies or clusters. To investigate the influence of density perturbations of various scale on the void structure, we shall use our models of the L100 series which have the highest resolution in mass and scale. To find haloes, we applied the Amiga halo finder by Knollmann & Knebe (2009). We characterise the web and void structure by the dependence of the halo mass function on the scale of density perturbations for various epochs, and by the number and radii of voids defined by haloes of various mass. Our results are shown in Figs. 10 and 11.
Figure 10 shows the cumulative mass functions of the AHF haloes for all models of the L100 series, for three epochs, z = 0, 2, 5. We see that in the models where the large-scale waves have been cut off, maximum haloes have much lower masses than in the full models. This effect can also be seen in Fig. 3. The differences between the models with various cutoff scales increase with time: at early epochs, halo masses are lower and time is needed for most massive haloes to grow.
To find voids, we used a simple void finder proposed by Einasto et al. (1989). For each vertex of the simulation grid, we first calculated its distance to the nearest AHF halo. The maxima of the void distance matrix correspond to the centres of voids, and their values are the void radii. The distribution of the AHF haloes is noisy, thus there are many nearby local maxima in the distance matrix. We define the position of the void centre as the location of the cell, which has the largest distance to a halo within a box of the size of ± 3 grid elements.
The left panels in Fig. 11 show the number of voids found for various AHF halo mass thresholds, which correspond to systems of galaxies of different mass. The right panels of the figure show mean radii of voids as a function of the AHF halo mass threshold. The void numbers and radii characterise the hierarchy of voids. We see that as the threshold halo mass used in the void search increases, the number of voids continuously decreases, and the void radii increase. This means that some filaments are fainter than the respective mass threshold limit, and do not contribute to the void definition. Both parameters also depend strongly on the highest density perturbations used in the models. Models cut at larger scales have more voids, but their radii are smaller. This effect can be clearly seen at all simulation epochs.
In the models L100.100 and L100.032, the dependence of the number of voids and their mean radii is a more-or-less continuous function of the halo threshold mass. In contrast, in the strongly cut models L100.016 and L100.008, at higher mass thresholds, the number of voids decreases very rapidly and void radii also increase more rapidly than in the models L100.100 and L100.032. This effect is due to the very sharp decrease in the number of haloes of high mass (see Fig. 10). These rare haloes define very large voids. The sizes of these voids are not characteristic of the overall cosmic web pattern of the particular model.
The simulation box used in the present void structure study has the size L = 100 h-1Mpc, thus very large perturbations responsible for the formation of rich superclusters are absent in the model. For this reason, the largest voids for the highest halo mass thresholds have radii ≃ 10 h-1Mpc. As shown by Suhhonenko et al. (2011), in models with cube sizes L = 265 and L = 768 h-1Mpc the maximum void radii are much larger (see Fig. 6 by Suhhonenko et al. 2011). This comparison shows that large-scale density perturbations are needed to form voids defined by superclusters.
6. Discussion
According to the current cosmological paradigm, the cosmic web with systems of galaxies of various scale and mass, from clusters to filaments and superclusters, and voids between them, is formed from tiny density perturbations during the very early stage of the evolution of the Universe. For the formation of the web and of voids between various objects of the web, the presence of a continuous spectrum of density perturbations of various scales is essential. The power spectrum of density perturbations has the highest power on small scales. Thus, the influence of small-scale perturbations relative to large-scale perturbations is strongest in the early period of structure evolution. Small-scale systems, i.e. small haloes in simulations and dwarf galaxies in the real world are the earliest compact objects to form. As shown by Suhhonenko et al. (2011), and confirmed in the present study, small-scale haloes form at early epochs everywhere. The wavelet analysis done by Einasto et al. (2011) shows that wavelets w1 at redshift z = 30 are almost identical in models L256.256 and L256.008 (see Fig. 8 there). The present study shows that this is also the case for the wavelets w1 of the models L100.100 and L100.008 at the epoch z = 10 (see Fig. 4).
Further evolution of the web depends on the presence of density perturbations on larger scales. In models where medium-scale density perturbations are absent, no systems of filaments and voids form (Suhhonenko et al. 2011). In models with density perturbation spectra cut on large scales, the cosmic web with filaments and voids has a characteristic scale of the largest scale present in the density perturbation field. The main quantitative characteristics of the web – the masses of haloes, the number and sizes of voids defined by haloes of various mass – depend on the largest scale perturbations present.
In the models with strongly cut power spectra (λcut ≤ 16 h-1Mpc), the maximum masses of haloes are lower than in the models with a full power spectrum. Their number is larger, but they define a cellular cosmic web with smaller mean void sizes (see Fig. 11). With the increase of the cut-off wavelength λcut, the maximum masses of haloes increase, and they define a cellular web with larger cells but fewer voids.
The wavelet analysis described in previous Sections shows a very important property of the evolution of density waves with time: the synchronisation of the phases of density waves on various scales. Einasto et al. (2011) discussed this property of the evolution of over-density features – clusters and superclusters of galaxies in numerical simulations. In the present paper, we have followed the evolution of both over- and under-density regions. The analogy in the evolution of over- and under-density regions is expected, since in the early linear stage of the evolution of structure positive and negative parts of density waves were similar and symmetrical.
The wavelet analysis leads us to the conclusion that the properties of the large-scale cosmic web with filaments and voids depend on two connected properties of the evolution of density perturbations. The first property is the synchronisation of density waves of medium and large scales. Due to the synchronisation of density waves of different scales, positive amplitude regions of density waves add together to form rich systems of galaxies, and negative amplitude regions of density waves add together to decrease the mean overall density in voids. The amplification of density perturbations is another property of density evolution. Due to the addition of negative amplitudes of medium and large scale perturbations, there is no possibility for the growth of the initial small-scale positive density peaks in void regions. For this reason, small-scale protohaloes dissolve there. In the absence of medium and large-scale density perturbations, these peaks would contract to form haloes, which would also fill the void regions, i.e. there would be no void phenomenon as observed.
Simulations with truncated power spectra were performed by Little et al. (1991) and Einasto & Gramann (1993). Little et al. (1991) used three-dimensional simulations of resolution 1283 with power spectra in the form P(k) ~ k-1 for k ≤ kc and P(k) = 0 for k > kc, i.e. the spectra were cut at small scales, in contrast to our study here. The cuts were scaled so that k = 1 represents the fundamental mode of the simulation box of the size L = 64 h-1Mpc. The authors used the cuts: k = 2, 4, 8, 16, 32, 64. The main result of the study was that the structure of the cosmic web depends on density perturbations of larger scale than the cut-off scale, in accordance with our results. Einasto & Gramann (1993) made a two-dimensional simulation of the resolution 5122 with the full power spectrum, and a power spectrum cut at the scale λt = L/4, where L is the size of the simulation box. The fine structure of filaments in both models was rather similar, only the location and strength of filaments was slightly different. This result is also in agreement with our present findings.
As the analysis shows, the phase synchronisation of both positive and negative sections of density waves is stronger for density waves of larger scales, λ ≥ 32 h-1Mpc. Scales larger than the sound horizon at recombination, ≈ 146 Mpc according to the most recent cosmological data by Jarosik et al. (2010), were outside the horizon most of the time. This scale, 105 h-1Mpc for the presently accepted Hubble constant h = 0.72, is surprisingly close to the characteristic scale of the supercluster-void network (Einasto et al. 1997a, 2001). The skeleton of the supercluster-void network was created during the very early post-inflation stage of the evolution of the Universe (Kofman & Shandarin 1988). This result is also true for large voids between superclusters of galaxies – the seeds for these supervoids were created in the very early Universe.
7. Conclusions
Our present study of the evolution of density perturbations of various scales has led to the following conclusions:
-
The formation of the cosmic web with filaments and voids is due to the synchronisation of density waves of medium and large scales, and the amplification of both over- and under-dense regions.
-
Voids are regions in space where medium- and large-scale density waves combine in similar under-density phases.
-
Owing to phase synchronisation, the mean density of matter in void regions is below the mean density, thus initial small-scale perturbations cannot grow.
Acknowledgments
We thank the referee for constructive suggestions. Our special thanks go to Rien van de Weygaert and other participants of the workshop “Cosmic Web Morphology and Topology”, held in Warsaw 12–17 July 2011, for a detailed discussion of void structure problems. The present study was supported by the Estonian Science Foundation grants Nos. 7146 and 8005, and by the Estonian Ministry for Education and Science grant SF0060067s08. It has also been supported by ICRAnet through a professorship for Jaan Einasto, and by the University of Valencia (Vicerrectorado de Investigación) through a visiting professorship for Enn Saar and by the Spanish MEC projects “ALHAMBRA” (AYA2006-14056) and “PAU” (CSD2007-00060), including FEDER contributions. J.E., I.S., and E.T. thank Leibniz-Institut für Astrophysik Potsdam (using DFG-grant Mu 1020/15-1), where part of this study was performed. J.E. also thanks the Aspen Center for Physics and the Johns Hopkins University for hospitality where this project was started and continued. In plotting of density fields and wavelets, we used the SAOImage DS9 program. A.A.S. acknowledges the RESCEU hospitality as a visiting professor. He was also partially supported by the Russian Foundation for Basic Research grant No. 11-02-00643 and by the Scientific Programme “Astronomy” of the Russian Academy of Sciences.
References
- Aragón-Calvo, M. A., Jones, B. J. T., van de Weygaert, R., & van der Hulst, J. M. 2007, A&A, 474, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aragon-Calvo, M. A., van de Weygaert, R., Araya-Melo, P. A., Platen, E., & Szalay, A. S. 2010a, MNRAS, 404, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Aragón-Calvo, M. A., van de Weygaert, R., & Jones, B. J. T. 2010b, MNRAS, 408, 2163 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S. V. W., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., & Weinberg, D. H. 2002, ApJ, 575, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Bertschinger, E. 1987, ApJ, 323, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Bertschinger, E. 1995 [arXiv:astro-ph/9506070] [Google Scholar]
- Bond, J. R., Kofman, L., & Pogosyan, D. 1996, Nature, 380, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, N. A., Strauss, M. A., & Cen, R. 2010a, MNRAS, 406, 1609 [NASA ADS] [Google Scholar]
- Bond, N. A., Strauss, M. A., & Cen, R. 2010b, MNRAS, 409, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Coil, A. L., White, M., et al. 2005, ApJ, 635, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Wechsler, R. H., & Kravtsov, A. V. 2006, ApJ, 647, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Colless, M., Gaztañaga, E., et al. 2004, MNRAS, 352, 828 [NASA ADS] [CrossRef] [Google Scholar]
- de Lapparent, V., Geller, M. J., & Huchra, J. P. 1986, ApJ, 302, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshkevich, A. G., Kotok, E. V., Poliudov, A. N., et al. 1980, MNRAS, 192, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., da Costa, L. N., Goldwirth, D. S., Lecar, M., & Piran, T. 1993, ApJ, 410, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., & Gramann, M. 1993, ApJ, 407, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Jõeveer, M., & Saar, E. 1980, MNRAS, 193, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Einasto, M., & Gramann, M. 1989, MNRAS, 238, 155 [NASA ADS] [Google Scholar]
- Einasto, J., Saar, E., Einasto, M., Freudling, W., & Gramann, M. 1994a, ApJ, 429, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Einasto, J., Tago, E., Dalton, G. B., & Andernach, H. 1994b, MNRAS, 269, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Einasto, M., Gottloeber, S., et al. 1997a, Nature, 385, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Tago, E., Jaaniste, J., Einasto, J., & Andernach, H. 1997b, A&AS, 123, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Einasto, J., Tago, E., Müller, V., & Andernach, H. 2001, AJ, 122, 2222 [CrossRef] [Google Scholar]
- Einasto, J., Hütsi, G., Saar, E., et al. 2011, A&A, 531, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fillmore, J. A., & Goldreich, P. 1984, ApJ, 281, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Forero-Romero, J. E., Hoffman, Y., Gottlöber, S., Klypin, A., & Yepes, G. 2009, MNRAS, 396, 1815 [NASA ADS] [CrossRef] [Google Scholar]
- Furlanetto, S. R., & Piran, T. 2006, MNRAS, 366, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, M. J., & Huchra, J. P. 1989, Science, 246, 897 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldberg, D. M., & Vogeley, M. S. 2004, ApJ, 605, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, D. M., Jones, T. D., Hoyle, F., et al. 2005, ApJ, 621, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlöber, S., Łokas, E. L., Klypin, A., & Hoffman, Y. 2003, MNRAS, 344, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., & Geller, M. J. 1999, AJ, 118, 2561 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, O., Porciani, C., Carollo, C. M., & Dekel, A. 2007, MNRAS, 375, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, M., & Gottlöber, S. 2010, Adv. Astron., 2010 [Google Scholar]
- Hoeft, M., Yepes, G., Gottlöber, S., & Springel, V. 2006, MNRAS, 371, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, Y., & Shaham, J. 1982, ApJ, 262, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, G. L., Salpeter, E. E., & Wasserman, I. 1983, ApJ, 268, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Vogeley, M. S. 2004, ApJ, 607, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Icke, V. 1984, MNRAS, 206, 1P [NASA ADS] [CrossRef] [Google Scholar]
- Ishiyama, T., Makino, J., Portegies Zwart, S., et al. 2011, ApJ, submitted [arXiv:1101.2020] [Google Scholar]
- Jarosik, N., Bennett, C. L., Dunkley, J., et al. 2011, ApJS, 192, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, B. J. T., van de Weygaert, R., & Aragón-Calvo, M. A. 2010, MNRAS, 408, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Jõeveer, M., & Einasto, J. 1978, in Large Scale Structures in the Universe, ed. M. S. Longair, & J. Einasto, IAU Symp., 79, 241 [Google Scholar]
- Jõeveer, M., Einasto, J., & Tago, E. 1978, MNRAS, 185, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., Sharina, M. E., et al. 2003, A&A, 398, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [Google Scholar]
- Karachentsev, I. D., Karachentseva, V., Huchtmeier, W., et al. 2007 [arXiv:astro-ph/0710.0520] [Google Scholar]
- Kirshner, R. P., Oemler, Jr., A., Schechter, P. L., & Shectman, S. A. 1981, ApJ, 248, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Kirshner, R. P., Oemler, Jr., A., Schechter, P. L., & Shectman, S. A. 1987, ApJ, 314, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A. A., & Shandarin, S. F. 1983, MNRAS, 204, 891 [NASA ADS] [Google Scholar]
- Knebe, A., Green, A., & Binney, J. 2001, MNRAS, 325, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Knollmann, S. R., & Knebe, A. 2009, ApJS, 182, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Kofman, L. A., & Shandarin, S. F. 1988, Nature, 334, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Berlind, A. A., Wechsler, R. H., et al. 2004, ApJ, 609, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Peebles, P. J. E., van Gorkom, J. H., van de Weygaert, R., & van der Hulst, J. M. 2011a, AJ, 141, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Platen, E., Aragón-Calvo, M. A., et al. 2011b, AJ, 141, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Lindner, U., Einasto, J., Einasto, M., et al. 1995, A&A, 301, 329 [NASA ADS] [Google Scholar]
- Little, B., Weinberg, D. H., & Park, C. 1991, MNRAS, 253, 295 [NASA ADS] [Google Scholar]
- Longair, M. S., & Einasto, J. 1978, The large scale structure of the universe, Proceedings of the Symposium, Tallinn, Estonian SSR, September 12–16, IAU Symp., 79, 1977 [Google Scholar]
- Martel, H., & Wasserman, I. 1990, ApJ, 348, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez, V. J., & Saar, E. 2002, Statistics of the Galaxy Distribution (Chapman & Hall/CRC) [Google Scholar]
- Melott, A. L., Einasto, J., Saar, E., et al. 1983, Phys. Rev. Lett., 51, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, V., Arbabi-Bidgoli, S., Einasto, J., & Tucker, D. 2000, MNRAS, 318, 280 [Google Scholar]
- Oort, J. H. 1983, ARA&A, 21, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, N., White, M., Norberg, P., & Porciani, C. 2009, MNRAS, 397, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- Patiri, S. G., Betancort-Rijo, J. E., Prada, F., Klypin, A., & Gottlöber, S. 2006, MNRAS, 369, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1971, Physical cosmology, Princeton Series in Physics (Princeton, N.J.: Princeton University Press) [Google Scholar]
- Peebles, P. J. E. 1982, ApJ, 257, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 2001, ApJ, 557, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Regos, E., & Geller, M. J. 1989, AJ, 98, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas, R. R., Vogeley, M. S., Hoyle, F., & Brinkmann, J. 2004, ApJ, 617, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Sahni, V., Sathyaprakah, B. S., & Shandarin, S. F. 1994, ApJ, 431, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U. 2000, MNRAS, 318, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U., Makarov, A., McDonald, P., et al. 2005, Phys. Rev. D, 71, 103515 [NASA ADS] [CrossRef] [Google Scholar]
- Shandarin, S. F. 2011, J. Cosmol. Astropart. Phys., Issue 05, 015 [Google Scholar]
- Sheth, R. K., & van de Weygaert, R. 2004, MNRAS, 350, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T., Pichon, C., Colombi, S., Novikov, D., & Pogosyan, D. 2008, MNRAS, 383, 1655 [Google Scholar]
- Sousbie, T., Colombi, S., & Pichon, C. 2009, MNRAS, 393, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New A, 6, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Stanonik, K., Platen, E., Aragón-Calvo, M. A., et al. 2009, ApJ, 696, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Starck, J., & Murtagh, F. 2002, Astronomical image and data analysis, ed. J.-L. Starck, & F. Murtagh [Google Scholar]
- Starck, J., Murtagh, F. D., & Bijaoui, A. 1998, Image Processing and Data Analysis, ed. J.-L. Starck, F. D. Murtagh, & A. Bijaoui [Google Scholar]
- Suhhonenko, I., Einasto, J., Liivamägi, L. J., et al. 2011, A&A, 531, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szomoru, A., van Gorkom, J. H., Gregg, M. D., & Strauss, M. A. 1996, AJ, 111, 2150 [NASA ADS] [CrossRef] [Google Scholar]
- Tarenghi, M., Tifft, W. G., Chincarini, G., Rood, H. J., & Thompson, L. A. 1978, in Large Scale Structures in the Universe, ed. M. S. Longair, & J. Einasto, IAU Symp., 79, 263 [Google Scholar]
- Tegmark, M., Strauss, M. A., Blanton, M. R., et al. 2004, Phys. Rev. D, 69, 103501 [CrossRef] [Google Scholar]
- Tegmark, M., Eisenstein, D. J., Strauss, M. A., et al. 2006, Phys. Rev. D, 74, 123507 [Google Scholar]
- Tifft, W. G., & Gregory, S. A. 1978, in Large Scale Structures in the Universe, ed. M. S. Longair, & J. Einasto, IAU Symp., 79, 267 [Google Scholar]
- Tikhonov, A. V., & Klypin, A. 2009, MNRAS, 395, 1915 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tinker, J. L., Weinberg, D. H., & Warren, M. S. 2006, ApJ, 647, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Norberg, P., Weinberg, D. H., & Warren, M. S. 2007, ApJ, 659, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008a, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Conroy, C., Norberg, P., et al. 2008b, ApJ, 686, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1978, in Large Scale Structures in the Universe, ed. M. S. Longair, & J. Einasto, IAU Symp., 79, 214 [Google Scholar]
- van de Weygaert, R., & Platen, E. 2009 [arXiv:0912.2997] [Google Scholar]
- van de Weygaert, R., & van Kampen, E. 1993, MNRAS, 263, 481 [NASA ADS] [Google Scholar]
- van de Weygaert, R., Aragon-Calvo, M. A., Jones, B. J. T., & Platen, E. 2009 [arXiv:0912.3448] [Google Scholar]
- van de Weygaert, R., Kreckel, K., Platen, E., et al. 2011 [arXiv:1101.4187] [Google Scholar]
- van den Bosch, F. C., Yang, X., Mo, H. J., et al. 2007, MNRAS, 376, 841 [NASA ADS] [CrossRef] [Google Scholar]
- von Benda-Beckmann, A. M., & Müller, V. 2008, MNRAS, 384, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- White, M., Zheng, Z., Brown, M. J. I., Dey, A., & Jannuzi, B. T. 2007, ApJ, 655, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Weinberg, D. H., Zheng, Z., et al. 2004, ApJ, 608, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2005, ApJ, 630, 1 [Google Scholar]
- Zeldovich, Y. B. 1970, A&A, 5, 84 [NASA ADS] [Google Scholar]
- Zeldovich, Y. B. 1978, in Large Scale Structures in the Universe, ed. M. S. Longair, & J. Einasto, IAU Symp., 79, 409 [Google Scholar]
- Zeldovich, Y. B., Einasto, J., & Shandarin, S. F. 1982, Nature, 300, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Berlind, A. A., Weinberg, D. H., et al. 2005, ApJ, 633, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Coil, A. L., & Zehavi, I. 2007, ApJ, 667, 760 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Density field and wavelets
A.1. Density field
For each particle, we calculated the global density at the location of the particle. For this purpose, we first found the high-resolution density field, using a B3 spline ![\appendix \setcounter{section}{1} \begin{equation} B_3(x)=\frac1{12}\left[|x-2|^3-4|x-1|^3+6|x|^3-4|x+1|^3+|x+2|^3\right]; \end{equation}](/articles/aa/full_html/2011/10/aa17248-11/aa17248-11-eq162.png) (A.1)this function differs from zero only in the interval x ∈ [− 2,2 ] . The one-dimensional B3 box spline kernel of width h = N is
(A.1)this function differs from zero only in the interval x ∈ [− 2,2 ] . The one-dimensional B3 box spline kernel of width h = N is 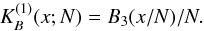 (A.2)This kernel preserves the interpolation property (mass conservation) for all kernel widths that are integer multiples of the grid step, h = N. The 3-D
(A.2)This kernel preserves the interpolation property (mass conservation) for all kernel widths that are integer multiples of the grid step, h = N. The 3-D 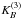 box spline kernel we use is given by the direct product of the three one-dimensional kernels
box spline kernel we use is given by the direct product of the three one-dimensional kernels 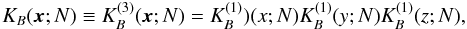 (A.3)where x ≡ { x,y,z } . To calculate the high-resolution density field, we use the kernel of scale, equal to the cell size of the particular simulation.
(A.3)where x ≡ { x,y,z } . To calculate the high-resolution density field, we use the kernel of scale, equal to the cell size of the particular simulation.
A.2. Wavelets
We use the à trous wavelet transform (for details see Starck et al. 1998; Starck & Murtagh 2002). The field is decomposed into several frequency bands as follows. The high-resolution (zero level) density field was calculated with the B3 spline kernel with width equal to the size of one cell of the field, every subsequent field being calculated with a kernel twice as wide. Wavelets were found by subtracting higher level density fields from the previous level fields. In such a way, each wavelet band contains waves twice the scale of the previous band, in the range 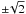 centered on the mean (central) scale. The sum of these bands restores the original density field.
centered on the mean (central) scale. The sum of these bands restores the original density field.
The “à trous algorithm” wavelet transform decomposes an n × n × n data set D as a superposition of the form  (A.4)where DJ is a J times smoothed version of the original data D, and wj represents the structure of D at scale 2j. The wavelet decomposition output consists of J three-dimensional mother fields Dj and wavelets wj of size n × n × n. Following the traditional indexing convention, we mark the mother fields and wavelets of the finest scale with the index j = 1. The smoothed version of the original data, DJ = D0, is the density field found with the kernel of the scale, equal to the cell size of the simulation L/Ngrid.
(A.4)where DJ is a J times smoothed version of the original data D, and wj represents the structure of D at scale 2j. The wavelet decomposition output consists of J three-dimensional mother fields Dj and wavelets wj of size n × n × n. Following the traditional indexing convention, we mark the mother fields and wavelets of the finest scale with the index j = 1. The smoothed version of the original data, DJ = D0, is the density field found with the kernel of the scale, equal to the cell size of the simulation L/Ngrid.
The wavelets can be found in a recursive manner, but we also needed to evaluate the partial density fields (mother fields of different order) for our analysis. Thus, we found the mother fields Dj first by convolving the field Dj − 1 by the B3 kernel of twice the scale used for calculating the field Dj − 1. We then found the wavelets of index j by subtracting the mother density fields  (A.5)In this construction, a wavelet of index j describes density waves between the scales Δj − 1 = lc × 2j − 1/2 and Δj = lc × 2j + 1/2. The scales are the diameters of kernels used in calculating of the density fields Dj − 1 and Dj.
(A.5)In this construction, a wavelet of index j describes density waves between the scales Δj − 1 = lc × 2j − 1/2 and Δj = lc × 2j + 1/2. The scales are the diameters of kernels used in calculating of the density fields Dj − 1 and Dj.
All Tables
All Figures
 |
Fig. 1 The left and right panels show the power spectra for the models of the series L256 at the epochs z = 30 and z = 0, respectively. |
| In the text | |
 |
Fig. 2 The high-resolution density fields of the model M256.256 are shown in the left column, at the k = 140 coordinate. The second, third, and fourth columns show the wavelet w5, w4, and w3 decompositions at the same k, respectively. The upper row gives data for the present epoch, z = 0, the second row for the redshift z = 1, the third row for the redshift z = 5, and the last row for the redshift z = 10. Densities are expressed on a linear scale. In wavelet panels, green and red colours show the positive regions of wavelets, and the blue colour shows negative (under-density) wavelet regions. Colour codes are plotted at the bottom of the figure for wavelet w3 at epoch z = 10. |
| In the text | |
 |
Fig. 3 Zoom-ins to the high-resolution density fields of the models L100.100 and L100.016, left and right columns, respectively. Zoom factor is 2, central 50 × 50 h-1Mpc (256 × 256 pixels) of all models are shown. Upper panels are for the present epoch z = 0, lower panels for the epoch z = 2. All panels are at the k = 51 coordinate. Cross sections (beams) at coordinates j = 222 and k = 51 for both models are shown in Fig. 5 for three redshifts to see the evolution of the density field and its wavelets. In the upper left corner of the figure there is a rich supercluster in the model L100.100, absent in the model L100.016. Both models have at the right edge of the figure a rich cluster. This cluster is well seen in Fig. 5 at i = 390 coordinate. Densities are expressed in the logarithmic scale, identical lower and upper limits for plotting with the SAO DS9 package are used. The border between the light blue and the dark green colours corresponds to the critical density Dloc = 1.6, which separates low-density haloes and haloes collapsed during the Hubble time (Kaiser 1984; Bardeen et al. 1986). Note that in both models and simulation epochs the majority of filaments in voids have densities below the critical density. |
| In the text | |
 |
Fig. 4 Wavelets w1 of models L100.100 and L100.008 at redshift z = 10 are shown in the left and right panels, respectively, at coordinate k = 51. Densities are expressed on a linear scale, only over-density regions are shown. As in Fig. 3, the central 256 × 256 pixels of the full models are shown. The characteristic scale of density perturbations corresponding to this wavelet is 0.4 h-1Mpc. Note the weakening of peak densities of the model L100.100 in the region of future large under-dense region, seen in Fig. 3. |
| In the text | |
 |
Fig. 5 The evolution of the local density and wavelets of the models L100.100 (left panels) and L100.016 (right panels) in beams along the i-coordinate at j = 220, k = 51. The same k-coordinate was used in plotting the density field in Fig. 3. Data are shown for epochs z = 0, 2, 5. To see better details only the region 144 ≤ i ≤ 400 of length 50 h-1Mpc is shown. The characteristic scale of the wavelet w5 is 12.5 h-1Mpc. Wavelets are divided by the factor f ∝ (1 + z)-1. |
| In the text | |
 |
Fig. 6 The local density and wavelets of the models L256.256 (left panel) and L256.008 (right panel) in beams along the i − coordinate at j = 90, k = 105 at the early epoch, z = 30. To enhance details, only the region 100 ≤ i ≤ 250 of length 75 h-1Mpc is shown. The characteristic scale of the wavelet w5 is 32 h-1Mpc. |
| In the text | |
 |
Fig. 7 Left panel: the distribution of void particle local densities of the model L100.100 as a function of redshift. Right panel: the distributions of void particle local densities at the present epoch of the models of the series L100 with different cutoff wavelengths. |
| In the text | |
 |
Fig. 8 The behaviour of the correlation coefficient for different redshift pairs (zi,zj) ∈ { (30,10);(30,5);(30,1);(30,0) } for all the six wavelet levels. The solid and dashed lines correspond to the under- and overdensities, respectively (10% of the most under/over-dense cells). We see that for the largest smoothing scale, i.e. w6, all the correlators stay quite close to r = 1, while later on, as the other redshift decreases below z = 30, the lines start to deviate from r = 1. Thus, on the largest scales the information is approximately preserved, while on the smallest scales the information gets gradually erased. |
| In the text | |
 |
Fig. 9 Correlators at fixed redshifts zi = zj = 30,10,5,1,0 from top to bottom (from light to dark blue) for the under-dense regions. For wm = 1, the curves are peaked at wn = 1, while they drop gradually as wn is increased to higher values. Similarly, the curves for wm = 2 are peaked at wn = 2, and get reduced as the distance increases from this point. For the other wm and wn values, the behaviour is very similar. We see that the lower the output redshift, the narrower the coupling kernels, i.e. a nonlinear evolution in under-dense regions leads to additional decoupling of nearby wavelet modes. |
| In the text | |
 |
Fig. 10 The cumulative mass functions of the AHF haloes of models of the L100 series with various cutoff scales. The upper, middle, and lower panels are for the redshifts z = 0, 2, 5, respectively. |
| In the text | |
 |
Fig. 11 The left panels show the numbers of voids, defined by the AHF haloes for various threshold masses and models, as shown in Fig. 10. The right panels show the mean radii of voids, defined by the AHF haloes for different threshold masses, Mth, and for various cut-off scales. The upper, middle, and lower panels are for the redshifts z = 0, 2, 5, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


