| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116993 | |
| Published online | 12 August 2011 | |
The two components of the evolved massive binary LZ Cephei
Testing the effects of binarity on stellar evolution
1
Institut d’Astrophysique et de Géophysique, Université de Liège, Bât. B5C, Allée du 6 Août 17, 4000 Liège, Belgium
e-mail: mahy@astro.ulg.ac.be
2
LUPM–UMR 5299, CNRS & Université Montpellier II, Place Eugène Bataillon, 34095 Montpellier Cedex 05, France
3
IRAP–UMR 5277, CNRS & Univ. de Toulouse, 14 Av. E. Belin, 31400 Toulouse, France
4
LAM–UMR 6110, CNRS & Université de Provence, rue Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
5
NASA/GSFC, Code 665, Greenbelt, MD 20771, USA
Received: 31 March 2011
Accepted: 29 June 2011
Aims. We present an in-depth study of the two components of the binary system LZ Cep to constrain the effects of binarity on the evolution of massive stars.
Methods. We analyzed a set of high-resolution, high signal-to-noise ratio optical spectra obtained over the orbital period of the system to perform a spectroscopic disentangling and derive an orbital solution. We subsequently determine the stellar properties of each component by means of an analysis with the CMFGEN atmosphere code. Finally, with the derived stellar parameters, we model the Hipparcos photometric light curve using the program NIGHTFALL to obtain the orbit inclination and the stellar masses.
Results. LZ Cep is a O 9III+ON 9.7V binary. It is as a semi-detached system in which either the primary or the secondary star almost fills up its Roche lobe. The dynamical masses are about 16.0 M⊙ (primary) and 6.5 M⊙ (secondary). The latter is lower than the typical mass of late-type O stars. The secondary component is chemically more evolved than the primary (which barely shows any sign of CNO processing), with strong helium and nitrogen enhancements as well as carbon and oxygen depletions. These properties (surface abundances and mass) are typical of Wolf-Rayet stars, although the spectral type is ON 9.7V. The luminosity of the secondary is consistent with that of core He-burning objects. The preferred, tentative evolutionary scenario to explain the observed properties involves mass transfer from the secondary – which was initially more massive- towards the primary. The secondary is now almost a core He-burning object, probably with only a thin envelope of H-rich and CNO processed material. A very inefficient mass transfer is necessary to explain the chemical appearance of the primary. Alternative scenarios are discussed but they are affected by greater uncertainties.
Key words: stars: early-type / binaries: general / stars: fundamental parameters / stars: winds, outflows
© ESO, 2011
1. Introduction
The binary fraction of massive stars is not tightly constrained, but studies of young open clusters indicate that it can easily reach 60% (e.g. Sana et al. 2008). The effects of binarity on stellar evolution depend not only on the properties of the components, but also on the mass ratio, the separation, and the eccentricity. Consequently, their study is complex, requiring the exploration of a large parameter space (de Mink et al. 2011). In the case of young systems with large separations, the components of the binary evolve independently, following single-star evolution (Pavlovski & Hensberge 2005). In evolved binary systems, the evolutionary scheme is completely different. If Roche lobe overflow occurs, the surface chemistry and rotational rate of the components are deeply affected. In particular, the mass gainer is expected to show large nitrogen surface abundance enhancements (Langer et al. 2008). To more clearly understand the physics of binary systems and test the predictions of theoretical models, it is thus important to quantitatively analyze the properties of massive binary systems with well-constrained orbital parameters.
 |
Fig. 1 NARVAL spectra between 4450 and 4570 Å. The upper part of the figure presents the daily spectra. The lower two spectra are the results of the spectral disentangling process. The two vertical dash lines correspond to the rest wavelengths of the He i 4471 and He ii 4542 lines. |
LZ Cep (HD 209481) is a double-lined spectroscopic binary system composed of a primary component with a spectral type O 8.5III and an O 9.5V secondary (Conti & Alschuler 1971). The projected rotational velocities were reported to be close to 155 km s-1 and 105 km s-1 by Howarth et al. (1991). The period of the system was found to be 3.070508 d by Kameswara Rao (1972), a value that was confirmed by Howarth et al. (1991) and Harries et al. (1998). The eccentricity estimated by Howarth et al. (1991) is about 0.031. Although small, this is significant enough to not be neglected. According to Lucy & Sweeney (1971), the null hypothesis of a circular orbit can be rejected with a significance level of about 0.05. However Harries et al. (1998) determined an orbital eccentricity close to zero in their orbital solution (e = 0.017 ± 0.084), implying that the circularization of the system is not clearly established. From the photometric point of view, LZ Cep is not an eclipsing system but ellipsoidal variations are clearly visible in the light curve. The photometric analysis indicates that this binary is an evolved system (Hill et al. 1976) with a secondary component that fills up its Roche lobe. Hence, the system is most likely to be in a configuration of post case A mass transfer i.e., a system where the mass transfer happened while both components were still in a hydrogen-burning core phase (Howarth et al. 1991).
LZ Cep is thus a target of choice for the study of the effects of binary interactions and their impacts on massive star evolution. The present paper is organized as follows. Section 2 presents the journal of observations and the data-reduction technique. We then devote Sect. 3 to the determination of the orbital solution and the spectroscopic classification. Using the radial velocities obtained from the orbital solution, we apply a disentangling program to separate the individual spectra of both components. In Sect. 4, we apply the CMFGEN atmosphere code on the separated spectra to determine the main stellar and wind parameters as well as the surface abundances of each star. These parameters provide us with information about the stars’ evolutionary status. The last step in our investigation is reported in Sect. 5 and consists of the analysis of the Hipparcos light curve, which provides the system inclination and consequently the real masses of the stars. All the parameters and results determined in the present paper are discussed in Sect. 6. Finally, we present our conclusions in Sect. 7.
2. Observations and data reduction
LZ Cep was observed with the spectropolarimeter NARVAL mounted on the Télescope Bernard Lyot (TBL) located at the Pic du Midi observatory in the French Pyrenees. Table 1 gives the journal of observations. A total of ten spectra over a period of 14 d were obtained between 2009 July 20 and 2009 August 3 (Fig. 1). This corresponds to more than four orbital periods of the system. The signal-to-noise ratio (SNR) per 2.6 km s-1 velocity bin is between 300 and 1300 depending on weather conditions and wavelength. A spectral resolution of 65 000 is achieved. The data were automatically reduced with the Libre ESpRIT package (Donati et al. 1997) installed at TBL. An exhaustive description of the reduction procedure is given in Donati et al. (1997) and we refer to this paper for information.
Journal of the observations.
3. Disentangling and orbital solution
The previous analyses of Howarth et al. (1991) and Harries et al. (1998) focused on the orbital elements of the system. In the present paper, we go one stage further and study the properties of the individual components. The first step is to separate the spectra of each star. We applied an iterative disentangling method consisting of using alternatively the spectrum of one component (shifted by its radial velocity) and subtracting it from the observed spectra to determine the mean spectrum of the other component. The separated spectral components, corrected by the brightness ratio (see below), are shown in Fig. 1 (the two bottom spectra) for the range 4450–4570 Å and in Figs. 3 and 4 (black lines) for a wider spectral band. This disentangling method, inspired by González & Levato (2006), requires the approximative knowledge of the radial velocities as input. We first measured these radial velocities by fitting two Gaussian profiles to the observed spectra. The cross-correlation technique was subsequently used by the disentangling program to refine the radial velocities from the disentangled spectra. This method ensures that radial velocities are obtained at all orbital phases, including those where the lines are heavily blended. The cross-correlation masks were built on a common basis of the Si iv 4089–4116, He i 4388, 4471, 4713, 4921, 5015, 5876, 6678, C iv 5801–5812, O iii 5592, and Hα lines. For the primary component, we added the He ii 4200, 4542, 5412 lines indicating, by the way, its earlier spectral type (Conti & Alschuler 1971). The list of the radial velocities obtained by cross-correlation is reported in Table 1.
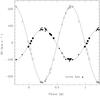 |
Fig. 2 Radial velocities as a function of orbital phase. The solid (open) symbols are for the primary (secondary). The circles are the data of the present paper, whilst the squares are the data of Harries et al. (1998). |
Orbital solution and stellar parameters.
We checked these radial velocities by computing the orbital solution of LZ Cep. For this purpose, we took into account the well-known period of the system (Porb = 3.070507 d, Petrie 1962) and used the Liège Orbital Solution Package (LOSP, Sana & Gosset, A&A, submitted). This software is based on the generalization of the SB1 method of Wolfe et al. (1967) to the SB2 case along the lines described in Rauw et al. (2000) and Sana et al. (2006a). We assigned a weight of 1.0 to all the measurements. Figure 2 represents the fitted radial velocity curves as a function of the phase. We added, for comparison, the radial velocities measured from the IUE spectra by Harries et al. (1998). To compare both datasets, it was necessary to shift the radial velocities of Harries et al. (1998) by − 9.4 km s-1 to obtain the same systemic velocity as that measured for our dataset. We represent these data by squares in Fig. 2. T0 is the phase of the conjunction with the primary star in front. We tried to include a non-zero eccentricity in the orbital solution but the fit residuals are smaller for a zero eccentricity, indicating that the system is circularized. Previous studies (Howarth et al. 1991; Harries et al. 1998) have shown that this system could be in a post case A mass transfer phase (see also Sect. 5). It is therefore likely that the tidal interactions have circularized that system. Other differences between our solution and that of Howarth et al. (1991) are notably a smaller value of K2, lower minimum masses, and a higher mass ratio. The orbital parameters are listed in the upper part of Table 2.
Finally, in the framework of the study of wind parameters (see Sect. 4), we also decided to separate the IUE spectra in the range 1200–1800 Å. We thus determined, from the orbital solution, the values of the radial velocities corresponding to the IUE spectra. We fixed these radial velocities in the disentangling program to obtain the resulting spectra shown in Fig. 5 (black line). Unfortunately, the disentangled spectrum recovered for the secondary is too noisy to help us constrain the wind parameters.
To pinpoint the nature of the components, we determined their spectral types. We measured the equivalent widths by fitting Gaussian functions to the line profiles. We did that for both the most deblended observed spectra and the disentangled spectra. The spectral-type determination is based on the quantitative classification criteria for O-type stars proposed by Conti & Alschuler (1971), Conti (1973), and Mathys (1988, 1989). We derived, from the ratios of the appropriate lines, the spectral classifications O 9III and ON 9.7V for the primary and the secondary star, respectively. The “N” classification of the secondary comes from the strength of the nitrogen lines – e.g. N ii 4037–41–43, N ii 4601–07–13 and N iii 4523–30–34. These results confirm the conclusion of Hilditch (1974), who reported that the secondary is of a different luminosity class than the primary component. Otherwise, the spectral types are slightly different from those quoted in the literature. Petrie (1962) quoted LZ Cep as a binary system composed of two O 9.5V stars, whilst Conti & Alschuler (1971) determined a spectral type O 8.5III for the primary and O 9.5V for the secondary component.
 |
Fig. 3 Best CMFGEN fit (red) of the disentangled optical spectrum (black) of the primary component of LZ Cep. No data are available in the immediate vicinity of He i 4921. |
In a second stage, we estimated the light ratio. For that purpose, we measured, for both stars, the equivalent widths of the He i 4026, 4143, 4388, 4471, 5876, He ii 4200, 4542, Si iv 4089, O iii 5592 lines and then computed the ratio of these lines and the corresponding theoretical average values reported in Conti & Alschuler (1971), Conti (1973) and Conti et al. (1977). Owing to the absence of O 9.7 stars in these three papers, we used an O 9.5 star as a reference for the secondary. We find that the primary star is about 1.85 times brighter than the secondary (l1/l2 = 1.85 ± 0.1). Alternatively we also measured the equivalent widths of the above-quoted lines in synthetic spectra computed with a similar effective temperature and log g to those of the primary and secondary components estimated (see Sect. 4). With these synthetic spectra, we obtained a light ratio of about l1/l2 = 1.91, which is consistent with our previous value (l1/l2 = 1.85 ± 0.1). Consequently, we adopt in the following a light ratio of about l1/l2 = 1.85 ± 0.1. Petrie (1962) reported a value of l2/l1 = 0.66 ± 0.1, which corresponds to l1/l2 = 1.52 ± 0.3 (the method they used is not however described). Another estimate was made by Harries et al. (1998). Although their method appears to be relevant, the result seems questionable, probably because of the confusion between the primary and secondary stars. The authors reported a value of about l1/l2 = 0.65 ± 0.1. However, when we compare the equivalent widths computed by Harries et al. (1998) with our measurements, no significant difference appears, indicating that the equivalent widths of the primary are larger than those measured for the secondary. We thus assume that the real determination of Harries et al. (1998) is l2/l1 = 0.65 ± 0.1, which corresponds to l1/l2 = 1.54 ± 0.3. Consequently, the discrepancy between our measurement and those of Harries et al. (1998) and Petrie (1962) is probably due to the sample of spectral lines that is larger in our analysis, leading to a more accurate determination of the light ratio1. As a comparison, if we use a smaller brightness ratio (l1/l2 ~ 1.54), we obtain absolute luminosities of log (L1/L⊙) = 5.08 and log (L2/L⊙) = 4.74. The effect on the determination of the abundances is however small and does not exceed the error bars quoted in Sect. 4.
Adopting our brightness ratio, we computed the luminosity of each component. The magnitude and color of the system are V = 5.55 and (B − V) = 0.06 (Maíz-Apellániz et al. 2004). The visual extinction directly follows from (B − V)0 = −0.27 (appropriate for late O stars, Martins & Plez 2006). With these photometric parameters and assuming a distance modulus for LZ Cep equal to 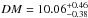 (Sota et al. 2011, and references therein), consistent with the value of 10.12 given by Petrie (1962), we found a visual absolute magnitude of the entire binary system to be equal to
(Sota et al. 2011, and references therein), consistent with the value of 10.12 given by Petrie (1962), we found a visual absolute magnitude of the entire binary system to be equal to 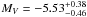 . We derived, by using the brightness ratio,
. We derived, by using the brightness ratio, 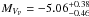 and
and 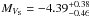 and with the bolometric corrections corresponding to the spectral types of both components (Martins & Plez 2006), we obtained absolute luminosities of
and with the bolometric corrections corresponding to the spectral types of both components (Martins & Plez 2006), we obtained absolute luminosities of 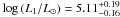 and
and 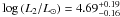 (more details about the method are given in Mahy et al. 2010). As a comparison, if we had taken into account a smaller brightness ratio (l1/l2 ~ 1.54), we would obtain absolute luminosities of log (L1/L⊙) = 5.08 and log (L2/L⊙) = 4.74. Accordingly, the brightness ratio computed in the present analysis does not significantly affect the determination of the results since these values remain within the measured error bars.
(more details about the method are given in Mahy et al. 2010). As a comparison, if we had taken into account a smaller brightness ratio (l1/l2 ~ 1.54), we would obtain absolute luminosities of log (L1/L⊙) = 5.08 and log (L2/L⊙) = 4.74. Accordingly, the brightness ratio computed in the present analysis does not significantly affect the determination of the results since these values remain within the measured error bars.
4. Spectroscopic analysis
The disentangled optical spectra of both components were each analyzed with the atmosphere code CMFGEN (Hillier & Miller 1998). The UV spectrum of the primary was also used. CMFGEN produces non-LTE models including the effects of winds and line-blanketing. The rate equations are solved iteratively together with the radiative transfer equation to provide the occupation numbers of energy levels and the radiation field. The computations are done in spherical geometry and in the co-moving frame. The temperature structure is a consequence of the radiative equilibrium condition. The velocity structure is an input of the calculation. In our case, we used TLUSTY hydrostatic structures in the photosphere connected to a β-velocity law for the wind part. The OSTAR2002 grid of TLUSTY models was used (Lanz & Hubeny 2003). The density structure directly follows from the mass-conservation equation. Once the atmosphere model is obtained, a formal solution of the radiative transfer equation is performed to yield the synthetic spectrum using an accurate line profile that accounts for both Stark broadening and a variable depth microturbulence. This last quantity varies from 10 km s-1 in the photosphere to 0.1 × v∞ in the outer atmosphere (v∞ being the terminal velocity). The spectrum is subsequently compared to the observational data to constrain the main parameters. In practice, we determine the following parameters:
-
the effective temperature Teff is determined from the ionization balance of He. The relative strength of He i and He ii directly depends on the temperature. We used He i 4471 and He ii 4542 as the main indicators. Other lines were also checked: He i 4026, He i 4389, He i 4713, He i 5876, He ii 4200, He ii 4686, and He ii 5412. An accuracy of ± 1000 K in the Teff determination was achieved;
-
gravity where a larger log g broadens the width of the Balmer lines wings. We thus used Hβ, Hγ, and Hδ as the main gravity diagnostics. The final log g are accurate to 0.1 dex;
-
luminosity: the knowledge of the effective temperature, the absolute V magnitude, and the extinction provides a direct estimate of the luminosity as described in Sect. 3. The uncertainty in the luminosity determination depends mainly in the uncertainty on the distance (see Sect. 3);
-
surface abundances, which were determined from the strength of the He, C, N, and O lines. The He lines of all ionization states are stronger when the helium content is higher. This effect is different from a change in Teff, which changes the relative strengths of lines from successive ionization states. We thus used the same lines as for the effective temperature determination to constrain the He content. For nitrogen, we mainly relied on several N ii lines between 4000 Å and 4700 Å, as well as the N iii lines in the 4500–4520 Å range. The main carbon indicators were the C iii lines around 4070 Å and C iii 5696 Å. For oxygen, we relied on the numerous O ii lines between 4000 and 4600 Å, as well as on O iii 5592 Å. The typical uncertainty in the CNO surface abundance is 50%. To estimate these uncertainties, we ran models with element abundances across a range of values both lower and higher than the preferred value and compared the corresponding spectra to the observed line profiles. When a clear discrepancy was seen between the model and data for all lines of the same element, we adopted the corresponding abundance as the maximum/minimum value of the possible chemical composition. An illustration is shown in Fig. 6. As a test, we conducted the same analysis for the primary with four additional sets of models with the following sets of parameters: Teff = 31 000 K and log g = 3.5; Teff = 33 000 K and log g = 3.5; Teff = 32 000 K and log g = 3.4; Teff = 32 000 K and log g = 3.6. We then estimated the best N/H abundance for each set of models (including also the best-fit combination, Teff = 32 000 K and log g = 3.5) by means of a chi-square method. We then computed the average and 1-σ dispersion of this set of five N/H values and found N/H = 8.5 ± 0.18 × 10-5. This is perfectly consistent with the value we estimate from Fig. 6. For the other elements and the secondary, we thus proceeded as described above, running models with various abundances for the best-fit model parameters (Teff, log g);
-
mass-loss rate: we used the UV resonance lines of the primary to estimate Ṁ. The C iv 1538–1545 and N v 1240 were the main diagnostics. The uncertainty in Ṁ is 0.1 dex. For the secondary, the UV spectrum was not good enough to allow this determination but to compute the atmosphere model associated with this star, we took a Ṁ = 3 × 10-8 M⊙ yr-1. We also used homogeneous models (i.e. no clumping was included), which provided a good fit to the UV lines. As a consequence, our determination should be seen as an upper limit. We also included X-ray emission so as to have a canonical value of
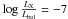 (Sana et al. 2006b). This turned out to be a crucial step in reproducing the N v 1240 profile;
(Sana et al. 2006b). This turned out to be a crucial step in reproducing the N v 1240 profile; -
terminal velocity: the blueward extension of the P-Cygni profiles of the primary UV spectrum are directly related to v∞. We thus used them to estimate this parameter, where v∞ is derived to within 100 km s-1;
-
rotational and macroturbulent velocity: we used the Fourier transform formalism (Simón-Díaz & Herrero 2007) to derive the projected rotational velocity (V sin i). The macroturbulent velocity was obtained by convolving the theoretical line profiles with a Gaussian profile in attempt to reproduce the shape of He i 4713.
The best-fits models of both components are shown in Figs. 3 and 4. The fit of the UV spectrum of the primary is shown in Fig. 5. The derived parameters are gathered in Table 2 (bottom part). The quality of the fit is on average very good. Only a few features are not reproduced. This is the case of the Si iii lines around 4550 Å. Increasing Teff leads to a better fit, but in that case the other diagnostics are less well reproduced. This problem is frequently observed in our models, and the origin is not known at present. Hence, we decided not to rely on these lines in the present study.
 |
Fig. 4 Same as for Fig. 3 but for the secondary component of LZ Cep. No data are available in the immediate vicinity of He i 4921. |
5. Light curve
To more clearly understand the binary system LZ Cep and, in particular, its geometry, we also performed an analysis of the Hipparcos light curve. This investigation was made with the NIGHTFALL program2. This software is based on a generalized Wilson-Devinney method assuming a standard Roche geometry. We performed a fit to the light curve by minimizing the free parameters. We fixed the effective temperatures to 32 000 K and 28 000 K for the primary and the secondary star, respectively, as determined by the CMFGEN analysis (see Sect. 4). The mass ratio and the orbital period are those obtained from the orbital solution (see Table 2). We stress that the zero phase of the light curve fit corresponds to the zero phase of the orbital solution.
The light curve (Fig. 7) does not exhibit any eclipses but ellipsoidal variations are clearly visible. The depth of the secondary minimum is very similar to that of the primary minimum. Howarth et al. (1991) considered two different models to explain the geometry of this binary system: a first one where both stars fill their Roche lobe, and a second one with a semi-detached configuration. The emphasis of their analysis was put on the second model with the secondary star filling its Roche lobe.
Parameters fitted from the Hipparcos light curve.
In our analysis, the NIGHTFALL program also provides two possible solutions that both converge toward a semi-detached system. The first possibility is a situation in which the primary component fills up its Roche lobe (Sol 1 in Table 3). This configuration favors an inclination of about 50.1°. The primary star would fill up its Roche lobe at about 98%, whilst the secondary component would at about 87%. The second possible configuration is a system where the secondary star fills up its Roche lobe (Sol 2 in Table 3). This configuration is closer to that found in the literature. Under this assumption, we found an inclination of about 48.1°. The volumes of the Roche lobes fill up at about 95% and 99% for the primary and the secondary components, respectively. As Howarth et al. (1991) noted and regardless of the chosen configuration, the inclination is well between 45° and 55° but, with the present investigation, we note that we improved to greater accuracy the true value of the inclination. In both configurations, we included the reflection effects, which are not negligible when one star fills out a large fraction of its Roche lobe. We also note that there is no photometric evidence of a non-zero eccentricity.
The error bars given in Table 3 are established by exploring the parameter space. We fixed one parameter and allowed the others to vary in order to reach the minimum of the χ2. The error bars were then determined for a variation in the χ2 corresponding to a 90% confidence level and the appropriate number of freedom degrees (for more details, see Linder et al. 2009).
Both models are extremely close to each other in terms of parameters values and it is difficult to favor one configuration without any eclipse and based on only the light curve fit. We can only safely conclude that LZ Cep is in a transitory state, where both components are close to entirely filling their Roche lobe. LZ Cep is close to being a contact binary.
6. Stellar evolution and binarity
The position of the two components of the LZ Cep system in the HR diagram is displayed in Fig. 8. The two stars are located significantly away from the zero-age main sequence. The isochrones reveal that the primary would be assigned an age of 4–6 Myr by using single-star evolutionary tracks. The secondary would have an age of 7–9 Myr. This difference in age could be due to a different rotation rate. As demonstrated by Brott et al. (2011), isochrones based on rapidly rotating star evolutionary models tend to be located closer to the ZAMS than isochrones based on tracks with lower rotation rates. This is found for stars with luminosities above 3.0 × 105 L⊙ in the Galaxy. However, this effect is significant only for values of V sin i larger than ~250 km s-1. Since the projected rotation rates we derive are 130 and 80 km s-1for the primary and secondary components, respectively, we can exclude rotation as an explanation to the age difference between both stars.
We determined various masses for the components of the LZ Cep system. From the orbital solution and the light curve analysis, we derived the true present masses of about 16 M⊙ and 6.5 M⊙ for the primary and the secondary components, respectively. These masses can be compared to the spectroscopic masses obtained from the luminosity, temperature, and gravity. We obtained 15.9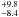 M⊙ for the primary and 4.1
M⊙ for the primary and 4.1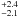 M⊙ for the secondary. Within the error bars, the agreement is very good for the primary, and marginal for the secondary. This could be due to the deformation of the secondary (see Fig. 7) and that we derive only an average gravity. The evolutionary masses derived using single-star evolutionary tracks are respectively 25.3
M⊙ for the secondary. Within the error bars, the agreement is very good for the primary, and marginal for the secondary. This could be due to the deformation of the secondary (see Fig. 7) and that we derive only an average gravity. The evolutionary masses derived using single-star evolutionary tracks are respectively 25.3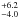 M⊙ and 18.0
M⊙ and 18.0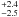 M⊙ for the primary and the secondary. The former masses, estimated from the orbital solution and the inclination, are in strong conflict with the latter ones. Under normal circumstances, a star of initial mass around 25 M⊙ does not lose 10 M⊙ through stellar winds before it enters the Wolf-Rayet phase (e.g. Meynet & Maeder 2000). Hence normal evolution cannot explain the mass discrepancy for the primary. In addition, if the discrepancy in mass concerned only one component, one could argue that mass was lost through Roche-lobe overflow and given to the other component. In our case, both stars however have evolutionary masses much larger than present masses. This is an indirect indication that the system was affected by binary interaction and that single-star evolutionary tracks cannot be used blindly to derive the initial masses of the components of LZ Cep. We also note that the spectroscopic masses we obtained are lower than expected for single-star evolution (see e.g. Martins et al. 2005). This is especially true for the secondary, for which a mass of 4.1
M⊙ for the primary and the secondary. The former masses, estimated from the orbital solution and the inclination, are in strong conflict with the latter ones. Under normal circumstances, a star of initial mass around 25 M⊙ does not lose 10 M⊙ through stellar winds before it enters the Wolf-Rayet phase (e.g. Meynet & Maeder 2000). Hence normal evolution cannot explain the mass discrepancy for the primary. In addition, if the discrepancy in mass concerned only one component, one could argue that mass was lost through Roche-lobe overflow and given to the other component. In our case, both stars however have evolutionary masses much larger than present masses. This is an indirect indication that the system was affected by binary interaction and that single-star evolutionary tracks cannot be used blindly to derive the initial masses of the components of LZ Cep. We also note that the spectroscopic masses we obtained are lower than expected for single-star evolution (see e.g. Martins et al. 2005). This is especially true for the secondary, for which a mass of 4.1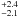 M⊙ is much lower than the 10–15 M⊙ of Martins et al. (2005). Having such a low mass but still the luminosity and effective temperature of an O star imply the occurrence of processes not present in single-star evolution.
M⊙ is much lower than the 10–15 M⊙ of Martins et al. (2005). Having such a low mass but still the luminosity and effective temperature of an O star imply the occurrence of processes not present in single-star evolution.
Another indication of interaction within the system comes from the analysis of the surface abundances. In Fig. 9, we show the nitrogen to carbon ratio as a function of the nitrogen to oxygen. In addition, single-star evolutionary tracks including rotational mixing from Meynet & Maeder (2003) are shown. We see that the primary, located at the bottom-left corner of Fig. 9, displays surface chemistry consistent with single star evolution. However, the secondary features extreme nitrogen enrichment and carbon/oxygen depletion. Such high N/C and N/O ratios are only reached during the Wolf-Rayet phase of single star evolution (the Wolf-Rayet phase is indicated by bold symbols in Fig. 9). Interestingly, this is consistent with the high helium content of the secondary He/H = 0.4, corresponding to Y = 0.6, which is only observed in advanced stages of evolution in single-star evolutionary tracks with initial masses of about 20 M⊙. This raises the question of whether the secondary is more evolved than the primary and currently in a state of central helium burning. Using the mass-luminosity relation of Schaerer & Maeder (1992) for core H-free stars, we find that a star with a current mass of about 6 M⊙ (resp. 5 M⊙) should have a luminosity 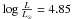 (resp. 4.69). This is remarkably consistent with the derived luminosity of the secondary (
(resp. 4.69). This is remarkably consistent with the derived luminosity of the secondary (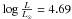 ).
).
 |
Fig. 5 Best-fit CMFGEN model (red) of the disentangled UV spectrum (black) of the primary component of LZ Cep. |
 |
Fig. 6 Illustration of the N/H determination for the primary component of LZ Cep. Colored lines represent the models and the black line is the disentangled spectrum. We estimate that the best-fit model abundance has N/H slightly above 8.0 × 10-5 and that models with N/H = 6.0 × 10-5 and N/H = 1.0 × 10-4 correspond to the extrema of the allowed N/H values. |
 |
Fig. 7 Top: photometry of LZ Cep from Hipparcos satellite. The red triangles are the observational data. A period of ~ 3.07 d is used. The solid line corresponds to the theoretical light curve fit with the parameters listed in Table 3. Bottom: a 3D view of both stars when the secondary star fills up its Roche lobe. |
 |
Fig. 8 HR diagram with the position of the two components of the LZ Cep system shown by the red squares. The primary is the most luminous star. The evolutionary tracks computed for an initial rotational velocity of 300 km s-1 and the isochrones are from Meynet & Maeder (2003). |
 |
Fig. 9 N/C versus N/O for the components of LZ Cep (red squares). The inset zooms on the primary value. The evolutionary tracks are from Meynet & Maeder (2003). The dotted line (resp. dashed, dot-dashed, short-dash long-dashed lines) are tracks for a 15 M⊙ (resp. 20, 25, 40 M⊙) star. The bold lines indicate the Wolf-Rayet phase of the evolution according to Meynet & Maeder (2003), i.e. X(H) < 0.4 and Teff > 10 000 K. |
All indications thus favor the scenario in which the secondary was initially more massive, evolved faster, transferred mass to the companion and is now close to being a core He-burning object. This could also explain the rather low gravity and mass of the secondary (if it is truly a main-sequence O star, log g should be much higher – see also above). However, there are two caveats to this scenario. First, the spectroscopic appearance of the secondary is not that of an evolved massive star. With a spectral type ON 9.7V, it resembles a normal main-sequence star. Said differently, despite of all the indications, the absence of strong mass loss characterizing evolved massive stars (and affecting spectral types) is challenging. Gräfener & Hamann (2008) demonstrated that the mass loss rate of Wolf-Rayet stars depended on the Eddington factor Γe. Estimating this factor from the parameters we determined, we obtain Γe ~ 0.17. This is rather low, and much lower than the range of values for which Gräfener & Hamann (2008) provide mass loss prescriptions for Wolf-Rayet stars (their computations are restricted to Γe > 0.4). Hence, the secondary may very well have a rather normal wind. If we use the mass loss recipe of Vink et al. (2001), we obtain log Ṁ ~ −7.0, which is much more typical of O stars. Consequently, it does not seem impossible that the secondary is an evolved object with a rather normal wind and thus the appearance of an O star.
The second caveat is the chemical composition of the primary. If almost all the envelope of the secondary was dumped onto the primary, the chemical pattern would be different. The primary should then show evidence of N enrichment and CO depletion because material from the secondary would be processed, the secondary being significantly evolved. According to our determinations, there are only weak signatures of CNO processing. This favors a weak accretion of material from the donor. A way out of this puzzle is to invoke a very non-conservative mass transfer, even though this kind of process was not observed in the two post Roche lobe overflow key systems: φ Per (Bozic et al. 1995) and RY Scuti (Grundstrom et al. 2007). All in all, the scenario according to which the secondary was initially more massive and evolved more rapidly to the core-He burning phase while filling its Roche lobe and transferring very inefficiently material onto the primary seems a valuable explanation of the system.
However other explanations can be invoked. de Mink et al. (2007) and Langer et al. (2008) argued that strong nitrogen enhancement can be produced in interacting binaries. Two effects are at work: the mass gainer receives N-rich material usually from the inner layers of the donor, and the angular momentum received from the primary triggers rotational mixing, which increases the surface nitrogen content of the secondary. In total, at solar metallicities, the enrichment can be a factor of ten relative to the initial N abundance. According to Table 2, the nitrogen surface abundance of the secondary star in LZ Cep is 25 times the initial value. This is qualitatively consistent with the predictions of binary evolution that depend on the orbital parameters and masses of the components. In contrast to the scenario described above, the primary is then the mass donor. Since rotational mixing is triggered by mass transfer, one also expects helium enrichment in the secondary, which is what we observe in the LZ Cep. However, according to de Mink et al. (2009), a mass fraction of Y = 0.6 can be reached only for very short periods and occurs only for stars more massive than ~40 M⊙. Another concern is that the rotational velocity of the secondary is not extreme. With V sin i = 80 km s-1, and assuming that the rotation axis is parallel to the orbital axis, this gives a rotation rate of ~100 km s-1. However as shown by Langer et al. (2008), the rotational velocity can reach very large values after mass transfer, and subsequently return to more moderate values. The question is whether rapid mixing can be triggered during this short spin-up phase. It seems unlikely, but further dedicated simulations should be run to help answer this unknown.
For the combination of the inclination, projected rotational velocities, and radius, we can estimate the rotational period of each star and verify whether synchronization has been achieved in the system. Assuming an inclination angle of 49.1° (the average of the two values from Table 3), we obtain a rotational period of 3.09 ± 0.24 d using R = 10.50 R⊙ (average of the polar radii for the primary) and 3.75 ± 0.31 d using R = 12.75 R⊙ (equatorial radius). Similarly, the rotational period of the secondary is 3.15 ± 0.45 d (polar radius) and 4.21 ± 0.60 d (equatorial radius). Compared to the orbital period (3.07 d), the true rotational periods of both components (which are probably in-between the polar and equatorial cases) are thus roughly from 10% to 20% larger, implying that the synchronous co-rotation is not completely established in the system. However, given the small differences and the similarity between the primary and secondary rotational periods, the system is certainly on the verge of achieving this.
All in all, we have thus gathered evidence of mass transfer and tidal interaction in the massive binary system LZ Cep. A scenario in which the secondary was initially the more massive star appears to explain more observational constraints, although it is not free of challenges. What is clear is that single-star evolutionary tracks are certainly not relevant to explaining the position of the two components in the HR diagram. This was highlighted by Wellstein et al. (2001), who computed evolutionary tracks for interacting binaries and showed that as soon as mass transfer occurs, dramatic deviations from single-star evolutionary track happen. Consequently, the evolutionary masses we derived in Table 2 are very uncertain.
7. Conclusion
We have presented a detailed analysis of the binary system LZ Cep. We used high-resolution and high SNR spectra collected with the instrument NARVAL on the TBL. We have derived an orbital solution from which we did not find evidence for a non-zero eccentricity. We have applied a spectral disentangling programme to our data set. This gave us the individual spectra of each component of the system. We have determined the combined spectral type of the system to be O 9III + ON 9.7 V. We have subsequently performed a quantitative spectroscopic analysis with the CMFGEN atmosphere code. Although the secondary star has a main-sequence luminosity class, its surface abundances indicates that the star has experienced significant helium and nitrogen enhancement, as well as carbon and oxygen depletion. The primary barely shows any sign of chemical processing. The analysis of the Hipparcos photometry has revealed ellipsoidal variations that can be explained by two configurations of this system: LZ Cep is a semi-detached system in which either the primary or the secondary almost entirely fills its Roche lobe. The ellipsoidal variations in the light curve correspond to an inclination of about 48°. Together with the spectroscopic orbital solution, this has allowed us to determine the masses of the system of about 16.0 M⊙ for the primary and 6.5 M⊙ for the secondary. These masses are in good agreement with the spectroscopic masses. The evolutionary masses obtained using single-star evolutionary tracks are higher. Our results indicate that LZ Cep is in a transitory state following mass transfer from the secondary – which was initially the most massive component – to the primary. The secondary is now (close to being) a core He-burning object. The mass transfer must have been very inefficient to account for the weak chemical processing at the surface of the primary. The caveats to this scenario have been discussed. The system is not yet completely synchronized, but the individual rotational periods are only 10 to 20% longer than the orbital period.
Our investigation of the binary system LZ Cep represents a significant improvement to previous studies. We have obtained the individual spectra of each component. This leads to the determination of a number of stellar parameters that could be used to constrain the evolutionary status of the system. This evolved system is thus particularly interesting because it provides observational constraints of theoretical binary evolutionary models. Similar analyses have been performed for B stars (e.g., see Pavlovski et al. 2009) but studies of systems composed of two evolved early-type stars are scarce (e.g., Plaskett’s star by Linder et al. 2008). We have emphasized the need for theoretical binary system evolutionary models because our comparison of the stellar properties of the components of evolved binary systems with those of single-star theoretical predictions has revealed discrepancies.
If we rely on the same spectral lines as Harries et al. (1998) for the determination, we obtain a brightness ratio that only slightly differs from their estimate.
For more details, see the Nightfall User Manual by Wichmann (1998) available at the URL: http://www.hs.uni-hamburg.de/DE/Ins/Per/Wichmann/Nightfall.html
Acknowledgments
We thank the anonymous referee for valuable comments that helped us to improve the presentation of the paper and the discussion of our results. L.M. thanks the PRODEX XMM/Integral contract (Belspo) and the Communauté française de Belgique – Action de recherche concertée – ARC – Académie Wallonie-Europe for their support. We thank John Hillier for making his code CMFGEN available and for constant support with its use.
References
- Bozic, H., Harmanec, P., Horn, J., et al. 1995, A&A, 304, 235 [NASA ADS] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conti, P. S. 1973, ApJ, 179, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Conti, P. S., & Alschuler, W. R. 1971, ApJ, 170, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Conti, P. S., Leep, E. M., & Lorre, J. J. 1977, ApJ, 214, 759 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Pols, O. R., & Hilditch, R. W. 2007, A&A, 467, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Cantiello, M., Langer, N., et al. 2009, A&A, 497, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., Langer, N., & Izzard, R. G. 2011, Bulletin de la Société Royale des Sciences de Liège, 80, 543 [Google Scholar]
- Donati, J., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- González, J. F., & Levato, H. 2006, A&A, 448, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grundstrom, E. D., Gies, D. R., Hillwig, T. C., et al. 2007, ApJ, 667, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Harries, T. J., Hilditch, R. W., & Hill, G. 1998, MNRAS, 295, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Hilditch, R. W. 1974, MNRAS, 169, 323 [NASA ADS] [Google Scholar]
- Hill, G., Hilditch, R. W., & Pfannenschmidt, E. L. 1976, Publications of the Dominion Astrophysical Observatory Victoria, 15, 1 [NASA ADS] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Stickland, D. J., Prinija, R. K., Koch, R. H., & Pfeiffer, R. J. 1991, The Observatory, 111, 167 [NASA ADS] [Google Scholar]
- Kameswara Rao, N. 1972, PASP, 84, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Cantiello, M., Yoon, S., et al. 2008, IAU Symp. 250, ed. F. Bresolin, P. A. Crowther, & J. Puls (Cambridge Univ. Press), 167 [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Linder, N., Rauw, G., Martins, F., et al. 2008, A&A, 489, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linder, N., Rauw, G., Manfroid, J., et al. 2009, A&A, 495, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Mahy, L., Rauw, G., Martins, F., et al. 2010, ApJ, 708, 1537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz-Apellániz, J., Walborn, N. R., Galué, H. Á., & Wei, L. H. 2004, ApJS, 151, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., & Plez, B. 2006, A&A, 457, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G. 1988, A&AS, 76, 427 [Google Scholar]
- Mathys, G. 1989, A&AS, 81, 237 [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlovski, K., & Hensberge, H. 2005, A&A, 439, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlovski, K., Tamajo, E., Koubský, P., et al. 2009, MNRAS, 400, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, R. M. 1962, AJ, 67, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Rauw, G., Sana, H., Gosset, E., et al. 2000, A&A, 360, 1003 [NASA ADS] [Google Scholar]
- Sana, H., Gosset, E., & Rauw, G. 2006a, MNRAS, 371, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Rauw, G., Nazé, Y., Gosset, E., & Vreux, J.-M. 2006b, MNRAS, 372, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Gosset, E., Nazé, Y., Rauw, G., & Linder, N. 2008, MNRAS, 386, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & Maeder, A. 1992, A&A, 263, 129 [NASA ADS] [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sota, A., Maíz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wichmann, R. 1998, Nightfall User Manual [Google Scholar]
- Wolfe, Jr., R. H., Horak, H. G., & Storer, N. W. 1967, The machine computation of spectroscopic binary elements, ed. M. Hack (New York: Gordon & Breach), 251 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 NARVAL spectra between 4450 and 4570 Å. The upper part of the figure presents the daily spectra. The lower two spectra are the results of the spectral disentangling process. The two vertical dash lines correspond to the rest wavelengths of the He i 4471 and He ii 4542 lines. |
| In the text | |
 |
Fig. 2 Radial velocities as a function of orbital phase. The solid (open) symbols are for the primary (secondary). The circles are the data of the present paper, whilst the squares are the data of Harries et al. (1998). |
| In the text | |
 |
Fig. 3 Best CMFGEN fit (red) of the disentangled optical spectrum (black) of the primary component of LZ Cep. No data are available in the immediate vicinity of He i 4921. |
| In the text | |
 |
Fig. 4 Same as for Fig. 3 but for the secondary component of LZ Cep. No data are available in the immediate vicinity of He i 4921. |
| In the text | |
 |
Fig. 5 Best-fit CMFGEN model (red) of the disentangled UV spectrum (black) of the primary component of LZ Cep. |
| In the text | |
 |
Fig. 6 Illustration of the N/H determination for the primary component of LZ Cep. Colored lines represent the models and the black line is the disentangled spectrum. We estimate that the best-fit model abundance has N/H slightly above 8.0 × 10-5 and that models with N/H = 6.0 × 10-5 and N/H = 1.0 × 10-4 correspond to the extrema of the allowed N/H values. |
| In the text | |
 |
Fig. 7 Top: photometry of LZ Cep from Hipparcos satellite. The red triangles are the observational data. A period of ~ 3.07 d is used. The solid line corresponds to the theoretical light curve fit with the parameters listed in Table 3. Bottom: a 3D view of both stars when the secondary star fills up its Roche lobe. |
| In the text | |
 |
Fig. 8 HR diagram with the position of the two components of the LZ Cep system shown by the red squares. The primary is the most luminous star. The evolutionary tracks computed for an initial rotational velocity of 300 km s-1 and the isochrones are from Meynet & Maeder (2003). |
| In the text | |
 |
Fig. 9 N/C versus N/O for the components of LZ Cep (red squares). The inset zooms on the primary value. The evolutionary tracks are from Meynet & Maeder (2003). The dotted line (resp. dashed, dot-dashed, short-dash long-dashed lines) are tracks for a 15 M⊙ (resp. 20, 25, 40 M⊙) star. The bold lines indicate the Wolf-Rayet phase of the evolution according to Meynet & Maeder (2003), i.e. X(H) < 0.4 and Teff > 10 000 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


