| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117080 | |
| Published online | 22 July 2011 | |
Reconstructing the intergalactic UV background with QSO absorption lines
Institut für Physik und Astronomie, Universität Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, 14476 Potsdam, Germany
e-mail: cfech@astro.physik.uni-potsdam.de
Received: 14 April 2011
Accepted: 6 June 2011
We present a new approach to observationally constraining the spectral energy distribution of the intergalactic UV background by studying metal absorption systems. We study single-component metal line systems that exhibit various well-measured species. Among the observed transitions, at least two ratios of ionization stages from the same element are required, e.g. C iii/C iv and Si iii/Si iv. For each system photoionization models are constructed by varying the spectrum of the ionizing radiation. The spectral energy distribution can then be constrained by comparing the models with the observed column density ratios. Extensive tests with artificial absorbers show that the spectrum of the ionizing radiation cannot be reconstructed unambiguously, but it is possible to constrain the main characteristics of the spectrum. Furthermore, the resulting physical parameters of the absorber, such as ionization parameter, metallicity, and relative abundances, may depend strongly on the adopted ionizing spectrum. Even in case of well-fitting models, the uncertainties can be as high as ~0.5 dex for the ionization parameter and up to ~1.5 dex for the metallicity. Therefore, it is essential to know the hardness of the UV background when estimating the metallicity of the intergalactic medium. Applying the procedure to a small sample of 3 observed single-component metal line systems yields a soft ionizing radiation at z > 2 and a slightly harder spectrum at z < 2. The resulting energy distributions exhibit strong He ii Lyα re-emission features, suggesting that reprocessing by intergalactic He ii is important. Comparing the observed systems to UV background spectra from the literature indicates that a recent model that includes sawtooth modulation due to reprocessing by intergalactic He ii with delayed helium reionization fits the investigated systems very well.
Key words: intergalactic medium / quasars: absorption lines / diffuse radiation
© ESO, 2011
1. Introduction
The intergalactic medium (IGM) observed in QSO absorption spectra at redshifts z < 6 is highly ionized. At redshifts z ≳ 1, photoionization is the dominant ionization process. To interpret quasar absorption spectra and to investigate the physics of the IGM, ionization corrections have to be applied, and a thorough understanding of the ionizing radiation field is required. Related key questions are the formation of galaxies and the enrichment of the IGM with heavy elements. For studies of the enrichment history, the spectrum and evolution of the UV background have to be known to estimate the metallicity of intergalactic absorbers. It is still under debate how and when metals are distributed into the IGM (e.g. Porciani & Madau 2005; Songaila 2006). However, the recently detected lack of C iv absorption systems at z ~ 6 suggests that the IGM has not been pre-enriched to a high level (Becker et al. 2009; Ryan-Weber et al. 2009). Galaxy formation is also influenced since the cooling of the gas is affected by the metallicity (Wiersma et al. 2009), as well as by the intensity and spectrum of the ionizing background. For instance, photoheating suppresses star formation in dwarf galaxies (e.g. Efstathiou 1992; Hoeft et al. 2006, but see also Gnedin 2010).
The highly photoionized stage of the intergalactic material is maintained by the UV background that is produced by the radiation of quasars and galaxies filtered by absorption and re-emission processes in the IGM. Its spectral energy distribution (SED) can be estimated from theoretical calculations based on the redshift-dependent properties of the sources and the absorbers (the hardness of the QSO spectra, their number density, the column density distribution of intergalactic absorbers, etc.). The UV background model from Haardt & Madau (2001, HM01) is usually adopted in absorption line studies. A particular application is to estimate the metallicity of the IGM, which is important for understanding the mechanisms and stellar sources of metal enrichment.
Alternative UV background models from other authors (Fardal et al. 1998; Faucher-Giguère et al. 2009) and recent upgrading (Madau & Haardt 2009) reveal the same characteristic spectral shape, which is determined by an underlying power-law slope of the quasar sources with additional contribution by galaxies at low energies. Absorption breaks and re-emission features due to the intergalactic H i and He ii are superimposed on the spectrum. The specifications of these characteristics depend on the details of the handling of the cosmological radiative transfer, as well as on the adopted properties of the quasars and galaxies as the sources of radiation. The spectrum in the energy range ~1–10 Ryd is particularly important since the species that are easily accessible in the optical have ionization potentials in this range (e.g. C iii 3.5 Ryd, C iv 4.74 Ryd, Si iii 2.46 Ryd, Si iv 3.32 Ryd, O vi 10.15 Ryd), which are, therefore, usually adopted to tracing the metallicity and the relative abundances of the IGM. However, from investigating intergalactic He ii absorption, which probes the spectral hardness of the ionizing radiation, it is known that the UV background is probably fluctuating (e.g. Kriss et al. 2001; Shull et al. 2004; Fechner et al. 2006a; Fechner & Reimers 2007; Shull et al. 2010). These fluctuations in spectral hardness can be attributed to variations in the IGM density, effects of radiative transport, as well as local sources close to the line of sight. Recently, Bolton & Viel (2011) have found from numerical simulations that spatial inhomogeneities of the spectral hardness of the UV background have only a little impact on the ionization balances of Si iv and C iv, because of the longer mean free path of photons with energies close to the He ii ionization edge. However, studies of individual intergalactic metal line systems indicate deviations from the standard HM01 spectrum, in particular in the important energy range 3–4 Ryd (e.g., Agafonova et al. 2005, 2007; Fechner et al. 2006b; Reimers et al. 2006).
In order to investigate in detail the SED of the UV background, metal line systems have to be studied by means of photoionization modeling. The ionization fractions within an absorber will depend on the spectrum and intensity of the ionizing radiation, as well as on the density of the absorbing material. Therefore, the ionizing spectrum can be reconstructed to a given level of confidence for appropriate systems. Suitable systems have to exhibit various different species, preferably at least two of each observed element to avoid degeneracy with the elemental abundance pattern. In principle, this can be done using the absorption features of C ii, C iii, C iv, Si ii, Si iii, Si iv, and possibly several low-ionization species at redshift z ~ 2.
In this paper we introduce a new approach to constraining the SED of the UV background by extensive photoionization modeling of metal line systems. The criteria applied to select appropriate absorption systems are explained in Sect. 2. Our new method is presented in Sect. 3. Its potential and limitations are illustrated in Sect. 4 by applying it to artificially constructed test absorbers. The selected observed absorption systems are investigated in Sect. 5, and the results are discussed and compared to the most recent model calculations in Sect. 6. We summarize our conclusions in Sect. 7. Throughout the paper abundances are given in the notation [X/Y] = log (X/Y) − log (X/Y)⊙ with solar abundances taken from Asplund et al. (2005).
2. Selection of appropriate systems
To explore the potential of a new approach to constraining the spectral shape of the UV background by modeling metal line systems, it is important to select appropriate absorption systems. Suitable systems should be as simple as possible to avoid systematics due to simplifying assumptions about the physical properties of the absorber. Therefore, we selected systems that (1) show absorption in one single component only, i.e. without any substructure; (2) are unblended and unsaturated in all important transitions; and (3) exhibit various species with at least two ratios of two different ions from the same element.
2.1. Selection criteria
These selection criteria are supposed to reduce implicit assumptions about the characteristics of the absorbing material like velocity structure, multiple gas phases, and elemental abundances.
-
(1)
Single-component systems. Systems exhibiting multiple component metal line features usually show strong H i absorption that has to be distributed to the individual components. In principle, the H i can be assigned to the individual components assuming the same metallicity throughout the system. However, analyses of damped Lyα (DLA) systems probed by gravitationally lensed sight lines have shown that the metallicity can vary on small scales (e.g. Lopez et al. 1999; Lopez & Ellison 2003; Richter et al. 2005). Selecting single-component systems avoids any assumptions about the velocity structure and the distribution of metals within the absorbing gas.
-
(2)
Unblended and unsaturated absorption features. Photoionization models are based on the column densities estimated from the observed absorption profiles. In particular, the ionization parameter , which is the ratio of the ionizing photon to hydrogen density, is fixed by a measured column density ratio. To keep the uncertainties of the model as low as possible, it is important to have exact column density estimates. Moreover, we consider the column density measurements to evaluate the tested SEDs, and the constraints will be stricter if the error bars of the column densities are small. Line parameters can be measured best if the absorption features are neither saturated nor blended.
-
(3)
Various species with at least two ratios of two different ions from the same element. The ionization parameter of an observed system can be constrained by comparing a measured column density ratio to predictions from photoionization calculations that adopt a radiation field. For a given normalization of the ionizing spectrum, the ionization parameter is uniquely related to the density of the absorber. In principle, a solution can be found for any SED, even though extremely hard/soft spectra will yield unrealistically low/high densities and probably unreasonable metallicity values. Thus, the derived physical parameters rely on a reasonable choice of the radiation field. If two or more column density ratios are available, both have to be reproduced at the same ionization parameter. This will be impossible for unrealistic ionizing spectra, thereby providing a tool to evaluate the plausibility of various SEDs. To be independent of assumptions about the relative abundances, which may deviate from solar in the IGM (e.g. Aguirre et al. 2004, 2008; Fechner & Richter 2009), the adopted ratios have to consider two species of the same element. For the systems that will be studied in the following the ratios C iii/C iv and Si iii/Si iv or Si ii/Si iii/Si iv and Al ii/Al iii, respectively, are available.
We searched in published data for metal absorption systems satisfying these selection criteria. Three systems at different redshifts were selected that are suitable for a feasibility study.
Fitted line parameters.
2.2. System at z = 1.7529 towards HE 1347-2457
HE 1347-2457 (zem = 2.61) has been observed as part of the ESO Large Program “Cosmic evolution of the IGM” (Bergeron et al. 2004) with UVES at the VLT. The optical spectrum has a resolution R ≈ 45 000 and a signal-to-noise ratio of S/N ~ 35−70. For details of the data reduction we refer to Aracil et al. (2004).
The system at z = 1.7529 exhibits one single absorption component predominately in low-ionization species. Features of C ii, Mg ii, Al ii, Al iii, Si ii, Si iii, Si iv, and also C iv were identified. Column densities were estimated by fitting Doppler profiles. The resulting line parameters are listed in the upper part of Table 1 and the observed features, together with the modeled profiles, are presented in Fig. 1.
Unfortunately, H i is only detected in Lyα, and the corresponding feature is saturated. Therefore, the column density estimate may be wrong, leading to an incorrect metallicity. However, since the absorption is optically thin (i.e. NH i ≲ 1017 cm-2), the modeled column density ratios of the metal ions do not depend on the exact value of the H i column density. Thus, our main conclusions will not be affected by this uncertainty. However, we should keep it in mind for the interpretation of derived metallicity. The features of C iv and Si iii, as well as Si iv, are mildly saturated. But since the estimated Doppler parameters of these species agree well, we have confidence in the column density measurements.
 |
Fig. 1 Profiles of the systems at z = 1.7529 towards HE 1347-2457. The histogram-like lines represent the observed data. The solid lines indicate the profiles from the line fit. |
2.3. System at z = 2.3799 towards HS 1700+6416
 |
Fig. 2 Profiles of the systems at z = 2.3799 towards HS 1700+6416. The histogram-like lines represent the observed data. The solid lines indicate the profiles from the line fit. |
The metal line systems in the line of sight towards the QSO HS 1700+6416 (zem = 2.72) have been studied by various authors (e.g. Vogel & Reimers 1995; Köhler et al. 1996; Petitjean et al. 1996; Tripp et al. 1997; Simcoe et al. 2006; Fechner et al. 2006b). We used the co-added spectrum described in Fechner et al. (2006b) of the data presented in Songaila (1998) and Simcoe et al. (2002). The resolution is R ~ 38 000 with S/N ~ 100 at 4000 Å.
The selected system at z = 2.3799 exhibits features of H i, C iii, C iv, Si iii, and Si iv. The line parameters derived by Doppler-profile fitting are summarized in the middle part of Table 1, and the observed features are presented in Fig. 2. Again the H i absorption is saturated. The column density estimate is based on a simultaneous fit of all available transitions of the Lyman series (Lyα, β, γ). Features of Si iii and Si iv are weak but clearly detected. The C iii profile is slightly saturated, and the corresponding column density estimate is the most uncertain one in this system.
2.4. System at z = 2.8266 towards HE 0940-1050
 |
Fig. 3 Profiles of the systems at z = 2.8266 towards HE 0940-1050. The histogram-like lines represent the observed data. The solid lines indicate the profiles from the line fit. |
As HE 1347-2457 the QSO HE 0940-1050 (zem = 3.08) is part of the ESO Large Program sample. Data quality and reduction process are equivalent for both lines of sight. We selected a system at z = 2.8266 showing absorption in C iii, C iv, Si iii, and Si iv. Again, the features of Si iii and Si iv are weak and the C iii estimate is the most uncertain due to interlopers from the Lyα forest. Redshifts and b-parameters of C iii and Si iii were fixed to the values derived for C iv and Si iv, respectively, to reduce the uncertainties in the column density estimates. Using the Lyman series up to Lyϵ, the column density of H i is well measured. We summarize the derived line parameters in the lower part of Table 1 and present the observed profiles in Fig. 3.
3. Modeling
Photoionization models were computed for each system using CLOUDY (v05.07.06; Ferland et al. 1998). The basic idea is to construct individual best-fitting models for several spectra of the ionizing radiation. Since the systems were selected to provide two independent column density ratios, the tested SEDs can then be evaluated for their consistency with the observations. Furthermore, the sensitivity of the resulting physical parameters of the absorbers, e.g. density and metallicity, on the spectrum of the ionizing radiation can be investigated.
For a given radiation field, the ionization parameter U is determined by matching the observed column density ratio of two species. Because of the uncertainties of the C iii measurement, we adopt Si iii/Si iv for all systems. The metallicity of the absorber is then adjusted to recover the absolute values of the measured column densities. We assume a solar abundance pattern, and reference solar abundances are taken from Asplund et al. (2005). The tested SEDs are scaled to JH i = 10-21.1 erg s-1cm-2 Hz-1sr-1 at 1 Ryd (Scott et al. 2000). With this normalization the number of ionizing photons of each SED is fixed and the derived ionization parameter corresponds to a density . Thus, for an individual SED, a best-fit model is found determined by the resulting values of and log U, respectively, the metallicity [Si/H], and the relative abundance [Si/C], which is scaled a posteriori to also match as well the measured column densities of the carbon species as accurate as possible.
This procedure is applied to various ionizing spectra. At first we adopt the UV background from Haardt & Madau (2001, HM01) at the appropriate redshift. Its SED at z ~ 2.0 is indicated as thick line in Fig. 4. The shape of this spectrum represents a mean UV background constituted by the radiation of galaxies and quasars, which is filtered when propagating through the IGM. The main characteristics are a break at 1 Ryd due to absorption by intergalactic H i, a second break at 4 Ryd due to absorption by intergalactic He ii, and a small peak at 3 Ryd due to He ii Lyα re-emission. The included galaxies are assumed to have an escape fraction of ionizing photons of 10%. Their soft radiation mainly contributes to the SED at energies ≲ 1 Ryd.
 |
Fig. 4 Spectral energy distribution of the ionizing radiation in comparison to the ionization potential of several species. The thick line represents the UV background at z ~ 2.0 according to the model of (Haardt & Madau 2001, HM01), which is adopted as ionizing radiation for test case A (see Sect. 4). The thin line indicates an example of a modified spectrum, where the main characteristics varied in this work are marked with arrows. They are measured in deviation from the HM01 spectrum in dex as indicated in the inset. These are (1) the height of the He ii Lyα re-emission peak at 3 Ryd Δ1; (2) the flux level in the energy range 3 < E < 4 Ryd Δ2; and (3) the depth of the He ii break at 4 Ryd Δ3. The presented modified SED can parameterized with Δ1 = + 0.5, Δ2 = −0.7, and Δ3 = −0.5, and is adopted for test case B in Sect. 4. |
Inspired by the results of Fechner et al. (2006b) and Agafonova et al. (2007), three characteristics of the HM01 spectrum are systematically varied: (1) the height of the 3 Ryd Lyα peak; (2) the depletion of the intensity in the range 3 < E < 4 Ryd; and (3) the strength of the 4 Ryd break. We measure each of the modifications in departure from the HM01 spectrum in dex denoted by Δ1, Δ2, and Δ3 in the following, as indicated in the inset in Fig. 4. Figure 4 shows an example of a modified SED with an enhanced 3 Ryd Lyα peak by Δ1 = 0.5, intensity depletion at 3–4 Ryd by Δ2 = −0.7, and a deeper break at > 4 Ryd by Δ3 = −0.5.
 |
Fig. 5 1σ (marked areas) and 3σ (dotted lines) confidence regions of the tested SED parameters for test cases A (upper panels) and B (lower panels). The three left panels show the projections into each of the three possible planes, i.e. Δ1 versus Δ2, Δ3 versus Δ2, and Δ1 versus Δ3, respectively. The right panels show the enhancement of the intensity break at 3 Ryd compared to the HM01 background, which means Δ1 − Δ2, versus the strength of the 4 Ryd break Δ3, where the dashed line indicates a linear fit of the correlation (see text). The parameters of the input SEDs are marked with stars. |
The parameter space explored is −0.4 ≤ Δ1 ≤ + 1.0 using a step size of 0.1 dex, i.e. we vary between spectra with no 3 Ryd Lyα peak at all (which is at Δ1 = −0.4 at the probed redshifts) to a pronounced peak 1.0 dex stronger than in the HM01 spectrum. The intensity between 3 and 4 Ryd is reduced by up to 1.0 dex (−1.0 ≤ Δ2 ≤ 0.0) with a step size of 0.1 dex. The depth of the 4 Ryd break is modified in the range −1.0 ≤ Δ3 ≤ + 0.4 with a step size of 0.2 dex. This means that the intensity at E > 4 Ryd is either reduced by up to 1 dex or increased by up to 0.4 dex, where the latter modification generates a substantially harder SED. Since all modifications are combined with each other in this feasibility study, 1320 models are computed in total for each system.
The resulting models are evaluated to investigate which of the tested SEDs are consistent with the observed metal line systems to a given level of confidence. Therefore, we use the second observed column density ratio. For the systems at z > 2, this is C iii/C iv. By comparing the modeled ratio to the observed value log (N1/N2) ± Δlog (N1/N2), where Δlog (N1/N2) denotes the 1σ error of the column density ratio, the confidence of the best-fit models are estimated. For the system at z = 1.7529, two more ratios are available (Si ii/Si iii and Al ii/Al iii), which are applied individually and in a combined manner, respectively, as presented in Sect. 5. Evaluation of the additional column density ratio then leads to the SED producing the overall best-fitting model. Furthermore, we can derive confidence levels for the parameters of the SED modifications.
4. Test cases
Input parameters and column densities of the test cases.
To test the ability of the procedure described above to recover the spectrum of the ionizing radiation we constructed two artificial systems. Presuming an absorber with , [Si/H] = −1.8, [Si/C] = + 0.7, and an observed H i column density of log NH i = 15.3 was exposed to an unmodified HM01 spectrum at z ~ 2 (Fig. 4), CLOUDY predicts column densities for C iii, C iv, Si iii, and Si iv listed in Table 2 as case A. As a second test case B the same absorber was exposed to a modified HM01 spectrum with Δ1 = + 0.5, Δ2 = −0.7, and Δ3 = −0.5. For both test cases, we ran the same grid of models to establish whether the presumed ionizing spectra can be recovered.
In the following the best-fit photoionization models are evaluated by considering different aspects of the robustness of the method and the influence of the individual parameters on the results. The Si iii/Si iv ratio was adopted to find the best-fit model for every individual SED. The C iii/C iv ratio was then used additionally to evaluate the goodness of the model with respect to the adopted SED. Assuming an uncertainty of Δlog N = 0.01 for each column densities we adopted a 1σ error of 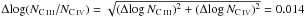 for the C iii/C iv ratio. Thus, models yielding |(C iii/C iv)obs − (C iii/C iv)mod| ≤ 0.014 reproduce the column densities within 1σ confidence. Here, (C iii/C iv)obs denotes the column density ratio of the test absorbers given in Table 2.
for the C iii/C iv ratio. Thus, models yielding |(C iii/C iv)obs − (C iii/C iv)mod| ≤ 0.014 reproduce the column densities within 1σ confidence. Here, (C iii/C iv)obs denotes the column density ratio of the test absorbers given in Table 2.
4.1. Recovery of the ionizing spectrum
In Fig. 5 the 1σ and 3σ confidence regions of the SED parameters are shown for test cases A (upper panels) and B (lower panels) projected into each of the three possible planes in parameter space (Δ1 versus Δ2, Δ3 versus Δ2, and Δ1 versus Δ3; from left to right). Even though the parameters of the input SEDs are within the 1σ confidence regions, they are not recovered unambiguously.
From the most left panel it can be seen that the favored Δ1 and Δ2 values seem to be correlated. This can be understood since both the height of the 3 Ryd Lyα peak and the intensity reduction in the range 3–4 Ryd are related to the He ii recombination re-emission. Since the models are based on the Si iii/Si iv ratio, they are particularly sensitive to the spectral shape at 3 Ryd since the ionization potentials of Si iii (2.46 Ryd) and Si iv (3.32 Ryd) are located in this energy range. Thus, the important characteristic is the strength of the intensity break at 3 Ryd rather than the absolute values of the intensity just below and above this energy. Therefore, we introduce the strength of the break a 3 Ryd relative to the HM01 spectrum as an alternative parameter, which is Δ1 − Δ2. The distribution of Δ1 − Δ2 for the 1σ-confidence models are shown in Fig. 6. For both test cases a clear maximum is seen. For test case A we recovered 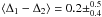 , which slightly overestimates the actual value (which is 0.0 since the ionizing radiation is the unmodified HM01 spectrum). Test case B led to
, which slightly overestimates the actual value (which is 0.0 since the ionizing radiation is the unmodified HM01 spectrum). Test case B led to 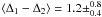 , which is recovered by the procedure even though with larger scatter.
, which is recovered by the procedure even though with larger scatter.
 |
Fig. 6 Distribution of Δ1 − Δ2 for UV background spectra that fit the observed column density ratios up to 1σ confidence for test cases A (left panel) and B (right panel). Input values are marked with an arrow. |
The confidence contours for this parameter versus the strength of the intensity break at 4 Ryd Δ3 are shown in the righthand panels of Fig. 5. The 3 Ryd break Δ1 − Δ2 appears to be weakly correlated with Δ3 in the sense that larger Δ3, i.e., harder spectra favor stronger breaks at 3 Ryd. Since the 4 Ryd break is the He ii ionization edge, it is also governed by the amount of He ii in the IGM. Therefore, a correlation between Δ1 − Δ2 and Δ3 is expected, since more He ii means both: stronger He ii Lyman continuum absorption, hence a stronger 4 Ryd break, as well as stronger He ii recombination re-emission and stronger He ii Lyman series absorption (see Fig. 1 of Madau & Haardt 2009, for illustration). Describing this correlation roughly as linear, we fit Δ1 − Δ2 = (0.50 ± 0.05)Δ3 + (0.22 ± 0.02) for case A and (0.49 ± 0.10)Δ3 + (1.40 ± 0.05) for case B (right panels of Fig. 5). In general, the adopted method does not lead to reasonable constraints on the intensity level at E > 4 Ryd. Models with 1σ confidence can be found for each value of Δ3 for case A, and only the hardest SEDs are excluded by the 1σ constraint for case B. However, a rough estimate of Δ3 by inserting the recovered Δ1 − Δ2 into the fitted relation yields Δ3 ≃ 0.0 and Δ3 ≃ − 0.4 for cases A and B, respectively, which recovers the input value within 0.1 dex. Fixing Δ3 to the derived value, the best-fit models are then found at (Δ1,Δ2,Δ3) ≃ (0.0,0.0,0.0) for case A and ( + 0.4, − 1.0, − 0.4) for case B. While the HM01 spectrum is perfectly reproduced, the main characteristics of the modified SED (enhanced 3 Ryd Lyα peak, depression of the intensity at energies >3 Ryd and >4 Ryd) are also recovered. Therefore, it should at least be possible to also give reliable constraints on the spectral shape of the UV background for observed metal line systems. We expect, however, to find various SEDs that fit the observed column densities to the same level of confidence. Furthermore, we should keep in mind that the parameters of the best-fit models are subject to high uncertainties. Strictly speaking, the parameter ranges marked in Fig. 5 indicate the actual error bars of our estimate.
4.2. Estimated physical parameters
 |
Fig. 7 Recovered physical parameters of the test systems A (left panels) and B (right panels). Marked areas in the upper, middle, and lower panels show the ionization parameter log U, metallicity [Si/H], and relative abundance [Si/C], respectively, in the dependence of the SED parameters Δ1, Δ2, and Δ3 (from the left to the right) estimated for all tested spectra. The narrower ranges represent the results of the models that are consistent with the “observed” column density ratios on a 1σ level. The actual input values (see Table 2) are indicated as stars. |
Recovered physical parameters for the test cases.
Usually, photoionization models for metal absorption systems are used to derive physical parameters of the absorbing material. Most important are the metallicity and the ionization parameter U, which is related to the density of the absorber for a given normalization of the ionizing spectrum. With our grid of best-fit models we are able to investigate the dependence of these physical quantities on the shape of the ionizing radiation. Since the test cases are based on CLOUDY calculations with a given ionizing spectra, it is easily verified that the ionization parameter (thus the density), the metallicity, and the [Si/C] relative abundance are reproduced well by the CLOUDY models if the correct SED is adopted. If system B is modeled with an HM01 background, as it would be in a standard analysis, the density would be slightly underestimated (by 0.05 dex), but the abundances would be heavily overestimated. The HM01 model yields [Si/H] = −0.8 and [Si/C] = + 1.2, which overestimate the actual values by 1.0 and 0.5 dex, respectively.
Generally, the physical parameters depend on the characteristics of the assumed ionizing spectrum. In particular, harder SEDs lead to higher metallicities. The marked areas in Fig. 7 show the ionization parameter log U (upper panels), the metallicity [Si/H] (middle panels), and the relative abundance [Si/C] (lower panels) resulting from the best-fit model of each tested spectrum versus the SED parameters Δ1, Δ2, and Δ3 (left, middle, right panels), respectively, for test cases A (left) and B (right). The parameters of the models with 1σ confidence are indicated by the narrower marked areas. Considering all models, harder spectra, i.e. larger Δ3 lead to higher metallicity estimates and higher [Si/C] as expected. The ionization parameter depends on Δ1, i.e. the height of the 3 Ryd Lyα peak, in the sense that a more pronounced peak leads to lower log U and thus to a higher density . This is due to using the Si iii/Si iv ratio to fix the ionization parameter since the ionization potential of Si iii, i.e. the energy to create Si iv from Si iii is 2.46 Ryd, which is affected by the value of Δ1 (see Fig. 4 and also Agafonova et al. 2007). The estimated [Si/C] abundance decreases with increasing 3 Ryd Lyα peak as well. Virtually no correlation is found between the flux level in the range 3 to 4 Ryd and the derived physical parameters.
Considering all tested spectra, the estimated values are spread over a wide range (see also Table 3). Therefore, if the explored SEDs represent realistic spectral shapes of the UV background, the uncertainties of the derived physical parameters are on the order of ≳ 1 dex. The values of the ionization parameter spread over Δlog U ≃ 0.9, where the corresponding densities cover . The abundance estimates are scattered over an even wider range yielding, Δ [Si/H] ≃ 2.4 and Δ [Si/C] ≃ 1.8 for both test cases.
The range of possible values can be further constrained if only those SEDs are taken into account that fit the additional column density ratio C iii/C iv within 1σ confidence (dark areas in Fig. 7). The mean values are listed in Table 3 where the quoted error bars refer to the range of covered values. The density recovered for case A is slightly underestimated (by ~0.1 dex), while it is slightly overestimated (by ~.2 dex) for case B. For both test cases, the mean 1σ-result overestimates the metallicity by slightly more than 0.1 dex. By the same amount the [Si/C] abundance is overestimated and underestimated in cases A and B, respectively. However, all values are well reproduced within the scatter.
The tightest constraints for the physical parameters are obtained by adopting the best-fit SEDs discussed in the previous section. We have found Δ3 ≃ 0.0 for case A and Δ3 ≃ −0.4 for case B. The results obtained when fixing these values and selecting the models with 1σ confidence are also listed in Table 3. All parameters are reproduced within 2σ, but not necessarily to an improved precision compared to the previous selection, particularly noticeable for case A.
For the recovered SED with (Δ1,Δ2,Δ3) = (0.0,0.0,0.0) for case A and (+0.4, −1.0, −0.4) for case B, the input values are well reproduced. Metallicity and [Si/C] are slightly overestimated (by ≲ 0.2 dex) in case B, which can be explained by the slightly harder recovered SED compared to the original one.
Thus, the shape of the ionizing spectrum, as well as the underlying physical quantities such as ionization parameter (i.e. density), metallicity, and relative abundance [Si/C] of the test cases, are recovered well by our procedure. We therefore are confident of also obtaining meaningful results for observed data, provided that the SED of the ionizing radiation is, in principle, similar to the HM01 spectrum.
5. Results from observations
The observed metal line systems presented in Sect. 2 are modeled in the same way as the test cases where the model grid is based on the unmodified HM01 spectrum at the appropriate redshift for each system. The ionization parameter of the best-fit model for each test SED is determined by matching the observed Si iii/Si iv ratio. To estimate the confidence of the fit we use in addition C iii/C iv for the systems at z = 2.3799 and z = 2.8266. For the system at z = 1.7529 both Si ii/Si iii and Al ii/Al iii are considered (see below). This means that at z > 2 we probe the same energy range as for the test cases. At z < 2 the height of the 3 Ryd Lyα peak, i.e. Δ1, is expected to have the strongest impact on the results since none of the ionization thresholds of the species taken into account are at E > 4 Ryd (see Fig. 4).
5.1. Constraints on the ionizing spectral energy distribution
The confidence contours with respect to the parameterization of the SED projected into all possible planes are presented in Figs. 8 and 10. Obviously, the distributions of the best-fit models of the z > 2 systems (Fig. 8) are similar to those found for the test cases, while the low-redshift system appears to be exposed to a different spectrum (Fig. 10). This could come from the different column density ratios adopted to evaluate the quality of the fit, but a real evolution of the UV background is also possible (Fechner et al. 2006b; Agafonova et al. 2007). The unmodified HM01 spectrum is not included in the confidence regions for any of the systems.
5.1.1. z > 2
 |
Fig. 8 Projected 1σ (marked areas) and 3σ (dotted lines) confidence contours of the SED parameters for the observed systems at z = 2.3799 (upper panels), and z = 2.8266 (lower panels). The projections in each of the three possible planes are shown (Δ1 versus Δ2, Δ3 versus Δ2, and Δ1 versus Δ3; from left to right). The rightmost panels display the confidence regions considering the enhancement of the break at 3 Ryd, i.e. Δ1 − Δ2 versus the strength of the 4 Ryd break Δ3, where the dashed lines indicate a fitted linear correlation (see text). The contours of the z = 2.8266 system are smoothed for a clearer presentation. |
 |
Fig. 9 Distribution of Δ1 − Δ2 for UV background spectra that fit the observed column density ratios up to 1σ confidence for the three observed systems at z = 1.7529 (left panel), z = 2.3799 (middle panel), and z = 2.8226 (right panel). |
In the case of the z > 2 systems, the SED parameters of the 1σ models are correlated in a similar way as those of the test cases. For both systems more enhanced 3 Ryd Lyα peaks, i.e. larger Δ1, are found for less depressed intensity in the 3-4 Ryd range, i.e. larger Δ2. In addition, Δ1 increases with increasing Δ3. That means harder spectra favor more pronounced 3 Ryd Lyα peaks.
The distribution of Δ1 − Δ2, which describes the intensity break at 3 Ryd for the most confident models, are presented in the middle and right panels of Fig. 9. The mean values are found to be 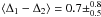 for the system at z = 2.3799 and
for the system at z = 2.3799 and 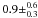 at z = 2.8266.
at z = 2.8266.
Comparing the intensity break at 3 Ryd Δ1 − Δ2 to the break at 4 Ryd Δ3 in the rightmost panels of Fig. 8 again yields a correlation between those parameters. A linear fit leads to Δ1 − Δ2 = (0.44 ± 0.04)Δ3 + (0.85 ± 0.02) for the system at z = 2.3799 and Δ1 − Δ2 = (0.31 ± 0.06)Δ3 + (1.02 ± 0.03) for the system at z = 2.8266 (Fig. 8). Analogously to the test cases, we compute rough estimates for the values Δ3 by inserting the mean Δ1 − Δ2 into the linear fits. This results into Δ3 ≃ − 0.3 for the system at z = 2.3799 and Δ3 ≃ − 0.4 for the system at z = 2.8266. The most confident models with this 4 Ryd break are found at (Δ1,Δ2,Δ3) = ( + 0.4,0.0, − 0.3) at z = 2.3799, where we have interpolated between the models with Δ3 = −0.2 and − 0.4, and ( + 0.3, − 0.6, − 0.4) at z = 2.8266, respectively. Since the unmodified HM01 spectrum has been reproduced well by the test model and at least the correct tendencies of the modified UV background have been recovered, we are led to the conclusion that both systems at z > 2 are ionized by a spectrum that is different from the HM01 background.
5.1.2. z < 2
 |
Fig. 10 Projected confidence contours of the SED parameters for the observed system at z = 1.7529 considering the Al ii/Al iii ratio (upper panels), the Si ii/Si iii ratio (middle panel), and the combination of both column density ratios (lower panel). The projections in each of the three possible planes are shown (Δ1 versus Δ2, Δ3 versus Δ2, and Δ1 versus Δ3; from left to right). The outer right panels display the confidence contours considering the enhancement of the break at 3 Ryd, i.e. Δ1 − Δ2 versus the strength of the 4 Ryd break Δ3. The upper and middle panels show the 1σ (marked areas) and 3σ (dotted lines) ranges of confidence. Since there are no SEDs that reproduce the Al ii/Al iii and Si ii/Si iii within < 3σ simultaneously, the lower panels indicate the regions in parameter space where both column density ratios are matched within 5σ confidence. |
The distribution of the parameters of the most confident models for the system at z = 1.7526 apparently differs from the z > 2 systems (Fig. 10). Since for this system two additional column density ratios are available, we first consider the 1σ and 3σ confidence regions for the Al ii/Al iii and Si ii/Si iii ratios separately (upper and middle panels of Fig. 10). Both ratios lead to rather tight constraints for the peak at 3 Ryd, Δ1, since all considered column density ratios (Si iii/Si iv, Si ii/Si iii, and Al ii/Al iii) are sensitive to the SED at E < 3 Ryd. While Al ii/Al iii requires Δ1 ≤ + 0.4, the Si ii/Si iii ratio is only reproduced with ~1σ confidence by models with Δ1 = + 1.0. Furthermore, Si ii/Si iii favors spectra with Δ3 ≳ − 0.4, while Al ii/Al iii leaves Δ3 unconstrained.
Since neither the 1σ nor the 3σ ranges of Al ii/Al iii and Si ii/Si iii overlap, we consider a wider range of confident SEDs and mark in the lower panels of Fig. 10 those regions in parameter space that reproduce Al ii/Al iii and Si ii/Si iii simultaneously to a 5σ level of confidence. Owing to the higher uncertainties of the column densities of silicon, the number of confident models derived from the Si ii/Si iii ratio strongly increases when wider σ-ranges are considered. Therefore, the joint 5σ confidence regions are mainly determined by the Al ii/Al iii constraints. The 3 Ryd Lyα peak is then found to be 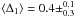 . Best-fit values of the break at 3 Ryd are in the range
. Best-fit values of the break at 3 Ryd are in the range 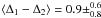 . Together with the well-constrained result for Δ1, we estimate Δ2 ~ −0.5. Furthermore, hard spectra with Δ3 > −0.2 are favored. The actual best-fit model is yielded at (Δ1,Δ2,Δ3) = ( + 0.4, − 0.5, + 0.4), suggesting that the system at z = 1.7529 favors a hard ionizing radiation.
. Together with the well-constrained result for Δ1, we estimate Δ2 ~ −0.5. Furthermore, hard spectra with Δ3 > −0.2 are favored. The actual best-fit model is yielded at (Δ1,Δ2,Δ3) = ( + 0.4, − 0.5, + 0.4), suggesting that the system at z = 1.7529 favors a hard ionizing radiation.
5.2. Physical parameters
 |
Fig. 11 Dependence of physical parameters on the adopted ionizing spectrum for the observed low-redshift system at z = 1.7529. The wide and narrow marked areas in the upper, middle, and lower panels show the ionization parameter log U, metallicity [Si/H], and relative abundance [Si/C], respectively, versus the parameters of the ionizing SED (Δ1, Δ2, Δ3; from the left to the right) for all best-fit models and those consistent with the observed column density ratios of Al ii/Al iii and Si ii/Si iii on a 5σ level, respectively. |
Results for the three studied metal line systems.
The estimated values for the ionization parameter log U, the metallicity [Si/H], and the relative abundance [Si/C] versus the SED parameters are shown in Figs. 11 and 12 and summarized in Table 4. The marked narrow areas in Fig. 11 indicate the range for those models of the system at z = 1.7529 that fit various measured column density ratios simultaneously with 5σ confidence, while the narrow areas in Fig. 12 mark the 1σ confidence regions for the systems at z > 2 based on the C iii/C iv ratio. For the system at z = 1.7529 (Fig. 11) these models yield physical parameters in an extremely narrow range. On average we find ⟨ log U ⟩ = −2.11 ± 0.04 corresponding to , ![\hbox{$\langle\mathrm{[Si/H]}\rangle = +0.01 \pm ^{0.08}_{0.14}$}](/articles/aa/full_html/2011/08/aa17080-11/aa17080-11-eq240.png) , and
, and ![\hbox{$\langle\mathrm{[Si/C]}\rangle = -0.86\pm^{0.09}_{0.13}$}](/articles/aa/full_html/2011/08/aa17080-11/aa17080-11-eq241.png) where the error bars denote the range of estimated values. Adopting the HM01 background leads to log U ≃ − 1.92 and [Si/H] ≃ − 0.22, roughly 0.2 dex higher and lower than the mean of the confident models reflecting that those spectra are considerably harder than HM01.
where the error bars denote the range of estimated values. Adopting the HM01 background leads to log U ≃ − 1.92 and [Si/H] ≃ − 0.22, roughly 0.2 dex higher and lower than the mean of the confident models reflecting that those spectra are considerably harder than HM01.
The corresponding plots for the z = 2.3799 and z = 2.8266 systems are given in the left and right panels of Fig. 12, respectively. The higher uncertainty of the C iii column density means a wider range of consistent models and parameter values is found. For the z = 2.3799 system, we derived 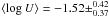 for the ionization parameter and a metallicity of
for the ionization parameter and a metallicity of ![\hbox{$\langle\mathrm{[Si/H]}\rangle = -2.41 \pm ^{0.57}_{0.63}$}](/articles/aa/full_html/2011/08/aa17080-11/aa17080-11-eq245.png) with 1σ confidence. The results derived for an HM01 spectrum (log U ≃ − 1.50 and [Si/H] ≃ − 2.12) are within this range, although the HM01 model is not within the 1σ confidence range. The system at z = 2.8266 yields ⟨ log U ⟩ = −1.04 ± 0.33 and
with 1σ confidence. The results derived for an HM01 spectrum (log U ≃ − 1.50 and [Si/H] ≃ − 2.12) are within this range, although the HM01 model is not within the 1σ confidence range. The system at z = 2.8266 yields ⟨ log U ⟩ = −1.04 ± 0.33 and ![\hbox{$\langle\mathrm{[Si/H]}\rangle = -1.31 \pm ^{0.75}_{0.70}$}](/articles/aa/full_html/2011/08/aa17080-11/aa17080-11-eq249.png) , which is also consistent with the HM01 result of log U ≃ − 1.00 and [Si/H] ≃ − 0.73 even though the HM01 spectrum significantly underestimates the observed C iii/C iv ratio. The 1σ results for the metallicity and hydrogen density of the z > 2 systems are already spread over more than one order of magnitude strongly depending on the hardness of the ionizing radiation and the strength of the Lyα peak at 3 Ryd.
, which is also consistent with the HM01 result of log U ≃ − 1.00 and [Si/H] ≃ − 0.73 even though the HM01 spectrum significantly underestimates the observed C iii/C iv ratio. The 1σ results for the metallicity and hydrogen density of the z > 2 systems are already spread over more than one order of magnitude strongly depending on the hardness of the ionizing radiation and the strength of the Lyα peak at 3 Ryd.
Following the analysis procedure applied to the test cases, we fix Δ3 to the recovered value, which is − 0.3 and − 0.4, respectively, and select the models that at least fit with 1σ confidence. The ranges of the physical parameters then strongly reduce (see Table 4). In particular, the metallicity is now tightly constrained with a spread of Δ [Si/H] ~ 0.1. The results for the recovered SEDs are also listed in Table 4. Compared to the HM01 result, we find only slightly different ionization parameters. But for both z > 2 systems, the metallicity derived from the recovered SED is lower by ~0.3 to 0.7 dex due to the softer spectrum. Furthermore, the enhancement of the 3 Ryd Lyα peak leads to a higher [Si/C] abundance by roughly 0.5 dex.
 |
Fig. 12 Dependence of physical parameters on the adopted ionizing spectrum for the observed systems at z > 2. The marked areas in the upper, middle, and lower panels show the ionization parameter log U, metallicity [Si/H], and relative abundance [Si/C], respectively, versus the parameters of the ionizing SED (Δ1, Δ2, Δ3; from the left to the right) for the best-fit models of the systems at z = 2.3799 (left) and z = 2.8266 (right). The narrower areas indicate the parameters of the models consistent with the observed C iii/C iv column density ratios on a 1σ level. |
6. Discussion
As shown in the previous section, evaluating best-fit photoionization models of three observed metal line systems suggests that the ionizing radiation differs from the usually adopted Haardt & Madau (2001) background spectrum. In two systems at z > 2 a softer spectrum has been recovered where the He ii re-emission peak at 3 Ryd is slightly enhanced and the intensity level in the range 3–4 Ryd is reduced. Measuring the deviation from the HM01 spectrum in dex, our fiducial SEDs can be parameterized with (Δ1,Δ2,Δ3) = ( + 0.4,0.0, − 0.3) at z = 2.3799 and ( + 0.3, − 0.6, − 0.4) at z = 2.8266. For one system at z = 1.7529, a hard spectrum that is even more different from HM01, is considered to yield ( + 0.4, − 0.5, + 0.4) as fiducial SED.
6.1. The spectrum of the UV background
Our fiducial spectra are shown in Fig. 13. We need to keep in mind that the uncertainties of these SEDs are high and hard to quantify since the parameters are mutually correlated. Nevertheless, in the following we compare our best-fit recovered SEDs to various UV background spectra from the literature, which are the classical Haardt & Madau (2001) spectrum, various upgradings based on Madau & Haardt (2009), and the independently computed background from Faucher-Giguère et al. (2009, see Fig. 13.
The recent model of Faucher-Giguère et al. (2009, FG09) at the appropriate redshift is indicated in each panel of Fig. 13. At each redshift the FG09 background is significantly flatter than our fiducial SEDs and even slightly flatter than the pure HM01 background. The FG09 spectra show only very weak recombination emission at 3 Ryd. According to the authors this comes from the combined effects of the saturation of re-emission in optically thick systems, leakage of the re-emitted photons at the ionizing edge, and the frequency dependence of the photoionization cross section. In addition to the weak 3 Ryd Lyα peak, the FG09 spectra show a high intensity in the 3–4 Ryd range, leading to a weak break at 3 Ryd, which is even less pronounced than in the HM01 spectrum. Since this feature is robustly constrained by our models to be greater than in the HM01 case, we conclude that the He ii Lyman continuum absorption and recombination re-emission may be underestimated in the FG09 models.
Furthermore, the break at 4 Ryd is weaker in the FG09 spectra than in the HM01 background. Consequently, the FG09 spectra provide a harder radiation field. As demonstrated by Faucher-Giguère et al. (2009), the depth of the 4 Ryd break mainly depends on the slope β of the H i column density distribution and the spectral index αQSO of the contributing QSOs. The steeper the column density distribution or the softer the QSO radiation, the stronger the break at the He ii edge. In both cases the number of He ii Lyman limit systems is increased, leading to more absorption just above 4 Ryd. Thus, comparison to our fiducial spectra at z > 2 suggest that either the H i column density distribution slope is steeper than the adopted β = 1.4 of Faucher-Giguère et al. (2009) or the contribution of QSOs to the UV background at these redshifts is less than assumed.
The recent finding of a flat, i.e. nearly constant, hydrogen photoionization rate at z > 2 by Faucher-Giguère et al. (2008) and Dall’Aglio et al. (2009) suggests that stars contribute significantly to the ionizing radiation at z ≳ 3. If galaxies dominate the UV background, a softer SED is expected. The studied systems may probe the transition from a QSO- to a galaxy-dominated background in the redshift range 2 ≲ z ≲ 3. Alternatively, the absorbers may be affected by an additional contribution from local soft radiation sources (Miralda-Escudé 2005; Schaye 2006).
Recently, Madau & Haardt (2009) have shown that resonant line absorption in the Lyman series of He ii leads to a sawtooth modulation of the UV background spectrum between 3 and 4 Ryd. The resulting energy distributions at the appropriate redshifts are also shown in Fig. 13 (MH09/HM+S). In this model only QSOs are considered as sources of radiation, and photoionization equilibrium with a uniform radiation field is assumed. Since the soft radiation contributed by galaxies is neglected, the sawtooth SED is much harder than the HM01 background, which also takes galaxy spectra into account.
A very recent upgrade of the HM spectrum (Haardt & Madau 2011, HM11) includes the sawtooth modulation, as well as the radiation of galaxies (for more details we refer to Haardt & Madau 2011). A rough comparison of the new model to the HM01 background at z ~ 3 shows that, along with the sawtooth modulation, the HM11 spectrum declines slightly more steeply between 1 and 3 Ryd and has a weaker break at 4 Ryd. At higher energies, the intensity of the HM11 spectrum drops significantly, in particular at E ≳ 45 Ryd, while the HM01 background is still flat in this energy regime.
A sawtooth model according to Madau & Haardt (2009) which additionally assumes late He ii reionization by artificially boosting the He ii/H i ratio by factors of 10, 30, and 500 (MH09/DR10, MH09/DR30, MH09/DR500), respectively, is also shown in Fig. 13. In these cases, the spectrum is suppressed above 4 Ryd, and the sawtooth modulation results in a net depression of the intensity level in the range 3–4 Ryd. Both effects increase with the amount of existing He ii, i.e. with the He ii/H i ratio. Furthermore, the re-emission peak at 3 Ryd is enhanced. Thus, at z > 2 the MH09/DR spectra show similar overall features to our recovered SEDs. In particular, for the system at z = 2.3799, the recovered spectrum near 4 Ryd follows the MH09/DR30 spectrum closely (middle panel of Fig. 13), and the 3 Ryd Lyα peak of the recovered SED and all the MH09/DR spectra are nearly identical for the system at z = 2.8266 (lower panel of Fig. 13).
 |
Fig. 13 Recovered SEDs in comparison to UV background spectra from the literature for the metal line systems at z = 1.7529 (upper panel), z = 2.3799 (middle panel), and z = 2.8266 (lower panel). Thick blue lines display our fiducial spectra described by (Δ1,Δ2,Δ3) = (+0.4, −0.5, +0.4) at z = 1.7529, (+0.4,0.0, −0.3) at z = 2.3799, and (+0.3, −0.6, −0.4) at z = 2.8266, compared to the unmodified Haardt & Madau (2001) background (thin black line; HM01), the sawtooth spectrum of Madau & Haardt (2009) in the Haardt & Madau (1996) uniform background limit (red dashed line; MH09/HM+S) and with delayed helium reionization boosting the He ii/H i by factors of 10, 30, and 500 compared to the MH09/HM+S case (thin solid lines; MH09/DR10, MH09/DR30, MH09/DR500), respectively, and the UV background spectrum of Faucher-Giguère et al. (2009, dotted line; FG09) at the appropriate redshifts. All spectra are normalized to log J = −21.1 at 1 Ryd. |
 |
Fig. 14 Comparison of predicted column density ratios to the observations for various UV background models from the literature. The adopted ionizing spectra are from Haardt & Madau (2001, HM01), Faucher-Giguère et al. (2009, FG09), Madau & Haardt (2009), assuming equilibrium conditions (MH09/HM+S) or delayed helium reionization with He ii/H i boosted by factors 10, 30, and 500 (MH09/DR10, MH09/DR30, MH09/DR500), respectively, and our recovered SEDs (see text). Shaded areas mark the observed ratio of Si ii/Si iii (upper panel, wider range) and Al ii/Al iii (upper panel, narrow range) for the z = 1.7529 system and C iii/C iv for the systems at z = 2.3799 (middle panel) and z = 2.8266 (lower panel). |
Comparison of UV background spectra from the literature.
For each UV background spectrum from the literature, we used CLOUDY to compute a best-fit photoionization model for each observed system. The resulting physical parameters are summarized in Table 5. The He ii/H i ratio log η is listed in addition to the hydrogen density , the ionization parameter log U, the metallicity [Si/H], and the relative abundance [Si/C]. The He ii/H i ratio measures the hardness of the ionizing radiation, which is mainly determined by the intensity level above 4 Ryd. Therefore, the strongly absorbed MH09/DR500 background yields the highest η-values indicating a soft radiation field, while the relatively flat MH09/HM+S and FG09 spectra lead to lower values corresponding to hard spectra. To evaluate the quality of the models we compared the predicted column density ratios to the observed values in Fig. 14. As above, the C iii/C iv ratio is adopted at z > 2 (lower panels), while Si ii/Si iii and Al ii/Al iii are used at z < 2 (upper panel).
For the low-redshift system, the quality of the fit is dominated by the Al ii/Al iii ratio, which is tightly constrained by the observations. Besides our fiducial model, the MH09/DR10 spectrum fits the observed column density ratios with 4.2σ confidence. Though our recovered SED suggests a hard ionizing radiation, the models based on the harder backgrounds FG09 and MH09/HM+S are less accurate. However, the selected 5σ-confidence models cover the range of hardness 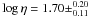 corresponding to
corresponding to 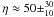 . The FG09 and MH09/HM+S spectra are even harder, thus yielding η ~ 30 and 20, respectively, while the η-value of the MH09/DR10 background (~60) matches the range of the recovered spectra. Comparison to direct measurements of the He ii/H i ratio at z ≳ 2 (Zheng et al. 2004; Fechner et al. 2006a; Fechner & Reimers 2007; Shull et al. 2010) shows that the recovered η-values are at the hard end of the expected range.
. The FG09 and MH09/HM+S spectra are even harder, thus yielding η ~ 30 and 20, respectively, while the η-value of the MH09/DR10 background (~60) matches the range of the recovered spectra. Comparison to direct measurements of the He ii/H i ratio at z ≳ 2 (Zheng et al. 2004; Fechner et al. 2006a; Fechner & Reimers 2007; Shull et al. 2010) shows that the recovered η-values are at the hard end of the expected range.
A hardening of the UV background at z < 2 has already been claimed by other studies (Fechner et al. 2006b; Agafonova et al. 2007). However, the results for the system at z = 1.7529 should be interpreted very cautiously. Absorption features of various species are detected in this system (see Fig. 1). In particular, the system exhibits strong lines of C iv and C ii simultaneously. Owing to their different ionization potentials (1.79 Ryd for C ii and 4.74 Ryd for C iv), both species probably do not live in the same gas phase. While the C ii absorption is thought to arise from the same phase as Si ii, Si iii, Al ii, and Al iii, C iv is expected to trace a more highly-ionized gas phase. Possibly, part of the Si iv absorption may arise from the C iv phase as well. If so, the measured Si iii/Si iv ratio used to constrain the models would actually be a lower limit, so our results would be biased. Thus, an independent confirmation for a z < 2 metal line system using C iii/C iv is desirable. But the short restwavelength of C iii (977.0201 Å) means this requires high-quality near-UV observations.
At z > 2 our fiducial SEDs optimally reproduce the observed C iii/C iv ratio since they are constructed to do so. Furthermore, the delayed reionization sawtooth models lead to surprisingly good fits for both systems. The column densities of the system at z = 2.3799 are optimally modeled by the MH09/DR30 spectrum. The other delayed reionization models lead to acceptable fits, as well as reproducing the C iii/C iv ratio within 2.5σ (MH09/DR10) and 4.7σ (MH09/DR500). The physical parameters derived when adopting the MH09/DR30 spectrum differ significantly from those estimated with our recovered SED by upto 0.5 dex (see Table 5). However, the values are consistent with the 1σ range listed in Table 4. The system at z = 2.8266 is fitted best by the MH09/DR500 spectrum (3.6σ confidence). Though the amount of He ii required to generate such a soft radiation field seems unrealistically high, we conclude that the ionizing radiation should indeed be rather soft.
At least for these two individual systems our findings are contrary to Vasiliev et al. (2010). They have compared the observed C iii/C iv ratio of 10 absorbers to (non-)equilibrium photoionization models for several UV background spectra from Madau & Haardt (2009). The authors come to the conclusion that the delayed reionization models (MH09/DR), hence a large fraction of He ii, is disfavored by their data.
6.2. Physical parameters
The physical parameters of the analyzed metal line systems are also given in Table 5. Though the various adopted ionizing spectra lead to different results for ionization parameter, i.e. hydrogen density, metallicity [Si/H], and [Si/C] abundance, the derived values indicate distinct results for the three systems.
The system at z = 1.7529 shows roughly solar [Si/H] with silicon depleted with respect to carbon with [Si/C] ~ −0.8 for all adopted spectra. This means that the system is apparently metal-rich with [C/H] ~ +0.8. The system at z = 2.3799 has subsolar metallicity, [Si/H] ~ [C/H] ~ −2.0, with roughly solar [Si/C]. The soft recovered SED and the even softer MH09/DR500 spectrum lead to enhanced silicon abundance of [Si/C] ~ +0.4, as would be expected in the IGM (Aguirre et al. 2008). The system at z = 2.8266 appears to be metal-rich as well. For the adopted spectra we find about solar metallicity, [C/H] ~ −0.1, and silicon is depleted with respect to carbon by [Si/C] ~ −0.6. The hard UV background of FG09 suggests enhanced silicon for this system (see Table 5).
Two of the analyzed systems have been investigated in detail by Agafonova et al. (2007, z = 2.3799 and Levshakov et al. (2009, z = 1.7925. For both systems the measured column densities are generally in good agreement. For the z = 2.3799 system, Agafonova et al. (2007) also estimate similar abundances ( [C/H] = −1.94 and [Si/C] = + 0.33), even though they applied a slightly different UV background spectrum,
However, for the system at z = 1.7529, Levshakov et al. (2009) estimate a significantly higher H i column density (log N(H i) ≃ 16.0 in comparison to our ~15.5). Since the Lyα feature is saturated and higher order Lyman series lines are not observed, the H i column density cannot be estimated unambiguously. But the difference may explain the different resulting metallicities. Levshakov et al. (2009) derive [C/H] = 0.1...0.2 and [Si/C] = −0.3, indicating a moderately metal-rich absorber. While Levshakov et al. (2009) also apply a hard but slightly different radiation field, our very high metallicity of [C/H] ~ +0.8 may be due to the underestimated H i column density.
Finding silicon depleted in intergalactic absorption systems as for the systems at z = 1.7529 and z = 2.8266 is rather unusual. According to Aguirre et al. (2008), [Si/C] is expected to be ~ +0.7, indicating enrichment by supernovae type II explosions. However, when studying metal-rich systems, Levshakov et al. (2009) have recently found that these absorbers often have underabundant silicon with respect to carbon. The authors conclude that silicon is depleted into dust, and therefore the absorber may by enriched by gas expelled from massive AGB-stars.
7. Summary and conclusions
We present a new, straightforward method of constraining the spectrum of the intergalactic UV background by means of photoionization modeling of metal line systems. This new method requires simple, one-component systems with unblended, unsaturated absorption features of various species. In particular, at least two different ionization stages of two different elements are needed. Then the column density ratio of two species of one element is used to construct a photoionization model of the system, while the second column density ratio is adopted to estimate the quality of the models for different ionizing spectra. Based on the UV background according to Haardt & Madau (2001, HM01), we parameterized three main characteristics of the spectrum: the He ii re-emission peak at 3 Ryd, Δ1, the intensity level in the range 3–4 Ryd, Δ2, which is related to the absorption due to the He ii Lyman series, and the break at 4 Ryd, the ionization edge of He ii, Δ3. The three parameters were measured in terms of deviation from the HM01 spectrum in dex.
The method was tested with artificially constructed systems using Si iii/Si iv to establish the photoionization models and C iii/C iv to evaluate the various SEDs. The main conclusions were:
-
The SED of the ionizing radiation cannot be reconstructedunambiguously. Instead, we find various spectra that reproducethe observed column densities to a 1σ confidence level.
-
The characteristics of the recovered SEDs are correlated. Evaluating the 1σ confident models yields that Δ1 is correlated with Δ2; i.e., the more pronounced the 3 Ryd Lyα peak, the more depressed the intensity between 3–4 Ryd. Therefore, we introduced (Δ1 − Δ2), which measures the break at 3 Ryd relative to the HM01 spectrum. Furthermore, (Δ1 − Δ2) is correlated with Δ3, which determines the hardness of the spectrum. This means that harder SEDs favor a more pronounced break at 3 Ryd.
-
Nevertheless, the main features of the ionizing spectrum can be recovered by estimating the average value of (Δ1 − Δ2) and inserting it into the (Δ1 − Δ2)-Δ3-relation.
Moreover, we investigated the dependence of the estimated physical parameters of the metal line system – i.e. the ionization parameter log U, the metallicity [Si/H], and the relative abundance [Si/C] – on the spectrum of the ionizing radiation.
-
The ionization parameter log U strongly depends on the 3 Ryd Lyα peak Δ1, where higher Δ1 leads to lower log U. This is due to adopting the Si iii/Si iv ratio to constrain the photoionization model since the ionization potentials of Si iii and Si iv are close to 3 Ryd (2.46 Ryd and 3.32 Ryd, respectively), making both column densities sensitive to the spectrum in this energy range.
-
The metallicity correlates with the 4 Ryd break Δ3, confirming the previous result that harder ionizing spectra lead to higher metallicities.
-
Considering all SEDs that reproduce the observed column densities with 1σ confidence, the resulting values of the physical parameters are spread over Δlog U ~ 0.5 dex, Δ [Si/H] ~ 1.5 dex, and Δ [Si/C] ~ 0.5 dex, respectively. In particular the uncertainty of the metallicity can be higher than one order of magnitude even for a well-fitting model if the spectrum of the ionizing radiation is not confirmed. However, the uncertainties decrease if the hardness of the SED can be constrained. For a fixed 4 Ryd break Δ3 the spread of log U and [Si/C] decrease by a factor of 2. In this case the spread of the metallicity decreases even more to Δ [Si/H] ≲ 0.5 due to the strong dependence on the hardness of the ionizing spectrum.
The method is applied to three appropriate metal line systems at redshifts z ≈ 1.75, 2.38, and 2.83. The recovered spectra differ from the HM01 background yielding the parameters (Δ1,Δ2,Δ3) = ( + 0.4, − 0.5, + 0.4), ( + 0.4,0.0, − 0.3), and ( + 0.3, − 0.6, − 0.4), respectively. However, the recovered SEDs are subject to high uncertainties.
-
(1)
All systems favor an enhanced peak at 3 Ryd, suggesting that the He ii recombination re-emission is stronger than predicted by the HM01 model.
-
(2)
At z < 2 the recovered SED is rather flat and hard. This is consistent with previous findings at similar redshifts by e.g. Agafonova et al. (2007). However, the adopted column density ratios are Si ii/Si iii/Si iv and Al ii/Al iii, while for the z > 2 systems we use Si iii/Si iv and C iii/C iv. Therefore, the hardening of the UV background at lower redshifts should be confirmed using UV data where the C iii λ977 line can be detected even at z < 2.
-
(3)
The recovered SEDs for the z > 2 systems tend to be softer than the HM01 background yielding a stronger break at 4 Ryd in combination with enhanced He ii recombination at 3 Ryd and intensity depression at 3-4 Ryd at least at z ≈ 2.83. Ionization of the observed systems by a soft radiation field implies that the absorbers contain much He ii. Indeed, the expected He ii/H i ratios are high, log η ~ 2.4 at z ≈ 2.38 and 2.8 at 2.83. This may suggest that metal line systems reside in dense environments, where they are shielded from the general UV background and are exposed to a filtered radiation field (Miralda-Escudé 2005; Schaye 2006). In particular, the system at z = 2.3799 towards HS 1700+6416 is located within a protocluster of galaxies reported by Steidel et al. (2005). Generally, metal line systems are thought to arise close to galaxies where the heavy elements are produced and then transported into the IGM by galactic winds. If this is true for the majority of metal line absorbers in QSO spectra, the usually adopted HM01 UV background might be too hard. Due to the strong dependence of the metallicity estimate on the hardness of the ionizing radiation, the derived metallicities might be overestimated by up to one order of magnitude. However, the estimated metallicity of the diffuse IGM (e.g. Schaye et al. 2003; Aguirre et al. 2008) is not supposed to be affected substantially.
-
(4)
Comparing our best-fit models to models derived with theoretical UV background spectra from the literature, we find a surprisingly good fit in the case of the sawtooth modulated UV background from Madau & Haardt (2009), when assuming delayed helium reionization. Madau & Haardt (2009) provide three different models that boost the He ii/H i ratio by a factor of 10, 30, and 500 with respect to the standard case. The boosting factor of the best-fit model increases with increasing redshift. From direct observations of the He ii absorption, it is known that it shows a Lyα forest structure, so helium is highly ionized at z ≲ 2.7 (Kriss et al. 2001; Zheng et al. 2004; Fechner et al. 2006a; Shull et al. 2010). Thus, the fraction of He ii at these redshifts should be lower. However, the observed systems are probably exposed to a surprisingly soft radiation. They may reside in dense environments where remaining patches of He ii might filter the UV background locally.
The application of our new method to three observed systems shows that it should be possible to infer constraints on the spectrum of the UV background. The recent finding of a rather soft ionizing radiation should be confirmed with a larger sample of systems in the future. However, systems that exhibit pronounced metal line features probably reside close to galaxies. They may not be representative to the general intergalactic medium since they live in special environments and may be affected by the radiation of local sources. Thus, they may be exposed to a softer radiation than the general UV background. As a preliminary result from the limited sample of systems investigated so far, we suggest that the Madau & Haardt (2009) spectrum with sawtooth modulation and delayed helium reionization is appropriate to study metal line systems. In comparison, the spectrum provided by Faucher-Giguère et al. (2009) seems to be too flat and featureless, although it might be a appropriate representation of the mean UV background in intergalactic space.
Acknowledgments
We thank Dieter Reimers and Philipp Richter for valuable comments on the manuscript and Francesco Haardt for providing the MH09 spectra.
References
- Agafonova, I. I., Centurión, M., Levshakov, S. A., & Molaro, P. 2005, A&A, 441, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agafonova, I. I., Levshakov, S. A., Reimers, D., et al. 2007, A&A, 461, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguirre, A., Schaye, J., Kim, T., et al. 2004, ApJ, 602, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Aguirre, A., Dow-Hygelund, C., Schaye, J., & Theuns, T. 2008, ApJ, 689, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Aracil, B., Petitjean, P., Pichon, C., & Bergeron, J. 2004, A&A, 419, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [arXiv:astro-ph/0410214] [Google Scholar]
- Becker, G. D., Rauch, M., & Sargent, W. L. W. 2009, ApJ, 698, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, J., Petitjean, P., Aracil, B., et al. 2004, The Messenger, 118, 40 [NASA ADS] [Google Scholar]
- Bolton, J. S., & Viel, M. 2011, MNRAS, 414, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Aglio, A., Wisotzki, L., & Worseck, G. 2009, ApJ, submitted [arXiv:0906.1484] [Google Scholar]
- Efstathiou, G. 1992, MNRAS, 256, 43P [Google Scholar]
- Fardal, M. A., Giroux, M. L., & Shull, J. M. 1998, AJ, 115, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008, ApJ, 688, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C., Lidz, A., Zaldarriaga, M., & Hernquist, L. 2009, ApJ, 703, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Fechner, C., & Reimers, D. 2007, A&A, 461, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fechner, C., & Richter, P. 2009, A&A, 496, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fechner, C., Reimers, D., Kriss, G. A., et al. 2006a, A&A, 455, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fechner, C., Reimers, D., Songaila, A., et al. 2006b, A&A, 455, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Gnedin, N. Y. 2010, ApJ, 721, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 1996, ApJ, 461, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 2001, in Clusters of Galaxies and the High Redshift Universe Observed in X-rays, ed. D. M. Neumann, & J. T. T. Van, 64 [arXiv:astro-ph/0106018] [Google Scholar]
- Haardt, F., & Madau, P. 2011, ApJ, submitted [arXiv:1105.2039] [Google Scholar]
- Hoeft, M., Yepes, G., Gottlöber, S., & Springel, V. 2006, MNRAS, 371, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, S., Reimers, D., & Wamsteker, W. 1996, A&A, 312, 33 [NASA ADS] [Google Scholar]
- Kriss, G. A., Shull, J. M., Oegerle, W., et al. 2001, Science, 293, 1112 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Levshakov, S. A., Agafonova, I. I., Molaro, P., Reimers, D., & Hou, J. L. 2009, A&A, 507, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez, S., & Ellison, S. L. 2003, A&A, 403, 573 [Google Scholar]
- Lopez, S., Reimers, D., Rauch, M., Sargent, W. L. W., & Smette, A. 1999, ApJ, 513, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Haardt, F. 2009, ApJ, 693, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escudé, J. 2005, ApJ, 620, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Petitjean, P., Riediger, R., & Rauch, M. 1996, A&A, 307, 417 [NASA ADS] [Google Scholar]
- Porciani, C., & Madau, P. 2005, ApJ, 625, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Reimers, D., Agafonova, I. I., Levshakov, S. A., et al. 2006, A&A, 449, 9 [Google Scholar]
- Richter, P., Ledoux, C., Petitjean, P., & Bergeron, J. 2005, A&A, 440, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryan-Weber, E. V., Pettini, M., Madau, P., & Zych, B. J. 2009, MNRAS, 395, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J. 2006, ApJ, 643, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Aguirre, A., Kim, T., et al. 2003, ApJ, 596, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, J., Bechtold, J., Dobrzycki, A., & Kulkarni, V. P. 2000, ApJS, 130, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., Tumlinson, J., Giroux, M. L., Kriss, G. A., & Reimers, D. 2004, ApJ, 600, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., France, K., Danforth, C. W., Smith, B., & Tumlinson, J. 2010, ApJ, 722, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Simcoe, R. A., Sargent, W. L. W., & Rauch, M. 2002, ApJ, 578, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Simcoe, R. A., Sargent, W. L. W., Rauch, M., & Becker, G. 2006, ApJ, 637, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A. 1998, AJ, 115, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A. 2006, AJ, 131, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2005, ApJ, 626, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Tripp, T. M., Lu, L., & Savage, B. D. 1997, ApJS, 112, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E. O., Sethi, S. K., & Nath, B. B. 2010, ApJ, 719, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Vogel, S., & Reimers, D. 1995, A&A, 294, 377 [NASA ADS] [Google Scholar]
- Wiersma, R. P. C., Schaye, J., & Smith, B. D. 2009, MNRAS, 393, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Kriss, G. A., Deharveng, J.-M., et al. 2004, ApJ, 605, 631 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Profiles of the systems at z = 1.7529 towards HE 1347-2457. The histogram-like lines represent the observed data. The solid lines indicate the profiles from the line fit. |
| In the text | |
 |
Fig. 2 Profiles of the systems at z = 2.3799 towards HS 1700+6416. The histogram-like lines represent the observed data. The solid lines indicate the profiles from the line fit. |
| In the text | |
 |
Fig. 3 Profiles of the systems at z = 2.8266 towards HE 0940-1050. The histogram-like lines represent the observed data. The solid lines indicate the profiles from the line fit. |
| In the text | |
 |
Fig. 4 Spectral energy distribution of the ionizing radiation in comparison to the ionization potential of several species. The thick line represents the UV background at z ~ 2.0 according to the model of (Haardt & Madau 2001, HM01), which is adopted as ionizing radiation for test case A (see Sect. 4). The thin line indicates an example of a modified spectrum, where the main characteristics varied in this work are marked with arrows. They are measured in deviation from the HM01 spectrum in dex as indicated in the inset. These are (1) the height of the He ii Lyα re-emission peak at 3 Ryd Δ1; (2) the flux level in the energy range 3 < E < 4 Ryd Δ2; and (3) the depth of the He ii break at 4 Ryd Δ3. The presented modified SED can parameterized with Δ1 = + 0.5, Δ2 = −0.7, and Δ3 = −0.5, and is adopted for test case B in Sect. 4. |
| In the text | |
 |
Fig. 5 1σ (marked areas) and 3σ (dotted lines) confidence regions of the tested SED parameters for test cases A (upper panels) and B (lower panels). The three left panels show the projections into each of the three possible planes, i.e. Δ1 versus Δ2, Δ3 versus Δ2, and Δ1 versus Δ3, respectively. The right panels show the enhancement of the intensity break at 3 Ryd compared to the HM01 background, which means Δ1 − Δ2, versus the strength of the 4 Ryd break Δ3, where the dashed line indicates a linear fit of the correlation (see text). The parameters of the input SEDs are marked with stars. |
| In the text | |
 |
Fig. 6 Distribution of Δ1 − Δ2 for UV background spectra that fit the observed column density ratios up to 1σ confidence for test cases A (left panel) and B (right panel). Input values are marked with an arrow. |
| In the text | |
 |
Fig. 7 Recovered physical parameters of the test systems A (left panels) and B (right panels). Marked areas in the upper, middle, and lower panels show the ionization parameter log U, metallicity [Si/H], and relative abundance [Si/C], respectively, in the dependence of the SED parameters Δ1, Δ2, and Δ3 (from the left to the right) estimated for all tested spectra. The narrower ranges represent the results of the models that are consistent with the “observed” column density ratios on a 1σ level. The actual input values (see Table 2) are indicated as stars. |
| In the text | |
 |
Fig. 8 Projected 1σ (marked areas) and 3σ (dotted lines) confidence contours of the SED parameters for the observed systems at z = 2.3799 (upper panels), and z = 2.8266 (lower panels). The projections in each of the three possible planes are shown (Δ1 versus Δ2, Δ3 versus Δ2, and Δ1 versus Δ3; from left to right). The rightmost panels display the confidence regions considering the enhancement of the break at 3 Ryd, i.e. Δ1 − Δ2 versus the strength of the 4 Ryd break Δ3, where the dashed lines indicate a fitted linear correlation (see text). The contours of the z = 2.8266 system are smoothed for a clearer presentation. |
| In the text | |
 |
Fig. 9 Distribution of Δ1 − Δ2 for UV background spectra that fit the observed column density ratios up to 1σ confidence for the three observed systems at z = 1.7529 (left panel), z = 2.3799 (middle panel), and z = 2.8226 (right panel). |
| In the text | |
 |
Fig. 10 Projected confidence contours of the SED parameters for the observed system at z = 1.7529 considering the Al ii/Al iii ratio (upper panels), the Si ii/Si iii ratio (middle panel), and the combination of both column density ratios (lower panel). The projections in each of the three possible planes are shown (Δ1 versus Δ2, Δ3 versus Δ2, and Δ1 versus Δ3; from left to right). The outer right panels display the confidence contours considering the enhancement of the break at 3 Ryd, i.e. Δ1 − Δ2 versus the strength of the 4 Ryd break Δ3. The upper and middle panels show the 1σ (marked areas) and 3σ (dotted lines) ranges of confidence. Since there are no SEDs that reproduce the Al ii/Al iii and Si ii/Si iii within < 3σ simultaneously, the lower panels indicate the regions in parameter space where both column density ratios are matched within 5σ confidence. |
| In the text | |
 |
Fig. 11 Dependence of physical parameters on the adopted ionizing spectrum for the observed low-redshift system at z = 1.7529. The wide and narrow marked areas in the upper, middle, and lower panels show the ionization parameter log U, metallicity [Si/H], and relative abundance [Si/C], respectively, versus the parameters of the ionizing SED (Δ1, Δ2, Δ3; from the left to the right) for all best-fit models and those consistent with the observed column density ratios of Al ii/Al iii and Si ii/Si iii on a 5σ level, respectively. |
| In the text | |
 |
Fig. 12 Dependence of physical parameters on the adopted ionizing spectrum for the observed systems at z > 2. The marked areas in the upper, middle, and lower panels show the ionization parameter log U, metallicity [Si/H], and relative abundance [Si/C], respectively, versus the parameters of the ionizing SED (Δ1, Δ2, Δ3; from the left to the right) for the best-fit models of the systems at z = 2.3799 (left) and z = 2.8266 (right). The narrower areas indicate the parameters of the models consistent with the observed C iii/C iv column density ratios on a 1σ level. |
| In the text | |
 |
Fig. 13 Recovered SEDs in comparison to UV background spectra from the literature for the metal line systems at z = 1.7529 (upper panel), z = 2.3799 (middle panel), and z = 2.8266 (lower panel). Thick blue lines display our fiducial spectra described by (Δ1,Δ2,Δ3) = (+0.4, −0.5, +0.4) at z = 1.7529, (+0.4,0.0, −0.3) at z = 2.3799, and (+0.3, −0.6, −0.4) at z = 2.8266, compared to the unmodified Haardt & Madau (2001) background (thin black line; HM01), the sawtooth spectrum of Madau & Haardt (2009) in the Haardt & Madau (1996) uniform background limit (red dashed line; MH09/HM+S) and with delayed helium reionization boosting the He ii/H i by factors of 10, 30, and 500 compared to the MH09/HM+S case (thin solid lines; MH09/DR10, MH09/DR30, MH09/DR500), respectively, and the UV background spectrum of Faucher-Giguère et al. (2009, dotted line; FG09) at the appropriate redshifts. All spectra are normalized to log J = −21.1 at 1 Ryd. |
| In the text | |
 |
Fig. 14 Comparison of predicted column density ratios to the observations for various UV background models from the literature. The adopted ionizing spectra are from Haardt & Madau (2001, HM01), Faucher-Giguère et al. (2009, FG09), Madau & Haardt (2009), assuming equilibrium conditions (MH09/HM+S) or delayed helium reionization with He ii/H i boosted by factors 10, 30, and 500 (MH09/DR10, MH09/DR30, MH09/DR500), respectively, and our recovered SEDs (see text). Shaded areas mark the observed ratio of Si ii/Si iii (upper panel, wider range) and Al ii/Al iii (upper panel, narrow range) for the z = 1.7529 system and C iii/C iv for the systems at z = 2.3799 (middle panel) and z = 2.8266 (lower panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


