| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117033 | |
| Published online | 21 July 2011 | |
The mass-loss return from evolved stars to the Large Magellanic Cloud
V. The GRAMS carbon-star model grid⋆
1
Institut d’Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
e-mail: srinivas@iap.fr
2
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
Received: 6 April 2011
Accepted: 9 June 2011
Context. Outflows from asymptotic giant branch (AGB) and red supergiant (RSG) stars inject dust into the interstellar medium. The total rate of dust return provides an important constraint to galactic chemical evolution models. However, this requires detailed radiative transfer (RT) modeling of individual stars, which becomes impractical for large data sets. An alternative approach is to select the best-fit spectral energy distribution (SED) from a grid of dust shell models, allowing for a faster determination of the luminosities and mass-loss rates for entire samples.
Aims. We have developed the Grid of RSG and AGB ModelS (GRAMS) to measure the mass-loss return from evolved stars. The models span the range of stellar, dust shell and grain properties relevant to evolved stars. The GRAMS model database will be made available to the scientific community. In this paper we present the carbon-rich AGB model grid and compare our results with photometry and spectra of Large Magellanic Cloud (LMC) carbon stars from the SAGE (Surveying the Agents of Galaxy Evolution) and SAGE-Spec programs.
Methods. We generate models for spherically symmetric dust shells using the 2Dust code, with hydrostatic models for the central stars. The model photospheres have effective temperatures between 2600 and 4000 K and luminosities from ~2000 L⊙ to ~40 000 L⊙. Assuming a constant expansion velocity, we explore five values of the inner radius Rin of the dust shell (1.5, 3, 4.5, 7 and 12 Rstar). We fix the outer radius at 1000 Rin. Based on the results from our previous study, we use amorphous carbon dust mixed with 10% silicon carbide by mass. The grain size distribution follows a power-law and an exponential falloff at large sizes. The models span twenty-six values of 11.3 μm optical depth, ranging from 0.001 to 4. For each model, 2Dust calculates the output SED from 0.2 to 200 μm.
Results. Over 12 000 models have dust temperatures below 1800 K. For these, we derive synthetic photometry in optical, near-infrared and mid-infrared filters for comparison with available data. We find good agreement with magnitudes and colors observed for LMC carbon-rich and extreme AGB star candidates from the SAGE survey, as well as spectroscopically confirmed carbon stars from the SAGE-Spec study. Our models reproduce the IRAC colors of most of the extreme AGB star candidates, consistent with the expectation that a majority of these enshrouded stars have carbon-rich dust. Finally, we fit the SEDs of some well-studied carbon stars and compare the resulting luminosities and mass-loss rates with those from previous studies.
Key words: stars: AGB and post-AGB / radiative transfer / stars: carbon / stars: mass-loss / circumstellar matter / Magellanic Clouds
The model grid is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/532/A54
© ESO, 2011
1. Introduction
During the final stages of their evolution, low- and intermediate-mass stars (0.8 to 8 M⊙) ascend the asymptotic giant branch (AGB). AGB stars are prominent members of stellar populations of ages ~0.2−2 Gyr. Characterized by mass-loss rates of up to 10-4 M⊙ yr-1, stars in the AGB phase inject a significant fraction of their mass into the interstellar medium (ISM). This mass loss is thought to occur in two steps: stellar pulsations first levitate material to the cool, outer layers where dust grains form. Interaction with stellar photons then accelerates the dust grains, which in turn drag the gas along with them (e.g., Goldreich & Scoville 1976; Höfner & Dorfi 1997; Wachter et al. 2002; Höfner 2009). AGB stars of masses ~1−4 M⊙ undergo the third dredge-up process (e.g., Iben 1983; Karakas et al. 2002) which transports the products of nuclear reactions, including carbon, into the outer layers. Each dredge-up event increases the carbon abundance relative to oxygen until eventually the C/O ratio exceeds unity and carbon stars are born. Carbon dust is more efficient at absorbing optical photons (e.g., Wallerstein & Knapp 1998) and it has higher emissivity at infrared (IR) wavelengths. High rates of mass loss from C-rich AGB stars make them major contributors of atomic carbon and carbonaceous dust grains (Dwek 1998; Matsuura et al. 2009; Srinivasan et al. 2009) to the ISM where they may subsequently be assimilated into star-forming regions. The thousands of carbon stars present in galaxies with intermediate-age stellar populations contribute substantially to their integrated bolometric and near-IR (NIR) luminosities (Frogel et al. 1990; Maraston 1998), and this contribution is somewhat higher at lower metallicity (e.g., Fig. 13 in Maraston 2005). Therefore, we must quantify the carbon-star dust output in order to study the dust cycle in galaxies as well as constrain stellar population synthesis models.
The study of Milky Way AGB stars is inhibited by the presence of substantial interstellar extinction, and large uncertainties in distance determinations. The Large Magellanic Cloud (LMC) offers the combination of proximity (~50 kpc; van Leeuwen et al. 2007), low line-of-sight extinction (E(B − V) ~ 0.075 mag; Schlegel et al. 1998) and favorable orientation (~24°; Weinberg & Nikolaev 2001). These properties allow in-depth studies of the entire LMC AGB population. One such study, the Spitzer Space Telescope (Werner et al. 2004) Legacy program SAGE (Surveying the Agents of a Galaxy’s Evolution; Meixner et al. 2006), imaged a 7 × 7° area centered on the LMC and found over 6 million point sources, including thousands of carbon-star candidates (Blum et al. 2006; Srinivasan et al. 2009). Follow-up spectroscopy from the Infrared Spectrometer (IRS, Houck et al. 2004) on Spitzer was obtained as part of the SAGE-Spec program (Kemper et al. 2010).
SAGE provides an ideal dataset for AGB studies. Srinivasan et al. (2009, hereafter Paper I) calculated mid-IR (MIR) excess fluxes for AGB candidates identified from SAGE photometry and used these to estimate the total dust injection rate into the LMC. A more precise estimate for the injection rate requires detailed radiative transfer (RT) modeling of the spectral energy distribution (SED) of each star in the candidate list. Many authors have computed such detailed models for LMC carbon stars (see, e.g., van Loon et al. 1999; Groenewegen et al. 2009; Srinivasan et al. 2010). The computation of individual models becomes time-consuming for large samples such as the SAGE dataset. For this purpose, an alternative would be to compare the observed SEDs to those of pre-computed models. Ideally, such a grid of models should account for the photospheric absorption due to atomic and molecular species (e.g., Gautschy-Loidl et al. 2004; Aringer et al. 2009) and dynamical effects such as pulsation-driven shocks (e.g., Höfner et al. 2003; Mattsson et al. 2007, 2010), as well as the reprocessing of stellar radiation by dust (e.g., Groenewegen 2006). The effects of stellar evolution can be folded into the grid either by performing the above calculations on stars sampled along AGB evolutionary tracks (see, e.g., Mattsson et al. 2007) or by folding the effects of dust into stellar population modeling (e.g., Marigo et al. 2008; González-Lópezlira et al. 2010).
The method of comparison with model grids is suitable for quickly constraining the general properties of large photometric datasets such as the LMC SAGE set. With the intention of quick SED fitting in mind, we have generated the Grid of RSG and AGB ModelS (GRAMS). The GRAMS grid consists of radiative transfer models computed using model stellar photosphere fluxes and assuming various values of stellar and dust shell parameters. While some model grids are available in the literature (e.g., Groenewegen 2006), they typically use only a few template solar-metallicity photospheric spectra as the basis for the grid. Our models cover a large region of the parameter space spanned by AGB stars. One of the motivations for our study is the recent availability of large sets of photosphere models with an improved treatment of molecular spectral features of low-metallicity stars (Gautschy-Loidl et al. 2004; Aringer et al. 2009). This enables us to probe the dependence of mass loss over a large range of stellar parameters. Other studies typically equate the dust temperature at the inner radius to the dust condensation temperature, which is usually fixed at 1000 K for carbon dust (see, e.g., van Loon et al. 1999; Groenewegen 2006). We circumvent this assumption by adopting a more general treatment – we specify the inner radius as input to the modeling and this automatically determines the temperature of the dust in the shell when the model is computed. The output SEDs are very sensitive to the inner radius Rin (see, e.g., Srinivasan et al. 2010) and we incorporate this dependence in our grid by computing models for different Rin values. We thus provide a large grid of models that is complementary to the currently available grids constructed by other authors. In previous papers in this series, we determined the properties of oxygen-rich (Sargent et al. 2010a, hereafter Paper II) as well as carbonaceous (Srinivasan et al. 2010, hereafter Paper III) dust grains for use with the grid. Groenewegen (2006) incorporate different dust species in their grid. While the current incarnation of our grid is computed for a fixed set of dust properties, we will investigate other types of dust in future versions.
Fitting the SEDs of our entire dataset will allow us to investigate the LMC AGB mass-loss return. In this paper, we provide the details of the GRAMS carbon-star grid. Our O-rich grid is described in a companion paper (Sargent et al. 2011, hereafter Paper IV). The remainder of the paper is organized as follows. We detail the parameter selection for the carbon-star grid in Sect. 2 and describe the computational procedure and the calculation of synthetic photometry for the resulting grid in Sect. 3. In Sect. 4, we compare the GRAMS synthetic photometry with SAGE observations on color–magnitude as well as color–color diagrams. As a further validation of the grid, we perform simple chi-squared fits to the SEDs of some sources that have been previously studied in detail. We present our conclusions in Sect. 6.
2. The model grid
We use the 2Dust code (Ueta & Meixner 2003) to populate the grid. 2Dust is a radiative transfer code for axisymmetric systems. While the mass loss is spherically symmetric for most of the AGB phase, the highly evolved AGB stars as well as their post-AGB successors exhibit bipolar geometries (e.g., Ueta et al. 2000; Meixner et al. 2002). The dust around post-AGB stars is also similar to AGB star circumstellar dust. We would like to produce models for these objects as well, but in this paper we assume spherically symmetric shells for simplicity. We will consider the effect of non-spherical geometries in future versions of the grid. In order to solve the radiative transfer equation, 2Dust discretizes the dust shell into a 2-dimensional polar grid. The code then computes the radiation field at each grid point, discretizing the field into a set of incoming rays (“characteristics”) that converge on the grid point from all directions. During each iteration, the code ensures self-consistency by requiring a global luminosity constancy throughout the dust shell. For a given stellar spectrum, dust shell geometry (inner and outer radius, density variation) and a set of dust grain properties (species, optical depth at a reference wavelength, grain size distribution), 2Dust calculates the luminosity1 and mass-loss rate for the system. The code then solves the radiative transfer for the output star+dust spectrum. In this section, we discuss our parameter selection and provide details of our computational procedure. Table 1 lists some of the input/output parameters as well as the range in each parameter covered by the GRAMS carbon-star grid.
GRAMS carbon-star model grid parameter coverage.
2.1. Input for the grid
2.1.1. Stellar spectrum
We represent the central stars using the Aringer et al. (2009) COMARCS hydrostatic models of AGB star photospheres. Aringer et al. (hereafter, A09) take into account the contribution to the emergent spectrum from atomic and molecular absorption lines, which can cause the optical and near-infrared spectrum to deviate significantly from that expected from a blackbody at the same effective temperature. The A09 set consists of spherically symmetric COMARCS hydrostatic models calculated with opacities generated for CO, C2, CN, C2H2, HCN, C3 and a number of other molecules using the COMA (Copenhagen Opacities for Model Atmospheres) code. The parameter coverage of the models reflects the range of effective temperatures, surface gravities and C/O ratios predicted by synthetic evolution models. These are the most accurate models available at present. A09 find good agreement between their models and data for warmer AGB stars. They do not account for dynamical effects and the processing of starlight by dust. In addition to an entire grid calculated for solar metallicity, there are subsets of models for metallicities of Z = 0.33 and 0.1 Z⊙, corresponding to the Magellanic Clouds (ZLMC/Z⊙ ~ 0.3−0.5 and ZSMC/Z⊙ ~ 0.1−0.2; Dufour et al. 1982; Bernard et al. 2008). As we are interested in first reproducing the observed range of colors for the LMC, we selected only their Z = 0.33 Z⊙ subset of 131 models of masses ≤ 5 M⊙. We briefly outline the range of values covered by this subset. For details on the entire grid, we refer the reader to Sect. 2.1 of A09.
The effective temperatures of the Z = 0.33 models (hereafter, the LMC set) range from 2600 K to 4000 K in increments of 100 K. While carbon stars may have lower effective temperatures than this range covers (Mattsson et al. 2008), the A09 models provide adequate coverage for the LMC C-rich sample (Groenewegen et al. 2009). As noted in A09, most models with temperatures hotter than 3500 K will not be on the AGB, but they are included in order to model carbon-rich objects in the post-AGB phase. The surface gravities range from log (g [cm s-1]) = 0 to − 1 in steps of 0.1, but not all log g values are available for a given temperature. In general, the cooler the temperature, the lower the minimum log g available. The LMC set was calculated completely for a stellar mass of 2 M⊙, resulting in 126 models. There are also three 1 M⊙ models with Teff = 2600 K and 3000 K, as well as one Teff = 3000 K model each for mass of 3 M⊙ and 5 M⊙. A09 find that a change in stellar mass has only a minor effect on the near-IR color and bolometric magnitude (see their Fig. 8). These models have C/O ratios of 1.4, 2 and 5. Higher C/O ratios are expected at lower Z due to the under-abundance of oxygen. Due to this fact, the C/O ratio can become significantly higher than unity within the first few dredge-up events. For the range of model parameters corresponding to each temperature range, see Table 1 in A09. The luminosities of the selected models are roughly in the range 1100 − 26 000 L⊙ (Mbol = −2.9 to − 6.3).
In Fig. 2, we compare this range to the luminosity distribution calculated for SAGE C-rich and extreme AGB candidates. Marigo et al. (1999) estimate that the observed LMC carbon-star luminosity function extends between Mbol = −3 and − 6.5; these numbers are in good agreement with ours2. IRAS 04496 − 6958 is the most luminous spectroscopically confirmed carbon star in the LMC (>30 000 L⊙; see, e.g., Speck et al. 2006). Based on SAGE photometry alone, we estimate its luminosity to be about 35 000 L⊙ (Mbol ≈ −6.7) which is still below the classical luminosity limit. Figure 2 also shows the GRAMS luminosity coverage. To fit the SEDs of the most luminous carbon stars, we may have to scale up the luminosities of our models in a procedure similar to that adopted in Sargent et al. (Paper IV) for RSGs and O-rich AGB stars. Our aim in constructing the GRAMS model grid is to span the range of parameters observed for LMC carbon stars; it is possible that in this attempt we may generate some models with extreme luminosities that are not representative of real carbon stars and may never be matched to data. We do not use luminosity scaling in the current version of the carbon star grid; however the scaling is easy to apply once the model grid has been generated, and we will consider such a scheme when we perform SED fitting of the SAGE data in upcoming papers.
2.1.2. Shell geometry
We assume a constant mass-loss rate at a constant outflow velocity 3exp, leading to an inverse-square density distribution in the shell. Models of stationary winds (e.g., Woitke 2006) show that the wind is accelerated from rest near the stellar surface to an almost constant speed within a few stellar radii. The acceleration of the wind therefore affects the density profile in the regions of the dust shell that contribute significantly to the optical extinction and mid-IR emission. In the current paper, we do not take this radial dependence of the outflow velocity into account; ignoring such complications enables us to generate a full grid spanning the observed range for a small set of parameters while allowing us to compensate for the simplifications at a later time. We also ignore any dependence of the expansion velocity on the metallicity or gas:dust ratio. As the dust mass-loss rate calculated by the code is directly proportionate to the value of 3exp chosen (see, e.g., Eq. (2) in Paper III), it is straightforward to incorporate the effect of changing 3exp once the grid has been populated. Following our discussion in Paper III, we use 3exp = 10 km s-1 for all our models. 2Dust accepts a user-defined density function, which can be used to study time-dependent mass loss. We will also consider this possibility in future versions of the grid.
As discussed in Paper III, the mass-loss rate and output spectrum are very sensitive to the value of the inner radius Rin. The inner radius determines the hottest temperature of the dust, which is one of the 2Dust output parameters. We calculate models for Rin = 1.5, 3, 4.5, 7 and 12 stellar radii. Simple energy-balance estimates suggest that amorphous carbon dust should form within a few stellar radii (Höfner 2007). A lower limit of about 1.3 Rin is suggested for SiC formation in extreme carbon stars by Speck et al. (2009). The range considered here also agrees with observations of Galactic carbon stars (e.g., IRC+10216; Danchi et al. 1995) and results from RT modeling of LMC stars (e.g., van Loon et al. 1999). We note here that 2Dust uses the inner radius as input to determine the dust temperature (Tin) as a function of radius in the shell. This means that we cannot directly restrict the range of Tin before the grid is computed. However, we filter out models with high and/or unphysical dust temperatures from the grid once it is generated (see Sect. 3.3 for details).
The outer radius determines the total amount of mass in the shell and the mass-loss timescale. While these are important quantities, we focus on obtaining mass-loss rates, which are only weakly sensitive to changes in the value of the outer radius. We ensure that the outer radius is large enough so that we do not miss any contributions to the flux from the outermost regions. While modeling the shell around OGLE LMC LPV 28579 in Paper III we found that a value of Rout = 1000 Rin was sufficiently large to satisfy this condition. We use the same value for all the models in our grid. For 3exp = 10 km s-1 and Rout = 1000 Rin, the mass-loss timescales corresponding to the smallest and largest circumstellar envelopes in our grid are 548 yr and 19 620 yr respectively.
2.1.3. Dust grain properties
We modeled the SAGE photometry and SAGE-Spec spectrum of OGLE LMC LPV 28579 in Paper III for the purpose of selecting a set of carbonaceous dust grain properties for GRAMS. As a result, we choose a mixture of amorphous carbon (AmC; optical constants from Zubko et al. 1996) with 10% silicon carbide by mass (optical constants from Pégourié 1988). As input, 2Dust also requires the optical depth specified at a reference wavelength. In Paper III, we used the SiC feature observed in the SAGE-Spec spectrum of LPV 28579 to constrain the optical depth as well as the SiC content of our dust model, so it was convenient to specify the optical depth at 11.3 μm. We follow the same practice in this paper, because the dust composition used in the grid is identical to that of Paper III3. We will revise the current convention when we incorporate more dust types into our grid. The values of τ11.3 in our grid range from 10-3 to 4. We consider five optical depths per decade between 10-3 and 0.1 (1, 2, 4, 6 and 8 × 10-3 and so on), and ten values between 0.1 and 1. Additionally, we calculate models for τ11.3 = 1.5, 2, 2.5, 3, 3.5 and 4, bringing the total to twenty-six unique optical depth values. The grain sizes are distributed according to n(a) ∝ a − γe − a/a0 (KMH distribution, Kim et al. 1994) with power-law index γ = 3.5, minimum grain size amin = 0.01 μm and exponential scale height a0 = 1 μm. For the AmC:SiC mixture considered here, the average grain size4 is about 0.1 μm, the value typically used in single-size models (e.g., Groenewegen 2006). The Mathis et al. (1977) (MRN) distribution, given by n(a) ∝ a − γ for amin < a < amax places a strict limit on the maximum grain size. In this sense, the KMH model represents a more realistic grain size prescription. In Paper III, we showed that the output spectrum showed only a weak dependence on the exponential factor a0 of the KMH model beyond a0 ≈ 0.1μm. Our choice of the KMH model thus means there is one less parameter to constrain. Owing to its maximum grain size requirement, the MRN distribution has a smaller average grain size. This results in higher absorption and therefore lower optical flux and more mid-IR emission. This effect was discussed in Ueta & Meixner (2003). In our study, we computed 2Dust models for a few GRAMS models using the MRN prescription and found that the maximum difference in fluxes is less than 5%.
3. Generating the grid
3.1. Preparation
We use 131 A09 photospheres and we explore five values for the inner radius as well as twenty-six optical depths, making a total of 17 030 output models. Generating such a huge grid of models requires that 2Dust be run in the non-interactive mode, with all the required information provided in the form of various input files (For details of the input format, we refer the user to Sect. 3.1 of the 2Dust manual5).
The A09 photospheric spectra comprise of fluxes at about 8 000 wavelengths ranging from ~0.44−25 μm. As we are interested in providing synthetic photometry over all the broadband filters available to us (optical U through MIPS24), we extrapolate the A09 fluxes onto a larger wavelength grid. On the long-wavelength side, we extend the grid beyond the MIPS24 band, to allow for future comparisons with MIPS 70 and 160 μm fluxes or other long-wavelength data, if available. However, this raw extrapolated spectrum cannot directly be fed into 2Dust; the computational speed of each run is approximately linearly proportional to the number of points in the wavelength grid (Sect. 3.1.5 of the 2Dust manual). We therefore sample the extrapolated spectrum at about 130 wavelengths ranging from 0.2 μm to about 200 μm. We sample more near- and mid-infrared wavelength points as we desire to fit the mid-IR photometry and spectra available as part of the SAGE and SAGE-Spec programs; the constraint on the total number of wavelength points then reduces the number of samples for λ < 1 μm. As a result of this undersampling, we expect that we may not reproduce many of the sharp atomic/molecular features observed in the optical spectra of AGB photospheres, which would affect the heating of dust grains as well as the broadband optical colors of the models with optically thin dust shells. This latter issue is of less concern since we are interested in reproducing the near- and mid-IR photometry. However, in order to have a more accurate treatment of dust heating, we will incorporate a better sampling in the optical in future versions of the grid. Figure 1 demonstrates the effect of undersampling on the output model for a Teff = 3300 K, log (g [cm s-1]) = −0.2 photosphere with an optically thin (τ11.3 = 2 × 10-3) dust shell. While the resulting GRAMS model does not reproduce all the narrow optical features, it shows some of the large-scale variation in the spectrum. The sampling described above also changes the integrated flux calculated for each model by at most a few percent – we found that the luminosities calculated from the raw and sampled spectra agreed to within 5% for 115 of the 131 A09 photospheres, with the maximum discrepancy being around 8%. For consistency, we only use the post-sampled luminosities to tag our resulting models.
 |
Fig. 1 Aringer et al. (2009) photosphere spectrum (gray) with Teff = 3300 K and log (g [cm s-1]) = −0.2, showing many strong features at shorter wavelengths. The vertical dashes show the wavelengths at which this spectrum was sampled for input to 2Dust. The resulting GRAMS output model with optical depth τ11.3 = 2 × 10-3 (black) incorporates some of the variation in the optical. |
The number of discrete radial zones in the shell (NRAD) directly determines the total memory allocated to the code. Based on our tests, we chose to have 64 radial zones for all of our models. The code converges to a solution when, at each grid point, the fractional change in the integrated flux between consecutive iterations is less than a user-defined tolerance level. This level is specified in the code in the form of the CONDITION parameter, which we fixed at 5 × 10-4 for all the models. The execution time is then most sensitive to the optical depth. There is a trade-off between output precision and execution efficiency, which are regulated internally by two parameters: one (VSPACE) sets the smallest line integration step size in terms of the local mean free path length, while the other (MXSTEP) sets the maximum number of allowed steps for line integration along each characteristic. The smallest step size is inversely proportionate to VSPACE value chosen, so large VSPACE values are required for higher precision in the results. However, VSPACE determines the actual number of steps along the characteristic, which cannot exceed MXSTEP. This latter value controls the array length for long characteristics and therefore the memory access time upon execution of the code. Therefore, we need to optimize the choices for MXSTEP and VSPACE as a function of optical depth in order for the code to converge in a reasonable amount of time. For this purpose, we ran a number of test models on a MacBook Pro laptop with a 3.06 GHz Intel Core 2 Duo processor and 8 GB RAM. The test models sampled optical depths over the entire range of values considered for the grid. These models explored various (MXSTEP, VSPACE) pairs, enabling us to select ideal values over different optical depth ranges. This information is incorporated into the input files for each model in the grid, and this input enables us to run 2Dust in the non-interactive mode in an automated fashion.
2Dust tracks the temperature of the dust grains during each iteration. Assuming radiative equilibrium, the code uses these temperatures to obtain the corresponding intensities κνBν from a look-up table, which is computed on execution. This table consists of a temperature grid whose lower and upper limits are TBOT = 2.7 K and TTOP = 1000 K (the typical value chosen for the condensation temperature of carbon dust) by default. It is not easy, however, to constrain Tcond as it depends on many factors such as the C/O ratio and the gas pressure (e.g., Sect. 3.4 of Speck et al. 2009,and references therein). A detailed treatment of Tcond is beyond the scope of our work. Speck et al. (2009) suggest that carbon dust can form at temperatures above 1400 K even at low mass-loss rates. They also find that for high C/O ratios, graphite grains can form at temperatures of ~1800 K. While our current models only consider amorphous carbon dust grains, we are interested in as few constraints on the output parameters as possible so as to be able to extend our treatment by including more grain types in the future if required. Therefore, we assume an upper limit of 1800 K for Tcond. We allow for slightly higher dust temperatures in the look-up table by setting TTOP to 2000 K to avoid convergence issues (see Sect. 3.3), and we enforce the 1800 K constraint on Tcond once the grid is generated.
3.2. Batch job submission
We automated the 2Dust execution using the Magique supercomputing cluster at the Institut d’Astrophysique de Paris. Magique is a cluster of 96 AMD operton nodes interconnected with a Gigabit ethernet network, 84 of which are reserved for scientific computation. Of these, we used the bisockets single and double core nodes (18 and 64 nodes respectively), which allowed 8 GB RAM per job. 2Dust was compiled using the Intel FORTRAN compiler ifort available on Magique. The batch queue system on the cluster is managed by PBSpro v8.0, which automatically allocates a position in the queue for submitted jobs and continuously monitors their status. Our jobs were grouped according to the A09 photosphere used and they were submitted for execution in batches consisting of up to five sets of photospheres (i.e., upto 650 models), depending on the queue status and the load on the cluster from other users. Depending on the optical depth, the time taken for a single model to converge ranged from under a minute to about two hours. We were able to generate the entire grid in under two weeks.
3.3. Filtering out models based on dust temperature
Not all combinations of input parameters detailed in Table 1 will result in realistic or even physical representations of the dust around carbon stars. For instance, we expect that the output dust temperatures for high Teff, low Rin and high τ11.3 may be higher than the dust condensation temperature Tcond. If the local radiation intensity is high enough to warm the dust grains to temperatures beyond TTOP (the maximum value in the lookup table, which was set to 2000 K as described in Sect. 3.1), the code is unable to track these temperatures and intensities, resulting in unphysical (extremely large or negative) dust temperatures in the inner regions of the shell. We found that 1860 models did not converge because of this issue. As expected, these models consisted mainly of shells that were too close to the star (Rin = 1.5Rstar), but also included some models with larger Rin and Teff values warmer than 3500 K. The number of converged models in our grid is therefore 15 170. We then impose the constraint that the dust temperatures be cooler than the chosen condensation temperature (Tcond = 1800 K, see Sect. 3.1), which eliminates 2915 more models. Our final grid thus consists of 12 243 models with dust temperatures cooler than 1800 K. The number will reduce further if we adopt a lower Tcond value; for instance, there are only ~ 9000 models with Tin < 1400 K.
3.4. Publicly available synthetic photometry
For comparison with photometric data, we convolved the SED output from each 2Dust model with the relative spectral response (RSR) curves for the various broadband filters. In particular, we produced synthetic photometry in this fashion for the MCPS UBVI 6, 2MASS JHKs7 and Spitzer IRAC8 and MIPS249 bands. We compare the synthetic photometry against SAGE data in the next section.
Synthetic photometry was also derived for the AKARI (Murakami et al. 2007) and WISE (Wright 2009) passbands10. The AKARI S11 band (centered around 11 μm) as well as the WISE W3 (centered around 12 μm) band directly sample the 11.3 μm SiC feature in carbon stars and the ~10 μm silicate feature in O-rich AGB stars. Ita et al. (2008) presented the AKARI survey of the LMC and discussed color–color and color–magnitude diagrams. The increase in SiC feature strength, therefore, is reflected in the [S11] − [L15] color.
Spectra and synthetic photometry for the GRAMS O-rich and C-rich models will soon be available on the 2Dust website at the Space Telescope Science Institute11. The format of the publicly-available data is still undergoing testing and will be refined through input from the end-users. In addition to the filters mentioned above, we can make synthetic photometry available for other filters on request.
4. Results
In this section, we demonstrate the coverage of various parameters by the GRAMS grid. We discuss the luminosities and dust mass-loss rates. We also compare the GRAMS synthetic photometry with data for the SAGE C-rich and extreme AGB candidates as well as SAGE-Spec carbon stars on color–magnitude diagrams (CMDs) and color–color diagrams (CCDs).
 |
Fig. 2 Top: the distribution of luminosities of LMC C-rich (solid) and extreme (dotted) AGB candidates from SAGE. The classical AGB luminosity limit is also shown (dashed line). Bottom: the range of luminosities and dust mass-loss rates covered by the GRAMS carbon star models. As discussed in Sect. 3.3, only models with Tin < 1800 K are shown. Gray symbols show the luminosities and mass-loss rates of LMC carbon stars as calculated from detailed modeling by van Loon et al. (1999) (triangles) and Groenewegen et al. (2009) (diamonds). |
4.1. Luminosities and dust mass-loss rates
The large number of A09 models provide us with a relatively dense coverage of the luminosities expected for LMC AGB stars. This fact is evident from Fig. 2, which compares the GRAMS model luminosities with the distribution of luminosities calculated in Paper I from SAGE photometry for C-rich and extreme AGB candidates12. The GRAMS models provide excellent coverage over the entire range of luminosities, except at the faint and bright ends. There is a gap visible between the two lowest available luminosities of 1100 L⊙ and 2200 L⊙. There are 50 candidates (8 C-rich, 42 extreme) brighter than the brightest C-rich GRAMS model available, and 60 candidates (45 C-rich, 15 extreme) fainter than ~2200 L⊙.
The dust mass-loss rates in the GRAMS grid range from 1.5 × 10-12 M⊙ yr-1 to 2.1 × 10-7 M⊙ yr-1. As mentioned in Sect. 2.1.3, 2Dust can only constrain the ratio Ṁdust/3exp, so the range of mass-loss rates produced by the grid depends on the value of 3exp chosen. The lowest values of mass-loss rates calculated from the IR excesses for SAGE carbon star candidates in Paper I were around 10-11 M⊙ yr-1. As we are interested in covering as much of the parameter space as possible, our grid contains mass-loss rates well below this limit. Carbon stars can have dust mass-loss rates up to a few times 10-7 M⊙ yr-1 (e.g., Groenewegen et al. 2009). Our grid does not currently have adequate coverage of the highest luminosities expected for carbon stars (see Sect. 2.1.1), but the models can be scaled to these higher luminosities as in Paper IV. This would also result in higher mass-loss rates. As an example, if we scale the brightest model (L = 2.6 × 104 L⊙) to the classical AGB limit (L = 5.3 × 104 L⊙) while keeping all the other parameters constant, the corresponding highest mass-loss rate is 3 × 10-7 M⊙ yr-1. The total (gas+dust) rate depends on the gas:dust ratio, Ψ. As AGB stars produce their own carbon, it is easier at lower metallicities to produce an excess abundance of carbon relative to oxygen; however, whether the gas:dust ratio shows a dependence on metallicity remains an open question (see, e.g., van Loon et al. 2008, and references therein). Using Ψ = 200, the value determined for Galactic carbon stars (Jura 1986), the range of gas mass-loss rates covered by the grid is 3.0 × 10-10 M⊙ yr-1 to 4.3 × 10-5 M⊙ yr-1. We plot the GRAMS dust mass-loss rates against their luminosities in Fig. 2. The luminosities and mass-loss rates determined for some LMC carbon stars that were modeled by van Loon et al. (1999) and Groenewegen et al. (2009) are also shown for comparison. The GRAMS grid has good coverage of the range of luminosities and mass-loss rates calculated by these studies, except at very high luminosities and mass-loss rates – in particular, there are three stars modeled by Groenewegen et al. (2009) with higher mass-loss rates. We would like to point out that this is no longer an issue if we adopt the same amorphous carbon dust opacities as in the Groenewegen et al. study (see Sect. 5.1.2 for details). The current optical depth limit of τ11.3 = 4 was chosen based on the reddest sources in the SAGE study – with the current set of models, we are able to produce redder mid-IR colors than those observed in the SAGE sample (see Sect. 4.2). The choice was also based on results from our empirical study (Paper I). As models with higher optical depth are computationally intensive, we decided to add optically thicker models in the future if required.
4.2. Color–magnitude and color–color diagrams
The figures in this section compare the GRAMS synthetic photometry with SAGE O-rich, C-rich and extreme AGB candidates. These plots demonstrate that the GRAMS grid is able to reproduce the range of observed colors for carbon star candidates. We also include sources from the SAGE-Spec study that display molecular features and/or dust signatures typical of carbon stars (Kemper et al. 2010; Woods et al. 2011). Only the subset of SAGE-Spec sources that had a full 5 − 37 μm spectrum are shown here. We refer the reader to Blum et al. (2006) for a detailed description of the various stellar populations observed in these diagrams and to Paper IV for discussion on the locations of the oxygen-rich AGB candidates and models.
We would like to emphasize that comparisons on CMDs and CCDs are only shown in order to demonstrate the coverage of the observed colors and magnitudes, and we are careful not to over-interpret the agreement. Some of our models may be unrealistic, yet others may correspond to unphysical parameter values. While we have made an effort to avoid unrealistic models by filtering out those with very high dust temperatures, our aim was to span a large parameter space and good agreement with data does not necessarily validate a model in the grid. Similarly, good agreement with data on a color–color diagram does not necessarily imply that a model is a good fit to the data. Two models with significantly different values for the same parameter (e.g., luminosity) but similar SED shapes might also end up close to each other on a color–color diagram, resulting in a large uncertainty for the parameter calculated for data based on just this diagram.
4.2.1. Ks vs. J − Ks CMD
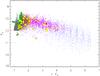 |
Fig. 3 the Ks vs. J − Ks CMD shows the model grid (light blue points) overlaid onto the SAGE AGB candidates from Paper I (gray: O-rich, orange: C-rich and pink: extreme). The yellow diamonds are SAGE sources identified as carbon-rich from their SAGE-Spec spectra. The large red triangle is OGLE LMC LPV 28579. Also shown are the Aringer et al. (2009) photospheres (green squares) used to generate the grid. The “spike” running across the O-rich AGB candidates consists of models with Teff warmer than 3500 K. The cloud of models with τ11.3 = 0.3 is seen at J − Ks ~ 3 mag. |
This CMD is used to distinguish between stars with oxygen-rich and carbon-rich dust chemistries (see Paper I and references therein) because of a clear division of the stellar distribution into two branches – the bluer branch, consisting of the O-rich AGB candidates, extends to brighter Ks magnitudes where the red supergiants are located. The red branch reaches a maximum brightness with increasing color, at which point the near-infrared flux becomes progressively attenuated by the increasing amount of circumstellar dust. This branch consists of the C-rich and extreme AGB candidates. The carbon stars along the boundary between the two branches (i.e., the bluest carbon stars) contain little or no dust around them; the GRAMS models for low optical depths (as well as the bare Aringer et al. (2009) photospheres) should lie along this boundary. Figure 3 shows the Ks vs. J − Ks CMD for SAGE AGB candidates, with the model grid points superimposed. As expected, most of the A09 photospheres lie along the O/C boundary on this diagram. The NIR fluxes of AGB stars are significantly affected by pulsation; for instance, the data of Whitelock et al. (2003) for selected LMC carbon stars suggests a median peak-to-peak variability of ~1.0 mag in the J and Ks bands. The agreement between the data and models is very good, considering that the A09 models do not include the effects of dynamical processes. A small number of A09 models possess much bluer colors and run across the O-rich AGB population. These are the warmer (Teff > 3500 K) photospheres which, as mentioned in Sect. 2.1.1, are probably more representative of the post-AGB phase. Overall, the GRAMS grid provides excellent coverage of the J − Ks colors observed for C-rich candidates and the extreme AGB candidates with detections in the near-infrared as well as carbon stars identified in the SAGE-Spec program. Photometry for OGLE LMC LPV 28579, which was studied in Paper III, is also shown. A series of vertical bands are visible in the models; these bands correspond to models with similar optical depths. For instance, the band with τ11.3 = 0.3 is seen just blueward of the photometry for OGLE LMC LPV 28579.
 |
Fig. 4 The [3.6] vs. J − [3.6] CMD, same symbols as in Fig. 3. The cloud of models with τ11.3 = 0.3 is seen at J − [3.6] ~ 5 mag. |
Aringer et al. (2009) noted that the H − Ks colors predicted by their models were systematically bluer than observations. They explained the disagreement at warmer temperatures as probably arising from the scaling of their C2 opacity. We observe a similar disagreement between our models and SAGE data in the H band. For this reason, we do not discuss the 2MASS color–color diagram or CMDs involving the H band.
4.2.2. [3.6] vs. J − [3.6] CMD
This CMD, shown in Fig. 4, is used in Blum et al. (2006) and Paper I to select extreme AGB stars. It is somewhat similar to the Ks vs. J − Ks CMD. The 3.6 μm magnitude is less affected by dust reddening and is therefore a better luminosity proxy for the extreme AGB candidates than the Ks magnitude. The GRAMS grid shows good coverage of the entire range of J − [3.6] color, reproducing the colors of almost all the extreme AGB stars with J-band detections. Once again, the models form vertical bands of increasing optical depth. OGLE LMC LPV 28579 is seen to lie on the τ11.3 = 0.3 group of models. However, there are many C-rich candidates with J − [3.6] colors up to ~ 0.3 mag bluer than the model photospheres. This discrepancy in color can arise from misclassification of O-rich AGB stars as carbon-rich (resulting from our somewhat artificial definition of the O/C boundary based on near-IR colors) as well as the photometric uncertainty associated with the SAGE 3.6 μm photometry for our list of AGB candidates, which can be as high as 0.2 − 0.3 mag13.
4.2.3. [24] vs. [8.0] − [24] CMD
Figure 5 shows the [24] vs. [8.0] − [24] CMD. In Paper I, we used this diagram to illustrate the “bright” and “faint” O-rich AGB populations observed in SAGE data. The carbon stars are superimposed over most of the bright O-rich population, while the faint population is clearly seen at [8.0]−[24] ≳ 1 mag and [24] ≳ 8 mag. The GRAMS models cover the entire range of MIPS 24 μm magnitudes observed for LMC carbon-stars. We note that there are several SAGE C-rich candidates as well as some SAGE-Spec carbon stars with [8.0]−[24] colors up to ~0.5 mag bluer than the bluest GRAMS models (in fact, bluer than the A09 photospheres). While this discrepancy might potentially hint at limitations of the underlying stellar models used to generate the grid, it is not inconsistent with the spread expected due to photometric uncertainties and variability. Using the uncertainties from Paper I for our C-rich and extreme AGB candidates, we estimate that the 3σ uncertainty in the [8.0] − [24] color can be up to about 0.55 mag (for more details, we refer the reader to the SAGE Data Products Description file). We calculate the median change in the color between the two epochs of SAGE observations for the variable stars from Vijh et al. (2009) to be around 0.1 mag. The observed discrepancy could thus be a combined effect of these uncertainties.
 |
Fig. 6 The Ks − [3.6] vs. J − Ks CCD, same symbols as in Fig. 3. The “arc" slightly blueward of OGLE LMC LPV 28579 consists of the τ11.3 = 0.3 models. The variation of the J − Ks color with effective temperature of the central star is depicted by the solid black curve for log g = 0, M = 2 M⊙, C/O = 2, τ11.3 = 0.6 and Rin = 7 Rstar (Teff decreases in the direction of increasing Ks − [3.6] color). |
There are also about 40 C-rich and extreme AGB candidates with [8] − [24] colors redder than the reddest models available (~3.3 mag). We note here that at redder colors the extreme AGB candidate sample may be contaminated by young stellar objects (see discussion in Paper I). However, three of the very red sources mentioned above – IRAS 04535–6616, 2MASS J05031662–6549450 and OGLE LMC LPV 16169 (not seen in Fig. 5 due to its extremely red color of 6.02 mag) – have been identified as carbon stars from their SAGE-Spec spectra. The first two are known C-rich AGB candidates; van Loon et al. (1997) discovered the near-IR counterpart of IRAS 04535–6616 and classified it as a carbon star based on its colors, while Kontizas et al. (2001) identified the carbonaceous nature of 2MASS J05031662–6549450 based on the detection of Swan C2 bands in its optical spectrum. OGLE LMC LPV 16169 is seen projected against NGC 1835, a low-metallicity ([Fe/H] = –1.8) globular cluster with a considerable number of RR Lyrae variables (e.g., Walker 1993). As an extremely dust-enshrouded star, its presence in the metal-poor, low-mass population of NGC 1835 makes OGLE LMC LPV 16169 a very interesting object worth studying in detail. To be able to model such extremely reddened sources, we will include higher optical depth models in future versions of the grid, and also consider more dust species.
4.2.4. Ks − [3.6] vs. J − Ks CCD
Figure 6 shows the Ks − [3.6] vs. J − Ks two-color diagram, which compares the emission from the warmest regions of the dust shell to that from the stellar photosphere. We show the GRAMS carbon-star grid superimposed on the SAGE AGB candidates from Paper I and the SAGE-Spec carbon stars on this diagram. The GRAMS models separate into groups of equal optical depth (in Fig. 6, OGLE LMC LPV 28579 is seen to fall close to the group of models with optical depth τ11.3 = 0.3). This is more obvious at redder colors because of the coarse sampling at higher optical depths in the current version of the model grid. The J − Ks color shows an interesting trend with effective temperature of the central star: for each set of models with the same optical depth and inner shell radius, decreasing Teff first causes a reddening in J − Ks, due to the increasing continuum flux in the Ks band relative to the J band. However, a lower Teff value also means increased strength in the ~2.3 μm CO absorption feature, which eventually counteracts the increase in continuum Ks flux and shifts the coolest models towards bluer J − Ks. This trend with Teff is depicted in Fig. 6 for the GRAMS models with log g = 0, M = 2 M⊙, C/O = 2, τ11.3 = 0.6 and Rin = 7 Rstar. At low optical depths (τ < 0.1), the Ks − [3.6] color is affected by the Ks band CO absorption feature as well as strong HCN + C2H2 absorption near 3 μm. With decreasing Teff, the Ks − [3.6] color first moves to bluer values, reaches a minimum then reverses this trend. This turnover trend is not seen in either color for GRAMS models with the highest optical depths (τ > 1) due to the large amounts of dust which overwhelms emission from the central star. For these models, a decrease in effective temperature is accompanied by a reddening in both colors.
The GRAMS models are able to reproduce the range of observed colors in this diagram. The colors of the bare photospheres are similar to the bluest carbon-star candidates on the boundary with the O-rich candidates, as would be expected if these represented carbon stars with little or no dust. However, at redder J − Ks colors, a significant fraction of C-rich and extreme AGB candidates are not covered by the models; in fact these sources are up to 0.8 mag bluer in Ks − [3.6] than the models. We have already mentioned that the photometric uncertainty in the 3.6 μm SAGE data can be up to a few tenths of a magnitude. This uncertainty alone is not sufficient to explain the observed discrepancy. LMC carbon stars are known to exhibit strong C2H2 absorption in the 3 μm region; as discussed previously, this can depress the flux in the 3.6 μm band. At higher dust optical depths, emission from the circumstellar dust may somewhat reduce this effect (see, e.g., van Loon et al. 2006), which would explain why our high τ11.3 models reproduce the colors of the reddest extreme AGB candidates on this plot.
4.2.5. [5.8] − [8.0] vs. [3.6] − [4.5] CCD
Figure 7 shows the IRAC-only two-color diagram. An increase in [3.6] − [4.5] color is accompanied by an increase in the [5.8] − [8.0] color for the extreme AGB candidates. This is simply a result of increasing dust emission in the mid-IR due to increasing optical depth. A significant fraction of the C-rich AGB candidates, however, show a decreasing [5.8] − [8.0] color with redder [3.6] − [4.5] colors. This trend is also seen to a smaller extent in the distribution of the bluest ([3.6] − [4.5] < 0) model grid points. There is a strong CO absorption feature in the 5.8 μm band (see, e.g., Fig. 2 in Paper III) which could be filled in by emission from dust with increasing optical depth.
The model colors agree well with those observed for the data, especially for the extreme AGB candidates. The photometric uncertainties as well as pulsation amplitudes in the IRAC bands are lower than in the near-IR, which may explain the smaller spread in the data around the models. At the bluest colors, there are many C-rich AGB candidates that are bluer than the model photospheres. This could be explained, once again, on the basis of the absorption features in the IRAC 3.6 (HCN + C2H2) and 5.8 μm (CO) bands.
We also note that the carbon-star models have continuous coverage of the extreme AGB candidates over the entire range of colors. Compare this to the oxygen-rich models from Paper IV, which do not reproduce the colors of the stars in the range 0.2 < [3.6] − [4.5] < 1 mag (see Fig. 5 and the discussion in Sect. 4.1.2 in Paper IV). This difference in relative coverage can be used to identify the chemical types of the extreme AGB candidates through SED fitting.
5. Discussion
5.1. Preliminary SED fits
5.1.1. Fits to the van Loon et al. (1999) sources
We are ultimately interested in fitting the SEDs of the entire SAGE AGB star candidate list. In this section, we evaluate simple chi-squared fits to the SEDs of spectroscopically confirmed carbon stars in the LMC for which detailed models already exist in the literature. Specifically, we consider the sources studied by van Loon et al. (1999) and Groenewegen et al. (2009, hereafter, vL99 and G09 respectively). We also compare the results of such SED fitting of the carbon star OGLE LMC LPV 28579 with the parameters derived from detailed modeling of this source in Paper III. The chi-squared fitting considered in this section allows a simple consistency check of the GRAMS grid. This technique is able to predict accurate luminosities and dust mass-loss rates (see Paper III), but it may not be able to produce strong constraints on other parameters. For instance, we expect that a set of reasonable fits to a reddened source (e.g., a carbon star from the vL99 or G09 sample) will exhibit considerable degeneracy in predicted stellar parameters. In what follows, therefore, we only compare the luminosities and dust mass-loss rates for the vL99 and G09 sources with the corresponding GRAMS best-fit values. We use the gas:dust ratio provided in vL99 and G09 (500 and 200 respectively) to convert their total mass-loss rates to dust rates. Our υexp value is kept fixed at the same value as that of G09. However, vL99 use a luminosity-dependent expansion velocity given by 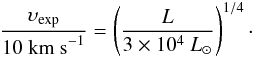 (1)For each vL99 source, we compare both the “scaled” (υexp as in Eq. (1)) and “unscaled” (υexp = 10 km s-1) versions of the dust mass-loss rate with our best-fit value in Sect. 5.1.1.
(1)For each vL99 source, we compare both the “scaled” (υexp as in Eq. (1)) and “unscaled” (υexp = 10 km s-1) versions of the dust mass-loss rate with our best-fit value in Sect. 5.1.1.
 |
Fig. 8 GRAMS fits to the SEDs of four carbon stars modeled by van Loon et al. (1999). |
Evolved AGB stars have significant variability amplitudes at visible wavelengths; this variation must be taken into account in order to reconstruct the SED from multi-wavelength photometry obtained at different pulsation phases. We will consider these details in future papers. Presently we fit only the JHKs and Spitzer bands for these sources. As discussed in Sect. 4.1, our models provide substantial coverage of the range of observed luminosities. Moreover, at the moment we would like to demonstrate the general agreement between fits from our model grid and those from detailed studies. For these reasons, we do not vary the model luminosities in order to find the best fit. We will treat the luminosity scale as an extra free parameter when we consider SED fitting in detail.
5.1.2. Fits to the Groenewegen et al. (2009) sources
In their paper, van Loon et al. modeled 31 carbon stars (57 LMC evolved stars total) with ISO photometry supplemented by ground-based near-IR photometry. ISO spectroscopy was also available for 10 of these stars. In Paper I, we used the vL99 mass-loss rates to estimate the total dust injection rate into the LMC from the entire AGB population. We found nearest-neighbor matches in our AGB candidate list (see Paper I) for all of the van Loon et al. carbon stars14. We fit GRAMS models to each of these stars, fitting only the near- and mid-IR bands as previously mentioned. Figure 8 shows best-fit GRAMS spectra for four of the vL99 stars. Overall, our best-fit spectra reproduce the observed photometry well. The best-fit luminosities and dust mass-loss rates also show a good agreement with the values calculated by van Loon et al., as shown in Figs. 10 and 11. These plots demonstrate the power of the simple model grid fitting technique to obtain reliable luminosities and mass-loss rates. The GRAMS luminosities are within a factor of ~1.75 of the vL99 values. The median discrepancy is –13%, with a standard deviation of 29% around this value. With the exception of TRM 45, for which we obtain a poor fit, our mass-loss rates agree with those of vL99 (unscaled) to within a factor of 4.5. Our rates are discrepant from the unscaled vL99 rates by a median value of 8% with a standard deviation of 83% and from the scaled versions by –13% with a standard deviation of 125%.
Groenewegen et al. used Spitzer IRS spectra to model 101 Magellanic Cloud carbon stars, using multi-epoch photometry to constrain the optical variability. Their dataset included 68 LMC carbon stars. We found counterparts in our list of AGB candidates for all but three of the G09 stars – MSX LMC 95, MSX LMC 1384 and NGC 1978 IR1. However, on searching the SAGE Archive point source lists, we were able to find a match for MSX LMC 95 in the IRAC Epoch 1 Archive. We also found detections for MSX LMC 1384 and NGC 1978 IR1 in the IRAC Mosaic Photometry catalog. Figure 9 shows the best-fit GRAMS spectra for four carbon stars studied by Groenewegen et al. (2009). The best-fit luminosities and dust mass-loss rates for the entire set are compared with the G09 estimates in Figs. 10 and 11 respectively. Once again, the luminosities predicted by GRAMS SED fitting are within a factor of ~1.75 of the values determined from detailed modeling. The median discrepancy is very low at –1%, with a standard deviation of 31%. However, the behavior of the mass-loss rates is different from that observed with the vL99 sample.
 |
Fig. 9 GRAMS fits to the SEDs of four carbon stars modeled by Groenewegen et al. (2009). |
While the luminosities are more or less evenly distributed about the 1:1 line for GRAMS fits to both the vL99 and G09 sources, our dust mass-loss rate estimates for most of the G09 sources are systematically lower than theirs by a factor of about 2–4. The median discrepancy in this case is –168%, with a standard deviation of almost 200% around this value. This discrepancy is due to our different choice of amorphous carbon optical constants. The Rouleau & Martin (1991) optical constants used in G09 give rise to a consistently lower absorption efficiency over the ~0.1–100 μm range (see, e.g., Fig. 1 of Suh 2000), thus requiring a higher dust shell mass in order to fit a given mid-IR flux. This in turn increases the calculated mass-loss rate. In order to verify the effect of this change, we performed detailed radiative transfer calculations on ten of the G09 sources using the GRAMS best-fit parameters from SED fitting as input, with two modifications: we used the Rouleau & Martin (1991) optical constants for amorphous carbon and set the SiC mass fraction to the value determined in G09 for each star. We found that in general the Rouleau & Martin (1991) optical constants gave mass-loss rates that were 2 − 4 times higher than those predicted by the GRAMS best fits, explaining the systematic offset observed in Fig. 11. For comparison, the Preibisch et al. (1993) amorphous carbon optical constants used by van Loon et al. (1999) have absorption efficiencies similar to that of the Zubko et al. (1996) dust model. We computed 2Dust models for five of the vL99 sources with the Preibisch et al. (1993) dust constants and found that the resulting dust mass-loss rates were at most 12% different from those predicted by the corresponding GRAMS best-fit models. In developing this first version of the model grid, we used a single set of dust properties. We will investigate the effect of varying the dust properties in detail in future versions of the grid.
 |
Fig. 10 Luminosities calculated from GRAMS SED fitting plotted against the luminosities obtained from detailed modeling by van Loon et al. (1999) (squares) and Groenewegen et al. (2009) (circles). The solid line represents a 1:1 agreement. |
 |
Fig. 11 Same as Fig. 10, but for dust mass-loss rates. Also shown are lines along which the GRAMS mass-loss rate is lower than the rates from detailed modeling (vL99 or G09) by a factor of 2 and 4 (dotted and dashed line respectively). |
 |
Fig. 12 GRAMS best-fit for TRM 88. The best-fit luminosity and mass-loss rates are more consistent with the vL99 estimates. |
TRM 88 was modeled by both vL99 and G09. Figure 12 shows the GRAMS best-fit spectrum to the observed photometry of TRM 88. The GRAMS best-fit luminosity (11 700 L⊙) and mass-loss rate (3.4 × 10-9 M⊙ yr-1) are closer to the values estimated by van Loon et al. In this case, the GRAMS fit is somewhat poor as it under-predicts the mid-IR emission resulting in a low mass-loss rate. The marginal quality of the fit is partly due to the fact that we have not taken the near-IR variability into account; the fluxes are currently weighted by their photometric errors which are quite small. The best-fit model has an optical depth τ11.3 = 0.1 and Rin = 12Rstar. We do not have enough resolution in optical depth (the closest higher optical depth is 0.2) and inner radius (we only explore four values) to provide a better fit to the data. Despite these details, we find good agreement with the vL99 results.
5.1.3. Fit to OGLE LMC LPV 28579
 |
Fig. 13 Best fit SEDs to the SAGE photometry (dots) and SAGE-Spec IRS spectrum for OGLE LMC LPV 28579. The solid curve is a result of the detailed model from Paper III, while the dashed curve is the GRAMS best-fit. A comparison of the fit parameters is also shown. |
In Paper III we presented a 2Dust model best-fit model for OGLE LMC LPV 28579. The dust properties determined for this best-fit model were subsequently used for the entire carbon-star grid. Our detailed model suggested a luminosity of 6580 L⊙ for the SAGE Epoch 1 observations, an optical depth of τ11.3 = 0.27, and a dust mass-loss rate of 2.5 × 10-9 M⊙ yr-1. The mass-loss rate derived for OGLE LMC LPV 28579 was found to be consistent with the rates derived from various empirical relationships (see discussion in Paper III for details). In this paper we fit the observed SED for OGLE LMC LPV 28579 using models from the GRAMS grid. This serves as a consistency check for the model grid. The best-fit GRAMS SED gives a luminosity of 6170 L⊙, τ11.3 = 0.3 and a dust mass-loss rate of 2.4 × 10-9 M⊙ yr-1. These numbers are within a few percent of the values calculated in Paper III. Figure 13 compares the best-fit models from both papers with the SAGE Epoch 1 photometry and SAGE-Spec spectrum for OGLE LMC LPV 28579. We also obtain good agreement with the values obtained for the optical depth, dust shell inner radius as well as temperature at the inner radius.
6. Summary
We constructed a grid of carbon star models using the radiative transfer code 2Dust and for a range of various stellar and dust shell parameters. We intend to use these models in conjunction with our models for O-rich AGB and red supergiant stars described in Sargent et al. (2011) to investigate the mass-loss return from evolved stars to the LMC. The models can also be used for similar estimates from large photometric samples of C-rich AGB stars. The grid covers luminosities from 2000 L⊙ to 26 000 L⊙ by using model photospheres spanning temperatures in the range 2600 − 4000 K. Assuming spherically symmetric dust shells, and constant expansion velocity and mass-loss rate, we perform radiative transfer using the 2Dust code for 11.3 μm optical depths ranging from 10-3 to 4 and values for the inner radii of 1.5, 3, 4.5, 7 and 12 times the stellar radius. This results in over 12 000 models with dust temperatures under 1800 K, with dust mass-loss rates in the range 10-12 − 10-7 M⊙ yr-1.
We synthesize photometry for these models in optical as well as near- and mid-infrared bands. The entire set of models, including spectra and synthetic photometry, will soon be available at the 2Dust website at STScI. We compare the resulting colors and magnitudes with those observed for AGB candidates in the SAGE survey and confirmed AGB stars from the SAGE-Spec survey, finding good overall agreement with these data. Using a chi-squared fitting routine, we obtain best-fit spectra, luminosities and mass-loss rates for spectroscopically identified carbon stars in the van Loon et al. (1999) and Groenewegen et al. (2009) samples. The luminosities predicted from simple fitting to the photometry are in good agreement with those determined by these detailed models. Our mass-loss rates for the van Loon et al. sample agree well with their values. However, our rates for the Groenewegen et al. sample are lower by a factor of 2–4, most likely due to a different choice of dust properties. We find excellent agreement between the results of detailed modeling of OGLE LMC LPV 28579 from Paper III and the fitting employed in this work.
One of the aims of our study is to provide a general-use fitter that can be applied to large sets of photometric data. This will be the focus of one of our future papers. The GRAMS grid will enable the assessment of mass-loss return from galaxy-wide point source catalogs from projects such as SAGE. While most extreme AGB stars are probably carbon-rich, some are very bright OH/IR stars. Currently, there is no way to clearly distinguish between these sources with photometry alone. We hope that a comparison of our results with ongoing studies such as AKARI and WISE that include filters sensitive to silicate and SiC features will enable us to define the separation between C-rich and O-rich sources in this extreme regime.
We calculate luminosities higher than the classical AGB limit (Mbol = −7.1, Paczyński 1970) for a handful of our extreme AGB candidates; while a majority of these are well-studied O-rich AGB stars, there are no carbon stars in this subsample.
For the GRAMS grid, averages over grain size space are computed by weighting according to grain surface area (Harrington averaging scheme, Harrington et al. 1988).
The 2Dust manual is available at http://www.stsci.edu/science/2dust/2dust_manual.pdf.gz
The MCPS magnitudes were placed on the Johnson-Kron-Cousins UBVI system. The detector quantum efficiency (QE) curve available on the Las Campanas Observatory website at http://www.lco.cl/lco/telescopes-information/irenee-du-pont/instruments/specs/du-pont-telescope-direct-ccd-camera-ccd was extrapolated to 0.3 μm. The QE was also assumed to drop linearly to zero from its value at 0.84 μm, the last wavelength provided on the graph, to 1.13 μm, the wavelength corresponding to a photon energy of 1.1 eV, which is the energy of the band gap of silicon. The B- and V-band transmission profiles were obtained from http://www.lco.cl/lco/telescopes-information/irenee-du-pont/instruments/website/direct-ccd-manuals/direct-ccd-manuals/3x3-filters-for-ccd-imaging (Harris B profile LC-3013 and Harris V profile LC-3009 respectively). The U- and I-band filter profiles were obtained from I. Thompson (2009, priv. comm.).
The 2MASS filter relative spectral responses (RSRs) derived by Cohen et al. (2003) were obtained from the 2MASS All-Sky Data Release Explanatory Supplement, available at http://www.ipac.caltech.edu/2mass/releases/allsky/doc/ sec6_4a.html
RSRs available at http://ssc.spitzer.caltech.edu/irac/ calibrationfiles/spectralresponse
RSR available at http://ssc.spitzer.caltech.edu/mips/ calibrationfiles/spectralresponse/
Filter response curves available at http://www.ir.isas.jaxa.jp/ASTRO-F/Observation/RSRF/ IRC_FAD/index.html and http://www.astro.ucla.edu/~wright/WISE/passbands.html respectively.
The luminosities in Paper I (Fig. 4), obtained using the trapezoidal rule, were overestimated for the brightest stars because of erroneous coefficients in the sum. In the present paper we have used the correct coefficients, leading to lower luminosities as shown in Fig. 2.
Also see the SAGE Data Products Description file available at http://irsa.ipac.caltech.edu/data/SPITZER/SAGE/doc/ SAGEDataProductsDescription_Sep09.pdf
We excluded IRAS 05289–6617 from further analysis because it lacked detections in the optical and near-IR bands as well as most of the Spitzer bands (see discussion in van Loon et al. 1999).
Acknowledgments
We would like to thank our referee, Jacco van Loon, for his constructive comments which helped improve the quality of the paper. We also thank Angela Speck for her valuable insight on dust condensation temperatures. This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under NASA contract 1407. We acknowledge funding from the NAG5-12595 grant and the SAGE-LMC Spitzer grant 1275598. The authors would also like to thank Bernie Shiao at STScI for his invaluable assistance with the SAGE database.
References
- Aringer, B., Girardi, L., Nowotny, W., Marigo, P., & Lederer, M. T. 2009, A&A, 503, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, R. D., Mould, J. R., Olsen, K. A., et al. 2006, AJ, 132, 2034 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J.-P., Reach, W. T., Paradis, D., et al. 2008, AJ, 136, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Danchi, W. C., Bester, M., Greenhill, L. J., et al. 1995, Ap&SS, 224, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Dufour, R. J., Shields, G. A., & Talbot, R. J., Jr. 1982, ApJ, 252, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Epchtein, N., de Batz, B., Copet, E., et al. 1994, Ap&SS, 217, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Frogel, J. A., Mould, J., & Blanco, V. M. 1990, ApJ, 352, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Gautschy-Loidl, R., Höfner, S., Jørgensen, U. G., & Hron, J. 2004, A&A, 422, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Scoville, N. 1976, ApJ, 205, 144 [Google Scholar]
- González-Lópezlira, R. A., Bruzual-A., G., Charlot, S., Ballesteros-Paredes, J., & Loinard, L. 2010, MNRAS, 403, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T. 2006, A&A, 448, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T., Sloan, G. C., Soszyński, I., & Petersen, E. A. 2009, A&A, 506, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrington, J. P., Monk, D. J., & Clegg, R. E. S. 1988, MNRAS, 231, 577 [NASA ADS] [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Höfner, S. 2007, Why Galaxies Care About AGB Stars: Their Importance as Actors and Probes, 378, 145 [Google Scholar]
- Höfner, S. 2009, AIP Conf. Ser., 1094, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Höfner, S., & Dorfi, E. A. 1997, A&A, 319, 648 [NASA ADS] [Google Scholar]
- Höfner, S., Gautschy-Loidl, R., Aringer, B., & Jørgensen, U. G. 2003, A&A, 399, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, I., Jr. 1983, ApJ, 275, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Ita, Y., Onaka, T., Kato, D., et al. 2008, PASJ, 60, 435 [Google Scholar]
- Jura, M. 1986, ApJ, 303, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Karakas, A. I., Lattanzio, J. C., & Pols, O. R. 2002, PASA, 19, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Kemper, F., Woods, P. M., Antoniou, V., et al. 2010, PASP, 122, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S.-H., Martin, P. G., & Hendry, P. D. 1994, ApJ, 422, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Kontizas, E., Dapergolas, A., Morgan, D. H., & Kontizas, M. 2001, A&A, 369, 932 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraemer, K. E., Sloan, G. C., Price, S. D., & Walker, H. J. 2002, ApJS, 140, 389 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Maraston, C. 1998, MNRAS, 300, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., & Girardi, L. 2007, A&A, 469, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., & Bressan, A. 1999, A&A, 344, 123 [NASA ADS] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuura, M., Zijlstra, A. A., van Loon, J. Th., et al. 2005, A&A, 434, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuura, M., Barlow, M. J., Zijlstra, A. A., et al. 2009, MNRAS, 396, 918 [NASA ADS] [CrossRef] [Google Scholar]
- Mattsson, L., Höfner, S., & Herwig, F. 2007, A&A, 470, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., Wahlin, R., Höfner, S., & Eriksson, K. 2008, A&A, 484, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattsson, L., Wahlin, R., & Höfner, S. 2010, A&A, 509, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meixner, M., Ueta, T., Bobrowsky, M., & Speck, A. 2002, ApJ, 571, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Meixner, M., Gordon, K. D., Indebetouw, R., et al. 2006, AJ, 132, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, 369 [Google Scholar]
- Paczyński, B. 1970, Acta Astron., 20, 47 [NASA ADS] [Google Scholar]
- Pégourié, B. 1988, A&A, 194, 335 [Google Scholar]
- Preibisch, T., Ossenkopf, V., Yorke, H. W., & Henning, T. 1993, A&A, 279, 577 [NASA ADS] [Google Scholar]
- Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, B. A., Srinivasan, S., Meixner, M., et al. 2010, ApJ, 716, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, B. A., Srinivasan, S., & Meixner, M. 2011, ApJ, 728, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Speck, A. K., Cami, J., Markwick-Kemper, C., et al. 2006, ApJ, 650, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Speck, A. K., Corman, A. B., Wakeman, K., Wheeler, C. H., & Thompson, G. 2009, ApJ, 691, 1202 [NASA ADS] [CrossRef] [Google Scholar]
- Srinivasan, S., Meixner, M., Leitherer, C., et al. 2009, AJ, 137, 4810 [NASA ADS] [CrossRef] [Google Scholar]
- Srinivasan, S., Sargent, B. A., Matsuura, M., et al. 2010, A&A, 524, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suh, K.-W. 2000, MNRAS, 315, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Ueta, T., & Meixner, M. 2003, ApJ, 586, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Ueta, T., Meixner, M., & Bobrowsky, M. 2000, ApJ, 528, 861 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F., Feast, M. W., Whitelock, P. A., & Laney, C. D. 2007, MNRAS, 379, 723 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T., Zijlstra, A. A., Whitelock, P. A., et al. 1997, A&A, 325, 585 [NASA ADS] [Google Scholar]
- van Loon, J. T., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 [NASA ADS] [Google Scholar]
- van Loon, J. T., Marshall, J. R., Cohen, M., et al. 2006, A&A, 447, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loon, J. T., Cohen, M., Oliveira, J. M., et al. 2008, A&A, 487, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vijh, U. P., Meixner, M., Babler, B., et al. 2009, AJ, 137, 3139 [NASA ADS] [CrossRef] [Google Scholar]
- Wachter, A., Schröder, K.-P., Winters, J. M., Arndt, T. U., & Sedlmayr, E. 2002, A&A, 384, 452 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, A. R. 1993, AJ, 105, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Wallerstein, G., & Knapp, G. R. 1998, ARA&A, 36, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, M. D., & Nikolaev, S. 2001, ApJ, 548, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Whitelock, P. A., Feast, M. W., van Loon, J. T., & Zijlstra, A. A. 2003, MNRAS, 342, 86 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Woitke, P. 2006, A&A, 452, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, P. M., Oliveira, J. M., Kemper, F., et al. 2011, MNRAS, 411, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L. 2009, ASP Conf. Ser., 418, 359 [NASA ADS] [Google Scholar]
- Zebrun, K., Soszynski, I., Wozniak, P. R., et al. 2001, Acta Astron., 51, 317 [NASA ADS] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Aringer et al. (2009) photosphere spectrum (gray) with Teff = 3300 K and log (g [cm s-1]) = −0.2, showing many strong features at shorter wavelengths. The vertical dashes show the wavelengths at which this spectrum was sampled for input to 2Dust. The resulting GRAMS output model with optical depth τ11.3 = 2 × 10-3 (black) incorporates some of the variation in the optical. |
| In the text | |
 |
Fig. 2 Top: the distribution of luminosities of LMC C-rich (solid) and extreme (dotted) AGB candidates from SAGE. The classical AGB luminosity limit is also shown (dashed line). Bottom: the range of luminosities and dust mass-loss rates covered by the GRAMS carbon star models. As discussed in Sect. 3.3, only models with Tin < 1800 K are shown. Gray symbols show the luminosities and mass-loss rates of LMC carbon stars as calculated from detailed modeling by van Loon et al. (1999) (triangles) and Groenewegen et al. (2009) (diamonds). |
| In the text | |
 |
Fig. 3 the Ks vs. J − Ks CMD shows the model grid (light blue points) overlaid onto the SAGE AGB candidates from Paper I (gray: O-rich, orange: C-rich and pink: extreme). The yellow diamonds are SAGE sources identified as carbon-rich from their SAGE-Spec spectra. The large red triangle is OGLE LMC LPV 28579. Also shown are the Aringer et al. (2009) photospheres (green squares) used to generate the grid. The “spike” running across the O-rich AGB candidates consists of models with Teff warmer than 3500 K. The cloud of models with τ11.3 = 0.3 is seen at J − Ks ~ 3 mag. |
| In the text | |
 |
Fig. 4 The [3.6] vs. J − [3.6] CMD, same symbols as in Fig. 3. The cloud of models with τ11.3 = 0.3 is seen at J − [3.6] ~ 5 mag. |
| In the text | |
 |
Fig. 5 The [24] vs. [8.0] − [24] CMD, same symbols as in Fig. 3. |
| In the text | |
 |
Fig. 6 The Ks − [3.6] vs. J − Ks CCD, same symbols as in Fig. 3. The “arc" slightly blueward of OGLE LMC LPV 28579 consists of the τ11.3 = 0.3 models. The variation of the J − Ks color with effective temperature of the central star is depicted by the solid black curve for log g = 0, M = 2 M⊙, C/O = 2, τ11.3 = 0.6 and Rin = 7 Rstar (Teff decreases in the direction of increasing Ks − [3.6] color). |
| In the text | |
 |
Fig. 7 The [3.6] − [4.5] vs. [5.8] − [8.0] CCD, same symbols as in Fig. 3. |
| In the text | |
 |
Fig. 8 GRAMS fits to the SEDs of four carbon stars modeled by van Loon et al. (1999). |
| In the text | |
 |
Fig. 9 GRAMS fits to the SEDs of four carbon stars modeled by Groenewegen et al. (2009). |
| In the text | |
 |
Fig. 10 Luminosities calculated from GRAMS SED fitting plotted against the luminosities obtained from detailed modeling by van Loon et al. (1999) (squares) and Groenewegen et al. (2009) (circles). The solid line represents a 1:1 agreement. |
| In the text | |
 |
Fig. 11 Same as Fig. 10, but for dust mass-loss rates. Also shown are lines along which the GRAMS mass-loss rate is lower than the rates from detailed modeling (vL99 or G09) by a factor of 2 and 4 (dotted and dashed line respectively). |
| In the text | |
 |
Fig. 12 GRAMS best-fit for TRM 88. The best-fit luminosity and mass-loss rates are more consistent with the vL99 estimates. |
| In the text | |
 |
Fig. 13 Best fit SEDs to the SAGE photometry (dots) and SAGE-Spec IRS spectrum for OGLE LMC LPV 28579. The solid curve is a result of the detailed model from Paper III, while the dashed curve is the GRAMS best-fit. A comparison of the fit parameters is also shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


