| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201116948 | |
| Published online | 20 June 2011 | |
A deep all-sky census of the Hyades⋆
1
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität
Heidelberg, Mönchhofstraße
12-14, 69120
Heidelberg,
Germany
e-mail: roeser@ari.uni-heidelberg.de;
elena@ari.uni-heidelberg.de;
apiskunov@ari.uni-heidelberg.de;
nkhar@ari.uni-heidelberg.de
2
Institute of Astronomy of the Russian Acad. Sci.,
48 Pyatnitskaya Str.,
109017
Moscow,
Russia
e-mail: piskunov@inasan.rssi.ru
3
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482
Potsdam,
Germany
e-mail: apiskunov@aip.de; nkharchenko@aip.de;
rdscholz@aip.de
4
Main Astronomical Observatory, 27 Academica Zabolotnogo Str., 03680
Kiev,
Ukraine
e-mail: nkhar@mao.kiev.ua
Received:
24
March
2011
Accepted:
12
May
2011
Aims. On the basis of the PPMXL catalogue we perform an all-sky census of the Hyades down to masses of about 0.2 m⊙ in a region up to 30 pc from the cluster centre.
Methods. We use the proper motions from PPMXL in the convergent point method to determine probable kinematic members. From 2MASS photometry and CMC14 r′-band photometry, we derive empirical colour-absolute magnitude diagrams and, finally, determine photometric membership for all kinematic candidates.
Results. This is the first deep (r′ ≤ 17) all-sky survey of the Hyades allowing a full three-dimensional analysis of the cluster. The survey is complete down to at least MKs = 7.3 or 0.25 m⊙. We find 724 stellar systems co-moving with the bulk Hyades space velocity, which represent a total mass of 435 m⊙. The tidal radius is about 9 pc, and 275 m⊙ (364 systems) are gravitationally bound. This is the cluster proper. Its mass density profile is perfectly fitted by a Plummer model with a central density of 2.21 m⊙ pc-3 and a core radius of rco = 3.10 pc, while the half-mass radius is rh = 4.1 pc. There are another 100 m⊙ in a volume between one and two tidal radii (halo), and another 60 m⊙ up to a distance of 30 pc from the centre. Strong mass segregation is inherent in the cluster. The present-day luminosity and mass functions are noticeably different in various parts of the cluster (core, corona, halo, and co-movers). They are strongly evolved compared to presently favoured initial mass functions. The analysis of the velocity dispersion of the cluster shows that about 20% of its members must be binaries. As a by-product, we find that presently available theoretical isochrones are not able to adequately describe the near-infrared colour-absolute magnitude relation for those cluster stars that are less massive than about 0.6 m⊙.
Key words: open clusters and associations: individual: Hyades / stars: luminosity function, mass function / Hertzsprung-Russell and C-M diagrams
Full Table 1 is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/531/A92
© ESO, 2011
1. Introduction
Without doubt, the Hyades are one of the best-studied open clusters in our Galaxy. Its proximity to the Sun has made it an interesting target for centuries, so it is impossible here to give appropriate credit to all the astronomers who worked on the Hyades. With no claim to completeness, we mention here the studies by van Bueren (1952), van Altena (1969), Pels et al. (1975), Hanson (1975), Gunn et al. (1988), and Reid (1992). Recently, Hogan et al. (2008) have surveyed some 275 deg2 of the Hyades based on a combination of 2MASS and UKIDSS observations.
Loosely speaking, we distinguish between pencil beam studies and those relying on an all-sky survey. All the above-mentioned studies are pencil beam studies since they only cover a limited field-of-view, even if it is as large as 275 deg2 in the case of Hogan et al. (2008). On the sphere, this only corresponds to a distance of 7.3 pc from the Hyades centre. Pencil beam studies are based on dedicated observations and may comprise a variety of astrophysical parameters. They can only indirectly reveal the full three-dimensional structure of the cluster.
An all-sky survey allows studying the cluster in its full three-dimensional extent, but one usually relies on the few available data entries in the survey, e.g. proper motions or photometry in a few bands. Of these studies we mention the work by Schwan (1991) using the old PPM and FK5 catalogues and the papers based on the Hipparcos observations by Perryman et al. (1998) and de Bruijne et al. (2001). These all-sky studies were restricted to stars brighter than about V ≈ 11 to 12 (Hipparcos) without being complete to this magnitude.
As far as membership of individual stars in the Hyades cluster is concerned, the results of the studies above were collected in the Prosser & Stauffer (P&S) database (presently available from Stauffer, 2010, priv. comm.) some fifteen years ago. Prosser & Stauffer’s database was assumed to be complete down to 0.1 m⊙ (Bouvier et al. 2008). Much effort has since been dedicated to the search for very low-mass (below 0.1 m⊙) Hyades candidates. These attempts have been partly unsuccessful (Gizis et al. 1999), or resulted in the confirmation of membership of only one M 8.5 dwarf (Reid & Hawley 1999). Hogan et al. (2008) report the detection of 12 L-dwarfs in a 275 deg2 field of view, and Bouvier et al. (2008) describe the detection of two brown dwarfs in an area of 16 deg2 around the Hyades centre.
Using PPMXL (Roeser et al. 2010) we can, for the first time, extend previous studies by going as deep in magnitude as the pencil beam studies and still performing an all-sky survey. We supply a complete sample of candidates within 30 pc from the centre, determine individual distances to the stars, and so resolve the full three-dimensional spatial structure of the Hyades, and its immediate neighbourhood, from the most massive stars down to almost 0.1 m⊙ by an application of the convergent method to the proper motions in PPMXL.
The paper has the following structure: in the next section we briefly introduce the observational dataset from PPMXL we are using. In Sect. 3 we describe the convergent point method. Then, in Sect. 4 we define our criteria for membership determination and discuss the amount of possible contamination of the sample. We compare the empirically derived colour-absolute magnitude diagram of the Hyades with theoretical isochrones in Sect. 4.4. In Sect. 5 we reveal the spatial structure of the Hyades and derive the shape parameters of the cluster. Section 6 is devoted to the present-day luminosity and mass functions. Then we discuss the internal velocity dispersion in Sect. 7, and, finally we summarise our results in Sect. 8.
2. Observations
As primary data of observations we use the PPMXL catalogue (Roeser et al. 2010). PPMXL contains positions and proper motions on the ICRS for some 900 million stars (from the brightest stars down to about V ≈ 20) and covers the complete sky. PPMXL also gives low-accuracy photometry from USNO-B1.0 (Monet et al. 2003), a subset of 410 million stars contains 2MASS (Skrutskie et al. 2006) photometry. The typical individual mean errors of the proper motions range from better than 2 mas/y for the brightest stars with Tycho-2 (Høg et al. 2000) observations to more than 10 mas/y for the faintest stars in the region south of –30° declination. For the 2.5 million brightest stars Tycho-2 B,V photometry is available.
For this work we cross-matched PPMXL with UCAC3 (Zacharias et al. 2010) and CMC14 (Copenhagen Univ. Obs. et al. 2006). We combined the positions and proper motions of PPMXL with the positions from CMC14 and from UCAC3. The latter had to be reconstructed because the original positions of UCAC3 are not published. With these data we performed a weighted least-squares adjustment to derive new, improved, mean positions and proper motions. In the following we refer to this subset of PPMXL as the Carlsberg-UCAC (CU) subset. It turned out that the most important feature in the CU is the accurate photometry in at least one optical band from CMC14, the r′-magnitudes in the SDSS system. CMC14 observed the sky in the declination range from –30 deg to about +52 deg, and it is 95% complete down to r′ = 16.8 and 80% to 17.0. Then completeness drops rapidly (when compared to SDSS). Its limiting magnitude is r′ = 17.8 (Copenhagen Univ. Obs. et al. 2006). The CU contains some 140 million stars, 90 million of which have r′-magnitudes from CMC14.
The astrometric information for the ≈120 000 Hipparcos stars is taken from the new reduction of the Hipparcos data by van Leeuwen (2007) instead of the data contained in PPMXL, the cross-matches with 2MASS are kept as are the B, V magnitudes from Tycho-2 of the Hipparcos stars.
3. Convergent point method
For a nearby open cluster like the Hyades the convergent point method is a suitable tool to determine membership when only proper motions and (for a representative subset) radial velocities are available. The method is textbook knowledge (see, e.g. Smart 1968), and an excellent recent description can be found in van Leeuwen (2009). Hence, we will not repeat a description here.
In this paper, we did not apply the convergent point method from scratch, but used the six-dimensional phase space parameters for the Hyades cluster centre from Table 7 in van Leeuwen (2009). We use the galactic rectangular coordinate system X,Y,Z with origin in the Sun, and axes pointing to the Galactic Centre (X), to the direction of galactic rotation (Y), and the North Galactic Pole (Z). In galactic coordinates, we adopt [xc, yc, zc] = [–43.1, 0.7, –17.3] pc for the position and [uc, vc, wc] = [–41.1, –19.2, –1.4] km s-1 for the mean motion of the cluster centre. In other words, the stars most accurately measured, Hipparcos stars from the new reduction by van Leeuwen (2007), determine the position and the motion of the Hyades cluster. Then the direction of the convergent point is also given, see Eq. (7) in van Leeuwen (2009).
Given the phase space parameters from van Leeuwen (2009), we search for all stars in the sky (in this case the PPMXL catalogue, resp. the CU subset) which have proper motions consistent with the given space velocity vc = [uc,vc,wc] of the cluster centre. For each line-of-sight (α,δ) we can then express the vector of the space velocity by one component vr parallel to the line-of-sight, the radial velocity, and one perpendicular to it vt, the tangential velocity (in the tangential plane). It is easy to see that, for a Hyades member, the component of vc parallel to the line-of-sight only depends on (α,δ), and not on the distance of a star from the Sun. Hence, the same is true for the component of vc in the tangential plane. The tangential velocity can be split into one component v∥ in the direction to the convergent point, and a component v⊥ perpendicular to it. The expectation value of the latter is zero.
The PPMXL catalogue gives for each star the positions (α,δ) and the proper motions (μα, μδ), i.e. four of the six components of the phase space coordinates, the radial velocity vr and the distance d from the Sun being the remaining two. A necessary condition for a star to be a kinematic member of the Hyades cluster is: 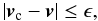 (1)where v = [u,v,w] is the space velocity of a candidate and ϵ is a suitable bound. As long as the radial velocity vr is not measured, we adopt as vr the projection of the cluster motion vc to the line-of-sight.
(1)where v = [u,v,w] is the space velocity of a candidate and ϵ is a suitable bound. As long as the radial velocity vr is not measured, we adopt as vr the projection of the cluster motion vc to the line-of-sight.
At each position (α,δ) the proper motions (μα, μδ) can be rotated into the direction of v∥ and v⊥. We call these motion components μ∥ and μ⊥. The remaining parameter, distance d or parallax ϖ, is given by 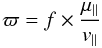 (2)where f = 4.74 km s-1 kpc-1 and ϖ is the so-called secular parallax. As the method fixes vr as explained above and ϖ from Eq. (2), the necessary condition (Eq. (1)) for kinematic membership shrinks to |v⊥| ≤ ϵ. Since the expectation value of v⊥ is zero,
(2)where f = 4.74 km s-1 kpc-1 and ϖ is the so-called secular parallax. As the method fixes vr as explained above and ϖ from Eq. (2), the necessary condition (Eq. (1)) for kinematic membership shrinks to |v⊥| ≤ ϵ. Since the expectation value of v⊥ is zero, 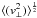 is a measure for the one-dimensional velocity dispersion of the cluster.
is a measure for the one-dimensional velocity dispersion of the cluster.
The convergent point method predicts the radial velocity vr and the distance d from the Sun for a cluster candidate. A final confirmation as a member can be obtained by directly measuring vr and ϖ. Other than from trigonometric parallaxes, the distance d from the Sun can be confirmed also by determining photometric parallaxes. The CU subset of PPMXL catalogue gives 2MASS J,H,Ks-photometry plus r′-magnitudes. For the 2.5 million brightest stars in PPMXL B and V magnitudes from Tycho-2 are available. These photometric data are used to confirm or reject photometrically the parallaxes from the convergent point method. The radial velocities vr can only be confirmed by direct measurements.
4. Membership determination
4.1. Kinematic membership
The Hyades have a tidal radius of about 10 pc (see, e.g. Perryman et al. 1998) and an average velocity dispersion in one dimension of 0.23 km s-1 (Gunn et al. 1988). In this paper we do not concentrate only on the gravitationally bound cluster itself, it is also interesting to investigate the situation in the immediate surroundings. There we expect to reveal former Hyades members which already left the cluster because of dynamical evolution.
Therefore, we allow a bound ϵ = 4 km s-1 for the velocity component v⊥. Additionally, we have to take into account that v∥ goes to zero when (α,δ) approaches the convergent point. This led us to set an upper bound η for the tangent of the angle between the proper motion vector and the direction to the convergent point 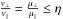 . At the cluster centre η = 1/6 corresponds to |v⊥| = 4 km s-1, so we set this condition to hold everywhere in the cluster.
. At the cluster centre η = 1/6 corresponds to |v⊥| = 4 km s-1, so we set this condition to hold everywhere in the cluster.
We also specified a third bound by requiring that the distance rc of a candidate from the cluster centre should be less than 30 pc which is sufficiently large compared to the tidal radius.
These kinematic selection criteria are fulfilled by 15 757 stars out of the 140 million contained in the CU subset. They are subject to the photometric selection described in the next section. At this stage we excluded all candidate white dwarfs from further consideration. White dwarfs in the Hyades are at the limit of being observed in 2MASS, and if so, the photometric accuracy is low. That prevents us from using photometric distances of white dwarfs from the CU to check their predicted secular parallaxes. We will investigate the white dwarfs associated with the Hyades in a separate study.
4.2. Photometric membership
In the following we will check if the kinematically selected stars populate allowed loci in the colour-absolute-magnitude diagrams. As the candidates occupy a large magnitude range, there is no unique CMD where all the stars have sufficiently accurate photometry. Stars brighter than V = 10 have good quality in B and V mainly from Tycho-2 (Høg et al. 2000), or ASCC-2.5 (Kharchenko 2001). On the other hand, stars fainter than about Ks = 5 have good quality photometry from 2MASS and CMC14.
Fortunately, the interstellar reddenning towards the Hyades is very low. In a critical review on reddening determinations of the Hyades Taylor (2006) concludes that E(B − V) ≤ 1.0 mmag, hence reddenning has been neglected in all future considerations.
 |
Fig. 1 The MKs vs. r′ − Ks diagram of the kinematic candidates (small dots). The vast majority of the stars have kinematically predicted parallaxes inconsistent with their photometric parallaxes. The candidates shown as thick dots are retained for further analysis. Stars brighter than MKs ≈ 3.5 are not contained in CMC14. |
 |
Fig. 2 The MKs vs. J − Ks diagram of the candidates. Stars which were marked as thick dots in Fig. 1 are also marked as thick dots here. |
For the absolutely brightest stars we rely on the classical MV vs. B − V diagram for cross-checking the kinematically predicted parallax ϖ with the photometric parallax. In fact, almost all the bright Hyades members have been observed by Hipparcos and their membership is settled (see, e.g. Perryman et al. 1998; de Bruijne et al. 2001; van Leeuwen 2009).
For stars with masses less than about 0.6 m⊙ and the age and metallicity of the Hyades there are discrepancies between different theoretical isochrones, especially in the NIR. We discuss this in more detail in Sect. 4.4. As a consequence of this, we have no choice but to select the Hyades candidates from an empirically derived colour-magnitude diagram obtained from the distribution of the kinematically selected candidates. In the MKs vs. J − Ks diagram the selection of low-mass stars (<0.6 m⊙) is hampered by the fact that the colour J − Ks is nearly constant. In a first step, we therefore used the MKs vs. r′ − Ks (Fig. 1) and the MKs vs. J − Ks (Fig. 2) diagrams to discard the large majority of the 15 757 kinematic candidates whose photometric parallaxes were inconsistent with the predicted secular ones.
In order to work out more clearly the empirical Hyades main sequence, we selected, in Figs. 1 and 2, only stars with |v⊥| ≤ 1 km s-1, i.e. the ≈9000 most probable kinematic candidates. In Fig. 1 we show the MKs vs. r′ − Ks diagram of all those 9000 stars (small dots) that have r′ magnitudes, i.e. that are contained in CMC14. The stars brighter than MKs ≈ 3.5 are missing. They are not contained in CMC14, but their photometric membership is determined from Tycho-2 B,V photometry. The Hyades main sequence stands out prominently, and the candidates are provisionally marked as thicker dots. Stars below the Hyades sequence appear as sub-luminous stars and must be much farther away than Hyades members. In other words, their parallax ϖ predicted from the kinematic selection is inconsistent with the photometric parallax, and hence these stars cannot belong to the Hyades. In the MKs vs. J − Ks diagram for the same stars (Fig. 2) we find a considerable density of stars at colours J − Ks between 0.8 and 1. We marked the candidate Hyades from Fig. 1 as thick dots also in Fig. 2. It is clearly visible that NIR photometry alone is not sufficient to properly select faint stars with MKs ≥ 5: from Fig. 1 we find no Hyades candidates with MKs > 9 although Fig. 2 suggests plenty of them. Instead, all the candidates with MKs > 9 have r′ − Ks colours which are to blue, and this means that their predicted secular parallaxes are too large. We conclude that stars with MKs > 9 in the Hyades are below the limiting magnitude of CMC14.
Even if we consider the finite width of the Hyades sequence caused by the presence of binaries, we still find a number of stars above the sequence in both CMDs (Figs. 1 and 2). In their majority they are field giants or very seldomly foreground dwarfs. The former are discarded via the two-colour, J − H vs. H − Ks, diagram. In the MKs vs. J − Ks diagram we note a few white dwarfs near J − Ks ≈ 0 and 11 ≤ MKs ≤ 14, but investigating them needs a different approach.
For the final selection we determined the lower bound of an empirical cluster sequence stepwise over r′ − Ks and J − Ks, and selected all stars between this lower bound and the upper limit given by binaries. Out of the 15 757 kinematically selected candidates, we could confirm the secular parallax via the photometric parallax for 775 stars.
4.3. Final membership selection
The sample of 775 kinematic and photometric candidates was cross-matched with the probable Hyades members from the P&S database. Out of their 536 candidates, 407 were identified in our sample. Further, we found 6 stars which belong to the Hyades with certainty but have been missing in our list due to erroneous proper motions in PPMXL (checked via Vizier and Aladin). These stars were added to our sample to give a total of 781. The membership of the majority of the remaining stars from the P&S database has not been confirmed since they did not pass either the kinematic or photometric criteria. A few stars from P&S are too faint to be observed in CMC14, so we could not check their membership in a proper way.
4.3.1. Contamination estimate
Although the kinematic and photometric criteria provide a powerful tool for selecting cluster candidates and enable us to isolate 781 candidates out of 140 million on the whole sky, we cannot exclude a certain contamination of our sample by field stars. The contamination can be estimated empirically by directly comparing the predicted parallaxes and radial velocities with the corresponding measurements as far as these are available. Another approach is to compute the probability of contamination from a kinematic model of the Galaxy, or, alternatively, by considering the observed velocity dispersion of field stars in the solar vicinity. In the following we apply these methods to estimate probable contamination of our Hyades sample.
For about 300 stars from the candidate list we could find Hipparcos parallaxes and/or radial velocities in Vizier/Simbad. We call them “control stars” in the following. Whereas for the majority of the control stars the predicted and measured parameters coincide well within the standard errors, 26 of them have observed parallaxes and/or radial velocities that differ significantly from the computed ones. We analysed their space coordinates predicted by the convergent point method and found that all of them are relatively far away from the cluster centre. Indeed, the membership was not confirmed for all control stars with |z − zc| > 20 pc (11 stars). The remaining 15 “wrong” control stars are located at distances rc from the cluster centre larger than 9 pc. From their distribution we estimate a 7.5% contamination at 9 pc <rc < 18 pc, 30% at 18 pc < rc < 30 pc and 100% whenever |z − zc| > 20 pc. Following this finding, we exclude all stars from the Hyades candidate sample which are located more than 20 pc away from the cluster centre in z-direction. This leaves us with a sample of 724 candidates, and the formal application of the empirical rule found above predicts some 65 field stars among these 724 Hyades candidates.
Since the control stars are relatively bright stars (see Fig. 4) that usually have astrometric and photometric data of better accuracy, we must consider the possibility that the contamination rate may be somewhat higher for the faintest stars of our sample. Therefore, we checked whether our empirical estimate from above coincides with the statistical predictions of galactic models within the complete magnitude range covered by our sample. We used the kinematic model of the Galaxy by Kharchenko & Schilbach (1996) to estimate the number of field stars within a circle of a radius 5 deg from the cluster centre and with proper motions compatible with Hyades membership in this region of the sky. The model predicts 5.06 such field stars in an area of 78.54 deg2 in the direction of the Hyades. That suits perfectly the number of 4.95 stars we obtain if we use the empirical rule of the contamination estimates from above.
Further, we computed the probability for field stars in the local solar neighbourhood to have, by chance, the same space velocities as the Hyades members. Jahreiß (2010, priv. comm.) has recently determined the K-band luminosity function of the stars in the solar neighbourhood from the CNS4, the new 4th Catalog of Nearby Stars (in prep.) from which we infer the volume density of the local sample. The CNS4 luminosity function is shown in Fig. 3a together with the luminosity functions of the 724 Hyades candidates at different distances from the cluster centre. The random contamination of our Hyades sample is now determined by the percentage of stars having the same space velocity [u,v,w] as the Hyades members with respect to the local standard of rest (LSR). Corrected for the solar motion from Piskunov et al. (2006), the LSR velocity of the Hyades is [–31.8, –7.1, +6.1]. Assuming that the velocity distribution of field stars follows a three-dimensional normal distribution with standard deviations given by the velocity dispersions, we compute the number of field stars with Hyades motion in the range 0 ≤ MKs ≤ 8. We used the data from Dehnen & Binney (1998) who determined the velocity dispersions of field stars of different colours in the solar neighbourhood from Hipparcos measurements. Taking into account that only two velocity components are observed, we find that the percentage of random field stars with Hyades motion is less than 0.6 × 10-2 of the local density, and this is plotted as the dotted line at the bottom of Fig. 3a.
 |
Fig. 3 The luminosity functions (LF) of the Hyades candidates and of field stars in the solar vicinity. a) Solid lines and symbols are the LFs of the Hyades at different distances from the cluster centre rc, black filled circles for rc < 9 pc, red open circles for 9 pc < rc < 18 pc, blue crosses for 18 pc < rc < 30 pc. The LF of nearby stars from the CNS4 (Jahreiß 2010, priv. comm.) is shown by the black dashed line whereas the black dotted line is the fraction of field stars with space velocities comparable to the velocity of the Hyades. b) The red open circles and blue crosses show the adopted contamination of the Hyades sample of 7.5% at 9 pc < rc < 18 pc and 30% at 18 pc < rc < 30 pc, respectively. The black dotted line is the same as in a). |
 |
Fig. 4 The MKs vs. J − Ks diagram of the 724 Hyades candidates. For MKs ≤ 2, the J − Ks colours from 2MASS are of low precision, because the stars are too bright in the J-band. Stars shown as green dots are those for which we were able to confirm their membership by comparing with measured trigonometric parallaxes and/or radial velocities. |
Description of the table containing the data of 724 Hyades candidates.
Since the spatial density of the Hyades candidates with rc < 9 pc is, on average, by two orders of magnitude higher than that expected from the local density of field stars, we conclude that contamination is negligible for this volume. With increasing distance from the cluster centre, the density of the Hyades stars is decreasing, and the probability of contamination becomes higher. For comparison we show in Fig. 3b the contribution of field stars (the same as in Fig. 3a) together with the contamination expected in outer regions, like what we obtained empirically a few paragraphs above. For 9 pc < rc < 18 pc, the contamination by field stars is always less than the estimated 7.5%, except for the faintest stars with MKs > 8 where our catalogue becomes incomplete. Also in the region 18 pc < rc < 30 pc, the contamination of 30% from our empirical finding coincides well with the statistical estimates in this magnitude range.
To summarise: in the following, our study is based on a sample of 724 Hyades candidates. The contamination by field stars is assumed to be dependent on the distance rc from the cluster centre: a negligible contamination at rc < 9 pc, 7.5% at 9 pc < rc < 18 pc, and 30% at 18 pc < rc < 30 pc. This is taken into account when we discuss the density distribution in the Hyades cluster, its luminosity and mass functions.
4.3.2. The final sample
The 724 Hyades candidates are listed in Table 1 organised as follows: in the first column we give a running number. The next six columns are the right ascension and declination for equinox and epoch J2000.0, the corresponding proper motions, and the mean errors of the proper motions. The following 12 columns (8 to 19) contain photometric data, i.e. magnitudes and their corresponding mean errors: Johnson B and V, mainly from ASCC-2.5, J,H and Ks from 2MASS, r′ from CMC14. All the following columns are derived quantities. Columns 20 and 21 are the secular parallax ϖ and its mean error, Col. 22 gives the predicted distance from the cluster centre, Col. 23 is the predicted radial velocity, Cols. 24 to 27 are v∥ and v⊥ with corresponding mean errors. In the last Col. 28 we give the mass of the stars as derived in Sect. 5 below. This table is available from the CDS, Strasbourg, France.
The MKs vs. J − Ks colour-magnitude diagram of the final sample is shown in Fig. 4. Since the CU subset of PPMXL is 95% complete down to r′ = 16.8, we find that our sample starts getting incomplete between MKs = 7 and MKs = 8. A subset of stars in Fig. 4 is shown as green dots. For these stars we were able to confirm their predicted secular parallaxes and/or radial velocities via measured trigonometric parallaxes and/or radial velocities.
4.4. Comparison with theoretical isochrones
The empirical selection of kinematic members was chosen as present-day theoretical isochrones fail to describe the main sequence of the Hyades. We compared the empirical colour-magnitude diagram MKs vs. J − Ks with 3 different theoretical isochrones. In the literature, we found estimates of the metallicity of the Hyades, e.g. as [Fe/H] = 0.14 ± 0.05 (Perryman et al. 1998), [Fe/H] = 0.144 ± 0.013 (Grenon 2002) and [Fe/H] = 0.13 ± 0.01 (Paulson et al. 2003). The age of the Hyades is given as 625 ± 50 Myr (Perryman et al. 1998) or 648 ± 45, the latter based on cooling white dwarfs (De Gennaro et al. 2009). From models taking into account stellar rotation of the turn-off stars Lebreton et al. (2001) estimate a range of 500 to 650 Myr for the Hyades age.
In Fig. 5 we compare the empirical colour-magnitude diagram with available theoretical isochrones for ages and metallicities as close to the Hyades values as possible. The isochrones are taken from Marigo et al. (2008) (PADOVA, 650 Myr, [Fe/H] = 0.14, filled red triangles), Dotter et al. (2008) (DARTMOUTH, 600 Myr, [Fe/H] = 0.21, open blue circles ) and Baraffe et al. (1998) (BCAH, 650 Myr, [Fe/H] = 0.0, open magenta triangles). In the latter case we used BCAH98_models.1. The BCAH models are insensitive to the L_mix parameter below 0.6 m⊙ (Baraffe et al. 1998). When isochrones were not given in 2MASS magnitude bands, we converted them using the formulae given in the 2MASS webpage www.ipac.caltech.edu/2mass/.
 |
Fig. 5 Comparison of the empirical MKs vs. J − Ks diagram of the Hyades candidates (masses less than about 1 m⊙) with different theoretical isochrones. The PADOVA isochrones are shown by filled red triangles (curve most to the left), the DARTMOUTH isochrones blue open circles, and the BCAH isochrones by the magenta open triangles (curve most to the right). |
We find that the DARTMOUTH isochrones describe the MKs vs. J − Ks of the Hyades perfectly in the regime brighter than MKs = 5.0, but fail to describe the situation for fainter stars. This is, Hyades stars with masses less than 0.65 m⊙ have colours redder in J − Ks than predicted by DARTMOUTH for stars with corresponding age and metallicity. The less massive the stars are, the greater the discrepancy. The PADOVA isochrones also coincide well with observations for J − Ks ≤ 0.7 (0.7 m⊙). For stars with masses less than 0.7 m⊙ the theoretical J − Ks is about 0.1 mag too small.
Finally, a comparison has been made with the BCAH isoschrones. They cover a mass range from 0.06 to 1.1 m⊙. For masses larger than 0.8 m⊙ (J − Ks = 0.6), BCAH gives MKs-magnitudes which are slightly too bright compared to PADOVA and DARTMOUTH. For 4.5 ≤ MKs ≤ 6.5 the theoretical J − Ks-colours are slightly too blue compared to observations. But for fainter stars the isochrones satisfactory describe the observations.
We conclude that all the isochrones have problems with masses around 0.6 m⊙, which is at the transition from pre-MS to MS at the age of the Hyades (see, e.g. Siess et al. 2000).
It is a mass-MV relation for masses above 1 m⊙, and a mass-MKs relation for masses lower than 1 m⊙.
5. Spatial structure
The analysis of the spatial structure of the cluster does not only require the three-dimensional distribution of the stars as particles, but also their individual masses. v For the 724 candidates we determined individual masses using the following mass-to-luminosity relations: for systems with MV ≤ 5.38 corresponding to m ≥ m⊙ we take the Mass-MV relationship for the Hyades derived by Pinsonneault et al. (2004). For MV > 5.38 masses are determined via the Mass-MKs relationship from the DARTMOUTH isochrones (Dotter et al. 2008). At the transition, we find an insignificant discontinuity in the mass determination of less than 0.005 m⊙. Finally for MKs > 5.5, masses are determined via the BCAH isochrones (Baraffe et al. 1998). The transition at MKs = 5.5 creates an insignificant step in the estimated masses of 0.01 m⊙. In the range 4.0 ≤ MKs ≤ 6.0 masses determined by either of the isochrones (DARTMOUTH or BCAH) do not differ by more than 0.03 m⊙. In our application of these mass-to-luminosity relations we ignore the possible binary nature of the stars in our sample, since we have information on binarity only for a minor portion of our sample.
Using the individual masses of stellar systems, we derive the cumulative mass function M(rc) depending on the distance rc from the cluster centre. This function is shown in Fig. 6. It is corrected for contamination as described in Sect. 4.3.1. In the galactic disk the sphere of influence of a gravitational body is given by 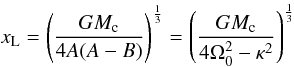 (3)where xL is the distance of the Lagrangian points from the centre, Mc is the total mass inside a distance xL from the centre, G = 4.3 × 10-3 pc/m⊙ (km s-1)2 is the gravitational constant, A and B are Oort’s constants, Ω0 the angular velocity and κ the epicyclic frequency at the position of the Sun. Here we use A (14.5 km s-1 kpc-1) and B (–13.0 km s-1 kpc-1) from Piskunov et al. (2006). The distance xL is often referred to as the tidal radius rt of a cluster and we use this definition in the following also. The tidal radius rt separates, in general, stars gravitationally bound to a cluster from those that are unbound. However, this definition is not to be understood that each star inside rt is bound, and all stars outside are unbound. Individual stars can, every now and then, change from a bound to an unbound state and vice versa (see Just et al. 2009, for the fraction of potential escapers with Jacobi energy above the critical value in the cluster). It is inherent in the convergent point method, that we find, in the first place, stars that are co-moving with the adopted space motion of the centre of the Hyades cluster. So, we cannot separate, from the beginning, the gravitationally bound Hyades cluster and its surroundings.
(3)where xL is the distance of the Lagrangian points from the centre, Mc is the total mass inside a distance xL from the centre, G = 4.3 × 10-3 pc/m⊙ (km s-1)2 is the gravitational constant, A and B are Oort’s constants, Ω0 the angular velocity and κ the epicyclic frequency at the position of the Sun. Here we use A (14.5 km s-1 kpc-1) and B (–13.0 km s-1 kpc-1) from Piskunov et al. (2006). The distance xL is often referred to as the tidal radius rt of a cluster and we use this definition in the following also. The tidal radius rt separates, in general, stars gravitationally bound to a cluster from those that are unbound. However, this definition is not to be understood that each star inside rt is bound, and all stars outside are unbound. Individual stars can, every now and then, change from a bound to an unbound state and vice versa (see Just et al. 2009, for the fraction of potential escapers with Jacobi energy above the critical value in the cluster). It is inherent in the convergent point method, that we find, in the first place, stars that are co-moving with the adopted space motion of the centre of the Hyades cluster. So, we cannot separate, from the beginning, the gravitationally bound Hyades cluster and its surroundings.
 |
Fig. 6 The cumulated mass as a function of the distance from the cluster centre rc. The thick black curve is the observed cumulated mass function as obtained from adding up all the individual masses within a distance rc. The (thinner) red curve is the relation from Eq. (3) between the tidal radius and the tidal mass in the gravitational field of the Galaxy near the position of the Sun. |
If we would add up the masses of all our Hyades co-moving stars within 30 pc from the centre we would get a tidal radius rt of 10.5 pc from Eq. (3). Now, it is clear that stars outside 10.5 pc are not gravitationally bound, and cannot self-consistently contribute to the determination of rt itself. In general, the tidal radius is the distance rt where M(rt) calculated via Eq. (3) equals the integrated mass of all stars up to the distance rt from the centre. The function shown as the thin red curve in Fig. 6 represents the relation from Eq. (3), and the black curve gives the counted integrated mass of our stars as a function of the distance from the centre. From Fig. 6 we find that the tidal radius comes out to be 9.0 pc and the corresponding tidal mass is 276 m⊙. Uncertainty in the determination of rt may come from the fact that we use system masses in the case of unresolved binaries, that we neglect the contribution from white dwarfs, and that our sample is getting incomplete at the lowest masses. The additional mass in white dwarfs, found so far in the Hyades, is very low. It has been estimated to be 6.4 m⊙ by von Hippel (1998). We show in Sect. 6.2 that incompleteness at the low-mass end of the mass function has only negligible influence on the tidal radius. We would miss less than 8% of the total mass in the unrealistic assumption that the logarithmic mass function were constant from 0.25 m⊙ down to 0.01 m⊙. The contribution due to unresolved binaries to the cluster mass is more substantial. Based on their radial velocity study, Gunn et al. (1988) argue that about 25% of the stars they measured are binaries. Assuming the average mass of the secondary of 2/3 of the primary’s mass, Gunn et al. (1988) estimate an increase in the total mass by 17%. Applying this correction would give us an increase in the tidal radius of only 5%, from 9.0 pc to 9.45 pc. Even a 50% increase in the total mass would only enlarge the tidal radius to 10.4 pc.
Another source of uncertainty for the determination of the tidal radius are the adopted values of Oort’s constants to characterise the tidal field of the Galaxy. Using different values for the parameters of galactic rotation, we could determine a tidal radius between 8.0 pc (using Ω0 = 30.6, and κ = 39.0, both in km s-1 kpc-1) and 9.3 pc (using A = −B = 13.75 km s-1 kpc-1). The Piskunov et al. (2006) values for A and B give a tidal radius in between these two approaches. So, for the rest of the paper, we use a tidal radius of rt = 9 pc. In models of star clusters, especially in N-body calculations, the Lagrangian radius for 50% of the cluster mass, plays an important role and is called half-mass radius rh. Estimated from a tidal mass of 276 m⊙, the half-mass radius is rh = 4.1 pc at the present state of evolution of the Hyades.
 |
Fig. 7 The dependence of number density, mass density, and average mass per star as a function of the logarithm of the distance from the centre rc. From top to bottom: a) the number density D of stars in the cluster obtained with a binning of 2 pc in steps of 1 pc. Outside 10 pc the bin size is increased to get a better signal-to-noise ratio. The error bars are Poisson errors; b) the observed mass density ρ (black dots) using the same binning and a density distribution (red crosses) from a Plummer model (Eq. (4) with Mt = 276 m⊙ and rco = 3.10 pc); c) the average mass per star obtained as ρ/D. Its decrease from the centre outbound characterises the mass segregation in the Hyades, at present time. |
In Fig. 7 we show the number density D, the mass density ρ, and the average mass per star as a function of the distance from the centre rc. The bottom part of Fig. 7 reveals the mass segregation in the Hyades; the average mass per star decreases from 1.4 m⊙ in the centre to about 0.5 m⊙ at the tidal radius rt. We discuss this in more detail in Sect. 6.2 together with the description of the mass function. The mass density of the Hyades, shown in the middle part of Fig. 7, is fitted to a Plummer model (Plummer 1915), where the mass density follows the equation ![\begin{equation} \rho({r_{\rm c}}) = {\frac{3 M_{\rm t}}{4\pi{r_{\rm co}}^3}\frac{1}{[1+(r_{\rm c}/{r_{\rm co}})^2]^{5/2}}}, \label{pluden} \end{equation}](/articles/aa/full_html/2011/07/aa16948-11/aa16948-11-eq151.png) (4)where rco is the so-called core radius of a cluster. Using the tidal mass of Mt = 276 m⊙ the best fit to the observed density distribution (black dots) in Fig. 7 is obtained with a core radius of rco = 3.10 pc. The core radius is easily seen in the two upper panels of Fig. 7 as the distance where the slope in the density and mass distributions significantly changes. The corresponding Plummer model (crosses in Fig. 7) shows excellent agreement with the observations. The model has a central mass density of 2.21 m⊙ pc-3 which coincides well with our innermost point of 2.14 m⊙ pc-3. The ratio of the half-mass radius rh to rco in the Hyades is 1.32 which also is in remarkable coincidence with the theoretical ratio of 1.3048 for a Plummer model (see Spitzer & Shull 1975).
(4)where rco is the so-called core radius of a cluster. Using the tidal mass of Mt = 276 m⊙ the best fit to the observed density distribution (black dots) in Fig. 7 is obtained with a core radius of rco = 3.10 pc. The core radius is easily seen in the two upper panels of Fig. 7 as the distance where the slope in the density and mass distributions significantly changes. The corresponding Plummer model (crosses in Fig. 7) shows excellent agreement with the observations. The model has a central mass density of 2.21 m⊙ pc-3 which coincides well with our innermost point of 2.14 m⊙ pc-3. The ratio of the half-mass radius rh to rco in the Hyades is 1.32 which also is in remarkable coincidence with the theoretical ratio of 1.3048 for a Plummer model (see Spitzer & Shull 1975).
Gunn et al. (1988) already found that the cluster conforms well to a Plummer model. Taking into account the incompleteness of their sample, they argue for a total mass of 390 m⊙. They use the projected density distribution to determine a core radius rco = 3.15 pc (0.07 radians) and a central density of 2.97 m⊙ pc-3, the latter being about 30% higher than ours. As the core radii rco in Gunn’s model and ours practically coincide, the difference in central density comes solely via the tidal mass of the cluster. So, either Gunn et al. (1988) have overestimated the tidal mass of 390 m⊙, or our stellar masses are underestimated essentially due to binarity. Using Gunn’s estimate on binarity (25%) we could account for an increase of 17% in total mass to get 323 m⊙. A mass of 390 m⊙ would require an increase of 37% in mass for all our stellar systems (more than 50% binaries), which, however, could also be possible. Perryman et al. (1998) also fit the observed density distribution to a Plummer model and find a smaller core radius of 2.9 pc and a central density of 1.8 m⊙ pc-3. This is not surprising as the Hipparcos sample is incomplete already at 0.6 to 0.7 m⊙.
In the following we call the region inside rco = 3.1 pc the core, the region between rco and rt the corona. In a volume between 1 and 2 rt, called halo, we find another 100 m⊙ in objects co-moving with the Hyades, but probably not gravitationally bound. Outside the halo up to the distance of 30 pc from the cluster centre there is another 60 m⊙ in co-moving stars.
5.1. The shape of the cluster
Since the convergent point method provides an individual distance from the Sun for each Hyades star, we can study the three-dimensional distribution of cluster members in more detail. The distribution of the 724 Hyades candidates in galactic rectangular coordinates is shown in Fig. 8a.
 |
Fig. 8 Observed a) and modelled b), c) spatial distribution in the Hyades. Blue points are for stars with masses m > 0.5 m⊙, red points for m ≤ 0.5 m⊙. In the modelled distribution, the dynamically unbound particles are marked by black crosses b) or black points c). Two large black circles in a) and b) indicate the distances rc from the cluster centre of 9 pc and 18 pc, whereas in c) the circles correspond to rc = 9 pc, rc = 18 pc, and rc = 30 pc. The last one restricts the area considered in this study. |
For comparison, we show in Fig. 8b a model distribution of stars predicted by the N-body simulation (Kharchenko et al. 2009) of an open cluster originally spheroidal, with an initial mass of 1000 m⊙ and the Salpeter IMF down to 0.1 m⊙. The model cluster is moving on a circular orbit in the external tidal field of the Milky Way. It is 650 Myr old and located close to the observed location of the Hyades (for more details of the model parameters, see Kharchenko et al. 2009). It is appropriate to note that the model has not been specifically tailored to fit the Hyades, but it is a general model for the evolution of a prototype open cluster in the disk at 8.5 kpc. The model does not take into account that the Hyades could undergo some irregular events (e.g., encounters with molecular clouds) during their life. As far as the observations are concerned, we note that our sample can be contaminated beyond rc = 9 pc. However, the model and observations show quite a good agreement in general. The main feature, an elongated shape with the minor axis directed towards the Galactic Poles, is clearly seen in both distributions.
In the following we analyse and compare the shapes of the observed Hyades cluster and the model cluster. The principal axes of the cluster ellipsoid are given as the eigenvectors and eigenvalues of the matrix formed by the 2nd order momenta Mxx,...Mzz of the space coordinates of the cluster stars 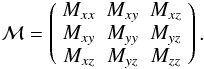 The coordinates x,y,z are counted relative to the cluster centre in the galactic coordinate system as defined in Sect. 3. Let A, B, C be the eigenvalues of ℳ with A being the highest, C the lowest eigenvalue. The corresponding eigenvectors are denoted by a, b and c.
The coordinates x,y,z are counted relative to the cluster centre in the galactic coordinate system as defined in Sect. 3. Let A, B, C be the eigenvalues of ℳ with A being the highest, C the lowest eigenvalue. The corresponding eigenvectors are denoted by a, b and c.
The results are given in Table 2. In the first column we indicate the data set used for the calculations (Observations or Model, within 30 pc, 18 pc, or 9 pc). Columns 2 and 3 give the axis ratios. Columns 4–6 describe the orientation of the ellipsoids in the XYZ-system where ψ is the angle between the X-axis and the projection of the semi-major axis a on the XZ-plane, ϕ is the angle between the X-axis and the projection of a on the XY-plane, and θ is the angle between the Y-axis and the projection of b on the YZ-plane. The numbers in brackets below each parameter give a measure of confidence. These are the lowest and highest values obtained for a given parameter from four subsets of data in the corresponding range of rc. The first two subsets were extracted from the sample arranged with increasing distance of stars from the cluster centre by sorting into two groups of even and odd entries. These two subsets contain, therefore, half of stars of the original sample and are supplementing each other. The other two subsets were extracted in the same way but from the sample arranged with increasing distance of stars from the Sun.
Shape parameters of the observed Hyades O, and the model cluster M.
Although the model particles are distributed more regularly than the real stars, both distributions show similar parameters and tendencies. If the area within rc = 30 pc is considered, the semi-major axis A of the observed as well as of the modelled ellipsoids is about a factor of two larger than the semi-minor axis C (C/A = 0.58 for O/30, and C/A = 0.44 for M/30). The axis a is located in the XY-plane (ψ ≈ 0°) but inclined to the X-axis by an angle ϕ of about 30°, whereas the second axis b seems to form a small angle θ with respect to the XY-plane. With decreasing rc the distribution of stars becomes more spherical, and the orientation angles lose their meaning.
An interesting feature in Fig. 8c, the tails parallel to the Y-axis, is predicted by the model (see also Fig. 3 in Kharchenko et al. 2009). These tails spread out to ≈700 pc from the cluster centre and they are sparsely populated by former cluster members, mainly low-mass stars with space velocities pretty different to that of the cluster itself. Therefore, even if the tails would not be destroyed by events not taken into account by the model, they are difficult to segregate from the field by use of kinematic criteria alone. From this point of view, all-sky surveys of chemical compositions of stars would be more promising to detect former members of an individual cluster.
6. The mass and luminosity functions
In this paper we derive the masses of our Hyades candidates (stellar systems) from a mass-luminosity relation (MLR). Hence the luminosity function and the mass function are not independent of each other, and cannot be discussed independently. From the point of view of an observer, the luminosities are the primary observable quantities and the masses are derived thereof. However, from theory, the primary astrophysical parameter is the initial mass function (IMF) which evolves into the present-day mass function (PDMF). In consequence, we shall epitomise the observed luminosity function in the next subsection, and discuss the PDMF in more detail.
In Sect. 5 we described the mass-luminosity relation we adopted to convert absolute magnitudes into masses. It is a mass-MV relation for masses above 1 m⊙, and a mass-MKs relation for masses lower than 1 m⊙. Our derived luminosity and mass functions in this section were corrected for contamination as described in Sect. 4.3.1 (7.5% for 9 pc < rc < 18 pc and 30% at 18 pc < rc < 30 pc). In Sect. 4.2 we found that our sample is getting incomplete between MKs = 7.3 and MKs = 8. Translated into mass, incompleteness in the mass functions sets on somewhere between 0.25 and 0.17 m⊙. The onset of incompleteness is shown by the dashed vertical lines in Figs. 9 and 10.
6.1. The luminosity function
The K-band luminosity function (KLF) is defined as the number of stars per magnitude bin and volume element 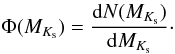 (5)The KLF is mostly used to characterise the stellar population in young or even embedded clusters. On the other hand, Jahreiß (2010, priv. comm.) has recently determined the KLF of the stars in the solar neighbourhood from the CNS4. We compare the KLF from the Hyades both with that of young clusters and with the older local population.
(5)The KLF is mostly used to characterise the stellar population in young or even embedded clusters. On the other hand, Jahreiß (2010, priv. comm.) has recently determined the KLF of the stars in the solar neighbourhood from the CNS4. We compare the KLF from the Hyades both with that of young clusters and with the older local population.
In different regimes of magnitude, the KLF is usually characterised by a power law in the form 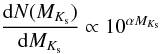 (6)with α as the slope of the power law. For young open clusters (see, e.g. Devine et al. 2008; Jose et al. 2008, as an overview) the slopes α of the KLF lie between 0.3 and 0.4 in ranges of MKs between 0 and 3, whereas the slope of the KLF of CNS4 (see Fig. 3) is steeper, about 0.5, in the corresponding magnitude range.
(6)with α as the slope of the power law. For young open clusters (see, e.g. Devine et al. 2008; Jose et al. 2008, as an overview) the slopes α of the KLF lie between 0.3 and 0.4 in ranges of MKs between 0 and 3, whereas the slope of the KLF of CNS4 (see Fig. 3) is steeper, about 0.5, in the corresponding magnitude range.
To be independent of binning we construct the luminosity function in steps of 0.1 mag with a binsize (kernel) of 1.5 mag. We also distinguish different regions of the cluster as defined in Sect. 5, the core region up to rc = 3.1 pc from the centre, the corona between core and tidal radius of 9 pc, the halo in the 1 to 2 tidal radii shell, and the co-movers outside 18 pc up to 30 pc from the cluster centre. We show the KLF for the different regions of the Hyades in Fig. 9.
 |
Fig. 9 The luminosity function of the Hyades in different regions. This luminosity function is constructed as a moving average with a rectangular kernel of 1.5 mag in steps of 0.1 mag. The upper (blue) curve refers to the core region inside 3.1 pc from the centre, the second (cyan) curve to the corona (3.1 pc to 9 pc), the third (green) to the halo (9 pc to 18 pc), and the fourth (red) to the co-movers outside 18 pc. The dashed vertical line at MKs = 7.3 marks the onset of incompleteness of our survey. The units are stars (systems) per pc-3 and 1 mag. |
Looking at the KLF of the different regions one feature immediately catches the eye: the luminosity function in the core of the Hyades is strikingly different from the other regions and also from the field star LF in Fig. 3. We observe a strong excess of luminous stars with MKs ≤ 5. This is a manifestation of mass segregation already seen in Fig. 7.
 |
Fig. 10 The present-day mass function (PDMF) of the Hyades. The lowest histogram (filled black dots) shows the PDMF in the core of the cluster (rc < 3.1 pc), the magenta triangles mark the PDMF within the tidal radius (rc < 9 pc), the blue squares stand for the PDMF in the region rc < 18 pc, and finally the filled red squares are the PDMF of all 724 stars within 30 pc from the centre. The PDMFs are corrected for field star contamination. The histograms give the actual star counts per logarithmic mass bin of 0.1. The dashed vertical line at about 0.25 m⊙ marks the onset of incompleteness of our survey. For comparison, we show a Kroupa (2001) mass function (solid line) with α = 2.35 for masses larger than 0.5 m⊙, and α = 1.35 below 0.5 m⊙. As an other extreme we show a mass function with slope α = 3.05 (dashed line) fitted to the high-mass portion of the observed PDMF. |
 |
Fig. 11 The mass function of the Hyades from this paper (black histogram with filled black dots). The blue curve (open squares) shows the Hyades PDMF from Bouvier et al. (2008), the red histogram with triangles is the PDMF from the 120 Myr old Pleiades from Moraux et al. (2003), and finally the green curve (filled squares) is the PDMF of Praesepe from Boudreault et al. (2010). The thin solid line shows again a Kroupa (2001) mass function. |
The maxima of the PDLFs in the different regions are reached at about MKs = 7, except for the additional maxima in the core at MKs = 4 and MKs = 1.5, caused by mass segregation. The local KLF from Fig. 3 is still increasing at MKs = 7, and reaches its maximum at MKs = 9 or later. This implies a lack of low-luminous stars in the Hyades compared to the field with all caution, because incompleteness in our sample starts at MKs = 7.3. In the optical regime, according to Kroupa et al. (1990), the maximum of the field star LF is located at MV = 12 which corresponds to MKs = 7.3. This is at a brighter magnitude than the Jahreiß (2010, priv. comm.) KLF. We have no explanation for this difference in the field star LF.
At absolute magnitudes 3 < MKs < 5 we find local maxima in all KLFs shown in Fig. 9. In the KLF of CNS4 we do not see a maximum but a flattening of the slope to α = 0.1. In the optical this phenomenon is known as the Wielen dip (Kroupa et al. 1990). Kroupa et al. (1990) located it at m = 0.6 m⊙. They explained the dip as a consequence of an inflection of the mass-luminosity relation which appears due to the formation of negative H-ions impacting the atmospheric opacity. A mass of 0.6 m⊙ corresponds to MKs = 5.1 in the MLR from Sect. 5. We observe strong Wielen dips (even local minima) in the luminosity functions in all regions of the Hyades in Fig. 9, strongest in the core region, where mass segregation is responsible for an apparently stronger Wielen dip.
For 1 ≤ MKs ≤ 4, we find the slope of the luminosity function in the halo to be α = 0.26, i.e. marginally flatter than in young open clusters and much flatter than in the field. This behaviour in a zone of co-moving, gravitationally unbound stars, shows that we find there an ensemble of “former” members representing the IMF of open clusters at least in this magnitude range. On the other hand, the slope is remarkably different from that in the field star KLF meaning that the halo is exclusively related to the cluster and not to the field. This can be considered as an alternative confirmation of low field star contamination (cf. Sect. 4.3.1).
6.2. The mass function
The mass function ξ(m) of a cluster is defined as the number of stars within a mass interval between m and m + dm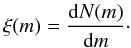 (7)Alternatively, we can describe it as a function of the logarithm of mass
(7)Alternatively, we can describe it as a function of the logarithm of mass 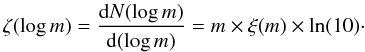 (8)So, ζ(log m) gives the number of stars (systems) in the interval between log m and log m + dlog m. In Figs. 10 and 11 we chose dlog m to be 0.1. The different regimes in the mass function ξ(m) are usually approximated by a power law with an exponent −α which transforms into −α + 1 for the logarithmic mass function ζ(log m). So, even if we show the logarithmic mass function in the figures below, we always refer to the exponent −α of ξ(m).
(8)So, ζ(log m) gives the number of stars (systems) in the interval between log m and log m + dlog m. In Figs. 10 and 11 we chose dlog m to be 0.1. The different regimes in the mass function ξ(m) are usually approximated by a power law with an exponent −α which transforms into −α + 1 for the logarithmic mass function ζ(log m). So, even if we show the logarithmic mass function in the figures below, we always refer to the exponent −α of ξ(m).
Figure 10 shows the mass function in different regions of the cluster. The lowest function (black) refers to the core region (rc < 3.1 pc). The mass function peaks sharply at about 1 m⊙. Towards larger masses the MF drops as a power law with exponent α = 2.7, even steeper than Salpeter. The most striking effect is the steep decline (α = −0.05) towards lower mass stars, again a clear indication for mass segregation.
The mass function for all stars within the tidal radius of the cluster rc ≤ 9 pc has its less prominent maximum at 0.9 m⊙, and follows about the same power law (α = 2.7) towards higher mass systems as in the core (provided that we neglect the four giants in the most massive bin). Towards low-mass stars the logarithmic mass function is almost flat (α = 0.93) down to the completeness limit. This mass function refers to the gravitationally bound stars of the Hyades cluster. Adding the formerly bound members with rc ≥ 9 pc shifts the maximum further towards lower mass stars. However, the logarithmic mass function for all 724 stars is almost flat in the mass range from 1 m⊙ to 0.2 m⊙. The mass function which we determined is incomplete for masses lower than about 0.25 m⊙. This has, however, not much influence on the total mass of the cluster. If we assume that the logarithmic mass function were constant below 0.25 m⊙ down to 0.01 m⊙, this would add merely 8% to the total mass of the cluster.
In Fig. 10 we compare the observed mass functions with a Kroupa (2001) IMF shown as the solid line. This IMF has α = 2.35 for masses larger than 0.5 m⊙, and α = 1.35 below 0.5 m⊙, down to the brown dwarf limit of 0.08 m⊙. Using the Kroupa IMF as a tangent to the observed mass function, we can estimate a minimum initial mass of the cluster, provided that all originally formed stars of about solar-mass are still contained within a radius of 30 pc. With these assumptions we get an initial cluster mass of 1100 m⊙ in 2300 stars (stellar systems). From this simple calculation we can conclude that about 40% of the original mass of the Hyades is still contained in the immediate neighbourhood of 30 pc around the centre. The remaining mass has left further into tails of the form predicted by, e.g. Kharchenko et al. (2009). More refined statements on the initial parameters of the Hyades are expected from dedicated N-body simulations which are underway.
A better fit to the high-mass end of the observed mass function requires a steeper slope of α = 3.05 in a mass range from 1 to 2.5 m⊙. This is shown as the dashed line in Fig. 10. We should point out again that in the mass functions presented here binaries are not resolved, and the masses are based on a specific mass-luminosity relation used to convert absolute magnitudes to masses. This makes us cautious, not to interpret the slope of the mass function at high masses in more depth.
In Fig. 11 we compare our PDMF of the Hyades with earlier results. This mass function (black histogram with filled black dots) is obtained within the 30 pc volume around the centre (top curve in Fig. 10). The PDMF from Bouvier et al. (2008) is shown as the blue histogram (open squares). On the high mass part it is derived from the P&S database. Bouvier et al. (2008) argue that the P&S database is essentially complete down to 0.1 m⊙, but having a 27% contamination by field dwarfs below 0.3 m⊙. The slope of their mass function between 0.2 and 1 m⊙ is found to be α = 0.6. Compared with our results this indicates that incompleteness in the P&S database begins near 1 m⊙ and increases towards lower masses. We attribute this to the fact that the P&S database is not based on a deep all-sky survey. As fainter stars show less concentration to the centre (mass segregation) they may be missed if the field-of-view is restricted. Bouvier et al. (2008) detected 3 new very low-mass stellar members, and constructed a PDMF down to 0.08 m⊙. Nevertheless, their PDMF practically shows a cut-off at 0.1 m⊙. We neither can confirm nor reject this on the basis of our analysis using the CU catalogue because of incompleteness below about 0.25 m⊙. Work is going on to exploit the faint PPMXL stars not in the CU subset to reach an all-sky completeness of the Hyades stars at least down to 0.1 m⊙. Hogan et al. (2008) did not try to derive a mass function from the 12 L-dwarfs in their surveyed 275 deg2 field. If we apply our Mass-MKs relationship, the 12 candidates range from 0.078 down to 0.06 m⊙. A larger field is needed to decide if the presently observed strong cut-off at 0.1 m⊙ will be confirmed or not.
Fig. 11 also shows the PDMF of the much younger (≈120 Myr) Pleiades cluster from Moraux et al. (2003). The maximum of the Pleiades PDMF in the logarithmic mass function is between 0.3 and 0.4 m⊙ compared to about 0.7 to 0.8 m⊙ in our mass function of the Hyades. If both clusters had a similar IMF then mass loss works more effectively the less massive the stars are. The similarity of the mass functions in the region above 1 m⊙ suggests that this effect is less prominent for the more massive stars in a cluster. A further similarity in the Hyades and Pleiades mass functions is the decline below 0.1 m⊙.
The green curve (filled squares) is the mass function of Praesepe recently derived by Boudreault et al. (2010). Given that Praesepe is practically of the same age as the Hyades, this mass function is quite unusual. With an α = 1.9 between 0.2 and 0.7 m⊙, the contribution of low-mass stars to the total mass of Praesepe is much more important than in the case of the Hyades and even the Pleiades. Contrary to the latter, it would mean that Praesepe could hold its low-mass stars in bound stage.
The thin solid line in Fig. 11 is again the universal IMF from Kroupa (2001). Prima facie one gets the impression that an IMF like Kroupa’s evolves via a Pleiades PDMF (120 Myr) to a Hyades PDMF due to dynamical and stellar evolution.
7. The internal velocity dispersion
For a cluster in a statistically steady state (Chandrasekhar 1942) the virial theorem 2T = −Ω holds (with T being the total kinetic and Ω the total potential energy of the system). For compact, isolated, massive and long living systems like globular clusters the assumption of statistically steady state is, in general, justified. However, this is not trivial if we were to consider a relatively old, low-mass open cluster dipped into the Galactic disk.
Strictly speaking, the virial theorem only holds for the cluster as an ensemble. For each well-defined subset of stars { m1,...,ms } we can postulate that the velocity dispersion is given by 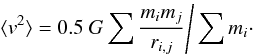 (9)where mi is the mass of an individual star in the subset, and mj runs along all stars within the tidal radius of the cluster, ri,j is the distance between stars i and j, G is the gravitational constant, and ⟨v2⟩ is defined as
(9)where mi is the mass of an individual star in the subset, and mj runs along all stars within the tidal radius of the cluster, ri,j is the distance between stars i and j, G is the gravitational constant, and ⟨v2⟩ is defined as 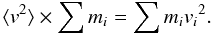 (10)The summation in Eq. (9) extends over all pairs of stars with i ≠ j. If the subset consists of all stars within the tidal radius then Eq. (9) gives 2T = −Ω.
(10)The summation in Eq. (9) extends over all pairs of stars with i ≠ j. If the subset consists of all stars within the tidal radius then Eq. (9) gives 2T = −Ω.
We use here the actual three-dimensional distribution of the Hyades stars and do not approximate the cluster by a Plummer model, albeit the fit of the Hyades to a Plummer model is excellent (see Sect. 5). The assumption of a statistically steady state, if at all, is only justified within the tidal radius of the cluster. We applied Eq. (9) to two distinct subsets of the Hyades, one containing all stars within the core radius rco (rc ≤ 3.1 pc) and the other within the tidal radius rt (rc ≤ 9.0 pc). The three-dimensional velocity dispersion comes out as 0.42 km s-1 and 0.32 km s-1, respectively. Putting an artificial particle in the centre we obtain the central velocity dispersion ⟨v2⟩1/2 = 0.45 km s-1.
Gunn et al. (1988) used their fit of the Hyades cluster to a Plummer model (cf. Sect. 5) to get 0.51 km s-1 for the central, and 0.40 km s-1 for the average velocity dispersion (or 0.23 km s-1 for 1D). The higher values can be explained by their assumption of a higher (tidal) mass for the Hyades. Perryman et al. (1998) derive a central velocity dispersion of 0.36 km s-1 from their fit to a Plummer model, which is too low because of their lower mass estimate for the cluster.
In principle, an empirical determination of the velocity dispersion is possible by exploiting the observed velocity distribution of cluster members. However, during their life, open clusters are permanently losing members part of which remain in the vicinity of their parent cluster and form sparse haloes and tails of co-moving stars. This makes it difficult to separate “actual” members by use of velocity observations and properly determine ⟨v2⟩1/2. For open clusters, one expects velocity dispersions ranging from a few hundred meters per second to 1–2 km s-1 i.e., at a level of accuracy of radial velocity measurements and/or tangential velocities of nearby stars. Empirically determined ⟨v2⟩ are thus sensitive to the adopted mean errors of input data used for computing internal spatial velocities of cluster members (see e.g., Appendix in Piskunov et al. 2007).
In the past, several attempts were undertaken to derive the velocity dispersion of the Hyades from proper motions and radial velocities. Schwan (1990) determined the velocity dispersion from 44 FK5 stars. Using v⊥, he obtained an 1d-velocity dispersion of 0.71 ± 0.41 km s-1. Based on only the vα-component, the velocity dispersion comes out to be 0.3 km s-1 which corresponds to about 0.5 km s-1 for the three-dimensional dispersion. Schwan (1990) explained this considerable difference by larger uncertainties in vδ-component of the velocity data. Perryman et al. (1998) used the Hipparcos parallaxes and proper motions, but were unable to determine the velocity dispersion, because the accuracy of the measured trigonometric parallaxes resulted in a too large mean error of the tangential velocities. de Bruijne et al. (2001) used the same data set as Perryman et al. (1998) but took the formally better secular parallaxes instead of the trigonometric parallaxes. They achieved a 1d-velocity dispersion of 0.3 km s-1 after consecutive rejection of stars with large offsets in the observed vs. computed tangential velocities. In the following we estimate the three-dimensional velocity dispersion in the Hyades via the one-dimensional velocity dispersion given by the velocity component perpendicular to the direction to the convergent point v⊥. The distribution of v⊥ versus the distance of stars from the cluster centre is shown in Fig. 12. Stars in red circles are outliers and are discussed a few paragraphs below.
 |
Fig. 12 The distribution of the tangential velocity components v⊥ perpendicular to the direction to the convergent point as a function of the distance from the cluster centre. The nine stars in red circles are outliers which are not considered in the determination of the velocity dispersion in Table 3. The vertical lines mark the core (dashed) and tidal (solid) radii. |
Let vi be the residual space velocity of the i-th member with respect to the bulk motion of the cluster, and 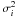 its individual mean error. We define the square of the velocity dispersion ⟨v2⟩ as
its individual mean error. We define the square of the velocity dispersion ⟨v2⟩ as 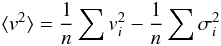 (11)where n is the number of stars in a given region. Provided that the space velocities of the cluster stars are randomly oriented, the first term on the right-hand side can be computed from the velocity components v⊥ and we can re-write Eq. (11) as
(11)where n is the number of stars in a given region. Provided that the space velocities of the cluster stars are randomly oriented, the first term on the right-hand side can be computed from the velocity components v⊥ and we can re-write Eq. (11) as 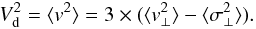 (12)The mean errors σVd (Trumpler & Weaver 1953) are computed as
(12)The mean errors σVd (Trumpler & Weaver 1953) are computed as 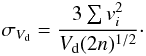 (13)Here we are obliged to rely on the quoted σi and to assume their uncertainties to be negligible.
(13)Here we are obliged to rely on the quoted σi and to assume their uncertainties to be negligible.
Since the kinematic candidates of the Hyades have different observing history, their individual mean errors σ⊥ vary significantly, from ≈0.1 km s-1 for bright (and high mass) Hipparcos stars to ≈1 km s-1 for the faintest (and lowest mass) stars in our sample. Therefore, they must be considered in different bins containing a sufficient number of stars of homogeneous accuracy. As a compromise, we divided our sample into four groups, according to the masses of stars included: masses higher than 1.45 m⊙, between 1.45 m⊙ and 1.05 m⊙, between 1.05 m⊙ and 0.71 m⊙, and less than 0.71 m⊙. We had to exclude the last group from consideration: there is no chance to use them for the determination of the velocity dispersion due to the low accuracy of their kinematic data. Further we rejected 5 stars from the calculation of 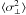 because their reported mean errors were significantly higher than the corresponding group average.
because their reported mean errors were significantly higher than the corresponding group average.
For each mass group, the mean values ⟨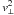 ⟩ were computed in two ranges of the distance from the cluster centre: rc ≤ 3.1 pc, and rc ≤ 9 pc. It is self-evident that stars with high |v⊥| can cause an oversize increasing of the velocity dispersion. Therefore, in each bin we applied a statistical test to reveal outliers at the 95% confidence level. In total, 9 stars were excluded from the calculation of the velocity dispersions. They are marked by red circles in Fig. 12. All these stars are double stars. Of these, six are found as Δμ-binaries in Wielen et al. (1999). The binary nature of the Δμ-stars is revealed from the significant difference between their short-scale (Hipparcos) and their long-scale (FK5, Tycho-2) proper motions. One more Δμ-binary is found in Frankowski et al. (2007). Another star is marked as double in the Hipparcos Double and Multiple Systems Annex, and the last one is WDS 04285+1742 from the 2011 version of the Washington Double Star catalog (Mason et al. 2001).
⟩ were computed in two ranges of the distance from the cluster centre: rc ≤ 3.1 pc, and rc ≤ 9 pc. It is self-evident that stars with high |v⊥| can cause an oversize increasing of the velocity dispersion. Therefore, in each bin we applied a statistical test to reveal outliers at the 95% confidence level. In total, 9 stars were excluded from the calculation of the velocity dispersions. They are marked by red circles in Fig. 12. All these stars are double stars. Of these, six are found as Δμ-binaries in Wielen et al. (1999). The binary nature of the Δμ-stars is revealed from the significant difference between their short-scale (Hipparcos) and their long-scale (FK5, Tycho-2) proper motions. One more Δμ-binary is found in Frankowski et al. (2007). Another star is marked as double in the Hipparcos Double and Multiple Systems Annex, and the last one is WDS 04285+1742 from the 2011 version of the Washington Double Star catalog (Mason et al. 2001).
For comparison, we also computed the velocity dispersion of stars at larger distances from the cluster centre by applying the same approach. Since there are only 8 stars at rc > 9 pc with masses larger than 1.45 m⊙, the calculations were carried out only for two mass groups. The results are given in Table 3 together with the theoretical velocity dispersion computed above from the virial theorem.
The increase of the velocity dispersion outside 9–11 pc from the cluster centre can be already observed in Fig. 12, and Table 3 confirms this impression. Partly, this may be explained by an increasing contamination by field stars. But more probably, this finding indicates the limiting distance for the gravitationally bound part of the Hyades cluster. The distance 9–11 pc is in good agreement with the conclusion on the cluster size we obtained from the density and mass distribution of stars in Sect. 5.
Within the first two bins (rc ≤ 9 pc), the velocity dispersion achieves ≈0.8 km s-1 which is higher by almost a factor of two than one would expect from Eq. (9). So, a factor of 4 in mass would be required to balance this discrepancy. Assuming additional mass hidden in double stars, white dwarfs, faint stars below the completeness limit of our survey, the current estimate of cluster mass of approximately 300 m⊙ can be hardly increased actually by more than 50%, a factor of 4 is excluded.
On the other hand, we can assume that 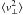 is overestimated and/or
is overestimated and/or 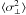 is underestimated in Eq. (12). A formal calculation shows that a decrease of the observed velocity dispersion by a factor of two can be achieved for the most massive stars (group I) by increasing the rms errors of proper motions by a factor of ≈3. However, this seems to be far from reality, especially for this mass group containing mainly stars with Hipparcos data.
is underestimated in Eq. (12). A formal calculation shows that a decrease of the observed velocity dispersion by a factor of two can be achieved for the most massive stars (group I) by increasing the rms errors of proper motions by a factor of ≈3. However, this seems to be far from reality, especially for this mass group containing mainly stars with Hipparcos data.
Alternatively, an additional dispersion can be introduced by the presence of double stars which can impact the proper motion measurements. The effect from neglecting the binary nature of the stars is twofold: the velocity dispersion contains a part that comes from orbital motion, and the total gravitational energy is increased to the higher mass in binaries. Indeed, we found that the high velocity dispersion is caused by only 20% of the stars with somewhat higher v⊥ velocities. From a statistical point-of-view, however, they cannot be considered as outliers and simply be excluded from the calculation of the velocity dispersion. But, we note that this number of 20% coincides well with the results by Gunn et al. (1988), who estimated the percentage of double stars to be 25% from their measurements of radial velocities of stars in the Hyades region and extrapolated this number to the complete cluster. As a further possibility to explain the high empirical velocity dispersion we can assume that a certain number of stars is just escaping the cluster. Simulations have been started to quantitatively investigate the importance of this effect.
In the discussion above we used the observed distribution of stars (with their masses) to derive the allowed velocity dispersion for the cluster to be in equilibrium. That is, the mass of the cluster was obtained by counting the members with their individual masses. At first sight, see Table 3 the observed velocity dispersion seemed to considerably exceed the allowed one. But, as we argued above, there are good reasons that both the observed distribution of masses and the observed velocity dispersion are consistent with each other.
Let us, at the end of this chapter, add a remark on the estimation of masses from an observed velocity distribution. Chandrasekhar (1942) introduces the “average” radius R of the cluster such that the equation 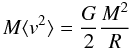 (14)holds. Here M is the total (gravitationally bound) mass of the cluster. This is fulfilled for
(14)holds. Here M is the total (gravitationally bound) mass of the cluster. This is fulfilled for 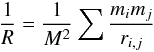 (15)where the summation is now carried out over all mi,mj with i ≠ j. The so-called “average” radius of the cluster is determined via the weighted mean over the inverse distances between individual stars. For the Hyades with their tidal mass of 276 m⊙ we find R = 4.53 pc, which in our case happens to be 1.5 times rco. The measured velocity dispersion can be used to determine the mass (virial mass) of an open cluster via
(15)where the summation is now carried out over all mi,mj with i ≠ j. The so-called “average” radius of the cluster is determined via the weighted mean over the inverse distances between individual stars. For the Hyades with their tidal mass of 276 m⊙ we find R = 4.53 pc, which in our case happens to be 1.5 times rco. The measured velocity dispersion can be used to determine the mass (virial mass) of an open cluster via 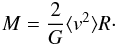 (16)The two terms on the right-hand side of Eq. (16), ⟨v2⟩ and R depend on the sample for which the velocity dispersion is measured. This should be taken into account when deriving the mass of a cluster from its velocity dispersion.
(16)The two terms on the right-hand side of Eq. (16), ⟨v2⟩ and R depend on the sample for which the velocity dispersion is measured. This should be taken into account when deriving the mass of a cluster from its velocity dispersion.
8. Summary
We used a subset of PPMXL, derived from a combination of PPMXL proper motions with UCAC3 and CMC14 observations, and augmented by CMC14 photometry to perform the most complete three dimensional census of the Hyades to date. This census yielded 724 stellar systems as candidates moving with the same space motion as the cluster. These candidates have been found from an application of the convergent point method, and we verified the resulting secular parallaxes by photometric parallaxes. Although we tested the full catalogue for stars co-moving with the Hyades centre, we restricted our analysis to stars with derived distances smaller than 30 pc from the cluster centre. We did not search for new white dwarfs, as they may be at the detection limit of the 2MASS, and need a separate approach. Our census is complete down to MKs ≈ 7.3, corresponding to masses of 0.25 m⊙. Incompleteness for more massive stars is no longer a question of limited field-size; the only reason for incompleteness may be possibly erroneous proper motions and/or photometry.
The secular parallaxes allow us to construct an empirical Colour-Magnitude Diagram (here MKs vs. J − Ks) from the brightest stars down to MKs ≈ 9. Comparing this with 3 different theoretical isochrones relevant to the metallicity and age of the Hyades we find that only the isochrones from Baraffe et al. (1998) more or less describe the loci of the Hyades stars fainter than about MKs = 5 in the CMD, whereas the isochrones from Marigo et al. (2008) and Dotter et al. (2008) predict J − Ks colours which are too blue.
Using the mass-luminosity relation described in Sect. 5 we derive M(r), the cumulative mass as a function of the distance from the cluster centre. M(r) is increasing up to our arbitrarily set limiting radius of 30 pc. If we consider the tidal field of the Galaxy via Eq. (3), we derive a tidal radius of about 9 pc, consistent with earlier determinations. The M/L relation gives us system masses for unresolved binaries. Using these individual masses we find that 276 m⊙ (364 stars) are bound within the tidal radius of the cluster, another 100 m⊙ (190 stars) are found in the halo up to 2 tidal radii, and another 60 m⊙ (170 stars) are found as co-movers outside 2 tidal radii. Here the masses are corrected for contamination, whereas the number of stars is given as counted.
The spatial distribution of the Hyades has a clear ellipsoidal shape considering both bound as well as unbound stars. The largest axis is almost parallel to the galactic plane, and forms an angle of about 30 deg with the galactocentric radius vector (in the direction of the galactic rotation). The ellipticity and the orientation of the principal axis may already reflect the onset of tidal tails as predicted by the models.
Within its tidal radius (rt = 9 pc) the spatial distribution follows excellently a Plummer model with core radius rco = 3.1 pc and a central density of 2.21 m⊙ pc-3. The half-mass radius of the cluster is rh = 4.1 pc, and the ratio rh/rco is 1.32, also in excellent agreement with the model value. The “average” cluster radius R determined from the distances between the stars is found to be 4.53 pc.
Mass segregation is clearly seen in the Hyades. The average mass per star drops from 1.1 m⊙ at the centre to 0.5 m⊙ at the tidal radius. This mass segregation is also seen in the Ks-band luminosity function KLF. In the core the KLF shows a peak at MKs ≈ 4 which is more prominent than the other at MKs = 7, whereas this is vice versa in the corona. We see clear indications for the presence of the so-called Wielen dip at about MKs = 5. Mass segregation exaggerates the Wielen dip in the core, while it is present in all other regimes (corona, halo and co-movers) as a flattening of the slope of the luminosity function.
Compared with the KLF of the field stars in the solar neighbourhood (Fig. 3) the Hyades KLF is generally flatter than the field KLF in all regions of the cluster in the range 1 < MKs < 6. The increase in the field KLF for MKs > 7 is not seen in the Hyades KLF with the caution that our sample is becoming incomplete there.
The mass function of all co-moving stars (bound or unbound) is complete down to 0.25 m⊙. About 94% of the total mass is in stars more massive than 0.25 m⊙. Hypothetically, even a constant logarithmic mass function at lower masses between 0.25 m⊙ and 0.01 m⊙ (for which we so far see no indication) would add only 8% to the total mass we determined. From literature there is no indication for a considerable amount of mass in white dwarfs. Hence, hidden mass could only be in unresolved binaries, and, indeed, we got hints to this from the observed high velocity dispersion. Adopting the estimate of 25% binaries from Gunn et al. (1988), the total mass would increase by 17%.
Mass segregation is also seen impressively in the mass function (Fig. 10). Whereas in the core, the PDMF sharply peaks at about 1 m⊙ and steeply drops to both sides, the number of lower mass stars increases up to the tidal radius to give a practically flat logarithmic mass function. If the IMF had been a Kroupa (2001) IMF we see strong dynamical evolution on the low-mass side. This would hold even more for a Salpeter IMF. A comparison with the mass function of a much younger cluster like the Pleiades supports this conclusion. Adopting a Kroupa IMF we derive a minimum mass of 1100 m⊙ for the cluster at formation.
The distribution of the velocity dispersion is clearly different inside and outside the tidal radius of the cluster. The observed velocity dispersion within the tidal radius is not sustained by the total gravitational energy of the cluster. A relatively high fraction of binaries is needed to overcome this discrepancy, because binaries not only increase the total mass, but their orbital motions also may strongly corrupt the proper motions used for the determination of the velocity dispersion. Our investigation on possible contamination by local field stars has shown that the population outside the tidal radius is strongly related to the cluster itself and consists of stars that left the cluster in the past.
Putting all together, we observe our neighbouring open cluster as an evolving object, which is permanently losing bound members that we can pin-point up to a certain distance once they left the cluster. The results that we obtained here for the spatial, the velocity and the mass distribution of the Hyades give starting conditions for ongoing N-body simulations to reveal the past and the future of this cluster
Acknowledgments
Part of this work was supported by DFG grant RO 528/10-1. We are grateful to Hartmut Jahreiß who furnished us with the KLF of the nearby stars prior to publication. We also thank Hans Zinnecker and Andreas Just for helpful discussions. We further thank the anonymous referee for his helpful comments. This paper is based on observations from the ESA Hipparcos satellite. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Boudreault, S., Bailer-Jones, C. A. L., Goldman, B., Henning, T., & Caballero, J. A. 2010, A&A, 510, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Kendall, T., Meeus, G., et al. 2008, A&A, 481, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1942, Principles of stellar dynamics (The University of Chicago Press) [Google Scholar]
- Copenhagen Univ. Obs., Inst. of Astronomy, Cambridge, UK, & Real Instituto Y Observatorio de La Armada, F. E. S. 2006, VizieR Online Data Catalog, 1304, [Google Scholar]
- de Bruijne, J. H. J., Hoogerwerf, R., & de Zeeuw, P. T. 2001, A&A, 367, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Gennaro, S., von Hippel, T., Jefferys, W. H., et al. 2009, ApJ, 696, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Binney, J. J. 1998, MNRAS, 298, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Devine, K. E., Churchwell, E. B., Indebetouw, R., Watson, C., & Crawford, S. M. 2008, AJ, 135, 2095 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Frankowski, A., Jancart, S., & Jorissen, A. 2007, A&A, 464, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizis, J. E., Reid, I. N., & Monet, D. G. 1999, AJ, 118, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Grenon, M. 2002, Highlights of Astronomy, 12, 680 [NASA ADS] [Google Scholar]
- Gunn, J. E., Griffin, R. F., Griffin, R. E. M., & Zimmerman, B. A. 1988, AJ, 96, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, R. B. 1975, AJ, 80, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Hogan, E., Jameson, R. F., Casewell, S. L., Osbourne, S. L., & Hambly, N. C. 2008, MNRAS, 388, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Jose, J., Pandey, A. K., Ojha, D. K., et al. 2008, MNRAS, 384, 1675 [NASA ADS] [CrossRef] [Google Scholar]
- Just, A., Berczik, P., Petrov, M. I., & Ernst, A. 2009, MNRAS, 392, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 409 [NASA ADS] [Google Scholar]
- Kharchenko, N., & Schilbach, E. 1996, Balt. Astron., 5, 337 [Google Scholar]
- Kharchenko, N. V., Berczik, P., Petrov, M. I., et al. 2009, A&A, 495, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1990, MNRAS, 244, 76 [NASA ADS] [Google Scholar]
- Lebreton, Y., Fernandes, J., & Lejeune, T. 2001, A&A, 374, 540 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Moraux, E., Bouvier, J., Stauffer, J. R., & Cuillandre, J.-C. 2003, A&A, 400, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paulson, D. B., Sneden, C., & Cochran, W. D. 2003, AJ, 125, 3185 [NASA ADS] [CrossRef] [Google Scholar]
- Pels, G., Oort, J. H., & Pels-Kluyver, H. A. 1975, A&A, 43, 423 [NASA ADS] [Google Scholar]
- Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS] [Google Scholar]
- Pinsonneault, M. H., Terndrup, D. M., Hanson, R. B., & Stauffer, J. R. 2004, ApJ, 600, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, A. E., Kharchenko, N. V., Röser, S., Schilbach, E., & Scholz, R.-D. 2006, A&A, 445, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, A. E., Schilbach, E., Kharchenko, N. V., Röser, S., & Scholz, R.-D. 2007, A&A, 468, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1915, MNRAS, 76, 107 [NASA ADS] [Google Scholar]
- Reid, N. 1992, MNRAS, 257, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, I. N., & Hawley, S. L. 1999, AJ, 117, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Schwan, H. 1990, A&A, 228, 69 [NASA ADS] [Google Scholar]
- Schwan, H. 1991, A&A, 243, 386 [NASA ADS] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smart, W. M. 1968 (London: Longmans) [Google Scholar]
- Spitzer, L., Jr., & Shull, J. M. 1975, ApJ, 200, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, B. J. 2006, AJ, 132, 2453 [NASA ADS] [CrossRef] [Google Scholar]
- Trumpler, R. J., & Weaver, H. F. 1953, Dover Books on Astronomy and Space Topics (New York: Dover Publications) [Google Scholar]
- van Altena, W. F. 1969, AJ, 74, 2 [NASA ADS] [CrossRef] [Google Scholar]
- van Bueren, H. G. 1952, Bull. Astron. Inst. Netherlands, 11, 385 [Google Scholar]
- van Leeuwen, F. 2007, Astrophys. Space Sci. Lib., 350, [Google Scholar]
- van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Hippel, T. 1998, AJ, 115, 1536 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R., Dettbarn, C., Jahreiß, H., Lenhardt, H., & Schwan, H. 1999, A&A, 346, 675 [NASA ADS] [Google Scholar]
- Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The MKs vs. r′ − Ks diagram of the kinematic candidates (small dots). The vast majority of the stars have kinematically predicted parallaxes inconsistent with their photometric parallaxes. The candidates shown as thick dots are retained for further analysis. Stars brighter than MKs ≈ 3.5 are not contained in CMC14. |
| In the text | |
 |
Fig. 2 The MKs vs. J − Ks diagram of the candidates. Stars which were marked as thick dots in Fig. 1 are also marked as thick dots here. |
| In the text | |
 |
Fig. 3 The luminosity functions (LF) of the Hyades candidates and of field stars in the solar vicinity. a) Solid lines and symbols are the LFs of the Hyades at different distances from the cluster centre rc, black filled circles for rc < 9 pc, red open circles for 9 pc < rc < 18 pc, blue crosses for 18 pc < rc < 30 pc. The LF of nearby stars from the CNS4 (Jahreiß 2010, priv. comm.) is shown by the black dashed line whereas the black dotted line is the fraction of field stars with space velocities comparable to the velocity of the Hyades. b) The red open circles and blue crosses show the adopted contamination of the Hyades sample of 7.5% at 9 pc < rc < 18 pc and 30% at 18 pc < rc < 30 pc, respectively. The black dotted line is the same as in a). |
| In the text | |
 |
Fig. 4 The MKs vs. J − Ks diagram of the 724 Hyades candidates. For MKs ≤ 2, the J − Ks colours from 2MASS are of low precision, because the stars are too bright in the J-band. Stars shown as green dots are those for which we were able to confirm their membership by comparing with measured trigonometric parallaxes and/or radial velocities. |
| In the text | |
 |
Fig. 5 Comparison of the empirical MKs vs. J − Ks diagram of the Hyades candidates (masses less than about 1 m⊙) with different theoretical isochrones. The PADOVA isochrones are shown by filled red triangles (curve most to the left), the DARTMOUTH isochrones blue open circles, and the BCAH isochrones by the magenta open triangles (curve most to the right). |
| In the text | |
 |
Fig. 6 The cumulated mass as a function of the distance from the cluster centre rc. The thick black curve is the observed cumulated mass function as obtained from adding up all the individual masses within a distance rc. The (thinner) red curve is the relation from Eq. (3) between the tidal radius and the tidal mass in the gravitational field of the Galaxy near the position of the Sun. |
| In the text | |
 |
Fig. 7 The dependence of number density, mass density, and average mass per star as a function of the logarithm of the distance from the centre rc. From top to bottom: a) the number density D of stars in the cluster obtained with a binning of 2 pc in steps of 1 pc. Outside 10 pc the bin size is increased to get a better signal-to-noise ratio. The error bars are Poisson errors; b) the observed mass density ρ (black dots) using the same binning and a density distribution (red crosses) from a Plummer model (Eq. (4) with Mt = 276 m⊙ and rco = 3.10 pc); c) the average mass per star obtained as ρ/D. Its decrease from the centre outbound characterises the mass segregation in the Hyades, at present time. |
| In the text | |
 |
Fig. 8 Observed a) and modelled b), c) spatial distribution in the Hyades. Blue points are for stars with masses m > 0.5 m⊙, red points for m ≤ 0.5 m⊙. In the modelled distribution, the dynamically unbound particles are marked by black crosses b) or black points c). Two large black circles in a) and b) indicate the distances rc from the cluster centre of 9 pc and 18 pc, whereas in c) the circles correspond to rc = 9 pc, rc = 18 pc, and rc = 30 pc. The last one restricts the area considered in this study. |
| In the text | |
 |
Fig. 9 The luminosity function of the Hyades in different regions. This luminosity function is constructed as a moving average with a rectangular kernel of 1.5 mag in steps of 0.1 mag. The upper (blue) curve refers to the core region inside 3.1 pc from the centre, the second (cyan) curve to the corona (3.1 pc to 9 pc), the third (green) to the halo (9 pc to 18 pc), and the fourth (red) to the co-movers outside 18 pc. The dashed vertical line at MKs = 7.3 marks the onset of incompleteness of our survey. The units are stars (systems) per pc-3 and 1 mag. |
| In the text | |
 |
Fig. 10 The present-day mass function (PDMF) of the Hyades. The lowest histogram (filled black dots) shows the PDMF in the core of the cluster (rc < 3.1 pc), the magenta triangles mark the PDMF within the tidal radius (rc < 9 pc), the blue squares stand for the PDMF in the region rc < 18 pc, and finally the filled red squares are the PDMF of all 724 stars within 30 pc from the centre. The PDMFs are corrected for field star contamination. The histograms give the actual star counts per logarithmic mass bin of 0.1. The dashed vertical line at about 0.25 m⊙ marks the onset of incompleteness of our survey. For comparison, we show a Kroupa (2001) mass function (solid line) with α = 2.35 for masses larger than 0.5 m⊙, and α = 1.35 below 0.5 m⊙. As an other extreme we show a mass function with slope α = 3.05 (dashed line) fitted to the high-mass portion of the observed PDMF. |
| In the text | |
 |
Fig. 11 The mass function of the Hyades from this paper (black histogram with filled black dots). The blue curve (open squares) shows the Hyades PDMF from Bouvier et al. (2008), the red histogram with triangles is the PDMF from the 120 Myr old Pleiades from Moraux et al. (2003), and finally the green curve (filled squares) is the PDMF of Praesepe from Boudreault et al. (2010). The thin solid line shows again a Kroupa (2001) mass function. |
| In the text | |
 |
Fig. 12 The distribution of the tangential velocity components v⊥ perpendicular to the direction to the convergent point as a function of the distance from the cluster centre. The nine stars in red circles are outliers which are not considered in the determination of the velocity dispersion in Table 3. The vertical lines mark the core (dashed) and tidal (solid) radii. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


