| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201016187 | |
| Published online | 01 June 2011 | |
The metal contents of two groups of galaxies
1
SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
e-mail: y.g.grange@sron.nl
2
Astronomical Institute, Utrecht University, PO Box 80000, 3508 TA Utrecht, The Netherlands
3
Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 382 Via Pueblo Mall, Stanford, CA 94305-4060, USA
4
Columbia Astrophysics Laboratory and Department of Astronomy, Columbia University, 550 West 120th Street, New York, NY 10027, USA
Received: 23 November 2010
Accepted: 30 March 2011
Context. The hot gas in clusters and groups of galaxies is continuously being enriched with metals from supernovae and stars. It is well established that the enrichment of the gas with elements from oxygen to iron is mainly caused by supernova explosions. The origins of nitrogen and carbon are still being debated. Possible candidates include massive, metal-rich stars, early generations of massive stars, intermediate- or low-mass stars and asymptotic giant branch (AGB) stars.
Aims. In this paper we accurately determine the metal abundances of the gas in the groups of galaxies NGC 5044 and NGC 5813, and discuss the nature of the objects that create these metals. We mainly focus on carbon and nitrogen.
Methods. We use spatially-resolved high-resolution X-ray spectroscopy from XMM-Newton. For the spectral fitting, multi-temperature hot gas models are used.
Results. The abundance ratios of carbon over oxygen and nitrogen over oxygen that we find are high compared to the ratios in the stars in the disk of our Galaxy. The oxygen and nitrogen abundances we derive are similar to what has been found in earlier work on other giant ellipticals in comparable environments. We show that the iron abundances in both our sources have a gradient along the cross-dispersion direction of the reflection gratingspectrometer (RGS).
Conclusions. We conclude that it is unlikely that the creation of nitrogen and carbon takes place in massive stars, which end their lives as core-collapse supernovae, enriching the medium with oxygen because oxygen should then also be enhanced. Therefore we favour low- and intermediate-mass stars as sources of these elements. The abundances in the hot gas can be explained best by a 30–40% contribution of type Ia supernovae based on the measured oxygen and iron abundances and under the assumption of a Salpeter initial mass function (IMF).
Key words: galaxies: abundances / X-rays: galaxies / galaxies: groups: general / galaxies: groups: individual: NGC 5044 / galaxies: groups: individual: NGC 5813 / galaxies: clusters: intracluster medium
© ESO, 2011
1. Introduction
Most of the galaxies in the Universe reside in groups (e.g. Tully 1987). Groups of galaxies typically contain up to tens of galaxies. Because their gravitational potential is relatively shallow, groups of galaxies are good laboratories for studying non-gravitational effects (see e.g. the review by Mulchaey 2004). The gravitational compression and infall shocks, which heat up the gas, depend on the depth of gravitational potential, therefore groups of galaxies are cooler than the more massive clusters.
Since the temperature of groups is rather low (~107 K), the emission lines of metals present in the medium are relatively strong. This yields insight into the abundance distribution of metals in the intragroup medium. Since all the metals in this medium have been produced by stars, metal abundances in the intragroup medium are a tracer of the history of stellar evolution.
X-ray spectroscopy of groups and clusters of galaxies is a powerful tool for measuring the abundances in the hot gas. The broad spectral band of the European photon imaging cameras (EPIC-MOS, Turner et al. 2001; and EPIC-pn, Strüder et al. 2001) and the high spectral resolution of the reflection gratingspectrometers (RGS, den Herder et al. 2001) on board XMM-Newton allow us to determine the key abundances needed to constrain supernova models and ratios (see e.g. the review by Böhringer & Werner 2010). While earlier work focussed on clusters, more recently, the metal contents of groups has been investigated in more detail (e.g. Rasmussen & Ponman 2007; Werner et al. 2009). Measurements with the RGS are the only way to constrain the carbon and nitrogen abundance in the hot gas.
The abundances observed in the intracluster medium are the result of the production of the elements in stars and the transport of the elements released to their current location. The metals with even atomic numbers from oxygen up to iron and nickel are produced in supernovae: oxygen, neon, and magnesium mainly in core-collapse supernovae, iron and nickel mainly in type Ia supernovae. Both types create significant amounts of silicon, sulfur, argon, and calcium. The relative fraction of these elements is however unknown and highly model dependent (see e.g. Iwamoto et al. 1999; Woosley et al. 2002). Carbon and nitrogen are produced by a variety of sources, the relative importance of which is still under debate (for an overview of possible sources of several elements, see Romano et al. 2010, and references therein). Based on optical observations of stars in our galaxies, most authors conclude that superwinds of massive metal-poor stars enriched the gas with carbon early in the Galaxy disk’s evolution. Some authors argue that at a later stage, a significant amount of carbon is created by low-mass stars (e.g. Cescutti et al. 2009). Others (e.g. Bensby & Feltzing 2006; Mattsson 2010) advocate at the enrichment at later stages is mainly due to intermediate-mass stars, during their AGB phase. Bensby & Feltzing (2006) conclude from the literature that it is likely that the enrichment with carbon is probably due to a complicated, and finely tuned set of objects. Nitrogen is created by the conversion of carbon and oxygen during the CNO cycles of hydrogen burning in low- and intermediate-mass stars (Edmunds & Pagel 1978; Chiappini et al. 2003) and metal-poor massive stars (Matteucci 1986; Meynet & Maeder 2002).
Several mechanisms have been proposed that enrich the gas in groups and clusters of galaxies with the metals created inside the galaxies. An overview of these mechanisms is given by Schindler & Diaferio (2008). Simulations suggest that the gas is mainly enriched by galactic winds, which are powered by core-collapse supernovae at early stages of the evolution. During the life time of the group, the winds get more and more driven by type Ia supernovae. Other mechanisms include e.g. uplift of metals by the central active galactic nucleus (AGN) and ram-pressure stripping of infalling galaxies. The relative importance of these processes is however yet unknown.
In this paper, we study two X-ray bright groups of galaxies, NGC 5044 and NGC 5813. Both groups are named after the giant elliptical galaxy in their core. Multiple dwarf galaxies are found around the central elliptical galaxy of these groups. NGC 5044 has previously been observed with several X-ray satellites (Einstein: Fabbiano et al. 1992; ROSAT: David et al. 1994; ASCA: Fukazawa et al. 1996). The X-ray emission is sharply peaked in the central region and the temperature declines towards the core. Recently, the kinematic structure of NGC 5044 was studied with Chandra by David et al. (2009). Chandra images show multiple filaments and cavities, which indicate activity of the central AGN (Gastaldello et al. 2009). XMM-Newton observations show a clear multi-temperature structure and Tamura et al. (2003) put constraints on the metal abundances. Since then, the models and instrumental calibration have been improved and longer observations have been performed to measure the abundances with a higher precision.
The group around NGC 5813 is part of a larger gravitationally bound system which also includes the group around NGC 5846. NGC 5813 has a kiloparsec size, kinematically decoupled core (Efstathiou et al. 1982) caused by a history of minor or intermediate mergers long ago. It is classified by Emsellem et al. (2007) as being a slow rotator, which they conclude is an extreme evolutionary end point reached in a deep potential well. In essence, this means that this group is extremely relaxed. Randall et al. (2011) studied the shocks caused by the AGN feedback in this group using data taken by Chandra, and conclude that the outflow of the central AGN is energetic enough to heat up the gas.
We have obtained deep XMM-Newton observations of these two groups. Exploiting the high spectral resolution and sensitivity of XMM-Newton, we aim to accurately determine metal abundances in the hot gas. Especially the carbon and nitrogen abundances contain clues on the likely candidates for their production. In addition, the ratio between type Ia and core-collapse supernovae can be constrained using the oxygen and iron abundance. We use the measured abundances in the intragroup medium to test supernova yield models.
Throughout this paper, we use H0 = 70 km s-1 Mpc-1, ΩM = 0.3, and ΩΛ = 0.7. At the redshift of NGC 5044 (z = 0.009), 1′ represents a distance of 11.1 kpc. At the redshift of NGC 5813 (z = 0.007), 1′ represents a distance of 7.92 kpc. The abundances are in units of the proto-solar abundances (Lodders 2003). Quoted statistical uncertainties are at a 1σ (68%) confidence level. Results obtained from the literature using different abundance scales (Anders & Grevesse 1989; and Grevesse & Sauval 1998) or significance levels (e.g. 90%) were converted to the units of this work before comparing them.
Log of the observations used.
2. Data reduction and analysis
All the data used for this research were obtained using the instruments on board of the XMM-Newton satellite. A log of the observations is presented in Table 1. The recent (2008 and 2009) data were obtained using the thin filter and for the archival data the medium filter was used. We use data from both the EPIC and the RGS. The EPIC-MOS was in full frame mode during all observations. For the EPIC-pn, the extended full frame mode was turned on during the 2005 observation of NGC 5813, while for all others it was in the full frame mode. In total, 153 ks of data are available for NGC 5044 and 173 ks for NGC 5813. The reduction was done with the XMM-Newton Science Analysis Software (SAS) version 9.0.0 with the calibration files created on 22 June 2009.
In order to reduce contamination from soft-proton flares, we created a lightcurve for each instrument and observation. For EPIC, the light curve was based on the data in the 10–12 keV energy band and for RGS we used the data from CCD number 9, where hardly any emission from the group is expected. We binned the light curve in 200 s intervals for RGS and 100 s intervals for EPIC. A Poissonian distribution was fitted to the count-rate histogram. We rejected all time bins for which the number of counts lies outside the interval 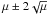 , where μ is the fitted average of the Poissonian. The clean exposure times are listed in Table 1. Since we cut off all data above μ + 2σ as well as all data under μ − 2σ, we do not expect the flux to change due to our filtering. To check whether a less severe filtering would significantly improve the statistics, we fitted RGS spectra for which we did not use any filtering at all. These fits are statistically comparable to the results of this work. In addition, we created a light curve from the events between 0.3 and 1 keV to check whether our spectra are contaminated by charge-exchange emission from the interactions between the solar wind and gas in the ecliptic plane of our solar system and the Earth’s atmosphere. This emission should show up as flares in the light curve under 1 keV. The light curve does not show significant flares in this energy region.
, where μ is the fitted average of the Poissonian. The clean exposure times are listed in Table 1. Since we cut off all data above μ + 2σ as well as all data under μ − 2σ, we do not expect the flux to change due to our filtering. To check whether a less severe filtering would significantly improve the statistics, we fitted RGS spectra for which we did not use any filtering at all. These fits are statistically comparable to the results of this work. In addition, we created a light curve from the events between 0.3 and 1 keV to check whether our spectra are contaminated by charge-exchange emission from the interactions between the solar wind and gas in the ecliptic plane of our solar system and the Earth’s atmosphere. This emission should show up as flares in the light curve under 1 keV. The light curve does not show significant flares in this energy region.
The RGS is a slitless instrument. This means that the zeropoint of the wavelength calibration is dependent on the position of the source in the detector field of view. We gauge our wavelength scale of RGS on the peak of the emission in the X-ray image. We also use this position as the source centre for the EPIC extraction region. For NGC 5044, we take α = 13h15m24s, δ = −16°23′08′′ and for NGC 5813, these coordinates are α = 15h01m11s, δ = 01°42′06′′. These coordinates are within 2′′ from the optical position of the central galaxy.
2.1. Reduction of the RGS data
The RGS data were reduced using the standard pipeline processing of the SAS. We subtracted from the total spectrum a model background spectrum which is created by the standard RGS pipeline. This method consists of selecting a template background file, based on the count rate in CCD 9 of the RGS. We do not explicitly model the cosmic X-ray background in RGS because any diffuse line source would be smeared out into a broad, nearly flat continuum-like component. We included 100% of the cross-dispersion direction in the spectrum because the extent of the sources is larger than the width of the RGS. All other options were left to their default values. To make one-dimensional spatial profiles of the parameters that we measured using RGS, we also created spectra based on five narrow regions in the cross-dispersion direction of the RGS, within 2′ from the core. During one of the observations of NGC 5813 (obsID 0302460101) the position angle differs by ~180° from the other two observations. We fitted the spectra from the cross-dispersion strips of this observation simultaneously with the spectra from the opposing regions of the other two observations. In the other cases, we assumed that the differences in roll angle were not large enough to introduce systematic effects. The relative position of the sources to the RGS detectors and the positive cross-dispersion directions are shown in Figs. 1 and 2.
Since, as mentioned before, RGS is a slitless instrument, all photons within the field of view end up in the final spectrum. This causes a broadening of the spectral lines. If a photon originates from an angle Δθ (in arc minutes) projected along the dispersion direction, it will be registered as having a wavelength which is shifted by Δλ (in Å) with respect to its original wavelength. The XMM-Newton Users Handbook gives the relation 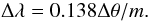 (1)Here, m is the (absolute value of the) spectral order. We extracted the brightness profile of the source in the dispersion direction from the EPIC-MOS image and used this to account for the broadening following the method developed by Tamura et al. (2004). We used the spectral data between 7 Å and 36 Å. This upper limit is chosen so that we include the C vi line at 33.7 Å.
(1)Here, m is the (absolute value of the) spectral order. We extracted the brightness profile of the source in the dispersion direction from the EPIC-MOS image and used this to account for the broadening following the method developed by Tamura et al. (2004). We used the spectral data between 7 Å and 36 Å. This upper limit is chosen so that we include the C vi line at 33.7 Å.
 |
Fig. 1 Smoothed Chandra image of NGC 5044. The edges of the RGS for obsID 0037950101 are indicated with black lines. The black arrow has length 1′, and points in the positive cross-dispersion direction. |
 |
Fig. 2 Smoothed Chandra image of NGC 5813. The edges of the RGS for obsID 0554680201 are indicated with black lines. The black arrow has length 1′, and points in the positive cross-dispersion direction. |
2.2. EPIC data reduction
Because we want to compare our EPIC results with RGS, we derived EPIC spectra from a circle with radius 3′ around the centre. The diameter corresponding to this radius is comparable to the cross-dispersion width of the RGS (5′). We identified point sources, based on visual selection, and excised a region with a radius of 15′′ around them. In total, we excised one point source from the NGC 5044 observation. Two point sources were removed which lie on the edge of the 3′ circle. From the field around NGC 5813, three point sources were identified and removed. Based on the spectrum, we created files containing the effective area and response matrix using the default SAS-tasks. To correct for vignetting effects, we created these files using a detector map of the source. Furthermore, we corrected the pn observations for out of time (OOT) events. We ignored all events corresponding to energies higher than 10 keV. For EPIC-MOS, we ignored the events below 0.4 keV. We also ignored all events below 1.5 keV in the EPIC-pn data because these data are affected by a gain shift, leading to large-scale systematic residuals below this energy. This effect seems to be present in both sources.
2.2.1. EPIC background
To correctly fit the EPIC spectra, we need to subtract or model the background. Snowden et al. (2004) used a method to subtract the EPIC-MOS instrumental background by scaling closed filter observations, as created by the XMM-Newton science operations centre (SOC). Other authors (Arnaud et al. 2001; Read & Ponman 2003; De Luca & Molendi 2004; Nevalainen et al. 2005) developed and used comparable methods. The methods mentioned are highly dependent on the region of the CCD outside the field of view. In the pn, this region is very small which makes the method sensitive to statistical fluctuations. Since we want to simultaneously fit the three instruments, we need to use a unified background subtraction method. Our method involves modelling the background by use of additional spectral models (see e.g. Leccardi & Molendi 2008; de Plaa et al. 2010), as follows. We modeled both instrumental and Cosmic X-ray background.
For the instrumental background, we used the closed filter observations, provided by the XMM-Newton SOC. We extracted a spectrum from these closed filter files, using the same procedure as for the actual data. We modelled this instrumental background using a broken power law, which describes the hard particle spectrum, and a number of delta functions that represent the fluorescence lines caused by the interaction of hard particles with the instrument itself. We list the fluorescence lines that we took into account in Table 2. Since high-energy particles are not focussed by the telescope in the same way as X-ray photons, we did not fold these models through the ancillary response file (ARF), which describes the effective area of the instrument. The instrument degrades with time, leading to an increase of the instrumental background. In addition, the instrumental powerlaw does not vary over the field of view, while the strength of the instrumental lines does depend on the position on the detector. During the fits to the core spectra, we fitted the instrumental background for each observation by allowing the normalisations of the instrumental background components to vary within a factor of 4 of the best-fit value, derived from the closed filter spectrum. We also left free the power-law break strength. We assumed that the two observations of NGC 5813 on February 2009 had the same instrumental background.
Instrumental lines modelled for EPIC-MOS and EPIC-pn.
The second group of components models the emission by the astrophysical back- and foreground. These X-rays are focussed by the mirror in the same way as source photons, and therefore these components should be folded through the ARF. At high energies (>2 keV), the background is dominated by the cosmic X-ray background of unresolved point sources. This component is modelled using a power-law, the extra-galactic power law (EPL). We fixed the photon index Γ to 1.41 and the 2−10 keV flux to 2.24 × 10-14 W m-2deg-2 (De Luca & Molendi 2004).
At lower energies (< 2keV), foreground emission from the local hot bubble (LHB) dominates the background spectrum. Contrary to the other X-ray background components, this one is not absorbed by the neutral gas of our Galaxy. Furthermore, the diffuse halo or disk of the Galaxy also contributes to the foreground at these low energies (Kuntz & Snowden 2001). We modelled these two components using a collisionally ionisation equilibrium (CIE) plasma model. Since the temperatures of these components vary across the sky, we had to fit the temperatures locally. Therefore, we extracted a spectrum from an annulus between 9′ and 12′ centred on the emission peak of the group. In this annulus the group emission is low. In addition to the background components, we added an extra CIE component to model any residual group emission. The best-fit values of the relevant parameters are listed in Table 3. We kept the parameters of the X-ray background model components frozen to the best-fit values while fitting the spectra in the core. The normalisations of the components were scaled to the size of the extraction region.
Relevant parameters of the fitted background components.
2.3. Spectral models
We fit our spectra using the SPEX package (Kaastra et al. 1996). Since clusters and groups are not isothermal, we used multi-temperature models. We fitted the spectra using two different empirical parametrisations of a differential emission measure (DEM) model. The emission measure Y = nenhdV with ne and nh the electron and proton densities and V the volume of the source.
The first parametrisation is the gdem model, in which the differential emission measure dY/dT as a function of temperature is distributed as (e.g. de Plaa et al. 2006) 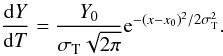 (2)In this equation, x = log (T) and x0 = log (T0).
(2)In this equation, x = log (T) and x0 = log (T0).
The second DEM model we fitted is the wdem model (Kaastra et al. 2004). The model consists of a number of thermal components distributed as a truncated power law. The model is characterised by: 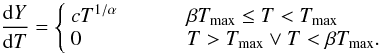 (3)For α → 0, the model becomes isothermal with temperature kTmax.
(3)For α → 0, the model becomes isothermal with temperature kTmax.
In order to compare the multi-temperature models, we calculated the emission-weighted temperature for wdem (see de Plaa et al. 2006, for the derivation), 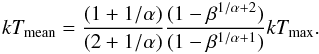 (4)For gdem the peak temperature is fitted.
(4)For gdem the peak temperature is fitted.
 |
Fig. 3 Fluxed, background-subtracted RGS spectrum of NGC 5044. The (red) line through the data points is the best fit. The most important spectral lines are indicated in the plot. |
The hot gas models allow us to determine the abundances of metals in the intragroup medium. Since the neon and magnesium abundance could not be constrained using EPIC, we fixed the ratio between these and iron to the values found in RGS. For the Galactic foreground absorption due to neutral gas, we used the H i column density from the Leiden/Argentine/Bonn survey (Kalberla et al. 2005). For NGC 5044 we used a column density of 4.87 × 1024 m-2 and for NGC 5813 the value is 4.37 × 1024 m-2.
3. Results
We fitted the spectra of NGC 5044 and NGC 5813 using the models described in Sect. 2.3. In order to easily compare the abundances found to other groups, we quote abundance ratios for most elements. We chose to quote the abundances relative to iron, because iron has the smallest statistical uncertainty of all measured abundances.
3.1. NGC 5044
In Fig. 3, we show the RGS spectrum of NGC 5044. The best-fit values are listed in Table 4. The spectrum shows a wealth of lines that can be used to constrain the abundances and multi-temperature structure of the gas. Most lines are fitted well, however both the Fe xviii and O viii-Lyβ line blend around 16 Å and the blend of Fe xviii and Fe xix near 14 Å are not fitted optimally. Near 11 Å the model is also underestimating the data.
Table 4 shows that this source has a significant temperature structure to which the gdem model fits slightly better than the wdem model. The derived abundance ratios, as reported in Table 4, are consistent. The absolute iron abundances derived from these models differ by about 3σ. The mean temperature is consistent between the two models.
The background for RGS at long wavelength is high for extended sources, and hence some systematic residuals remain near the C vi line at ~ 34 Å.
 |
Fig. 4 Iron and temperature profiles in the cross-dispersion direction based the fits to the RGS data of NGC 5044 using the gdem model. |
Figure 4 shows the profiles of the gdem peak temperature and iron abundance as measured along the cross-dispersion direction of RGS (see Fig. 1 for the physical direction of the cross-dispersion direction). The temperature shows an increase from the centre of the galaxy towards the outer parts, as is normal in the cooling cores of groups and clusters of galaxies. The iron abundance shows a hint of a linear decrease over the cross-dispersion direction. Fitting a linear model to the data yields a normalisation of 0.663 ± 0.016 solar at r = 0 and the slope of the line is −0.08 ± 0.02 solar per arc minute.
 |
Fig. 5 O/Fe and N/Fe profiles (in proto-solar units by Lodders 2003) based on the fits to the RGS data of NGC 5044 using the gdem model. The nitrogen abundance could not be constrained in the rightmost bin and is therefore not present in the plot. |
The profiles of the relative abundances of oxygen and nitrogen are presented in Fig. 5. The oxygen over iron abundance shows no significant variation over the cross-dispersion direction. The nitrogen abundance is poorly constrained. The EPIC spectrum, (Fig. 6) shows systematic residuals above 2 keV, where the background is becoming more important possibly to a low contribution of quiescent soft-protons. The residuals also show some systematic effects in the iron-L complex at energies below 2 keV.
 |
Fig. 6 EPIC spectrum of NGC 5044. The top panel shows the data points with the model as a histogram through them. Upper data set: EPIC-pn, bottom data set: EPIC-MOS. The bottom plot shows the fitting residuals. Squares: EPIC-pn, circles: EPIC-MOS. |
The iron abundance derived using the EPIC data is significantly higher than the one derived from RGS. For the oxygen over iron ratio, the value derived from EPIC is lower than the RGS value. The abundance ratios of silicon, sulfur, argon, calcium and nickel over iron are high. The EPIC fits give a temperature structure with a higher peak temperature and a lower emission measure than for those of the RGS. For the EPIC spectra, the derived temperature structure is broader than what we find for the RGS spectra.
Fitted values to the NGC 5044 spectra.
3.2. NGC 5813
We present the RGS spectrum of NGC 5813 in Fig. 7. The model is underestimating the line flux of the oxygen and iron line blend near 16 Å, which is also the case for NGC 5044. Contrary to the fit for NGC 5044, the 14 Å blend is well fitted by the model.
 |
Fig. 7 Fluxed RGS spectrum of NGC 5813. The (red) line through the data points is the best fit. The most important spectral lines are indicated in the plot. |
The values and accuracies of the carbon and nitrogen abundances are well defined and comparable to what we find for NGC 5044. Also for this source, the background at ~34 Å introduces extra uncertainty in the measured carbon abundance.
The fits to the RGS spectrum of NGC 5813 show no significant difference between wdem and gdem. Both models converge to the single-temperature limit with essentially the same values for all parameters and the same statistical significance.
 |
Fig. 8 Iron and temperature profiles in the cross-dispersion direction based on the fits to the RGS data of NGC 5813 using the gdem model. |
The RGS profiles along the cross-dispersion direction of the gdem peak temperature and the iron abundance that we obtained from the RGS data are shown in Fig. 8. For the physical meaning of the cross-dispersion direction, see Fig. 2. A decrease towards the centre of the temperature is observed, like in cool-core groups. However, the central temperature gradient is shallower than for NGC 5044. The iron abundance appears to be asymmetrically distributed around the core. A linear fit to this data set yields a normalisation of 0.650 ± 0.018 solar at r = 0 and a slope of − 0.13 ± 0.03 solar per arc minute.
 |
Fig. 9 O/Fe and N/Fe profiles (in proto-solar units by Lodders 2003) based the fits to the RGS data of NGC 5813 using the gdem model. |
In Fig. 9, the radial profiles of oxygen and nitrogen over iron abundances are shown. The O/Fe abundance ratio is flat, with a hint of a decrease from the negative to the positive cross-dispersion direction.
 |
Fig. 10 EPIC spectrum of NGC 5813. The top panel shows the data points with the model as a histogram through them. Upper data set: EPIC-pn, bottom data set: EPIC-MOS. The bottom plot shows the fitting residuals. Squares: EPIC-pn, circles: EPIC-MOS. |
The EPIC spectra of NGC 5813 are shown in Fig. 10. In the iron-L complex, around 1.2 keV some residuals remain which do not show up as strong in the spectra of NGC 5044. Between 3 keV and 5 keV, the systematic residuals are similar to the same spectral regions in NGC 5044.
As can be seen in Table 5, the iron abundance in EPIC is 16% higher than the value deduced from RGS. The emission measure is lower by 24%, while the O/Fe ratio is 20% lower. Contrary to RGS, EPIC shows a significant temperature structure with the gdem model. Silicon, sulfur, argon and calcium to iron abundance ratios are high. The nickel to iron abundance is low.
Fitted values to the NGC 5813 spectra.
4. Discussion
We accurately determined the metal abundances of the hot gas in two groups of galaxies. In the following sections we focus the discussion of four main points. First, the derivation of the temperature structure, including the fitting of the iron-L complex and its effects on the reported abundance ratios. Second, we show how our abundance ratios compare to what was earlier reported in the literature. After this the supernova models and numbers using the abundances found in the gas are discussed. Finally we address the stellar origins of the carbon, nitrogen and oxygen abundances.
4.1. Temperature structure
In general, multi-temperature models fit the spectra of both groups well. In the EPIC spectrum of NGC 5813 we find some systematic effects in the residuals near 1.2 keV. Brickhouse et al. (2000) encountered the same feature in Capella, which has a thermal component with a temperature comparable to our sources. They solve this problem by adding lines caused by transitions of Fe xvii, Fe xviii and Fe xix to the model. The abundances of Capella significantly increased when doing this. We recalculated the best fitted model using an experimental version of the line list that is being implemented in SPEX1, which contains many more transitions, including the ones probably causing the feature. Doing this did improve the fit near 1.2 keV. To date it is however not possible yet to use the new list for fitting yet.
In RGS, we find that some lines in the iron-L complex are not well fitted in both groups. In Table 6, we list the ten strongest lines between 15.3 Å and 16.7 Å in the fitted models to our sources. The eight brightest lines are the same for both sources but their order in the list is slightly different. Most of these strongest lines are due to the Fe xviii ion.
The ten strongest modelled lines around the 16 Å blend, using the fitted model to the sources.
We investigated whether these model errors could be caused by the use of an outdated ionisation balance. We fitted the spectra of NGC 5044 again using the ionisation balance by Bryans et al. (2009) instead of the default ionisation balance of SPEX (Arnaud & Raymond 1992, for iron; and Arnaud & Rothenflug 1985, for the other elements). Statistically, the fit did not improve by this (C-stat 2824 cf. 2418 for the original balance). The fit around the 16 Å line did not improve either. We also recalculated the best fitted model using the forementioned experimental version of the SPEX line list. This also did not improve the fit near the blend.
Work by Audard et al. (2001) using a MEKAL model on Capella shows that the spectral lines around 16 Å are indeed not fitted well. The fact that the other line blend of Fe xviii and Fe xix is correctly fitted in one of the cases hints towards uncertainties in the unresolved spectral lines at these wavelengths. Since most of the lines of iron are fitted correctly when using the abundances that we find, the effect of single poorly fitted lines on the iron abundance should be limited. Werner et al. (2009) show an indication for resonant scattering of one of the Fe xvii lines in NGC 5813 which could cause a slight underestimation of the iron abundances. Although they try to take this effect into account, the 16 Å line is not perfectly fitted in that work as well. Since the blend at 16 Å also consists of the O viii − Lyα an resonant scattering effect on this line might also influence the underestimation of the flux at this blend.
Line ratios that differ from the ones calculated using the ionisation balance at a given temperature might be caused by non-equilibrium effects. To test for the presence of these effects, the CIE model allows for fitting of the ratio between the ionisation balance temperature and the electron temperature. The best-fit ratio we find is 1.21 ± 0.03 for NGC 5044 and 1.30 ± 0.05 for NGC 5813. The fitting of this parameter improves the C-statistic with ~50. However, the problems with the 14 Å and 16 Å lines are not solved. Moreover, due to the high densities and collisional timescales in the cores of the groups of galaxies studied, it is highly unlikely that non-equilibrium effects are present.
Clusters and groups of galaxies intrinsically contain multiple gas components with different temperatures. Therefore, we need multi-temperature models to constrain temperature structures and abundances correctly (e.g. Peterson et al. 2003; Kaastra et al. 2004). Knowing this, it is remarkable that NGC 5813 shows a single-temperature spectrum in RGS. This is fully consistent between the wdem and gdem fits of the RGS data and was previously found by Werner et al. (2009). In the cross-dispersion direction of RGS we do measure a significant but relatively small rise of the temperature near the outermost bin (between 1′ and 2′). In the EPIC data, the gdem models have a σT of 0.057 ± 0.004, corresponding to a 0.09 keV spread in the temperature.
The analysis of Chandra data by Randall et al. (2011) shows a high-resolution temperature map of the inner region of NGC 5813 (r < 3′). The temperatures range from ~0.6 keV to ~0.7 keV. To investigate whether some, maybe unresolved, temperature structure would cause an effect comparable to our results, we simulated a spectrum consisting of two CIE components. We choose to set one of these components to have a temperature of 0.6 keV and put the other at 0.7 keV. The normalisations were fixed to half the value found for NGC 5813 and all other parameters were fixed to the best-fit values derived from the RGS data of NGC 5813. We then fitted this spectrum under the assumption of one single gdem distribution and found a σT of 0 and a value for the ion to electron temperature ratio that is the same as we find in our fits. A fit to the NGC 5813 data using two distinct CIE models caused both temperatures to converge to the value found using a single gdem model. The effect found by leaving the ratio between the electron and ionisation balance temperature free could in both sources be caused by the part of the temperature structure that can not be resolved using the models.
4.2. Abundances
The oxygen abundances as measured by EPIC are lower than what is measured using RGS. Oxygen lines can not be well resolved by EPIC due to its relatively poor spectral resolution and uncertain calibration (e.g. de Plaa et al. 2007). Since we ignore EPIC-pn in the region of the oxygen line, instrumental effects are probably due to the cross-calibration between RGS and EPIC-MOS. Since the RGS spectra resolve the O viii line at ~19 Å, we use the RGS value. For NGC 5044 we could fit the EPIC spectrum leaving the instrumental power-law normalisation to vary within a factor 2. For NGC 5813, we needed to increase the factor to 4 and to leave the photon index break free. This effect could be due to a possible low contribution of quiescent soft-protons. We compared the abundances and temperature for those fits to a fit leaving only the normalisation free within a factor of 2. The abundances of nickel, argon and sulfur did significantly differ between those fits. We therefore decided not to use the abundances of nickel, argon and sulfur for further analysis in NGC 5813.
To check for a potential residual low-mass X-ray binary contribution to our spectra, we added a power-law to the spectral model in RGS. This did not improve the fit in any way, whether or not we fixed the photon index to a value of 1.5. For NGC 5813 this is in agreement with the results of Randall et al. (2011).
The values found in the literature for NGC 5044 and NGC 5813 are summarised in Tables 7 and 8. Most other work has been carried out using spectra based on different extraction regions, instruments or models. All these can have an effect on the fitted temperatures and absolute abundance values. Abundance ratios do however generally not change with radius (e.g. Simionescu et al. 2009). Because of this, the derived values for those should be comparable. Differences in those values therefore are an indication of the systematic effects introduced by the usage of different instruments and models.
Literature values of the parameters for NGC 5044.
Literature values of the parameters for NGC 5813.
Tamura et al. (2003, T03) fitted the RGS spectrum of NGC 5044 (obsID 0037950101) in the 0′−1′ cross-dispersion region using a model consisting of two temperature components. Buote et al. (2003, B03) used a two-temperature APEC model to constrain the parameters of NGC 5044 using Chandra. The abundance ratio of oxygen over iron is comparable between the two RGS observations and lower in Chandra. The nitrogen to iron abundance ratio we measure is higher than derived by T03. This may be caused by the different background subtraction, extraction regions and temperature structure model (note that the background is relatively large at this wavelength and therefore sensitive to systematic effects). The same holds for the silicon value derived from RGS by T03. The value we derive from EPIC does however agree with the value of B03 derived from ACIS and EPIC. For the magnesium over iron ratio, the value we measure is somewhat lower than found by both T03 and B03, but still acceptably close. The lower sulfur over iron ratio found by B03 can be explained by their higher temperature, at which the emission in the sulfur lines is higher and hence a lower abundances is needed to obtain the same line power. For neon, the values reported by the three studies do not agree well. Since the neon lines in the spectrum are relatively weak and blend with iron, some systematic effects could still play a role because the often imperfect fit to the iron-L complex. We decided not to use it for further analysis.
Werner et al. (2009, W09) fitted the RGS spectrum of NGC 5813 in a strip with width 0.5′ (based on obsID 0302460101) in the cross-dispersion direction. For their fits, they take resonant scattering of the strongest Fe xvii lines into account. Randall et al. (2011, R11) present results of an RGS fit to the same data set, using a strip of 1′ and they also present the results of Chandra analysis. The temperature found by W09 is close to what we measure in the inner bins of the cross-dispersion profile. The oxygen over iron abundance ratio that we find is consistent with W09 and the RGS value found by R11. The value reported by R11 based on ACIS is much lower. As we noted before, RGS has the resolving power to constrain the oxygen abundance using the O viii − Lyα line as opposed to the CCD instruments where this line is part of a blend. The nitrogen over iron abundance ratio we find is consistent with the value by W09. There is a good agreement between the Chandra ACIS results and our work based on EPIC for the abundance ratios of magnesium, silicon and sulfur over iron. However, the neon abundance is rather different and it is excluded from further analysis.
Abundances reported in M 87 by Werner et al. (2006).
We can compare the abundances that we find to those in other giant ellipticals in the cores of groups or clusters. The central galaxy of the Virgo cluster, M 87, was studied by Werner et al. (2006). We show the values in Table 9 and compare our results with their findings because all three sources contain a giant elliptical galaxy. The absolute iron abundance that we find is about half the iron abundance in M 87. As mentioned before, absolute abundances are however sensitive to bias. The O/Fe ratio found for NGC 5044 is close to that of M 87, while NGC 5813 has a somewhat higher value. The N/Fe ratio found for our groups is in good agreement with M 87. We do find a value of C/Fe which is about a factor of 2 higher than in M 87. It should however be noted that the model background of the RGS suffers from severe problems in the CCD chip on which the carbon line is projected.
Werner et al. (2009) present the RGS-measured abundances of five bright elliptical galaxies, including NGC 5813. The fits are based on single-temperature models and include corrections for resonant scattering effects. The abundances are shown in Table 10.
Abundances reported by Werner et al. (2009).
The fits presented in this table are based on relatively short observations (17−81 ks) which translates in relatively large error bars on the parameters. The ratio of nitrogen to iron is higher than solar for all objects. It appears that data from the shorter observations hint towards higher values for this ratio although we do not have enough data to confirm this. For NGC 5813 the longer observation shows a lower abundance ratio. For the oxygen over iron ratio, the values of the abundances are all comparable with what we measure in our groups. As mentioned before, the neon abundance is very hard to constrain. The measured values are sometimes hardly significant and there is some spread. The absolute iron abundances do also show some spread. Those are however, as mentioned before, sensitive to biases.
The abundances of carbon, nitrogen, oxygen (in RGS), silicon and sulfur can be constrained based on single, isolated lines and are much more robust than the abundances of neon and magnesium because these metals are only constrained using lines that are blended with iron lines. The calcium and argon abundances measured are high with large error bars. Moreover they may be somewhat biased by residual background in the relevant energy band. The peak of the calcium and argon lines is 5−10% above the continuum, while the continuum shows systematic offsets of 10−20% at the wavelengths of these elements (see e.g. Fig. 10). In NGC 5044, the relative abundances measured with RGS are also consistent for the two DEM parametrisations. The iron abundance itself differs significantly, as well as the normalisation of the hot gas model.
The abundance ratios give an insight in the processes that create the metals in a cluster or group of galaxies. Most of the metals in galaxies are created by supernovae. Some metals, especially carbon and nitrogen, are however not so efficiently created by supernovae and result from stellar winds of main sequence or AGB stars. We discuss both points in a bit more detail.
4.3. Relative supernova yields
For years, the oxygen and iron abundances of our Galaxy have been used to determine the ratio between type Ia and core-collapse supernovae (see e.g. the reviews by Rana 1991; Woosley et al. 2002). In general type Ia supernovae are believed to yield most of the iron in the Galaxy while core-collapse supernovae would be responsible for the oxygen. The spread of the yields between the different models is however large. Attempts have been made to constrain the supernova ratios and models using the abundances in the hot gas of clusters of galaxies (see e.g. de Plaa et al. 2007).
The abundances that we measure in the gas do not directly reflect the chemical yield of supernovae during the total history of the group. But the abundances do provide constraints on the ratio of type Ia to core-collapse supernovae contributing to the gas (see Humphrey & Buote 2006; de Plaa et al. 2007). If we assume that all iron and oxygen have been created by supernovae, we can use the ratio of these two abundances to find the ratio between type Ia and core-collapse supernovae that enriched the gas. We write 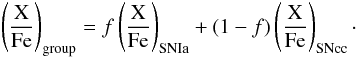 (5)Here X is the abundance of an element, Fe the iron abundance and f represents the fraction of the iron that was created by type Ia supernovae. The supernova models that we use are the best-fit models found by de Plaa et al. (2007). For core-collapse supernovae, this is the model by Nomoto et al. (2006), using stars with Z = 0.02 and a Salpeter initial mass function (IMF; Salpeter 1955).
(5)Here X is the abundance of an element, Fe the iron abundance and f represents the fraction of the iron that was created by type Ia supernovae. The supernova models that we use are the best-fit models found by de Plaa et al. (2007). For core-collapse supernovae, this is the model by Nomoto et al. (2006), using stars with Z = 0.02 and a Salpeter initial mass function (IMF; Salpeter 1955).
Since the yield of a core-collapse supernova depends on the mass, the typical core-collapse yield we use is the IMF weighted integrated yield (Tsujimoto et al. 1995).
Comparison of the supernova yields to the measured abundances.
For the type Ia supernovae, we use four different models. First we use two delayed detonation (DDT) models by Badenes et al. (2003). The DDTc model compared best to the abundances found in the Tycho supernova remnant (Badenes et al. 2006). Badenes et al. (2008) propose that SNR 0509 − 67.5 is best fitted by the DDTa model from Badenes et al. (2003). The difference between the DDT models is due to the different input parameters for the density of the ambient medium and the kinetic energy of the ejecta. The DDTa model predicts lower amounts of silicon to calcium than DDTc (Table 11). We also compare our data to the W7 and WDD2 model from Iwamoto et al. (1999) because they are commonly used in the literature. These two models do also predict higher amounts of silicon and sulfur than the DDTa model. There is also some spread in the yields of argon and nickel between the four models. The DDTc model predicts the highest argon value, which is still lower than we measure for NGC 5044. The nickel abundance predicted by the W7 model is higher than what we find while for the other models it is significantly lower. The amount of produced iron predicted by the DDTa model is higher than in the other models. This translates in the lower number ratio for comparable f.
To find the value for f, we use the oxygen over iron abundance. We then use this value for f to predict the abundance ratios of the other elements expected by the models and compare these to our results. This is shown in Table 11. We find a value for f which is consistent with the value found for NGC 5044 by Böhringer et al. (2005), based on the abundances reported by Buote et al. (2003), using oxygen, iron and silicon abundances. The number is also consistent with M 87 (Werner et al. 2006). This means that the stellar population of our sources is similar to the population of M 87. If we use the abundances of the solar neighbourhood as input (i.e. O/Fe ≡ 1), we find a ratio of ~0% of the supernovae being of type Ia. The stellar population of the group is significantly older than in the surroundings of our Sun. By fitting supernova yields to multiple abundance values, de Plaa et al. (2007) derived from a sample of clusters that 44 ± 5% of the contributing supernovae is of type Ia. This means that the stellar population in our groups seems to be slightly younger than or comparable to the average population in clusters of galaxies. The magnesium abundance predicted by the supernova models is lower than the value we measured. The measured silicon abundances are higher than the values found using the DDTc model, and even more higher than the DDTa model. The DDTc model reproduces a high calcium abundance, but this is still lower than our measurements.
We have compared the abundances with the metallicities of stars in the disk of our own Galaxy (by Chen et al. 2000; Shi et al. 2002; Bensby & Feltzing 2006). Based on this we can indicate what the differences are between the large ellipticals in the centre of groups and our Galactic environment. For comparison with Galactic stars, we use [X/Y] = log (X/Y) − log (X/Y)⊙ as parameter, converting the abundances from the proto-solar abundances of Lodders (2003) to the photospheric solar abundances of Lodders (2003). However, the difference between the photospheric and solar abundance is 0.07 dex for all elements for which we present a ratio (C, N, O, Fe). The absolute values of the abundances change, but the ratios are the same in both abundance systems. The abundance ratios measured in Galactic stars are calibrated on a measured solar spectrum. We assume that this difference between the measured solar spectrum and the recent Lodders abundances are small compared to our uncertainties.
Since star formation has continued in our Galaxy, we can assume that the metallicities in young stars, which are located in the disk of the Galaxy, are comparable to the metallicities in the ambient medium. The oxygen to iron abundance ratio which we find for our sources is [O/Fe] = −0.222 ± 0.022 at [Fe/H] = −0.210 ± 0.011 for NGC 5044 and [O/Fe] = −0.137 ± 0.018 at [Fe/H] = −0.269 ± 0.014 for NGC 5813. The ratios are low compared to the set of stars by Bensby & Feltzing (2006). Therefore we can state that the contribution of core-collapse supernovae is relatively low in our sources compared to the core-collapse contribution in our Galaxy.
4.4. Carbon and nitrogen progenitors
For nitrogen and carbon, the measured abundance values are respectively factors 8 and 7 higher than predicted by supernovae only. For nitrogen, this number is much lower than the factor of 313 which was found by Werner et al. (2006). The difference mostly rises from the fact that the supernova models we used for type Ia’s include nitrogen creation. For the same reason the ratio we find for carbon is lower than the value of 10 reported by Werner et al. (2006).
Conclusions about the parent stellar population based on the carbon and nitrogen abundance in the hot intragroup medium should be drawn with care. First of all, these metals are still being created and a fraction could still be locked up in stars. On the other hand, the stellar mass fraction of groups and clusters is 10 − 20% of the gas mass (Ettori et al. 2009). This amount is comparable to the corresponding uncertainties on carbon and nitrogen and therefore the effect of those metals being locked up in stars is limited. Furthermore, the secondary creation of carbon and nitrogen depends on the metallicity of the environment in which a star was formed. The formation of the less massive stars, which at this moment still enrich the gas, did however happen long ago during a relatively short period of the groups’ life time. The metallicities of those stars around the time they formed are likely to be comparable to each other. In addition, our observations do not directly show how and when elements were ejected into the hot medium. As mentioned before, multiple mechanisms exist that enrich the medium with metals created in the galaxies. All mechanisms act on their typical time scale. Therefore, the measured abundance ratios are the ratios in the intragroup gas, and not necessarily the ratios in the constituent galaxies. Since core-collapse supernovae, which can eject metals in a wind, seem to have decreased significantly in rate during the life time of the group, it is likely that other enrichment mechanisms took over. It was shown that jets from the AGN in the centre of the giant elliptical galaxy can drag out metals from the galaxies into the hot gas (Simionescu et al. 2008, 2009; Kirkpatrick et al. 2011). Both NGC 5044 and NGC 5813 show evidence of AGN activity (David et al. 2009; Randall et al. 2011), therefore AGN uplift is probably the currently dominating enrichment mechanism.
Comparison of the measured abundance ratios to the stars in the disk of our galaxy.
The exact scenario for the creation of nitrogen is not yet fully understood (see e.g. Schiavon 2007; Pipino et al. 2009). Models suggest that core-collapse supernovae produce much more oxygen than nitrogen. Nitrogen may instead be produced by low- and intermediate-mass stars. A high nitrogen over oxygen ratio would then hint towards lower present star formation. The comparison of the nitrogen to oxygen ratios of the two studied groups and the ranges of those values quoted in the literature (Chen et al. 2000; Shi et al. 2002; Bensby & Feltzing 2006) are shown in Table 12. Based on the high nitrogen to oxygen abundance ratio in the two studied groups, we can conclude that following the initial starburst the star-formation rate in these giant elliptical galaxies was significantly lower than in the Milky Way. This agrees well with the general assumption that the present star formation rate in elliptical galaxies is negligible. Due to the continuous evolution of low- and intermediate-mass stars, nitrogen is still being enhanced while hardly any new oxygen is created.
When we compare the carbon and nitrogen to iron abundance ratios that we find to the typical abundance ratios in disk stars of our own Galaxy, we conclude that both the carbon and nitrogen abundances are comparable to the stars with the highest ratios in disk of our Galaxy. The fact that the nitrogen and carbon abundance ratios are higher than the ones in most of the stars of our Galaxy, while the abundance ratio of oxygen over iron is relatively low seems to point towards intermediate-mass stars in AGB phase as sources of carbon and nitrogen creation in our sources, because the mass range of the progenitors of white dwarfs involved in type Ia supernovae (3−8 M⊙) is the same as for AGB stars. It should be noted that this conclusion is based on simple arguments and should be verified by more detailed population synthesis studies.
5. Conclusions
We present the results of the analysis of NGC 5044 and NGC 5813 data, obtained with the RGS and EPIC instruments aboard XMM-Newton. From the analysis we conclude that:
-
The relatively low ratio of the oxygen over iron abundance,combined with the high abundance ratios to iron for carbon andnitrogen suggest that the bulk of the carbon and nitrogen are notcreated by massive stars which end their lives as core-collapsesupernovae.
-
From the oxygen and iron abundance, and under the assumption of a Salpeter IMF, we find for both studied groups that about 80% of the iron is formed by type Ia supernovae. This means that of the contributing supernovae roughly 30–40% are type Ia supernovae while the other ~ 60–70% are of the core-collapse type.
-
The relative contribution of core collapse supernovae to type Ia supernovae is comparable with what was previously found for M 87. This means that the giant elliptical galaxies in our study have a stellar and chemical evolution history comparable to the central giant elliptical galaxy of the Virgo cluster. Both stellar populations tend to be older than in the surroundings of our Sun.
-
A wdem and gdem model give comparable results in terms of abundances for the RGS observations of NGC 5044 and NGC 5813
-
Low temperature plasma models have problems fitting the line blends of Fe xviii, Fe xix and O viii near 14 Å and 16 Å.
Acknowledgments
The anonymous referee is thanked for the useful comments on how to improve the science of the paper. We thank Joke Claeys, Sjors Broersen and Ton Raassen for their useful comments on the manuscript. Carles Badenes is kindly thanked for providing the yields of his supernova models. The Netherlands Institute for Space Research, (SRON) is supported financially by NWO, The Netherlands Organisation for Scientific Research. N.W. was supported by the National Aeronautics and Space Administration through Chandra Postdoctoral Fellowship Award Number PF8-90056 issued by the Chandra X-ray Observatory Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of the National Aeronautics and Space Administration under contract NAS8-03060. Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, M., & Raymond, J. 1992, ApJ, 398, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS] [Google Scholar]
- Arnaud, M., Neumann, D. M., Aghanim, N., et al. 2001, A&A, 365, L80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audard, M., Behar, E., Güdel, M., et al. 2001, A&A, 365, L329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badenes, C., Bravo, E., Borkowski, K. J., & Domínguez, I. 2003, ApJ, 593, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Borkowski, K. J., Hughes, J. P., Hwang, U., & Bravo, E. 2006, ApJ, 645, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Hughes, J. P., Cassam-Chenaï, G., & Bravo, E. 2008, ApJ, 680, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., & Feltzing, S. 2006, MNRAS, 367, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., & Werner, N. 2010, A&ARv, 18, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Matsushita, K., Finoguenov, A., Xue, Y., & Churazov, E. 2005, Adv. Space Res., 36, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Brickhouse, N. S., Dupree, A. K., Edgar, R. J., et al. 2000, ApJ, 530, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Bryans, P., Landi, E., & Savin, D. W. 2009, ApJ, 691, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., Lewis, A. D., Brighenti, F., & Mathews, W. G. 2003, ApJ, 595, 151, (B03) [NASA ADS] [CrossRef] [Google Scholar]
- Cescutti, G., Matteucci, F., McWilliam, A., & Chiappini, C. 2009, A&A, 505, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Romano, D., & Matteucci, F. 2003, MNRAS, 339, 63 [NASA ADS] [CrossRef] [Google Scholar]
- David, L. P., Jones, C., Forman, W., & Daines, S. 1994, ApJ, 428, 544 [NASA ADS] [CrossRef] [Google Scholar]
- David, L. P., Jones, C., Forman, W., et al. 2009, ApJ, 705, 624 [NASA ADS] [CrossRef] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Werner, N., Bykov, A. M., et al. 2006, A&A, 452, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Werner, N., Bleeker, J. A. M., et al. 2007, A&A, 465, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Werner, N., Simionescu, A., et al. 2010, A&A, 523, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edmunds, M. G., & Pagel, B. E. J. 1978, MNRAS, 185, 77P [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G., Ellis, R. S., & Carter, D. 1982, MNRAS, 201, 975 [NASA ADS] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Morandi, A., Tozzi, P., et al. 2009, A&A, 501, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabbiano, G., Kim, D., & Trinchieri, G. 1992, ApJS, 80, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukazawa, Y., Makishima, K., Matsushita, K., et al. 1996, PASJ, 48, 395 [NASA ADS] [Google Scholar]
- Gastaldello, F., Buote, D. A., Temi, P., et al. 2009, ApJ, 693, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Humphrey, P. J., & Buote, D. A. 2006, ApJ, 639, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, ed. K. Yamashita, & T. Watanabe (Tokyo: Univ. Ac. Press), 411 [Google Scholar]
- Kaastra, J. S., Tamura, T., Peterson, J. R., et al. 2004, A&A, 413, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirkpatrick, C. C., McNamara, B. R., & Cavagnolo, K. W. 2011, ApJ, 731, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntz, K. D., & Snowden, S. L. 2001, ApJ, 554, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 1986, MNRAS, 221, 911 [NASA ADS] [Google Scholar]
- Mattsson, L. 2010, A&A, 515, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2002, A&A, 381, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulchaey, J. S. 2004, in Clusters of Galaxies: Probes of Cosmological Structure and Galaxy Evolution, ed. J. S. Mulchaey, A. Dressler, & A. Oemler (Cambridge: Cambridge Univ. Press), 353 [Google Scholar]
- Nevalainen, J., Markevitch, M., & Lumb, D. 2005, ApJ, 629, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Tominaga, N., Umeda, H., Kobayashi, C., & Maeda, K. 2006, Nucl. Phys. A, 777, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, J. R., Kahn, S. M., Paerels, F. B. S., et al. 2003, ApJ, 590, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., Chiappini, C., Graves, G., & Matteucci, F. 2009, MNRAS, 396, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Rana, N. C. 1991, ARA&A, 29, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, S. W., Forman, W. R., Giacintucci, S., et al. 2011, ApJ, 726, 86 (R11) [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, J., & Ponman, T. J. 2007, MNRAS, 380, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Read, A. M., & Ponman, T. J. 2003, A&A, 409, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schiavon, R. P. 2007, ApJS, 171, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Schindler, S., & Diaferio, A. 2008, Space Sci. Rev., 134, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, J. R., Zhao, G., & Chen, Y. Q. 2002, A&A, 381, 982 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simionescu, A., Werner, N., Finoguenov, A., Böhringer, H., & Brüggen, M. 2008, A&A, 482, 97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simionescu, A., Werner, N., Böhringer, H., et al. 2009, A&A, 493, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snowden, S. L., Collier, M. R., & Kuntz, K. D. 2004, ApJ, 610, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamura, T., Kaastra, J. S., Makishima, K., & Takahashi, I. 2003, A&A, 399, 497 (T03) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamura, T., Kaastra, J. S., den Herder, J. W. A., Bleeker, J. A. M., & Peterson, J. R. 2004, A&A, 420, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B. 1987, ApJ, 321, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, N., Böhringer, H., Kaastra, J. S., et al. 2006, A&A, 459, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, N., Zhuravleva, I., Churazov, E., et al. 2009, MNRAS, 398, 23 (W09) [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
The ten strongest modelled lines around the 16 Å blend, using the fitted model to the sources.
Comparison of the measured abundance ratios to the stars in the disk of our galaxy.
All Figures
 |
Fig. 1 Smoothed Chandra image of NGC 5044. The edges of the RGS for obsID 0037950101 are indicated with black lines. The black arrow has length 1′, and points in the positive cross-dispersion direction. |
| In the text | |
 |
Fig. 2 Smoothed Chandra image of NGC 5813. The edges of the RGS for obsID 0554680201 are indicated with black lines. The black arrow has length 1′, and points in the positive cross-dispersion direction. |
| In the text | |
 |
Fig. 3 Fluxed, background-subtracted RGS spectrum of NGC 5044. The (red) line through the data points is the best fit. The most important spectral lines are indicated in the plot. |
| In the text | |
 |
Fig. 4 Iron and temperature profiles in the cross-dispersion direction based the fits to the RGS data of NGC 5044 using the gdem model. |
| In the text | |
 |
Fig. 5 O/Fe and N/Fe profiles (in proto-solar units by Lodders 2003) based on the fits to the RGS data of NGC 5044 using the gdem model. The nitrogen abundance could not be constrained in the rightmost bin and is therefore not present in the plot. |
| In the text | |
 |
Fig. 6 EPIC spectrum of NGC 5044. The top panel shows the data points with the model as a histogram through them. Upper data set: EPIC-pn, bottom data set: EPIC-MOS. The bottom plot shows the fitting residuals. Squares: EPIC-pn, circles: EPIC-MOS. |
| In the text | |
 |
Fig. 7 Fluxed RGS spectrum of NGC 5813. The (red) line through the data points is the best fit. The most important spectral lines are indicated in the plot. |
| In the text | |
 |
Fig. 8 Iron and temperature profiles in the cross-dispersion direction based on the fits to the RGS data of NGC 5813 using the gdem model. |
| In the text | |
 |
Fig. 9 O/Fe and N/Fe profiles (in proto-solar units by Lodders 2003) based the fits to the RGS data of NGC 5813 using the gdem model. |
| In the text | |
 |
Fig. 10 EPIC spectrum of NGC 5813. The top panel shows the data points with the model as a histogram through them. Upper data set: EPIC-pn, bottom data set: EPIC-MOS. The bottom plot shows the fitting residuals. Squares: EPIC-pn, circles: EPIC-MOS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


