| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201015959 | |
| Published online | 24 June 2011 | |
Azimuthal variations of magnetic field strength and inclination on penumbral boundaries
Astronomical Institute of the Academy of Sciences, Fričova 298, 25165 Ondřejov, Czech Republic
e-mail: jurcak@asu.cas.cz
Received: 20 October 2010
Accepted: 5 May 2011
Aims. I try to determine the properties of the magnetic field on the inner and outer penumbral boundaries and find out if either magnetic field strength or inclination are constant there and if these plasma parameters depend on the sunspot area.
Methods. The spectropolarimetric data obtained with the Hinode satellite were analysed. Active regions located mostly around the disc centre were selected to compare sunspots of different sizes. The magnetic field strength and inclination were estimated using the inversions of observed Stokes profiles.
Results. Both the magnetic field strength and inclination do not vary along individual outer penumbral boundaries, and the magnetic field probably becomes weaker and more vertical with decreasing sunspot area. The magnetic field strength and inclination are changing along the inner penumbral boundaries and also depend on the umbral area. Weaker magnetic fields are more vertical on the inner penumbral boundaries, which leads to a constant vertical component of the magnetic field on these boundaries. The vertical component of the magnetic field is possibly independent of the umbral area.
Conclusions. The inner penumbral boundaries are defined by the critical value of the vertical component of the magnetic field. This implies that the penumbral filaments have a convective origin.
Key words: sunspots / Sun: photosphere / Sun: magnetic topology / techniques: polarimetric
© ESO, 2011
1. Introduction
Sunspots are distinguished from pores by the presence of penumbra. The formation of penumbra was observationally described by e.g., Leka & Skumanich (1998), Yang et al. (2003), and Schlichenmaier et al. (2010). As shown by Schlichenmaier et al. (2010), it takes about four hours to form a penumbra around half of the umbra, but single penumbral filaments develop faster (within 30 min). Such rapid development of penumbra is supported by theoretical simulations (Simon & Weiss 1970; Rucklidge et al. 1995; Tildesley & Weiss 2004) that also show that sunspots generally have higher magnetic flux than pores. With increasing magnetic flux the magnetic field inclination (angle from the local normal line) increases on the edge of the flux tube, and if some critical value of inclination is reached, the penumbra develops as the filamentary convection sets in. The critical value of 45° was derived by Rucklidge et al. (1995) and recently confirmed by Rempel et al. (2009a).
The configuration of magnetic field in sunspots has been studied for a long time. From the earliest analyses, the radial dependence (azimuthal averages around a spot) of magnetic field strength and inclination were investigated. From these azimuthal averages, it is possible to determine the typical values on the penumbral boundaries. Apart from the oldest studies (see review by Solanki 2003, and references therein), the typical values of magnetic field strength and inclination found at outer penumbral boundaries are around 800 G and 70°, respectively (e.g., Lites et al. 1990; Solanki et al. 1992; Balthasar & Schmidt 1993; Keppens & Martinez Pillet 1996; Westendorp Plaza et al. 2001; Mathew et al. 2003; Borrero et al. 2004; Bellot Rubio et al. 2004; Balthasar & Collados 2005; Sánchez Cuberes et al. 2005; Beck 2008). At the inner penumbral boundary, the magnetic field strength reaches values around 2000 G and inclination around 35°. The higher range of these values is on the inner penumbral boundary.
Both the magnetic field strength and the inclination depend on the height in the atmosphere in the penumbra as was shown by, e.g., Balthasar & Schmidt (1993, using different spectral lines) or later by, e.g., Westendorp Plaza et al. (2001, using the inversion code and allowing for changes in plasma parameters with height). The magnetic field strength increases with height, while the inclination decreases; i.e., the field becomes more vertical. Such changes with height can be explained by the uncombed model of the penumbra fine structure proposed by Solanki & Montavon (1993), where horizontal magnetic flux tubes are embedded in a more vertical and stronger magnetic field. The analyses of observations suggest that these horizontal flux tubes are located deep in the atmosphere (Bellot Rubio et al. 2003; Borrero et al. 2006; Jurčák et al. 2007; Jurčák & Bellot Rubio 2008) and azimuthal averaging through this deep photospheric layers decreases the magnetic field strength and increases the inclination angle.
The values of magnetic field inclination found in the higher photospheric layers using height-dependent models of atmosphere (Westendorp Plaza et al. 2001; Mathew et al. 2003; Borrero et al. 2005; Sánchez Cuberes et al. 2005) or using the two-component model of atmosphere (Borrero et al. 2004; Bellot Rubio et al. 2004; Langhans et al. 2005) are similar to those derived from the simplistic simulations of sunspots by e.g., (Jahn 1989) and (Jahn & Schmidt 1994). It is difficult to compare the observed values with the results of a three-dimensional MHD simulations of a sunspot, since the penumbra is not fully developed in these simulations, and its boundaries can hardly be defined (see e.g., Rempel et al. 2009b).
To my knowledge, apart from highly mentioned studies of radial dependence of magnetic field strength and inclination, no one has yet tried to estimate the properties of the magnetic field right at the penumbra boundaries. It is the aim of this paper to determine these parameters and find out whether they are the same for sunspots of different sizes, and if they are even constant along the boundaries in a given sunspot.
2. Observations
All the analysed data were taken with the spectropolarimeter (SP, part of the Solar Optical Telescope, Tsuneta et al. 2008) onboard the Hinode satellite (Kosugi et al. 2007). The Hinode SP acquires all four Stokes profiles of two neutral iron lines at 630.15 nm and 630.25 nm. The list of analysed observations is given in Table 1.
I analysed altogether ten umbra/penumbra boundaries (marked 1U−10U in the first column) and nine penumbra/quiet Sun boundaries (1P−9P). I selected only sunspots with definite inner or outer boundaries; i.e., I omitted sunspots with light bridges or complex and undeveloped penumbrae. Moreover, the observed active regions have to be located close to the disc centre as is explained in Sect. 3.
The date and time of the observations are listed in the second column, where the time corresponds to the scan taken in the middle of the appropriate structure. The third and fifth columns list the areas of regions enclosed in the boundaries and the heliocentric angles, respectively. As shown in the fourth column, I used data taken in two scanning modes, normal (N) and fast (F). In both modes, the resulting noise level is around 10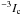 . The pixel size is approximately
. The pixel size is approximately 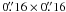 and
and 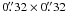 for the normal and fast modes, respectively. The diffraction limit of the Solar Optical Telescope is 0
for the normal and fast modes, respectively. The diffraction limit of the Solar Optical Telescope is 0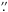 3 at 630 nm, and the spatial resolution is slightly worse because of the aliasing induced by the CCD pixel size. The data were calibrated with the standard routines available in the Hinode SolarSoft package.
3 at 630 nm, and the spatial resolution is slightly worse because of the aliasing induced by the CCD pixel size. The data were calibrated with the standard routines available in the Hinode SolarSoft package.
Observed targets.
Number of nodes.
3. Data analysis
The penumbral boundaries were determined from maps of continuum intensity. These are created from intensities observed on the far red wing of the Stokes I profile of the 630.25 nm line. No absolute values of continuum intensity were used to determine the penumbral boundaries. For each analysed sunspot, the average intensity of the umbra, penumbra, and QS were taken, then the continuum intensity map smoothed to avoid the filamentary structure, and then the find continuum intensities were used to define the penumbral boundaries. In Figs. 1a and b, I show the boundaries 1U, 1P and 3U, 3P, respectively. This definition of penumbral boundaries is more precise than in the studies of the radial dependencies of magnetic field parameters, where the azimuthal averages are made along either circles or ellipses inscribed into sunspots.
 |
Fig. 1 Maps of continuum intensity (a, b)) with marked penumbral boundaries (1U and 1P in a; 3U and 3P in b)). The white arrows point to the disc centre, and their length is proportional to the heliocentric angle. Plots c, d) show the magnetic field strengths dependent on the position angle (ψ) along the penumbral boundaries, where the ∗ and + symbols represent the inner and outer penumbral boundaries, respectively. The colours of symbols correspond to the position on the boundary. The small black symbols are the fits of the measured magnetic field strengths with resulting formulas written in the plots. The magnetic field on the 1P and 3P boundaries is increased by 1 kG for display purposes. |
The Stokes profiles observed at pixels creating the boundaries were inverted using the inversion code SIR (Stokes Inversion based on Response functions, Ruiz Cobo & del Toro Iniesta 1992). I used three cycles of inversion, where the number of nodes are listed in Table 2. As I use the spectral PSF of the Hinode SP, the macroturbulence is not allowed in the inversion.
The main advantage of the Hinode SP data is the absence of the stray light induced by the Earth’s atmosphere. This is even more important on the penumbral boundaries, where the stray light either from the quiet Sun (QS) regions or from the penumbra significantly influences the resulting values (Solanki 2003). As shown by Wedemeyer-Böhm (2008), there is an instrumental stray light component of about 5% in the broadband filter imager of the Hinode SOT. A similar value can also be expected in the Hinode SP instrument. Such a low level of unpolarised stray light does not influence the resulting values of plasma parameters.
Orozco Suárez et al. (2007) have simulated the Hinode SP data using the magnetoconvective simulations to show that it is important to include a stray-light contamination in the Milne-Eddington inversion. They find very high values of about 80%. Such high contamination cannot be a real stray light and has to be interpreted at least partly as a magnetic filling factor. Following their paper, I used the local polarised stray light to represent an unresolved magnetic component. The resulting values of plasma parameters do not change significantly with the increasing stray-light factor because the inverted Stokes profiles are very similar to the profiles of the stray light. Moreover, the uncertainties of plasma parameters determined by the inversion code increase with an increasing stray-light component. Therefore, I also omitted the local polarised stray light in the inversion scheme.
Because determining the azimuthal variations in magnetic field strength and inclination is the aim of this paper, I hereafter concentrate on these plasma parameters. In the first cycle of the inversion, with one node, the plasma parameters are constant with height. In second and third cycles, the plasma parameters change with height, and from their stratifications I obtain values typical of the lower part of the photosphere (averaged between log (τ) = −0.2 and −0.8) and higher regions (log (τ) between −1.5 and −2).
The magnetic field strength and inclination obtained in the lower atmosphere in the second and third cycles have the largest variations along the boundaries and also depend on the continuum intensity at umbra/penumbra boundaries. Since the inverted spectral lines of neutral iron are most sensitive to the plasma parameters between log (τ) = −1 and −2 (Cabrera Solana et al. 2005), the results from the first cycle of the inversion are comparable to those obtained in the higher atmosphere in later cycles. Hereafter, I use the values of magnetic field strength and inclination obtained in the higher photosphere in the second cycle of the inversion (three nodes), because they are the least dependent on the continuum intensity and have the smallest variation along the penumbral boundaries.
To study the azimuthal variation in the magnetic field inclination, it is necessary to transform it from the line-of-sight (LOS) reference frame to the local reference frame (LRF). To do so, I first solve the 180° azimuth ambiguity by assuming that the magnetic field azimuth retrieved on the penumbral boundaries is close to the azimuth of the radially opening lines from the centres of the sunspots. Then, I use routines from the AZAM code developed for the Advanced Stokes Polarimeter (Lites et al. 1995) to transform the values of magnetic field azimuth and inclination to the LRF. For sunspots with negative polarity, I changed the reference frame, so the values of magnetic field inclination are comparable in all studied cases.
Only one SP scan was taken far from the disc centre, and the continuum intensity map is shown in Fig. 1b. Magnetic field strength along the penumbral boundaries 3U and 3P are shown in Fig. 1d, and it is clear that the retrieved values depend on the position on the boundary with respect to the direction to the disc centre (ψ = 0). This effect was discussed by Rimmele (1995) who concluded that we see into deeper geometrical depths in the centre-side penumbra due to the different opacities along the LOS. Westendorp Plaza et al. (2001) confirm this LOS effect, but find that deeper layers are probed in the limb-side penumbra. The weaker magnetic field strength found in the centre-side penumbra (Fig. 1d), and also the less inclined magnetic field there suggest that a higher atmosphere is seen in these regions and confirms the findings of Westendorp Plaza et al. (2001).
There is no such effect for observations taken close to the disc centre, Fig. 1c. There is no dependence at all on the 1P boundary, and although the magnetic field strength changes on the 1U boundary, it is not related to the direction to the disc centre and is caused by the real changes in B at this boundary. Because the LOS effect cannot be removed, I only concentrate on observations taken close to the disc centre, where this effect is to some extent still present, but does not obviously influence the azimuthal variations of the retrieved plasma parameters.
To determine whether the plasma parameters depend on the position on the boundary, I fit them with the function 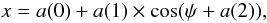 (1)where x is the plasma parameter that depend on the position angle ψ, the a(0) parameter corresponds to the mean value of the plasma parameter along the boundary, the a(1) parameter represents the eventual amplitude of the azimuthal dependence, and a(2) is the difference between the maximum of the cos function and the direction towards the disc centre. Examples of fits are shown in Figs. 1c and d by the small black symbols along with the resulting equations. The reliability of the fit can be estimated from comparison of the standard deviations of the given plasma parameter from its median value (σmed) and from the fitted curve σfit.
(1)where x is the plasma parameter that depend on the position angle ψ, the a(0) parameter corresponds to the mean value of the plasma parameter along the boundary, the a(1) parameter represents the eventual amplitude of the azimuthal dependence, and a(2) is the difference between the maximum of the cos function and the direction towards the disc centre. Examples of fits are shown in Figs. 1c and d by the small black symbols along with the resulting equations. The reliability of the fit can be estimated from comparison of the standard deviations of the given plasma parameter from its median value (σmed) and from the fitted curve σfit.
4. Results
In Fig. 2, I show the changes in magnetic field strength (B) and inclination (γ) across the penumbra. It is important to know how these plasma parameters depend on the determined position of the penumbral boundary; i.e., if the movement of the boundary by few pixels influences the retrieved value of the given plasma parameter.
In agreement with previous studies (e.g. Westendorp Plaza et al. 2001; Mathew et al. 2003; Borrero et al. 2004; Bellot Rubio et al. 2004), the magnetic field inclination does not change significantly around the outer penumbral boundary, and its position thus does not significantly influence this plasma parameter. I found similar behaviour also for magnetic field strength, and it was also reported by, e.g., Balthasar & Schmidt (1993) and Mathew et al. (2003). Others (e.g. Westendorp Plaza et al. 2001; Borrero et al. 2004; Bellot Rubio et al. 2004) find that B steadily decreases around the outer penumbral boundary. Around the inner penumbral boundary, I found a strong dependence of both plasma parameters on the exact position. This is confirmed by all these studies.
 |
Fig. 2 Changes in magnetic field strength (upper plot) and inclination (lower plot) along three paths across the penumbra. In the lower right part is the continuum intensity map with marked region with the three shown paths and their colour codes. The black lines in the plots of plasma parameters correspond to the penumbral boundaries shown in the continuum map. |
The behaviour of B and γ across the penumbra shows that the results on the outer penumbral boundary are not significantly affected by the position of this boundary. For example in Fig. 1a, the outer penumbral boundary is located slightly inside the penumbra, but the few pixels between the found and the real penumbral boundary would not cause remarkable differences in the absolute values of magnetic field strength and inclination. On the inner penumbral boundary, the situation is different because the plasma parameters are changing significantly. However, this boundary is defined more precisely than the outer penumbral boundary and only a strong intrusion of bright penumbral filaments into the umbra causes observable changes in the plasma parameters. The peak value of magnetic field strength on the inner penumbral boundary in Fig. 1c is caused by such an intrusion of bright filaments into umbra as shown in Fig. 1a.
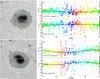 |
Fig. 3 Maps of continuum intensity (a, b)) with marked penumbral boundaries 5P and 6P, respectively. The white arrows are analogous to those in Fig 1. Plots c, d) show the magnetic field strengths (top) and inclination (bottom) dependent on the position along the penumbral boundaries. The colours of symbols correspond to the position on the boundary. The small black symbols are the fits of the observed values with formulas written in the plots. |
4.1. Outer penumbral boundaries
In Fig. 1c, I show the changes of magnetic field on the outer penumbral boundary P1. There are no systematic changes in B on this boundary. Although not displayed, the magnetic field inclination along the P1 boundary shows a similar behaviour. There is, however, a large scatter of the values of B and γ on this boundary. This is probably not caused by the penumbral fine structure, as there is no correlation between the continuum intensity and the retrieved plasma parameters. To some extent, these variations can be caused by the position of the boundary with respect to the real penumbral edge, but this scatter is mostly caused by the inversion uncertainties.
In Fig. 3, I show similar behaviour of magnetic field strength and inclination on the outer penumbral boundaries 5P and 6P. The sunspots have similar areas, but they have different SP scan types.
The 5P boundary is reconstructed from a normal SP scan. There are no significant dependencies of either B or γ on the position at the boundary. The highest scatter of the obtained values of the studied plasma parameters is in a region marked by blue colour, where a pore-like structure can be seen on the 5P boundary in Fig. 3a. There, the magnetic field is stronger and more vertical than the surrounding regions. In regions marked by yellow and orange, there are some local variations in magnetic field strength and inclination. There is no structure visible in the intensity map that can explain these changes.
On the 6P boundary, the strongest variations in B and γ are seen in the region where the boundary encircles nearby pore. As in the case of the 5P boundary, a stronger and more vertical field is retrieved there. The fits of the magnetic field strength and inclination on this boundary have larger amplitudes then those obtained on the 5P boundary. However, the a(2) parameter is significantly different between B and γ fits and not close to either 0° or 180°. This means that the azimuthal changes are not caused by the LOS effect.
Plasma properties at the outer penumbral boundaries.
In Table 3, I show the median values of magnetic field strength and inclination (second column) on all outer penumbral boundaries observed close to the disc centre along with their standard deviations (third column). The fourth to sixth columns show the resulting parameters of equation (1), and the seventh column the standard deviations from the fitted curve.
As can be seen in Table 3, the magnetic field strength does not depend on ψ at the outer penumbral boundary. The σmed and σfit values are comparable for all analysed sunspots. On average, the uncertainty of the magnetic field strength on the outer penumbral boundary is 195 G. This value is higher than the error computed by the inversion code for B at the studied height in the atmosphere, which is on average 90 G and 85 G for the normal and fast scan, respectively. This increased uncertainty is caused by the variation in magnetic field strength due to some fine structures on the outer penumbral boundaries, e.g. pore-like structures on 5P and 6P boundaries.
The magnetic field inclination has on average an error of 5° as determined by the inversion code SIR, and this error is same for normal and fast scans. This is again much lower than the standard deviations of γ determined for individual boundaries, on average 15°. For boundaries 7P, 8P, and 9P, I use the σfit values to determine the average standard deviation.
The 8P and 9P boundaries are observed the furthest from the disc centre, the retrieved parameters a(1) show large azimuthal variations, and the maximal values of γ are reached in the direction towards the disc centre as the a(2) parameters are close to 0°. These changes can therefore be ascribed to the LOS effect. However, similar parameters of the fit are also obtained for the 7P boundary, which is observed closer to the disc centre than 2P and 5P boundaries. The pronounced LOS effect in the case of the 7P boundary is possibly caused by the lower spatial resolution combined with the used inversion scheme.
The magnetic field strength ranges from 530 G to 690 G on the outer penumbral boundary. This is slightly lower than values derived by e.g. Westendorp Plaza et al. (2001) or Mathew et al. (2003) who found 750 G and 700 G, respectively. Even higher values of B are found from two-component inversion of the penumbra, around 1000 G by Bellot Rubio et al. (2004) and Borrero et al. (2004). Only Sánchez Cuberes et al. (2005) find lower values of magnetic field strength (around 400 G) at a comparable height in the photosphere using SIR inversion with the fixed stray-light factor set to 5%.
The magnetic field inclination is in the range of 73° to 80° on the studied outer penumbral boundaries. This is more than the values obtained from two-component inversions of the penumbra (Bellot Rubio et al. 2004; Borrero et al. 2004), but comparable to results of e.g. Mathew et al. (2003), Sánchez Cuberes et al. (2005), and Langhans et al. (2005).
4.2. Inner penumbral boundaries
In Fig. 1c, I show the changes of B along the inner penumbral boundary 1U. The magnetic field strength is not constant along this boundary. The changes are more complex than the cos function, which does not reproduce the observed dependence of B on ψ very well in this case. Neither minimum nor maximum values of magnetic field strength are reached in the direction towards disc centre. This means that the variation in B is not caused by the LOS effect, so it represents a real change of this plasma parameter on the inner penumbral boundary. The magnetic field inclination shows similar behaviour on this boundary.
In Fig. 4, I show the behaviour of magnetic field strength and inclination on inner penumbral boundaries 2U and 7U. The 2U boundary encircles the same sunspot as the 1U boundary, but this scan was taken nine hours later. Again, both B and γ show complex behaviour along the 2U boundary. It is clear that the stronger the magnetic field, the more horizontal it is.
The 7U boundary encircles much smaller umbra. Also in this case, the magnetic field strength and inclination change along the boundary. The changes are nicely fitted by the cos function, but neither minimum nor maximum values are reached on the centre-side part of the boundary; i.e., these changes are again not caused by the LOS effect. As in the case of the 2U boundary, the strongest magnetic field is also the most horizontal.
Plasma properties at the inner penumbral boundaries.
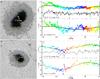 |
Fig. 4 Analogous to Fig. 3, but for boundaries 2U a, c) and 7U b, d). The solid black lines in B plots mark the vertical component of the magnetic field strength. |
In Table 4, I show the properties of B and γ at all the studied inner penumbral boundaries observed close to the disc centre. The columns are analogous to those in Table 3. Unlike at the outer penumbral boundaries, there are significant azimuthal changes in both B and γ on these boundaries. Therefore, the σmed values are higher than the σfit values. The only exception is the 6U boundary, where a(1) parameters of both magnetic field strength and inclination are negligible.
The a(2) parameters of B and γ fits are similar for a given inner penumbral boundary, and this means that there is a close relation between these parameters. On all boundaries, the stronger magnetic field is more horizontal, as shown cases Fig. 4. This is a local property on the inner penumbral boundary and does not contradict the overall behaviour found for radial dependencies in the sunspot, where a weaker field is more horizontal as shown in Fig. 2 and by e.g. Westendorp Plaza et al. (2001), Mathew et al. (2003), and Sánchez Cuberes et al. (2005).
As there are significant changes in the studied plasma parameters along the inner penumbral boundaries, the standard deviations from the median values are very large, on average 330 G for B and 7° for γ, especially compared to the average errors of B and γ computed by the inversion code SIR on the inner penumbral boundaries, which are 65 G and 1.5°, respectively.
As mentioned in Sect. 1, the previously reported values of magnetic field strength and inclination on the umbra/penumbra boundary have a high span. This high span is confirmed by the studied sample. The magnetic field strength ranges from 1930 G to 2480 G and magnetic field inclination from 28° to 38°. These values are comparable to previous studies (Westendorp Plaza et al. 2001; Borrero et al. 2004; Bellot Rubio et al. 2004), although lower values of B and higher values of γ were found by Mathew et al. (2003) and Sánchez Cuberes et al. (2005), among others.
Using the resulting values of magnetic field strength and inclination, I derive the vertical component of the magnetic field (Bver) on the inner penumbral boundaries. In Fig. 4, the Bver is shown along 2U and 7U boundaries. The Bver does not show any azimuthal variations along these boundaries, although both B and γ vary. There are some local fluctuations of Bver that are caused by fine structure at the inner penumbral boundaries. At the 2U boundary (Fig. 4c), the vertical component of the magnetic field drops by 300 G in regions where the bright penumbral filaments protrude deeply into the umbra, ψ = [ − 170°,170°] . At the 7U boundary (Fig. 4d), similar decrease in Bver can be seen around ψ = −40°, which corresponds to a small intrusion of umbra into penumbra.
Vertical component of the magnetic field on the inner penumbral boundaries.
In Table 5, I show the median values of Bver at the studied boundaries along with their standard deviations. The uncertainties are significantly lower than those of the magnetic field strength listed in the second column of Table 4, because the vertical component of magnetic field does not vary along the boundaries. The average uncertainty is 190 G including all listed inner penumbral boundaries and 170 G, if the 5U boundary is omitted (the origin of the high σver on this boundary is unknown). Using the average errors of B and γ computed by the inversion code SIR on the inner penumbral boundaries, the error of Bver is 98 G. The value of Bver on the inner penumbral boundary is usually not specified in previous studies, but using the average values of B and γ from azimuthal averages, the vertical component of the magnetic field strength would be comparable to the values listed in Table 5.
5. Discussion
In Fig. 5, I show the dependence of magnetic field strength on the cos(γ) on both inner and outer penumbral boundaries. There is an obvious difference between these boundaries. On the inner penumbral boundaries, the stronger field is associated with more inclined field lines, as discussed in Sect. 4.2 for individual boundaries. From Fig. 5 is clear that this relation also applies generally, as smaller umbrae have weaker and more vertical magnetic fields on their boundaries than the bigger ones.
 |
Fig. 5 The scatter plot showing the dependence of B on the cos(γ) on inner (+ symbols) and outer (⋄ symbols) penumbral boundaries. The colours of symbols represent individual boundaries. |
There is no obvious dependence of magnetic field strength on the inclination angle on the outer penumbral boundaries, especially for cos(γ) < 0.5, where 88% of the studied pixels is located. For higher values of cos(γ), i.e., more vertical field, there is a trend toward an increasing magnetic field. This can again be explained by the pore structures located around the outer penumbral boundaries (e.g. Fig. 3b), which are associated with a stronger and more vertical magnetic field.
In Fig. 6, I show the dependencies of the median values of magnetic field strength and inclination (from Table 3) on the sunspot area. The plots also mark the uncertainties of these plasma parameters (second column of Table 3). In case of boundaries 7P, 8P, and 9P, where I find azimuthal variations of γ caused by the LOS effect, I use the a(0) and σfit values from Table 3.
 |
Fig. 6 Plots of magnetic field strength (top) and inclination (bottom) reached at the outer penumbral boundaries as a function of sunspot area. The errorbars mark the standard deviations. The solid and dashed lines represent the linear and constant fit of the B and γ values, respectively. The parameters of the fit along with χ2 values are written in the plots. |
The magnetic field strength (upper plot in Fig. 6) is most probably decreasing with decreasing sunspot area as the linear fit of B on the outer penumbral boundaries has roughly seven times lower χ2 value than the fit with a constant value. On the other hand, the mean standard deviation of magnetic field strength is 195 G, and this value is higher than the difference of B between the largest and smallest sunspots as derived from the linear fit (130 G). Although the trend toward decreasing B with sunspot area is clear, it is uncertain owing to large errors of magnetic field strength on the outer penumbral boundaries.
Also in the case of magnetic field inclination, there seems to be a decrease in this parameter with decreasing sunspot area. Compared to B, the effect is even more uncertain because the linear fit only has a two times lower χ2 value than the fit with a constant value. Moreover, the gradient results into a 5° difference of γ between the smallest and largest analysed sunspots and this is much smaller than the mean σ of this plasma parameter on the outer penumbral boundary (15°).
Presuming that gradients of both B and γ with sunspot area are real means that the vertical component of the magnetic field can be the parameter that is independent of the sunspot area. The linear fits of B and γ shown in Fig. 6 results in the mean value of Bver of 129 G and a difference of 30 G between the smallest and largest sunspots. However, if the linear fit of the magnetic field inclination is taken only from 1P to 6P boundaries (omitting the boundaries with the pronounced LOS effect), the resulting gradient is lower, the mean value of Bver is 120 G, and the difference between the smallest and largest sunspots is only 8 G. Using the values of B and γ directly from the inversion on all boundaries, the average value of Bver is 126 ± 185 G.
 |
Fig. 7 Plots of magnetic field strength (top) and inclination (bottom) reached at the inner penumbral boundaries as a function of umbral area. In the plot of magnetic field strength, the values of Bver are shown under the thin solid line. The values of vertical component of the magnetic field are decreased by 800 G for display purposes. See caption of Fig. 6 for explanation of errorbars, lines, etc. |
In Fig. 7, I show the dependence of magnetic field strength and inclination obtained at the inner penumbral boundaries on the umbral area. In the upper plot, I also show the variation in Bver with umbral area. The results are analogous to what I find on the outer penumbral boundary. Both B and γ decrease with decreasing umbral area.
For magnetic field strength, the χ2 value of the linear fit is three times lower than the one obtained with a fit with a constant value. The found gradient corresponds to the difference of B of 550 G between the smallest and the largest observed umbra. This is larger than the average uncertainty of magnetic field strength on these boundaries (330 G). Therefore, the change in B on the inner penumbral boundaries with umbral area is trustworthy. The same applies also to the magnetic field inclination on the inner penumbral boundaries. For this plasma parameter, the χ2 value of the linear fit is five times lower than the one obtained with a fit with a constant value. The gradient results in the difference of 10° between the smallest and the largest sunspots, which is again greater than the average uncertainty of γ on these boundaries (7°).
In the case of the vertical component of the magnetic field, there seems to be a small change with umbral area. The linear fit is less than two times better than a fit with a constant value. On the other hand, the linear fit results in a difference of Bver of 245 G between the smallest and the largest observed umbrae, and this is larger than the average uncertainty of Bver on these boundaries (190 G).
On some of the inner penumbral boundaries, the azimuthal changes of magnetic field inclination are reproduced very well by the cos fits, but these variations are not caused by the LOS effect because the a(2) parameters are not close to 0° or 180°. Such azimuthal changes in γ can be reproduced, if I assume that the axis of a flux tube creating the sunspot is inclined with respect to the local normal line (which would correspond to the a(1) parameter from the fitted function), and the opening of the field lines is constant with respect to the axis of the flux tube (a(0) parameter). If I assume a(1) = 4° and a(0) = 34°, the azimuthal variation of inclination around the 7U boundary (Fig. 4b) is reproduced. The observed variations of magnetic field strength are consequences of the inclination variations, as the Bver is constant along the inner penumbral boundaries.
 |
Fig. 8 Analogous to Fig. 4, but for a 4U boundary and a boundary along umbra with only partially developed penumbra (not listed in Table 1). The red and blue arrows points in the direction of maximal γ and B, respectively. The solid black lines mark the umbra/QS region at the lower boundary. |
In Fig. 8b, I show similar behaviour along the 4U boundary. This boundary is observed in an active region, where the umbrae of opposing polarities are divided by a penumbra. The smaller umbra does not have a fully developed penumbra (Fig. 8a). Therefore, this boundary (hereafter called U) is not listed in Table 1, but the variations of B and γ along this boundary are displayed in Fig. 8c. The cos fit of the γ variations along the U boundary shows that the flux tube creating this umbra is inclined by 14° with respect to the local normal line and bends toward the larger umbra of opposite polarity.
From Fig. 8c is also clear that the penumbra is not developed in regions where both B and γ reach their minimal values. According to the simulations mentioned in Sect. 1, the penumbra develops if some critical value of magnetic field inclination is reached. It is not possible to determine the critical value observationally from the behaviour of γ along the U boundary. However, from the shape of the U boundary it is clear, that once the penumbra is formed, the filaments protrude deeper into the umbra (see the sharp change in the boundary location around the black lines in Fig. 8a, which mark the umbra/QS region). The penumbral filaments move inwards because the Bver is only around 1500 G at this part of the U boundary, where it is at least 1700 G in developed sunspots as shown in Table 5.
6. Summary and conclusions
I have analysed the properties of the magnetic field on inner and outer penumbral edges. For this purpose, I chose the active regions of various sizes observed by Hinode SP close to the disc centre. There, the magnetic field strength and inclination are not biased by the LOS effect; i.e., similar geometrical heights are probed all along the penumbral boundaries. In Fig. 9, I show the simplified scheme of a sunspot, where all the found properties are summarised.
Both the magnetic field strength and inclination do not vary along the individual outer penumbral boundaries. If there are some variations, they are below the achieved accuracy, which is given by the uncertainties from the inversion, the variation in the boundary with respect to the real penumbral edge, and the occurrence of fine structures with different plasma properties around the outer penumbral boundaries. The resulting values are summarised in Table 3. On average, the magnetic field strength is 598 ± 195 G and magnetic field inclination is 77° ± 15°.
Most likely, the magnetic field strength on the outer penumbral boundary is decreasing with the decreasing sunspot area (upper plot in Fig. 6). Owing to the high uncertainties, the trend cannot be confirmed. Also the magnetic field inclination seems to be decreasing with the decreasing sunspot area, but this trend is well below the achieved precisions (lower plot in Fig. 6). If these trends are assumed to be real, it means that the vertical component of the magnetic field is independent of the sunspot area and that it reaches 126 ± 185 G.
The magnetic field strength and inclination vary along the inner penumbral boundaries. In most of the cases, neither of these parameters is constant and the uncertainties of these parameters are high (Table 4). In the studied sample of inner penumbral boundaries, the average magnetic field strength reaches 2220 ± 330 G, and the average magnetic field inclination is 33° ± 7°. The magnetic field strengths and inclinations found on individual inner penumbral boundaries undoubtedly depend on the umbral area. Both of these parameters on average decrease with the decreasing umbral area (Fig. 7).
At all inner penumbral boundaries, there is a clear relation between the magnetic field strength and inclination, with the correlation coefficient of 0.72 computed from all pixels on all studied boundaries. The weaker the field is, the more vertical it is. Together with the fact that the average values of B and γ depend on the sunspot area, it means that on the boundaries of smaller umbrae a weaker and more vertical field is found compared to larger umbrae (Fig. 5). This behaviour of B and γ results in a vertical component of the magnetic field that does not vary along the individual inner penumbral boundaries (Figs. 4, 8b). The achieved precision in determining Bver is not good enough to determine whether it depends on the umbral size (Fig. 7). The values of Bver are listed in Table 5 with their uncertainties, and on average it is 1860 ± 190 G.
 |
Fig. 9 Simplified scheme of a sunspot. The field lines marked |B1| and |B2| are symmetric with respect to the field line |B0|. |
It means that the vertical component of the magnetic field is the crucial parameter defining the inner penumbral boundary. This finding was not described before. The mechanism that causes the penumbral filamentary structure only works in regions where Bver is smaller than some crucial value.
Theoretical computations by Chandrasekhar (1961) show that the convection in the inclined magnetic field is sensitive to the vertical component, while the horizontal component influences the shape of the convective cell creating a convective roll oriented parallel to this horizontal component (for details see Thomas & Weiss 2008). If this simplified theory is correct, the critical value of Bver implies the convective origin of penumbral filaments. The magnetic flux tube model by Schlichenmaier et al. (1998) predicts that the inward motion of penumbral filaments is stopped when the subphotospheric part of the flux tube is almost vertical. Because I find the magnetic field inclination changing along individual boundaries, the scenario can only be maintained only by assuming different gradients of γ with height at various locations in a given spot. This would result in the same inclination of magnetic field in the subphotospheric layers of this spot. However, information about the magnetic field structure in the subphotospheric layers cannot be determined from the available data, so it remains an open question.
Acknowledgments
I thank the referee for suggestions and comments that significantly improved this paper. The support from GA AS CR IAA 300030808 is gratefully acknowledged. Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in cooperation with ESA and NSC (Norway).
References
- Balthasar, H., & Collados, M. 2005, A&A, 429, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balthasar, H., & Schmidt, W. 1993, A&A, 279, 243 [NASA ADS] [Google Scholar]
- Beck, C. 2008, A&A, 480, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L. R., Balthasar, H., Collados, M., & Schlichenmaier, R. 2003, A&A, 403, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L. R., Balthasar, H., & Collados, M. 2004, A&A, 427, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Solanki, S. K., Bellot Rubio, L. R., Lagg, A., & Mathew, S. K. 2004, A&A, 422, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Lagg, A., Solanki, S. K., & Collados, M. 2005, A&A, 436, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Solanki, S. K., Lagg, A., Socas-Navarro, H., & Lites, B. 2006, A&A, 450, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrera Solana, D., Bellot Rubio, L. R., & del Toro Iniesta, J. C. 2005, A&A, 439, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and hydromagnetic stability (Oxford: Clarendon Press) [Google Scholar]
- Jahn, K. 1989, A&A, 222, 264 [NASA ADS] [Google Scholar]
- Jahn, K., & Schmidt, H. U. 1994, A&A, 290, 295 [NASA ADS] [Google Scholar]
- Jurčák, J., & Bellot Rubio, L. R. 2008, A&A, 481, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jurčák, J., Bellot Rubio, L., Ichimoto, K., et al. 2007, PASJ, 59, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., & Martinez Pillet, V. 1996, A&A, 316, 229 [NASA ADS] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Langhans, K., Scharmer, G. B., Kiselman, D., Löfdahl, M. G., & Berger, T. E. 2005, A&A, 436, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leka, K. D., & Skumanich, A. 1998, ApJ, 507, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Skumanich, A., & Scharmer, G. B. 1990, ApJ, 355, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Low, B. C., Martínez Pillet, V., et al. 1995, ApJ, 446, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Mathew, S. K., Lagg, A., Solanki, S. K., et al. 2003, A&A, 410, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., Del Toro Iniesta, J. C., et al. 2007, PASJ, 59, 837 [Google Scholar]
- Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009a, Science, 325, 171 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Rempel, M., Schüssler, M., & Knölker, M. 2009b, ApJ, 691, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmele, T. R. 1995, A&A, 298, 260 [NASA ADS] [Google Scholar]
- Rucklidge, A. M., Schmidt, H. U., & Weiss, N. O. 1995, MNRAS, 273, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Cuberes, M., Puschmann, K. G., & Wiehr, E. 2005, A&A, 440, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichenmaier, R., Jahn, K., & Schmidt, H. U. 1998, A&A, 337, 897 [NASA ADS] [Google Scholar]
- Schlichenmaier, R., Rezaei, R., Bello González, N., & Waldmann, T. A. 2010, A&A, 512, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, G. W., & Weiss, N. O. 1970, Sol. Phys., 13, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Solanki, S. K., & Montavon, C. A. P. 1993, A&A, 275, 283 [NASA ADS] [Google Scholar]
- Solanki, S. K., Rueedi, I., & Livingston, W. 1992, A&A, 263, 339 [NASA ADS] [Google Scholar]
- Thomas, J. H., & Weiss, N. O. 2008, Sunspots and Starspots (Cambridge University Press) [Google Scholar]
- Tildesley, M. J., & Weiss, N. O. 2004, MNRAS, 350, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer-Böhm, S. 2008, A&A, 487, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 2001, ApJ, 547, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, G., Xu, Y., Wang, H., & Denker, C. 2003, ApJ, 597, 1190 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Maps of continuum intensity (a, b)) with marked penumbral boundaries (1U and 1P in a; 3U and 3P in b)). The white arrows point to the disc centre, and their length is proportional to the heliocentric angle. Plots c, d) show the magnetic field strengths dependent on the position angle (ψ) along the penumbral boundaries, where the ∗ and + symbols represent the inner and outer penumbral boundaries, respectively. The colours of symbols correspond to the position on the boundary. The small black symbols are the fits of the measured magnetic field strengths with resulting formulas written in the plots. The magnetic field on the 1P and 3P boundaries is increased by 1 kG for display purposes. |
| In the text | |
 |
Fig. 2 Changes in magnetic field strength (upper plot) and inclination (lower plot) along three paths across the penumbra. In the lower right part is the continuum intensity map with marked region with the three shown paths and their colour codes. The black lines in the plots of plasma parameters correspond to the penumbral boundaries shown in the continuum map. |
| In the text | |
 |
Fig. 3 Maps of continuum intensity (a, b)) with marked penumbral boundaries 5P and 6P, respectively. The white arrows are analogous to those in Fig 1. Plots c, d) show the magnetic field strengths (top) and inclination (bottom) dependent on the position along the penumbral boundaries. The colours of symbols correspond to the position on the boundary. The small black symbols are the fits of the observed values with formulas written in the plots. |
| In the text | |
 |
Fig. 4 Analogous to Fig. 3, but for boundaries 2U a, c) and 7U b, d). The solid black lines in B plots mark the vertical component of the magnetic field strength. |
| In the text | |
 |
Fig. 5 The scatter plot showing the dependence of B on the cos(γ) on inner (+ symbols) and outer (⋄ symbols) penumbral boundaries. The colours of symbols represent individual boundaries. |
| In the text | |
 |
Fig. 6 Plots of magnetic field strength (top) and inclination (bottom) reached at the outer penumbral boundaries as a function of sunspot area. The errorbars mark the standard deviations. The solid and dashed lines represent the linear and constant fit of the B and γ values, respectively. The parameters of the fit along with χ2 values are written in the plots. |
| In the text | |
 |
Fig. 7 Plots of magnetic field strength (top) and inclination (bottom) reached at the inner penumbral boundaries as a function of umbral area. In the plot of magnetic field strength, the values of Bver are shown under the thin solid line. The values of vertical component of the magnetic field are decreased by 800 G for display purposes. See caption of Fig. 6 for explanation of errorbars, lines, etc. |
| In the text | |
 |
Fig. 8 Analogous to Fig. 4, but for a 4U boundary and a boundary along umbra with only partially developed penumbra (not listed in Table 1). The red and blue arrows points in the direction of maximal γ and B, respectively. The solid black lines mark the umbra/QS region at the lower boundary. |
| In the text | |
 |
Fig. 9 Simplified scheme of a sunspot. The field lines marked |B1| and |B2| are symmetric with respect to the field line |B0|. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


