| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116668 | |
| Published online | 22 April 2011 | |
Solar winds along curved magnetic field lines
1
Shandong Provincial Key Laboratory of Optical Astronomy &
Solar-Terrestrial Environment, School of Space Science and Physics, Shandong
University at Weihai,
264209
Weihai,
PR China
e-mail: bbl@sdu.edu.cn
2
State Key Laboratory of Space Weather, Chinese Academy of
Sciences, 100190
Beijing, PR
China
Received:
7
February
2011
Accepted:
24
March
2011
Context. Both remote-sensing measurements using the interplanetary scintillation (IPS) technique and in-situ measurements by the Ulysses spacecraft show a bimodal structure for the solar wind at solar minimum conditions. At present it still remains to address why the fast wind is fast and the slow wind is slow. While a robust empirical correlation exists between the coronal expansion rate fc of the flow tubes and the speeds v measured in situ, a more detailed data analysis suggests that v depends on more than just fc.
Aims. We examine whether the non-radial shape of field lines, which naturally accompanies any non-radial expansion, could be an additional geometrical factor.
Methods. We solved the transport equations incorporating the heating from turbulent Alfvén waves for an electron-proton solar wind along curved field lines given by an analytical magnetic field model, which is representative of a solar minimum corona.
Results. The field line shape is found to influence the solar wind parameters substantially, reducing the asymptotic speed by up to ~130 km s-1 or by ~28% in relative terms, compared with the case where the field line curvature is neglected. This effect was interpreted in the general framework of energy addition in the solar wind: compared to the straight case, the field line curvature enhances the effective energy deposition to the subsonic flow, which results in a higher proton flux and a lower terminal proton speed.
Conclusions. Our computations suggest that the field line curvature could be a geometrical factor which, in addition to the tube expansion, substantially influences the solar wind speed. Furthermore, although the field line curvature is unlikely to affect the polar fast solar wind at solar minima, it does help make the wind at low latitudes slow, which in turn helps better reproduce the Ulysses measurements.
Key words: waves / solar wind / stars: winds, outflows
© ESO, 2011
1. Introduction
Around solar minima the global distribution of the solar wind exhibits a simple bimodal structure: a band around the helioequator with an angular width ~50° of the slow wind (speed v ≲ 500 km s-1) is sandwiched between the high-latitude fast winds (v ≳ 650 km s-1) (e.g., Plate 1 in McComas et al. 2000). This picture was established indirectly by interplanetary scintillation (IPS) measurements in 1974 and 1985, corresponding to the minimum of solar cycles (SC) 20 and 21, respectively (Kojima & Kakinuma 1990). However, it became definitive only when Ulysses finished the first polar orbit, which encompasses the minimum of SC 22 (McComas et al. 2000). The bimodal picture continued for the SC 23 minimum as shown by Ulysses during its third polar orbit (McComas et al. 2008; Ebert et al. 2009).
What makes the fast solar wind fast and slow wind slow? In the context of the Ulysses measurements, what produces the pronounced latitudinal variation of v? Considering the well-established empirical relation between v and the coronal expansion rate fc of flow tubes (Wang & Sheeley 1990), one may expect that the speed profile results from the differences in fc of tubes reaching different latitudes in interplanetary space. Models that incorporate heating rates closely related to the magnetic field B indeed suggest that varying the spatial distribution of B, or equivalently that of the expansion rate, can result in considerable changes in wind parameters (for a summary of geometrical models, see Cranmer 2005; for more recent models adopting empirical heating terms, see Wang 2011). For instance, the most recent models based on the anisotropic turbulence, which self-consistently accommodate the heating from interactions of counter-propagating Alfvén waves, indicate that by varying the B profile alone, the modeled latitudinal dependence of wind speed at 1 AU can agree fairly well with the Ulysses measurements (Fig. 12 in Cranmer et al. 2007).
While the fc − v relationship is strikingly robust, the significant spread in v in a given fc interval means that v is a function of more than fc, and the angular distance θb of the field line footpoint to its nearest coronal hole boundary was proved a good candidate for this additional factor (Arge et al. 2004). For a given fc, the smaller θb, the lower is the speed. Because one naturally expects that the open field line becomes increasingly curved while its footpoint becomes closer to the coronal hole boundary, a natural alternative to θb would be the shape of field lines. Surprisingly, the possible effect of field line curvature has not been examined yet. Instead, the available turbulent-heating-based models tend to assume a radially directed flow tube, even though the non-radial tube expansion has been examined in considerable detail (e.g., Chen & Hu 2002; Cranmer et al. 2007; Wang 2011).
The aim of this study is to examine how the field line shape affects the solar wind parameters in general, and whether it helps reproduce the Ulysses measurements in particular. It should be noted that while fully multi-dimensional models incorporating turbulent or empirical heating rates (e.g., Usmanov et al. 2000; Chen & Hu 2001; Li et al. 2004; Cohen et al. 2007; Lionello et al. 2009; Feng et al. 2010; van der Holst et al. 2010) certainly have taken account of both a non-radial expansion and the field line curvature, the two effects cannot be separated. Therefore we choose to solve the transport equations along field lines in a prescribed magnetic field configuration typical of the solar minimum corona, thereby allowing us to switch on and off the effect of the field line shape. The solar wind model we employ incorporates a physically motivated boundary condition, distinguishes between electrons and protons, adopts reasonably complete energy equations including radiative losses, electron heat conduction, and the solar wind heating from parallel propagating turbulent Alfvén waves.
The paper is organized as follows. In Sect. 2 we give a brief overview of the model and describe how it is implemented. The numerical solutions are then presented in Sect. 3. Finally, Sect. 4 summarizes the results, ending with some concluding remarks.
2. Model description and solution method
We consider a time-independent electron-proton solar wind flowing in the meridional plane and incorporating turbulent heating from Alfvén waves. Since the equations are quite well-known, we simply note that the mass or energy exchange between neighboring flow tubes is prohibited, permitting the decomposition of the vector equations (e.g., Eqs. (2) to (7) in Li et al. 2005, and references therein) into a force balance condition transverse to B and a set of conservation equations along it. For mathematical details, please see the appendix of Li & Li (2006). Here we replace the former with a prescribed magnetic field, and treat only the conservation equations in detail. The Alfvén waves are assumed to propagate along B and to be dissipated at the Kolmogorov rate Qwav = ρδv3/Lc, where ρ = nmp is the mass density with n and mp being the number density and proton mass, respectively. Moreover, δv is the rms value of the wave velocity fluctuations, and Lc the correlation length. By standard treatment, the wave heating Qwav goes entirely to protons, and Lc = Lc0(B0/B)1/2, where the subscript 0 denotes values at the field line footpoint at the Sun. This form of dissipation and its variants, first proposed by Hollweg (1986), have been a common practice in solar wind modeling ever since (see e.g., the review by Hollweg & Isenberg 2002).
The conservation equations along an arbitrary magnetic line of force read ![\begin{eqnarray} \label{eq_n}&& \frac{\left(n v A\right)'}{A} =0, \\ \label{eq_v}&& v v' +\frac{p_{\rm p}'}{\rho} +\frac{p_{\rm e}'}{\rho}-\left(\frac{G M_\odot}{r}\right)' = \frac{F}{\rho}, \\ \label{eq_Ts}&& T_{\rm s}'+(\gamma-1)T_{\rm s}[\ln(vA)]' =\frac{\gamma-1}{nk_{\rm B} v}\Bigg[\frac{\delta E_{\rm s}}{\delta t}+Q_{\rm s} -L-\frac{\left(q_{\rm s} A\right)'}{A}\Bigg], \\ \label{eq_pw} &&\frac{\left(F_{\rm w} A\right)'}{A} + v F = -\qwav, \end{eqnarray}](/articles/aa/full_html/2011/05/aa16668-11/aa16668-11-eq22.png) \arraycolsep1.75ptwhere
v is the wind speed,
A ∝ 1/B is the cross-sectional area
of the flux tube, and the prime ′ denotes the derivative with respect to the arc
length l, measured from the footpoint of the field line. The species
pressures ps (s = e,p) are related to species
temperatures Ts via
ps = nkBTs
in which kB is the Boltzmann constant. The gravitational
constant is denoted by G, and M⊙ is the mass
of the Sun. Note that the gravitational acceleration is put in the form of a directional
derivative. In addition, the force density acting on the fluid is caused by Alfvén waves,
\arraycolsep1.75ptwhere
v is the wind speed,
A ∝ 1/B is the cross-sectional area
of the flux tube, and the prime ′ denotes the derivative with respect to the arc
length l, measured from the footpoint of the field line. The species
pressures ps (s = e,p) are related to species
temperatures Ts via
ps = nkBTs
in which kB is the Boltzmann constant. The gravitational
constant is denoted by G, and M⊙ is the mass
of the Sun. Note that the gravitational acceleration is put in the form of a directional
derivative. In addition, the force density acting on the fluid is caused by Alfvén waves,
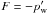 where
pw = ρδv2/2
is the wave pressure. The adiabatic index γ = 5/3, and
δEs/δt
represents the energy exchange rates of species s due to Coulomb collisions
with the other species. To evaluate them, we take the Coulomb logarithm to be 23. For
simplicity, the proton heat flux is neglected (qp = 0), whereas
the electron one is taken to be the Spitzer law
where
pw = ρδv2/2
is the wave pressure. The adiabatic index γ = 5/3, and
δEs/δt
represents the energy exchange rates of species s due to Coulomb collisions
with the other species. To evaluate them, we take the Coulomb logarithm to be 23. For
simplicity, the proton heat flux is neglected (qp = 0), whereas
the electron one is taken to be the Spitzer law 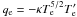 where
κ = 7.8 × 10-7
erg K−7/2 cm-1 s-1. Moreover, the
heating rates applied to species s is denoted by
Qs. For the protons, one has
Qp = Qwav. On the other hand,
optically thin radiative losses are accounted for by the term L, which is
included in the electron version of Eq. (3)
and is described by the parametrization scheme of Rosner
et al. (1978). Some electron heating is also included, expressed by
where
κ = 7.8 × 10-7
erg K−7/2 cm-1 s-1. Moreover, the
heating rates applied to species s is denoted by
Qs. For the protons, one has
Qp = Qwav. On the other hand,
optically thin radiative losses are accounted for by the term L, which is
included in the electron version of Eq. (3)
and is described by the parametrization scheme of Rosner
et al. (1978). Some electron heating is also included, expressed by
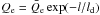 where
where 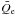 is the magnitude and ld the scale length of this heating. For
simplicity, here we assume that this electron heating is associated with no momentum
deposition. Equation (4) describes the wave
evolution, in which
Fw = pw(3v + 2vA)
is the wave energy flux density with
is the magnitude and ld the scale length of this heating. For
simplicity, here we assume that this electron heating is associated with no momentum
deposition. Equation (4) describes the wave
evolution, in which
Fw = pw(3v + 2vA)
is the wave energy flux density with 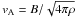 the Alfvén speed.
the Alfvén speed.
Given the governing equations, one may say a few words on the effect of the magnetic field
line shape before actually solving them. Consider the case, referred to as Case S, where we
put dl = dr in ′ (note that ′ is
also involved in qe) and
l = r − R⊙ in
Qe. Here r is the heliocentric distance and
R⊙ the solar radius. As such, Case S differs from the
original case, called Case C, only in that the field lines are straight in the former, but
allowed to be curved in the latter. It then follows that if the wind energetics is not
self-consistently considered, say, if one prescribes an r-distribution of
the temperatures Te and Tp, then
Eqs. (1) and (2) indicate that no matter how curved the field line may be, the same
r-profiles for n and v result. This
applies even if the waves are considered as long as the wave dissipation is neglected. To
understand this, one may readily derive from Eq. (4) a conservation law which reads (e.g. Hu et al.
1997) 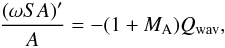 (5)where
ωS = 2pwvA(1 + MA)
is the wave action flux density, and
MA = v/vA
is the Alfvénic Mach number. If Qwav = 0, one finds that
ωSA is a constant, enabling the wave pressure
pw to be expressed as a functional of flow parameters as well
as B. As such multiplying Eqs. (1) and (2) by a factor
dl/dr does not invalidate the equal
signs. This means that any two field lines that have identical radial distributions of
B,Te and Tp will
yield identical radial distributions of n,v and
pw, provided that the base values for n and
δv are the same for the two lines. However, if the energy equation is
explicitly considered, as we will do, and the adopted heating rates play a role in
determining the solar wind mass flux, then the field line shape will likely play a role (see
also the discussion section).
(5)where
ωS = 2pwvA(1 + MA)
is the wave action flux density, and
MA = v/vA
is the Alfvénic Mach number. If Qwav = 0, one finds that
ωSA is a constant, enabling the wave pressure
pw to be expressed as a functional of flow parameters as well
as B. As such multiplying Eqs. (1) and (2) by a factor
dl/dr does not invalidate the equal
signs. This means that any two field lines that have identical radial distributions of
B,Te and Tp will
yield identical radial distributions of n,v and
pw, provided that the base values for n and
δv are the same for the two lines. However, if the energy equation is
explicitly considered, as we will do, and the adopted heating rates play a role in
determining the solar wind mass flux, then the field line shape will likely play a role (see
also the discussion section).
For the meridional magnetic field, we adopt the Banaszkiewicz et al. (1998) model for which we use the reference values [Q,K,a1] = [1.5,1,1.538]. This set of parameters is supported by images obtained with the instruments on board the SOlar and Heliospheric Observatory (SOHO) spacecraft at solar minimum (see e.g., Fig. 1 in Forsyth & Marsch 1999), and has found extensive applications in solar wind models (e.g., Hackenberg et al. 2000; Cranmer et al. 2007; Li & Li 2008). Another parameter M, which controls the magnetic field strength, is chosen such that B at the Earth orbit is 3.5γ, consistent with Ulysses measurements (Smith & Balogh 1995; also Smith 2011).
 |
Fig. 1 Adopted meridional magnetic field configuration in the corona. a) A quadrant is shown where the magnetic axis points upward, and the thick contours delineate the lines of force for which the expansion factors f = (A/A0)(R⊙/r)2 are plotted in b) as a function of heliocentric distance r. The field lines are labeled with the colatitude at which they intersect the Earth orbit (1 AU). Here A denotes the cross-sectional area of the flow tube, the subscript 0 represents values at the inner boundary R⊙. |
The meridional magnetic field configuration is depicted in Fig. 1a, where the thick contours indicate the lines of force along which we compute the expansion factor f = (A/A0)(R⊙/r)2, given in Fig. 1b. The field lines are labeled with the colatitude at which the lines are located at 1 AU. From Fig. 1a one can see that the open field lines occupy only a minor fraction of the solar surface, with colatitudes θ ≤ 30° to be specific. If one identifies this area as the coronal hole (CH) (see e.g., Wang 2011), one can indeed see that when their footpoints approach the CH boundary, the open field lines become progressively more curved. Furthermore, Fig. 1b shows that while in the inner corona, say at r = 1.7 R⊙, the expansion factor f increases when the field lines become closer to the CH edge, the opposite is true at large distances, say r ≳ 20 R⊙. As was first pointed out by Wang & Sheeley (1990), this tendency is due to the inclusion of the current sheet component in the magnetic field, and the low densities in the fast wind in interplanetary space were attributed to that flow tubes originating near the CH center experienced the most significant net expansion.
Given a B profile along a field line, the governing equations are put in a
time-dependent form, discretized onto a non-uniformly spaced grid, and then advanced in time
from an arbitrary initial state by a fully implicit scheme (Hu et al. 1997) until a steady state is reached, which is then taken as our
solution. For the solutions found, the mass, momentum, and energy are found to be conserved
to better than 1%. At the top boundary (1 AU), all flow parameters are linearly extrapolated
for simplicity. At the base (1 R⊙) the flow speed
v is determined by mass conservation, whereas the species temperatures
are fixed at
Te0 = Tp0 = T0 = 5 × 105 K,
corresponding to mid-transition region. Because the processes taking place below this level
should influence the mass supply to the solar wind (e.g., Hansteen & Leer 1995; Lie-Svendsen et al.
2002), they should be taken into account and can be well represented by the
radiation equilibrium boundary (REB) condition (Withbroe
1988; Lionello et al. 2001). The REB
condition translates into
n0 = 4.8 × 103qe0 in
cgs units for our chosen T0. As such, the base density
n0 is not fixed but allowed to adjust to the downward heat
flux, which in turn depends on how the fluid is heated close to the base. Without the basal
electron heating, the Te gradient and hence the electron heat
flux density qe0 at the base are too low, leading to
n0T0 ≪ 1.6 × 1014 cm-3
K, the value inferred from measurements with the Solar Ultraviolet Measurements of Emitted
Radiation (SUMER) on SOHO for coronal holes (Warren
& Hassler 1999). The values adopted for Qe are
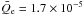 erg cm-3 s-1,
and ld = 0.06 R⊙. With such a
short scale length, Qe rapidly gives way to the more gradual
proton heating Qwav, for which we use a base wave amplitude
δv0 = 27 km s-1 and a base value
for the correlation length Lc0 of 1.5 × 104 km. (Note
that even though this Lc0 translates into approximately
0.02 R⊙, it does not mean that the wave dissipation is
extremely concentrated at the base. A length scale comparable to
ld involved in Qe can be given by
erg cm-3 s-1,
and ld = 0.06 R⊙. With such a
short scale length, Qe rapidly gives way to the more gradual
proton heating Qwav, for which we use a base wave amplitude
δv0 = 27 km s-1 and a base value
for the correlation length Lc0 of 1.5 × 104 km. (Note
that even though this Lc0 translates into approximately
0.02 R⊙, it does not mean that the wave dissipation is
extremely concentrated at the base. A length scale comparable to
ld involved in Qe can be given by
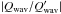 , for which one finds a value
ranging from 0.086 R⊙ at the base to
0.59 R⊙ at 2 R⊙ for the
solution labeled case C in Fig. 2.)
, for which one finds a value
ranging from 0.086 R⊙ at the base to
0.59 R⊙ at 2 R⊙ for the
solution labeled case C in Fig. 2.)
3. Numerical results
To examine the extent to which the wind parameters are affected by the field line shape, we will compare solutions that incorporate the curvature effect (Case C) and those that neglect it (Case S).
 |
Fig. 2 Alfvén wave-turbulence-based solar wind models incorporating effects of field line shape. Radial profiles are shown for a) the solar wind speed v, and b) the electron and proton temperatures Te and Tp. The curved (straight) case in which the field line shape is considered (neglected) is given by the solid (dashed) lines. In a), the asterisks indicate the sonic point where v equals the effective sonic speed cS defined by Eq. (6), while the vertical bars represent wind speeds measured by tracking small density inhomogeneities (blobs) in SOHO/LASCO images as given by Wang et al. (2000). The triangles in b) give the hydrogen kinetic temperatures derived from H I Lyα measurements with SOHO/UVCS for a typical solar minimum streamer (Strachan et al. 2002). |
Figure 2 presents the radial profiles of (a) the wind
speed v and (b) the electron and proton temperatures
Te and Tp for the solutions
computed along the tube labeled 88 in Fig. 1a. For this
field line the effect of the field line curvature is almost maximal. The solid and dashed
curves correspond to Cases C and S, respectively. The asterisks in Fig. 2a refer to the sonic point where v equals the effective
sound speed cS given by (e.g., Eq. (36) in Hackenberg et al. 2000) 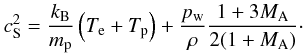 (6)Moreover,
in Fig. 2a the vertical bars give the range of wind
speeds derived by tracking a collection of small inhomogeneities (the blobs) in images
obtained with the Large Angle Spectrometric COronagraph (LASCO) on board SOHO (Wang et al. 2000). The triangles in Fig. 2b represent the hydrogen kinetic temperatures derived from
the H I Lyα profiles measured with the UltraViolet Coronagraph Spectrometer
(UVCS) on SOHO for a typical solar minimum streamer (Strachan et al. 2002).
(6)Moreover,
in Fig. 2a the vertical bars give the range of wind
speeds derived by tracking a collection of small inhomogeneities (the blobs) in images
obtained with the Large Angle Spectrometric COronagraph (LASCO) on board SOHO (Wang et al. 2000). The triangles in Fig. 2b represent the hydrogen kinetic temperatures derived from
the H I Lyα profiles measured with the UltraViolet Coronagraph Spectrometer
(UVCS) on SOHO for a typical solar minimum streamer (Strachan et al. 2002).
The solution for Case C (solid curves) agrees well with available measurements. For instance, the model yields the following parameters at 1 AU: vE = 333 km s-1, (nv)E = 3.65 × 108 cm2 s-1, Te = 1.4 × 105 K and Tp = 2.7 × 104 K, all of which match the in-situ measurements by both Helios (Schwenn 1990) and Ulysses (McComas et al. 2000, 2008; Ebert et al. 2009) of the low latitude slow winds. Here the subscript E denotes the Earth orbit. Figure 2a indicates that the wind speed starts with 6.4 km s-1 at the base, which is in line with the Doppler speed measured with Ne VIII (e.g., Xia et al. 2003), whose formation temperature is close to our base temperature. The speed profile is not monotonic but possesses a local minimum at 1.63 R⊙ where v = 25.1 km s-1. The sonic point, denoted by rC, is located at 4.15 R⊙. Between 3 and 20 R⊙ the computed speeds are in line with the blob measurements. Moreover, for r ≲ 3 R⊙ the modeled v is no higher than 98.8 km s-1, which would be below the sensitivity of the Doppler dimming of H I Lyα (Kohl et al. 2006), and in this sense is compatible with the fact that there is not much empirical knowledge about the proton speed in the inner portion of the slow wind. Moving to Fig. 2b one may see that because of the applied electron heating both Te and Tp increase near the base. At 1.19 R⊙ the electron temperature Te attains its maximum of 9.8 × 105 K. Below this height, Te and Tp stay close to each other owing to Coulomb coupling. However, while Te decreases monotonically with distance above this height, Tp further increases to 2.14 × 106 K at 1.6 R⊙ beyond which Tp declines with a slope steeper than Te and is overtaken by Te at 30.1 R⊙. In the range from 1.75 to 5.11 R⊙ the modeled proton temperature reproduces the H I measurements fairly satisfactorily, which indicates that the heating mechanism we employ performs well in heating the inner solar wind.
Compared with Case C, at 1 AU Case S yields a significantly higher proton speed and a
substantially lower proton flux density. The parameters at 1 AU now read
vE = 461 km s-1,
(nv)E = 3.14 × 108 cm2 s-1,
Te = 7.5 × 104 K, and
Tp = 4.65 × 104 K. In addition, Case S yields a
sonic point at rC = 3.24 R⊙,
closer to the Sun than in Case C. The differences between the temperatures in the two cases
can be readily understood by examining Eq. (3). A higher speed in Case S leads to a more prominent adiabatic cooling (the second
term on the left-hand side), which accounts for a steeper, negative
Te gradient and hence a lower asymptotic
Te; on the other hand, while the same also happens to protons,
the reduced proton flux results in a higher
Qwav/(nv), which leads to
a steeper, positive Tp gradient and eventually a higher
asymptotic Tp. However, the question remains as to how
neglecting the curvature of the field line leads to the changes in the proton speed and
flux? This is understandable if one follows the comprehensive discussion by Leer & Holzer (1980): the more energy is
deposited in the subsonic region of the flow, the higher the proton flux; and the larger the
energy deposition per particle, the higher the terminal speed. Let us first examine the
subsonic physics, from R⊙ to the sonic point
rC. The contribution from the electron heating, measured as an
energy flux density scaled to 1 AU 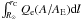 ,
increases only slightly from 0.3 in Case C to 0.337 in Case S (here and hereafter the energy
flux densities are in erg cm-2 s-1). However, the effect of
energy addition to protons, which eventually derives from Alfvén waves since
,
increases only slightly from 0.3 in Case C to 0.337 in Case S (here and hereafter the energy
flux densities are in erg cm-2 s-1). However, the effect of
energy addition to protons, which eventually derives from Alfvén waves since
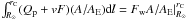 ,
reduces more significantly from 1.089 in Case C to 0.931 in Case S. And this reduction is a
direct consequence of the field line shape. To see this, we note that the wave action
Eq. (5) is a proper starting point, because
its right-hand side (RHS) evaluates the consequence of the “genuine” dissipation while its
LHS involves the wave ponderomotive force, which also contributes to the wave energy loss.
Without dissipation, we saw that the field line shape is unable to make the radial
distributions different in Case C from those in Case S, even when the ponderomotive
force is allowed for. Expressing Eq. (5) in
the integral form yields
,
reduces more significantly from 1.089 in Case C to 0.931 in Case S. And this reduction is a
direct consequence of the field line shape. To see this, we note that the wave action
Eq. (5) is a proper starting point, because
its right-hand side (RHS) evaluates the consequence of the “genuine” dissipation while its
LHS involves the wave ponderomotive force, which also contributes to the wave energy loss.
Without dissipation, we saw that the field line shape is unable to make the radial
distributions different in Case C from those in Case S, even when the ponderomotive
force is allowed for. Expressing Eq. (5) in
the integral form yields 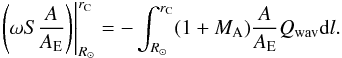 (7)Now
that in general
dl/dr > 1,
which is particularly true in the inner flow where MA ≪ 1, the
RHS of Eq. (7) means that
Qwav of similar amount effectively contributes more to the
wave energy reduction in the curved than in the straight case. Now let us discuss the
asymptotic speeds. The net energy added to the solar wind, i.e., the electron heating plus
wave dissipation plus enthalpy flux subtracted by radiative losses and the net electron heat
flux flowing out of the computational domain, yields an energy flux scaled to 1 AU of 1.495
(1.553) in Case C (S). Divided by the proton flux density, this gives 0.41
(0.495) × 10-8 erg per particle in Case C (S), which explains the higher
terminal speed in Case S.
(7)Now
that in general
dl/dr > 1,
which is particularly true in the inner flow where MA ≪ 1, the
RHS of Eq. (7) means that
Qwav of similar amount effectively contributes more to the
wave energy reduction in the curved than in the straight case. Now let us discuss the
asymptotic speeds. The net energy added to the solar wind, i.e., the electron heating plus
wave dissipation plus enthalpy flux subtracted by radiative losses and the net electron heat
flux flowing out of the computational domain, yields an energy flux scaled to 1 AU of 1.495
(1.553) in Case C (S). Divided by the proton flux density, this gives 0.41
(0.495) × 10-8 erg per particle in Case C (S), which explains the higher
terminal speed in Case S.
Now we return to the question what geometrical factor(s) besides the tube expansion may also affect the solar wind speed v. The comparison between the straight and curved cases shows that the field line shape could be one. In this regard, the physical basis for the empirical relation found by Arge et al. (2004) may be simply that θb, which measures how far the open field line footpoint is away from the coronal hole boundary, also characterizes the field line shape.
 |
Fig. 3 Distribution with colatitude θ of the computed solar wind speed v at 1 AU and the coronal expansion factor fc of the flow tube intersecting the Earth orbit at θ. The model result incorporating (neglecting) the field line shape, called Case C (S), is given by the solid (dashed) line. They are obtained by varying the flow tube alone but keeping all other parameters unchanged. Cases C and S both take the radial variation of the magnetic field strength into account, and differ from each other only in that Case C considers the field line shape whereas Case S neglects it. The blue continuous curve gives the daily averaged speed measurements by Ulysses during the first half of its latitude scan from Sep. 12, 1994 to Mar. 4, 1995. As for fc, it is taken to have the value of f at a heliocentric distance of 1.7 R⊙. |
What role does the shape of field lines play in shaping the latitudinal profile of the solar wind speed at 1 AU? This is examined in Fig. 3, which compares the speed profile in Case C (the solid curve) and in Case S (the dashed curve). The model results are obtained by varying only the flow tube along which the governing equations are solved, but keeping everything else untouched. In addition to the speed v at 1 AU, Fig. 3 also displays as a function of colatitude θ the coronal expansion factor fc of the flow tube that reaches 1 AU at θ. Here fc is defined as (A/A0)(R⊙/rcor)2, where rcor is taken to be 1.7 R⊙ (see Fig. 1b). For comparison, the solid curve in blue gives the daily averages of the Ulysses measurements of the wind speed during the first half of the fast latitude scan from Sep. 12, 1994 to Mar. 4, 1995. From Fig. 3 one can see that while the speed v in both models is inversely correlated with fc, the results in Case C provide a stronger latitudinal variation. Indeed, the reduction in the wind speed caused by the field line shape is larger than 10% throughout the latitudinal range θ ≳ 70°, with the largest relative difference being 27.8%, which occurs close to the equator. Furthermore, without more tweaking of the heating parameters, such as varying the base values of the wave amplitude δv0 and the correlation length Lc0 from tube to tube as was done by e.g., Li et al. (2004), the modeled latitudinal dependence for θ ≲ 70° is too strong to reproduce the measured profile for the fast wind. Despite this, the low-latitude portion of Fig. 3 indicates that in addition to a more pronounced coronal expansion rate, the field line curvature is also an important factor that makes the slow wind there slow.
4. Summary and concluding remarks
Both remote-sensing measurements using the interplanetary scintillation (IPS) technique and in-situ measurements by the Ulysses spacecraft show a latitudinal gradient in the wind properties, the speed in particular, at solar minimum conditions (Kojima & Kakinuma 1990; McComas et al. 2000, 2008). What makes the fast wind fast and the slow wind slow still seems elusive. While there exists a robust empirical correlation between the coronal expansion rate fc of the flow tubes and the speeds v measured in situ (Wang & Sheeley 1990), a more detailed data analysis suggests that v depends on more than just fc (Arge et al. 2004). We examined whether the non-radial shape of field lines, which naturally accompanies any non-radial expansion, could be an additional geometrical factor. To this end, we solved the transport equations for an electron-proton solar wind, which incorporate the heating from turbulent Alfvén waves dissipated at the Kolmogorov rate, along curved field lines given by the Banaszkiewicz et al. (1998) model, which is representative of a solar minimum corona. The shape of field lines was found to substantially influence the solar wind parameters, reducing the terminal speed by as much as ~130 km s-1 or up to 28%, compared to the straight case where field line curvature is neglected. And this effect was interpreted in the general framework of energy addition in the solar wind by Leer & Holzer (1980): compared with the straight case, even though the wave dissipation rates may be similar, the field line curvature enhances the effective wave energy deposition in the subsonic region of the flow, which results in a higher proton flux and a lower terminal proton speed. Our results suggest that the experimental finding by Arge et al. (2004) may be interpreted in view of the fact that flow tubes with identical coronal expansion rates may differ substantially in their curvature. On the other hand, even though the field line curvature is unlikely to affect the polar fast solar wind at solar minima, it does considerably help the wind at low latitudes become slow, which in turn helps to better reproduce the Ulysses measurements.
Could this effect have to do with the particular boundary conditions or the energy deposition mechanism employed here? This proves very unlikely. We tested cases where the inner boundary is placed at the lower transition region where T = 105 K, or the “coronal base” where T = 106 K. Adjusting the heating parameters in a way that realistic values can be obtained for the proton flux and asymptotic speed, and comparing solutions with field line curvature switched on and off, the conclusion is the same. On the other hand, using a different heating function where Qp is given by the dissipation of some unspecified mechanical energy flux at a constant scale length, the conclusion is the same. Moreover, this effect is not related to the heat conduction, even though the effective electron heat conductivity is reduced by a factor dr/dl in the curved case. Indeed, turning off the electron heat flux, in which case we have to fix the base density though, we reach the same conclusion. All of these additional computations corroborate our interpretation that the changes brought forth by the field line shape are simply related to the differential arc-length dl involved in Eq. (7), whereby the more curved the field lines are in the subsonic region, the greater is the wave energy reduction there, hence the higher the proton flux, and with the total input energy flux barely changing, the lower the terminal proton speed. The effect of the field line shape therefore should happen in quite general situations where the wave dissipation rate Qwav is not directly proportional to the spatial derivative of background parameters and the energy deposition in the subsonic region plays a significant role in determining the solar wind flux. From this perspective one may expect that the effect of field line curvature is not restricted to flow tubes rooted at any particular latitude on the Sun. Instead, it should play a role for any flow tube that is curved. Moreover, this effect should also exhibit some influence on the flow if one employs the anisotropic turbulence treatment of the Alfvén waves to incorporate the finite-wavelength non-WKB effects, as is actively pursued at present (Cranmer et al. 2007; Verdini et al. 2010). Compared with a radial one, a curved line of force is likely to enhance the non-WKB effect (i.e., reflection) in the near-Sun region (Fig. 16 in Heinemann & Olbert 1980). However, to predict what happens next is not as straightforward as what was done here. Let us neglect the wave dissipation for the moment, i.e., the waves interact with the flow only via their ponderomotive force. The enhanced reflection then tends to lead to a reduction of this force, and hence to a reduced mass flux as well as a lower terminal speed. Unlike the dissipationless case discussed in Sect. 2, this tendency exists both when the wind temperatures are prescribed (Fig. 10 in MacGregor & Charbonneau 1994) and when the wind energetics is self-consistently treated (Fig. 4 in Li & Li 2008). The case with turbulent dissipation is considerably more complicated. The enhancement of wave reflection in the subsonic flow means an enhancement of the ingoing component of the waves. With the turbulent dissipation trying to diminish both outgoing and reflected components to similar extents, a substantial fraction of the reflected component may end up in the supersonic portion of the flow, and its consequent dissipation may lead to a higher terminal speed with the mass flux barely altered. However, this is not the whole story because the ponderomotive force is altered in a similar fashion to the dissipationless case. As such, the net outcome has to be told by a detailed numerical study, which is beyond the scope of this paper. Nonetheless, it seems fair to say that if one tries to reproduce the Ulysses measurements, especially those of the slow solar wind at low latitudes, the field line shape has to be accounted for.
That said, let us say a few words on the situations where the curvature effects are unlikely to be important. This may happen, for instance, 1) in the spectral erosion scenario where the solar wind is heated by high-frequency Alfvén waves (with frequencies up to 10 kHz) that are directly launched by chromospheric magnetic reconnections, since now the dissipation rate is proportional to the directional derivative of the proton gyro-frequency and therefore the background magnetic field strength (Marsch & Tu 1997; Hackenberg et al. 2000); 2) in the scenario for the solar wind generation where both the energy Fw0 and mass injection Fm0 rates are fixed (e.g., Fisk 2003; Tu et al. 2005). To illustrate this, consider the scenario by Fisk (2003) where the energy and mass injection occurs at some level where the temperature is on the order of 1 MK, which means, roughly speaking, the contributions like enthalpy, heat flux and radiative losses may be neglected when considering the overall energy balance between the injection point and 1 AU. Evidently the
mass flux density at 1 AU is simply
Fm0A0/AE,
and from energy conservation it follows that the terminal proton speed is approximately
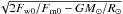 .
As such, the terminal mass flux density is determined by the net expansion of the flow tube
from its footpoint to 1 AU, but the speed is related to neither the tube expansion nor the
field line shape.
.
As such, the terminal mass flux density is determined by the net expansion of the flow tube
from its footpoint to 1 AU, but the speed is related to neither the tube expansion nor the
field line shape.
Acknowledgments
We thank the referee (Dr. Andrea Verdini) for his comments, which helped us clarify the possible effects of the magnetic field line shape on a turbulence-heated solar wind where the non-WKB effects are considered. The Ulysses data are obtained from the CDAWeb database. The SWOOPS team (PI: D. J. McComas) is gratefully acknowledged. This research is supported by the grant NNSFC 40904047, and also by the Specialized Research Fund for State Key Laboratories. Y.C. is supported by grants NNSFC 40825014 and 40890162, and LDX by NNSFC 40974105.
References
- Arge, C. N., Luhmann, J. G., Odstrcil, D., Schrijver, C. J., & Li, Y. 2004, J. Atm. Solar-Terrestrial Phys., 66, 1295 [Google Scholar]
- Banaszkiewicz, M., Axford, W. I., & McKenzie, J. F. 1998, A&A, 337, 940 [NASA ADS] [Google Scholar]
- Chen, Y., & Hu, Y. Q. 2001, Sol. Phys., 199, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., & Hu, Y. Q. 2002, Ap&SS, 282, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, O., Sokolov, I. V., Roussev, I. I., et al. 2007, ApJ, 654, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R. 2005, Solar Wind 11/SOHO 16, Connecting Sun and Heliosphere, 592, 159 [NASA ADS] [Google Scholar]
- Cranmer, S. R., van Ballegooijen, A. A., & Edgar, R. J. 2007, ApJS, 171, 520 [Google Scholar]
- Ebert, R. W., McComas, D. J., Elliott, H. A., Forsyth, R. J., & Gosling, J. T. 2009, J. Geophys. Res., 114(A01), 109 [Google Scholar]
- Feng, X., Yang, L., Xiang, C., et al. 2010, ApJ, 723, 300 [Google Scholar]
- Fisk, L. A. 2003, J. Geophys. Res., 108, 1157 [Google Scholar]
- Forsyth, R. J., & Marsch, E. 1999, Space Sci. Rev., 89, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Hackenberg, P., Marsch, E., & Mann, G. 2000, A&A, 360, 1139 [NASA ADS] [Google Scholar]
- Hansteen, V. H., & Leer, E. 1995, J. Geophys. Res., 100, 21577 [NASA ADS] [CrossRef] [Google Scholar]
- Heinemann, M., & Olbert, S. 1980, J. Geophys. Res., 85, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Hollweg, J. V. 1986, J. Geophys. Res., 91, 4111 [Google Scholar]
- Hollweg, J. V., & Isenberg, P. A. 2002, J. Geophys. Res., 107, 1147 [CrossRef] [Google Scholar]
- Hu, Y. Q., Esser, R., & Habbal, S. R. 1997, J. Geophys. Res., 102, 14661 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., Noci, G., Cranmer, S. R., & Raymond, J. C. 2006, A&ARv, 13, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Kojima, M., & Kakinuma, T. 1990, Space Sci. Rev., 53, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Leer, E., & Holzer, T. E. 1980, J. Geophys. Res., 85, 4681 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., & Li, X. 2006, A&A, 456, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, B., & Li, X. 2008, ApJ, 682, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., Li, X., Hu, Y.-Q., & Habbal, S. R. 2004, J. Geophys. Res., 109, 103 [CrossRef] [Google Scholar]
- Li, B., Habbal, S. R., Li, X., & Mountford, C. 2005, J. Geophys. Res., 110, 112 [CrossRef] [Google Scholar]
- Lie-Svendsen, Ø., Hansteen, V. H., Leer, E., & Holzer, T. E. 2002, ApJ, 566, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Lionello, R., Linker, J. A., & Mikić, Z. 2001, ApJ, 546, 542 [Google Scholar]
- Lionello, R., Linker, J. A., & Mikić, Z. 2009, ApJ, 690, 902 [CrossRef] [Google Scholar]
- MacGregor, K. B., & Charbonneau, P. 1994, ApJ, 430, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., & Tu, C.-Y. 1997, A&A, 319, L17 [NASA ADS] [Google Scholar]
- McComas, D. J., Barraclough, B. L., Funsten, H. O., et al. 2000, J. Geophys. Res., 105, 10419 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Ebert, R. W., Elliott, H. A., et al. 2008, Geophys. Res. Lett., 35, 18103 [NASA ADS] [CrossRef] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Schwenn, R. 1990, in Physics of the Inner Heliosphere I, ed. R. Schwenn, & E. Marsch, 99 [Google Scholar]
- Smith, E. J. 2011, J. Atm. Solar-Terrestrail Phys., 73, 277 [Google Scholar]
- Smith, E. J., & Balogh, A. 1995, Geophys. Res. Lett., 22, 3317 [NASA ADS] [CrossRef] [Google Scholar]
- Strachan, L., Suleiman, R., Panasyuk, A. V., Biesecker, D. A., & Kohl, J. L. 2002, ApJ, 571, 1008 [Google Scholar]
- Tu, C.-Y., Zhou, C., Marsch, E., et al. 2005, Science, 308, 519 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Usmanov, A. V., Goldstein, M. L., Besser, B. P., & Fritzer, J. M. 2000, J. Geophys. Res., 105, 12675 [NASA ADS] [CrossRef] [Google Scholar]
- van der Holst, B., Manchester, W. B., Frazin, R. A., et al. 2010, ApJ, 725, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Verdini, A., Velli, M., Matthaeus, W. H., Oughton, S., & Dmitruk, P. 2010, ApJ, 708, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M. 2011, Space Sci. Rev., doi:10.1007/s11214-010-9733-0 [Google Scholar]
- Wang, Y.-M., & Sheeley, N. R., Jr. 1990, ApJ, 355, 726 [Google Scholar]
- Wang, Y.-M., Sheeley, N. R., Socker, D. G., Howard, R. A., & Rich, N. B. 2000, J. Geophys. Res., 105, 25133 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, H. P., & Hassler, D. M. 1999, J. Geophys. Res., 104, 9781 [NASA ADS] [CrossRef] [Google Scholar]
- Withbroe, G. L. 1988, ApJ, 325, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, L. D., Marsch, E., & Curdt, W. 2003, A&A, 399, L5 [Google Scholar]
All Figures
 |
Fig. 1 Adopted meridional magnetic field configuration in the corona. a) A quadrant is shown where the magnetic axis points upward, and the thick contours delineate the lines of force for which the expansion factors f = (A/A0)(R⊙/r)2 are plotted in b) as a function of heliocentric distance r. The field lines are labeled with the colatitude at which they intersect the Earth orbit (1 AU). Here A denotes the cross-sectional area of the flow tube, the subscript 0 represents values at the inner boundary R⊙. |
| In the text | |
 |
Fig. 2 Alfvén wave-turbulence-based solar wind models incorporating effects of field line shape. Radial profiles are shown for a) the solar wind speed v, and b) the electron and proton temperatures Te and Tp. The curved (straight) case in which the field line shape is considered (neglected) is given by the solid (dashed) lines. In a), the asterisks indicate the sonic point where v equals the effective sonic speed cS defined by Eq. (6), while the vertical bars represent wind speeds measured by tracking small density inhomogeneities (blobs) in SOHO/LASCO images as given by Wang et al. (2000). The triangles in b) give the hydrogen kinetic temperatures derived from H I Lyα measurements with SOHO/UVCS for a typical solar minimum streamer (Strachan et al. 2002). |
| In the text | |
 |
Fig. 3 Distribution with colatitude θ of the computed solar wind speed v at 1 AU and the coronal expansion factor fc of the flow tube intersecting the Earth orbit at θ. The model result incorporating (neglecting) the field line shape, called Case C (S), is given by the solid (dashed) line. They are obtained by varying the flow tube alone but keeping all other parameters unchanged. Cases C and S both take the radial variation of the magnetic field strength into account, and differ from each other only in that Case C considers the field line shape whereas Case S neglects it. The blue continuous curve gives the daily averaged speed measurements by Ulysses during the first half of its latitude scan from Sep. 12, 1994 to Mar. 4, 1995. As for fc, it is taken to have the value of f at a heliocentric distance of 1.7 R⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


