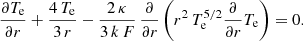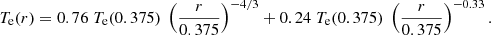| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 7 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202244128 | |
| Published online | 18 September 2023 | |
The nature of the solar wind electron temperature and electron heat flux
I. Case of a radial interplanetary magnetic field
1
Department of Chemistry, University of British Columbia, Vancouver V6T 1Z1, Canada
e-mail: damahubert@gmail.com
2
Space Sciences Laboratory, University of California, Berkeley, CA 94720, USA
e-mail: salem@ssl.berkeley.edu
Received:
27
May
2022
Accepted:
22
February
2023
Aims. We analyze the properties of a phenomenological model of the solar wind electron energy equation in a spherical expansion, with a radial power law for the electron heat flux, a radial interplanetary magnetic field (IMF), and a constant or smooth increase of the solar wind speed.
Methods. We define a critical electron heat flux that is a fraction of the electron thermal energy convected at the solar wind speed, and which plays a crucial role in the electron energy equation solution. When the electron heat flux is equal to the critical heat flux, the electron temperature is driven solely by the dissipation of the heat flux and the electron temperature is a simple radial power law. This defines an heat dissipation dominated (HDD) expansion of the electrons. When the electron heat flux is not equal to the critical electron heat flux, both adiabatic cooling and dissipation of the heat flux drive the electron temperature evolution. These two processes are quantitatively evaluated all along the expansion, in a composite expression of the electron temperature.
Results. We establish generic radial electron temperature laws for different values of the electron heat flux index α. We discuss the derivation of the electron temperature as ∝r−2/7 in the solar wind. We show that a model of the electron energy equation where the Spitzer and Härm (SH) heat conduction law is a closure, with a constant or smooth increase of the solar wind speed and a radial IMF, is an HDD expansion. We also show that the electron temperature follows a radial power law as ∝r−0.4. We obtain constraints on the nature of the electron temperature and the electron heat flux power law index for the SH law to be verified in a large range of radial distance from the Sun. An application of the generic temperature law to kinetic numerical simulations of the solar wind accurately predicts the electron temperature characteristics and evolution.
Key words: Sun: heliosphere / solar wind / plasmas / conduction / magnetic fields / methods: analytical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In this work, we consider what processes govern the radial evolution of the solar wind electron temperature and electron heat flux. This has been an outstanding question since it was found that the Spitzer & Härm (1953, hereafter SH) electron heat conduction law overestimates the solar wind electron heat flux (see Scime et al. 1994, and references therein). In the collisional (Knudsen number < 0.3) slow solar wind at 1 astronomical unit (AU), the electron heat flux has been observed to be consistent with the SH law (Salem et al. 2003; Bale et al. 2013); but this property is not verified in the less collisional fast solar wind. However, simulations by Landi et al. (2014), taking a radial variation of the heat flux into account, indicate that the SH law is not approached until Knudsen numbers < 0.02. Landi et al. (2012) also stressed that to be finally established this property should be verified based on a large range of radial distances from the Sun. Moreover, it is necessary to address the origin of the halo component of the electron distribution function, which is not included in the establishment of the SH law. It is more likely the result of wave-particle interactions (Pilipp et al. 1987; Vocks et al. 2005; Salem et al. 2007) or a natural outcome of a generalized Ohm’s law (Scudder 2019).
A solar wind electron temperature profile as r−2/7 is considered as the radial electron temperature in collisional heat flux models with the SH law as the closure of the energy equation (Salem et al. 2003; Landi et al. 2012; Bale et al. 2013). This radial power law was obtained by Hartle & Sturrock (1968) in a two-fluid model with a radial interplanetary magnetic field (IMF) for distances r > 102 RS where RS is the solar radius. In the two-fluid model of Olsen & Leer (1996) in a radial IMF, the electron temperature shows a different profile that is not ∝r−2/7 at 1 AU. In these two-fluid models, no adiabatic cooling is mentioned. In their comprehensive analysis, Meyer-Vernet & Issautier (1998) studied the electron distribution function (EDF) evolution in the exospheric paradigm, for electrons that are either in a Maxwellian or Kappa state at the exobase. These authors show that in a radial IMF at large radial distance, the truncated EDF carries an electron heat flux ∝r−2 and the temperature evolution of the EDF is composed of an adiabatic component and an isothermal contribution, with the same weight at the radial distance of one AU. This exospheric approach is the only model that predicts an electron adiabatic cooling contribution in the solar wind expansion, but no observation, up to now, has confirmed this prediction. Horaites et al. (2015) obtained a scale-invariant solution of the Fokker-Planck equation with the assumption of a power law decrease of the electron temperature; they found a solution with an electron temperature of ∝r−0.5 and an electron heat flux of ∝r−11/4. An electron temperature of ∝r−0.4 was recently derived by Boldyrev et al. (2020), using a model where core electrons are heated through collisions with the strahl electrons.
The Helios and Ulysses missions have provided unique opportunities to study the physics of solar wind electrons along large radial distances from the Sun. Pilipp et al. (1990) analyzed Helios 1 and 2 data collected between 0.3 and 1 AU. They established radial power laws of the electron temperature and electron heat flux, finding in some cases variable power law indices with respect to the radial distance. They also conclude that in the high-speed solar wind the total electron temperature cannot be explained only by the electron heat flux dissipation. Štverák et al. (2015), in revisiting the same data from Helios 1 and 2, found a constant power law index respectively for the radial electron temperature and the radial electron heat flux. Moreover, they found that the electrons do not need a significant external heating mechanism to explain the temperature gradients. Scime et al. (1994), in analyzing Ulysses data collected in the ecliptic plane from 1 to 5 AU, found electron temperature and electron heat flux as radial power laws with a constant power law index. Ulysses measurements, from the south solar pole to the north solar pole, during a period of stationary fast solar wind, show a constant radial power law for the core electron temperature (Issautier et al. 1998), a constant radial power law for the total electron temperature (Le Chat et al. 2011), and a constant radial power law for the electron heat flux as well (Scime et al. 1999). In particle simulations in a radial IMF performed by Landi et al. (2012), the electron temperature and heat flux are expressed with a range of values of the power law indices. Indeed, in these simulations, with different electron densities at the lower boundary, the electron temperature decreases as ∝rβ with β in the range of −0.8 to −0.6, and the electron heat flux decreases as ∝rα with α in the range of −2.5 to −2.3, whether the solar wind is slow or fast. Considering individual simulations, we find that the power law indices of the electron temperature and of the electron heat flux are not exactly constant with respect to the radial distance. From all these results, we conclude that the radial variation of the electron temperature and of the electron heat flux are commonly expressed as radial power laws, with constant or sometimes variable power law indices.
To provide a complete answer to our original question – which also stands as one of the goals of the Parker Solar Probe Mission (Fox et al. 2016; Viall & Borovsky 2020) – we need to solve the Fokker-Planck equation, to run numerical particle simulations, or to solve transport equations describing properly the solar wind plasma (Cranmer & Schiff 2021), implementing the IMF and wave-particle processes within each of these approaches. Then, from the output of these approaches, we would have to identify the nature of the electron heat flux to quantify the adiabatic cooling and the electron heat flux dissipation, as well as the IMF and the electron-wave interaction effects on the radial evolution of the electron temperature. In this study, we undertake a portion of this program through a phenomenological approach, supported by observations of the electron heat flux as a radial power law. Our goal is to study the adiabatic cooling, the electron heat flux dissipation, and the role of the IMF on the radial electron temperature of the solar wind; in addition, we aim to analyse the relevance of the electron heat flux as a radial power law through the solution of the electron energy equation. We also revisit results obtained with the SH law as a closure of the electron energy equation, as they display some discrepancies, and address the validity of the SH law at large radial distance from the Sun. In Paper I, we consider a radial IMF case, given its relevance to theoretical studies and numerical simulations. Paper II is devoted to the spiral IMF case (Parker 1958).
In Sect. 2 of this paper, a phenomenological model of the solar wind electron energy equation, within an electron heat flux as a radial power law is set up and its solution is analyzed for a constant or smooth increase of the solar wind speed. In Sect. 3, we provide an expression of the electron temperature in an electron solar wind model with the SH law as a closure to the energy equation; we also address the conditions for the validity of the SH law in a range of large radial distances. In Sect. 4, we apply the electron temperature law derived in Sect. 2 to the study of the electron temperature obtained in numerical simulations by Landi et al. (2012). In Sect. 5, the results are discussed and concluded.
2. Phenomenological electron energy equation model
We consider a solar wind composed of electrons and protons with isotropic temperatures, Te and Tp. Neutrality and zero electrical current are assumed through the equality of the density, n, of the two components and the equality of their flow speed, V. Spherical expansion implies a flow tube cross-section, S = r2, with the radial distance, r, from the Sun. The time stationary equation describing the radial evolution of the electron temperature in a radial IMF is:
In this equation, me and mp are the electron and the proton mass, respectively, and νep is the electron-proton collisional frequency.
We limit the analysis of Eq. (1) to large distances from the Sun, where the solar wind speed V is constant. We do develop further (in a subsection of this paper), the case of non-constant speed V with r V−1∂V/∂r = δ, where “δ” is positive and small to fit the solar wind speed profile. Indeed, Yeh (1971) noted that this latter condition does not affect the solution of Eq. (1) with a constant speed in a qualitative way. At such distances, typically r ≥ r0 ≊ 0.1 AU, the thermal energy exchange between the electrons and the protons is very small, owing to the small electron-to-proton mass ratio and to the small electron-proton energy exchange rate. Hartle & Sturrock (1968) showed, based on a two fluid model of the solar wind, that the electron and the proton temperatures are decoupled. Therefore, the collisional right hand side is ignored in Eq. (1). We assume that the electron heat flux intensity is a radial power law, qe(r) = q0 (r/r0)α, with q0 = qe(r0) > 0 and that α, the power law index, is constant. From the above definitions and assumptions and the consequence of a spherical expansion with n V = n0 V0(r/r0)−2, n0 = n(r0) and V0 = V(r0), Eq. (1) becomes:
Equation (2) is a first-order linear, non-homogeneous, differential equation, where the electron temperature is coupled to the heat flux through the third term in the left-hand side. With C as a constant of integration, defined at some original distance, r0, the electron temperature is:
where
The special case with α = −2 leads to Ir(−2, r) = 0, and corresponds to the conservation of the electron heat flux in a spherical expansion with a radial IMF. Therefore, the electron temperature evolution in Eq. (3) is not coupled to the electron heat flux dissipation, and the electron temperature is the adiabatic law. In the following, we consider α ≠ −2. As long as the constant of integration is not equal to zero, the electron temperature in Eq. (3) exhibits two contributions: The first contribution is the intrinsic adiabatic cooling and the second is due to the dissipation of the electron heat flux. From Eq. (4), we have two distinct cases, with α ≠ −10/3 and α = −10/3, for analysis.
2.1. Case with α ≠ −10/3
Following straightforward algebra, the constant of integration in Eq. (3), evaluated at some distance r0 is:
The constant C in Eq. (5) is a function of the electron temperature, the distance, r0, the power law index α, the flow speed, V0, the electron heat flux, q0, and the electron density, n0, at r0. It may be equal to zero or positive or negative.
2.1.1. Case C = 0
As the electron heat flux q0 is positive, we deduce a necessary condition on the power law index α, for C = 0, it is: −10/3 < α < −2. Then the adiabatic contribution to the electron temperature in Eq. (3) disappears and the electron temperature is entirely governed by the dissipation of the electron heat flux. We define this situation as an heat dissipation dominated (HDD) expansion of the electrons. The electron temperature is expressed as a simple radial power law as:
With the constant of integration C = 0 we obtain, from Eq. (5), a specific expression of the electron heat flux at r0, in term of a fraction of the electron thermal energy convected at the solar wind speed, as:
It is straightforward to show that as Eq. (7) is verified at r0, its generalization to any radial distance r is also verified.
We note that the expression in Eq. (7) increases to infinity as α converges to −2, while the intensity of the electron heat flux, q0, is always limited to the free streaming electron heat flux calculated at r0, 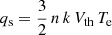 , where Vth is the electron thermal speed (Hundhausen 1972). Then, for C = 0, which corresponds to a HDD expansion of the electrons, we get a second condition on the power law index α ≤ α1 = −2 (5V0 + 3Vth)/3 (V0 + Vth), with Vth calculated at r0; for example, with a solar wind flow speed of 550 km s−1 and an electron temperature of 3 × 105 K in r0, we get α ≤ −2.2.
, where Vth is the electron thermal speed (Hundhausen 1972). Then, for C = 0, which corresponds to a HDD expansion of the electrons, we get a second condition on the power law index α ≤ α1 = −2 (5V0 + 3Vth)/3 (V0 + Vth), with Vth calculated at r0; for example, with a solar wind flow speed of 550 km s−1 and an electron temperature of 3 × 105 K in r0, we get α ≤ −2.2.
2.1.2. Case C ≠ 0
As C ≠ 0, Eq. (7) is not verified, and it is pertinent to define a critical electron heat flux as:
We first consider the case of C < 0. The constant of integration in Eq. (5) can be negative under two simultaneous conditions: the first implies the power law index −10/3 < α < −2 and the second, obtained by introducing the critical electron heat flux into the constant C to obtain 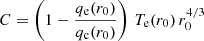 , is qe(r0) > qc(r0); this second condition restrains the range of power law index to −10/3 < α < α1. The expression of the electron temperature is then:
, is qe(r0) > qc(r0); this second condition restrains the range of power law index to −10/3 < α < α1. The expression of the electron temperature is then:
Therefore, the electron temperature contains two contributions: a negative one, decreasing as an adiabatic law with the exponent −4/3, and a second contribution induced by the dissipation of the electron heat flux. At large radial distances, the second contribution in Eq. (9) is dominant. For α → −10/3, the critical electron heat flux decreases to zero, then the addition in Eq. (9) of the two contributions due to the electron heat flux decreases to zero and the electron temperature reaches the adiabatic law.
When the constant of integration C is positive (C > 0), the electron temperature has the same expression as in Eq. (9). The constant C is obviously positive if the second contribution in Eq. (5) is positive, that is, whether α > −2 or α < −10/3. For these two values of α, the critical electron heat flux is negative. For α > −2 the electron temperature (in Eq. (9)) decreases to negative values as r increases: this range of power law indices must be rejected as unphysical; for α < −10/3, the first contribution in Eq. (9) is dominant at any radial distances, the second contribution being negative. The constant C is also positive if the second contribution in Eq. (5) is negative, which implies −10/3 < α < −2, with also qe(r0) < qc(r0). At large radial distance, the electron temperature is provided by the second contribution in Eq. (9).
As noted above, the critical electron heat flux, in Eq. (8), is strongly dependent on the power law index α. For α → −2, the critical electron heat flux increases to infinity and becomes much higher than any realistic electron heat flux that is limited by the free streaming electron heat flux. In such a limit, with α → −2, the contribution of the dissipated electron heat flux to the electron temperature, in Eq. (9), decreases to zero and we obtain the usual adiabatic law of the electron temperature.
The generic expression of the electron temperature in Eq. (9) is valid for any values of C equal to zero, negative or positive; for C = 0, we have qc(r) = qe(r0). Figure 1 shows the evolution of the electron temperature from 0.1 AU to 20 AU for an electron heat flux power law index α = −2.5 and three different values of the electron heat flux at 0.1 AU. With an electron temperature of 5 × 105 K at r0 = 0.1 AU, a solar wind speed of 550 km s−1, the critical electron heat flux is 0.24 qs, where qs is the free streaming heat flux. The solid curve in Fig. 1 shows the electron temperature for an electron heat flux equal to the critical heat flux. Therefore, the electron temperature is given by Eq. (6) or by Eq. (9) and represents the electron temperature driven only by the dissipation of the heat flux in an HDD expansion of the electrons. The dotted curve in Fig. 1, obtained from Eq. (9), shows the electron temperature obtained with a heat flux equal to half the critical heat flux at 0.1 AU; we note the concave shape of the curve up to around 1 AU, due to the adiabatic cooling, while at larger distance the temperature is driven mainly by the dissipation of the heat flux. The dashed curve in Fig. 1 shows the electron temperature obtained with an electron heat flux equal to twice the critical heat flux at 0.1 AU. This curve is convex due to the balance between the adiabatic cooling and the effect of the dissipation of the large electron heat flux, such that the electron temperature increases from 0.1 AU up to around 0.15 AU. At large distance, the three curves are nearly parallel: they represent the common effect of the electron heat flux dissipation on the electron temperature, with a radial power law of ∝r−0.5.
 |
Fig. 1. Evolution of the electron temperature given by Eq. (9) from 0.1 AU to 20 AU for α = −2.5, with three different values of the electron heat flux ratio qe(r0)/qc(r0): equal to 1 (solid line), 0.5 (dotted line), and 2 (dashed line), at r0 = 0.1 AU. |
2.2. Case with α = −10/3
For α = −10/3, the expression in Eq. (4) is Ir(−10/3, r) = − 4log(r)/3; then the constant of integration defined from Eq. (3) at some origin, r0, is:
The constant C can be equal to zero, negative or positive. For C = 0, we define a HDD expansion, where the electron temperature is:
In this HDD expansion, with C = 0, we obtain from Eq. (10) an expression of the electron heat flux at r0, qe(r0), in terms of the electron thermal energy convected at the solar wind speed. For C ≠ 0, as with the case α ≠ −10/3, we define a critical electron heat flux as:
We note that in Eq. (12), the fraction of thermal energy is a function of the radial distance contrary to the case with α ≠ −10/3. The electron temperature for α = −10/3, with the constant C negative or positive, is directly obtained as:
This expression of the electron temperature is also valid for C = 0, because then qe(r0) = qc(r0) and Eq. (13) is reduced to Eq. (11).
2.3. Case of a smooth increase of the solar wind speed
The solution of the empirical electron energy equation, with the assumption of a constant solar wind speed, is directly extended to the range of radial distances of increasing speeds, such that r V−1 ∂V/∂r = δ, where “δ” is a small positive constant to fit the solar wind speed profile. For example, for a solar wind of 320 km s−1 at 0.3 AU and 380 km s−1 at 1 AU, we get δ = 0.14 (Maksimovic et al. 2020); with a solar wind speed increasing from 600 km s−1 in 0.1 AU up to 700 km s−1 in 1 AU, we get δ = 0.07.
With an increasing solar wind speed, V(r) = V(r0) (r/r0)δ, the coefficient 4/3 in the second term of Eq. (2) is replaced by (4 + 2δ)/3. The solution of the new energy equation is qualitatively the same as the solution in Sects. 2.1 and 2.2. We define new critical electron heat fluxes, new HHD expansion models, new generic temperature profiles respectively for α ≠ −(10 + 2δ)/3, and for α = −(10 + 2δ)/3. The electron temperature expression established for α ≠ −(10 + 2δ)/3 is similar to Eq. (9), with the adiabatic power coefficient −4/3 replaced by −(4 + 2δ)/3, while interestingly the power coefficient due to the dissipation of the electron heat flux, α + 2, remains the same. The temperature law established for α = −(10 + 2δ)/3 is similar to Eq. (13), with the power coefficient −4/3 replaced by −(4 + 2δ)/3. In conclusion, the electron temperature profile is insignificantly different than the one with the speed V(r0) as δ ≪ 1.
3. The SH thermal conduction law and the solar wind
Let us consider the electron energy equation in a spherical expansion with a constant flow speed, a radial IMF, no thermal energy exchange between the electrons and the protons, and with the electron heat flux provided by the SH law 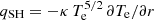 , where κ is constant. Within these assumptions and introducing the electron particle flux F = n V0 r2 into Eq. (1), we get an equation similar to Eq. (2), that is:
, where κ is constant. Within these assumptions and introducing the electron particle flux F = n V0 r2 into Eq. (1), we get an equation similar to Eq. (2), that is:
We consider what the expression is for the electron temperature decreasing to zero at large radial distance in a radial IMF and a constant solar wind speed. Yeh (1971) verified that 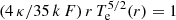 , where k is the Boltzmann constant and 4 π F is the total electron flux, is an exact solution of the electron energy equation.
, where k is the Boltzmann constant and 4 π F is the total electron flux, is an exact solution of the electron energy equation.
This “isolated solution” of the electron temperature is a simple radial power law, Te ∝ r−2/5, which does not contain an adiabatic contribution. With this expression of the electron temperature, the SH law becomes a radial power law with a constant index, α ≠ −10/3, which leads to an HDD expansion, characterized by a simple radial power law of the temperature, namely, the “isolated solution”. As shown in Sect. 2.1, there must be a critical electron heat flux such that qSH(r) = a n(r) k V0 Te(r), where “a” is constant. The solution of the homogeneous electron energy equation, with the convective form of the electron heat flux, is the electron temperature Te(r) = Te(r0)(r/r0)−4/(3 + 2 a) with a given electron temperature Te(r0) at r0. From the two expressions of the electron heat flux, the SH law, and the convective form, with this electron temperature, we obtain a condition for the two expressions of the heat flux to be equal: a = 3.5 with 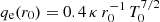 . Then Te(r) = Te(r0) (r/r0)−0.4 and qe(r) = qe(r0) (r/r0)−2.4.
. Then Te(r) = Te(r0) (r/r0)−0.4 and qe(r) = qe(r0) (r/r0)−2.4.
The solution of the electron energy equation with the SH law as a closure can be extended to the range of radial distances, such that V−1 ∂V/∂r = δ where “δ” is a positive constant. Indeed, the coefficient 4/3 in the second term of Eq. (14) is replaced by (4 + 2δ)/3 and we can verify that 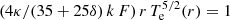 is a solution of the new equation derived from Eq. (14). Therefore, all the above developments are applicable, and the electron temperature is Te(r) = Te(r0) (r/r0)−0.4 in the range of radial distances, such that V(r) = V(r0) (r/r0)δ.
is a solution of the new equation derived from Eq. (14). Therefore, all the above developments are applicable, and the electron temperature is Te(r) = Te(r0) (r/r0)−0.4 in the range of radial distances, such that V(r) = V(r0) (r/r0)δ.
We go on to address the conditions for the SH law to be verified along large radial distance from the Sun. We need to have 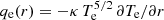 , whatever the distance r is, with qe(r) as the measured electron heat flux and Te(r) as the measured electron temperature. With the assumption that the electron heat flux is a radial power law with qe(r)∝rα, with α being a constant, the above condition provides a constraint on the electron temperature: it must also be a radial power law with a constant index, Te(r)∝rβ with α = 7β/2 − 1; moreover, at some distance, r0, we must have the equality of the above two expressions. Assuming that the electron temperature is driven by the energy equation within the power law electron heat flux, we obtain the result that the electron temperature must be driven by an HDD expansion, with β = α + 2. Then we directly get two more conditions: α = −2.4 and β = −0.4. We note that the solution of the electron energy equation, within the SH law as a closure, provides the same criteria for the SH law to be valid in a range of large radial distance from the Sun; these are qe ∝ r−2.4 and Te ∝ r−2/5, as long as the electron heat flux is equal to the one predicted by the SH law at some radial distance,
, whatever the distance r is, with qe(r) as the measured electron heat flux and Te(r) as the measured electron temperature. With the assumption that the electron heat flux is a radial power law with qe(r)∝rα, with α being a constant, the above condition provides a constraint on the electron temperature: it must also be a radial power law with a constant index, Te(r)∝rβ with α = 7β/2 − 1; moreover, at some distance, r0, we must have the equality of the above two expressions. Assuming that the electron temperature is driven by the energy equation within the power law electron heat flux, we obtain the result that the electron temperature must be driven by an HDD expansion, with β = α + 2. Then we directly get two more conditions: α = −2.4 and β = −0.4. We note that the solution of the electron energy equation, within the SH law as a closure, provides the same criteria for the SH law to be valid in a range of large radial distance from the Sun; these are qe ∝ r−2.4 and Te ∝ r−2/5, as long as the electron heat flux is equal to the one predicted by the SH law at some radial distance, 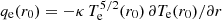 .
.
4. Analysis of numerical simulations
Now we apply the generic temperature law of Eq. (9) to the kinetic numerical simulations of Landi et al. (2012). This work concentrates on the electron heat flux and temperature properties in a slow and fast solar wind expansion in a radial IMF, for the radial distances of 0.3 to 6 AU. At 0.3 AU, where the EDF is isotropic and Maxwellian. From this original state, the EDF builds up, in the expansion, a core-strahl structure typical of solar wind observations (i.e., Salem et al. 2023), carrying a heat flux. The velocity moments of the EDF are calculated every 0.15 AU from 0.375 to 6.075 AU. The electron temperatures, in Fig. 7 of Landi et al. (2012), refer to fast solar winds with different densities at the origin. They all show a concave shape with an important decrease up to around 1.5 AU, then flatten further. The electron heat fluxes in Fig. 11 of Landi et al. (2012), typical of slow and fast wind, display also a concave shape. Landi et al. (2012) found that in all their simulations, the heat flux decreases approximately as a radial power law, with a power law index in the range −2.3 to −2.5. We obtained the plasma parameters of the original simulation by Landi et al. (2012) for a fast solar wind of 700 km s−1, in the range of 0.375−6.075 AU: The electron density, the electron temperature, the electron heat flux, with an electron density of 23 cm−3 at the origin 0.3 AU. The curve joining the diamonds in Fig. 2 represents the electron heat flux obtained in these simulations; the concave shape in a log-log representation indicates that the heat flux is not a pure radial power law. The solid line in Fig. 2 is a model of the electron heat flux as a radial power law obtained through a linear regression process; we obtained a power law index of α = −2.33.
 |
Fig. 2. Simulated electron heat flux from 0.375 AU to 6.075 AU (Landi et al. 2012), shown as the line joining the diamonds. Solid line represents a linear regression through the simulated data. |
With the power law index of α = −2.33, we calculate the critical electron heat flux at the origin r0 = 0.375 AU from Eq. (8) and find qc(0.375) = 7.6 × 10−5 W m−2 s−1. The ratio of the electron heat flux to the critical heat flux at r0 = 0.375 AU is 0.24. Therefore, the electron temperature law as given from Eq. (9) is:
Figure 3 shows the electron temperature from 0.375 to 6.075 AU, obtained from Eq. (15) in solid line and in dashed line the electron temperature issued from the numerical simulations. The solid curve in Fig. 3 shows an important decrease up to around 1.5 AU, then it flattens further. This important decrease, at short radial distances, is the effect of the adiabatic cooling identified in the first contribution in Eq. (15); the second contribution in Eq. (15) is provided by the dissipation of the electron heat flux. The solid curve in Fig. 3 is very close to the dashed curve, indicating that the predicted temperature law in Eq. (15) matches the numerical simulations very well. From the electron temperature expression in Eq. (15), showing an important adiabatic contribution, we can conclude that the SH law is not verified in these numerical simulations.
 |
Fig. 3. Predicted electron temperature from Eq. (15) in the range of 0.375−6.075 AU, shown as a solid line. Dashed line represents the simulated electron temperature. |
5. Discussion and conclusions
The assumption that the electron heat flux follows a radial power law, with a constant power law index α, sheds new light on the nature of the solar wind electron energy equation solution, with a radial IMF. We also provide a solution of the solar wind electron energy equation within the Spitzer & Härm (1953; SH) law and for a radial IMF. The properties of these two models established for a constant solar wind speed are extended directly to a smoothly increasing solar wind flow speed. We discuss the conditions for the validity of the SH law along large radial distance from the Sun in a radial IMF. The application of the phenomenological model to published numerical simulations is commented.
A key result in Sect. 2 is the definition of a critical electron heat flux as a portion of the electron thermal energy convected at the solar wind flow speed. Indeed, comparing the actual electron heat flux intensity to the critical heat flux at some original distance, r0, we can quantitatively evaluate the contributions of the adiabatic cooling and of the heat flux dissipation to the electron temperature radial evolution. If the actual electron heat flux intensity is equal to the critical heat flux, there is no adiabatic cooling contribution to the electron temperature; then, the electron temperature is completely driven by the dissipation of the electron heat flux. We define this situation as an HDD expansion of the electrons. In order to define an HDD expansion, the power law index α of the electron heat flux must be in the range of: −10/3 ≤ α < −2. There is also another constraint on α, as the critical electron heat flux increases to infinity as α converges to −2. This constraint is related to the electron thermal velocity and the solar wind speed, such that α ≤ α1, where α1 is derived from the equality of the critical heat flux to the free streaming heat flux at some origin, r0. In an HDD expansion, the electron temperature is Te(r) = Te(r0) (r/r0)α + 2 with α ≠ −10/3 and Te(r) = (log(r0))−1 Te(r0) (r/r0)−4/3 log(r), with α = −10/3.
For an electron heat flux intensity not equal to the critical heat flux at some original distance, the electron temperature evolution is the result of an adiabatic cooling and of the dissipation of the heat flux. Then, the electron temperature follows the generic laws in Eq. (9) with α ≠ −10/3 and in Eq. (13) with α = −10/3, where the adiabatic cooling and the heat flux dissipation contributions are directly evaluated all along the expansion. Our study also shows that the range of power law indices of the electron heat flux is limited to α ≤ −2. Indeed, for α > −2, the electron temperature decreases to negative values as the radial distance increases. For α → −2, and for α → −10/3, the electron temperature follows the adiabatic law.
The expression of the critical electron heat flux as a convective heat flux is of the same nature as the one proposed, phenomenologically, by Hollweg (1974) and discussed by Landi & Pantellini (2003) and by Landi et al. (2012, 2014). The theoretical derivation of the solar wind electron heat flux, as a fraction “a” of the thermal energy, ankVTe, convected at the solar wind flow speed is still an open question. In the lower corona, Smith et al. (2012) find that the fraction “a” is clearly a function of the radial distance. Landi et al. (2012, 2014), with a constant solar wind speed, find that the fraction “a” is also a function of the radial distance, which decreases near the lower boundary of the simulations, r0 = 0.3 AU, and then increases smoothly further. We believe that this decrease could be related to the choice of the EDF being Maxwellian at the lower boundary of the simulations. In our study, for α ≠ −10/3, the fraction a = −(3α + 10)/2(α + 2) in the critical electron heat flux is constant, but for α = −10/3, the fraction a = 9 (8log(r))−1 is a function of the radial distance. The electron energy equation with a convective model of heat flux and a constant fraction “a” is homogeneous and provides obviously an HDD expansion, the solution of which is ∝r−4/(3 + 2 a). For the particular case with α = −10/3, the specific convective model of electron heat flux in Eq. (12), with the non-constant fraction “a” of the thermal energy, provides also an HDD expansion of the electrons; this temperature is given in Eq. (11).
In Sect. 3, we show that the electron energy equation, within the SH heat conduction law, a constant solar wind speed or a smooth increase solar wind speed and a radial IMF, is an HDD expansion model. We show that the electron temperature is Te(r) = Te(r0) (r/r0)−0.4 and that the electron heat flux, while expressed through the SH heat conduction law, verifies the radial power law qe(r) = qe(r0) (r/r0)−2.4. As long as the electron temperature at the original distance r0 is given, the electron heat flux at r0 is defined as 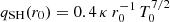 . The equality of the Spitzer & Härm (1953) electron heat flux and the critical electron heat flux at r0 implies a restriction on the product of the electron density and the flow speed, n(r0) V0 = qSH(r0)/(3.5 k Te(r0)). Therefore, a range of densities at r0 is allowed, setting a constraint on the flow speed V0; we note that the higher the density, the lower the flow speed. The ∝r−0.4 power law recently derived by Boldyrev et al. (2020) is the temperature of the electrons of the core distribution, while the same law in Sect. 3 is obtained for the whole electron population subjected to the SH law heat conduction.
. The equality of the Spitzer & Härm (1953) electron heat flux and the critical electron heat flux at r0 implies a restriction on the product of the electron density and the flow speed, n(r0) V0 = qSH(r0)/(3.5 k Te(r0)). Therefore, a range of densities at r0 is allowed, setting a constraint on the flow speed V0; we note that the higher the density, the lower the flow speed. The ∝r−0.4 power law recently derived by Boldyrev et al. (2020) is the temperature of the electrons of the core distribution, while the same law in Sect. 3 is obtained for the whole electron population subjected to the SH law heat conduction.
The solution of the electron temperature obtained by Hartle & Sturrock (1968) as ∝r−2/7 has to be considered in the limit of r → ∞, as stressed by Hundhausen (1972). Indeed, implementing the electron temperature as ∝r−2/7 in the SH law, we would obtain a conservative electron heat flux, which provides (from Eq. (14)) an electron temperature as Te(r) = T0 (r/r0)−4/3. This is obviously in contradiction to the assumption of Te ∝ r−2/7.
With similar assumptions for the study of the electron energy equation, we would directly obtain a solution for the energy equation of the one-fluid model, with a temperature of ∝r−0.4; this solution can be extended to a smoothly increasing flow speed as well. The temperature law in a one-fluid model, as ∝r−0.4, was obtained for the first time by Whang & Chang (1965), for radial distances larger than some 15 RS where the solar wind speed increases smoothly. Yeh (1971) solves the one-fluid model with a radial IMF, a constant velocity, through the splitting of the second-order differential equation in two simultaneous first-order differential equations. They find that in the limit of small radial distances, the temperature is ∝r−0.4, while in the limit of large radial distances (r → ∞), the temperature is ∝r−2/7.
We have established necessary conditions for the SH law to be verified in the solar wind in a radial IMF: the power law index of the electron heat flux must be α = −2.4, with the electron temperature as a solution of the energy equation in an HDD expansion and a power law index of β = −0.4, and the intensity of the electron heat flux at some distance has to be equal to the SH law. We note that these new requirements are straightforward: they provide two specific power laws for the electron temperature and electron heat flux as function of the radial distance. These offer a way to check the validity of the SH law at any radial distance by comparing observations to these power laws. Indeed, the validity of the SH law at one given distance, as that obtained in Wind data at 1 AU (Bale et al. 2013) and in numerical simulations (Landi et al. 2012), may be simply coincidental. Let us stress that the direct solution of the energy equation with the SH law as a closure provides the same electron temperature law as the one obtained from the general requirement for the validity of the SH law. The radial electron temperature law as ∝r−0.4 should be the reference for discussions of the validity of the SH law in the solar wind, in the case of a radial IMF.
The application of the generic electron temperature law obtained in Sect. 2 to the numerical simulation data from Landi et al. (2012) predicts very well the electron temperature at 6.075 AU from the original electron temperature at 0.375 AU. It also reproduces very well the decrease in the electron temperature, due to the adiabatic cooling, in the range of radial distances up to around 1.5 AU, while at further radial distances, the electron temperature is driven mainly by the dissipation of the electron heat flux. This numerical simulation does not correspond to an HDD expansion. We believe that the concave shape of the electron heat flux, obtained in all the simulations by Landi et al. (2012), is more likely related to the Maxwellian EDF at the origin r0 = 0.3 AU. Indeed, some collisions are needed, along a mean-free path, for the electron microscopic state to reach the typical core-strahl feature observed in the solar wind (Pilipp et al. 1987; Salem et al. 2023). Let us stress that while the electron heat flux is not a pure power law, its modeling as a power law with a constant power law index predicts a temperature law very close to the simulated data. This indicates that the proposed method for predicting the electron temperature from the electron heat flux as a power law, is robust; it is worth noting that it is simple as well.
In the work by Landi et al. (2012), the electron temperature evolution is interpreted with respect to the temperature law derived in the exospheric approach by Meyer-Vernet & Issautier (1998). This theory predicts that at large radial distances from the Sun, the electron temperature is controlled by an adiabatic cooling of the core population of the EDF and an isothermal contribution from the hot population of the EDF, with the same weight at 1 AU. However, in Fig. 8 of Landi et al. (2012), we cannot identify such a behaviour with regard to the temperature of the core and the hot electron populations. In fact, the exospheric approach can not be directly applied to these simulations as collisions are an important ingredient. We stress that in the exospheric model, the identification of a core population and an escaping population relies on the physics of the model, while in simulations or in observed solar wind data, the identification of these two populations relies sometimes on fitting processes with some ambiguities. Indeed, some electrons are part of both populations. In the present work, the electron population is considered as a whole, while the adiabatic cooling and the dissipation of the electron heat flux (in Eq. (15)) illustrate, at the level of the electron energetics, the “competition” between radial expansion and Coulomb collisions in shaping the electron velocity distribution, as described by Landi et al. (2012) in their paper. Our results show that the electron heat flux as a radial power law is the most pertinent in modeling observational solar wind data: it is simple to implement, with only two fitting parameters, flexible with a large range of possible power law indices, and neutral with respect whether the observed thermal flux is a conduction flux or a convective flux. The phenomenological model of the electron energy equation, with an electron heat flux as a radial power law is effective: It enables us to evaluate, directly and quantitatively, the contribution of the adiabatic cooling and of the heat flux dissipation to the evolution of the electron temperature in the solar wind expansion. In Paper II, we go on to analyse the electron temperature in a spiral IMF topology and apply our findings to the analysis of solar wind data collected by the Ulysses mission at high latitudes.
Acknowledgments
D. Hubert is grateful for the extended hospitality at the Department of Chemistry of British Columbia University. He thanks warmly Bernie Shizgal for his interest in this field and Catherine Lacombe for pertinent remarks. Particular thanks to Simone Landi who provided the numerical simulations data analyzed in this article. Work at UC Berkeley was supported by NASA grant NNX16AI59G and by NSF SHINE grants 1622498 and 2203319.
References
- Bale, S. D., Pulupa, M., Salem, C., Chen, C. H. K., & Quataert, E. 2013, ApJ, 769, L22 [Google Scholar]
- Boldyrev, S., Forest, C., & Egedal, J. 2020, Proc. Natl. Acad. Sci., 117, 9232 [Google Scholar]
- Cranmer, S. R., & Schiff, A. J. 2021, J. Geophys. Res.: Space Phys., 126, e29666 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
- Hartle, R. E., & Sturrock, P. A. 1968, ApJ, 151, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Hollweg, J. V. 1974, J. Geophys. Res.: Space Phys., 79, 3845 [NASA ADS] [CrossRef] [Google Scholar]
- Horaites, K., Boldyrev, S., Krasheninnikov, S. I., et al. 2015, Phys. Rev. Lett., 114, 245003 [NASA ADS] [CrossRef] [Google Scholar]
- Hundhausen, A. J. 1972, Coronal Expansion and Solar Wind (New-York: Springer-Verlag) [CrossRef] [Google Scholar]
- Issautier, K., Meyer-Vernet, N., Moncuquet, M., & Hoang, S. 1998, J. Geophys. Res.: Space Phys., 103, 1969 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, S., & Pantellini, F. 2003, A&A, 400, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landi, S., Matteini, L., & Pantellini, F. 2012, ApJ, 760, 143 [Google Scholar]
- Landi, S., Matteini, L., & Pantellini, F. 2014, ApJ, 790, L12 [Google Scholar]
- Le Chat, G., Issautier, K., Meyer-Vernet, N., & Hoang, S. 2011, Sol. Phys., 271, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Maksimovic, M., Bale, S. D., Berčič, L., et al. 2020, ApJS, 246, 62 [Google Scholar]
- Meyer-Vernet, N., & Issautier, K. 1998, J. Geophys. Res.: Space Phys., 103, 29705 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, E. L., & Leer, E. 1996, J. Geophys. Res.: Space Phys., 101, 15591 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Pilipp, W. G., Muehlhaeuser, K.-H., Miggenrieder, H., Montgomery, M. D., & Rosenbauer, H. 1987, J. Geophys. Res.: Space Phys., 92, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Pilipp, W. G., Muehlhaeuser, K.-H., Miggenrieder, H., Rosenbauer, H., & Schwenn, R. 1990, J. Geophys. Res.: Space Phys., 95, 6305 [NASA ADS] [CrossRef] [Google Scholar]
- Salem, C., Hubert, D., Lacombe, C., et al. 2003, ApJ, 585, 1147 [Google Scholar]
- Salem, C., Bale, S. D., & Maksimovic, M. 2007, ESA SP, 641, 9 [NASA ADS] [Google Scholar]
- Salem, C. S., Pulupa, M., Bale, S. D., & Verscharen, D. 2023, A&A, 675, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scime, E. E., Bame, S. J., Feldman, W. C., et al. 1994, J. Geophys. Res.: Space Phys., 99, 23 [NASA ADS] [Google Scholar]
- Scime, E. E., Badeau, A. E., Jr., & Littleton, J. E. 1999, Geophys. Res. Lett., 26, 2129 [NASA ADS] [CrossRef] [Google Scholar]
- Scudder, J. D. 2019, ApJ, 885, 138 [Google Scholar]
- Smith, H. M., Marsch, E., & Helander, P. 2012, ApJ, 753, 31 [Google Scholar]
- Spitzer, L., & Härm, R. 1953, Phys. Rev., 89, 977 [Google Scholar]
- Štverák, Š., Trávníček, P. M., & Hellinger, P. 2015, J. Geophys. Res.: Space Phys., 120, 8177 [NASA ADS] [CrossRef] [Google Scholar]
- Viall, N. M., & Borovsky, J. E. 2020, J. Geophys. Res.: Space Phys., 125, e26005 [NASA ADS] [CrossRef] [Google Scholar]
- Vocks, C., Salem, C., Lin, R. P., & Mann, G. 2005, ApJ, 627, 540 [Google Scholar]
- Whang, Y. C., & Chang, C. C. 1965, J. Geophys. Res., 70, 4175 [NASA ADS] [CrossRef] [Google Scholar]
- Yeh, T. 1971, J. Geophys. Res.: Space Phys., 76, 7508 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Evolution of the electron temperature given by Eq. (9) from 0.1 AU to 20 AU for α = −2.5, with three different values of the electron heat flux ratio qe(r0)/qc(r0): equal to 1 (solid line), 0.5 (dotted line), and 2 (dashed line), at r0 = 0.1 AU. |
| In the text | |
 |
Fig. 2. Simulated electron heat flux from 0.375 AU to 6.075 AU (Landi et al. 2012), shown as the line joining the diamonds. Solid line represents a linear regression through the simulated data. |
| In the text | |
 |
Fig. 3. Predicted electron temperature from Eq. (15) in the range of 0.375−6.075 AU, shown as a solid line. Dashed line represents the simulated electron temperature. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



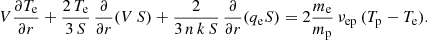
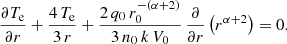
![$$ \begin{aligned} T_{\rm e}(r) = r^{-4/3} \left[C - \frac{2\,q_0\, r_0^{-\alpha -2}}{3\,n_0\,k\,V_0}\,I_r(\alpha ,r)\right], \end{aligned} $$](/articles/aa/full_html/2023/09/aa44128-22/aa44128-22-eq3.gif)
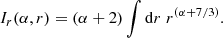
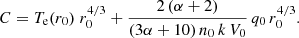
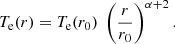
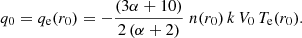
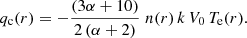
![$$ \begin{aligned} T_{\rm e}(r) = \left[1-\frac{q_{\rm e}(r_0)}{q_{\rm c}(r_0)}\right]T_{\rm e}(r_0)\left(\frac{r}{r_0}\right)^{-4/3}+\frac{q_{\rm e}(r_0)}{q_{\rm c}(r_0)}\,T_{\rm e}(r_0)\left(\frac{r}{r_0}\right)^{\alpha +2}. \end{aligned} $$](/articles/aa/full_html/2023/09/aa44128-22/aa44128-22-eq11.gif)
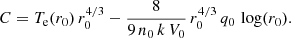
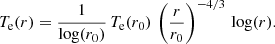
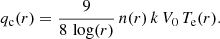
![$$ \begin{aligned} T_{\rm e}(r) = \left[1-\frac{q_{\rm e}(r_0)}{q_{\rm c}(r_0)}\right]T_{\rm e}(r_0)\left(\frac{r}{r_0}\right)^{-4/3} \\ + \frac{q_{\rm e}(r_0)}{q_{\rm c}(r_0)}\,T_{\rm e}(r_0)\left(\frac{r}{r_0}\right)^{-4/3}\frac{\log (r)}{\log (r_0)}\cdot \end{aligned} $$](/articles/aa/full_html/2023/09/aa44128-22/aa44128-22-eq15.gif)