| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A153 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201016358 | |
| Published online | 22 April 2011 | |
Horizontal flow fields observed in Hinode G-band images
I. Methods
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482
Potsdam, Germany
e-mail: mverma@aip.de; cdenker@aip.de
Received:
19
December
2010
Accepted:
10
March
2011
Context. The interaction of plasma motions and magnetic fields is an important mechanism, which drives the solar activity in all its facets. For example, photospheric flows are responsible for the advection of magnetic flux, the redistribution of flux during the decay of sunspots, and the build-up of magnetic shear in flaring active regions.
Aims. Systematic studies based on G-band data from the Japanese Hinode mission provide the means to gather statistical properties of horizontal flow fields. This facilitates comparative studies of solar features, e.g., G-band bright points, magnetic knots, pores, and sunspots at various stages of evolution and in distinct magnetic environments, which advances our understanding of the dynamic Sun.
Methods. We adapted local correlation tracking (LCT) to measure horizontal flow fields based on G-band images obtained with the Solar Optical Telescope on board Hinode. A total of about 200 time-series with a duration between 1–16 h and a cadence between 15–90 s were analyzed. Selecting a high-cadence (Δt = 15 s) as well as a long-duration (ΔT = 16 h) time-series enabled us to optimize and validate the LCT input parameters, which ensures a robust, reliable, uniform, and accurate processing of a huge data volume.
Results. The LCT algorithm produces best results for G-band images with a cadence of 60–90 s. If the cadence is lower, the velocity of slowly moving features will not be reliably detected. If the cadence is higher, the scene on the Sun will have evolved too much to bear any resemblance with the earlier situation. Consequently, in both instances horizontal proper motions are underestimated. The most reliable and yet detailed flow maps are produced using a Gaussian kernel with a size of 2560 km × 2560 km and a full-width-at-half-maximum (FWHM) of 1200 km (corresponding to the size of a typical granule) as sampling window.
Conclusions. Horizontal flow maps and graphics for visualizing the properties of photospheric flow fields are typical examples for value-added data products, which can be extracted from solar databases. The results of this study will be made available within the “small projects” section of the German Astrophysical Virtual Observatory (GAVO).
Key words: Sun: photosphere / Sun: surface magnetism / sunspots / Sun: granulation / techniques: image processing / methods: data analysis
© ESO, 2011
1. Introduction
Data from space do not suffer the deleterious effects of Earth’s turbulent atmosphere, which blur and distort images so that features may fade into obscuration, which makes it difficult to follow them from image to image. The huge volume of the Hinode G-band images with good spatial resolution, cadence, and coverage provide time-series of consistent quality to quantify photospheric proper motions, which can be used in comparative studies.
Various techniques have been developed in the past decades to measure horizontal proper motions on the solar surface. Basically, they can be divided into two classes. The first class includes feature tracking (FT) methods, which follow the footprints of individual features in images of a time-series (see e.g. Strous 1995). Tracking facular points of opposite magnetic polarity in an emerging flux region effectively demonstrated the potential of the FT techniques (Strous et al. 1996). However, the steps of image processing (segmentation, labeling, and identification) rely on prior knowledge about the object under investigation. Therefore, FT methods seem to be better suited for case studies rather than bulk processing of huge data volumes, where the reduction of dimensionality is a desirable feature. The balltracking method developed by Potts et al. (2004) can also be subsumed under FT techniques, because artificial tracer particles are introduced to follow the footprints of local intensity minima. The balltracking method works well for granulation so that it is a good choice for the characterization of supergranulation (Potts & Diver 2008). Nevertheless, it might introduce a scale dependence when tracking on other (small-scale) features such as bright points, penumbral grains, and umbral dots.
 |
Fig. 1 Calibrated G-band images of active regions a) NOAA 10960 and b) NOAA 10930 observed on 2007 June 4 and 2006 December 7, respectively. The FOV is 111″ × 111″. The annotation of the axes refers to heliocentric coordinates given in seconds of arc. The region in the rectangular white box is used for further analysis, zooming in on a quiet Sun region that contains numerous G-band bright points that outline the supergranular boundaries. The images were normalized in a way that the mode of the quiet Sun intensity distribution corresponds to unity. |
The second class is based on local correlation tracking (LCT), where displacement vectors are derived by cross-correlating small regions in consecutive images of a time-series. The principles of LCT are laid out in the seminal work of November & Simon (1988). Leaving behind the underlying velocity assumption of LCT, Schuck (2006) developed a technique to track optical flows and named it the differential affine velocity estimators (DAVE). Chae & Sakurai (2008) presented a formulation of the non-linear case and called it accordingly the nonlinear affine velocity estimators (NAVE). These authors also provide a detailed parameter study of LCT, DAVE, and NAVE based on images reflecting analytical solutions of the continuity equation as well as on magnetogram data from Hinode and MHD simulations. Similarly, Welsch et al. (2007) compared these velocity inversion techniques based on MHD simulations, with the known velocity field.
Various other technical aspects have to be considered while implementing techniques for optical flow tracking. Because interpolations are required in the various data reduction steps, we refer to Potts et al. (2003), who describe the systematic errors that can be introduced by unsuitable interpolation schemes. More recently, Löfdahl (2010) discussed image-shift measurements in the context of solar wavefront sensors, which are also applicable to the LCT implementations.
Hinode G-band images offer an excellent opportunity for systematic statistical studies of flow fields because of their uniform quality in the absence of seeing distortions, thus allowing us to directly compare flow fields in different solar settings. In Sect. 2 we introduce the high-cadence and long-duration datasets that are used to find the optimal parameters for computing LCT maps based on time-series of Hinode G-band images. The implementation of the algorithm is described in Sect. 3. Section 4 presents the results of this parameter study and justifies our choice of LCT parameters, which will be used to create value-added data to complement the Hinode database. The most important parameters are summarized in Sect. 5, which also introduces some of the future uses of such a database.
2. Observations
Images obtained in the Fraunhofer G-band (bandhead of the CH molecule at λ430.5 nm) have high contrasts, and small-scale magnetic features can be easily identified with bright points (Berger et al. 1995). Despite the observational advantages of this “proxy-magnetometry” (Leenaarts et al. 2006), the theoretical description of the molecular line-formation process is far from easy (cf. Sánchez Almeida et al. 2001; Steiner et al. 2001; Schüssler et al. 2003). The LCT techniques, however, can take full advantage of the high contrast and the rich structural contents of G-band images. On Hinode (Kosugi et al. 2007) these observations are carried out by the broad-band filter imager (BFI) of the Solar Optical Telescope (SOT, Tsuneta et al. 2008).
Our initial selection criteria were that at least 100 G-band images had to be recorded on a given day, which should additionally have a cadence of better than 100 s. It turned out that these criteria restricted us to data with only half the spatial resolution (0.11″ pixel-1), where 2 × 2 pixels were binned into one. In total 48 datasets with 2048 × 1024 pixels and 153 datasets with 1024 × 1024 pixels were selected for further analysis. The time intervals covered by these datasets range from one to 16 h. The bulk statistical analysis will be presented in forthcoming publications. Here, we will discuss the LCT algorithm in detail and justify our choice of input parameters. For this purpose, we selected two datasets: one with a high cadence and another one with a long duration. In addition, we picked a dataset without binning to study the dependence of flow maps on the spatial resolution of the input data.
2.1. High-cadence sequence
The LCT depends on several input parameters such as the time interval between successive images and the sampling window’s size and form. We analyzed a one-hour time-series with a cadence of 15 s to validate the intrinsic accuracy of the LCT algorithm. The data were captured from 14:27–15:27 UT on 2007 June 4 (see Fig. 1a). The time-series contains 238 images with 1024 × 1024 pixels. The observations were centered on the active region NOAA 10960, which was located on the solar disk at heliocentric coordinates E630″ and S125″ (μ = 0.75). The active region was in the maximum growth phase and had a complex magnetic field configuration. NOAA 10960 was classified as a βγδ-region and was the source of many M-class flares, including a major M8.9 flare at 05:06 UT on 2007 June 4, which has been analyzed in a multi-wavelength study by Kumar et al. (2010).
2.2. Long-duration sequence
Solar features evolve on different time scales from about five minutes for granulation to several tens of hours for supergranulation. Obviously, the time over which individual LCT maps are averaged plays a decisive role in the interpretation of these average flow maps. Hence, we selected a time-series with 16 hours of continuous data captured on 2006 December 7 (see Fig. 1b). This long-duration sequence starts at 02:30 UT and ends at 18:30 UT. It includes 960 images with 1024 × 1024 pixels and has a cadence of 60 s. Owing to memory constrains imposed by the subsonic filtering we chose an area of 210 × 595 pixels centered on a region with granulation and G-band bright points (white box Fig. 1b). This region is to the west of the active region NOAA 10930, located at heliocentric coordinates E777″ and S88″ (μ = 0.59). The sunspot group was classified as a βγδ-region that exhibits a complex magnetic topology and produced numerous C-, M-, and X-class flares. This region has been extensively studied, especially around the time of an X3.4 flare on 2006 December 13 (e.g., Schrijver et al. 2008). The LCT techniques were used by Tan et al. (2009) to study horizontal proper motions associated with penumbral filaments in a rapidly rotating δ-spot.
2.3. High-spatial resolution sequence
Only a few datasets of G-band images exist with the full spatial resolution of 0.055″ pixel-1 and a cadence suitable for LCT. We selected a one-hour time-series, which was acquired starting at 04:00 UT on 2006 November 26. This high-spatial resolution sequence contains 118 images with 2048 × 2048 pixels and has a time cadence of about 30 s. The observations were centered on a quiet Sun region near the disk center at heliocentric coordinates E108″ and S125″ (μ = 0.99), which contains only a few G-band bright points and no major magnetic flux concentrations.
3. Implementation of the LCT algorithm
3.1. Preprocessing of the G-band images
The data analysis was carried out in the interactive data language (IDL)1. Datasets are split in 60-min sequences with 30 min overlap between consecutive sequences. In preparation for the LCT algorithm, basic data calibration was performed, which consists of subtraction of dark current , correction of gain, and removal of spikes caused by high-energy particles. Figure 1 contains sample G-band images for the high-cadence and the long-duration dataset after basic calibration. After initial data calibration, the geometric foreshortening corrected and the images were resampled in a regular grid with a spacing of 80 km × 80 km, i.e., the images appear as if observed at the center of the solar disk. Residual effects of projecting the surface of a sphere onto a plane are neglected, since the FOV of the G-band images is still relatively small. A grid size of 80 km was chosen so that the fine structure contents of the G-band images were not diminished. Pixels close to the solar limb were projected onto several pixels in planar coordinates. Thus, the accuracy of the flow maps at these locations is not as good as for locations close to disk center.
In a 60-min sequence are l = 0,1,2,..., L − 1 calibrated and deprojected images, where L is the total number of images in a particular sequence. For an image with N × M pixels the intensity distribution is represented by i(x,y) with x = x0,x1,...,xN−1 and y = y0,y1,...,yM − 1 as pixel coordinates. The indices are typically dropped to ease the notation. The data processing makes extensive use of the fast fourier transform (FFT). The FFT of the intensity distribution i(x,y) is simply denoted by ℱ(i(x,y)).
3.2. Aligning the images within a time-series
In principle, images could be aligned using the pointing information of the spacecraft. However, we calculate shifts between consecutive images il−1(x,y) and il(x,y) by computing the cross-correlation using only the central part of the images, which is half of the original image size. These shifts are then applied in succession to align all images with respect to the first image using cubic spline interpolation with subpixel accuracy. The signature of the 5-min oscillation is removed from the time-series by applying a 3D Fourier filter. This filter, sometimes called a subsonic filter, has a cut-off velocity of cs ≈ 8 km s-1 corresponding to the photospheric sound speed. Because the subsonic filter uses a 3D Fourier transform, some edge effects are sometimes noted for the first and last few images of a time-series. For this reason we decided to discard the images during the first and last two minutes of the time-series after applying the subsonic filter. Therefore, the final time-series is shortened by this amount of time (see Sect. 3.5).
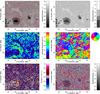 |
Fig. 2 a) The average (60-min) G-band image after correction of geometrical foreshortening corresponding to the G-band image shown in Fig. 1a. The red arrows indicate the magnitude and direction of the horizontal proper motions. Arrows with a length corresponding to the grid size indicate velocities of 1 km s-1. b) Adaptive and fixed intensity thresholds are used to identify conglomerates of G-band bright points, granulation, penumbrae, umbrae, and pores. Color codes are used to point out c) flow speed and d) direction in high-resolution flow maps. The flow direction is encoded according to the 12 colors of the compass rose. Sources and sinks in a flow field can be identified in e) a divergence map. The f) forward cork maps provides additional means of visualizing converging motions. Test particles are subsequently superimposed on an average G-band image after they have followed the flows for two (blue), four (orange), and eight (red) hours. The conspicuous network of corks is related to the spatial scales of the meso-and supergranulation. |
3.3. LCT algorithm
The LCT algorithm is based on ideas put forward by November & Simon (1988). The algorithm was adapted to subimages with sizes
of 32 × 32 pixels corresponding to 2560 km × 2560 km, so that structures with dimensions
smaller than a granule will contribute to the correlation signal. Because
cross-correlation techniques are sensitive to strong intensity gradients, a high-pass
filter was applied to the entire image, suppressing gradients related to structures larger
than granules. The high-pass filter is implemented as a Gaussian with a FWHM
of 15 pixels (1200 km). To indicate that we refer to an subimage with 32 ×
32 pixels and not the entire image, we use the notation
i(x′,y′). The Gaussian kernel used in
the high-pass filter then becomes 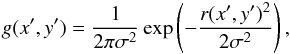 (1)where
(1)where 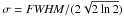 and
r(x′,y′) = (x′2 + y′2)1/2.
The high-pass filtered image can be expressed as
and
r(x′,y′) = (x′2 + y′2)1/2.
The high-pass filtered image can be expressed as
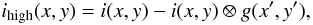 (2)where ⊗ denotes a convolution. The result
is an image rich in detail, where the low spatial frequencies have been removed.
(2)where ⊗ denotes a convolution. The result
is an image rich in detail, where the low spatial frequencies have been removed.
The core of the LCT algorithm is the cross-correlation
cl(x,y,x′,y′)
computed over a 32 × 32 pixel region centered on the coordinates (x,y)
for each pixel in image pairs
il − 1(x,y) and
il(x,y), which can be
written as ![\begin{eqnarray} c_l(x, y, x^\prime, y^\prime) & = & \Re\big\{ {\cal F}^{-1} \big[ {\cal F} \big( i_{l-1}(x, y, x^\prime, y^\prime) g(x^\prime, y^\prime) \big) \nonumber\\ & & \times {\cal F}^{\ast} \big( i_l(x, y, x^\prime, y^\prime) g(x^\prime, y^\prime) \big) \big] \big\} d(x^\prime, y^\prime), \end{eqnarray}](/articles/aa/full_html/2011/05/aa16358-10/aa16358-10-eq38.png) (3)where
g(x′,y′) denotes a weighting function
also serving as an apodising window. This function has the same form as the Gaussian
kernel previously used in the high-pass filter. This ensures that the displacement vectors
are computed without preference in azimuthal direction. We also multiplied the
cross-correlation functions by a mask
d(x′,y′) so that the maximum of the
cross-correlation function is forced to be within a distance of
cs, lim = 12 pixels from its center. The typical time
interval between consecutive images is in the range from 60–90 s, i.e., a feature moving
at the photospheric sound speed of cs ≈ 8 km s-1
would travel 480–720 km, corresponding to 6–9 pixels. This justifies our choice of
cs, lim, which also takes into account some numerical
errors. The position of the maximum of the cross-correlation function is calculated with
subpixel accuracy by a parabolafit to the neighboring pixels. The numerical accuracy of
the parabola fit is about one fifth of a pixel or 16 km on the solar surface, which
corresponds to about 200 m s-1 for proper motions measured from a single pair
of G-band images. Therefore, many flow maps had to be averaged to determine reliable
horizontal proper motions.
(3)where
g(x′,y′) denotes a weighting function
also serving as an apodising window. This function has the same form as the Gaussian
kernel previously used in the high-pass filter. This ensures that the displacement vectors
are computed without preference in azimuthal direction. We also multiplied the
cross-correlation functions by a mask
d(x′,y′) so that the maximum of the
cross-correlation function is forced to be within a distance of
cs, lim = 12 pixels from its center. The typical time
interval between consecutive images is in the range from 60–90 s, i.e., a feature moving
at the photospheric sound speed of cs ≈ 8 km s-1
would travel 480–720 km, corresponding to 6–9 pixels. This justifies our choice of
cs, lim, which also takes into account some numerical
errors. The position of the maximum of the cross-correlation function is calculated with
subpixel accuracy by a parabolafit to the neighboring pixels. The numerical accuracy of
the parabola fit is about one fifth of a pixel or 16 km on the solar surface, which
corresponds to about 200 m s-1 for proper motions measured from a single pair
of G-band images. Therefore, many flow maps had to be averaged to determine reliable
horizontal proper motions.
3.4. LCT data products
Once the individual flow maps were calculated they were saved in binary format. In addition, average maps of horizontal speed and flow direction as well as the x- and y-components of the horizontal flow velocity (vx,vy) were stored in native IDL format. Some auxiliary variables were saved as well so that they can be used, e.g., in annotating plots depicting the flow fields. A sample of these plots for a 60-min average flow field is shown in Fig. 2. In Fig. 2a horizontal proper motions are plotted as red arrows with a 60-min averaged G-band image as a background. The moat flow starting at the sunspot penumbra and terminating at the surrounding G-band network is clearly discernible.
In Fig. 2b we used an adaptive thresholding
algorithm to discern between granulation, G-band bright points, and strong magnetic
features. Indiscriminately, we used a fixed intensity threshold of
Imag = 0.8 for strong magnetic features and an adaptive
threshold for G-band bright points, which can be given as 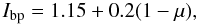 (4)where
μ = cos(θ) is the cosine of the heliocentric angle
θ. The darkest parts of sunspots (umbrae) and pores can be identified
using another fixed threshold of Idark = 0.6, while sunspot
penumbrae cover intermediate intensities from Idark to
Imag, allotting the range Imag
to Ibp to granulation. The adaptive threshold was necessary,
as a first order approximation, to account for the center-to-limb variation (CLV) of the
G-band bright points, which exhibit much higher contrasts near the solar limb. This
adaptive thresholding algorithm allows us to study the properties of horizontal proper
motions for different solar features.
(4)where
μ = cos(θ) is the cosine of the heliocentric angle
θ. The darkest parts of sunspots (umbrae) and pores can be identified
using another fixed threshold of Idark = 0.6, while sunspot
penumbrae cover intermediate intensities from Idark to
Imag, allotting the range Imag
to Ibp to granulation. The adaptive threshold was necessary,
as a first order approximation, to account for the center-to-limb variation (CLV) of the
G-band bright points, which exhibit much higher contrasts near the solar limb. This
adaptive thresholding algorithm allows us to study the properties of horizontal proper
motions for different solar features.
Apart from the conventional way of displaying velocity vectors as arrows we present two-dimensional high-resolution speed (Fig. 2c) and azimuth (Fig. 2d) maps. In these maps, the physical quantities are computed for each individual pixel so that the fine structure of the flow field becomes accessible. The color scale for the speed values is the same for all plots in this study. Indeed, we used the same color scale for all flow maps in the database so that flows for different scenes on the Sun can be directly compared. In the azimuth map the direction is encoded in a 12-color compass-rose, which can be found to the very right of this panel. In principle more colors could be used to illustrate the flow direction. However, such plots would become very crowded and are very hard to interpret. The essential features of the flow field, i.e., inward motion of the penumbral grains in the inner penumbra and outward motions related to Evershed and moat flows, can easily be identified.
Divergence (Fig. 2e) and vorticity maps were also compiled for each time-series. The maximum values for divergence (1.5 × 10-3 s-1) and vorticity (0.6 × 10-3 s-1) in these maps are an order of magnitude higher than values found for quiet Sun granulation in previous studies. However, higher values are not surprising, because we calculated them for each pixel in the high-resolution maps capturing more of the small-scale motions. Reassuringly, our values of the 10th percentile for divergence (4.3 × 10-4 s-1) and vorticity (1.9 × 10-4 s-1) are essentially the same as reported by Simon et al. (1994). On the other hand, in the present study the divergence is four times and the vorticity is two times higher than the values presented by Strous et al. (1996) but their values were computed in the proximity of an emerging active region. In summary and keeping in mind the different LCT parameters used in the different studies, the statistical properties of the flow fields as presented in this study agree with previous investigations.
In order to visualize the temporal evolution of the horizontal proper motions, we computed forward (Fig. 2f) and inverse cork maps. Evenly spread test particles are allowed to float forward in time with a given horizontal speed for a certain time interval (see Molowny-Horas 1994). In the inverse cork map the particles float backward in time. This is accomplished by simply reversing the sign of the velocity components. The forward cork map is used to visualize regions of converging flows, and the inverse map is a good tool to study divergence regions. We tracked test particles for consecutively two, four, and eight hours. These particles were initially distributed on an equidistantly spaced grid with a spacing of 10 pixels, i.e., one particle was placed every 0.8 Mm. The most conspicuous feature of the forward cork map are the tracer particles that outline the network of G-band bright points, which corresponds to the supergranular boundaries.
We prepared overview web pages for the respective dates when suitable time-series of G-band images were available, which contain all six plots of Fig. 2 along with vorticity and inverse cork maps. The results of this study will ultimately be published as a small GAVO2 project as a value-added product of the Hinode database.
3.5. Timing issues related to the image capture
Local correlation tracking delivers localized displacements observed in image pairs.
These displacements in conjunction with the time that has elapsed between the acquisition
of both images yield localized velocity vectors. Therefore, accurate knowledge of the time
interval between consecutive images used in the LCT algorithm is essential. The time
interval Δt for the high-cadence image sequence observed on 2007 June 4
has a bimodal distribution with values Δt of 14.4 s (60.7%) and 16 s
(39.3%). The average value is 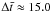 s.
The difference of 1.6 s is an artifact of the polarization modulation. The polarization
modulation unit (PMU) is located just behind the telescope exit slit within the optical
telescope assembly but in front of the tip-tilt mirror that is employed by the correlation
tracker (see Tsuneta et al. 2008). A common CCD
camera is assigned to both the broad- and narrowband filter imagers (BFI and NFI). The
critical timing between camera and PMU is handled by the focal plane package. The PMU is a
continuously rotating waveplate, which is always turned on – even for non-polarimetric
data such as G-band images. Its rotation period is T = 1.6 s and all
exposure timing is controlled with the clock of the PMU. This is the reason for the
non-uniformity in the observed time-interval Δt.
s.
The difference of 1.6 s is an artifact of the polarization modulation. The polarization
modulation unit (PMU) is located just behind the telescope exit slit within the optical
telescope assembly but in front of the tip-tilt mirror that is employed by the correlation
tracker (see Tsuneta et al. 2008). A common CCD
camera is assigned to both the broad- and narrowband filter imagers (BFI and NFI). The
critical timing between camera and PMU is handled by the focal plane package. The PMU is a
continuously rotating waveplate, which is always turned on – even for non-polarimetric
data such as G-band images. Its rotation period is T = 1.6 s and all
exposure timing is controlled with the clock of the PMU. This is the reason for the
non-uniformity in the observed time-interval Δt.
However, we do not find a bimodal pattern in the LCT displacements but only fluctuations
related to evolving features on the Sun and some residual numerical effects. Therefore, we
opted to use the fixed time interval 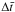 in the data analysis. Sometimes a “traffic jam” in the data transfer might result in even
larger timing errors. On the other hand, averaging individual LCT maps over an hour (or
longer) will only result in velocity errors of less than a tenth of a percent, i.e., the
speed measured by the LCT algorithm is not significantly affected. In summary, accurate
timing has to be ensured to obtain reliable LCT flow maps and all data were checked for
consistency between recorded time stamps and measured horizontal displacements. Because
the individual flow maps during the first and last two minutes of the one-hour sequences
do not reflect the true proper motions but are artifacts of the subsonic filtering, we
excluded them from the calculation of the average flow maps.
in the data analysis. Sometimes a “traffic jam” in the data transfer might result in even
larger timing errors. On the other hand, averaging individual LCT maps over an hour (or
longer) will only result in velocity errors of less than a tenth of a percent, i.e., the
speed measured by the LCT algorithm is not significantly affected. In summary, accurate
timing has to be ensured to obtain reliable LCT flow maps and all data were checked for
consistency between recorded time stamps and measured horizontal displacements. Because
the individual flow maps during the first and last two minutes of the one-hour sequences
do not reflect the true proper motions but are artifacts of the subsonic filtering, we
excluded them from the calculation of the average flow maps.
4. Results
4.1. Statistical properties of flow maps and time cadence selection
The one-hour time-series on 2007 June 4 contains 238 G-band images, i.e., the time cadence is ≈15 s. This higher temporal resolution allows us to study the intrinsic accuracy of the LCT algorithm. We calculated LCT maps using seven different time intervals Δt = 15, 30, 60, 90, 120, 240, and 480 s. Note that the time interval over which flow maps are averaged is reduced to ΔT = 3600 s − Δt, i.e., in case of the longest time cadence by as much as 8 min. However, these slightly different averaging times will not change the results discussed below. When using all individual LCT maps to compute the average horizontal proper motion, we refer to these data as the entire sequence. On the other hand, when we split the entire sequence into four disjunct sets, we refer to them as interleaved datasets, i.e., every fourth LCT map is employed to compute the average horizontal proper motion. Because these flow maps cover exactly the same period of time, differences can be directly attributed to the numerical accuracy of the LCT algorithm.
For the entire sequence and interleaved datasets we computed statistical parameters that describe the distribution of horizontal proper motions for granulation in the vicinity of active region NOAA 10960. We used the adaptive thresholding algorithm (Eq. (4)) to select only granulation excluding G-band bright points. The proper motions accordingly refer to plasma motions in the absence of any strong magnetic field concentrations. This selection facilitates comparing horizontal flow speeds and their distributions in all cases of the present work.
We calculated the mean 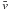 ,
median vmed, maximum vmax, and
10th percentile v10 of the horizontal flow speeds. Since the
maximum speed vmax is only based on a single value, it is
easily influenced by numerical errors and the data calibration. The 10th percentile
v10 is more robust because it describes a property of the
entire distribution, i.e., the high-velocity tail. Along with these quantities we also
calculated the variance
,
median vmed, maximum vmax, and
10th percentile v10 of the horizontal flow speeds. Since the
maximum speed vmax is only based on a single value, it is
easily influenced by numerical errors and the data calibration. The 10th percentile
v10 is more robust because it describes a property of the
entire distribution, i.e., the high-velocity tail. Along with these quantities we also
calculated the variance 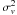 , standard deviation
σv, skewness
γ1,v, and kurtosis
γ2,v. The last two statistical parameters
describe the deviation of the distribution from a normal distribution.
, standard deviation
σv, skewness
γ1,v, and kurtosis
γ2,v. The last two statistical parameters
describe the deviation of the distribution from a normal distribution.
We find an increase of the average velocity with increasing time cadence
Δt starting from about 0.40 km s-1 for
Δt = 15 s, arriving at a maximum value of about 0.47 km s-1
for Δt = 60–90 s, and then decreasing from about 0.45 km s-1
for Δt = 120 s to 0.34 km s-1 for Δt = 240 s,
reaching the lowest value of about 0.23 km s-1 for Δt = 480 s.
Other statistical parameters such as vmed,
v10, vmax,
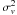 , and
σv follow the same trend.
, and
σv follow the same trend.
The initially increasing values can be explained by the time required for a solar feature to move from one to the next pixel. Three velocity values have to be considered: (1) the photospheric sound speed of ≈8 km s-1, (2) the maximum photospheric velocity of ≈2 km s-1 measured by LCT techniques, and (3) the average speed for the proper motion of the granulation of ≈0.5 km s-1. For Δt = 15 s the average displacement is around one tenth of a pixel, whereas the numerical accuracy for a single measurement is only one fifth of a pixel, because the maximum of the cross-correlation function can only be determined with this precision. Thus, in this case a solar feature has insufficient time to move, which results in underestimating its velocity.
For Δt = 60–90 s, the horizontal displacement is sufficiently large so that a feature could have moved to one of the neighboring pixels. The speed in individual LCT maps is now well within the range where numerical accuracy issues are negligible. Starting at Δt = 120 s the mean velocity becomes lower, while there is sufficient time for a solar feature to move quite some distance, the feature might have evolved too much, so that the LCT algorithm might not any longer trace the same feature. This leads to diminished horizontal velocities.
Thus, 60–90 s is the good choice for measuring of horizontal flow speeds with LCT
techniques. In this range of the time cadence, the mean values
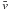 of the interleaved datasets are essentially the same. Their deviations are much smaller
than the previously discussed systematic trends. In summary, all flow maps for the
database were calculated using Δt = 60–90 s. If the time interval
Δt was shorter, a multiple of the time interval
Δt′ = nΔt with
n = 2,3, or 4 was used.
of the interleaved datasets are essentially the same. Their deviations are much smaller
than the previously discussed systematic trends. In summary, all flow maps for the
database were calculated using Δt = 60–90 s. If the time interval
Δt was shorter, a multiple of the time interval
Δt′ = nΔt with
n = 2,3, or 4 was used.
4.2. Determining the duration of the time averages
How many individual LCT maps have to be averaged to yield a reliable flow map? As previously discussed, the parabola fit to the maximum of the cross-correlation sets one limitation. However, there are also method-independent issues to be considered. Solar features evolve over time so that a global pattern reveals itself only after averaging many individual LCT maps. We computed the mean horizontal flow speed as a function of the number of individual LCT maps that were used to arrive at an average flow map. The number of flow maps corresponds to the time interval ΔT over which the individual flow maps were averaged.
 |
Fig. 3 Mean horizontal flow speed as a function of averaged LCT maps for time cadences Δt of 15 s (thick dashed), 30 s (thick dash-dotted curve), 60 s (thick dash-triple-dotted curve), 90 s (thick long dashed curve), 120 s (thin dashed), 240 s (thin dotted), and 480 s (thin solid). |
Figure 3 presents this functional dependence for the time cadences from Δt = 15 s to 480 s. All curves start with high velocities when only a few individual LCT maps are averaged. It takes about 20 min before the curves level out and approach an asymptotic value, indicating that these average flow maps are still dominated by the motions of fine structure contained within the sampling window. As discussed in the context of the statistical properties of the flow maps, short time cadences Δt tend to underestimate the flow speed. If flow speeds have been computed for time intervals shorter than 20 min, feature tracking methods are more appropriate than LCT techniques in particular for small-scale features.
 |
Fig. 4 Horizontal flow speed (left) and azimuth maps (right) measured using Gaussian kernels with 64 × 64 pixels and various FWHM. The FWHM of 7.5, 15, 22.5, and 30 pixels correspond to 600, 1200, 1800, and 2400 km on the solar surface, respectively. The bottom row depicts smoothed versions of the FWHM = 1200 km speed and azimuth maps. The color coding is the same as in Fig. 2. |
We find that all curves up to Δt = 90 s are stacked on top of each other without crossing the next higher curve at any point. Starting at Δt = 120 s we find that the curves corresponding to the longer time cadences cross the other curves after about 20–25 min. This is another indication that solar features have evolved too much so that LCT fails to properly track their motion. This behavior provides an explanation for the spread of velocity values found in literature. In particular, short time-series, as often encountered in ground-based observations, might be biased toward higher velocities. In summary, our choice of 60-min averages for LCT maps is a conservative one that gives the solar features sufficient time to reveal the global flow pattern.
4.3. Selection of the sampling window
How do the horizontal proper motions depend on size and FWHM of the
Gaussian kernel used in the LCT algorithm? To answer this question, we calculated
horizontal proper motions using a Gaussian kernel with 64 × 64 pixels, which is equivalent
to 5120 km × 5120 km on the solar surface. This larger kernel was chosen to encompass
successively broader FWHM. We choose four FWHM of 7.5,
15, 22.5, and 30 pixels corresponding to 600, 1200, 1800, and 2400 km, respectively. The
FWHM of 1200 km matches the size of a granule. Individual LCT maps are
produced from image pairs separated by 60 s in time. We computed the statistical
parameters relating to granulation for the entire sequence and the interleaved datasets.
All statistical parameters are decreasing with increasing FWHM. For
FWHM = 600 km the mean velocity is
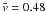 km s-1,
which decreases to
km s-1,
which decreases to 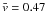 km s-1
for FWHM = 1200 km,
km s-1
for FWHM = 1200 km, 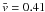 km s-1
for FWHM = 1800 km, and further to
km s-1
for FWHM = 1800 km, and further to
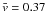 km s-1
for FWHM = 2400 km. Small-scale features, which exhibited the highest
proper motions, are lumped together with regions of low flow speeds when the FWHM
increases. This effect is displayed in Fig. 4, which shows the speed and azimuth maps for the four FWHM. As
before, for a given FWHM all statistical parameters agree with each other
for up to three significant digits, i.e., there is no indication that the algorithm’s
numerical accuracy depends on the FWHM of the kernel used in LCT.
km s-1
for FWHM = 2400 km. Small-scale features, which exhibited the highest
proper motions, are lumped together with regions of low flow speeds when the FWHM
increases. This effect is displayed in Fig. 4, which shows the speed and azimuth maps for the four FWHM. As
before, for a given FWHM all statistical parameters agree with each other
for up to three significant digits, i.e., there is no indication that the algorithm’s
numerical accuracy depends on the FWHM of the kernel used in LCT.
In the case of FWHM = 1200 km, the statistical parameters are very close to the ones calculated for the same FWHM, but with a kernel of 32 × 32 pixels. This is not surprising, because the Gaussian kernel assigns a much stronger weight to features in the center of the subimage, i.e., the periphery in the 64 × 64 pixels FOV has only a small influence in determining the displacement vector for a pair of subimages. This of course only holds true as long as the wings of the Gaussian do not significantly extend beyond the edges of the kernel. Convolving the average flow map (FWHM = 1200 km) with a Gaussian kernel, which had a size of 32 × 32 pixels and FWHM = 26.4 pixels (2112 km), we arrive at a smoothed version (see bottom row in Fig. 4), which is virtually identical with the flow map with FWHM = 2400 km.
In conclusion, it makes no difference, whether one uses a larger FWHM while computing LCT maps or one smoothes the maps after computation. In both cases, the results are virtually the same. Because only minor changes in the LCT results were observed for kernels with 32 × 32 pixels as compared to 64 × 64 pixels, the smaller kernel was chosen because it significantly reduced the computing time. Furthermore, the smallest FWHM produces the most detailed flow maps. However, we chose a FWHM of 1200 km, favoring the spatial scales of granulation, which covers the largest fraction of the observed area. Additional smoothing can still be applied in the later data analysis stages to either reduce noise or to track flows on larger spatial scales. For case studies regarding the fine structure of sunspots, a smaller FWHM might be more appropriate.
4.4. Numerical errors in calculating flow maps
We computed the pixel-to-pixel rms-error for the magnitude and direction of the flow velocity using the interleaved datasets for different time cadences Δt and for different FWHM of the sampling window. Six difference maps (sets 1–2, 1–3, 1–4, 2–3, 2–4, and 3–4) can be computed from the four interleaved datasets, thus for each pixel we can derive the errors, which are primarily due to numerical errors inherent to the LCT algorithm. The rms-error in velocity is 15–90 m s-1 from shortest to longest cadence. The corresponding rms-error in direction is 5°–30°. However, for cadences in the range of 60–90 s, which is the range used to create the database, the rms-error of the velocity is typically in the range from 35–70 m s-1, while the values for the direction vary by as much as 10°–15°. The largest variations in direction are observed near the boundaries of patches showing coherent flows. Even after correcting the 2π ambiguity in the difference maps, we find high values at these locations. As a side note, the rms-error in direction justifies our choice of a color wheel with only twelve segments in the display of the azimuth maps. One segment covers 30° so that pixel-to-pixel variations of about ± 15° are suppressed. Otherwise, the azimuth maps would appear too crowded and consequently the overall flow pattern is no longer perceptible.
 |
Fig. 5 Time-averaged G-band images with horizontal flow vectors computed for ΔT = 1, 2, 4, 8, and 16 h. Arrows with a length corresponding to the grid spacing indicate velocities of 1 km s-1. The background images are displayed in the intensity range 0.5 ≤ I/I0 ≤ 1.5. |
For a different FWHM of the sampling window, rms-errors for speed and direction decrease with increasing FWHM. The velocity error is 35 m s-1 and the error in direction is about 10° for a FWHM of 1200 km. These errors decrease to 15 m s-1 and 5° for a FWHM = 1800 km and to 10 m s-1 and 4° for a FWHM = 2400 km. Here, the decreasing rms-errors can be attributed to the smoothing effect of a wider sampling window, i.e., more pixels are used with higher weights in the cross-correlation. Furthermore, the rms-error in magnitude and direction for the time cadence Δt = 60 s is nearly the same regardless of the size of the Gaussian kernel (32 × 32 pixels vs. 64 × 64 pixels).
Finally, we calculated Pearson’s correlation coefficient between LCT maps of the interleaved datasets. Pearson’s correlation coefficient indicates the degree of a linear relationship between two variables. A positive value of unity indicates that the datasets are identical, disregarding a linear scaling factor. The linear correlation coefficient for different time cadences Δt decreases from 0.99 to 0.93 starting at the shortest and ending at the longest cadence. The high degree of correlation indicates that all essential features of the flow field are captured by the LCT algorithm. The monotonic decrease, however, indicates that numerical errors increase when the cadences Δt become too large.
4.5. Long-lived features in flow maps
The one-hour time interval over which the LCT maps are averaged is insufficient to identify features that need longer to evolve, such as meso- and supergranulation. Therefore, to clearly identify the boundaries of these large-scale convective cells and to visualize the effects of longer time averages, we averaged LCT maps over ΔT = 1, 2, 4, 8, and 16 h, utilizing the long-duration dataset with 960 images and a time cadence Δt = 60 s.
As before, we calculated the statistical parameters for the entire sequence and the
interleaved datasets for granulation. All velocity values decrease with increasing time
intervals over which the individual LCT maps are averaged. For ΔT = 1 h
the mean velocity is 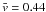 km s-1,
which decreases to
km s-1,
which decreases to 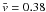 km s-1
for ΔT = 2 h,
km s-1
for ΔT = 2 h, 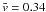 km s-1
for ΔT = 4 h,
km s-1
for ΔT = 4 h, 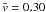 km s-1
for ΔT = 8 h, and further to
km s-1
for ΔT = 8 h, and further to 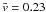 km s-1
for ΔT = 16 h. The mean speed approaches a value for the global flow
field with increasing ΔT. However, the value for
ΔT = 1 h is only slightly lower than previously computed for the
high-cadence sequence. These small deviations (<0.05 km s-1) reflect only
minute differences between the scenes on the solar surface.
km s-1
for ΔT = 16 h. The mean speed approaches a value for the global flow
field with increasing ΔT. However, the value for
ΔT = 1 h is only slightly lower than previously computed for the
high-cadence sequence. These small deviations (<0.05 km s-1) reflect only
minute differences between the scenes on the solar surface.
 |
Fig. 6 Relative frequency distributions of horizontal proper motions for quiet Sun (left) and G-band bright points (right) calculated over ΔT = 1 h (solid curve), 2 h (dotted curve), 4 h (dashed curve), 8 h (dash-dot-dotted curve), and 16 h (dash-triple dotted curve). |
Parameters describing the horizontal proper motions of granulation and G-band bright points calculated over ΔT = 1,2,4,8,and 16 h.
Figure 5 contains the time-averaged G-band images with superposed arrows indicating speed and direction of the horizontal proper motions for ΔT = 1, 2, 4, 8, and 16 h. The region shows granulation and G-band bright points to the west of active region NOAA 11930. Magnetic features dominate the long-duration time averages, i.e., the flow speed is low where strong magnetic fields are present in the chromospheric network, and conversely the speed is high where G-band bright points outline the boundaries of large-scale convective cells. The high speeds associated with the local convective pattern of granules have diminished for the long-duration flow maps and only the converging motion toward the cell boundaries remains, which explains the statistical properties of the velocity values discussed above. The overall visual impression of the vector maps is that the arrows are more ordered in the long-duration maps, whereas in the short-duration maps (ΔT = 1 and 2 h) a larger scatter of the flow vectors is observed on smaller scales. Nonetheless, the imprint of the the meso- and/or supergranulation is already visible in the short-duration flow maps and becomes more prominent the longer the time interval is over which the LCT maps are averaged. Strong converging motions can be found in Fig. 5 near the vertical alignment of G-band bright points in the northeast corner of the FOV and at the boundary of the larger supergranular cell in the southeast corner of the FOV. The supergranule also contains substructures on smaller scales, e.g., a strong divergence center exactly in the central FOV, which can be clearly seen after averaging for at least ΔT = 2 h.
We plotted the relative frequency distributions of the flow fields spanning time intervals of ΔT = 1, 2, 4, 8, and 16 h in Fig. 6 to gain insight into the statistical properties of the long-duration datasets – this time both for granulation and for G-band bright points. The statistical parameters characterizing these distributions are provided in Table 1 for reference. The distribution describing granulation for the shortest time interval (ΔT = 1 h) is the broadest and has an extended high-velocity tail. Interestingly, for velocities up to 0.6 km s-1 this distribution is virtually the same as the distribution for an averaging time, which is twice as long (ΔT = 2 h). The only difference is the high-velocity tail. This indicates that proper motions on small scales still make their presence known if individual LCT maps are not averaged for at least two hours. The peaks of these distributions are shifted toward lower velocity values (from 0.43 to 0.23 km s-1) for longer ΔT. In addition, their standard deviations are progressively becoming smaller (from 0.24 to 0.12 km s-1). The progression of the frequency distributions shown in the left panel of Fig. 6 supports the conclusion that the essential features of long-duration LCT maps have been captured for ΔT = 8–16 h.
The frequency distributions for G-band bright points differ in some aspects from those for granulation. The high-velocity tail is less prominent and all statistical parameters describing the distributions are reduced by about a factor of two. The two distribution with the shortest time intervals (ΔT = 1 and 2 h) show a hint of a bimodal distribution, and they are skewed toward higher velocity values. However, this might be an artifact of the adaptive thresholding algorithm, because the areas covered by G-band bright points are smaller and well defined in the short-duration intensity maps. Thus, considering the FWHM = 1200 km of the sampling window, a larger contribution from granulation is expected, if more isolated G-band bright points are present in the maps, which are used for thresholding. Equation (4) was slightly modified to accommodate the longer time intervals, which leads to a fuzzier appearance of the area covered by G-band bright points and results in a diminished contrast of the G-band bright points. Because no contemporary magnetograms with a comparable spatial resolution were available, we cannot comment on the influence of flux emergence or dispersal during the observed time interval. However, the active region NOAA 10930 showed pronounced activity. In particular, the penumbra of the small sunspot just to the east of the FOV decayed and resulted in continuous flaring in the active region.
Even though long-duration time averages are an important tool when studying large-scale convective patterns or the persistent motions in an active region, the scarcity of such datasets argues against their use for comprehensive and comparative studies. Since most of the characteristics of flow fields are already captured in one-hour averages, we opted for ΔT = 1 h. Furthermore, selecting ΔT = 1 h allows us to study changes in long-duration time-series by computing averaged flow maps every 30 min. Another consideration is that one hour is more then ten times the typical lifetime of granules, so that the proper motions of individual granules should be negligible and global motion patterns will reveal themselves.
Statistical parameters describing the frequency distributions of the horizontal proper motions of various solar features.
Statistical parameters describing the frequency distributions of the horizontal proper motions for various image scales.
 |
Fig. 7 Relative frequency distributions of horizontal proper motions computed for all solar features (solid curve), G-band bright points (dotted curve), granulation (dashed curve), umbra (dash-dotted curve) and penumbra (dash-dot-dotted curve). |
 |
Fig. 8 Time-averaged G-band images with horizontal flow vectors (top) and flow speed maps (bottom) for different spatial resolution. Arrows with the length corresponding to the grid spacing indicate velocities of 0.5 km s-1. |
4.6. Frequency distributions for different solar features
The simplest approach to describe flow fields would be to compute the overall frequency distributions for a particular FOV. However, this simplistic approach is insufficient to recover the underlying physics of plasma motions in the presence (or absence) of strong magnetic field. We used the adaptive thresholding algorithm (Eq. (4)) described in Sect. 3.4 to compute frequency distributions for granulation, penumbrae, umbrae/pores, G-band bright points, and the entire FOV regardless of the features contained in this region. For this case study, we used the high-cadence sequence (see Fig. 2b for the thresholded image) with Δt = 60 s, ΔT = 1 h, and a FWHM = 1200 km. The respective distributions are shown in Fig. 7 and the corresponding statistical parameters are summarized in Table 2. Similar plots and tables will be included in the database subsuming the more than 200 datasets that were analyzed as part of this study. We provide Fig. 7 and Table 2 to facilitate the comparison with other case studies. However, these data are not representative (in the sense of a mean value) for all datasets contained in the database.
Summary of LCT results in previous studies.
A barely detectable shoulder in the frequency distribution for the entire FOV and the
extended high-velocity tail already hint that this distribution contains contributions
from various solar features. Its mean velocity 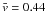 km s-1
is slightly lower than the corresponding value for granulation
km s-1
is slightly lower than the corresponding value for granulation
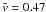 km s-1
that dominates the FOV. The distribution for granulation is broader and a low value of
kurtosis (γ2,v = 0.08) leads to a flatter
peak, where any indication of a shoulder is absent. There is a noticeable difference in
the distributions of strong magnetic elements and granulation. The distributions for
G-band bright points, umbral and penumbral regions are narrow, have sharp peaks, and are
shifted toward lower velocities. The mean velocity for these regions varies from
km s-1
that dominates the FOV. The distribution for granulation is broader and a low value of
kurtosis (γ2,v = 0.08) leads to a flatter
peak, where any indication of a shoulder is absent. There is a noticeable difference in
the distributions of strong magnetic elements and granulation. The distributions for
G-band bright points, umbral and penumbral regions are narrow, have sharp peaks, and are
shifted toward lower velocities. The mean velocity for these regions varies from
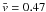 km s-1
for penumbrae to
km s-1
for penumbrae to 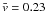 km s-1
for umbrae/pores and G-band bright points. Interestingly, the distributions for the
umbrae/pores and the G-band bright points are virtually identical, while that for the
penumbra has significant contributions at velocities above 0.4 km s-1. This is
indicative of the more complex flow fields in the penumbra, where penumbral grains move
preferentially in the radial direction – inward in the inner penumbra and outward in the
outer penumbra. This also illustrates that some of the small-scale horizontal proper
motions can be captured with the current implementation of the LCT algorithm.
km s-1
for umbrae/pores and G-band bright points. Interestingly, the distributions for the
umbrae/pores and the G-band bright points are virtually identical, while that for the
penumbra has significant contributions at velocities above 0.4 km s-1. This is
indicative of the more complex flow fields in the penumbra, where penumbral grains move
preferentially in the radial direction – inward in the inner penumbra and outward in the
outer penumbra. This also illustrates that some of the small-scale horizontal proper
motions can be captured with the current implementation of the LCT algorithm.
4.7. Flow maps for different spatial resolution
Finally, we will address the question of how the spatial resolution affects the determination of the horizontal proper motions. We used the high-spatial resolution sequence of Sect. 2.3 and treated it exactly like as all the other data with the exception that the G-band images were sampled at 40, 80, 120, 160, and 200 km after correction of geometrical foreshortening. Multiple of 40 km were chosen to match the Hinode SOT/BFI pixel size of 0.055″. Obviously the number of pixels in the sampling window had to be adjusted. However, shape, size, and FWHM = 1200 km of the sampling window were not changed.
The values describing the respective frequency distributions are given in Table 3. They were computed for areas where the granulation covered the full FOV. However, to visualize the minute changes in the flow maps, we show in Fig. 8 only an area of 8 Mm × 8 Mm. In the top row of Fig. 8 the flow vectors are superposed on one-hour average G-band images with different image scales. This scene on the Sun is dominated by converging motions toward the X-shaped alignment of G-band bright points. The grid spacing corresponds to 320 km and the length of the arrows was chosen so that an arrow with a length of exactly the grid spacing corresponds to 0.5 km s-1. The differences are so minute that they only show up in difference images of the LCT maps. The bottom row of Fig. 8 shows the flow speed for each pixel in the FOV at the same color scale as used in all the other figures. The overall appearance of the flow field is the same. However, the low resolution maps look blockier owing to the coarser sampling, and some of the fine structure starts to fade out.
In summary, the average velocity diminishes from 0.54 km s-1 at the highest spatial resolution to 0.47 km s-1 at the lowest resolution. This trend is the same for all other parameters with the exception of kurtosis and skewness, which show some (negligible) scatter. Changes of less than 15% in velocity cannot explain the broad range of velocity values for the horizontal proper motion reported in literature. Note, however, that the Hinode data are not susceptible to the adverse affect of seeing, i.e., ground-based LCT measurements will be much more affected depending on the spatial resolution. Even though seeing should not introduce a systematic bias in LCT (see November & Simon 1988), it will still affect the noise in the LCT measurements.
5. Conclusions
Many case studies exist in the literature that describe horizontal proper motions based on LCT or FT techniques. Even though most of them agree on the morphology of the observed flows, significant differences are found when quantifying the flow properties. Besides obvious differences inherent to the techniques, the choice of parameters such as sampling window, time cadence, and duration can significantly impact the outcome. Some results of previous studies are provided in Table 4 for convenience and to ease the comparison with the present investigation.
We presented the implementation of an LCT algorithm, which was used to create a database of flow maps derived from time-series of G-band images observed with Hinode/SOT. The parameter study and error analysis will also be beneficial to other studies using LCT techniques. Even for observations from the ground our results provide guidance, since LCT techniques are not biased by seeing (see November & Simon 1988) so that our error estimates can be understood as a lower limit.
Justifying the choice of parameters for LCT and FT algorithms is always a challenging task, which should be driven by the scientific purpose of the study. In the present study, the emphasis was on creating a database of flow maps that can be used in statistical investigations regardless of the type of solar feature, location on the Sun, or solar activity. Below, we summarize our choice of LCT parameters.
The flow maps are based on time-series of G-band images with cadences Δt between 60 s and 90 s. If the cadence is shorter, features with low velocities cannot be accurately tracked, whereas in longer cadences the features will have evolved too much for the algorithm to recognize them any longer. Our cadence selection is conservative in the sense that we limit our database in favor of better comparability. Note that there is a significant number of G-band time-series with cadences of about 2 min that are not included in our database.
The evolution of individual features (granules, bright points, penumbral grains, umbral dots, etc.) dominate flow fields on short time scales. Therefore, averaging over time scales significantly longer than the lifetime of the aforementioned features is necessary to yield the global flow field. Our choice of ΔT = 1 h over which the flow maps are averaged ensures that the global flow fields has emerged from the motions of individual features and that sufficient flow maps were averaged to reduce the numerical rms-errors for magnitude and direction of the flow vectors to reasonable values of 35–70 m s-1 and 10–15°, respectively. Note that ΔT = 1 h is not an appropriate choice for studies focusing on meso- and supergranulation because the associated flow pattern is still very noisy and could be more easily perceived in longer time averages. However, long-duration time-series are rare to facilitate these studies. Whenever, time-series with longer durations were available, we computed one-hour flow maps with an overlap of 30 min so that the temporal evolution of the flow field can be monitored, which is of particular interest for the investigation of explosive events such as flares, filament eruptions, and coronal mass ejections.
In principle, the spatial resolution of Hinode/SOT would allow one to track features that are smaller than one second of arc. Our choice of a Gaussian sampling window with 32 × 32 pixels and a FWHM of 1200 km was again motivated by establishing a database of flow maps for statistical studies. Therefore, we used a FWHM, which corresponds approximately to the size of a granule, which is one of the “largest” elements of solar fine structures. Tracking flows on larger spatial scales can still be accomplished by smoothing the flow maps after the fact.
In forthcoming studies, we will use the database of flow maps to study the statistical properties of pores, the motions in sunspot penumbrae, and their relation to the flow pattern observed in the moat of sunspots. Several years of G-band time-series and more than 1000 individual flow maps facilitate the study of these flows during the life cycle of solar features and environment, i.e., as a function of solar activity or the complexity of the surrounding magnetic field. Once thoroughly tested, the value-added Hinode/SOT data will be made available as a small project within the scope of GAVO.
Acknowledgments
Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC
(UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). We thank Drs. K. G. Puschmann and N. Deng for carefully reading the manuscript and for providing comments significantly enhancing the contents of this article. M.V. expresses her gratitude for the generous financial support by the German Academic Exchange Service (DAAD) in the form of a Ph.D. scholarship.
References
- Berger, T. E., Schrijver, C. J., Shine, R. A., et al. 1995, ApJ, 454, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Löfdahl, M. G., Shine, R. S., & Title, A. M. 1998, ApJ, 495, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, P. N., Scharmer, G. B., Ferguson, S., Shine, R. A., & Tarbell, T. D. 1988, Nature, 335, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., & Sakurai, T. 2008, ApJ, 689, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Srivastava, A. K., Filippov, B., & Uddin, W. 2010, Sol. Phys., 266, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Rutten, R. J., Carlsson, M., & Uitenbroek, H. 2006, A&A, 452, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Löfdahl, M. G. 2010, A&A, 524, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molowny-Horas, R. 1994, Sol. Phys., 154, 29 [NASA ADS] [CrossRef] [Google Scholar]
- November, L. J. 1989, in High Spatial Resolution Solar Observations, ed. O. von der Lühe, Proc. 10th Sacramento Peak Summer Workshop, 457 [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Potts, H. E., & Diver, D. A. 2008, Sol. Phys., 248, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Potts, H. E., Barrett, R. K., & Diver, D. A. 2003, Sol. Phys., 217, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Potts, H. E., Barrett, R. K., & Diver, D. A. 2004, A&A, 424, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Almeida, J., Asensio Ramos, A., Trujillo Bueno, J., & Cernicharo, J. 2001, ApJ, 555, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., DeRosa, M. L., Metcalf, T., et al. 2008, ApJ, 675, 1637 [Google Scholar]
- Schuck, P. W. 2006, ApJ, 646, 1358 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., Shelyag, S., Berdyugina, S., Vögler, A., & Solanki, S. K. 2003, ApJL, 597, L173 [CrossRef] [Google Scholar]
- Shine, R. A., Simon, G. W., & Hurlburt, N. E. 2000, Sol. Phys., 193, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, G. W., Brandt, P. N., November, L. J., Scharmer, G. B., & Shine, R. A. 1994, in Solar Surface Magnetism, ed. R. J. Rutten, & C. J. Schrijver, 261 [Google Scholar]
- Steiner, O., Hauschildt, P. H., & Bruls, J. 2001, A&A, 372, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strous, L. H. 1995, in Helioseismology, ESA Special Publication, 376, 213 [Google Scholar]
- Strous, L. H., Scharmer, G., Tarbell, T. D., Title, A. M., & Zwaan, C. 1996, A&A, 306, 947 [NASA ADS] [Google Scholar]
- Tan, C., Chen, P. F., Abramenko, V., & Wang, H. 2009, ApJ, 690, 1820 [NASA ADS] [CrossRef] [Google Scholar]
- Title, A. M., Tarbell, T. D., Topka, K. P., et al. 1989, ApJ, 336, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Welsch, B. T., Abbett, W. P., De Rosa, M. L., et al. 2007, ApJ, 670, 1434 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters describing the horizontal proper motions of granulation and G-band bright points calculated over ΔT = 1,2,4,8,and 16 h.
Statistical parameters describing the frequency distributions of the horizontal proper motions of various solar features.
Statistical parameters describing the frequency distributions of the horizontal proper motions for various image scales.
All Figures
 |
Fig. 1 Calibrated G-band images of active regions a) NOAA 10960 and b) NOAA 10930 observed on 2007 June 4 and 2006 December 7, respectively. The FOV is 111″ × 111″. The annotation of the axes refers to heliocentric coordinates given in seconds of arc. The region in the rectangular white box is used for further analysis, zooming in on a quiet Sun region that contains numerous G-band bright points that outline the supergranular boundaries. The images were normalized in a way that the mode of the quiet Sun intensity distribution corresponds to unity. |
| In the text | |
 |
Fig. 2 a) The average (60-min) G-band image after correction of geometrical foreshortening corresponding to the G-band image shown in Fig. 1a. The red arrows indicate the magnitude and direction of the horizontal proper motions. Arrows with a length corresponding to the grid size indicate velocities of 1 km s-1. b) Adaptive and fixed intensity thresholds are used to identify conglomerates of G-band bright points, granulation, penumbrae, umbrae, and pores. Color codes are used to point out c) flow speed and d) direction in high-resolution flow maps. The flow direction is encoded according to the 12 colors of the compass rose. Sources and sinks in a flow field can be identified in e) a divergence map. The f) forward cork maps provides additional means of visualizing converging motions. Test particles are subsequently superimposed on an average G-band image after they have followed the flows for two (blue), four (orange), and eight (red) hours. The conspicuous network of corks is related to the spatial scales of the meso-and supergranulation. |
| In the text | |
 |
Fig. 3 Mean horizontal flow speed as a function of averaged LCT maps for time cadences Δt of 15 s (thick dashed), 30 s (thick dash-dotted curve), 60 s (thick dash-triple-dotted curve), 90 s (thick long dashed curve), 120 s (thin dashed), 240 s (thin dotted), and 480 s (thin solid). |
| In the text | |
 |
Fig. 4 Horizontal flow speed (left) and azimuth maps (right) measured using Gaussian kernels with 64 × 64 pixels and various FWHM. The FWHM of 7.5, 15, 22.5, and 30 pixels correspond to 600, 1200, 1800, and 2400 km on the solar surface, respectively. The bottom row depicts smoothed versions of the FWHM = 1200 km speed and azimuth maps. The color coding is the same as in Fig. 2. |
| In the text | |
 |
Fig. 5 Time-averaged G-band images with horizontal flow vectors computed for ΔT = 1, 2, 4, 8, and 16 h. Arrows with a length corresponding to the grid spacing indicate velocities of 1 km s-1. The background images are displayed in the intensity range 0.5 ≤ I/I0 ≤ 1.5. |
| In the text | |
 |
Fig. 6 Relative frequency distributions of horizontal proper motions for quiet Sun (left) and G-band bright points (right) calculated over ΔT = 1 h (solid curve), 2 h (dotted curve), 4 h (dashed curve), 8 h (dash-dot-dotted curve), and 16 h (dash-triple dotted curve). |
| In the text | |
 |
Fig. 7 Relative frequency distributions of horizontal proper motions computed for all solar features (solid curve), G-band bright points (dotted curve), granulation (dashed curve), umbra (dash-dotted curve) and penumbra (dash-dot-dotted curve). |
| In the text | |
 |
Fig. 8 Time-averaged G-band images with horizontal flow vectors (top) and flow speed maps (bottom) for different spatial resolution. Arrows with the length corresponding to the grid spacing indicate velocities of 0.5 km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


