| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201016095 | |
| Published online | 09 March 2011 | |
Non-LTE calculations for neutral Na in late-type stars using improved atomic data
1
European Southern Observatory (ESO), Karl-Schwarzschild-Strasse 2, 85748
Garching bei München,
Germany
2
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Strasse 1, 85741
Garching bei München,
Germany
e-mail: klind@mpa-garching.mpg.de
3
Department of Physics & Astronomy, Uppsala
University, Box
515, 75120
Uppsala,
Sweden
4
Department of Theoretical Physics, Herzen
University, St.
Petersburg
191186,
Russia
Received:
7
November
2010
Accepted:
17
January
2011
Neutral sodium is a minority species in the atmospheres of late-type stars, and line formation in local thermodynamic equilibrium (LTE) is often a poor assumption, in particular for strong lines. We present an extensive grid of non-LTE calculations for several Na I lines in cool stellar atmospheres, including metal-rich and metal-poor dwarfs and giants. For the first time, we constructed a Na model atom that incorporates accurate quantum mechanical calculations for collisional excitation and ionisation by electrons as well as collisional excitation and charge exchange reactions with neutral hydrogen. Similar to Li I, the new rates for hydrogen impact excitation do not affect the statistical equilibrium calculations, while charge exchange reactions have a small but non-negligible influence. The presented LTE and non-LTE curves-of-growth can be interpolated to obtain non-LTE abundances and abundance corrections for arbitrary stellar parameter combinations and line strengths. The typical corrections for weak lines are −0.1... −0.2 dex, whereas saturated lines may overestimate the abundance in LTE by more than 0.5 dex. The non-LTE Na abundances appear very robust with respect to uncertainties in the input collisional data.
Key words: stars: abundances / stars: late-type / line: formation
© ESO, 2011
1. Introduction
Sodium has established itself as an important tracer of Galactic chemical evolution, and numerous investigations of the Na abundances of late-type stars, residing in different regions of the Galaxy, have been conducted (e.g. Takeda et al. 2003; Gehren et al. 2006; Andrievsky et al. 2007). Na is mainly synthesised during hydrostatic carbon-burning in massive stars, through the reaction 12C(12C, p)23Na. As pointed out by Woosley & Weaver (1995), the production is dependent on the available neutron excess through secondary reactions, which implies metal-dependent yields. In addition, there is a production channel via proton-capture reactions, 22Ne(p, γ)23Na (Denisenkov & Denisenkova 1990). The latter, the so-called NeNa-cycle, occurs when temperatures are high enough for H-burning through the CNO-cycle, e.g. in the cores or H-burning shells of intermediate mass and massive stars.
Abundance studies of late-type stars in the thin disk show a steady increase from solar to positive [Na/Fe] ratios at super-solar metallicities, while thin and thick disk stars instead form a decreasing trend slightly below solar metallicities (e.g. Edvardsson et al. 1993; Reddy et al. 2003; Bensby et al. 2003; Shi et al. 2004). Relying exclusively on weak lines for the analysis, LTE has been proved a reasonable approximation in this metallicity regime. For metal-poor stars the situation is different, especially in cases where the strong Na I D resonance lines (588.9/589.5 nm) are the only available abundance indicators. As shown by Takeda et al. (2003) and Gehren et al. (2006), [Na/Fe] ratios are slightly subsolar (−0.1... −0.5) in metal-poor stars in the thick disk and the halo in the metallicity range [Fe/H] = −3.0... −1.0. This deficiency is only recovered through non-LTE analysis, because LTE investigations tend to overestimate the abundances, sometimes by as much as ~0.5 dex (see Sect. 3.1). Moreover, almost solar values are obtained from non-LTE analysis of extremely metal-poor stars below [Fe/H] < −3.0, where LTE analysis, at least of giants, instead yields positive ratios, [Na/Fe] ≈ 0.3 (Cayrel et al. 2004; Andrievsky et al. 2007). Interestingly, Nissen & Schuster (2010) found evidence for systematic Na abundance differences of the order of 0.2 dex between α-poor and α-rich halo stars, with important implications for the presumably separate origin of these two Galactic components. To place all Galactic stellar populations on an absolute Na abundance scale to the same and better precision, non-LTE is clearly required.
In globular clusters, Na is of particular interest, because the large overabundances of this element, compared with those of field stars of similar metallicities, imply a chemical evolution scenario that is specific to these dense stellar systems (e.g. Gratton et al. 2004). By detailed mapping of the Na abundance and its correlating behaviour with similar-mass and lighter elements we may distinguish between stars formed in different formation episodes in globular clusters and eventually identify the elusive self-enrichment process that so efficiently polluted the star-forming gas with the nucleosynthesis products of hot H-burning through the CNO-cycle and the related NeNa- and MgAl-chains (i.e. enhancement of N, Na, and Al, and depletion of C, O, and Mg, see e.g. Lind et al. 2011; and Carretta et al. 2009).
In this study we present 1D, non-LTE calculations for several neutral Na lines for a large stellar grid. The given non-LTE abundances can be interpolated to arbitrary stellar-parameter combinations and will consequently be useful for Na abundance analyses with a variety of applications. In a forthcoming paper we will apply the non-LTE modelling procedure described here to individual stars, and extend it to using 3D hydrodynamical model atmospheres.
Typically, the largest uncertainties affecting the non-LTE calculations in stellar atmospheres are collisional cross-sections, especially for collisions with hydrogen atoms (e.g. Asplund 2005). As described in Sects. 2.3 and 2.4, recent quantum mechanical calculations of cross-sections for collisions with both electrons and hydrogen have significantly improved the situation for sodium, and a reliable atom can now be constructed. In this study, we put extra emphasis on assessing to which extent the remaining uncertainties in collisional rates influence the statistical equilibrium of Na I.
2. Non-LTE modelling procedure
We used the code MULTI, version 2.3 (Carlsson 1986, 1992) to simultaneously solve the statistical equilibrium and radiative transfer problems in a plane-parallel stellar atmosphere. Na was considered a trace element, i.e. we neglected feedback effects from changes in its level populations on the atmospheric structure. The LTE assumption was used for all other species in the computation of background continuum and line opacity. A simultaneously computed line-blanketed radiation field was therefore used in the calculation of photoionisation rates.
A grid of 764 1D, LTE, opacity-sampling marcs model atmospheres (Gustafsson et al. 2008) was used in the analysis. The models span Teff = 4000...8000 K, log g = 1.0...5.0, and [Fe/H] = −5.0... +0.5. Sodium abundances vary from [Na/Fe] = −2.0... +2.0, in steps of 0.25 dex. The highest effective temperature is 5500 K for models with log g = 1.0, 6500 K for log g = 2.0, and 8000 K for log g ≥ 3.0. For models with log g ≥ 3.0, we adopted microturbulence parameters ξt = 1.0 and 2.0 km s-1 and for models with log g ≤ 3.0, we adopted ξt = 1.0,2.0, and 5.0 km s-1. All models have a standard composition, i.e. with scaled solar abundances according to Grevesse et al. (2007), plus 0.4 dex enhancement of alpha-elements in all metal-poor models ([Fe/H] ≤ −1.0).
We define a non-LTE correction for each abundance point as the difference between the LTE sodium abundance and the non-LTE abundance that corresponds to the same equivalent width. Corrections are given for equivalent widths in the range 0.01–500 pm. The equivalent width was obtained by numerical integration over the line profile, considering a spectral region that extends ± 0.3–3 nm from the line centre, depending on the typical line strength.
2.1. Structure of the model atom
The model atom we constructed for Na consists of 22 energy levels of Na I, plus the Na II continuum (see Fig. 1). The energy levels are coupled by radiative transitions and by collisional transitions with electrons and neutral hydrogen. Experimentally measured energies were taken from the compilation by Sansonetti (2008) (for highly excited states isoelectronic fitting was used). Because we are not concerned with modelling the detailed structure of highly excited levels, we collapsed all sublevels for n = 7−12 into super-levels. The fine-structure components of the 3p level were accounted for in the statistical equilibrium calculations by treating 3p1/2 and 3p3/2 as separate, collisionally coupled levels1. In addition, the fine-structure components of the 3p–3d and 3p–4d transitions, as well as the hyper-fine structure components of the 3s–3p1/2 and 3s–3p3/2 transitions, were accounted for by computing the line profile as a linear combination of the subcomponents (see Table 1).
The collisional transition probabilities were computed for the 3p level, not for its fine-structure components. To calculate these we assume that the ionisation and excitation rates of the sublevels were equal to that of the collapsed level. We further assume that the de-excitation rates to 3s scale with the statistical weights, i.e. the de-excitation rate from 3p3/2 is twice as large as from 3p1/2, and the sum of the rates is equal to that of the collapsed level. The collisional cross-section for electron impact excitation between the two fine-structure levels was estimated with the impact parameter method of Seaton (1962). We note that the detailed rates are not important for the non-LTE problem.
 |
Fig. 1 Schematic term diagram of the 23-level Na I model atom. The dashed line marks the Na II continuum. The highest level considered in Na I is n = 12. |
2.2. Radiative transitions
In total, 166 allowed bound-bound radiative transitions were included, adopting where possible oscillator strengths from the ab initio calculations of Froese Fischer2. For most remaining transitions, we used the calculated transition probabilities by Taylor, as part of the Opacity Project (TOPbase, Cunto & Mendoza 1992)3. The two sets of f-values typically agree within 3% for the strongest, most important transitions. For the Na D lines, accurate experimental data exist, and we adopted the values listed in the NIST data base4 (see Table 1).
Photoionisation cross-sections for levels with l ≤ 4 were drawn from the TOP-base (computations by K.T. Taylor). For the highly excited collapsed levels we adopted hydrogenic cross-sections.
Line data for the 11 lines considered in the spectrum synthesis.
2.3. Collisions with electrons
Cross-sections for collisional excitation by electrons can be estimated using general recipes based on the Born approximation, which is known to overestimate the cross-sections at low impact energies (e.g. Park 1971). Those near-threshold energies are most relevant for stellar atmospheres that host electrons with typical kinetic energies of the order of 1 eV. Seaton (1962) tried to rectify the Born cross-sections by modifying the transition probability for low-impact parameters, thus accounting for strong coupling between states, which was previously neglected (the so-called impact parameter approximation). Another approach is to empirically adjust the Born rates to reach better agreement with experimental data, which was advocated by van Regemorter (1962) and Park (1971). Without any alternatives, non-LTE applications have long had to rely almost exclusively on these simple semi-empirical formulae.
 |
Fig. 2 Three sample excitation cross-sections for collisions between Na I and electrons. The black solid lines represent R-matrix calculations (Feautrier et al. 2010; Gao et al. 2010) and the red dashed lines represent the analytical fitting functions derived by Igenbergs et al. (2008). The transitions are marked with labels next to the energy thresholds. |
Nowadays, much more rigorous quantum mechanical calculations can be performed for simple atoms like Na. Igenbergs et al. (2008) present new convergent close-coupling (CCC) calculations for excitation and ionisation of neutral Na by electron collisions, which agree well with experimental data when available (e.g. with the measurements by Phelps & Lin 1981). Additionally, R-matrix calculations that are able to recover the detailed resonant structures of the cross-sections at threshold impact energies (<5 eV) have been performed by Gao et al. (2010). Here, we adopted cross-sections calculated with the R-matrix method in a manner similar to that described in Gao et al., including seven real spectroscopic states of Na I (3s, 3p, 4s, 3d, 4p, 4d, and 4f) and four polarised pseudo-orbitals to take into account the polarisation effects between the scattered electron and the target electrons (see Feautrier et al., in prep.). The calculations were performed for impact energies in the range 0–14 eV. Figure 2 compares the cross-sections obtained for some sample transitions with the R-matrix method and the analytical fitting functions by Igenbergs et al. (2008). The two methods agree very well; the typical difference between calculated rate coefficients in the temperature regime 2000–20 000 K is only a factor of two, although individual rates could differ by up to a factor of ten.
For more highly excited states of Na I, quantum mechanical data are lacking and we are still dependent on general formulae. However, the empirically adjusted rates by Park (1971) perform surprisingly well compared with the newer data, with half of the transitions at 6000 K agreeing within a factor of three and 90% of the transitions agreeing to within a factor of ten. We adopted these for transitions involving levels above 5s.
Cross-sections for ionisation by electron impact have also been calculated with the CCC method up to 5s by Igenbergs et al. (2008), and compare well with existing experimental data for the ground and first excited states. For ionisation from more highly excited levels, we relied on the general recipe given in Allen (2000). Also, to bridge the small energy gap between the ionisation edge and the minimum energy for which the analytical fits to the ionisation cross-sections are valid (see Table 2 in Igenbergs et al.), we assumed that the cross-sections for all levels were given by the general recipe (Allen 2000) at the edge.
In Sect. 3.2 we evaluate the influence from uncertainties in collisional rates on the statistical equilibrium of Na I by multiplying and dividing all electron collisional rates by a factor of two, which given the present data may be indicative of the true uncertainty of the data for the most important transitions.
2.4. Collisions with hydrogen
Neutral hydrogen atoms are the most abundant atomic species in late-type stellar atmospheres. Still, collisional cross-sections between hydrogen and other atoms are notorious sources of uncertainty for non-LTE applications, and some empirical calibration of the classical recipe by Drawin (1968) is usually the only option, using a general rate scaling factor SH. Again, the situation for Na today is improved in this respect.
Belyaev et al. (2010) have performed quantum-scattering calculations of cross-sections for inelastic collisions between H + Na with impact energies ranging from threshold up to 10 eV. Using these cross-sections, Barklem et al. (2010) present for the first time quantum mechanical rate coefficients for a large number of bound-bound transitions in Na I, caused by collisions with neutral hydrogen, as well as charge exchange reactions between sodium and hydrogen (Na∗ + H ⇆ Na + + H−). We use the rate coefficients given in Barklem et al. (2010) involving all levels and all possible transitions below the ionic limit, i.e. up to 5p (for levels above the ionic limit, charge exchange is not possibile). The bound-bound rates for allowed transitions are smaller than what is found with the commonly used classical recipe by Drawin by one to six orders of magnitude, depending on the transition (see Fig. 3). The Drawin recipe is not applicable to forbidden bound-bound transitions, ionisation or charge exchange.
We estimate the bound-bound collisional rates for transitions between highly excited levels with the free electron model described by Kaulakys (1991), which is applicable to Rydberg atoms (Eq. (18) in Kaulakys, using non-hydrogenic wave-functions in momentum space calculated using the methods of Hoang Binh & Van Regemorter 1997). Figure 3 compares the rate coefficients found by Barklem et al. (2010) with those given by the Drawin recipe for transitions between low excited states, and also compares the rates by Kaulakys and Drawin for transitions between highly excited states. It is easily appreciated from these figures that for Na no single scaling factor can be applied to the Drawin recipe to reproduce either the quantum mechanical rates or the Kaulakys rates.
 |
Fig. 3 Comparison between rate coefficients at T = 6000 K for collisional excitation of Na I by neutral hydrogen atoms. Only optically allowed transitions are shown and x-axis represents the energy of the transition. Top: the ratio between the unscaled Drawin formula and the free electron model of Kaulakys (1991) for transitions between highly excited states. Bottom: the ratio between the unscaled Drawin formula and the quantum mechanical calculations by Barklem et al. (2010) for transitions between levels up to 5s. |
Barklem et al. (2010) also provide estimates of the rate uncertainty, so called fluctuation factors. In Sect. 3.2 we discuss the effect on the non-LTE calculations when multiplying all quantum mechanical rates by the maximum fluctuation factors or by the suggested minimum value (0.5).
2.5. Line broadening
For line broadening caused by collisions with neutral hydrogen, we use the ABO theory by Anstee & O’Mara (1995) and Barklem & O’Mara (1997) whenever applicable, and otherwise adopt the C6 constant for van der Waals-broadening by Unsöld (1955). The latter are enhanced by a factor of 2 (Δlog C6 ≈ 0.8), which is typically required to match the observed line profiles in the Sun (e.g. Mashonkina et al. 2000). Stark broadening constants (C4) are estimated from the tables of Dimitrijević & Sahal-Bréchot (1985, 1990). The line data are summarised in Table 1 for the 11 principally considered transitions.
 |
Fig. 4 Contour diagrams illustrating how the abundance corrections vary with effective temperature and surface gravity for four commonly analysed lines of Na I. Only the results for ξ = 2 km s-1 and [Na/Fe] = 0 are shown. |
3. Discussion
3.1. Departures from LTE
There is a great regularity in the statistical equilibrium of Na over the whole stellar grid covered by our analysis. As we will describe below, the non-LTE abundance corrections are dependent on the line strength and much of the model dependence can therefore be easily understood through the variation of the excitation and ionisation equilibrium with temperature and density. Figure 4 shows contour plots of how the inferred corrections vary with effective temperature and surface gravity at [Na/Fe] = 0.
To describe the non-LTE line formation of Na lines, we define the departure coefficient
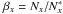 , which represents the population of a
certain level x in non-LTE, divided by the corresponding population in
LTE. Given a specific background continuum opacity, the strength and shape of a spectral
line are determined by the line opacity, which is proportional to the population of the
lower level of the transition, and the source function
Sν, which is proportional to the
population ratio between the upper and lower level5.
Lifting the assumption of LTE, both line formation depth and source function may change
and thus alter the strength and shape of the spectral line.
, which represents the population of a
certain level x in non-LTE, divided by the corresponding population in
LTE. Given a specific background continuum opacity, the strength and shape of a spectral
line are determined by the line opacity, which is proportional to the population of the
lower level of the transition, and the source function
Sν, which is proportional to the
population ratio between the upper and lower level5.
Lifting the assumption of LTE, both line formation depth and source function may change
and thus alter the strength and shape of the spectral line.
The strong Na I D doublet lines at 588.9/589.5 nm are commonly used in abundance studies
of metal-poor stars. Indeed, in certain cases (warm, metal-poor dwarfs) they are the only
lines that are sufficiently strong. The doublet originates from the resonance line
transition between the ground state (3s) and the two fine structure components of the
first excited state (3p1/2 and 3p3/2). We found empirically that as
a general rule the line source function perfectly resembles that of a pure scattering line
in a two-level atom, i.e. to a very good approximation
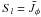 at all depths, where
at all depths, where 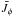 is the profile-averaged mean intensity. This merely reflects that for these lines, the
photon absorption and emission rates strongly dominate the collisional rates and all
interactions with other levels, including the continuum. Although in principle for a
two-level atom,
is the profile-averaged mean intensity. This merely reflects that for these lines, the
photon absorption and emission rates strongly dominate the collisional rates and all
interactions with other levels, including the continuum. Although in principle for a
two-level atom, 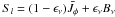 ,
the probability for true absorption, ϵν, is
very close to zero at shallow depths where
,
the probability for true absorption, ϵν, is
very close to zero at shallow depths where 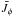 departs from Bν, so the approximation of a
pure scattering line still holds at all depths.
departs from Bν, so the approximation of a
pure scattering line still holds at all depths.
The ratio between the population of the upper and lower level is therefore always set by the mean intensity, and, for a specific line strength, this is correctly established with a simple two-level atom. However, the actual population of the ground level, which governs the line opacity and typical formation depth of the line, is underestimated when more highly excited levels of Na I are neglected. As described by Bruls et al. (1992), a number of high-excitation levels and a ladder of high-probability transitions connecting these with lower excitation levels must be established to obtain the correct populations. This is needed because the first and second excited states have photoionisation thresholds in the ultra-violet, where the radiation field exceeds the Planck function (Jν > Bν), and pushes the ionisation balance to overionisation of Na I. The situation is reversed for more highly excited levels since their photoionisation thresholds lie in the near-infrared regime, where the radiation field is instead subthermal. This photoionisation/recombination picture has been described previously by Takeda et al. (2003) and Mashonkina et al. (2000).
We can now qualitatively understand the non-LTE formation, starting with the Na I resonance lines. When either line is weak, it will obviously have little influence on its own radiation field. Therefore, Jν − Bν > 0 at shallow optical depths, as is the case for neighbouring continuum regions. This is governed by the temperature gradient, which determines how rapidly Bν decreases with optical depth. At these wavelengths, the gradient is steep enough to produce a Jν − Bν excess and, consequently, a line source function that is stronger than in LTE (βu/βl > 1). This would tend to weaken the resonance lines compared with LTE, but the effect is small because the lines are formed deep in the atmosphere, where the radiation field is close to thermal. On the other hand, the photoionisation balance of Na I is always shifted to overrecombination in the line-forming regions. The ground state of Na I is thus overpopulated compared with LTE (βl > 1), and the combined effect is generally a moderate line strengthening. The resulting abundance corrections for the resonance lines are always minor, |ΔA| < 0.1 dex at line strengths below 5 pm. However, these lines are only that weak in extremely metal-poor stars.
As the line strength increases towards saturation in any given model, Jν drops, and the line source function becomes weaker than in LTE. This is naturally accompanied by a decrease in the excitation rate. Also the ionisation rates drop with increasing abundance as the photoionising radiation field weakens. This enhances photorecombination from the Na II reservoir, and all levels of Na I are increasingly overpopulated. The combination of higher line opacity and a weaker source function produce significant line strengthening in non-LTE, with negative abundance corrections as a result. This behaviour is illustrated in Fig. 5 for a metal-poor dwarf and giant. We note that even if the statistical equilibrium is not necessarily pushed further from LTE, the abundance corrections become larger and larger as the line saturates, simply because the abundance sensitivity to equivalent width is small in this regime.
With further strengthening, the line enters onto the damping part of the curve-of-growth with the development of broad wings. Because photons from a wider frequency range are then able to excite the atoms, the excitation rate actually increases again, lessening the overpopulation in deep layers. The abundance sensitivity to line strength also starts to increase again, consequently the abundance corrections, as we define them here, reach a minimum value when the line is fully saturated (see Fig. 5) and then become less negative with higher abundance, although these strong lines are hardly suitable for accurate abundance analysis through equivalent width measurements. Line profile analysis especially of the wings is more appropriate, but that is not addressed here.
 |
Fig. 5 Non-LTE abundance corrections as functions of equivalent width for selected Na I lines for a metal-poor turn-off star (top: Teff = 6400 K, log g = 4.0, [Fe/H] = −2, and ξt = 2.0 km s-1) and metal-poor giant (bottom: Teff = 5000 K, log g = 2.0, [Fe/H] = −2, and ξt = 2.0 km s-1). The black bullets indicate the predicted line strength and abundance corrections at [Na/Fe] = 0. |
Even if the two-level approximation holds true only for the source function of the resonance lines, the subordinate transitions (with 3p as lower level) show a very similar behaviour. At low line strength each line has a “plateau” of close-to-constant, small abundance corrections, which becomes increasingly negative as the line saturates around 20 pm. This general behaviour with line strength has been discovered previously e.g. by Takeda et al. (2003). The strongest subordinate transitions, 3p–3d at 818.3/819.4 nm, follow an almost identical behaviour as the resonance lines, but are offset to more negative corrections. The latter is because of the shallower temperature gradient with continuum optical depth in the near-infrared wavelength, which produces a Jν − Bν deficiency in the line, and a source function that is weaker than in LTE also when the lines are very weak.
Naturally, the abundance corrections at a given line strength are still somewhat model-dependent. For saturated lines, the corrections are more negative for hotter models and models with lower surface gravity, whereas the metallicity dependence seems almost negligible. Fully unsaturated lines (below 5 pm) almost always have corrections in the range −0.1... −0.2 dex.
We note the very close resemblance in the non-LTE line formation of sodium and the lighter alkali atom lithium, whose departures from LTE have been described e.g by Carlsson et al. (1994) and Lind et al. (2009). There are many striking similarities between the two elements, especially in the shape of the abundance correction curves. Differences mainly arise from the higher degree of overionisation of Li, which in turn is a direct result of the larger photoionisation cross-section from the first excited state of Li I (2p), compared to Na I (3p). The abundance corrections at low line strengths thus tend to be somewhat higher, even positive, for Li (overionisation causes underpopulation of Li I, thus weakening the spectral lines).
3.2. The influence of collisions
As described in Sects. 2.3 and 2.4, the statistical equilibrium of Na I was calculated by accounting for collisional excitation and ionisation by electrons and hydrogen atoms. We now discuss the impact on the derived abundance corrections when varying the strength of collisional rates.
When multiplying/dividing all rates for collisional excitation and ionisation by electrons by a factor of two, the solar equivalent widths of Na I lines change systematically by typically 1%. This propagates to less than ~0.01 dex in terms of non-LTE abundance corrections, and is therefore negligible. A somewhat larger impact is seen for hotter, higher surface gravity models, where electrons are more abundant. Still, the non-LTE equivalent widths calculated for a Teff = 8000 K, log (g) = 5.0, solar metallicity model are affected by only 2–4%, corresponding to approximately 0.02 dex for relevant lines. Giants and cooler dwarfs are less sensitive, because they have lower densities of the colliding free electrons. The Na non-LTE calculations thus seem robust with respect to input atomic data for collisions with electrons.
 |
Fig. 6 Departure coefficients for a solar model, for the Na I levels indicated with labels in the plot. Solid: neglecting collisions with neutral hydrogen. Dotted: including charge exchange reactions and bound-bound collisional excitation by neutral hydrogen. Bullets: including only charge exchange reactions in collisions with hydrogen. |
The quantum mechanical calculations by Barklem et al. (2010) result in rate coefficients for collisional excitation by hydrogen atoms that are lower than the commonly used classical Drawin recipe by one to six orders of magnitude. The new rates thus have very little influence on the statistical equilibrium of Na I, in the stellar parameter range that we consider here. However, again analogously to Li, charge exchange reactions turn out to be more influential. Figure 6 illustrates how the departure coefficients of low excited levels change for a solar model, when including and neglecting collisions with neutral hydrogen.
It is conceptually correct to say that higher collisional rates have a thermalising effect, i.e. they tend to drive the level population towards LTE. However, as seen for the Sun in Fig. 6, this is not generally true for all levels. The populations of the ground state and first excited states are instead pushed farther away from LTE in optically thin atmospheric layers, when charge exchange is included. This seemingly contradictory behaviour can be understood by realising that the collisional cross-sections of 3s and 3p are very small, and the changes in their level population are rather a secondary effect, stemming from the thermalisation of higher excited levels. Especially 4s, whose departure coefficients are also displayed in Fig. 6, has a large cross-section for charge exchange and the level becomes almost thermalised with the inclusion of this process. In deeper layers, where β4s > 1, the overpopulation of the level decreases, which also propagates to lower excited levels. In shallow layers, where β4s < 1, the added neutralisation channel through charge exchange reactions lessens the underpopulation of 4s, but further increases the overpopulation of lower levels. In practice, higher excited levels than 4s influence the outcome as well, but to a lesser extent.
Even if the statistical equilibrium is indeed influenced by hydrogen collisions, this need not necessarily be the case for the the emergent spectral lines. This is because the source functions remain unchanged, and as discussed above, the effect on the level populations of 3s and 3p is opposite in different regimes of the atmosphere, so that the net effect on the line strength is small. The situation is different from that of Li, for which charge exchange reactions always lead to more neutralisation throughout the atmosphere, with significant line strengthening as a result (Barklem et al. 2003; Lind et al. 2009).
Charge exchange is most important in cool, high surface gravity models, for which abundance corrections are affected by up to ~0.2 dex, whereas the effect in solar-type stars is only ~0.01 dex. This is a direct reflection of the ionisation equilibrium of hydrogen, because H− is abundant in cool, dense atmospheres. We therefore tested how the uncertainty in collisional rates affects the abundance corrections for the extreme case of a Teff = 4000 K, log g = 5.0 model. When multiplying and dividing all rates with their maximum fluctuation factors (see Sect. 2.4), the abundance corrections vary with typically 0.04 dex for such a model. For the Sun, the corresponding variation is <0.01 dex, i.e. essentially irrelevant for practical purposes.
 |
Fig. 7 Comparison between the abundance corrections determined in this study (lines connected with bullets) and earlier studies, as indicated in each panel (lines connected with plus signs). Effective temperature is used as reference axis, with surface gravity values for each model indicated along the top axis of each panel. All calculations assumed [Na/Fe] = 0.0. |
3.3. Consequences for stellar abundance analysis
Obviously, it is always preferable to base the abundance analysis on unsaturated spectral lines, not least because non-LTE abundance corrections for fully saturated lines may reach −1 dex in extreme cases. This means that equivalent width measurements of the resonance lines should be used only as a last resort for metal-poor stars, when the 818.3/819.4 nm doublet lines are not detectable or too severely blended with telluric lines. At metallicities in the range [Fe/H] = −2.0... −1.0, the 568.2/568.8 nm doublet lines are usually to be preferred, whereas the 615.4/616.0 are good indicators for solar metallicity stars. Given the estimated uncertainties in collisional data, the non-LTE modelling gives abundances for weak lines that normally can be trusted to high precision.
 |
Fig. 8 Top: temperature difference between atlas9 models with respect to marcs models (Gustafsson et al. 2008), for a metal-poor giant (Teff = 5000 K, log g = 2.0, [Fe/H] = −2.0, ξt = 2.0 km s-1). The dotted line represents an atlas9 model with scaled solar composition and convective overshoot from the Kurucz 1993-grid. The dashed line has the same composition, but without overshoot. The dashed-dotted line represents a 0.4 dex alpha-enhanced atlas9 model without overshoot from the 2004-grid by Castelli & Kurucz. Middle: difference between LTE abundance as function of line strength for the same models with respect to marcs. The abundances are based on the 819.4 nm Na I line and vary from left to right between [Na/Fe] = −2.0... +2.0. Bottom: same as the middle panel, but for non-LTE abundances. |
Figure 7 compares our inferred corrections with those of Andrievsky et al. (2007), Shi et al. (2004), Takeda et al. (2003) and Mashonkina et al. (2000) for selected models within the grid. Overall, the agreement between the studies is never worse than 0.2 dex and they usually agree to within 0.1 dex. Considering that all studies have (to various degree) differences in input atomic data, atmospheric models, and the numerical methods, this is not surprising. Still, all statistical equilibrium calculations in 1D are conceptually similar and a better consensus between independent studies is clearly desired to ensure that accurate Na abundances can be derived. In particular, we note the sometimes highly significant discrepancies with the non-LTE calculations published by Gratton et al. (1999). Their abundance corrections show an increasing trend toward positive values (up to +0.5 dex, depending on the line) for very low surface gravity stars, which is not seen in our calculations.
While our model atom is superior to previous studies in that it contains more reliable atomic data for collisions, we do not expect that this is the primary reason behind some of the larger offsets compared with previous studies. As discussed in Sect. 3.2, the sensitivity to the detailed collisional rates is fairly low for the specific case of Na in the stellar parameter range covered and we suspect that the differences in the model atmospheric structure have a larger impact. Takeda et al. (2003), Mashonkina et al. (2000) and Andrievsky et al. (2007) all use Kurucz atlas9 models, while Shi et al. (2004) use the grid by Fuhrmann et al. (1997). The atmospheric temperature gradient is inevitably different for models of identical stellar parameters, for example because of differences in the treatment of convection, equation of state, and opacity. This is illustrated in the top panel of Fig. 8, which shows the difference in temperature stratification for different versions of atlas9 models with respect to a marcs model for a metal-poor giant6. As can be seen in this figure, the stratification is critically dependent on the inclusion of convective overshooting in the 1993 grid by Kurucz. The most up-to-date versions of atlas9 (Castelli & Kurucz 2004) and marcs (Gustafsson et al. 2008) both neglect overshoot, and the models shown have similar, but not identical parameters for the mixing length, but nevertheless show differences on the 100 K level.
The middle and lower panels of Fig. 8 illustrate the effect on derived LTE and non-LTE Na abundances for the 819.4 nm line, when using different atmospheric models. In both cases the line strengths appear, as expected, to be connected to the temperatures around log (τ500) = 0. The higher temperatures of the atlas9 models, especially the one with overshoot, weakens the line compared to marcs for a given Na abundance (i.e. a given line strength generally corresponds to a higher LTE abundance). However, in non-LTE the difference is lessened because of a higher degree of overpopulation of neutral Na in the temperature “jump” in the overshooting model. This in turn is caused by the flatter temperature gradient and consequently the less efficient overionising ultra-violet flux in this region. This comparison implies that differences between 1D atmospheric models can produce differences of the order of ~0.1 dex in Na abundance for such a metal-poor giant.
4. Concluding remarks
Using our calculated abundance corrections and/or non-LTE curves-of-growth for 11 important neutral Na I lines, Na abundances that are superiour to those inferred with the LTE assumption can easily be obtained for late-type dwarf and giant stars. The results show a low sensitivity to uncertainties in input atomic data for collisional cross-sections, but are sensitive to the detailed structure of the atmosphere. To minimize the influence from possible systematic errors in the model, unsaturated lines are definitely to be preferred as abundance indicators. As always, a good test of the soundness of the modelling procedure is to compare Na abundances from lines of different strengths.
Our results satisfactorily agree with earlier non-LTE studies of Na I that treated the strength of hydrogen collisions as a free parameter, even though the new quantum mechanical rates for hydrogen impact excitation are considerably lower than the traditational estimates. This low sensitivity of non-LTE abundances to hydrogen collisions stems from a cancellation between effects in different line-forming regions.
In a forthcoming paper we will explore the impact of the model atmosphere on the abundance determination more closely, and extend our work to include 3D, hydrodynamical model atmospheres, superseding the crude mixing length recipes used for convection in static 1D models. The model atom presented here will then be applied to specific cases of solar-metallicity and metal-poor dwarfs and giants, and we will discuss the Galactic chemical evolution of Na.
Accounting for the fine-structure components of the 3p level simplifies the numerical procedure, while also predicting correct line formation depths for the individual lines (e.g. Mashonkina et al. 2000).
Multi-configuration Hartree-Fock computations (MCHF). http://www.vuse.vanderbilt.edu/~cff/mchf_collection/
The atlas9 models were retrieved from http://kurucz.harvard.edu/grids/, with convective overshoot (gridm20), without overshoot (gridm20NOVER), and using more up-to-date opacities and abundances (gridm20a2ODFNEW).
Acknowledgments
We gratefully acknowledge the support of the Royal Swedish Academy of Sciences, Göran Gustafssons Stiftelse and the Swedish Research Council. P.S.B. is a Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. A.K.B. acknowledges the support from the Russian Foundation for Basic Research (Grant No. 10-03-00807-a). Special thanks to N. Feautrier for assistance with the draft and for providing us with collisional data before publication.
References
- Allen, C. W. 2000, Allen’s Astrophysical Quantities, 4th edn. (Berlin: Springer) [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2007, A&A, 464, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
- Barklem, P. S., Belyaev, A. K., & Asplund, M. 2003, A&A, 409, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Belyaev, A. K., Dickinson, A. S., & Gadéa, F. X. 2010, A&A, 519, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belyaev, A. K., Barklem, P. S., Dickinson, A. S., & Gadéa, F. X. 2010, Phys. Rev. A, 81, 032706 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruls, J. H. M. J., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 265, 237 [NASA ADS] [Google Scholar]
- Carlsson, M. 1986, Uppsala Astronomical Observatory Reports, 33 [Google Scholar]
- Carlsson, M. 1992, in Cool Stars, Stellar Systems, and the Sun, ed. M. S. Giampapa, & J. A. Bookbinder, ASP Conf. Ser., 26, 499 [Google Scholar]
- Carlsson, M., Rutten, R. J., Bruls, J. H. M. J., & Shchukina, N. G. 1994, A&A, 288, 860 [NASA ADS] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, [arXiv:astro-ph/0405087] [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunto, W., & Mendoza, C. 1992, Rev. Mex. Astron. Astrofis., 23, 107 [NASA ADS] [Google Scholar]
- Denisenkov, P. A., & Denisenkova, S. N. 1990, SvA Lett., 16, 275 [Google Scholar]
- Dimitrijević, M. S., & Sahal-Bréchot, S. 1985, J. Quant. Spectrosc. Rad. Trans., 34, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitrijević, M. S., & Sahal-Bréchot, S. 1990, J. Quant. Spectrosc. Rad. Trans., 44, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Drawin, H.-W. 1968, Z. Phys., 211, 404 [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M., Frank, C., Reetz, J., & Gehren, T. 1997, A&A, 323, 909 [NASA ADS] [Google Scholar]
- Gao, X., Han, X., Voky, L., Feautrier, N., & Li, J. 2010, Phys. Rev. A, 81, 022703 [NASA ADS] [CrossRef] [Google Scholar]
- Gehren, T., Shi, J. R., Zhang, H. W., Zhao, G., & Korn, A. J. 2006, A&A, 451, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R., Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., Carretta, E., Eriksson, K., & Gustafsson, B. 1999, A&A, 350, 955 [NASA ADS] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoang Binh, D., & Van Regemorter, H. 1997, J. Phys. B At. Mol. Phys., 30, 2403 [Google Scholar]
- Igenbergs, K., Schweinzer, J., Bray, I., Bridi, D., & Aumayr, F. 2008, Atomic Data and Nuclear Data Tables, 94, 981 [Google Scholar]
- Kaulakys, B. 1991, J. Phys. B At. Mol. Phys., 24, L127 [Google Scholar]
- Lind, K., Asplund, M., & Barklem, P. S. 2009, A&A, 503, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Charbonnel, C., Decressin, T., et al. 2011, A&A, 527, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L. I., Shimanskiĭ, V. V., & Sakhibullin, N. A. 2000, Astron. Rep., 44, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Park, C. 1971, J. Quant. Spectrosc. Rad. Trans., 11, 7 [Google Scholar]
- Phelps, J. O., & Lin, C. C. 1981, Phys. Rev. A, 24, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Tomkin, J., Lambert, D. L., & Allen de Prieto, C. 2003, MNRAS, 340, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Sansonetti, J. E. 2008, J. Phys. Chem. Ref. Data, 37, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1962, Proc. Phys. Soc., 79, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, J. R., Gehren, T., & Zhao, G. 2004, A&A, 423, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sydoryk, I., Bezuglov, N. N., Beterov, I. I., et al. 2008, Phys. Rev. A, 77, 042511 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Zhao, G., Takada-Hidai, M., et al. 2003, Chinese J. Astron. Astrophys., 3, 316 [Google Scholar]
- Unsöld, A. 1955, Physik der Sternatmospharen, MIT besonderer Berucksichtigung der Sonne (Berlin, Springer) [Google Scholar]
- van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic term diagram of the 23-level Na I model atom. The dashed line marks the Na II continuum. The highest level considered in Na I is n = 12. |
| In the text | |
 |
Fig. 2 Three sample excitation cross-sections for collisions between Na I and electrons. The black solid lines represent R-matrix calculations (Feautrier et al. 2010; Gao et al. 2010) and the red dashed lines represent the analytical fitting functions derived by Igenbergs et al. (2008). The transitions are marked with labels next to the energy thresholds. |
| In the text | |
 |
Fig. 3 Comparison between rate coefficients at T = 6000 K for collisional excitation of Na I by neutral hydrogen atoms. Only optically allowed transitions are shown and x-axis represents the energy of the transition. Top: the ratio between the unscaled Drawin formula and the free electron model of Kaulakys (1991) for transitions between highly excited states. Bottom: the ratio between the unscaled Drawin formula and the quantum mechanical calculations by Barklem et al. (2010) for transitions between levels up to 5s. |
| In the text | |
 |
Fig. 4 Contour diagrams illustrating how the abundance corrections vary with effective temperature and surface gravity for four commonly analysed lines of Na I. Only the results for ξ = 2 km s-1 and [Na/Fe] = 0 are shown. |
| In the text | |
 |
Fig. 5 Non-LTE abundance corrections as functions of equivalent width for selected Na I lines for a metal-poor turn-off star (top: Teff = 6400 K, log g = 4.0, [Fe/H] = −2, and ξt = 2.0 km s-1) and metal-poor giant (bottom: Teff = 5000 K, log g = 2.0, [Fe/H] = −2, and ξt = 2.0 km s-1). The black bullets indicate the predicted line strength and abundance corrections at [Na/Fe] = 0. |
| In the text | |
 |
Fig. 6 Departure coefficients for a solar model, for the Na I levels indicated with labels in the plot. Solid: neglecting collisions with neutral hydrogen. Dotted: including charge exchange reactions and bound-bound collisional excitation by neutral hydrogen. Bullets: including only charge exchange reactions in collisions with hydrogen. |
| In the text | |
 |
Fig. 7 Comparison between the abundance corrections determined in this study (lines connected with bullets) and earlier studies, as indicated in each panel (lines connected with plus signs). Effective temperature is used as reference axis, with surface gravity values for each model indicated along the top axis of each panel. All calculations assumed [Na/Fe] = 0.0. |
| In the text | |
 |
Fig. 8 Top: temperature difference between atlas9 models with respect to marcs models (Gustafsson et al. 2008), for a metal-poor giant (Teff = 5000 K, log g = 2.0, [Fe/H] = −2.0, ξt = 2.0 km s-1). The dotted line represents an atlas9 model with scaled solar composition and convective overshoot from the Kurucz 1993-grid. The dashed line has the same composition, but without overshoot. The dashed-dotted line represents a 0.4 dex alpha-enhanced atlas9 model without overshoot from the 2004-grid by Castelli & Kurucz. Middle: difference between LTE abundance as function of line strength for the same models with respect to marcs. The abundances are based on the 819.4 nm Na I line and vary from left to right between [Na/Fe] = −2.0... +2.0. Bottom: same as the middle panel, but for non-LTE abundances. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


