| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201015926 | |
| Published online | 17 February 2011 | |
First stars
XIV. Sulfur abundances in extremely metal-poor stars⋆
1
GEPI Observatoire de Paris, CNRS, Université Paris Diderot,
92195
Meudon Cedex,
France
e-mail: monique.spite@obspm.fr
2
Zentrum für Astronomie der Universität Heidelberg,
Landessternwarte, Königstuhl
12, 69117
Heidelberg,
Germany
3
Department of Astronomy and Astronomical Observatory, Odessa
National University, and Isaac Newton Institute of Chile, Odessa branch, Shevchenko Park, 65014
Odessa,
Ukraine
4
Las Cumbres Observatory, Goleta, CA
93117,
USA
5
Observatoire de la Côte d’Azur, CNRS UMR6202,
BP4229,
06304
Nice Cedex 4,
France
6
GRAAL, Université de Montpellier II, 34095
Montpellier Cedex 05,
France
7
The Niels Bohr Institute, Astronomy, Juliane Maries Vej 30, 2100
Copenhagen,
Denmark
8
Nordic Optical Telescope, Apartado 474,
38700
Santa Cruz de La Palma,
Spain
9
Universidade de São Paulo, Departamento de
Astronomia, Rua do Matão
1226, 05508-900
São Paulo,
Brazil
10
Department of Physics & Astronomy and JINA: Joint
Institute for Nuclear Astrophysics, Michigan State University,
East Lansing,
MI
48824,
USA
11
Istituto Nazionale di Astrofisica, Osservatorio Astronomico di
Trieste, via Tiepolo 11, 34143
Trieste,
Italy
12
European Southern Observatory (ESO), Karl-Schwarschild-Str. 2, 85748
Garching b. München,
Germany
Received:
14
October
2010
Accepted:
9
December
2010
Context. Precise S abundances are important in the study of the early chemical evolution of the Galaxy. In particular the site of the formation remains uncertain because, at low metallicity, the trend of this α-element versus [Fe/H] remains unclear. Moreover, although sulfur is not bound significantly in dust grains in the ISM, it seems to behave differently in DLAs and old metal-poor stars.
Aims. We attempt a precise measurement of the S abundance in a sample of extremely metal-poor stars observed with the ESO VLT equipped with UVES, taking into account NLTE and 3D effects.
Methods. The NLTE profiles of the lines of multiplet 1 of S I were computed with a version of the program MULTI, including opacity sources from ATLAS9 and based on a new model atom for S. These profiles were fitted to the observed spectra.
Results. We find that sulfur in EMP stars behaves like the other α-elements, with [S/Fe] remaining approximately constant below [Fe/H] = –3. However, [S/Mg] seems to decrease slightly with increasing [Mg/H]. The overall abundance patterns of O, Na, Mg, Al, S, and K are most closely matched by the SN model yields by Heger & Woosley. The [S/Zn] ratio in EMP stars is solar, as also found in DLAs. We derive an upper limit to the sulfur abundance [S/Fe] < +0.5 for the ultra metal-poor star CS 22949-037. This, along with a previously reported measurement of zinc, argues against the conjecture that the light-element abundance pattern of this star (and by analogy, the hyper iron-poor stars HE 0107-5240 and HE 1327-2326) would be due to dust depletion.
Key words: Galaxy: abundances / Galaxy: halo / Galaxy: evolution / stars: abundances / supernovae: general
© ESO, 2011
1. Introduction
The determination of the abundance of sulfur in the atmosphere of old Galactic stars is of interest for two primary reasons:
-
First, since unlike most other heavy elements, sulfur is generallyconsidered not to be significantly bound in interstellar dustgrains, it is a good indicator of the chemical composition of theISM and thus allows a direct comparison between the abundancesin the DLAs (damped Lyα clouds) and early Galactic matter.
-
Secondly, the formation of sulfur remains controversial. Sulfur is generally considered as an α-capture element such as magnesium and calcium, formed preferentially in massive type II supernovae, including those of the first generations of stars. In analogy with other α-elements, [S/Fe] is expected to be constant and positive at low metallicity (see e.g. François 1987, 1988). However, the trend of [S/Fe] versus [Fe/H] in the early Galaxy is still debated: Israelian & Rebolo (2001) and Takada-Hidai et al. (2002) found [S/Fe] to rise with decreasing [Fe/H], while Ryde & Lambert (2004) and Nissen et al. (2004, 2007) found [S/Fe] to remain flat. Finally, Caffau et al. (2005, 2010a), combining their own data with a large sample from the literature covering the multiplets 1, 3, 6, and 8 of S I (see Table 1), suggest a bimodal distribution of [S/Fe] for [Fe/H] < −1.0 to explain the high value of [S/Fe] found in several metal-poor stars.
A rise in [S/Fe] with decreasing [Fe/H] is difficult to explain. It has been suggested that SNe with high explosion energies (hypernovae) could have made a substantial contribution to the nucleosynthesis of elements in the early Galaxy (Israelian & Rebolo 2001; Nakamura et al. 2001), or even that they may be responsible for a delayed deposition of the supernova-synthesized products into the interstellar medium (Ramaty et al. 2000).
Parameters of the sulfur lines.
On the other hand, Takeda et al. (2005) noted that, even taking into account the non-LTE effects on the formation of the S lines, the resulting abundance of sulfur depended on the multiplet used for this determination. There was, in particular, an apparent discrepancy between the abundance trends deduced from multiplets 6 and 1.
Taking advantage of a new model atom of sulfur (Korotin 2008, 2009a,b), based on new radiative photoionization rates, we here report S abundances for 33 very metal-poor stars, including 21 extremely metal-poor (EMP) stars with [Fe/H] < −2.9. Our study is based on a precise high-resolution NLTE analysis of the lines of the multiplet (hereafter Mult.) 1 of S I at λλ 921.29, 922.81, and 923.75 nm (see Table 1).
2. Observations and reduction
All stars were observed as part of the ESO large programme “First Stars”, using the high-resolution spectrograph UVES (Dekker et al. 2000) at the ESO-VLT. The spectra were discussed in detail by Cayrel et al. (2004) and Bonifacio et al. (2007, 2009). The resolving power of the spectra is R ≈ 43 000 with 5 pixels per spectral resolution element. The spectra were reduced using the UVES context within MIDAS (Ballester et al. 2000). The signal-to-noise ratio (S/N) per pixel in the region of the S I lines is typically ~180 for the giants and ~90 for the dwarfs (or 400 and 200 per resolution element, see Cayrel et al. 2004).
Three Ba-poor giants (McWilliam et al. 1995) were also observed as part of the programme, under similar conditions as the other metal-poor stars (see also Andrievsky et al. 2011). The S abundance could be determined for one of them (CS 22949-048), which has been added to the sample.
3. Choice of sulfur lines and determination of fundamental atmospheric parameters
In cool stars, five multiplets of S I can be observed in the red and near-infrared spectral region (Table 1): Mult. 1 at about 922 nm, Mult. 3 at 1045 nm, Mult. 6 at 869 nm, and Mult. 8 at 675 nm (Caffau et al. 2005, 2010a), and Mult. 1F, the forbidden line at 1082.1 nm (Ryde 2006; Caffau & Ludwig 2007). However, in EMP stars, the lines of multiplets 6 and 8 are too weak to permit a precise analysis (see Fig. 1). The lines of Mult. 3 and Mult. 1F, are non-detectable in stars with [Fe/H] < −2.9, and are in any case outside the range of our spectra. The S abundances reported in this paper are therefore derived from the lines of Mult. 1 at 921.286, 922.809, and 923.754 nm.
 |
Fig. 1 Spectra of BD+17 3248 and HD 2796, showing the line at 869.46 nm in Mult. 6 of S I. We detect the line in BD+17 3248 ([Fe/H] = –2.1), but not in HD 2796 ([Fe/H] = –2.5). A synthetic spectrum (full line) corresponding to the equivalent width of 0.26 pm found by Israelian and Rebolo for this line has been superimposed on our spectrum of HD 2796. |
The line at 922.809 nm is located in the wing of the Paschen ζ line, and the absorption from the hydrogen line has been taken into account in the computations (see Fig. 2). This spectral region is also crowded with telluric absorption lines of H2O. Since no hot star was included among the programme stars, we did not try to remove these telluric lines, but carefully computed their position relative to the stellar lines using only S I lines free of contamination. At least one or two lines in each spectrum in general are free of blending.
 |
Fig. 2 Spectrum of the giant star CS 29491-053 ([Fe/H] = –3.0) in the region of the S I lines of multiplet 1 (wavelength in nm). The synthetic spectrum (red line) has been computed for the adopted abundance (Table 3), and for an abundance 2.5 times smaller (thin blue line). The S line at 922.8 nm lies in the wing of the hydrogen line Pζ; all other lines in this region are of telluric origin. In our analysis, all S lines blended with telluric lines have been rejected. |
Table 2 provides equivalent widths of the S I lines, since they were published neither in Cayrel et al. (2004) nor Bonifacio et al. (2009). In this spectral region, the observed spectra are affected by fringing, which is not completely compensated when dividing by a flat field (Nissen et al. 2007). The continuum level is therefore often not well defined, and we estimate that the error in the equivalent width can reach 0.4 pm for giants and 0.5 pm for dwarfs. Since in all the cases, the sulfur lines in Table 2 are “weak”, the uncertainties, as a first approximation, are proportional to the EWs of the lines: Δ(log ab) = Δ(log EW). However, these equivalent widths were not used in the computations since we directly compared synthetic and observed spectra; they are given here only for comparison.
Equivalent widths (pm) of the S I lines of multiplet 1.
In total, we could thus determine S abundances in 26 giants and 7 turnoff stars from our original sample.
4. NLTE calculations and 3D correction
The atmospheric parameters of the stars (Teff, log g, [Fe/H]) were adopted from Cayrel et al. (2004), Hill et al. (2002), and Bonifacio et al. (2007) and for the Ba-poor star from Andrievsky et al. (2011). To summarize, the temperature of the giants were inferred from their colours by adopting the calibration of Alonso et al. (1996), and the temperature of the turnoff stars from the wings of the Hα line. The random error in the temperature is about 80 K (1σ). For a given stellar temperature, the ionization equilibrium provides an estimate of the stellar gravity with an internal accuracy of about 0.1 dex in log g, and the microturbulence velocity vt can be constrained to within 0.2 km s-1. The adopted parameters are given in Table 3. Table 4 lists the uncertainty in the sulfur abundance originating in the errors in Teff, log g, and vt. Because gravity is determined from the ionization equilibrium, a variation in Teff will change log g and also sometimes slightly influences vt. Hence, the total error budget is not the quadratic sum of the various sources of uncertainties, but contains significant covariance terms (see Cayrel et al. 2004, for more details).
Adopted atmospheric parameters and NLTE S abundances for our sample of EMP stars.
Abundance uncertainties linked to stellar parameters.
Our log g value may be affected by NLTE effects (overionization) and the uncertainties in the oscillator strengths of the Fe and Ti lines. This was discussed in Cayrel et al. (2004), their Sect. 3.1.: even for giants the spectroscopic log g and the log g value deduced from isochrones should not differ by more than about 0.3 dex.
For the non-LTE computations of the sulfur abundance, Kurucz models without overshooting were used (Castelli et al. 1997). These models have been shown to provide LTE abundances very similar (within 0.05 dex) to those of the MARCS models used by Cayrel et al. (2004) and Bonifacio et al. (2009).
It has been shown (see Takeda et al. 2005; Korotin 2008) that Mult. 1 of S I is affected by a significant negative non-LTE correction. To compute NLTE profiles of the S I lines, we used the model atom of Korotin (2008), which contains 64 levels of S I and the ground level of S II. The radiative photoionization rates of all the levels taken into account are based on the new detailed ionization cross-sections listed in the Opacity Project TopBase (hereafter TopBase)1. The oscillator strengths of the lines are also taken from TopBase.
 |
Fig. 3 NLTE correction for the 921.2 nm sulfur line in metal-poor stars as a function of the temperature, the gravity, and the metallicity for [Fe/H] = –2, [Fe/H] = –3 (dashed lines) and [Fe/H] = –4 (solid line). This correction has been computed for [S/H] = [Fe/H]. |
We also computed the 3D correction (as explained in Caffau et al. 2010b; or Caffau & Ludwig 2007). This correction is small, but positive (Table 3), and has been computed and applied separately.
4.1. Test of coherence
With the model atom adopted here, there is good agreement (to within 0.1 dex) in the Sun and in Procyon between the S abundances derived from the different multiplets when 3D models are used. For Procyon, we found ϵ(S) = 7.23 ± 0.03 from the 3D, LTE computations of Caffau et al. (2007) with a Korotin’s NLTE correction (private communication). For the Sun, the mean sulfur abundance derived from these computations is log ϵ(S) = 7.16 ± 0.05, for log ϵ(H) = 12.0 (Caffau et al. (2010b). This value is very close to the meteoritic value (7.17 ± 0.02, following Lodders et al. 2009). The solar abundance log ϵ(S) = 7.16 has been adopted as a reference in our computations.
Moreover, for the most metal-rich star of our sample, BD+17 3248, the S abundance could be determined from the lines of the Mult. 1 and the main line of Mult. 6 (Fig. 1a). The agreement between the NLTE S abundances derived from multiplets 6 and 1 is very good when the 3D correction is also included (−0.02 for Mult. 6, +0.10 for Mult. 1): ϵ(S) = 5.28 ± 0.2 from Mult. 6 and ϵ(S) = 5.22 ± 0.1 from Mult. 1.
5. Results
In Table 3, we present the result of the computations for our sample of stars. The S abundances were derived from fits of synthetic spectra (Fig. 2). The sulfur abundances could not be determined for the most metal-poor stars ([Fe/H] < −3.6 for giants, [Fe/H] < −3.2 for dwarfs), because the lines were too weak to be measured reliably. However, an upper limit to the sulfur abundance was given for CS 22949-037 because this upper limit can help us to explain the chemical anomalies of this star (see Sect. 5.3). The error in the sulfur abundance, given in Table 3, represents the uncertainty in the spectral fitting. This error strongly dominates the total error in both [S/Fe] and [S/Mg].
5.1. [S/Fe] vs. [Fe/H] and comparison to previous studies
Figure 4 shows [S/Fe] as a function of [Fe/H] for our sample of EMP stars. Below [Fe/H] = –2.9, the slope of the relation is very small: a = −0.012 ± 0.006, thus [S/Fe] is practically constant with a mean of ![\hbox{$\rm \overline{[S/Fe]}=+0.35 \pm 0.10$}](/articles/aa/full_html/2011/04/aa15926-10/aa15926-10-eq169.png) . The level of this plateau is in good agreement with the value found by Nissen et al. (2004, 2007) and Caffau et al. (2005),
. The level of this plateau is in good agreement with the value found by Nissen et al. (2004, 2007) and Caffau et al. (2005), ![\hbox{$\rm \overline{[S/Fe]} \approx +0.35$}](/articles/aa/full_html/2011/04/aa15926-10/aa15926-10-eq170.png) (found for the most metal-poor stars of their sample).
(found for the most metal-poor stars of their sample).
 |
Fig. 4 Final NLTE [S/Fe] ratios for our EMP stars. Solid symbols show the turnoff stars, open symbols the giants. |
Behavior of stars with −2.5 < [Fe/H] It is interesting that none of the stars in Fig. 4 is found to be “S-rich” ([S/Fe] > +0.7), in contrast to several stars in the interval −2 < [Fe/H] < −1 (Israelian & Rebolo 2001; Takada-Hidai et al. 2002; Takeda et al. 2005; Caffau et al. 2005).
The most S-rich star in Israelian & Rebolo (2001) is HD 2796, for which [S/Fe] = +0.8. It is included in our sample, but its very high S abundance is not confirmed by our measurement of the lines of Mult. 1 from which we find [S/Fe] = +0.3. Israelian & Rebolo found that EW = 0.26 pm for the main line of Mult. 6 in this star, but although our spectrum has a very high S/N in this region (over 500/pix at 869 nm), we do not detect the line (Fig. 1b). Its equivalent width is clearly smaller than 0.26 pm, the error in the equivalent width was probably underestimated by Israelian and Rebolo. Ryde & Lambert (2004), reanalysed three other S-rich stars from the list of Israelian & Rebolo with 0.55 < [S/Fe] < 0.7 and for all of them they also found a normal sulfur abundance.
In Caffau et al. (2005), three other stars were found to be S-rich (with [S/Fe] > +0.7), BD+02 263, BD+05 3640 and CD-45 13178 (HD 181743), their metallicities being in the interval −2.2 < [Fe/H] < −1.1, thus outside the range of metallicity explored in our paper. Moreover, in HD 181743, Nissen et al. (2007) found from the Mult. 1 a normal abundance of sulfur ([S/Fe] = +0.34), but on the other hand, in BD+05 3640 the high sulfur abundance has been confirmed (but at a lower level) by Caffau et al. (2010a) by the analysis of the Mult. 3.
It remains unclear wether S-rich stars exist with metallicities in the interval −2.5 < [Fe/H] < −1.1.
Recently, Takeda & Takada-Hidai (2011) measured the Mult. 3 of S I in metal-poor stars and found [S/Fe] to be constant in the interval −2.5 < [Fe/H] < −1.1, but to increase suddenly for [Fe/H] < −2.6. They have only five stars with [Fe/H] < −2.6, and in one of them the S line cannot be detected. For G 64-37, the uncertainty is so high that the detection is in doubt (see their Fig. 13). Of the three remaining stars, two of them are in common with our sample: HD 122563 and BD–18 5550. For these stars, we find “normal” S abundances of [S/Fe] = +0.42 and +0.38 from Mult. 1 (Table 3).
To understand the cause of this discrepancy, we remeasured the equivalent widths of the 1045.5449 nm line in the spectra of Takeda & Takada-Hidai (2011), neglecting the other two lines, which are even fainter. The lines of Mult. 3 used by Takeda & Takada-Hidai are weaker than those of Mult. 1 and their spectra have only half the resolution of ours. For HD 122563, we find that EW = 1.5 pm, corresponding to [S/Fe] = +0.45, in excellent agreement with our determination. Since the sulfur lines are weak, the value of [S/Fe] found by Takeda & Takada-Hidai was simply corrected by Δ[S/Fe] = log (EW2/EW1), where EW1 and EW2 represent the old and new equivalent widths. BD–18 5550 is the most S-rich star in the sample of Takeda & Takada-Hidai with [S/Fe] = +0.76, against our value of +0.38 from Mult. 1 (see Fig. 5). For this star, the S/N of the spectrum of Takeda and Takada-Hidai seems to be rather high, but we note that the full width at half maximum (FWHM) of the lines is much larger in this spectrum than in the spectrum of HD 122563, while in our UVES spectra the FWHM of the lines in both stars is about the same. If we fix the FWHM of the lines in BD–18 5550 to the same value as in HD 122563, we find the equivalent width of the 1045.5449 nm line to be about 1.2 pm and [S/Fe] = +0.62. Adopting the Cayrel formula (Cayrel 1988) to estimate the precision of this measurement (with S/N = 150), we find the error of this equivalent width to be close to 0.5 pm. Hence, the error in the abundance ratio should be about 0.2 dex, which makes their result compatible with ours.
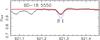 |
Fig. 5 Spectrum of BD–18 5550 in the region of Mult. 1 of S I. Only the main line can be measured in our spectrum, as the others are severely blended with telluric lines. The thick line shows the theoretical profile computed with our value of the S abundance (Table 3). The profile computed with the abundance adopted by Takeda & Takada-Hidai (2011) (thin line), is not compatible with the observed spectrum. |
5.2. [S/Mg] vs. predicted supernova yields
It is often noted that magnesium should be a more reliable reference element than iron, because Mg is only formed in massive SN II and its production is less affected by explosive nucleosynthesis, mixing, and “fallback”. As a consequence, the predictions for [S/Mg] should be more robust than for [S/Fe] (Woosley & Weaver 1995; Shigeyama & Tsujimoto 1998).
The NLTE abundance of Mg for our sample of stars was computed by Andrievsky et al. (2010). Figure 6 shows the observed value of [S/Mg] as a function of [Fe/H] and [Mg/H]. The scatter is small, but two stars seem to have a high [S/Mg] ratio: BS 17570–063 ([Fe/H] = –2.92) and CS 22189–009 ([Fe/H] = –3.49). In both cases, the high [S/Mg] ratio seems to be real, and not the consequence of an uncertainty in the magnesium abundance (see Fig. 6). The full spread of NLTE [Mg/Fe] for the metal-poor stars below [Fe/H] < −1 is definitely larger than expected from the error estimate of the analysis itself (see Gehren et al. 2006; Andrievsky et al. 2010; and also Cayrel et al. 2004) and the anomalies of the magnesium abundances are not clearly correlated with the other elements.
In the interval −3.4 < [Fe/H] < −2.5, we can define a mean value of [S/Mg] as done for O, Na, Al and K by Andrievsky et al. (2010): ![\hbox{$\rm \overline{[S/Mg]}=-0.32 \pm 0.14$}](/articles/aa/full_html/2011/04/aa15926-10/aa15926-10-eq191.png) . In the same metallicity interval, the scatter in [S/Fe] around the mean is only 0.12 dex (see Fig. 4). It appears that, as already observed in LTE (Cayrel et al. 2004), the scatter of the abundance ratios is slightly larger when Mg rather than Fe is used as the reference element. This is surprising because Fe forms in processes quite different from those forming Mg and S (explosive burning for Fe, and mainly hydrostatic C, Ne, and O burning for Mg and S).
. In the same metallicity interval, the scatter in [S/Fe] around the mean is only 0.12 dex (see Fig. 4). It appears that, as already observed in LTE (Cayrel et al. 2004), the scatter of the abundance ratios is slightly larger when Mg rather than Fe is used as the reference element. This is surprising because Fe forms in processes quite different from those forming Mg and S (explosive burning for Fe, and mainly hydrostatic C, Ne, and O burning for Mg and S).
For [Mg/H] < −2.7, a slight increase in [Na/Mg], [Al/Mg], and [K/Mg] as [Mg/H] decreases was seen by Andrievsky et al. (2010). A slight increase in [S/Mg] is also possible (Fig. 6), but there are very few stars with [Mg/H] < −2.7 in our sample. We plan to discuss the evolution of [S/Mg] in the Galaxy in more detail when we have completed a new precise analysis of disk stars, including NLTE and 3D corrections.
5.3. The case of the peculiar C-rich star CS 22949-037
CS 22949-037 is a very peculiar giant: it is extremely metal-poor ([Fe/H] ≈ −4.0), and its unusual chemical composition was first pointed out by McWilliam et al. (1995) and later studied in more detail by Norris et al. (2001) and Depagne et al. (2002). This star exhibits light element (C-N-O, Na, Mg) enhancements that are quite similar to those associated with the hyper iron-poor stars HE 0107-5240 and HE 1327-2326 with [Fe/H] < −5 (see Frebel et al. 2005, 2008). It is generally admitted that these stars are the product of specific zero-metal supernovae. However, Venn & Lambert (2008) argued that this abundance pattern might be associated with the same peculiarity that is used to account for λ Boo stars (presumably related to dust depletion). If this were so, the abundance of the elements should be smoothly correlated with the condensation temperature Tcond. The abundances of S and Zn could help us to choose between the two hypotheses, because their temperatures are intermediate between those of O and Na, both of which are strongly enhanced in CS 22949-037. If dust depletion is responsible for the pattern of CS 22949-037 we would expect that sulfur and zinc also be strongly enhanced in this star. The abundance of zinc was measured in CS 22949-037 by Depagne et al. (2002). The sulfur lines are not visible in this star but (as can be seen in Table 3) an upper limit can be estimated as [S/H] < −3.5 or [S/Fe] < +0.5. In Fig. 7, we have plotted [X/H] vs. Tcond. The abundances [X/H] of C, N, O, Ca, Fe, and Zn are taken from Depagne et al. (2002); for the other elements Na, Mg, Al, S, Sr, and Ba, the NLTE abundances (Andrievsky et al. 2007, 2008, 2009, 2010, 2011) have been preferred. The oxygen abundance, determined from the forbidden line, is insensitive to the NLTE effects. It can be seen that CS 22949-037 does not show any clear signature of dust depletion.
 |
Fig. 7 [X/H] abundances in CS 22949-037 against the solar condensation temperatures (Lodders 2003). There is no correlation between Tcond and the abundance of the elements, in particular S and Zn have a condensation temperature lower than Na and they are more deficient, at variance with the abundances in λ Boo stars. (The filled circles represent the abundances corrected or not sensitive to NLTE effects, the open symbols are abundances that could not be corrected for NLTE effects). |
 |
Fig. 8 Comparison of the most recent O, Na Mg, Al, S, and K abundances in EMP stars to the predicted yields of metal-poor SNe and hypernovae. The solid lines represent the predictions of different models, and the dots the mean values of the observed abundances in the interval −3.0 < [Mg/H] < −2.0. |
5.4. Comparison with predicted SN yields
In Fig. 8, we compare the abundance ratios of the light metals to some predicted abundances in the ejecta of metal-poor SNe or hypernovae following Woosley & Weaver (1995), Kobayashi et al. (2006), and Heger & Woosley (2010). The mean values of the observed abundances of the different elements are computed in the interval −3.0 < [Mg/H] < −2.0, their uncertainty being of the order of 0.1 dex. The amount of ejected S seems to be generally overestimated by the models. If we consider all the elements from O to K, the best agreement is obtained with the predictions by the models of Heger & Woosley 2010 (hypotheses B or D, with a low mass cutoff at 10 M⊙), mainly because their predictions show a better agreement with the observed K abundance.
5.5. [S/Zn] in metal-poor stars and damped Lyα systems
Nissen et al. (2004) suggested that the [S/Zn] ratio is higher in stars than in damped Lyα systems. Neither S nor Zn shows much affinity for dust, although MgS has been recently proposed as a possible grain constituent by Zhang et al. (2009). Thus, depletion onto dust in DLAs probably cannot explain this difference. Nissen et al. (2007) have shown that in the interval −2.5 < [Zn/H] < 0 this effect is considerably reduced if one adopts the non-LTE corrections to the abundances of S and Zn.
Figure 9 shows [S/Zn] vs. [Zn/H] for our sample of metal-poor stars and for the most metal-poor DLAs with both Zn and S abundance determinations (Table 5). Since the Zn line is very weak in turnoff stars, we could only measure Zn abundances in our giant stars (Cayrel et al. 2004). Following Takeda et al. (2005), non-LTE effects for Zn are not very important in these stars (≤+0.1 dex), but we have applied the small correction obtained by interpolation in their tables.
 |
Fig. 9 [S/Zn] vs. [Zn/H] in EMP stars (circles) and in metal-poor DLAs (triangles). |
[Zn/H] and [S/Zn] in the most metal-poor DLAs.
With stellar NLTE effects taken into account for both S and Zn, Fig. 9 shows that the sulfur abundance in metal-poor stars is rather similar to that in DLAs – if anything slightly lower. However, the chemical evolution of the Galactic halo might still be different from the average of DLAs.
In EMP stars as in DLAs, the [S/Zn] ratio is approximately solar. This is due to positive values of both [S/Fe] (Fig. 4) and [Zn/Fe] at very low metallicity (Cayrel et al. 2004; see also Primas et al. 2000; and Nissen et al. 2004). We will discuss the evolution of the [S/Zn] ratio in the Galaxy in more detail when we have completed a new precise analysis of S abundances in less metal-poor stars.
6. Conclusions
We have determined S abundances in 33 metal-poor stars, including 21 with [Fe/H] < −2.9, and find [S/Fe] to be fairly constant at [S/Fe] = 0.35 ± 0.10. However, a slight increase in [S/Mg] when [Mg/H] decreases cannot be excluded (Fig. 6). The same effect is also observed for Na, Al, and K (Spite et al. 2009; Andrievsky et al. 2010).
We do not confirm earlier claims of a significant rise in [S/Fe] with decreasing [Fe/H], but corroborate the findings of Nissen et al. (2004, 2007) and Ryde & Lambert (2004) that S behaves like the other α-elements, also at very low metallicity.
The low sulfur abundance (along with a low abundance of zinc) in CS 22949-037 suggests that the abundance pattern in this star (and thus by analogy in the hyper iron-poor stars HE 0107-5240 and HE 1327-2326) is the result of specific zero-metal supernovae and is unrelated to dust depletion as suggested by Venn & Lambert (2008).
When the NLTE effects are taken into account, the pattern of the light elements from O to K relative to magnesium, is rather well represented by ejecta of zero-metal supernovae (Heger & Woosley 2010).
The ratio [S/Zn] is found to be approximately solar as it is in DLAs since [S/Fe] and [Zn/Fe] are both equally positive at low metallicity.
Acknowledgments
S.M.A. gratefully acknowledges the support and hospitality of Observatoire de Paris-Meudon. M.S., E.C., F.S., P.B., R.C., P.F. and V.H. acknowledge the support of CNRS (PNCG and PNPS). BB acknowledges grants from FAPESP and CNPq. B.N. and J.A. acknowledge the support of the Carlsberg Foundation and the Danish Natural Science Research Council and TCB acknowledges partial funding of this work from grants PHY 02-16783 and PHY 08-22648: Physics Frontiers Center/Joint Institute for Nuclear Astrophysics (JINA), awarded by the US National Science Foundation. We also thank the anonymous referee for his helpful comments.
References
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2007, A&A, 464, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2008, A&A, 481, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2009, A&A, 494, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrievsky, S. M., Spite, M., Korotin, S. A., et al. 2010, A&A, 509, 88 [Google Scholar]
- Andrievsky, S. M., Spite, F., Korotin, S. A., et al. 2011, A&A, submitted [Google Scholar]
- Ballester, P., Modigliani, A., Boitiquin, O., et al. 2000, ESO Messenger, 101, 31 [Google Scholar]
- Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 (First Stars VII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Spite, M., Cayrel, R., et al. 2009, A&A, 501, 519 (First Stars XII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., & Ludwig, H.-G. 2007, A&A, 467, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Bonifacio, P., Faraggiana, R., et al. 2005, A&A, 441, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Faraggiana, R., Bonifacio, P., Ludwig, H.-G., & Steffen, M. 2007, A&A, 470, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Sbordone, L., Faraggiana, R., et al. 2010a, AN, 331, 725 [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2010b, Sol. Phys., 66 [Google Scholar]
- Carlsson, M. 1986, Uppsala Obs. Rep. 33 [Google Scholar]
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
- Cayrel, R. 1988, in The impact of very high S / N spectroscopy on stellar physics, ed. G. Cayrel de Strobel, M. Spite (Dordrecht: Kluwer Academic Publishers), Proc. IAU Symp., 132, 345 [Google Scholar]
- Cayrel, R., Depagne, E., Spite, M., et al. 2004, A&A, 416, 1117 (First Stars V) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centurión, M., Molaro, P., & Vladilo, G. 2003, A&A, 403, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., et al. 2000, in Optical and IR Telescopes Instrumentation and Detectors, ed. I. Masanori, & A. F. Morwood, Proc. SPIE, 4008, 534 [Google Scholar]
- Depagne, E., Hill, V., Spite, M., et al. 2004, A&A, 416, 1117 (First Stars II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessauges-Zavadsky, M., Calura, F., Prochaska, J. X., D’Odorico, S., & Matteucci, F. 2004, A&A, 416, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessauges-Zavadsky, M., Prochaska, J. X., D’Odorico, S., Calura, F., & Matteucci, F. 2006, A&A, 445, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessauges-Zavadsky, M., Calura, F., Prochaska, J. X., D’Odorico, S., & Matteucci, F. 2007, A&A, 470, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, S. L., & Lopez, S. 2001, A&A, 380, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- François, P. 1987, A&A, 176, 294 [NASA ADS] [Google Scholar]
- François, P. 1988, A&A, 195, 226 [NASA ADS] [Google Scholar]
- Frebel, A., Aoki, W., Christlieb, N., et al. 2005, Nature, 434, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Frebel, A., Collet, R., Eriksson, K. et al. 2008, ApJ, 684, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Gehren, T., Shi, J. R., Zhang, H. W. et al. 2006, A&A, 451, 1065 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., & Woosley, S. E. 2010, ApJ, 724, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Plez, B., Cayrel, R., et al. 2002, A&A, 387, 560 (First Stars I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Israelian, G., & Rebolo, R. 2001, ApJ, 557, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Umeda, H., Nomoto, K., Tominaga, N., & Ohkubo, T. 2006, ApJ, 653,1145 [NASA ADS] [CrossRef] [Google Scholar]
- Korotin, S. A. 2008, Odessa Astron. Pub. 21, 42 [Google Scholar]
- Korotin, S. A. 2009a, Astronomicheski’ Zhurnal, 86, 702 [Google Scholar]
- Korotin, S. A. 2009b, Astr. Rep., 53, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Korotin, S. A., Andrievsky, S. M., & Luck, R. E. 1999, A&A, 351, 168 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1992, RMxAA, 23, 181 [Google Scholar]
- Ledoux, C., Petitjean, P., & Srianand, R. 2003, MNRAS, 346, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt-Börnstein, New Series, Astronomy and Astrophysics (Berlin: Springer Verlag) [Google Scholar]
- Lopez, S., & Ellison, S. L. 2003, A&A, 403, 573 [Google Scholar]
- Lopez, S., Reimers, D., D’Odorico, S., & Prochaska, J. X. 2002, A&A, 385, 778 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, P., Vladilo, G., & Centurión, M. 1998, MNRAS, 293, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, T., Umeda, H., Iwamoto, K., et al. 2001, ApJ, 555, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P., Chen, Y. Q., Asplund, M., & Pettini, M. 2004, A&A, 415, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., Akerman, C., Asplund, M., et al. 2007, A&A, 469, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, J. E., Ryan, S. G., & Beers, T. C. 2001, ApJ, 561, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., et al. 2007, A&A, 474, 393 [Google Scholar]
- Pettini, M., Smith, L. J., Hunstead, R. W., & King, D. L. 1994, ApJ, 426, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Ellison, S. L., Steidel, C. C., Shapley, A. E., & Bowen, D. V., 2000, ApJ, 532, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Primas, F., Brugamyer, E., Sneden, C., et al. 2000, in The First Stars: Proceedings of the MPA/ESO Workshop, ESO astrophysics symposia, ed. A. Weiss, T. G. Abel, V. Hill. (Springer-Verlag), 51 [Google Scholar]
- Prochaska, J. X., Wolfe, A. M., Tytler, D., et al. 2001, ApJS, 137, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ramaty, R., Scully, S., Lingenfelter, R., & Kozlovsky, B. 2000, ApJ, 534, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N. 2006, A&A, 455, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryde, N., & Lambert, D. L. 2004, A&A, 415, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shigeyama, T., & Tsujimoto, T. 1998, ApJ, 507, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M., Spite, F., Bonifacio, P., et al. 2009, in Chemical Abundances in the Universe: Connecting First Stars to Planets, ed. K. Cunha, M. Spite, & B. Barbuy, Proc. IAU Symp., 265, 380 [Google Scholar]
- Srianand, R., Petitjean, P., Ledoux, C., Ferland, G., & Shaw, G. 2005, MNRAS, 362, 549 [Google Scholar]
- Takada-Hidai, M., Takeda, Y., Sato, S., et al. 2002, ApJ, 573, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., & Takada-Hidai, M. 2011, PASJ, in press [arXiv:1009.0824] [Google Scholar]
- Takeda, Y., Hashimoto, O., Taguchi, H., et al. 2005, PASJ, 57, 751 [NASA ADS] [Google Scholar]
- Venn, K. A., & Lambert, D. L. 2008, ApJ, 677, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Jiang, B. W., & Li, A. 2009, ApJ, 702, 680 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Adopted atmospheric parameters and NLTE S abundances for our sample of EMP stars.
All Figures
 |
Fig. 1 Spectra of BD+17 3248 and HD 2796, showing the line at 869.46 nm in Mult. 6 of S I. We detect the line in BD+17 3248 ([Fe/H] = –2.1), but not in HD 2796 ([Fe/H] = –2.5). A synthetic spectrum (full line) corresponding to the equivalent width of 0.26 pm found by Israelian and Rebolo for this line has been superimposed on our spectrum of HD 2796. |
| In the text | |
 |
Fig. 2 Spectrum of the giant star CS 29491-053 ([Fe/H] = –3.0) in the region of the S I lines of multiplet 1 (wavelength in nm). The synthetic spectrum (red line) has been computed for the adopted abundance (Table 3), and for an abundance 2.5 times smaller (thin blue line). The S line at 922.8 nm lies in the wing of the hydrogen line Pζ; all other lines in this region are of telluric origin. In our analysis, all S lines blended with telluric lines have been rejected. |
| In the text | |
 |
Fig. 3 NLTE correction for the 921.2 nm sulfur line in metal-poor stars as a function of the temperature, the gravity, and the metallicity for [Fe/H] = –2, [Fe/H] = –3 (dashed lines) and [Fe/H] = –4 (solid line). This correction has been computed for [S/H] = [Fe/H]. |
| In the text | |
 |
Fig. 4 Final NLTE [S/Fe] ratios for our EMP stars. Solid symbols show the turnoff stars, open symbols the giants. |
| In the text | |
 |
Fig. 5 Spectrum of BD–18 5550 in the region of Mult. 1 of S I. Only the main line can be measured in our spectrum, as the others are severely blended with telluric lines. The thick line shows the theoretical profile computed with our value of the S abundance (Table 3). The profile computed with the abundance adopted by Takeda & Takada-Hidai (2011) (thin line), is not compatible with the observed spectrum. |
| In the text | |
 |
Fig. 6 [S/Mg] vs. [Fe/H] (top) and [Mg/H] (bottom). Symbols as in Fig. 4. |
| In the text | |
 |
Fig. 7 [X/H] abundances in CS 22949-037 against the solar condensation temperatures (Lodders 2003). There is no correlation between Tcond and the abundance of the elements, in particular S and Zn have a condensation temperature lower than Na and they are more deficient, at variance with the abundances in λ Boo stars. (The filled circles represent the abundances corrected or not sensitive to NLTE effects, the open symbols are abundances that could not be corrected for NLTE effects). |
| In the text | |
 |
Fig. 8 Comparison of the most recent O, Na Mg, Al, S, and K abundances in EMP stars to the predicted yields of metal-poor SNe and hypernovae. The solid lines represent the predictions of different models, and the dots the mean values of the observed abundances in the interval −3.0 < [Mg/H] < −2.0. |
| In the text | |
 |
Fig. 9 [S/Zn] vs. [Zn/H] in EMP stars (circles) and in metal-poor DLAs (triangles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


