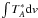| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015837 | |
| Published online | 22 February 2011 | |
A line-confusion limited millimeter survey of Orion KL
II. Silicon-bearing species⋆,⋆⋆
1
Centro de Astrobiología (CSIC-INTA). Departamento de Astrofísica Molecular.
Ctra. de Aljalvir Km 4,
28850 Torrejón de Ardoz,
Madrid,
Spain
e-mail: terceromb@cab.inta-csic.es
2
LERMA and UMR 8112 of CNRS, Observatoire de Paris-Meudon,
92195
Meudon Cedex,
France
3
Department of Physics and Astronomy, University College
London, Gower Street, WC1E
6BT, London,
UK
4
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA
22903,
USA
e-mail: jcernicharo@cab.inta-csic.es; lucie@damir.iem.csic.es; sv@star.ucl.ac.uk; nmarceli@nrao.edu
Received: 29 September 2010
Accepted: 3 December 2010
Aims. We present a study of the silicon-bearing species detected in a line-confusion limited survey towards Orion KL performed with the IRAM 30-m telescope. The analysis of the line survey is organized by families of molecules. Our aim is to derive physical and chemical conditions for each family taking all observed lines into account from all isotopologs of each species. The large number of transitions in different vibrationally excited states covered by our data, which range from 80 to 280 GHz, let us provide reliable source-average column densities (hence, isotopolog abundances and vibrational temperatures) for the detected molecules. In addition, we provide a wide study of the physical properties of the source based on the different spectral components found in the emission lines.
Methods. We modeled the lines of the detected molecules using a radiative transfer code, which permit us to choose between large velocity gradient (LVG) and local thermodynamic equilibrium (LTE) approximations depending on the physical conditions of the gas. We used appropriate collisional rates for the LVG calculations. To qualitatively investigate the origin of the SiS and SiO emissions in Orion KL we ran a grid of chemical models.
Results. For the v = 1 state of SiO, we detected the J = 2−1 line and, for the first time in this source, emission in the J = 4−3 transition, both of them showing a strong masering effect. For SiO v = 0, we detected 28SiO, 29SiO, and 30SiO; in addition, we have mapped the J = 5−4 SiO line. For SiS, we have detected the main species, 29SiS, and SiS v = 1. Unlikely other species detected in Orion KL (IRc2), the emission peak of SiS appears at a velocity of ≃ 15.5 km s-1. A study of the 5−4 SiO line around IRc2 shows this feature as an extended component that probably arises from the interaction of the outflow with the ambient cloud. We derive an SiO/SiS column density ratio of ≃ 13 in the plateau component, four times lower than the cosmic O/S ratio ≃ 48. In addition, we provide upper limits to the column density of several non-detected silicon-bearing species. The results of our chemical models show that while it is possible to reproduce SiO in the gas phase (as well as on the grains), SiS is a product of surface reactions, most likely involving direct reactions of sulfur with silicon.
Key words: surveys / stars: formation / ISM: abundances / ISM: clouds / ISM: molecules / radio lines: ISM
Appendices are only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
The Orion BN/KL (Becklin & Neugebauer 1967; Kleinmann & Low 1967) nebula is one of the most studied star formation regions in the Milky Way. At a distance of 414 pc (Menten et al. 2007), the nebula is embedded in a giant molecular cloud harboring practically all phases of the interstellar medium, from hot and diluted plasma, to PDRs, protostellar cores, molecular outflows, SiO and H2O masering regions, high density cores, intermediate and high mass star formation, protoplanetary disks, and proplydes (see, e.g., Genzel et al. 1980; Genzel & Stuzki 1989; Wright et al. 1995; Cernicharo et al. 1990, 1994; Plambeck et al. 2009).
Together with Sgr B2, Orion BN/KL nebula exhibits a rich spectrum (see, e.g., Tercero et al. 2010, hereafter Paper I, and references therein) produced by complex organic molecules, which are formed through reactions on the grain surfaces during the collapse phase followed by evaporation when radiation from a newly formed star becomes available. The high temperature of the gas cause the molecular lines to be particularly strong in Orion, allowing several line surveys of this source over the past 20 years. Recently, we have performed a line survey towards Orion IRc2 source between 80 and 280 GHz (Paper I), limited not by sensitivity but only by line confusion. The data provide a significant number of transitions for all molecules detected so far towards this source. Although the physical structure of the Orion is rather complex, the many transitions observed for each species allows the different cloud components to be modeled and reliable physical parameters to be derived. In addition, the line survey provides deep insight into the chemistry of the Orion KL region and allows refining our knowledge of its chemical structure by searching for new molecular species and new isotopologs and vibrationally excited states of molecules already known to exist in this source. In a first paper, we presented the line survey and analyzed the CS-bearing species by deriving the abundance of CS, OCS, CCS, CCCS, H2CS, and HCS+ (Paper I). In this paper, we analyze the silicon-bearing species SiO and SiS. SiO has been observed with single dishes and interferometers (see, e.g., Plambeck et al. 2009, and references therein), while only a few observations are available for SiS (Dickinson & Rodríguez-Kuiper 1981; Ziurys 1988, 1991).
The SiO lines in Orion show a complex pattern of thermal and maser emission. The masers seem to arise from a small region around the radio continuum source I (Churchwell et al. 1987), a young star with a very high luminosity without any infrared counterpart, ≃105 L⊙ (Gezari et al. 1998; Greenhill et al. 2004). This source is also driving the low velocity outflow observed in SiO (Beuther et al. 2005; Plambeck et al. 2009) and in other molecular species (Paper I). Recent studies have discussed the driving source of the high velocity outflow. Whereas Beuther & Nissen (2008) claim that SMA1 (a submillimeter source not detected at IR and centimeter wavelengths, predicted by de Vicente et al. 2002, and detected by Beuther et al. 2004) is the host of the high velocity outflow (based on combined observations of J = 2−1 C18O from the SMA and the IRAM 30 m telescope), Plambeck et al. (2009) defend this outflow as a continuation of the low-velocity outflow (based on CARMA observations of SiO v = 0 J = 2−1).
The SiO v = 1 maser emission was modeled in early interferometric observations as arising from a rotating and expanding disk (Plambeck et al. 1990). However, maser emission was also found in the v = 0 J = 2−1 line by Wright et al. (1995), adding more complexity to the modeling of the structure of the emitting source. Recently, Goddi et al. (2009) have found maser emission in the v = 0 J = 1−0 transition of 29SiO and 30SiO associated with source I. In addition, observations of Plambeck et al. (2009) clearly show that the emission of this line arises essentially from an outflow driven by source I. Although our single-dish data cannot provide a view of the spatial structure of the thermal and maser emission around that source, the observed maser and thermal lines can provide useful constraint on the physical conditions of the gas.
In addition to the study of SiO and SiS, we derive upper limits to the abundance of SiC, SiC2, c-SiC3, SiC4, SiN, SiCN, SiNC, ob-SiC3, l-SiC3, Si3, SiCCO, SiCCS, SiH2, H2CSi, and the different isomers of Si2H2. The observations are described in Sect. 2. The results for SiO and SiS are analyzed in Sect. 3. Section 4 is devoted to the modeling of the observed lines. All these results are discussed in Sect. 5 in terms of comparisons with chemical models predictions for silicon-bearing species. The effect of the new collisional rates for SiO and SiS is analyzed in Appendix A.
2. Observations and data analysis
ηMB and HPBW along the covered frequency range.
The observations were carried out using the IRAM 30 m radiotelescope during 2004 September (3 mm and 1.3 mm windows), 2005 March (full 2 mm window), 2005 April (completion of 3 mm and 1.3 mm windows), 2007 January (maps and different positions), and March 2008 (2D line survey using a multibeam receiver). Four SIS receivers operating at 3, 2, and 1.3 mm were used simultaneously with image sideband rejections within 20−27 dB (3 mm receivers), 12−16 dB (2 mm receivers), and 13 dB (1.3 mm receivers). System temperatures were 100−350 K for the 3 mm receivers, 200−500 K for the 2 mm receivers, and 200−800 K for the 1.3 mm receivers, depending on the particular frequency, weather conditions, and source elevation. For the spectra between 172−178 GHz, the system temperature was significantly higher, 1000−4000 K, owing to the proximity of the atmospheric water line at 183.3 GHz. The intensity scale was calibrated using two absorbers at different temperatures and using the atmospheric transmission model (ATM, Cernicharo 1985; Pardo et al. 2001a). The half power beam width (HPBW) and the main beam efficiency (ηMB) along the covered frequency range are given in Table 1.
Pointing and focus were regularly checked on the nearby quasars 0420−014 and 0528+134. The observations were made in the balanced wobbler-switching mode, with a wobbling frequency of 0.5 Hz and a beam throw in azimuth of ± 240′′. No contamination from the off position affected our observations except for a marginal one at the lowest elevations (~25°) for molecules having emission along the extended ridge.
The backends used were two filter banks with 512 × 1 MHz channels and a correlator providing two 512 MHz bandwidths and 1.25 MHz resolution. We pointed towards the (survey) position α = 5h35m14.5s, δ = −5°22′30.0′′ (J2000.0) corresponding to IRc2.
The spectra shown in the figures are in units of main beam temperature, TMB. In spite of the good image band rejection of the receivers, each setting was repeated at a slightly shifted frequency (10−20 MHz) in order to identify and remove all features arising from the image side band. In the data reduction we have removed most of them above 0.05 K (see Paper I for further explanation of this procedure).
Emission lines of SiO, SiO isotopologs, and SiO vibrationally excited present in the frequency range of the Orion KL survey.
2.1. 2D survey observations
The HERA multibeam receiver was used to carry out a systematic line survey between 216−250 GHz over a region of 144 × 144′′ (2 × 2′ approximately) with a 4′′ spacing. System temperatures were around 400−500 K. The sensitivity of the resulting maps was comparable to those of the pointed line survey with the single pixel SIS receivers. The 2D line survey observations were performed in on-the-fly mapping mode, with position switching using a emission-free reference position at an offset (−600′′, 0) from IRc2. We used WILMA as the main backend, covering the full 1 GHz bandwidth provided by HERA with 2 MHz of spectral resolution. We also used the versatile VESPA spectrometer in parallel to get some interesting lines within the 1 GHz range with higher spectral resolution (320 kHz), as we did for J = 5−4 SiO (from all the 2D survey data only the map of this line is shown in this paper). A full description of the 2D line survey will be published elsewhere (Marcelino et al., in prep.).
3. Results
The line survey has been presented elsewhere (Paper I). This paper is devoted to study the emission of silicon-bearing molecules: we detected SiO, 29SiO, 30SiO, SiO v = 1, SiS, 29SiS, and SiS v = 1. For Si18O and Si17O we have evidence of their presence, but all their lines in our frequency range are blended with other molecules. We report the detection of the transition J = 4−3 of SiO v = 1 for the first time for this source. While this transitions shows strong maser emission, rotational lines for v ≥ 2 in the covered frequencies lack maser emission. In the following sections we describe the data and the results for each molecular species.
3.1. SiO
 |
Fig. 1 Observed lines (histogram spectra) and model (thin curves) of SiO and its isotopologs. The dashed line shows a radial velocity at 9 km s-1. |
Five rotational transitions of silicon monoxide (SiO) fall in the covered frequency range of our line survey. For its isotopologs (29SiO, 30SiO, Si18O, and Si17O) and SiO vibrationally excited four rotational transitions are within our frequency range.
 |
Fig. 2 Observed lines of vibrationally excited SiO v = 1 showing maser emission in the transitions J = 2−1 and J = 4−3. The dashed lines show radial velocities at −3.4, + 5.1, and + 13.9 km s-1. |
The rotational constants used to derive the line parameters were taken from Sanz et al. (2003) (for SiO, 29SiO, 30SiO, Si18O, SiO v = 1) and for Si17O, the line parameters were derived from the Dunham coefficients, Yijs, of 28SiO and the isotopic relations 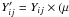 (Si17O)/μ(SiO))(i+2j)/2 (where μ is the reduced mass of the isotopolog). The dipole moment (μ = 3.098D) was reported by Raymonda et al. (1970). Line parameters and observed intensities for all these lines are given in Table 2. Figure 1 shows the observed lines of SiO and its isotopologs, together with the results from our best model (see Sect. 4.1). Figure 2 shows the SiO v = 1 lines within our line survey. The J = 2−1 and J = 4−3 lines show maser emission whereas the J = 5−4 and J = 6−5 are blended with other abundant molecules in Orion and their possible contribution to the observed features is rather weak and two orders of magnitude below the observed emission in the J = 2−1 and J = 4−3 maser emission. Rotational lines from SiO v ≥ 2 are below the detection limit of this line survey. Only v = 2 J = 2−1 seems to have a very weak emission, TMB ≃ 0.06 K, at the velocity of the red component of the maser.
(Si17O)/μ(SiO))(i+2j)/2 (where μ is the reduced mass of the isotopolog). The dipole moment (μ = 3.098D) was reported by Raymonda et al. (1970). Line parameters and observed intensities for all these lines are given in Table 2. Figure 1 shows the observed lines of SiO and its isotopologs, together with the results from our best model (see Sect. 4.1). Figure 2 shows the SiO v = 1 lines within our line survey. The J = 2−1 and J = 4−3 lines show maser emission whereas the J = 5−4 and J = 6−5 are blended with other abundant molecules in Orion and their possible contribution to the observed features is rather weak and two orders of magnitude below the observed emission in the J = 2−1 and J = 4−3 maser emission. Rotational lines from SiO v ≥ 2 are below the detection limit of this line survey. Only v = 2 J = 2−1 seems to have a very weak emission, TMB ≃ 0.06 K, at the velocity of the red component of the maser.
The line profiles indicate the contribution to the emerging intensities from different velocity components: the extended and compact molecular ridge (difficult to separate), the hot core, the high-velocity outflow, and the low-velocity plateau. The last appears as the most significant contribution to the line profile and intensity.
Table C.1, only available electronically, gives the parameters for the different cloud components derived by fitting several Gaussian profiles to the observed transitions of SiO and to selected lines of 29SiO and 30SiO. The profiles are separated into two components: one wide component that corresponds to the low and high velocity outflows (the plateau) and a narrow one consisting of a mix of the ridge components with the plateau.
The broad component from the plateau dominates the line profiles and hides the contribution of the hot core at 5 km s-1, which is only marginally detected as a blue shoulder in the emission from the isotopologs. We interpret this behavior as due to the opacity of the SiO lines in the high velocity gas, which could absorb the emission from the hot core (studied for HDO by Pardo et al. 2001b). However, the line profiles of the 29SiO and 30SiO isotopologs, for which the high-velocity gas should be thinner, clearly need a component at the velocity of the hot core (see also the discussion for SiS below) in order to reproduce their line profiles.
3.1.1. J = 5–4 SiO map
From the 2D survey data of Orion KL, a map of the SiO J = 5−4 intensity at different velocity ranges is shown in Fig. B.1. The velocity structure of the SiO emission shows the contribution from all the cloud components quoted above, and we note the spatial displacement of the emission peak with velocity. Particularly interesting is the spatial distribution of the red and blue wings at the largest velocities (panels top left and bottom right). The high-velocity outflow appears as an elliptical shell of gas around IRc2. Recently, Plambeck et al. (2009) have obtained a map with an angular resolution of ≃ 0.5′′ of the v = 0 J = 2−1 line of SiO. Their data for the extreme red velocities, 29−52 km s-1, indicates that the emission is shifted towards the E from source I by 5−10′′. However, blue extreme velocities, −20 to −40 km s-1, are found several arcseconds W and NW of source I. Wright et al. (1996) obtain a similar result in their aperture synthesis ( ≃ 4′′ resolution) v = 0 J = 2−1 SiO velocity map of the extreme velocities (vLSR < −11 km s-1 and vLSR > 29 km s-1). These results are in very good agreement with our lower angular resolution map. Plambeck et al. (2009) find that the bulk of the emission arises from a bipolar outflow covering velocities from −13 to 16 km s-1, driven by source I and with an extent of ≃ 6′′ along the NE-SW direction. The high-velocity outflow, or extreme velocities, seems to be a continuation of the low-velocity outflow but less spatially structured. This “EW bipolarity” of the SiO high-velocity outflow has already been noted by Olofsson et al. (1981). We have obtained angular source sizes between 16′′ for the central velocities to 23′′ for the extreme velocities, assuming emission within the half flux level and corrected for the size of the telescope beam at the observing frequency. The distribution of the high-velocity gas is very similar to what was found in the extended maser emission of H2O at 183.3 GHz found by Cernicharo et al. (1990, 1994).
3.2. SiS
Nine transitions of silicon monosulfide 28Si32S v = 0, 1 and of its rare isotopologs are present in the covered frequency range. Spectroscopic constants are from Sanz et al. (2003). The dipole moment (μ = 1.730D) was taken from Hoeft et al. (1969). Line frequencies and observational line parameters are given in Table 3. The observed line profiles and the results from our best model (see Sect. 4.2) are shown in Fig. 3, for the main isotopolog, and in Fig. B.2 (for 29SiS and SiS v=1). The lines from the other isotopologs are blended with strong lines arising from other molecular species. Only one line (J = 9−8 transition) is free of blending for Si34S. The line intensities arising from the isotopologs 30SiS and Si33S are below the confusion limit of our line survey.
The line profiles of the most abundant isotopolog display three components: a wide component that corresponds to the plateau, the hot core (clearly seen in the profile of the J = 14−13 transition), and a narrower one at vLSR ≃ 15.5 km s-1. No emission has been observed from the ridge component. Line parameters are given in Table C.2, only available electronically (in the wide-component emission the plateau and the hot core are merged).
The velocity of the emission peak for the main isotopolog is at vLSR ≃ 15.5 km s-1, which coincides with the LSR velocity of the red component of the SiO v = 1 maser emission (which could be a fortuitous agreement, see Sect. 3.2.1). Previous works discuss the SiS in Orion KL and its association with the SiO v = 1 maser (Dickinson & Rodríguez-Kuiper 1981; Sutton et al. 1985; Ziurys 1988, 1991; Schilke et al. 1997).
Although confusion is great when considering the weak lines of 29SiS and SiS v = 1, we found their emission peaks at vLSR ≃ 13.5 km s-1 (see Fig. B.2), a mixture of all cloud components, but dominated by the 15.5 km s-1 feature.
Emission lines of SiS, 29SiS, and SiS v = 1 present in the frequency range of the Orion KL survey.
3.2.1. The feature at 15.5 km s-1
At the position of the line survey (IRc2), only SiS (v = 0, 1) lines and one component of the SiO maser emission (v = 1) show an intensity peak at 15.5 km s-1. Wright et al. (1990) measured the absolute position of the SiO masers to an accuracy of  coinciding with the position of radio source I (very close to IRc2). In order to check the origin of this feature we observed the line profiles of several molecules around IRc2. We find that the line profiles of SiO show large changes with position. Figure 4 central panel displays a 20′′ × 20′′ map centered on IRc2 of the J = 5−4 line of SiO, and the small panels around the map show the line profile of the J = 5−4 transition of SiO at selected positions and show strong differences across the cloud. The intensity peak of SiO lines is at 15.5 km s-1 at the positions Δα = −10′′, Δδ = + 6′′ and Δα = −6′′, Δδ = + 14′′. A comparison of the J = 5−4 SiO line at (−10′′, 6′′) with the emission of the J = 14−13 SiS line at (0, 0) is shown in the right panel.
coinciding with the position of radio source I (very close to IRc2). In order to check the origin of this feature we observed the line profiles of several molecules around IRc2. We find that the line profiles of SiO show large changes with position. Figure 4 central panel displays a 20′′ × 20′′ map centered on IRc2 of the J = 5−4 line of SiO, and the small panels around the map show the line profile of the J = 5−4 transition of SiO at selected positions and show strong differences across the cloud. The intensity peak of SiO lines is at 15.5 km s-1 at the positions Δα = −10′′, Δδ = + 6′′ and Δα = −6′′, Δδ = + 14′′. A comparison of the J = 5−4 SiO line at (−10′′, 6′′) with the emission of the J = 14−13 SiS line at (0, 0) is shown in the right panel.
In our map, this extended feature is seen around the position Δα = −7′′, Δδ = + 7′′ (near the BN object) with a radius of ≃ 5 arcsec. Figure B.3 shows emission lines from different molecules at a position offset (−15′′, 15′′) from IRc2. Only molecules with a strong emission from the plateau component (SO, 34SO, SO2, and SiO) show the 15.5 km s-1 component at this position. Hence, this feature is not a particularity of SiS but arises probably from the interaction of the outflow with the ambient cloud. Lines toward Orion KL showing a strong intensity and eventually high opacity in the plateau could, in turn, hide interesting details of other components (hot core, feature at 15.5 km s-1), making line interpretation a very difficult task.
 |
Fig. 3 Observed lines (histogram spectra) and model (thin curves) of SiS. The dashed line shows a radial velocity at 15.5 km s-1. |
4. Physical parameters of the clouds
Column densities for all detected species have been calculated using an excitation and radiative transfer code developed by J. Cernicharo (Cernicharo, in prep.). Depending on the selected molecule or physical conditions, we assume the large velocity gradient (LVG; Sobolev 1958; Sobolev 1960) or local thermodynamic equilibrium (LTE) approximations. Table 4 summarizes the physical parameters we obtained for each spectral cloud component from modeling SiO and SiS. For the new feature at 15.5 km s-1 we derived the following parameters from the modeling of the SiS lines: TK = 200 K, n(H2) = 5 × 106 cm-3, and vhalfpowerintensity = 7.5 km s-1. We assume uniform physical conditions: kinetic temperature, density, radial velocity, and line width. We adopted these values from the data analysis (Gaussian fits and an attempt to simulate the line widths and intensities with LTE and LVG codes) as representative parameters for the different species. Our modeling also takes the size of each component into account and its offset position with respect to IRc2. Corrections for beam dilution are applied for each line depending on their frequency.
The only free parameter is, therefore, the column density of the corresponding observed species. Considering the reduced size of most cloud components, the contribution from the error beam is negligible except for the extended ridge, which has a small contribution for all observed lines.
In addition to line opacity effects, we discussed other sources of uncertainty in Paper I.
4.1. SiO
LTE conditions were assumed for the hot core, while LVG calculations were performed for the extended ridge, compact ridge, plateau, and high-velocity plateau, with collisional cross sections of SiO-p-H2 taken from Dayou & Balança (2006) (see Appendix A) for temperatures between 10 K to 300 K including levels up to J = 20 (Eup = 437 K).
The SiO lines appear to be optically thick and therefore the derived SiO column density could be significantly underestimated. The lines of the isotopologs are, however, mostly optically thin so we can estimate the SiO column density assuming standard isotopic abundance ratios (28Si/29Si ≃ 20 and 28Si/30Si ≃ 30; Anders & Grevesse 1989). The results are shown in Table 5. Due to the weakness of the less abundant isotopologs lines (Si18O and Si17O) and large line overlap problems, we can only obtain upper limits for their column density. We estimated the uncertainty between 20−30% for the 29SiO and 30SiO results.
The cloud component with the highest column density corresponds to the plateau with N(SiO)plateau = (4.7 ± 1.0) × 1015 cm-2, while the total column density of SiO is N(SiO) = (7.4 ± 2.0) × 1015 cm-2, both results in agreement with those obtained from the line survey of Orion using the Odin satellite (Persson et al. 2007). Our study provides a column density between six times to one order of magnitude higher than obtained in the surveys at high frequency by Schilke et al. (2001) and Comito et al. (2005). Higher column densities have been reported by Ziurys & Friberg (1987) and Wright et al. (1996), while Johansson et al. (1984) and Sutton et al. (1995) obtained a beam average column density in good agreement with our results. These differences are mostly caused by the different assumptions on the physical conditions and cloud structure in the interpretation of the observations.
We derive a column density 29SiO/30SiO ratio of 2, 2, 1.7, 1.4, 1.25 for the extended ridge, compact ridge, plateau, high-velocity plateau, and hot core, respectively, in agreement with the standard solar value of 29Si/30Si ≃ 1.5 (Anders & Grevesse 1989). We can estimate a lower limit for the isotopic ratio 16O/18O and an estimation of 18O/17O by means of the total column density ratios N(Si16O)/N(Si18O) ≳ 239 and N(Si18O)/N(Si17O) ≃ 2 with large uncertainty due to the severe blending of their lines with other species. These values are two times lower than those of the solar system. In Paper I we derived N(16OCS)/N(18OCS) = 250 ± 135, while Persson et al. (2007) obtain a 18O/17O ratio of 3.6 from C18O/C17O.
We also modeled the 5−4 SiO line in the offset position (−10′′, 6′′) from IRc2 (see Fig. 4) in order to provide a column density for the 15.5 km s-1 feature. Using the same column densities obtained above for the different components, we added the feature at 15.5 km s-1 with a column density of (1.0 ± 0.3) × 1015 cm-2.
4.1.1. SiO maser lines
The SiO maser emission in Orion was discovered by Snyder & Buhl (1974) through its v = 1 J = 2−1 transition. Plambeck et al. (1990) suggested that the emission arises from an expanding rotating disk around IRc2. The emission from this line has been found by several authors to be confined to a region of 20−100 AU (3−10 × 1014 cm) around the radiocontinuum source I (Churchwell et al. 1987) and to trace a protostellar wind and/or outflow expanding with a velocity ≃ 20 km s-1 (Plambeck et al. 1990; Menten & Reid 1995; Greenhill et al. 1998; Doeleman et al. 1999; Plambeck et al. 2003; Doeleman et al. 2004; Greenhill et al. 2004; Matthews et al. 2007). Source I has not infrared counterpart in the range 4−22 μm (Greenhill et al. 2004), suggesting that it is surrounded by a dusty disk producing severe extinction. Source I is placed between Orion IRc2 and the hot core and excites the masers of SiO and H2O (Genzel & Stuzki 1989; Plambeck et al. 1995). Several other lines of SiO in v = 1 and 2 have been searched towards this source and some of them have been detected (v = 1 J = 1−0, J = 2−1, J = 3−2; see references above). The v = 1 J = 4−3 line was searched without success by Schwartz et al. (1982). In our line survey we covered the J = 2−1, 4−3, 5−4, and 6−5 lines of all vibrational states of SiO. As shown in Fig. 2, only the v = 1 J = 2−1 and 4−3 transitions have been unambiguously detected (the J = 4−3 for the first time). For the rotational lines of the v = 2 level the range of velocities covered by the SiO v = 1 J = 2−1 maser is always contaminated by other lines. The v = 2 J = 2−1 line shows a weak feature coincident with the red emission at 15 km s-1, but it arises from the 42,3−31,2 line of E-CH3OCOH as confirmed from the observed intensities of other lines of this species. The v = 2 J = 4−3 line shows a strong feature at the velocity of the blue component of the maser, but it arises from (CH3)2CO. The other lines from v = 2, 3, and 4 are always blended with other lines. In our survey we covered the same rotational and vibrational quantum numbers of the SiO isotopologs. None of them shows any maser effect within the sensitivity of our observations.
The observation of several ro-vibrational lines of SiO can be used to constraint the physical properties of the gas on spatial scales from a few ten to a few hundred AU from the source. Goddi et al. (2009) have modeled the emission of several isotopologs of SiO and they conclude that, while the v = 0 J = 1−0 maser emission arises from a region with radius > 100 AU and densities < 107 cm-3, the v = 1, 2 J = 1−0 and J = 2−1 are produced in a region of ≃ 100 AU around source I. Our observed intensity ratio v = 1 J = 2−1/J = 4−3 is ≃ 5−10 depending on the velocity component. We obtain this behavior for column densities of ≃ 1019 cm-2 and densities ≃ 108 cm-3. For higher densities the ratio increases and the predicted intensities of the J = 2−1 and J = 4−3 lines, although high, are not compatible with the inferred brightness temperatures that could be well above 105 K. We ran several models with different physical parameters. Our results suggest that the gas responsible for maser emission could have densities up to 108 cm-3, sizes of 100 AU, and gas temperatures around 600−800 K, a factor of two below those of Goddi et al. (2009). With these parameters for the emitting region the abundance of SiO should be as high as 10-4.
González-Alfonso & Cernicharo (1997) have shown that the masers of SiO and their isotopologs are affected by line overlap in the infrared between themselves. Such overlaps seem to have little effect on the emission of SiO, 29SiO, and 30SiO in v ≠ 0 for which maser emission has been found in evolved stars (Cernicharo et al. 1991b; González-Alfonso et al. 1996).
 |
Fig. 4 Central panel shows a 20′′ × 20′′ map, centered on IRc2, of the J = 5−4 line of SiO; the right panel shows a comparison between the J = 5−4 line at an offset (−10′′, 6′′), and the SiS J = 14−13 line towards IRc2, and the resulting model for each line (thin curves). The rest of the panels show the SiO J = 5−4 line at different positions. |
Physical parameters of Orion KL components.
Column densities of the different SiO isotopologs calculated with LVG and LTE codes.
4.2. SiS
In the same way as for SiO, LTE conditions were assumed for the hot core, while LVG calculations were performed for the 15.5 km s-1 feature and the plateau, with collisional cross sections SiS-o-H2 for 41 levels and 5 < Tk < 300 K taken from Klos & Lique (2008) (see Appendix A). The fits are shown in Figs. 3 and B.2. The column density results are shown in Table 6. We estimated the uncertainty to be about 20−30% for the results of SiS and 50% for 29SiS and SiS v = 1. Our highest value of the column density for SiS corresponds to the feature at 15.5 km s-1 obtaining N(SiS)15.5km s-1feature = (7.0 ± 1.7) × 1014 cm-2, and the total column density for SiS is N(SiS)total = (1.35 ± 0.40) × 1015 cm-2. A similar value was obtained by Ziurys (1988) and Ziurys (1991), whereas Dickinson & Rodríguez-Kuiper (1981) found N(SiS) = (1−2) × 1013 cm-2.
Assuming that SiS emission is optically thin, as indicated by our calculations, we derive an isotopic abundance of 28Si/29Si ≃ 14, 35, and 30 for the 15.5 km s-1 feature, the plateau, and the hot core, respectively i.e. close to the solar system value. We provide an average value of 28Si/29Si = 26 ± 10.
The N(SiO)/N(SiS) column density ratio observed in the plateau is ≃ 13, in good agreement with Dickinson & Rodríguez-Kuiper (1981) and four times lower than the cosmic O/S ratio of 48 (Anders & Grevesse 1989). Ziurys (1991) found an N(SiO)/N(SiS) ratio ≃ 40−80. We can also derive this ratio by means of N(29SiO)/N(29SiS), obtaining a value ≃ 25 for the plateau. To compare column density ratios, we have to assume that the region of the line formation is the same for each molecule and the excitation temperature is similar for both species, so we only provide this ratio for the plateau component. In the previous work of this line survey (Paper I), we derived O/S ratios using different species/families of molecules: N(HCO+)/N(HCS + ) ≃ 13, N(H2CO)/N(H2CS) ≃ 12, and N(CO)/N(CS) ≃ 370; in addition, Persson et al. (2007) find N(H2O)/N(H2S) ≃ 20 and N(H2CO)/N(H2CS) ≃ 15. All these values, excep N(CO)/N(CS) ≃ 370, show a similar O/S ratio, indicating that the different formation paths of different molecules maintain a constant ratio O/S in the same particular region of the cloud.
From the column density obtained for SiS in the ground and the vibrationally excited states, it is easy to estimate a vibrational temperature by means of 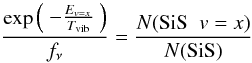 (1)where Eν = x is the excitation energy of the vibrational state (Ev = 1 = 1077 K, Tvib the vibrational temperature, fν the vibrational partition function, N(SiS v = x) the column density of the vibrational state, and N(SiS) the column density of SiS in the ground state. The vibrational partition function can be approximated by
(1)where Eν = x is the excitation energy of the vibrational state (Ev = 1 = 1077 K, Tvib the vibrational temperature, fν the vibrational partition function, N(SiS v = x) the column density of the vibrational state, and N(SiS) the column density of SiS in the ground state. The vibrational partition function can be approximated by 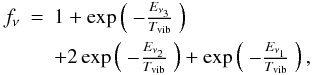 (2)which leads to fν ≃ 1 for low Tvib.
(2)which leads to fν ≃ 1 for low Tvib.
We obtain Tvib = 500 ± 200 K in the 15.5 km s-1 component. This value is higher than the kinetic temperature we have assumed for that component (200 K). This result could indicate an inner hotter emitting region for vibrationally excited SiS, suggesting that the excitation temperature varies across the feature at 15.5 km s-1. In Paper I we calculated the vibrational temperature in the hot core component for OCS ν2 = 1 and ν3 = 1 obtaining ≃ 210 K and an upper limit of 300 K for CS v = 1. As we indicated in our previous paper, all these results could point to radiative pumping effects in the populations of the vibrationally excited states of these molecules (taking the magnitude of the collisional rates of these species into account).
Higher angular resolution observations are needed to resolve any possible excitation gradient and temperature profile in the feature at 15.5 km s-1 and in the hot core component.
4.3. Other silicon-bearing molecules
Column densities of different SiS species calculated with LVG and LTE codes.
Upper limits for the column density of non-detected silicon-bearing molecules in Orion KL.
We provide upper limits for the column density of several silicon molecules not detected in our line survey. We assumed the four typical spectroscopic components of Orion KL (hot core, extended ridge, compact ridge, and plateau) plus the 15.5 feature, and an LTE approximation for all these molecules. Table 7 shows the results, the dipole moment of each species, and references for the spectroscopic constants.
SiC.- Millar (1980) predicted SiC to be an abundant form of silicon in dense clouds on the basis of gas-phase chemistry models. This molecule was detected by Cernicharo et al. (1989) towards the envelope of the red giant star IRC+101216, but not in Orion (see Schilke et al. 1997 for the attempts of detection in this source). We obtained an upper limit for its total column density of 1.3 × 1014 cm-2 providing an abundance ratio of N(SiO)/N(SiC) ≳ 57.
SiC2.- We did not detect silicon dicarbide in our line survey. Turner (1991) reported the detection of this molecule in the hot core of Orion KL. However, this result is quite uncertain due to the few observed transitions (three) and their weakness. We searched for other lines of SiC2 in our line survey, and we conclude that the intensities of the lines from this molecule are below the confusion limit, as many of these lines are blended or missing. We obtain an upper limit to its column density of 3.5 × 1013 cm-2 and an abundance ratio N(SiO)/N(SiC2) ≳ 211. This molecule and its isotopologs have also been detected towards IRC+101216 by Thaddeus et al. (1984) (SiC2), Cernicharo et al. (1986) (29SiC2 and 30SiC2), and Cernicharo et al. (1991a) (Si13CC).
c-SiC3.- Apponi et al. (1999a) detect rhomboidal SiC3 in the expanding envelope of the evolved carbon star IRC+10216. For this molecule we calculated an upper limit to its column density in Orion KL of 1.3 × 1013 cm-2, and a ratio N(SiO)/N(SiC3) ≳ 570.
SiC4.- SiC4 was first detected in space by Ohishi et al. (1989) in the envelope of IRC+10216. For this molecule we calculated an upper limit to its column density in Orion KL of 3.5 × 1012 cm-2, and a ratio N(SiO)/N(SiC4) ≳ 2114.
SiN.- Silicon nitride has been detected in IRC+10216 by Turner et al. (1992) and in the galactic center cloud SgrB2(M) by Schilke et al. (2003). We did not find SiN above the confusion limit in Orion; however, some U-lines in our survey could be assigned to SiN (see Fig. B.4, panels 1, 6, and 9), but we consider that the evidence for its presence in Orion is not strong enough within the our survey coverage. We provide an upper limit of 6.1 × 1013 cm-2, and N(SiO)/N(SiN) ≳ 121.
SiCN.- Cyanosilylidyne was identified in spectra recorded toward IRC+10216 by Guélin et al. (2000). The calculated upper limit to its column density in Orion KL is 3.1 × 1013 cm-2, deriving the ratio N(SiO)/N(SiCN) ≳ 240.
SiNC.- The isocyanosilylidyne isomer has a thermodynamic stability that is very similar to that of SiCN, but a slightly smaller dipole moment. It was detected toward IRC+10216 by Guélin et al. (2004). We provide an upper limit of 3.1 × 1013 cm-2 to its column density and a ratio N(SiO)/N(SiNC) ≳ 240.
SiH, SiH4.- In our frequency range there are no transitions of SiH, a molecule tentatively detected by Schilke et al. (2001) towards Orion KL, so we cannot assess that detection. The other silicon molecule detected in the space (in IRC+10216) is SiH4 (Golhaber & Betz 1984), but this molecule can only be observed at IR wavelengths.
ob-SiC3, l-SiC3, Si3, SiCCO, SiCCS, o-SiH2, o-H2CSi, p-H2CSi, mb-Si2H2, o-db-Si2H2.- These molecules have not been detected in the space yet. Upper limits for their column density are shown in Table 7.
5. Discussion
SiO is a key tracer of shocked emission. Many interferometric observations show that thermal and maser SiO emission depicted the low-velocity outflow centered on source I in Orion KL (Blake et al. 1996; Wright et al. 1996; Beuther et al. 2005; Plambeck et al. 2009; Goddi et al. 2009; Zapata et al. 2009). In addition, SiO traces many other molecular outflows in different sources (Jiménez-Serra et al. 2004; Gibb et al. 2007; De Buizer et al. 2009; Zapata et al. 2009). Mookerjea et al. (2007) have not found emission from SiO at the position of the hot molecular core in G34.26+0.15. This hot core does not have a central source, but it is instead externally heated, similar to the Orion compact ridge, by shocks, ionization fronts, and stellar winds. Mookerjea et al. (2007) point out that the lack of SiO in this hot core rules out any significant role played by shocks in determining the hot core chemistry. Observations of SiO in the L1448-mm outflow permit to distinguish between the shock precursor and the postshock components (Jiménez-Serra et al. 2005). They observed an enhancement in the abundances of SiO (and another shock tracers) by one order of magnitude in the shock precursor component and three orders of magnitude in the postshock gas (leading to the broadening of the line profiles), evidence of recent ejection of SiO from grains (Flower et al. 1996).
5.1. Molecular abundances
Molecular abundances were derived using the H2 column density calculated by means of the C18O column density (1.5 × 1016, 1.5 × 1016, 1 × 1017, 5 × 1016 cm-2, and 2 × 1017 cm-2 for the extended ridge, compact ridge, plateau, high velocity plateau, and hot core, respectively) and the isotopic abundance 16O/18O = 250, both provided in Paper I, assuming that CO is a robust tracer of H2 and therefore their abundance ratio is roughly constant, ranging from CO/H2 ≃ 5 × 10-5 (for the ridge components) to 2 × 10-4 (for the hot core and the plateau). In spite of the large uncertainty in this calculation, we include it as a more intuitive result for the molecules described in the paper. We obtained N(H2) = 7.5 × 1022, 7.5 × 1022, 2.1 × 1023, 6.2 × 1022, and 4.2 × 1023 cm-2 for the extended ridge, compact ridge, plateau, high velocity plateau, and hot core, respectively; for the 15.5 km s-1 component, we assume N(H2) = 1.0 × 1023 cm-2 as an average value in Orion KL. In addition, we assume that the H2 column density spatially coincides with the emission from the species considered. Our estimated source average abundances for each Orion KL component are summarized in Table C.3, together with comparison values from other authors (Sutton et al. 1995; Persson et al. 2007; and Ziurys 1988). The differences between the abundances shown in Table C.3 mostly come from the different H2 column density considered, to the assumed cloud component of the molecular emission, and to discrepancies in the sizes of these components.
5.2. Origin of the SiO and SiS emission
 |
Fig. 5 Column densities of SiO (solid line) and SiS (dotted line) as a function of time from Phase II of the hot core model with an initial elemental abundance of 1 × 10-6 for sulfur and 8 × 10-8 for silicon. The different plots show different efficiencies for the formation of SiS on the grain, namely: 100% (top left), 0% (top right), 30% (bottom left), 10% (bottom right). |
To qualitatively investigate the origin of the SiS and SiO emissions in Orion KL we ran a grid of models using the chemical model UCL_CHEM (Viti et al. 2004a,b; Lerate et al. 2010), a time and depth dependent gas-grain model.
We modeled the hot core and the plateau separately. Both models are two-phase calculation. In Phase I we follow the chemical and dynamical evolution of a collapsing core up to a final density of 5 × 107 cm-3 for the hot core component and 106 cm-3 for the plateau component as derived in Sect. 4. The initial gas is at typical densities of ~ 200 cm-3 and in atomic form (apart from a fraction of hydrogen already in molecular form), and it undergoes a free-fall collapse (Rawlings et al. 1992) until the final densities are reached. During this time, atoms and molecules from the gas freeze onto the dust grains and hydrogenate where possible. The advantage of this approach is that the ice composition is not assumed but is derived by a time-dependent computation of the chemical evolution of the gas/dust interaction process. However, the ice composition does depend on the percentage of gas depleted on to the grains during the collapse, and this in turns depend on the density, as well as on the sticking coefficient and other properties of the species and of the grains (see Rawlings et al. 1992). In our model we can vary this percentage (reflecting the uncertainty on the grain properties and sticking probabilities), and the degree (or efficiency) of depletion (as well as the viability of different surface reactions) is explored in this study. Our initial elemental abundances for Phase I are as in Bell et al. (2006) (see Table 1). We also ran some models where the initial abundances of both S and Si were either depleted or enhanced by a factor of 10 with respect to these values, reflecting the uncertainty of their degree of depletion onto dust. In Phase II, we follow the chemical evolution of the remnant core. For the hot core models, we simulate the effect of the presence of an infrared source in the center of the core or in its vicinity by subjecting the core to an increase in gas and dust temperature, up to T = 300 K. This increase in temperature is based on the luminosity of the protostar by using the observational luminosity function of Molinari et al. (2000). The models we use have been published before. For the models describing the hot core we refer the reader to Viti et al. (2004a) and Lerate et al. (2010), while for the models describing the plateau we refer the reader to Lerate et al. (2008), Lerate et al. (2010), and Viti et al. (2004b). In both models the presence of a non dissociative C-shock (modeled as in Bergin et al. 1997) can be simulated. If a shock is included in the model, then sputtering also occurs and is faster than thermal evaporation. We ran a total of six models for the hot core component and two models for the plateau component. For the hot core model, we investigated the sensitivity of the chemical abundances to the degree of gas depleted onto the grains during the formation of the core: the branching ratios of surface reactions relevant to the formation of SiO and SiS; the initial abundances of sulfur and silicon; likelihood that the gas is subjected to a non-dissociative shock during the hot core lifetime. For the plateau models, we only varied the initial sulfur and silicon abundances.
We were able to reproduce the observed column density of SiO with most models. The only constraint we found was that the temperature of the gas must be at least ~ 100 K or, alternatively, must have undergone a shock. SiS, on the other hand, is difficult to produce, Si surface reactions (and subsequent evaporation or sputtering of the mantles) seem to be necessary. We find that the only models that succeed in reproducing the data are those where a percentage (even as low as 5%) of sulfur on the grains react with Si to form SiS. Figure 5 shows the column density of SiO and SiS as a function of time during Phase II of the hot core for models differing only in the mantle formation efficiency of SiS (i.e. on how efficient Si bonds with S). A qualitative match with the observation can be achieved, at early times, by those models where only 5%−10% of sulfur on the grains react with Si to form SiS, or at late times if a higher percentage of sulfur is involved in the formation of SiS.
Exact ages cannot, however, be derived from these considerations as the relationship of the time dependencies with the efficiency of SiS formation on grains will depend on the desorption times of SiO and SiS.
In conclusion, while it is possible to reproduce SiO in the gas phase (as well as on the grains), our models indicate that SiS is a product of surface reactions, most likely involving direct reactions of sulfur with silicon.
6. Summary
In Paper I we presented a line survey of Orion KL taken with the 30 m IRAM telescope. The sensitivity achieved allows for a line confusion limited survey. Thanks to the wide frequency range covered and data quality, we decided to present the line survey in a series of papers focused on different molecular families. In this paper we presented the study of the emission from silicon-bearing species, SiO and SiS, as well as their isotopologs and their vibrationally excited states.
For the v = 1 state of SiO we have detected the J = 2−1 line and, for the first time in this source, emission in the J = 4−3 transition, both of them showing strong masering effect. The well known components of Orion (hot core, plateau, high velocity plateau, extended ridge, and compact ridge) contribute to the observed emission from SiO and its isotopologs whereas for SiS, 29SiS, and SiS v = 1 we have found emission from the hot core, the plateau, and a feature at 15.5 km s-1. To check the origin of this feature, we observed the line profiles of J = 5−4 SiO around IRc2 and of different molecules at an offset position (−15′′, 15′′) from IRc2. We conclude that this extended feature is seen around the position Δα = −7′′, Δδ = + 7′′ (near the BN object) with a radius of ≃ 5 arcsec and probably arises from the interaction of the outflow with the ambient cloud.
The physical parameters obtained for each Orion KL component agree with those we can find in the Orion literature. For the feature at vLSR = 15.5 km s-1, we derived TK = 200 K, n(H2) = 5 × 106 cm-3, and vhalfpowerintensity = 7.5 km s-1. Column densities were calculated with radiative transfer codes based on either the LVG or the LTE approximations taking the physical structure of the source into account and using the new SiO-p-H2 and SiS-o-H2 collisional rates. The results are provided as source-averaged column densities. In this way, we obtained a total column density of (7.4 ± 2.0) × 1015 and (1.35 ± 0.40) × 1015 cm-2 for SiO and SiS, respectively.
We derived several column density ratios, which permit us to provide the following average isotopic abundances: 28Si/29Si = 26 ± 10, 29Si/30Si = 1.7 ± 0.6, 16O/18O ≳ 239, 18O/17O ≃ 2. We also investigated the origin of the SiS and SiO emission in Orion KL by a gas-grain chemical model and find that, while SiO can be easily formed in the gas phase, SiS seems to be a product of grain surface reactions, most likely involving direct reactions of sulfur with silicon.
The resulting vibrational temperature for SiS v = 1 in the feature at 15.5 km s-1 is ≃ 500 K, higher than the kinetic temperature derived for this component, indicating an IR pumping or a warmer component difficult to see in the lines of the ground vibrational state.
Finally, we derived upper limits for the column density of nondetected molecules (silicon-bearing species). For the detected species in other sources SiC, SiC2, c-SiC3, SiC4, SiN, SiCN, and SiNC the upper limits for their column density are 1.3 × 1014, 3.5 × 1013, 1.3 × 1013, 3.5 × 1012, 6.1 × 1013, 3.1 × 1013, and 3.1 × 1013 cm-2, respectively.
Online material
Appendix A: Density diagnostic
In this section we study the influence of collisional rates on the modeling of the SiO and SiS lines observed in our line survey of Orion. Although most of the emission in Orion arises from regions of high volume density, the intensity of the high-velocity wings apparent in the SiO and SiS line profiles arise from a region, the plateau, in which the density is not enough to thermalize the rotational levels of high dipole moment molecules such as SiO (3.1 D) and SiS (1.73 D). Collisional rates are then needed for each species to derive the physical conditions. For SiO previous calculations by Green and collaborators (Bieniek & Green 1983; Turner et al. 1992; see http://www.giss.nasa.gov/data/mcrates#sio) have provided collisional rates for this molecule and temperatures 20−1500 K. These collisional rates have been recalculated using a new SiO-p-H2 surface by Dayou & Balança (2006). However, no collisional rates were available of SiS until recently: Vincent et al. (2007) and Klos & Lique (2008) have calculated the state-to-state collisional rates for the system SiS-He and SiS-H2, respectively.
We tested the influence of collisional rates on the modeling of the SiO and SiS lines observed in our line survey of Orion. Using the recent rates quoted above we computed line-intensity ratios between some transitions to provide tools for estimating the physical conditions in astrophysical sources. We covered volume densities between 102−109 cm-3 and kinetic temperatures from 10 to 300 K including levels up to J = 20 for SiO and J = 40 for SiS. In the following, we analyze the excitation conditions for 1 → 0, 2 → 1, 3 → 2, 5 → 4, 12 → 11, and 19 → 18 for both molecules.
A.1. SiO
 |
Fig. A.1 Intensity ratio between two transitions for SiO as a function of H2 density with the SiO column densities equal to 1012, 1013, 1014, and 1015 cm-2 and temperatures from 10 K to 100 K. |
 |
Fig. A.3 Comparison of the line intensities predicted using two different sets of collisional rates (see text) for different lines, column densities, and densities. |
The line-intensity ratios for SiO are shown in Figs. A.1 (kinetic temperature between 10 and 100 K) and A.2 (for a temperature of 300 K). In Fig. A.1 we notice that the intensity ratio TB(3 → 2)/TB(2 → 1) is particularly sensitive to densities of about 104 to 106 cm-3, whereas for TB(5 → 4)/TB(1 → 0) it shows important variations in the density range 106 to 107 cm-3. Using the intensity ratio TB(5 → 4)/TB(12 → 11), we can explore density values around 107−5 × 108 cm-3. For TK = 300 K and TB(12 → 11)/TB(19 → 18), we can trace densities above 105 cm-3, as seen in Fig. A.2. For lower densities, the 19−18 line will be very weak.
To illustrate this point, we deduce the intensity ratio TB(2 → 1)/TB(3 → 2) of SiO from our observations, and find ≃ 2.6 (see Table 2), which corresponds, depending on the column density and for TK = 100 K, on densities between 105.5 and 107 cm-3. Our results for the physical parameters of the different cloud components discussed in previous sections are given in Table 4.
The collisional rates calculated by Turner et al. (1992) have been used in the past to describe collisions of SiO molecules with H2. We used the new rates of Dayou & Balança (2006) throughout this paper. As a first step in modeling SiO emission in warm clouds, we compared the results using both sets of collisional rates for a wide range of physical conditions: TK = 10−300 K, N(SiO) = 1012−1015 cm-2, and n(H2) = 1−109 cm-3. Figure A.3 shows the brightness temperature (TB) ratio (predictions using the Dayou & Balança 2006 rates over those obtained from Turner et al. 1992 rates) as a function of H2 density for different values of the SiO column density and temperature and for the six first transitions of this molecule. The plots in Fig. A.3 show that the difference in the predicted line intensities between both sets of collisional rates never exceed 40% (J = 6−5 line), because it is always below 20% for all other rotational lines and kinetic temperatures. The lowest temperature for the collisional rates of Turner et al. (1992) is 20 K. We have extrapolated these rates to obtain the corresponding ones at 10 K. For most transitions the predicted line intensities from the Dayou & Balança (2006) rates are lower than those predicted from Turner et al. (1992) rates for densities below ≃ 105 cm-3. Although the differences in line intensities are not significant for determining the physical properties of the emitting gas in interstellar clouds, we adopted in our SiO calculations the new rates of Dayou & Balança (2006).
A.2. SiS
 |
Fig. A.4 Intensity ratio between two transitions for SiS as a function of H2 density with the SiS column density equal to 1012, 1013, 1014, and 1015 cm-2. |
We performed the same study for SiS using the rates calculated by Vincent et al. (2007). Figures A.4 and A.5 show our results. We observe the same trends as for SiO, but for lower densities. Thus, the TB(3 → 2)/TB(2 → 1) ratio increases in the density range 103 to 105 cm-3, the second one TB(5 → 4)/TB(1 → 0) in 104 to 105 cm-3, and the last graphs of Fig. A.4 show that TB(5 → 4)/TB(12 → 11) varies mostly between 105 and a few 106 cm-3. In Fig. A.5, we can see that for TK = 300 K, TB(12 → 11)/TB(19 → 18) are useful for densities around 105 cm-3. Two of those lines have been detected in our survey, the transitions 5 → 4 and 12 → 11, with an intensity ratio of ≃ 0.12. For TK = 100 K we can derive a volume density ≃ 105.5 cm-3.
Before 2007, no collisional data was available for SiS, so most authors have adopted the SiO collisional rates for SiS. As quoted above, the system SiS-He has been studied by Vincent et al. (2007). Lique et al. (2008) have compared these rates with the correspondings for the SiS-H2 system. They show that, when scaled by the square root of the collision reduced mass, the SiS-He rates were a reasonable approximation to describe collisions with H2. We have updated the LVG code by adding the new SiS-He and SiS-H2 rates. We calculated the line intensities and compared the results to those obtained with rates for SiO from Turner et al. (1992) (multiplied by a factor 2 to take the larger geometrical size of the SiS molecule into account). Figure A.6 shows the line intensity ratio (brightness temperature obtained with rates from Vincent et al. 2007 over those calculated with rates from Turner et al. 1992) as a function of n(H2) for the first six rotational transitions. The discrepancies in the line intensities between the two cases do not exceed 50%. As for SiO, we notice that the differencies between the two sets of collisional rates are the same for all column densities: the line intensity predicted with rates for SiS are lower than those predicted from Turner et al. (1992) rates for densities up to ≃ 103. These differences are quite small and do not affect the determination of the physical parameters performed by authors who previously used the Turner et al. (1992) rates in their models to interpret SiS observations. We also tried to describe SiS excitation by collisions with the rate coefficients for the system CS-He from Green & Chapman (1978) with an appropriate scaling factor. The predicted intensities show reasonable agreement with those derived from SiS-He or SiS-H2 collisional rates. These results show that, with the actual calibration accuracy for the SiS observations, determination of the properties of the emitting gas is not very sensitive to small differences in collisional rates. It is a rather curious result that the predicted line intensities with both sets of collisional rates, deduced from two different potential energy surfaces, moreover, with different propensity rules, produce similar intensity ratios (when the scaling factor is adequately selected). Determining the SiS column densities, we used the SiS-H2 rates (Klos & Lique 2008), although no significant differences were found when we used the SiS-He ones.
To better quantify the effects of the use of scaled SiO-He rates in predicting SiS intensities, we considered a case in which the lines are optically thin, for instance, n(H2) = 105 cm-3, TK = 40 K, and N(SiS) = 3 × 1012 cm-2. The predicted line intensities from SiS-He rates are TB(2 → 1, 4 → 3, 6 → 5) = 0.08,
0.26, 0.33 K. To obtain these results from scaled SiO-He rates, we need a density of 7 × 104 cm-3, or must reduce the scaling factor from 2 to ≃ 1.5, i.e., an error lower than two in density.
We compared predictions from the SiS-He rates with those obtained from the SiS-H2 rates and found insignificant variation between both.
Appendix B: Online figures
 |
Fig. B.1 Integrated intensity of the J = 5−4 transition of SiO at different velocity ranges (indicated at the top of each panel). In some panels, the integrated intensity of the maps has been multiplied by a scale factor (indicated in the panels) to maintain the same color dynamics for all maps. The step in integrated intensity ( |
 |
Fig. B.2 Observed lines (histogram spectra) and model (thin curves) of 29SiS and SiS v = 1. The dashed line shows a radial velocity at 13.5 km s-1. |
 |
Fig. B.3 Observed lines of different molecules at a position (−15′′, 15′′) offset IRc2. The dashed line shows a radial velocity at 15.5 km s-1. |
 |
Fig. B.4 Observed lines (histogram spectra) and model (thin curves) of SiN. |
Appendix C: Online tables
SiO and SiO isotopologs velocity components.
SiS velocity components.
Molecular abundances.
Acknowledgments
We thank the Spanish MEC for funding support through grants AYA2003-2785, AYA2006-14876, AYA2009-07304, ESP2004-665 and AP2003-4619 (M. A.), Consolider project CSD2009-00038 the DGU of the Madrid Community government for support under IV-PRICIT project S-0505/ESP-0237 (ASTROCAM).
References
- Alberts, I. L., Grev, R. S., & Schaefer III, H. F. 1990, J. Chem. Phys., 93, 5046 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989 GeCoA, 53, 197 [Google Scholar]
- Andreazza, C. M., & Marinho, E. P. 2007, MNRAS, 380, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Apponi, A. J., McCarthy, M. C., Gottlieb, C. A., & Thaddeus, P. 1999a, ApJ, 516, 103 [Google Scholar]
- Apponi, A. J., McCarthy, M. C., Gottlieb, C. A., & Thaddeus, P. 1999b, J. Chem. Phys., 111, 3911 [NASA ADS] [CrossRef] [Google Scholar]
- Apponi, A. J., McCarthy, M. C., Gottlieb, C. A., & Thaddeus, P. 2000, ApJ, 536, L55 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bell, T. A., Roueff, E., Viti, S., & Williams, D. A. 2006, MNRAS, 371, 1865 [NASA ADS] [CrossRef] [Google Scholar]
- Becklin, E. E., & Neugebauer, G. 1967, ApJ, 147, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Goldsmith, P. F., Snell, R. L., & Langer, W. D. 1997, ApJ, 482, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., & Nissen, H. D. 2008, ApJ, 679, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Zhang, Q., Greenhill, L. J., et al. 2004, ApJ, 616, L31 [Google Scholar]
- Beuther, H., Zhang, Q., Greenhill, L. J., et al. 2005, ApJ, 632, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Bieniek, R. J., & Green, S. 1983, ApJ, 265, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzocchi, L., Degli Esposti, C., & Dore, L. 2006, A&A, 455, 1161 [Google Scholar]
- Blake, G. A., Mundy, L. G., Carlstrom, J. E., et al. 1996, ApJ, 472, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Bogey, M., Demuynck, C., & Destombes, J. L. 1990, A&A, 232, L19 [NASA ADS] [Google Scholar]
- Bogey, M., Bolvin, H., Cordonnier, M., et al. 1994, J. Chem. Phys., 100, 8614 [NASA ADS] [CrossRef] [Google Scholar]
- Botschwina, P. 2005, JMoSt: THEOCHEM, 724, 95 [Google Scholar]
- Botschwina, P., Sanz, M. E., McCarthy, M. C., & Thaddeus, P. 2002, J. Chem. Phys., 116, 10719 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J. 1985, Internal IRAM report (Granada: IRAM) [Google Scholar]
- Cernicharo, J., Kahane, C., Gómez-Gonzalez, J., & Guélin, M. 1986, A&A, 167, L9 [NASA ADS] [Google Scholar]
- Cernicharo, J., Gottlieb, C. A., Guelin, M., Thaddeus, P., & Vrtilek, J. M. 1989, ApJ, 341, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Thum, C., Hein, H., et al. 1990, A&A, 231, L15 [NASA ADS] [Google Scholar]
- Cernicharo, J., Guélin, M., Kahane, C., Bogey, M., & Demuynck, C. 1991a, A&A, 246, 213 [NASA ADS] [Google Scholar]
- Cernicharo, J., Bujarrabal, V., & Lucas, R. 1991b, A&A, 249, L27 [NASA ADS] [Google Scholar]
- Cernicharo, J., González-Alfonso, E., Alcolea, J., Bachiller, R., & John, D. 1994, ApJ, 432, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churchwell, E., Felli, M., Wood, D. O. D., & Massi, M.- 1987, ApJ, 321, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Comito, C., Schilke, P., Philips, T. G., et al. 2005, ApJS, 165, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cordonnier, M., Bogey, M., Demuynck, C., & Destombes, J.-L. 1992, J. Chem. Phys., 97, 7984 [NASA ADS] [CrossRef] [Google Scholar]
- Dayou, F., & Balança, C. 2006, A&A, 459, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Buizer, J. M., Redman, R. O., Longmore, S. N., Caswell, J., & Feldman, P. A. 2009, A&A, 493, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vicente, P., Martín-Pintado, J., Neri, R., & Rodríguez-Franco, A. 2002, ApJ, 574, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, D. F., & Rodríguez-Kuiper, E. 1981, ApJ, 247, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Lonsdale, C. J., & Pelkey, S. 1999, ApJ, 510, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Lonsdale, C. J., Kondratko, P. T., & Predmore, C. R. 2004, ApJ, 607, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forets, G., Field, D., & May, P. W. 1996, MNRAS, 280, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, W. 1993, CP, 174, 45 [NASA ADS] [Google Scholar]
- Genzel, R., & Stuzki, J. 1989, ApJ, 574, 258 [Google Scholar]
- Genzel, R., Downes, D., Schwartz, P. R., et al. 1980, ApJ, 239, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Gezari, D. Y., Backman, D. E., & Werner, M. W. 1998, ApJ, 509, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, A. G., Davis, C. J., & Moore, T. J. T. 2007, MNRAS, 382, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Goddi, C., Greenhill, L. J., Chandler, C. J., et al. 2009, ApJ, 698, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Goldhaber, D. M., & Betz, A. L. 1984, ApJ, 279, L55 [NASA ADS] [CrossRef] [Google Scholar]
- González-Alfonso, E., & Cernicharo, J. 1997, A&A, 322, 938 [NASA ADS] [Google Scholar]
- González-Alfonso, E., Alcolea, J., & Cernicharo, J. 1996, A&A, 313, L13 [NASA ADS] [Google Scholar]
- Gordon, V. D., Nathan, E. S., Apponi, A. J., et al. 2000, J. Chem. Phys., 113, 5311 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A., Vrtilek, J. M., & Thaddeus, P. 1989, ApJ, 343, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S., & Chapman, S. 1978, ApJS, 37, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Greenhill, L. J., Gwinn, C. R., Schwartz, C., Moran, J. M., & Diamond, P. J. 1998, Nature, 396, 650 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Greenhill, L. J., Gezari, D. Y., Danchi, W. C., et al. 2004, ApJ, 605, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Grev, R. S., & Schaefer III, H. F. 1992, J. Chem. Phys., 97, 7990 [NASA ADS] [CrossRef] [Google Scholar]
- Guélin, M., Muller, S., Cernicharo, J., et al. 2000, A&A, 363, L9 [NASA ADS] [Google Scholar]
- Guélin, M., Muller, S., Cernicharo, J., McCarthy, M. C., & Thaddeus, P. 2004, A&A, 426, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, E., & Ishikawa, H. 1999, J. Chem. Phys., 110, 4254 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, J., Lovas, F. J., Tiemann, E., & Törring, T. 1969, ZNatA, 24, 1422 [Google Scholar]
- Izuha, M., Yamamoto, S., & Saito, S. 1996, J. Chem. Phys., 105, 4923 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Martíń-Pintado, J., Rodríguez-Franco, A., & Marcelino, N. 2004, ApJ, 603, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Martín-Pintado, J., & Rodríguez-Franco, A. 2005, ApJ, 627, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Johansson, L. E. B., Andersson, C., Elldér, J., et al. 1984, A&A, 130, 227 [NASA ADS] [PubMed] [Google Scholar]
- Kerkines, I. S. K., & Mavridis, A. 2005, J. Chem. Phys., 123, l4301 [Google Scholar]
- Kleinmann, D. E., & Low, F. J. 1967, ApJ, 149, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Klos, J., & Lique, F. 2008, MNRAS, 390, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Langhoff, S. R., & Bauschlicher, C. W., Jr. 1990, J. Chem. Phys., 93, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Lerate, M. R., Yates, J., Viti, S., et al. 2008, MNRAS, 387, L1660 [NASA ADS] [CrossRef] [Google Scholar]
- Lerate, M. R., Yatesi, J., Barlow, M. J., Viti, S., & Swinyard, B. M. 2010, MNRAS, 406, L445 [CrossRef] [Google Scholar]
- Lique, F., Tobola, R., Klos, J., et al. 2008, A&A, 478, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthews, L. D., Goddi, C., Greenhill, L. J., et al. 2007, in Astrophysical Masers and their Environments, ed. J. M. Chapman, & W. A. Baan (Dordrecht: Kluwer), IAU Symp., 242, 130 [Google Scholar]
- McCarthy, M. C., Apponi, A. J., & Thaddeus, P. 1999, J. Chem. Phys., 111, 7175 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., Apponi, A. J., Gottlieb, C. A., & Thaddeus, P. 2000, ApJ, 538, 766 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., Apponi, A. J., Gottlieb, C. A., & Thaddeus, P. 2001, J. Chem. Phys., 115, 870 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., & Thaddeus, P. 2003a, ApJ, 592L, 91 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., & Thaddeus, P. 2003b, JMoSp, 222, 248 [NASA ADS] [Google Scholar]
- Menten, K. M., & Reid, M. J. 1995, ApJ, 445, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Reid, M. J., Forbrich, J., & Brunthaler, A. 2007, ApJ, 474, 515 [Google Scholar]
- Millar, T. J. 1980, Ap&SS, 72, 509M [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Brand, J., Cesaroni, R., & Palla, F. 2000, A&A, 355, 617 [NASA ADS] [Google Scholar]
- Mookerjea, B., Casper, E., Mundy, L. G., & Looney, L. W. 2007, ApJ, 659, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Ohishi, M., Kaifu, N., Kawaguchi, K., et al. 1989, ApJ, 345L, 83 [Google Scholar]
- Olofsson, H., Hjalmarson, A., & Rydbeck, O. E. H. 1981, A&A, 100, L30 [NASA ADS] [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001a, IEEE Tras. Antennas and Propagation, 49, 12 [Google Scholar]
- Pardo, J. R., Cernicharo, J., Herpin, F., et al. 2001b, ApJ, 562, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Persson, C. M., Olofsson, A. O. H., Koning, N., et al. 2007, A&A, 476, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plambeck, R. L., Wright, M. C. H., & Carlstrom, J. E. 1990, ApJ, 348, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Plambeck, R. L., Wright, M. C. H., Mundy, L. G., & Looney, L. W. 1995, ApJ, 502, L75 [Google Scholar]
- Plambeck, R. L., Wright, M. C. H., & Rao, R. 2003, ApJ, 594, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Plambeck, R. L., Wright, M. C. H., Friedel, et al. 2009, ApJ, 704, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Raymonda, J. W., Muenter, J. S., & Klemperer, W. A. 1970, J. Chem. Phys., 52, 3458 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, J. M. C., Hartquist, T. W., Menten, K. M., & Williams, D. A. 1992, MNRAS, 255, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, S., Endo, Y., & Hirota, E. 1983, J. Chem. Phys., 78, 6447 [NASA ADS] [CrossRef] [Google Scholar]
- Sanz, M. E., McCarthy, M. C., & Thaddeus, P. 2003, J. Chem. Phys., 119, v22, 11715 [NASA ADS] [CrossRef] [Google Scholar]
- Sanz, M. E., Alonso, J. L., Blanco, S., Lesarri, A., & López, J. C. 2005, ApJ, 621, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Groesbeck, T. D., Blake, G. A., & Philips, T. G. 1997, ApJS, 108, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Benford, C. J., Hunter, T. R., Lis, D. C., & Philips, T. G. 2001, ApJS, 132, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Leurini, S., Menten, K. M., & Alcolea, J. 2003, A&A, 412, 15 [Google Scholar]
- Schwartz, P. R., Zuckerman, B., & Bologna, J. M. 1982, ApJ, 256, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, L. E., & Buhl, D. 1974, ApJ, 189, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, V. V. 1958, en Theorical Astrophysics, edn. Ambartsumyan (London: Pergamon Press Ltd.), 29 [Google Scholar]
- Sobolev, V. V. 1960, en Moving Envelopes of Stars (Hardvard University Press) [Google Scholar]
- Suenram, R. D., Lovas, F. J., & Matsumura, K. 1989, ApJ, 342, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Blake, G. A., Masson, C. R., & Philips, T. G. 1985, ApJS, 58, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, E. C., Peng, R., Danchi, W. C., et al. 1995, ApJS, 97, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Tercero, B., Pardo, J. R., Cernicharo, & Goicoechea, J. R. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thaddeus, P., Cummins, S. E., & Linke, R. A. 1984, ApJ, 283, 45 [Google Scholar]
- Turner, B. E. 1991, ApJS, 76, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E., Chan, K.-W., Green, S., & Lubowich, D. A. 1992, ApJ, 399, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, I., Ögüt, S., & Chelikowsky, J. R. 1997, PhRvL, 78, 4805 [NASA ADS] [Google Scholar]
- Vincent, L., Lique, F., Spielfiedel, A., & Feautrier, N. 2007, A&A, 472, 1037 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viti, S., Codella, C., Benedettini, M., & Bachiller, R. 2004a, MNRAS, 350, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Collings, M. P., Dever, J. W., McCoustra, M. R. S., & Williams, D. A. 2004b, MNRAS, 354, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, M. C. H., Carlstrom, J. E., Plambeck, R. L., & Welch, W. J. 1990, AJ, 99, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, M. C. H., Plambeck, R. L., Mundy, L. G., & Looney, L. W. 1995, ApJ, 455, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, M. C. H., Plambeck, R. L., & Wilner, D. J. 1996, ApJ, 469, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Zapata, L. A., Menten, K., Reid, M., & Beuther, H. 2009, ApJ, 691, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M. 1988, ApJ, 324, 544 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ziurys, L. M. 1991, ApJ, 379, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M., & Friberg, P. 1987, ApJ, 314, L49 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Emission lines of SiO, SiO isotopologs, and SiO vibrationally excited present in the frequency range of the Orion KL survey.
Emission lines of SiS, 29SiS, and SiS v = 1 present in the frequency range of the Orion KL survey.
Column densities of the different SiO isotopologs calculated with LVG and LTE codes.
Upper limits for the column density of non-detected silicon-bearing molecules in Orion KL.
All Figures
 |
Fig. 1 Observed lines (histogram spectra) and model (thin curves) of SiO and its isotopologs. The dashed line shows a radial velocity at 9 km s-1. |
| In the text | |
 |
Fig. 2 Observed lines of vibrationally excited SiO v = 1 showing maser emission in the transitions J = 2−1 and J = 4−3. The dashed lines show radial velocities at −3.4, + 5.1, and + 13.9 km s-1. |
| In the text | |
 |
Fig. 3 Observed lines (histogram spectra) and model (thin curves) of SiS. The dashed line shows a radial velocity at 15.5 km s-1. |
| In the text | |
 |
Fig. 4 Central panel shows a 20′′ × 20′′ map, centered on IRc2, of the J = 5−4 line of SiO; the right panel shows a comparison between the J = 5−4 line at an offset (−10′′, 6′′), and the SiS J = 14−13 line towards IRc2, and the resulting model for each line (thin curves). The rest of the panels show the SiO J = 5−4 line at different positions. |
| In the text | |
 |
Fig. 5 Column densities of SiO (solid line) and SiS (dotted line) as a function of time from Phase II of the hot core model with an initial elemental abundance of 1 × 10-6 for sulfur and 8 × 10-8 for silicon. The different plots show different efficiencies for the formation of SiS on the grain, namely: 100% (top left), 0% (top right), 30% (bottom left), 10% (bottom right). |
| In the text | |
 |
Fig. A.1 Intensity ratio between two transitions for SiO as a function of H2 density with the SiO column densities equal to 1012, 1013, 1014, and 1015 cm-2 and temperatures from 10 K to 100 K. |
| In the text | |
 |
Fig. A.2 Same as A.1 but for T = 300 K. |
| In the text | |
 |
Fig. A.3 Comparison of the line intensities predicted using two different sets of collisional rates (see text) for different lines, column densities, and densities. |
| In the text | |
 |
Fig. A.4 Intensity ratio between two transitions for SiS as a function of H2 density with the SiS column density equal to 1012, 1013, 1014, and 1015 cm-2. |
| In the text | |
 |
Fig. A.5 Same as A.4 but for T = 300 K. |
| In the text | |
 |
Fig. A.6 Same as A.3 for SiS with the SiS column density equal to 1012, 1013, 1014, and 1015 cm-2. |
| In the text | |
 |
Fig. B.1 Integrated intensity of the J = 5−4 transition of SiO at different velocity ranges (indicated at the top of each panel). In some panels, the integrated intensity of the maps has been multiplied by a scale factor (indicated in the panels) to maintain the same color dynamics for all maps. The step in integrated intensity ( |
| In the text | |
 |
Fig. B.2 Observed lines (histogram spectra) and model (thin curves) of 29SiS and SiS v = 1. The dashed line shows a radial velocity at 13.5 km s-1. |
| In the text | |
 |
Fig. B.3 Observed lines of different molecules at a position (−15′′, 15′′) offset IRc2. The dashed line shows a radial velocity at 15.5 km s-1. |
| In the text | |
 |
Fig. B.4 Observed lines (histogram spectra) and model (thin curves) of SiN. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.