| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 14 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201015586 | |
| Published online | 03 March 2011 | |
Detection of new point sources in WMAP cosmic microwave background maps at high Galactic latitude
A new technique to extract point sources from CMB maps
1 Centro de Astrofísica, Universidade
do Porto, Rua das
Estrelas, 4150-762 Porto, Portugal
e-mail: eramos@astro.up.pt
2 Departamento de Física e Astronomia
da Faculdade de Ciências da Universidade do Porto, Rua do Campo Alegre, 687, 4169-007
Porto,
Portugal
3 Chip Computers Consulting s.r.l.,
Viale Don L. Sturzo 82, S. Liberale di Marcon, 30020
Venice,
Italy
e-mail: robertovio@tin.it
4 ESO, Karl-Schwarzschild-Strasse 2,
85748
Garching,
Germany
5 INAF-Osservatorio Astronomico di
Trieste, via Tiepolo 11, 34143
Trieste,
Italy
e-mail: pandrean@eso.org
Received: 14 August 2010
Accepted: 10 January 2011
In experimental microwave maps, point sources can strongly affect the estimate of the power spectrum and/or the test of Gaussianity of the cosmic microwave background (CMB) component. As a consequence, their removal from the sky maps represents a critical step in the analysis of the CMB data. Before removing a source, however, it is necessary to detect it, and source extraction is a delicate preliminary operation. In the literature, various techniques have been presented to detect point sources in the sky maps. The most sophisticated ones exploit the multi-frequency nature of the observations that is typical of the CMB experiments. These techniques have “optimal” theoretical properties and, at least in principle, are capable of remarkable performances. Yet they are fairly difficult to use, which deteriorates the quality of the obtainable results. We present a new technique, the weighted matched filter (WMF), which is quite simple to use and therefore more robust in practical applications. This technique shows particular efficiency in the detection of sources whose spectra have a slope different from zero. We apply this method to three Southern Hemisphere sky regions – each with an area of 400 deg2 – of the seven-year Wilkinson Microwave Anisotropy Probe (WMAP) maps and compare the resulting sources with those of the two seven-year WMAP point source catalogues. In these selected regions we find seven additional sources not previously listed in WMAP catalogues and discuss their most likely identification and spectral properties.
Key words: methods: data analysis / cosmic background radiation / methods: statistical / radio continuum: galaxies
© ESO, 2011
1. Introduction
The detection of point sources embedded in a noise background is a critical problem in the analysis of the experimental cosmic microwave background (CMB) maps. The estimate of the power spectrum of the CMB component and the test of its possible non-Gaussian nature need “a priori” detection and removal of these sources. The former operation in particular, is very delicate because usually there is a diffuse background of astrophysical nature and/or the inevitable instrumental noise. With the increasing high sensitivities of instruments to detect the CMB signal, the astrophysical foregrounds have become the major source of contamination with respect to the instrumental noise. In CMB experiments, the foreground signals at high galactic latitudes come mainly from the emission of extragalactic point sources. Given its importance, this subject has been extensively considered in the literature (see e.g. Herranz & Sanz 2008; Carvalho et al. 2009, and references therein). Among the various proposed techniques, the multi-frequency approaches appear to be the most promising ones. A good example is the multi-frequency matched filter (MMF), a well known technique in the community of the “digital signal processing” (e.g. see Kay 1998), which recently has been proposed by Herranz et al. (2002) and Lanz et al. (2010). Although in principle this technique has “optimal” properties, its use is fairly difficult and this could limit the actual performance in real experimental scenarios. In addition, most of the detection methods available in the literature have been developed in the context of full-sky observations. These experiments undoubtedly represent an important tool to better understand the physical properties of CMB. However, they suffer the drawback of the Galactic contamination that despite the optimism expressed in many papers, could not yet been completely removed. We present a new technique, which we call weighted matched filter (WMF), tailored to the detection of point sources in regions where the Galactic contamination can be considered negligible. This technique also takes into account the instrumental noise and can be applied to small sky regions.
Observational radio data such as those provided by the Wilkinson Microwave Anisotropy Probe (WMAP) satellite should be a test to the robustness of the WMF to detect extragalactic point sources. Because this technique can be used on small sky patches, we plan in the future to exploit the high sensitivity and angular resolution of the Atacama Large Millimeter/submillimeter Array (ALMA), and to test the technique’s applicability to this facility, we plan to apply the WMF to simulated ALMA data (Ramos et al., in prep.).
The paper is structured as follows: in Sect. 2 the mathematics of the WMF is described. Associated numerical experiments are shown in Sect. 3. The application of the WMF to the WMAP observational data and the identification of the new discovered sources are presented in Sect. 4. Conclusions and future development of this work are discussed in Sect. 5. To speed up the reading of the article most of the mathematical technical details are deferred to the appendix.
2. Point source detection at high Galactic latitude
In the context of point source detection, data can be thought of as two-dimensional discrete maps 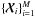 , each of them containing Np pixels, corresponding to M different observing frequencies (channels), with the form
, each of them containing Np pixels, corresponding to M different observing frequencies (channels), with the form 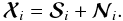 (1)Here,
(1)Here, 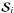 corresponds to the contribution of the point sources at the ith frequency, whereas
corresponds to the contribution of the point sources at the ith frequency, whereas 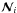 denotes the corresponding noise component. At high Galactic latitudes, the CMB component is expected to be the dominant one. Hence,
denotes the corresponding noise component. At high Galactic latitudes, the CMB component is expected to be the dominant one. Hence, 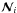 may be modelled by
may be modelled by 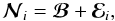 (2)where ℬ is the contribution of the CMB component that is the same at all frequencies (in terms of thermodynamic temperature units), and ℰi is the instrumental noise corresponding to the ith channel.
(2)where ℬ is the contribution of the CMB component that is the same at all frequencies (in terms of thermodynamic temperature units), and ℰi is the instrumental noise corresponding to the ith channel.
The contribution of the point sources is assumed to have the form 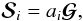 (3)with ai the amplitude of the source to the ith channel, and where all the sources are assumed to have the same profile
(3)with ai the amplitude of the source to the ith channel, and where all the sources are assumed to have the same profile 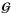 independently of the observing frequency. Although this will not be true generally, it is possible to meet this condition by convolving the images with an appropriate kernel. In the following, the components { ℰi } are considered to be realizations of a Gaussian, stationary, zero-mean, stochastic process.
independently of the observing frequency. Although this will not be true generally, it is possible to meet this condition by convolving the images with an appropriate kernel. In the following, the components { ℰi } are considered to be realizations of a Gaussian, stationary, zero-mean, stochastic process.
The main feature of model (1)–(2) is that the CMB contribution does not change with the frequency. Hence, it is possible to linearly combine the maps 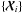 in a single map
in a single map 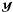 in a way that the CMB contribution is zeroed. In particular,
in a way that the CMB contribution is zeroed. In particular, 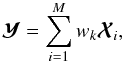 (4)where the weights w are chosen to fulfill the criteria
(4)where the weights w are chosen to fulfill the criteria  with w = [w1,w2,...,wM] T, a = [a1,a2,...,aM] T, and 1 = (1,1,....1)T. Here, symbol “
with w = [w1,w2,...,wM] T, a = [a1,a2,...,aM] T, and 1 = (1,1,....1)T. Here, symbol “ ” denotes the matrix transpose. The first constraint (5) implies that the contribution of ℬ in
” denotes the matrix transpose. The first constraint (5) implies that the contribution of ℬ in 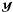 is completely removed, whereas the second one (6) provides a normalizing factor. The advantage of this procedure is that one deals with a map contaminated only by the instrumental noise. It is easier to deal with this kind of noise than with ℬ because the correlation length of
is completely removed, whereas the second one (6) provides a normalizing factor. The advantage of this procedure is that one deals with a map contaminated only by the instrumental noise. It is easier to deal with this kind of noise than with ℬ because the correlation length of 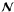 is much shorter than that of ℬ. This is particularly useful in situations where only small patches of sky are available and the auto-covariance function of the noise (a piece of information necessary to any detection method) has to be estimated from the data. Moreover, working with a single map allows one to use detection techniques such as the classical matched filter (MF) (see Appendix A), whose robustness is proved by many years of applications in many different fields of science and engineering (Vio et al. 2002, 2004). We call here the coupling of the weighted combination of the maps with the MF, the weighted matched filter (WMF).
is much shorter than that of ℬ. This is particularly useful in situations where only small patches of sky are available and the auto-covariance function of the noise (a piece of information necessary to any detection method) has to be estimated from the data. Moreover, working with a single map allows one to use detection techniques such as the classical matched filter (MF) (see Appendix A), whose robustness is proved by many years of applications in many different fields of science and engineering (Vio et al. 2002, 2004). We call here the coupling of the weighted combination of the maps with the MF, the weighted matched filter (WMF).
For M = 2, (i.e. two maps are available), the only possible solution is wT = [1/(a1 − a2), −1/(a1 − a2)] . However, for M > 2 more degrees of freedom are available. This allows the selection of the weights in a way that specific conditions are satisfied. In particular, the peak signal-to-noise ratio of 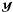 ,
, 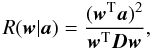 (7)can be maximized, i.e.1
(7)can be maximized, i.e.1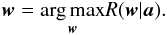 (8)Here, D is the M × M cross-covariance matrix of the noise processes whose (i,j)th entry (D)ij is given by
(8)Here, D is the M × M cross-covariance matrix of the noise processes whose (i,j)th entry (D)ij is given by 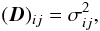 (9)with
(9)with 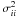 the variance of ℰi and
the variance of ℰi and 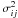 the covariance between ℰi and ℰj. Because of the constraint (6), condition (8) can be reformulated as
the covariance between ℰi and ℰj. Because of the constraint (6), condition (8) can be reformulated as ![\begin{equation} \label{eq:R} \wb = \underset{ \wb }{\arg\min} [{\wb^{\rm T} \Db \wb}]. \end{equation}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq39.png) (10)This approach differs from that proposed by Chen & Wright (2009), which consists in the minimization of the simpler quantity wTw (i.e. instrumental noise is not taken into account). Moreover, these authors seem to adopt a numerical approach for this operation (no details are provided with respect to this). A simple analytic solution of problem (10) with the constraints (5)-(6) can be obtained by means of the Lagrange multipliers method, i.e.
(10)This approach differs from that proposed by Chen & Wright (2009), which consists in the minimization of the simpler quantity wTw (i.e. instrumental noise is not taken into account). Moreover, these authors seem to adopt a numerical approach for this operation (no details are provided with respect to this). A simple analytic solution of problem (10) with the constraints (5)-(6) can be obtained by means of the Lagrange multipliers method, i.e. 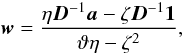 (11)where
(11)where  This result is similar to that obtained by Remazeilles et al. (2011) and Hurier et al. (2010), but in a completely different context, where the problem of interest is the separation of CMB and Sunyaev-Zel’dovich effect through the internal linear composition approach. The main difference with solution (11) is that in Remazeilles et al. (2011) and Hurier et al. (2010) the empirical covariance matrix of the observed maps
This result is similar to that obtained by Remazeilles et al. (2011) and Hurier et al. (2010), but in a completely different context, where the problem of interest is the separation of CMB and Sunyaev-Zel’dovich effect through the internal linear composition approach. The main difference with solution (11) is that in Remazeilles et al. (2011) and Hurier et al. (2010) the empirical covariance matrix of the observed maps 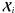 is used, instead of the matrix D in (11).
is used, instead of the matrix D in (11).
3. Numerical experiments
To test the performances of the WMF we carried out several numerical experiments. We considered a scenario where four different observing frequencies are available. We made the simplifying assumption that all channels have the same point-spread function (PSF), which is a two-dimensional circular symmetric Gaussian normalized to have a peak value equal to one and with a dispersion set to three pixels. Here the CMB component ℬ is simulated on a regular two-dimensional grid containing (101 × 101) pixels with size 3.52′ × 3.52′. The instrumental noise ℰi is assumed to be a Gaussian white-noise process with variance equal to one in units of the standard deviation of the CMB signal. This scenario mimics that expected for the low-frequency instrument mounted on the PLANCK satellite (Vio et al. 2003). The amplitudes { ai } of the point sources are assumed to follow a power-law 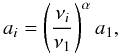 (15)where νi, i = 1,2,3,4 are the observing frequencies (i = 1 → 30 GHz, i = 2 → 44 GHz, i = 3 → 70 GHz, i = 4 → 100 GHz), a1 = 0.5 (in units of the standard deviation of the CMB signal) and α is the source spectral index. The value of a1 has been chosen to reproduce an experimental situation characterized by a comparatively low signal-to-noise ratio.
(15)where νi, i = 1,2,3,4 are the observing frequencies (i = 1 → 30 GHz, i = 2 → 44 GHz, i = 3 → 70 GHz, i = 4 → 100 GHz), a1 = 0.5 (in units of the standard deviation of the CMB signal) and α is the source spectral index. The value of a1 has been chosen to reproduce an experimental situation characterized by a comparatively low signal-to-noise ratio.
Figure 1 shows the “probability of detection”, PD, against the “probability of false alarm”, PFA (i.e. the probability of a false detection), for the WMF (see Appendix A). Four different values of α are considered, i.e. α = 3,1,0.5,0.05 (negative values of α provide similar results). For comparison we also show the results obtained with the classical multi-frequency matched filter (MMF), and those obtained using the WMF with the weights w = [ρ,ρ,..., − (M − 1)ρ] T, 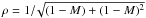 . This last method, which we name uniformly weighted matched filter (UWMF), corresponds to a situation where only one signal is used to eliminate the component ℬ, whereas the others are given an identical weight. Quantity ρ is fixed in a way that wT1 = 0 and wTw = 1. In this experiment MMF and UWMF are used as upper and lower limit, respectively, for the results obtainable by WMF. This is because under the conditions we are working with, no detection method can outperform MMF (see Appendix A). On the other hand, it is generally not expected that UWMF achieves good performances, because the weights are computed without considering the noise level in the map and the characteristics of the source spectra. In this kind of diagram, one method is superior to another one when for a fixed PFA, the corresponding PD is greater. More specifically, the relation PD to PFA should always be well above a 45° straight line (the dashed line in the figure), because this corresponds to a detection performance identical to that of flipping a coin, ignoring all data.
. This last method, which we name uniformly weighted matched filter (UWMF), corresponds to a situation where only one signal is used to eliminate the component ℬ, whereas the others are given an identical weight. Quantity ρ is fixed in a way that wT1 = 0 and wTw = 1. In this experiment MMF and UWMF are used as upper and lower limit, respectively, for the results obtainable by WMF. This is because under the conditions we are working with, no detection method can outperform MMF (see Appendix A). On the other hand, it is generally not expected that UWMF achieves good performances, because the weights are computed without considering the noise level in the map and the characteristics of the source spectra. In this kind of diagram, one method is superior to another one when for a fixed PFA, the corresponding PD is greater. More specifically, the relation PD to PFA should always be well above a 45° straight line (the dashed line in the figure), because this corresponds to a detection performance identical to that of flipping a coin, ignoring all data.
Figure 1 shows that when α > 1, the WMF and MMF have very similar performances. When 0.5 ≤ α ≤ 1, the behaviour of both filters is still reasonably similar. For α ≈ 0 (i.e. for sources with a flat spectrum), the performance of the WMF becomes close to that of the UWMF. This happens because for α close to zero, not only the CMB has the same contribution at the various frequencies, but the intensity of the sources is constant as well. In this case, a simple alternative is to average the maps and then apply the classic MF to the resulting map. We call this method average matched filter (AMF). A point to stress is that for the AMF one needs to know the auto-covariance matrix of the CMB as for the MMF, but the advantage over the MMF is that only one map has to be handled. For comparison, we show in Fig. 1 the performance of the AMF as well.
From these considerations, it appears that an effective and indeed the most straightforward procedure to detect less common sources (those with spectra different from flat) consists of using the WMF, optimized for different values of α. The reliability of this procedure is supported by Fig. 2, which shows the relative decrease of the probability of detection, 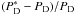 , against PFA when the WMF is applied to a source whose true spectral index α is erroneously assumed to be α ∗ . Here, PD and
, against PFA when the WMF is applied to a source whose true spectral index α is erroneously assumed to be α ∗ . Here, PD and 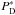 are the probability of detection when the WMF is applied assuming the true and the wrong spectral index, respectively. The set of values [3,1,0.5,0.05] is used for both α and α ∗ . This figure shows that a remarkable decrease of the probability of detection is to be expected only if α is quite different from α ∗ .
are the probability of detection when the WMF is applied assuming the true and the wrong spectral index, respectively. The set of values [3,1,0.5,0.05] is used for both α and α ∗ . This figure shows that a remarkable decrease of the probability of detection is to be expected only if α is quite different from α ∗ .
 |
Fig. 1 Probability of detection PD against probability of false alarm PFA for the detection methods in the numerical experiment described in Sect. 3. The sources are assumed to have an intensity ai at the ith frequency given by ai = (νi/ν1)αa1, with a1 = 0.5. Four values for α are considered, α = 3,1,0.5,0.05. The results are shown for the different methods: the weighted matched filter (WMF), the multi-frequency matched filter (MMF), the uniformly weighted matched filter (UWMF) and the average matched filter (AMF). The MMF is used as benchmark because it has the best theoretical detection performance. The UWMF shows the worst possible results obtainable with the WMF approach. The AMF shows which results are obtainable when the maps are simply averaged. A method is superior to another one when for a fixed PFA the corresponding PD is greater (for a given method, the relation PD to PFA should always be well above a 45° straight line, the dashed line in the figure). With increasing α, the behaviour of MMF and WMF becomes similar. For an α close to zero, the MMF and AMF show a very similar performance. |
 |
Fig. 2 Relative decrease of the probability of detection, |
4. Application to WMAP data
4.1. WMAP maps
The Wilkinson Microwave Anisotropy Probe (WMAP) satellite (Bennett et al. 2003a) was designed to produce microwave full-sky maps of the CMB radiation. With the aim of separating the CMB signal from foreground components, the maps were obtained at five different frequency bands, centred at 23 GHz (K band), 33 GHz (Ka band), 41 GHz (Q band), 61 GHz (V band), and 94 GHz (W band). Despite the limited angular resolution of WMAP, with a full width at half maximum (FWHM) of about 13 arcmin (W band), it is presently the only instrument that can offer a millimeter wavelength all-sky survey, which provides a unique tool for the study of radio sources.
The seven-year full sky temperature and polarization maps per frequency band, namely the Stokes I, Q and U parameters, are available from the LAMBDA website2. The maps of the five frequency bands have different resolutions, from roughly 0.21° (W band) to about 0.82° (K band). With the goal of testing the proposed WMF method to identify radio point sources we used the Stokes I (temperature) co-added maps (combination of the individual differencing assemblies of a single frequency band) to a common 1°FWHM Gaussian beam, from which the CMB dipole was removed (for more details see Jarosik et al. 2011). These maps were generated as a nested HEALPix3 sky projection (Górski et al. 2005) with a resolution of Nside = 512 (corresponding to the label WMAP resolution of Res 9).
4.2. Selection of the sky regions
The drawback in using the CMB experiments for cosmological studies is the foreground contamination from the Galaxy and extragalactic sources. In particular, the extragalactic point sources contaminate the CMB maps at frequencies below 60 GHz, and at high frequencies the statistical properties are still barely known. At high Galactic latitudes (|b| > 15°) and for frequencies between 30 and 150 GHz, the CMB signal dominates the Galactic one (e.g. Bennett et al. 2003b; Tegmark et al. 2000). Therefore, a strategic way to obtain more accurate cosmological information is to observe at high Galactic latitudes, where the foreground contamination is expected to be lower. We selected three particular sky regions, each with an area of 20° × 20° centred at a galactic longitude (l) and latitude (b) of (l,b) = (258.18°, −46.33°), (l,b) = (252.07°,−38.78°) and (l,b) = (272.48°,−54.63°) denoted here by the first, second, and third sky region, respectively. The first coordinates were chosen because this region is of particular interest to the EBEx experiment (Reichborn-Kjennerud et al. 2010), towards which we plan follow-up observations with the Atacama Large Millimetre/submillimetre Array (ALMA). The centres of the other two regions are two point sources identified in the first one. We extracted these three sky regions from the smoothed full-sky maps per frequency band and projected them in squared maps of (512 × 512) pixels using the HEALPix software. In Fig. 3 we show the resulting maps in all the frequency bands for the first region. We applied the WMF method to the three regions mentioned above and present the linear composition map for the first region in Fig. 3. To fix the detection threshold, we considered an approach based on the empirical probability density function (EPDF) of the pixel values of the linear composition maps after the application of the filter. This is the procedure typically used for the detection of point sources in the CMB context. Many authors set this threshold to five times the standard deviation of the pixel values in the map (5σ level). This method, however, suffers the impact of the point sources themselves (e.g. see Leach et al. 2008). For this reason, we adopted a different approach that much less depends on the amount of the spurious contributions. In particular, we claim a detection when the fluxes in the corresponding pixels have values above a threshold given by the 98th percentile computed over all pixels in the respective sky region. The choice of this approach is forced by the difficulties in the computation of the detection threshold starting from an “a priori” PFA, because we could not use the level of the pixel noise provided by the WMAP team (defined as 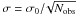 , where σ0 and Nobs are values taken from the LAMBDA website4). The reason is that before their linear composition, the maps have been manipulated to obtain a common spatial resolution as well as to convert them from spherical to rectangular coordinates (our codes are developed for the case of small patches of sky). Moreover, the noise in the WMAP maps is not spatially uniform. The EPDF for the first region can be seen in Fig. 4, where is clear that the bulk of the pixel values is confined in a very restricted range, of about [−10, 15] in internal units of our codes with a standard deviation of about σ15 = 2.98 units. Because the CMB component is absent in the linear composition map, it is reasonable to assume that these values are a result only of the noise. The EPDF presents a long tail up to a value of about 132 units that is owing to the presence of the point sources. The 98th empirical percentile of the EPDF roughly corresponds to the 5σ15 level. Similar values are found for the other regions.
, where σ0 and Nobs are values taken from the LAMBDA website4). The reason is that before their linear composition, the maps have been manipulated to obtain a common spatial resolution as well as to convert them from spherical to rectangular coordinates (our codes are developed for the case of small patches of sky). Moreover, the noise in the WMAP maps is not spatially uniform. The EPDF for the first region can be seen in Fig. 4, where is clear that the bulk of the pixel values is confined in a very restricted range, of about [−10, 15] in internal units of our codes with a standard deviation of about σ15 = 2.98 units. Because the CMB component is absent in the linear composition map, it is reasonable to assume that these values are a result only of the noise. The EPDF presents a long tail up to a value of about 132 units that is owing to the presence of the point sources. The 98th empirical percentile of the EPDF roughly corresponds to the 5σ15 level. Similar values are found for the other regions.
 |
Fig. 3 Squared WMAP maps per frequency band for the first sky region, centred at (l,b) = (258.18°, −46.33°) with an area of 20° × 20°. The map in the bottom right corner corresponds to the linear composition map obtained with the WMF. |
 |
Fig. 4 Empirical probability density function (EPDF) of the pixel values for the linear composition map of the first sky region after the application of the filter. The EPDF is different from zero in the range [− 11, 132] . Here, only the range [− 10, 30] is shown because outside this interval the EPDF is close to zero. The vertical red and green lines show the detection threshold based on the 98th percentile and the 5σ15 level, respectively. Here, σ15 is the standard deviation of the pixels with values less or equal to 15. The cyan line provides the Gaussian probability density function with zero mean and standard deviation given by σ15. |
 |
Fig. 5 Left panel: linearly composed image obtained with the WMF for the first sky region centred at (l,b) = (258.18°, −46.33°). Right panel: to enhance the source appearence it is shown the same image with the lowest pixel values zeroed (98% of the total). |
 |
Fig. 7 Spectral energy distribution for the new sources using the derived WMAP data and NED data of the possible counterparts. The arrows represent upper limits corresponding to 3σ, where σ was obtained from the pixel noise. The WMAP data are plotted with data from MRC 0427-539B and IC 2082 for Source # 1, PKS 0437-454 for Source # 2, PKS 0212-620 for Source # 3, PKS 0313-66019.0 for Source # 4 and PKS 0235-618 for Source # 5. For the Sources # 1, # 4, and # 5 , it is also plotted the BCES(Y | X) ordinary least-squares regression lines. |
New detected sources and possible counterparts.
 |
Fig. 8 Same as Fig. 7, with WMAP data plotted with data from SUMSS J032356-602410, PKS 0322-605 and PMN J0323-6026 for Source # 6 and PKS 0226-559 for Source # 7. |
4.3. Identification of the WMAP point sources
The WMAP seven-year point source catalogues contain information on the point sources in the five frequency bands from 23 to 94 GHz, based on data from the first seven years of the WMAP sky survey from 10 Aug. 2001 to 9 Aug. 2008, inclusive. The WMAP team has produced two point source catalogues using different methods for the identification of the sources, namely the Five-band search technique and the three-band CMB-free technique5. The former catalogue contains 471 point sources and is complete to 2 Jy for regions of the sky away from the Galactic plane. The latter catalogue was built using the three frequency bands from 41 to 94 GHz. This last method identifies 417 point sources in a linear combination map for which the weights were obtained in a way that the CMB contribution was removed and point sources with a flat spectrum were preserved.
In the three sky regions selected for this work all sources found with the WMF were cross-checked with those found in both WMAP seven-year catalogues. All sources found by the WMAP team for the selected regions are detected by WMF. However, the WMF allows us to find more sources that are not listed in any of these catalogues. Those new sources can be seen in Figs. 5 and 6. We labelled them Source 1 and 2 in the first region and 3, 4, 5, 6, and 7 in the third region. All sources detected by the WMF in the second region are listed already in the WMAP catalogues, except two (Source 1 and 2) that are already identified in the first region.
Because our detection method is sensitive to the source spectral index, we investigated which kind of spectral type radio source populations were detected by WMAP. The Five-band catalogue provides an estimate of the spectral index (α) defined by a power-law of the form F ∝ ν − α, where F is the flux density and ν is the frequency. We made use of this information to study the distribution of the spectral indices. The α lies in the range [− 2.1, 1.3] and three main spectral classes can be identified: about 81% of the population have a flat spectrum (−0.5 ≤ α ≤ 0.5), 16% show an inverted spectrum (α < −0.5), and the remaining 3% show a steep spectrum (α > 0.5).
We tested different values for α with the WMF, and the new sources are detected for spectral indices in the range obtained from the Five-band catalogue, except for an α close to 0. As explained in Sect. 3, the WMF is more efficient in finding sources with a spectral index different from zero. For strictly flat spectrum sources (α ≃ 0) the method erases not only the CMB component, but also the sources with an equal intensity in all WMAP bands. Therefore, this method is optimized for the sources with a flux dependent on the frequency.
4.3.1. Sources fluxes
To identify the newly detected sources we needed an estimate of the fluxes measured by WMAP. To this aim we used the original seven-year maps and integrated the flux density at the source location within the WMAP beam, which we assumed to have a Gaussian profile with a FWHM as given in Hinshaw et al. (2009). Conversion factors from mK to Jy were derived by comparing our derived fluxes with those given in the WMAP catalogues.
4.3.2. Cross-identification of the newly discovered WMAP point sources
To identify possible counterparts, we cross-correlated the new WMAP sources with catalogues found in the NED database, AT20G Catalogue (Murphy et al. 2010) and NEWPS sources (Massardi et al. 2009). We checked all sources with a radio counterpart within a selected radius of 12′, which corresponds to three times the mean position uncertainty of the WMAP satellite (Gold et al. 2011).
We summarize in Table 1 a list of possible counterparts. Figures 7 and 8 show the reconstructed radio spectral energy distributions (SED) of the most likely counterparts with the WMAP data. The linear regression lines and respective spectral indices were obtained through the BCES(Y | X) ordinary least-squares method, which takes into account measurement errors (Akritas & Bershady 1996).
Here we briefly discuss the most likely identifications of the new sources, which we associate with the brightest radio sources within our search radius.
-
Source # 1: The strongest radio sources within our search radiusare MRC 0427-539B, of which only one flux value at408 MHz is available, and IC 2082, which is aGalaxy pair (Gpair) with radio data from 408 MHzto 22 GHz. We plot the corresponding radio SED ofboth sources assuming that the WMAP fluxes belong to them.Both spectra are plotted in Fig. 7. In both cases wealso plot for reference the best fit through the data, which indicatesa spectral behaviour of a steep spectrum with a spectral index ofabout 0.60 ± 0.07 and 1.00 ± 0.09, respectively.
-
Source # 2: The most likely association is the radio source PKS 0437-454, which has data between 2.7 and 150 GHz. Our reconstructed SED is reported in Fig. 7. Here the distribution of fluxes is complex and may show a SED with different components. The uncertainties of the identification and the source fluxes do not allow us to proceed the investigation with the present data.
-
Source # 3: The closest radio source with the highest fluxes is PKS 0212-620, which is a candidate QSO with radio data from 843 MHz to 20 GHz. The fluxes are shown in Fig. 7. The source seems to be variable, and differences in flux values at the same frequency confirm this (see Sadler et al. 2006).
-
Source # 4: The most likely association is PKS 0313-660, which has data from 843 MHz to 20 GHz and is identified as a QSO. The SED built with WMAP data is reported in Fig. 7 and the fit gives the spectral index of ~ −0.15 ± 0.01.
-
Source # 5: The most probable identification is the QSO PKS 0235-618, which has radio data in the range 408 MHz to 20 GHz. The SED built with WMAP data is reported in Fig. 7, resulting in a fit with a spectral index of ~ 0.09 ± 0.01.
-
Source # 6: There are three sources with bright radio fluxes, namely SUMSS J032356-602410, PKS 0322-605 and PMN J0323-6026. We report the radio SEDs in Fig. 8. For the first and second possible counterpart, only one flux value is available. The PMN J0323-6026 has data from 843 MHz to 20 GHz and is a variable QSO (see Sadler et al. 2006).
-
Source # 7: The closest and most likely association is PKS 0226-559 with radio data from 843 MHz to 8.4 GHz, which is identified as a flat spectrum (at frequencies lower than 8GHz) radio QSO (Healey et al. 2007). The reconstructed SED with the WMAP data is shown in Fig. 8. At high frequencies the spectrum appears to decrease with frequency and is no longer flat.
Most of all other possible radio counterparts for which we do not give any SED (see Table 1) have only one radio detection mostly at 843 GHz of the order of mJy or do not have published radio data.
5. Conclusions
A new technique was presented, the weighted matched filter (WMF), to extract point sources from astrophysical maps. This method is quite simple to use and more robust in practical applications. It achieves an optimal performance for extracting sources with a spectrum different from a strictly flat one. We showed the reliability of this technique with some numerical simulations.
The WMF was applied to three Southern Hemisphere sky regions – each with an area of 400 deg2 – of the seven-year WMAP temperature maps and compared the resulting sources with those of the two seven-year WMAP point source catalogues.
We found in these three regions seven additional sources not previously listed in WMAP catalogues and discussed their most likely identification and spectral properties.
We plan to investigate and further explore the application of the WMF technique and the identification of the new sources in future experiments, namely with Planck observational data and with simulations aimed at reproducing the sky at the ALMA frequencies and spatial resolution.
Acknowledgments
E. P. Ramos was financially supported by a grant from Fundação para a Ciência e a Tecnologia (POPH-QREN-SFRH/BD/45613/2008) and project PTDC/CTE-AST/64711/2006. E. P. Ramos and R. Vio thank ESO for its hospitality and support through the DGDF funding programme.
References
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Bay, M., Halpern, M., et al. 2003a, ApJ, 583, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Hill, R. S., Hinshaw, G., et al. 2003b, ApJS, 148, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Carvalho, P., Rocha, G., & Hobson, M. P. 2009, MNRAS, 393, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Wright, E. L. 2009, ApJ, 694, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Gold, B., Odegard, N., Weiland, J. L., et al. 2011, ApJS, 192, 15 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Healey, S. E., Romani R. W., Taylor G. B., et al. 2007, ApJS, 171, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Herranz, D., & Sanz, J. L. 2008, IEEE J. Selected Topics in Signal Processing, 2, 727 [Google Scholar]
- Herranz, D., Sanz, J. L., Hobson, M. P., et al. 2002, MNRAS, 336, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Hirshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJ, 180, 225 [NASA ADS] [Google Scholar]
- Hurier, G., Hidelbrandt, S. R., & Macias-Perez, J. F. 2010, [arXiv:1007.1149v2] [Google Scholar]
- Jarosik, N., et al. 2011, ApJS, 192, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kay, S. M. 1998, Fundamentals of Statistical Signal Processing: Detection Theory (London: Prentice Hall) [Google Scholar]
- Lanz, L. F., Herranz, D., Sanz, J. L., et al. 2010, MNRAS, 403, 212 [Google Scholar]
- Leach, S. M., Cardoso, J.-F., Baccigalupi, C., et al. 2008, A&A, 491, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massardi, M., Lopez-Caniego, M., Gonzalez-Nuevo, J., et al. 2009, MNRAS, 392, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, T., Sadler, E. M., Ekers, R. D., et al. 2010, MNRAS, 402, 2403 [NASA ADS] [CrossRef] [Google Scholar]
- Reichborn-Kjennerud, B., Aboobaker, A. M., Ade, P., et al. 2010, Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy V, ed. W. S. Holland, & J. Zmuidzinas, Proc. SPIE, 7741, 77411C [Google Scholar]
- Remazeilles, M., Delabrouille, J., & Cardoso, J. F. 2011, MNRAS, 410, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Sadler, E. M., Ricci, R., Ekers, R. D., et al. 2006, MNRAS, 371, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Eisenstein, D. J., Hu, W., & de Oliveira-Costa, A. 2000, ApJ, 530, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Vio, R., Tenorio, L., & Wamsteker, W. 2002, A&A, 391, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vio, R., Nagy, J. G., Tenorio, L., et al. 2003, A&A, 401, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vio, R., Andreani, P., & Wamsteker, W. 2004, A&A, 414, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: The classic matched filter method to detect point sources in CMB maps
This appendix integrates the missing information of Sects. 2 and 3. We present here the classic matched filter method to detect point sources in multi-frequency observations. The goal is to facilitate the comparison of this approach with that proposed in this work. Arguments will be developed starting from the one-dimensional signal and single frequency case. The two-dimensional signal and multi-frequency case is developed in the second part.
A.1. One-dimensional signal and single-frequency case
In CMB observations, the following conditions are commonly assumed:
-
1.
The point sources have a known spatial profiles = ag. The amplitude “a” is a scalar quantity that differs from source to source, whereas g is a function which, owing to the instrument beam, is identical for all the sources. Function g is normalized in a way that max { g [0] ,g [1] ,...,g [N − 1] } = 1, where N is the length of the function.
-
2.
The point sources are embedded in a noise background n, i.e. the observed signal x is given by x = s + n. In other words, noise is additive.
-
3.
Noise n is the realization of a stationary stochastic process with known covariance matrix
![\appendix \setcounter{section}{1} \begin{equation} \label{eq:C} \Cb = {\rm E}[\nb \nb^{\rm T}]. \end{equation}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq141.png) (A.1)Because of the Galactic contribution, especially at low Galactic latitudes, this hypothesis is not always satisfied, but we assume that it holds locally. This allows the computation of statistics such as the mean or the covariance matrix that otherwise could not be possible. Without loss of generality, it is assumed that E [n] = 0.
(A.1)Because of the Galactic contribution, especially at low Galactic latitudes, this hypothesis is not always satisfied, but we assume that it holds locally. This allows the computation of statistics such as the mean or the covariance matrix that otherwise could not be possible. Without loss of generality, it is assumed that E [n] = 0.
Under these conditions, the detection problem consists in deciding whether x is a pure noise n (hypothesis H0) or also contains the contribution of a source s (hypothesis H1). In this way, the source detection problem is equivalent to a decision problem where two hypotheses hold: 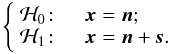 (A.2)Under ℋ0 the probability density function of x is given by p(x | ℋ0), whereas under ℋ1 by p(x | ℋ1). At this point, it is necessary to fix the criterion to use for the detection, which depends on the particular case of interest. For example, one could decide that the non-detection or the misidentification of a bright source could be more important than the detection of a fainter one, or vice versa. A very common and effective criterion is the Neyman-Pearson criterion, which consists of the maximization of the probability of detection PD under the constraint that the probability of false alarm PFA (i.e., the probability of a false detection) does not exceed a fixed value α. The Neyman-Pearson theorem (e.g., see Kay 1998) is a powerful tool that allows one to design a decision process that pursues this aim: to maximize PD for a given PFA = α, decide ℋ1 if the likelihood ratio (LR)
(A.2)Under ℋ0 the probability density function of x is given by p(x | ℋ0), whereas under ℋ1 by p(x | ℋ1). At this point, it is necessary to fix the criterion to use for the detection, which depends on the particular case of interest. For example, one could decide that the non-detection or the misidentification of a bright source could be more important than the detection of a fainter one, or vice versa. A very common and effective criterion is the Neyman-Pearson criterion, which consists of the maximization of the probability of detection PD under the constraint that the probability of false alarm PFA (i.e., the probability of a false detection) does not exceed a fixed value α. The Neyman-Pearson theorem (e.g., see Kay 1998) is a powerful tool that allows one to design a decision process that pursues this aim: to maximize PD for a given PFA = α, decide ℋ1 if the likelihood ratio (LR)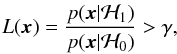 (A.3)where the threshold γ is found from
(A.3)where the threshold γ is found from 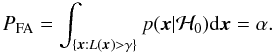 (A.4)The test of the ratio (A.3) is called the likelihood ratio test (LRT).
(A.4)The test of the ratio (A.3) is called the likelihood ratio test (LRT).
An important example for the application of LRT is the case of a Gaussian noise n with correlation function C. In CMB experiments this condition is satisfied only for observations at high Galactic latitudes where the CMB emission and the instrumental noise are the dominant contributions. At lower latitudes, it is often assumed to hold locally. For example, the contribution to x of components that in small sky patches show linear spatial trends are often approximated with stationary Gaussian processes with a steep spectrum (e.g. 1/f noises). This is usually assumed, even for unrealistic Gaussianity conditions, because it allows an analytical treatment of the problem of interest and the results can be used as a benchmark in the analysis of more complex scenarios. When n is Gaussian, ![\appendix \setcounter{section}{1} \begin{eqnarray} p(\xb | \Hc_0) & =& \Delta \exp\left[ -\frac{1}{2} \xb^{\rm T} \Cb^{-1} \xb \right]; \label {eq:t1} \\ p(\xb | \Hc_1) & =& \Delta \exp\left[ -\frac{1}{2} (\xb - \ssb)^{\rm T} \Cb^{-1} (\xb -\ssb) \right], \label{eq:t2} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq161.png) with
with 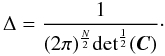 (A.7)The LRT is given by
(A.7)The LRT is given by ![\appendix \setcounter{section}{1} \begin{equation} l(\xb) = \ln[L(\xb)] = \xb^{\rm T} \Cb^{-1} \ssb - \frac{1}{2} \ssb^{\rm T} \Cb^{-1} \ssb > \gamma'. \end{equation}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq163.png) (A.8)Hence, it follows that ℋ1 has to be chosen when the statistic T(x) (called NP detector) is
(A.8)Hence, it follows that ℋ1 has to be chosen when the statistic T(x) (called NP detector) is 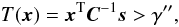 (A.9)with γ′′ in a way that
(A.9)with γ′′ in a way that ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:pfa} \PFA = Q \left( \frac{\gamma''}{\left[ \ssb^{\rm T} \Cb^{-1} \ssb \right]^{1/2}} \right) = \alpha, \end{equation}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq167.png) (A.10)i.e.,
(A.10)i.e., 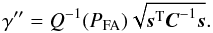 (A.11)Here, Q(x) is the complementary cumulative distribution function
(A.11)Here, Q(x) is the complementary cumulative distribution function 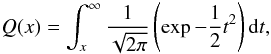 (A.12)and Q-1 the corresponding inverse function. Equation (A.10)has this form because T(x) is a Gaussian random variable with variance sTC-1s and expected values equal to zero under ℋ0 and sTC-1s under ℋ1 (see Fig. A.1). For the same reason, the PD is given by
(A.12)and Q-1 the corresponding inverse function. Equation (A.10)has this form because T(x) is a Gaussian random variable with variance sTC-1s and expected values equal to zero under ℋ0 and sTC-1s under ℋ1 (see Fig. A.1). For the same reason, the PD is given by 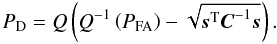 (A.13)Equation (A.9)can be written in the form
(A.13)Equation (A.9)can be written in the form 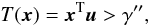 (A.14)with
(A.14)with 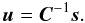 (A.15)From this equation u can be thought of as a linear filter of signal x. It is called matched filter (MF).
(A.15)From this equation u can be thought of as a linear filter of signal x. It is called matched filter (MF).
A.1.1. Some comments on the use of the matched filter in practical applications
 |
Fig. A.1 Probability density function of the statistic T(x) under the hypothesis ℋ0 (noise-only hypothesis) and ℋ1 (signal-present hypothesis). The detection-threshold is given by γ′′. The probability of false alarm (PFA) and the probability of detection (PD) are shown in green and yellow colors, respectively. |
There are several important points to stress about the MF when used in practical applications:
-
T(x) is a sufficient statistic (Kay 1998). Loosely speaking, this means that T(x) is able to summarize all relevant information in the data concerning the decision (A.2). No other statistic can perform better.
-
If the amplitude “a” of the source is unknown, then Eq. (A.9) can be rewritten in the form
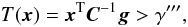 (A.16)with
(A.16)with 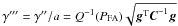 . In other words, a statistic is obtained independently of “a”. As a consequence of the Neyman-Person theorem, for an unknown amplitude of the source, T(x) still maximizes PD for a fixed PFA. The only consequence is that PD cannot be evaluated in advance. In principle this can be done “a posteriori” by using the maximum likelihood estimate of the amplitude,
. In other words, a statistic is obtained independently of “a”. As a consequence of the Neyman-Person theorem, for an unknown amplitude of the source, T(x) still maximizes PD for a fixed PFA. The only consequence is that PD cannot be evaluated in advance. In principle this can be done “a posteriori” by using the maximum likelihood estimate of the amplitude, 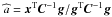 . However, this is of little interest, because in real experiments one is typically interested in the detection of sources with amplitudes that are characterized by a probability density function p(a). In this case, once PFA is fixed to a value α and changing “a” across the domain of p(a), the quantity 1 − PD, with PD given by Eq. (A.13) and s = ag, provides an estimate of the fraction of undetected sources as a function of their amplitude.
. However, this is of little interest, because in real experiments one is typically interested in the detection of sources with amplitudes that are characterized by a probability density function p(a). In this case, once PFA is fixed to a value α and changing “a” across the domain of p(a), the quantity 1 − PD, with PD given by Eq. (A.13) and s = ag, provides an estimate of the fraction of undetected sources as a function of their amplitude. -
If
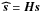 and
and 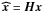 , then
, then 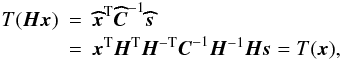 (A.17)with H any invertible linear operator (matrix). A useful consequence of this property is that if the signal x is convolved with a function (e.g., the beam of an instrument), this operation does not modify the optimality of MF. In this case, the operator H transforms the covariance matrix C into HCHT. This is useful in situations where more signals are available that are obtained with different point-spread functions.
(A.17)with H any invertible linear operator (matrix). A useful consequence of this property is that if the signal x is convolved with a function (e.g., the beam of an instrument), this operation does not modify the optimality of MF. In this case, the operator H transforms the covariance matrix C into HCHT. This is useful in situations where more signals are available that are obtained with different point-spread functions.
A.2. One-dimensional signal and multiple-frequency case
In the context of CMB observations, the complexity increases because there are M signals xk = sk + nk, sk = akgk, k = 1,2,...,M, coming from the same sky area that are taken at different observing frequencies. Here, ak is the amplitude of the source at the kth observing frequency, whereas gk is the corresponding spatial profile. For ease of notation, all signals are assumed to have the same length N. In general, the amplitudes { ak } as well as the profiles { gk } are different for different k. However, if one sets ![\appendix \setcounter{section}{1} \begin{eqnarray} \xb & =& [\xb_1^{\rm T}, \xb_2^{\rm T}, \ldots, \xb_M^{\rm T}]^{\rm T}, \label{eq:mxb} \\ \ssb & =& [\ssb_1^{\rm T}, \ssb_2^{\rm T}, \ldots, \ssb_M^{\rm T}]^{\rm T}, \label{eq:msb} \\ \nb & =& [\nb_1^{\rm T}, \nb_2^{\rm T}, \ldots, \nb_M^{\rm T}]^{\rm T}, \label{eq:mnb} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq200.png) it is possible to obtain a problem that is formally identical to that treated in the previous section. Hence, the MF is still given by Eqs. (A.14)–(A.15)and is named multi-frequency matched filter (MMF). The only difference with the classic MF is that now C is a (NM) × (NM) block matrix with Toeplitz blocks (BTB):
it is possible to obtain a problem that is formally identical to that treated in the previous section. Hence, the MF is still given by Eqs. (A.14)–(A.15)and is named multi-frequency matched filter (MMF). The only difference with the classic MF is that now C is a (NM) × (NM) block matrix with Toeplitz blocks (BTB): 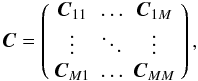 (A.21)i.e., each of the Cij blocks is constituted by a N × N Toeplitz matrix. In particular,
(A.21)i.e., each of the Cij blocks is constituted by a N × N Toeplitz matrix. In particular, ![\appendix \setcounter{section}{1} \hbox{$\Cb_{ii} = {\rm E}[\nb_i \nb_i^{\rm T}]$}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq205.png) provides the autocovariance matrix of the ith noise, whereas
provides the autocovariance matrix of the ith noise, whereas ![\appendix \setcounter{section}{1} \hbox{$\Cb_{ij} = {\rm E}[\nb_i \nb_j^{\rm T}]$}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq207.png) , i ≠ j, the cross-covariance matrix between the ith and the jth ones.
, i ≠ j, the cross-covariance matrix between the ith and the jth ones.
Despite these similarities, when M > 1, there are additional difficulties: T(x) cannot be written in a form equivalent to Eq. (A.16). For unknown amplitudes { ak } T(x) cannot be computed. In other words, if the spectral characteristics of the radiation emitted by a source are not fixed, then the MMF is not applicable.
A.3. Extension to two-dimensional signals
The extension of MF to the two-dimensional signals 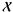 and
and 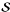 is conceptually trivial. For the one-dimensional case, setting6
is conceptually trivial. For the one-dimensional case, setting6![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:stack1} \ssb & =& {\rm VEC}[\Smatb];\\ \label{eq:stack2} \xb & =& {\rm VEC}[\Xmatb]; \\ \label{eq:stack3} \nb & =& {\rm VEC}[\Nmatb], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq214.png) formally the problem becomes the same as that given by Eq. (A.2). For multi-frequency observations, the situation is more complex because MF has to be applied to M signals at the same time. However, with the notation
formally the problem becomes the same as that given by Eq. (A.2). For multi-frequency observations, the situation is more complex because MF has to be applied to M signals at the same time. However, with the notation ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:stack12} \ssb & =& {\rm VEC}\left[ {\rm VEC}[ \Smatb_1 ], {\rm VEC}[ \Smatb_2 ], \ldots, {\rm VEC}[ \Smatb_M ] \right]; \\ \label{eq:stack22} \xb & = &{\rm VEC}\left[ {\rm VEC}[ \Xmatb_1 ], {\rm VEC}[ \Xmatb_2 ], \ldots, {\rm VEC}[ \Xmatb_M ] \right]; \\ \label{eq:stack32} \nb & =& {\rm VEC}\left[ {\rm VEC}[ \Nmatb_1 ], {\rm VEC}[ \Nmatb_2 ], \ldots, {\rm VEC}[ \Nmatb_M ] \right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15586-10/aa15586-10-eq215.png) it is also possible to obtain a problem that is formally identical to that given by Eq. (A.2). The only difference is that now in Eq. (A.21), C is a (MNp) × (MNp) block matrix. If the signals
it is also possible to obtain a problem that is formally identical to that given by Eq. (A.2). The only difference is that now in Eq. (A.21), C is a (MNp) × (MNp) block matrix. If the signals 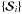 are two-dimensional Nr × Nc maps, then each of the Cij blocks is constituted by a (NrNc) × (NrNc) block Toeplitz with Toeplitz blocks (BTTB) matrix. In particular, Cii provides the autocovariance matrix of the ith map, whereas Cij, i ≠ j, the cross-covariance matrix between the ith and the jth maps.
are two-dimensional Nr × Nc maps, then each of the Cij blocks is constituted by a (NrNc) × (NrNc) block Toeplitz with Toeplitz blocks (BTTB) matrix. In particular, Cii provides the autocovariance matrix of the ith map, whereas Cij, i ≠ j, the cross-covariance matrix between the ith and the jth maps.
Especially for the multi-frequency case, the implementation of the MF is not trivial. Even for moderate size signals, the matrix C rapidly becomes huge. As a consequence, it is necessary to implement numerical methods that are able to exploit the specific structure of C. Typically, they are based on Fourier approaches. This subject, however, is beyond the aim of the present work.
All Tables
All Figures
 |
Fig. 1 Probability of detection PD against probability of false alarm PFA for the detection methods in the numerical experiment described in Sect. 3. The sources are assumed to have an intensity ai at the ith frequency given by ai = (νi/ν1)αa1, with a1 = 0.5. Four values for α are considered, α = 3,1,0.5,0.05. The results are shown for the different methods: the weighted matched filter (WMF), the multi-frequency matched filter (MMF), the uniformly weighted matched filter (UWMF) and the average matched filter (AMF). The MMF is used as benchmark because it has the best theoretical detection performance. The UWMF shows the worst possible results obtainable with the WMF approach. The AMF shows which results are obtainable when the maps are simply averaged. A method is superior to another one when for a fixed PFA the corresponding PD is greater (for a given method, the relation PD to PFA should always be well above a 45° straight line, the dashed line in the figure). With increasing α, the behaviour of MMF and WMF becomes similar. For an α close to zero, the MMF and AMF show a very similar performance. |
| In the text | |
 |
Fig. 2 Relative decrease of the probability of detection, |
| In the text | |
 |
Fig. 3 Squared WMAP maps per frequency band for the first sky region, centred at (l,b) = (258.18°, −46.33°) with an area of 20° × 20°. The map in the bottom right corner corresponds to the linear composition map obtained with the WMF. |
| In the text | |
 |
Fig. 4 Empirical probability density function (EPDF) of the pixel values for the linear composition map of the first sky region after the application of the filter. The EPDF is different from zero in the range [− 11, 132] . Here, only the range [− 10, 30] is shown because outside this interval the EPDF is close to zero. The vertical red and green lines show the detection threshold based on the 98th percentile and the 5σ15 level, respectively. Here, σ15 is the standard deviation of the pixels with values less or equal to 15. The cyan line provides the Gaussian probability density function with zero mean and standard deviation given by σ15. |
| In the text | |
 |
Fig. 5 Left panel: linearly composed image obtained with the WMF for the first sky region centred at (l,b) = (258.18°, −46.33°). Right panel: to enhance the source appearence it is shown the same image with the lowest pixel values zeroed (98% of the total). |
| In the text | |
 |
Fig. 6 Same as Fig. 5 for the third sky region centred at (l,b) = (272.48°,−54.63°). |
| In the text | |
 |
Fig. 7 Spectral energy distribution for the new sources using the derived WMAP data and NED data of the possible counterparts. The arrows represent upper limits corresponding to 3σ, where σ was obtained from the pixel noise. The WMAP data are plotted with data from MRC 0427-539B and IC 2082 for Source # 1, PKS 0437-454 for Source # 2, PKS 0212-620 for Source # 3, PKS 0313-66019.0 for Source # 4 and PKS 0235-618 for Source # 5. For the Sources # 1, # 4, and # 5 , it is also plotted the BCES(Y | X) ordinary least-squares regression lines. |
| In the text | |
 |
Fig. 8 Same as Fig. 7, with WMAP data plotted with data from SUMSS J032356-602410, PKS 0322-605 and PMN J0323-6026 for Source # 6 and PKS 0226-559 for Source # 7. |
| In the text | |
 |
Fig. A.1 Probability density function of the statistic T(x) under the hypothesis ℋ0 (noise-only hypothesis) and ℋ1 (signal-present hypothesis). The detection-threshold is given by γ′′. The probability of false alarm (PFA) and the probability of detection (PD) are shown in green and yellow colors, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


