| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014778 | |
| Published online | 17 March 2011 | |
Theoretical light curves of type Ia supernovae
1 Hamburger Sternwarte, Gojenbergsweg
112, 21029 Hamburg, Germany
e-mail: djack@hs.uni-hamburg.de; yeti@hs.uni-hamburg.de
2 Homer L. Dodge Department of Physics
and Astronomy, University of Oklahoma, 440 W Brooks, Rm 100, Norman, OK
73019-2061,
USA
e-mail: baron@ou.edu
Received: 13 April 2010
Accepted: 9 February 2011
Aims. We present the first theoretical SN Ia light curves calculated with the time-dependent version of the general purpose model atmosphere code PHOENIX. Our goal is to produce light curves and spectra of hydro models of all types of supernovae.
Methods. We extend our model atmosphere code PHOENIX to calculate type Ia supernovae light curves. A simple solver was implemented which keeps track of energy conservation in the atmosphere during the free expansion phase.
Results. The correct operation of the new additions to PHOENIX were verified in test calculations. Furthermore, we calculated theoretical light curves and compared them to the observed SN Ia light curves of SN 1999ee and SN 2002bo. We obtained LTE as well as NLTE model light curves.
Conclusions. We have verified the correct operation of our extension into the time domain. We have calculated the first SN Ia model light curves using PHOENIX in both LTE and NLTE. For future work the infrared model light curves need to be further investigated.
Key words: supernovae: general / radiative transfer / methods: numerical
© ESO, 2011
1. Introduction
All types of supernovae are important for the role that they play in understanding stellar evolution, galactic nucleosynthesis, and as cosmological probes. Type Ia supernovae are of particular cosmological interest, e.g., because the dark energy was discovered with type Ia supernovae (Riess et al. 1998; Perlmutter et al. 1999).
In dark energy studies, the goal now is to characterize the nature of the dark energy as a function of redshift. While there are other probes that will be used (gravitational lensing, baryon acoustic oscillations), a JDEM or Euclid mission will likely consider supernovae in some form. In planning for future dark energy studies both from space and from the ground, it is important to know whether the mission will require spectroscopy of modest resolution, or whether pure imaging or grism spectroscopy will be adequate. Several purely spectral indicators of peak luminosity have been proposed (Nugent et al. 1995; Hachinger et al. 2006; Bongard et al. 2006; Bronder et al. 2008; Foley et al. 2008; Chotard et al. 2011). What is required is an empirical and theoretical comparison of both light curve shape luminosity indicators (Pskovskii 1977; Phillips 1993; Riess et al. 1996; Goldhaber et al. 2001) and spectral indicators.
To make this comparison one needs to know more about the physics going on in a supernova explosion and to be able to calculate light curves and spectra self-consistently. Thus, we need to extend our code to time-dependent problems. While our primary focus is on type Ia supernovae, the time-dependent radiative transfer code is applicable to all types of supernovae, as well as to other objects, e.g., stellar pulsations.
In the following we present the methods we used to implement time dependence. First we focus on solving the energy equation (first law) and then present our first theoretical LTE light curves of type Ia supernova events. In a further section, we present results of NLTE model light curve calculations.
2. Energy solver
In our previous paper (Jack et al. 2009), we presented our approach to calculate light curves of type Ia supernovae events. We implemented a simple energy solver into our general purpose model atmosphere code PHOENIX where we kept track of the overall energy change of the radiating fluid and the energy exchange between the matter and radiation. Simple test light curves confirmed that our approach worked correctly. We now present a new approach to calculate theoretical light curves of SNe Ia. Again, we are using a simple solver where we keep track of the energy conservation. In the new approach, we consider only the energy density of the material. We assume free expansion and do not solve the equations of hydrodynamics. In order to obtain the result for the new time step, we use an explicit scheme. We apply this scheme and compute time steps until radiative equilibrium is reached. These are the points in our light curves.
The direct change of the energy density of the material considering absorption and emission of radiation and energy deposition by gamma rays is given by Eq. (96.7) in Mihalas & Mihalas (1984)![\begin{equation} \rho\left[\frac{\dx e}{\dx t}+p\frac{\dx}{\dx t}\left(\frac{1}{\rho}\right)\right]= \int\left(c\chi E-4\pi\eta\right)+\rho\epsilon, \end{equation}](/articles/aa/full_html/2011/04/aa14778-10/aa14778-10-eq1.png) (1)where ρ is the density, p the gas pressure and e is the energy density of the material. The quantities of the radiation field are χ which is the absorption coefficient, η is the emission coefficient and
(1)where ρ is the density, p the gas pressure and e is the energy density of the material. The quantities of the radiation field are χ which is the absorption coefficient, η is the emission coefficient and 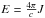 is the radiation energy density with the mean intensity J. To obtain E, the radiative transfer equation in spherical symmetry is solved including special relativity. All additional energy sources are put in ϵ such as the energy input from gamma ray deposition. This equation represents the first law of thermodynamics for the material. The change of the energy density of the material depends on the coupling of matter and radiation field, the absorption of gamma-radiation and positron annihilation energy, the expansion work and the change of the ionization and excitation of matter.
is the radiation energy density with the mean intensity J. To obtain E, the radiative transfer equation in spherical symmetry is solved including special relativity. All additional energy sources are put in ϵ such as the energy input from gamma ray deposition. This equation represents the first law of thermodynamics for the material. The change of the energy density of the material depends on the coupling of matter and radiation field, the absorption of gamma-radiation and positron annihilation energy, the expansion work and the change of the ionization and excitation of matter.
Dividing equation 1 by the material density ρ we obtain 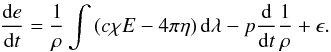 (2)The radiation energy density is given by
(2)The radiation energy density is given by 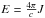 , where J is the mean intensity. Using this, we obtain for the radiation term
, where J is the mean intensity. Using this, we obtain for the radiation term 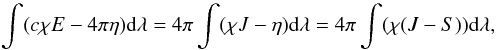 (3)where
(3)where 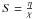 is the source function. All these quantities can be derived from the solution of the radiative transfer equation. The term of the change of the energy density by the radiation is therefore given by
is the source function. All these quantities can be derived from the solution of the radiative transfer equation. The term of the change of the energy density by the radiation is therefore given by 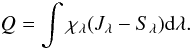 (4)Another change of the energy density is due to the work W done by the adiabatic expansion of the SN Ia atmosphere. For a discrete step this work is given by
(4)Another change of the energy density is due to the work W done by the adiabatic expansion of the SN Ia atmosphere. For a discrete step this work is given by 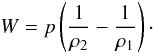 (5)The expansion is assumed to be homologous. Since we solve the energy equation for the matter, we do not include the radiation pressure work. Since the system is radiation dominated there is the possibility of numerical inaccuracies in coupling the matter and radiation only by Q. For the calculation of the new radii and densities as well as a discussion about the accuracy of this assumption see Jack et al. (2009).
(5)The expansion is assumed to be homologous. Since we solve the energy equation for the matter, we do not include the radiation pressure work. Since the system is radiation dominated there is the possibility of numerical inaccuracies in coupling the matter and radiation only by Q. For the calculation of the new radii and densities as well as a discussion about the accuracy of this assumption see Jack et al. (2009).
Including all energy changing effects, the new energy density of the material e2 after a discrete time step Δt is explicitly given by 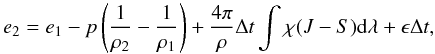 (6)where e1 is the old energy density.
(6)where e1 is the old energy density.
To obtain all the needed quantities we have to solve the spherically symmetric special relativistic radiative transfer equation. The advantage of our new approach is that we do not have to iterate for each time step. In our previous paper the calculation of each time step involved an iteration process to obtain the new matter temperature. With the new approach we can calculate the new temperature for the next time step directly from all the known quantities.
The translational energy density of the material is given by 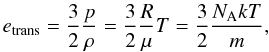 (7)with the mean molecular weigh μ and the universal gas constant R. The gas pressure is represented by p and the density by ρ. T stands for the temperature of the material. This equation of the energy density is now used to determine the new temperature after the next time step.
(7)with the mean molecular weigh μ and the universal gas constant R. The gas pressure is represented by p and the density by ρ. T stands for the temperature of the material. This equation of the energy density is now used to determine the new temperature after the next time step.
During the first phase of the SN Ia envelope evolution, the material of the atmosphere is hot and, therefore, highly ionized. The energy change due to ionization and excitation changes of the atoms present in the SN Ia atmosphere cannot be neglected. PHOENIX already solves the equation of state (EOS), where all the excitation and ionization stages of the present atoms and molecules are included. Using the EOS, we obtain the overall energy density of the material by the sum of the ionization energy eions and the translational energy etrans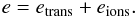 (8)Hence, the energy density change of the material goes into a change of the translational energy and the ionization energy, which both depend on the temperature. Therefore, we obtain the new temperature by an iteration scheme. The matter density at the next point in time is determined by homologous expansion. A first temperature guess is used, and the EOS is solved to obtain the ionization energy density. Combined with the translational energy density, the overall energy density is computed. This is checked against the target energy density, which we obtained Eq. (6). If the obtained energy density is incorrect, a new temperature guess is made. This new temperature guess is obtained by assuming a linear dependence of the energy density and temperature. The current temperature guess is iterated to the target energy density. It takes about 5–10 iteration steps to determine the new temperature. If the EOS delivers the correct target energy density, the new temperature of the next time step has been found. The accuracy relative of the energy density in this iteration process is set to 10-5.
(8)Hence, the energy density change of the material goes into a change of the translational energy and the ionization energy, which both depend on the temperature. Therefore, we obtain the new temperature by an iteration scheme. The matter density at the next point in time is determined by homologous expansion. A first temperature guess is used, and the EOS is solved to obtain the ionization energy density. Combined with the translational energy density, the overall energy density is computed. This is checked against the target energy density, which we obtained Eq. (6). If the obtained energy density is incorrect, a new temperature guess is made. This new temperature guess is obtained by assuming a linear dependence of the energy density and temperature. The current temperature guess is iterated to the target energy density. It takes about 5–10 iteration steps to determine the new temperature. If the EOS delivers the correct target energy density, the new temperature of the next time step has been found. The accuracy relative of the energy density in this iteration process is set to 10-5.
2.1. γ-ray deposition
The maximum of the light curve of an SN Ia event is observed around 20 days after explosion. Causing this later maximum of the light curve of an SN Ia event is the energy release into the envelope caused by the radioactive decay of 56Ni and its also radioactive decay product 56Co. Therefore, this energy deposition has a strong influence on the energy change of the SN Ia envelope structure. Hence, the energy deposition due to radioactive decay has to be taken into account for the calculation of the SN Ia envelope evolution.
The energy deposition due to the γ-rays emitted by radioactive isotopes needs to be computed by a radiative transfer solver for the γ-rays. In this work, we solve the γ-ray deposition with the assumption of a gray atmosphere for the γ-rays. Jeffery (1998) did a detailed study of the γ-ray deposition and pointed out that this is an adequate approach to calculate γ-ray deposition in SN Ia atmospheres. In the decay of a 56Ni nucleus, a γ-photon is emitted with an energy of 2.136 MeV. The 56Co nucleus decays to an 56Fe nucleus and emits a γ-photon, which has an energy of 4.566 MeV. In the decay of 56Co about 19% of the energy is released by positrons. The positrons are assumed to be locally trapped. They annihilate by emitting two photons each with an energy of 512 keV, which has to be taken into account for the energy deposition calculation. The opacity is considered to be constant and a pure absorption opacity, meaning that no scattering is assumed. As in Jeffery (1998), κγ = 0.06 ⟨ Z/A ⟩ cm2 g-1 was chosen as the opacity. ⟨ Z/A ⟩ is the proton fraction, which is counts both bound and free electrons, since the electron binding energy is small compared to the energy of gamma rays. The energy deposition into the atmosphere per unit time is given by 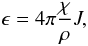 (9)where J is the mean intensity, which has been obtained by solving the gray radiative transfer for the γ-rays. This obtained energy deposition has to be taken into account for the calculation of the overall energy change.
(9)where J is the mean intensity, which has been obtained by solving the gray radiative transfer for the γ-rays. This obtained energy deposition has to be taken into account for the calculation of the overall energy change.
2.2. Adaptive time step procedure
The timescale for energy changes in the SN Ia envelope will change during the evolution of the light curve. In order to save computation time, the light curves have to be calculated with the optimal time step size for each phase of light curve evolution. Therefore, we implemented an adaptive time step routine to determine the optimal time step size for the current time step.
The energy change Δe of the energy of the material e may be approximated by 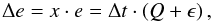 (10)where Q is the energy change of the interaction with the radiation, and ϵ is the energy deposition by the gamma rays. The energy change due to the expansion is ignored in this case. On the one hand, this energy change depends on the new matter density after the time step, which is unknown because it depends on the size of the time step itself. Furthermore, the energy change because of the expansion is small compared to the changes caused by the energy transport and the energy deposition by γ-rays. The idea of the adaptive time step procedure is to limit the energy change to a prescribed amount of the energy of the material. Thus, rewriting Eq. (10), we obtain the time step size Δt for the current time step by
(10)where Q is the energy change of the interaction with the radiation, and ϵ is the energy deposition by the gamma rays. The energy change due to the expansion is ignored in this case. On the one hand, this energy change depends on the new matter density after the time step, which is unknown because it depends on the size of the time step itself. Furthermore, the energy change because of the expansion is small compared to the changes caused by the energy transport and the energy deposition by γ-rays. The idea of the adaptive time step procedure is to limit the energy change to a prescribed amount of the energy of the material. Thus, rewriting Eq. (10), we obtain the time step size Δt for the current time step by 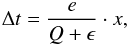 (11)where x is the introduced limiting energy change factor. The factor x ranges between xmin and xmax, which mark the largest and smallest allowed energy change. These are input parameters for the adaptive time step procedure. The time step size is calculated for every layer, and the minimum time step size of all layers is used for the energy solver.
(11)where x is the introduced limiting energy change factor. The factor x ranges between xmin and xmax, which mark the largest and smallest allowed energy change. These are input parameters for the adaptive time step procedure. The time step size is calculated for every layer, and the minimum time step size of all layers is used for the energy solver.
Each time the adaptive time step procedure is called, it checks if the energy changes of the time step before were too big or could have been bigger. If the minimum time step size is in a different layer, the same value of x is kept for the next time step. If the minimum is in the same layer and the sign of the energy change does not change, the previous time step might have been too small. Thus, the factor x is increased for the following time step. If the sign changes, the last time step might have been too large, therefore, the factor x is decreased. This means that for each time step, the allowed energy change is adapted and the factor x is updated to get the optimal time step during the whole evolution of the SN Ia atmosphere.
3. Test calculations
All new implemented physical processes of the simple energy solver have to be tested. For the test atmosphere, the atmosphere structure and abundances of the W7 deflagration model (Nomoto 1984) are used. The atmosphere structure is expanded to a point in time of 10 days after the explosion. The densities and radii are determined by free homologous expansion and can be computed easily. To perform the test calculations, we obtained an initial temperature structure with the PHOENIX temperature correction procedure (Hauschildt et al. 2003). This temperature structure is the result of a simple approach that does not represent the temperature structure of an SN Ia precisely. However, for the test calculations for our energy solver, this simple temperature structure is sufficient. With this initial atmosphere structure, the energy solver is applied for different test cases. All contributions to the energy change are tested separately.
3.1. Energy transport
In this section, the energy transport through the atmosphere is tested. The energy solver considers only the energy change caused by emission and absorption of radiation, where the result of the radiative transfer equation is needed. All other influences are neglected. As a first test, we check how the initial temperature structure changes if the energy solver is changing the SN Ia envelope. As the initial atmosphere structure is already in radiative equilibrium, the energy solver should not change the temperature structure significantly, because it also pushes the atmosphere towards a radiative equilibrium state.
 |
Fig. 1 Temperature structures of a test atmosphere obtained with the energy solver and the PHOENIX temperature correction procedure. |
In Fig. 1, a comparison of the temperature structure of the energy solver to the result of the temperature correction procedure is shown. The differences in the temperature structure for most layers are less than 1%. But the temperature differences of the inner layers are clearly higher. These differences arise in the PHOENIX temperature correction result which produces a spike in the temperature structure. This is likely due to the boundary condition in the temperature correction. Hence, the resulting temperature structure obtained with the energy solver is more accurate. Here, the temperature structure is smooth. In order to obtain an atmosphere in radiative equilibrium, the energy transport part of the energy solver can be used instead of the temperature correction procedure. The main problem is that about a few hundred time steps are needed to obtain the resulting atmosphere structure in radiative equilibrium, while the temperature correction needs fewer iteration steps and is, therefore, significantly faster.
3.2. Expansion
In a further test calculation, the expansion part of the energy solver is checked. The only energy change considered is the adiabatic cooling due to free expansion of the SN Ia envelope. The energy deposition by γ-rays or an energy change due to energy transport is disabled. For this test case, the expectation is that the atmosphere should just cool down, so the temperature of the atmosphere and the observed luminosity should be decreasing.
 |
Fig. 2 Light curve of a test atmosphere that is just expanding and adiabatically cooling. |
 |
Fig. 3 Initial and final temperature structure of a test atmosphere which is just expanding and adiabatically cooling. |
The observed luminosity is shown in Fig. 2. The observed luminosity of the SN Ia atmosphere decreases in time. The temperature structure of the first and the last time step is plotted in Fig. 3. The adiabatic expansion has cooled the atmosphere everywhere, and the new temperature structure is now significantly lower than the initial one.
3.3. Energy deposition
To test the energy deposition by the radioactive decay of nickel and cobalt into the SN Ia atmosphere, a test case is considered, where only this γ-ray deposition is calculated with the energy solver. The energy change due to free expansion and energy transport are neglected to see the direct effect of the additional energy put into the test SN Ia atmosphere.
 |
Fig. 4 Light curve of a test atmosphere with energy deposition. Because of the additional energy, the luminosity increases with time. |
The results of the energy deposition by γ-rays calculation with the energy solver is shown in Fig. 4, where the light curve is plotted. Due to the energy added to the atmosphere, the luminosity seen by an observer increases with time.
3.4. Realistic test scenario
After all single effects have been tested, we now calculate a test case where all effects are considered for the solution of the energy solver. Again, the same initial temperature structure is used and we start our calculation at day 10 after the explosion. Free expansion as well as energy deposition and energy transport are active for this computation.
 |
Fig. 5 Model light curve of a realistic test scenario. |
 |
Fig. 6 The initial temperature structure for the static solution of the equation of radiative equilibrium and the relaxed temperature structure obtained 1 min later by advancing the energy solver in the test scenario. All influences on the SN Ia atmosphere are considered. |
The observed light curve is shown in Fig. 5. The luminosity increases because of the energy input from deposition of energy from the γ-rays produced by decay of nickel and cobalt. It takes a certain time, until the whole atmosphere has relaxed to this new condition. The atmosphere is then in radiative equilibrium state, and the luminosity stays constant. The initial and final temperature structure are plotted in Fig. 6. The energy input caused by radioactive decay has increased the temperature of the whole atmosphere. The atmosphere is heated by γ-ray deposition in the inner part of the atmosphere. Due to this additional energy, the luminosity of these layers increases and the heat is radiated away and absorbed by the surrounding layers. This energy transport takes care that the deposited energy is moving through the whole atmosphere so that the temperature increases everywhere and the additional energy from the radioactive decay is radiated away towards the observer. The atmosphere is then in radiative equilibrium.
4. SN Ia model light curves
We now present our first theoretical SN Ia light curves obtained with our extensions to the general purpose model atmosphere code PHOENIX and compare them to observed SN Ia light curves. The online supernova spectrum archive (SUSPECT) (Richardson et al. 2001, 2002)1 provides numerous of observations of different types of supernovae. For this work, the observed light curves of SN 2002bo and SN 1999ee are used to compare them to our results of model light curves. Photometric light curve observations of SN 2002bo in different photometric bands (Benetti et al. 2004) have been obtained. SN 1999ee also has observed spectra (Hamuy et al. 2002) and photometry (Stritzinger et al. 2002).
4.1. Method
The energy solver is now applied to calculate synthetic light curves of SNe Ia. The SN Ia light curve evolution is calculated during the free expansion phase. For the initial model atmosphere structure, the results of the explosion calculation of other groups are used as the input structure. Each layer has a certain expansion velocity, which does not change during the evolution, because homologous expansion is assumed. We start the model light curve calculation a few days after explosion. In the first few days the SN Ia envelope is optically thick and compact. Another point is, in the first few days the SNe Ia light curves are quite faint, and there are almost no observations of this early time phase that have been obtained. Thus, for the model light curve calculation, it is adequate to start the light curve calculation a few days after the explosion. The initial structure is given by the result of the explosion model simulation. The results of the explosion model give the expansion velocities, density structure and the non-homogeneous abundances of all chemical elements present in the SN Ia envelope. The envelope expands for the first few days by assuming homologous expansion. The radii are determined by the expansion velocities and time after explosion. For the first temperature structure guess, the PHOENIX temperature correction procedure is used to obtain an initial temperature structure, which is in radiative equilibrium. Alternatively we could calculate RE models starting at day one.
For the computation of an SN Ia model light curve, we let the energy solver change the obtained initial model atmosphere structure. The atmosphere structure adapts to the new conditions caused by γ-ray deposition and other energy effects. After a certain time, the atmosphere eventually reaches the radiative equilibrium state. A typical time step of an energy change in the model atmosphere is about 0.1 s. It takes about 500 time steps to reach radiative equilibrium depending on in which evolution phase the SN Ia is. For the later phase after the maximum of the SN Ia light curve, fewer time steps are needed. We use this first radiative equilibrium atmosphere structure to calculate a more detailed spectrum, where more wavelength points are used. This model spectrum is then used to obtain the first point of the model light curve for each band by using the filter functions described below. It certainly would require too much computation time to calculate a whole light curve evolution by using the typical time steps of about 0.1 s. Therefore, to obtain the next point of the light curve, big time steps are computed. For these big time steps, the atmosphere is only expanding. This means that neither energy deposition by γ-rays or energy transport through the atmosphere is considered for the solution of the energy solver. After half a day computed with big time steps, the whole energy solver changes the atmosphere structure again and the next point in the light curve is obtained after the atmosphere structure moves back to radiative equilibrium. Even with the use of these big time steps, the radiative transfer for a light curve of 50 days has to be solved about 10 000 times. For normal model atmosphere calculation in PHOENIX with the temperature correction procedure, the radiative transfer equation has to be solved about 100 times, at most. Therefore, the computation of a whole SN Ia model light curve is very computationally expensive, because the solution of the radiative transfer equation has to be obtained too many times. It takes a huge amount of computation time to calculate even simple SN Ia model light curves, even when using only a few wavelength points. Basically, the SN Ia model light curve is a curve consisting of half day points, where the atmosphere is in radiative equilibrium. During the later phase after maximum light, the big time steps have been performed for one or even two days, as the energy changes is the SN Ia atmosphere become smaller.
 |
Fig. 7 A typical model spectrum of an SN Ia together with the filter functions for the U,B,V,R and I band. These are used to determine the luminosity in each band for the model light curves. |
As described above, a model spectrum is calculated with the obtained atmosphere structure, which is in radiative equilibrium at each half day point of the light curve. To obtain a model light curve for different photometric bands, filter functions were used to calculate the luminosity in different bands. In Fig. 7, an SN Ia model spectrum and the filter functions for the U,B,V,R and I bands are shown. These filter functions are described in Hamuy et al. (1992). With these filter functions, SNe Ia model light curves can now be obtained for these five different photometric bands.
4.2. Light curves of LTE models
For the first calculations of theoretical light curves, the model atmosphere of the SN Ia is considered to be in LTE. For a first approach to obtain model light curves this is adequate. Another reason for the assumption of LTE is that model light curve calculations with an atmosphere treated in NLTE use more computation time. In order to obtain an SN Ia model light curve in reasonable computation time, a model atmosphere in LTE is a necessary assumption. For the model light curve calculations presented in this section the following parameters were chosen. The model atmosphere is divided into 128 layers. The radiative transfer is solved including atomic lines of the Kurucz atomic data line list. The number of wavelength points used for the solution of the radiative transfer is about 2400. For the inner boundary condition of the radiation, we use the nebular boundary condition, which means that the radiation is just passing through the inner empty region, therefore all the radiation is produced by the ejecta itself, there is no inner lightbulb. The outer boundary condition is zero.
For the first LTE light curve calculation, the W7 deflagration explosion model is used to obtain model light curves of SNe Ia in different photometric bands. The first point of the light curve was calculated at three days after the explosion. The method to obtain the theoretical light curves is described in Sect. 4.1.
 |
Fig. 8 The energy change due to the expansion for several days. |
Before we present our resulting model light curves, we present plots of various terms that change the energy density for several moments in time. In Fig. 8, the energy change due to the expansion is shown for several moments in time. The energy change is decreasing for later days in the light evolution. The additional energy input due to the radioactive decay is shown in Fig. 9. With increasing time, the amount of energy input into the atmosphere decreases. It also shows, that the additional energy is located in the inner part of the envelope, where the 56Ni has been produced. Figure 10 shows the energy loss due to the emission of radiation. The temperature structures of the atmosphere for several moments in time are shown in Fig. 11.
 |
Fig. 9 The energy change due to the additional energy input for several days. |
 |
Fig. 10 The energy change due to the radiation for several days. |
 |
Fig. 11 Temperature profiles as a function of time. |
 |
Fig. 12 LTE model light curve of the W7 explosion model in the V band compared to two observed SN Ia light curves of SN 1999ee and SN 2002bo. |
 |
Fig. 13 U band light curve of the LTE model light curve compared to SN 1999ee. |
Figure 12 shows the LTE SN Ia model light curve of the W7-based explosion model in the optical V band. The theoretical light curve accurately reproduces the observed light curves of two SNe Ia. The steep rise of the model light curve beginning at three days after explosion is in agreement with the observed light curves. The maximum of the W7-based model light curve seems to be later than that of the observed light curves. At 20 days after the explosion, the model light curve has its maximum, while the maximum of the observed light curves is around 17 days after the explosion. After maximum, the decline of the light curve of the W7-based model well reproduces the observed light curve. Even up to the later phase at 50 days after the explosion, where the atmosphere becomes significantly thinner, the fit to the observed light curves is quite accurate.
The theoretical light curve in the ultraviolet U band is shown in Fig. 13. Only an observed light curve of SN 1999ee is available. The observational data are scattered. The rise in the beginning as well as the maximum phase is well represented by the model light curve. However, the decline of the theoretical light curve seems to be too steep. This same effect is present in the model light curve of the B band, which is shown in Fig. 14. The first days of the model light curve are too bright compared to both observed SN Ia light curves. The maximum phase of the model light curve is in good agreement with the observed ones. At day 50, the model light curve becomes brighter than the observed light curves.
 |
Fig. 14 LTE light curves of the W7 explosion model. The B band model light curve is too bright during the first few days. |
 |
Fig. 15 The theoretical light curve in the R band seems to rise after a first decline after the maximum phase. |
 |
Fig. 16 LTE light curves of the W7 explosion model. For the I band the model light curve has no distinctive maximum. At 30 days after the explosion the model light curve is way too bright in comparison to the observed ones. |
In Fig. 15, a plot of the model light curve of the R band is shown. The steep rise in the beginning and the maximum phase of the observed SN Ia light curves is well represented by the computed model light curve. However, the theoretical light curve fit becomes worse for later phases. The luminosity of the model light curve seems to rise again at around day 25 after the explosion. Up to day 45, the model light curve has a second bump, which is not observed in the light curves of SN 1999ee and SN 2002bo. In the infrared I band, the decline after the maximum phase is missing, as shown in Fig. 16. As in the R band, the rise in the beginning and maximum are well represented in the model light curve. However, at maximum, the luminosity of the SN Ia model light curve rises further, which is not seen in the observed light curves of SN 2002bo and 1999ee. Around day 30, the difference between model and observed light curve in the I band are about 1 mag. Up to day 50, the model light curve declines, while the observed light curves show their second maximum around 40 days after explosion.
 |
Fig. 17 Comparison of U − B for the theoretical and observed light curves. |
 |
Fig. 18 Comparison of B − V for the theoretical and observed light curves. |
In Fig. 17, we compared the relation U − B of the theoretical and observed light curves. The same comparision for the B − V relation is shown in Fig. 18.
4.3. Dynamical models
We have three different results of explosion calculations of SN Ia events. The structure of these models are results from hydrodynamical explosion calculations. One is the W7 deflagration model of Nomoto et al. (1984). The W7 dynamical model assumes that the ongoing explosion is a deflagration. The flame propagates with a velocity lower than the speed of sound outwards. Another possible explosion model is the delayed detonation model. The explosion starts with a deflagration which eventually proceeds to a detonation. We used two different dynamical models named as DD25 and DD16. For more detailed information about the used delayed detonation models see Höflich et al. (2002).
 |
Fig. 19 V band light curves for three different dynamical models W7, DD16 and DD25. The DD25 dynamical model is fainter because less nickel was produced during the explosion. The W7 and DD15 dynamical model light curves are quite similar. |
The resulting optical model light curves of the V band are plotted in Fig. 19. The light curve of the DD16 is fainter than the other ones. This is due to the fact that in this explosion model less 56Ni is produced. The W7 and DD25 model are quite similar. DD25 is slightly brighter than W7. The shape of the light curves are in good agreement with the observed ones. The maximum of the DD16 is later than the one of the W7 and DD25.
 |
Fig. 20 I band light curves for the dynamical models W7, DD16 and DD25 are compared to the two observed SN Ia light curves. |
In Fig. 20 the light curves in the I band of the three dynamical models are shown. The infrared light curves deviate strongly from the observations. As in the optical light curve, the DD16 light curve is fainter than W7 and DD25. DD16 also has only one maximum and a decline. However, this maximum is later than the observed ones. The DD25 and W7 light curves are still rising after the observed light curves have reached their maximum and are declining. The theoretical light curves in the infrared must be improved for all explosion models.
5. Light curves of NLTE models
The LTE model light curves in the V Band and most other bands are in quite good agreement with observed SN Ia light curves. However, in the near-infrared of the I band, the model light curves need improvements especially for the later phase to fit the observational light curves more accurately. So far, the SN Ia model atmosphere is considered to be in LTE during the whole evolution time. In this section, we calculate the model light curves with the assumption of an atmosphere which is not in LTE. The computation of model light curves with SN Ia model atmospheres in NLTE requires a huge amount of computation time. At first, we model light curves with atmospheres in NLTE that are computed with LTE temperature structures. More realistic NLTE model light curves with a temperature structure that adapts to NLTE conditions are computed to investigate the NLTE effects on the model light curves.
The first approach to compute NLTE model light curves is to consider the atmosphere to be in NLTE, but use a fixed LTE temperature structure. For this computation of NLTE model light curves, we used the calculated radiative equilibrium LTE temperature structure of the W7 deflagration model. We keep this temperature structure constant and perform 20 iterations to let the NLTE converge, which is mainly the occupation numbers of the species that are considered for the NLTE calculation. We considered the following species for the calculations in NLTE: H I, He I, He II, C I-III, O I-III, Ne I, Na I, Mg I-III, Si I-III, S I-III, Ca II, Ti II, Fe I-III and Co II. These are the species that are most abundant in SN Ia atmospheres and mainly contribute to the spectrum. There is only little H and He in SN Ia, and in W7, there is none. However, considering H I, He I and He II in NLTE does not cost much computation time. The advantage of this approach to an NLTE model light curve is that no temperature iterations have to be performed. This reduces the computation time significantly, although about 200 000 wavelength points are calculated instead of 2400 in case of LTE.
 |
Fig. 21 Model light curves of the W7 explosion model in the V band. The NLTE model atmosphere has an LTE temperature structure. |
In Fig. 21, the SN Ia model light curve in the V band of an NLTE calculation with an LTE temperature structure is shown. The NLTE light curve is fainter than the LTE light curve. During the maximum phase there is about 0.4 mag difference between both light curves. We have to point out that for our NLTE models, the energy is not conserved because the radiation does not thermalize within the envelope. After maximum the NLTE model light curve approaches the LTE light curve and agrees with the observed light curves as well as the LTE light curve. However, the NLTE model light curve in the V band does not agree with the observed light curves very accurately. With the assumption of an atmosphere in LTE, a better fit is obtained, although NLTE is more accurate.
 |
Fig. 22 Model light curves of the W7 model in the U band. The NLTE model atmosphere has an LTE temperature structure. |
 |
Fig. 23 Model light curves of the W7 model in the B band. The NLTE model atmosphere has an LTE temperature structure. |
The NLTE model light curve of the U band is shown in Fig. 22. The NLTE light curve shows almost no deviations from the LTE light curve. During the later phase the steep decline is also present in the NLTE model light curves. In Fig. 23, the NLTE model light curve in the B band is presented. The NLTE model light curve is slightly fainter than the LTE light curve. The shape of the NLTE light curve seems to be the same as for the LTE light curve. The NLTE model light curve is also an accurate fit to the observed light curves.
 |
Fig. 24 NLTE and LTE model light curves in the R band of the W7 model. The NLTE model atmosphere has an LTE temperature structure. |
 |
Fig. 25 NLTE and LTE model light curves of the W7 model. The NLTE model atmosphere has an LTE temperature structure. In the I band the NLTE light curve is somewhat of an improvement. |
In Fig. 24, the NLTE model light curve of the R band is shown. The luminosity of the NLTE light curve is fainter than the LTE light curve. It has almost the same shape. But for the phase after 25 days after the explosion, the NLTE model light curve rises again. The assumption of NLTE does not improve the fit to the observed light curves of SN 1999ee and SN 2002bo. The infrared NLTE light curve for the I band is shown in Fig. 25. During the maximum phase, the NLTE light curve is fainter than the LTE light curve. A distinctive maximum is missing in the NLTE model light curve. For the phase between day 15 and day 25, the NLTE model light curve fits the observed SN Ia light curves very accurately. Here, there is a significant improvement compared to the light curve of the LTE model atmosphere. But, after day 25 the NLTE model light curve starts to rise and becomes too bright. This is the same problem that already emerged in the LTE light curve.
5.1. NLTE atmosphere structures
We perform a more realistic NLTE calculation of the SN Ia model atmosphere evolution. The temperature structure is now changing and adapting to the new conditions of NLTE. The calculation of an NLTE model light curve takes a huge amount of computation time. Considerably more wavelength points are needed for the calculation of the solution of the radiative transfer. For all the species considered in NLTE, the rate equations have to be solved. Note that a time step in the NLTE calculation is not a real time step. The rate equation changes the energy of the atmosphere, but this is not included in the energy solver. However, it is adequate as the goal is to obtain a temperature structure, where the atmosphere is in radiative equilibrium.
In a first try to calculate a more realistic NLTE light curve, numerous species up to calcium are considered to be in NLTE. These are the species H I, He I, He II, C I-III, O I-III, Ne I, Na I, Mg I-III, Si I-III, S I-III and Ca II. Higher species are neglected because they have more levels, which would increase the computation time significantly. Nevertheless, the computation of an NLTE light curve needs significantly more time than LTE. For this computation of NLTE model light curves, about 200 000 wavelength points need to be calculated, compared to about 2400 wavelength points for a pure LTE light curve calculation. To obtain an NLTE model light curve in a reasonable time, we started the calculation at day 10 after the explosion and used the LTE temperature structure as the initial atmosphere structure. The main focus is to check if the infrared light curves during the later phase can be further improved.
 |
Fig. 26 NLTE and LTE model light curves of the W7 explosion model in the V band. |
 |
Fig. 27 NLTE and LTE model light curves of the W7 explosion model in the I band. |
In Fig. 26, the NLTE and LTE light curves of the W7 deflagration model in the V band are shown. The maximum phase is not well fitted by the NLTE model light curve. The LTE light curve fits the observed light curves better. At day 20 the NLTE and LTE light curves are almost the same. Compared to the NLTE light curve obtained with the LTE temperature structure, there are only small differences to the NLTE calculation where the temperature structure adapts to the NLTE conditions.
In Fig. 27, the I band model light curves of NLTE and LTE are shown. During the maximum phase, the NLTE light curve is fainter than the LTE light curve. Between day 15 and day 25 the NLTE model light curve fits the observed light curves quite accurately. Here, the use of NLTE improves the fit to the observed light curves. However, we obtained this improvement also with the NLTE model light curve calculated with the LTE temperature structure. At day 25 the NLTE model light curve starts to rise again. Although the consideration of NLTE improves the model light curve in the I band, the problem with a rise in brightness after the maximum remains.
 |
Fig. 28 Light curves in the I band. The light curve with variable scattering is fainter than the LTE light curve. |
5.2. Line scattering
The fits to the infrared light curves need to be improved, as they are too bright during the phase of 20 to 50 days after the explosion in all models. We found that a change in the ratio of line scattering to absorption in the LTE case improves the fits to the I band light curve. The resulting light curve is shown in Fig. 28. The line scattering is here roughly inversely proportional to the density and was for the figure “hand tuned” to produce a good match. As the density becomes lower due to the ongoing expansion, the scattering becomes more important, as expected. A more detailed investigation of the IR line scattering and its effects on SN Ia light curve modeling will be a topic of future work. To treat this effect more accurately, very detailed NLTE model atoms are required that include the important infrared lines. In the atomic data we have presently available, these lines are mostly “predicted” lines and were not included in the our current NLTE model atoms. This result indicates that an accurate treatment of line scattering and NLTE effects in the IR lines is very important to model and interpret the IR light curves of SNe.
6. Conclusion
We have presented a new approach for an energy solver which can be applied to expanding SN Ia envelopes to compute SN Ia model light curves. Test calculations confirm that the implemented code works properly. We applied the energy solver to calculate SN Ia model light curves during the free expansion phase.
We present the first PHOENIX light curves of type Ia supernovae in different photometric bands. At first, we solved the radiative transfer equation with the assumption of the atmosphere being in LTE. The model light curves were in decent agreement with the observed ones at early times. However, in the infrared I band, the theoretical light curves do not fit the observed light curves. Blinnikov et al. (2006) had the same deviations in their model light curves compared to observations. Their light curve in the I band is also too bright and further rising, even after the maximum in observed light curves. Kasen (2006) presented a detailed study of SN Ia light curves in the near IR. His I band light curve fits the observations better. He also showed how variable and dependent on different parameters the light curves in the near infrared can be.
Three different dynamical models were compared to observed SN Ia light curves. The delayed detonation model DD 16 is unlikely to be the best explosion model because the model light curves are too faint to fit the observed light curves due to the low 56Ni mass. The results of the W7 model are the best fit to the observed light curves.
For the later phase of the light curves, especially in the infrared, we need the atmosphere to be considered in NLTE. We showed that NLTE model light curves computed with an LTE temperature structure leads to improvements in the model light curves. For future work more investigation of the infrared model light curves and the NLTE needs to be performed. The focus has to lie on the influence of line scattering on the shape of the light curves. It would also be interesting to look in detail on the spectral evolution during the free expansion phase. Further improvements may be achieved with a full 3D radiative transfer and energy solver.
Acknowledgments
This work was supported in part by the Deutsche Forschungsgemeinschaft (DFG) via the SFB 676, NSF grant AST-0707704, and US DOE Grant DE-FG02-07ER41517. This research used resources of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231, and the Höchstleistungs Rechenzentrum Nord (HLRN). We thank all these institutions for generous allocations of computation time.
References
- Benetti, S., Meikle, P., Stehle, M., et al. 2004, MNRAS, 348, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., Roepke, F. K., Sorokina, E. I., et al. 2006, A&A, 453, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bongard, S., Baron, E., Smadja, G., Branch, D., & Hauschildt, P. 2006, ApJ, 647, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Bronder, T. J., Hook, I. M., Astier, P., et al. 2008, A&A, 477, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chotard, N., et al. 2011, A&A, submitted [Google Scholar]
- Foley, R. J., Filippenko, A. V., & Jha, S. W. 2008, ApJ, 686, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Goldhaber, G., Groom, D. E., Kim, A., et al. 2001, ApJ, 558, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hachinger, S., Mazzali, P. A., & Benetti, S. 2006, MNRAS, 370, 299 [NASA ADS] [Google Scholar]
- Hamuy, M., Walker, A. R., Suntzeff, N. B., et al. 1992, PASP, 104, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Maza, J., Pinto, P. A., et al. 2002, AJ, 124, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Barman, T. S., Baron, E., & Allard, F. 2003, in Stellar Atmospheric Modeling, ed. I. Hubeny, D. Mihalas, & K. Werner (San Francisco: ASP), 227 [Google Scholar]
- Höflich, P., Gerardy, C., Fesen, R., & Sakai, S. 2002, ApJ, 568, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Jack, D., Hauschildt, P. H., & Baron, E. 2009, A&A, 502, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffery, D. J. 1998 [arXiv:astro-ph/9811356] [Google Scholar]
- Kasen, D. 2006, ApJ, 649, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of Radiation Hydrodynamics (Oxford: Oxford University) [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Nugent, P., Phillips, M., Baron, E., Branch, D., & Hauschildt, P. 1995, ApJ, 455, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Pskovskii, I. P. 1977, SvA, 21, 675 [Google Scholar]
- Richardson, D., Thomas, R. C., Casebeer, D., et al. 2001, BAAS, 33, 1428 [NASA ADS] [Google Scholar]
- Richardson, D., Thomas, R., Casebeer, D., Branch, D., & Baron, E. 2002, BAAS, 34, 1205 [NASA ADS] [Google Scholar]
- Riess, A. G., Press, W. H., & Kirshner, R. P. 1996, ApJ, 473, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Hamuy, M., Suntzeff, N. B., et al. 2002, AJ, 124, 2100 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Temperature structures of a test atmosphere obtained with the energy solver and the PHOENIX temperature correction procedure. |
| In the text | |
 |
Fig. 2 Light curve of a test atmosphere that is just expanding and adiabatically cooling. |
| In the text | |
 |
Fig. 3 Initial and final temperature structure of a test atmosphere which is just expanding and adiabatically cooling. |
| In the text | |
 |
Fig. 4 Light curve of a test atmosphere with energy deposition. Because of the additional energy, the luminosity increases with time. |
| In the text | |
 |
Fig. 5 Model light curve of a realistic test scenario. |
| In the text | |
 |
Fig. 6 The initial temperature structure for the static solution of the equation of radiative equilibrium and the relaxed temperature structure obtained 1 min later by advancing the energy solver in the test scenario. All influences on the SN Ia atmosphere are considered. |
| In the text | |
 |
Fig. 7 A typical model spectrum of an SN Ia together with the filter functions for the U,B,V,R and I band. These are used to determine the luminosity in each band for the model light curves. |
| In the text | |
 |
Fig. 8 The energy change due to the expansion for several days. |
| In the text | |
 |
Fig. 9 The energy change due to the additional energy input for several days. |
| In the text | |
 |
Fig. 10 The energy change due to the radiation for several days. |
| In the text | |
 |
Fig. 11 Temperature profiles as a function of time. |
| In the text | |
 |
Fig. 12 LTE model light curve of the W7 explosion model in the V band compared to two observed SN Ia light curves of SN 1999ee and SN 2002bo. |
| In the text | |
 |
Fig. 13 U band light curve of the LTE model light curve compared to SN 1999ee. |
| In the text | |
 |
Fig. 14 LTE light curves of the W7 explosion model. The B band model light curve is too bright during the first few days. |
| In the text | |
 |
Fig. 15 The theoretical light curve in the R band seems to rise after a first decline after the maximum phase. |
| In the text | |
 |
Fig. 16 LTE light curves of the W7 explosion model. For the I band the model light curve has no distinctive maximum. At 30 days after the explosion the model light curve is way too bright in comparison to the observed ones. |
| In the text | |
 |
Fig. 17 Comparison of U − B for the theoretical and observed light curves. |
| In the text | |
 |
Fig. 18 Comparison of B − V for the theoretical and observed light curves. |
| In the text | |
 |
Fig. 19 V band light curves for three different dynamical models W7, DD16 and DD25. The DD25 dynamical model is fainter because less nickel was produced during the explosion. The W7 and DD15 dynamical model light curves are quite similar. |
| In the text | |
 |
Fig. 20 I band light curves for the dynamical models W7, DD16 and DD25 are compared to the two observed SN Ia light curves. |
| In the text | |
 |
Fig. 21 Model light curves of the W7 explosion model in the V band. The NLTE model atmosphere has an LTE temperature structure. |
| In the text | |
 |
Fig. 22 Model light curves of the W7 model in the U band. The NLTE model atmosphere has an LTE temperature structure. |
| In the text | |
 |
Fig. 23 Model light curves of the W7 model in the B band. The NLTE model atmosphere has an LTE temperature structure. |
| In the text | |
 |
Fig. 24 NLTE and LTE model light curves in the R band of the W7 model. The NLTE model atmosphere has an LTE temperature structure. |
| In the text | |
 |
Fig. 25 NLTE and LTE model light curves of the W7 model. The NLTE model atmosphere has an LTE temperature structure. In the I band the NLTE light curve is somewhat of an improvement. |
| In the text | |
 |
Fig. 26 NLTE and LTE model light curves of the W7 explosion model in the V band. |
| In the text | |
 |
Fig. 27 NLTE and LTE model light curves of the W7 explosion model in the I band. |
| In the text | |
 |
Fig. 28 Light curves in the I band. The light curve with variable scattering is fainter than the LTE light curve. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


