| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 19 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201015482 | |
| Published online | 28 January 2011 | |
Star formation in the outer Galaxy: membership and fundamental parameters of the young open cluster NGC 1893⋆
1
INAF - Osservatorio Astronomico di Palermo, Piazza del Parlamento
1,
90134
Palermo,
Italy
e-mail: loredana@astropa.unipa.it
2
Centro de Astrobiología / CSIC-INTA, LAEFF Campus, PO Box 78,
28691 Villanueva de la Cañada, Madrid, Spain
3
ESO, Karl-Scharzschild-Strasse 2, 85748
Garching-bei-Mnchen,
Germany
Received:
27
July
2010
Accepted:
3
September
2010
Context. Different environmental conditions can play a crucial role in determining final products of the star formation process, and in this context, less favorable activities of star formation are expected in the external regions of our Galaxy.
Aims. We studied the properties of the young open cluster NGC 1893 located about 12 Kpc from the galactic center, to investigate how different physical conditions can affect the process of star formation.
Methods. By adopting a multiwavelength approach, we compiled a catalog extending from X-rays to NIR data to derive the cluster membership. In addition, optical and NIR photometric properties are used to evaluate the cluster parameters.
Results. We find 415 diskless candidate members and 1061 young stellar objects with a circumstellar disk or class II candidate members, 125 of which are also Hα emitters. Considering the diskless candidate members, we find that the cluster distance is 3.6 ± 0.2 kpc and the mean interstellar reddening is E(B − V) = 0.6 ± 0.1 with evidence of differential reddening in the whole surveyed region.
Conclusions. NGC 1893 contains a conspicuous population of pre-main sequence stars, together with the well-studied main sequence cluster population. We found a disk fraction of about 70% similar to the one found in clusters of similar age in the solar neighbor and then, despite expected unfavorable conditions for star formation, we conclude that very rich young clusters can also form in the outer regions of our Galaxy.
Key words: open clusters and associations: individual: NGC 1893 / stars: pre-main sequence / stars: formation / Hertzsprung-Russell and C-M diagrams / infrared: stars
Full Tables 5–8 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/527/A77
© ESO, 2011
1. Introduction
The sequence of events that characterize the star formation (SF) process starts from the compression of gas in a giant molecular cloud that produces molecular cores. These collapse into protostars evolving in pre-main sequence (PMS) objects through accretion of material and circumstellar disk formation (Zinnecker & Yorke 2007). Within this standard picture, however, different environmental properties may play a key role by changing the physical conditions during the SF process and possibly the final products, for example the initial mass function (IMF).
Optical observations of the cluster NGC 1893.
The SF regions with peculiar properties are therefore crucial to a complete understanding of the SF process since they are the natural places where different initial conditions can lead to the formation of clusters with nonstandard IMF, dynamical evolution, and/or disk fraction and evolution. In this context, clusters in the outer Galaxy are very interesting since they are located in regions where surface and volume densities of atomic and molecular hydrogen are much lower than in the inner Galaxy (Wouterloot et al. 1990), while metal content is, on average, smaller (Wilson & Matteucci 1992) so that higher temperatures of the cloud are expected due to lower radiative losses. In addition, the lack of prominent spiral arms and the presence of few supernovae as external triggers for SF are further indications of less likely SF conditions.
We have identified NGC 1893 as a very promising cluster for this kind of investigations since it is very young (~1–2 Myr), about 12 Kpc distant from the Galactic center, with known massive members and indication of a large PMS population (Vallenari et al. 1999; Sharma et al. 2007). This SF region, located at the center of the Aur OB2 associations, is associated with the HII region IC 410 and the two pennant nebulae, Sim 19 and Sim 130 (Gaze & Shajn 1952). It is obscured by several dust clouds and contains at least five O-type stars (Hiltner 1966). The presence of several O-type stars and emission line B-type stars (Marco & Negueruela 2002), likely in the PMS phase, is a strong indication that very recent SF events have occurred in this cluster.
Several photometric and low-resolution spectroscopic works have been devoted to this cluster since the first study by Hoag et al. (1961). Many of them are, however, aimed at studying the NGC 1893 massive stars, which are in the MS phase (Becker & Fenkart 1971; Moffat 1972; Cuffey 1973; Humphreys 1978; Tapia et al. 1991; Fitzsimmons 1993; Massey et al. 1995; Marco et al. 2001; Marco & Negueruela 2002). Evidence of a large population of PMS stars in this cluster has been found by Vallenari et al. (1999) by using near-infrared photometry, even if their data did not allow them to distinguish the young population from the contaminating field stars. Only recently, Sharma et al. (2007) presented a study about the low-mass population in NGC 1893 based on deep optical photometry down to V ~ 22 and NIR 2MASS (Cutri et al. 2003) catalog. Several conclusions have been drawn in this work about the IMF, the dynamical evolution and the effects of massive cluster stars on the low-mass population. However, their results are based on a statistical subtraction of the field star population falling in the same region and suffer from the large statistical uncertainties related to the membership. In fact, the main challenge of the analysis of the low-mass population in very young clusters is the membership derivation since PMS stars usually lie in the same region as occupied by contaminating field stars, and it is therefore crucial an accurate analysis to identify cluster members.
We have started a project aimed at the detailed study of the star formation process in NGC 1893 and in particular the unknown low-mass population: the first results, based on the joint Chandra-Spitzer large program The Initial Mass Function in the Outer Galaxy: the star forming region NGC1893 (P.I. G. Micela), have been published in Caramazza et al. (2008,hereafter Paper I). In this paper, a conspicuous sample of low-mass cluster members with circumstellar disk and of more evolved diskless candidate members belonging to this region has been identified by using Spitzer-IRAC and Chandra X-ray data.
We present here the results for the membership and cluster parameters based on a multiwavelength approach including new deep optical and JHK photometry that allow us to derive a more complete census of the low-mass population in this cluster. Knowledge of individual members is used to derive cluster parameters (reddening and distance) in a more accurate way than previously reported in the literature. Detailed studies on the X-ray coronal properties, disk fraction and evolution, and IMF will be presented in forthcoming papers.
The present paper is organized as follow. In Sect. 2 we present the observations, the data reduction method, and a description of the procedure used to derive the photometry and the astrometry. The whole catalog is presented in Sect. 3, while Sect. 4 includes the comparison with previous works; Sect. 5 describes how we identify cluster candidate members by using VRIJHK, Hα and X-rays data, while in Sect. 6 the cluster parameters are derived and a comparison with literature results is presented in Sect. 7. In Sect. 8 individual masses and ages are derived, while in Sect. 9 we present our summary and conclusions.
2. Observations, data reduction and photometry
We present here new optical and near infrared (NIR) data for the cluster, collected from the Telescopio Nazionale Galileo (TNG) at the Roque de los Muchachos Observatory (ORM, Canary Islands, Spain), and from the 2.2 m telescope at the Calar Alto Observatory (Spain).
2.1. Optical data
Optical observations were acquired in service mode using two different telescopes, with the standard VRI and Hα photometric filters. The Device Optimized for the LOw RESolution (DOLORES) mounted on the TNG was used in service mode during three nights in 2007, and the Calar Alto Faint Object Spectrograph (CAFOS), mounted on the 2.2 m telescope in Calar Alto German-Spanish Observatory (Spain), observed for three nights in 2007 and 2008, as detailed in Table 1. Standard fields were taken with both instruments to perform the required photometric calibration.
DOLORES is a focal reducer instrument equipped with a 2048 × 2048 square pixel CCD, with
a scale of 0.252 /px and a field of
view (FoV) of 8.6′ × 8.6′. A mosaic of four fields was made, covering an approximate
area of 22.2′ × 18.0′. The standard VRI filters were used in the four
fields, as well as the Hα narrow band filter centered on 6658 Å, with a
full width half maximum (FWHM) of 57 Å. We also observed the standard
field SA 98 (Landolt 1992,
α = 6h:52m:04.1s,
δ = −00d:19m:37.9s).
/px and a field of
view (FoV) of 8.6′ × 8.6′. A mosaic of four fields was made, covering an approximate
area of 22.2′ × 18.0′. The standard VRI filters were used in the four
fields, as well as the Hα narrow band filter centered on 6658 Å, with a
full width half maximum (FWHM) of 57 Å. We also observed the standard
field SA 98 (Landolt 1992,
α = 6h:52m:04.1s,
δ = −00d:19m:37.9s).
CAFOS is a focal reducer instrument that works with a CCD of 2048 × 2048 square pixels,
and has a scale of 0.53 /px, covering a
circular FoV of 16′ diameter. With this FoV we covered the central areas of the cluster
not observed by the four DOLORES fields. Standard VRI filters were used,
together with an Hα filter centered at 6577 Å with FWHM
of 98 Å. The fields used as standards for the photometric calibration were RU 149
(α = 07h:24m:40.8s,
δ = −00d:34m:10.0s), PG 2331
(α = 23h:34m:14.1s,
δ = + 05d:46m:25.9s), and SA 95
(α = 03h:53m:32.9s,
δ = + 00d:00m:48.3s). In this case,
we noticed some variability in the photometric conditions of the last two nights in Calar
Alto. To improve the quality of the photometric calibration, we also used a set of local
standards of the cluster, selected during the TNG data calibration, as explained below. A
combined image of the four TNG fields in the I band, with the shape of
the CAFOS FoV overplotted, is shown in Fig. 1.
/px, covering a
circular FoV of 16′ diameter. With this FoV we covered the central areas of the cluster
not observed by the four DOLORES fields. Standard VRI filters were used,
together with an Hα filter centered at 6577 Å with FWHM
of 98 Å. The fields used as standards for the photometric calibration were RU 149
(α = 07h:24m:40.8s,
δ = −00d:34m:10.0s), PG 2331
(α = 23h:34m:14.1s,
δ = + 05d:46m:25.9s), and SA 95
(α = 03h:53m:32.9s,
δ = + 00d:00m:48.3s). In this case,
we noticed some variability in the photometric conditions of the last two nights in Calar
Alto. To improve the quality of the photometric calibration, we also used a set of local
standards of the cluster, selected during the TNG data calibration, as explained below. A
combined image of the four TNG fields in the I band, with the shape of
the CAFOS FoV overplotted, is shown in Fig. 1.
Optical data were reduced using the standard Image Reduction and Analysis Facility (IRAF) routines, including the bias and flatfield subtraction. Bias correction was applied by using zero images and the local overscan strip in each image. Some nonstandard steps were taken due to various problems that arose during the reduction, with details described below.
For the DOLORES observations a combination of sky flat-fields was used to create a master flat field in each band, using the task flatcombine. Once the images were corrected from flat-field, a strong illumination pattern was still present in the images of the I band. An illumination function was created using the flat-field (with the task mkillumflat), and conveniently removed from images. A pattern of interference fringing was still present in the I band images, with no variations found in the different nights. We constructed a fringing image by combining 15 images in the I band of the three nights, so the stars in the different fields are canceled. The selected images were of short exposure (2–60 s) to reduce the number of stars in the fields. The resulting fringing pattern was successfully corrected using the task mkfringecor and applied to every image in the I band.
For the CAFOS data, dome flats were used to correct the images from local irregularities. The singular circular shape of the FoV required special care: the values of all the pixels outside the FoV (easy to filter because they are well below the background) were set to a very large number. In this way no unreal features are created in the target images after subsequent flat-field removal, resulting in a value well below background outside the FoV. The remaining reduction followed the standard path.
 |
Fig. 1 Upper panel: I band combined image of the four DOLORES frames of 740 s; the overplotted circle indicates the CAFOS FoV. Bottom panel: Js band combined image of the NICS frames reduced and coadded with SNAP. |
2.2. NIR data
NIR observations were acquired in service mode at the TNG, using the large field Near
Infrared Camera Spectrometer (NICS), which is a camera equipped with a 1024 × 1024 square
pixels HgCdTe HAWAII infrared array, with a scale of
0.25 /pix and a FoV of
4.2
/pix and a FoV of
4.2 × 4.2
× 4.2 (Baffa et al. 2001). Our observations were acquired with
the Js(1.25 μ), H(1.63 μ) and
K′(2.12 μ) filters during eight nights in 2007 and 2008. We observed the
whole field with a raster of 4 × 4 pointings, at each pointing we obtained a series of
NINT dithered exposures. Each exposure is a repetition of a DIT (Detector Integration
Time) times NDIT (number of DIT), to avoid saturation of the background. Details are given
in Table 2.
(Baffa et al. 2001). Our observations were acquired with
the Js(1.25 μ), H(1.63 μ) and
K′(2.12 μ) filters during eight nights in 2007 and 2008. We observed the
whole field with a raster of 4 × 4 pointings, at each pointing we obtained a series of
NINT dithered exposures. Each exposure is a repetition of a DIT (Detector Integration
Time) times NDIT (number of DIT), to avoid saturation of the background. Details are given
in Table 2.
Near infrared observations of the cluster NGC 1893 from NICS; NINTs is the number of single frames.
Raw IR images taken with NICS were reduced by using the Speedy Near-IR data Automatic reduction Pipeline (SNAP) implemented for NICS using the “full dither” options. We forced the script to use an external master flat field obtained by a median combination of single flat fields taken during the same night or the nearest night. After a bad pixel correction, the pipeline performs the source detection on the sky subtracted and flat-fielded images. A double iteration is performed to obtain a coadded image for each filter by using the offsets among the images computed by a cross-correlation algorithm after the field distortion has been corrected. A combined image in the Js band of the NICS images reduced and coadded with SNAP is shown in Fig. 1 (bottom panel).
2.3. Photometry and data selection
Sources detection and point spread function (PSF) photometry were done using the routines within the Fortran stand-alone versions of the DAOPHOT II and ALLSTAR packages (Stetson 1987a), improved with the use of ALLFRAME (Stetson 1994). Instrumental PSF photometry was corrected by using appropriate aperture corrections derived by growth curves computed with the DAOGROW code (Stetson 1990). Details on the photometric calibration are given in the appendix.
To perform an accurate analysis of the color-magnitude and color-color diagrams and to compare them with appropriate theoretical models, we selected the optical photometric catalogs obtained from the Dolores and Cafos images by considering only objects with photometric error smaller than a magnitude-dependent limit and with the DAOPHOT parameter sharp smaller than 0.5, i.e. objects with brightness distribution consistent with point-like sources. The Dolores and Cafos final catalogs include 7144 and 3222 objects, respectively.
The photometric JHK catalog obtained using NICS images was selected by
considering only objects with magnitude errors smaller than
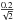 in order to have color errors smaller than 0.2. This criterion was adopted in order to
discard false detections found in the spots due to saturated objects. After this
selection, our JHK catalog contained 11181 entries including multiple
items for the objects located in the overlapping regions of the 16 fields. To filter out
the redundant detections, we first estimated an appropriate matching radius by computing
the offset cumulative distribution of the objects in adjacent fields within a relatively
large radius equal to 3
in order to have color errors smaller than 0.2. This criterion was adopted in order to
discard false detections found in the spots due to saturated objects. After this
selection, our JHK catalog contained 11181 entries including multiple
items for the objects located in the overlapping regions of the 16 fields. To filter out
the redundant detections, we first estimated an appropriate matching radius by computing
the offset cumulative distribution of the objects in adjacent fields within a relatively
large radius equal to 3 using a binsize
of 0.2
using a binsize
of 0.2 , as shown in
Fig. 2.
, as shown in
Fig. 2.
We compared this distribution with the expected cumulative distribution of spurious
identifications (dashed line in Fig. 2) computed by
using the relation ![\begin{equation} \frac{{\rm d}N}{{\rm d}r}=\sum_{i=1,j=2}^{15,16}\frac{n_i*n_j}{A_{ij}}[\pi (r+{\rm d}r)^2-\pi r^2] \label{spureq} \end{equation}](/articles/aa/full_html/2011/03/aa15482-10/aa15482-10-eq39.png) (1)where
ni and
nj are the total number of objects in the
i-th and j-th fields, respectively, falling in the
common area Aij. The difference between the
measured offset distribution and the expected spurious one is the true
distribution (Fig. 2) which tends to flatten
at separations greater than 1.1
(1)where
ni and
nj are the total number of objects in the
i-th and j-th fields, respectively, falling in the
common area Aij. The difference between the
measured offset distribution and the expected spurious one is the true
distribution (Fig. 2) which tends to flatten
at separations greater than 1.1 . Using this value
as the final matching radius, we included less than 10% of spurious matches and most of
the true identifications.
. Using this value
as the final matching radius, we included less than 10% of spurious matches and most of
the true identifications.
Therefore, we matched each star of our catalog with those of adjacent fields and
considered those falling within 1.1 as the same
object. The final catalog composed of single items includes 9 880 objects with K magnitude
down to 17.78.
as the same
object. The final catalog composed of single items includes 9 880 objects with K magnitude
down to 17.78.
2.4. Astrometry
 |
Fig. 2 Cumulative distribution of offsets between objects falling in adjacent fields (dotted line). The expected offset cumulative distribution of spurious matches (dashed line, see Eq. (1) and the true distribution (solid line, see text) are also shown. |
In order to assign celestial coordinates to the stars in the optical catalogs, we used the 2MASS catalog (Cutri et al. 2003) as reference. The transformation between the two coordinate systems was made by applying the appropriate sky projection using several tasks of the imcoords IRAF package. To determine this transformation we first identified three stars common to the 2MASS observations and to each of our fields through visual inspection. With these initial coordinates, we used the task ccxymatch to match the pixel coordinate list of each of our fields and the celestial coordinate list of the 2MASS catalog. The resulting single-matched coordinate list is used as input for the task ccmap to derive the final sky projection. This sky map is set in the master image of each field with the task ccsetwcs, and the catalog of stars converted into celestial coordinates using the xy2sky program of the WCSTools UNIX package developed at the Smithsonian Astrophysical Observatory. The celestial coordinates were assigned to the stars in the NIR catalog by using the WCSTools package.
To verify the results and estimate the astrometric accuracy, we matched the three entire
catalogs DOLORES, CAFOS, and NICS with the 2MASS catalog, as reference to find the
astrometric solution, and considered the offset distribution within a relatively high
value (2 ). From this
distribution we subtracted the expected distribution of spurious identifications (Eq. (1))
to obtain the distribution of true identifications. For the matches
DOLORES-2MASS, CAFOS-2MASS and NICS-2MASS, the 1 σ corresponding values
are 0.24
). From this
distribution we subtracted the expected distribution of spurious identifications (Eq. (1))
to obtain the distribution of true identifications. For the matches
DOLORES-2MASS, CAFOS-2MASS and NICS-2MASS, the 1 σ corresponding values
are 0.24 ,
0.22
,
0.22 and
0.19
and
0.19 , which are then
the final accuracies for each catalog.
, which are then
the final accuracies for each catalog.
3. Catalog
The aim of this section is to describe the multiwavelength catalog obtained with the following data:
-
the new optical VRI photometry from the DOLORES@TNGand CAFOS@2.2m telescope of the Calar Alto Observatorypresented here;
-
the new deep JHK photometry from NICS@TNG telescope presented here;
-
the Spitzer/IRAC photometry published in Paper I;
-
the Chandra/ACIS-I X-ray detections published in Paper I.
Figure 3 shows the fields of view of all involved observations, viz. DOLORES, CAFOS, NICS, plus the Chandra-ACIS1.
 |
Fig. 3 FoVs of our observations: DOLORES (solid boxes), CAFOS (solid circle), NICS (dotted boxes) plus the Chandra-ACIS (dashed box). In the upper-left and bottom-left corners of the DOLORES (D) and NICS (N) boxes, respectively, the corresponding field number is indicated. The IRAC FoV is larger than all the previous ones and is not shown here. |
To match these catalogs we first derived an appropriate matching
radius for each pair of catalogs, and then identified the common objects by considering the
nearest neighbor match within the adopted radius. With the aim of including as many
counterparts as possible between the catalogs, we initially computed the offset distribution
within a radius larger than the expected astrometric accuracy of the two matched catalogs
and the distribution of the spurious identifications according to Eq. 1. To match the objects we used the radius at
which the true distribution (see Sect. 2.3) starts to flatten and in all cases, we have less than 10% spurious
identifications. We derived a matching radius of 0.7 between the NICS and
IRAC catalogs. The IRAC catalog includes 15 277 objects having at least one magnitude among
the four IRAC filters; 7194 sources fall within the NICS FoV, 5020 with a counterpart in the
NICS catalog. Most of the NICS objects with no IRAC counterpart are fainter than
K = 15, since NICS data are deeper than IRAC observations.
between the NICS and
IRAC catalogs. The IRAC catalog includes 15 277 objects having at least one magnitude among
the four IRAC filters; 7194 sources fall within the NICS FoV, 5020 with a counterpart in the
NICS catalog. Most of the NICS objects with no IRAC counterpart are fainter than
K = 15, since NICS data are deeper than IRAC observations.
Using the same method described as before, we found that a matching radius of
0.7  is appropriate to
cross-match the DOLORES optical catalog with both the NICS and IRAC catalogs. For the
DOLORES-NICS matches, we found 5285 common objects. Using the same radius, we
cross-correlated the DOLORES objects without an NICS counterpart with the IRAC catalog and
found a further 629 objects, mostly located outside the NICS images, for a total of 5914
DOLORES optical detections with at least one NICS or IRAC counterpart. A radius of
0.7
is appropriate to
cross-match the DOLORES optical catalog with both the NICS and IRAC catalogs. For the
DOLORES-NICS matches, we found 5285 common objects. Using the same radius, we
cross-correlated the DOLORES objects without an NICS counterpart with the IRAC catalog and
found a further 629 objects, mostly located outside the NICS images, for a total of 5914
DOLORES optical detections with at least one NICS or IRAC counterpart. A radius of
0.7  was used also to
cross-correlate the CAFOS and NICS catalogs, finding 2915 common objects, while a radius of
0.9
was used also to
cross-correlate the CAFOS and NICS catalogs, finding 2915 common objects, while a radius of
0.9 was adopted to match
the CAFOS unmatched objects with the IRAC catalog, finding another 64 objects.
was adopted to match
the CAFOS unmatched objects with the IRAC catalog, finding another 64 objects.
The X-ray ACIS-I catalog includes 1021 sources. As mentioned in Paper I, 717 of them have a
single counterpart in the IRAC catalog, while 2 sources have a double identification. For
the match between the NICS and X-ray ACIS-I catalogs, we used the same procedure as in
Paper I; i.e., we considered three different matching radii,
0.7 ,
1.5
,
1.5 , and
2.5
, and
2.5 , in order to take the
degrading of the ACIS point spread function (PSF) off axis into account. We found a total of
752 X-ray sources with a single counterpart in the NICS catalog and 10 X-ray sources with
two IR counterparts 642 already having an IRAC detection.
, in order to take the
degrading of the ACIS point spread function (PSF) off axis into account. We found a total of
752 X-ray sources with a single counterpart in the NICS catalog and 10 X-ray sources with
two IR counterparts 642 already having an IRAC detection.
The entire catalog includes 21 688 objects, with 9531 having only the IRAC counterpart since the Spitzer/IRAC FoV is larger than in the other observations.
4. Photometry comparison
We compared the photometry obtained with DOLORES and CAFOS data to check the consistency of our data. We limited the comparison to V = 22 since the limiting magnitudes in the CAFOS and DOLORES catalogs are V ~ 22 and V ~ 24.3, respectively, if we consider magnitudes with errors smaller than 0.1. The results of the statistical comparison between the catalogs are shown in Table 3 where we also show the analogous results from the comparison with the catalog of Sharma et al. (2007), which is the only VRI photometric catalog available in literature. For this comparison, we limited the Sharma et al. (2007) catalog to V < 20 to avoid effects of large photometric errors. Our catalogs, obtained with CAFOS and DOLORES observations are in excellent agreement, as expected, since the CAFOS one has been calibrated by using the DOLORES catalog. We also found good agreement with the Sharma et al. (2007) photometry since in all bands we have smaller offsets than 0.04 mag, and the standard deviation is always smaller than 0.2 mag. The mean offsets in the V − I color are all smaller than 0.05 mag.
Good agreement is found also from the comparison between our JHK photometry, obtained with NICS data, and the 2MASS catalog, as shown by the corresponding statistical values given in Table 3.
Comparison of the optical and NIR photometric catalogs, here and in the literature, giving the statistical values and the number (N) of objects on which they have been computed.
5. Member selection
In this section we complement our optical photometric catalog by using the V and I magnitudes by Sharma et al. (2007) for the objects detected in X-rays with Chandra/ACIS-I or in the NIR with NICS and/or IRAC falling outside our optical fields or in saturated or corrupted regions of the V and I images. This is only for the purpose of finding as complete a list of cluster candidate members as possible, while in the next sections, where we derive cluster parameters, stellar masses, and ages, we only use our photometry to make certain we have a homogeneous photometric system.
5.1. Candidate members with circumstellar disk
Deep infrared observations in the JHK bands presented in this paper allow us to enlarge the sample of NGC 1893 members published in Paper I based on X-ray detection and/or infrared photometry in the four IRAC bands.
As in Damiani et al. (2006) and in Guarcello et al. (2007, 2009), we selected YSOs with circumstellar disk by using reddening-independent
indices that allow us to distinguish objects reddened by the interstellar medium from
those with IR excesses due to the disk. We defined a generic index as 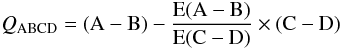 (2)where
(A − B) and (C − D) are two different colors, while E(A − B)/E(C − D) depends only on the
adopted reddening law. In our case we used the reddening laws of Munari & Carraro (1996) and Rieke & Lebofsky (1985) for optical and JHK bands,
respectively, since they are the ones that better follow our data in the color-color
diagrams. For the IRAC bands we adopted the mean of the extinctions relative to the
K band, derived for five SFRs in Flaherty et al. (2007). With the magnitudes available in our multiband catalog,
we defined 20 reddening independent Q-indices by using the couples of
colors given in Table 4. These indices allow us to
select as completely as possible all the objects showing excesses in a given color. For
example, indices involving the (V − I) colors should
select YSOs with excess in the NIR band, if the (V − I)
colors derive from the photosphere. However, in the case of accretion, the
V band can be affected by the veiling contribution, in which case, the
Q index is the combination of excesses in two colors.
(2)where
(A − B) and (C − D) are two different colors, while E(A − B)/E(C − D) depends only on the
adopted reddening law. In our case we used the reddening laws of Munari & Carraro (1996) and Rieke & Lebofsky (1985) for optical and JHK bands,
respectively, since they are the ones that better follow our data in the color-color
diagrams. For the IRAC bands we adopted the mean of the extinctions relative to the
K band, derived for five SFRs in Flaherty et al. (2007). With the magnitudes available in our multiband catalog,
we defined 20 reddening independent Q-indices by using the couples of
colors given in Table 4. These indices allow us to
select as completely as possible all the objects showing excesses in a given color. For
example, indices involving the (V − I) colors should
select YSOs with excess in the NIR band, if the (V − I)
colors derive from the photosphere. However, in the case of accretion, the
V band can be affected by the veiling contribution, in which case, the
Q index is the combination of excesses in two colors.
For each reddening-independent Q-index we adopted a conservative limit that was chosen by considering the expected colors of main-sequence stars (Kenyon & Hartmann 1995) for the colors involving the VIJHK band. For the colors involving the IRAC magnitudes [3.6], [4.5], [5.8], and [8.0], we defined the limit by considering the Q-indices of the objects that in the [3.6]–[4.5] vs. [5.8]–[8.0] diagram have colors compatible with zero within 2σ. By assuming these limits, given for each index in Table 4, we consider objects with infrared excess the ones with Q-index smaller within 3σ than the adopted limit in a given index.
We note, however, that with the Q-index method all the selected objects have a disk, but there is an ambiguous region where stars with disks cannot be distinguished from reddened objects so that the list of candidate members with a disk can be incomplete.
With this criterion, we selected 984 class II YSOs. By comparing the class II YSOs with the 242 class II YSOs selected in Paper I we found that 187 are common to the two samples, only 19 are class II according to the IRAC colors but not according to our indices, and 36 are class II according to the IRAC colors that fall outside of the NICS FoV.
In our list of class II candidate members. we found 5 of the 7 YSOs classified in Paper I as class 0/I candidate members, for which we maintained the 0/I classification and discarded them from our sample of class II candidate members. In summary, we have 1034 (984+19+36-5) class II YSOs of which 792 are new candidate members with a disk found in this work. These include 17 objects classified in Paper I as diskless candidate members. We checked that the NICS photometry is of good quality, so we classified these objects as class II candidate members.
The V vs. V − I diagram of the objects with a circumstellar disk is presented in Fig. 4 where the 10 Myr solar metallicity isochrone of Siess et al. (2000) is drawn after assuming a distance of 3.6 kpc and E(B − V) = 0.6 (see Sect. 6). From now on the theoretical models are plotted by using the Munari & Carraro (1996) and Rieke & Lebofsky (1985) reddening laws for the optical and NIR bands and the Kenyon & Hartmann (1995) conversions to transform theoretical temperatures and luminosities in the observational plane. The 10 Myr isochrone is used here only to distinguish the PMS region from the stars that have colors apparently inconsistent with a PMS nature.
We found that, among the 1034 class II candidate members, there are 170 YSOs in the region below the 10 Myr isochrone. We do not interpret them to be actually older than the other members, but rather guess they are candidate members for which optical colors are not purely photospheric. Most of these objects show excesses in the JHK-IRAC colors, and therefore the anomalous optical colors and/or magnitudes could be due to phenomena related to the disk presence, such as veiling, scattering, or other effects due to the disk’s angle of inclination (see Guarcello et al. 2010, for a discussion).
In fact, by using the synthetic photometry derived from the Robitaille et al. (2006) models, stars with circumstellar disk with age younger than 10 Myr can have optical colors and magnitudes apparently compatible with an older age. However, we cannot exclude that a small fraction of these objects could also be extragalactic sources, as expected since the cluster NGC 1893 lies in the direction of the galactic anticenter. We defer to a future work accurate analysis of the disk properties of these objects by means of spectroscopic data.
 |
Fig. 4 V vs. V − I diagram of all objects with optical magnitudes in our catalog. Class II YSOs are indicated by squares. Solid line is the 10 Myr solar metallicity isochrone of Siess et al. (2000) assuming a distance of 3.6 kpc and E(B − V) = 0.6. |
5.2. Candidate diskless members
We define as diskless candidate members all the objects having an X-ray counterpart in the Chandra-ACIS catalog, showing any IR excess, i.e. not belonging to the sample of class II YSOs, defined in the previous section, and falling in the PMS region of the V vs. V − I diagram, i.e. those with colors redder than the 10 Myr solar metallicity isochrone of Siess et al. (2000) drawn assuming a distance of 3.6 kpc and E(B − V) = 0.6 (see Sect. 6).
To define the PMS region, we have been guided by the bulk of objects with X-ray counterpart, as shown in Fig. 5 which depicts the V vs. V − I diagram of all objects with optical magnitudes in our catalog. Stars with X-ray counterpart are indicated with × symbols.
In the sample of diskless candidate members we also include the objects with X-ray emission that do not show any IR excess and have already reached the MS phase at the cluster age, i.e. those with V < 15.
With the above conditions, we found 434 diskless YSOs, 85 of which are in the sample of 110 diskless YSOs found in Paper I. If we discard the 17 objects considered here as class II YSOs from the 110 diskless YSOs defined in Paper I, the remaining 8 diskless YSOs classified in Paper I have neither V nor I magnitudes. By using the literature B and V magnitudes by Massey et al. (1995) of these 8 objects, we found that 5 fall in the cluster MS region and the other 3 lie in the PMS region. We therefore included them in our sample of diskless cluster candidate members.
In summary, we have a total of 442 diskless YSOs, shown in the V vs. V − I diagram in Fig. 5.
 |
Fig. 5 V vs. V − I diagram of all objects with optical magnitudes in our catalog. X-ray detections are indicated by × symbols, while those selected as diskless YSOs are indicated by filled circles. Solid line is as in Fig. 4. |
5.3. Hα emitters
Optical photometry of Class 0/I and Class II candidate members.
In the case of stars with accretion from circumstellar disk, the Hα line is much enlarged so the (R − Hα) index is a measure of the Hα flux in excess. To identify stars with Hα emission, we used the R vs. R − Hα diagram shown in Fig. 6, where we defined the normal star limit by performing a linear fit of the R magnitudes of all diskless YSOs having R − Hα < −3. Then we estimated a typical error in the R − Hα index per bin of 0.5 mag, as the average of the R − Hα errors in each bin. We added these errors to the R − Hα derived from the linear fit to obtain the limit indicated in the figure. We defined those with R − Hα larger within 3σ than this limit as Hα emitters. Among the 269 objects that satisfy this condition, we consider only the 125 stars for which we have an additional membership indication as cluster Hα emitters, viz. 98 class II and 27 objects previously classified as diskless candidate members.
We included in the class II sample those 27 Hα emitters that we had classified as diskless in the previous section. This is not a contradiction in the classification but only a limit in the selection of candidate members with a disk, since there is a region in which the excesses by disks cannot be distinguished from reddened objects.
In summary, we have a sample of 1061 class II candidate members, 125 of which are Hα emitters, plus 415 diskless stars. Optical photometry and classification of class II and diskless candidates members are given in Tables 5 and 6, while new JHK photometry and Spitzer-IRAC magnitudes from Paper I of class II and diskless candidates members are given in Tables 7 and 82.
Optical photometry of diskless candidate members.
NIR photometry of Class 0/I and Class II candidate members.
NIR photometry of diskless candidate members.
 |
Fig. 6 R vs. R-Hα diagram of all objects; diskless YSOs are indicated with filled circles while Hα emitters with at least an other membership indication are indicated as empty circles. Solid line is the limit we defined to distinguish diskless YSOs from high Hα emitters. |
6. Cluster parameters
Metallicity, interstellar reddening, and cluster distance are fundamental for comparing the observed CMD with theoretical tracks and isochrones from which we estimate masses and ages of cluster candidate members. However, as already discussed in several papers (e.g. Hillenbrand 1997; Gullbring et al. 1998), class II YSOs typically experience accretion phenomena, scattering, and/or reflection processes due to the dust grains in their circumstellar disks that may alter their photospheric colors, even in the optical bands. In such cases, comparison of observed magnitudes and colors with models can be unreliable and the results should be interpreted with caution. To get around this problem, we derived cluster parameters by considering only cluster candidate members without a circumstellar disk (class III YSOs), for which the observed colors can be directly compared with evolutionary tracks and isochrones once the interstellar reddening is considered.
6.1. Metallicity
In this work we adopt models computed for solar metallicity, since there are ambiguous indications in the literature about the metallicity in NGC 1893. In a paper focused on the Galactic metallicity, Rolleston et al. (1993) and Rolleston et al. (2000) derived C, N, O, Mg, Al, and Si abundances of 80 B-type main sequence stars, 8 of which are NGC 1893 members. After discarding two high rotator objects, they performed an LTE analysis from which they derive only a slight indication of under solar abundance for NGC 1893. More recently, Daflon & Cunha (2004) derived non-LTE chemical abundances in young OB stars from high-resolution echelle spectra. The two NGC 1893 cluster members again show a marginal indication of subsolar metallicity, but from the chemical analysis of 69 young stars with Galactocentric distances between 4.7 and 13.2 kpc, Daflon & Cunha (2004) find metallicity slopes consistent with a flattening of the radial gradient. Even if Rolleston et al. (2000) find indications of steeper slopes, the available studies do not show strong evidence of subsolar metallicity and therefore, as assumed in previous studies, we adopt a solar metallicity for NGC 1893.
6.2. Interstellar reddening
Color–color diagram using UBV photometry is the classical tool for deriving the mean interstellar reddening of a given cluster by comparing expected photospheric colors with those observed for diskless cluster members. Figure 7 shows the U − B vs. B − V diagram obtained with UBV photometry by Massey et al. (1995) and Sharma et al. (2007). We find that most of the bluest diskless YSOs are compatible with a reddening E(B − V) = 0.6 ± 0.1 from the comparison with the solar metallicity ZAMS of Siess et al. (2000), transformed into the observed colors by using the Kenyon & Hartmann (1995) relations. Diskless candidate members with B − V ≳ 0.6 can be compatible with lower reddenings down to E(B − V) = 0.2 or with higher reddenings, at least up to E(B − V) = 1.3, as shown by the ZAMS reddened with E(B − V) = 0.2 and E(B − V) = 1.3 (Fig. 7).
 |
Fig. 7 U − B vs. B − V diagram obtained by using Massey et al. (1995) and Sharma et al. (2007) photometry (dots); filled circles are diskless candidate members, squares are those compatible with reddening 0.5 < E(B − V) < 0.7 based on the expected photospheric colors by Kenyon & Hartmann (1995) drawn at the E(B − V) values indicated on each line. The reddening vector obtained using the Munari & Carraro (1996) reddening law is also shown. |
This allows us to deduce that the cluster region is affected by a significant differential reddening and that the interstellar reddening cannot be photometrically derived for the reddest objects. On the contrary, it can be unequivocally derived for the bluest objects, i.e. those for which the 0.5 < E(B − V) < 0.7. This result has been checked by computing individual reddenings for the 12 diskless YSOs with U − B ≲ 0.5 for which spectral types are available (Hiltner 1966; Massey et al. 1995; Marco & Negueruela 2002); we found that among the bluest objects (B − V ≲ 0.5), all the reddening values are compatible with E(B − V) = 0.6 ± 0.1, while among the reddest ones (B − V ≳ 0.5), four have E(B − V) ~ 0.2 and one has E(B − V) = 0.68.
The mean reddening E(B − V) = 0.6 ± 0.1 we derive for NGC 1893 is also consistent in the V vs. V − I CMD shown in Fig. 8, showing all objects in the FoV with error in V − I smaller than 0.1 and diskless candidate cluster members. The solar metallicity ZAMS of Siess et al. (2000) at a distance of 3.6 kpc (see Sect. 6.3) and reddened using E(B − V) = 0.4 is also drawn. The value E(B − V) = 0.4 is assumed for foreground objects that we expect to be less reddened than cluster members. To fit the highest mass range not covered by the Siess et al. (2000) ZAMS, we used the theoretical isochrone at solar metallicity of 1.5 Myr of Marigo et al. (2008) reddened with E(B − V) = 0.5, 0.6 and 0.7 at a distance of 3.6 kpc. In this diagram, diskless candidate cluster members show a wide spread that can be due to several effects, such as differential reddening, binarity, and/or age spread. This is also true in the V ≲ 16 range, where we can have objects in PMS or MS phase. However, those with 0.5 < E(B − V) < 0.7, as derived from Fig. 7 are well-fitted by the 1.5 Myr isochrone if a reddening E(B − V) = 0.6 ± 0.1 is adopted, in agreement with the value we derived by using the U − B vs. B − V diagram. In contrast, the other bright objects show a significant spread and can be both PMS objects or very reddened MS members. We also note that the choice of the 1.5 Myr isochrone is not critical for this result since in this mass range, isochrones degenerate in a vertical shape branch. For this reason in the V vs. V − I diagram, MS members cannot be used to constrain neither ages, nor the cluster distance, while they can constrain the cluster reddening.
Our result is also consistent in the low-mass range, as can be seen by using the V − I vs. J − K diagram shown in Fig. 9, where we present the color-color diagram of all objects. Diskless candidate members are used to estimate the cluster reddening by considering the locus of expected photospheric colors by Kenyon & Hartmann (1995). We take advantage of the fact that the expected photometric colors for low mass stars are almost vertical in this diagram.
To estimate the cluster reddening, we also considered the distribution of the J − K colors of diskless candidate members within fixed ranges of 0.2 magnitudes in the interval 1.3 < V − I < 3.0, and we considered, for each V − I bin, the peaks of the J − K distribution to derive the fiducial cluster sequence, indicated by the error bars in the bottom panel of Fig. 9. Comparison of this fiducial sequence with the lines allows us to confirm that the NGC 1893 mean reddening is E(B − V) = 0.6 ± 0.1. However, since the population of low-mass stars is larger and spatially spread over the whole region affected by a higher differential reddening, we note that low-mass candidate cluster members can individually have E(B − V) higher or lower values. As shown later, by using IR colors, we estimate that the reddening in this region is not higher than about E(B − V) = 1.3 (AV = 4 mag).
 |
Fig. 8 V vs. V − I diagram of all the objects (dots) with errors in V − I smaller than 0.1. Filled circles are the diskless candidate cluster members, while squares indicate those with E(B − V) between 0.5 and 0.7, according to Fig. 7. Solid line is the solar metallicity ZAMS of Siess et al. (2000) at a distance of 3.6 kpc and reddening E(B − V) = 0.4. Dashed lines indicate the 1.5 Myr Marigo et al. (2008) isochrone of solar metallicity for masses larger than 2 M⊙ at 3.6 kpc and for E(B − V) = 0.5, 0.6 and 0.7. The reddening vector obtained using the Munari & Carraro (1996) reddening laws is also shown. |
The spread of low-mass candidate cluster members in the V vs. V − I diagram is not only due to differential reddening. In fact, if we select the sample of low-mass diskless candidate members from the V − I vs. J − K diagram with 0.5 < E(B − V) < 0.7, we find that they show the same spread in the V vs. V − I diagram as all diskless, so we conclude that the low-mass star spread in the V vs. V − I diagram could also come from an intrinsic age spread and/or binarity.
We note that the E(B − V) value we derived both for low-mass and high-mass candidate cluster members, is independent of other adopted parameters such as distance, ages, and metallicity. However, further spectroscopic observations should be obtained to derive spectral types, hence individual reddening values.
 |
Fig. 9 Color–color diagram of objects with error in color smaller than 0.1 (dots). Solid lines are the photospheric colors by Kenyon & Hartmann (1995) at the three E(B − V) values indicated on each line. Filled circles in the upper panel are the NGC 1893 candidate cluster members without circumstellar disk, while error bars in the bottom panel indicate the cluster sequence fiducial line derived as described in the text. The reddening vector obtained using the Munari & Carraro (1996) and Rieke & Lebofsky (1985) reddening laws is also shown. |
6.3. Distance
The distance of NGC 1893 is a very uncertain parameter ranging from 3.2 to 6.0 kpc (see Sect. 7). Using broad band optical or NIR photometry of candidate cluster members and the isochrone fitting method, it is very difficult to derive the cluster distance. In fact, very young clusters such as NGC 1893 include a population of PMS stars, which lie in an ample region of the CMD diagram, and a small population, more or less rich, depending on the cluster age, of higher mass objects already on the MS phase and hence on a well-defined locus of the CMD. Nevertheless, the MS star distribution on the CMD is usually almost vertical and therefore quite ineffective for an accurate distance derivation. In addition, for clusters younger than about 15 Myr, the flattening of the isochrones between the two phases (PMS and MS) ends on the MS at a given magnitude that is strongly dependent on the isochrone age. Unfortunately, unless individual ages of PMS cluster members are well known, it is very hard to constrain the cluster distance by looking for this magnitude, even if the cluster mean reddening is fixed and a large population of high-mass and low-mass cluster members is known.
 |
Fig. 10 V vs. U − B diagram from the Massey et al. (1995) and Sharma et al. (2007) photometry (upper panels) and V vs. V − I diagram of all the objects with errors in V − I smaller than 0.1 and located in the regions with AV > 3.8 (bottom panels). Filled circles are the diskless candidate cluster members; squares are those with 0.5 < E(B − V) < 0.7; solid line is the 3.0 Myr isochrone of solar metallicity using E(B − V) = 0.6, while dashed line is the solar metallicity ZAMS of Siess et al. (2000) using E(B − V) = 0.4; both are drawn assuming a distance of 3.6 kpc. The reddening vector obtained using the Munari & Carraro (1996) reddening laws is also shown. |
However, in the V vs. U − B diagram, the MS population is separated quite well from the bulk of the remaining objects that are field stars and candidate PMS cluster members. This is evident in the upper panels of Fig. 10, obtained by using the UBV photometry by Massey et al. (1995) and Sharma et al. (2007), and where diskless candidate cluster members selected by us are indicated. Among these objects, we indicate those that, according to the U − B vs. B − V diagram, have 0.5 < E(B − V) < 0.7. We use these objects here to constrain the cluster distance by again comparing the solar metallicity isochrone of 1.5 Myr of Marigo et al. (2008) reddened with E(B − V) = 0.6. By taking advantage of the slightly curved shape of the isochrone in this CMD, we find that a good fitting is achieved if a distance of 3.6 kpc is adopted with an error of about 200 pc. With our data, we can rule out a distance of 3200 pc or 4300 pc for NGC 1893 which are values previously given in the literature (Sharma et al. 2007; Tapia et al. 1991; Massey et al. 1995).
A distance of 3.6 kpc for NGC 1893 is also consistent with that derived by using an independent method based on the nebula properties. In fact, as already done in previous works (Prisinzano et al. 2005; Guarcello et al. 2007), we assume that the nebula surrounding the cluster obscures many background objects, and this allows us to see mainly foreground stars, which are mostly in MS, with distances smaller than or equal to the nebula distance. Among these, those located at the nebula distance define the blue envelope of the CMD diagram that can be fitted by the ZAMS locus. With the plausible assumption that the nebula is located at the same distance of NGC 1893 and by considering only very highly reddened regions around the cluster (to minimize the spread due to background objects), it is possible to derive the cluster distance by fitting the ZAMS to the blue envelope of the CMD.
By a visual inspection of our observations in the optical, JHK, and
Spitzer/IRAC bands, we note that the nebula is not evenly spatially distributed, lying
mostly in the western region of our FoV. For this reason, we selected the MS stars to be
used for the ZAMS isochrone fitting by using the most obscured regions. The latter have
been selected by means of a reddening map based on the distribution of the
H − K colors, as in Damiani et al. (2006, see this paper for details) by using
H − K = 0.1 as the limit for the intrinsic color
expected for background giants. As in Damiani et al.
(2006), for the map computation we excluded all objects classified as candidate
cluster members. The AV map was derived by using a cell size
of 3.1 ×
2.6
×
2.6 within the FoV
defined by our NICS/JHK observations and by the
E(K − H) map, obtained as the median
of H − K colors in each cell minus the expected 0.1
value. We find that the whole region is affected by
2.2 ≲ AV ≲ 4, with the reddest regions being the western ones.
As already mentioned, the whole region is not affected by very high
AV values, and this can be also confirmed by the
distribution of field stars in the J − H vs.
H − K diagrams. This is likely due to a low absolute
reddening affecting the galactic anticenter direction.
within the FoV
defined by our NICS/JHK observations and by the
E(K − H) map, obtained as the median
of H − K colors in each cell minus the expected 0.1
value. We find that the whole region is affected by
2.2 ≲ AV ≲ 4, with the reddest regions being the western ones.
As already mentioned, the whole region is not affected by very high
AV values, and this can be also confirmed by the
distribution of field stars in the J − H vs.
H − K diagrams. This is likely due to a low absolute
reddening affecting the galactic anticenter direction.
By using the resulting AV map, we selected all the objects within the regions with AV > 3.8 and error in the V − I colors smaller than 0.1; the CMD diagram of these objects is shown in the bottom panels of Fig. 10 where we also show the solar metallicity ZAMS of Siess et al. (2000) adopting E(B − V) = 0.4, which is the minimum reddening we associate to field stars according to the bright stars in this diagram, and the solar metallicity 1.5 Myr isochrone of Marigo et al. (2008) for stars with mass M > 1.5 M⊙, adopting E(B − V) = 0.6.
As already mentioned, we derived the cluster distance as that value for which a good ZAMS fitting to MS stars of the blue envelope of this diagram is achieved. Since the maximum AV is about 4, even in the most obscured regions, a little fraction of faint background objects could be visible. In fact, as shown in Fig.10 (bottom panel), objects with V > 21 do not follow the ZAMS shape, most likely because this region is populated by field stars or extragalactic objects, which are expected to be visible in the galactic anticenter direction where the cluster NGC 1893 is located. Therefore, we only consider field stars with V < 21 for the ZAMS fitting; nevertheless, since the bright population of field stars (V ≲ 17) is poorly populated, we considered, in this range, the candidate cluster members with V ≲ 16 that are on the MS phase and with 0.5 < E(B − V) < 0.7. We note that V ≃ 16 is the magnitude of the Turn On, i.e. the magnitude where the PMS joins the cluster MS. We fitted the candidate MS cluster members assuming the mean cluster reddening E(B − V) = 0.6 and we found that a good fit is obtained both for the MS stars in the blue envelope and for the bright candidate cluster members on MS if a distance of ~3.6 kpc (see bottom panel of Fig. 10) is used. By taking the solar galactocentric distance of 8.5 Kpc, we deduce that NGC 1893 is located at a distance of about 12.1 Kpc from the Galactic center.
7. Comparison with previously published cluster parameters
The cluster distance we derived (3.6 ± 0.2 kpc) is marginally consistent with the one recently derived by Sharma et al. (2007) (d = 3250 pc) by fitting the 4 Myr isochrone of Bertelli et al. (1994) to the MS field stars and assuming E(B − V) = 0.4, which is the value taken for the MS field stars. This method is similar to ours, since the 4 Myr isochrone of Bertelli et al. (1994) instead corresponds to the ZAMS locus, if we consider that stars 4 Myr old with masses lower than about 2 M⊙ are still in PMS.
We find good agreement with the value derived by Cuffey (1973) who used UBV magnitudes to derive that the reddening in front of the cluster amounts to E(B − V) = 0.4, while the distance is 3.6 kpc. Among the first distance values published for NGC 1893, Becker & Fenkart (1971) found d = 3700 pc and AV = 1.68, corresponding to E(B − V) = 0.54, by using simultaneously two color–magnitude diagrams. Moffat (1972) derived a distance of 3980 pc and a reddening E(B − V) = 0.55 using photographic UBV photometry and the ZAMS fitting to the unreddened CMD. Humphreys (1978) found a distance modulus of 12.52 corresponding to a distance of about 3200 pc, by using V, B − V photometry of three O type main sequence stars of NGC 1893 in a paper devoted to the fundamental properties of the most luminous stars in our Galaxy.
A larger distance of 4300 pc has been derived by Tapia
et al. (1991) by using Str mgren
ubvy, Hβ and JHK photometry. They
derived spectral types and approximate luminosity classes from the
m1 and c1 indices that, together
with literature slit spectral types, are used to estimate reddening and absorption, hence
intrinsic colors and magnitudes for candidate cluster members. The corrected distance
modulus is derived as the difference between the unabsorbed V magnitude and
the absolute magnitude predicted for the given spectral type. A similar value, equal to
4800 pc, has been found by Fitzsimmons (1993), by
again using Str
mgren
ubvy, Hβ and JHK photometry. They
derived spectral types and approximate luminosity classes from the
m1 and c1 indices that, together
with literature slit spectral types, are used to estimate reddening and absorption, hence
intrinsic colors and magnitudes for candidate cluster members. The corrected distance
modulus is derived as the difference between the unabsorbed V magnitude and
the absolute magnitude predicted for the given spectral type. A similar value, equal to
4800 pc, has been found by Fitzsimmons (1993), by
again using Str mgren
ubvy photometry and the theoretical ZAMS fitting.
mgren
ubvy photometry and the theoretical ZAMS fitting.
CCD UBV photometry and multiobject fiber spectroscopy were used by Massey et al. (1995) to determine a distance of 4400 pc and reddening E(B − V) = 0.53 ± 0.2. These values are derived by using individual reddening from spectroscopy and appropriate spectral type-MV calibration for O and B-type stars. The derived distance was obtained by including only stars with inferred color excess E(B − V) between 0.41 and 0.70 Vallenari et al. (1999) used J and K photometry and UBV literature photometry to derive E(J − K) from 0.15 to 0.5, corresponding to 0.25 < E(B − V) < 0.8 in the whole region they study. In addition, they find two main dark regions where E(J − K) is 0.45–0.55 (or E(B − V) = 0.7−0.9) which is higher than the value derived in the regions outside the dark clumps.
The most discordant distance value for NGC 1893 with respect to the one found in this paper
is that derived by Marco et al. (2001) equal to
6000 pc. They used photometric Str mgren
indices (magnitude limit V ≃ 15.9) to compute the interstellar reddening
E(b − y) of cluster members. They find
values up to E(b − y) = 0.607, but they
estimate the average interstellar reddening
E(b − y) = 0.33 ± 0.03 by considering
only stars with E(b − y) < 0.4.
They used this average reddening to derive individual magnitudes and colors
(V0, (b − y)0 and
c0). By fitting an empirical ZAMS in the
MV vs. c0 diagram, they derive a
dereddened distance modulus of 13.9. Considering that the cluster is affected by a
significant differential reddening, we suppose that the photometric intrinsic parameters
derived by Marco et al. (2001), based on the average
reddening, could be the origin of their overestimate of the cluster distance.
mgren
indices (magnitude limit V ≃ 15.9) to compute the interstellar reddening
E(b − y) of cluster members. They find
values up to E(b − y) = 0.607, but they
estimate the average interstellar reddening
E(b − y) = 0.33 ± 0.03 by considering
only stars with E(b − y) < 0.4.
They used this average reddening to derive individual magnitudes and colors
(V0, (b − y)0 and
c0). By fitting an empirical ZAMS in the
MV vs. c0 diagram, they derive a
dereddened distance modulus of 13.9. Considering that the cluster is affected by a
significant differential reddening, we suppose that the photometric intrinsic parameters
derived by Marco et al. (2001), based on the average
reddening, could be the origin of their overestimate of the cluster distance.
 |
Fig. 11 V vs. V − I diagram of all objects with optical magnitudes in our catalog (dots). diskless and class II candidate members are indicated with filled circles and empty squares, respectively. Lines are the Siess et al. (2000) tracks and isochrones of masses and ages indicated on each line. |
8. Masses and ages
Assuming the cluster parameters derived by us in the previous sections, we were able to compute masses and ages of all objects we selected as candidate cluster members. However, as mentioned before, the position in the color–magnitude diagram of class II candidate members can be influenced by effects of the presence of circumstellar disk. Since our data do not allow disentangling the purely photospheric spectrum of the stars, to which theoretical models are referred, from that in excess due to these effects, we assume that masses and ages of diskless stars can be accurately derived within the uncertainties due to photometric errors, reddening, and the theoretical models, while masses and ages of class II stars should be taken with caution, especially those of the 170 candidate members falling outside the PMS region with ages apparently older than 10 Myr.
Masses and ages were computed by interpolating the solar metallicity Siess et al. (2000) tracks on the V vs. V − I plane, using the TRIGRID idl function. Figure 11 shows the V vs. V − I diagram with the Siess et al. (2000) tracks and isochrones superposed.
For the diskless sample, we find stars with masses between 0.3 and 6.7 M⊙3. We also find 11 objects classified as diskless candidate members with mass higher than 7 M⊙. The median value and the standard deviation of diskless member ages are 1.4 Myr and 1.8 Myr, respectively. For the class II sample, if we discard the 170 stars with optical anomalous photometry, we find stars with masses between 0.2 and 6.9 M⊙, and have a further 10 objects classified as class II candidate members with mass higher than 7 M⊙. The median value and the standard deviation of ages of candidate members with a disk are 1.6 Myr and 2.2 Myr, respectively, with a few stars again 9–10 Myr old. We conclude that, apart from the 170 objects with anomalous optical indices, the remaining class II stars show very similar mass and age distributions to those of diskless YSOs as shown in Fig. 12 where the age distribution of diskless and class II candidate members are shown. This reflects the similar spread observed in the V vs. V − I diagram by the two populations of candidate members. Apparently the colors of class II candidate members are not substantially modified by phenomena related to accretion. The peak in the observed mass function lies between 0.4 and 0.5 M⊙; however, the IMF will be computed in an other work where we will discuss the biases from the adopted methods and where we will compare the IMF with that of other clusters of similar age.
9. Summary and conclusions
We used new deep optical NIR data in the VRIJHK and Hα bands, along with published X-ray and Spitzer-IRAC data to compile a multiband photometric catalog in the direction of the young distant open cluster NGC 1893, located towards the galactic anticenter. Using these data and different membership criteria, we made the most complete census of candidate members available for this cluster. Reddening-independent indices involving optical and/or NIR colors allowed us to derive a list of 1061 candidate members with a circumstellar disk, with 125 among them being also Hα emitters. Among the disk bearing candidate members, 170 show anomalous optical magnitudes and colors that are likely caused by gas and/or dust in the disk. In addition, X-ray detections and optical magnitudes allowed us to distinguish 415 candidate members without a disk.
We used these last 415 YSOs and their photometric properties to assess the cluster parameters, viz. interstellar reddening and distance. Disk-less candidate members are, in fact, the most reliable objects to compare with theoretical tracks and isochrones, since their colors are purely photospheric and do not suffer from additional effects of the presence of circumstellar disks.
Bright diskless members in the U − B vs. B − V diagram, obtained from literature data, are consistent with an interstellar reddening E(B − V) = 0.6 ± 0.1. This value is also consistent whit the one derived by using the same bright candidate members in the independent V vs. V − I diagram and most of the low-mass diskless candidate members in the V − I vs. J − K diagram. However, we find evidence of differential reddening in this region.
Using the V vs. B − V (from the literature) diagram, and assuming the mean cluster reddening E(B − V) = 0.6, we find that the main sequence members selected in this work are well-fitted by a 1.5 Myr isochrone, if a distance of 3.6 ± 0.2 kpc is adopted. In the MS cluster region, isochrones degenerate and therefore our distance estimate is independent of the age adopted for MS members. The value of 3.6 kpc is consistent with the cluster distance we derived with the main sequence blue envelope traced in the V vs. V − I diagram by foreground field stars located at the cluster distance. Therefore, using independent methods and data, we are able to firmly evaluate the cluster distance for which values between 3250 and 6000 pc are given in the most recent literature.
 |
Fig. 12 Age distribution of diskless and class II candidate members in the PMS region. Class II YSOs with anomalous blue colors are not included in this sample. |
Finally, we derived masses and ages of selected candidate members in the optical PMS region down to about 0.2 M⊙; median ages for diskless and class II stars, are, respectively, 1.4 and 1.6 Myr, with a standard deviation of 1.8 and 2.2 Myr for the two samples. Few cluster candidate members are older with ages up to about 10 Myr.
If we consider that 1005 of the 1061 class II candidate members are within the Chandra FoV, where we selected the diskless candidate members, we find a disk fraction of about 71% of stars. This value is an upper limit since the diskless member selection is based on the X-ray observations that reach a mass limit higher than the one we can reach with NIR observations used to select class II stars. However, the disk fraction we find is similar to the 67% value we found in Paper I and in agreement with the disk fraction found in clusters of similar age (Haisch et al. 2001), if we assume a median age of 1.5 Myr for NGC 1893. A detailed analysis of the disk fraction as a function of stellar masses and cluster location will be the subject of a forthcoming paper (Sanz-Forcada et al., in preparation).
We therefore conclude that, despite its peculiar location in the Galaxy, NGC 1893 includes a rich population of young stars, with general properties similar to those found in young clusters in the solar neighborhood.
The upper limit is imposed by the adopted Siess et al. (2000) models.
Acknowledgments
Part of this work was financially supported by the PRIN-INAF (P.I. Lanza) and the EC MC RTN CONSTELLATION (MRTNCT2006035890). We thank Donata Randazzo for careful reading of the paper.
References
- Baffa, C., Comoretto, G., Gennari, S., et al. 2001, A&A, 378, 722 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, W., & Fenkart, R. 1971, A&AS, 4, 241 [Google Scholar]
- Bertelli, G., Bressan, A., Chiosi, C., et al. 1994, A&AS, 106, 275 [Google Scholar]
- Caramazza, M., Micela, G., Prisinzano, L., et al. 2008, A&A, 488, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuffey, J. 1973, AJ, 78, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources, ed. U. of Massachusets and Infrared Processing and Analysis Center, IPAC/California Institute of Technology [Google Scholar]
- Daflon, S., & Cunha, K. 2004, ApJ, 617, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Damiani, F., Prisinzano, L., Micela, G., et al. 2006, A&A, 459, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzsimmons, A. 1993, A&AS, 99, 15 [Google Scholar]
- Flaherty, K. M., Pipher, J. L., Megeath, S. T., et al. 2007, ApJ, 663, 1069 [CrossRef] [Google Scholar]
- Gaze, V. F., & Shajn, G. A. 1952, Izvestiya Ordena Trudovogo Krasnogo Znameni Krymskoj Astrofizicheskoj Observatorii, 9, 52 [Google Scholar]
- Ghinassi, F., Licandro, J., Oliva, E., et al. 2002, A&A, 386, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guarcello, M. G., Prisinzano, L., Micela, G., et al. 2007, A&A, 462, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guarcello, M. G., Micela, G., Damiani, F., et al. 2009, A&A, 496, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guarcello, M. G., Damiani, F., Micela, G., et al. 2010, A&A, 521, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gullbring, E., Hartmann, L., Briceno, C., et al. 1998, ApJ, 492, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hiltner, W. A. 1966, in Spectral Classification and Multicolour Photometry, ed. K. Loden, L. O. Loden, & U. Sinnerstad, IAU Symp., 24, 373 [Google Scholar]
- Hoag, A. A., Johnson, H. L., Iriarte, B., et al. 1961, Publications of the US Naval Observatory Second Series, 17, 345 [Google Scholar]
- Humphreys, R. M. 1978, ApJS, 38, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Currie, M. J., Varricatt, W. P., et al. 2006, MNRAS, 373, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Marco, A., & Negueruela, I. 2002, A&A, 393, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marco, A., Bernabeu, G., & Negueruela, I. 2001, AJ, 121, 2075 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, P., Johnson, K. E., & Degioia-Eastwood, K. 1995, ApJ, 454, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Moffat, A. F. J. 1972, A&AS, 7, 355 [Google Scholar]
- Munari, U., & Carraro, G. 1996, A&A, 314, 108 [NASA ADS] [Google Scholar]
- Prisinzano, L., Damiani, F., Micela, G., et al. 2005, A&A, 430, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., et al. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Rolleston, W. R. J., Brown, P. J. F., Dufton, P. L., et al. 1993, A&A, 270, 107 [NASA ADS] [Google Scholar]
- Rolleston, W. R. J., Smartt, S. J., Dufton, P. L., & Ryans, R. S. I. 2000, A&A, 363, 537 [NASA ADS] [Google Scholar]
- Sánchez, S. F., Aceituno, J., Thiele, U., et al. 2007, PASP, 119, 1186 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, S., Pandey, A. K., Ojha, D. K., et al. 2007, MNRAS, 380, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Stetson, P. B. 1987a, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987b, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1990, PASP, 102, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1994, PASP, 106, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 2000, PASP, 112, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 2005, PASP, 117, 563 [CrossRef] [Google Scholar]
- Tapia, M., Costero, R., Echevarria, J., et al. 1991, MNRAS, 253, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Vallenari, A., Richichi, A., Carraro, G., et al. 1999, A&A, 349, 825 [NASA ADS] [Google Scholar]
- Wilson, T. L., & Matteucci, F. 1992, A&ARv, 4, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wouterloot, J. G. A., Brand, J., Burton, W. B., et al. 1990, A&A, 230, 21 [NASA ADS] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Photometric calibration
A.1. DOLORES
Photometric calibration of DOLORES observations was computed by using the images of the
Landolt (1992) standard field SA 98. We used
the v, r, i, hα instrumental magnitudes,
and considered the V, R, and I
magnitudes of the Johnson-Kron-Cousins photometric system of standard stars in these
fields (Stetson 2000);
Hα is the magnitude in the corresponding nonstandard
filter. We calculated the transformation coefficients between the instrumental and
standard systems by using the CCDSTD code (Stetson
2005) and the following equations: 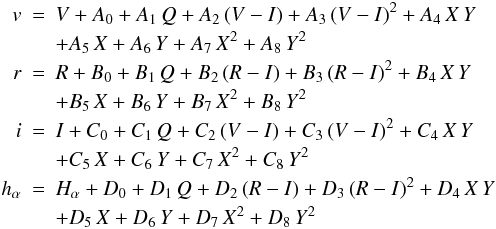 (A.1)where
Q is the airmass, A0,
B0, and C0 are the magnitude
zero points; A1, B1, and
C1 are the extinction coefficients;
A2, B2, and
C2 and A3,
B3, and C3 are the color
terms, and the rest of the terms are related to the geometrical coordinates
(X,Y) of the plate. Stars with magnitude residual values above the
3σ level were not considered for the coefficient fitting.
Coefficients calculated during calibration are listed in Table A.1. DOLORES extinction
terms are set to those provided by the telescope website. We followed the same
nomenclature for the Hα filter, but since we had no standard
measurements in this band, we applied the same calibration as for the R
band (therefore
Di = Ci)
in the case of DOLORES.
(A.1)where
Q is the airmass, A0,
B0, and C0 are the magnitude
zero points; A1, B1, and
C1 are the extinction coefficients;
A2, B2, and
C2 and A3,
B3, and C3 are the color
terms, and the rest of the terms are related to the geometrical coordinates
(X,Y) of the plate. Stars with magnitude residual values above the
3σ level were not considered for the coefficient fitting.
Coefficients calculated during calibration are listed in Table A.1. DOLORES extinction
terms are set to those provided by the telescope website. We followed the same
nomenclature for the Hα filter, but since we had no standard
measurements in this band, we applied the same calibration as for the R
band (therefore
Di = Ci)
in the case of DOLORES.
A.2. CAFOS
We tried to calibrate the CAFOS observations following the same procedure as for DOLORES, using the site extinction terms as provided by Sánchez et al. (2007); however, we noticed substantial discrepancies in the final magnitudes calculated for CAFOS when compared to DOLORES results. The variable atmospheric conditions detected during the observations, also noted in the seeing, could be responsible for the inconsistencies. We decided to use the DOLORES photometry to calibrate the CAFOS fields, by selecting the local standards used in DOLORES fields that are also common to the CAFOS FoV, and using a total of 417 CAFOS counterparts as standards for the calibration, so we calibrated the CAFOS observations in the same photometric system of DOLORES. The second and third nights of CAFOS observations also required setting the “cloud” variable in the CCDSTD setting. As explained by Stetson (2000) this variable allows different atmospheric conditions (thin clouds) to be considered during the night, setting all the extinction terms to 0 in this case (Table A.1), and fitting the zero points and the other terms. CAFOS observations used the DOLORES standard stars falling in the field to calibrate the Hα observations, with Di coefficients as listed in Table A.1.
A.3. NICS
We used the stand-alone DAOPHOT II/ALLSTAR code (Stetson 1987b) to obtain the instrumental photometry for the combined images obtained with SNAP for each filter (JHK) and for each of the 16 fields observed around the cluster NGC 1893. For most of the images we performed the PSF photometry assuming the Moffat function with β = 2.5, typically used to model stellar profiles as an analytic first approximation to the PSF, while for 6 images we used the more complex Penny function in order to take into account the elongated shape of the PSF likely due to some aberration. In addition we treated the variable PSF by using the DAOPHOT option that considers a PSF, which varies quadratically with position in the frame.
Since the PSF photometry is relative to the model stellar profile of a given frame, we needed to derive the aperture correction to the instrumental photometry; so we performed aperture photometry at different radii on a sample of isolated and relatively bright stars from which we derived growth curves with the DAOGROW code (Stetson 1990). The aperture correction was computed using the selected stars as the median of the difference between the PSF magnitudes and the aperture magnitudes obtained at the radius including all the stellar flux.
To discard false identifications due to the spots either of very bright objects or just falling at the edge of the images, we selected the list of objects detected by considering only those following the typical exponential profile of the magnitude errors. Then for each of the 16 observed fields, we merged the three lists with JHK magnitudes with DAOMATCH/DAOMASTER (Stetson 1987b) in order to have a single list with objects with at least two among the JHK magnitudes.
The NICS filters used for our observations (Js, H, K′) are those of the Mauna Kea Observatories (MKO) near-infrared filter set (Ghinassi et al. 2002), and therefore we calibrated our catalog in the MKO photometric system. To this aim we used as standard stars, the 2MASS counterparts falling in our fields with PH_QUAL flag equal to “AAA” and CC_FLG flag equal to “000”. We first converted the 2MASS catalog in the MKO system by using the inverted transformations given in the 2MASS web page4 maintained by Carpenter (see also Leggett et al. 2006).
By using instrumental magnitudes for the standard stars, that we indicate as j, h, k, and those of the 2MASS catalog in the MKO system, that we indicate as JMKO, HMKO, KMKO, we performed a linear fit of the magnitude differences for each field as a function of the colors as in the following equations:
 (A.2)From
the linear fit we derived the zero points, indicated by coefficients with subscript 0
and the color terms, indicated by coefficients with subscript 1 given in Table A.2. The
final photometric catalog in the MKO system was obtained by imposing these coefficients
and the analogous equations to the instrumental magnitudes of all detected objects.
(A.2)From
the linear fit we derived the zero points, indicated by coefficients with subscript 0
and the color terms, indicated by coefficients with subscript 1 given in Table A.2. The
final photometric catalog in the MKO system was obtained by imposing these coefficients
and the analogous equations to the instrumental magnitudes of all detected objects.
All Tables
Near infrared observations of the cluster NGC 1893 from NICS; NINTs is the number of single frames.
Comparison of the optical and NIR photometric catalogs, here and in the literature, giving the statistical values and the number (N) of objects on which they have been computed.
All Figures
 |
Fig. 1 Upper panel: I band combined image of the four DOLORES frames of 740 s; the overplotted circle indicates the CAFOS FoV. Bottom panel: Js band combined image of the NICS frames reduced and coadded with SNAP. |
| In the text | |
 |
Fig. 2 Cumulative distribution of offsets between objects falling in adjacent fields (dotted line). The expected offset cumulative distribution of spurious matches (dashed line, see Eq. (1) and the true distribution (solid line, see text) are also shown. |
| In the text | |
 |
Fig. 3 FoVs of our observations: DOLORES (solid boxes), CAFOS (solid circle), NICS (dotted boxes) plus the Chandra-ACIS (dashed box). In the upper-left and bottom-left corners of the DOLORES (D) and NICS (N) boxes, respectively, the corresponding field number is indicated. The IRAC FoV is larger than all the previous ones and is not shown here. |
| In the text | |
 |
Fig. 4 V vs. V − I diagram of all objects with optical magnitudes in our catalog. Class II YSOs are indicated by squares. Solid line is the 10 Myr solar metallicity isochrone of Siess et al. (2000) assuming a distance of 3.6 kpc and E(B − V) = 0.6. |
| In the text | |
 |
Fig. 5 V vs. V − I diagram of all objects with optical magnitudes in our catalog. X-ray detections are indicated by × symbols, while those selected as diskless YSOs are indicated by filled circles. Solid line is as in Fig. 4. |
| In the text | |
 |
Fig. 6 R vs. R-Hα diagram of all objects; diskless YSOs are indicated with filled circles while Hα emitters with at least an other membership indication are indicated as empty circles. Solid line is the limit we defined to distinguish diskless YSOs from high Hα emitters. |
| In the text | |
 |
Fig. 7 U − B vs. B − V diagram obtained by using Massey et al. (1995) and Sharma et al. (2007) photometry (dots); filled circles are diskless candidate members, squares are those compatible with reddening 0.5 < E(B − V) < 0.7 based on the expected photospheric colors by Kenyon & Hartmann (1995) drawn at the E(B − V) values indicated on each line. The reddening vector obtained using the Munari & Carraro (1996) reddening law is also shown. |
| In the text | |
 |
Fig. 8 V vs. V − I diagram of all the objects (dots) with errors in V − I smaller than 0.1. Filled circles are the diskless candidate cluster members, while squares indicate those with E(B − V) between 0.5 and 0.7, according to Fig. 7. Solid line is the solar metallicity ZAMS of Siess et al. (2000) at a distance of 3.6 kpc and reddening E(B − V) = 0.4. Dashed lines indicate the 1.5 Myr Marigo et al. (2008) isochrone of solar metallicity for masses larger than 2 M⊙ at 3.6 kpc and for E(B − V) = 0.5, 0.6 and 0.7. The reddening vector obtained using the Munari & Carraro (1996) reddening laws is also shown. |
| In the text | |
 |
Fig. 9 Color–color diagram of objects with error in color smaller than 0.1 (dots). Solid lines are the photospheric colors by Kenyon & Hartmann (1995) at the three E(B − V) values indicated on each line. Filled circles in the upper panel are the NGC 1893 candidate cluster members without circumstellar disk, while error bars in the bottom panel indicate the cluster sequence fiducial line derived as described in the text. The reddening vector obtained using the Munari & Carraro (1996) and Rieke & Lebofsky (1985) reddening laws is also shown. |
| In the text | |
 |
Fig. 10 V vs. U − B diagram from the Massey et al. (1995) and Sharma et al. (2007) photometry (upper panels) and V vs. V − I diagram of all the objects with errors in V − I smaller than 0.1 and located in the regions with AV > 3.8 (bottom panels). Filled circles are the diskless candidate cluster members; squares are those with 0.5 < E(B − V) < 0.7; solid line is the 3.0 Myr isochrone of solar metallicity using E(B − V) = 0.6, while dashed line is the solar metallicity ZAMS of Siess et al. (2000) using E(B − V) = 0.4; both are drawn assuming a distance of 3.6 kpc. The reddening vector obtained using the Munari & Carraro (1996) reddening laws is also shown. |
| In the text | |
 |
Fig. 11 V vs. V − I diagram of all objects with optical magnitudes in our catalog (dots). diskless and class II candidate members are indicated with filled circles and empty squares, respectively. Lines are the Siess et al. (2000) tracks and isochrones of masses and ages indicated on each line. |
| In the text | |
 |
Fig. 12 Age distribution of diskless and class II candidate members in the PMS region. Class II YSOs with anomalous blue colors are not included in this sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


