| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201015199 | |
| Published online | 31 January 2011 | |
TASTE: The Asiago Search for Transit timing variations of Exoplanets⋆
I. Overview and improved parameters for HAT-P-3b and HAT-P-14b
1
Dipartimento di AstronomiaUniversità degli Studi di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova, Italy
e-mail: valerio.nascimbeni@unipd.it; giampaolo.piotto@unipd.it, mario.damasso@studenti.unipd.it
2
Space Telescope Science Institute, 3700 San Martin Drive, MD
21218, Baltimore, USA
e-mail: bedin@stsci.edu
3
Astronomical Observatory of the Autonomous Region of the Aosta
Valley, Loc. Lignan
39, 11020
Nus (AO),
Italy
Received: 11 June 2010
Accepted: 24 November 2010
A promising method for detecting earth-sized exoplanets is the timing analysis of a known transit. The technique allows a search for variations in either the transit duration or the center induced by the perturbation of a third body, e.g. a second planet or an exomoon. By applying this method, the TASTE (The Asiago search for transit timing variations of Exoplanets) project will collect high-precision, short-cadence light curves for a selected sample of transits by using imaging differential photometry at the Asiago 1.82 m telescope. The first light curves show that our project can achieve a competitive timing accuracy, as well as a significant improvement of the orbital parameters. We derived refined ephemerides for HAT-P-3b and HAT-P-14b with a timing accuracy of 11 and 25 s, respectively.
Key words: techniques: photometric / planetary systems / stars: individual: HAT-P-14 / stars: individual: HAT-P-3
Photometric data is only a vailable in electronic form at CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsweb.u-strasbg.fr/viz-bin/qcat?J/A+A/527/A85
© ESO, 2011
1. Introduction
Among the techniques developed to discover exoplanets, the photometric transit method is one of the most promising having already discovered more than 100 planets. Transits also give us the unique opportunity of a nearly complete characterization of an extrasolar planetary system, by measuring orbital and physical parameters that would otherwise be inaccessible: the planetary radius Rp, the orbital inclination i, the “real” planetary mass Mp (which cannot be provided by the radial velocities alone), and hence the average density (ρp).
The great opportunities provided by transits do however exist with some disadvantages. To obtain a light curve of a typical target with a significant signal-to-noise ratio (S/N), an extremely high photometric precision needs to be reached and sustained for several hours. Many systematic trends can arise from various sources. Known as correlated or red noise, this effect plagues to a variable extent the ground-based photometry in particular (Pont et al. 2006) and specific techniques have been developed to deal with it (e.g., Tamuz et al. 2005). The simultaneous requirement of both precision and stability makes a sub-millimagnitude light curve a real challenge for ground-based instruments.
In spite of these difficulties, even exoearths might be within the reach of ground-based facilities. Several indirect methods for detecting them have been proposed. One of these is Transit Time Variation (TTV) analysis. In principle, a single planet on a Keplerian orbit should be seen to transit at very regular time intervals. However, if there were a second planet (not necessarily transiting) in the same system, it would gravitationally perturbate the orbit of the transiting one, breaking its strict periodicity and varying the measured mid-transit time relative to the expected one (Holman & Murray 2005). The amplitude of the TTV is dependent upon the mass of the perturber (more massive planets leading to a larger effect) and is strongly enhanced if the hidden planet is locked in a low-order orbital resonance with the primary, such as 1:2 or 2:3 (Agol et al. 2005). In that case, even a terrestrial planet could be responsible for a TTV on the order of tens or hundreds of seconds. It should be noted that such resonant orbits have already been detected with the radial velocity (RV) method in some planetary systems (Tinney et al. 2006).
Many ground-based projects about TTV analysis are currently ongoing. The most notable are RISE1 (Steele et al. 2008), which published null TTV detections of TrES-3b and HAT-P-3b (Gibson et al. 2009, 2010), and the Transit Light Curve project (Holman et al. 2006). Most of these works use an instrumental setup that is specifically designed to get high-precision light curves with a short cadence, sometimes of a few seconds. A very high sampling rate is required to accurately determine the instant at which the mid-transit occurs. Systematic trends have to be carefully corrected, because they can perturb the light curve from its ideal symmetric shape, biasing the estimated timing and, possibly, mimicking a TTV (Gibson et al. 2009). Despite the efforts of these and other authors, achieving a timing accuracy ≲ 10 s is still an ambitious target, typical values ranging from 15 to 30 s for the most accurate published works.
Interestingly, even though five years have elapsed since the first TTV study (Steffen & Agol 2005), no clear evidence has so far been found for a genuine perturbation by a previously unknown planet, although we note that Holman et al. (2010) announced the Kepler discovery of a pair of giant planets orbiting the same star in a 2:1 resonance, and showing an impressive TTV signature (120–240 s). Some ambiguous results have instead been reported for OGLE-TR-111 (Pont et al. 2004; Díaz et al. 2008) and a (yet unconfirmed) claim for WASP-3b (Pollacco et al. 2008) was published by Maciejewski et al. (2010). Perhaps small planets in orbital resonances are less common than previously expected by migration models such as that of Cresswell & Nelson (2006), which would be by itself a significant result. We note that the timing precision reached by most of the earlier studies was around 50–100 s, and that the effects of red noise were then more poorly understood than they are today.
Compared to TTV, Transit Duration Variation (TDV) analysis is a more recently developed method, whose theory is more subtle. A periodic change in the transit duration may arise from the presence of a satellite, or exomoon, which makes the planet oscillate around the planet-satellite barycenter along its path (Kipping 2009a); in addition, a periodic TTV signal is expected for the same reason. Here TTV and TDV are strictly complementary: a π/2 phase difference between the two signals is the expected distinctive signature of an exomoon, and the ratio of their amplitudes allows the satellite mass and its distance from the planet to be determined separately (Kipping 2009b). For the most part, timing surveys are focused only on the TTV. A tricky problem in determining the duration is that it is very dependent upon the limb darkening (LD) parameters, which are poorly constrained. Moreover, the LD is wavelength-dependent, making the comparison of TDV data extracted with different instrumental setups prone to systematics.
Our primary aim is to collect a database of high-precision light curves that will be suitable for a simultaneous TTV/TDV analysis, optimizing every task from the observation/calibration setup to the data extraction with fully home-made software tools, optimized for this specific program. Our survey is based on data collected at the Asiago Observatory2. Some feasibility tests were also performed at the Osservatorio Astronomico della regione autonoma Valle d’Aosta3 (OAVdA) observatory, which hosts a 0.81m telescope as its main instrument. Once the necessary fine tuning are completed, it will be useful as an auxiliary facility for our program, improving the efficiency of our survey.
In this first paper of this series, we present preliminary results, describing in detail: the strategy, facility, observations, data reduction, and analysis. We demonstrate that – even at this early stage – our photometry and time resolution are competitive compared with those derived by instruments of the same class. Two targets of our survey are shown as examples, and we present improved orbital and physical parameters of the recently discovered HAT-P-14b (Torres et al. 2010) and of HAT-P-3 (Torres et al. 2007), based on our new data.
2. Target selection
The selected sample of targets for the TASTE project, and their parameters.
For each studied exoplanet, a TTV/TDV analysis requires the construction of a homogeneous database of photometric high-precision light curves (RMS: ~ 1 mmag), all calibrated in time, at a high-accuracy level ( ≲ 1 s). Thus, it is necessary to perform a careful selection of the targets, based on both observational and physical criteria. Among the 81 transiting exoplanets known at the time of the submission (exoplanet.eu database), we assigned a rating to each candidate by taking into account the following observational constraints:
-
declinationδ > + 0°;
-
magnitude of the host star 9 < V < 13;
-
orbital period P ≲ 5 days;
-
total duration d ≲ 200 min;
-
transit depth ≳ 5 mmag;
-
the presence of suitable reference star(s) within the field of view of our detectors.
As demonstrated by our tests on the Asiago 1.82 m telescope, this first set of requirements gives us the chance to collect each season a reasonable number of full transits with a high sampling rate and a high S/N.
Targets lying within the CoRoT or Kepler fields were excluded; targets discovered more than four years ago, or for which accurate TTV/TDV studies have been already published, were assigned a lower ranking. The last two criteria take into account the probability of a large TTV/TDV effect (both periodic or secular) being detected by space missions or previous ground-base studies. In addition, we evaluated other factors specific to the detectability of the TTV/TDV signal:
-
the computed TTV2:1 effect induced by a 1 M⊕ exoplanet in a 2:1 resonant external orbit (Agol et al. 2005);
-
the computed TTVm effect induced by a 1 M⊕ exomoon at one third of the Hill radius (Kipping 2009a), which can be conservatively assumed to be the allowed region for a stable satellite;
-
the computed TDVm effect induced by the same exomoon, for both the V (velocity change) and the TIP (impact parameter) components of the perturbation discussed by Kipping (2009b).
Targets with TTV2:1 < 30 s were excluded. Among the remainder, a higher priority was set for targets with a total TDVm > 5 s. We briefly discuss in Sect. 5.5 how a TTV/TDV signal will be detected.
Finally, a sample of twelve exoplanets was selected. The list sorted in order of RA, along with a summary of their parameters can be seen in Table 1. Few targets were added to the list, as backup choices or because of their interesting properties, though they do not fully comply with the selection criteria. For instance, HAT-P-14b is quite a massive planet, but its highly “grazing” configuration makes it very sensitive to changes in the transit duration. On the other hand, two targets were included because a TTV is expected by previous studies: the above-mentioned WASP-3b and HAT-P-13b, for which a TTV is predicted by the perturbation of a known – but non-transiting – outer planet (Bakos et al. 2009).
3. Instrumental setup and observational strategy
The facility used for the present work is the Asiago Astrophysical Observatory, located at Mount Ekar (elevation: 1366 m) in northern Italy. Its 1.82 m Cassegrain is the largest optical telescope within Italian territory.
The instrument for imaging at the 1.82 m is the Asiago Faint Object Spectrograph and Camera (AFOSC), a focal-reducer type camera. Its 9′ × 9′ field of view is large enough to allow a careful selection of the stars to be used as reference sources in differential photometry. When used as an imager, AFOSC is equipped with a set of standard Bessel UBVR filters, and a Gunn i filter.
The CCD detector was recently upgraded, by installing a 2k × 2k pixels thinned, back-illuminated E2V 42-20, which provides a ~90% quantum efficiency in the R band spectral region. Its pixel size implies a 0.26′′/pixel scale, which severely oversamples the stellar profiles considering the typical seeing of the site. Despite the thermoelectrical cooling, usually set at −60 °C, the measured dark current is quite low, peaking at 0.2 e−/s/pix in the hottest regions. The cosmetics are very good, with only a bad column starting from a hot pixel group. The 500 MHz read-out mode provides a 2.7 e−/ADU gain and a ~7.6 e− read-out noise (RON), which may seem quite high compared to the current standards but does not represent an obstacle for our project because it is in a shot-noise (and scintillation-) limited regime (as we later illustrate).
The camera controller software has been customized to meet our needs for a very high sampling rate. Binning factors of up to 4 × 4 are available, which help us to lower the readout time while at the same time decreasing the readout noise. For the same reason, sub-windowing is used when only a part of the field is necessary to image a suitable set of reference stars. Significant effort has been devoted to shortening as much as possible the dead technical time between consecutive frames. The total overhead is now 3.4 s when reading a full frame, and 2.2 s for one quarter of a 1024 × 1024 frame. This performance allows us to achieve a sampling of about 7 s and 5 s, respectively, while keeping a duty-cycle >50%.
We ran tests of the accuracy of the mechanical shutter. For exposures as short as 1s, the effective integration time is repeatable to within 0.05 s and the travel time is regular to about two parts in 104, allowing sub-millimagnitude photometry. However, we do not wish to reach such short exposures, since the duty-cycle would get very low ( < 20%) and a non-negligible fraction of the overall S/N of our light curve would be lost, nullifying the advantages of a fast sampling. When a target is too bright to be imaged with ≥ 2 s exposures, we choose instead to apply a slight defocus to avoid saturation. The defocusing technique also minimizes systematic errors caused by a non-perfect flat field correction (Southworth et al. 2009a,b). The 1.82 m autoguide is not accurate enough to keep the stars on the same physical pixel during the whole series, but our data analysis will take into account the motion of the centroids as a possible source of systematic errors.
Only a good pre-reduction strategy would guarantee the extremely precise photometry required by the goals of the project, and much of the efforts are devoted to this task. Even very small instrumental drifts (over a timescale of just a few hours) could easily reach amplitudes of a few mmag. Bias, dark, and flat-field frames are taken just before and after the photometric series. In this way, at the data-reduction stage it becomes possible to linearly interpolate between the pre- and post- master-bias, -flats, and -darks to “customize” the calibration frames for each individual scientific frame of the time series. The master-bias, master-flat, and master-dark frames collected on each night are also stored for a long-term calibration analysis, in order to highlight any change or drift that may be correlated with seasonal trends (such as temperature) or the detector decay (cosmetics).
Summary of the observed transits at the 1.82 m Asiago telescope.
Even when taking the greatest care, smooth gradients on the order of ≲ 5% are evident when comparing dome flats with a more accurate sky flat. Therefore, sky flats, taken at both the sunset and dawn twilights and then interpolated, provide a more effective means of flat-fielding our data. Dome flats are taken in any case, not only as a backup means of performing the flat-field calibration, but also to check for short-period variations in sensitivity. Even when dealing with the highest quality flats, accuracy at low spatial frequencies is challenged by “sky concentration”, typically affecting focal reducers (Andersen et al. 1995) where scattered light is directed preferentially at the center of the field. As we later show, a very smooth gradient is not a problem as long as the tracking drifts are carefully monitored and constrained to within a few pixels.
4. Observations
 |
Fig. 1 Left: A 15′ × 15′ image from PSS2-red centered on HAT-P-14 (red circle) North is up, East is to the left. For reference, the blue circles highlight the brightest stars in the field (corresponding numbers give their R magnitude and B − R color). The AFOSC full-frame FOV (red square) is also shown. Right: Example of the typical image quality obtained with AFOSC on a 2 s single frame during the 2010 Mar. 12 run. The two main reference stars are marked with blue circles. The two green circles indicate the annulus within which the local sky was estimated. |
After a tuning phase that lasted some months mostly involving hardware/software tests and closed-dome calibrations, the first scientific observations on real transits were performed in February 2010, namely for XO-3b (Johns-Krull et al. 2008) on 2010 February 13, and WASP-12b (Hebb et al. 2009) on 2010 February 144. In both cases, clouds and high humidity prevented a full transit from being monitored. However, a data analysis of that light curves revealed some problems (such as dome turbulence, hardware/software bugs) for which later countermeasures were taken. All the observations reported here were carried out with the AFOSC R filter. The log of the observations shown in Table 2.
The first complete light curve was measured for HAT-P-14b on the night of 2010 March 12. HAT-P-14b is a “hot Jupiter” discovered by Torres et al. (2010), orbiting a slightly evolved F dwarf (V = 9.98). This planet is more massive and eccentric than the average of its class. In addition, its grazing inclination generates a V-shaped light curve, which differs from the usual U-shaped ones. That transit was the first one available, just 24 h after its publication, with an ingress and egress time predicted by Torres et al. (2010) at 2:16 and 4:28 UT of 2010 March 12. A V = 9.39 reference star lies 4.4′ from HAT-P-14. The reference star has a color very similar to the target. We chose the full-frame readout in order to include a third V = 10.53 star to be used as a cross-check source. They are labeled #1 and #2 in the finding chart of Fig. 1, respectively. The sky was photometric during the entire series. Astronomical twilight was expected at 3:51 UT, but observations lasted until the autoguide was possible, at nearly the end of the nautical twilight. The series was stopped at 4:54 UT after 200 min without interruptions; 2247 frames (in 4 × 4-binning mode) were collected. A high but quite stable seeing (~2.5′′) and a slight defocusing allowed for constant 2 s exposure times and a 37% duty-cycle. In addition to the dome flats, twilight flats were taken at dawn.
Finally, a complete transit of HAT-P-3b was observed during the night of 2010 April 7. HAT-P-3 is a V = 11.86 K dwarf, which hosts a quite light (0.60 MJ) transiting hot Jupiter with a short period of P ~ 2.9 days (Torres et al. 2007). The transit of HAT-P-3b exhibits a depth that is twice as large (0.013 mag) as that of HAT-P-14b. The field is very poor, allowing only one star with a significant flux (V ~ 10.9) and a B − R color not too different from that of the target (1.4 versus 0.8), at about 6.8′. To reduce our overhead, we chose to read only a 90 × 500 pixel CCD window (4 × 4 binned). Seeing was excellent (FWHM ≲ 1′′), so stars were defocused at about 2′′FWHM to prevent saturation of the brighter one. A full time-series covering 70 min of pre-ingress and 60 min of post-egress was taken, with a constant 5 s time sampling. The focus had be adjusted twice during the series, because of the slow thermal expansion of the secondary mirror. In the end, 2882 frames were collected, with an overall duty-cycle of 40%.
5. Data reduction and analysis
To maintain full control of the error budget and extract the maximal amount of information from the available data, we implemented and used independent software tools specifically developed for this project. The resulting pipeline, coded in Fortan 77/90 for the most part, is usable but still in active development. As a crosscheck, its output is frequently compared with that obtained using other publicly available softwares.
The key concept of our pipeline is the use of a fully empirical approach to perform every task, from the pre-processing, passing through the light curve extraction, to the estimate of the transit parameters along with their associated errors. We care about keeping our code as flexible as possible, so that future data sets coming from a different instrumental setup could be treated with minimal changes.
5.1. Aperture photometry with STARSKY
For our typical observing conditions (highly variable PSF due to seeing and defocus, lack of stellar crowding), the method of choice is differential aperture photometry, which allows us to normalize the flux of the target with a “reference flux” constructed by combining one or more reference stars. Given the small size of our field, this differential measure automatically cancels out first-order systematic trends, such as transparency variations. We carry out this task with a code named STARSKY. The final aim of our empirical approach is to obtain a light curve whose measured scatter is as small as possible.
Each frame is calibrated using the supplied master-bias, -flat, and -dark. These master frames are linearly interpolated when two given epochs (before and after the observations) are available, accordingly to our pre-reduction strategy. A precise centroid and an estimate of the FWHM of the stellar profiles is then computed by a Gaussian fit for each target or reference star in an input list. The sky level is estimated over an annulus either as a k-σ clipped median or by fitting a plane with an iterative k-σ rejection. The k factor is tunable, k = 3 usually being the best choice. The annuli are dynamically adjusted for each frame i by multiplying the input values of the inner and outer radii by the quantity Bi/ ⟨ Bi ⟩ , that is the mean FWHM of the profiles, normalized by its median over the full time-series.
After the sky is subtracted, fluxes are evaluated by summation over a set of user-defined circular apertures; partial pixels are handled by numerical integration of the fraction of pixel area falling inside a given aperture. We considered “optimal” extraction (Naylor et al. 1998) as a possible alternative to classical aperture photometry, but the high spatial variability of the PSF prevented us from such a choice. Anyway, the advantages of that approach would have been partly nullified by the very low contribution of the background noise to the typical S/N of our sources.
The expected total noise for each source is given theoretically by Merline & Howell (1995) as 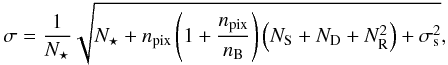 (1)where N ⋆ is the total number of photons collected from the star, and NS, ND, and NR the average photons per pixel coming from the sky, the dark current, and the readout noise, respectively. These quantities are assumed to have been estimated over an aperture covering npix pixels and the sky over an annulus covering nB pixels. The σs term is the contribution from the atmospheric scintillation, given by Dravins et al. (1998) as
(1)where N ⋆ is the total number of photons collected from the star, and NS, ND, and NR the average photons per pixel coming from the sky, the dark current, and the readout noise, respectively. These quantities are assumed to have been estimated over an aperture covering npix pixels and the sky over an annulus covering nB pixels. The σs term is the contribution from the atmospheric scintillation, given by Dravins et al. (1998) as 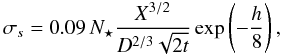 (2)where X is the airmass, D the diameter of the telescope in cm, t the exposure time in s, h the observatory altitude in km. In the typical observing conditions that we have to deal with (bright targets, short exposures, almost negligible dark current), the noise budget is largely dominated by photon “shot” noise and scintillation. Figure 2 shows how, in typical conditions, scintillation is dominant for bright targets (R ≲ 11), while shot noise is dominant for faint targets (R ≳ 11). Read-out noise is nearly negligible in our magnitude range.
(2)where X is the airmass, D the diameter of the telescope in cm, t the exposure time in s, h the observatory altitude in km. In the typical observing conditions that we have to deal with (bright targets, short exposures, almost negligible dark current), the noise budget is largely dominated by photon “shot” noise and scintillation. Figure 2 shows how, in typical conditions, scintillation is dominant for bright targets (R ≲ 11), while shot noise is dominant for faint targets (R ≳ 11). Read-out noise is nearly negligible in our magnitude range.
 |
Fig. 2 Expected noise budget in mmag of a single 2 s exposure taken at the Asiago 1.82 m telescope under typical observing conditions (4 × 4 binning, airmass 1.2, 7′′ aperture), as function of the R magnitude of the target. Measured off-transit scatters are shown for the observed light curves of HAT-P-14 and HAT-P-3. |
Once we compute the “absolute” fluxes of each source along with the associated expected errors, we need to combine the flux from the reference stars to be used as optimal “reference flux” for our differential photometry. For each reference star i of flux Fi – and for each image – we chose to calculate the reference flux 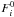 as the weighted mean of the instrumental magnitudes of all the other reference stars Fj ≠ i. This averaging technique was proven to be formally correct by Broeg et al. (2005). During the first iteration, the weights
as the weighted mean of the instrumental magnitudes of all the other reference stars Fj ≠ i. This averaging technique was proven to be formally correct by Broeg et al. (2005). During the first iteration, the weights 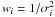 are set according to the expected amount of noise given by Eq. (1). A differential light curve is constructed by normalizing the raw flux Fi to the reference flux
are set according to the expected amount of noise given by Eq. (1). A differential light curve is constructed by normalizing the raw flux Fi to the reference flux 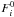 . The scatter
. The scatter 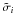 of each differential light curve is estimated as the 68.27th percentile of the residuals from its median value, after the outliers have been rejected with an iterative 4-σ clipping algorithm. Then we iterate the process of re-evaluating the reference flux
of each differential light curve is estimated as the 68.27th percentile of the residuals from its median value, after the outliers have been rejected with an iterative 4-σ clipping algorithm. Then we iterate the process of re-evaluating the reference flux 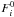 by using this time the measured scatters
by using this time the measured scatters 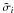 for the weights wi, constructing a new differential light curve
for the weights wi, constructing a new differential light curve 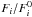 , and so forth, until convergence is reached.
, and so forth, until convergence is reached.
To detect possible systematic trends or intrinsic variability among the reference stars, two diagnostics are computed for each light curve:
-
dsys, the ratio
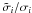 of the measured photometric scatter to the expected amount of noise given by Eq. (1).
of the measured photometric scatter to the expected amount of noise given by Eq. (1). -
psys, the ratio of the
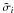 to the same scatter measured after a low-order polynomial (whose degree is user-defined) has been fitted and subtracted from the whole light curve.
to the same scatter measured after a low-order polynomial (whose degree is user-defined) has been fitted and subtracted from the whole light curve.
In the ideal case, i.e. without systematics and unknown sources of random errors, we would get dsys = psys = 1. A situation in which dsys ≫ 1, psys ≃ 1 is indicative of short-period systematics and/or an underestimated budget noise, while psys ≫ 1 reveals long-term systematic trends (as these might also depend, for example, on airmasses). For the initial set of reference stars, the reference flux 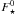 is computed by combining all their fluxes and used to normalize the light curve of the target F ⋆ , and the off-transit scatter
is computed by combining all their fluxes and used to normalize the light curve of the target F ⋆ , and the off-transit scatter 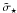 is then evaluated. The reference star(s) with the highest values of dsys and psys are removed from the list of the valid reference stars and
is then evaluated. The reference star(s) with the highest values of dsys and psys are removed from the list of the valid reference stars and 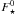 is re-evaluated without them, to check whether the off-transit measured
is re-evaluated without them, to check whether the off-transit measured 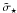 decreases. If so, dsys and psys are calculated for the remaining reference stars and a new selection is done, iterating until
decreases. If so, dsys and psys are calculated for the remaining reference stars and a new selection is done, iterating until 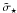 is minimized. Given the small number of reference stars in our fields, each light curve is visually inspected to search for unexpected behaviour.
is minimized. Given the small number of reference stars in our fields, each light curve is visually inspected to search for unexpected behaviour.
We incorporate an additional routine to perform empirical systematic correction. We search for correlations between the fluxes 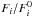 and relevant quantities such as airmass, (x, y) centroid positions, FWHM of the stellar profiles and other relevant parameters, which we then fit with low-order polynomials and subtract. A systematic correction is again considered effective if the out-of-transit
and relevant quantities such as airmass, (x, y) centroid positions, FWHM of the stellar profiles and other relevant parameters, which we then fit with low-order polynomials and subtract. A systematic correction is again considered effective if the out-of-transit 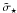 decreases when it is applied. A further cross-check is performed by sorting the stars by their B − R colors to see whether dsys and psys are higher for stars bluer or redder than average, as we would expect in the case of color-dependent systematics.
decreases when it is applied. A further cross-check is performed by sorting the stars by their B − R colors to see whether dsys and psys are higher for stars bluer or redder than average, as we would expect in the case of color-dependent systematics.
Finally the light curve of the target is normalized to one by dividing it by its off-transit median flux, after a 4-σ iterative clipping, as explained above. The error bar associated with each photometric point is assigned in this way: the expected noise for all the stars is computed using Eq. (1), the error is then propagated to the reference flux for the target 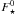 and to the differential flux
and to the differential flux 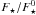 . This is an important step, because often the error in the estimate of the reference flux is not negligible when compared with that on the raw flux of the target, especially when dealing with faint and/or an insufficient number of reference stars. Neglecting the uncertainities in the reference sources, indeed, ensures that σ in Eq. (1) is underestimated. The presence of red noise would also lead to an underestimated σ.
. This is an important step, because often the error in the estimate of the reference flux is not negligible when compared with that on the raw flux of the target, especially when dealing with faint and/or an insufficient number of reference stars. Neglecting the uncertainities in the reference sources, indeed, ensures that σ in Eq. (1) is underestimated. The presence of red noise would also lead to an underestimated σ.
5.2. Light curve fitting
To extract the best estimate of the transit parameters, we need to fit a suitable model to our light curves. The details of the fitting process can appreciably affect the results. It is even trickier to obtain a realistic estimate of the errors in the fitted quantities, i.e. taking into account the role played by systematic errors and input parameters that must be held fixed at a constant value (above all, the limb darkening coefficients). All the light curves in this work were fitted with the JKTEBOP code5 (Southworth et al. 2004), which was originally developed for the analysis of detached binary systems, of which planetary transits are a special case; it has already been used in several works about high-precision transit photometry (Southworth 2008) and also specifically for TTV analysis (Coughlin et al. 2008). The package models the two components of the system as biaxial ellipsoids and performs a numerical integration in concentric annuli over the surface of each component to estimate the flux coming from the system. It then fits the model to the data with a Levenberg-Marquardt (L-M) least squares algorithm. We chose JKTEBOP among other commonly used modeling/fitting algorithms (such as those based on the analytic light curves from Mandel & Agol 2002) because it does not rely on small/spherical planet approximations, it converges rapidly toward a reliable solution (Giménez 2006), minimizes the correlation between the fitted parameters (Southworth 2008) and includes several routines for the estimation of realistic errors.
JKTEBOP can compute the limb darkening (LD) effect with several different non-linear laws, as a simple linear dependence has been proven to be not accurate enough when dealing with high precision light curves (Southworth et al. 2007). We chose to use a quadratic LD law, labeling with u1 the linear term and u2 the quadratic term. These two quantities are strongly correlated and therefore difficult to fit simultaneously; we instead usually fix u2 to its theoretical value, i.e. attempt to find only the u1 term. In some cases this second strategy may also deliver unphysical results for u1 (e.g. negative values) and so both u1 and u2 have to be fixed. We take the theoretical LD coefficients by interpolating over the grid tabulated by Claret (2000) with the ATLAS model, using the log g, Teff, and [M/H] estimated for the host star from the highest quality available spectroscopic follow-up.
Since the internal errors in the L-M fit are known to be too optimistic, JKTEBOP also includes some subroutines to estimate realistic uncertainties in every fitted parameter, using Monte Carlo and bootstrapping methods (Southworth 2008). We chose one of the most conservative approaches, i.e. the uncertainties given by a “prayer bead” empirical algorithm, also known as “residual-permutation” (RP). The RP algorithm evaluates a best-fit solution to the N data points, and the residuals of the fit are then all cyclically shifted to the next data point; a new fit is next found and the new residuals are shifted again, this iteration continuing until the residuals return to the original position (that is, after N fits). The errors are then evaluated based on the final distribution of the fitted parameters. This algorithm automatically takes into account the effects of both red noise and random errors (Jenkins et al. 2002). Its main advantage over the other Monte Carlo Markov Chain and bootstrapping methods is that it propagates over the light curve the photometric features of the actual correlated noise, without being sensitive to the choice of an averaging time or to a specific error-rescaling method. We also perform Monte Carlo tests for comparison, to check whether the errors estimated by the two different methods are consistent with each other. In our analysis, we always choose the most conservative error. As shown in the discussion, we performed thorough cross-checks to assess the reliability of the parameters and the associated uncertaintes derived by JKTEBOP.
We have already begun to implement from scratch an independent pipeline that will replace JKTEBOP for our purposes, i.e. following the same flexible and empirical approach that characterizes STARSKY. Once completed and tested, it will allow us to perform the entire data reduction and analysis with fully customized and optimized tools.
5.3. HAT-P-14b
At V = 9.98, R ~ 9.7, HAT-P-14 is the brightest star in the sample surveyed by TASTE. In our AFOSC field of view, only two stars provide a non-negligible flux compared to the target, and can be chosen as primary reference stars: they are named ref#1 (R ~ 9.1) and ref#2 (R ~ 10.7) in the right panel of Fig. 1. In addition, light curves were extracted for another eleven stars, with 12.8 ≲ R ≲ 16 and 0.6 ≲ (B − R) ≲ 2.3, just to check for systematic errors depending upon colors or upon (x, y) position.
For the inner and outer sky annuli we chose an initial value of 33 and 47 binned pixels, respectively (one 4 × 4 binned pixel ≃ 1′′), to be dynamically adapted to each frame as explained in Sect. 5.1. The aperture fluxes of the stars were evaluated over 20 different circular apertures, their radii being equally spaced between 4.0 and 20.0 pixels. The two available master-bias (taken just before and after the series) were interpolated for each frame, while flat fielding was performed with a constant master-flat taken at the morning twilight. We verified that dark correction is not necessary – in fact, its sole effect on photometry is to add noise. Measured background levels and raw aperture fluxes confirm that the sky was photometric. The typical gaussian FWHM of the profiles was quite stable through the series at about 2.5′′, because of a mix of atmospheric seeing and slight defocus. The telescope guide drifted slowly and monotonically by about 1.6′′ in 200 min, mostly along the RA axis.
The algorithms used for the iterative rejection of the reference stars (described in Sect. 5.1) simplify in this case to only three possible choices: 1, 1+2, and 2. When using ref#2 as a single reference source, the off-transit light curve of HAT-P-14b shows clear short- and long-term systematic errors, as confirmed by the dsys and psys diagnostics. The brighter ref#1 has instead dsys ≃ psys ≃ 1 for most of the aperture sizes. We note that the color (B − R)#1 = 0.7 matches exactly the target, while (B − R)#2 is 1.2. To summarize, STARSKY selected the flux from ref#1 enclosed by a 7.2 pixel aperture as the best reference flux. The differential light curve obtained for HAT-P-14 is shown with green points in the upper panel of Fig. 3.
 |
Fig. 3 Top: light curve for HAT-P-14b (V ~ 9.98, ΔV = 0.007), observed on March 13, 2010 with the Asiago 1.82 m. Unbinned points are shown in green and 120s-binned points in black. Off-transit magnitude has been set to zero. Bottom: residuals after the best-fit model is subtracted. |
Using JKTEBOP, we chose to fit the light curve by fixing both the LD coefficients at their theoretical values of u1 = 0.33 and u2 = 0.09, which were computed assuming the stellar parameters given by Torres et al. (2010) of Teff = 6600 K, vmic = 0.85 km s-1, log g = 4.25, and [Fe/H] = + 0.11. Attempts to fit u1 failed, as our single light curve does not provide enough S/N for such a shallow transit. As soon as additional time series for HAT-P-14b are collected, a simultaneous fit will allow us to get an empirical estimate for u1 and u2.
The final fitted model is plotted as a red line in Fig. 3. When the model is subtracted from the data, the unbinned light curve shows an RMS scatter of 2.2 mmag. Once the points are binned to 120 s (i.e. ~22 frames per bin), the scatter decreases to 0.54 mmag, showing only a small amount of red noise. The errors do not show any significant correlation with airmass, seeing, or positions, therefore no systematic correction was applied. In spite of an increase in the sky level of about two order of magnitudes, the systematics were tightly constrained to within 1 mmag even in the last part of the curve, when twilight occurred. The fitted parameters are reported in Table 3, along with the 1-σ errors estimated by the residual-permutation algorithm.
Fitted parameters for HAT-P-14b (top panel) and HAT-P-3b (bottom panel).
5.4. HAT-P-3b
As reported above, the field surrounding HAT-P-3 (V = 11.86, R ~ 10.9, B − R = 1.6) is extremely sparsely populated, containing only one suitable reference star: TYC 3466-1158-1 (R ~ 10.6, B − R = 1.4). The narrow 1.5′ × 8′ stripe we analyzed lacks in sources brighter than R = 17, leaving us with no other possible reference stars. The inner and outer sky annulus radii were set to 30 and 47 binned pixels, dynamically adjusted throughout the series; we used 20 circular apertures for the star fluxes, equally spaced between 4.0 and 10.0 pixels.
As for HAT-P-14, we interpolated the bias correction for each frame, while a constant master-flat correction was applied, taken at the morning twilight. The sky was photometric; the FWHM of the profiles changed through the series in the range 1.5′′–2.3′′, because of the afore mentioned thermal focus drift (Sect. 4) and the consequent adjustments. At the same time, the shape of the PSFs changed noticeably, becoming asymmetric in the second part of the series. The telescope guide drifted monotonically by about 3.6′′ in 250 min, along both axes. Reflecting the change of scale due to the focus adjustments, we noticed a small differential drift, which caused the relative distance between the two main stars to change by about 0.8′′.
TYC 3466-1158-1 turned out to be a good choice, showing no long-term systematic trends (psys ≃ 1) similar to those expected from differential extinction. However, dsys = 1.24 indicates that there is a non-negligible level of short-term systematics, probably owing to small pixel-to-pixel residual errors in the flat-field correction, combined with the PSF unpredictable (also spatial-) variability, which led to changes in the photometric zero point. An intrinsic microvariability of TYC 3466-1158-1 is a possible cause that should not be ruled out. In addition, a part of the S/N that would be achievable on HAT-P-3 is inevitably lost because of the paucity of reference flux. STARSKY selected 6.1 pixels as the best aperture. The differential light curve obtained for HAT-P-3 is shown with green points in the upper panel of Fig. 4.
 |
Fig. 4 Top: light curve for HAT-P-3b (V = 11.86, ΔV = 0.013), observed on April 7, 2010 with the Asiago 1.82 m telescope. Unbinned points are shown in green and 120 s-binned points in black. Off-transit magnitude has been set to zero. Bottom: residuals after the best-fit model is subtracted. |
The light curve was fitted by fixing both the LD coefficients at their theoretical values u1 = 0.47, u2 = 0.24, which werecomputed assuming the stellar parameters given by Torres et al. (2007) of Teff = 5185 K, vmic = 2.0 km s-1, log g = 4.61, and [ Fe/H ] = + 0.27. Attempts to fit u1 failed, as our single light curve does not provide enough S/N. The final fitted model is plotted as a red line in Fig. 4. When the model is subtracted from the data, the unbinned light curve shows an RMS scatter of 3.7 mmag. Once the points are binned to 120 s (i.e. ~24 frames per bin), the scatter decreases to 0.93 mmag. Though a small amount of systematic noise was detected, it does not show a significant correlation with airmass, seeing, or positions, therefore no correction was applied. As for HAT-P-14, the increase in the sky level near the end of the series does not cause significant trends: even in the last few minutes, the binned points are well within 2-σ off the model. The fitted parameters are reported in the Table 3, along with the 1-σ errors estimated by the residual-permutation algorithm.
5.5. TTV analysis
When TASTE begins to accumulate multiple transits for a given target, a search for TTV will be carried out using specially developed software tools, now still at the development stage.
In principle, at least three measurements are needed to detect a TTV. In a “real world case”, the signal could be multimodal, noisy, and/or unevenly sampled, and the number of observed points required for a TTV detection is strongly dependent on the signal itself. Previous works (Gibson et al. 2009, among others) have shown that it is risky to rely only on unexpectedly large amounts of scatter in the (O − C) diagrams. The solid detection of a TTV requires instead the identification of periodic structure in the timing residuals. For typical targets, a number of transits between 5 and 10 is sufficient to place very stringent upper limits on the system. The TTV signals of Kepler-9b (~2 min) and Kepler-9c (~4 min) are the only ones detected so far (Holman et al. 2010), which were sampled, respectively, with 6 and 9 observed transits with a timing accuracy of about 80 s (that is, working at S/N ~ 2–3).
If the O − C residuals for a given TASTE target show an anomalous scatter (reduced χ2 ≫ 1), possible periodicities will be searched for by a periodogram, folding the residuals over the significant frequency peaks. Even in the case of null detection, upper limits will be estimated by fitting synthetic TTV signals to our data. These will be calculated by integrating the equations of motion on a grid of eccentricities, masses, and periods of the hypotetical perturber and mapping the χ2 over the parameter space.
6. Discussion
The overall photometric performances of our system met our expectations. The scatter measured in the whole light curve of our targets is in good agreement with the theoretical expected amount of noise, as shown in Fig. 2. This holds both for HAT-P-14 and HAT-P-3, which are, respectively, the brightest, and close to the faintest magnitude limits of our surveyed sample. In particular, the noise measured for HAT-P-14 (~0.5 mmag on 120 s bins) is indicative of a very small amount of systematic error, and of the same order as achieved by state-of-the-art photometry with medium class telescopes (e.g., see Southworth et al. 2009b, with data acquired in a much better site).
HAT-P-14b was very recently discovered and no specific TTV studies for it have yet been performed. The shallowness and grazing shape of its transit make it one of the most difficult targets in our sample. The O − C diagram (observed minus computed) for the transit central times, relative to the ephemeris published by Torres et al. (2010) is shown in Fig. 5; we plotted the five measurements made by Torres et al. (2010), as well as the first TASTE point. The improvement with respect to the original data and due to our 25 s timing accuracy is remarkable. Because of the better accuracy and the longer than one-year baseline, we were able to improve the ephemeris by using all the weighted available points.
 |
Fig. 5 O − C diagram for the central time of the HAT-P-14b transit. The last point is from TASTE (2010, Mar. 12), the others from Torres et al. (2010) from which the C ephemeris is taken. The red line is the weighted fit for our refined ephemeris. |
Our best-fit value for the relative radius Rp/R ⋆ of HAT-P-14b is ~4% larger than that reported by Torres et al. (2010), though the two estimates are consistent to within 1-σ. Despite the lower scatter in our light curve, we cannot so far improve the precision in Rp/R ⋆ over the previous measure, which is based on a simultaneous fit of five transits. We instead refined the other orbital parameters, which are in good agreement with Torres et al. (2010) except for our derived inclination i, which is slightly larger6.
 |
Fig. 6 O − C diagram for the central time of the HAT-P-3b transit. The last point is from TASTE (2010, Apr. 7), the others from Gibson et al. (2010) from which the C ephemeris is taken. The point by Torres et al. (2007) is omitted. The red line is the weighted fit for our refined ephemeris. |
As for HAT-P-3b, a TTV null detection was found recently, and published by Gibson et al. (2010), placing a constraint on planets with masses higher than 0.33 and 1.81 M⊕ (in inner and outer 2:1 resonances, respectively). The very accurate ephemeris that they calculated (which accumulated only ~90 s of uncertainty at our epoch) allows us to cross-check very strictly the timing accuracy we reached. Our estimated error (~11 s) is smaller by a factor 2–5 than the RISE single measurements. Our measure is indeed well within the range predicted by the previous ephemeris, as can be seen from Fig. 6. Our improved ephemeris is therefore nearly unchanged except for the smaller error on both P and Tc. The other parameters are in excellent agreement with the results by Gibson et al. (2010), with uncertainties that are similar overall.
To assess the reliability of our analysis, we performed a cross-check by analyzing with JKTEBOP the seven light curves of HAT-P-3b used by Gibson et al. (2010) in their TTV study. We corrected the raw light curves by fitting the out-of-transit flux with a linear function, as described by the authors. We then fixed both the LD quadratic coefficients at the values used in that study and ran JKTEBOP by estimating the errors with the RP algorithm. As an additional test, we also determined the central times by fitting a Mandel and Agol model with a L-M least squares algorithm. The results are shown in Fig. 7, where we plotted the difference between our timings and those published, for each of the seven RISE transits. Our measurements are fully consistent with the results of Gibson et al. (2010), as are the associated error bars. The three transits that display the largest deviation are problematic in various ways (Fig. 8): two are partial transits with a strong variation in scatter during the series (RISE #2, RISE #3), while the third displays clear systematic errors in the out-of-transit part (RISE # 7). Even the highest quality RISE curves (#1, #5), despite their smaller scatter, display an amount of red noise that is larger than that detected on the TASTE transit, as can be seen by binning each curve and comparing the resulting RMS with the one expected by a 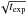 scaling law.
scaling law.
 |
Fig. 7 Central times measured on seven light curves of HAT-P-3 collected by Gibson et al. (2010). Comparison between the values published in the original study (black circles and error bars) and those found by our re-analysis with JKTEBOP (blue circles with green error bars from RP algorithm) and a Mandel and Agol model (red circles, slightly displaced on the right for clarity). The numbering of the RISE transits is consistent with Fig. 8. |
 |
Fig. 8 Raw light curves for seven transit of HAT-P-3b by Gibson et al. (2010) (RISE#1, ..., RISE#7) and the TASTE transit shown in Fig. 4. The light curves are shown in the same scale and without binning. |
7. Conclusions
The primary aim of the TASTE project is to collect a library of high-precision, short-cadence light curves for a selected sample of transits, by performing differential photometry at the Asiago 1.82 m telescope. The focus of the project is on the search for TTV and TDV effects induced by other planets (or moons) in the limited number of monitored systems. An important additional advantage is the opportunity to perform a long-term photometric follow-up, leading to an extremely precise characterization of each target, as done e.g. by the TLC project (Holman et al. 2006). By keeping in mind both of the above-mentioned goals, a careful selection of the targets was performed, as described in Sect. 2.
Many improvements are still possible, above all increases in the duty-cycle, which was only ~40% for the two time series that have been presented in this work. Recent tests have demonstrated that, when reading a narrow CCD window, a further reduction of the technical overhead from 3–3.5 s to about 1.6 s is possible. This would lead to a ≳ 70% duty-cycle (for 4 s exposures) for most of our surveyed targets, decreasing the photometric scatter on average by 30–35%. The real-time computing of our photometry will also allow us to perform a nearly-instant correction of the small tracking drifts that we mentioned in Sect. 5, minimizing any residual systematics caused by an imperfect flat-field correction.
The fine tuning of our instrumental setup will proceed in step with the additional improvement of our photometric code and the implementation of a brand new independent software tool for the light curve analysis. However, the first results reported here already show the feasibility of our project. We have already began to collect light curves for two targets in our sample (HAT-P-14b and HAT-P-3b), which will define the “zero epoch” of our analysis. In both cases, the achieved photometric precision is very close to the theoretical limits, and the systematics are constrained to well within the milli-magnitude. The overall measured scatter is close to that of the present optimal value achievable 1–2 m class telescopes, as obtained by long-cadence photometry on similar targets. The timing accuracy that we have reached, estimated by JKTEBOP algorithms, demonstrates that TASTE is very competitive compared to the performances of other similar projects. With only one transit available for each target, we have been able to derive a refined ephemeris and an independent parameter estimate for both targets.
After the submission of the present paper, an additional study of HAT-P-14b appeared on astro-ph (Simpson et al. 2010).
Acknowledgments
We thank M. Fiaschi for the support in the optimization for our purposes of AFOSC data acquisition software, and L. Malavolta for the night support during the observations of HAT-P-14b and HAT-P-3b.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, M. I., Freyhammer, L., & Storm, J. 1995, in European Southern Observatory Astrophysics Symposia, ed. P. Benvenuti, 53, 87 [Google Scholar]
- Bakos, G. Á., Howard, A. W., Noyes, R. W., et al. 2009, ApJ, 707, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Broeg, C., Fernández, M., & Neuhäuser, R. 2005, Astron. Nachr., 326, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Coughlin, J. L., Stringfellow, G. S., Becker, A. C., et al. 2008, ApJ, 689, L149 [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2006, A&A, 450, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Rojo, P., Melita, M., et al. 2008, ApJ, 682, L49 [CrossRef] [Google Scholar]
- Dravins, D., Lindegren, L., Mezey, E., & Young, A. T. 1998, PASP, 110, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Pollacco, D., Simpson, E. K., et al. 2009, ApJ, 700, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, N. P., Pollacco, D. L., Barros, S., et al. 2010, MNRAS, 401, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A. 2006, A&A, 450, 1231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Holman, M. J., Winn, J. N., Latham, D. W., et al. 2006, ApJ, 652, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jenkins, J. M., Caldwell, D. A., & Borucki, W. J. 2002, ApJ, 564, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Johns-Krull, C. M., McCullough, P. R., Burke, C. J., et al. 2008, ApJ, 677, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009a, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009b, MNRAS, 396, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, G., Dimitrov, D., Neuhaeuser, R., et al. 2010, MNRAS [arXiv:1009.4567] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Merline, W. J., & Howell, S. B. 1995, Exp. Astron., 6, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Naylor, T. 1998, MNRAS, 296, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2008, MNRAS, 385, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Bouchy, F., Queloz, D., et al. 2004, A&A, 426, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, E. K., Barros, S. C. C., Brown, D. J. A., et al. 2010, AJ, submitted [arXiv:1009.3470] [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Wheatley, P. J., & Sams, G. 2007, MNRAS, 379, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Hinse, T. C., Burgdorf, M. J., et al. 2009a, MNRAS, 399, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Hinse, T. C., Jørgensen, U. G., et al. 2009b, MNRAS, 396, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Steele, I. A., Bates, S. D., Gibson, N., et al. 2008, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 7014 [Google Scholar]
- Steffen, J. H., & Agol, E. 2005, MNRAS, 364, L96 [Google Scholar]
- Tamuz, O., Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2006, ApJ, 647, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Bakos, G. Á., Kovács, G., et al. 2007, ApJ, 666, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Bakos, G. A., Hartman, J., et al. 2010, ApJ, 715, 458 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: A 15′ × 15′ image from PSS2-red centered on HAT-P-14 (red circle) North is up, East is to the left. For reference, the blue circles highlight the brightest stars in the field (corresponding numbers give their R magnitude and B − R color). The AFOSC full-frame FOV (red square) is also shown. Right: Example of the typical image quality obtained with AFOSC on a 2 s single frame during the 2010 Mar. 12 run. The two main reference stars are marked with blue circles. The two green circles indicate the annulus within which the local sky was estimated. |
| In the text | |
 |
Fig. 2 Expected noise budget in mmag of a single 2 s exposure taken at the Asiago 1.82 m telescope under typical observing conditions (4 × 4 binning, airmass 1.2, 7′′ aperture), as function of the R magnitude of the target. Measured off-transit scatters are shown for the observed light curves of HAT-P-14 and HAT-P-3. |
| In the text | |
 |
Fig. 3 Top: light curve for HAT-P-14b (V ~ 9.98, ΔV = 0.007), observed on March 13, 2010 with the Asiago 1.82 m. Unbinned points are shown in green and 120s-binned points in black. Off-transit magnitude has been set to zero. Bottom: residuals after the best-fit model is subtracted. |
| In the text | |
 |
Fig. 4 Top: light curve for HAT-P-3b (V = 11.86, ΔV = 0.013), observed on April 7, 2010 with the Asiago 1.82 m telescope. Unbinned points are shown in green and 120 s-binned points in black. Off-transit magnitude has been set to zero. Bottom: residuals after the best-fit model is subtracted. |
| In the text | |
 |
Fig. 5 O − C diagram for the central time of the HAT-P-14b transit. The last point is from TASTE (2010, Mar. 12), the others from Torres et al. (2010) from which the C ephemeris is taken. The red line is the weighted fit for our refined ephemeris. |
| In the text | |
 |
Fig. 6 O − C diagram for the central time of the HAT-P-3b transit. The last point is from TASTE (2010, Apr. 7), the others from Gibson et al. (2010) from which the C ephemeris is taken. The point by Torres et al. (2007) is omitted. The red line is the weighted fit for our refined ephemeris. |
| In the text | |
 |
Fig. 7 Central times measured on seven light curves of HAT-P-3 collected by Gibson et al. (2010). Comparison between the values published in the original study (black circles and error bars) and those found by our re-analysis with JKTEBOP (blue circles with green error bars from RP algorithm) and a Mandel and Agol model (red circles, slightly displaced on the right for clarity). The numbering of the RISE transits is consistent with Fig. 8. |
| In the text | |
 |
Fig. 8 Raw light curves for seven transit of HAT-P-3b by Gibson et al. (2010) (RISE#1, ..., RISE#7) and the TASTE transit shown in Fig. 4. The light curves are shown in the same scale and without binning. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


