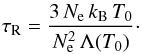| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A134 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014045 | |
| Published online | 12 January 2011 | |
Hinode observations and 3D magnetic structure of an X-ray bright point
1
Jeremiah Horrocks Institute, University of Central Lancashire,
Preston,
PR1 2HE,
UK
e-mail: CAlexander@uclan.ac.uk
2
Department of Applied Mathematics and Theoretical Physics,
University of Cambridge, Wilberforce Road, Cambridge, CB3
0WA, UK
3
Institute of Mathematics, University of St Andrews,
The North Haugh, St Andrews,
Fife, KY16 9SS, UK
Received: 12 January 2010
Accepted: 23 November 2010
Aims. We present complete Hinode Solar Optical Telescope (SOT), X-Ray Telescope (XRT)and EUV Imaging Spectrometer (EIS) observations of an X-ray bright point (XBP) observed on the 10, 11 of October 2007 over its entire lifetime (~12 h). We aim to show how the measured plasma parameters of the XBP change over time and also what kind of similarities the X-ray emission has to a potential magnetic field model.
Methods. Information from all three instruments on-board Hinode was used to study its entire evolution. XRT data was used to investigate the structure of the bright point and to measure the X-ray emission. The EIS instrument was used to measure various plasma parameters over the entire lifetime of the XBP. Lastly, the SOT was used to measure the magnetic field strength and provide a basis for potential field extrapolations of the photospheric fields to be made. These were performed and then compared to the observed coronal features.
Results. The XBP measured ~15″ in size and was found to be formed directly above an area of merging and cancelling magnetic flux on the photosphere. A good correlation between the rate of X-ray emission and decrease in total magnetic flux was found. The magnetic fragments of the XBP were found to vary on very short timescales (minutes), however the global quasi-bipolar structure remained throughout the lifetime of the XBP. The potential field extrapolations were a good visual fit to the observed coronal loops in most cases, meaning that the magnetic field was not too far from a potential state. Electron density measurements were obtained using a line ratio of Fe xii and the average density was found to be 4.95 × 109 cm-3 with the volumetric plasma filling factor calculated to have an average value of 0.04. Emission measure loci plots were then used to infer a steady temperature of log Te [K] ~ 6.1. The calculated Fe xii Doppler shifts show velocity changes in and around the bright point of ±15 km s-1 which are observed to change on a timescale of less than 30 min.
Key words: techniques: spectroscopic / Sun: corona / Sun: magnetic topology
© ESO, 2011
1. Introduction
X-ray bright points (hereafter XBPs) were first observed by Vaiana et al. (1970) while studying images of the X-ray corona taken during an Aerobee rocket flight in 1969. The first detailed study was from Golub et al. (1974) using data from Skylab. It was found that XBPs have an average lifetime of 8 h, an average size of 30″, and are composed of a diffuse aspect and a bright core. The enhanced X-ray emission is due to electron density being typically 2–4 times higher than the coronal average of around 5 × 108 cm-3. NIXT (Normal Incidence X-ray Telescope), as well as TRACE (TRAnsition region and Coronal Explorer) observations later showed that XBPs are normally composed of multiple compact loops.
About one-third of bright points are associated with emerging ephemeral regions, while two-thirds are associated with canceling magnetic fragments (see e.g., Harvey 1985; Brown et al. 2001). The process of flux emergence and cancellation in connection with XBP occurrence is quite complex, as shown by Harvey et al. (1994): XBPs can occur from magnetic bipoles emerging, cancelling, emerging then cancelling, or even when no visible bipole exists. They also stated that two thirds of all magnetic bipoles observed have no corresponding XBP and that bright points only occur when the magnetic field lines of the bipoles interact and reconnect with the overlying global magnetic field.
As in the general case of the solar corona, it is quite clear that the XBP emission is powered by the release of magnetic energy, however the details are elusive.Various models have been put forward. For example, Priest et al. (1994) proposed the Converging Flux Model to explain the interaction of the magnetic field and the creation of an XBP. The model consists of three main stages: (1) “The Preinteraction Phase” where the two unconnected areas of opposite magnetic polarity approach one another, (2) “The Interaction Phase” where energy is released as the fields of the two areas reconnect creating the XBP, and (3) “The Cancellation Phase” where the fragments cancel each other and disappear. Another possibility is “stick slip” magnetic reconnection, which should occur along separator field lines and should be associated with sporadic energy releases, as proposed by Longcope (1998).
It is still not clear if XBPs are heated in a steady or impulsive way. For example, Nolte et al. (1979) used X-ray imaging at about 90s cadence for a period of 25 min for a few XBPs to show that the emission appeared as steady, although rapid disappearances were found, following brightening. Habbal & Withbroe (1981), on the other hand, found evidence of variations of EUV emission in chromospheric, transition region and coronal lines, on timescales as short as 5.5 min (the cadence of their Skylab observations). Some work based on SOHO/CDS and SUMER spectroscopic observations to study XBPs at transition region temperatures followed (see e.g., Madjarska et al. 2003; Ugarte-Urra 2004; Ugarte-Urra et al. 2005).
In this work we present a case study of one particular X-ray bright point observed with the Hinode satellite over a period of 12 h. We have utilised all three instruments in order to investigate the measurable physical characteristics of the feature such as temperature, density, filling factor, Doppler velocities, cooling time and magnetic field strengths over the entire lifetime of the XBP. Once these measurements have been made, conclusions can be drawn about the likely source of the XBPs heating.
Measurements of EUV coronal line profiles and photospheric magnetic fields, together with estimates of coronal magnetic fields are fundamental to test theories. A large literature exists, however a comprehensive study has been lacking. The suite of instruments aboard Hinode (Kosugi et al. 2007) is extremely well suited to study XBPs for a variety of reasons. First, XPBs small sizes and short lifetimes mean that their entire evolution, from birth to disappearance, can be followed with the Hinode instruments. Indeed, telemetry limitations and high temporal cadence normally constrain the FOV of the Hinode instruments to be of the order of a few arcmin2. Second, the temporal cadence and spatial resolutions of the Hinode X-Ray Telescope (XRT) and the Solar Optical Telescope (SOT) are higher compared to what was available with previous instruments. XRT has a resolution of 2″ (Golub et al. 2007) while SOT provides imaging and spectropolarimetry at 0.32 and 0.16″ resolution, i.e. far superior than what was previously achieved with e.g. the SOHO/MDI instrument. As we shall describe below, SOT data show that the rate of magnetic flux density emergence and cancellation in quiet Sun areas, where most XBPs are formed, occur on timescales much shorter (i.e. minutes) than previously thought (clearly seen in the SOT movie1). Third, the Hinode EIS instrument (Culhane et al. 2007) is far superior than any previous spectrometers flown on satellites in providing accurate measurements of coronal densities and temperatures for XBPs. Also, for the first time it allows detailed studies of line widths and Doppler-shifts in coronal lines, something that has already added a new dimension into the problem of understanding how plasma is heated and cools in active regions (see e.g., Del Zanna 2008b).
We surveyed the entire Hinode database to find a suitable well-observed case to be studied. From the Hinode observations, described in Sect. 2, we obtained the physical properties of an XBP such as density, temperature, velocity flows, magnetic field strengths during its lifetime. We also estimated cooling times. To our knowledge, this is the first time that such a complete set of physical parameters is presented for the entire lifetime of an XBP.
As regards measurements of electron temperatures, in most previous literature they were obtained with broad-band filter ratios, which are inherently subject to large uncertainties. A few more direct measurements using spectral lines exist, however this is the first time that the emission measure loci (EML) method (see below) is applied to measure the temperature of an XBP at different times over the feature’s lifetime.
Few results exist in the literature regarding direct measurements of XBP electron densities at coronal temperatures. In most cases, only measurements at one point in time are provided, whilst we provide here several measurements which span the lifetime of an XBP.
Previous estimates of cooling times in most cases have not been based on direct measurements of densities and temperatures. For example, Habbal et al. (1990) assumed the temperature was the peak formation temperature of the lines, while the density was estimated from an assumed constant pressure. Also, most previous estimates of radiative losses have used power-law fits, whilst we actually calculate the coronal radiative losses with the latest atomic data (CHIANTI v.6).
In terms of Doppler-shifts, very few previous measurements of XBPs exist in the literature. A few measurements from SOHO SUMER (e.g., Madjarska et al. 2003) have been published, but were limited to low-temperature lines. Brosius et al. (2007) provided Doppler measurements at “coronal” temperatures along the slit during an EUNIS rocket flight, but lacked spatial and temporal information. Pérez-Suárez et al. (2008) presented one Dopplergram in Fe xii from a single observation, and found spatially-variable red and blue-shifts. We present here for the first time a complete sequence of Dopplergrams of an XBP. It has been unclear whether the observed velocities are a direct measure of reconnection outflows or if they are signatures of chromospheric evaporation, or something else.
We also modelled the evolution of the coronal magnetic field with potential field extrapolations, and discuss energetics and correlations between magnetic fields and coronal emission.
2. Observations and data analysis
We used the on-line Hinode SDC Archive Search2 to look for good observations of XBPs. The criteria were that the XBP should be well within the field-of-views of the Hinode instruments and observed over many hours. A few cases were found, and were selected for more detailed study. Here, we present results concerning one of them. The X-ray bright point studied here was observed between 2007 October 10 18:45 UT and 2007 October 11 07:17 UT with the Hinode satellite. Figure 1 shows the location of the XBP on the 11th October 2007, in a quiet Sun region close to Sun centre. This position makes line-of-sight analysis more accurate.
The Hinode observations consist of a long sequence of XRT, SOT and EIS observations. The Hinode spacecraft in its normal mode tracks a solar feature, as the Sun rotates, so in theory the FOV should be the same over time for the various instruments. However, thermal changes along the orbit affect each of the instruments in different ways, creating a considerable “jitter” of a few arcseconds over short (minutes) time-scales. The fact that the pointing of the instruments is not stable requires a significant amount of extra analysis, described below.
2.1. XRT
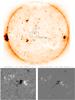 |
Fig. 1 The top panel shows a negative image of full disk XRT Al_poly/Open filter showing the location of the XBP at 00:07:11 UT on 11 October 2007. The over-plotted boxes show the EIS and SOT full fields of view. The lower left panel shows SOHO/MDI data with the three magnetic source regions labelled as they are referred to in the text. The lower right panel shows same-time SOT/NB data. The field-of-view of both lower images is 100″ × 85″. |
The XRT data we consider here were taken with the Al-poly/Open filters and a FOV of 384″ × 256″. The XRT has a lower energy X-ray cut-off than the SXT (Soft X-Ray Telescope) aboard Yohkoh meaning that the XRT can observe coronal plasma with temperatures of 1 × 106 K or lower (Kosugi et al. 2007). The data were processed using XRT_PREP and the XRT jitter has been corrected for by cross-correlating successive images. The pointing of the partial-frame images were obtained by cross-correlating with same-time full-disk XRT and EIT images. The pointing of the partial-frame images is susceptible to error due to spacecraft movement. In order to correct for this, each partial-frame image must be aligned with a similar full-disk image. The pointing of the full-disk images can be trusted more due to the visible limb offering context. In the case of XRT, each partial-frame image was compared to a same-time full-disk XRT image (or EIT 195 image if no full-disk XRT was available). By matching up the features, the partial-frame images can be corrected to full-disk pointing. Figure 2 shows a sequence of XRT images (negative) over a time-span of 12 h. The XBP was composed of two main areas, a compact bright structure (size of approximately 10 Mm) and a secondary, fainter loop system to the East. The secondary one is clearly increasing in brightness during the evolution of the XBP. We will return to this point later.
2.2. SOT
The SOT observed the XBP with both the Narrow-band Filter Imager (NFI) and the Spectropolarimeter (SP). The NFI was used in the NB mode, where imaging in the V, I Stokes parameters is performed in the Na i line. The FOV was 276″ × 164″ and the temporal cadence was about 1 minute. The FG data were processed using the standard processing routine FG_PREP. The Stokes I and V data were used to obtain, as described below, line-of-sight (LOS) magnetic field density maps. The SOT has an internal mechanism which tracks a solar feature. Despite this, a considerable “jitter” of a few arcseconds over short (minutes) time-scales is still present in both the SP and FG data. This jitter in the FG data was corrected for by cross-correlating successive images. Figure 3 shows a selection of these images with the same FOV and timings of the XRT images of Fig. 2.
As with the partial-frame XRT images, the SOT/FG Stokes V images are likely to have slight errors in their pointing values. This can again be corrected for by aligning each SOT magnetogram with a same-time SOHO/MDI LOS magnetogram which has more accurate pointing values as it is full-disk. The pointing of the full-disk images was obtained by fitting the visible limb. The features of the bright point seen in each magnetogram can easily be matched up in order to check how misaligned each partial-frame is and correct for it. Figure 1 shows two near-simultaneous observations of SOHO/MDI and Hinode SOT/NB. Notice the striking difference in resolution between the full-disk MDI and SOT/NB. Once all the corrections were applied, and the FOV reduced, a movie of the SOT/FG V images was made. Notice in Fig. 2 that the brightest part of the XBP is associated with the largest magnetic fragment concentrations, which are converging and cancelling over time. The fainter XRT loops connect the main negative polarity (N1) with the fragments of positive polarity located NE of the main feature (P2).
 |
Fig. 2 Evolution of negative XRT images with co-aligned SOT contours overlaid. Unfilled grey contours indicate negative magnetic flux and the filled grey contours represent positive flux (contours are at level ± 250 G). The FOV is 80″ × 70″. |
 |
Fig. 3 Hinode SOT NB FG V images of the bright point during times corresponding to those of the X-ray XRT images of Fig. 2. The FOV is 80″ × 70″ and the range of the data is ± 350 Gauss. |
The SOT contours in Fig. 2 are coloured to show the different polarities (unfilled grey contours for negative flux, and filled grey contours for positive flux). It can be seen that over time the main negative polarity splits into two segments: one that goes on to cancel with the west positive fragments (P1), and one that moves towards the secondary positive fragments in the east (P2). It can be seen that the bright point does not occur exactly in-between the cancelling magnetic features as one would expect. The XBP seems to be concentrated over the central area of negative flux which is most likely due to the influence of the secondary positive flux fragments. It may also be a line of sight difference between the fragments which are observed on the photosphere and the XBP on the corona.
The SP provides the line profiles in all Stokes parameters (I,Q,U,V) and is sensitive to magnetic flux of 1–5 Gauss (longitudinal) and 30–50 Gauss (transverse) (Tsuneta et al. 2008). The SP performed various scans over the XBP, with the 0.16″ slit over a FOV of 157″ × 162″. The data can provide vector magnetograms but there are drawbacks in using the SP data: the long time (typically 30 min–1 h) to scan an area means fast-changing features are missed, and the thermal/orbital effects that exist are difficult to correct for.
We used the SP data processed in the standard way within SolarSoft. The processing makes various corrections, including an approximate one for the instrument jittering, and provides apparent longitudinal and transverse magnetic field density maps. We have used the longitudinal maps to calibrate the NFI data. A section of one SP longitudinal map over the XBP took approximately 15 min to be rastered over. We averaged the FG V, I images obtained during this time and used them to obtain a calibration of the FG data, using the apparent SP longitudinal map. First, the FG data have been re-binned to the same spatial scale as the SP data. Second, the two datasets have been co-aligned, and an area centred on the XBP selected. Then, we performed a linear correlation between the SP density and the V/I values (see, e.g., Chae et al. 2007). This linear relation can be seen in Fig. 4.
 |
Fig. 4 Graph showing linear relation between SOT/SP data and SOT/NB data. |
Small discrepancies between the SP and FG dataset are present, due to the different scales and method of observations, and the fast temporal evolution of the magnetic fragments. The calibration leaves an uncertainty of the order of 10–20 Gauss. It was found that the stronger magnetic fragments (i.e. the main polarity fragments labelled P1 and N1 in Fig. 1) have typical flux densities of 100–250 Gauss.
2.3. EIS
The EIS instrument aboard Hinode observes emission lines with wavelengths in the ranges 165–211 Å and 246–291 Å (Culhane et al. 2007). EIS is used to measure line intensities, Doppler velocities (i.e. to show plasma flows), temperatures and densities in the upper transition region and coronal part of the solar atmosphere. The spatial resolution is only of the order of 3–4″ however the spectral resolution is very high and allows measurements of Doppler-shifts of only a few km s-1.
 |
Fig. 5 Negative EIS intensity maps of the XBP in different spectral lines observed on 11-Oct.-2007 at 00.10.47 UT. The FOV is 70″ × 70″. |
The EIS observations were successive repetitions of an EIS study (CAM_QS_2AS_CONTEXT) which was designed by one of us (GDZ), as part of a campaign to observe the quiet Sun. This study included 32 spectral windows and lines formed over a range of temperatures. The 2″ slit covered a field of view of 120″ × 360″ with an exposure time of 30 s. The time between successive files was 30 min with a total of 22 rasters being performed.
The SolarSoft routine EIS_PREP was used to process the raw data. The cfit package (Haugan 1997) was then used to fit Gaussian profiles to all the lines observed, using custom-written programs to obtain intensity, position and width.
Some of the prominent EIS lines present in the CAM_QS_2AS_CONTEXT study used.
 |
Fig. 6 Emission Measure Loci curves of the XBP for temperature analysis. |
The line fitting produced information on 32 spectral lines and from these results, a few lines were chosen to be looked at in more detail. These lines, along with their wavelengths and approximate temperatures, are shown in Table 1. These lines show how the features of the bright point change at different wavelengths and represent the XBP from the chromosphere, through the transition region to the corona.
The EIS instrument has a complex internal and external jittering. Only some corrections can be applied. This was done by co-aligning the monochromatic EIS images in the hot lines with XRT images taken at similar times. The co-alignment is very accurate (1–2″), however the fast jittering of the EIS instrument while it scans means that locations of EIS features can only be obtained with an accuracy of 3–4″.
As described in Del Zanna (2008a), one of the problems in the analysis of EIS data is the offset in both N-S (18″) and E-W (2″) directions between the two channels. The offset in the E-W direction means that observations in the two channels were not simultaneous nor co-spatial however this only affects rapid variations and not the observations considered here.
Figure 5 shows monochromatic images of a selection of EIS lines. The primary part of the XBP is very compact in the hottest lines (e.g. Fe xvi). The transition region lines (e.g. Fe viii) and particularly the chromospheric He ii consistently show a bipolar structure in the main body of the XBP, which we interpret as the footpoint locations of the (unresolved) system of hot loops. The strong He ii 256.32 Å line (seen in the first panel of Fig. 5) is blended with many coronal transitions, from Si x, Fe xiii, Fe xii, and Fe x at least, the dominant one being Si x. However, at the footpoints of coronal loops, the He ii emission is so bright that blending with coronal lines can become negligible. Indeed the morphology of this line is similar to that one of lines formed in the transition region. This morphology is also similar to that one noticed by Kankelborg et al. (1996) in the high-resolution (1″) images obtained by the MSSTA rocket: XBPs have associated very strong neutral hydrogen Lyα emission, often resolved as a pair of footpoints. Fe xii 195.119 has the most intense emission suggesting that the bright point has a maximum temperature within the range 6.1 ≤ log T/K ≤ 6.3 and very little plasma emitting above 3 MK. The secondary loop structure to the east of the main bright point is also clearly shown in this image.
3. Results
3.1. Temperatures
The temperature of the XBP was investigated using the emission measure loci (EML) method (see e.g., Jordan et al. 1987; Del Zanna et al. 2002). Figure 6 shows an example of one of the 22 plots that was made for each time-step. It was constructed by plotting the ratio of the background-corrected intensity values of the bright point in eight strong emission lines (see Table 1) with the calculated contribution function and plotting these against an array of temperatures. In order to determine the temperature where the greatest number of intersections occurred, a simple histogram plot was made (Fig. 6 lower panel). This histogram has a bin size of log T/K = 0.05 and clearly shows that the specific temperature of log T/K = 6.05 has the most intersections. This method was applied to each of the 22 EIS files studied and it was found that over the time period (12 h) the XBP was nearly isothermal with an average temperature of 1.3 MK. The crossing point of the EM loci curves was found to shift slightly from file to file meaning the indicated temperature varied from 1.2–1.7 MK. The ionization equilibrium values of Mazzotta et al. (1998) were used, together with elemental abundances of Grevesse & Sauval (1998).
The EML method is a direct and accurate way of determining the plasma thermal distribution, although still relies on the accuracy of the atomic calculations and on the validity of ionization equilibrium in a low-density plasma. One important result of the EML method is that the XBP was nearly isothermal during its entire lifetime. It should be noted that the assumption that the temperature in which a line is formed is equal to the peak formation temperature is not consistent with the data here.
3.2. Electron densities and spectroscopic filling factors
The CHIANTI (v6) package (Dere et al. 1997; Landi et al. 2006) was used to calculate the density of the central part of the bright point using the Fe xii (186.854 + 186.887 Å)/(195.119 + 195.179 Å) line intensity ratio, with the values of intensity corrected for background emission. This was done for each EIS raster. The density of the bright point was found to be fairly steady around 4.95 × 109 cm-3, although it did decline by around 40% in the last hour of the data set (see Table 3), when the main part of the XBP became faint. We would like to point out that the Fe xii lines used here often produce densities higher than other ions (see e.g., Young et al. 2009), when densities are of the order of 1010 cm-3 or more, so it is possible that our electron densities are slightly over-estimated here. Our densities are however similar to those found in the literature. For example, Ugarte-Urra (2004) used various instruments on-board SOHO to observe two bright points. For one of the XBPs they used the Si ix (349.86/345.10) line ratio to calculate a density value of ~5 × 108 cm-3 which they found to be in agreement with the result of Del Zanna & Mason (2003) for a similar bright point. Ugarte-Urra et al. (2005) measured electron densities for six bright points observed with SOHO/CDS, obtained with a range of ions. Values ranged between 109 and 109.9 cm-3. Pérez-Suárez et al. (2008) found values around 109.5 cm-3 for one XBP using Hinode/EIS lines from Fe xii and Fe xiii. Tian et al. (2008) found values around 109.4 cm-3 for one XBP using a few Hinode/EIS line ratios. Dere (2008) and Dere (2009) used the Fe xii ratio to provide densities for several XBPs which were also in-line with these values.
Using the densities calculated from the Fe xii line ratio together with the calibrated intensity seen with EIS Fe xii 195.119, an estimate of the spectroscopic filling factor for the bright point in each EIS raster can be made. The average filling factor for this bright point was found to be 0.04. This is in excellent agreement with the results of both Dere (2008) and Dere (2009) who studied various quiet sun coronal bright points using EIS. The filling factor was found using the equation: 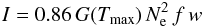 (1)where I is the intensity (erg cm-2 s-1 sr-1) of the Fe xii 195.119 Å, G is the contribution function, Ne is the electron density (cm-3), f is the filling factor, and w is the width of the XBP along the line of sight. We are approximating that the depth of the bright point is equal to the observed width. In Dere (2008) an average density of 4 × 109 cm-3 and an average filling factor of 0.015 was found. Dere (2009) used the better spatial resolution of TRACE to recalculate the bright point widths of the same data set (plus an additional EIS raster) and found a lower average density of 3 × 109 cm-3 and an average filling factor of 0.04.
(1)where I is the intensity (erg cm-2 s-1 sr-1) of the Fe xii 195.119 Å, G is the contribution function, Ne is the electron density (cm-3), f is the filling factor, and w is the width of the XBP along the line of sight. We are approximating that the depth of the bright point is equal to the observed width. In Dere (2008) an average density of 4 × 109 cm-3 and an average filling factor of 0.015 was found. Dere (2009) used the better spatial resolution of TRACE to recalculate the bright point widths of the same data set (plus an additional EIS raster) and found a lower average density of 3 × 109 cm-3 and an average filling factor of 0.04.
Table 3 shows a summary of the values of filling factor found for the bright point over the time series. The width of the XBP at different times was found by using the method described by Dere (2008) where the width of the XBP was defined as the width of the feature at half the maximum intensity (see Fig. 7).
 |
Fig. 7 Example showing how the width of the XBP was calculated. The left figure shows an EIS Fe xii 195.119 Å image with a cross-section taken through the middle of the bright point. The right figure is the intensity plotted along this cross-section. A fit of the curve was made and the FWHM of this curve was determined to be the width. |
3.3. Timescales of energy losses
With the information we have already calculated it is trivial to calculate the timescales of energy losses within the XBP. This will give us a more thorough view of the processes at work within the XBP. The timescale for radiative losses is given by the following equation:
 |
Fig. 8 Sequence of Dopplergrams of area around XBP from 18:45 on the 10-October-2007 every 30 min until 06:32 on the 11-October-2007. The numbers in the bottom-left of each image correspond to their entries in Table 3 (NB file 22 is not shown in this plot). Velocities were found using EIS Fe xii 195.119 Å. The velocities shown are between ± 20 km s-1 and are over-plotted with intensity contours. The field-of-view of each box is 70″ × 70″. |
This timescale represents how long a feature should last if its primary method of energy loss is through radiation. In the equation, Λ(T0) stands for the radiative loss function (erg cm3 s-1). This was calculated using the CHIANTI RAD_LOSS procedure. Also in the equation, T0 represents the measured temperature, kB represents Boltzmann’s constant, and Ne is the measured electron density.
The equation to calculate the timescale of the bright point if its primary method of energy loss is through conduction is given by the following equation:
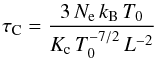 (3)In this equation Kc represents the coefficient of classical heat conductivity and has a value of 8 × 10-7 erg cm-1 s-1 K−7/2. The L represents the approximate size of the bright point in centimetres and was valued at 1.09 × 109 cm for a bright point of 15″ size.
(3)In this equation Kc represents the coefficient of classical heat conductivity and has a value of 8 × 10-7 erg cm-1 s-1 K−7/2. The L represents the approximate size of the bright point in centimetres and was valued at 1.09 × 109 cm for a bright point of 15″ size.
3.4. Velocities
We have also looked at Doppler-shifts and line widths. As described in Del Zanna (2008a), a strong (75 km s-1) orbital variation of the wavelength scale is present. This variation is non-reproducible and is different for the two bands. It has been corrected for (with custom-written software) by obtaining an average time-dependent wavelength scale for the two bands using the brightest lines and the standard wavelength-to-pixel calibration. Rest wavelengths were obtained from a quiet Sun area far away from the XBP. Count rates were such that Doppler-shifts in only a few stronger lines could be measured. The best measurements are those from the strongest line in the EIS wavelengths, the Fe xii 195.12 Å self-blend.
The line widths do not vary significantly over time and in the XBP location, however Doppler-shifts do.
The velocity flows in and around the bright point were studied over a 12 h period at intervals of 30 min (the minimum time between the rasters). Figure 8 shows a time series of the red-shifts and blue-shifts that were observed. It can be seen that even on the relatively short timescale of 30 min, changes are observed in the strength and structure of the velocity flows suggesting that these flows are occurring on timescales smaller than the observations we have. It can be clearly seen that initially there are blue-shifts observed in the boundary between the two loop systems as well as on the other side of the cooler loop system (i.e. above the magnetic area P2). It can also be seen that there is a persistent red-shift observed in the main part of the XBP which also corresponds to the area where the polarities N1 and P1 are meeting and cancelling. Figure 8 shows that these red and blue-shifts are changing in strength and position from one image to another. As the cancellation of the XBP magnetic fragments progresses, it can be seen that a new area of red-shift has emerged in the secondary loop area. This is most likely due to the migration of part of N1 that splits off and moves towards P2 at around 03.00 UT. This new red-shift indicates that a secondary cancellation is occurring.
Density and temperature values and corresponding timescales for radiative and conductive processes (see text).
3.5. 3D magnetic field structure
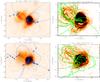 |
Fig. 9 Figure showing two examples of our comparison between the X-ray emission seen in XRT and the similarities to the potential field model we applied. The two figures on the left show negative XRT images overlaid with the photospheric footprints of the calculated topological structure of the extrapolated magnetic field. Positive magnetic sources are labelled as ⊕ , negative magnetic sources as ⊗ , positive null points as ▾, negative null points as ▴, spines as solid curves, and the intersections of separatrix surfaces with the photosphere as dashed curves. It is possible to form a good impression of the whole 3D magnetic field structure, given that each null point’s associated 3D separatrix surface must close via spine field-lines in the photosphere in cases where its own two separatrix traces do not terminate at the same source. No field-line can cross a separatrix surface or a spine. The two figures on the left show the same XRT images after being put through an edge-detection process. These images have then been overlaid with field-lines (in green) generated by the potential field model to identify any structural similarities. |
We reconstructed the coronal magnetic field near the bright point from the SOT NB/FG data which we calibrated. By identifying the strong photospheric magnetic features, tracking them in time, and modelling them as point magnetic sources, we were able to extrapolate a sequence of potential magnetic fields for the solar atmosphere close to the bright point. This was useful for our analysis because we could then calculate the 3D magnetic topological structure of these fields. Such a topology consists of magnetic null points (where the magnitude of the magnetic field is zero, Parnell et al. 1996) and their associated field-lines: spines, separatrix surfaces, and separators (a good review is given by Longcope 2005). These elements together make up the topological skeleton of the magnetic field, and they are prime locations for magnetic reconnection (Priest et al. 2005). As the heating of the bright point could have been caused by magnetic reconnection (Brown et al. 2001), it makes sense to use topological analysis to determine where the likely reconnection sites are and how they change in time. These can be compared with the observed heating/brightening locations (from XRT) to determine the role of magnetic reconnection in heating the bright point.
In order to take advantage of the simultaneous observations that we had for this bright point, we chose XRT and SOT/NB data that were taken as close to the EIS file times as possible. The SOT/NB data were analysed using the YAFTA feature tracking algorithm (Welsch et al. 2004), which was set to detect and track magnetic features with a minimum magnetic flux density of 250 G in each pixel, and a minimum size of 20 pixels. Ten or more strong magnetic features were detected in all frames.
The tracked features were then modelled as point magnetic sources, with magnetic field strengths and (flux-weighted) locations determined by their parent features. MPOLE (Longcope & Klapper 2002) was used to extrapolate a potential magnetic field for each time-frame and calculate its topological skeleton. Figure 9 (left column) shows the photospheric footprints of the topological skeletons of the magnetic fields, superimposed on the XRT emission, for two representative time-frames within the observation period. The photospheric footprint of the topological skeleton means that only those parts of the skeleton that lie in the photospheric plane are shown; magnetic sources, null points, spines, and the intersections of the separatrix surfaces with the photosphere. The right-hand column in Fig. 9 shows the same XRT images after being processed with edge-detection software. Over-plotted on these figures are example field-lines based on the calculated topological skeleton. This is to look for similarities between the observed loop structure and that predicted by the potential field model.
4. Discussion and conclusions
4.1. Energy timescale
It can be seen in Table 2 that the average results for the bright point for both τR and τC are different to the values calculated for a similar bright point studied by Ugarte-Urra (2004). This is due to the slight differences in density and temperature of the two bright points as well as having a more up-to-date figure for the radiative loss function Λ. The size of the bright point in the study was also smaller so the timescales are bound to be different. The figures calculated for our bright point indicate that the corona cools via conduction in around half an hour whereas energy is lost via radiative methods over a manner of minutes. This illustrates that there must be a continuous heating method present in the XBP for it to last longer than these timescales.
4.2. Magnetic Topology
The fundamental large-scale structure of the bright point’s magnetic field is two sets of magnetic loops sitting next to each other length-ways, and orientated approximately east-north-east to west-south-west on the Sun. These loops spring from three main regions of strong magnetic field on the photosphere; a central negative region (N1) flanked by positive regions to both west (P1) and east (P2), as can clearly be seen in Fig. 1 (lower panels).
Early on, the strongest brightening in XRT issues from the loops joining N1 to P1; this can be considered as the main bright point. However, fainter loops can also be seen joining N1 to P2 (seen clearly in Fig. 2). As time goes on, the brightening in the N1-P1 loops become more concentrated close to N1, and eventually dims to about the same level as the N1-P2 loops, which remain faint but distinct throughout.
Figure 10a shows how the magnetic fluxes of N1 (solid curve), P1 (dot-dot-dashed curve) and P2 (dashed curve) varied over time. After 23:00 UT, the fluxes of N1 and P1 are both clearly decreasing, suggesting that magnetic cancellation took place between the two main bright point sources at least from 23:00 to 07:00 UT.
The distances between N1 and P1 (solid curve) and between N1 and P2 (dashed curve) can be seen in Fig. 10(b). This graph shows that both pairs of sources moved closer together during the observational period, although the change was more steady and significant for N1 and P1. So we have a pair of sources moving closer together while their magnetic fluxes are decreasing; both indications of magnetic cancellation. Finally, we used our topological model of the bright point’s magnetic field to calculate the changing amounts of flux joining each pair of sources. This is shown in Fig. 10c, with the flux joining N1 to P1 shown as a solid curve, and the flux joining N1 to P2 shown as a dashed curve. The magnetic connection between N1 and P1 steadily weakens over the whole observation period. After 23:00 UT, the magnetic connection between N1 and P2 also weakens. This weakening must be due to magnetic cancellation between both source pairs.
 |
Fig. 10 From top to bottom: a) Evolution of the magnetic flux of each source region. N1 = solid curve, P1 = dot-dot-dashed curve, P2 = dashed curve. b) Evolution of the distances between the source regions. N1-P1 = solid curve, N1-P2 = dashed curve. c) Evolution of the magnetic flux joining the pairs of source regions. N1-P1 = solid curve, N1-P2 = dashed curve. |
Values calculated for the 22 EIS files observed over the 10–11 October 2007.
4.3. Relation between photospheric fields and coronal signatures
Several authors have found it useful to study the magnetic field of an area of coronal activity and use the extrapolated field lines to look for similarities in the coronal emission. Pérez-Suárez et al. (2008) used SOHO/MDI to compare the extrapolated field lines of an XBP with what they saw in XRT images. They found that the bright point X-ray structure was very similar to that predicted by the potential field model used.
It is very clear that the XRT brightenings join our two pairs of magnetic source regions. As can be seen in Fig. 9, our XBP shows a good agreement between the positions and angles of the observed magnetic loops and the extrapolated magnetic field-lines of the potential-field model. This implies that our model does a good job of capturing the large-scale features of the XBPs 3D magnetic field for most of its observed lifetime. The Hinode/XRT observations of the XBP do not show significant variations on short timescales (the same was found by Nolte et al. 1979 with X-ray imaging). This is in disagreement with the “stick slip” magnetic reconnection model proposed by Longcope (1998). This of course does not mean that impulsive heating does not occur, but if it does, it does on very short time-scales (seconds) and/or sub-resolution spatial scales.
It is interesting to look for correlations between the X-ray emission and the total magnetic flux density over time. An area around the main polarity of the XBP was selected (areas P1 and N1 in Fig. 1), and the light curve of the XRT count rates obtained. This is shown in Fig. 11. It can be seen that the XRT data shows a significant variation up until midnight where the count rates decrease in intensity then level out to background levels. A good correlation between flux densities and XRT intensities is found. In Fig. 10 both the positive and negative SOT fluxes show the same gradual decrease after 00.00 UT suggesting this is when the cancellation begins. Figure 10a also shows that the greatest loss of magnetic flux joining P1 and N1 takes place between 11pm and 1am, which suggests that the midnight spike in the XRT intensity is due to energy release from this magnetic cancellation event. There are two or three significant peaks seen in the XRT intensities before the cancellation begins which we cannot fully explain. These are most likely due to heating or reconnection events that we can’t link to motions of the magnetic fragments.
The fact that the magnetic field of the XBP is quite close to being potential means that the energy powering the XRT spikes should come from physical cancellation of the magnetic fields rather that from magnetic reconnection converting stored magnetic energy to heat.
 |
Fig. 11 XRT intensity (count rates) of the XBP area as a function of time. |
4.4. Relation between magnetic field and observed plasma velocity flows
The Dopplergrams clearly indicate a variable pattern. This is somewhat puzzling, considering that the overall intensity pattern does not change so rapidly. Similar patterns of blue and red-shifts were found in active regions (see e.g., Del Zanna 2008b), but they were stationary over long times. It seems unlikely that the Doppler motions are related to reconnection outflows. Also, the flow patterns do not support the idea of “stick slip” magnetic reconnection, which should occur along separator field lines.
It is quite possible that the Doppler-motions are related to chromospheric evaporation (blue-shifts) and subsequent draining (red-shifts) following cooling. However, Brosius et al. (2007) suggested the possibility that, if outflows are connected to chromospheric evaporation, they would likely decrease in time, something that we do not observe.
We have found no clear correlation between the Doppler-motions and the coronal magnetic field as obtained from the extrapolations, and we have no clear explanation of these observed velocity flows. Higher cadence observations with EIS will better reveal the pattern and links between what we see in the magnetic structure on the photosphere and the corresponding changes in the plasma velocities observed in the corona.
Available on-line: www.star.uclan.ac.uk/~cea/publications
Acknowledgments
C.E.A. is grateful for STFC Studentship support. GDZ acknowledges support from STFC via the Advanced Fellowship program. CHIANTI is a collaborative project involving researchers at NRL (USA) and the Universities of: Cambridge (UK), George Mason (USA), and Florence (Italy). Hinode is a Japanese mission developed and launched by ISAS/JAXA, with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in co-operation with ESA and NSC (Norway).
References
- Brosius, J. W., Rabin, D. M., & Thomas, R. J. 2007, ApJ, 656, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, D. S., Parnell, C. E., Deluca, E. E., Golub, L., & McMullen, R. A. 2001, 201, 305 [Google Scholar]
- Chae, J., Moon, Y.-J., Park, Y.-D., et al. 2007, PASJ, 59, 619 [NASA ADS] [Google Scholar]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [Google Scholar]
- Del Zanna, G. 2008a, A&A, 481, L69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G. 2008b, A&A, 481, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., & Mason, H. E. 2003, A&A, 406, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Landini, M., & Mason, H. E. 2002, A&A, 385, 968 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P. 2008, A&A, 491, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P. 2009, A&A, 497, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Golub, L., Krieger, A. S., Silk, J. K., Timothy, A. F., & Vaiana, G. S. 1974, ApJ, 189, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Golub, L., Deluca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Habbal, S. R., & Withbroe, G. L. 1981, Sol. Phys., 69, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Habbal, S. R., Withbroe, G. L., & Dowdy, Jr., J. F. 1990, ApJ, 352, 333 [Google Scholar]
- Harvey, K. L. 1985, Australian J. Phys., 38, 875 [Google Scholar]
- Harvey, K. L., Strong, K. S., Nitta, N., & Tsuneta, S. 1994, in Solar Active Region Evolution: Comparing Models with Observations, ed. K. S. Balasubramaniam, & G. W. Simon, ASP Conf. Ser., 68, 377 [Google Scholar]
- Haugan, S. V. H. 1997, The Component Fitting System (CFIT) for IDL, CDS software note no. 47, Tech. Rep. [Google Scholar]
- Jordan, C., Ayres, T. R., Brown, A., Linsky, J. L., & Simon, T. 1987, MNRAS, 225, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Kankelborg, C. C., Walker, II, A. B. C., Hoover, R. B., & Barbee, Jr., T. W. 1996, ApJ, 466, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W. 1998, ApJ, 507, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W. 2005, Living Rev. Sol. Phys., 2, 7 [Google Scholar]
- Longcope, D. W., & Klapper, I. 2002, 579, 468 [Google Scholar]
- Madjarska, M. S., Doyle, J. G., Teriaca, L., & Banerjee, D. 2003, A&A, 398, 775 [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [Google Scholar]
- Nolte, J. T., Solodyna, C. V., & Gerassimenko, M. 1979, Sol. Phys., 63, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., Smith, J. M., Neukirch, T., & Priest, E. R. 1996, 3, 759 [Google Scholar]
- Pérez-Suárez, D., Maclean, R. C., Doyle, J. G., & Madjarska, M. S. 2008, A&A, 492, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Priest, E. R., Parnell, C. E., & Martin, S. F. 1994, ApJ, 427, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., Longcope, D. W., & Heyvaerts, J. 2005, 624, 1057 [Google Scholar]
- Tian, H., Curdt, W., Marsch, E., & He, J. 2008, ApJ, 681, L121 [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Ugarte-Urra, I. 2004, Ph.D. thesis, AA (Armagh Observatory, College Hill, Armagh BT61 9DG, N. Ireland, UK) [Google Scholar]
- Ugarte-Urra, I., Doyle, J. G., & Del Zanna, G. 2005, A&A, 435, 1169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaiana, G. S., Speybroeck, L. P., & Krieger, A. S. 1970, Bull. Am. Phys. Soc., 15, 611 [Google Scholar]
- Welsch, B. T., Fisher, G. H., Abbett, W. P., & Régnier, S. 2004, ApJ, 610, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., Watanabe, T., Hara, H., & Mariska, J. T. 2009, A&A, 495, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Density and temperature values and corresponding timescales for radiative and conductive processes (see text).
All Figures
 |
Fig. 1 The top panel shows a negative image of full disk XRT Al_poly/Open filter showing the location of the XBP at 00:07:11 UT on 11 October 2007. The over-plotted boxes show the EIS and SOT full fields of view. The lower left panel shows SOHO/MDI data with the three magnetic source regions labelled as they are referred to in the text. The lower right panel shows same-time SOT/NB data. The field-of-view of both lower images is 100″ × 85″. |
| In the text | |
 |
Fig. 2 Evolution of negative XRT images with co-aligned SOT contours overlaid. Unfilled grey contours indicate negative magnetic flux and the filled grey contours represent positive flux (contours are at level ± 250 G). The FOV is 80″ × 70″. |
| In the text | |
 |
Fig. 3 Hinode SOT NB FG V images of the bright point during times corresponding to those of the X-ray XRT images of Fig. 2. The FOV is 80″ × 70″ and the range of the data is ± 350 Gauss. |
| In the text | |
 |
Fig. 4 Graph showing linear relation between SOT/SP data and SOT/NB data. |
| In the text | |
 |
Fig. 5 Negative EIS intensity maps of the XBP in different spectral lines observed on 11-Oct.-2007 at 00.10.47 UT. The FOV is 70″ × 70″. |
| In the text | |
 |
Fig. 6 Emission Measure Loci curves of the XBP for temperature analysis. |
| In the text | |
 |
Fig. 7 Example showing how the width of the XBP was calculated. The left figure shows an EIS Fe xii 195.119 Å image with a cross-section taken through the middle of the bright point. The right figure is the intensity plotted along this cross-section. A fit of the curve was made and the FWHM of this curve was determined to be the width. |
| In the text | |
 |
Fig. 8 Sequence of Dopplergrams of area around XBP from 18:45 on the 10-October-2007 every 30 min until 06:32 on the 11-October-2007. The numbers in the bottom-left of each image correspond to their entries in Table 3 (NB file 22 is not shown in this plot). Velocities were found using EIS Fe xii 195.119 Å. The velocities shown are between ± 20 km s-1 and are over-plotted with intensity contours. The field-of-view of each box is 70″ × 70″. |
| In the text | |
 |
Fig. 9 Figure showing two examples of our comparison between the X-ray emission seen in XRT and the similarities to the potential field model we applied. The two figures on the left show negative XRT images overlaid with the photospheric footprints of the calculated topological structure of the extrapolated magnetic field. Positive magnetic sources are labelled as ⊕ , negative magnetic sources as ⊗ , positive null points as ▾, negative null points as ▴, spines as solid curves, and the intersections of separatrix surfaces with the photosphere as dashed curves. It is possible to form a good impression of the whole 3D magnetic field structure, given that each null point’s associated 3D separatrix surface must close via spine field-lines in the photosphere in cases where its own two separatrix traces do not terminate at the same source. No field-line can cross a separatrix surface or a spine. The two figures on the left show the same XRT images after being put through an edge-detection process. These images have then been overlaid with field-lines (in green) generated by the potential field model to identify any structural similarities. |
| In the text | |
 |
Fig. 10 From top to bottom: a) Evolution of the magnetic flux of each source region. N1 = solid curve, P1 = dot-dot-dashed curve, P2 = dashed curve. b) Evolution of the distances between the source regions. N1-P1 = solid curve, N1-P2 = dashed curve. c) Evolution of the magnetic flux joining the pairs of source regions. N1-P1 = solid curve, N1-P2 = dashed curve. |
| In the text | |
 |
Fig. 11 XRT intensity (count rates) of the XBP area as a function of time. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.