| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201015699 | |
| Published online | 03 December 2010 | |
Large-scale bias of dark matter halos
Institut de Physique Théorique, CEA Saclay,
91191
Gif-sur-Yvette,
France
e-mail: patrick.valageas@cea.fr
Received:
6
September
2010
Accepted:
3
November
2010
Aims. We build a simple analytical model for the bias of dark matter halos that applies to objects defined by an arbitrary density threshold, 200 ≤ δ∗ ≤ 1600, and that provides accurate predictions from low-mass to high-mass halos.
Methods. We point out that it is possible to build simple and efficient models, with no free parameter for the halo bias, by using integral constraints that govern the behavior of low-mass and typical halos, whereas the properties of rare massive halos are derived through explicit asymptotic approaches. We also describe how to take into account the impact of halo motions on their bias, using their linear displacement field.
Results. We obtain a good agreement with numerical simulations for the halo mass functions and large-scale bias at redshifts 0 ≤ z ≤ 2.5, for halos defined by a nonlinear density threshold 200 ≤ δ∗ ≤ 1600. We also evaluate the impact on the halo bias of two common approximations, i) neglecting halo motions, and ii) linearizing the halo two-point correlation.
Key words: large-scale structure of Universe / gravitation / methods: analytical
© ESO, 2010
1. Introduction
A fundamental test of cosmological models is provided by the distribution of nonlinear virialized objects, such as galaxies or clusters of galaxies. First, this allows to check that nonlinear objects form through the amplification by gravitational instability of small (nearly Gaussian) primordial density fluctuations (Peebles 1980). Second, quantitative comparisons between theoretical predictions and observations allow to derive constraints on cosmological parameters (Zheng & Weinberg 2007). Indeed, observations show that galaxies and clusters do not follow a Poisson distribution but show significant large-scale correlations (e.g., McCracken et al. 2008; Padilla et al. 2004). In particular, at large scales their two-point correlation function is roughly proportional to the underlying matter correlation, with a multiplicative factor b2, called the bias, that is greater for more massive objects.
Following the spirit of the Press-Schechter picture (Press & Schechter 1974), where nonlinear virialized objects are identified with high-density fluctuations in the initial (linear) density field, Kaiser (1984) showed how such a behavior for the halo correlation naturally arises. Similar results are obtained for the clustering of density peaks instead of overdensities above a given threshold (Bardeen et al. 1986). Indeed, distant high-density regions are correlated through their common longwavelength modes of the linear density field, and the effect is greater for more massive and extreme objects. A somewhat simpler derivation can be obtained through the peak-background split argument (Cole & Kaiser 1989; Bond et al. 1991). This rests on the same physics, which is that within a large region characterized by a positive mean density contrast local density peaks beyond a given density threshold are more frequent than in the mean, which yields a positive correlation between rare massive halos and the larger-scale matter density field.
Along these lines, a simple analytical model that compares reasonably well with numerical simulations was presented by Mo & White (1996), while a better agreement was obtained by Sheth & Tormen (1999), at the cost of adding a few parameters fitted to the simulations (through the halo mass function). More complex models, that also apply to redshift space and take into account subleading scale-dependent terms can be found for instance in Desjacques (2008); Desjacques & Sheth (2010). On the other hand, various fitting formulas have been proposed from measures in numerical simulations (Hamana et al. 2001; Pillepich et al. 2010; Tinker et al. 2010; Manera et al. 2010). In particular, Tinker et al. (2010) have recently studied the dependence of the halo bias on the density contrast δ∗ used to define the halos. In the paper we present a simple analytical model for the halo bias that extends a previous work (Valageas 2009) to arbitrary density thresholds in the range 200 ≤ δ∗ ≤ 1600. This is of practical interest as the definition of halos can vary among authors, and it can happen that observations only extend to smaller radii than the usual virial radius, which corresponds to objects defined by higher density thresholds. In addition, we also improve on Valageas (2009) by simplifying somewhat the model, especially the treatment of halo motions, while obtaining a better accuracy for low-mass halos. This should allow an easier generalization to more complex cases, such as non-Gaussian initial conditions. This simple model also allows us to evaluate the inaccuracies implied by two approximations that are frequently used, that is, neglecting halo motions and linearizing the halo correlation function over the matter correlation function.
In Sect. 2 we describe our model for the bias of halos defined by a nonlinear density contrast δ∗ = 200. We explain how the standard model of Kaiser (1984) for the correlation of rare massive halos is modified once we take into account the motion of halos. Then, we point out that normalization conditions can be very useful to constrain the bias of intermediate and low mass halos, which allows to build a simple and efficient model. Next, we show that we obtain a good agreement with numerical simulations. In Sect. 3 we extend this model for the bias, as well as for the halo mass function, to the case of halos defined by a larger nonlinear density contrast, and we compare our results with numerical simulations for 200 ≤ δ∗ ≤ 1600. Finally, we estimate the importance of halo motions and of the nonlinearity of the bias in Sects. 4 and 5, and we conclude in Sect. 6.
2. Bias of dark matter halos
Following Kaiser (1984) we estimate the two-point correlation function of dark matter halos, whence their bias, from the probability to reach a linear density threshold δL ∗ (associated with the formation of virialized halos of nonlinear density contrast δ∗). As in Valageas (2009), we improve this model by taking into account the motion of halos, associated with the change from Lagrangian to Eulerian space (i.e., from the linear density field to the actual nonlinear density field). However, we simplify the prescription used in Valageas (2009) as we no longer use a spherical collapse model to estimate these displacements but use the initial momenta of both halos (i.e., the linear displacement field). In addition, we add a further ingredient to the study of Valageas (2009), as we explicitly enforce the normalization to unity of the halo bias (when integrated over all halo masses). We describe below this simple model.
2.1. Lagrangian space
We first consider the two-point correlation function of halos in Lagrangian space, that
is within the linear density field
δL(q), where we identify
future halos of Eulerian radius r and nonlinear density contrast
δ∗ (with typically δ∗ ~ 200)
with spherical regions of Lagrangian radius q and linear density contrast
δL ∗ . Thanks to the conservation of mass, the Lagrangian
and Eulerian properties of halos of mass M are related by  (1)where
(1)where
 is the mean
matter density. As pointed out in Valageas (2009),
the function ℱ describes the spherical collapse dynamics, so that in a ΛCDM cosmology with
Ωm = 0.27, ΩΛ = 0.73, we have
δL ∗ ≃ 1.59 at z = 0 for
δ∗ = 200, instead of the usual value
δc ≃ 1.675 associated with full collapse to a point, that is
with δ∗ = ∞.
is the mean
matter density. As pointed out in Valageas (2009),
the function ℱ describes the spherical collapse dynamics, so that in a ΛCDM cosmology with
Ωm = 0.27, ΩΛ = 0.73, we have
δL ∗ ≃ 1.59 at z = 0 for
δ∗ = 200, instead of the usual value
δc ≃ 1.675 associated with full collapse to a point, that is
with δ∗ = ∞.
Defining halos by the linear threshold δL ∗ = ℱ-1(δ∗), rather than by the full collapse value δc, is closer to observational and numerical procedures, since (in the best cases) one defines “halos” in galaxy or cluster surveys, and in numerical simulations, by the radius and mass of overdensities within a given nonlinear density threshold δ∗. Moreover, this gives the freedom to chose different thresholds, such as δ∗ = 200 or 100 (Valageas 2009). As discussed in Sect. 3 in Valageas (2009), for massive (M ~ 1015 h-1M⊙) and rare halos, the choice δ∗ = 200 also roughly corresponds to the separation between outer shells, dominated by radial accretion, and inner shells, with a significant transverse velocity dispersion, that have experienced shell crossing. The case of typical halos (i.e. below the knee of the halo mass function) is more intricate as they do not show such a clear separation. This can also be seen in numerical simulations, such as Fig. 3 in Cuesta et al. (2008). At high redshift, where nonlinear objects have a smaller mass, this “virialization” radius shifts to higher density contrasts for ΛCDM cosmologies, because of the change of slope of the linear matter power spectrum with scale (e.g., δ∗ ~ 500 for M ~ 1011 h-1M⊙, as seen in Fig. 5 in Valageas 2009).
Then, defining the halo correlation as the fractional excess of halo pairs (Kaiser 1984; Peebles
1980), we write in Lagrangian space ![\begin{eqnarray} \nb_{\rm L}(M_1,M_2;\vs_1,\vs_2) \dd M_1 \dd M_2 \dd \vs_1 \dd \vs_2 & = & \nonumber \\ \label{xiL-def}&& \hspace{-4cm} \nb_{\rm L}(M_1) \nb_{\rm L}(M_2) [ 1 + \xi_{\rm L}(M_1,M_2;s) ] \dd M_1 \dd M_2 \dd \vs_1 \dd \vs_2 . \end{eqnarray}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq29.png) (2)Here
and in the following we use the letter s for the position of
halos in Lagrangian space to avoid confusion with their Lagrangian radius
q, and we introduced the Lagrangian distance,
s = |s2 − s1| ,
between both objects. We also note with a subscript L the quantities
associated with the linear fields or the Lagrangian space. Then, following Kaiser (1984) and Valageas (2009), we obtain the fractional excess of halo pairs from the
bivariate density distribution
(2)Here
and in the following we use the letter s for the position of
halos in Lagrangian space to avoid confusion with their Lagrangian radius
q, and we introduced the Lagrangian distance,
s = |s2 − s1| ,
between both objects. We also note with a subscript L the quantities
associated with the linear fields or the Lagrangian space. Then, following Kaiser (1984) and Valageas (2009), we obtain the fractional excess of halo pairs from the
bivariate density distribution  over the two spheres of radii q1 and
q2,
over the two spheres of radii q1 and
q2,  where
we considered a single population, that is halos defined by the same density thresholds
δL ∗ and
δ∗ = ℱ(δL ∗ ). Here we assumed
Gaussian initial conditions and we introduced the cross-correlation of the smoothed linear
density contrast at scales q1 and
q2, at positions s1
and s2,
where
we considered a single population, that is halos defined by the same density thresholds
δL ∗ and
δ∗ = ℱ(δL ∗ ). Here we assumed
Gaussian initial conditions and we introduced the cross-correlation of the smoothed linear
density contrast at scales q1 and
q2, at positions s1
and s2,  (5)where
(5)where
 is the Fourier transform of
the top-hat window of radius q,
is the Fourier transform of
the top-hat window of radius q,  (6)and
PL(k) is the linear matter power spectrum,
defined by
(6)and
PL(k) is the linear matter power spectrum,
defined by  (7)
(7) (8)In particular,
σq = σq,q(0)
is the usual rms linear density contrast at scale q. In Eq. (4) we also used the short-hand notation
(8)In particular,
σq = σq,q(0)
is the usual rms linear density contrast at scale q. In Eq. (4) we also used the short-hand notation
 ,
,
 , and
, and
 , for the covariances over the
two spherical Lagrangian regions.
, for the covariances over the
two spherical Lagrangian regions.
Of course, the prescription (4) only applies to the limit of rare events (i.e., large mass M) and large separations, where halos are isolated and almost spherical, so that we can neglect tidal effects as well as violent processes such as mergings. We shall come back to this point in Sect. 2.3 below. The Eq. (4) expresses the fact that if we have a rare overdensity at position s1 the probability to have a second overdensity at a nearby position s2 is amplified, with respect to random locations, because of common longwavelength modes.
2.2. Eulerian space
We must now convert the expression (4) into a model for the halo correlation in Eulerian space, that is within the actual nonlinear density field. Indeed, even halos that have not been destroyed or strongly modified by merging events have had time to move since the early times associated with the linear density field (which formally corresponds to z → ∞). In particular, the particles they are made of have moved even before the formation of the final halo. This leads to two effects with respect to the halo correlation: i) the Eulerian-space distance x between the two halos is not identical to the Lagrangian-space distance s, ii) the halo number densities are modified because the Lagrangian-Eulerian mapping modifies local volumes (i.e., dx ≠ ds). These effects were estimated in Valageas (2009) from a spherical collapse model. Here we present a simpler method, which has the advantage of being more flexible and more closely related to the estimate (4), based on the linear density field. Moreover, it avoids the need to use a spherical dynamics approximation. As a further simplification, we also neglect the second effect ii), due to the change of volume between Eulerian and Lagrangian spaces, because it is a subdominant prefactor.
Thus, we simply estimate the displacement
Ψ(M,s) of a
halo of mass M and Lagrangian position s
from the linear displacement field (see also Desjacques
2008, for a somewhat different implementation in the case of density peaks). This
gives for the Eulerian position of its center of mass,  (9)with
(9)with  (10)This coincides with the
use of the Zeldovich approximation (Zeldovich 1970)
for the dynamics of the particles that make up the halo of mass M.
However, since the halo scale q introduces a natural cutoff at high
k (through the factor
(10)This coincides with the
use of the Zeldovich approximation (Zeldovich 1970)
for the dynamics of the particles that make up the halo of mass M.
However, since the halo scale q introduces a natural cutoff at high
k (through the factor  ), which for large masses
and rare events is within the linear regime, the approximation (9) should fare much better than what could be
expected from an analysis of the Zeldovich dynamics for individual particle trajectories.
For instance, the “truncated Zeldovich approximation”, where one suppresses the initial
power at high k, provides a good description of large-scale clustering
and yields a significant improvement over the unsmoothed Zeldovich approximation (Coles et al. 1993; Melott et al. 1994). Physically, this means that small-scale nonlinear processes
such as virialization within bound objects conserve momentum and do not affect the
large-scale properties of the system.
), which for large masses
and rare events is within the linear regime, the approximation (9) should fare much better than what could be
expected from an analysis of the Zeldovich dynamics for individual particle trajectories.
For instance, the “truncated Zeldovich approximation”, where one suppresses the initial
power at high k, provides a good description of large-scale clustering
and yields a significant improvement over the unsmoothed Zeldovich approximation (Coles et al. 1993; Melott et al. 1994). Physically, this means that small-scale nonlinear processes
such as virialization within bound objects conserve momentum and do not affect the
large-scale properties of the system.
Then, for Gaussian initial conditions we can obtain the trivariate probability
distribution  ,
where Ψ12 ∥ is the linear relative displacement of the halos along their
Lagrangian separation vector,
,
where Ψ12 ∥ is the linear relative displacement of the halos along their
Lagrangian separation vector, ![\begin{equation} \Psi_{L12\parallel} = \frac{[\vPsi_{\rm L}(M_2,\vs_2)-\vPsi_{\rm L}(M_1,\vs_1)]\cdot (\vs_2-\vs_1)}{|\vs_2-\vs_1|} \cdot \label{Psi12-def} \end{equation}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq61.png) (11)In particular, the mean
conditional relative displacement, at fixed linear density contrasts
δL1 and δL2 within the two
spheres of radii q1 and q2, reads
as
(11)In particular, the mean
conditional relative displacement, at fixed linear density contrasts
δL1 and δL2 within the two
spheres of radii q1 and q2, reads
as  (12)where we introduced the
covariance
(12)where we introduced the
covariance  (13)which writes as
(13)which writes as
 (14)with
(14)with
 (15)where again
s = |s2 − s1| .
We introduced a minus sign in the definition (13) to avoid a minus sign in Eqs. (14)–(15). Although
(15)where again
s = |s2 − s1| .
We introduced a minus sign in the definition (13) to avoid a minus sign in Eqs. (14)–(15). Although
 is not
guaranteed to be always positive, it is usually positive, which expresses through (13) that in the mean two rare overdensities
tend to move closer, as could be expected through their mutual gravitational attraction.
By symmetry, the mean conditional relative displacement along the orthogonal directions
vanishes,
⟨ ΨL12 ⊥ ⟩ δL1,δL2 = 0.
Then, at lowest order the mean Eulerian-space distance x between both
halos reads as
is not
guaranteed to be always positive, it is usually positive, which expresses through (13) that in the mean two rare overdensities
tend to move closer, as could be expected through their mutual gravitational attraction.
By symmetry, the mean conditional relative displacement along the orthogonal directions
vanishes,
⟨ ΨL12 ⊥ ⟩ δL1,δL2 = 0.
Then, at lowest order the mean Eulerian-space distance x between both
halos reads as  (16)where we considered a
single population defined by the same density threshold δL ∗ .
Neglecting the width of the distribution
(16)where we considered a
single population defined by the same density threshold δL ∗ .
Neglecting the width of the distribution  ,
whence of
,
whence of  ,
and in the limit of large separation, s → ∞, where
,
and in the limit of large separation, s → ∞, where
 , we can
invert Eq. (16) as
, we can
invert Eq. (16) as ![\begin{equation} s(M_1,M_2;x) \simeq x \left[ 1 + \frac{\deltaLs}{3} \frac{\sigma^2_{q_1,q_2,x}(\sigma^2_1+\sigma^2_2-2\sigma^2_{12})} {\sigma_1^2\sigma_2^2-\sigma_{12}^4} \right] , \label{s-x} \end{equation}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq75.png) (17)where
(17)where
 is also
evaluated at distance x.
is also
evaluated at distance x.
It is interesting to note that the expression (17) is very close to the one obtained in Valageas (2009) from a spherical collapse model. The main difference is that
this new result involves the quantity  defined in
Eq. (15), which contains the three
windows
defined in
Eq. (15), which contains the three
windows  , and
, and
 , whereas the former result
only involved quantities such as
, whereas the former result
only involved quantities such as 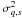 and
and
 that only contain two windows.
The reason is that the model used in Valageas
(2009) treated each halo as a test particle within the spherical gravitational
field built by the other halo, whereas in the derivation of Eq. (17) above we did not need to make this
approximation and we simultaneously take into account the effect of both halos on the
initial gravitational field. Nevertheless, it is reassuring that both models give similar
results, as could be expected from qualitative arguments (for rare and well-separated
halos).
that only contain two windows.
The reason is that the model used in Valageas
(2009) treated each halo as a test particle within the spherical gravitational
field built by the other halo, whereas in the derivation of Eq. (17) above we did not need to make this
approximation and we simultaneously take into account the effect of both halos on the
initial gravitational field. Nevertheless, it is reassuring that both models give similar
results, as could be expected from qualitative arguments (for rare and well-separated
halos).
Equation (17) gives the “typical”
Lagrangian-space distance s between two halos that are observed in the
nonlinear density field at the Eulerian distance x. This takes care of
the first effect i) associated with halo motions. As noticed above, the second effect ii)
of halo displacements is to change volumes so that
dx ≠ ds. Then, by
conservation of the number of pairs, the Lagrangian-space and Eulerian-space correlations
at distances s and x are
related by ![\begin{equation} [1+\xi(M_1,M_2;x)] \dd\vx = [1+\xi_{\rm L}(M_1,M_2;s)] \dd\vs , \end{equation}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq82.png) (18)and we could use
again Eqs. (9) and (17) to estimate the factor
|ds/dx| .
However, for rare massive halos, of Lagrangian radius q, this is a
subdominant effect, since from Eq. (17) we
have
(18)and we could use
again Eqs. (9) and (17) to estimate the factor
|ds/dx| .
However, for rare massive halos, of Lagrangian radius q, this is a
subdominant effect, since from Eq. (17) we
have  , whereas
the argument of the exponential (4) behaves
as
, whereas
the argument of the exponential (4) behaves
as  . Thus, the
latter is larger than the former by a factor
. Thus, the
latter is larger than the former by a factor  , which is
much greater than unity (and this is further amplified for very rare halos by the
exponential). Therefore, to avoid introducing unnecessary approximations and to make the
model as simple as possible, we neglect this volume effect and we only keep the
exponential behavior of the two-point correlation of rare halos. This gives for equal-mass
halos, with
M1 = M2 = M and
q1 = q2 = q,
, which is
much greater than unity (and this is further amplified for very rare halos by the
exponential). Therefore, to avoid introducing unnecessary approximations and to make the
model as simple as possible, we neglect this volume effect and we only keep the
exponential behavior of the two-point correlation of rare halos. This gives for equal-mass
halos, with
M1 = M2 = M and
q1 = q2 = q,
![\begin{equation} 1+\xi(M,x) \simeq e^{\deltaLs^2 \sigma^2_{q,q}(s)/ [\sigma^2_q(\sigma^2_q+\sigma^2_{q,q}(s))]} , \label{xi-M} \end{equation}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq89.png) (19)whereas the Lagrangian
distance reads from Eq. (17) as
(19)whereas the Lagrangian
distance reads from Eq. (17) as
 (20)Then, since at large
distance the dark matter two-point correlation function is within the linear regime and
reads as
(20)Then, since at large
distance the dark matter two-point correlation function is within the linear regime and
reads as  , we obtain for the bias of
halos of mass M,
, we obtain for the bias of
halos of mass M, ![\begin{eqnarray} b^2_{\rm r.e.}(M,x) & = & \frac{\xi(M,x)}{\xi(x)} \\ \label{b2-def}& = & \frac{1}{\sigma^2_{0,0}(x)} \left[ e^{\deltaLs^2 \sigma^2_{q,q}(s)/ [\sigma^2_q(\sigma^2_q+\sigma^2_{q,q}(s))]} -1 \right] . \end{eqnarray}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq92.png) Here
the subscript “r.e.” stands for the “rare-event” limit to recall that the results obtained
so far have been derived for very massive and rare halos, and do not apply to small
objects.
Here
the subscript “r.e.” stands for the “rare-event” limit to recall that the results obtained
so far have been derived for very massive and rare halos, and do not apply to small
objects.
2.3. Normalization
It is very difficult to derive an approximate model for the bias, and even the mass
function, of small halos. Indeed, such objects associated with typical density
fluctuations have been strongly distorted by tidal effects and have often undergone
various merging events. Then, it is not possible to identify in a simple manner the
precursors of these halos in the initial linear density field. In this article we propose
the following simple prescription to bypass this problem: we add to the asymptotic
result (22) a constant term with respect
to the halo mass, b0(x), which we obtain from
the normalization of the bias. More precisely, making the approximation that the bias
factorizes (which however is not exact, even in the large-mass regime, see Eq. (22) and Fig. 12 in Valageas (2009)), as  (23)we model the bias
b(M,x) as
(23)we model the bias
b(M,x) as  (24)Here
br.e.(M,x)
is given by Eq. (22) (taking the
square-root of this positive quantity), while
b0(x) is set by the normalization (at fixed
distance x)
(24)Here
br.e.(M,x)
is given by Eq. (22) (taking the
square-root of this positive quantity), while
b0(x) is set by the normalization (at fixed
distance x)  (25)whence
(25)whence
 (26)where we used
(26)where we used
 (27)Here we introduced the
scaled mass function of dark matter halos, that is, we write the halo mass function as
(27)Here we introduced the
scaled mass function of dark matter halos, that is, we write the halo mass function as
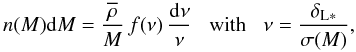 (28)where
δL ∗ is the linear density threshold that defines these
halos, given by Eq. (1), and
σ(M) = σq.
The well-know constraints (27) and (25) follow from the requirement that all the
mass is accounted for by the mass function of halos (whatever the choice of
δL ∗ ), which leads to Eq. (27), so that the density field on large scales (beyond the size of
these halos) can be written in terms of the halo mass function, as in the usual halo model
(Cooray & Sheth 2002) (the so-called
“two-halo term”). Then, requiring that one recovers the dark matter two-point correlation
function leads to the constraint (25),
provided the bias can be factorized as (23) (otherwise the constraint involves a bidimensional integral over
b2(M1,M2)).
(28)where
δL ∗ is the linear density threshold that defines these
halos, given by Eq. (1), and
σ(M) = σq.
The well-know constraints (27) and (25) follow from the requirement that all the
mass is accounted for by the mass function of halos (whatever the choice of
δL ∗ ), which leads to Eq. (27), so that the density field on large scales (beyond the size of
these halos) can be written in terms of the halo mass function, as in the usual halo model
(Cooray & Sheth 2002) (the so-called
“two-halo term”). Then, requiring that one recovers the dark matter two-point correlation
function leads to the constraint (25),
provided the bias can be factorized as (23) (otherwise the constraint involves a bidimensional integral over
b2(M1,M2)).
We do not claim here that the halo bias has a nonzero asymptote at low mass. In fact, the asymptotic behavior of the low-mass tail of the bias (and of the mass function itself) is largely unknown, but numerical simulations show that the dependence on mass flattens below ν ~ 1 and seems roughly constant down to ν ~ 0.3. Then, the prescription (24) is intended to describe both this behavior (since from expression (22) we can see that br.e.(M) → 0 for M → 0, or more precisely when σq → ∞) and the constraint (25). Indeed, if the asymptotic behavior (22) provides a good description for ν > 1 we can expect the constraint (25) to provide a good estimate for the (almost constant) value of b(M) in the regime ν < 1. Moreover, it is always useful to make sure normalization constraints such as (25) are satisfied by the models. Indeed, this ensures that the models are self-consistent and that absurd results will not be produced by the violation of basic internal constraints.
Another advantage of this simple prescription is that our model (24) of the halo bias has no specific free parameter, apart from those already contained in the halo mass function (especially its low-mass tail). This is why we prefer to keep a simple constant term b0, instead of introducing for instance higher-order polynomials (over ν or M) that would require some fitting over numerical simulations. This provides a greater flexibility to the model, which can be used for a variety of cosmologies.
 |
Fig. 1 The halo bias b(M,x) as a function of σ(M), at distance x = 50 h-1Mpc, for halos defined by the nonlinear density contrast δ∗ = 200. We plot our results at redshifts z = 0 (left panel), z = 1.25 (middle panel), and z = 2.5 (right panel). The black solid line, “δL ∗ ”, is the theoretical prediction (24), the red dashed line, “s = x”, corresponds to the approximation where halo motions are neglected, and the green dot-dashed line, “δc”, corresponds to the use of δc = 1.686 instead of δL ∗ . The blue dashed line, “SMT”, is the fit from Sheth et al. (2001), and the points are the results from numerical simulations of Tinker et al. (2010). |
Finally, for numerical computations we use the mass function given in Valageas (2009), ![\begin{equation} f(\nu) = 0.502 \left[ (0.6 \,\nu)^{2.5} + (0.62 \, \nu)^{0.5} \right] \, e^{-\nu^2/2} , \label{fnu-fit} \end{equation}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq120.png) (29)which has been shown to
agree with numerical simulations (for halos defined by
δ∗ = 200). The exponential falloff,
e−ν2/2,
where ν is defined by Eqs. (28) and (1), is consistent with
the exponential term of Eq. (4). Indeed,
both the 1-point distribution (i.e. the mass function) and the 2-point distribution (i.e.
the halo correlation or bias) are obtained in the large-mass limit from spherical
overdensities δL ∗ in the linear density field, with
δL ∗ = ℱ-1(δ∗) and
δ∗ = 200. Note also that the normalization of the mass
function (29) is not a free parameter
since it is set by the constraint (27).
This is why we prefer to use the mass function (29), so that the model is fully self-consistent and large-mass tails do not
involve free parameters.
(29)which has been shown to
agree with numerical simulations (for halos defined by
δ∗ = 200). The exponential falloff,
e−ν2/2,
where ν is defined by Eqs. (28) and (1), is consistent with
the exponential term of Eq. (4). Indeed,
both the 1-point distribution (i.e. the mass function) and the 2-point distribution (i.e.
the halo correlation or bias) are obtained in the large-mass limit from spherical
overdensities δL ∗ in the linear density field, with
δL ∗ = ℱ-1(δ∗) and
δ∗ = 200. Note also that the normalization of the mass
function (29) is not a free parameter
since it is set by the constraint (27).
This is why we prefer to use the mass function (29), so that the model is fully self-consistent and large-mass tails do not
involve free parameters.
In particular, following Cole & Kaiser
(1989), applying the peak-background split argument to Eq. (29) gives
 , in the
rare-event and large-distance limits. This agrees with the asymptotic behavior of
Eq. (22), except that Eq. (22) also yields the prefactor
σq,q(s)/σ0,0(x),
which is different from unity. This expresses the facts that i) contributions to the
correlation of objects of size q are damped for high wavenumbers,
k ≫ 1/q, and ii) halo motions are
nonzero and correlated, s ≠ x. Of course, these two
effects are neglected by the peak-background split argument.
, in the
rare-event and large-distance limits. This agrees with the asymptotic behavior of
Eq. (22), except that Eq. (22) also yields the prefactor
σq,q(s)/σ0,0(x),
which is different from unity. This expresses the facts that i) contributions to the
correlation of objects of size q are damped for high wavenumbers,
k ≫ 1/q, and ii) halo motions are
nonzero and correlated, s ≠ x. Of course, these two
effects are neglected by the peak-background split argument.
2.4. Comparison with numerical simulations
We now compare the model defined by Eqs. (20), (22), (24), and (26), with results from numerical simulations. We first consider in Fig. 1 the dependence on halo mass M of the large-scale bias, for halos defined by the nonlinear density contrast δ∗ = 200 (whence δL ∗ ≃ 1.59) at distance x = 50 h-1Mpc. We show our results at redshifts z = 0,1.25, and 2.5. We can see that we obtain a good agreement with the numerical simulations of Tinker et al. (2010). This was expected at high masses, where the arguments based on the clustering of rare overdensities in the linear Gaussian density field apply (as introduced by Kaiser 1984, and implemented in a slightly modified variant here). An improvement over previous models of this kind (Kaiser 1984; Valageas 2009) is the good agreement at low mass, which is obtained through the constant term b0 in Eq. (24), associated with the normalization of the halo bias through Eq. (26). Thus, it appears that this constraint is sufficient to obtain a good description of the halo bias over the whole range σ(M) < 10. Indeed, as explained in Sect. 2.3, since the model is reasonably successful at large mass, σ < 1, the integral constraint (25) ensures that the value of the bias over the range 1 < σ < 10, which contains the other half of the total matter content, has the correct magnitude, although the detailed shape has no reason to be exact a priori. In particular, at low masses, σ > 10, which represent a small fraction of the total matter density field and do not significantly contribute to the integral (25), the normalization (25) becomes largely irrelevant (since large changes of b(M) would not significantly change the overall normalization) so that there is no reason a priori to trust our model. Thus, it may happen that at very low masses the bias goes to zero, for instance as a power law over M. However, this is beyond the reach of current numerical simulations and it is not a serious practical problem, for the same reason that this only concerns a small fraction of the matter content and of the halo population.
As is well known, the dependence on redshift, at fixed σ(M), is quite weak over the range 0 ≤ z ≤ 2.5. There appears to be a slight growth of the bias at larger redshift, in the regime of rare halos (σ(M) < 0.5). This is most clearly seen by the comparison with the dashed line associated with the fit from Sheth et al. (2001), which is independent of z and is identical in the three panels. This small growth is also reproduced by our model (24), as shown by the solid line. This confirms the validity of this approach, and more generally of such models that follow Kaiser (1984). However, for practical purposes it is probably sufficient to neglect the dependence on redshift in this range.
It is interesting to note that the bias obtained from Eq. (8) of Sheth et al. (2001) behaves at large masses as
 , with a parameter
a ≃ 0.707 obtained from fits to the halo mass function (through the
peak-background split argument), whereas we have noticed in Sect. 2.3 that Eq. (22) yields
, with a parameter
a ≃ 0.707 obtained from fits to the halo mass function (through the
peak-background split argument), whereas we have noticed in Sect. 2.3 that Eq. (22) yields
 . In order to explain why both
predictions are rather close (especially at z = 0 in Fig. 1) despite these different forms, and without introducing
such a parameter a in Eq. (22), we have also plotted the curves obtained by setting
s = x (i.e. neglecting halo motions) or
δL ∗ = δc, with the usual value
δc = 1.686. We can see that the change from
δc to δL ∗ makes almost no
difference for the halo bias (for δ∗ = 200), while taking
into account halo motions leads to a significant reduction at z = 0 for
massive halos. Indeed, since rare halos tend to move closer, neglecting halo motions
underestimates their initial distance and overestimates their correlation. This effect is
greater at lower redshift, associated with more massive objects, and leads to a bias that
happens to be very close to the prediction from Sheth
et al. (2001) at z = 0.
. In order to explain why both
predictions are rather close (especially at z = 0 in Fig. 1) despite these different forms, and without introducing
such a parameter a in Eq. (22), we have also plotted the curves obtained by setting
s = x (i.e. neglecting halo motions) or
δL ∗ = δc, with the usual value
δc = 1.686. We can see that the change from
δc to δL ∗ makes almost no
difference for the halo bias (for δ∗ = 200), while taking
into account halo motions leads to a significant reduction at z = 0 for
massive halos. Indeed, since rare halos tend to move closer, neglecting halo motions
underestimates their initial distance and overestimates their correlation. This effect is
greater at lower redshift, associated with more massive objects, and leads to a bias that
happens to be very close to the prediction from Sheth
et al. (2001) at z = 0.
Thus, taking into account halo motions has the same effect (i.e. reducing the bias at low z) as the parameter a of Sheth et al. (2001). Within the peak-background split approach, the latter is not a new free parameter for the bias, since it is set by the halo mass function itself. However, within our approach, we do not need to introduce such a parameter, neither for the halo mass function (29) nor for the bias (22). We can note that the very weak dependence on redshift of the halo bias, in the range 0 ≤ z ≤ 2.5, is somewhat misleading, since within this model it arises from the partial cancellation between two opposite trends (as the “s = x” curve decreases at higher z while the full prediction grows to get closer to it).
 |
Fig. 2 The mean bias |
In Fig. 1 we have considered the bias at the
distance x = 50 h-1Mpc, which is the
typical distance where the large-scale halo bias is measured in numerical simulations,
with box sizes of order 500 h-1Mpc (Tinker et al. 2010). The bias measured in such simulations is almost
scale-independent over the range
20 < x < 110 h-1Mpc,
as seen for instance in Fig. 10 of Manera et al.
(2010) and Fig. 17 of Manera & Gaztanaga
(2010). This agrees with the standard large-scale behavior
 . In our
model, there is an additional prefactor
σq,q(s)/σ0,0(x),
due to halo motions and to the fact that high wavenumbers do not contribute to halo
correlations. Therefore, we show in Fig. 2 the
dependence on scale of the bias
. In our
model, there is an additional prefactor
σq,q(s)/σ0,0(x),
due to halo motions and to the fact that high wavenumbers do not contribute to halo
correlations. Therefore, we show in Fig. 2 the
dependence on scale of the bias  , at z = 0 for
five mass bins
[M1,M2] ,
defined as
, at z = 0 for
five mass bins
[M1,M2] ,
defined as  (30)We can check that we
obtain a weak dependence on scale over the range
20 < x < 100 h-1Mpc
(and we obtain similar results at higher redshift). At smaller scales, the upturn for the
bias of the most massive halos (upper dotted curve) is due to the fact that the argument
of the exponential in Eq. (22) becomes
large so that the linear approximation is no longer valid. We shall come back to this
point in Sect. 5 below. At even smaller scales, of
the order of the radius of the halos, exclusion constraints that we have not taken into
account come into play and imply a halo correlation equal to −1. It is clear that our
model only applies to the larger scales, shown in Fig. 2, where halos are well separated.
(30)We can check that we
obtain a weak dependence on scale over the range
20 < x < 100 h-1Mpc
(and we obtain similar results at higher redshift). At smaller scales, the upturn for the
bias of the most massive halos (upper dotted curve) is due to the fact that the argument
of the exponential in Eq. (22) becomes
large so that the linear approximation is no longer valid. We shall come back to this
point in Sect. 5 below. At even smaller scales, of
the order of the radius of the halos, exclusion constraints that we have not taken into
account come into play and imply a halo correlation equal to −1. It is clear that our
model only applies to the larger scales, shown in Fig. 2, where halos are well separated.
At larger scales, the bias is difficult to measure (because the two-point correlation
functions are quite small) and actually becomes meaningless. Indeed, as pointed out in
Valageas (2010) for more general initial
conditions, and in previous studies where halos are identified with density peaks (Coles 1989; Lumsden
et al. 1989; Desjacques 2008), since the
halo correlation is not exactly proportional to the matter correlation (because of the
smoothing at scale q in 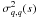 , of halo motions, and of
subleading terms) their zero-crossings do not exactly coincide. This implies that the
ratio
b2 = ξ(M,x)/ξ(x)
shows wild oscillations and divergent peaks at the scale where the matter two-point
correlation changes sign (typically at
x ~ 120 h-1Mpc). Therefore, at very large
scales,
x > 100 h-1Mpc, it
is no longer useful to introduce the ratio b2, and it is best
to work with the halo and matter correlations themselves (note that this conclusion is
quite general and not specific to the model studied here).
, of halo motions, and of
subleading terms) their zero-crossings do not exactly coincide. This implies that the
ratio
b2 = ξ(M,x)/ξ(x)
shows wild oscillations and divergent peaks at the scale where the matter two-point
correlation changes sign (typically at
x ~ 120 h-1Mpc). Therefore, at very large
scales,
x > 100 h-1Mpc, it
is no longer useful to introduce the ratio b2, and it is best
to work with the halo and matter correlations themselves (note that this conclusion is
quite general and not specific to the model studied here).
3. Extension to higher density contrasts
The results obtained in Sect. 2 applied to halos defined by a nonlinear density contrast δ∗ such that δ∗ ≲ 200, so that the large-mass tails could be derived from the spherical collapse dynamics associated with Eq. (1) (and we focused on the case δ∗ = 200, which is of practical interest). As pointed out in Valageas (2009), for larger density contrasts shell crossing plays a key role and even in the rare-event or large-mass limit Eq. (1) no longer applies. Indeed, as discussed in Valageas (2002), because of a strong radial-orbit instability spherical dynamics is no longer a useful guide. More precisely, the properties of the density field in such high-density regions are no longer governed by initial configurations that are spherically symmetric (whence with purely radial motions) and one must take into account (infinitesimally) small deviations from spherical symmetry, that are amplified in a non-perturbative manner after collapse. This is a significant difficulty for precise and robust modeling of halos defined by high density thresholds. Therefore, we investigate in this paper a very simple model that tries to bypass this problem by relating inner high-density shells to outer lower-density radii.
As we have seen in Sect. 2, in order to obtain a reasonably successful model for the distribution (i.e., the bias) of dark matter halos, defined by δ∗ = 200, it is sufficient to derive the large-mass tail, following the standard ideas of Kaiser (1984) where rare nonlinear objects are identified in the initial (linear) density field. Then, normalization conditions constrain the bias of typical halos (σ(M) ≳ 1) and automatically provide reasonable estimates in this range. The advantage of this procedure is to bypass a detailed treatment of typical or low-mass halos, which would require taking into account tidal effects and mergings (but see Blanchard et al. 1992).
In this spirit, in order to extend our model to higher density thresholds
δ∗, we only need to explicitly consider rare massive halos.
Then, since these halos are isolated and relaxed objects, we assume that they can be
described by a mean mass profile
M(< r), with a mean density
within radius r that behaves as  (31)where
M(<r) is the mass enclosed
within radius r. Here we could have used a more detailed density profile,
such as the usual NFW profile (Navarro et al. 1997),
as described in Hu & Kravtsov (2003).
However, this would also introduce a further dependence on mass and redshift through the
concentration parameter c(M,z) that parametrizes such
profiles. Therefore, in view of the approximations involved in our approach we think that
such refinements are beyond the scope of this study and we prefer to use a single power-law
index α. This should be sufficient as long as we do not consider too wide a
range of contrasts δ∗, over which the slope of the density
profile shows significant changes. Then, from Eq. (31) we can relate the mass
Mδ∗, enclosed with the radius
defined by the nonlinear density contrast δ∗, to
M200, associated with δ∗ = 200,
by
(31)where
M(<r) is the mass enclosed
within radius r. Here we could have used a more detailed density profile,
such as the usual NFW profile (Navarro et al. 1997),
as described in Hu & Kravtsov (2003).
However, this would also introduce a further dependence on mass and redshift through the
concentration parameter c(M,z) that parametrizes such
profiles. Therefore, in view of the approximations involved in our approach we think that
such refinements are beyond the scope of this study and we prefer to use a single power-law
index α. This should be sufficient as long as we do not consider too wide a
range of contrasts δ∗, over which the slope of the density
profile shows significant changes. Then, from Eq. (31) we can relate the mass
Mδ∗, enclosed with the radius
defined by the nonlinear density contrast δ∗, to
M200, associated with δ∗ = 200,
by  (32)With the same one-to-one
identification, we can define a reduced variable
νδ∗ as
(32)With the same one-to-one
identification, we can define a reduced variable
νδ∗ as  (33)where
ν200(M200) is given by the second
Eq. (28) and
M200 is obtained as a function of
Mδ∗ through Eq. (32), and the large-mass tail of the halo mass
function is still given by
(33)where
ν200(M200) is given by the second
Eq. (28) and
M200 is obtained as a function of
Mδ∗ through Eq. (32), and the large-mass tail of the halo mass
function is still given by  . This
one-to-one identification of rare massive halos also implies that their spatial distribution
remains the same, independently of the choice of δ∗, so that
the large-mass two-point correlation and bias are still given by Eqs. (19) and (22),
. This
one-to-one identification of rare massive halos also implies that their spatial distribution
remains the same, independently of the choice of δ∗, so that
the large-mass two-point correlation and bias are still given by Eqs. (19) and (22),  (34)Next, in order to
describe typical halos we again take advantage of normalization constraints. First, to
ensure that the mass function remains normalized to unity as in Eq. (27), we choose the approximation
(34)Next, in order to
describe typical halos we again take advantage of normalization constraints. First, to
ensure that the mass function remains normalized to unity as in Eq. (27), we choose the approximation  (35)where the reduced
function f(ν) is still given by Eq. (29) and the reduced variable ν
is given by Eq. (33). Here the mass
M200 is still defined by Eq. (32) but since there is no longer a one-to-one identification (except at
very large mass, as explained below) M200 must be seen as an
“effective mass” rather than the mass within δ∗ = 200 of the
same individual object. This prescription automatically provides both the right large-mass
cutoff, as explained below Eq. (33)
(provided the mean profile (31) is correct)
and the normalization (27). Note that this
is a normalization in terms of mass, which ensures that by counting such halos we recover
the mean matter density of the Universe. Thus, a fixed range
[ν1,ν2] is
associated with the same fraction of matter, independently of the choice of
δ∗, but it is divided into a larger number of smaller
objects for larger δ∗, because of the prefactor
(35)where the reduced
function f(ν) is still given by Eq. (29) and the reduced variable ν
is given by Eq. (33). Here the mass
M200 is still defined by Eq. (32) but since there is no longer a one-to-one identification (except at
very large mass, as explained below) M200 must be seen as an
“effective mass” rather than the mass within δ∗ = 200 of the
same individual object. This prescription automatically provides both the right large-mass
cutoff, as explained below Eq. (33)
(provided the mean profile (31) is correct)
and the normalization (27). Note that this
is a normalization in terms of mass, which ensures that by counting such halos we recover
the mean matter density of the Universe. Thus, a fixed range
[ν1,ν2] is
associated with the same fraction of matter, independently of the choice of
δ∗, but it is divided into a larger number of smaller
objects for larger δ∗, because of the prefactor
 in
Eq. (35). Indeed, a given
ν is associated to a fixed M200, through the
second Eq. (28), and to a mass
Mδ∗ ∝ (1 + δ∗)−(3−α)/α
through Eq. (32). Thus, through the
normalization constraint and the form (35)
we include some dependence of the halo multiplicity on the choice of
δ∗ (as expected, a higher threshold
δ∗ leads to a larger number of objects), and the one-to-one
identification used in Eqs. (32)–(34) only applies in an asymptotic sense at high
mass.
in
Eq. (35). Indeed, a given
ν is associated to a fixed M200, through the
second Eq. (28), and to a mass
Mδ∗ ∝ (1 + δ∗)−(3−α)/α
through Eq. (32). Thus, through the
normalization constraint and the form (35)
we include some dependence of the halo multiplicity on the choice of
δ∗ (as expected, a higher threshold
δ∗ leads to a larger number of objects), and the one-to-one
identification used in Eqs. (32)–(34) only applies in an asymptotic sense at high
mass.
 |
Fig. 3 The halo mass functions at redshift z = 0, for halos defined by a nonlinear density contrast δ∗ = 200,400,800, and 1600. The solid line is our model (35), the dashed line is the fit from Sheth & Tormen (1999), which does not change with δ∗, and the points are the results from numerical simulations in Tinker et al. (2008). The value of the parameter α in Eq. (31) is set to α = 2.2. Here M = Mδ∗ is the halo mass enclosed within the radius defined by the density threshold δ∗. |
 |
Fig. 4 The halo bias b(M,x) as a function of σ(M), at distance x = 50 h-1Mpc and redshift z = 0. We show our results for halos defined by a density threshold δ∗ = 400 (left panel), δ∗ = 800 (middle panel), and δ∗ = 1600 (right panel). The solid line is our model (36), with α = 2.2 as for the mass functions of Fig. 3. The dashed line is the fit from Sheth et al. (2001), for halos with δ∗ = 200, which is the same in all panels and in Fig. 1. The points are the results from numerical simulations of Tinker et al. (2010). |
Second, to ensure that the halo bias also remains normalized to unity, as in Eq. (25), we also add to the large-mass term
br.e.;δ∗(Mδ∗,x)
a mass-independent term
b0;δ∗(x), as in
Eq. (24). Then, thanks to the
choice (35) we find that the
normalization (25) yields
b0;δ∗(x) = b0;200(x).
Combining with Eq. (34) this gives for the
total halo bias,  (36)This automatically
satisfies both the expected large-mass behavior (where the halos labeled by
δ∗ and 200 are the same objects) and the normalization
constraint. Since at moderate and low mass we no longer have a one-to-one identification
between halos, as we have seen from the mass function (35), the equality (36)
should not be seen as the result of a strict one-to-one identification,
even though it happens to give a similar expression.
(36)This automatically
satisfies both the expected large-mass behavior (where the halos labeled by
δ∗ and 200 are the same objects) and the normalization
constraint. Since at moderate and low mass we no longer have a one-to-one identification
between halos, as we have seen from the mass function (35), the equality (36)
should not be seen as the result of a strict one-to-one identification,
even though it happens to give a similar expression.
We first show in Fig. 3 the halo mass functions we obtain with our simple model at redshift z = 0. In the following, for simplicity we do not write the subscript δ∗, so that in each panel of Fig. 3 the mass M is actually the mass Mδ∗ enclosed within the radius defined by the density threshold δ∗, as labeled in each plot.
For δ∗ > 200 we set the parameter α of Eq. (31) to α = 2.2. Within our approach, this is the only new parameter that is needed to obtain the mass functions for arbitrary δ∗ from the one at δ∗ = 200 given by Eq. (29). We choose a value such that the large-mass tail is correctly reproduced for 200 ≤ δ∗ ≤ 1600. This gives a reasonable value for the slope of the density profile around the virial radius (i.e. ρ (<r) ~ r-2.2). For larger values of the density threshold, which correspond to smaller radii within massive halos, a smaller value of α would probably be required in order to follow the flattening of the halo profile, down to α ≃ −1. Since for practical purposes one usually considers density thresholds in the range 170 ≤ δ∗ ≤ 500 to define dark matter halos, we do not investigate further this point. As seen in Fig. 3, our simple model is already sufficient to reproduce the shift of the large-mass tail over the range 200 ≤ δ∗ ≤ 1600. This is most clearly seen by comparison with the fixed dashed line that applies to δ∗ = 200, taken from Sheth & Tormen (1999).
For high values of the threshold δ∗, especially in the lower right panel at δ∗ = 1600, it appears that our model overestimates the mass function for intermediate-mass halos, σ(M) ~ 1.5. On the other hand, it seems that in numerical simulations some fraction of matter is lost as we consider higher thresholds δ∗, so that the normalization (27) no longer holds (the integral would be smaller than unity for large δ∗). This may have a physical meaning, for instance if some regions of space are smooth and show a maximum density contrast, in which case they are no longer included as we select a higher threshold. A second factor is that at some level the distribution of the matter content of the Universe over a set of halos is not a very well defined procedure. More precisely, even though one may always build a well-defined algorithm to redistribute particles in a collection of halos within numerical simulations, to some degree it involves some arbitrariness from a physical point of view. This is clear from the fact that one cannot build a partition of a 3D box with spheres, and this means that the description of the matter distribution in terms of spherical halos can only be approximate. This may also lead to a violation of the normalization (27). A detailed investigation of such effects is beyond the scope of this paper and we prefer to stick to our simple model and to fixed normalizations such as Eq. (27). For practical purposes, the accuracy of the model (35) should be sufficient, and appears to be quite satisfactory in view of its simplicity.
We compare in Fig. 4 the halo bias predicted by our model, Eq. (36), with results from numerical simulations (Tinker et al. 2010), for the density thresholds δ∗ = 400,800, and 1600. Although the theoretical curve corresponds to z = 0, in order to increase the statistics we plot the numerical data obtained for 0 ≤ z ≤ 2.5, since the dependence on redshift is quite weak (see Fig. 1). Of course, for the parameter α we use the same value as the one used for the mass functions shown in Fig. 3, α = 2.2.
We can see that as the density threshold δ∗ increases the
bias at fixed σ(M) grows, especially at large masses. This
is most clearly seen through the comparison with the fixed dashed line, which corresponds to
the fit from Sheth et al. (2001) for halos defined by
δ∗ = 200. This moderate dependence on
δ∗ is also reproduced by our simple model (36), which shows a reasonable agreement with
N-body simulations over this range, 200 ≤ δ∗ ≤ 1600. In fact,
for a constant parameter α, as in Fig. 4, we can see from Eq. (36) that
as δ∗ grows the curve b(M)
is simply shifted by a uniform translation towards the left in the (lnM,b)
plane, since at fixed bias b, whence at fixed “effective mass”
M200, we have ![\hbox{$\ln M = \ln M_{200} + \frac{3-\alpha}{\alpha} \ln [201/(1+\deltas)]$}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq199.png) . Since
σ(M) is not exactly a power law, this horizontal
translation is not exactly uniform in the
(ln(1/σ),b) plane of Fig. 4. As noticed above, in order to cover a larger range of
density thresholds δ∗, or to improve the accuracy, it would be
necessary to use a slope α in Eq. (31) that runs with M and δ∗, in
order to take into account the dependence on mass of the halo profile and the flattening of
the slope at inner radii. However, we can see in Fig. 4
that the simple model with a constant value, α = 2.2, already provides a
good match to numerical simulations.
. Since
σ(M) is not exactly a power law, this horizontal
translation is not exactly uniform in the
(ln(1/σ),b) plane of Fig. 4. As noticed above, in order to cover a larger range of
density thresholds δ∗, or to improve the accuracy, it would be
necessary to use a slope α in Eq. (31) that runs with M and δ∗, in
order to take into account the dependence on mass of the halo profile and the flattening of
the slope at inner radii. However, we can see in Fig. 4
that the simple model with a constant value, α = 2.2, already provides a
good match to numerical simulations.
An advantage of this simple approximation is that it is straightforward to satisfy the normalization (25), as shown by the simple consequence (36). This ensures that our underlying halo model is self-consistent, in the sense that if we describe the matter distribution through a standard halo model (Cooray & Sheth 2002), but with arbitrary threshold δ∗ to define the halos, by integrating over these halos we recover both the total matter density (through the halo mass function) and the matter two-point correlation (through the halo bias). This means that, despite the approximate nature of such halo descriptions noticed above in the discussion of Fig. 3, our model automatically satisfies these two integral constraints.
We think such properties should be taken into account in the building of models for the matter distribution. As seen in this work, they can serve as a useful guide, which can be sufficient to provide reasonable quantitative estimates over tightly constrained domains. A second benefit is that they avoid introducing small inconsistencies, which may lead to spurious quantitative discrepancies for quantities that would be computed in later steps by integrating over the halo populations.
 |
Fig. 5 The ratio bs = x/b, as a function of σ(M), at redshifts z = 0,1.25, and 2.5. The bias b is the one obtained in Sect. 2 and shown in Fig. 1, whereas bs = x is obtained by making the approximation s = x in Eq. (22). |
4. Impact of halo motions
We now take advantage of the simple analytical model presented in Sect. 2 to estimate the impact of halo motions on their observed two-point correlation. Thus, focusing on halos defined by the nonlinear density threshold δ∗ = 200, we plot in Fig. 5 the ratio bs = x/b, where b is the bias obtained in Sect. 2 and shown by the solid line in Fig. 1, while bs = x is the bias obtained with the approximation s = x (i.e. we substitute s → x in Eq. (22)), which was plotted as the red dashed line in Fig. 1. Therefore, this ratio measures the effect on the bias of halo motions, which are neglected in the usual approach (Kaiser 1984) or in the peak-background split method (Cole & Kaiser 1989; Mo & White 1996).
For rare massive halos, where the asymptotic expression (22) applies, we have s > x within our complete approach, as can be checked from Eq. (20). Thus, as could be expected, rare massive halos tend to move closer because of their mutual gravitational attraction. Although this might seem contradictory with large-scale homogeneity (one may ask how could all halos move closer to each other ?), this is not the case. For instance, let us consider an infinite regular 3D grid of cell size L, and let us put two halos separated by a small distance, ℓ ≪ L, around each vertex (so that the vertex is the center of the pair). Then, if at a later time we independently shrink each pair around its vertex, ℓ → ℓ′ with ℓ′ < ℓ, we can see that on the mean halos have moved closer. Indeed, the distances between different pairs have not changed while they have been reduced within each pair. However, the system has clearly remained homogeneous on large scales (there is not coherent shrinking of all halos positions towards a central point, as one might have been afraid of). This simple picture shows how small scale motions can have a nonzero effect on the mean, while preserving large-scale statistical homogeneity.
Then, it is clear from Eq. (22) that the
predicted bias, or the predicted two-point correlation function, of rare massive halos is
smaller when we take into account the fact that
s > x than when we neglect this
distinction. Indeed, cross-correlations, such as 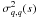 , of the linear density
fluctuations at scale q over a large distance s are
decreasing functions of s. This implies that by making the approximation
“s = x” we overestimate the initial cross-correlation
between massive halos observed at distance x, and this explains why the
ratio
bs = x/b
is larger than unity at large masses in Fig. 5. This
effect increases at larger masses, which have a large bias and show a stronger sensitivity
to the large-scale correlations. Of course, this agrees with the behavior found in
Fig. 1. At small masses the ratio
bs = x/b
becomes slightly smaller than unity. This is a direct consequence of the normalization
constraint (25), which implies that the
greater value of the bias at high mass, within the approximation
“s = x”, must be compensated by a smaller value at small
mass. The effect is rather small in this range since massive halos are rare so that their
bias does not contribute much to the normalization (25).
, of the linear density
fluctuations at scale q over a large distance s are
decreasing functions of s. This implies that by making the approximation
“s = x” we overestimate the initial cross-correlation
between massive halos observed at distance x, and this explains why the
ratio
bs = x/b
is larger than unity at large masses in Fig. 5. This
effect increases at larger masses, which have a large bias and show a stronger sensitivity
to the large-scale correlations. Of course, this agrees with the behavior found in
Fig. 1. At small masses the ratio
bs = x/b
becomes slightly smaller than unity. This is a direct consequence of the normalization
constraint (25), which implies that the
greater value of the bias at high mass, within the approximation
“s = x”, must be compensated by a smaller value at small
mass. The effect is rather small in this range since massive halos are rare so that their
bias does not contribute much to the normalization (25).
We can see in Fig. 5 that the effect of halo motions is smaller at higher redshift for a fixed value of σ(M), which actually corresponds to a smaller mass at higher z. Thus, if one only considers typical halos, or a population defined by a fixed upper bound on 1/σ(M) (this roughly corresponds to a fixed comoving number density), the average halo motion can be neglected at high z. We show in Fig. 6 the same ratio bs = x/b at redshifts z = 0,1.25, and 2.5, but as a function of M instead of 1/σ(M). Then, we can see that the effect of the average halo motion now increases at higher redshift, for a fixed mass M.
At z = 0, neglecting this effect leads to an overestimation of the bias b(M) by a factor 1.5 at M ~ 3 × 1015 h-1M⊙, that is, σ(M) ~ 0.34. Therefore, it cannot be neglected for massive halos.
 |
Fig. 7 The ratio bL/b, as a function of σ(M), at redshifts z = 0,1.25, and 2.5. The bias b is the one obtained in Sect. 2 and shown in Fig. 1, whereas bL is obtained by using the “linear” approximation (37) in Eq. (24). |
5. Impact of exponential nonlinearity
At large distance cross-correlations such as  become very
small and one can expand the exponential in Eq. (22), to obtain the linearized form
become very
small and one can expand the exponential in Eq. (22), to obtain the linearized form  (37)At zeroth-order
over
(37)At zeroth-order
over 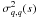 , where
s = x, this gives the well-known result of Kaiser (1984),
, where
s = x, this gives the well-known result of Kaiser (1984),  , which shows
how the bias of massive halos grows as
, which shows
how the bias of massive halos grows as  , in agreement with
Fig. 1. Linearized expressions such as (37), that is, where one looks for an expression
of the halo two-point correlation function, or of the halo power spectrum, that is linear
over the matter two-point correlation or power spectrum, are widely used. In terms of the
“local bias model” (Fry & Gaztanaga 1993;
Mo et al. 1997; Manera & Gaztanaga 2010), this also corresponds to the approximation of
“linear bias”, where the halo density field,
nM(x), is
written as a linear function of the matter density field, such as
, in agreement with
Fig. 1. Linearized expressions such as (37), that is, where one looks for an expression
of the halo two-point correlation function, or of the halo power spectrum, that is linear
over the matter two-point correlation or power spectrum, are widely used. In terms of the
“local bias model” (Fry & Gaztanaga 1993;
Mo et al. 1997; Manera & Gaztanaga 2010), this also corresponds to the approximation of
“linear bias”, where the halo density field,
nM(x), is
written as a linear function of the matter density field, such as
![\hbox{$n_M(\vx) = \nb_M [1 + b_1(M) \delta_M(\vx) ]$}](/articles/aa/full_html/2011/01/aa15699-10/aa15699-10-eq219.png) (where
δM(x) is the
matter density contrast smoothed on scale M), with a constant linear bias
factor b1. However, as pointed out by Politzer & Wise (1984), even when the cross-correlation
(where
δM(x) is the
matter density contrast smoothed on scale M), with a constant linear bias
factor b1. However, as pointed out by Politzer & Wise (1984), even when the cross-correlation
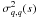 is small the argument of the
exponential (22) can be large, because of
the factor
is small the argument of the
exponential (22) can be large, because of
the factor  . For
instance, at fixed scales q and s the argument grows as
1/σ2 as the amplitude of the linear matter
power spectrum decreases. Therefore, we investigate in this section the impact of the
exponential non-linearity (22) on the halo
bias.
. For
instance, at fixed scales q and s the argument grows as
1/σ2 as the amplitude of the linear matter
power spectrum decreases. Therefore, we investigate in this section the impact of the
exponential non-linearity (22) on the halo
bias.
Thus, we show in Fig. 7 the ratio
bL/b, where
b is again the bias obtained in Sect. 2 and Fig. 1, while
bL is the bias obtained with the approximation (37), which we substitute into Eq. (24). We still take into account halo motions
through Eq. (20), as well as normalizations
to unity. Therefore, this ratio measures the effect of the exponential non-linearity (22). In agreement with the previous discussion,
we can see in Fig. 7 that by linearizing the
expression (22) we underestimate the halo
bias at large masses. Indeed, the argument in Eq. (22) scales as  , which grows at
large mass. However, this effect is only significant at very large masses and typical
objects are not affected by this linearization. As shown by Figs. 7 and 8, this effect decreases at
higher redshift for a fixed value of σ(M), but increases
at higher redshift for a fixed mass M. Therefore, although for typical
halos such a “linearization” of the bias is a very good approximation, for very massive
objects it can lead to a significant underestimation, especially at high redshift. As
noticed in Fig. 2 (upper dotted curve), this effect
also becomes more important at smaller distance x, as
, which grows at
large mass. However, this effect is only significant at very large masses and typical
objects are not affected by this linearization. As shown by Figs. 7 and 8, this effect decreases at
higher redshift for a fixed value of σ(M), but increases
at higher redshift for a fixed mass M. Therefore, although for typical
halos such a “linearization” of the bias is a very good approximation, for very massive
objects it can lead to a significant underestimation, especially at high redshift. As
noticed in Fig. 2 (upper dotted curve), this effect
also becomes more important at smaller distance x, as
 is larger.
is larger.
6. Conclusion
We have described in this paper a simple analytical model for the bias of dark matter halos. It extends previous works, which focused on halos defined by their virial density contrast (δ∗ ~ 200), to the more general case of halos defined by an arbitrary density threshold in the range 200 ≤ δ∗ ≤ 1600. This is coupled to a model for the halo mass function that is also generalized to these density thresholds, and we have checked that these simple models yield a good agreement with numerical simulations at redshifts 0 ≤ z ≤ 2.5.
Our approach also improves over some previous works by including the effect of halo motions on their two-point correlation function. This arises from the fact that massive halos move closer on the mean, because of their mutual gravitational attraction, which implies that their mean distance at a given time is smaller than the Lagrangian separation of the two regions they originate from in the primordial density field. We estimate this effect from the linear displacement of halos, which provides a simple approximation that could be easily used in more complex cases, such as non-Gaussian initial conditions.
Another feature of our model is that it contains no free parameters for the bias. More precisely, the only parameters that appear are related to the halo mass functions. As in most other approaches, a few parameters are needed to describe the shape of the mass function (of halos defined by δ∗ = 200) at low and intermediate masses, but the large mass tail is governed by the cutoff e−ν2/2 without further tuning. Then, the extension to halo populations defined by larger density contrasts only involves a single parameter, α ≃ 2.2, which is related to the slope of halo density profiles around the virial radius. Then, no further parameters are required to compute the bias of these halo.
As stressed in this paper, this is possible thanks to the use of integral constraints for both the halo mass function and bias. This allows us to focus on rare and massive objects, where reliable predictions can be derived. Then, the behavior of intermediate and small halos, which is beyond the reach of analytical approaches because of strong tidal effects and mergings, is strongly constrained by these integral conditions, and we have shown that this is sufficient to build simple and efficient models. Of course, this simplicity has a cost: we cannot expect a priori high accuracy at very low mass, and there is no systematic procedure (such as expansions over some parameters) to improve the model up to arbitrarily high accuracy. However, we have seen that we already obtain a good agreement with numerical simulations, and this approach should be quite robust. Another advantage is that by explicitly taking into account such integral constraints we make sure our model is self-consistent, and we avoid any risk to introduce spurious discrepancies that may arise in integral quantities because of small inconsistencies.
Finally, we have evaluated the quantitative impact on halo bias of two common approximations, i) neglecting halo motions, and ii) linearizing the halo two-point correlation over the matter power spectrum. This could be useful to check the range of validity of these approximations.
It would be interesting to generalize this work to more complex cases, such as non-Gaussian initial conditions. However, we leave this to future studies.
Acknowledgments
The author thanks J. L. Tinker for sending his numerical results for the halo bias, used in Figs. 1 and 4.
References
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchard, A., Valls-Gabaud, D., & Mamon, G. A. 1992, A&A, 264, 365 [NASA ADS] [Google Scholar]
- Bond, J. R., Cole, S., Efstathiou, G., & Kaiser, N. 1991, ApJ, 379, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., & Kaiser, N. 1989, MNRAS, 237, 1127 [NASA ADS] [Google Scholar]
- Coles, P. 1989, MNRAS, 238, 319 [NASA ADS] [Google Scholar]
- Coles, P., Melott, A. L., & Shandarin, S. F. 1993, MNRAS, 260, 765 [NASA ADS] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cuesta, A. J., Prada, F., Klypin, A., & Moles, M. 2008, MNRAS, 389, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Desjacques, V. 2008, Phys. Rev. D, 78, 103503 [NASA ADS] [CrossRef] [Google Scholar]
- Desjacques, V., & Sheth, R. K. 2010, Phys. Rev. D, 81, 023526 [NASA ADS] [CrossRef] [Google Scholar]
- Fry, J. N., & Gaztanaga, E. 1993, ApJ, 413, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Hamana, T., Yoshida, N., Suto, Y., & Evrard, A. E. 2001, ApJ, 561, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Kravtsov, A. V. 2003, ApJ, 584, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Heavens, A. F., & Peacock, J. A. 1989, MNRAS, 238, 293 [NASA ADS] [Google Scholar]
- Manera, M., & Gaztanaga, E. 2010 [arXiv:0912.0446] [Google Scholar]
- Manera, M., Sheth, R. K., & Scoccimarro, R. 2010, MNRAS, 402, 589 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Ilbert, O., Mellier, Y., et al., 2008, A&A, 479, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melott, A. L., Pellman, T. F., & Shandarin, S. F. 1994, MNRAS, 269, 626 [NASA ADS] [Google Scholar]
- Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., Jing, Y. P., & White, S. D. M. 1997, MNRAS, 284, 189 [NASA ADS] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Padilla, N. D., Baugh, C. M., Eke, V. R., et al. 2004, MNRAS, 352, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The large scale structure of the universe (Princeton: Princeton university press) [Google Scholar]
- Pillepich, A., Porciani, C., & Hahn, O. 2010, MNRAS, 402, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Politzer, H. D., & Wise, M. B. 1984, ApJ, 285, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Tormen, G. 1999, MNRAS, 308, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Robertson, B. E., Kravtsov, A. V. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Valageas, P. 2002, A&A, 382, 450 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P. 2009, A&A, 508, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P. 2010, A&A, 514, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeldovich, Y. B. 1970, A&A, 5, 84 [NASA ADS] [Google Scholar]
- Zheng, Z., & Weinberg, D. H. 2007, ApJ, 659, 1 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 The halo bias b(M,x) as a function of σ(M), at distance x = 50 h-1Mpc, for halos defined by the nonlinear density contrast δ∗ = 200. We plot our results at redshifts z = 0 (left panel), z = 1.25 (middle panel), and z = 2.5 (right panel). The black solid line, “δL ∗ ”, is the theoretical prediction (24), the red dashed line, “s = x”, corresponds to the approximation where halo motions are neglected, and the green dot-dashed line, “δc”, corresponds to the use of δc = 1.686 instead of δL ∗ . The blue dashed line, “SMT”, is the fit from Sheth et al. (2001), and the points are the results from numerical simulations of Tinker et al. (2010). |
| In the text | |
 |
Fig. 2 The mean bias |
| In the text | |
 |
Fig. 3 The halo mass functions at redshift z = 0, for halos defined by a nonlinear density contrast δ∗ = 200,400,800, and 1600. The solid line is our model (35), the dashed line is the fit from Sheth & Tormen (1999), which does not change with δ∗, and the points are the results from numerical simulations in Tinker et al. (2008). The value of the parameter α in Eq. (31) is set to α = 2.2. Here M = Mδ∗ is the halo mass enclosed within the radius defined by the density threshold δ∗. |
| In the text | |
 |
Fig. 4 The halo bias b(M,x) as a function of σ(M), at distance x = 50 h-1Mpc and redshift z = 0. We show our results for halos defined by a density threshold δ∗ = 400 (left panel), δ∗ = 800 (middle panel), and δ∗ = 1600 (right panel). The solid line is our model (36), with α = 2.2 as for the mass functions of Fig. 3. The dashed line is the fit from Sheth et al. (2001), for halos with δ∗ = 200, which is the same in all panels and in Fig. 1. The points are the results from numerical simulations of Tinker et al. (2010). |
| In the text | |
 |
Fig. 5 The ratio bs = x/b, as a function of σ(M), at redshifts z = 0,1.25, and 2.5. The bias b is the one obtained in Sect. 2 and shown in Fig. 1, whereas bs = x is obtained by making the approximation s = x in Eq. (22). |
| In the text | |
 |
Fig. 6 The ratio bs = x/b, as in Fig. 5, but as a function of M, at redshifts z = 0,1.25, and 2.5. |
| In the text | |
 |
Fig. 7 The ratio bL/b, as a function of σ(M), at redshifts z = 0,1.25, and 2.5. The bias b is the one obtained in Sect. 2 and shown in Fig. 1, whereas bL is obtained by using the “linear” approximation (37) in Eq. (24). |
| In the text | |
 |
Fig. 8 The ratio bL/b, as in Fig. 7, but as a function of M, at redshifts z = 0,1.25, and 2.5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


