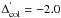| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201015662 | |
| Published online | 06 December 2010 | |
Mining SDSS in search of multiple populations in globular clusters
1
Department of AstronomyUniversity of Bologna,
via Ranzani 1,
40127
Bologna,
Italy
e-mail: carmela.lardo2@unibo.it
2
INAF - Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
Received:
31
August
2010
Accepted:
6
October
2010
Several recent studies have reported the detection of an anomalous color spread along the red giant branch (RGB) of some globular clusters (GC) that appears only when color indices including a near ultraviolet band (such as Johnson U or Strömgren u) are considered. This anomalous spread in color indexes such as U − B or cy has been shown to correlate with variations in the abundances of light elements such as C, N, O, Na, etc., which, in turn, are generally believed to be associated with subsequent star formation episodes that occurred in the earliest few 108 yr of the cluster’s life. Here we use publicly available u, g, r Sloan Digital Sky Survey photometry to search for anomalous u − g spreads in the RGBs of nine Galactic GCs. In seven of them (M 2, M 3, M 5, M 13, M 15, M 92 and M 53), we find evidence of a statistically significant spread in the u − g color, not seen in g − r and not accounted for by observational effects. In the case of M 5, we demonstrate that the observed u − g color spread correlates with the observed abundances of Na, the redder stars being richer in Na than the bluer ones. In all the seven clusters displaying a significant u − g color spread, we find that the stars on the red and blue sides of the RGB, in (g, u − g) color magnitude diagrams, have significantly different radial distributions. In particular, the red stars (generally identified with the second generation of cluster stars, in the current scenario) are always more centrally concentrated than blue stars (generally identified with the first generation) over the range sampled by the data (0.5 rh ≲ r ≲ 5 rh), in qualitative agreement with the predictions of some recent models of the formation and chemical evolution of GCs. Our results suggest that the difference in the radial distribution between first and second generation stars may be a general characteristic of GCs.
Key words: stars: abundances / globular clusters: general
© ESO, 2010
1. Introduction
Globular clusters (GCs) have long been considered as examples of the theoretical concept of a simple stellar population, i.e., a population of stars that is strictly coeval and chemically homogeneous (Renzini & Buzzoni 1986). This traditional paradigm remains valid in some cases, but recent photometric and spectroscopic observational results strongly indicate that most GCs have been sites of two or even more star-formation episodes, producing a peculiar chemical (self-)enrichment pattern (see Piotto 2009; Carretta et al. 2010d, and references therein, for review and discussion).
In general, GCs are largely homogeneous if we consider Fe-peak elements but exhibit a significant spread in the abundance of lighter elements, with strong anti-correlations between, for example, the abundances of Na and O, or Mg and Al, as well as bimodal distributions of CH and CN line strengths (see Carretta et al. 2010d; Martell & Smith 2009, and references therein). While these anomalies have been known for decades (see Kraft 1994, for a review of early results), it has only recently been established that (a) they can also be traced in un-evolved stars (Gratton et al. 2001; Ramírez & Cohen 2002; Carretta et al. 2004), hence cannot be due to mixing processes; and (b) they seem to be a characteristic feature of GCs (Carretta et al. 2010d). Interestingly enough, these chemical inhomogeneities are not confined only to Galactic GCs (Colucci et al. 2009; Mucciarelli et al. 2009; Johnson et al. 2006; Letarte et al. 2006, and references therein).
The scenario generally invoked to explain the above phenomena, foresees two subsequent generations of stars in the first few hundred Myr of cluster life, with ejecta from the massive stars of the first generation enriching the intra cluster medium (ICM) before the formation of the second one. Intermediate-mass asymptotic giant branch stars (IM-AGBs; Ventura & D’Antona 2008) or fast rotating massive stars (FRMSs; Decressin et al. 2007) have been proposed as the ICM polluters that most likely explain the observed patterns (see Renzini 2008, for a discussion of the merits of the two models).
In this context, several results imply that the spread in light-element abundances of GCs can be traced by photometric indices with near ultraviolet (wide or intermediate) passbands, encompassing the wavelength range 3000 Å ≲ λ ≲ 4000 Å. For instance, Yong et al. (2008) demonstrated that the cy index (including the near-ultraviolet Strömgren u passband, akin to the c1 index used by Grundahl & Briley 2001; Grundahl et al. 2002, to trace NH1) very clearly traces the differences in N abundances among the stars of NGC 6752, over a range of ~2.0 dex in [N/Fe]. As the abundance of N is found to correlate (or anti-correlate) very well with other light elements exhibiting abundance spreads in GCs (O, Na, Mg, Al), differences in these elements can also be correlated with cy variations, as demonstrated by Carretta et al. (2009b). These authors used their Na and O abundance determinations for NGC 6752 to show that stars with different abundances of these elements lie on different sides of the cluster RGB in the (V, cy) plane, and concluded that Na-poor (Na-rich) stars are also N-poor (N-rich; see also Milone et al. 2010, for further results on NGC 6752 and discussion). Moreover, the well-known anti-correlation between Na and O implies that Na-rich stars are also O-poor and vice versa. Yong et al. (2008) noted that available Strömgren photometry of Galactic GCs (Grundahl & Andersen 1999) suggests that a significant spread in N abundance may be a general property of GCs. In particular, their Fig. 14 shows remarkable spreads in cy, at any magnitude along the RGB of NGC 288, NGC 362, M 5, M 3, M 13, NGC 6752, M 15, M 92, and NGC 6397.
Marino et al. (2008) were able to demonstrate for M 4 that a bimodal Na-O distribution, correlated with a bimodal distribution in CN strength, was also clearly associated with a bimodal spread in the color of RGB stars in the U vs. (U − B) CMD, not seen with other color indices. In this case, as in all cases in which the U − B color spread in the RGB has been correlated with O, Na abundances, the Na-rich/CN-strong stars lie on the red side of the RGB, while Na-poor/CN-weak stars populate a bluer portion of the branch. In line with Yong et al. (2008), Marino et al. (2008) attribute the spread in (U − B) color to strength variations of several NH and CN bands included within the U passband, in particular the NH band around 3360 Å, and the CN bands around 3590 Å, 3883 Å and 4215 Å. They performed synthetic U, B photometry of theoretical spectra with different strengths of the NH and CN features, mimicking the observed spectra of M 4 stars, finding that the resulting variation in the U − B color goes in the right direction but has an amplitude four times smaller than the observed color spread.
Kravtsov et al. (2010a,b) used U band photometry to identify multiple populations within the clusters NGC 3201 and NGC 1261. The spread in U − B color among RGB stars of NGC 3201 was shown to correlate with Na abundance by Carretta et al. (2010d). Finally, Han et al. (2009) showed that the RGB of NGC 1851, which is narrow and well defined in optical CMDs not including U photometry, is clearly split into two parallel branches in the U vs. U − I colour. Han et al. (2009) suggest that the splitting is caused by a combination of effects due to variations in the abundances of not only of C, N, O but also of heavier elements (Ca, Si, Ti, and Fe) and helium. The presence of a small (but real) spread in iron and α-elements abundance in this cluster was recently confirmed spectroscopically by Carretta et al. (2010e, see also their Fig. 4. Additional results and a more general discussion about the possible role of heavy elements variations in producing the RGB color spreads in GCs can be found in Lee et al. (2009) and Carretta et al. (2010b).
While the details of the process remain still unclear, it seems reasonably well established that (at least) light-element abundance spreads in GCs are correlated with spreads in the colors of RGB stars if near ultraviolet filters are adopted. This opens an interesting window in investigating the origin of the chemical evolution of GCs as accurate U photometry for very large sample of GC stars can be obtained in a much easier way and for much more distant clusters than the mid-to-high-resolution spectroscopy needed to obtain direct chemical abundance estimates (which, however, provides more information). In particular, wide-field photometry capable of discriminating between N-rich and N-poor stars would provide the large samples and the wide radial coverage that are needed to compare the radial distributions of the two groups; this may provide a very interesting insight into the process of GC formation and early chemical enrichment (see D’Ercole et al. 2008; Decressin et al. 2007; Renzini 2008).
Globular cluster sample.
Prompted by these considerations we decided to test whether additional observational evidence of color spreads in the RGB of GCs could be derived from the publicly available Sloan Digital Sky Survey photometry (SDSS; see Abazajian et al. 2009, and references therein), as it provides multicolor photometry including a u passband2 and incorporates several Galactic GCs. In the following, we use the accurate ugriz SDSS photometry by An et al. (2008) of nine GCs selected from their sample to show that: (a) the u − g color index indeed correlates with spectroscopic Na, O abundances and that the associated spread in color can be detected in SDSS data, at least in clusters of intermediate to high metallicity; (b) a statistically significant intrinsic u − g spread among RGB stars is detected in seven of the nine clusters considered in the present study; and, finally; (c) in these seven clusters the radial distribution of stars lying on the blue side of the RGB (in u − g) differs significantly from that of stars lying on the red side, the latter being more centrally concentrated than the former.
In Sect. 2, we briefly describe the adopted photometric data set and present evidence of a correlation between light-element abundances and u − g spread along the RGB for the cluster M 5. In Sect. 3, we analyze the g, g − r and g, u − g CMDs of the considered clusters in search of u − g color spread in the RGB that cannot be accounted for by observational effects. We finally discuss our results in Sect. 4. Some preliminary results from this study were presented by M. Bellazzini at the meeting “The Giant Branches” held in Leiden in May 20093.
2. The data set
An et al. (2008, An08 hereafter) reanalyzed SDSS images of the GCs (and open clusters) included in the survey using the DAOPHOT/ALLFRAME suite of programs (Stetson 1987, 1994). These programs are known to perform more effectively than the survey photometric pipeline in the high-crowding conditions typical of dense star clusters.
We limited our analysis to the most favorable cases, excluding clusters with |b| ≤ 20° – to avoid strong contamination from Galactic field stars – and/or with E(B − V) ≥ 0.15 – i.e., clusters with relatively high extinction. Moreover, we decided to include in our sample only clusters with more than 100 candidate RGB stars between the horizontal branch (HB) and two magnitudes below this level, to ensure a solid statistic basis to our analysis. According to these criteria, among the seventeen clusters considered by An08 we selected the nine GCs listed in Table 1.
Only stars with valid magnitude estimates in both g and r have been retained for subsequent analysis. When An08 provided more that one catalog per cluster (i.e., in cases of clusters imaged in different overlapping SDSS “plates”, see Abazajian et al. 2009, An08, and references therein), we merged the catalogs into a single one including all the cluster stars listed by An08 without duplications. The final catalogs cover fields including the vast majority of cluster stars but does not reach the tidal radius (except for NGC 2419, see below).
In some cases, the available photometry was highly incomplete and/or was characterized by large uncertainties in the innermost regions of the cluster, because of the high degree of crowding. In most cases the final catalog also covered a field of view including regions where the contamination from Galactic stars was not negligible. To avoid the inclusion of cluster stars with poor-quality photometry and contamination from fore/background Galactic stars, we limited the analysis to a radial corona between the rin and rout values specified in Table 1. In this table, rin and rout are also expressed in units of core, half-light, and tidal radii (rc, rh, and rt, respectively), to provide a more objective idea of the actual radial sampling and of the cluster-to-cluster differences in the radial sampling. We note that: (a) in all the considered cases we sample the clusters out to >4 rh, and in most cases out to 6−10 rh; (b) in the cases in which we excluded the innermost 1′ from the analysis, the innermost regions between ~1−3 rc were lost, the completeness in these inner parts possibly being remarkably low also in clusters for which we retained the central region4; and (c) the considered clusters span a wide range of central density (more than 4 orders of magnitude, see Harris 1996), hence the different radial ranges also sample regions in widely different dynamical conditions, depending on the considered cluster.
The reddening for the GCs are taken from Harris (1996). The coefficients of the adopted extinction laws (Aλ/AV) are taken from the computations by Girardi et al. (2004) for cool giants (Teff = 4000, log g = 2.00 and [M/H] = −2), and assuming AV = 3.1 E(B − V). In particular: Au = 4.84 E(B − V), Ag = 3.64 E(B − V), and Ar = 2.71 E(B − V), and E(u − g) = 1.20 E(B − V) and E(g − r) = 0.93 E(B − V).
2.1. Na abundances and u – g colors in RGBs
For two of the selected clusters, M 5 and M 15, we found a significant sample of stars for which there are spectroscopic Na abundances over a remarkably wide luminosity range along the RGB, from Carretta et al. (2009a,b). Following the criteria used by these authors, we divide the RGB stars between a candidate first generation and a candidate second generation (P and I+E components, respectively, adopting their nomenclature5) by adopting a threshold in sodium abundance that depends on the cluster metallicity. In particular, stars having [Na/Fe] min ≤ [Na/Fe] < [Na/Fe] min + 0.3 are assigned to the Na-poor P component, while stars having [Na/Fe] ≥ [Na/Fe] min + 0.3 are assigned to the Na-rich I+E component (see Carretta et al. 2009b, for further details). The resulting thresholds are [Na/Fe] = +0.10 for M 5 and [Na/Fe] = +0.22 for M 15; we stress, however, that the results presented below are not particularly sensitive to the adopted threshold.
 |
Fig. 1 g, g − r and g, u − g CMDs for M 5, M 15. The stars for which spectroscopic abundances are available from from Carretta et al. (2009a,b) are marked according to their Na abundances: Na-poor stars are marked as blue open circles, while Na-rich stars are marked with red open triangles. Stars plotted as heavy dark dots are those selected as candidate RGB stars from the g, g − r CMD. |
The upper panel of Fig. 1 shows that, in the case of M 5, the Na-poor and Na-rich stars, that are tightly aligned along the narrow cluster RGB in the g, g − r CMD, are clearly separated into two parallel sequences in the much broader giant branch seen in the g, u − g diagram, the Na-rich stars appearing systematically redder than Na-poor ones (at least below the HB level), a behavior strictly analogous to that observed by Marino et al. (2008) in M 4, by Milone et al. (2010) in NGC 6752, using U photometry, and by Carretta et al. (2009b), again in NGC 6752, but using Strömgren u photometry.
This result clearly indicates that SDSS u photometry can also be used to trace the UV color spread correlated with the light-element abundance spread described in Sect. 1, above. We note that most of the RGB stars displaying the color segregation as a function of Na abundance are fainter than the RGB bump (at g ≃ 15.4, see Fig. 2, below), as expected if the observed chemical anomalies are not due to extra-mixing phenomena known to occur in evolutionary phases brighter than this feature (Gratton et al. 2000; Smith & Martell 2003).
However, the clear u − g color segregation between Na-poor and Na-rich stars observed in M 5 is not seen in M 15 (lower panel of Fig. 1). A likely explanation of this different behavior calls into play the difference in overall metal content between the two clusters. The iron abundance in M 5 is ten times higher than in M 15 and the average abundance of the light elements should scale similarly. Hence, the same degree of N abundance with respect to iron (as expressed by [N/Fe]) corresponds to very different absolute abundances of N ([N/H]). This, in turn, should correspond to significant differences in the strength of the absorption features that are supposed to drive the spreads observed in broad-band near-ultraviolet photometry (see also Martell et al. 2008). In particular, the strengths of spectral lines of diatomic molecules (such as CN, NH) depend quadratically on the overall metallicity and it has been noted that CN bands become very weak in the spectra of GC giants for [Fe/H] ≲ −1.8 (Smith 2002). In this context, we note that the clusters for which the color spread in the RGB has been detected using the broad U (or u, in the present case) filter and correlated with spectroscopic light-element abundances, have intermediate metallicities, i.e. [Fe/H] = −1.34 for M 5, [Fe/H] = −1.17 for M 4, [Fe/H] = −1.51 for NGC 3201, [Fe/H] = −1.55 for NGC 6752 (metallicities from Carretta et al. 2009b), and [Fe/H] = −1.18 for NGC 1851, (metallicity from Carretta et al. 2010e).
On the other hand, we need also consider that the RGBs of M 5 and M 15 seem to display similar spreads in the (V, cy) plane (Yong et al. 2008), thus not supporting the above hypothesis. It is difficult to draw a firm conclusion at the present stage, in particular if we consider that we still lack a detailed theoretical understanding of the mechanism at the origin of the color spread. This kind of investigation is clearly beyond the scope of the present paper. For our present purposes, we take as the basis of the further analysis of the clusters in our sample the clear evidence that, at least in some cases, star-to-star differences in light-element abundances in the RGB of GCs can be discerned with the u − g color.
In particular, the sought-after anomaly should be distinguishable as a significant color spread in the RGB in the (g, u − g) CMD, not seen in the (g, g − r) CMD and unaccounted for by other effects, such as an increase in the photometric error and/or an increase in the amplitude of the effect of differential extinction (see below). Independently of its true origin, we refer in the following section to the observational effect under consideration as a UV-spread (UV-s hereafter, for brevity) and we will look for its presence in the clusters of our sample, trying to establish, in the various cases, wether it is (at least partially) due to intrinsic star-to-star physical differences or it can be fully accounted for by trivial effects.
 |
Fig. 2 g − r, g and g, u − g CMDs for the GCs in our sample. In some cases, the RGB is truncated due to SDSS saturation. The red arrows in the upper right corner of each panel are the reddening vectors whose amplitudes correspond to the average E(B − V) values reported in Table 1. Horizontal black arrows mark the position of the RGB bump. Stars selected as candidate RGB on the (g, g − r) CMDs are plotted as heavy dark dots, the remaining ones as lighter red dots. The curves approximately tracing the red edges of the RGBs are used as references to compute the color spread distributions shown in Fig. 3; the two horizontal segments display the portion of the RGB that is used to compute those distributions. In most cases, note that the asymptotic giant branch starts above the bright end of the adopted selection box (NGC 2419 is an obvious exception). |
3. Detecting anomalous u – g spreads
In Fig. 2, we present the g, g − r CMDs, flanked by their g, u − g counterparts for all the clusters listed in Table 1. In all cases, two horizontal segments enclose the magnitude range to which we limit our analysis of the color spread: we tried to select similar portions of the RGB in all clusters, possibly spanning a wide region below the horizontal branch. Given the different distances and reddenings of the various clusters, this was not always possible (in particular, for NGC 2419 which is far more distant than the other GCs in our sample). This gives rise to differences in the sensitivity of the adopted method as (a) the color spread corresponding to a given abundance spread is always observed to decrease with increasing luminosity along the RGB, virtually disappearing at the RGB tip (Yong et al. 2008; Marino et al. 2008; Milone et al. 2010); and (b) the same portion of the RGB occurs at different apparent magnitudes in different clusters, which is indicative of different photometric accuracy.
The line located approximately at the red edge of the RGB, within the two horizontal segments, is a ridge line following the curvature of the observed RGB, and is taken as a reference to compute the color spreads, that is the difference between the color of a given star and the color of the ridge line at the same magnitude, Δcol, where col = g − r or col = u − g. Both Δg − r and Δu−g are computed only for stars selected as candidate RGB in the g,g − r CMDs (heavier dots in Fig. 2). To limit the effects of possible spurious u − g outliers, we considered only stars for which −0.2 ≤ Δu−g ≤ 0.05; these limits were found to be appropriate for all clusters except NGC 2419 for which we adopted −0.8 ≤ Δu−g ≤ 0.05.
There are several cases in Fig. 2 in which a conspicuous broadening of the RGB in u − g with respect to g − r is apparent. However, as anticipated above, a few factors unrelated to physical differences among cluster stars may also (in principle) produce this effect. These factors and the methods we adopted to keep their effect under control can be summarized as follows:
-
1.
Field contamination. The degree of contamination by Galacticfore/background stars is very modest, because of thecombination between the relatively high (absolute) Galacticlatitude of the considered clusters (all have |b| > 25° and four |b| > 70°) and the relatively small area of the considered annular fields. We used the Galactic model TRILEGAL (Girardi et al. 2005) to obtain a conservative estimate of the degree of contamination affecting the samples of candidate RGB stars considered in the present analysis (see Fig. 2). We found that the fraction of Galactic field stars in our samples is lower than 5% for seven of the nine clusters, reaching 8% for M 15 and 10% for M 92. Moreover, the effect of even this small degree of contamination should be minimized by the way in which we selected candidate RGB stars. In the following, we analyze the color spreads of candidate RGB stars selected in the g, g − r CMD as the most tightly clustered along the narrow RGB sequence in this plane (heavy dark dots in Fig. 2). This means that we compare the g − r and u − g color spreads produced by exactly the same stars. Hence, any field star artificially broadening the distribution of Δcol in u − g should also have a similar effect on g − r.
-
2.
Blendings and artifacts. Any photometry of crowded fields (especially ground-based seeing-limited ones) is expected to include some fraction of sources that are either blends of two (or more) fainter stars, or non-stellar sources, such as unresolved distant galaxies or flukes in the halo of bright stars, both misclassified as stars. While it is likely that our samples of RGB candidates include some of these sources, their effect is expected to broaden the distribution of Δcol by a similar amount in both of the considered colors, given the adopted selection, as for the case of contamination described above.

Fig. 3 Distributions of u − g (solid histograms) and g − r (dashed histograms) color spreads (with respect to the RGB fiducials of Fig. 2) for the clusters in our sample. Panels marked with a) show the distributions of absolute color spreads, while those marked with b) show the normalized color spreads, in units of σ.
-
3.
Differential reddening. In principle, if there is a star-to-star difference in the degree of stellar extinction (due to spatial a variation in the reddening over the considered field of view) this will produce a larger color spread in u − g than in g − r, mimicking the effect we are looking for. However, the ratio of the expected spreads is quite small
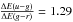 , meaning that a
difference of 0.02 mag in E(B − V)
would correspond to 0.019
in E(g − r) and 0.024
in E(u − g), i.e. a mere
difference of 5 millimag between g − r
and u − g. The clusters considered here have,
in general, low average reddening values (four having
E(B − V) ≤ 0.02, seven
E(B − V) ≤ 0.06, and all nine
E(B − V) ≤ 0.11) and, as far as
we know, no indication of differential reddening has ever been reported in the
literature. In the cases for which we report the detection of significant
u − g spread, the full width at half maximum
(FWHM) of the distribution spread
in u − g is ≳2 times larger than
in g − r, more than the factor of 1.29 that can be
attributable to differential reddening alone. Finally, the case of M 5 presented here
as well as the previous cases reported in the literature (see Sect. 1) suggests that differential reddening does not play
a major role in producing the UV-s, in the cases where this has been revealed up to
now. We conclude that the effects of differential reddening for the considered sample,
should be negligible.
, meaning that a
difference of 0.02 mag in E(B − V)
would correspond to 0.019
in E(g − r) and 0.024
in E(u − g), i.e. a mere
difference of 5 millimag between g − r
and u − g. The clusters considered here have,
in general, low average reddening values (four having
E(B − V) ≤ 0.02, seven
E(B − V) ≤ 0.06, and all nine
E(B − V) ≤ 0.11) and, as far as
we know, no indication of differential reddening has ever been reported in the
literature. In the cases for which we report the detection of significant
u − g spread, the full width at half maximum
(FWHM) of the distribution spread
in u − g is ≳2 times larger than
in g − r, more than the factor of 1.29 that can be
attributable to differential reddening alone. Finally, the case of M 5 presented here
as well as the previous cases reported in the literature (see Sect. 1) suggests that differential reddening does not play
a major role in producing the UV-s, in the cases where this has been revealed up to
now. We conclude that the effects of differential reddening for the considered sample,
should be negligible. -
4.
Photometric errors. Since all the SDSS observations are performed at fixed exposure time and RGB stars emit much less light in the near-UV than in the visible range6, any given star in our sample has larger photometric errors in u than in either g or r: as a consequence, the color spread due to photometric errors is larger in u − g than in g − r. We see below that this is the most serious problem in the present analysis, as there are cases in which a large observed UV-s can be fully accounted for by (relatively) large photometric errors that hide any (possible) underlying signal associated to real differences among stars. To take this effect into due account, we divided the color spread of each star by the associated photometric uncertainty in each color
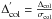 (normalized color spread), which should be
(approximately) expressed in units of standard deviations. Comparing
(normalized color spread), which should be
(approximately) expressed in units of standard deviations. Comparing
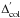 distributions
in g − r
and u − g, we can check whether there is any
significant UV-s in addition to that due to photometric errors; if the latter were the
main contributor to the observed u-g spread, the two distributions
should be indistinguishable.
distributions
in g − r
and u − g, we can check whether there is any
significant UV-s in addition to that due to photometric errors; if the latter were the
main contributor to the observed u-g spread, the two distributions
should be indistinguishable.
In Fig. 3, we plot the distribution of Δcol
and 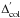 for all the
considered clusters. Histograms in g − r are plotted as
dotted lines, and those in u − g as continuous lines. The
for all the
considered clusters. Histograms in g − r are plotted as
dotted lines, and those in u − g as continuous lines. The
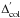 distributions have
been shifted by (small) arbitrary amounts to ensure that their maxima approximately coincide
with
distributions have
been shifted by (small) arbitrary amounts to ensure that their maxima approximately coincide
with 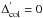 , to allow
a more direct comparison between the distributions in the two color indices7. We shall see below that the significance of the detected
differences is maintained independently of the adopted shifts.
, to allow
a more direct comparison between the distributions in the two color indices7. We shall see below that the significance of the detected
differences is maintained independently of the adopted shifts.
Dimensions of the samples and results of KS tests.
It may be useful to start the discussion of Fig. 3
from the pair of panels in the lower right corner (NGC 2419). As readily visible in the CMD
of Fig. 2, there is an impressive broadening of the
RGB color spread passing from g − r
to u − g in this case. The broadening in
u − g color is so large that we had to adopt a different
horizontal scale in this panel to accommodate the bulk of the
Δu−g distribution. However,
the distributions of 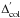 are
indistinguishable, with essentially all the stars lying within ±3σ of the
mean, as expected for (approximately) normal errors8.
Hence, all the UV-s observed in NGC 2419 can be accounted for by the effect of photometric
errors. We note that this does not mean that there is no underlying spread in
light-element abundance, but that the photometric accuracy is not sufficient to reveal it,
if it exists. The same is true for NGC 5466, while the case of M 15 is discussed
in more detail below.
are
indistinguishable, with essentially all the stars lying within ±3σ of the
mean, as expected for (approximately) normal errors8.
Hence, all the UV-s observed in NGC 2419 can be accounted for by the effect of photometric
errors. We note that this does not mean that there is no underlying spread in
light-element abundance, but that the photometric accuracy is not sufficient to reveal it,
if it exists. The same is true for NGC 5466, while the case of M 15 is discussed
in more detail below.
On the other hand, in all the cases considered in the left raster of panels pairs of
Fig. 3 (M 5, M 53, M 13, M 3, and M 2), plus M 92 in
the right raster of panels, the differences in the Δcol distributions correspond
to significant differences in the distributions of 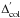 , implying that
the detected UV-s cannot be entirely accounted for by observational effects, thus requiring
the presence of some physical star-to-star difference. In particular,
the
, implying that
the detected UV-s cannot be entirely accounted for by observational effects, thus requiring
the presence of some physical star-to-star difference. In particular,
the  distributions
display extended tails toward the blue that are completely lacking in the remarkably
symmetric g − r distributions. In the case of M 5, we know
from Sect. 2 that the observed
u − g spread correlates with Na abundances (and it is
likely to be caused by differences in N abundances, Yong
et al. 2008). It is interesting to note that the Δcol distribution of
this cluster appears to be bimodal (as in the case of M 4 Marino et al. 2008), even if it is not possible to firmly establish the
statistical significance of this feature. Hints of multi-modality are indeed visible in all
the Δcol (and
distributions
display extended tails toward the blue that are completely lacking in the remarkably
symmetric g − r distributions. In the case of M 5, we know
from Sect. 2 that the observed
u − g spread correlates with Na abundances (and it is
likely to be caused by differences in N abundances, Yong
et al. 2008). It is interesting to note that the Δcol distribution of
this cluster appears to be bimodal (as in the case of M 4 Marino et al. 2008), even if it is not possible to firmly establish the
statistical significance of this feature. Hints of multi-modality are indeed visible in all
the Δcol (and 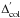 ) distributions
of these six clusters.
) distributions
of these six clusters.
A Kolmogorov-Smirnov (KS) test would be the most straightforward non-parametric way to
quantitatively establish the statistical significance of the detected differences between
the u − g
and g − r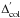 distributions.
However, it is well known that this test is very sensitive to offsets between distributions
and the shifts adopted in Fig. 3 are quite arbitrary.
In principle, a given choice of the shift between the two distribution may add spurious
significance to their mutual difference measured by the KS test. To circumvent this problem,
we proceeded as follows: (a) keeping the
g − r distributions shown in Fig. 3 fixed, we moved the u − g distribution
from − 5 to + 5
distributions.
However, it is well known that this test is very sensitive to offsets between distributions
and the shifts adopted in Fig. 3 are quite arbitrary.
In principle, a given choice of the shift between the two distribution may add spurious
significance to their mutual difference measured by the KS test. To circumvent this problem,
we proceeded as follows: (a) keeping the
g − r distributions shown in Fig. 3 fixed, we moved the u − g distribution
from − 5 to + 5 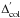 units in steps
of 0.1; (b) at each step, we performed the KS test computing the probability that the two
samples are drawn from the same parent population,
units in steps
of 0.1; (b) at each step, we performed the KS test computing the probability that the two
samples are drawn from the same parent population, 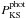 ; and,
(c) we adopted the value of the shift that
maximize
; and,
(c) we adopted the value of the shift that
maximize 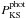 , i.e. the
shift that minimize the significance of the difference between the two
distributions. In this way, we are guaranteed that the residual differences considered by
the KS test are genuine differences in the shape of the distributions, not
due to unphysical shifts. The adopted differential shifts and the corresponding values
of
, i.e. the
shift that minimize the significance of the difference between the two
distributions. In this way, we are guaranteed that the residual differences considered by
the KS test are genuine differences in the shape of the distributions, not
due to unphysical shifts. The adopted differential shifts and the corresponding values
of 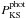 are reported in
Table 2. The significance of the difference in
the u − g and
g − r distributions
of
are reported in
Table 2. The significance of the difference in
the u − g and
g − r distributions
of 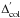 is very high for all
the clusters whose distributions are plotted in the left hand of Fig. 3 plus M 92 (
is very high for all
the clusters whose distributions are plotted in the left hand of Fig. 3 plus M 92 (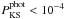 ).
In particular, we note that the difference is also significant in the case of M 15:
the probability that the u − g and
g − r distributions
of
).
In particular, we note that the difference is also significant in the case of M 15:
the probability that the u − g and
g − r distributions
of 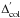 measured in this
cluster are drawn from the same parent population is just 0.08%. A careful inspection of the
measured in this
cluster are drawn from the same parent population is just 0.08%. A careful inspection of the
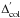 distributions for
this cluster in Fig. 3 reveals that while the wings
virtually coincide, the core of the g − r distribution is
far more peaked than its u − g counterpart, which exhibits
hints of bi-modality (compare with the cases of NGC 5466 and NGC 2419, where the
distributions nearly coincide in both the wings and the core). Hence, while
the amplitude of the effect is insufficient to provide an obvious color segregation in the
CMD of this cluster (see Fig. 1), the underlying signal
is there and can be revealed once the much larger photometric sample is considered and the
observational effects are properly taken into account, in agreement with the results of
Yong et al. (2008). This conclusion is strongly
supported by the behavior of the radial distributions of RGB stars as a function of their
color spread in this cluster, as discussed in the following section.
distributions for
this cluster in Fig. 3 reveals that while the wings
virtually coincide, the core of the g − r distribution is
far more peaked than its u − g counterpart, which exhibits
hints of bi-modality (compare with the cases of NGC 5466 and NGC 2419, where the
distributions nearly coincide in both the wings and the core). Hence, while
the amplitude of the effect is insufficient to provide an obvious color segregation in the
CMD of this cluster (see Fig. 1), the underlying signal
is there and can be revealed once the much larger photometric sample is considered and the
observational effects are properly taken into account, in agreement with the results of
Yong et al. (2008). This conclusion is strongly
supported by the behavior of the radial distributions of RGB stars as a function of their
color spread in this cluster, as discussed in the following section.
We note that the four clusters displaying the most obvious and significant difference in
their  and
and
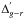 distributions
have metallicity around [Fe/H] = −1.5, while M 53, M 92, and M 15, which have
larger
distributions
have metallicity around [Fe/H] = −1.5, while M 53, M 92, and M 15, which have
larger 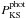 , are significantly
more metal-poor ([Fe/H] ≲ −2.0). This is likely due to the weakening of the intrinsic
UV-s effect at low metallicity, discussed in Sect. 2.1.
, are significantly
more metal-poor ([Fe/H] ≲ −2.0). This is likely due to the weakening of the intrinsic
UV-s effect at low metallicity, discussed in Sect. 2.1.
3.1. The radial distribution of UV-red and UV-blue stars
As anticipated in Sect. 1, it would be very interesting to check whether RGB stars with different u − g colors (at the same magnitude) may have different radial distributions. According to some models of the early enrichment of GCs, at the end of the enrichment phase (lasting a few hundred Myr), stars from the first generation (P) should be significantly less concentrated toward the center of the cluster than stars of later generation(s) (I+E), born from material polluted by the ashes of P stars (D’Ercole et al. 2008). While it may be expected that this difference should have been largely erased long ago by the dynamical evolution of the cluster (D’Ercole et al. 2008; Decressin et al. 2008), the (sparse) available observational evidence about radial distributions of the two populations is in qualitative agreement with the prediction of the above quoted model. For example, Kravtsov et al. (2010b,a) found that the stars on the red side of of the broad U − I distribution of the RGB of NGC 1261 and NGC 3201 are significantly more centrally concentrated than those on the blue side. In the case of NGC 3201, Carretta et al. (2010a) used detailed Na, O abundances from high resolution spectroscopy to show that Na-rich RGB stars are redder (in U − I) and more centrally concentrated than Na-poor RGB stars.
Carretta et al. (2009b) merged the spectroscopic sample of RGB stars in 19 GCs, normalizing the distance of each star from the center of its cluster by the cluster rh, and compared the radial distributions of P, I, and E stars. They found that I stars are significantly more centrally concentrated that P stars, while E stars appear slightly less concentrated than P stars. However, as discussed in detail by Carretta et al. (2009b), this result may be affected by serious selection biases, inherent to the process of efficient fiber allocation in multi-object spectroscopy of Galactic GC stars.
A difference in the radial distribution of the two sub giant branches of NGC 1851 (whose stars are presumed to differ in terms of CNO abundance; Cassisi et al. 2008) was detected by Zoccali et al. (2009), but the result was not fully confirmed by Milone et al. (2009). However, Carretta et al. (2010e) find that the radial distribution of the RGB stars they analyzed depends on their iron abundance, more metal-poor stars being more centrally concentrated than their more metal-rich counterparts.
Different populations with different radial distributions are known to be present in ω Centauri (Pancino et al. 2003; Sollima et al. 2007; Villanova et al. 2007), but this system is more complex and may have a different origin with from classical GCs (see Carretta et al. 2010c, and references therein).
To follow-up this line of investigation with our sample, we divided the selected
RGB candidates in each of the considered clusters into two sub-samples, according to the
value of their normalized u − g spread
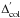 . For brevity, we
dub UV-blue the stars having
. For brevity, we
dub UV-blue the stars having 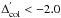 and UV-red those having
and UV-red those having
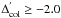 , in the scale of
Fig. 3 (i.e. using the shifts adopted there). It is
important to recall that any observational effect potentially affecting the radial
distributions (notably, the radial variation in the degree of completeness, due to the
increase in crowding toward the center) must affect the two sub-samples exactly in the
same way, as they have the same distribution of magnitudes.
, in the scale of
Fig. 3 (i.e. using the shifts adopted there). It is
important to recall that any observational effect potentially affecting the radial
distributions (notably, the radial variation in the degree of completeness, due to the
increase in crowding toward the center) must affect the two sub-samples exactly in the
same way, as they have the same distribution of magnitudes.
The comparison between the radial distributions of UV-blue and UV-red RGB stars for all
the considered clusters is presented in Fig. 4;
the probability that the two distributions are drawn from the same parent population
according to a KS test (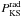 ) is
reported in the last column of Table 2. In all the
clusters for which we detected a significant intrinsic
u − g spread (including M 15), the UV-red population
is obviously more centrally concentrated than the UV-blue one,
with
) is
reported in the last column of Table 2. In all the
clusters for which we detected a significant intrinsic
u − g spread (including M 15), the UV-red population
is obviously more centrally concentrated than the UV-blue one,
with 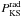 always lower (and
in most cases much lower) than 0.02%. We note that this result is very
insensitive to the actual choice of the
always lower (and
in most cases much lower) than 0.02%. We note that this result is very
insensitive to the actual choice of the 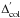 threshold;
the difference remains highly significant for a large range of adopted thresholds
(in particular, for the whole range
threshold;
the difference remains highly significant for a large range of adopted thresholds
(in particular, for the whole range 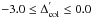 ).
).
 |
Fig. 4 Comparison between the radial distribution of UV-blue (continuous blue line) and UV-red (dashed red line) for all the considered clusters. The data within the radius marked by the dotted lines in the plots of the distributions for M 53, M 2, and M 13 were not included in the analysis (see Sects. 2 and 2.1). See Table 2 for the significance of the detected differences, as measured by the KS test. |
This result clearly provides further support to the physical significance of the u − g spread: it is very hard to conceive how any spurious observational effect can be associated with such a strong difference in the radial distribution. Moreover, it suggests that the higher degree of central concentration of UV-red (putative I+E) stars with respect to UV-blue (putative P) stars may be a general characteristic of all GCs where intrinsic UV-s can be detected, therefore any model intended to explain the origin of the spread in light-element abundances in GCs should also be able to reproduce this feature.
Figure 4 aims to demonstrate the high level of
statistical significance of the detected differences between the radial distributions of
UV-red and UV-blue stars. To allow a more direct comparison with the predictions of
chemo-hydro-dynamical models (D’Ercole et al. 2008;
Decressin et al. 2008, 2010), in Fig. 5 we present the
radial profile of the ratio of the number of UV-red to UV-blue stars
(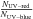 ),
where the radial coordinate is expressed in units of the clusters core
radii (rc), and the distances of 1−5 half-light
radii (rh) are also indicated (vertical dashed lines). This
ratio should approximately scale as the ratio of second generation(s) (I+E) to first
generation (P) stars, whose radial distribution is a typical outcome of the considered
models. However, we stress that while the overall shape of the observed profiles does not
change much when different thresholds between UV-blue and UV-red stars are adopted9, the true values
of NUV − red/NUV − blue
depends on the adopted threshold, hence they cannot be directly compared with
second-to-first generation ratios computed elsewhere. The only safe conclusion that we can
draw here is that UV-red stars are more abundant than UV-blue stars (in the innermost
~3−4 rh) for any threshold
),
where the radial coordinate is expressed in units of the clusters core
radii (rc), and the distances of 1−5 half-light
radii (rh) are also indicated (vertical dashed lines). This
ratio should approximately scale as the ratio of second generation(s) (I+E) to first
generation (P) stars, whose radial distribution is a typical outcome of the considered
models. However, we stress that while the overall shape of the observed profiles does not
change much when different thresholds between UV-blue and UV-red stars are adopted9, the true values
of NUV − red/NUV − blue
depends on the adopted threshold, hence they cannot be directly compared with
second-to-first generation ratios computed elsewhere. The only safe conclusion that we can
draw here is that UV-red stars are more abundant than UV-blue stars (in the innermost
~3−4 rh) for any threshold
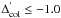 , albeit with
cluster-to-cluster differences of a factor of a few; this is in qualitative agreement with
the predictions by D’Ercole et al. (2008) and Decressin et al. (2010), and with the observations by
Carretta et al. (2010d).
, albeit with
cluster-to-cluster differences of a factor of a few; this is in qualitative agreement with
the predictions by D’Ercole et al. (2008) and Decressin et al. (2010), and with the observations by
Carretta et al. (2010d).
The profiles shown in Fig. 5 cover the range given by ≃0.5−1 rh and >4 rh. In nearly all cases, the profiles display a relatively steep decline from the innermost bin out to a radius of ~3 rh where they flatten at a level NUV−red/NUV−blue ≲ 1, remaining approximately flat out to the last observed point. Hints of another increase at rh ≳ 10 rh are seen in the profiles of M 3 and M 2 but their significance seems only marginal, if any. A notable exception to this general trend is provided by M 13, whose profile is nearly flat out to ~3 rh, then declines into another flat branch at r ~ 4 rh.
 |
Fig. 5 Ratio of the number of UV-red to UV-blue stars as a function of distance from the
cluster center, for the seven clusters in which we detected a significant intrinsic
UV-s. The radial coordinate is expressed in units of cluster core radii, the dashed
vertical lines marks the radial distances corresponding to 1−5 half-light radii
(rc and rh from Harris 1996). The ratio is computed in radial
bins 2.5′ wide in steps of 0.5′. Note that the actual value of the ratio depends on
the adopted threshold between UV-red and UV-blue stars: here we adopted
|
It is interesting to compare the observed profiles with the model predictions shown in Fig. 18 of D’Ercole et al. (2008). In that specific model, after 25 half-light relaxation times of evolution, the profile of the second-to-first generation number ratio is nearly flat within r ≃ 0.5 rh (a region always entirely enclosed in the innermost bin of our profiles, or not even included in the considered sample, in the cases of M 2 and M 53), then has declined by a factor of a few by ≃2 rh, at the limit of that figure. This is in fair agreement with the observed profiles10; a broad agreement is also found with some of the models presented in Decressin et al. (2010, see the middle bottom and right bottom panels of their Fig. 1. A detailed comparison with models is far beyond the scope of the present paper. On the other hand, we feel that Fig. 5 provides a very useful set of observational constraints that must be reproduced by models of GC formation. Unfortunately, our data do not sufficiently probe the innermost regions (r ≤ 0.5 rh) of the considered clusters; and complementary HST observations are probably needed to check this part of the profiles. Finally, a fully meaningful comparison with the profiles of Fig. 5 would require dedicated models for each cluster, taking into account its specific structural and dynamical properties, as well as accounting for its evolution for a Hubble time.
3.2. Comments on individual clusters
In this section, we briefly report on previous results about abundance and/or UV color spreads in the clusters considered in the present paper.
Five of our clusters were also considered in the study by Yong et al. (2008), namely M 5, M 3, M 13, M 15, and M 92. These clusters display a significant spread at all evolutionary stages in the V, cy CMD (from photometry by Grundahl et al. 1999). According to Yong et al. (2008), the observed spreads are comparable to that seen in NGC 6752, suggesting that all these clusters exhibit a ≃2.0 dex dispersion in [N/Fe], i.e., the value found in NGC 6752.
Grundahl et al. (1998) provided evidence of stars from two different populations in the horizontal branch of M 13. In particular, they noted that at any given (b − y)0 color, there is a large spread in the c0 index (defined as c0 = c1 − 0.2 E(b − y)) that they interpreted as being due to star-to-star-variations in CNO abundances.
Turning to spectroscopic analyses, Martell et al. (2008) showed that M 53 has a broad but not strongly bimodal distribution of CN band strength, with CN and CH band strengths that are anticorrelated for unevolved stars.
For the well-studied cluster M 5, Smith & Norris (1983) showed that the cyanogen distribution is strongly bimodal for a sample of 29 stars near the RGB tip. The classic Na/O anti-correlation has been found by Sneden et al. (1992) and confirmed by Ivans et al. (2001). This was further correlated with the CN strength index, δS(3839): stars with larger CN indices also have larger Na and Al abundances and lower O abundances than stars with lower CN indices. Finally, Briley et al. (1992) and Cohen et al. (2002) found strong (and anti-correlated) variations in the abundances of C and N of stars down to the base of the RGB of M 5.
An extended Na/O anti-correlation was found also in the extremely metal-poor cluster M 92 (Sneden et al. 1991), as well as strong (and anticorrelated) variations in the abundances of C and N (Carbon et al. 1982).
Spectroscopic observations revealed star-to-star variations in the abundances of the CNO group elements among the M 3 giants (Pilachowski & Sneden 2001), with both oxygen-rich and oxygen-poor stars coexisting in the cluster (Kraft et al. 1992; Cohen et al. 2005).
Lee (2000) claimed the existence of a C-N anticorrelation among stars on the lower RGB of M 15, although no bimodality is found (Cohen et al. 2005). Kayser et al. (2008) showed a weak indication of a bimodality in the CH-CN plane (two clumps separated at CN ~ −0.6), although the observational errors are large compared to the separation of the two clumps. Pancino et al. (2010) detected a clear and bimodal CN and CH anticorrelation among the unevolved stars measured by Kayser et al. (2008). Finally, Smith & Mateo (1990) found a CN-CH band strength anticorrelation and a possible bi-modality in their sample of red giants in the cluster M 2.
We note that for all the clusters in which we detected a significant intrinsic u − g spread, there was previous evidence of inhomogeneity in their stellar population reported in literature, supporting our findings.
Previous detections of differences in radial distributions between different populations in GCs were limited to the cases of ω Cen, NGC 1851, NGC 1261, and NGC 3201, as discussed in Sect. 3.1. The results presented here more than doubles the number of GCs where these differences are detected at a very high degree of significance.
4. Summary and conclusions
We have used publicly available u,g,r photometry from An et al. (2008) to search for anomalous spread in near UV color (u − g) along the RGB of nine high-latitude, low-reddening, and well populated Galactic GCs. This anomalous spread (UV-s) was detected before in some clusters, using colors including other broad/intermediate band filters, such as Johnson’s U or Strömgren u, and it was shown to be associated with the well known spread in the abundance of light elements (C, N, O, Na, etc.; see Carretta et al. 2009b, and references therein). The main results of our analysis can be summarized as follows:
-
1.
We have introduced a method to remove the effect of pho-tometric errors from the observed color spread, normalizingthe color residual about a fiducial RGB lineof each considered star by the associated photometric er-ror (
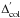 ).
By comparing the distribution of
).
By comparing the distribution of  with that
of
with that
of 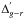 of the same
sample of candidate RGB stars, we revealed anomalous
u − g spreads in seven of the nine clusters. The
observed effect has a very high statistical significance in all seven cases: according
to Kolmogorv-Smirnov tests, the probability that the observed
of the same
sample of candidate RGB stars, we revealed anomalous
u − g spreads in seven of the nine clusters. The
observed effect has a very high statistical significance in all seven cases: according
to Kolmogorv-Smirnov tests, the probability that the observed
 and
and
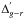 distribution
are drawn from the same parent population are always lower that 0.1%, but typically
much lower than this. The lack of detection of any significant intrinsic
u − g spread in the two remaining clusters
(NGC 2419 and NGC 5466) may be due to a real lack of chemical spread but it may also
be associated with insufficient photometric accuracy and/or radial sampling. NGC 2419
is far more distant than any other cluster in the sample and its RGB is observed at
much fainter apparent magnitudes, implying much larger photometric errors in the range
of interest; for the same reason, the available photometry for this cluster samples
mostly the portion of the RGB between the HB and the tip, where the amplitude of the
UV-s effect is known to decrease. The radial range explored here for NGC 5466 is the
smallest of the whole sample,
r ≤ 4.1 rh. There are indications
that the UV-s effect may be weaker at very low metallicity and this may also hamper
our ability to detect it in clusters with [Fe/H] ≲ −1.8.
distribution
are drawn from the same parent population are always lower that 0.1%, but typically
much lower than this. The lack of detection of any significant intrinsic
u − g spread in the two remaining clusters
(NGC 2419 and NGC 5466) may be due to a real lack of chemical spread but it may also
be associated with insufficient photometric accuracy and/or radial sampling. NGC 2419
is far more distant than any other cluster in the sample and its RGB is observed at
much fainter apparent magnitudes, implying much larger photometric errors in the range
of interest; for the same reason, the available photometry for this cluster samples
mostly the portion of the RGB between the HB and the tip, where the amplitude of the
UV-s effect is known to decrease. The radial range explored here for NGC 5466 is the
smallest of the whole sample,
r ≤ 4.1 rh. There are indications
that the UV-s effect may be weaker at very low metallicity and this may also hamper
our ability to detect it in clusters with [Fe/H] ≲ −1.8. -
2.
In the case of M 5 ([Fe/H] = –1.34), we have demonstrated that the Na abundance correlates with the u − g color along the RGB, in the same way as in other clusters studied in the literature: Na-rich cluster stars have redder u − g colors than Na-poor cluster stars of the same magnitude, while they are indistinguishable in g − r. The same effect is not seen in M 15 ([Fe/H] = −2.32): we attribute this to the weakening of the UV-s with decreasing metallicity, which is probably associated with the extreme weakening of CN lines for [Fe/H] ≲ −1.8 (Smith 2002), as CN and NH features in the region 3000 Å ≤ λ ≤ 4000 Å are thought to be at the origin of the effect. However, the case of M 5 illustrates that light-element abundance variations can be traced with the u − g color as done before with U − B, U − V, U − I, and cy indices (see, for example Yong et al. 2008; Marino et al. 2008; Han et al. 2009; Carretta et al. 2009b, 2010d).
-
3.
Dividing the RGB stars of each cluster into UV-blue and UV-red subsamples, according to their
 , we found
that UV-red stars are more centrally concentrated than UV-blue stars in all the seven
clusters in which we detected a significant intrinsic UV-s. Kolmogorv-Smirnov tests
have proven that the difference in the radial distributions of the two groups are
highly significant in all cases: the probability that UV-blue and UV-red stars be
drawn from the same radial distribution is always lower than 0.02%.
, we found
that UV-red stars are more centrally concentrated than UV-blue stars in all the seven
clusters in which we detected a significant intrinsic UV-s. Kolmogorv-Smirnov tests
have proven that the difference in the radial distributions of the two groups are
highly significant in all cases: the probability that UV-blue and UV-red stars be
drawn from the same radial distribution is always lower than 0.02%. -
4.
The radial profiles of the ratio of UV-red to UV-blue stars typically show an approximately linear decline from the first sampled point (at ≃0.5−1 rh) out to 3−4 rh, where they flatten and remain approximately flat out to the last sampled point (at ≃4−8 rh). This behavior is in qualitative agreement with the predictions of most recent models of formation and chemical evolution of globular clusters. It is interesting to note that in M 13 the profile is flat in the innermost ~3 rh, then declines at larger radii. The shape of the observed profile provides a quantitative basis to test these theoretical scenarios, once specific models reproducing the present-day status of the considered clusters become available.
The results presented here clearly suggest that the difference in the radial distribution of first and second generation stars may be a general characteristic of globular clusters. Moreover, it has been demonstrated that near UV photometry can be a very efficient tool to trace light element spreads in very large samples of RGB stars in clusters, and it is especially well suited to studying the radial distribution of the various cluster populations. It must be considered that the very encouraging results presented in this paper have been obtained with a relatively small (2.5 m aperture) ground-based telescope, under non-ideal seeing conditions (≤1.6″ FWHM, An et al. 2008). A survey performed with larger telescopes and/or under good seeing conditions (e.g., with service mode observations) and complemented with HST observations of the cluster cores would provide a completely new insight into the problem, and would surely contribute to shedding light on the mysterious earliest phases of the evolution of globular clusters.
In particular, cy = c1 − (b − y) and c1 = (u − v) − (v − b), see Yong et al. (2008), and references therein.
The SDSS u filter has λeff = 3521 Å and FWHM = 555 Å. For details about the photometric filters quoted in this paper see the Asiago Database of Photometric Systems http://ulisse.pd.astro.it/Astro/ADPS/ (Moro & Munari 2000).
This should not affect the results presented below, as in all the cases we compare RGB stars having the same distribution in magnitude, see Sect. 3.1.
P stands for the first – Primordial – generation (Na-poor stars), while Na-rich stars are divided into I (Intermediate) and E (Extreme) subsequent generations. For homogeneity, we follow the nomenclature by Carretta et al. but we always consider all Na-rich stars as a single class (I+E), for simplicity.
There are other factors concurring to lower the signal-to-noise ratio of u observations with respect to g or r ones. For example: (1) CCDs are less sensitive in near-UV than in visible bands; (2) as in the SDSS the photometry of a given field is taken simultaneously in all the ugriz passbands and the seeing worsens at shorter wavelengths, u images hence experiencing the worst seeing; (3) at fixed atmospheric transparency conditions and air mass, u light suffers from the highest amount of atmospheric extinction.
In particular, the g − r distribution has been shifted
to ensure that its well defined maximum occurs at 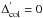 , while for the broader
u − g distributions, with less clear peaks, we
searched for a compromise between placing the peak at
, while for the broader
u − g distributions, with less clear peaks, we
searched for a compromise between placing the peak at
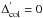 and matching the right (red) edge
of the two distributions, to make the comparison easier.
and matching the right (red) edge
of the two distributions, to make the comparison easier.
Over the range 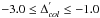 . In particular, the slope
of the inner rising branch of the profile changes with the adopted threshold (the relative
height of the central peak grows by a factor of ≲3−4 changing the threshold from −1
to −3) but the radius where the profile flattens remains unchanged. In Fig. 5, we have adopted
. In particular, the slope
of the inner rising branch of the profile changes with the adopted threshold (the relative
height of the central peak grows by a factor of ≲3−4 changing the threshold from −1
to −3) but the radius where the profile flattens remains unchanged. In Fig. 5, we have adopted
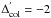 , as above.
, as above.
Acknowledgments
We are grateful to E. Vesperini for useful discussions and comments. This research is partially supported by the PRIN-INAF 2009 (“Formation and Early Evolution of Massive Star Clusters”, P.I. R. Gratton). This research has made use of NASA’s Astrophysics Data System Bibliographic Services. This research has made use of the SIMBAD database and VizieR catalogue access tool, operated at CDS, Strasbourg, France. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- An, D., Johnson, J. A., Clem, J. L., et al. 2008, ApJS, 179, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M. 2007, A&A, 473, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briley, M. M., Smith, G. H., Bell, R. A., Oke, J. B., & Hesser, J. E. 1992, ApJ, 387, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Carbon, D. F., Romanishin, W., Langer, G. E., et al. 1982, ApJS, 49, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Gratton, R. G., Bragaglia, A., Bonifacio, P., & Pasquini, L. 2004, A&A, 416, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009a, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009b, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., D’Orazi, V., Lucatello, S., & Gratton, R. G. 2010a, A&A, 519, A71 [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., et al. 2010b, ApJ, 712, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010c, ApJ, 714, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010d, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Gratton, R. G., Lucatello, S., et al. 2010e, ApJ, 722, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Briley, M. M., & Stetson, P. B. 2002, AJ, 123, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Briley, M. M., & Stetson, P. B. 2005, AJ, 130, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Colucci, J. E., Bernstein, R. A., Cameron, S., McWilliam, A., & Cohen, J. G. 2009, ApJ, 704, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Baumgardt, H., & Kroupa, P. 2008, A&A, 492, 101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Baumgardt, H., Charbonnel, C., & Kroupa, P. 2010, A&A, 516, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Grebel, E. K., Odenkirchen, M., & Chiosi, C. 2004, A&A, 422, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Groenewegen, M. A. T., Hatziminaoglou, E., & da Costa, L. 2005, A&A, 436, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Carretta, E., Matteucci, F., & Sneden, C. 2000, A&A, 358, 671 [NASA ADS] [Google Scholar]
- Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grundahl, F., & Andersen, M. I. 1999, in Galaxy Evolution: Connecting the Distant Universe with the Local Fossil Record, ed. M. Spite, 197 [Google Scholar]
- Grundahl, F., & Briley, M. 2001, Nucl. Phys. A, 688, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Grundahl, F., Vandenberg, D. A., & Andersen, M. I. 1998, ApJ, 500, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Grundahl, F., Catelan, M., Landsman, W. B., Stetson, P. B., & Andersen, M. I. 1999, ApJ, 524, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Grundahl, F., Briley, M., Nissen, P. E., & Feltzing, S. 2002, A&A, 385, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, S., Lee, Y., Joo, S., et al. 2009, ApJ, 707, L190 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Ivans, I. I., Kraft, R. P., Sneden, C., et al. 2001, AJ, 122, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Ivans, I. I., & Stetson, P. B. 2006, ApJ, 640, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Kayser, A., Hilker, M., Grebel, E. K., & Willemsen, P. G. 2008, A&A, 486, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraft, R. P. 1994, PASP, 106, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., Sneden, C., Langer, G. E., & Prosser, C. F. 1992, AJ, 104, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, V., Alcaíno, G., Marconi, G., & Alvarado, F. 2010a, A&A, 512, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kravtsov, V., Alcaíno, G., Marconi, G., & Alvarado, F. 2010b, A&A, 516, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, J.-W., Kang, Y.-W., Lee, J., & Lee, Y.-W. 2009, Nature, 462, 480 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lee, S. G. 2000, J. Korean Astron. Soc., 33, 137 [NASA ADS] [Google Scholar]
- Letarte, B., Hill, V., Jablonka, P., et al. 2006, A&A, 453, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marino, A. F., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martell, S. L., & Smith, G. H. 2009, PASP, 121, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Martell, S. L., Smith, G. H., & Briley, M. M. 2008, PASP, 120, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Stetson, P. B., Piotto, G., et al. 2009, A&A, 503, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Piotto, G., King, I. R., et al. 2010, ApJ, 709, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Moro, D., & Munari, U. 2000, A&AS, 147, 361 [Google Scholar]
- Mucciarelli, A., Origlia, L., Ferraro, F. R., & Pancino, E. 2009, ApJ, 695, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E., Seleznev, A., Ferraro, F. R., Bellazzini, M., & Piotto, G. 2003, MNRAS, 345, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E., Rejkuba, M., Zoccali, M., & Carrera, R. 2010, A&A, 524, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilachowski, C. A., & Sneden, C. 2001, BAAS, 33, 1513 [NASA ADS] [Google Scholar]
- Piotto, G. 2009, in IAU Symp. 258, ed. E. E. Mamajek, D. R. Soderblom, & R. F. G. Wyse, 233 [Google Scholar]
- Ramírez, S. V., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Renzini, A. 2008, MNRAS, 391, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Buzzoni, A. 1986, in Spectral Evolution of Galaxies, ed. C. Chiosi, & A. Renzini, Astrophys. Space Sci. Libr., 122, 195 [Google Scholar]
- Smith, G. H. 2002, PASP, 114, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H., & Mateo, M. 1990, ApJ, 353, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H., & Martell, S. L. 2003, PASP, 115, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. H., & Norris, J. 1983, ApJ, 264, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Kraft, R. P., Prosser, C. F., & Langer, G. E. 1991, AJ, 102, 2001 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Kraft, R. P., Prosser, C. F., & Langer, G. E. 1992, AJ, 104, 2121 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Ferraro, F. R., Bellazzini, M., et al. 2007, ApJ, 654, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1994, in The Restoration of HST Images and Spectra – II, ed. R. J. Hanisch, & R. L. White, 308 [Google Scholar]
- Ventura, P., & D’Antona, F. 2008, MNRAS, 385, 2034 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Piotto, G., King, I. R., et al. 2007, ApJ, 663, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Grundahl, F., Johnson, J. A., & Asplund, M. 2008, ApJ, 684, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Pancino, E., Catelan, M., et al. 2009, ApJ, 697, L22 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 g, g − r and g, u − g CMDs for M 5, M 15. The stars for which spectroscopic abundances are available from from Carretta et al. (2009a,b) are marked according to their Na abundances: Na-poor stars are marked as blue open circles, while Na-rich stars are marked with red open triangles. Stars plotted as heavy dark dots are those selected as candidate RGB stars from the g, g − r CMD. |
| In the text | |
 |
Fig. 2 g − r, g and g, u − g CMDs for the GCs in our sample. In some cases, the RGB is truncated due to SDSS saturation. The red arrows in the upper right corner of each panel are the reddening vectors whose amplitudes correspond to the average E(B − V) values reported in Table 1. Horizontal black arrows mark the position of the RGB bump. Stars selected as candidate RGB on the (g, g − r) CMDs are plotted as heavy dark dots, the remaining ones as lighter red dots. The curves approximately tracing the red edges of the RGBs are used as references to compute the color spread distributions shown in Fig. 3; the two horizontal segments display the portion of the RGB that is used to compute those distributions. In most cases, note that the asymptotic giant branch starts above the bright end of the adopted selection box (NGC 2419 is an obvious exception). |
| In the text | |
 |
Fig. 3 Distributions of u − g (solid histograms) and g − r (dashed histograms) color spreads (with respect to the RGB fiducials of Fig. 2) for the clusters in our sample. Panels marked with a) show the distributions of absolute color spreads, while those marked with b) show the normalized color spreads, in units of σ. |
| In the text | |
 |
Fig. 4 Comparison between the radial distribution of UV-blue (continuous blue line) and UV-red (dashed red line) for all the considered clusters. The data within the radius marked by the dotted lines in the plots of the distributions for M 53, M 2, and M 13 were not included in the analysis (see Sects. 2 and 2.1). See Table 2 for the significance of the detected differences, as measured by the KS test. |
| In the text | |
 |
Fig. 5 Ratio of the number of UV-red to UV-blue stars as a function of distance from the
cluster center, for the seven clusters in which we detected a significant intrinsic
UV-s. The radial coordinate is expressed in units of cluster core radii, the dashed
vertical lines marks the radial distances corresponding to 1−5 half-light radii
(rc and rh from Harris 1996). The ratio is computed in radial
bins 2.5′ wide in steps of 0.5′. Note that the actual value of the ratio depends on
the adopted threshold between UV-red and UV-blue stars: here we adopted
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.