| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014758 | |
| Published online | 26 November 2010 | |
Development of electric currents in a magnetic field configuration containing a magnetic null point
1
Max-Planck-Institut für Sonnensystemforschung (MPS),
Katlenburg-Lindau,
Germany
e-mail: santos@mps.mpg.de
2 Geophysical Institute, University of Alaska Fairbanks (UAF),
Fairbanks, USA
e-mail: ao@how.gi.alaska.edu
Received:
9
April
2010
Accepted:
14
September
2010
Context. In the past the role of magnetic null points in the generation of electric currents was investigated mainly in the close vicinity of the null, with perturbations being applied at nearby boundaries, or for a magnetic null configuration with a dome-shaped fan. In the solar atmosphere, however, electric currents are generated by perturbations originating at the photosphere, far away from coronal 3D nulls, and the occurence of magnetic nulls with a dome-shaped fan is apparently not common.
Aims. We investigate the consequences of photospheric motion for the development of electric currents in a coronal magnetic field configuration containing a null, located far away from the boundaries, and the influence of topological structures on the spatial distribution of the currents.
Methods. We use a 3D resistive MHD code to investigate the consequences of photospheric plasma motion for the generation of currents in a coronal magnetic field containing a null. The plasma is considered fully compressible and is initially in hydrostatic equilibrium. The initial magnetic field is potential (current free).
Results. The photospheric plasma motion causes magnetic field perturbations that propagate to the corona along the field lines at the local Alfvén speed. The Alfvénic wave perturbations correspond to a propagating current directed mainly parallel to the magnetic field. Perpendicular currents connect to return currents to close the current system. The magnetic perturbations eventually reach the vicinity of the null. However, the currents forming in and around the null, near the fan surface or near the spine field lines, are not always the strongest currents developing in the simulation box. In our simulation, the strongest currents develop close to the bottom boundary, where the plasma is moved, and below the null point, in a region where field line connectivity considerably changes.
Conclusions. Our simulation shows that the presence of a magnetic null point does not necessarily mean that the strongest currents will form in or around the null, at the fan surface or at the spine. Our results indicate that regions of considerable change in field line connectivity are fundamental for the development of strong and thin current sheets. Regions of connectivity change are important because they combine perturbations that are generated at different locations on the Sun. Our results also suggest that it is more important how the perturbations are mapped and combined in regions of considerable connectivity change than what is the driver of the perturbations itself. The driver does not necessarily need to create strong currents where it is applied. However, when the perturbations produced by the driver combine in the regions of considerable connectivity change, they can increase the current in regions for which the length scale is much smaller than the characteristic length scale of the system. The location of regions of connectivity change, combined with the mapping of the perturbations to those regions, can be a useful tool to predict where and when solar flares will occur.
Key words: Sun: atmosphere / Sun: magnetic topology / magnetic reconnection / magnetohydrodynamics
© ESO, 2010
1. Introduction
Magnetic reconnection is a physical process related to changes of the magnetic field connectivity. In the course of reconnection the free magnetic energy, which is stored in the system as electric currents, is converted into kinetic and thermal energy (Dungey 1953; Cowling 1953).
In three dimensions reconnection can take place either in configurations containing null points (Priest & Titov 1996) or at places of non vanishing field strength, the so called finite-B-reconnection (Hesse & Schindler 1988). In both cases the formation of the current sheets is very important (Priest & Démoulin 1995; Büchner 2006). Global topological features influence the current sheet formation. Magnetohydrodynamic (MHD) simulations of electric current development in magnetic field configurations containing no null point have been carried out in the past (De Moortel & Galsgaard 2006a,b; Galsgaard et al. 2003b; Pontin et al. 2005; Wilmot-Smith & De Moortel 2007; Wilmot-Smith & Priest 2007; Parnell et al. 2008; Linton & Priest 2003; Aulanier et al. 2006). They have shown that topological features like separators, separatrices, quasi-separatrices (QSL) and hyperbolic-flux-tubes (HFT) are the preferred location for electric current development. Several authors (Pontin & Craig 2005; Pontin et al. 2007b,a; Pontin & Galsgaard 2007; Pariat et al. 2009; Masson et al. 2009) investigated the formation of electric currents in magnetic field configurations containing a null point. They all start with a potential null and perturb the system either by moving the plasma at the boundaries near fan and spine field lines, or by adding a perturbation field and letting the system relax. In both cases similar results are obtained: strong currents develop preferentially in and around the null region, along the fan plane or along the spine. The preferred location depends on the driver used to generated the magnetic perturbations. Shear of the magnetic field lines generates strong currents in and around the null, while rotation of the fan (spine) field lines generates strong current systems at the spine (fan). The authors have noticed that the peak current strength depends on the plasma β, the resistivity η and on the amplitude of the plasma velocity used to perturb the system. Higher driver velocities increase the current peak value. Also important is the compressibility of the plasma, which is measured by the polytropic index (γ). For higher values of γ the current sheets spread more and the peak value of the current decreases.
Some of these previous investigations (Pontin & Craig 2005; Pontin et al. 2007b,a; Pontin & Galsgaard 2007) were, however, performed in a region very close to the null. The authors do not consider the global magnetic field structure of the corona and the formation and closure of larger scale current systems away from the null. In the solar atmosphere the energy input is caused by the photospheric plasma motion, while coronal null points can be located tens of Mm away from those regions. Investigations of the global magnetic field structure (Pariat et al. 2009; Masson et al. 2009) consider a specific example of a magnetic field configuration containing a null, the dome-shaped fan null. However, this is not the only possible magnetic field configuration containing a magnetic null. Indeed, a dome-shaped fan null is not even frequently observed in the solar atmosphere. We address these two points by running numerical experiments for a complementary magnetic field configuration containing a null point. In our simulation a null point located high in the simulation box (≈32 Mm) is connected to the bottom boundary by the fan and spine field lines. We move the plasma at the bottom of the simulation box in regions close to the foot points of the fan and spine field lines and follow the formation of electric currents as the Alfvénic perturbation generated by the plasma motion propagates along the field lines. The model setup is described in detail in Sect. 2, while the results obtained for the different runs are presented in Sect. 3. In Sect. 4 we summarize and discuss our results, and in Sect. 5 we present our main conclusions.
2. Model setup
The model solves the following set of resistive MHD equations (in normalized units):
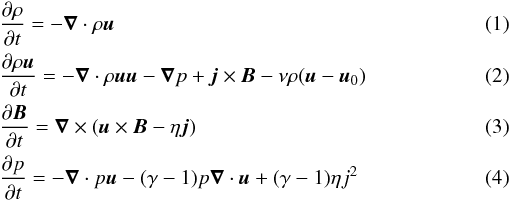 together
with Ohm’s law, Ampère’s law and taking into account the ideal gas equation for a fully
ionized plasma
together
with Ohm’s law, Ampère’s law and taking into account the ideal gas equation for a fully
ionized plasma  Here
ρ is the plasma mass density, u is the
plasma velocity, B is the magnetic field,
p is the thermal pressure, T is the plasma temperature and
γ is the polytropic index (
Here
ρ is the plasma mass density, u is the
plasma velocity, B is the magnetic field,
p is the thermal pressure, T is the plasma temperature and
γ is the polytropic index (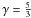 ). The
quantity u0 denotes the velocity of a neutral
gas, to which the plasma is coupled. To decrease the numerical errors in evaluating the
electric current density we solve
∇ × B1, where
B1 = B − BP.
The field BP is the initial
potential field, which is current free
(∇ × BP = 0).
Hence,
∇ × B1 = ∇ × B.
This assumption is valid at any time instant.
). The
quantity u0 denotes the velocity of a neutral
gas, to which the plasma is coupled. To decrease the numerical errors in evaluating the
electric current density we solve
∇ × B1, where
B1 = B − BP.
The field BP is the initial
potential field, which is current free
(∇ × BP = 0).
Hence,
∇ × B1 = ∇ × B.
This assumption is valid at any time instant.
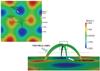 |
Fig. 1 Magnetic field lines connecting the null point, which is located inside the black box, to the bottom boundary. Also shown is the Z component of the magnetic field at the bottom of the simulation box. The color code represents the intensity of the magnetic field in normalized units. The view in the bottom panel is along the positive Y-axis. |
The system of equations is solved in an equidistant cartesian grid (131 × 131 ×
131 grid points) that covers a 3D volume of 21 × 21 ×
21 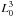 . The simulation
box has six boundaries: four lateral, top and bottom boundaries. The lateral boundaries use
line symmetric boundary conditions consistent with the set of MHD equations (Otto et al. 2007), while the top and bottom boundaries
are open. By open boundaries we mean that at the physical boundary the gradients of all
quantities in the direction normal to the boundary are equal to the gradients in the same
direction immediately at the first layer inside the simulation box. This provides a smooth
transition for the forces when they go through the physical boundary. The magnetic field
also satisfies ∇·B = 0. The
normalization of the macroscopic variables is chosen as
B0 = 100 G, L0 = 107 m,
T0 = 106 K,
. The simulation
box has six boundaries: four lateral, top and bottom boundaries. The lateral boundaries use
line symmetric boundary conditions consistent with the set of MHD equations (Otto et al. 2007), while the top and bottom boundaries
are open. By open boundaries we mean that at the physical boundary the gradients of all
quantities in the direction normal to the boundary are equal to the gradients in the same
direction immediately at the first layer inside the simulation box. This provides a smooth
transition for the forces when they go through the physical boundary. The magnetic field
also satisfies ∇·B = 0. The
normalization of the macroscopic variables is chosen as
B0 = 100 G, L0 = 107 m,
T0 = 106 K, 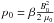 ,
,
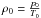 ,
,
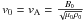 and
and 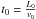 .
We consider a constant background magnetic diffusivity of
η′ ≈ 10-6 in normalized units, which corresponds to
η ≈ 106 m2/s in real physical units.
.
We consider a constant background magnetic diffusivity of
η′ ≈ 10-6 in normalized units, which corresponds to
η ≈ 106 m2/s in real physical units.
The initial magnetic field is obtained analytically by
![\begin{eqnarray} && B_{x} = \exp \left( - \lambda_{2} z \right) \left[ 25\sin\frac{2\pi}{L}x \right] \nonumber \\ &&\qquad +\, \exp\left(-\lambda_{4}z\right)\left[-125\sin\frac{4\pi}{L}x\right] \nonumber \\ &&\qquad + \frac{75\exp\left(-\lambda_{22}z\right)}{\sqrt{2}} \left[-\cos\frac{2\pi}{L}x\sin\frac{2\pi}{L}y \!+\! \sin\frac{2\pi}{L}x\cos\frac{2\pi}{L}y \right] \end{eqnarray}](/articles/aa/full_html/2011/01/aa14758-10/aa14758-10-eq35.png) (8)
(8)![\begin{eqnarray} && B_{y} = \exp\left(-\lambda_{2}z\right)\left[25\sin\frac{2\pi}{L}y\right] \nonumber \\ &&\qquad + \, \exp\left(-\lambda_{4}z\right)\left[125\sin\frac{4\pi}{L}y\right] \nonumber \\ &&\qquad + \frac{75\exp\left(-\lambda_{22}z\right)}{\sqrt{2}}\left[-\sin\frac{2\pi}{L}x\cos\frac{2\pi}{L}y \!+ \!\cos\frac{2\pi}{L}x\sin\frac{2\pi}{L}y\right] \end{eqnarray}](/articles/aa/full_html/2011/01/aa14758-10/aa14758-10-eq36.png) (9)
(9)![\begin{eqnarray} && B_{z} = \exp\left(-\lambda_{2}z\right)\left[25\cos\frac{2\pi}{L}y + 25\cos\frac{2\pi}{L}x\right] \nonumber \\ &&\qquad +\, \exp\left(-\lambda_{4}z\right)\left[125\cos\frac{4\pi}{L}y-125\cos\frac{4\pi}{L}x\right] \nonumber \\ &&\qquad + 75\exp\left(-\lambda_{22}z\right)\left[\sin\frac{2\pi}{L}x\sin\frac{2\pi}{L}y \!+\! \cos\frac{2\pi}{L}x\cos\frac{2\pi}{L}y\right], \end{eqnarray}](/articles/aa/full_html/2011/01/aa14758-10/aa14758-10-eq37.png) (10)where
L is the length-scale used in the
normalization (L0) and the different
coefficients λ are given in Table 1. This magnetic field configuration contains a magnetic null point located at the
center of the simulation box in X and Y, and
around 3.2 L0 in the Z direction (≈32 Mm).
Note that this null is much higher in the corona than the nulls obtained from quiet-Sun
photospheric magnetic field extrapolations (Régnier et al.
2008; Longcope & Parnell 2009).
Indeed, the height of the null depends on the smallest wavenumber present in the spatial
Fourier spectrum of the vertical component of the photospheric magnetic
field (Bz(z = 0)). Hence,
the height of our null corresponds to photospheric magnetic fields containing large scale
field structures, as in the case of active regions. The null point is connected to the
bottom of the simulation box by spine and fan field lines. The Jacobian matrix, evaluating
the structure around the null, has the eigenvalues of the matrix at the null point of
about (2, −1.7, −0.3) (Guo et al. 2010). The first
positive eigenvalue defines the spine, while the last two indicate the fan surface.
Figure 1 shows a lateral and top view of the field
lines connecting the null to the bottom of the simulation box, the location of the null
(small box) and the distribution of the Z component of the magnetic field
at the bottom of the simulation box. The plasma is initially at hydrostatic equilibrium
(p = const.) with constant temperature
T = 0.1T0 and constant density
ρ = 10ρ0. The plasma beta is around 0.03 in
the strong magnetic field regions and reaches infinity at the null.
(10)where
L is the length-scale used in the
normalization (L0) and the different
coefficients λ are given in Table 1. This magnetic field configuration contains a magnetic null point located at the
center of the simulation box in X and Y, and
around 3.2 L0 in the Z direction (≈32 Mm).
Note that this null is much higher in the corona than the nulls obtained from quiet-Sun
photospheric magnetic field extrapolations (Régnier et al.
2008; Longcope & Parnell 2009).
Indeed, the height of the null depends on the smallest wavenumber present in the spatial
Fourier spectrum of the vertical component of the photospheric magnetic
field (Bz(z = 0)). Hence,
the height of our null corresponds to photospheric magnetic fields containing large scale
field structures, as in the case of active regions. The null point is connected to the
bottom of the simulation box by spine and fan field lines. The Jacobian matrix, evaluating
the structure around the null, has the eigenvalues of the matrix at the null point of
about (2, −1.7, −0.3) (Guo et al. 2010). The first
positive eigenvalue defines the spine, while the last two indicate the fan surface.
Figure 1 shows a lateral and top view of the field
lines connecting the null to the bottom of the simulation box, the location of the null
(small box) and the distribution of the Z component of the magnetic field
at the bottom of the simulation box. The plasma is initially at hydrostatic equilibrium
(p = const.) with constant temperature
T = 0.1T0 and constant density
ρ = 10ρ0. The plasma beta is around 0.03 in
the strong magnetic field regions and reaches infinity at the null.
Coefficients in the exponentials used in the field expansion.
The initial equilibrium of the system is perturbed by coupling the plasma to a moving background neutral gas. The transfer of momentum is provided by a collision term in the momentum equation. The collision frequency between plasma and neutral gas is chosen to be higher than the inverse of the Alfvén time for z ≤ L0 and to vanish for z > L0. The velocity field of the neutral gas motion is imposed in form of vortices in a way that ∇·v vanishes (no compression, no emerging magnetic flux through the boundary).
We performed three different numerical experiments. In the first experiment, we imposed two velocity vortices that rotate the plasma at the foot points of the field lines close to the fan plane. Both velocity vortices rotate clockwise and have a maximum velocity of approximately 50 km s-1. In the second experiment, the velocity vortices are centered at the foot points of the spine field lines. The vortices have the same characteristic as those used in the first experiment. In the third experiment, we re-run the case of the motion of the spine foot points with one of the vortices rotating clockwise, while the other rotates counterclockwise. These three patterns of motion should generate perturbations in the magnetic field that propagate to the null, in the first experiment along the fan and in the second and third experiments along the spine field lines. Our aim is to investigate the formation of the resulting global current system including currents forming near the null and currents forming away from the null, e.g. close to topological boundaries.
3. Results
The motion of the neutral gas transfers momentum to the plasma, which starts to move in the same way. The normalized background plasma resistivity is chosen to be as low as possible to allow almost ideal conditions. Hence, plasma and magnetic flux move together. The plasma motion perturbs the magnetic field at the bottom of the simulation box, creating a small bending of the magnetic field. This perturbation in the magnetic field propagates along the magnetic field at the local Alfvén speed (torsional Alfvén waves). Because the magnetic field is stronger at the bottom of the simulation box and decreases upward, the Alfvén speed decreases with height. The magnetic bending associated with the Alfvénic waves corresponds to electric current perturbations according to ∇ × B. Because the plasma motion is mainly horizontal in regions of strong vertical B fields, the generated currents will be mainly parallel to the magnetic field. The currents should satisfy ∇·J = 0, hence, perpendicular currents might connect to return currents to close the current system. The currents propagate along the field lines at the local Alfvén speed, following the perturbations of the magnetic field.
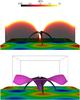 |
Fig. 2 Top panel: color-coded values of plasma β in a plane of x constant located at the center of the simulation box. The values of β are saturated at 15 for a better visualization. Bottom panel: isosurface of β = 1 layer in a subvolume (black box) close to the center of the simulation box (view is along the positive X-axis). Also shown are the fan and spine field lines, together with the Z component of the magnetic field at the bottom boundary of the simulation box. |
It is known that fast-mode waves can also be generated by nonlinear coupling to the helical Alfvén wave (Nakariakov et al. 1997). This happens mainly when the driver velocity presents a near discontinuity. In principle this is not the case in our simulations because the driver is defined by the collision term in the momentum equation, which couples the plasma to the neutral gas at a time scale proportional to the inverse of the collision frequency. Wave mode conversion can also happen in the region where β ≈ 1 (Galsgaard et al. 2003a; McLaughlin & Hood 2006). In this region, a low β fast wave is transformed into high β fast and slow waves. These waves correspond to currents that can accumulate close to the null and along separatrices. At the null itself the Alfvén speed vanishes and, as a consequence, Alfvénic perturbations cannot reach it. However, because of the non-zero sound speed at the null, perturbations can still reach the null as pure acoustic waves. Figure 2 shows the values of β in a plane x=constant located at the center of the simulation box (top panel) and an isosurface showing the location of the β = 1 layer in our initial configuration (bottom panel).
3.1. Locating regions of connectivity change
Regions where the coronal magnetic field considerably changes its connectivity to the photospheric sources are important because magnetic field perturbations that are generated at different locations of the solar surface can be combined there. Depending on the relative direction of these perturbations, they can give rise to strong and thin electric current sheets.
 |
Fig. 3 Spatial distribution of the measure of connectivity change ⟨ cosθ ⟩ i,j,k above the region containing the quadrupolar field. Values lower than 1 hint at a possible change of the global connectivity (view is along the positive X-axis). Also shown are the spine and fan field lines, together with the magnetic field at the bottom of the simulation box. |
 |
Fig. 4 Plasma velocity vector (black arrows) at the beginning of the simulation for the case where the foot points of fan field lines are moved. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
We determine the location of regions where the magnetic field presents connectivity changes. In regions of connectivity changes, the angle between the magnetic field vector at two neighboring points should increase from 0 to 180 degrees. Consequently, if we aim to check if at the point (i,j,k) the magnetic field changes its connectivity, we compare the angle between the magnetic field vector at this point and the magnetic field on the six neighboring points of the simulation grid. To create a quantitative measure to verify the change in connectivity, we average the information about the angle variation between those points.
 |
Fig. 5 Lateral view along the positive Y-axis of the distribution of the vector current density inside the simulation volume at different instants of time. The arrows show the vector direction, the color code its amplitude and the size of the arrows the relative strength of the currents. Also shown are the spine and fan field lines, colored by the amplitude of the current, together with the Z component of the magnetic field at the bottom of the simulation box. |
The cosine of the angle between magnetic field vectors at a
point (i,j,k) and at its neighboring
point (i + 1,j,k) is given by
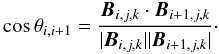 (11)The point
(i,j,k) has six neighbors, and the average of the cosine of the angle
between the vector Bi,j,k and
its neighbors is calculated as
(11)The point
(i,j,k) has six neighbors, and the average of the cosine of the angle
between the vector Bi,j,k and
its neighbors is calculated as 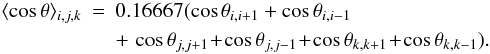 (12)We
use this average ⟨ cosθ ⟩ i,j,k at the
point (i,j,k) to determine if the magnetic field presents any change in
connectivity around this point.
If ⟨ cosθ ⟩ i,j,k is equal to 1,
the magnetic field at grid point (i,j,k) is aligned with the magnetic
field at its neighboring points.
If ⟨ cosθ ⟩ i,j,k is less than 1, at least
one of the magnetic field vectors is changing its direction around the
point (i,j,k). The advantage of this method compared to the squashing
factor Q (Titov et al. 2002) is that it directly
diagnoses the location in the grid where the change of connectivity occurs. However, we
are aware that the method is sensitive only to local changes of the connectivity around
the grid point (i,j,k).
(12)We
use this average ⟨ cosθ ⟩ i,j,k at the
point (i,j,k) to determine if the magnetic field presents any change in
connectivity around this point.
If ⟨ cosθ ⟩ i,j,k is equal to 1,
the magnetic field at grid point (i,j,k) is aligned with the magnetic
field at its neighboring points.
If ⟨ cosθ ⟩ i,j,k is less than 1, at least
one of the magnetic field vectors is changing its direction around the
point (i,j,k). The advantage of this method compared to the squashing
factor Q (Titov et al. 2002) is that it directly
diagnoses the location in the grid where the change of connectivity occurs. However, we
are aware that the method is sensitive only to local changes of the connectivity around
the grid point (i,j,k).
Figure 3 shows a volume-rendering visualization of ⟨ cosθ ⟩ i,j,k calculated in a subvolume containing the quadrupolar structure that is located close to the center of the simulation box. The null point is the region with the strongest change in connectivity. However, changes in connectivity also take place along a column above and below the null region. Even if the changes in connectivity through this column are less intense than at the null proper, the region might contribute to the development of strong and thin electric currents. This happens because, different from what happens in the null, the Alfvén speed is not zero there and, consequently, magnetic perturbations can reach that area. The region of change in connectivity below the null is also closer to the source of perturbations. This means that perturbations arrive there first and only later at the null region. However, clearly, to form strong current systems in that region the perturbations have to be started at the footpoints of field lines connecting to that area, and the perturbations should be combined in a way that ∇ × B increases. Only then electric currents can be generated there.
 |
Fig. 6 Current density vectors in a volume subset close to the null point region, at the center of the simulation box. Right column shows a view along the fan plane, positive X-axis, while the left column shows a view along the spine plane, positive Y-axis. Arrows show the vector direction, the color code its amplitude and the size of the arrows the relative strength of the currents. Also shown are the spine and fan field lines, colored by the amplitude of the currents, together with the Z component of the magnetic field at the bottom of the simulation box. |
3.2. Motion of fan foot points
As can be seen in Fig. 1, the fan field lines are mainly anchored in the two positive polarities composing the central quadrupolar region at the bottom boundary of the simulation box, with some of the fan field lines connecting also to weaker positive polarities around the two main polarities and to the walls of the simulation box. In the first numerical experiment we perturb the system by two velocity vortices, each of which is centered in one of the positive polarities where the fan field lines are anchored. Both vortices rotate clockwise. Figure 4 depicts the plasma velocity field at the very beginning of the simulation (black arrows). The figure also shows the spine and fan field lines, and color-coded the strength of the vertical (Z-) component of the magnetic field at the bottom of the simulation box. The rotation of the plasma in regions of strong positive Bz produces currents directed mainly parallel to the magnetic field lines. Electric currents perpendicular to the magnetic field are also present and connect to return currents that close the current system. Figure 5 shows the current density vectors at four instants of time. While the arrows point in the current direction, the color-coding indicates the current density, and the length of the arrows corresponds to the relative strength of the currents. The color code is saturated at a normalized value of 2 for a better visualization of the strong currents. Also shown are the fan and spine field lines and, color-coded, the value of the vertical (Z-) component of the magnetic field at the bottom of the simulation box. At t = 12.5 τA the current system is already well stablished. In our simulation the current system assumes the form of two fountains with their center mapping back to the center of the plasma velocity vortices. The current perturbations propagate along the field lines. At t = 25.0 τA they reach the center of the simulation box. At t = 37.5 τA a strong current sheet starts to form at the center of the simulation box, below the null point. The current sheet dimensions along the Z direction are much larger than in the X and Y directions. We will refer to this below as the current channel.
 |
Fig. 7 Top – surfaces for the x, y, and z constant, showing the distribution of the current amplitude in the region around the current channel. The three surfaces intersect in a point close to the center of the current channel in Z direction. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. Bottom – distribution of the current density amplitude along three lines in X, Y, and Z direction. The lines intersect at the same point of intersection of the planes. |
 |
Fig. 8 Lateral (top) and top (bottom) view of the parallel current density distribution in the central region of the simulation box. Red represents parallel currents and blue anti-parallel currents. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
 |
Fig. 9 Top view of the plasma flow field showing a stagnation flow pattern, which is characteristic of reconnection. The arrows show the velocity vector direction, the color code its amplitude and the size of the arrows the relative strength of the velocity. Also shown are the spine and fan field lines, together with the Z component of the magnetic field. |
The formation of the current channel is evident in Fig. 6, which shows the evolution from two viewpoints: along the fan (right column), view in the direction of the positive X-axis, and along the spine (left column), view in the direction of the positive Y-axis. Let us have a closer look at a smaller volume around the center of the simulation box to analyze the temporal evolution of the electric currents around the current channel. The figure shows the current density vectors (arrows). The color of the arrows depicts the current density amplitude and their size its strength. The field lines shown in the figure are the spine and fan field lines. Also shown is the Z component of the magnetic field at the bottom of the simulation box. At t = 37.5 τA the current channel is visible as a region of high current density depicted by red arrows in the figure. It is located at the center of the volume subset and below the null point. The current system extends along the Z direction and spreads preferentially along the direction of the fan plane.
In Fig. 7 the current density magnitude is shown in three planes for x, y, and z constant, at time t = 50.0 τA. The x, y, and z values are chosen in a way that the planes intersect in a point close to the center of the current channel in the Z direction. Also shown is the line plot of the current amplitude for three lines in the X, Y, and Z directions, intersecting at the point of intersection of the three planes. This figure shows that the current channel extends along the Z direction and reaches a peak strength at z ≈ 2.0 L0. The current spreads along the X and Y directions in the plane of z = const., assuming a double Y form.
 |
Fig. 10 Plasma velocity vector (black arrows) at the beginning of the simulation for the case where the foot points of the spine field lines are moved. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
Let us now focus on the component of the electric current parallel to the magnetic field
(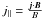 ).
Parallel currents are important because they can give rise to parallel electric fields,
a signature of reconnection and a measure of the reconnection rate. Figure 8 shows a lateral and top view of the distribution of the
parallel currents close to the center of the simulation box, constructed using volume
rendering. Dark red and dark blue regions correspond to parallel and anti-parallel
currents, respectively. The current channel contains the strongest field-aligned current
in the system. Parallel currents are also present along the fan plane, along the spine and
in the regions where the plasma is moved. However, they are weaker than the currents in
the current channel.
).
Parallel currents are important because they can give rise to parallel electric fields,
a signature of reconnection and a measure of the reconnection rate. Figure 8 shows a lateral and top view of the distribution of the
parallel currents close to the center of the simulation box, constructed using volume
rendering. Dark red and dark blue regions correspond to parallel and anti-parallel
currents, respectively. The current channel contains the strongest field-aligned current
in the system. Parallel currents are also present along the fan plane, along the spine and
in the regions where the plasma is moved. However, they are weaker than the currents in
the current channel.
A signature of reconnection in addition to parallel electric fields is the occurrence of stagnation flows. Figure 9 shows a top view of the plasma velocity field close to the region of interest. The arrows represent the velocity vector, the color code gives the amplitude of the velocity and the size of the arrows represent the relative strength of the velocity. Also shown are the fan and spine field lines, and the Z component of the magnetic field at the bottom of the simulation box. Close to the current channel the plasma motion turns into a a stagnation flow with an inflow and an outflow region. This means that reconnection can happen through the region where the current channel is formed and that plasma can be accelerated when it crosses this region as soon as the plasma becomes non-ideal there (e.g. resistive).
3.3. Motion of spine foot points
The spine field lines connect the null and the negative polarities of the central quadrupolar region. In this section we describe two different numerical experiments where a region close to the foot points of the spine field lines is perturbed. The aim is to investigate the influence of the driver properties on the formation of strong current sheets, in particular the strong current channel below the null.
3.3.1. Vortices with the same sense of rotation
In the second numerical experiment, the center of the velocity vortices coincides with the foot points of the spine field lines. The direction of rotation, the velocity amplitude, and the radius of the velocity vortices are the same as in the previous numerical experiment. Figure 10 shows the velocity of the plasma at the very beginning of the simulation run (black arrows).
Because the polarity at the foot points of the spine field lines is opposite to that of the fan field lines, the currents generated near the spine field lines will have opposite direction with respect to those generated in the first numerical experiment. Figure 11 shows the current density vectors at four different instants of time. As in the first numerical experiment, the plasma motion generates magnetic field perturbations that correspond to electric currents. The currents are mainly field aligned currents, with perpendicular currents connecting to return currents in order to close the current loop system. The currents spread along the field lines, as does the magnetic field perturbation. According to the global structure of the magnetic field, the current system assumes the form of two current fountains. Because the vortices are now centered at the foot points of the spine field lines, the perturbation propagates along those lines and the fountains are bent along the spine. At t = 21 τA the magnetic perturbation reaches the center of the simulation box and, as in the first numerical experiment, a strong current channel forms below the null point. Again, the currents are the strongest in this region and in the regions where the motion is applied.
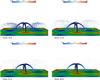 |
Fig. 11 Same as Fig. 5 but for the case where the foot points of the spine field lines are moved. The view is along the positive X-axis. |
Figure 12 shows the temporal evolution of the current density vectors close to the central region of the simulation box from two different view points, along the spine (left column) and along the fan plane (right column). The current channel is already forming as early as at t = 21.0 τA. At t = 43 τA the current density vectors start to point in random directions (see the view along the spine) in what corresponds to a disruption of the current channel.
In Fig. 13 the current density magnitude is shown in three planes, for x, y, and z constant, intersecting in a point close to the center of the current channel in the Z direction at t = 43 τA. Also shown is the line plot of the current strength along three lines, in X, Y, and Z directions, intersecting at the same point of intersection of the three planes. The current channel extends along the Z direction, with the current strength also spreading in the X and Y direction in the plane of z constant. Differently from the previous case, the current system now forms a double peak in Z direction (at z ≈ 1.5 and z ≈ 2.0) after the disruption of the current channel.
A lateral and top view of the distribution of the parallel currents close to the center of the simulation box is shown in Fig. 14. Like in the first numerical experiment, the current channel is the strongest field-aligned current system present in this region. Parallel currents are also present along the fan plane, along the spine and in the regions where the plasma is moved. However, they are much weaker than the currents in the current channel.
Finally, Fig. 15 shows a top view of the plasma velocity field close to the region of interest. Like in the first numerical experiment, the plasma presents a stagnation flow close to the current channel. This is a signature that reconnection is happening on the region where the strong parallel currents are formed and that plasma is accelerated when it crosses the current channel region.
3.3.2. Vortices with an opposite sense of rotation
In the third numerical experiment we invert the sense of rotation of one of the vortices responsible for moving the footpoints of the spine field lines. Now, one of the vortices is moving counterclockwise, while the other mantains the clockwise rotation of the second experiment. Figure 16 shows the velocity of the plasma at the very beginning of the simulation (black arrows). Also shown are the fan and spine field lines, and the Z component of the magnetic field at the bottom of the simulation box.
As before, the plasma motion causes a perturbation in the magnetic field that travels along the field lines at the local Alfvén speed. The perturbations of the magnetic field generate electric currents according to ∇ × B. The currents are mainly parallel to the magnetic field, with perpendicular currents connecting to return currents to close the current system. There is, however, an important difference regarding the results obtained for the electric current between the third and the other two numerical experiments. Figure 17 shows the current density vectors in the simulation volume (top panel) and a close-up view at the region where the current channel in the previous cases was formed (bottom panel), both at t = 49.5 τA. From the figure we can see that in this case no strong current channel is forming below the magnetic null. The current is distributed mainly along the spine field lines and the strong currents are located at the bottom boundary, where the plasma is moved by the interaction with the neutral gas.
Figure 18 shows the spatial distribution of parallel currents in a subvolume of the simulation box that contains the quadrupolar region. The figure also shows the spine and fan field lines together with the Z component of the magnetic field at the bottom boundary of the simulation box. The parallel currents are distributed mainly along the spine field lines. They are stronger close to the bottom boundary, where the plasma is moved. Again there is no strong current channel below the null region. While no current channel is formed in this case of plasma motion, the plasma velocity presents a random distribution around that region. There are no signs of plasma acceleration in this case. Figure 19 shows the plasma velocity vectors. The arrows depict the velocity direction, while the color and the size of the arrows indicate the velocity amplitude. Also shown are the fan and spine field lines, together with the Z component of the magnetic field at the bottom boundary.
 |
Fig. 16 Plasma velocity vector (black arrows) at the very beginning of the simulation for the case where the foot points of the spine field lines are moved. One of the vortices rotates clockwise, while the other rotates counterclockwise. Also shown are the fan and spine field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
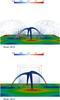 |
Fig. 17 Top – lateral view along the positive X-axis of the distribution of current density vectors inside the simulation box at t = 49.5 τA. The arrows show the current density direction, while the color and size of the arrows represent the current density amplitude. Bottom – close-up of the central region in the simulation box, where the current channel developed in the previous numerical experiments. The view direction is the same as in the top panel. |
 |
Fig. 18 Lateral (top panel) and top (bottom panel) view of the parallel current density distribution in the central region of the simulation box. Red represents parallel currents and blue anti-parallel currents. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
 |
Fig. 19 Top view of plasma flow field at t = 49.5 τA. The arrows show the velocity vector direction, the color code its amplitude and the size of the arrows the relative strength of the velocity. Also shown are the spine and fan field lines together with the Z component of the magnetic field. |
4. Summary and discussion
We performed three different numerical experiments in which the system is perturbed by moving the plasma at the footpoints of field lines connecting to a magnetic null. The motion of the plasma causes magnetic field perturbations that are associated to electric currents. Both the magnetic field perturbations and electric currents propagate along the magnetic field lines at the local Alfvén speed.
Our magnetic configuration is given analytically. It has a null point located in the middle of the box in the X–Y direction, at a height of ≈32 Mm. The null point is connected to the bottom of the simulation box (photosphere) via spine and fan field lines. Considerable changes in field line connectivity happen at the null and in a column extending above and below it. Regions of connectivity change are important for the interaction of magnetic field perturbations that are generated at different places on the solar surface. Their combination can generate strong and thin current sheets, far away from the places where the perturbations were launched.
This is exactly what happened in the first two numerical experiments. The perturbations propagate from the foot points of spine and fan field lines along the magnetic field. They accumulate in regions where the magnetic field considerably changes its connectivity. The structure and rotation sense of the drivers used in the first two numerical experiments produced magnetic field perturbations that, when combined in this region of considerable connectivity change, generated a strong and thin current channel. Because the current channel is closer to the bottom boundary, where perturbations start to propagate, the current channel forms long before the perturbations reach the null. The continuous action of the driver amplified the currents in the current channel in a way that even after the perturbations arrived at the null, the current channel carried the strongest current system present in the simulation box. The currents in the current channel appear mainly along the magnetic field. They generate parallel electric fields according to E∥ = ηj∥. From the results obtained in the first two numerical experiments, we conclude that the presence of a null does not necessarily imply that the strongest currents will develop near the null, along the spine, or along the fan field lines. There can be other places, where field line connectivity considerably changes, which are, more favorable for the development of strong and thin current (sheets or channels) concentrations depending on the particular magnetic field configuration and structure of the driving plasma motion.
In a third numerical experiment the sense of rotation of one of the vortices used to perturb the footpoints of the spine field lines was reversed (one of the vortices rotates clockwise, while the other rotates counterclockwise). There, the interaction of the perturbations in the region where the connectivity of the magnetic field considerably changes did not generate a current channel. The currents are distributed mainly along the spine field lines and are strongest in the regions where the plasma is moved (close to the bottom boundary). This result shows how important the driver is for the formation of strong and thin current sheets in places of connectivity change. The presence of regions of strong connectivity change is a necessary but not sufficient condition for the occurrence of strong and thin current sheets, and the plasma has to be driven in an appropriate way.
Note that the results obtained here, even if they are applied to a symmetric quadrupole, could be generalized to any quadrupolar configuration. The break in symmetry would only change the position of the null, the spine, the fan, and the region of connectivity change. However, strong currents would still preferentially form in this region of considerable connectivity change. It is also a challenge to find drivers in the solar photosphere that are perfectly symmetric or anti-symmetric. In this case, results like those obtained in the third numerical experiment would be very difficult to find and the common situation would be that of currents always forming in regions of considerable connectivity change.
5. Conclusions
Our investigation shows the importance of places where the connectivity of the magnetic field considerably changes for the development of strong current concentrations. Based on the results obtained here we can arrive at the following conclusions:
-
1.
The presence of a magnetic null does not necessary mean thatthe strongest currents will form in or around the null,at the spine or the fan field lines.
-
2.
Regions where the magnetic field connectivity considerably changes are decisive for the formation of strong and thin current sheets, because they combine perturbations that are generated at different locations of the solar surface.
-
3.
The mapping and combination of perturbations generated by the photospheric driver at the regions of considerable connectivity change determine if strong and thin current sheets will form in those regions. The presence of regions of considerable connectivity change is a necessary but not a sufficient condition for the formation of strong and thin current sheets.
-
4.
The location of regions of considerable connectivity change, combined with the mapping of the perturbations to those regions, can be used as a tool to predict where and when solar flares will occur.
Acknowledgments
J.C.S. and A.O. thank the Max-Planck Society for funding their work by the Inter-institutional Research Initiative “Turbulent transport and ion heating, reconnection and electron acceleration in solar and fusion plasmas”, project MIF-IF-A-AERO8047. J.C.S. thanks the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for funding his post doc fellowship under the project 201318/2008-3. The authors would like to thank the anonimous referee for improving the quality of the paper.
References
- Aulanier, G., Pariat, E., Démoulin, P., & Devore, C. R. 2006, Sol. Phys., 238, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Büchner, J. 2006, Space Sci. Rev., 122, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Cowling, T. G. 1953, ed. G. P. Kuiper (Chicago: University of Chicago Press) [Google Scholar]
- De Moortel, I., & Galsgaard, K. 2006a, A&A, 451, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Galsgaard, K. 2006b, A&A, 459, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dungey, J. W. 1953, Phil. Mag., 44, 725 [Google Scholar]
- Galsgaard, K., Priest, E. R., & Titov, V. S. 2003a, J. Geophys. Res., Space Phys., 108, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., Titov, V. S., & Neukirch, T. 2003b, ApJ, 595, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J., Büchner, J., Otto, A., et al. 2010, A&A, 513, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hesse, M., & Schindler, K. 1988, J. Geophys. Res., 93, 5559 [NASA ADS] [CrossRef] [Google Scholar]
- Linton, M. G., & Priest, E. R. 2003, ApJ, 595, 1259 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Parnell, C. E. 2009, Sol. Phys., 254, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Pariat, E., Aulanier, G., & Schrijver, C. J. 2009, ApJ, 700, 559 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2006, A&A, 459, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Roberts, B., & Murawski, K. 1997, Sol. Phys., 175, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Otto, A., Büchner, J., & Nikutowski, B. 2007, A&A, 468, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., Haynes, A. L., & Galsgaard, K. 2008, ApJ, 675, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., & Craig, I. J. D. 2005, Phys. Plasmas, 12, 072112 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., & Galsgaard, K. 2007, J. Geophys. Res., Space Phys., 112, 3103 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Galsgaard, K., Hornig, G., & Priest, E. R. 2005, Phys. Plasmas, 12, 052307 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007a, Phys. Plasmas, 14, 052106 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007b, Phys. Plasmas, 14, 052109 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Démoulin, P. 1995, J. Geophys. Res., 100, 23443 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Titov, V. S. 1996, R. Soc. London Proc. Ser. A, 354, 2951 [Google Scholar]
- Régnier, S., Parnell, C. E., & Haynes, A. L. 2008, A&A, 484, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titov, V. S., Hornig, G., & Démoulin, P. 2002, J. Geophys. Res., Space Phys., 107, 1164 [Google Scholar]
- Wilmot-Smith, A. L., & De Moortel, I. 2007, A&A, 473, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilmot-Smith, A. L., & Priest, E. R. 2007, Phys. Plasmas, 14, 102903 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Magnetic field lines connecting the null point, which is located inside the black box, to the bottom boundary. Also shown is the Z component of the magnetic field at the bottom of the simulation box. The color code represents the intensity of the magnetic field in normalized units. The view in the bottom panel is along the positive Y-axis. |
| In the text | |
 |
Fig. 2 Top panel: color-coded values of plasma β in a plane of x constant located at the center of the simulation box. The values of β are saturated at 15 for a better visualization. Bottom panel: isosurface of β = 1 layer in a subvolume (black box) close to the center of the simulation box (view is along the positive X-axis). Also shown are the fan and spine field lines, together with the Z component of the magnetic field at the bottom boundary of the simulation box. |
| In the text | |
 |
Fig. 3 Spatial distribution of the measure of connectivity change ⟨ cosθ ⟩ i,j,k above the region containing the quadrupolar field. Values lower than 1 hint at a possible change of the global connectivity (view is along the positive X-axis). Also shown are the spine and fan field lines, together with the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 4 Plasma velocity vector (black arrows) at the beginning of the simulation for the case where the foot points of fan field lines are moved. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 5 Lateral view along the positive Y-axis of the distribution of the vector current density inside the simulation volume at different instants of time. The arrows show the vector direction, the color code its amplitude and the size of the arrows the relative strength of the currents. Also shown are the spine and fan field lines, colored by the amplitude of the current, together with the Z component of the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 6 Current density vectors in a volume subset close to the null point region, at the center of the simulation box. Right column shows a view along the fan plane, positive X-axis, while the left column shows a view along the spine plane, positive Y-axis. Arrows show the vector direction, the color code its amplitude and the size of the arrows the relative strength of the currents. Also shown are the spine and fan field lines, colored by the amplitude of the currents, together with the Z component of the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 7 Top – surfaces for the x, y, and z constant, showing the distribution of the current amplitude in the region around the current channel. The three surfaces intersect in a point close to the center of the current channel in Z direction. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. Bottom – distribution of the current density amplitude along three lines in X, Y, and Z direction. The lines intersect at the same point of intersection of the planes. |
| In the text | |
 |
Fig. 8 Lateral (top) and top (bottom) view of the parallel current density distribution in the central region of the simulation box. Red represents parallel currents and blue anti-parallel currents. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 9 Top view of the plasma flow field showing a stagnation flow pattern, which is characteristic of reconnection. The arrows show the velocity vector direction, the color code its amplitude and the size of the arrows the relative strength of the velocity. Also shown are the spine and fan field lines, together with the Z component of the magnetic field. |
| In the text | |
 |
Fig. 10 Plasma velocity vector (black arrows) at the beginning of the simulation for the case where the foot points of the spine field lines are moved. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 11 Same as Fig. 5 but for the case where the foot points of the spine field lines are moved. The view is along the positive X-axis. |
| In the text | |
 |
Fig. 12 Same as Fig. 6 but for the case where the foot points of the spine field lines are moved. |
| In the text | |
 |
Fig. 13 Same as Fig. 7 but for the case where the foot points of the spine field lines are moved. |
| In the text | |
 |
Fig. 14 Same as Fig. 8 but for the case where the foot points of the spine field lines are moved. |
| In the text | |
 |
Fig. 15 Same as Fig. 9 but for the case where the foot points of the spine field lines are moved. |
| In the text | |
 |
Fig. 16 Plasma velocity vector (black arrows) at the very beginning of the simulation for the case where the foot points of the spine field lines are moved. One of the vortices rotates clockwise, while the other rotates counterclockwise. Also shown are the fan and spine field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 17 Top – lateral view along the positive X-axis of the distribution of current density vectors inside the simulation box at t = 49.5 τA. The arrows show the current density direction, while the color and size of the arrows represent the current density amplitude. Bottom – close-up of the central region in the simulation box, where the current channel developed in the previous numerical experiments. The view direction is the same as in the top panel. |
| In the text | |
 |
Fig. 18 Lateral (top panel) and top (bottom panel) view of the parallel current density distribution in the central region of the simulation box. Red represents parallel currents and blue anti-parallel currents. Also shown are the spine and fan field lines, together with the Z component of the magnetic field at the bottom of the simulation box. |
| In the text | |
 |
Fig. 19 Top view of plasma flow field at t = 49.5 τA. The arrows show the velocity vector direction, the color code its amplitude and the size of the arrows the relative strength of the velocity. Also shown are the spine and fan field lines together with the Z component of the magnetic field. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


