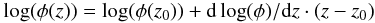| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015195 | |
| Published online | 22 November 2010 | |
The bright end of the z ~ 7 UV luminosity function from a wide and deep HAWK-I survey
1 INAF-Osservatorio Astronomico di Roma, via Frascati 33,
00040 Monteporzio ( RM), Italy
e-mail: castellano@oa-roma.inaf.it
2
NOAO, 950 N. Cherry Avenue, Tucson, AZ
85719,
USA
3
Department of Astronomy, University of
Massachusetts, 710 North Pleasant
Street, Amherst,
MA
01003,
USA
4
Lick Observatory, University of California, Santa Cruz,
CA
95064,
USA
5
Laboratoire d’Astrophysique de Marseille, OAMP, Université
Aix-Marseille & CNRS, 38 rue Frédéric Joliot Curie, 13388
Marseille Cedex 13,
France
6
INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125
Firenze,
Italy
7
INAF-Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131
Trieste,
Italy
8
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching,
Germany
9
INAF-Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio
5, 35122
Padova,
Italy
Received: 10 June 2010
Accepted: 29 July 2010
Aims. We perform a deep search for galaxies in the redshift range 6.5 ≤ z ≤ 7.5 to measure the evolution of the number density of luminous galaxies in this redshift range and derive useful constraints on the evolution of their luminosity function.
Methods. We present here the second half of an ESO Large Programme, which exploits the unique combination of area and sensitivity provided in the near-IR by the camera Hawk-I at the VLT. We have obtained ~30 observing hours with Hawk-I in the Y-band of two high galactic latitude fields. We combined the Y-band data with deep J and K Hawk-I observations, as well as FORS1/FORS2 U, B, V, R, I, and Z observations to select z-drop galaxies with Z − Y > 1, no optical detection, and flat Y − J and Y − K colour terms.
Results. We detect eight high-quality candidates in the magnitude range Y = 25.5−26.5 that we add to the z-drop candidates selected in two Hawk-I pointings over the GOODS-South field. We use this full sample of 15 objects found in ~161 arcmin2 of our survey to constrain the average physical properties and the evolution of the number density of z ~ 7 LBGs. A stacking analysis yields a best-fit SED with photometric redshift 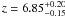 and an
and an 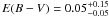 . We compute a binned estimate of the z ~ 7 LF and explore the effects of photometric scatter and model uncertainties on the statistical constraints. After accounting for the expected incompleteness through MonteCarlo simulations, we strengthen our previous finding that a Schechter luminosity function constant from z = 6 to z = 7 is ruled out at a ≳ 99% confidence level, even including the effects of cosmic variance. For galaxies brighter than M1500 = −19.0, we derive a luminosity density
. We compute a binned estimate of the z ~ 7 LF and explore the effects of photometric scatter and model uncertainties on the statistical constraints. After accounting for the expected incompleteness through MonteCarlo simulations, we strengthen our previous finding that a Schechter luminosity function constant from z = 6 to z = 7 is ruled out at a ≳ 99% confidence level, even including the effects of cosmic variance. For galaxies brighter than M1500 = −19.0, we derive a luminosity density 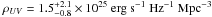 , implying a decrease by a factor 3.5 from z = 6 to z ≃ 6.8. We find that under standard assumptions, the emission rate of ionizing photons coming from UV bright galaxies is lower by at least a factor of two than the value required for reionization. Finally, we exploit deep Hawk-I J and K band observations to derive an upper limit on the number density of M1500 ≲ −22.0 LBGs at z ~ 8 (Y-dropouts).
, implying a decrease by a factor 3.5 from z = 6 to z ≃ 6.8. We find that under standard assumptions, the emission rate of ionizing photons coming from UV bright galaxies is lower by at least a factor of two than the value required for reionization. Finally, we exploit deep Hawk-I J and K band observations to derive an upper limit on the number density of M1500 ≲ −22.0 LBGs at z ~ 8 (Y-dropouts).
Key words: galaxies: distances and redshifts / galaxies: high-redshift / galaxies: luminosity function, mass function / galaxies: evolution
© ESO, 2010
1. Introduction
The search and study of galaxy populations at very high redshift is one of the most promising research areas of today astrophysics and cosmology. It derives its importance through two different and interrelated aspects: 1) the estimate of the UV photon budget provided by star-forming galaxies and its role on the reionization of the universe at z > 6; 2) the study of the formation and the physical properties of the first bulding blocks of present-day galaxies.
There is observational evidence that the Universe is highly ionized at z ~ 6 (e.g. Fan et al. 2006; Totani et al. 2006), in agreement with the latest WMAP estimates of the Thomson optical depth (Komatsu et al. 2010), although significant uncertainties remain on the homogeneity (e.g. Mesinger & Furlanetto 2009) and on the exact timeline of the reionization process (e.g. Gallerani et al. 2006). Whether the UV light emitted by star-forming galaxies is capable of reionizing the Universe by these epochs remains an open question that should be answered through the analysis of large samples of high-redshift objects.
The search for high-redshift star-forming galaxies has been carried out so far mainly with renditions of the Lyman Break, or “drop-out” technique that has been proved to be extremely efficient at redshift from 2 to 6 (e.g. Steidel et al. 1995, 1999; Adelberger et al. 2004; Dickinson et al. 2004; Giavalisco et al. 2004; Ouchi et al. 2004; Bouwens et al. 2007; McLure et al. 2009), or through narrow-band studies targeting the Lyα emission (e.g. Iye et al. 2006; Kashikawa et al. 2006; Ouchi et al. 2009b). The application of the Lyman Break technique at z > 6 has been performed, at first, in small areas with deep near-IR J + H NICMOS data (e.g. Bouwens et al. 2004), and it has recently acquired momentum thanks to the installation of the WFC3 camera onboard of the Hubble Space Telescope which yielded a sample of several faint Lyman Break Galaxies (LBGs) (Bouwens et al. 2010c; Oesch et al. 2010; McLure et al. 2010; Bunker et al. 2010; Yan et al. 2010; Wilkins et al. 2010a,b). In the meantime, ground based surveys (Ouchi et al. 2009a; Capak et al. 2009; Hickey et al. 2010; Castellano et al. 2010, C10 hereafter), together with a refined analysis of archival NICMOS observations (Bouwens et al. 2010a) have expanded the number of bright LBGs known.
The basic feature of the high-redshift galaxy population that can be analysed through the present datasets is its UV luminosity function (LF). The current picture of the evolution of the UV LF points to a factor of 6−11 decrease in the number density of UV bright galaxies from z ~ 3 to z ~ 6 (e.g. Stanway et al. 2003; Shimasaku et al. 2005; Bouwens et al. 2006), although some uncertainties are still present on the exact amount of evolution in the different parameters of the Schechter function (Dickinson et al. 2004; Giavalisco et al. 2004; Sawicki & Thompson 2006; Iwata et al. 2007; Yoshida et al. 2006; Bouwens et al. 2006, 2007; Beckwith et al. 2006). At redshift above 6, most of the analyses indicate a strong evolution in the LF, mainly through a dimming of the characteristic magnitude M ∗ and/or a decrease of the normalization factor φ (Bouwens et al. 2008; McLure et al. 2010; Ouchi et al. 2009a; Yan et al. 2010; Castellano et al. 2010; Bouwens et al. 2010a). The recent WFC3-based analysis by Oesch et al. (2010) also found evidence for a steep faint-end (α ~ −1.8), in agreement with the predictions of theoretical models (Trenti et al. 2010; Salvaterra et al. 2010). Lyman Break Galaxies searches around lensing clusters have also been performed, finding discrepant results that highlight the many challenges and uncertainties in these investigations (Richard et al. 2006, 2008; Bradley et al. 2008; Bouwens et al. 2009; Zheng et al. 2009). Along with improved constraints on the LF at z ~ 7, the latest analysis of the WFC3 data have also provided a first estimate of the evolution at z ~ 8−9 that points to a further decrease in the LBG number density, and thus in the total amount of UV photons produced by young stars at these early epochs.
The discrepancies among different works, both at z ~ 3−5 and at z ~ 6−9 are most probably due to the effect of cosmic variance (e.g. Trenti & Stiavelli 2008; Robertson 2010), but also to the difficulties in avoiding systematic effects in the different estimates of completeness level, contamination from lower redshift interlopers, volume elements, and redshift distributions in the various samples (Stanway et al. 2008), all worsened by the known degeneracy among the parameters adopted to fit the LF.
The strong decrease observed in the UV emission that comes from relatively bright sources seems to imply that reionization cannot be explained on the basis of UV bright galaxies only. An increased number of low-luminosity galaxies indicated by the steep faint end of the Schechter LF might play a decisive role in the reionization process. Large and reliable samples of high-z galaxies both at the bright and at the faint end of the LF are thus necessary to shed light on this issue and possibly to highlight the need to search for even more intriguing sources of the reionizing radiation with future facilities (see e.g. Venkatesan et al. 2003; Madau et al. 2004).
The latest surveys have also given us the opportunity of analysing the physical properties of high-redshift galaxies, whose knowledge is also a decisive factor to understand the very role of these sources in the reionization process. Recent studies have given the first estimates of masses, ages, and SFRs for single z ≳ 6.5 objects, the first constraints on the stellar mass density at these epochs, and have also raised an interesting debate about the possibilty that the first galaxes might be characterized by peculiar properties, like a very low dust content, nearly primordial metallicity or top-heavy stellar initial mass functions (Finkelstein et al. 2010; Bouwens et al. 2010a; González et al. 2010; Labbé et al. 2010; Salvaterra et al. 2010; Schaerer & de Barros 2010).
To give an answer to some of the above problems we are using the new VLT IR imager Hawk-I (Pirard et al. 2004; Casali et al. 2006; Kissler-Patig et al. 2008) to conduct a deep, medium area survey in the Y band over four independent pointings, aimed at the detection of relatively bright LBGs at 6.5 < z < 7.5. Thanks to the extreme efficiency and large field of view (7.5 × 7.5 arcmin) of Hawk-I, it is possible to easily reach Y ~ 26.5 AB at >5σ (roughly corresponding to M1500 = −20.5 at z = 7), over large areas in a reasonable amount of time (15 h).
In C10 we discussed the results of the first half of our survey, covering a large fraction of the GOODS-S field, and we estimated a statistically significant (~99% c.l.) decrease, with respect to z ~ 6, of the number density of UV-bright galaxies. In this paper we present the z ~ 7 candidates found in the second half of the survey, covering two other independent fields. We will constrain the evolution of the LF combining this new sample with the GOODS one.
The paper is organised as follows. In Sect. 2 we present the imaging set and the multiwavelength catalogue; in Sect. 3 the LBG selection criteria and the potential interlopers affecting the selection are discussed; in Sect. 4 we present our final sample of candidate z-drop LBGs. In Sect. 5 we discuss a stacking analysis of all the z-drop galaxies found in the four Hawk-I pointings that are used to constrain the z > 6 UV LF in Sect. 6. In Sect. 7 we derive an upper limit on the number density of very bright z ~ 8 LBGs. A summary of our methods and results is provided in Sect. 8.
Throughout the whole paper, observed and rest-frame magnitudes are in the AB system, and we adopt the Λ-CDM concordance model (H0 = 70 km s-1 Mpc, ΩM = 0.3, and ΩΛ = 0.7).
2. Data
2.1. Observations
BDF – observations.
NTTDF – observations.
This work is based on deep Y-band images obtained with the IR camera Hawk-I at the VLT, and on deep optical FORS2 observations. We use data collected through a dedicated ESO Large Programme in 2008 and 2009. The first set of data, which covers two adjacent regions of the GOODS-S field, has been presented in C10. Here we present the analysis of two other pointings (Fig. 1), chosen for the wealth of deep, public observations previously exploited by other authors to search for z ~ 4−6 LBGs: the BDF field at RA = 336.98°, Dec = −35.17° (Lehnert & Bremer 2003), and the New Technology Telescope Deep Field (NTTDF) at RA = 181.36°, Dec = −7.72° (Arnouts et al. 1999; Fontana et al. 2000, 2003). The total exposure time is 15h49m for BDF and 15h03m for the NTTDF in the Y band.
The Y-band images were reduced with standard techniques for IR data – flat fielding, sky subtraction among consecutive frames, and final coaddition. The reduction procedure, which is described in detail in our first paper C10, has been specifically designed to enhance the reliability of the images at the faintest fluxes, and to get rid of persistence effects and cross-talk resonances.
We determine an FWHM of 0.52 ± 0.01 arcsec (≃ 4.9 pixels) in the final coadded BDF image and 0.49 ± 0.01 arcsec (≃ 4.6 pixels) in the NTTDF one. Image zeropoints were computed using the standard stars that were observed during the same night and at similar airmasses. Reference fluxes were converted to the photometric system and filter set used in this paper, as described in C10.
We obtained the absolute rms maps for each pointing by computing the rms in each individual image (using the Poisson statistics and the instrumental gain) and self-consistently propagating this rms over the whole data reduction process. The typical 5σ magnitude in one arcsec2 is in the range 26.7−26.8 over more than 60% of the whole image, and >26.2 in 85% of the image – the rest of the images are shallower because of the gaps between the four Hawk-I chips.
 |
Fig. 1 Colour-composite image of the BDF (left) and NTTDF (right) fields, created using the weighted mean of Hawk-I Y, J, and K images as red, the FORS2 Z as green, and the weighted mean of FORS1/FORS2 optical images as blue. |
A wide wavelength coverage is needed to reliably select high-redshift LBGs excluding lower redshift interlopers and red and dusty galaxies at intermediate redshift. To this aim we obtained or re-reduced deep observations of both fields ranging from the blue to the near-IR, matching all images to the Y band pixel-size and astrometric solution. Along with the main Y-band pointings, we also acquired deep J and Ks Hawk-I observations of both fields. We also obtained ~7 h of FORS2 Z-band coverage for each field, which we coadded with the already existing FORS2 images (Fontana et al. 2003) to reach the required depth. We also re-reduced the archive U, B, V, R, I FORS2 and FORS1 observations of the NTTDF, and the FORS2 R and I images of the BDF. Finally, we obtained ~4 h of V-FORS2 observations on the BDF. The full dataset is presented in Tables 1 and 2.
2.2. The photometric catalogue
2.2.1. Detection
We obtained the photometric catalogue using the SExtractor code V2.5 (Bertin & Arnouts 1996) and the Y band as detection image with the rms map derived as described above. Because high-redshift galaxies are almost unresolved in ground-based images, and SExtractor’s are known to underestimate the total flux of faint objects (Y > 24 in our case), we chose to use aperture-corrected total magnitudes. We computed aperture magnitudes in a 2 FWHM diameter and corrected them to total magnitudes adopting aperture corrections from bright non-saturated stars in each field. While this choice might give slightly underestimated fluxes for the more extended high-redshift candidates, we can easily take into account this systematic through the simulations that we use to estimate the LF (Sect. 6.1), which are based on the observed profile of LBGs with known spectroscopic redshifts 5.5 < z < 6.2 (Vanzella et al. 2009) in the GOODS-S ACS images.
We optimised the SExtractor parameters involved in the detection process through the analysis of a “negative” image as discussed in C10, adopting the set of parameters that minimises the ratio between “negative” and “positive” detections at the faint end of the number counts. As expected, we find that the best parameters for faint objects detection on BDF and NTTDF Y-band images are the same adopted for the similar set of images over GOODS-South: we require 10 contiguous pixels each at S/N > 0.727, corresponding to a 2.3σ detection, and we restrict the analysis to the regions where the rms is less than ~1.5 times the lowest value. With this choice of parameters, we do not find any detection on the negative images at Y < 26.2, and a fraction of negative detections less than 5% of the real ones at fainter magnitudes. However, a posteriori, the latter value overestimates the actual rate of spurious detections. Indeed, all spurious sources should appear as “drop-out” candidates with a single-band detection. On the contrary, all the Y > 26.2 objects in our z-drop sample are confirmed by detections in other IR bands. Indeed, as we discuss also in C10, the test on the negative image is probably influenced by non-trivial issues concerning the subtraction of the background or a potential asymmetry in the noise distribution.
2.2.2. The multicolour catalogue
A multiwavelength catalogue containing self-consistent magnitudes in all available bands was built running SExtractor in dual mode using the Y-band Hawk-I image as the detection image with the detection parameters indicated above. Aperture fluxes were computed within a 2 FWHM aperture and converted to total applying appropriate aperture corrections in each band.
The typical 1σ limiting magnitudes in a 2 FWHM aperture are in the range 27.8−29.3 for the optical bands, J ~ 26.5−26.7, and Ks ~ 26.0−26.3. The corresponding 1σ limiting magnitude in the Z band, which is used to define the “dropout” selection, is ~28.6 in BDF and ~28.4 in the NTTDF (see Tables 1 and 2).
For each field we defined the total areas where the image depth is sufficiently homogeneous. The candidates found in this area will be used for the evaluation of the LF. We used Y-band detected objects only in the regions selected on the basis of the negative image test explained above. In addition, we also masked borders, CCD defects and noisiest regions in the other images of our data-set. The areas selected in this way correspond to ~71% of the Y-band coverage in the BDF, and ~56% in the NTTDF (owing to strong vignetting in the Z-band image). As a result, the total area used for z-drop detection amounts to 71.7 arcmin2. We will subtract from this value the fraction of area covered by lower redshift objects (~9%) to estimate effective volumes in Sects. 6 and 7.
3. The selection of z > 6.5 galaxies
3.1. The dropout criterion
We select candidate z > 6.5 galaxies with the “drop-out” technique adapted to our filter set and imaging depth.
In order to individuate the appropriate selection criteria we estimated the expected colours of high-redshift star-forming galaxies (black points in the right panel of Fig. 2) on the basis of the models of Charlot and Bruzual 2007 (Bruzual 2007a,b) with the same range of free parameters as in C10: Metallicity: 0.02, 0.2 and 1 Z⊙; age from 0.01 Gyr to the maximal age of the Universe at a given z; E(B − V) = 0...0.2 (Calzetti et al. 2000). Ly-α rest-frame equivalent width in the range 0−200 Å. Intergalactic absorption following Madau (1995). The same range of model parameters will be employed as baseline for the Monte Carlo simulations used to estimate the LF in a self consistent way, see Sect. 6.
As shown in the left panel of Fig. 2, galaxies at z > 6.5 show an increasing Z − Y colour, which is due to the sampling within these two filters of the sharp drop shortward of the Lyman-α, where most of the photons are absorbed by the intervening HI in the intergalactic medium. The drop in the flux observed shortward of the Y band is analogous to the one used to select star-forming galaxies at lower redshifts, like i-drops at z ~ 5, V-drops at z ~ 4 etc.: the major difference with respect to the standard Lyman Break technique is that the Y band does not sample the continuum around 1500 Å but a region shortward of it, contaminated by both the larger IGM absorption at z > 6 and by the Lyman-α emission line. These effects can only be accurately accounted for by realistic imaging simulations, as we discuss in detail in C10 and in Sect. 6.1 of this paper. Following this test, we choose Z − Y > 1 as our main selection criterion to select z > 6.5 galaxies. Given that the Z-band observations as well as the optical ones used here are slightly shallower than the GOODS-ACS ones, we limit our selection at Y < 26.5 instead of the Y < 26.8 adopted in C10.
 |
Fig. 2 Left: Z − Y colour of star-forming galaxies as a function of redshift. In the upper part, the efficiency curve of the two filters is shown, computed at the observed wavelength of a Lyman-α emission at the corresponding redshift. Right: Z − Y vs. Y − J colour diagram showing the expected colours of LBGs (same as in left panel, black points), passively evolving galaxies (red squares) and reddened starbursts (green circles) at 1.5 < z < 4 and cool dwarf stars from the templates of Tsuji et al. (2004) (magenta stars). Galaxy colours are computed according to CB07 models, see text for details on the adopted parameters. In both panels the lines indicate the relevant colour selection criteria discussed in Sect. 3 |
The selection of z-drop galaxies cannot be solely based on the Z − Y colour, since other classes of objects can display a red Z − Y colour similar to that of z > 6.5 galaxies. Selection criteria, both in the optical and in the IR bands, are thus necessary to individuate a reliable sample of z ~ 7 galaxies.
3.2. IR colour selection
We tailored our IR colour selection to exclude any possible contamination in our z-drop sample from known classes of lower redshift objects:
-
i)
we modelled passively evolving galaxies and dusty starburstgalaxies at z > 1.5 with a suitable set of spectral synthesis models. We used the same CB07 library as for high-redshift galaxies to predict the colours of these objects at 1.5 < z < 4 with a combination of short star-formation exponential timescales (0.1−1 Gyr) and ages >1 Gyr to reproduce passively evolving galaxies, and constant star-forming models with 0.5 < E(B − V) < 1.5 (adopting a Calzetti et al. 2000, extinction law) for the dusty starbursts. As is evident from Fig. 2 (right panel) these galaxies also show a large IR colour term. To exclude these objects, we adopt the same additional criteria on IR colours as in C10: (Z − Y) > (Y − K); (Z − Y) > 0.5 + 2.0(Y − J); (Y − J) < 1.5; (Y − K) < 2.0;
-
ii)
cool (Teff < 1500 K), low-mass stars, and substellar objects of the T spectral class have infrared spectra that are dominated by the CH4 and H2O absorption bands and by H2 resonant absorption (e.g. Chabrier et al. 2005; Burgasser et al. 2006) which produces a sharp break in their IR colours. We used the most up-to-date estimate of the T-dwarfs number density (as observed in the J band) of Burgasser et al. (2007) to compute the expected number of faint, cool dwarfs in our fields. Adopting an average Y − J colour of 0.8 mag estimated from the catalogue of observed dwarfs compiled by Leggett et al. (2010), and considering the dependence on galactic latitude as in Burgasser (2004), we estimated that ~0.6 stars of spectral types T0-T8 with Y < 26.5 are expected to fall in each of our fields. However, the exact number of expected contaminating dwarfs depends on the still uncertain parameters that constrains the IMF and their spatial distribution inside the disk and the halo of the Galaxy: a pessisimistic estimate (see C10) gives nearly twice surface density of cool dwarfs in our pointings. For this reason we used the synthetic spectral libraries by Tsuji et al. (2004) (see also Tsuji 2002, 2005) to check whether it is possible to define selection criteria that distinguish between LBGs and cool dwarfs. As shown in the right panel of Fig. 2, cool dwarfs appear redder than z-dropouts in the Y − J colour, and the Y − J criterion we adopt allows us to exclude these objects from our selection window. We note that the brown dwarf discovered in the NTTDF by Cuby et al. (1999), having Z − Y ~ 2 and no optical detection, is consistently excluded from our high-z sample on the basis of its Y − J colour;
-
iii)
finally, we cross-checked each object selected according to the above criteria against variability by analysing images acquired at different epochs. The BDF observations have been split in two separated epochs with a gap of three months (September and December 2009), while the NTTDF have been observed during four runs in January, February, April, and May 2009. We verified that all the objects in our sample are clearly detected and that they have a consistent total flux (within 2σ) in the different epochs. In the NTTDF case, we checked that a detection >3σ of the faintest candidate (Y ~ 26.5) was possible in the two epochs with longer integration time.
We summarise here the full set of colour selection criteria: 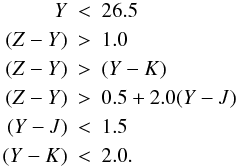
3.3. Comparison with the GOODS-ACS dataset
In our analysis of the GOODS-South field we exploited the ACS V2.0 B, V, I, Z observations (Giavalisco and the GOODS Team, in preparation) to select z-drop galaxies and to exclude lower redshift interlopers with significant detection in the optical bands. The main concern we have to consider to provide a z-drop selection as clean as the one in the GOODS field regards the difference in resolution between FORS2 optical observations of BDF and NTTDF and their corresponding ACS-GOODS images that we used to remove interlopers from the colour-selected sample.
Indeed, in C10 we found that a sample of galaxies selected with IR criteria only is also populated by faint contaminants that show significant detection in filters covering wavelengths shorter than the redshifted Lyman limit at z > 6 (U, B, V, R, I), where high redshift LBGs are not expected to present any flux. These objects are in most cases clearly extended, but their spectral energy distributions cannot be reproduced by a straightforward application of the CB07 models. While determining their nature is beyond the scope of the present analysis, we note that they might be faint galaxies with a very blue continuum, whose SED is altered by strong emission lines as in unobscured AGNs, or in star-forming galaxies like the blue compact dwarf galaxies (Izotov et al. 2004, 2007) or the ultra-strong-emission line galaxies (USELs, Hu et al. 2009). Potential contamination of z ~ 7 samples owing to an unknown class of objects without optical detection (<2σ) has also been suggested by Capak et al. (2009). Their objects are brighter than those found in our fields, but display similar colours. Given the unknown nature of these contaminants, the only feasible approach is at present to adopt more stringent criteria on the optical non-detections. Follow-up spectroscopy of z ~ 7 candidates and faint contaminants is needed to fully evaluate the impact of this population on high-redshift studies.
In our analysis of the GOODS-South field we adopted very strict selection criteria in the blue bands in order to exclude these contaminants, measuring the S/N ratios in small apertures (0.6′′) exploiting the high resolution of ACS images. In order to obtain optical selection criteria that are as effective as those used with the GOODS dataset, we performed tests computing S/N ratios and photometry on the GOODS-ACS images degraded and smoothed to the depth/seeing of the BDF and NTTDF corresponding ones. We then re-selected GOODS dropouts on “mock” BDF/GOODS and NTTDF/GOODS catalogues built in the same way as the real BDF and NTTDF catalogues. We verified that the criteria already adopted in the GOODS fields are effective in the NTTDF case: S/N < 2σS/N in all the optical bands and <1σS/N in at least four of them. In the BDF, given the absence of U and B images and the slightly shallower I imaging, we adopted the conservative criterion S/N < 1σS/N in all the optical bands. We verified that this criterion allows us to safely remove all those objects, up to Y = 26.5, which have been verified to be lower redshift contaminants on the basis of GOODS-ACS and, whenever possible, UDF-ACS photometry. The parameter σS/N indicated above is the rms of the S/N distribution estimated, as in C10, dropping random apertures in portions of the images free of detected objects. This procedure allows us to take into account the sky-noise distribution and the presence of faint, undetected foreground objects at the same time.
Candidates in the BDF and NTTDF fields.
 |
Fig. 3 Thumbnails showing the images of the eight selected high-redshift candidates in the different observed bands. |
4. Detected z > 6.5 galaxies
Adopting the selection criteria outlined above we find a total of eight candidates, three in the BDF and five in the NTTDF field, whose coordinates, Y magnitudes, and Z − Y colours are listed in Table 3. Thumbnails of the candidates are presented in Fig. 3. We note that two of them are clearly detected, and two others are marginally detected (S/N ~ 2), in the Z band. Three of the five candidates present in the NTTDF are also detected at S/N ~ 2−4 in the J and K bands, thanks to the slightly deeper images available for this field (see Table 2). We also verified that each candidate is undetected in the image obtained as the weighted sum of its V, R, and I observations.
As a final check we performed a stacking of all the objects in the available images. This test allows us to confirm the non-detection in the optical images, and to obtain a clear detection in the J (S/N ~ 5) and K band (S/N ~ 4) stacked images. The stacked object shows an average colour Z − Y ≃ 1.6.
 |
Fig. 4 Thumbnails showing the stacked images of the 15 high-redshift candidates selected in the GOODS1, GOODS2, BDF and NTTDF fields. The observed bands are shown in the legends. |
Below we will combine this sample of z-drop candidates found in the BDF and NTTDF pointings with the sample discussed in C10, which was obtained from the two pointings over the GOODS-South field, to find their average properties through a stacking analysis, and to constrain their LF. The GOODS z-drop sample includes seven candidates in the range Y ~ 25.5−26.7, selected through colour-selection criteria analogous to those outlined above, whose reliability has also been checked on the available IRAC and NICMOS observations.
5. Mean properties of Hawk-I z ~ 7 galaxies
We performed a weighted mean of the images in the available filters from the U to the K band for all the 15 objects detected in the Hawk-I fields. We did not attempt a similar stacking of the IRAC images, because most of our GOODS candidates are partially or extremely blended with other foreground sources, and the candidates in the other fields are either not covered by IRAC observations or are present in shallower exposures compared to GOODS. We matched the ACS images to the Hawk-I PSF and masked all foreground objects that surround the candidates in each image. The stacked object shows an S/N ≳ 5 detection in the Z, J, and K bands and a non-detection in all the optical bands, corresponding to an (optical − Y) colour of >4 mag. We used the magnitudes estimated for the stacked object to find the photometric redshift and physical parameters through our photo-z code (Giallongo et al. 1998; Fontana et al. 2000) exploiting a χ2 minimisation procedure to find the best-fitting spectral template to the observed colours among the full CB07 library. While the ACS optical filters used in the GOODS field have different passbands with respect to the FORS2 ones used in BDF and NTTDF fields, this is not a significant concern because they all span a wavelength range where no flux is expected for z > 6 objects. In turn, the small difference between FORS2 and ACS Z-band filters does not provide significant variations in the redshift selection window defined by the Z − Y colour, which is the main constraint to the photometric redshift. The resulting SED provides a unique photometric redshift solution at 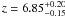 . Relevant thumbnails and SED are shown in Figs. 4 and 5. Given the absence of IRAC, most physical parameters are largely unconstrained, apart from the E(B − V) parameter whose estimate is mostly based on the Y − J and Y − K colours. We find that our stacked SED is fitted by an
. Relevant thumbnails and SED are shown in Figs. 4 and 5. Given the absence of IRAC, most physical parameters are largely unconstrained, apart from the E(B − V) parameter whose estimate is mostly based on the Y − J and Y − K colours. We find that our stacked SED is fitted by an 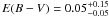 at a 68% confidence level. This value is consistent with the E(B − V) distribution obtained from the analysis of z ~ 7−8 objects by Finkelstein et al. (2010) and by Schaerer & de Barros (2010). Our best-fit E(B − V) indicates a low dust content for z ~ 7 galaxies, in agreement also with the best-fit AV values found by González et al. (2010) and by Labbé et al. (2010) for the mean SED of their z-drop samples, and with the blue UV continuum slope measured by Bouwens et al. (2010d).
at a 68% confidence level. This value is consistent with the E(B − V) distribution obtained from the analysis of z ~ 7−8 objects by Finkelstein et al. (2010) and by Schaerer & de Barros (2010). Our best-fit E(B − V) indicates a low dust content for z ~ 7 galaxies, in agreement also with the best-fit AV values found by González et al. (2010) and by Labbé et al. (2010) for the mean SED of their z-drop samples, and with the blue UV continuum slope measured by Bouwens et al. (2010d).
6. The evolution of the luminosity function
6.1. Monte Carlo simulations
 |
Fig. 5 Best-fit SED to the stacked photometry, with relevant photometric redshift at z = 6.85. |
When small galaxy samples are used to constrain the high-redshift LF, it is necessary to exploit detailed imaging simulations to appropriately treat the systematic effects that arise from faint object detection and from the application of colour selection criteria. To this aim we use the CB07 synthetic libraries described in Sect. 3 to produce a set of ~8 × 105 simulated LBGs for each field with redshift in the range 5.5 < z < 8.0 and observed magnitudes computed in the same filter set as we used for the observations. These galaxies are placed at random positions of the Y-band images, and the catalogues are extracted in the same way as in the original frames. To avoid an excessive crowding in the simulated images, we include only 200 objects each time, after masking the regions of the images where real objects are present. As in C10, we randomly assign the light profile of one of the four most distant spectroscopically confirmed LBGs that were observed with ACS in GOODS (z = 5.5−6.2, Vanzella et al. 2009) to each of our simulated galaxies, after convolving it with the relevant Hawk-I PSFs.
6.2. Stepwise luminosity function
The magnitude range covered by our survey, Y ≃ 25.5−26.7, roughly corresponds to the UV continuum magnitude range at M ≲ M ∗ . For this reason, we first performed a binned estimate of the number density of the Hawk-I z-drop galaxies through the stepwise method (see, e.g. Bouwens et al. 2008). The stepwise estimate is a non-parametric method based on the assumption that the rest-frame LF of galaxies can be approximated by a binned distribution, where the number density φi in each bin is a free parameter. To also evalute the potential systematics and the effects of observational uncertainties in this kind of estimates, we used two different procedures to compute the stepwise LF. The first one is the procedure commonly adopted in the literature based on the average relation between the observed Y and the UV continuum magnitude at 1500 Å (M1500), and on an estimate of the completeness in the different UV magnitude bins. The second more conservative procedure considers the uncertainties in the Y − M1500 conversion due to photometric scatter, to the redshift distribution and to the intrinsic properties of different galaxy models. In a separate work we will combine this stepwise analysis with similar estimates at fainter and brighter magnitudes to determine the Schechter parameters at z ~ 7 in a self-consistent way (Grazian et al. 2010, in preparation).
6.2.1. Stepwise luminosity function from the average Y−UV relation
Through a linear regression we computed the average Y − M1500 relation at the median redshift of our sample (z = 6.8) for the CB07 models of z-drop galaxies. We then divided our sample into two bins centered at M1500 = −21.1 and M1500 = −20.4, and used the imaging simulations to estimate the completeness of our selection. Finally, we converted the redshift-dependent completeness distribution into effective volumes of our survey at these magnitudes. The values of the stepwise LF estimated in this way are reported in Table 4 and plotted as filled squares in Fig. 6, with vertical error bars given by Poisson uncertainties in the number counts. The horizontal error bars indicate the relevant magnitude range of each bin.
6.2.2. Introducing photometric uncertainties in the stepwise luminosity function
A more conservative estimate can be computed assuming a stepwise LF made of three bins in the wider magnitude range −22.0 < M1500 < −19.0. This interval takes into account the photometric scatter and the variation of the Y − M1500 relation with redshift and galaxy models (see Fig. 7). We assume a fixed, constant, reference density φref and exploit the set of simulations described in Sect. 6.1 to compute for each field the distribution of observed magnitudes originating in each rest-frame bin for LBGs in the redshift range sampled by our colour selection. The simulated number counts are then scaled to the relevant observed areas and summed. Finally, we find the combination of binned densities φi = wi·φref, which best reproduces the total number counts of our survey, where wi are multiplicative factors to the reference density that we determine by comparing observed and simulated distributions through a simple χ2 test. We plot as black empty circles in Fig. 6 the two bins at M1500 < −19.8. The third and faintest bin at M1500 > −19.8 yields only a conservative upper limit and is not represented in the figure, but it is necessary in this procedure to consider the effect of Malmquist bias. Vertical error bars indicate the statistical uncertainties given by the χ2 test.
Stepwise determination of the UV LF.
 |
Fig. 6 Number densities in two rest-frame magnitude intervals estimated for our Hawk-I data set in a stepwise form with a standard Y − UV conversion of the observed number counts as discussed in the text (black filled squares), or with a χ2 method considering also photometric and model uncertainties (black empty circles). Other points are from Bouwens et al. (2010a) (NICMOS, red empty squares), Ouchi et al. (2009a) (SUBARU, blue empty squares and upper limits) and Oesch et al. (2010) (WFC3-UDF, magenta empty circles). For comparison we show the recent determinations of the LF at z ~ 6 by Bouwens et al. (2007) (B07, green dot-dashed line) and McLure et al. (2009) (M09, blue dashed line). The black solid line is the best-fit LF obtained by combining the stepwise points shown in the figure with new determinations of the binned densities from WFC3-UDF and WFC3-ERS data (Grazian et al. in preparation). |
The two methods give consistent results and perfectly agree with other stepwise estimates in the same magnitude range (see Fig. 6). However, the error bars and the relevant magnitude range are much larger when using the χ2 minimization procedure. While an average conversion from observed to rest-frame magnitudes along with an estimate of effective volumes can provide a first order-of-magnitude estimate of the binned number density of LBGs, we emphasize that significant statistical uncertainties can arise owing to photometric scatter, and to the different relation between Y and UV continuum magnitudes for different galaxy models and redshifts.
 |
Fig. 7 Normalized distribution of UV continuum magnitudes (estimated from the average Y − M1500 relation) for the 15 Hawk-I candidates divided in two bins (dashed histograms). The solid curves show the expected distributions of UV magnitudes for objects in the same observed ranges when photometric uncertainties are taken into account through Monte Carlo simulations. |
6.3. Maximum-likelihood luminosity function
We estimate how significant the evolution of the LF at z > 6 is adopting a maximum-likelihood approach. This method allows us to compare the observed number counts with those predicted for different evolving Schechter LFs (Schechter 1976) after accounting for the expected systematics in the detection process (e.g. Bouwens et al. 2007; Mannucci et al. 2007; McLure et al. 2009). As in C10, we assume that the LF can be described by a Schechter function with parameters φ and M ∗ evolving from their value at z0 = 6.0 (McLure et al. 2009) according to the following parametrisation:
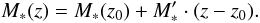 Since our faint limit is close to the expected value of the characteristic luminosity M ∗ , we fix the faint end slope to the value α = −1.71 of the z ~ 6 LF by McLure et al. (2009). We explicitly tested that no appreciable differences are found when fixing α to different values (α = −1.4,−2.0). For a broad range of values of the evolving terms
Since our faint limit is close to the expected value of the characteristic luminosity M ∗ , we fix the faint end slope to the value α = −1.71 of the z ~ 6 LF by McLure et al. (2009). We explicitly tested that no appreciable differences are found when fixing α to different values (α = −1.4,−2.0). For a broad range of values of the evolving terms 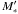 and dlog (φ)/dz (see Fig. 8) we simulate with a Monte Carlo approach the redshift z and UV magnitude M1500 for a population of 3 × 105 galaxies. These objects are randomly extracted from the larger database of simulated galaxies described in Sect. 6.1, which encompasses a broad range of the physical parameters determining the rest-frame photometry, like E(B − V), metallicity, Lyα EW etc.
and dlog (φ)/dz (see Fig. 8) we simulate with a Monte Carlo approach the redshift z and UV magnitude M1500 for a population of 3 × 105 galaxies. These objects are randomly extracted from the larger database of simulated galaxies described in Sect. 6.1, which encompasses a broad range of the physical parameters determining the rest-frame photometry, like E(B − V), metallicity, Lyα EW etc.
The distributions of Y magnitudes and Z − Y colours for each simulated population are scaled to the observed area in each of the fields and compared to the observed ones with a maximum-likelihood test, under the assumption of simple Poissonian statistics. For each of the two distributions and for each field we build the likelihood function ℒ: 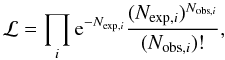 (1)where Nobs,i is the observed number of sources in the magnitude (colour) interval i, Nexp,i is the expected number of sources in the same magnitude (colour) interval, and Πi is the product symbol. For each field, we associate to every model a likelihood computed as the product of those obtained for the magnitude and colour distributions separately. We then compute a final likelihood as the product of the GOODS, BDF, and NTTDF likelihoods.
(1)where Nobs,i is the observed number of sources in the magnitude (colour) interval i, Nexp,i is the expected number of sources in the same magnitude (colour) interval, and Πi is the product symbol. For each field, we associate to every model a likelihood computed as the product of those obtained for the magnitude and colour distributions separately. We then compute a final likelihood as the product of the GOODS, BDF, and NTTDF likelihoods.
 |
Fig. 8 χ2 contour levels for the dlog (φ)/dz, |
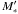 and dlog (φ)/dz (left and bottom axes) and for the resulting Schechter parameters at the median redshift z = 6.8 of our sample (top and right axes) for the combination of all four Hawk-I fields. In the same plot, the colour code refers to the χ2 distribution obtained under the usual assumption χ2 = −2.0·ln(ℒ) (e.g. Cash 1979). We reject at ≳ 99% confidence level the hypothesis that the LF remains constant in both parameters above z = 6 (dlog (φ)/dz = 0 and
and dlog (φ)/dz (left and bottom axes) and for the resulting Schechter parameters at the median redshift z = 6.8 of our sample (top and right axes) for the combination of all four Hawk-I fields. In the same plot, the colour code refers to the χ2 distribution obtained under the usual assumption χ2 = −2.0·ln(ℒ) (e.g. Cash 1979). We reject at ≳ 99% confidence level the hypothesis that the LF remains constant in both parameters above z = 6 (dlog (φ)/dz = 0 and  , black point in Fig. 8). In Fig. 8 we also show the 99% c.l. region on the Schechter evolutionary terms estimated on the basis of the two GOODS-South pointings only (C10). Although the degeneracy between M ∗ and φ is still present, the analysis of the BDF and NTTDF fields considerably reduces the allowed parameter space.
, black point in Fig. 8). In Fig. 8 we also show the 99% c.l. region on the Schechter evolutionary terms estimated on the basis of the two GOODS-South pointings only (C10). Although the degeneracy between M ∗ and φ is still present, the analysis of the BDF and NTTDF fields considerably reduces the allowed parameter space.
The region of allowed values for the LF parameters in our final likelihood map points to a pronounced decrease of φ along with a brightening of M ∗ with redshift. However, the best-fit values for M ∗ and φ at z ~ 7 derived by Ouchi et al. (2009a) and by Bouwens et al. (2008) (see also Bouwens et al. 2010b), indicating a constant or slightly dimming M ∗ , still fall within the 2σ region constrained by our maximum likelihood (grey points in Fig. 8), and they are consistent with our estimate once the uncertainties are considered. We argue that cosmic variance (see Sect. 6.4) and the limited sample of very bright objects available may explain the discrepancies among different results: in our case, an inspection of the likelihood maps obtained separately on each field shows that the NTTDF, having two bright objects (Y ~ 25.5−25.7, approximately M1500 ≲ −21.2 at z = 6.8), has a great effect in skewing the total likelihood towards brighter values of M ∗ . We also note that some theoretical models (e.g. Trenti et al. 2010; Finlator et al. 2010) predict a dimming of M ∗ with redshift. However, several model parameters are largely unconstrained by the observations, while a high dust extinction might be required to match observed and predicted LFs at the bright end (Lacey et al. 2010).
6.4. Cosmic variance
The effects of cosmic variance are reduced in our case, because our data come from three independent areas, albeit of different sizes (the GOODS-South field being covered by two of the four Hawk-I pointings). We evaluate the possible impact of cosmic variance using the mock catalogues of the Millennium Simulation (Kitzbichler & White 2007) in the same way as discussed in C10. For each of the three Hawk-I areas (GOODS-South, BDF, NTTDF) we extract 200 fields of the same size from independent Millennium light-cones and apply corresponding photometric selection criteria on galaxies at 6.5 < z < 7.4 (bracketing the peak of our selection window), without any constraint on the distribution of host haloes. We estimate that a cosmic variance of ~21% affects the total number counts of z-drop LBGs in our survey. We find that the evolution is still confirmed at a ≳ 99% confidence level by our maximum-likelihood approach, even allowing a ~21% variation in the total number density. Indeed, after accounting for all observational effects, we estimate that we would have observed ~30 z-drops in our survey for a non-evolving LF: a factor of two higher than the observed number. However, while cosmic variance has no significant effect on our conclusion that the LF strongly evolves from z ~ 7 to z ~ 6, it can have a great effect in determining the form of this evolution. Cosmic variance is strongly luminosity-dependent, and it is as high as 41% for galaxies brighter than Y = 25.8 in our survey, thus affecting the determination of the M ∗ parameter.
6.5. UV luminosity density, star-formation rate density and constraints on cosmic reionization
While the M ∗ and φ parameters are highly degenerate, the number density of bright galaxies, i.e. the integral of the bright end of the LF, is much better constrained, and so are the derived integral quantities such as the UV luminosity density (ρUV) and star-formation rate density (SFRD).
We conservatively consider the model LFs within the 95% c.l. region of our likelihood analysis to derive the ρUV by integrating L·Φ(L) up to the luminosity corresponding to M1500 = −19.0. We convert these values into a SFRD following the standard formula by Madau et al. (1998) and applying the extinction correction of Meurer et al. (1999) (considering an average UV slope β = −2.0). Finally, we use ρUV to evaluate the emission rate Ṅion of hydrogen ionizing photons per Mpc3 following Bolton & Haehnelt (2007). We consider an escape fraction fesc = 0.2, a spectral index αs = 3.0 and an ionizing emission density at the Lyman limit ϵg = ρUV/6.0.
We report in Table 5 the range of values for ρUV, SFRD, and log (Ṅion). These values are perfectly consistent with the analogous ones presented in C10 and derived from the LFs in the 68% c.l. region of the GOODS likelihood. Considering the same integral of the z = 6 UV LF of McLure et al. (2009), our estimated ρUV implies a drop of a factor ~3.5 in the UV luminosity density from z = 6. The lower limit for the ionization rate required to balance recombination at z = 7, computed according to Madau et al. (1999) and assuming an HII clumping factor equal to one, is log (Ṅrec) = 50.1, which is a factor of two higher than the highest value allowed by our analysis. This demonstrates that under usual assumptions bright UV galaxies alone cannot keep the universe reionized at z ~ 7. By varying the escape fraction, we obtain that values higher than fesc = 0.5 are required to reconcile the emission rate from bright galaxies with the one required for reionization. This demonstrates that either UV bright galaxies at z ~ 7 have different physical properties with respect to lower redshift LBGs, or, that most probably a crucial contribution to the reionization process comes from galaxies at the faint end of the LFs or from other kind of sources. Once different integration limits are taken into account, our estimates agree with the results obtained by Bouwens et al. (2008); Ouchi et al. (2009a); González et al. (2010).
7. Constraints on the number density of Lyman Break Galaxies at z ~ 8
We exploited deep Hawk-I J- and K-band observations to put an upper limit on the number density z ≳ 7.5, Y-drop galaxies in our survey. We used the observations of the BDF and NTTDF fields presented in Sect. 2 and deep observations of the two GOODS-South pointings obtained both in our programme and through a similar ESO observing programme (Clément et al., in preparation). We obtained a multicolour catalogue with the J-band as detection image using SExtractor in dual mode over the full imaging set presented in this paper and in C10. We used the same detection parameters and 2 FWHM apertures adopted for the Y-detected catalogue, computing aperture-corrected total magnitudes through appropriate corrections in each band. We chose the colour selection criteria in order to isolate galaxies with the Lyman-break sampled by the Y − J colour, and to exclude contamination from lower redshift galaxies on the basis of the expected colours for passive and dusty-starburst galaxies modelled as described in Sect. 3.2: 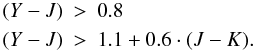 We also required no detection in the optical bands adopting the same S/N criteria outlined for the selection of z-drop galaxies. We limited our selection to J = 24.5, 24.8, 25.0 in the BDF, NTTDF, and GOODS pointings respectively, up to which we estimate that our catalogues are 100% complete, and we used the same area chosen for the selection of z-drop galaxies in order to avoid the noisiest regions in any image.
We also required no detection in the optical bands adopting the same S/N criteria outlined for the selection of z-drop galaxies. We limited our selection to J = 24.5, 24.8, 25.0 in the BDF, NTTDF, and GOODS pointings respectively, up to which we estimate that our catalogues are 100% complete, and we used the same area chosen for the selection of z-drop galaxies in order to avoid the noisiest regions in any image.
With these criteria we found no candidate Y-drop galaxy in our survey. Considering the average J − M1500 relation at the median redshift of our colour selection (z = 8), we are probing the M < M ∗ region of the LF at M1500 ~ −22.5. We report in Table 6 an upper limit on the number density of very bright Y-drop LBGs that is estimated as the inverse of the volume sampled by our survey in the redshift interval 7.5 < z < 9.0.
LBG number density at z ~ 8.
8. Summary and conclusions
We here presented the results of a Y-band survey of the two high galactic latitude BDF and NTTDF fields aimed at detecting galaxies at z ≳ 6.5 and measuring their number density. The survey is based on deep observations obtained through a dedicated ESO Large Programme. We made use of Y, J, and K band observations performed with Hawk-I, the new near-IR camera installed at the VLT, and of FORS2 Z-band observations. We matched and combined these data with deep archive FORS1 and FORS2 observations in the U, B, V, R, I filters to detect high-redshift LBGs with the main criterion Z − Y > 1, requiring no optical detection and flat Y − J and Y − K colours. The colour selection criteria were tailored in order to exclude lower redshift passive galaxies and dusty starbursts, galactic T-dwarfs and galaxies exhibiting high Z − Y colours as well as significant emission in the optical bands, which are possibly intermediate redshift sources with bright emission lines.
As a result, we isolated eight highly reliable z-drop candidates in the magnitude range Y ≃ 25.5−26.5 over a total area of 70.1 arcmin2. We combined this z-drop sample with the similar one extracted from two pointings over the GOODS-South field that comprises seven galaxies at Y < 26.7.
We performed a stacking analysis of the 15 objects to estimate the average properties of M ~ M ∗ galaxies at z ≳ 6.5. The photometric redshift of the stacked object is 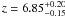 which perfectly agrees with the estimated selection window of our survey. The stacked SED is fitted by an
which perfectly agrees with the estimated selection window of our survey. The stacked SED is fitted by an 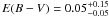 at a 68% confidence level, indicating a low dust content that agrees with the previous analysis of z ~ 7−8 objects (Finkelstein et al. 2010; Schaerer & de Barros 2010; González et al. 2010).
at a 68% confidence level, indicating a low dust content that agrees with the previous analysis of z ~ 7−8 objects (Finkelstein et al. 2010; Schaerer & de Barros 2010; González et al. 2010).
We then estimated the number density and the LF evolution on the basis of detailed Monte Carlo imaging simulations that account for all uncertainties involved in the observations: detection completeness, photometric scatter, and random fluctuations in the S/N measure due to overlapping unresolved sources, or other effects. We first computed a binned estimate of the galaxy number density at z ~ 7 following two different procedures. The first one, which is based on an average Y − M1500 relation and on an estimate of the redshift dependent completeness of our selection, is the procedure commonly adopted in the literature. The second method is more conservative, and exploits a χ2 minimization to compare the observed number counts to those predicted on the basis of Monte Carlo simulations for different combinations of galaxy densities. This second procedure intrinsically considers the uncertainties in the Y − M1500 conversion owing to photometric scatter, to the redshift distribution and to the intrinsic properties of different galaxy models. We find that the two procedures are consistent and agree with similar analyses from the literature. However, the more conservative procedure highlights that sources of statistical uncertainty are usually underestimated.
To assess the degree of evolution of the UV LF at z > 6.0, we also simulated galaxy populations following different UV Schechter functions with linearly evolving parameters log (φ) and M ∗ . For each of the four Hawk-I pointings we compared the resulting distributions of simulated magnitudes and colours with the observed ones following a maximum-likelihood approach. We find strong evidence of evolution of the LF above z = 6: our analysis rules out at a >99% confidence level that the LF remains constant in both φ and M ∗ above z = 6. Our likelihood maps for the Schechter parameters indicate a strong evolution in φ and a brightening of M ∗ with redshift. However, the detection of two bright objects (Y ~ 25.5−25.7, corresponding to M1500 ≲ −21.2) in the NTTDF pointing have a major role in skewing the evolution of M ∗ towards bright values. The two Schechter parameters are, however, highly degenerate and our findings are also consistent within the uncertainties with a milder evolution of φ and a constant or slightly dimming M ∗ as indicated by other authors (Bouwens et al. 2008; Ouchi et al. 2009a). We estimate that the possible effect of cosmic variance is incapable of reconciling the observed number density of z-drop galaxies with the one predicted for a non-evolving LF. However, the strong dependence on luminosity of the cosmic variance, and the relatively small magnitude range probed by our survey at M ≲ M ∗ , can influence the determination of the form of the evolving LF and provide an explanation for the difference between the evolution we determine and other estimates in the literature.
The uncertainty and the degeneracy in the M ∗ and φ best-fit values are not reflected in a comparable uncertainty in the number density of bright galaxies. We conservatively consider the model LFs within the 95% c.l. region of our likelihood analysis to derive for galaxies at M1500 < −19.0 an UV luminosity density 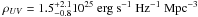 , a star-formation rate density
, a star-formation rate density 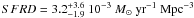 and an emission rate of hydrogen ionizing photons
and an emission rate of hydrogen ionizing photons 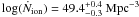 . The UV luminosity density is lower than the corresponding one at z ~ 6 by a factor ~3.5, while Ṅion is lower by at least a factor of ~2 than the lower limit required for reionization according to Madau et al. (1999), considering fesc = 0.2 and an HII clumping factor equal to one. This implies that UV bright galaxies alone cannot reionize the universe, unless their physical parameters are very different from those of lower redshift LBGs (e.g. fesc > 0.5, harder UV spectrum etc.). Most probably, the crucial contribution to reionization comes from galaxies at the faint end of the LF or from other kind of sources. Finally, we exploit the Hawk-I J and K band observations of our survey to derive an upper limit of 2 × 10-6 Mpc-3 for the number density of M ~ −22.5 LBGs at z ~ 8 from the non-detection of Y-drop galaxies up to J ~ 25.
. The UV luminosity density is lower than the corresponding one at z ~ 6 by a factor ~3.5, while Ṅion is lower by at least a factor of ~2 than the lower limit required for reionization according to Madau et al. (1999), considering fesc = 0.2 and an HII clumping factor equal to one. This implies that UV bright galaxies alone cannot reionize the universe, unless their physical parameters are very different from those of lower redshift LBGs (e.g. fesc > 0.5, harder UV spectrum etc.). Most probably, the crucial contribution to reionization comes from galaxies at the faint end of the LF or from other kind of sources. Finally, we exploit the Hawk-I J and K band observations of our survey to derive an upper limit of 2 × 10-6 Mpc-3 for the number density of M ~ −22.5 LBGs at z ~ 8 from the non-detection of Y-drop galaxies up to J ~ 25.
Acknowledgments
We would like to thank Adam Burgasser for providing assistance in using his results on the T-dwarfs number density. Observations were carried out using the Very Large Telescope at the ESO Paranal Observatory under Programme IDs LP181.A-0717, LP168.A-0485, ID 170.A-0788, ID 181.A-0485, ID 283.A-5052 and the ESO Science Archive under Programme IDs 67.A-0249, 71.A-0584, 73.A-0564, 68.A-0563, 69.A-0539, 70.A-0048, 64.O-0643, 66.A-0572, 68.A-0544, 164.O-0561, 163.N-0210, and 60.A-9120. We acknowledge support from Agenzia Spaziale Italiana.
References
- Adelberger, K. L., Steidel, C. C., Shapley, A. E., et al. 2004, ApJ, 607, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., D’Odorico, S., Cristiani, S., et al. 1999, A&A, 341, 641 [NASA ADS] [Google Scholar]
- Beckwith, S. V. W., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolton, J. S., & Haehnelt, M. G. 2007, MNRAS, 382, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Thompson, R. I., Illingworth, G. D., et al. 2004, ApJ, 616, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Blakeslee, J. P., & Franx, M. 2006, ApJ, 653, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., & Ford, H. 2007, ApJ, 670, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., & Ford, H. 2008, ApJ, 686, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Bradley, L. D., et al. 2009, ApJ, 690, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Gonzalez, V., et al. 2010a [arXiv:1003.1706] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010b, ApJ, submitted [arXiv:1006.4360] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010c, ApJ, 709, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010d, ApJ, 708, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, L. D., Bouwens, R. J., Ford, H. C., et al. 2008, ApJ, 678, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, A. G. 2007a, in IAU Symp. 241, ed. A. Vazdekis, & R. F. Peletier, 125 [Google Scholar]
- Bruzual, G. 2007b, in From Stars to Galaxies: Building the Pieces to Build Up the Universe, ed. A. Vallenari, R. Tantalo, L. Portinari, & A. Moretti, ASP Conf. Ser., 374, 303 [Google Scholar]
- Bunker, A., Wilkins, S., Ellis, R., et al. 2010, MNRAS, accepted [arXiv:0909.2255] [Google Scholar]
- Burgasser, A. J. 2004, ApJS, 155, 191 [Google Scholar]
- Burgasser, A. J., Geballe, T. R., Leggett, S. K., Kirkpatrick, J. D., & Golimowski, D. A. 2006, ApJ, 637, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Mobasher, B., Scoville, N. Z., et al. 2009, ApJ, submitted [Google Scholar]
- Casali, M., Pirard, J.-F., Kissler-Patig, M., et al. 2006, in SPIE Conf. Ser., 6269 [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Castellano, M., Fontana, A., Boutsia, K., et al. 2010, A&A, 511, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. H. 2005, [arXiv:astro-ph/050998] [Google Scholar]
- Cuby, J. G., Saracco, P., Moorwood, A. F. M., et al. 1999, A&A, 349, L41 [NASA ADS] [Google Scholar]
- Dickinson, M., Stern, D., Giavalisco, M., et al. 2004, ApJ, 600, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finkelstein, S. L., Papovich, C., Giavalisco, M., et al. 2010, ApJ, 719, 1250 [Google Scholar]
- Finlator, K., Oppenheimer, B. D., & Davé, R. 2010, MNRAS, accepted [arXiv:1005.4066] [Google Scholar]
- Fontana, A., D’Odorico, S., Poli, F., et al. 2000, AJ, 120, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Fontana, A., Poli, F., Menci, N., et al. 2003, ApJ, 587, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Gallerani, S., Choudhury, T. R., & Ferrara, A. 2006, MNRAS, 370, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., D’Odorico, S., Fontana, A., et al. 1998, AJ, 115, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Dickinson, M., Ferguson, H. C., et al. 2004, ApJ, 600, L103 [NASA ADS] [CrossRef] [Google Scholar]
- González, V., Labbé, I., Bouwens, R. J., et al. 2010, ApJ, 713, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Hickey, S., Bunker, A., Jarvis, M. J., Chiu, K., & Bonfield, D. 2010, MNRAS, 404, 212 [NASA ADS] [Google Scholar]
- Hu, E. M., Cowie, L. L., Kakazu, Y., & Barger, A. J. 2009, ApJ, 698, 2014 [NASA ADS] [CrossRef] [Google Scholar]
- Iwata, I., Ohta, K., Tamura, N., et al. 2007, MNRAS, 376, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Iye, M., Ota, K., Kashikawa, N., et al. 2006, Nature, 443, 186 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Izotov, Y. I., Papaderos, P., Guseva, N. G., Fricke, K. J., & Thuan, T. X. 2004, A&A, 421, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Guseva, N. G. 2007, ApJ, 671, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Kashikawa, N., Shimasaku, K., Malkan, M. A., et al. 2006, ApJ, 648, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kissler-Patig, M., Pirard, J.-F., Casali, M., et al. 2008, A&A, 491, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2010, ApJS, submitted [Google Scholar]
- Labbé, I., González, V., Bouwens, R. J., et al. 2010, ApJ, 708, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., & Benson, A. J., 2010, MNRAS, submitted [Google Scholar]
- Leggett, S. K., Burningham, B., Saumon, D., et al. 2010, ApJ, 710, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Bremer, M. 2003, ApJ, 593, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P. 1995, ApJ, 441, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Pozzetti, L., & Dickinson, M. 1998, ApJ, 498, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Haardt, F., & Rees, M. J. 1999, ApJ, 514, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Rees, M. J., Volonteri, M., Haardt, F., & Oh, S. P. 2004, ApJ, 604, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Buttery, H., Maiolino, R., Marconi, A., & Pozzetti, L. 2007, A&A, 461, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLure, R. J., Cirasuolo, M., Dunlop, J. S., Foucaud, S., & Almaini, O. 2009, MNRAS, 395, 2196 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Dunlop, J. S., Cirasuolo, M., et al. 2010, MNRAS, 403, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Mesinger, A., & Furlanetto, S. 2009, MNRAS, 400, 1461 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., et al. 2010, ApJ, 709, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Okamura, S., et al. 2004, ApJ, 611, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Mobasher, B., Shimasaku, K., et al. 2009a, ApJ, 706, 1136 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ono, Y., Egami, E., et al. 2009b, ApJ, 696, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Pirard, J.-F., Kissler-Patig, M., Moorwood, A., et al. 2004, in SPIE Conf. Ser. 5492, ed. A. F. M. Moorwood, & M. Iye, 1763 [Google Scholar]
- Richard, J., Pelló, R., Schaerer, D., Le Borgne, J.-F., & Kneib, J.-P. 2006, A&A, 456, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, J., Stark, D. P., Ellis, R. S., et al. 2008, ApJ, 685, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E. 2010, ApJ, 713, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Ferrara, A., & Dayal, P. 2010, MNRAS, submitted [Google Scholar]
- Sawicki, M., & Thompson, D. 2006, ApJ, 648, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & de Barros, S. 2010, A&A, 515, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Shimasaku, K., Ouchi, M., Furusawa, H., et al. 2005, PASJ, 57, 447 [NASA ADS] [Google Scholar]
- Stanway, E. R., Bunker, A. J., & McMahon, R. G. 2003, MNRAS, 342, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Bremer, M. N., & Lehnert, M. D. 2008, MNRAS, 385, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Pettini, M., & Hamilton, D. 1995, AJ, 110, 2519 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Giavalisco, M., Dickinson, M., & Pettini, M. 1999, ApJ, 519, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Totani, T., Kawai, N., Kosugi, G., et al. 2006, PASJ, 58, 485 [NASA ADS] [Google Scholar]
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [Google Scholar]
- Trenti, M., Stiavelli, M., Bouwens, R. J., et al. 2010, ApJ, 714, L202 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 2002, ApJ, 575, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T. 2005, ApJ, 621, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuji, T., Nakajima, T., & Yanagisawa, K. 2004, ApJ, 607, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Giavalisco, M., Dickinson, M., et al. 2009, ApJ, 695, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Venkatesan, A., Tumlinson, J., & Shull, J. M. 2003, ApJ, 584, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Bunker, A. J., Ellis, R. S., et al. 2010a, MNRAS, 403, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Bunker, A. J., Lorenzoni, S., & Caruana, J. 2010b, MNRAS, submitted [Google Scholar]
- Yan, H., Windhorst, R., Hathi, N., et al. 2010, AAS Meeting, BAAS, 42, 495 [NASA ADS] [Google Scholar]
- Yoshida, M., Shimasaku, K., Kashikawa, N., et al. 2006, ApJ, 653, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Bradley, L. D., Bouwens, R. J., et al. 2009, ApJ, 697, 1907 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Colour-composite image of the BDF (left) and NTTDF (right) fields, created using the weighted mean of Hawk-I Y, J, and K images as red, the FORS2 Z as green, and the weighted mean of FORS1/FORS2 optical images as blue. |
| In the text | |
 |
Fig. 2 Left: Z − Y colour of star-forming galaxies as a function of redshift. In the upper part, the efficiency curve of the two filters is shown, computed at the observed wavelength of a Lyman-α emission at the corresponding redshift. Right: Z − Y vs. Y − J colour diagram showing the expected colours of LBGs (same as in left panel, black points), passively evolving galaxies (red squares) and reddened starbursts (green circles) at 1.5 < z < 4 and cool dwarf stars from the templates of Tsuji et al. (2004) (magenta stars). Galaxy colours are computed according to CB07 models, see text for details on the adopted parameters. In both panels the lines indicate the relevant colour selection criteria discussed in Sect. 3 |
| In the text | |
 |
Fig. 3 Thumbnails showing the images of the eight selected high-redshift candidates in the different observed bands. |
| In the text | |
 |
Fig. 4 Thumbnails showing the stacked images of the 15 high-redshift candidates selected in the GOODS1, GOODS2, BDF and NTTDF fields. The observed bands are shown in the legends. |
| In the text | |
 |
Fig. 5 Best-fit SED to the stacked photometry, with relevant photometric redshift at z = 6.85. |
| In the text | |
 |
Fig. 6 Number densities in two rest-frame magnitude intervals estimated for our Hawk-I data set in a stepwise form with a standard Y − UV conversion of the observed number counts as discussed in the text (black filled squares), or with a χ2 method considering also photometric and model uncertainties (black empty circles). Other points are from Bouwens et al. (2010a) (NICMOS, red empty squares), Ouchi et al. (2009a) (SUBARU, blue empty squares and upper limits) and Oesch et al. (2010) (WFC3-UDF, magenta empty circles). For comparison we show the recent determinations of the LF at z ~ 6 by Bouwens et al. (2007) (B07, green dot-dashed line) and McLure et al. (2009) (M09, blue dashed line). The black solid line is the best-fit LF obtained by combining the stepwise points shown in the figure with new determinations of the binned densities from WFC3-UDF and WFC3-ERS data (Grazian et al. in preparation). |
| In the text | |
 |
Fig. 7 Normalized distribution of UV continuum magnitudes (estimated from the average Y − M1500 relation) for the 15 Hawk-I candidates divided in two bins (dashed histograms). The solid curves show the expected distributions of UV magnitudes for objects in the same observed ranges when photometric uncertainties are taken into account through Monte Carlo simulations. |
| In the text | |
 |
Fig. 8 χ2 contour levels for the dlog (φ)/dz, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.