© ESO, 2010

1. Introduction

Piskunov et al. (2007, 2008a,b) developed an approach to determining the masses of open star clusters (OCs) and applied it to determine the initial and present-day mass function of OCs in the solar neighborhood. The method is based on the determination of the tidal radius r_t from the cumulative number of cluster members as a function of projected distance from the cluster center. For each cluster, the tidal radius r_t is determined from projected number density profiles by fitting a King 1962 profile (King 1962). The identification of the King cutoff radius r_t with the “Jacobi” radius r_J (i.e., the dynamical tidal radius, which is the distance from the cluster center to the Lagrange points L₁ and L₂) then yields the OC mass from the standard formula given here by Eq. (9) solved for M_cl. The application of this dynamical mass estimate for tidally limited clusters to an unbiased OC catalog yields a mass determination that is independent of the classical methods. A detailed comparison with other cluster mass determinations is also made. In a second step, the method is extended to all OCs of an unbiased cluster catalog by establishing a transformation of the observed semi-major axis and central surface density to r_t. These results were then used to derive the cluster present-day mass function (CPDMF) and the initial mass function of OCs (CIMF) in the extended solar neighborhood. Adopting a constant cluster formation rate over the past 10 Gyr yields a surface density of 18M_⊙pc^-2 of stars born in OCs. This corresponds to a fraction of 37% of disk stars born in OCs (Röser et al. 2010). This is large compared to the classical values of the order of 10% or less (e.g., Wielen 1971; Miller & Scalo 1978).

Some crucial assumptions enter the dynamical mass determination based on fitting a King profile: a) The OC fills its Roche lobe in the tidal field of the Milky Way. For compact (e.g. Roche-lobe underfilling) clusters, r_J and as a consequence the mass can be underestimated by a large amount; b) The effect of mass segregation can be neglected, i.e., star counts on the upper main sequence, which dominate the observed cluster members, are representative of the mass distribution; c) The elliptic shape of the clusters and the contamination by tidal tail stars do not result in a systematic bias. Shape parameters were measured by Kharchenko et al. (2009) and the distribution of tidal tail stars have been investigated in detail (e.g. Just et al. 2009); d) The tidal radius r_t determined by fitting the cumulative projected mass profile represents the Jacobi radius r_J used to derive the cluster mass. Since the cluster mass depends on the third power of r_J, the method is very sensitive to systematic errors in the derivation of r_J.

In the present paper, we quantify the possible bias introduced by identifying the tidal radius r_t inferred from a King profile fitting with the Jacobi radius r_J used for the mass determination by Piskunov et al. (2007). We applied the King profile fitting procedure to a direct N-body simulation of a dissolving star cluster at different evolutionary states. We simulated a star cluster on a circular orbit at R_C = 8.5 kpc which evolved in the tidal field of the Milky Way including stellar evolution. We took snapshots of the evolved model with all stellar masses and positions at four different times and projected the snapshots from the perspective of an observer on Earth (at R₀ = 8 kpc) onto the sky, at different positions along its orbit. After all, we determined the model’s limiting radius r_t by fitting the projected cumulative mass profile with Eq. (6) and compared r_t to the actual Jacobi radius r_J.

The paper is organized as follows. In Sect. 2 we discuss the method of N-body simulations in the external potential of the Milky Way and Sect. 3 contains the theory of the cluster geometry in a tidal field. In Sect. 4, we show a simple iterative method to determine the Jacobi radius of an N-body model of a star cluster in a tidal field. In Sect. 5, the projection and fitting methods are described. Finally, Sect. 6 contains our results and Sect. 7 our conclusions.

2. Numerical simulation

We analyze in detail a numerical simulation of a star cluster with initial mass M₀ = 10⁴   M_⊙ on a circular orbit in an analytic Milky Way potential. It is the fiducial cluster simulation (run 10) discussed in Just et al. (2009). We chose this cluster because it is representative of the high-mass end of the observed OCs. Since the total mass of the cluster system is dominated by the high-mass end, the correction of biases in the mass determination are most important in that parameter regime. The cluster was set up as a W₀ = 6 King model with a half-mass radius of 8 pc. The extension of the cluster initially exceeds the Roche lobe initially leading to an enhanced mass loss in the first 0.5 Gyr. We used a Salpeter IMF and included mass loss by stellar evolution. The total lifetime of the cluster at a circular orbit with R_C = 8.5 kpc is 6.3 Gyr. For details of the evolution we refer to Just et al. (2009).

In a high-resolution simulation of a dissolving star cluster with N = 40404 particles in the tidal field of the Milky Way the direct N-body code φgrape¹ (Harfst et al. 2007) was used with the micro-grape6 special-purpose hardware at the Astronomisches Rechen-Institut (ARI) in Heidelberg². φgrape is an acronym for Parallel Hermite Integration with grape. The code is written in ansi-c and uses a fourth-order Hermite scheme (Makino & Aarseth 1992) for the orbit integration. It is parallelized and uses the MPI library to communicate between the processors. The force computations are executed on the fast special-purpose hardware grape. The special-purpose micro-grape6 hardware cards are designed especially to calculate gravitational forces in N-body simulations rapidly using parallelization with pipelining (see Harfst et al. 2007, and references therein).

The code φgrape does not adopt regularization as the codes nbody4 or nbody6++ (Aarseth 1999, 2003; Spurzem 1999) do. Rather, it uses a standard Plummer type N-body gravitational softening. The softening length in the model used for the current work was ϵ = 10^-3 pc. We tested for different softening lengths ϵ = 10^-3,10^-4, and 10^-5 pc that there are no significant differences regarding shape evolution and star-cluster mass loss.

For the simulation of a star cluster in the tidal field of the Galaxy, the N-body problem is solved in an analytic background potential. We use an axisymmetric three-component model, where the bulge, disc, and halo are described by Plummer-Kuzmin models (Miyamoto & Nagai 1975) with the potential 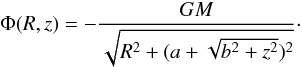$\mathrm{\Phi }\mathrm{\left(}\mathit{R,z}\mathrm{\right)}\mathrm{=}\mathrm{-}\frac{\mathit{GM}}{\sqrt{{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathrm{(}\mathit{a}\mathrm{+}\sqrt{{\mathit{b}}^{\mathrm{2}}\mathrm{+}{\mathit{z}}^{\mathrm{2}}}{\mathrm{)}}^{\mathrm{2}}}}\mathrm{·}$(1)The parameters a,b, and M of the Milky Way model are given in Table 1 for the three components.

The top panel of Fig. 1 shows the rotation curve of the three-component model of the Milky Way. The parameters of the three-component model are chosen such that the rotation curve matches that of the Milky Way (Dauphole & Colin 1995). At the solar radius R₀ = 8.0 kpc, which was assumed in this study, the value of the circular velocity is V₀ = 234.2 km s^-1. The values of Oort’s constants A and B are consistent with the observed values (A,B) = (14.5 ± 0.8, −13.0 ± 1.1) km s^-1/kpc derived by Piskunov et al. (2006). More generally, the dimensionless epicyclic and vertical frequency parameters are given by 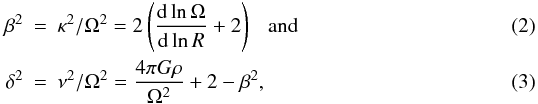$\begin{array}{ccc}{\mathit{\beta }}^{\mathrm{2}}& \mathrm{=}& {\mathit{\kappa }}^{\mathrm{2}}\mathit{/}{\mathrm{\Omega }}^{\mathrm{2}}\mathrm{=}\mathrm{2}\left(\frac{\mathrm{d}\ln \mathrm{\Omega }}{\mathrm{d}\ln \mathit{R}}\mathrm{+}\mathrm{2}\right)\mathrm{and}\\ {\mathit{\delta }}^{\mathrm{2}}& \mathrm{=}& {\mathit{\nu }}^{\mathrm{2}}\mathit{/}{\mathrm{\Omega }}^{\mathrm{2}}\mathrm{=}\frac{\mathrm{4}\mathit{\pi G\rho }}{{\mathrm{\Omega }}^{\mathrm{2}}}\mathrm{+}\mathrm{2}\mathrm{-}{\mathit{\beta }}^{\mathrm{2}}\mathit{,}\end{array}$where κ, ν, and Ω are the epicyclic, vertical, and circular frequencies of a near-circular orbit and ρ is the local Galactic density (see Oort 1965, for the derivation of δ²). The bottom panel of Fig. 1 shows the course of the epicyclic and vertical frequency parameters β and δ.

At the radius R_C = 8.5 kpc of the circular orbit considered in this study, we obtain (β_C,δ_C) = (1.37,2.86) and the circular velocity V_C = 233.3 km s^-1. The orbital timescale at R_C = 8.5 kpc is T_orb ≈ 224 Myr.

3. Cluster geometry

According to King (1962), the projected density profile Σ(r) of a star cluster can be approximated by 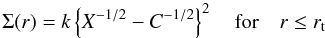$\mathrm{\Sigma }\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{=}\mathit{k}{\mathrm{\{}{\mathit{X}}^{\mathrm{-}\mathrm{1}\mathit{/}\mathrm{2}}\mathrm{-}{\mathit{C}}^{\mathrm{-}\mathrm{1}\mathit{/}\mathrm{2}}\mathrm{\}}}^{\mathrm{2}} \mathrm{for} \mathit{r}\mathrm{\le }{\mathit{r}}_{\mathrm{t}}$(4)with normalization constant k and 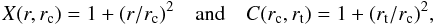$\mathit{X}\mathrm{\left(}\mathit{r,}{\mathit{r}}_{\mathrm{c}}\mathrm{\right)}\mathrm{=}\mathrm{1}\mathrm{+}\mathrm{(}\mathit{r}\mathit{/}{\mathit{r}}_{\mathrm{c}}{\mathrm{)}}^{\mathrm{2}} \mathrm{and} \mathit{C}\mathrm{(}{\mathit{r}}_{\mathrm{c}}\mathit{,}{\mathit{r}}_{\mathrm{t}}\mathrm{)}\mathrm{=}\mathrm{1}\mathrm{+}\mathrm{(}{\mathit{r}}_{\mathrm{t}}\mathit{/}{\mathit{r}}_{\mathrm{c}}{\mathrm{)}}^{\mathrm{2}}\mathit{,}$(5)where r_c is the core radius and r_t is the (tidal) cutoff radius where the projected density of the model drops to zero. Integration yields the cumulative form of the King (1962) profile, 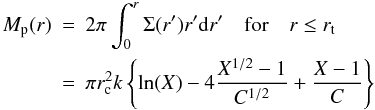$\begin{array}{ccc}{\mathit{M}}_{\mathrm{p}}\mathrm{\left(}\mathit{r}\mathrm{\right)}& \mathrm{=}& \mathrm{2}\mathit{\pi }{\mathrm{\int }}_{\mathrm{0}}^{\mathit{r}}\mathrm{\Sigma }\mathrm{\left(}{\mathit{r}}^{\mathrm{\prime }}\mathrm{\right)}{\mathit{r}}^{\mathrm{\prime }}\mathrm{d}{\mathit{r}}^{\mathrm{\prime }} \mathrm{for} \mathit{r}\mathrm{\le }{\mathit{r}}_{\mathrm{t}}\\ & \mathrm{=}& \mathit{\pi }{\mathit{r}}_{\mathrm{c}}^{\mathrm{2}}\mathit{k}\left\{\ln \mathrm{\left(}\mathit{X}\mathrm{\right)}\mathrm{-}\mathrm{4}\frac{{\mathit{X}}^{\mathrm{1}\mathit{/}\mathrm{2}}\mathrm{-}\mathrm{1}}{{\mathit{C}}^{\mathrm{1}\mathit{/}\mathrm{2}}}\mathrm{+}\frac{\mathit{X}\mathrm{-}\mathrm{1}}{\mathit{C}}\right\}\end{array}$(6)where M_p(r) is the projected cumulative mass of the model, i.e. the mass in projection on the sky within a circle of radius r. For r > r_t, we force the integrated profile (Eq. (6)) to the finite value 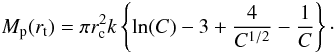${\mathit{M}}_{\mathrm{p}}\mathrm{\left(}{\mathit{r}}_{\mathrm{t}}\mathrm{\right)}\mathrm{=}\mathit{\pi }{\mathit{r}}_{\mathrm{c}}^{\mathrm{2}}\mathit{k}\left\{\ln \mathrm{\left(}\mathit{C}\mathrm{\right)}\mathrm{-}\mathrm{3}\mathrm{+}\frac{\mathrm{4}}{{\mathit{C}}^{\mathrm{1}\mathit{/}\mathrm{2}}}\mathrm{-}\frac{\mathrm{1}}{\mathit{C}}\right\}\mathrm{·}$(7)We do not use the identification of M_p(r_t) with the cluster mass, since in practice the equations are applied to star counts and the effective mass-of-light ratio enters the normalization constant k.

Already King (1961) remarks that the tidal forces from the galaxy distort only the outer regions of a star cluster. We quantify these deviations from spherical symmetry caused by the tidal field in this section. We employ a coordinate system (x, y, z) of “principal axes of the star cluster”. Its origin is the cluster center. The x-axis points away from the Galactic center, the y-axis points in the direction of the Galactic rotation and the z-axis is directed towards the Galactic north pole. Figure 2 shows a “principal axis plane cut” through the equipotential surfaces of the effective potential around a star cluster on a circular orbit in the tidal field of the Milky Way. To second order, the effective potential is given by 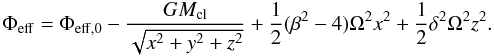$\begin{array}{ccc}{\mathrm{\Phi }}_{\mathrm{eff}}\mathrm{=}{\mathrm{\Phi }}_{\mathrm{eff}\mathit{,}\mathrm{0}}\mathrm{-}\frac{\mathit{G}{\mathit{M}}_{\mathrm{cl}}}{\sqrt{{\mathit{x}}^{\mathrm{2}}\mathrm{+}{\mathit{y}}^{\mathrm{2}}\mathrm{+}{\mathit{z}}^{\mathrm{2}}}}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}\mathrm{(}{\mathit{\beta }}^{\mathrm{2}}\mathrm{-}\mathrm{4}\mathrm{)}{\mathrm{\Omega }}^{\mathrm{2}}{\mathit{x}}^{\mathrm{2}}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\delta }}^{\mathrm{2}}{\mathrm{\Omega }}^{\mathrm{2}}{\mathit{z}}^{\mathrm{2}}\mathit{.}& & \end{array}$(8)For the cluster, we assumed a Kepler potential, which is a very good approximation in the outer parts (Just et al. 2009). The unit in Fig. 2 is the Jacobi radius r_J. The Jacobi radius is defined as the distance from the cluster center to the Lagrange points L₁ and L₂. It is given by ${\mathit{r}}_{\mathrm{J}}\mathrm{=}{\left[\frac{\mathit{G}{\mathit{M}}_{\mathrm{cl}}}{\mathrm{(}\mathrm{4}\mathrm{-}{\mathit{\beta }}^{\mathrm{2}}\mathrm{)}{\mathrm{\Omega }}^{\mathrm{2}}}\right]}^{\mathrm{1}\mathit{/}\mathrm{3}}$(9)(see King 1962). The value of the effective potential on the critical equipotential surface, which connects L₁ and L₂, can be easily calculated from Eqs. (8) and (9). 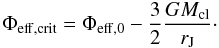It is given by ${\mathrm{\Phi }}_{\mathrm{eff}\mathit{,}\mathrm{crit}}\mathrm{=}{\mathrm{\Phi }}_{\mathrm{eff}\mathit{,}\mathrm{0}}\mathrm{-}\frac{\mathrm{3}}{\mathrm{2}}\frac{\mathit{G}{\mathit{M}}_{\mathrm{cl}}}{{\mathit{r}}_{\mathrm{J}}}\mathrm{·}$(10)Assuming that x_max = r_J, the radius in the y-direction of the last closed (critical) equipotential surface follows from Eqs. (8) and (10), 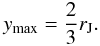${\mathit{y}}_{\max }\mathrm{=}\frac{\mathrm{2}}{\mathrm{3}}{\mathit{r}}_{\mathrm{J}}\mathit{.}$(11)For the radius in z-direction, we have to solve a cubic equation 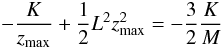$\mathrm{-}\frac{\mathit{K}}{{\mathit{z}}_{\max }}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{L}}^{\mathrm{2}}{\mathit{z}}_{\max }^{\mathrm{2}}\mathrm{=}\mathrm{-}\frac{\mathrm{3}}{\mathrm{2}}\frac{\mathit{K}}{\mathit{M}}$(12)with the constants 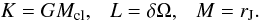$\mathit{K}\mathrm{=}\mathit{G}{\mathit{M}}_{\mathrm{cl}}\mathit{,}\mathit{L}\mathrm{=}\mathit{\delta }\mathrm{\Omega }\mathit{,}\mathit{M}\mathrm{=}{\mathit{r}}_{\mathrm{J}}\mathit{.}$(13)The only real solution is given by ${\mathit{z}}_{\max }\mathrm{=}\frac{{\left\{\mathit{K}\left[\mathit{K}\mathrm{+}\mathrm{2}\mathit{L}\left(\mathit{L}{\mathit{M}}^{\mathrm{3}}\mathrm{+}\sqrt{\mathit{K}{\mathit{M}}^{\mathrm{3}}\mathrm{+}{\mathit{L}}^{\mathrm{2}}{\mathit{M}}^{\mathrm{6}}}\right)\right]\right\}}^{\mathrm{1}\mathit{/}\mathrm{3}}\mathrm{-}{\mathit{K}}^{\mathrm{2}\mathit{/}\mathrm{3}}}{\mathit{L}{\left(\mathit{L}{\mathit{M}}^{\mathrm{3}}\mathrm{+}\sqrt{\mathit{K}{\mathit{M}}^{\mathrm{3}}\mathrm{+}{\mathit{L}}^{\mathrm{2}}{\mathit{M}}^{\mathrm{6}}}\right)}^{\mathrm{1}\mathit{/}\mathrm{3}}}\mathrm{·}$(14)For (β,δ) = (β_C,δ_C) = (1.37,2.86), we obtain ${\mathit{z}}_{\max }\mathrm{\approx }\mathrm{0.503}{\mathit{r}}_{\mathrm{J}}$(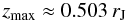15)(e.g. Wielen 1974). More generally, the ratios of the principal axes y_maxtox_max and z_maxtox_max of all closed equipotential surfaces are shown in Fig. 3 as a function of the parameter γ = x/r_J. At the center of the cluster we have γ = 0, while γ = 1 corresponds to the critical equipotential surface through x = r_J.

Figure 4 shows the logarithmically color-coded surface density Σ of projections of the simulated N-body model of the star cluster onto its principal axis planes at time T₄ = 1.31 Gyr. The surface density Σ has been calculated from the N-body snapshot file with the method of Casertano & Hut (1985) (their Eq. (II.6) with j = 20). The contours correspond to Δlog Σ ≈ 2 dex. The extent of the last closed (critical) equipotential surface is marked with dashed lines. The contours of constant surface density roughly follow the equipotential surfaces from Fig. 2.

4. Jacobi radius of the model

We determined the Jacobi radius of our simulated N-body model iteratively from Eq. (9). The gravitational constant G and the quantities β and Ω are known but M_cl, the cluster mass within r = r_J is unknown since r_J is unknown. Our iteration is given by ${\mathit{r}}_{\mathit{n}\mathrm{+}\mathrm{1}}\mathrm{=}{\left[\frac{\mathit{G}{\mathit{M}}_{\mathrm{enc}}\mathrm{\left(}{\mathit{r}}_{\mathit{n}}\mathrm{\right)}}{\mathrm{(}\mathrm{4}\mathrm{-}{\mathit{\beta }}^{\mathrm{2}}\mathrm{)}{\mathrm{\Omega }}^{\mathrm{2}}}\right]}^{\mathrm{1}\mathit{/}\mathrm{3}}$(16)where M_enc(r) is the enclosed mass of cluster stars within radius r around the cluster center. Starting with r₀ = ∞, the iteration theoretically converges towards r_∞ = r_J. In practice, a few iterations are sufficient to determine r_J accurately. We note that this simple method does not rely on numerical fits of the effective potential to the envelope of the spatial distribution of Jacobi energies of the cluster stars. It can easily be applied to an N-body snapshot file that contains masses and positions of the individual particles at a certain time.

5. Projection and fitting

We calculate the projection at the sky in Galactic coordinates (l,b) and ignore for simplicity the perspective effects. Strictly speaking the projection of the cluster model is consistent only in the midplane b = 0° corresponding to the circular orbit in the Galactic plane. The rotation angle α is related to the Galactic longitude l by the law of sines 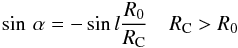$\sin \mathit{\alpha }\mathrm{=}\mathrm{-}\sin \mathit{l}\frac{{\mathit{R}}_{\mathrm{0}}}{{\mathit{R}}_{\mathrm{C}}} {\mathit{R}}_{\mathrm{C}}\mathit{>}{\mathit{R}}_{\mathrm{0}}$(17)where R₀ = 8 kpc at the solar circle and R_C = 8.5 kpc at the cluster orbit. At the Galactic coordinates (l,b) = (0,0) and (l,b) = (180°,0), the “system (x, y, z) of principal axes of the cluster” with origin at the cluster center is not rotated. We note that at l = 90° and l = 270° we have the maximum rotation angle 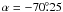and 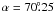, respectively.

A sketch of the projection of the simulated N-body model of the star cluster onto the plane of the sky is illustrated in Fig. 5. Four orbital positions of the dissolving star cluster with its tidal tails are marked in the sketch.

To demonstrate the effect of different projections also in Galactic latitude, we add the cases of a certain height of the cluster orbit above and below the plane of the solar circle (dotted lines in Fig. 5). The effect of the corresponding vertical oscillation of the cluster orbit on the intrinsic structure of the cluster and of a variation in δ in Eq. (2) are neglected in this study.

For all positions of the cluster on its orbit, we rotate the cluster around the z axis and then around the y′ axis by the ordered pair of angles (α,  −b) to simulate the perspective of the cluster for an observer on earth. After the projection, we determine the polar symmetric profile of the projected cumulative mass M_p(r) from our N-body data file by summations over radius and polar angle and apply a fit with Eq. (6). For the fitting, we used the mpfit package in idl (Markwardt 2009; Moré 1978, for the Levenberg-Marquardt algorithm).

6. Results

We now discuss projections according to Eq. (17) in detail. Figure 6 shows examples of fits (upper panels) with the corresponding projections (lower panels). The resulting parameter ratio r_t/r_J is given in the upper panels and the (l, b) coordinates in the corresponding lower panels. In the upper panels, the solid (black) line represents the data and dotted (blue) line the fit. The dashed (red) lines indicate r_c (left dashed line) and r_t (right dashed line) derived in the fit with Eq. (6). In the lower panels, the dashed (red) line indicates r_J.

We derived the ratio r_t/r_J for all projection directions in (l,b) at four different evolution times of the cluster. The projections are performed in steps of 4 degrees from b =  −90° to b =  +90° and l = 0 to l = 360°. The full N-body snapshot file with N = 40404 particles has been used for the projection and fitting procedure as described in Sect. 5. Figure 7 shows parameter surfaces of r_t/r_J as a function of Galactic coordinates of the cluster center at times T₁ = 0.62 Gyr (top left), T₂ = 0.84 Gyr (top right), T₃ = 1.06 Gyr (bottom left) and T₄ = 1.31 Gyr (bottom right). A squeezed Hammer-Aitoff projection of Galactic coordinates has been used (see Appendix A). The total number of fits for each plot in Fig. 7 is N_fits = 4186. We note that in the plot for T₁, a peak around (l,b) ≈ (270°,0) (see also Fig. A.1 in Appendix A) is not resolved (white colored area). Here r_t/r_J reaches a factor of 1.52.

It can be seen that the cluster masses are typically overestimated. The strongest bias to high masses at time T₁ (including the peak) shows that the unbound stars stay for a long time close to the cluster and contribute to the outer density profile in the fitting procedure. This bias depends on the initial conditions. At later times T₃, T₄, the cluster mass distribution becomes stable and the bias is independent of the age of the cluster.

Figure 8 shows a histogram of the fraction on the sky per bin in M_t/M_cl = (r_t/r_J)³ for the parameter surface in Fig. 7 corresponding to time T₄, where the “tidal” masses M_t and M_cl are calculated with Eq. (9) from r_t and r_J, respectively. The solid line shows the distribution for projections in the range  −20° < b <  +20°. The most frequent overestimation of the mass is M_t/M_cl = 1.18. The dashed line shows the distribution for projections in the range  −40° < b <  +40°. The most frequent ratio is the same as for the solid line. However, the ratios extend up to M_t/M_cl = 1.7. The dotted line shows the distribution for all projections.The most frequent ratio is the same as for the other two lines, but the ratios extend up to M_t/M_cl ≈ 2.1.

Figure 9 shows the mean mass  ⟨ M_t/M_cl ⟩  as a function of the Galactic latitude b, where M_t is the mass of cluster stars within radius r_t derived from the fitting procedure. Shown are the curves corresponding to times T₁ − T₄. All curves show a local minimum located roughly at b = 0°. For time T₁, the mean overestimation of the mass reaches 2.5 in the direction of the Galactic poles.

Only a small fraction of cluster stars are usually identified as members leading to an increased statistical uncertainty in the fitting procedure. The uppermost plot in Fig. 10 shows the parameter surface derived for the 400 most massive (i.e. the brightest) stars in the simulation at time T₄ (data courtesy of Beuria). The small values of r_t/r_J are caused by mass segregation. The stronger asymmetries with respect to b = 0° compared to the plots in Fig. 7 are due to a slightly asymmetric distribution of the 400 mass-segregated stars in position space.

In order to measure the statistical scatter in r_t, we applied a bootstrap analysis. We divided the N-body snapshot file for time T₄ with N = 40404 particles into 100 small-number samples of N_sample = 400 particles each (the remaining particles were dropped out of the analysis). For each of these small-number samples we applied the procedure described above. The resulting total number of projections and fits was therefore N_fits = 418600. The middle and bottom plots in Fig. 10 show the results of the bootstrap analysis. The middle plot of Fig. 10 shows the mean value of r_t/r_J averaged over the 100 samples. The bottom plot shows the relative standard deviation Δr_t/r_t evaluated by averaging over the 100 samples. The uncertainty in a single determination of r_t is between 10% and 20%. The highest uncertainty is expected for r_t-determinations in the vicinity of the peak around (l,b) ≈ (270°,0).

A comparison with the uppermost plot in Fig. 10 shows that the derived limiting radii for the sample of the most massive stars are systematically lower because of mass segregation. The differences are typically on a 1 − 2σ level.

7. Conclusions

In this paper, we have confirmed that star cluster masses are typically overestimated if the method of Piskunov et al. (2007) is applied to a complete sample. Moreover, we have quantified the methodological error in our analysis.

Figures 7 and 10 show that at certain Galactic coordinates the King (1962) profile fits are particularly biased. A high bias is predicted for (l,b) ≈ (270°,0) (see Figs. 7, 10, and A.1). The corresponding rotation angle of the cluster is α = 70°, where the projection is parallel to the inner end of the tidal arms (see lower left plots in Fig. 6). For (l,b) = (90°,0), there is no corresponding peak in the parameter surface (most clearly visible for T₁) because of the asymmetry between the leading and trailing tidal tails (see the sketch in Fig. 5). For Galactic latitudes beyond b ≈  ±40° (cf. Fig. A.1), the bias becomes large but only a few OCs occupy this regime.

For the parameter surfaces in Fig. 7, the masses are biased within the ranges [1.3M_cl, 3.5M_cl] (at T₁), [1.1M_cl, 2.3M_cl] (at T₂), [1.0M_cl, 2.0M_cl] (at T₃) and [1.0M_cl, 2.1M_cl] (at T₄) depending on the evolutionary state of the star cluster in the tidal field of the Galaxy. The bias depends strongly on the projection angles, which transform differently into Galactic coordinates for different orbital radii of the OC.

Furthermore, we have demonstrated using a bootstrap analysis that the relative error in a single determination of the limiting radius r_t is between 10% and 20% (at time T₄) corresponding to an uncertainty in the mass of  ≈ 50% for samples of N_sample = 400 particles (which are typical of rich OCs).

We have shown that the mass segregation of the brightest stars in a cluster can alter the r_t/r_J factor significantly, which is an important result for the data analysis of observations. The mass segregation results in a concentrated core that causes an underestimation of the tidal radius. For a younger cluster age, one would expect a smaller amount of mass segregation.

To apply a quantitative correction for the bias in the cluster mass determination by identifying r_t with r_J an extensive parameter study of cluster parameters is necessary. The influence of mass-segregation on selection effects caused by the brightness limit of the observations should be considered by such a study, because stellar evolution is taken into account. For young clusters, the bias factor can be particularly sensitive to the initial conditions. The final goal is to find an agreement between the OC mass determinations by the different methods. This would allow an interesting insight into the OC properties such as the IMF, mass-to-light ratio, and mass segregation.

---

Acknowledgments

The authors thank J. Beuria for his help with the Hammer-Aitoff projections and the provision of the data for the uppermost plot in Fig. 10. P.B. and M.I.P. acknowledge the special support by the Ukrainian National Academy of Sciences under the Main Astronomical Observatory GRAPE/GRID computing cluster project. P.B. acknowledges the support from the Volkswagen Foundation GRACE Project No. I80 041-043. M.I.P. acknowledges support by the University of Vienna through the frame of the Initiative Kolleg (IK) “The Cosmic Matter Circuit” I033-N and computing time on the Grape Cluster of the University of Vienna.

References

Appendix A: Squeezed Hammer-Aitoff projection

The squeezed Hammer-Aitoff projection is given by 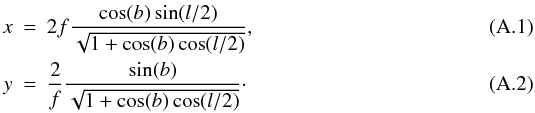$\begin{array}{ccc}\mathit{x}& \mathrm{=}& \mathrm{2}\mathit{f}\frac{\cos \mathrm{\left(}\mathit{b}\mathrm{\right)}\sin \mathrm{(}\mathit{l}\mathit{/}\mathrm{2}\mathrm{)}}{\sqrt{\mathrm{1}\mathrm{+}\cos \mathrm{\left(}\mathit{b}\mathrm{\right)}\cos \mathrm{(}\mathit{l}\mathit{/}\mathrm{2}\mathrm{)}}}\mathit{,}\\ \mathit{y}& \mathrm{=}& \frac{\mathrm{2}}{\mathit{f}}\frac{\sin \mathrm{\left(}\mathit{b}\mathrm{\right)}}{\sqrt{\mathrm{1}\mathrm{+}\cos \mathrm{\left(}\mathit{b}\mathrm{\right)}\cos \mathrm{(}\mathit{l}\mathit{/}\mathrm{2}\mathrm{)}}}\mathrm{·}\end{array}$It represents the standard Hammer-Aitoff equal-area projection, where we have also introduced a free squeezing factor f. The squeezing leaves the area element 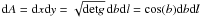invariant, where g is the first fundamental form calculated from Eqs. (A.1) and (A.2). The ratio of diameters of the elliptic projection area is given by d_x/d_y = f². For the standard Hammer-Aitoff projection, we have 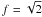. For a projection onto a circular area one can set f = 1. The inverse projection is given by 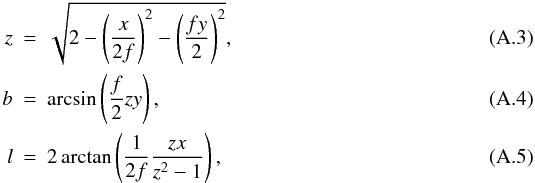$\begin{array}{ccc}\mathit{z}& \mathrm{=}& \sqrt{\mathrm{2}\mathrm{-}{\left(\frac{\mathit{x}}{\mathrm{2}\mathit{f}}\right)}^{\mathrm{2}}\mathrm{-}{\left(\frac{\mathit{fy}}{\mathrm{2}}\right)}^{\mathrm{2}}}\mathit{,}\\ \mathit{b}& \mathrm{=}& \arcsin \left(\frac{\mathit{f}}{\mathrm{2}}\mathit{zy}\right)\mathit{,}\\ \mathit{l}& \mathrm{=}& \mathrm{2}\arctan \left(\frac{\mathrm{1}}{\mathrm{2}\mathit{f}}\frac{\mathit{zx}}{{\mathit{z}}^{\mathrm{2}}\mathrm{-}\mathrm{1}}\right)\mathit{,}\end{array}$where we have introduced the auxiliary variable z.

We assumed that f = 1.2 for Figs. 7 and 10. The resulting coordinate system (which is hidden in Figs. 7 and 10) can be seen in Fig. A.1. We modified idl routines by Landsman to incorporate the free squeezing factor.

All Tables

All Figures