| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201014736 | |
| Published online | 22 November 2010 | |
QPOs in the time domain: an autocorrelation analysis
1
Astrophysics Science Division, NASA/Goddard Space Flight
Center
Greenbelt, MD
20771, USA
e-mail: Demos.Kazanas@nasa.gov
2
University of Maryland, Baltimore County
(UMBC/CRESST), Baltimore, MD
21250,
USA
e-mail: Keigo.Fukumura@nasa.gov
3
University Space Research Association,
10211 Wincopin Circle, Suite 620,
Columbia, MD
21044,
USA
e-mail: Chris.R.Shrader@nasa.gov
4
Columbia University, Department of Mechanical
Engineering, New
York, NY
10027,
USA
e-mail: jianwdong@caa.columbia.edu
Received:
5
April
2010
Accepted:
7
September
2010
Context. Motivated by the recent proposal that one can obtain quasi-periodic oscillations (QPOs) by photon echoes manifesting as non-trivial features in the autocorrelation function (ACF), we study the ACFs of the light curves of three accreting black hole candidates and a neutron star already known to exhibit QPOs namely, GRS 1915+105, XTE J1550-564, XTE J1859+226 and Cygnus X-2.
Aims. We present a comparative study of the timing properties of these systems in the frequency and time domain in search for similarities/differences that may provide clues to the physics underlying the QPO phenomenon.
Methods. We compute and focus on the form of the ACFs in search of systematics or specific temporal properties at the time scales associated with the known QPO frequencies in comparison with the corresponding PDS.
Results. Even within our small object sample we find both similarities as well as significant and subtle differences in the form of the ACFs both amongst black holes and between black holes and neutron stars to warrant a closer look at the QPO phenomenon in the time domain: the QPO features manifest as an oscillatory behavior of the ACF at lags near zero; the oscillation damps exponentially on time scales equal to the inverse QPO width to a level of a percent or so. In black holes this oscillatory behavior is preserved and easily discerned at much longer lags while this is not the case for the neutron star system Cyg X-2. The ACF of GRS 1915+105 provides an exception to this general behavior in that its decay is linear in time indicating an undamped oscillation of coherent phase. We present simple ad hoc models that reproduce these diverse time domain behaviors and we speculate that their origin is the phase coherence of the underlying oscillation.
Conclusions. It appears plausible that time domain analyses, complementary to the more common frequency domain ones, could impose tighter constraints and provide clues for the driving mechanisms behind the QPO phenomenon.
Key words: black hole physics / stars: oscillations / X-rays: stars / binaries: general / X-rays: binaries
© ESO, 2010
1. Introduction
In the past several decades the study of accretion powered sources, i.e. neutron stars and black holes, whether at the galactic or extragalactic scales, has been one of the central themes of high energy astrophysics. However, the small angular size of these systems puts them beyond the imaging capabilities of present and perhaps foreseeable future telescopes. Therefore, by necessity, the study of the structure and dynamics of the accretion flows responsible for their observed luminosity is effected through studies of their spectra and variability.
For the galactic sources in particular, most of their luminosity is emitted at X-ray energies (E ~ 0.1−20 keV) and their spectra at their highest energies, E ≳ 5 keV, are thought to be produced by the Comptonization process, while at lower energies they exhibit a quasi-thermal component, usually fit by the spectrum of a multi-color disk (MCD). However, spectral studies alone, in particular of spectra due to Comptonization, constrain mainly the column density of the hot gas along the observer’s line of sight. This is not sufficient to provide information about the accreting flow dynamics, which require in addition knowledge of source size (e.g. Hua et al. 1999); this is usually estimated from the source variability, thus arguing for the combined spectro-temporal analysis of the physics of accretion flows.
The variability of these sources, as conventionally determined through their power density spectra (PDS), spans many decades in Fourier frequency at roughly constant power (ν ~ 10-2 − 103 Hz extending in some cases to frequencies as low as 10-6 Hz), presumably an indication that the associated flows span also a large number of decades in radius. However, in addition to these broad power spectra of aperiodic variability, the PDS of accretion powered sources exhibit often excess variability also at particular narrow frequency bands known as quasi-periodic oscillations (QPOs). These are presumably associated with frequencies characteristic of the flow dynamics and/or the radiative transfer of the photons in the accretion flow.
QPOs are found in the PDS of both accreting galactic black hole candidates (GBHCs, e.g. Remillard & McClintock 2006) and neutron stars in low-mass X-ray binaries (LMXBs, e.g. van der Klis 2006). Perhaps with exception of the neutron star kHz QPO, their frequencies are generally lower than those characteristic of the dynamics of accretion onto an object of size a few Schwarzschild radii. Roughly twenty five years of QPO observations have produced a rich phenomenology which to date remains by and large unaccounted for. The generic QPO model, employing qualitative arguments about the dynamics or kinematics of the accretion flow and parameters chosen to reproduce the frequencies already observed, has rather limited predictive power. In the absence of a general, robust theoretical framework that it can reproduce the observed phenomenology it is not even clear whether the physics underlying the QPOs at the different frequency regimes and different sources involve similar or fundamentally different processes. Most interestingly, discerning the corresponding oscillations in the source light curves (LCs) has remained difficult (particularly more so in active galactic nuclei; e.g. Vaughan & Uttley 2005), even though on occasion the PDS exhibit QPOs with large Q-values (Q ≃ 10, where Q ≡ ν0/Δν ≃ 10 and Δν is the QPO FWHM); an exception are the light curves that yield the low frequency (<0.1 Hz) QPOs of GRS 1915+105 of Fig. 1c, in which the corresponding oscillations are possible to discern in the LC.
It is generally believed that the QPO phenomenon involves an oscillation of sorts; e.g. orbiting blobs of gas (clumpy hot spots) in the context of general relativistic diskoseismology under strong gravity (e.g. Schnittman 2005). However, while sufficient, this is not necessary, neither the PDS provides any clues on the shape of the oscillating signal. Specifically, one could also obtain QPO-like features in the PDS of a time series, among others, if the latter involves a given signal and its “echo”, i.e. a well defined lag of itself (see, e.g., Kazanas & Hua 1999), which in accretion powered sources will most likely be the result of a specific geometric arrangement of the system (e.g. a warped disk). We have recently shown the possibility of (harmonically spaced) “echo” QPOs due to general relativistic frame-dragging in the (simulated) inherently aperiodic LCs of rapidly rotating black holes (i.e. black holes with a/M ≳ 0.94 where a is specific spin and M is mass of a black hole) (Fukumura & Kazanas 2008; Fukumura et al. 2009). At this point it is not clear whether any of the observed GBHCs exhibit these “ergospheric” (or any other type of echo) QPOs (there is a search of the existing data bases going on). However, should the physics underlying certain harmonically spaced QPOs (often seen in the PDS of accreting sources) be an echo rather than an oscillation, the ACF would provide an indispensable analysis tool in verifying this because of its unique signature, namely its double peak structure (harmonically spaced QPOs are normally attributed to an underlying oscillation of non-sinusoidal shape).
The timing analysis of accretion powered sources, especially those that exhibit the QPO phenomenon is typically performed in the frequency domain through the use of FFT and the corresponding power density spectra (PDS). However, as argued above, analysis in the time domain through the ACF may also provide useful, complementary information as we will exhibit further on. As well known, the PDS and ACF are related through a Fourier transform and one might think that one of them might suffice to obtain all relevant knowledge about the signal. However, each of these variability metrics emphasizes different aspects of the underlying signal and the simultaneous transform of the always present noise might permit discerning different clues of the process underlying the QPO phenomenon in the two different domains.
We note that to date analyses of QPO properties the time-domain (i.e. through ACF) are precious few in the literature (see, e.g. Fig. 4 in Ebisawa et al. 1989, for the ACF associated with the QPO of LMC X-1). Motivated by this fact and the above discussion we have decided to take a closer look at the ACFs of sources which are known to exhibit harmonically spaced QPOs at well defined frequencies, thus shifting the emphasis of the analysis from the frequency to the time domain.
With these considerations in mind we present in Sect. 2 the PDS analysis of the time series of four accretion-powered sources known to exhibit prominent QPOs with harmonically spaced peaks. Of these, three are GBHCs and one is a well known accreting LMXB neutron star. Comparative analysis of the ACFs are then presented in Sect. 3. In Sect. 4 we present explicit examples of time series with similar PDS but very different ACFs in order to demonstrate the complementary roles of PDS and ACF. We finally summarize and review these findings and draw some general conclusions in Sect. 5.
2. Source selection and their pds analysis
The sources used in our analysis were selected by the requirement that they exhibit large amplitude QPOs at well defined frequencies and that they represent different types of objects, in order to test whether their overall morphological properties play a role in the type of QPOs and ACFs we obtain. The sources we have chosen usually exhibit QPOs in more than one frequency range, typically at a few Hz and also at tens to a hundred Hz. Since the lower frequency QPOs are the more prominent ones, we focus our analysis at these. Actually, it is not obvious that the ACF analysis we present herein can discern the higher frequency species of these features, but the answer to this question will have to wait for a more detailed analysis.
 |
Fig. 1 Leahy-normalized power density spectra (PDS) annotating the identified low-frequency features for a) XTE J1550-564 (νsub ~ 2.8,νf ~ 5.3 and ν1 ~ 10.9 Hz); b) XTE J1859+226 (νf ~ 1.2 and ν1 ~ 2.4 Hz); c) GRS 1915+105 (νf ~ 67,ν1 ~ 136,ν2 ~ 205,ν3 ~ 267 and νu ~ 781 mHz) and (d) Cygnus X-2 (νf ~ 14.9 and ν1 ~ 29.1 Hz) with the spectral resolution and (fundamental) QPO cycles f ≡ νfT indicated where T ⋍ 1 ks (see the text for notations). |
With the above very general criteria we focused on the following sources:
-
1.
XTE J1550-564: This is a well known X-raynova, discovered by the ASM aboard RXTE in September1998 (Smith 1998). The fact that the source remained activefor an extended period afforded the opportunity to study itsspectral and temporal properties as a function of the sourceflux. It was thus found to cover well known spectral statesof this class, namely the very high (VHS), high (HS), in-termediate (IS) and low (LS) states, characterized respec-tively by decreasing ratios between the flux of the MCD tothe power-law component of their spectra (see Remillard etal. 2002a; Remillard & McClintock 2006).At the same time it exhibited a QPO at frequencyν ≃ 5 Hz along with its first harmonic and subharmonic frequencies at ν ≃ 10 and 2.5 Hz respectively Wijnands et al. (1999). Such QPOs have been empirically categorized as type A, B or C, depending on the QPO frequency, amplitude (rms %), phase-lag, Q-value and on the photon energy spectrum. Remillard et al. (2002a), Remillard et al. (2002b), among others, have reported the presence of high frequency QPOs (HFQPOs) at frequencies 184 and 276 Hz, consistent with the often seen 2:3 ratio. Their analysis also indicated the disappearance of the QPO power as the power-law component of the spectrum decreased below ~ 20% of the total X-ray flux.
-
2.
XTE J1859+226: This is another GBHC that exhibits rich QPO behavior including several low frequency QPOs (LFQPOs) in the frequency range 1 − 9 Hz, including the presence of subharmonic frequencies like XTE J1550-564 (Casella et al. 2004). These authors noted also the occurrence of type A, B, C QPOs in this source. This source, however, exhibits different behavior in the time lags between the fundamental and the first harmonic from that of XTE J1550-564 (both of which have hard lags), in that its subharmonic exhibits soft lag while its fundamental hard.
-
3.
GRS 1915+105: This is a GBHC source, known also as a microquasar because it exhibits VLBI outflows of relativistic speeds. It is the GBHC source with the highest mass function, indicating a black hole of mass M ≃ 15 M⊙. It is known to exhibit statistically significant, high-Q, harmonically spaced LFQPOs, with fundamental frequency ν ≃ 67 mHz and its first, second, third and possibly even higher harmonics (Cui 1999); it also exhibits a broad QPO at ν ≃ 0.841 Hz (see Fig. 1c) and pair of HFQPOs at frequencies ν1,2 = 40,67 Hz (Cui 1999, Strohmayer 2001), having the commensurate ratio of 2:3, a common property of the HFQPOs of GBHCs.
-
4.
Cygnus X-2: This is a typical LMXB Z–source containing a neutron star accreting at the Eddington limit (van der Klis 2006). Hasinger et al. (1986) discovered a QPO at frequency 30 Hz increasing to 45 Hz with increasing source luminosity. HFQPOs (at νl ~ 700 Hz and νu ~ 1000 Hz) were then discovered by Wijnands et al. (1998), while correlations between the QPO frequencies, the flux and the spectral index were established in Titarchuk et al. (2007).
In Fig. 1 we show the Leahy normalized PDS (Leahy normalization provides the fractional amplitude relative to a χ2 process with 2 degrees of freedom which is known to have amplitude 2 and variance 4; see Leahy et al. 1983) of each of the above sources obtained at the specific date indicated along with the binned frequency resolution and the number of QPO cycles f ≡ νfT at the fundamental QPO frequency νf where T is the duration of the observed LC. While the variability properties are not stationary but vary with (or without) the source flux, we believe that the above are representative of the general PDS form of accretion powered sources; these exhibit a flat (white noise-type) or red noise low frequency regime, complemented in some cases by LFQPOs, which breaks to a steeper spectrum above a few Hz. At higher frequencies the PDS of the GBHCs continue to decrease (with exception the presence of HFQPOs), while those of neutron stars recover at the highest frequencies (kHz) where they exhibit prominent kHz QPOs. This difference between the overall form of the PDS of GBHCs and LMXB neutron stars has, in fact, been proposed as a discriminant of the nature of the accreting object (Sunyaev & Revnivtsev 2000). These PDS while not identical they all exhibit prominent QPOs with at least one harmonic beyond the fundamental, the latter being their unifying characteristic. In fact, the most similar in their overall PDS form are the GBHC XTE J1859+226 and the neutron star Cyg X-2.
 |
Fig. 2 ACFs corresponding to Fig. 1 for both long time-lags (extended to hundreds of seconds) and shorter time-lags (insets) with the temporal resolution ΔT indicated (T ⋍ 1 ks). Vertical lines correspond to the QPO peaks in the PDS from Fig. 1. The error bars in each of the above ACF has been estimated to be on the order of ≃ 0.001−0.01. |
The data used in producing the ACFs and PDSs in this paper contain photons in the energy range 5 ≲ E ≲ 13 keV for all sources; they were also obtained at the following dates: (a) XTE J1550-564 in Oct. 22 (1998); (b) XTE J1859+226 in Oct. 11 (1999); (c) GRS 1915+105 in May 5 (1996); and (d) Cygnus X-2 in March 3 (1996), with exposure times of approximately T ≃ 1 ks in all cases.
3. Autocorrelation function (ACF) analysis
For a discrete LC, I(ti),(photon counts) defined at times ti, the mean-subtracted normalized ACF is given by ![\begin{eqnarray} \textmd{ACF}(\tau_i) &\equiv& \sum_{k=1}^N \left[\bar{I}(t_k) \bar{I}(t_k+\tau_i)\right] / \sum_{k=1}^N \bar{I}^2(t_k), \label{eq:ACF} \end{eqnarray}](/articles/aa/full_html/2010/16/aa14736-10/aa14736-10-eq43.png) (1)where N is the entire number of time bins in the LC (sampling number) with a constant sampling time (temporal resolution) of ΔT ≡ ti + 1 − ti where T = NΔT with τi denoting the characteristic time-lag in the LC (see, for some of its applications, Fukumura & Kazanas 2008; Fukumura et al. 2009);
(1)where N is the entire number of time bins in the LC (sampling number) with a constant sampling time (temporal resolution) of ΔT ≡ ti + 1 − ti where T = NΔT with τi denoting the characteristic time-lag in the LC (see, for some of its applications, Fukumura & Kazanas 2008; Fukumura et al. 2009); 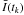 is the mean-subtracted LC defined as
is the mean-subtracted LC defined as 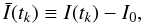 (2)with I0 the mean value of I(tk) over the interval T, a definition which allows the ACF(τi) to be either positive or negative. Note that with this definition the ACF obtains its maximum value of unity at τi = 0. Because of the finite length of the observed signal (i.e. the LC) the ACF must also, by definition, decline to zero at τi = T.
(2)with I0 the mean value of I(tk) over the interval T, a definition which allows the ACF(τi) to be either positive or negative. Note that with this definition the ACF obtains its maximum value of unity at τi = 0. Because of the finite length of the observed signal (i.e. the LC) the ACF must also, by definition, decline to zero at τi = T.
In Fig. 2 we show the ACFs corresponding to the LCs whose PDS are shown in Fig. 1. The main figure of each panel exhibits the ACF at long lags (τ ≫ 1/Δν) with its behavior near τ ≃ 0 shown in the inset. The differences and similarities of the ACFs are apparent in these figures: 1. they all decrease from the value 1 at τ = 0 to 0.1 or 0.2 after one oscillation period; 2. the ACF of XTE 1550-564, XTE 1859+226 and Cyg X-2 are quite similar amongst themselves in that they all exhibit near τ = 0 the form of a damped oscillation with period that of the QPO fundamental and decay time equal to the inverse of its width, i.e. τ ≃ 1/Δν; 3. the ACF of GRS 1915+105 is markedly different from those of the other three sources in that in reaching the value 0.2 after the first period it oscillates throughout the duration of the LC at the frequency of the QPO fundamental and with an amplitude that decreases linearly rather than exponentially to zero at lag equal to the observation time. As such it resembles the long time ACF behavior of a pure sinusoid or any undamped oscillation with coherent phase; 4. despite their overall similarity, the ACF of the GBHCs XTE 1550-564 XTE 1859+226 and that of the neutron star Cyg X-2 differ in their long time behavior: for τ ≫ 1/Δν they all attain small amplitudes ~2 × 10-2 for the GBHCs in (a) and (b) and ≲10-2 for Cyg X-2 in (d); however the GBHC ACFs exhibit an oscillatory behavior at the QPO fundamental frequency for lags τ equal to the observation duration, while the about zero fluctuations of the Cyg X-2 ACF appear totally random.
4. The power spectrum – autocorrelation synergy
To demonstrate the complementary nature of the PDS and ACF we present in this section an explicit example of the synergy between analysis in the frequency and time domains involving two different time series which both exhibit well defined harmonically spaced QPOs in their PDS. The LCs are given in Fig. 3a and b, one of which is a simulated Poisson noise-like LC while the second is that of GRS 1915+105. Visual inspection of these time series suggests the first one (Fig. 3a) to be totally aperiodic (and indeed it was constructed as such) with the second one (Fig. 3b) exhibiting a roughly periodic variability with period of order of 15 s.
 |
Fig. 3 The light curves (upper panels) of T = 200 s and the corresponding power spectra (lower panels) from a Kerr “echo” as discussed in the text (left panels) and from observations of GRS 1915+105 (right panels). |
 |
Fig. 4 a) The ACF corresponding to the model LC of Fig. 3a showing three characteristic peaks at τ = 0 (self-correlation), ⋍ 14 (shown with arrow) and ⋍28 s. b) The ACF corresponding to the light curve of Fig. 3b for GRS 1915+105 (similar to Fig. 2c except for only T = 200 s here). While the addition of noise can make both LCs look random, their ACFs are fundamentally different. |
The normalized PDS derived from these LCs are shown respectively in Fig. 3c and d. Their broad band form is different considering the Poisson character of the first LC and the ∝ 1/ν of the second; however, despite the fundamentally different apperance, they both exhibit harmonically spaced QPOs at approximately the same frequencies (albeit of different Q-values, a fact not surprising considering the completely incoherent character of the first LC). According to conventional wisdom, based on the PDS shown in Fig. 3c one would suspect a hidden periodicity within the LC of Fig. 3a. This is indeed the case with many QPOs of GBHCs or LMXBs, but from the algorithm used to produce it we know there is none!
With this in mind we present the corresponding ACFs of both LCs in Fig. 4. It can be seen these are drastically different; in fact the ACF of the first light curve is different from of the ACFs of any of the sources presented in this paper despite the presence of strong QPO in all: it consists of two narrow peaks at τ = 0 (self-correlation) and τ ≃ 14 s, a well known characteristic of an echo in the signal (Fukumura & Kazanas 2008; Fukumura et al. 2009, albeit of a lag much larger than the one specific to these references). The ACF of GRS 1915+105 does exhibit a (clearly non-sinusoidal) oscillation at the fundamental QPO period (as one would expect from an oscillating source) but, as discussed above, it decreases linearly with time to zero at a lag equal to the LC duration; this linear decrease is a property of an oscillation with a phase that is preserved over the observation interval (e.g. Morgan et al. 1997), as one can easily attest by computing the ACF of a simple sinusoid.
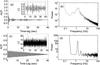 |
Fig. 5 Modeled ACFs (left panels) and their 40 s-long LCs (insets) for a random-phase ensemble of ~100 damped-sinusoidal waves (upper panels) and |sin(ωt)| function (lower panels) with period of 0.7 s. The corresponding PDS (right panels) showing prominent QPO peaks at ~1.4 Hz as expected. The damping time in a), b) is ~10 s. |
Motivated by the preservation of the oscillatory phase as the main ingredient behind the differences in the ACFs between GRS 1915+105 and the rest of the sources we present below two further examples of model LCs along with their ACF and PDS that provide support to this view and presumably shed some light into the nature of the oscillations associated with the observed QPOs in accretion powered sources. In Fig. 5a we present a LC (40-s long) by randomly adding ~100 damped oscillations of the form ∝ sin(ωt) × e( − t/t0)2 [where ω ≃ 0.75 Hz is the angular frequency and t0 ~ 5(2π/ω) is the e-folding decay time scale] with random phases (inset) along with its ACF (main figure); the ACF has a form very similar to those of three of the sources in our sample, including the long time, low amplitude oscillations. In Fig. 5c present an oscillation of the form ∝ |sin(ωt)| over 40 s with a mean rate of 60 cts/s along with the relevant Poisson noise (inset); the corresponding ACF is shown in the main figure which (modulo the single rather than double peaked oscillation) bears great resemblance to that of GRS 1915+105: its amplitude drops to 0.2 after one period (the result of the presence of Poisson noise) and subsequently decreases linearly to zero at the length of the LC, as is the case with the ACF of GRS 1915+105. Figures 5d present the corresponding PDS in which QPOs are apparent, with high Q-values and higher harmonics for the case of the LC that preserves the coherence of the oscillation phase.
As an additional argument for the complementary nature of the time and frequency domain analysis, we note that the long term oscillatory nature of the ACF in three of our sources, i.e. those of the GBHCs, while obvious in the ACF, is in no way apparent in the corresponding low frequency part of the PDS. One could argue that the high Q-values of the QPOs of GRS 1915+105 may be indicative of the phase coherence of the underlying oscillation; while this property is captured quantitatively by the ACF it is impervious to the PDS which erases all phase information. In the same vein, the difference in the long term ACF behavior between Cyg X-2 (totally aperiodic) and those of XTE J1550-564 and XTE J1859+226 (essentially periodic oscillations) is also absent if one restricts oneself to study of the PDS alone.
5. Discussion and conclusions
We have presented above a systematic, combined time-frequency study of the variability properties of four galactic sources known to exhibit QPO features. While our sample is rather limited, it indicates that the ACFs could prove useful in providing insights into the variability of these objects in addition to those of their PDS. Our analysis makes clear that the properties of the oscillations leading to the 67 mHz QPO of GRS 1915+105 are very different from those producing the dominant QPO peaks of the other sources, in that they continue with essentially the same phase for the duration of the observation (the random walk in phase by ~5 s over the 1000 s LC segment discussed by Morgan et al. 1997, is too small to interfere with the overall ACF form and we believe it to be the source of the observed QPO width). By contrast the ACF of the other three sources do resemble those of a damped oscillator, indicating that, whatever the underlying oscillation, it occurs in trains of limited duration Δτ ≃ 1/Δν with phase random beyond this time interval and perhaps for this reason not discernible in the LC.
Viewed in greater detail, there are several points to note in the ACF morphology: the ACFs exhibit their first major peak at lag τ = 1/νf, νf being the QPO fundamental frequency. This could serve to distinguish between the fundamental and its subharmonic in XTE J1550-564, which occurs close to the second ACF maximum. The frequency of the first QPO harmonic, easily discernible in the PDS of all sources, associates in the three sources other than GRS 1915+105, with the first ACF minimum. In this very different source, it associates with a secondary, albeit small amplitude, maximum with no ACF features corresponding to the second or third harmonics of its PDS. Furthermore, the ACF of GRS 1915+105 exhibits an additional peak at τ ≃ 1 s (inset in Fig. 2c), which presumably corresponds to the broad QPO at ν ≃ 1 Hz in the PDS. This is of interest because it is not accompanied by additional oscillatory peaks as is the case with the ACFs of the other sources. As such, it is unlikely that it represents an independent oscillation of the type observed in the ACFs of the other three sources and for this reason it may deserve closer attention.
Considering the ACFs of the other three sources, they all appear consistent with a damped oscillation. However, there are a number of differences between those of the GBHCs and the LMXB accreting neutron star Cyg X-2: in the GBHC ACFs the damped oscillation is almost symmetric about zero, while in Cyg X-2 remains largely positive. Furthermore, at lags τ ≫ 1/Δν the black hole ACFs continue to exhibit a small amplitude but persistent oscillatory behavior that lasts through the lag span of the entire observation. By contrast, that of Cyg X-2 exhibits nothing but statistical fluctuations with no indication of an oscillatory behavior, perhaps because of input from a non oscillating source such as the neutron star boundary layer.
Our analysis and simple model light curve examples has shown the ACF to provide important additional information beyond that of the PDS. This may in certain cases prove useful in figuring out the underlying source of periodicity and its long term properties, something not apparent in the PDS. We also provided an example in which a strictly random source would produce QPO features in the power spectra, whose nature while apparent in the ACF is completely hidden in the PDS. Most of the sources we have examined have ACFs consistent with the simplest QPO model, that of a damped oscillations of random phases. We do not know if this is a general property of these sources. In face of our limited sample, we do not want to prejudge the outcome of such analyses of much larger samples nor the efficacy of simple models and considerations such as those discussed just above in providing successful interpretations of the data. We anticipate, however, they will be the subject of future publications.
Acknowledgments
The authors would like to thank the anonymous referee for a number of useful suggestions that helped improve an earlier version of the paper. They would also like to thank to Stratos Boutloukos, Fotis Gavriil, Nikolai Shaposhnikov and Tod Strohmayer for useful discussions and comments.
References
- Casella, P., Belloni, T., Homan, J., & Stella, L. 2004, A&A, 426, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cui, W. 1999, ApJ, 524, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisawa, K., Mitsuda, K., & Inoue, H. 1989, PASJ, 41, 519 [NASA ADS] [Google Scholar]
- Fukumura, K., & Kazanas, D. 2008, ApJ, 679, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Fukumura, K., Kazanas, D., & Stephenson, G. 2009, ApJ, 695, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Langmeier, A., Sztajno, M., Truemper, J., & Lewin, W. H. G. 1986, Nature, 319, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Hua, X.-M., Kazanas, D., & Cui, W. 1999, ApJ, 512, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Kazanas, D., & Hua, X.-M., 1999, ApJ, 519, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., Darbro, W., Elsner, R. F., et al. 1983, ApJ, 266, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, E. W., Remillard, R. A., & Greiner, J. 1997, ApJ, 482, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., Sobczak, G. J., Muno, M. P., & McClintock, J. E. 2002a, ApJ, 564, 962 [Google Scholar]
- Remillard, R. A., Muno, M. P., McClintock, J. E., & Orosz, J. A. 2002b, ApJ, 580, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D. 2005, ApJ, 621, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. A. 1998, IAU Circ., 7008, 1 [NASA ADS] [Google Scholar]
- Strohmayer, T. E. 2001, ApJ, 554, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R., & Revnivtsev, M. 2000, A&A, 358, 617 [NASA ADS] [Google Scholar]
- Titarchuk, L., Kuznetsov, S., & Shaposhnikov, N. 2007, ApJ, 667, 404 [NASA ADS] [CrossRef] [Google Scholar]
- van der Klis, M. 2006, in Compact stellar X-ray sources, ed. W. H. G. Lewin, & M. van der Klis (Cambridge University Press) [arXiv:astro-ph/0410551] [Google Scholar]
- Vaughan, S., & Uttley, P. 2005, MNRAS, 362, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Homan, J., van der Klis, M., et al. 1998, ApJ, 493, 87 [Google Scholar]
- Wijnands, R., Homan, J., & van der Klis, M. 1999, ApJ, 526, L33 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Leahy-normalized power density spectra (PDS) annotating the identified low-frequency features for a) XTE J1550-564 (νsub ~ 2.8,νf ~ 5.3 and ν1 ~ 10.9 Hz); b) XTE J1859+226 (νf ~ 1.2 and ν1 ~ 2.4 Hz); c) GRS 1915+105 (νf ~ 67,ν1 ~ 136,ν2 ~ 205,ν3 ~ 267 and νu ~ 781 mHz) and (d) Cygnus X-2 (νf ~ 14.9 and ν1 ~ 29.1 Hz) with the spectral resolution and (fundamental) QPO cycles f ≡ νfT indicated where T ⋍ 1 ks (see the text for notations). |
| In the text | |
 |
Fig. 2 ACFs corresponding to Fig. 1 for both long time-lags (extended to hundreds of seconds) and shorter time-lags (insets) with the temporal resolution ΔT indicated (T ⋍ 1 ks). Vertical lines correspond to the QPO peaks in the PDS from Fig. 1. The error bars in each of the above ACF has been estimated to be on the order of ≃ 0.001−0.01. |
| In the text | |
 |
Fig. 3 The light curves (upper panels) of T = 200 s and the corresponding power spectra (lower panels) from a Kerr “echo” as discussed in the text (left panels) and from observations of GRS 1915+105 (right panels). |
| In the text | |
 |
Fig. 4 a) The ACF corresponding to the model LC of Fig. 3a showing three characteristic peaks at τ = 0 (self-correlation), ⋍ 14 (shown with arrow) and ⋍28 s. b) The ACF corresponding to the light curve of Fig. 3b for GRS 1915+105 (similar to Fig. 2c except for only T = 200 s here). While the addition of noise can make both LCs look random, their ACFs are fundamentally different. |
| In the text | |
 |
Fig. 5 Modeled ACFs (left panels) and their 40 s-long LCs (insets) for a random-phase ensemble of ~100 damped-sinusoidal waves (upper panels) and |sin(ωt)| function (lower panels) with period of 0.7 s. The corresponding PDS (right panels) showing prominent QPO peaks at ~1.4 Hz as expected. The damping time in a), b) is ~10 s. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


