| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913372 | |
| Published online | 23 November 2010 | |
LABOCA observations of giant molecular clouds in the southwest region of the Small Magellanic Cloud
1
Université de Strasbourg, Observatoire Astronomique de
Strasbourg,
France
2
CNRS, Observatoire Astronomique de Strasbourg, UMR7550,
67000
Strasbourg,
France
e-mail: caroline.bot@astro.unistra.fr
3
Departamento de Astronomia, Universidad de Chile,
Casilla 36-D, Santiago, Chile
4
Institut d’Astrophysique Spatiale, Université Paris-Sud,
91405,
Orsay,
France
5 Argelander-Institut für Astronomie, Universität Bonn, Germany
6 Universidad Católica del Norte, Chile
7
Max Planck Institute for Astronomy, Heidelberg, Germany
8 University of Maryland, MD, USA
9 Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD21218, USA
10
Steward Observatory, University of Arizona,
Tucson,
AZ
85721,
USA
Received: 29 September 2009
Accepted: 27 August 2010
Context. The amount of molecular gas is a key to understanding the future star formation in a galaxy. Because H2 is difficult to observe directly in dense and cold clouds, tracers such as the CO molecule are used. However, at low metallicities especially, CO only traces the shielded interiors of the clouds. In this context, millimeter dust emission can be used as a tracer to unveil the total dense gas masses. However, the comparison of masses deduced from the continuum SIMBA 1.2 mm emission and virial masses (understood to trace the entire potential of the clouds) in a sample of giant molecular clouds in the Small Magellanic Cloud (SMC) by previous studies found a discrepancy between these two quantities that requires explanation.
Aims. We attempt to more accurately assess possible uncertainties in the dust emission observed in the sample of giant molecular clouds from the SMC. We focus on the mass comparison in the densest parts of the giant molecular clouds where CO is detected to confirm the mass discrepancy previously observed.
Methods. New observations of the southwest region of the SMC were obtained with the LABOCA camera on the APEX telescope. All the giant molecular clouds previously observed in CO are detected and their emission at 870 μm is compared to ancillary data. The different contributions to the sub-millimeter emission are estimated, as well as dust properties (temperatures, emissivities), to determine molecular cloud masses precisely.
Results. The (sub-)millimeter emission observed in the giant molecular clouds in the southwest region of the SMC is dominated by dust emission, and masses are deduced for the part of each cloud where CO is detected and compared to the virial masses. The mass discrepancy between both methods is confirmed at 870 μm using the LABOCA observations: the virial masses are on average 4 times lower than the masses of dense gas inferred from dust emission, in contrast to what is observed for equivalent clouds in our Galaxy.
Conclusions. At present, the origin of this mass discrepancy in the SMC remains unknown. The direct interpretation of this effect is that the CO linewidth used to compute virial masses do not measure the full velocity distribution of the gas. Geometrical effects and uncertainties in the dust properties are also discussed.
Key words: ISM: clouds / submillimeter / ISM: molecules / Magellanic Clouds
© ESO, 2010
1. Introduction
Star formation is observed to occur within molecular clouds. The star formation rate in a galaxy therefore depends on the amount of molecular gas available, but this quantity remains difficult to estimate precisely. In particular, at low metallicities, the relationship between H2 and CO (the most widely used tracer of molecular gas) remains unclear.
The Small Magellanic Cloud (SMC) is one of the closest and easiest to observe, low metallicity galaxies. Owing to its proximity, molecular clouds in this galaxy can be resolved at various wavelength. Numerous molecular clouds in the Magellanic clouds have been observed in CO lines (Israel et al. 1993; Rubio et al. 1993a,b, 1996) and found to have weak CO emission. If the CO molecule accurately traces the molecular gas, then the star formation per unit CO emission in the SMC is higher than in most galaxies. This effect is observed in other low metallicity dwarf galaxies (Leroy et al. 2006) and could be an “evolutionary effect” or indicate that CO observations largely underestimate the amount of molecular gas in these conditions. At low metallicities, CO may indeed be photodissociated and trace only the densest parts of the clouds, while H2 molecules have the capacity to self-shield and would be present at larger radii than the CO molecule.
This “underestimation” by CO of the molecular content of SMC molecular clouds has been seen and studied mainly by determining the XCO = NH2/ICO factor. Using CO data only, the velocity dispersion inferred from the CO line width is understood to trace the gravitational potential of the cloud and therefore the total molecular content, which can be compared to the CO intensity in the same region. Analyzing NANTEN data for the whole SMC, Mizuno et al. (2001) found XCO = (1−5) × 1021 cm-2(Kkms-1)-1. Blitz et al. (2007) corrected these data for sensitivity and resolution effects and found XCO = (1 − 1.5) × 1021 cm-2(Kkms-1)-1. These values are systematically larger than the canonical Galactic value XCO = 2.3 × 1020 cm-2(Kkms-1)-1 (Strong et al. 1988), supporting the idea that CO is present only in part of the molecular cloud. The XCO factor appears to depend on radius (Rubio et al. 1993a) and on the smallest resolved scales, the values of XCO determined for individual resolved clouds are almost similar to the Galactic value (Bolatto et al. 2003; Israel et al. 2003; Bolatto et al. 2008).
To more clearly understand the total molecular content and its relationship to CO emission, other tracers of the dense and molecular gas at low metallicities are used. Dust continuum emission can be used to trace the dense and cold interstellar medium where the gas is molecular, thus be used to determine the total mass of dense gas in clouds. Israel (1997) was the first to introduce this method in the Magellanic Clouds, by comparing IRAS and CO data, and he deduced higher H2 masses than those found using CO data alone. Leroy et al. (2007) attempted to spatially trace molecular hydrogen using far infrared emission observed with Spitzer data in the SMC. In dense regions, they detected large quantities of dust that were not associated with either Hi or CO emission. A study of the star-forming region N83 confirms this result on smaller scales (Leroy et al. 2009). However, the dust emission in the far-infrared is sensitive to the dust temperature, leading to large uncertainties in the cloud masses. In the sub-millimeter and the millimeter range, dust emission is difficult to observe but depends only linearly on the dust temperature and is optically thin. With SIMBA on the SEST telescope, Rubio et al. (2004) observed for the first time the 1.2 mm emission from dust in a quiescent molecular cloud in the SMC. The dense gas mass deduced was several times higher than the dynamical mass inferred from CO observations of this cloud. Bot et al. (2007) extended this study with SIMBA to a larger sample of molecular clouds in the southwest region of the SMC. In all clouds, the gas mass deduced from the dust emission is systematically higher than the virial mass implied by CO data, even for conservative values of the dust emissivities and free-free contribution to the millimeter emission. All these studies agree that molecular clouds in the SMC are more massive than what can be deduced from CO emission. This mass difference can be explained by scenario where CO traces only the densest parts of the molecular clouds.
However, in the case of virial equilibrium, it is often assumed that the observed motions are balanced by the gravitational pressure and that the dynamical masses obtained from molecular line observations trace the total molecular masses (e.g. MacLaren et al. 1988; Rosolowsky et al. 2003; Du & Yang 2008; Dunham et al. 2010). The result from Bot et al. (2007) where the virial masses in the SMC systematically underestimate the true mass of the clouds (as traced by the dust mass) remains unexpected. Partial support of the clouds by a magnetic field has been invoked to explain this mass discrepancy. However, these results need to be confirmed with observations in the sub-millimeter range to more certainly exclude any possible contamination of the fluxes (free-free emission, CO line contribution), as well as unknown instrumental effects and dust properties. This study focuses on the parts of the giant molecular clouds that are detected in CO. These regions represent only the highest density parts of the giant molecular clouds but are most appropriate for the comparison with CO and the check of a mass discrepancy.
We present new observations of the sample of molecular clouds in the southwest region of the SMC taken with the LABOCA camera on the APEX telescope (Sect. 2). These observations at 870 μm complement the SIMBA data at 1.2 mm, CO and radio data, as well as 160 μm Spitzer data from the combined S3MC and SAGE-SMC surveys (Bolatto et al. 2007; Gordon et al. 2009). We compile spectral energy distributions (SEDs) of each giant molecular cloud (GMC) detected in both the sub-millimeter and CO and assess the possible contaminations and uncertainties (Sect. 2.3). The dust emission in each cloud is then used to determine dense gas masses for each molecular cloud in the southwest region of the SMC. These mass estimates are compared to virial masses and confirm the existence of a mass discrepancy (Sect. 3).
2. Data and methods
2.1. The data
The dust continuum observations were obtained using the Large APEX BOlometer CAmera (LABOCA, Siringo et al. 2009) on the Atacama Pathfinder Experiment (APEX, Güsten et al. 2006) telescope in Chile. LABOCA is a bolometer array consisting of 295 receivers packed in a hexagonal structure resulting in a total field of view of 114. It has a central frequency of 345 GHz (~870 μm) with a bandwidth of 60 GHz and the beam-size (HPBW) was measured to be 192.
The 870 μm LABOCA observations were performed during October 2007. The weather conditions were mostly good to excellent with a precipitable water vapor (PWV) content typically between 0.5 and 0.9 mm resulting in zenith opacities on the order of 0.2. The pointing was checked regularly on strong continuum sources and planets, and the pointing accuracy was found to be mostly superior to 3″. The focus settings were determined from observations of planets typically once per night and during changes in the weather conditions, sunset, and sunrise. To obtain the atmospheric opacity the sky emission was measured regularly about every two hours. Calibration factors were derived by observing Neptune and Uranus as well as secondary calibrators. Relative offsets and relative gains (flatfield) in the individual bolometer channels are determined about once per month and are provided by the APEX staff. The scientific mapping was carried out in spiral raster mode with the raster pattern alternating between 2 × 2 and 3 × 3 spirals to achieve an optimal sampling of the region of interest. Nine-position raster maps were completed in a 140′′ spiral at 1′′/s speed and 60° inclination. Raster lengths were varied in the x and y directions between 1000′′ and 1200′′, and the spacings between 500′′ and 600′′. Dithering of between 100′′ and 120′′ from the central position was performed. Additional observations of the central 6′ × 6′ region in a four-by-four points raster were performed to increase the signal-to-noise ratio. In total, we obtained 101 maps and a pure on-source integration time of 8.9 h. The final rms achieved was 8 mJy/beam.
The LABOCA data were reduced using the reduction package BoA1 (Schuller et al., in prep.). The processing of the raw time series, i.e. the time-ordered data stream (down-sampled to 25 Hz) of each channel and scan, consisted of the following steps: (1) calibration correction by applying a linearly interpolated calibration factor; (2) opacity correction by applying the linearly interpolated opacity at the elevation of the scan; (3) correction for temperature drifts due to the cryosystem, using two bolometers that have been sealed to block the sky signal for this purpose; (4) flat fielding by applying the relative bolometer gains; conversion from counts to Jansky and (5) flagging of bad channels. In addition to the known dead or noisy channels, bad channels were identified as those with an rms in their time series a given ratio r higher or 1/r lower than the median rms of all channels. The additional reduction included (in part on several occasions) the following tasks: (1) correlated noise removal from the full array; (2) correlated noise removal from groups sharing the same amplifier box and the same wiring; (3) baseline subtraction; (4) despiking; (5) flagging of data outside suitable telescope scanning velocity and/or acceleration limits; and (6) flagging of bad channels. Each reduced scan (i.e. raster pattern) was then gridded into a weighted intensity map and a corresponding weight map. The weights of the data points contributing to a certain pixel of the intensity map were evaluated to be 1/σ2, where σ denotes the rms of the reduced time series of the corresponding channel and subscan. Individual maps were then coadded, again noise-weighted, to build the final intensity map and the corresponding weight map, which in turn allows us to retrieve the rms for each pixel and to construct a signal-to-noise ratio (S/N) map.
 |
Fig. 1 Top image: LABOCA image in the southwest region of the SMC (Units are in Jy/beam). Middle and bottom images: LABOCA images convolved to a ~40′′ resolution with CO and MIPS 160 μm contours overlaid, respectively. All the molecular clouds observed in CO are detected at 870 μm. Extended emission is well recovered in the LABOCA map and the 870 μm emission matches well the 160 μm one. |
The described data reduction is affected by the presence of astronomical signals in the time series, which leads to a flux loss due to the subtraction of correlated noise. In the case of strong sources, this is revealed by the appearance of areas of negative fluxes adjacent to the sources. Moreover, the source emission wrongly contributes to the determination of the rms and weights. To minimise these effects, we applied an iterative approach by subsequently improving a model of the flux distribution of the astronomical source.
Observed fluxes from the far-infrared to the radio for our sample of giant molecular clouds.
In a first step, a map was produced by a “blind” execution of the reduction as described above. A first source model was constructed from the resulting map by extracting all pixels above a given S/N threshold (typically 3) and setting the remaining pixels to zero. This model was converted to a time series for each channel and subtracted from the data before any baseline subtraction, despiking, and correlated noise suppression. After the weight determination and before the map was built, the model was re-introduced into the time stream. The resulting map was used to extract a new source model. In subsequent iterations, this process was repeated until the measured flux distribution converges. As a result, most of the faint extended emission was recovered in the reduction.
The 20′ × 20′ image of the southwest region of the SMC that was obtained, is presented in Fig. 1. It is the first sub-millimeter map of a large region in the Small Magellanic Cloud. This southwest region of the SMC has had most of its known molecular clouds mapped at a 43′′ resolution and at high sensitivity in the CO (J = 1−0) line with SEST (Rubio et al. 1993a,b). All the GMCs observed in CO lines with SEST (shown as contours in Fig. 1) are detected with the present LABOCA observation. There is also extended emission well outside observed CO peaks. If the 870 μm emission originates from dust, this result shows that there is far more dense gas than traced by current CO observations. Comparing with the MIPS 160 μm map of the same region, we see that the spatial distribution of the 870 μm emission is well correlated with the one observed in the far-infrared. A short analysis of the dust emission outside the observed CO is presented in Appendix B.
The present paper compares the 870 μm and CO data and is therefore restricted to the regions where CO has been observed and detected. The entities for which we deduce masses in the following and that are referred to as “clouds” are the densest parts of the molecular clouds, associated with CO emission.
For comparison, we complement these data with SIMBA observations at 1.2 mm previously studied (Bot et al. 2007) and Spitzer MIPS observations at 160 μm in the same region from the combined S3MC and SAGE-SMC surveys (Bolatto et al. 2007; Gordon et al. 2009). Furthermore, to estimate the contribution of free-free emission to the observed millimeter emission, we also use radio ATCA maps at 8.6, 4.8 GHz obtained from J. Dickel 2.
2.2. Flux estimates
To estimate the LABOCA, SIMBA, MIPS, and radio fluxes in a way that is comparable to CO, we do the following. All maps were convolved to the 43′′ CO(1–0) resolution and projected onto the same sampling grid. Because we are interested in comparing the LABOCA, SIMBA, MIPS, and CO fluxes, it is important to remove the extended emission from all maps to compare emission in the region detected with all tracers (the peaks of the GMCs). To do so, we begin by masking the region where CO is detected and fit in each map (LABOCA, radio, SIMBA, MIPS) a 2D plane to the emission outside the CO detected region. The fitted plane is then removed from the maps (in units of surface brightness) to leave only the peak of emission where CO was observed. The integrated fluxes are then computed in a region above a defined WCO threshold. This threshold is defined individually for each cloud so that the area of the cloud we sample is similar to the one that was used to determine the virial masses and CO luminosities of the clouds (Rubio et al. 1993b). This method enables us to analyze the emission coming from the dust associated with the CO emission only. It attempts to filter extended envelopes around the clouds – uncertainties in this filtering process will be discussed in Sect. 4.1 – as well as possible emission associated with Hi. Using an Hi map of the Small Magellanic Cloud (Stanimirovic et al. 1999), we estimated that the remaining Hi column densities associated with the peaks of the molecular clouds we study, after filtering, are less than a few percent of the total hydrogen column densities as determined from the dust millimeter emission. The fluxes obtained are summarized in Table 1 and are used to build the SED for each cloud (cf. Fig. 2).
2.3. Origin of the 870 μm emission
At long wavelengths such as 870 μm, the broad-band flux densities determined from the maps may contain non-negligible contributions from thermal free-free continuum emission and CO line emission.
2.3.1. Free-free contribution
In Bot et al. (2007), estimates of the free-free emission and the CO line at 1.2 mm were found to provide negligible contributions to the measured fluxes. Even if we expect this to be the case at 870 μm, it is safe to quantify these contributions here too. Furthermore, the free-free estimates obtained in Bot et al. (2007) were derived from the Payne et al. (2004) radio catalog, which had integrated fluxes in regions that could differ in size from the molecular clouds we study, and when no source was present in the catalog it was not clear whether this was a non-detection or a non-observation. In this section, the use of the radio maps directly enables us to derive far more accurate estimates of the free-free contribution to the (sub-)millimeter emission for the regions we are interested in.
 |
Fig. 2 SEDs from the far-infrared to the radio, observed for each cloud. The fluxes observed at 160 μm, 870 μm and 1.2 mm are fitted with a single modified black body either with an emissivity index of 1 (dashed blue line) or 2 (plain red line) or with a free emissivity index (dotted green line). Radio fluxes (or upper limits) computed in the same regions are overplotted and the extrapolated free-free emission is displayed as a black line. This shows clearly that the sub-millimeter and millimeter emission is dominated by dust emission rather than free-free. |
All regions observed at 870 μm and in CO(1–0) also have radio emission that is detected at 4.8 or 8.64 GHz. A few regions (e.g. LIRS49) display an inverted spectrum (which may be caused by different spatial filtering between the observations at the two frequencies). But in most cases, the radio spectral index is flat, consistent with an origin of the emission that is mostly free-free. For free-free emission, the flux density scales as 0.95 − 0.16lnν with ν in GHz (Reynolds 1992), and is fitted to the radio emission detected at the highest frequency (plain black line in Fig. 2). Comparing this scaling with the emission at 870 μm and 1.2 mm, the free-free contribution to the (sub-) millimeter emission is not significant (we estimate it to be between 1 and 8% of the 870 μm emission and remove it from the observed LABOCA and SIMBA fluxes).
2.3.2. CO(3-2) line contribution
The J = 3−2 CO emission contribution to the 870 μm broad band emission is computed using the measured CO(3–2) line, when available, from Nikolić et al. (2007), or otherwise, by applying a high CO(3–2)/CO(2–1) ratio3 of 2 to the CO(2–1) observed emission. Using a Jy/K conversion factor of 8.4 and a bandwidth for the LABOCA bandpass of 60 GHz, we find that the CO(3–2) line contribution to the observed emission is insignificant in all clouds (it represents at most 0.3% of the emission at 870 μm).
The 870 μm and 1.2 mm fluxes in each cloud are then dominated by dust continuum emission.
2.4. Method
In Sects. 2.3.1 and 2.3.2, we showed that the emission detected by LABOCA at 870 μm is dominated by dust emission. The method to determine hydrogen masses from dust emission is then similar to the one described by Bot et al. (2007). In short, the hydrogen column density in each molecular cloud can be deduced from 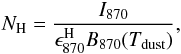 (1)where Tdust is the dust temperature,
(1)where Tdust is the dust temperature, 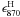 is the emissivity of dust per hydrogen atom at 870 μm, and Bλ is the Planck law. To infer dense gas masses from the dust emission detected with LABOCA, we therefore have to know the dust temperature in the clouds of the SMC and the dust emissivity at 870 μm.
is the emissivity of dust per hydrogen atom at 870 μm, and Bλ is the Planck law. To infer dense gas masses from the dust emission detected with LABOCA, we therefore have to know the dust temperature in the clouds of the SMC and the dust emissivity at 870 μm.
2.4.1. Dust temperatures and emissivity index
In Bot et al. (2007), it was assumed that the spectral dependance of this dust emission in the (sub-)millimeter is similar to that in our galaxy (Sν ∝ νβBν(Tdust) with β = 2.0) with a single temperature of 15 K, typical of GMCs in the Milky Way. Even though the dust temperature dependence of the submillimeter emission is mild, the uncertainty in this parameter can create scatter in the mass determined for the sample. Both the dust temperature and the emissivity index in the molecular clouds of the SMC can be more tightly constrained by comparing the LABOCA, SIMBA, and Spitzer MIPS fluxes for each cloud.
A modified blackbody fits to the MIPS, LABOCA, and SIMBA fluxes is made for each region with both the dust temperature and the emissivity index as free parameters (dashed line in Fig. 2). This fit infers values of β between 1.9 and 4 (cf. Table 2) and very low dust temperatures. However, high values (e.g. β ~ 3) are not believed to be physical and could be a consequence of filtering in the SIMBA data (cf. Sect. 2), even though by focusing on emission peaks we attempt to limit this effect. Alternatively, it could be due to a mix of temperatures within the regions we sample.
We note that since there is most probably a range of temperatures within the beam, the dust temperature determined from a single modified blackbody fit is an upper limit to the mean temperature. Since lower temperatures would give higher dust masses, our simple fit gives lower limits to the mass and is thus a conservative estimate to determine the dense cloud masses.
Results from modified blackbody fits to the MIPS, LABOCA, and SIMBA fluxes for each molecular cloud.
Using the SED compiled for each cloud (Fig. 2), we observe that in all the molecular clouds of this study, the emission is consistent with a modified black body with a standard spectral index of β = 2. Fixing the dust emissivity to this standard value, we observe low dust temperatures (12 K on average) for all the molecular clouds studied here. The temperatures range is small (from 10.2 to 13 K) and consistent with a constant temperature at a 3σ level. However, these low dust temperatures (which correspond to a radiation field intensity that would be 10 times lower than the canonical value from the solar neighbourhood, Mathis et al. 1983) are surprising. Indeed, some regions such as LIRS36 or LIRS49 harbour active starforming regions and our regions could contain, at least partly, dust heated by the surrounding stars. However, because our study focuses on regions where CO is detected, it is possible that the dust in these regions is predominantly cold. Even though, it is surprising that dust temperature in giant molecular clouds of the SMC are lower than what is observed for molecular clouds in the Milky Way, especially since at low metallicity the dust shielding should be lower.
The temperature and emissivity index of the dust associated with the 870 μm emission is therefore still difficult to constrain, and more data in the 100–300 μm wavelength regime are needed to provide tight enough constraints. In the following, we assume that β = 2 and the temperatures (Tdust ~ 12 K) determined in this case from the fitting procedure, but we also compute lower limits to the mass estimates using a low value of the emissivity index β = 1. A fit to the SED with β = 1 (dashed blue line in Fig. 2) leads to dust temperatures of Tdust ~ 19 K (last column in Table 2). In the following, we therefore also compute lower limits to the molecular cloud masses using Tdust = 19 K.
2.4.2. Dust emissivity at 870 μm
To determine gas masses from the dust (sub-)millimeter emission at 870 μm, it is crucial to know the dust emissivity in this wavelength regime. This quantity can be expressed as 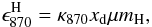 (2)where κ870 is the absorption coefficient per unit of dust mass, xd is the dust-to-gas mass ratio (in the following, we adopt a dust-to-gas ratio 0.17 times the one in the solar neighbourhood, as determined by Bot et al. (2007) from abundance studies) and μmH is the gas weight per hydrogen, taking into account the contribution of He.
(2)where κ870 is the absorption coefficient per unit of dust mass, xd is the dust-to-gas mass ratio (in the following, we adopt a dust-to-gas ratio 0.17 times the one in the solar neighbourhood, as determined by Bot et al. (2007) from abundance studies) and μmH is the gas weight per hydrogen, taking into account the contribution of He.
The long-wavelength emissivity of dust in the difuse medium was modeled and tabulated by Li & Draine (2001). At 850 μm, they found that κ850 μm = 0.4 cm2/g. However, this value may not be representative of the dust properties in molecular clouds. In particular, coagulation processes can occur between grains. The large fluffy aggregates created this way have different absorption/emission properties than those in the diffuse medium. Enhancements in the dust emissivity can be attributed to coagulation processes. This emissivity enhancement is observed in our galaxy (Cambrésy et al. 2001; Stepnik et al. 2003; Bot et al. 2007) and for giant molecular clouds, the dust emissivity in the (sub-)millimeter regime is enhanced by a factor 2–3 with respect to the diffuse medium.
To determine the dust opacity appropriate to the GMCs probed by our observations, we chose to estimate it directly from sub-millimeter observations in a Galactic molecular environment. Without any additional information, we assume that the molecular ring in our Galaxy can be used as a reference for the giant molecular clouds of the SMC. In particular, this implies that dust evolution (like coagulation) occur in the same way in SMC GMCs as in our Galaxy.
The method used is similar to the one by Bot et al. (2007): a map of the dust emission in our Galaxy at 870 μm is created using FIRAS data. In the molecular ring, the 870 μm dust emission correlated with Hi is substracted from the observed emission using the correlation observed at high Galactic latitude. The remaining emission correlates with the CO intensity (Dame et al. 2001) and a linear fit to the correlation implies that 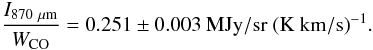 (3)We checked that in individual GMCs in our solar neighbourhood, this ratio is similar (~0.26 ± 0.18 – the uncertainty here reflecting the dispersion between clouds) and is therefore characteristic of the dust emission in GMCs in the Milky Way. Assuming a standard conversion factor between the CO intensity and the molecular gas column densities (XCO = N(H2)/WCO = 1.8 × 1020mol cm-2 (K km/s)-1, Dame et al. 2001; Grenier et al. 2005), a dust temperature in Galactic GMCs of 15 K as in Bot et al. (2007), we can deduce a dust emissivity at 870 μm for the molecular ring. By multiplying this value with the SMC dust-to-gas ratio, we obtain a dust emissivity suitable for SMC GMCs of
(3)We checked that in individual GMCs in our solar neighbourhood, this ratio is similar (~0.26 ± 0.18 – the uncertainty here reflecting the dispersion between clouds) and is therefore characteristic of the dust emission in GMCs in the Milky Way. Assuming a standard conversion factor between the CO intensity and the molecular gas column densities (XCO = N(H2)/WCO = 1.8 × 1020mol cm-2 (K km/s)-1, Dame et al. 2001; Grenier et al. 2005), a dust temperature in Galactic GMCs of 15 K as in Bot et al. (2007), we can deduce a dust emissivity at 870 μm for the molecular ring. By multiplying this value with the SMC dust-to-gas ratio, we obtain a dust emissivity suitable for SMC GMCs of 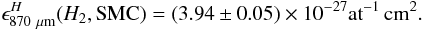 (4)This dust emissivity in molecular regions corresponds to an opacity κ870 = 1.26 ± 0.02 cm2/g.
(4)This dust emissivity in molecular regions corresponds to an opacity κ870 = 1.26 ± 0.02 cm2/g.
Mass estimates for the individual GMCs observed in the southwest region of the SMC.
The uncertainties quoted above for the different values correspond to formal uncertainties in the fitting procedures and do reflect neither the intrinsic scatter in the 870 μm-WCO correlation, nor the systematic uncertainty due to the assumptions, which are by far the dominant source of error. For example, it is unclear whether “coagulation” of dust grains occurs in the SMC and this will be discussed further in Sect. 4.2. However, to our current knowledge, most systematic effects will increase the mass estimated from the dust emission.
Using Eq. (4) and a dust temperature between 12 and 19 K, we can therefore determine gas masses directly from the observed 870 μm dust-emission continuum in the CO-detected GMCs of the SMC.
3. Results
Gas masses for all the GMCs of the southwest region of the SMC observed in CO are deduced from the LABOCA sub-millimeter emission and are summarized in Table 3. These masses are compared to the masses deduced from the application of the virial theorem to the CO line width and radii (cf. Table 3 and Fig. 3). For comparison purposes, we took from Bot et al. (2007) the masses determined from dust millimeter emission and the virial masses for a reference sample of similar molecular clouds in the solar neighbourhood.
For self-gravitating clouds, the velocity dispersion of the CO clumps balances the gravitational pressure and the virial masses should be similar to the cloud masses inferred from dust emission. However, we observe that the GMC masses deduced from dust emission are systematically larger than the virial masses determined for the same clouds. Our study with LABOCA data at 870 μm therefore confirms the results obtained by Rubio et al. (2004) and Bot et al. (2007) with SIMBA data. We find a median mass ratio 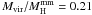 (0.41 for the upper limit to the dust temperature), in contrast to the mass ratio obtained for equivalent clouds in the Milky Way, which is always above 1.
(0.41 for the upper limit to the dust temperature), in contrast to the mass ratio obtained for equivalent clouds in the Milky Way, which is always above 1.
 |
Fig. 3 Comparison between the two molecular mass estimates: masses deduced from sub-millimeter dust emission and virial masses. The mass deduced from the LABOCA emission in the SMC are shown for a dust temperature as estimated from the SED fitting with β = 2 (Tdust ~ 12 K, black diamonds) and for a dust temperature of 19 K as an upper limit (green rhombs). Galactic GMCs studied with the same method are shown for comparison (blue stars). In the SMC, the molecular mass deduced from the sub-millimeter are systematically larger than the one deduced from the virial theorem applied to CO data, even with an upper limit to the dust temperature, in contrast to what is seen for equivalent Galactic clouds. |
The most straightforward interpretation of the mass discrepancy we observe in the SMC is then that the CO linewidth does not measure the full velocity distribution of the gas. There are two independent reasons why this could be true.
The CO emitting regions may be located in only the interior of the molecular clouds, in regions shielded from the UV radiation field (Lequeux et al. 1994; Glover & Mac Low 2010). If the (unresolved) CO emitting clumps are not evenly distributed in the region detected by the CO observations, the observed line width may not reflect the full velocity dispersion of the cloud.
The CO line may originate in the densest regions created by shocks in a turbulent medium (Klessen et al. 2009). Simulations of a turbulent interstellar medium indicate that these dense regions with CO might not always be the most shielded ones (Glover et al. 2010). In this case, the velocity dispersion in the CO emitting regions would not be representative of the velocity dispersion of the molecular gas located also in lower density regions. The CO line width would then underestimate the velocity dispersion of the molecular gas because of its preferential location in the densest and less turbulent regions. This difference has been observed between the CO and HI line width in high latitude clouds in the solar neighborhood on a few parsec scale (Barriault et al. 2010), but it is unclear whether this difference would exist on larger scales where many shocks at different locations of the cloud must be occurring.
Owing to the low metallicity of the SMC, a Galactic analog to understand the CO emitting clouds in the SMC may be denser molecular environments. Indeed, if the H2 abundance varies as the product of the mean gas number density and the metallicity (Glover & Mac Low 2010), the motions observed in CO and the mass observed in the dust continuum can be compared to the velocity of molecular cores and the relation to their envelopes in our Galaxy. In “extinction super cores”, Kirk et al. (2007) observed that the inner N2H+ or C18O starless cores have a velocity dispersion that is systematically lower than the one expected for a gravitational support of the region in extinction. The motions between the densest molecular entities are hence insufficient to support the envelopes against gravity, similarly to what we observe in the giant molecular clouds in the southwest of the SMC.
4. Discussion
Our analysis of the two mass estimates was performed in such a way as to avoid as much as possible the known caveats (CO-devoid envelope, enhanced dust emissivity): fluxes were extracted from regions restricted to where CO is observed, we attempted to remove the extended emission surrounding the CO peaks, and the dust emissivity was measured for molecular environments. The impact of these effects on the masses deduced is assessed in Appendix A. Here we discuss the possible remaining biasses that could affect the analysis and cause the mass discrepancy. We also discuss alternative interpretations of the mass discrepancy we observe.
4.1. Unresolved CO clouds and geometrical effects
In the scenario where CO is confined inside a large H2 envelope, the dust emission traces the total cloud mass (CO-emitting cloud+envelope). To minimize the effect of the CO-devoid envelope on the dust emission, we performed a local estimate of the extended emission around the CO-detected region and removed it from the measured (sub-)millimeter fluxes. However, the effectiveness of this removal depends on both the size of the envelope and the density profile of the cloud.
For the same configuration, the virial mass was inferred from both the CO velocities and the radius of the CO cloud. This radius may be overestimated from the observations if the CO clumps are not resolved and the virial masses overestimated. The dimension differences between the dust emitting region, the CO emitting region, and the area deduced from the observations (i.e., the aperture) may then still bias the ratio Mvir/Mmm in either direction (enhancing or decreasing the mass ratio).
The exact magnitude of these biases is a complicated function of the real structure of the cloud (e.g. density), the definition of the CO cloud and aperture, and the extent of any CO-free dusty envelope surrounding the cloud. We tested the magnitude of a geometric bias for a range of density profiles with a simple model, in which the CO cloud and the envelope are spherical. A circular aperture defines the radius that enters the virial mass calculation, while also defining the impact of the background subtraction on the mass deduced from the dust emission. We found that for a simple model in which dust emerges from a cloud twice the size of the CO cloud and the aperture covers the portion of the cloud not showing CO emission, the bias almost never exceeds ~ 30%. However, if the CO cloud is actually substantially smaller than the values quoted in Table 1 (e.g. CO clumps are not resolved at the SEST resolution), if the dust envelope is very large compared to the CO cloud, or if the aperture extends too far from the surface of the cloud, these effects can be larger. Conversely, for shallow density profiles and aperture definitions too close to the surface of the cloud, it is possible to overcorrect for a dusty envelope, meaning that our measurement of Mmm would in fact be too low and exacerbating the difference between Mvir and Mmm. This effect was explored in more detail for the N83 region in the Wing of the SMC (Leroy et al. 2009) and could play a role in the mass discrepancy despite our attempt to limit the mass comparison to the CO peaks of the molecular clouds.
To assess these biases, we performed the mass calculations without the extended emission subtraction and with deconvolved CO radii. The results are presented in Appendix A and demonstrate that, as far as can be tested with the current observations, both effects seem to enhance the mass discrepancy.
Observations of higher resolution and comparisons to models and simulations of cloud structure should enable to assess more accurately whether geometric effects can drive the observed difference. Here we note the possible concern and that we have done our best to correct for it given the data available (via the extended-emission fitting procedure).
4.2. The dust-to-gas ratio and the dust emissivity
To compute molecular cloud masses from the dust emission, we assumed that the dust properties in the Small Magellanic Cloud are similar to those that we observe in our Galaxy, except for their lower dust content with respect to the gas due to the metallicity. Hence, one possible way to understand the mass discrepancy we observe is to question our understanding of dust emission in the SMC.
Unfortunately, our current knowledge of dust grains in the SMC may differ from that in our Galaxy. Israel et al. (2010) observed a millimeter-emission excess in the Small Magellanic Cloud, on the scale of the galaxy, that is not explained by current standard models of dust emission (Bot et al. 2010). The nature of this excess remains unclear but it may be associated with spinning dust emission. Given that dust emission in the SMC is poorly understood on a global scale, the interpretation of a similar excess emission on the scale of individual molecular clouds can be very uncertain. Nevertheless, we do our best within the current knowledge on dust properties in the SMC, i.e. we assume that large dust grains in thermal equilibrium emit most of the sub-millimeter dust emission.
Biases caused by our uncertainties in the dust temperature and emissivity index (note that these quantities are not independent) were assessed by adopting an extreme value β = 1 giving Tdust ~ 19 K for a fit of the observed far-infrared to millimeter SEDs. In Fig. 3, we observe that the lower limit to the molecular cloud masses obtained with these parameters is still higher than the virial masses.
In Sect. 2.4.2, we assumed that the dust emissivity in the SMC is equivalent to that observed in GMCs of the Milky Way, and scaled it accordingly to the dust-to-gas ratio difference between the two galaxies. However, there is no ground-based evidence that this is the case. First, the knowledge of the dust-to-gas ratio in the SMC is quite uncertain. Second, the grain opacity may be different. In the following, we discuss how these two quantities can vary.
The dust-to-gas ratio estimate we use is based on abundance measures toward the star AV 304 (Rolleston et al. 2003), using Galactic depletions computed from Sofia & Meyer (2001b,a). These abundances are consistent with all HII region abundances published for the SMC (Vermeij & van der Hulst 2002; Pérez-Montero & Díaz 2005; Lebouteiller et al. 2008) expect for one (N13, for which a close to solar O/H abundance has been deduced), so we believe our metallicity estimate is accurate for the SMC. The depletion factors may be higher than in the Milky Way, increasing the dust-to-gas ratio and decreasing the mass discrepancy. However, to correct for the mass discrepancy that we observe as the dust-to-gas ratio varies, all metals would have to be depleted onto dust grains. It therefore seems unlikely that a change of the dust-to-gas ratio could explain the mass discrepancy we observe.
Grain coagulation can make the sub-millimeter dust emissivity larger than the value measured for the diffuse medium by Li & Draine (2001) . An enhancement (a factor of 3) is found for Galactic GMCs. We assumed that the same enhancement factor applies to the SMC clouds in our study. Could this enhancement be larger in the SMC and explain the mass discrepancy? By applying an upper limit to the dust temperature, we observed in the last section that the virial mass for the SMC GMCs is at least 2 to 5 times smaller than the mass deduced from the dust millimeter emission. To ensure that 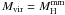 , the dust emissivity in the SMC would then need to be at least 2 to 5 times larger than the value we use. We note that this enhancement would lower dust temperatures by a factor
, the dust emissivity in the SMC would then need to be at least 2 to 5 times larger than the value we use. We note that this enhancement would lower dust temperatures by a factor 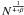 (where N is the factor of emissivity enhancement), since the dust grains would radiate more efficiently. Coagulation could therefore explain both the mass discrepancy and the low dust temperatures we observed when fitting the SEDs with an emissivity index β = 2.
(where N is the factor of emissivity enhancement), since the dust grains would radiate more efficiently. Coagulation could therefore explain both the mass discrepancy and the low dust temperatures we observed when fitting the SEDs with an emissivity index β = 2.
Voshchinnikov et al. (2006) analyzed the influence of grain porosity on the dust properties. They show that as the porosity increases, the millimeter mass absorption increases and the dust temperature decreases. Using their results, we see that the mass absorption coefficient for a porous composite grain (amorphous carbon+astronomical silicate) can be up to 22 times the Li & Draine (2001) value at 1 mm. Therefore, in theory the mass discrepancy between the virial theorem and dust estimates could be due to a larger fraction of porous grains or a larger porosity of the grains in the SMC GMCs than in the Milky Way.
However, since grains coagulation is proportional to the density of dust particles, one would expect less coagulation of dust grains in the SMC than in our Galaxy, due to the lower dust content. Models of the regulation of the grain size distribution by shattering and coagulation (Hirashita & Yan 2008) indeed imply that, for a MRN grain size distribution (Mathis et al. 1977), the importance of both of these processes is significantly lower at low metallicities such as those in the SMC. But the grain size distribution in the SMC seems to differ significantly from that in our Galaxy: the differences between the SMC and Milky Way diffuse ISM extinction curves and infrared SEDs indicate that a larger fraction of the dust mass is in small dust grains (Weingartner & Draine 2001; Bot et al. 2004; Bernard et al. 2008). This enhancement in small dust particles is therefore also likely to impact the grain coagulation process. Using the dust grain size distribution for the SMC and the Milky Way (for RV = 3.1) given by Weingartner & Draine (2001) and a simple coagulation model (using the collision rates due to turbulence from Draine (1985) and assuming that grain stick when they collide), we observe that for a given total dust mass, small grains (10 Å < a < 0.1 μm) may coagulate twice as quickly onto big grains than in our Galaxy. The greater fraction of small grains in the grain size distribution of the SMC therefore seems to encourage coagulation processes, while the low metallicity of the SMC may discourage them. More detailed models would be needed to quantify the likelyhood of finding large porous aggregates in the SMC. These models are beyond the scope of the current paper. It seems unlikely at present that large porous aggregates would be much easier to form in the SMC than in our galaxy. But the type of aggregates formed in the SMC (and hence their porosity) may differ from those in the Milky Way because of the different size distribution and this could also potentially affect the dust emissivity.
We cannot completely exclude at present that the mass difference we observe for SMC GMCs between the two methods (virial theorem and dust millimeter emission) is due to a higher sub-mm emissivity than that measured in Galactic GMCs. The production of large porous grains in the SMC by coagulation would indeed explain both the mass difference and the low temperatures observed. However our current understanding of dust in the SMC does not favor more coagulation in this environment than in our Galaxy.
5. Conclusion
We analyzed our LABOCA observations at 870 μm obtained for the southwest region of the Small Magellanic Cloud. All the GMCs observed previously in CO were detected. We have compiled SEDs by comparing the fluxes measured at 160 μm, 870 μm, 1.2 mm, 3 cm and 6 cm for each cloud. We have found that the sub-millimeter and millimeter emission, in all clouds in this study, is always dominated by dust emission. By fitting the SEDs with a modified blackbody and a standard β = 2, we have inferred low dust temperatures Tdust ~ 12 K. Given the uncertainties, we also assumed that β = 1 (giving fitted temperatures around Tdust ~ 19 K) to be able to deduce lower limits to the molecular cloud masses obtained from the dust emission. We have used a dust emissivity at 870 μm that we determined in the molecular regions of our Galaxy and scaled to the dust-to-gas ratio of the SMC, to inger mass estimates for the molecular clouds observed (as well as lower limits to these masses) from the 870 μm dust emission, and compared these estimates to virial masses deduced from CO observations.
We have confirmed the discrepancy between the virial masses and those deduced from dust emission found previously for the molecular clouds of the SMC. This discrepancy has now been observed at two different wavelengths with two different instruments and as such can no longer be attributed to instrumental effects. Furthermore, uncertainties in the origin of the sub-millimeter emission have been assessed (free-free contribution, CO line contribution). The mass ratio 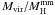 observed in the SMC is clearly below one, even for conservative assumptions about the dust emissivity, dust temperature, etc. In contrast, for similar clouds in the solar neighbourhoods, the observed values are systematically above 1. The direct interpretation of this result is that the CO line widths do not trace the full velocity dispersion of the gas in GMCs of the SMC. This may be due to the turbulent nature of the intersellar gas and the formation of CO in the densest structures.
observed in the SMC is clearly below one, even for conservative assumptions about the dust emissivity, dust temperature, etc. In contrast, for similar clouds in the solar neighbourhoods, the observed values are systematically above 1. The direct interpretation of this result is that the CO line widths do not trace the full velocity dispersion of the gas in GMCs of the SMC. This may be due to the turbulent nature of the intersellar gas and the formation of CO in the densest structures.
This low mass ratio in the SMC is unexpected for large molecular clouds and will have to be studied in greater detail to assess its origin. The dust properties in the SMC may differ from those in our Galaxy and we cannot completely exclude that an enhanced grain coagulation in the SMC could increase the dust emissivity and lead to an overestimate of the true mass by the dust millimeter emission, Herschel observations will provide more information in this respect by complementing the wavelength coverage. The cloud+envelope geometry may also play a role in enhancing or decreasing the mass discrepancy and higher resolution observations will be needed to assess this uncertainty.
Further investigations will be necessary to more clearly understand the origin of this discrepancy, and ascertain whether it is a general property of clouds in low metallicity galaxies or tells us something about the molecular cloud properties. These studies will be performed by Herschel, which is sensitive to dust emission on all angular scales and will provide a finer spectral sampling of the far-infrared and sub-mm emission. Spectroscopic observations of the C+ line with Herschel will also probe the extended envelopes of the molecular clouds and enable us to test whether the C+ linewidths are comparable to those observed in CO (i.e. test whether CO velocities trace the motions inside the molecular clouds).
Acknowledgments
M.R. wishes to acknowledge support from FONDECYT grant No. 1080335. M.R. is supported by the Chilean Center for Astrophysics FONDAP No. 15010003. M.R., F.B., and C.B. have been supported by the ECOS-CONICYT C08U03 project.
References
- Barriault, L., Joncas, G., Falgarone, E., et al. 2010, MNRAS, 859 [Google Scholar]
- Bernard, J.-P., Reach, W. T., Paradis, D., et al. 2008, AJ, 136, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., Fukui, Y., Kawamura, A., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil, 81 [Google Scholar]
- Bolatto, A. D., Leroy, A., Israel, F. P., & Jackson, J. M. 2003, ApJ, 595, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Simon, J. D., Stanimirović, S., et al. 2007, ApJ, 655, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Rosolowsky, E., Walter, F., & Blitz, L. 2008, ApJ, 686, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Bot, C., Boulanger, F., Lagache, G., Cambrésy, L., & Egret, D. 2004, A&A, 423, 567 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bot, C., Boulanger, F., Rubio, M., & Rantakyro, F. 2007, A&A, 471, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bot, C., Ysard, N., Paradis, D., et al. 2010, A&A, accepted [Google Scholar]
- Cambrésy, L., Boulanger, F., Lagache, G., & Stepnik, B. 2001, A&A, 375, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1985, in Protostars and Planets II, ed. D. C. Black & M. S. Matthews, 621 [Google Scholar]
- Du, F., & Yang, J. 2008, ApJ, 686, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. K., Rosolowsky, E., Evans, II, N. J., et al. 2010, ApJ, 717, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Mac Low, M. 2010, MNRAS, accepted [arXiv:1003.1340] [Google Scholar]
- Glover, S. C. O., Federrath, C., Mac Low, M., & Klessen, R. S. 2010, MNRAS, 404, 2 [NASA ADS] [Google Scholar]
- Gordon, K., Meixner, M., Blum, R., et al. 2009, ApJ [Google Scholar]
- Grenier, I. A., Casandjian, J., & Terrier, R. 2005, Science, 307, 1292 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirashita, H., & Yan, H. 2009, MNRAS, 394, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, F. P. 1997, A&A, 328, 471 [NASA ADS] [Google Scholar]
- Israel, F. P., Johansson, L. E. B., Lequeux, J., et al. 1993, A&A, 276, 25 [NASA ADS] [Google Scholar]
- Israel, F. P., Johansson, L. E. B., Rubio, M., et al. 2003, A&A, 406, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Israel, F. P., Wall, W. F., Raban, D., et al. 2010, A&A, 519, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, H., Johnstone, D., & Tafalla, M. 2007, ApJ, 668, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Krumholz, M. R., & Heitsch, F. 2009, Adv. Sci. Lett., Special issue on Computational Astrophysics, in press [ArXiv:0906.4452] [Google Scholar]
- Lebouteiller, V., Bernard-Salas, J., Brandl, B., et al. 2008, ApJ, 680, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Le Bourlot, J., Des Forets, G. P., et al. 1994, A&A, 292, 371 [NASA ADS] [Google Scholar]
- Leroy, A. k., Bolatto, A., Walter, F., & Blitz, L. 2006, ApJ, 643, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. k., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. k., Bolatto, A., Bot, C., et al. 2009, ApJ, 702, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Mizuno, N., Rubio, M., Mizuno, A., et al. 2001, PASJ, 53, L45 [NASA ADS] [Google Scholar]
- Nikolić, S., Garay, G., Rubio, M., & Johansson, L. E. B. 2007, A&A, 471, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Payne, J. L., Filipović, M. D., Reid, W., et al. 2004, MNRAS, 408 [Google Scholar]
- Pérez-Montero, E., & Díaz, A. I. 2005, MNRAS, 361, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, R. J. 1992, ApJ, 392, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Rolleston, W. R. J., Venn, K., Tolstoy, E., & Dufton, P. L. 2003, A&A, 400, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosolowsky, E., Engargiola, G., Plambeck, R., & Blitz, L. 2003, ApJ, 599, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Rubio, M., Lequeux, J., & Boulanger, F. 1993a, A&A, 271, 9 [NASA ADS] [Google Scholar]
- Rubio, M., Lequeux, J., Boulanger, F., et al. 1993b, A&A, 271, 1 [NASA ADS] [Google Scholar]
- Rubio, M., Lequeux, J., Boulanger, F., et al. 1996, A&AS, 118, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubio, M., Boulanger, F., Rantakyro, F., & Contursi, A. 2004, A&A, 425, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siringo, G., Kreysa, E., & Kovacs, A. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofia, U. J., & Meyer, D. M. 2001a, ApJ, 558, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., & Meyer, D. M. 2001b, ApJ, 554, L221 [NASA ADS] [CrossRef] [Google Scholar]
- Stanimirovic, S., Staveley-Smith, L., Dickey, J. M., Sault, R. J., & Snowden, S. L. 1999, MNRAS, 302, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2003, A&A, 398, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strong, A. W., Bloemen, J. B. G. M., Dame, T. M., et al. 1988, A&A, 207, 1 [NASA ADS] [Google Scholar]
- Vermeij, R., & van der Hulst, J. M. 2002, A&A, 391, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchinnikov, N. V., Il’in, V. B., Henning, T., & Dubkova, D. N. 2006, A&A, 445, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Systematics
A.1. Effect of the local background subtraction on the masses derived from the sub-mm emission
For this study, we tried to minimize the effect of CO-devoid envelope on the dust emission by performing a local background subtraction. This option was chosen to be conservative to compute masses from dust sub-millimeter emission that are comparable to virial masses obtained from CO observations. However, it can lead to complicated uncertainties as discussed in Sect. 4.1.
In this appendix, we test the impact of the background subtraction on our results by repeating the analysis of the molecular clouds in the southwest region of the SMC, but without local background subtraction. Instead, we took the same background region for all clouds in all maps at the location 00:46:02.85–73:19:26.5 (J2000). The fluxes obtained from 160 μm to 6 cm are given in Table A.1, and are on average 1.5 times higher at 870 μm. Additional steps of the analysis were then reproduced in the same manner as described in Sect. 2.4 and the masses obtained are given in Table A.2. We found a median mass ratio 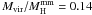 (0.23 for the upper limit to the dust temperature), i.e. 1.5 times lower than with the local background subtraction. This confirms that our attempt to minimize the effect of an extended envelope by subtracting a local background from the emission observed in each cloud, decreases the mass discrepancy observed between the submillimeter emission and the virial masses.
(0.23 for the upper limit to the dust temperature), i.e. 1.5 times lower than with the local background subtraction. This confirms that our attempt to minimize the effect of an extended envelope by subtracting a local background from the emission observed in each cloud, decreases the mass discrepancy observed between the submillimeter emission and the virial masses.
A.2. Deconvolved CO cloud radii
We used the sizes of the CO clouds reported by Rubio et al. (1993b) and Lequeux et al. (1994). Their sizes are the observed sizes that were not deconvolved by the beam size as the CO clouds were most often of larger sizes than the SEST beam. If one deconvolves their observed sizes assuming the standard aproximation of a source size smaller than the beam size, then the cloud sizes become smaller than the observed sizes published and used in the main text of this paper. The radii obtained for the deconvolved CO clouds are given in Table A.1. For a 43′′ beam, the deconvolved sizes are smaller than the observed sizes by a fraction of 0.3 to 0.8. In some cases, when the CO map is fully sampled, the observed CO radius can be smaller than the beam size. In this case, the deconvolved radius is indicated in Table A.1 as “NaN” and we used the observed radius to compute virial masses. Since deconvolved radii are smaller than the observed ones, lower virial masses were measured for the clouds by a similar fraction (see Table A.2). Thus the difference between the gas mass derived from the dust emission becomes even larger.
Combining the effect of deconvolved radii with the lack of the envelope subtraction (from Appendix A.1), we obtained a median mass ratio 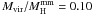 (0.16 for the upper limit on the dust temperature), i.e. twice as low as that presented in the main text of this paper. This confirms that our different attempts to minimize known caveats such as a CO-devoid envelope and the resolution of the CO observations, decrease the mass discrepancy. The mass discrepancy observed in the southwest region molecular clouds may then be at least twice as high as the one reported.
(0.16 for the upper limit on the dust temperature), i.e. twice as low as that presented in the main text of this paper. This confirms that our different attempts to minimize known caveats such as a CO-devoid envelope and the resolution of the CO observations, decrease the mass discrepancy. The mass discrepancy observed in the southwest region molecular clouds may then be at least twice as high as the one reported.
Appendix B: Sub-mm dust emission outside the CO clouds
The LABOCA 870 μm map of the south-west region presented in this study shows extended sub-millimeter emission well outside the molecular clouds observed in CO. In this appendix, we present a short analysis of this extended dust emission outside the CO peaks. We compile the SEDs from 160 μm to 6 cm by extracting fluxes at each wavelength for a region defined as being observed at all wavelengths and being outside the CO peaks studied. This region corresponds to a solid angle of 1.00787 × 10-7 sr. For the extended emission observed in this region, the spatial filtering in the SIMBA 1.2 mm observations is no longer negligible and the flux obtained at 1.2 mm is considered a lower limit. The SEDs obtained is shown in Fig. B.1.
A free-free emission model is fitted to the 3 cm radio flux and extrapolated to 160 and 870 μm. The free-free contribution is then removed from the observed flux at 160 and 870 μm before fitting a modified black-body spectrum with a spectral index of 1 (blue dashed line) or 2 (plain red line). The dust temperatures deduced are 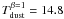 K and
K and 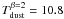 K, respectively. The dust temperature observed in the region surrounding the CO peaks is therefore similar to those observed in the CO-detected regions in our observations.
K, respectively. The dust temperature observed in the region surrounding the CO peaks is therefore similar to those observed in the CO-detected regions in our observations.
 |
Fig. B.1 SED from the far-infrared to the radio, observed for the region outside the molecular clouds observed in CO. The fluxes observed at 160 μm and 870 μm are fitted with a single modified black-body with either an emissivity index of 1 (dashed blue line) or 2 (plain red line). Radio fluxes computed in the same regions are overplotted and the extrapolated free-free emission is displayed as a black line. |
The hydrogen mass of this region inferred from the dust emission fit is 9.3 × 104 M⊙ for a standard spectral index β = 2 (5.2 × 104 M⊙ for β = 1). This is comparable to the mass, deduced from the sub-mm dust emission, of the smallest CO-detected molecular clouds of this study.
Using the Hi observations of the SMC from Stanimirovic et al. (1999), we estimated the neutral hydrogen mass in this region to be 2.5 × 104 M⊙, i.e. 2 to 4 times lower than the mass of the gas deduced from the dust emission. Most of the gas detected by means of the extended sub-mm emission outside CO-detected molecular clouds is then probably cold molecular hydrogen. This is consistent our finding that we observe no correlation between the 870 μm emission and the Hi 21 cm emission.
All Tables
Observed fluxes from the far-infrared to the radio for our sample of giant molecular clouds.
Results from modified blackbody fits to the MIPS, LABOCA, and SIMBA fluxes for each molecular cloud.
Mass estimates for the individual GMCs observed in the southwest region of the SMC.
All Figures
 |
Fig. 1 Top image: LABOCA image in the southwest region of the SMC (Units are in Jy/beam). Middle and bottom images: LABOCA images convolved to a ~40′′ resolution with CO and MIPS 160 μm contours overlaid, respectively. All the molecular clouds observed in CO are detected at 870 μm. Extended emission is well recovered in the LABOCA map and the 870 μm emission matches well the 160 μm one. |
| In the text | |
 |
Fig. 2 SEDs from the far-infrared to the radio, observed for each cloud. The fluxes observed at 160 μm, 870 μm and 1.2 mm are fitted with a single modified black body either with an emissivity index of 1 (dashed blue line) or 2 (plain red line) or with a free emissivity index (dotted green line). Radio fluxes (or upper limits) computed in the same regions are overplotted and the extrapolated free-free emission is displayed as a black line. This shows clearly that the sub-millimeter and millimeter emission is dominated by dust emission rather than free-free. |
| In the text | |
 |
Fig. 3 Comparison between the two molecular mass estimates: masses deduced from sub-millimeter dust emission and virial masses. The mass deduced from the LABOCA emission in the SMC are shown for a dust temperature as estimated from the SED fitting with β = 2 (Tdust ~ 12 K, black diamonds) and for a dust temperature of 19 K as an upper limit (green rhombs). Galactic GMCs studied with the same method are shown for comparison (blue stars). In the SMC, the molecular mass deduced from the sub-millimeter are systematically larger than the one deduced from the virial theorem applied to CO data, even with an upper limit to the dust temperature, in contrast to what is seen for equivalent Galactic clouds. |
| In the text | |
 |
Fig. B.1 SED from the far-infrared to the radio, observed for the region outside the molecular clouds observed in CO. The fluxes observed at 160 μm and 870 μm are fitted with a single modified black-body with either an emissivity index of 1 (dashed blue line) or 2 (plain red line). Radio fluxes computed in the same regions are overplotted and the extrapolated free-free emission is displayed as a black line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


