| Issue |
A&A
Volume 523, November-December 2010
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014855 | |
| Published online | 16 November 2010 | |
Detection of the Small Magellanic Cloud in gamma-rays with Fermi/LAT
1
Space Science DivisionNaval Research Laboratory,
Washington,
DC
20375,
USA
2
National Research Council Research Associate, National Academy of
Sciences, Washington,
DC
20001,
USA
3
W. W. Hansen Experimental Physics Laboratory, Kavli Institute for
Particle Astrophysics and Cosmology, Department of Physics and SLAC National
Accelerator Laboratory, Stanford University, Stanford, CA
94305,
USA
4
Istituto Nazionale di Fisica Nucleare, Sezione di Pisa, 56127
Pisa,
Italy
5
Laboratoire AIM, CEA-IRFU/CNRS/Université Paris Diderot, Service
d’Astrophysique, CEA Saclay, 91191
Gif sur Yvette,
France
6
Istituto Nazionale di Fisica Nucleare, Sezione di Trieste, 34127
Trieste,
Italy
7
Dipartimento di Fisica, Università di Trieste,
34127
Trieste,
Italy
8
Istituto Nazionale di Fisica Nucleare, Sezione di Padova, 35131
Padova,
Italy
9
Dipartimento di Fisica “G. Galilei”, Università di
Padova, 35131
Padova,
Italy
10
Istituto Nazionale di Fisica Nucleare, Sezione di Perugia, 06123
Perugia,
Italy
11
Dipartimento di Fisica, Università degli Studi di
Perugia, 06123
Perugia,
Italy
12
Centre d’Étude Spatiale des Rayonnements, CNRS/UPS, BP 44346,
31028
Toulouse Cedex 4,
France
e-mail: knodlseder@cesr.fr;jean@cesr.fr
13
Department of Physics, Center for Cosmology and Astro-Particle
Physics, The Ohio State University, Columbus, OH
43210,
USA
14
Dipartimento di Fisica “M. Merlin” dell’Università e del
Politecnico di Bari, 70126
Bari,
Italy
15
Istituto Nazionale di Fisica Nucleare, Sezione di Bari, 70126
Bari,
Italy
16
Laboratoire Leprince-Ringuet, École polytechnique, CNRS/IN2P3, Palaiseau,
France
17
Institut de Ciencies de l’Espai (IEEC-CSIC), Campus UAB,
08193
Barcelona,
Spain
18
INAF-Istituto di Astrofisica Spaziale e Fisica Cosmica, 20133
Milano,
Italy
19
NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
20
Center for Research and Exploration in Space Science and
Technology (CRESST) and NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
21
Department of Physics and Center for Space Sciences and
Technology, University of Maryland Baltimore County, Baltimore, MD
21250,
USA
22
George Mason University, Fairfax, VA
22030,
USA
23
Laboratoire de Physique Théorique et Astroparticules, Université
Montpellier 2, CNRS/IN2P3, Montpellier, France
24
Department of Physics, Stockholm University,
AlbaNova, 106 91
Stockholm,
Sweden
25
The Oskar Klein Centre for Cosmoparticle Physics, AlbaNova, 106 91
Stockholm,
Sweden
26
Royal Swedish Academy of Sciences Research Fellow, funded by a grant from
the
K. A. Wallenberg Foundation,
Sweden
27 CNRS/IN2P3, Centre d’Études Nucléaires BordeauxGradignan,
UMR 5797, Gradignan, 33175, France
28 Université de Bordeaux, Centre d’Études Nucléaires Bordeaux
Gradignan, UMR 5797, Gradignan, 33175, France
29
Department of Physical Sciences, Hiroshima
University, Higashi-Hiroshima, Hiroshima
739-8526,
Japan
30 Agenzia Spaziale Italiana (ASI) Science Data Center, 00044
Frascati ( Roma), Italy
31
INAF Istituto di Radioastronomia, 40129
Bologna,
Italy
32
Center for Space Plasma and Aeronomic Research (CSPAR), University
of Alabama in Huntsville, Huntsville, AL
35899,
USA
33
Institució Catalana de Recerca i Estudis Avançats (ICREA), Barcelona,
Spain
34 Research Institute for Science and Engineering, Waseda
University, 3-4-1, Okubo, Shinjuku, Tokyo, 169-8555 Japan
35
Department of Physics, University of Washington,
Seattle, WA
98195-1560,
USA
36
Max-Planck Institut für extraterrestrische Physik, 85748
Garching,
Germany
e-mail: martinp@mpe.mpg.de
37
Department of Physics and Department of Astronomy, University of
Maryland, College
Park, MD
20742,
USA
38
Istituto Nazionale di Fisica Nucleare, Sezione di Roma “Tor
Vergata”, 00133
Roma,
Italy
39
Department of Physics and Astronomy, University of
Denver, Denver,
CO
80208,
USA
40
Hiroshima Astrophysical Science Center, Hiroshima University, Higashi-Hiroshima,
Hiroshima
739-8526,
Japan
41
Institute of Space and Astronautical Science, JAXA, 3-1-1 Yoshinodai,
Sagamihara, Kanagawa
229-8510,
Japan
42
Institut für Astro- und Teilchenphysik and Institut für
Theoretische Physik, Leopold-Franzens-Universität Innsbruck, 6020
Innsbruck,
Austria
43
Santa Cruz Institute for Particle Physics, Department of Physics
and Department of Astronomy and Astrophysics, University of California at Santa
Cruz, Santa Cruz,
CA
95064,
USA
44
Space Sciences Division, NASA Ames Research Center, Moffett Field, CA
94035-1000,
USA
45
NYCB Real-Time Computing Inc., Lattingtown, NY
11560-1025,
USA
46
Department of Chemistry and Physics, Purdue University
Calumet, Hammond,
IN
46323-2094,
USA
48
Consorzio Interuniversitario per la Fisica Spaziale (CIFS), 10133
Torino,
Italy
49
INTEGRAL Science Data Centre, 1290
Versoix,
Switzerland
50
Dipartimento di Fisica, Università di Roma “Tor
Vergata”, 00133
Roma,
Italy
51
Department of Physics, Royal Institute of Technology
(KTH), AlbaNova,
106 91
Stockholm,
Sweden
52
School of Pure and Applied Natural Sciences, University of Kalmar, 391 82
Kalmar,
Sweden
Received:
23
April
2010
Accepted:
1
August
2010
Context. The flux of gamma rays with energies greater than 100 MeV is dominated by diffuse emission coming from cosmic-rays (CRs) illuminating the interstellar medium (ISM) of our Galaxy through the processes of Bremsstrahlung, pion production and decay, and inverse-Compton scattering. The study of this diffuse emission provides insight into the origin and transport of cosmic rays.
Aims. We searched for gamma-ray emission from the Small Magellanic Cloud (SMC) in order to derive constraints on the cosmic-ray population and transport in an external system with properties different from the Milky Way.
Methods. We analysed the first 17 months of continuous all-sky observations by the Large Area Telescope (LAT) of the Fermi mission to determine the spatial distribution, flux and spectrum of the gamma-ray emission from the SMC. We also used past radio synchrotron observations of the SMC to study the population of CR electrons specifically.
Results. We obtained the first detection of the SMC in high-energy gamma rays, with an integrated >100 MeV flux of (3.7 ± 0.7) × 10-8 ph cm-2 s-1, with additional systematic uncertainty of ≤16%. The emission is steady and from an extended source ~3° in size. It is not clearly correlated with the distribution of massive stars or neutral gas, nor with known pulsars or supernova remnants, but a certain correlation with supergiant shells is observed.
Conclusions. The observed flux implies an upper limit on the average CR nuclei density in the SMC of ~15% of the value measured locally in the Milky Way. The population of high-energy pulsars of the SMC may account for a substantial fraction of the gamma-ray flux, which would make the inferred CR nuclei density even lower. The average density of CR electrons derived from radio synchrotron observations is consistent with the same reduction factor but the uncertainties are large. From our current knowledge of the SMC, such a low CR density does not seem to be due to a lower rate of CR injection and rather indicates a smaller CR confinement volume characteristic size.
Key words: acceleration of particles / cosmic rays / Magellanic Clouds / gamma rays: general
© ESO, 2010
1. Introduction
Gamma rays with energies greater than 100 MeV are the observable manifestations of various populations of non-thermal particles. The sky in this energy range was unveiled by SAS-2 and COS-B in the 1970s, then mapped by CGRO/EGRET in the 1990s, and is now surveyed by AGILE since 2007 and Fermi/LAT since 2008. At low Galactic latitudes, many supernova remnants (SNRs) and pulsars have revealed themselves as accelerators of particles up to TeV energies, but a lot of localised sources are still formally unidentified. Most of the emission, however, is of diffuse nature and arises from the interaction of Galactic cosmic-rays (CRs) with interstellar matter and radiation. The pervasiveness of this emission, which accounts for 80−90% of the flux above 100 MeV, indicates that CRs diffuse far from their sources filling the entire Galaxy.
Since their discovery at the beginning of the 20th century, it has been realised that CRs are not simply a side-product of the most energetic phenomena of the Universe, but actually form an essential component of the Milky Way (MW). Galactic CRs affect the physical state of the interstellar medium (ISM) by heating/ionising its atomic and molecular phases (Ferrière 2001) and are thought to alter the spectrum of interstellar turbulence as they get reaccelerated by draining energy from magnetohydrodynamic waves (Ptuskin et al. 2006). Ionisation by low-energy CRs is important for the chemical processes operating inside dense molecular clouds, where Lyman photons cannot penetrate (Indriolo et al. 2009). Because of their high energy density (~1 eV cm-3) and corresponding pressure, CRs also contribute to supporting interstellar gas against gravity (Ferriere 1998). In addition, CRs are essential for the Parker dynamo mechanism, which may be the source of the large-scale magnetic fields in galaxies like the Milky Way (Hanasz et al. 2004, 2009).
Direct measurements of the CR composition and spectrum in the interplanetary medium, together with imaging of the Galactic diffuse emission in the radio and MeV-GeV domain, have provided a wealth of information on Galactic CRs. Combined with models of increasing sophistication, from simple leaky box to analytic diffusion models (e.g. Aharonian & Atoyan 2000) to more elaborate numerical calculations (such as GALPROP, see Strong et al. 2004), these data permitted deriving important constraints on the transport of CRs inside our Galaxy: the time spent in the Galactic volume, the amount of matter traversed, the extent of spatial diffusion, and the role of reacceleration and convection (see the review by Strong et al. 2007).
Resolved gamma-ray observations of externally-viewed galaxies provide the possibility to make further progress understanding the origin and propagation of CRs. The Magellanic Clouds offer a great opportunity in this regard due their proximity and their significantly contrasting geometries and physical conditions (gas, stars, magnetic field, ...) compared to the Milky Way. The Large Magellanic Cloud (LMC) was observed by EGRET with a measured flux >100 MeV of (1.9 ± 0.4) × 10-7 ph cm-2 s-1 that was found to be consistent with a model in which CRs interact with the ISM of the galaxy, under the assumption that the CRs, magnetic pressure, and thermal gas are in dynamical balance with the gravitational attraction (Fichtel et al. 1991; Sreekumar et al. 1992). While it was clear that the LMC was an extended object, the sensitivity of EGRET precluded resolving any features. The LMC has now been resolved by Fermi/LAT. The higher sensitivity and angular resolution of the instrument revealed a good correlation between gamma-ray emission and massive star forming regions, thereby providing evidence for CR acceleration in these regions and suggesting a relatively small diffusion length for GeV CRs (Abdo et al. 2009h). In contrast, the Small Magellanic Cloud (SMC) was not detected by EGRET but the upper-limit thus derived allowed to dismiss a metagalactic origin for the bulk of CRs with energies 1015−1016 eV (Sreekumar et al. 1993), while the most energetic particles are thought to come from extragalactic sources lying within the Greisen-Zatsepin-Kuz’min (GZK) horizon (The Pierre Auger Collaboration et al. 2007, 2008, 2009).
In this paper, we report the detection and resolving of the SMC in high-energy gamma-rays using Fermi/LAT. In the following, we describe the various analyses performed on the Fermi/LAT data in order to derive the morphology, the flux and the spectrum of the SMC in gamma-rays. We then discuss plausible origins for the detected emission before considering the consequences of our result on the CR population and transport in the SMC.
2. Observations
2.1. Data preparation
The characteristics and performance of the LAT aboard Fermi are described in detail by Atwood et al. (2009). We used the LAT Science Tools package, which is available from the Fermi Science Support Center, with the P6_V3 post-launch instrument response functions (IRFs). These take into account pile-up and accidental coincidence effects in the detector subsystems that were not considered in the definition of the pre-launch IRFs.
For the analysis, we selected all events within a square region-of-interest (ROI) of size 20° × 20° centred on (l,b) = (302.8°, −44.3°) and aligned in Galactic coordinates1. The data used in this work amount to 504 days of sky survey observations over the period August 8th 2008 – December 25th 2009 during which a total exposure of ~4.5 × 1010 cm2 s (at 1 GeV) was obtained for the SMC. Events of the Diffuse class (which are the least contaminated by the cosmic-ray background, see Atwood et al. 2009) and coming from zenith angles <105° (to greatly reduce the contribution by Earth albedo gamma rays, see Abdo et al. 2009g) were used. To further reduce the effect of Earth albedo, the time intervals when the Earth was appreciably within the field of view (specifically, when the centre of the field of view was more than 52° from the zenith) were excluded from this analysis. We further restricted the analysis to photon energies above 200 MeV because the effective area for Diffuse class events changes rapidly at lower energies, and up to 20 GeV because the number of counts is quite low beyond this limit.
2.2. Background modelling
At the mid-latitude position of the SMC (b ~ −45°), the gamma-ray background is a combination of extragalactic and Galactic diffuse emissions. The extragalactic component comprises resolved sources, which often can be associated with known blazars and other extragalactic source classes, and a diffuse component, which is attributed to unresolved sources and eventually intrinsically diffuse processes (Abdo et al. 2009f, 2010b).
The 1FGL catalog (Abdo et al. 2010a) has been derived from 11 months of survey data (comparable to the data volume used in this analysis) and contains 622 sources for latitudes | b | ≥30°, corresponding to a source density of 99 sources per steradian. Our ROI covers a solid angle of 0.12 sr, thus we expect about 12 resolved background sources in our field. Among those, 1−2 should spatially overlap with the SMC for an assumed angular size ~6−8° for the galaxy.
Spatial and spectral characteristics of each component of the celestial background model used in the analysis.
Within the ROI but outside the boundaries of the SMC, we found a total of 7 significant point sources, in rough agreement with expectations. One of these is the globular cluster 47 Tuc, which was found to be a strong source of gamma-rays, presumably due to its population of millisecond pulsars (Abdo et al. 2009d). Although we found no counterparts for the other 1FGL sources in the CRATES catalogue of flat-spectrum radio sources (Healey et al. 2007) using the procedure described in Abdo et al. (2009b), they are likely to be background blazars due to their high latitude positions. Searching for background sources within the SMC boundaries is more difficult due to possible confusion with point sources in the galaxy itself or with local emission maxima in its diffuse emission. However, background blazars may reveal themselves by their flaring activity. We therefore searched for excess emission above the time-averaged level on a monthly basis but found no indication for a flare coming from the direction of the SMC (see Sect. 4.1).
We modelled the celestial background emission within the ROI by fitting components for the diffuse Galactic and extragalactic backgrounds, 47 Tuc, and the 6 background objects from the 1FGL catalogue.
The LAT standard background model gll_iem_v02 for the Galactic diffuse emission was found to be inadequate for the specific SMC region. Subtracting this fitted model (and the other background components described below) from the data left strong positive residuals at low latitudes (b ~ −35°) that were found to be correlated with other tracers of the interstellar gas, such as the E(B − V) reddening map built by Schlegel et al. (1998) from COBE/DIRBE and IRAS/ISSA submillimeter observations of dust emission (the suitability of E(B − V) as gas tracer was illustrated for instance in Abdo et al. 2009i). A dedicated model for the Galactic diffuse emission in the SMC region, based on this E(B − V) map and an inverse-Compton (IC) intensity map computed using the GALPROP code for CR propagation in the Galaxy (Strong et al. 2000) and its model for the interstellar radiation field (Porter et al. 2008), turned out to improve the situation and yielded a better likelihood. The E(B − V) map is converted to hydrogen column density map using the best-fit relation obtained by Grenier et al. (2005), and a 5° × 3° region around the SMC is excluded and filled by the inpainting method described by Elad et al. (2005). As such, it is intended to trace the emission due to CRs interacting with interstellar matter in our Galaxy, and it is fitted assuming a power-law spectral shape with normalisation and spectral index as free parameters. The IC map2 gives the emission arising from CRs interacting with interstellar radiation and is fitted with the spectral shape as calculated with GALPROP.
An isotropic background component was fitted assuming a power-law spectral shape with normalisation and spectral index as free parameters. This component is designed to account for the diffuse/unresolved extragalactic emission, along with residual instrumental background.
The 6 background 1FGL objects are modelled as point sources at the positions given in the catalog and having power-law spectral shapes with normalisation and spectral indices as free parameters. Last, the globular cluster 47 Tuc lying close to the SMC (in the plane of the sky) was modelled as a point source at its SIMBAD position with an exponentially cutoff power-law spectral shape with normalisation, spectral index, and cutoff energy as free parameters (in agreement with the dedicated study of Abdo et al. 2009d). The characteristics of our complete celestial background model are listed in Table 1.
3. Emission morphology
To investigate the spatial distribution of gamma-ray emission toward the SMC, we first binned all photons into a counts map of size 20° × 20° centred on (l,b) = (302.8°, −44.3°) and aligned in Galactic coordinates. Figure 1 shows the counts map for the full ROI, with a pixel size of 0.05° × 0.05° and a smoothing of the statistical fluctuations with a 2D Gaussian kernel of width σ = 0.4°. The region is clearly dominated by 47 Tuc close to the centre, and by the Galactic diffuse emission at low latitudes.
The top panel of Fig. 2 shows the counts map for the full ROI after subtraction of the background model (by a binned maximum likelihood analysis with 10 logarithmically-spaced energy bins), with a pixel size of 0.05° × 0.05° and a smoothing of the statistical fluctuations with a 2D Gaussian kernel of width σ = 0.4°. The map suggests that the background is properly removed by our treatment. In particular, the intensity gradient due to the diffuse Galactic emission increasing as we move toward the Galactic plane as well as the 6 background 1FGL objects and 47 Tuc have disappeared. The only remaining feature is a clear excess at the position of the SMC. We emphasise here that, whatever the Galactic diffuse model used (the standard gll_iem_v02 model or our dedicated one), residual emission at the position of the SMC was observed and the excess counts were distributed in a very similar way. In addition, the characteristics of this residual emission were found to be insensitive to the inpainting or interpolation method used in the preparation of the E(B − V) map for the dedicated model.
The bottom panel of Fig. 2 is a zoom on the centre of the ROI showing residual emission over a few degrees and spatially coincident with the SMC, as traced by H I column density contours (from Stanimirovic et al. 1999). In Sect. 3.1, we show that the extension of this excess emission is real, and not just an effect of the IRF. The total number of excess 200 MeV−20 GeV photons above the background in a 4° × 4° square covering the residual excess amounts to ~450 counts, whereas the background in the same area amounts to ~1820 counts. Such modest statistics obviously limit the precision of the conclusions about the spatial distribution of the extended emission from the SMC.
The residual counts map shows several spots with intensities of ~40−50 counts/deg2, similar to the peak residual intensity associated with the SMC (~65 counts/deg2). None of these spots actually is significant except for the excess at (l,b) ~ (296°, −36°) which is at the ~4σ level. In contrast, the significance of the SMC emission is ~11σ (see Sect. 3.1), mainly because it is significantly extended while the other hot spots of the residual counts map are mostly point-like. We also checked that adding these hot spots as point sources in our model fitting did not alter the characteristics derived for the SMC emission.
 |
Fig. 1 200 MeV−20 GeV counts map of the region of interest centred on the SMC, after smoothing with a 2D Gaussian kernel with σ = 0.4°. The positions of the background point sources are marked by white circles, with circle size indicating position uncertainty. |
 |
Fig. 2 200 MeV−20 GeV residual counts maps after subtraction of the fitted celestial background model and a smoothing with a 2D Gaussian kernel with σ = 0.4°. Upper plot corresponds to the full region of interest and lower plot is a zoom on the SMC. The positions of the background point sources are marked by white circles in the top panel, with circle size indicating position uncertainty, and the SMC is traced by H I column density contours in the bottom panel. |
3.1. Geometrical models
We assessed the spatial distribution of the SMC emission using simple parameterized
geometrical models for the gamma-ray intensity distribution. We considered point-like and
2D Gaussian models with free geometric parameters, and for each model we assumed a
power-law spectrum with normalisation and spectral index also treated as free parameters.
In our procedure, the spatial and spectral parameters of the models are adjusted using a
binned maximum likelihood analysis with spatial pixels of
0.1° × 0.1° and 10 logarithmically spaced energy bins covering the
energy range 200 MeV−20 GeV. For each model of the SMC, we computed the so-called
Test Statistic (TS) which is defined as twice the difference between
the log-likelihood ℒ1 that is obtained by fitting the model on top of the
background model to the data, and the log-likelihood ℒ0 that is obtained by
fitting the background model only, i.e. TS = 2(ℒ1 − ℒ0). Under the
hypothesis that the background model satisfactorily explains our data, and if the number
of counts is high enough, the TS follows a 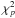 distribution with
p degrees of freedom, where p is the number of
additional free parameters in the maximization of ℒ1 with respect to those used
in the maximisation of ℒ0 (in the present case, p is the
number of free parameters of our model of the SMC). If, however, the TS takes a value that
is statistically unlikely for a
distribution with
p degrees of freedom, where p is the number of
additional free parameters in the maximization of ℒ1 with respect to those used
in the maximisation of ℒ0 (in the present case, p is the
number of free parameters of our model of the SMC). If, however, the TS takes a value that
is statistically unlikely for a 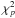 distribution, this means that
the background model is not an adequate enough representation of the observations and can
be improved by the additional SMC component (see Cash
1979).
distribution, this means that
the background model is not an adequate enough representation of the observations and can
be improved by the additional SMC component (see Cash
1979).
We first aimed at explaining the gamma-ray emission from the SMC by a combination of point sources. For this purpose we successively added point sources to our model and optimised at each step the location, flux, and spectral index of the new component by maximisation of the likelihood criterion. We stopped the procedure when adding a new point source did not improve the TS value by more than 10 (which formally corresponds to a 2σ detection for an additional model component with 4 degrees of freedom). From this method, we obtained a model of the residual emission from the SMC region consisting of 3 point sources and yielding a TS of 130.4 for a total number of 12 free parameters. This model will be referred to as 3PS hereafter. The strongest point source (PS1) is located at (l,b) = (301.7° ± 0.2°, −44.4° ± 0.2°) and alone gives a TS of 98.2 for 4 degrees of freedom. We note here that the position of PS1 approximately corresponds to the position of the source 1FGL J0101.3-7257 that is associated with the SMC in the catalog. The second point source (PS2) is located at (l,b) = (303.4° ± 0.3°, −43.6° ± 0.3°) and increases the TS to 119.2 for an additional 4 degrees of freedom. The third point source (PS3) is located at (l,b) = (302.1° ± 0.6°, −45.4° ± 0.5°) and further increases the TS to 130.4 for 4 more degrees of freedom. Quoted uncertainties correspond to 2σ intervals. These point sources correspond to the strongest maxima in the residual emission from the SMC and their positions may mark specific sites or objects in the galaxy: strong concentrations of CRs and/or gas if gamma-rays come primarily from CR-ISMinteractions, or high-energy objects like pulsars. The maxima also could be statistical fluctuations.
Next, instead of using a set of point sources we considered a 2D Gaussian shaped intensity profile to build a model that is more appropriate for extended and diffuse emission structures. Due to limited statistics, we restricted ourselves to a single Gaussian (we will see later that the photon statistics are currently insufficient to allow a more sophisticated model). The best fit 2D Gaussian has a width σ = 0.9° ± 0.5°, corresponding to a characteristic angular size of ~3°, and is centred on (l,b) = (302.1° ± 0.4°, −44.4° ± 0.4°). Quoted uncertainties correspond to 2σ intervals. The TS obtained for this model, referred to as 2DG in the following, is 136.6, which is above the TS of the 3PS model for fewer degrees of freedom (5 instead of 12). The significance of the extension, when comparing the 2DG model with respect to the single point-source PS1 model, is above 6σ. These results suggest that the emission from the SMC is diffuse in nature.
Finally, we tested the possibility that the gamma-ray emission from the SMC is not completely diffuse and has a point-source component, as might be expected for a pulsar adding its radiation to the diffuse emission arising for instance from CR-ISMinteractions. We took this hypothetical point source to be the PS1 component of the 3PS model. Essentially, we evaluated how the inferred diffuse emission is impacted when the maximum of the residual emission from the SMC is attributed to a point-like object. In this case, the best-fit 2D Gaussian was found to be quite similar in terms of position and width, but the associated flux dropped by ~20% (see Table 2). The TS value for this model is 138.8, a modest increase of 2.2 compared to the 2DG model. This attempt to improve our representation of the emission from the SMC actually reveals the limits on the spatial information that can be derived from the current set of observations. Yet, it also confirms that most of the emission is diffuse in nature: a higher TS is achieved for fewer degrees of freedom when complementing the PS1 component with an extended component rather than with more point sources, and in that case ~80% of the flux comes from the extended component.
Comparison of the different spatial models used to represent the emission from the SMC.
3.2. Tracer maps
The morphology study presented in 3.1, based on analytical intensity distributions, indicates that the emission from the SMC is of diffuse nature. This supports the idea that the observed emission can be attributed to CRs interacting with the ISM, although at this point we cannot dismiss the scenario of an ensemble of weak unresolved point sources in the galaxy like pulsars. To test the former hypothesis further, we compared our data to spatial templates that trace various components of the SMC relevant to CR-ISMinteractions. In the 200 MeV−20 GeV energy range, the gamma-ray emission from CR-ISMinteractions is dominated by the decay of neutral pions π0 created by inelastic collisions between CR nuclei and interstellar gas particles (see for example Strong et al. 2004). As tracers of CR-ISMinteractions, we therefore used a map of neutral atomic hydrogen, the major target for CR nuclei in the SMC (molecular hydrogen comprises <10% of the gas mass in the SMC, see 5.1), and a map of the ionised hydrogen that indirectly traces massive stars, that are putative accelerators of CRs (through their winds and/or explosions).
For the neutral atomic hydrogen distribution, we used the map of Stanimirovic et al. (1999) that is based on a combination of data from the ATCA and Parkes observatories. The map was converted into hydrogen column densities under the assumption of optically thin emission. The conversion of H I spectral line observations to H I column densities can actually be achieved under various hypotheses, optically thin or thick emission, with various spin temperatures in the latter case, but Stanimirovic et al. (1999) showed that the correction for self-absorption in the SMC is a relatively small effect. In addition, the photon statistics in our gamma-ray data are very likely not high enough for the above subtleties to have an important effect on the results. The adopted scheme for the preparation of the H I map proved to affect only marginally the detection significance in the analysis of the Fermi/LAT observations of the diffuse gamma-ray emission of the LMC (which has a 7 times greater flux than the SMC, see Abdo et al. 2009h).
For the ionised hydrogen tracer, we extracted from the full-sky composite Hα map of Finkbeiner (2003) a circular region of 3° in radius around the position (l,b) = (302.8°, −44.3°). A foreground Galactic contribution to the observed emission is estimated from the off-source Hα intensity in the nearby area outside our selection, and subtracted from the circular region. We note that a more accurate tracer of massive stars in the SMC could be obtained by taking into account foreground extinction by dust in the Milky Way and internal extinction in the SMC (see for instance Mao et al. 2008), but we again emphasise that the current photon statistics of our observations does not justify such efforts.
Both maps were convolved with the IRFs and fitted individually to the data (together with the background model) using a binned likelihood analysis with 10 energy bins and assuming a power-law spectral shape with free normalisation and spectral index for each model. This led to the following results: the H I map gives a TS of 120.8 while the Hα map gives a TS of 114.4, for 2 degrees of freedom in each case. The gas distribution traces the gamma-ray emission slightly better than the massive stars distribution. We note here that, even under the assumption of gamma-ray emission from CR-ISMinteractions, H I or Hα distributions may not be the best representations of the emission. Indeed, an intensity distribution correlated with CR sources, such as massive stars, would mean CRs with GeV energies are confined relatively close to their sources in a uniform hydrogen density. On the other hand, an intensity distribution correlated with the CR targets would imply a uniform CR density. Yet, while the CR diffusion length may indeed be short (Abdo et al. 2009h), we know that in the Milky Way both the gas and the CRs are not uniformly distributed and this is likely to be the case in the SMC as well.
As in 3.1 for the 2D Gaussian model, we tested the possibility that the gamma-ray emission from the SMC has a composite origin and includes at least one strong point source. We again assumed this hypothetical point source to be the PS1 component of the 3PS model, and we complemented it with the tracer maps. In this case, the PS1+H I model gives a TS of 135.2 while the PS1+Hα model gives a TS of 128.0. The conclusions actually are the same as in 3.1: an extended component in addition to PS1 is more significant than other point sources like PS2 and PS3, and in that case ~80% of the flux is associated with that extended component (see Table 2).
3.3. Correlations
The results obtained for the various spatial models tested to account for the SMC emission are summarised in Table 2. The model that best fits the data is the 2DG model, which gives the highest detection significance at a level of 10.9σ. Yet, the photon statistics of the set of observations used here are not sufficient to conclusively distinguish the various extended emission morphologies tested in this study.
In Fig. 3, we plot the extent of the 2DG model, computed as the sum of the σ of the Gaussian and the uncertainty in the position of its centroid, over the smoothed gamma-ray emission from the SMC. Although being statistically less likely than the 2DG model, the 3PS model gives indications on emission maxima that may correspond to particular sites or objects in the galaxy. We therefore marked these positions and their typical 2σ uncertainty domains in Fig. 3. For comparison, we also show in Fig. 3 the Hα emission contours of the SMC and the locations of the currently-known pulsars and SNRs3.
The position of the maximum of the emission is consistent in both the 3PS and 2DG models. Even when a hypothetical point source is placed at the emission maximum, the best-fit 2D Gaussian accounting for the remaining flux is centred at about this same position (see model PS1+Gaussian in Table 2). From Figs. 2 and 3, this place does not seem to correspond to any particular site or object in the SMC; it is neither a strong concentration of gas or massive stars, nor the direction to one of the pulsars or SNRs of the galaxy. However, it is consistent with the centre of supergiant shell 304A (Stanimirovic et al. 1999), located at (l,b) = (301.8°, −44.5°). Although they are not highly significant (detection at the 2−3σ level), we note that PS2 is found near the peak hydrogen density and close to the centre of supergiant shell 37A (Stanimirovic et al. 1999), while the position of PS3 is consistent within uncertainties with NGC346, the most active star-forming region of the SMC.
Regarding the tracers of CR-ISMinteractions, both the H I and Hα maps are relatively good tracers of the extended emission from the SMC. The photon statistics of the available SMC observations are not sufficient to conclusively distinguish one tracer from the other. In the case of the LMC, the gamma-ray emission is found to be strongly correlated with massive star forming regions and poorly correlated with gas density (Abdo et al. 2009h). Additional observations of the SMC with Fermi are needed to clarify the differences and similarities in the gamma-ray emission of the two Magellanic Clouds. From these, important information will very likely be obtained about the origin and transport of the CRs.
 |
Fig. 3 Residual counts map after subtraction of the fitted celestial background model and smoothing with a 2D Gaussian kernel with σ = 0.4°. Logarithmically-spaced Hα emission contours of the SMC are shown, together with the locations of the currently-known pulsars and SNRs in the galaxy (stars and points respectively). Black circles mark the extent of the 2DG model and the positions of the components of the 3PS model (including in all cases the 2σ uncertainty in the position). |
4. Emission lightcurve and spectrum
4.1. Variability
As noted earlier, emission from within the SMC boundaries could arise from background blazars and be incorrectly interpreted as local emission maxima of the diffuse emission from the galaxy. Background blazars may however reveal themselves by their flaring activity and we therefore searched for any excess emission above the time-averaged level.
We first considered the time variability of the integrated gamma-ray emission from the SMC by using the extended 2DG model (on top of our background model). As before, the spectrum of the 2DG model was assumed to be a power law, with the spectral index now fixed to the average value obtained from the fit to the entire data set. The same was done for 47 Tuc to allow comparison (and check that no cross-talk occurs between these two neighbouring sources), while the parameters of all other components of our background model were fixed to the average values obtained from the fit to the entire data set. The light curves of the 2DG and 47 Tuc models were then derived on a monthly basis. The result is shown in Fig. 4. There is no indication for a flare coming from the direction of the SMC or from 47 Tuc (in agreement with the dedicated analysis of the latter, see Abdo et al. 2009d).
Since background blazars obviously would appear as point-like sources, we also derived the light curves for the three point sources of the 3PS model. In this case as well, we found no indication for flaring activity from any of the three directions.
 |
Fig. 4 Monthly light curve of the SMC obtained with the 2DG spatial model and a power-law spectral shape with fixed index. Also shown for comparison is the light curve of 47 Tuc. |
4.2. Spectrum and flux
 |
Fig. 5 Spectrum of the SMC. The LAT data points (in black) come from independent fits of the 2DG plus background models in 6 different energy bins. The curves correspond the components and total of a spectral model of CR-ISMinteractions in the SMC fitted to the data using a binned maximum likelihood analysis (see text). |
Best-fit spectral parameters obtained from a maximum likelihood analysis with spatial model 2DG.
So far the analysis was done assuming that the spectrum of the SMC emission is well described by a power law. To determine the spectrum of the gamma-ray emission from the SMC without any assumption on the spectral shape, we fitted our background and 2 DG models to the data independently in 6 logarithmically-spaced energy bins covering the energy range 200 MeV−20 GeV. The result is shown in Fig. 5. The spectrum is relatively flat (Γ ~ 2) over most of the energy range, with a possible maximum around one GeV and a break or cutoff around a few GeV.
To determine the integrated gamma-ray flux of the spectrum, we fitted both simple power-law and exponentially cutoff power-law spectral models of the form N(E) = k(E / E0)−Γexp(−E / Ec) to the data by means of a binned maximum likelihood analysis over the energy range 200 MeV−20 GeV. This analysis is more reliable than fitting the spectra of Fig. 5 directly since it accounts for the Poissonian statistics of the data. The spectral parameters thus obtained are listed in Table 3. The best-fit model is the exponentially cutoff power law. The improvement over the simple power-law model is ΔTS = 6 for one more degree of freedom, which corresponds to a significance of 2.4σ only. This is most likely because the limited statistics at high energies prevent the clear detection of a cutoff in the spectrum. In the following, we will use the flux value associated with the exponentially cutoff power-law model because it is more relevant to the physical sources we will consider than the simple power-law model: we indeed discuss CRs-ISM interactions as a likely source of the SMC emission and the corresponding radiation is usually dominated by a ~GeV bump due to π0 decay, and this feature is better represented with an exponentially cutoff power-law model (see Sect. 5.1 and Fig. 5); alternatively, we consider pulsars as another plausible source of the SMC emission and the typical spectrum of the latter is characterised by a cutoff at a few GeV (see Sect. 5.2). We note that the relatively small difference between both spectral models ensures that the morphological analysis of the SMC emission presented in 3, and performed with an assumed simple power-law spectral shape, remains valid.
The integrated flux of the best-fit model is (1.9 ± 0.2) × 10-8 ph cm-2 s-1 for photons in the 200 MeV−20 GeV range, and (3.7 ± 0.7) × 10-8 ph cm-2 s-1 for photons in the 100 MeV−500 GeV range, all uncertainties being purely statistical. Since we restricted our analysis to photons >200 MeV the extrapolation down to 100 MeV may introduce a systematic uncertainty if the low-energy spectrum of the source deviates from our fitted model. In addition, systematic uncertainties on the LAT instrument response function translate into systematic uncertainties on the spectral parameters that are given in Table 3. The >100 MeV flux is provided to facilitate comparison with the upper limit from CGRO/EGRET. Sreekumar et al. (1993) gives an upper limit of 5.0 × 10-8 ph cm-2 s-1 from the first years of observations of the SMC with CGRO/EGRET, which is compatible with our extrapolated flux, whatever the spectral model used.
5. Gamma-ray sources in the SMC
Cosmic-ray interactions with the ISM may well be the primary source of gamma rays in the SMC. The resulting emission is expected to be intrinsically diffuse in nature and our analysis indeed suggests that the gamma-ray emission from the SMC does not originate in a small number of individual point sources. When trying to account for the emission from the SMC with a combination of point sources, we detected only three point sources with significance above 2σ within the boundaries of the galaxy. In contrast, we found a model with less degrees of freedom that resulted in a larger TS value when we allowed for the source to be extended (model 2DG). The SMC emission is therefore more likely diffuse in nature. Alternatively, it could be composed of a large number of unresolved and faint sources that can not be detected individually by Fermi/LAT. In the following, we examine these two possibilities in turn.
5.1. CRs – ISM interactions
In this section, we make the assumption that a large fraction of the gamma-ray emission
from the SMC indeed originates from CRs interacting with the interstellar gas and
radiation field. We first computed the average integrated
>100 MeV gamma-ray emissivity per hydrogen atom of the SMC using
the following relation: 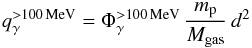 (1)where
Φγ is the integrated >100 MeV
photon flux from the SMC, Mgas is the total gas content of the
galaxy, d is the distance to the galaxy and
mp is the proton mass. In a more practical form (where
>100 MeV is implied):
(1)where
Φγ is the integrated >100 MeV
photon flux from the SMC, Mgas is the total gas content of the
galaxy, d is the distance to the galaxy and
mp is the proton mass. In a more practical form (where
>100 MeV is implied): 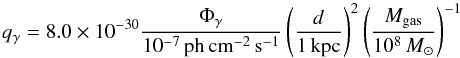 (2)where
the emissivity qγ is in
ph s-1 sr-1 H-1. With Eqs. (1) and (2), we focus on the gamma-rays produced by the interaction of CRs with
interstellar matter. These are produced by two processes: decay of neutral pions
π0 created by inelastic collisions between CR nuclei and ISM
gas particles, or Bremsstrahlung of CR electrons and positrons. In the local Galactic
conditions, the contribution of Bremsstrahlung becomes small beyond a few 100 MeV (see for
instance Abdo et al. 2009e), and we will therefore
consider in the following that gamma-rays from interactions with interstellar matter are
mostly due to the hadronic component of CRs. The questions of the average electron
spectrum and electron-to-proton ratio in the SMC are addressed in Sects. 6.1 and 6.2.
(2)where
the emissivity qγ is in
ph s-1 sr-1 H-1. With Eqs. (1) and (2), we focus on the gamma-rays produced by the interaction of CRs with
interstellar matter. These are produced by two processes: decay of neutral pions
π0 created by inelastic collisions between CR nuclei and ISM
gas particles, or Bremsstrahlung of CR electrons and positrons. In the local Galactic
conditions, the contribution of Bremsstrahlung becomes small beyond a few 100 MeV (see for
instance Abdo et al. 2009e), and we will therefore
consider in the following that gamma-rays from interactions with interstellar matter are
mostly due to the hadronic component of CRs. The questions of the average electron
spectrum and electron-to-proton ratio in the SMC are addressed in Sects. 6.1 and 6.2.
The SMC is a gas-rich system (compared to typical spiral galaxies, see Hunter 1997). The total mass of neutral atomic hydrogen (HI) has been determined from 21 cm radio observations with the Parkes and ATCA facilities; after correction for self-absorption, it was found to amount to 4.2 × 108M⊙ (Stanimirovic et al. 1999). The total mass of molecular hydrogen (H2) has been determined from far-infrared observations with the Spitzer space telescope and found to be 3.2 × 107M⊙. The ratio of molecular to atomic gas is therefore 2−3 times lower than in spiral galaxies (Leroy et al. 2007). We thus obtain a HI+H2 gas mass of ~4.5 × 108M⊙. This estimate, combined with the gamma-ray flux found in 4.2, translates into an average gamma-ray emissivity >100 MeV of (2.5 ± 0.5) × 10-27 ph s-1 sr-1 H-1 for an adopted distance to the SMC of 61.5 kpc (Cioni et al. 2000; Hilditch et al. 2005; Keller & Wood 2006), with the uncertainty reflecting only the uncertainty on the gamma-ray flux.
The average gamma-ray emissivity of the SMC is a factor of 6−7 times smaller than the emissivity qγ = (1.63 ± 0.05) × 10-26 ph s-1 sr-1 H-1 that has been determined with Fermi/LAT for the local ISM of our own Galaxy (Abdo et al. 2009e). However, these quantities are not directly comparable for the reasons we list below.
First, our derivation of the average gamma-ray emissivity per H-atom of the SMC implicitly assumes that all gamma-rays are produced by π0 decay after hadronic interactions. Yet, we know from the study of the Galactic high-energy diffuse emission that another process of leptonic origin, the inverse-Compton scattering, can account for a certain part of the flux in the 200 MeV−20 GeV energy range. The contribution of inverse-Compton was subtracted prior to the determination of the local emissivity using predictions from the GALPROP model, but the average emissivity of the SMC was computed from a mix of π0 decay and inverse-Compton gamma-rays in unknown proportions.
Second, some of the observed emission from the SMC may arise from unresolved point sources like pulsars, and this would overestimate the flux due to CRs interacting with interstellar matter (see Sect. 5.2). In contrast, the local emissivity was determined for high-latitude regions of the Galaxy, mostly within 1 kpc from the solar system. The observations were cleaned for point sources (at least for the point sources detected by the LAT over the first 6 months) and it seems reasonable to assume that the emission from the small volume under investigation was left relatively free of contamination by isolated objects.
Last, the emissivity is computed from the mass of hydrogen and as evident from Eq. (1), the higher the mass for a given gamma-ray flux, the lower the emissivity. The value we used for the SMC (4.5 × 108M⊙) is probably a lower limit of the total mass of gas in the galaxy. First, we neglected the ionised gas, which can account for up to 10% (in the case of the MW, see Cordes & Lazio 2002). More important is the possibility that the total SMC gas mass is not completely traced by the usual methods. This additional gas could be in the form of cold atomic gas being optically thick (thus not detectable at 21 cm), or molecular gas free of CO (thus not detectable at 2.6 mm). The latter scenario would be particularly relevant for a low-metallicity system such as the SMC, in which CO may be underabundant and/or not efficiently shielded from dissociating radiation because of a low dust content. In contrast, the high-latitude observations of the solar neighbourhood are probably not too much affected by this dark gas because the latter surrounds the CO clouds and is thus mostly confined to the Galactic plane. In their analysis of a region of the second Galactic quadrant, Abdo et al. (2009i) found that most of the dark gas is confined to Galactic latitudes | b | ≤20°, whereas Abdo et al. (2009e) derived the local emissivity from a region of the third Galactic quadrant with | b | ≥22°. In addition, it is worth noting that Abdo et al. (2009e) found good agreement between the emissivity inferred from the diffuse gamma-ray emission and the emissivity computed from the measured spectrum of CRs without resorting to any dark gas contribution.
On the whole, this means that the true average emissivity for the SMC is very likely below the above-mentioned value. The average gamma-ray emissivity of the SMC should therefore be regarded as being at least 6−7 times smaller than the local value. We emphasise, however, that depending on the actual relative distributions of gas and CRs in the SMC, the emissivity may reach higher values in some places. This was clearly illustrated in the recent Fermi/LAT study of the LMC. The average emissivity of the LMC is found to be 2−4 times smaller than the local value. Yet, the gamma-ray emission from the LMC is observed to be poorly correlated with the gas density, and this translates into a gamma-ray emissivity being higher than the local value in several places (see Fig. 10 in Abdo et al. 2009h). For the SMC, the current photon statistics are insufficient to build an emissivity map of the galaxy, so we must confine ourselves to the global average.
In comparing the gamma-ray emissivities per H-atom of the local Galaxy and the SMC, one should also not forget the effect of the chemical composition of both the ISM and the CRs. The latter is usually taken into account through the so-called nuclear enhancement factor ϵN, which is a multiplicative factor applied to the emissivity due to proton-proton reactions only. Recent calculations by Mori (2009) yielded ϵN = 1.85 for CRs having the composition measured at Earth and interacting with an ISM of solar metallicity. The Z = 0.2 Z⊙ metallicity of the SMC (Dufour 1984) corresponds to ϵN = 1.72, so we can consider that the effect of the low-metallicity of the SMC on the gamma-ray emissivity is negligible.
Our result, together with the above arguments, indicates that the average density of CR nuclei in the SMC is at least 6−7 times smaller than in the MW at the position of the solar system if the energy spectrum of both populations of CR nuclei are assumed similar. Yet, there is no reason for the CR spectrum not to vary from one galaxy to another. Indeed, the spectrum of the large-scale, steady-state population of CRs is very likely shaped primarily by transport, since we do not expect the diffusive shock acceleration mechanism to be strongly different, and transport of CRs may be highly dependent on characteristics of the host galaxy like geometry, magnetic field strength and topology, or level of interstellar and magnetic field turbulence. The actual spectrum of CR nuclei can be derived from the shape of the gamma-ray spectrum. However, our data do not have sufficient statistics to be conclusively constraining in this regard. These issues are addressed in more detail in 6.2 through modelling of the gamma-ray emission from CR-ISMinteractions in the SMC.
5.2. Isolated sources
The current Fermi/LAT observations of the SMC are limited in their capability to rule out the possibility that a sizeable fraction of the diffuse gamma-ray emission is due to a large number of unresolved and faint sources. In this section, we estimate that contribution to the observed emission.
The 1FGL catalog contains a total of 1451 sources, about half of which were associated with candidate sources. Most of the associated sources are active galactic nuclei, and the remaining associated sources are mostly Galactic objects (see for instance Abdo et al. 2009b). Although there is still a large number of unidentified sources, many of which lie in the Galactic plane, the Galactic population of gamma-ray sources seems to be dominated by pulsars. In the following, we will therefore focus on this class of object as possible sources of gamma-ray emission in the SMC.
The first Fermi/LAT catalogue of gamma-ray pulsars based on the first six months of LAT observations contains 46 objects, most of which are normal non-recycled pulsars (Abdo et al. 2009a). From distance estimates and using a flux correction factor fΩ = 1, the observed fluxes were converted into gamma-ray luminosities >100 MeV approximately ranging from 1034 to 1036 erg s-1 for most normal non-recycled pulsars. The inferred luminosities suffer from large uncertainties on the distance estimates, which are manifest from the >100% efficiencies implied for several objects. Another source of error is the assumption of a uniform beaming factor fΩ = 1 across the sky, which is not realised in many emission models and thus overestimates the gamma-ray luminosity in some cases. The characteristic ages for most normal non-recycled pulsars range from 104 to 106 yrs, and their typical spectrum has been found to be an exponentially cut-off power law with index 1.4 and cut-off energy 2.2 GeV. In the following, we will assume that normal gamma-ray pulsars have a mean luminosity of 1035 erg s-1 and a mean lifetime of 105 yrs. Adopting the above mentioned mean spectrum, the energy luminosity of 1035 erg s-1 translates approximately into a photon luminosity of 1038 ph s-1.
Crawford et al. (2001) estimated the number of active radio pulsars in the SMC to 5100 ± 3600, under the assumption that radio pulsars form at the same rate as SNII and have a mean lifetime of 10 Myr. This would imply 51 ± 36 gamma-ray pulsars, under the hypothesis that all young pulsars are gamma-ray emitters with a lifetime of 0.1 Myr. We currently know 6 pulsars in the SMC4, 5 discovered in radio and 1 in X-rays (Manchester et al. 2005; Lamb et al. 2002). Most of these pulsars have characteristic ages above 1 Myr and may therefore be too old for substantial gamma-ray emission. A possible exception is J0100-7211, which is an Anomalous X-ray Pulsar candidate with an estimated age of 6800 yrs (McGarry et al. 2005).
A mean luminosity of 1038 ph s-1 per pulsar in the SMC translates into a photon flux at Earth of ~2 × 10-10 ph cm-2 s-1. The 51 ± 36 gamma-ray pulsars would therefore give rise to a gamma-ray flux of (1.0 ± 0.7) × 10-8 ph cm-2 s-1, to be compared with the observed value of (3.7 ± 0.7) × 10-8 ph cm-2 s-1. Taking a lifetime of 1 Myr instead of 0.1 Myr for gamma-ray pulsars leads to the conclusion that the entire SMC emission can be accounted for by pulsars. Yet, these estimates suffers from large uncertainties, first in the birth rate of gamma-ray pulsars and then for the gamma-ray emission from a typical pulsar population. A more reliable calculation would require a complete population synthesis including, in particular, the time evolution of the gamma-ray luminosity. However, such a simulation is quite sensitive to the as yet unsettled magnetospheric processes governing high-energy emission (see Abdo et al. 2009a, and references therein). Nevertheless, the above calculation shows that a substantial fraction of the observed emission could be accounted for by normal pulsars. Adding other objects like millisecond pulsars would further increase the contribution of isolated sources.
On the whole, this means that the density of CRs in the SMC may be even smaller than the values discussed previously, and hence significantly below the local value. This also implies that the gamma-ray emission of the SMC may be of a different composition compared to the Milky Way. In the Galaxy, only 10−20% of the gamma-ray emission can be attributed to isolated sources while the rest is of diffuse nature, but in the SMC the proportions may be inverted. Such a scenario would require a lower mean SN rate per unit volume (to form gamma-ray pulsars without increasing the mean CR injection rate per unit volume) and/or a lower confinement of CRs (to reduce the accumulation of particles in the ISM). We will discuss this in more detail in 6.3.
On that issue, we note that the refinement of the emission morphology that will result from increased exposure may allow the assessment of the relative contributions of each kind of source. Also, the typical spectrum of pulsars has a specific shape that may not be consistent with the better-defined high-energy spectrum that will follow from better statistics.
6. The CR population of the SMC
In this section, we focus on the implications in terms of CR population of the detection of the SMC in gamma-rays. We again assume that the entire emission is due to CR-ISMinteractions and we derive the characteristics of the CR population of the SMC using a more detailed approach than the simple emissivity calculation performed in Sect. 5.1. In order to broaden the issue, we investigated the population of CR electrons in the SMC. Compared to CR nuclei, CR electrons undergo severe radiative energy losses. While the main loss mechanism for nuclei above 1 GeV is escape from the host galaxy, the CR electrons lose the bulk of their energy through inverse-Compton scattering of the interstellar radiation field and synchrotron radiation on the galactic magnetic field. Hence, the most energetic CR electrons do not travel far from their source regions before losing most of their energy. By considering the conditions for the CR nuclei and electrons in the SMC, it may be possible to assess if the lower density of CRs in the SMC is due to injection or to transport. In addition, we discuss the aspects of injection and/or transport that may drive the large-scale properties of the CR population of the SMC and their differences with respect to the Galaxy.
6.1. Constraints from synchrotron emission
When accelerated in the large-scale magnetic field of a galaxy, CR electrons manifest
themselves through diffuse synchrotron emission. From Longair (1994), the synchrotron radiation spectrum of a power-law energy
distribution of electrons is (with some changes in the units): 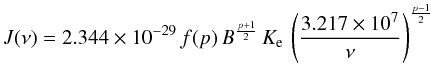 (3)where
ν is the radiation frequency in Hz,
J(ν) is the emissivity per unit volume in
W m-3 Hz-1, B is the magnetic field in
μG,
Ne(E) = Ke(E / E0)−p
is the energy spectrum of CR electrons in cm-3 GeV-1 and
f(p) is a numerical factor depending on the slope of
the particle spectrum. Then, the intensity of a given object is given by:
(3)where
ν is the radiation frequency in Hz,
J(ν) is the emissivity per unit volume in
W m-3 Hz-1, B is the magnetic field in
μG,
Ne(E) = Ke(E / E0)−p
is the energy spectrum of CR electrons in cm-3 GeV-1 and
f(p) is a numerical factor depending on the slope of
the particle spectrum. Then, the intensity of a given object is given by: 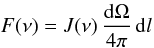 (4)where dΩ is the
solid angle subtended by the diffuse source, in sr, and dl is the mean
depth of the emitting medium along the line of sight, in m. The intensity
F(ν) is in W m-2 Hz-1 (which
corresponds to 1026 Jy).
(4)where dΩ is the
solid angle subtended by the diffuse source, in sr, and dl is the mean
depth of the emitting medium along the line of sight, in m. The intensity
F(ν) is in W m-2 Hz-1 (which
corresponds to 1026 Jy).
The radio continuum emission from galaxies usually has a steep spectrum at lower frequencies, due to synchrotron emission from non-thermal particles, followed by a flatter spectrum at higher frequencies, due to free-free emission from thermal particles (with a typical index of −0.1). Haynes et al. (1991) determined a spectral index of −0.85 ± 0.10 for the non-thermal radio continuum emission of the SMC, with a flux density5 of 34 ± 6 Jy at 1.4 GHz.
From Eq. (3), the radio measurements give p = −2.7 ± 0.2 for the average spectral index of the CR electron distribution of the SMC. The normalisation of the CR electron spectrum can be obtained from the flux density at a given frequency if we know the magnetic field strength and the spatial distribution of the synchrotron-emitting medium (see Eq. (3)).
The large-scale magnetic field of the SMC was recently studied by Mao et al. (2008) using optical starlight polarisation and rotation measures for background extragalactic radio sources. The authors determined that the coherent magnetic field in the SMC has a strength of ~1.7 μG and lies almost entirely in the plane of the sky. The SMC also seems to have a random magnetic field with an estimated strength of ~2−3 μG depending on the method used. The observed synchrotron emission from the SMC actually arises from the total magnetic field projected onto the plane of the sky Btotal, ⊥ , and Mao et al. (2008) estimated this component to have a strength of ~3 μG.
The 3D structure of the SMC is quite controversial and this directly affects the interpretation of the radio synchrotron emission. The size and appearance of the SMC in the sky is biased by observations of young stars and gas, which suggest a very irregular and asymmetric shape while the old stellar population seems to follow a very regular distribution (Gonidakis et al. 2009). Yet, for the purpose of interpreting radio synchrotron emission from CR electrons, young, massive stars are more relevant than old stars since they are putative sources of CRs. From a visual inspection of the radio maps of the SMC, it appears that the emitting regions can be enclosed in a circle of 5° in diameter corresponding to a solid angle of dΩ = 6 × 10-3 sr. However, the majority of the emission likely comes from half of this solid angle. The issue of the extension of the SMC along the line of sight is important as well. Past estimates of the depth of the galaxy range from a few kpc to a few 10 kpc (see the review by Stanimirović et al. 2004, Sect. 4.2). Currently, lower values are favoured. The deviations of pulsating red giants in the SMC from the mean period-luminosity relations indicate a distribution over a distance range of 3.2 ± 1.6 kpc (Lah et al. 2005). This result is reminiscent of the distance dispersion of ± 3.3 kpc found by Welch et al. (1987) from an analysis of Cepheid variables in the SMC (and put forward as an argument that the SMC is not extended beyond its tidal radius and is therefore not undergoing disintegration). In the following, we will adopt a mean depth along the line of sight of dl = 4 kpc. In our further calculations, however, we will also consider larger depth such as the 10 ± 6 kpc found by Mao et al. (2008) when deriving the line of sight magnetic field of the SMC from rotation measures.
From the above data and Eqs. (3) and (4), we computed the normalisation factor for the CR electron population of the SMC and obtained Ke = 2.5 × 10-12 cm-3 GeV-1. This corresponds to an energy density of wCR,e = 3.6 × 10-3 eV cm-3 for particles above 1 GeV with a spectral index of p = −2.7. For comparison, the local energy density of CR electrons estimated from the recent Fermi/LAT measurement is wCR,e ≃ 6.0 × 10-3 eV cm-3 for particles above 1 GeV with a spectral index of p = −3.0 (Abdo et al. 2009c, assuming the spectral slope measured over the 20 GeV−1 TeV range extends down to 1 GeV).
The average density of CR electrons in the SMC from this argument is ~60% of the Galactic local value. Yet, when taking into account the uncertainties on the radio data (spectral index and intensity), we find that the CR density derived for the SMC undergo relative variations from −50% to +70%. Also, the depth of the galaxy may be larger than the 4 kpc we adopted and assuming a depth of 10 kpc instead of 4 kpc would decrease the CR electron energy density by 60%. On the other hand, the size of the synchrotron emitting region may be smaller by 50% compared to the value used so far and this would nearly compensate an increased depth.
Large uncertainties therefore affect the derivation of the CR electron density in the SMC from radio synchrotron observations. At present, it is consistent with the local value and with a 6−7 reduction factor as observed for CR nuclei (the latter case implying the same electron-to-proton ratio as measured locally). CR electrons also manifest themselves through inverse-Compton gamma-ray emission, which offers an alternative to address the above questions. However, as discussed in the next section, the statistical limitations of the current high-energy observations are not very constraining either.
6.2. Constraints from gamma-ray emission
We simulated a gamma-ray spectrum for the SMC using a one-zone model of CR-ISMinteractions that takes into account π0 decay following proton-proton interactions, Bremsstrahlung from CR electrons and inverse-Compton scattering of cosmic-ray electrons on optical, infrared and cosmic microwave background photons. In this model, the various quantities involved in the CR-ISMinteractions are represented as average values over a given volume or gas mass, depending of the emission process. For the CR population, we used the proton, electron and positron spectra presented in Abdo et al. (2009e) for the local Galactic environment, with a global scaling factor to account for the CR density difference between the SMC and the local MW (see below).
We calculated the π0 production by proton-proton interactions following the prescription of Kamae et al. (2006). The π0 and Bremsstrahlung emissivities were calculated assuming an average SMC metallicity of Z = 0.2Z⊙ (Dufour 1984), which implies a nuclear enhancement factor of ϵN = 1.72 for the π0 emissivity (Mori 2009). These average emissivities are then multiplied by the the total hydrogen mass of the SMC (4.5 × 108M⊙, see Sect. 5.1) to give the total π0 and Bremsstrahlung gamma-ray luminosity.
The inverse Compton component was calculated from the method described by Blumenthal & Gould (1970) using the CMB, optical and infrared interstellar radiation fields (ISRFs). The optical and infrared ISRFs were taken from the GALPROP model of the MW (Porter et al. 2008) and averaged over a cylindrical volume with a 15 kpc radius and a 4 kpc thickness. The resulting average optical and infrared ISRFs were rescaled according to the stellar luminosity density and observed infrared emission for the SMC (factors of ~1.2 and ~1.25 respectively, see Bot et al. 2004). The inverse Compton gamma-ray luminosity was then calculated assuming that the CR electrons of SMC interact with the target photons in a cylinder with a 1.6 kpc radius (radius of the SMC gamma-ray emission, see 3.1) and a 4 kpc height (depth of the SMC along the line of sight, see 6.1).
The spectral profile thus obtained is associated with the 2DG intensity distribution to form a complete model for the SMC emission. The scaling factor rc of our model with respect to the data, which we refer to as the cosmic-ray enhancement factor, is then a direct measure of the average density of CRs in the SMC with respect to that in the vicinity of the Earth. From a binned maximum likelihood analysis, we found rc = 0.14 with a statistical uncertainty of ± 0.01. Systematic errors due to uncertainties in the effective area of the instrument amount to ± 0.01, and an additional uncertainty of ± 0.01 comes from the uncertainty on the extent of the source (the σ of the 2D Gaussian model). The rc factor obtained from this spectral modelling is consistent with the estimate made in 5.1.
From this one-zone model of CR-ISMinteractions in the SMC, the assumption of CR spectra and CR electron-to-proton ratio identical to the locally observed values does not conflict with the gamma-ray spectrum.
6.3. Injection and transport
The average density of CR nuclei in the SMC seems to be at least 6−7 times smaller than in our local environment, if we assume a similar spectrum for the particles. The energy distribution of CR nuclei is poorly constrained by our gamma-ray spectrum. The density of CR electrons in the SMC was found to be ~2 times smaller than in our local environment, but due to uncertainties on the radio data and other parameters, it could be down to 10 times smaller or consistent with the local value. The specifics of CR injection and transport in the SMC with respect to the Milky Way lead to lower average CR densities and possibly also to a higher electron-to-proton ratio, although a similar electron-to-proton ratio cannot be excluded.
Similar results were obtained in a recent study of the LMC based on Fermi/LAT observations. We report here the main conclusions of that work for comparison. The gamma-ray emission from the LMC is clearly of diffuse nature, with an extension of angular size ~3.5°. The total flux from the LMC is (2.6 ± 0.2 ± 0.4) × 10-7 ph cm-2 s-1, which is about 7 times the flux we obtained for the SMC. The spectrum was found to be well represented by a power law with an index of about −2.0 and a cut-off at a few GeV, quite similar to what we obtained for the SMC. These observations, combined with the properties of the LMC, imply a CR density that is 2−4 times smaller than the local Galactic value, possibly even less. Regarding CR electrons in the LMC, the authors did not explicitly estimate their density but they showed that the assumption of a CR electron-to-proton ratio identical to the locally observed value does not conflict with the gamma-ray spectrum or the radio synchrotron observations of the LMC.
A lower density of CR nuclei in a steady-state system can result from a lower rate of CR injection and/or a reduced confinement in the volume of the galaxy. To first order, the injection rate can be simply related to the rate of supernovae or to the rate of star formation (Pavlidou & Fields 2001), because we do not expect the diffusive shock acceleration process occurring in supernova explosions to strongly differ from one galaxy to another. Conversely, CR confinement may be highly dependent on some characteristics of the galaxy like geometry, magnetic field strength and topology or the presence of a galactic wind and/or halo. In the following, we discuss those specifics of the SMC that may explain the lower CR densities.
The star formation history derived by Harris & Zaritsky (2004) from UBVI photometry of over 6 million SMC stars show that the star formation rate (SFR) in the SMC over the last Gyr has an underlying constant value of ~0.1 M⊙ yr-1, with episodes of enhanced activity at 60 and 400 Myr where the value was increased by factors of 2−3. Based on far-infrared dust emission and Hα emission, Wilke et al. (2004) deduced a present-day SFR of ~0.05 M⊙ yr-1, in good agreement with the value of Harris & Zaritsky (2004) and with previous estimates. By comparison, a review of the SFR estimates for the Milky Way by Diehl et al. (2006) shows that a value of 4 ± 2M⊙ yr-1 can be adopted. The SFR in our Galaxy is therefore about 40 times higher than in the SMC. We note that a similar scaling is found for the supernova rates: the commonly adopted value for the Milky Way is ~3 per century, while the estimates for the SMC are ~0.1 per century (Tammann et al. 1994).
Yet, for the issue of steady-state CR density in a given system, it is not the absolute rate of star formation or supernovae that matters, but the rate by unit volume. Estimating the volumes in which star formation occurs is not an easy task, especially for the SMC, the exact morphology of which is still unclear (see Sect. 6.1). So instead of trying to compute these volumes, we used the interstellar radiation field density as an indicator of the star formation per unit volume. The average temperature of the dust is observed to be higher in the SMC than in the Milky Way, suggesting a stronger interstellar radiation field (Stanimirovic et al. 2000; Wilke et al. 2004). This could be due to the lower metallicity of the SMC, but may also be the consequence of a higher SFR per unit volume. If the rate of CR injection per unit volume actually is higher in the SMC than in the Galaxy, then the average lower CR densities we inferred for the SMC could be due to some properties of their transport in the ISM.
In a basic picture, the diffusion of CRs in the ISM is governed by two parameters: the spatial diffusion coefficient Dxx and the confinement volume characteristic size lconf (both parameters being energy-dependent). The main ISM characteristic thought to affect Dxx is the B / δB parameter (see the review by Strong et al. 2007). From the estimate of the random and ordered magnetic field strengths in the SMC by Mao et al. (2008), there is no reason to think that Dxx in the SMC could be substantially different from Dxx in the Galaxy. We are therefore left with the confinement volume size lconf as the potential explanation for the lower CR density of the SMC. Below, we make a first-order comparison of this parameter for the SMC and MW.
Neglecting energy losses, the steady-state average CR density in a galaxy can be
approximated by (see for instance Pavlidou &
Fields 2001): 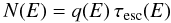 (5)where
τesc is the characteristic escape time and
q(E) the source term. For a diffusive process, the
confinement volume size can be approximated by:
(5)where
τesc is the characteristic escape time and
q(E) the source term. For a diffusive process, the
confinement volume size can be approximated by:
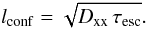 (6)From spectral modelling,
we found that the mean CR density in the SMC is ~15% or less the CR density in the local
Galaxy. Assuming a similar diffusion coefficient and a potentially higher injection rate
in the SMC, the above equations imply a mean CR confinement time in the SMC of ~15% the
Galactic value, which is typically ~107 yrs, and a mean CR confinement volume
size in the SMC at least 3 times smaller than in the MW.
(6)From spectral modelling,
we found that the mean CR density in the SMC is ~15% or less the CR density in the local
Galaxy. Assuming a similar diffusion coefficient and a potentially higher injection rate
in the SMC, the above equations imply a mean CR confinement time in the SMC of ~15% the
Galactic value, which is typically ~107 yrs, and a mean CR confinement volume
size in the SMC at least 3 times smaller than in the MW.
Similar conclusions can probably be drawn for the LMC. Discussing the possible physical reasons to this is beyond the scope of that paper. It may be a simple size effect like the surface-to-volume ratio (injection being proportional to volume while escape is proportional to surface), or a more sophisticated process involving the equilibrium of the various galactic components (CRs, gas and magnetic field resisting to gravitational attraction). It should be noted that the comparison of the Magellanic Clouds to the Milky Way in terms of a large-scale characteristic such as the CR population may be complicated by the fact that smaller galaxies are probably more affected by the stochasticity of star formation and by tidal interactions with their neighbours. The concept of steady-state CR population may simply not apply in these cases.
These rough estimates, however, hold for a mean CR density computed under the assumption of a uniformly distributed CR population. As mentioned in 5.1, if CRs are poorly correlated with the gas, then the CR density can be expected to vary over the SMC volume and may well reach values above the local Galactic one. If some correlation of the CRs with supergiant shells exists, as mentioned in 3.3 and as was found to be the case in the LMC (Abdo et al. 2009h), the mean CR confinement time and volume may well differ from the average values computed above. For instance, the dynamical ages of the three supergiant shells of the SMC are ~1.5 × 107 yrs (Stanimirovic et al. 1999). If CRs can be efficiently confined in the superbubbles interiors for this duration, the CR confinement time would be about an order of magnitude above the average value computed above. Such a scenario may be further explored observationally by looking for a correlation of the GeV signal with diffuse X-ray emission, the latter having the potential to reveal the hot gas filling the superbubble cavities. On the theoretical side, additional works are needed to better understand the transport of CRs in a hot, tenuous and presumably highly turbulent medium and determine the time scale over which CRs can be retained within supergiant shells.
7. Conclusion
From the first 17 months of Fermi/LAT observations, we obtained the first detection of the SMC in high energy gamma-rays. The flux in the 200 MeV−20 GeV energy range of the data is (1.9 ± 0.2) × 10-8 ph cm-2 s-1, and increases to (3.7 ± 1.7) × 10-8 ph cm-2 s-1 when extrapolated to the 100 MeV−500 GeV range from our best-fit spectral model. The latter value is consistent with the upper limit derived from the CGRO/EGRET data.
The emission is steady and from an extended source ~3° in size. It is not clearly correlated with the distribution of massive stars or neutral gas, nor with known pulsars or supernova remnants. However, a certain correlation of the gamma-ray emission with supergiant shells is observed. In the recent Fermi/LAT study of the LMC, the gamma-ray emission was observed to be poorly correlated with gas density but strongly correlated with tracers of massive star forming regions such as ionised gas, Wolf-Rayet stars, and supergiant shells. Better statistics from increased exposure may reveal patterns in the SMC emission and clarify the differences and similarities in the gamma-ray emission of the two Magellanic Clouds.
If the gamma-rays from the SMC are produced by CR-ISMinteractions, the observed flux implies an average density of CR nuclei in the SMC of ~15% the value measured locally in the MW. This value should be considered an upper limit since a substantial fraction of the emission may be due to the population of high-energy pulsars of the SMC and the gas mass used for the calculation may be underestimated. The average density of CR electrons derived from radio synchrotron observations of the SMC is consistent with the same reduction factor, but large uncertainties on the radio data and on the geometry of the galaxy also allow higher values. From our current knowledge on the SMC, such a low CR density does not seem to be due to a lower rate of CR injection but may indicate some dependence on CR transport effects, such as a smaller CR confinement volume characteristic size.
From GALPROP run 54_87Xexph7S, which is available from http://galprop.stanford.edu.
We used the ATNF catalogue version 1.36 from the web page http://www.atnf.csiro.au/research/pulsar/psrcat/ (Manchester et al. 2005) and SNRs data come from Rosa Williams web page http://www.astro.illinois.edu/projects/atlas/.
These 6 objects actually are those listed in the ATNF catalogue referred to previously, but there are in fact many more known pulsars in the SMC. Galache et al. (2008) lists about 30 X-ray pulsars that are presumably parts of Be/X-ray binaries. Yet, these pulsars are not expected to be powerful gamma-ray emitters because of their long periods ≥10 s.
Acknowledgments
The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique / Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the and the Centre National d’Études Spatiales in France.
References
- Abdo, A. A., Ackermann, M., Ajello, M., Atwood, W. B., & Axelsson. 2009a, ApJS, submitted [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJS, 183, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009c, Phys. Rev. Lett., 102, 181101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009d, Science, 325, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009e, ApJ, 703, 1249 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009f, ApJ, 700, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009g, Phys. Rev. D, 80, 122004 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009h, A&A, submitted [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009i, ApJ, submitted [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, submitted [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, Phys. Rev. Lett., 104, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 2000, A&A, 362, 937 [NASA ADS] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bot, C., Boulanger, F., Lagache, G., Cambrésy, L., & Egret, D. 2004, A&A, 423, 567 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cioni, M., van der Marel, R. P., Loup, C., & Habing, H. J. 2000, A&A, 359, 601 [NASA ADS] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, [arXiv:astro-ph:0207156] [Google Scholar]
- Crawford, F., Kaspi, V. M., Manchester, R. N., et al. 2001, ApJ, 553, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, R., Halloin, H., Kretschmer, K., et al. 2006, Nature, 439, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dufour, R. J. 1984, in Structure and Evolution of the Magellanic Clouds, ed. S. van den Bergh, & K. S. D. Boer, IAU Symp., 108, 353 [Google Scholar]
- Elad, M., Starck, J. L., Donoho, D., & Querre, P. 2005, Applied and Computational Harmonic Analysis, 19, 340 [CrossRef] [Google Scholar]
- Ferriere, K. 1998, ApJ, 497, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. M. 2001, Rev. Mod. Phys., 73, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Fichtel, C. E., Stone, R. G., Ozel, M. E., & Sreekumar, P. 1991, ApJ, 374, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Galache, J. L., Corbet, R. H. D., Coe, M. J., et al. 2008, ApJS, 177, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Gonidakis, I., Livanou, E., Kontizas, E., et al. 2009, A&A, 496, 375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grenier, I. A., Casandjian, J., & Terrier, R. 2005, Science, 307, 1292 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hanasz, M., Kowal, G., Otmianowska-Mazur, K., & Lesch, H. 2004, ApJ, 605, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasz, M., Otmianowska-Mazur, K., Kowal, G., & Lesch, H. 2009, A&A, 498, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, J., & Zaritsky, D. 2004, AJ, 127, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, R. F., Klein, U., Wayte, S. R., et al. 1991, A&A, 252, 475 [NASA ADS] [Google Scholar]
- Healey, S. E., Romani, R. W., Taylor, G. B., et al. 2007, ApJS, 171, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Hilditch, R. W., Howarth, I. D., & Harries, T. J. 2005, MNRAS, 357, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. 1997, PASP, 109, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Fields, B. D., & McCall, B. J. 2009, ApJ, 694, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kamae, T., Karlsson, N., Mizuno, T., Abe, T., & Koi, T. 2006, ApJ, 647, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., & Wood, P. R. 2006, ApJ, 642, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Lah, P., Kiss, L. L., & Bedding, T. R. 2005, MNRAS, 359, L42 [NASA ADS] [Google Scholar]
- Lamb, R. C., Fox, D. W., Macomb, D. J., & Prince, T. A. 2002, ApJ, 574, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, M. S. 1994, High energy astrophysics, Volume 2, Stars, the Galaxy and the interstellar medium, ed. M. S. Longair (Cambridge Univeristy Press) [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., Gaensler, B. M., Stanimirović, S., et al. 2008, ApJ, 688, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- McGarry, M. B., Gaensler, B. M., Ransom, S. M., Kaspi, V. M., & Veljkovik, S. 2005, ApJ, 627, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M. 2009, Astropart. Phys., 31, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlidou, V., & Fields, B. D. 2001, ApJ, 558, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, T. A., Moskalenko, I. V., Strong, A. W., Orlando, E., & Bouchet, L. 2008, ApJ, 682, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S., Moskalenko, I. V., Jones, F. C., Strong, A. W., & Zirakashvili, V. N. 2006, ApJ, 642, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Sreekumar, P., Bertsch, D. L., Dingus, B. L., et al. 1993, Phys. Rev. Lett., 70, 127 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sreekumar, P., Bertsch, D. L., Dingus, B. L., et al. 1992, ApJ, 400, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Stanimirovic, S., Staveley-Smith, L., Dickey, J. M., Sault, R. J., & Snowden, S. L. 1999, MNRAS, 302, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Stanimirovic, S., Staveley-Smith, L., van der Hulst, J. M., et al. 2000, MNRAS, 315, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Stanimirović, S., Staveley-Smith, L., & Jones, P. A. 2004, ApJ, 604, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Reimer, O. 2000, ApJ, 537, 763 [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Reimer, O. 2004, ApJ, 613, 956 [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Annual Review of Nuclear and Particle Science, 57, 285 [Google Scholar]
- Tammann, G. A., Loeffler, W., & Schroeder, A. 1994, ApJS, 92, 487 [NASA ADS] [CrossRef] [Google Scholar]
- The Pierre Auger Collaboration, Abraham, J., Abreu, P., et al. 2007, Science, 318, 938 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- The Pierre Auger Collaboration, Abraham, J., Abreu, P., et al. 2008, Astropart. Phys., 29, 188 [NASA ADS] [CrossRef] [Google Scholar]
- The Pierre Auger Collaboration, Roulet, E., et al. 2009, Nucl. Phys. B Proc. Suppl., 190, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Welch, D. L., McLaren, R. A., Madore, B. F., & McAlary, C. W. 1987, ApJ, 321, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Wilke, K., Klaas, U., Lemke, D., et al. 2004, A&A, 414, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Spatial and spectral characteristics of each component of the celestial background model used in the analysis.
Comparison of the different spatial models used to represent the emission from the SMC.
Best-fit spectral parameters obtained from a maximum likelihood analysis with spatial model 2DG.
All Figures
 |
Fig. 1 200 MeV−20 GeV counts map of the region of interest centred on the SMC, after smoothing with a 2D Gaussian kernel with σ = 0.4°. The positions of the background point sources are marked by white circles, with circle size indicating position uncertainty. |
| In the text | |
 |
Fig. 2 200 MeV−20 GeV residual counts maps after subtraction of the fitted celestial background model and a smoothing with a 2D Gaussian kernel with σ = 0.4°. Upper plot corresponds to the full region of interest and lower plot is a zoom on the SMC. The positions of the background point sources are marked by white circles in the top panel, with circle size indicating position uncertainty, and the SMC is traced by H I column density contours in the bottom panel. |
| In the text | |
 |
Fig. 3 Residual counts map after subtraction of the fitted celestial background model and smoothing with a 2D Gaussian kernel with σ = 0.4°. Logarithmically-spaced Hα emission contours of the SMC are shown, together with the locations of the currently-known pulsars and SNRs in the galaxy (stars and points respectively). Black circles mark the extent of the 2DG model and the positions of the components of the 3PS model (including in all cases the 2σ uncertainty in the position). |
| In the text | |
 |
Fig. 4 Monthly light curve of the SMC obtained with the 2DG spatial model and a power-law spectral shape with fixed index. Also shown for comparison is the light curve of 47 Tuc. |
| In the text | |
 |
Fig. 5 Spectrum of the SMC. The LAT data points (in black) come from independent fits of the 2DG plus background models in 6 different energy bins. The curves correspond the components and total of a spectral model of CR-ISMinteractions in the SMC fitted to the data using a binned maximum likelihood analysis (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


