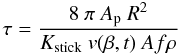| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201014928 | |
| Published online | 03 November 2010 | |
Comet 67P/Churyumov-Gerasimenko: the GIADA dust environment model of the Rosetta mission target
1
INAF – Osservatorio Astronomico di Trieste, via Tiepolo
11, 34143
Trieste,
Italy
e-mail: fulle@oats.inaf.it
2
ESA – ESTEC,
Keplerlaan 1, 2201AZ
Noordwijk, The
Netherlands
3
INAF – Osservatorio Astronomico di Capodimonte,
via Moiariello 16,
80131
Napoli,
Italy
4
Università Parthenope, Dip. Scienze Applicate, Centro Direzionale Isola
C4, 80143
Napoli,
Italy
5
Max-Planck-Institut fuer Kernphysik, Saupfercheckweg 1, 69117
Heidelberg,
Germany
6
Laboratory for Atmospheric and Space Physics, University of
Colorado, 1234 Innovation
Dr, Boulder,
CO, 80303-7814, USA
7
Seoul National University, Dept. of Physics and Astronomy, Seoul
151-742,
Korea
8 CARA – Unione Astrofili Italiani, UAI
9
Osservatorio di Talmassons, CAST, Italy
10
Instituto de Astrofísica de Andalucía,
CSIC, PO Box,
3004
Granada,
Spain
Received: 4 May 2010
Accepted: 2 July 2010
Context. The ESA Rosetta spacecraft will reach the short-period comet 67P/Churyumov-Gerasimenko in 2014. Orbiting strategy, orbiter safety conditions, landing scenarios and expected results from dust collectors depend on models of the 67P dust environment. Many papers already tackled this matter, analysing a limited set of observations, and therefore often reaching conflicting conclusions.
Aims. We consider a set of observations representative of all ground-based and IR (thermal infrared) Spitzer data collected over the last three perihelion passages, to determine the 67P dust environment after the end of the gas drag on dust (at about 20 nucleus radii) consistent with available 67P gas and dust coma photometry, images of the dust coma, tail and trail, at optical and IR wavelengths.
Methods. In order to obtain the best fit to 67P data, we consider three independent tail and trail simulation codes (developed by three independent groups), which parametrise cometary dust by the quantity β, the ratio between solar radiation pressure and gravity forces. GIADA, the dust monitor instrument of the Rosetta orbiter, will provide an experimental determination of the β-dust mass relation.
Results. A 67P environment model based on a perihelion-symmetric dust velocity and on a perihelion-asymmetric dust size distribution, is consistent with all available data. During most Rosetta operations, the dust cross-section is dominated by mm to cm-sized grains, while the ejected dust mass is dominated by grains larger than a few mm, with a dust-to-gas ratio of 3 around perihelion.
Conclusions. 67P onsets its activity at Sun-distances rh ≥ 3.4 AU; the dust geometric albedo is 0.04 ± 0.02; at 3.0 AU, 10 g grains escape the nucleus gravity field (10 kg grains at perihelion) with a dust mass-loss rate of 10−40 kg s-1 (500 kg s-1 at perihelion); 67P’s activity depends on seasons, with the northern heminucleus (rich in large grains and CN depleted) active before perihelion.
Key words: space vehicles: instruments / comets: individual: 67P/Churyumov-Gerasimenko
© ESO, 2010
1. Introduction
Comets are considered to be formed by the most primordial material in the Solar System, and spend most of their life in the coldest regions of the planetary system. Therefore, cometary nuclei are likely composed of relatively unprocessed material, and may even preserve pre-solar grains. A deeper knowledge of their nature will constrain the evolutionary processes such as radial mixing in the solar nebula from the hottest internal regions to the colder outer part beyond Neptune (Brownlee et al. 2006). In particular, the Jupiter Family Comets (i.e., Short Period Comets with aphelion at Jupiter’s orbit; see Marsden 2009, for the current definition of comet families) likely originate from the trans-Neptunian reservoir known as the Kuiper Belt (Fernández 1980; Duncan et al. 1988), and are fragments of larger Kuiper Belt Objects (Farinella & Davis 1996; Duncan et al. 2004). They should be studied in the framework of a global evolutionary process of the Solar System (see e.g. Morbidelli 2005).
Few cometary nuclei have been directly studied in situ: after the pioneering comet missions VEGA (Sagdeev et al. 1986) and Giotto (Reinhard 1986) to comets 1P/Halley, 21P/Giacobini-Zinner and 26P/Grigg-Skjellerup, 19P/Borrelly was reached by the Deep Space 1 mission (Soderblom et al. 2002), 81P/Wild 2 by the Stardust mission (Brownlee et al. 2006) and 9P/Tempel 1 by the Deep Impact mission (A’Hearn et al. 2005). All these missions contributed to a revision of the early view of a comet as a dirty snowball (Whipple 1950): the dominant component of a cometary nucleus is not water ice; the solid content and its distribution on the nucleus surface play a crucial role in the cometary activity (formation of crusts, fragmentation and outbursts, etc.); also organic materials (e.g. CHON particles) are present.
The future of cometary exploration is the European Space Agency’s mission Rosetta (Glassmeier et al. 2009; Schulz 2009): this Planetary Cornerstone Mission of the long-term programme Horizon 2000 will rendez-vous in 2014 with comet 67P/Churyumov-Gerasimenko (Churyumov 2004; Lamy et al. 2009, and references therein). Rosetta has been launched from the Guiana Space Center in Kourou, French Guiana, on 2004, March 2, and is presently in the second half of its 10-years travel across the Solar System towards its target. Rosetta will explore the composition of the cometary nucleus and the processes altering it by means of the 12 orbiter instruments and the 10 Philae lander instruments (see a detailed description of each instrument in the recent Rosetta book, Schulz et al. 2009).
Among the orbiter payload, the GIADA (Grain Impact Analyser and Dust Accumulator) instrument (Colangeli et al. 2009) will exploit the unique possibility offered by Rosetta to obtain time-resolved information about the dust environment and its evolution in the cometary coma. GIADA is composed of three different sub-systems, which will provide data on dynamical and physical properties of grains in a wide size (grains larger than 15 μm in diameter) and velocity (up to 300 m s-1) range (Table 1). A grain detection system (GDS) optically detects the transit of each single grain entering the GIADA instrument and crossing a laser curtain, without affecting its dynamical properties (Mazzotta Epifani et al. 2002). An impact sensor (IS) measures the momentum released by the same grain at the impact by means of five piezoelectric sensors. The scalar velocity is derived from the time of flight between the two sub-systems, and provides the mass of each single grain (Esposito et al. 2002). In addition, five micro balance systems (MBSs) point towards different space directions and measure the cumulative deposition in time of dust smaller than a few μm (Palomba et al. 2002).
Thanks to its different sensors, GIADA will be able to accomplish several scientific measurements, described in detail in Colangeli et al. (2009). Some of them are summarised below:
-
In situ and original (at nucleus) dust sizedistribution and dust mass-loss rate,by distinguishing the contributions of direct andreflected (by the solar pressure) grain populations.
-
Distribution of the dust velocity vs. grain mass, by measuring the scalar velocity and momentum of single dust grains.
-
Time (along the mission) and space (across the coma) evolution of the dust environment, allowing us to infer grain fragmentation and emission from active nucleus areas.
In order to predict the expected results from the GIADA instrument and the safety conditions of the whole spacecraft with regard to the dust environment, it is mandatory to extract all possible dust parameters from available ground-based observations. Since 2002 a series of publications have been dedicated to the observation and modelling of the tail, neckline, and trail of comet 67P. Each model is able to reproduce a subset of the observations of typically three images. Fulle et al. (2004) and Moreno et al. (2004) analysed one R-band image of the neckline observed by the Telescopio Nazionale Galileo (TNG) in 2003, March (heliocentric distance rh = 2.6 AU); both obtained that the only way to fit it by assuming a very strong asymmetry of the dust size distribution vs. perihelion. The adopted inversion technique (Fulle 1989) allowed them to infer the dust-loss rate from about 3 AU inbound. 67P also develops a prominent trail. Ishiguro (2008) analysed 3 R-band images of the 67P trail collected between 2002, September and 2003, February (rh = 1.3−2.2 AU), shortly after the comet’s perihelion passage in 2002, August. The images show a dust trail (composed of large particles older than one orbital period) on the projected orbit of the comet, and a tail and neckline of smaller particles emitted during the 2002 apparition. These phenomena are distinguishable because they are projected onto the sky at different position angles. During all observations in the following years, the position angles of trail and neckline differed by not more than a few degrees, which makes it necessary to model trail and neckline at the same time. Kelley et al. (2008) observed the 67P tail and trail in 2003, June (rh = 3.2 AU, outbound) in visible light from Mount Palomar and in 2004, February (rh = 4.5 AU, outbound) with Spitzer/MIPS at 24 micron. Kelley et al. (2009) analysed Spitzer/MIPS24 observations made in 2006, August/September (rh = 5.5 AU, inbound) and 2007, May (rh = 4.8 AU, inbound). Agarwal et al. (2010) modelled one optical image from 2004, April (rh = 4.7 AU, outbound), and two 24 micron images from 2005, August (rh = 5.7 AU, outbound) and 2006, April (rh = 5.7 AU, inbound).
Three models were based on these sequences of trail observations. Ishiguro (2008) and Kelley et al. (2008, 2009) found that a cone-shaped emission centred on the sub-solar point reproduces their images better than isotropic emission, while Agarwal et al. (2010) assume isotropic emission. All three models describe the dust size distribution as a power-law with a variable exponent α. Ishiguro (2008) and Kelley et al. (2008, 2009) found that α = −3.5 reproduces their observations best, while Agarwal et al. (2010) obtained the most appropriate solutions with α = −4.1. The emission speeds v in all models are described by 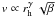 , where β is the ratio between solar gravity and radiation pressure forces. Ishiguro (2008) and Kelley et al. (2008, 2009) assumed γ = −0.5, which represents the variation of insolation with heliocentric distance. Agarwal et al. (2010) assume γ = −3, based on the observed water production rate of the comet and the consequential gas-dust coupling assuming isotropic emission. The speeds in Agarwal et al. (2010) are lower than the subsolar speeds in Ishiguro (2008) and Kelley et al. (2008, 2009) by factors of two at perihelion and ten at 3 AU. The β-parameter of the largest particle that can leave the comet’s gravity field depends on the escape speed from the comet and on the adopted v(β,rh). In Agarwal et al. (2010), the minimum β-value therefore depends on the heliocentric distance, while Ishiguro (2008) and Kelley et al. (2009) assumed a fixed minimum β = 10-4 (10-5 in Kelley et al. 2008). Due to the shallow dependence of v on rh in their models, also grains of β = 10-5 can be emitted at aphelion. All three models also describe the dust production rate as proportional to
, where β is the ratio between solar gravity and radiation pressure forces. Ishiguro (2008) and Kelley et al. (2008, 2009) assumed γ = −0.5, which represents the variation of insolation with heliocentric distance. Agarwal et al. (2010) assume γ = −3, based on the observed water production rate of the comet and the consequential gas-dust coupling assuming isotropic emission. The speeds in Agarwal et al. (2010) are lower than the subsolar speeds in Ishiguro (2008) and Kelley et al. (2008, 2009) by factors of two at perihelion and ten at 3 AU. The β-parameter of the largest particle that can leave the comet’s gravity field depends on the escape speed from the comet and on the adopted v(β,rh). In Agarwal et al. (2010), the minimum β-value therefore depends on the heliocentric distance, while Ishiguro (2008) and Kelley et al. (2009) assumed a fixed minimum β = 10-4 (10-5 in Kelley et al. 2008). Due to the shallow dependence of v on rh in their models, also grains of β = 10-5 can be emitted at aphelion. All three models also describe the dust production rate as proportional to 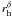 . Ishiguro (2008) treated the exponent as a free parameter and found the best fit with exponent δ = −3. Kelley et al. (2008, 2009) assumed an exponent of δ = −5.8, and Agarwal et al. (2010) assumed δ = −8. The total dust mass production per orbit in Ishiguro (2008) is a factor of 2.5 lower than in Agarwal et al. (2010), while Kelley et al. (2008, 2009) did not specify absolute production rates.
. Ishiguro (2008) treated the exponent as a free parameter and found the best fit with exponent δ = −3. Kelley et al. (2008, 2009) assumed an exponent of δ = −5.8, and Agarwal et al. (2010) assumed δ = −8. The total dust mass production per orbit in Ishiguro (2008) is a factor of 2.5 lower than in Agarwal et al. (2010), while Kelley et al. (2008, 2009) did not specify absolute production rates.
Sensitivity and upper limits of quantities measured by GIADA sub-systems (actual grain sizes depend on the chemical composition, we show the values of silicate and carbon grains, respectively).
This short review of all available 67P models points out that an agreement on the 67P dust environment is still lacking. A model able to fit all available coma, tail, neckline, and trail data is clearly required, and this is the aim of this paper.
2. 67P dust data
Astronomical observations of the cometary dust environment constrain our modelling in two ways:
-
Coma photometry (Afρ) constrains the dust production as a function of heliocentric distance, and is a model input.
-
We derive dust properties (time-dependent size distribution and emission speed) by fitting the morphology of coma, tail, and trail in a series of images of the cometary environment.
The quantity Afρ describes the coma photometry in a standardised way. A series of observations of the dust coma (usually in the R-passband to avoid most intense molecular emissions) provides the time evolution of the total brightness scattered by dust. Afρ (A’Hearn et al. 1984) is the product of the dust geometric albedo A times the filling factor f (proportional to the dust optical thickness) times the radius ρ of the observed coma (this implies Af is proportional to the coma surface brightness). In case of isotropic and steady ejection of dust from a point-like source, Afρ is proportional to the dust-loss rate times the dust cross section divided by the dust velocity; all these quantities are convoluted over the whole range of ejected dust masses (Fulle 2004). Afρ is measured in meters and needs further constraints to be converted into a real mass-loss rate (measured in kg s-1). Moreover, it is independent of the observation coma radius ρ only if the surface brightness of the dust coma is proportional to ρ-1. The geometric albedo A is defined at zero phase angle (see e.g. Hanner et al. 1981, for its definition).
We consider Afρ data from the European network of comet amateur observers (CARA, see e.g. Milani et al. 2008; Moreno 2009), which organised an observational campaign of comet 67P during 2008 and 2009, monitoring its photometry from 3 AU before perihelion to 1.5 AU after perihelion (Fig. 1). In addition, we use pre-perihelion Afρ data obtained in 2008 beyond 2 AU from VLT images available in the ESO public archive, and data from previous perihelion passages collected by CARA and in the Lowell Cometary Database (e.g. available at The Small Bodies Node, NASA, http://pdssbn.astro.umd.edu/). All these observations do not show changes of the photometric evolution from one perihelion passage to another.
 |
Fig. 1 Afρdata of comet 67P. Squares: pre-perihelion measurements on 2008 VLT images (this paper); Triangles: pre-perihelion measurements of the CARA 2008 campaign (http://cara.uai.it); Diamonds: post-perihelion measurements available in the Lowell Comet Database related to 1982 and 1983, and in the CARA Archive related to 1996. All measurements refer to the seeing-disc (upper error bar) and outermost (lower error bar) coma visible in the images. The interpolations (solid line: pre-perihelion; dashed line: post-perihelion) are the input to the dust environment model discussed in this paper. |
All Afρ observations show that the ρ-dependence of 67P coma brightness is closer to ρ-2 than to ρ-1 (Tozzi et al. 2009). In such a case, the Afρ value cannot be uniquely defined. This explains why the error bars in Fig. 1 are larger at the VLT data than at the CARA data: these are not due to photometric uncertainties, but simply reflect the covered range of Afρ values from the outer (lowest values) to the inner coma (highest values measured at the seeing-disc). The VLT images show the outer part of the coma to a fainter limit than the CARA images, because the telescope has a bigger mirror and because the sky at Mount Paranal is much darker than in Europe. On the other hand, the bright inner coma is better resolved in the VLT data due to better seeing. From the available 67P photometry we extract the interpolated Afρ curve: this is one of the inputs of our dust environment model, and is defined at about 20 nuclear radii, where the gas drag on dust grains ends. This distance is not resolved in the VLT images. If the 67P coma brightness is proportional to ρ-2 also in the unresolved part, at about 20 nuclear radii much higher Afρ values are probable.
The definition of Afρ shows that in order to convert this quantity into a dust loss rate, we need other data able to provide the dust size distribution and ejection velocity. Cometary data providing both quantities are images of the coma, tail, and trail, sampling the comet orbit in the most uniform way. Table 2 lists the images we have selected. Images collected beyond 2 AU before perihelion are fundamental to infer the environment the Rosetta spacecraft will probe on its arrival at the comet; this requirement is satisfied by the VLT images. We retrieved images of 67P from the ESO archive obtained with the FORS2 instrument on the 8.2-m VLT UT1 (Antu). We selected those images obtained through the R-SPECIAL filter. The observations were acquired during several consecutive days on 2008, June, September, and October. During those observing runs, no day-to-day variations in the images were detected, so we just selected one date for each observing run (see Table 2). The image scale in the default readout mode used during those observations was 0.25 arcsec px-1, providing a FOV of 6.8 × 6.8 arcmin2. Differential telescope tracking was applied to follow the motion of the comet. The images acquired were reduced by standard techniques, and the calibration was performed using both field stars and photometric standard star fields near the comet position. We used the median of the calibrated images from each night for analysis.
67P tail & trail database. θ: observation true anomaly.
The CAST (Circolo Astrofili Talmassons) observation close to the 2009 perihelion shows both a tail (composed of dust ejected shortly before perihelion) and a perspective sunward tail (composed of dust ejected at 3 AU before perihelion) of similar brightness: this strongly constrains models aimed to determine the dust-loss rate at 3 AU pre-perihelion vs. that at perihelion. This observation was made with a 1575 × 1088 pixel CCD camera at a 0.35 m telescope with a FOV of 21 × 14.5 arcmin2 and spatial resolution of 0.8 arcsec px-1, using a Cousins R filter. A total of 20 images of 30 s exposure each were acquired, which were dark- and flat-field corrected with standard techniques. Calibration was done according to the standard CARA procedure (e.g. Milani et al. 2008) using Hipparcos stars. Between the VLT and CAST data, the image collected at the Sierra Nevada Observatory of the Instituto de Astrofísica de Andalucía (IAA) fills the gap of dust coma and tail evolution between 1.9 and 1.3 AU. These observations were made on 2008, December 11 with a 2048 × 2048 pixel CCD camera at the 1.52 m telescope, using a Johnson R filter. We used a 2 × 2 binning readout, with a spatial resolution of 0.46 arcsec px-1, and a FOV of 7.8 × 7.8 arcmin2. A total of fifteen 67P images during a time interval of 15 min were acquired. The images were reduced by standard techniques and calibrated using field stars with the Carlsberg Meridian Catalog 14 (CMC-14). The median of those calibrated images was then taken for analysis.
In addition, we use several post-perihelion images from the previous apparition of the comet. The first of these was made on 2002, December 2 (rh = 1.72 AU) with the 1.05 m Schmidt telescope at the KISO observatory in Nagano, Japan. The image is in the R-filter, and has a FOV of about 30 × 30 arcmin2. It shows the coma, a tail with a neckline, and a trail of old particles (Ishiguro 2008). The next image was obtained with the Telescopio Nazionale Galileo (TNG) on La Palma on 2003, March 27 (rh = 2.58 AU) in R-band (Fulle et al. 2004). The 2002 and 2003 observations (Ishiguro 2008; Fulle et al. 2004) are fundamental to constrain the parameters of dust ejected shortly after perihelion (visible in the anti-sunward tail) with respect to those of dust ejected beyond 2 AU before perihelion (visible in the neckline). Finally, we fit our model to three images of the 67P dust trail acquired between 2004 and 2006 (Agarwal et al. 2010): One image was obtained on 2004, April 18−21 (rh = 4.69 AU) with the Wide Field Imager at the ESO/MPG 2.2 m telescope on La Silla, Chile, without filter. The FOV covers 40 arcmin of the projected orbit of the comet. It shows a bright bulge extending over about 10 arcmin behind the nucleus and uniform brightness further away. Two images were taken on 2005, August 29 (rh = 5.69 AU outbound) and on 2006, April 8 (rh = 5.66 AU inbound) with the MIPS instrument on board the Spitzer Space Telescope at 24 μm. The observations cover 20 arcmin and 40 arcmin of the projected orbit, respectively. They also show the bright bulge behind the nucleus and a flatter profile further away. Between 2004 and 2006, the bulge stretched out along the orbit, became flatter, and fell back behind the nucleus, the latter indicating that it consists of particles with longer orbital periods than the nucleus. The three trail images mainly constrain the dust size distribution and emission speed around perihelion. The 24 micron data (thermal infrared) also put a constraint on the dust albedo.
3. Model inputs from GIADA
The models of trails and tails, which we have applied to all 67P dust data (see the next section) parameterise the dust grains by means of the quantity β, i.e. the ratio between solar radiation pressure and solar gravity forces, which (together with the emission velocity) determines their Sun-centered Keplerian orbit (Fulle 2004). In order to extract the dust mass-loss rate from these models, β has to be converted into the corresponding dust mass. The β-parameter depends on the ratio between dust cross section σ and mass m times the scattering efficiency Qpr (Burns et al. 1979): β = Cpr Qpr σ m-1, with Cpr = 8 × 10-4 kg m-2. Also the dust dynamics during the gas drag in the inner coma (of size of about 20 nucleus radii) depends on the ratio σ m-1 (e.g. Wallis 1982). The GIADA instrument on the Rosetta orbiter will measure the cross section and mass of each in situ detected grain. Since cometary grains are not spheres, their cross section exposed to solar flux or gas flux cannot be uniquely defined; according to all possible shapes and spins, we can only define the averaged cross section vs. a fixed mass. GIADA will perform the simultaneous measurement of a sampled cross section vs. mass of thousands of grains, thus allowing us to establish the cross section distribution vs. dust mass. Therefore, GIADA output is of fundamental importance not only as input for the tail and trail models which will be applied in this paper, but also for coma dynamical models aimed to interpret all dust data (fluences and coma images) collected during the Rosetta mission. Moreover, we can already use the output of the GIADA instrument obtained during its calibration, which was performed by means of realistic, non-spherical cosmic dust analogues. The conversion from β to dust mass obtained in this way will be then refined as soon as in situ data will be available.
To test the scientific performances of the GDS+IS component of GIADA instrument, grains of several materials considered to be terrestrial analogues of cometary grains were used: andesite and nontronite, i.e. two members of the silicate family, and amorphous carbon, characterised by an albedo as low as expected for real cometary grains. Here we present only the results for the carbon grains used for the scientific calibration of the GIADA model, flying on-board the Rosetta spacecraft. These grains have been obtained by grinding pure carbon electrodes (99% graphite) and then by sieving the obtained dust in electronic sieves of two size ranges: 100−200 and 200−500 μm. Two equipments have been used during the calibration campaign to shoot or drop each single grain of the sample (around 100) across the GDS laser curtain and towards the IS impact plate. The two systems allowed us to cover the velocity range of grains entering the GIADA instrument from about 1 to 102 m s-1. For each grain, the equivalent radius was measured under a microscope before being shot or dropped across the GDS+IS system; it has been converted to scattering cross section by means of the classic BHMIE algorithm for Mie-scattering from a sphere (Bohren & Huffmann 1983). The GDS engineering calibration factor Signal/Csca [V m-2] has been derived by a rms fit to the experimental points. To simulate the GDS operation at the comet, the calibrated scattering cross section of each grain, as read by the GIADA – GDS subsystem, has been obtained for each grain. The mass of the same grain has been obtained from the IS calibration factors and data, by means of the formula Vout = C(x,y) a Qb, where (x,y) is the impact position on the IS plate, C(x,y), a and b are the IS calibration factors, Vout is the output signal from the central piezoelectric sensor (PZTA) of IS after the grain impact, and Q is the grain momentum Q = m v, where m is the mass and v the impact velocity provided by the time of flight between GDS and IS. The impact position has been extracted from the delay time of signals among the five IS piezoelectric sensors placed under the IS sensor plate. Therefore, m = v-1 [Vout (a C(x,y))-1] 1/b.
The results in Fig. 2 show us that the Mie theory applied to carbon grains (i.e., taking into account carbon refraction index and bulk density) predicts a trend which is inconsistent with the experimental data. This is because the Mie theory assumes that grains are spheres, and a sphere has always the lowest possible cross section with respect to a fixed mass. Since all grains were not spherical, all data must (as they do) lie to the left of the Mie line. When we consider spheres of equivalent bulk density of 102 and 103 kg m-3, in a log–log plot we obtain two straight lines, which confine all calibration data. We conclude that in terms of the ratio between cross section and mass, real carbon grains of any shape and spin are equivalent to spheres with a bulk density between 102 and 103 kg m-3. Such a range of equivalent bulk densities will be updated as soon as in situ data on true cometary grains will become available. The equivalent bulk density of 103 kg m-3 corresponds to the grains as close as possible to carbon spheres: these grains will be hereafter named quasi-spherical or compact grains; those corresponding to a bulk density of 102 kg m-3 will be named very non-spherical or fluffy grains. We point out that this lower density value corresponds to that found for the dust in comet 1P/Halley (Fulle et al. 2000). Since the chemical composition of real cometary grains will be much less homogeneous than that of grains used to calibrate the GIADA detector, we must expect an even wider range of equivalent bulk densities. However, the conversion from β to dust mass will remain that of spheres (of yet to be defined equivalent bulk densities), provided that a line of slope 2/3 in a log–log plot will still fit the data cloud in Fig. 2. For fractals we expect a slope steeper than 2/3, so that β will not be proportional to the inverse of the dust size anymore. The cloud of data in Fig. 2 suggests a slope lower than 2/3, which cannot be explained by dust shapes approaching fractals. This may be due to a bias in the selection of the grain shapes during calibration, a bias which will likely disappear in real cometary grains.
 |
Fig. 2 Results of the calibration of the GIADA GDS+IS sub-system. The thin solid line was computed by the Mie theory applied to carbon spheres. The thick lines provide the geometric cross section of spheres of a bulk density of 102 (left) and 103 (right) kg m-3. |
4. Models of coma, tail and trail
As discussed above, the models used to fit coma and tail data parameterise the dust in terms of the β quantity, which will be then converted into dust mass according to the procedure described in Sect. 3, assuming Qpr = 1 (large absorbing grains). All available coma and tail images of 67P have a resolution insufficient to resolve the inner coma (of the size of about 20 nucleus radii), where dust is accelerated by gas with probably time-dependent anisotropy patterns. In all available images, outside the nucleus pixel the motion of dust grains is ballistic, i.e. determined by solar radiation pressure and gravity forces, with no influence of the nucleus gravity. Therefore, the motion of each dust grain is determined uniquely by the parameter β and by the ejection velocity vector from the inner coma, which fix the Keplerian orbit of each dust grain around the Sun. The codes adopted here randomly eject millions of sample grains from the (point source) inner coma, parameterised by β and the time of ejection. Each grain is followed in its Keplerian motion around the Sun, and model images are reconstructed at each time corresponding to an available observation by projecting the position in space of all grains on the sky. The column dust density of the model image (i.e. the filling factor f in the definition of the quantity Afρ) depends on the total dust cross section and loss rate: both these quantities are other input parameters of the coma and tail models. However, it is possible to establish a simple relationship between Afρ data and the dust ejection velocity, the total dust cross section and the loss rate for isotropic ejection (Fulle 2004). Therefore, if we assume isotropic dust ejection, coma and tail models depend on two β-and-time-dependent parameters only: the dust ejection velocity from the inner coma and the dust size distribution. Given these two quantities, we can extract from Afρ data a dust-loss rate times the mean geometric albedo Ap, which allows us to directly compute coma and tail images in Af units. For this reason, we calibrated all observations of coma and tail in the same Af units: this allows us a direct comparison with the absolute brightness of coma and tail models independent of actual Ap-values; and also to easily estimate the Afρ values at given distances ρ from the comet nucleus. Since the real dust ejection is probably very anisotropic, the model Afρ values may be slightly different with respect to the input Afρ data (Fig. 1).
 |
Fig. 3 Dust environment of comet 67P. Panel a): maximum mass escaping the 67P inner coma (of size of about 20 nucleus radii) for compact (solid line) and fluffy (dotted line) grains. Panel b): pre-perihelion (solid line) and post-perihelion (dashed line) dust mass-loss rate provided by the interpolated values of Afρ (see Fig. 1), the dust velocity (panel c)), the differential size distribution (panel d)), and the assumed value of the geometric albedo Ap = 0.04: the mass-loss rate values are inversely proportional to Ap. Panel c): dust ejection velocity from the inner coma for compact (solid line) and fluffy (dotted line) grains; its intersection with the assumed escape velocity (dot-dashed line) provides the sun distance where 1 mg grains are able to escape the inner coma (panel a)). Panel d): pre-perihelion (solid line) and post-perihelion (dashed line) power index of the differential dust size distribution for grains of β > 5 × 10-4; two-dot-dashed line: power index of the dust distribution for grains of β < 5 × 10-4. |
In order to test our results, we consider two independent coma and tail codes, the Granada code (Moreno et al. 2004; Moreno 2009) and the Trieste code (Fulle 1989, 2004). Both models assume the ejection of 2.6 × 103 grains uniformly distributed over all solid angles. Time and β ranges are sampled in 260 and 105 bins, respectively. Dust ejection along the orbit is uniformly sampled at steps of 1° of true anomaly, from true anomaly −130° to +130° (heliocentric distance of 3.4 AU), i.e. two years centred on the perihelion passage. The fit of the VLT image of 2008, June was impossible with activity onset closer to the Sun. Regarding the β-range, the highest β is set to one; the smallest β value depends on the escape velocity at about 20 nucleus radii from the nucleus surface, where the gas drag on grains becomes negligible. Given the nucleus radius of about 2 km determined for 67P (Lamy et al. 2007), we obtain an escape velocity of 0.5 m s-1 if the nucleus bulk density is 103 kg m-3. Since the estimated nucleus bulk density ranges from 370 kg m-3 (Lamy et al. 2007) to 600 kg m-3 (Davidsson & Gutiérrez 2005), the nucleus is probably very non-spherical, and the coma gas density changes of orders of magnitude between the day and night sides: then, the actual value of the escape velocity is very ill-determined. Therefore, 67P will be probably able to eject grains bigger than the values obtained in this paper. We get the minimum β-value (i.e. the largest ejected mass) when the dust ejection velocity reaches the escape velocity. Following dust drag models (e.g. Wallis 1982), and assuming that the dust mass m is m ∝ σ3 /2, we get that the dust velocity depends on 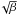 ; the dust velocity is then
; the dust velocity is then 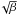 times a time-dependent velocity, a free parameter of the models. The dust size distribution is assumed to be a power law of β, with the time-dependent power index variable over subsets of the total β-range. The resulting dust environment best fitting to all available 67P images is summarised in Fig. 3 and will be discussed in the next section.
times a time-dependent velocity, a free parameter of the models. The dust size distribution is assumed to be a power law of β, with the time-dependent power index variable over subsets of the total β-range. The resulting dust environment best fitting to all available 67P images is summarised in Fig. 3 and will be discussed in the next section.
For the simulation of the 2004–2006 trail images, we used the trail simulation code described in Agarwal et al. (2010). In contrast to the previously described Monte Carlo codes, this code uses an analytical approach to calculate the images of dust shells characterised by a fixed emission time, β-parameter, and emission speed. The final image is a composite of images of individual dust shells emitted at discrete times (in one day steps) during the time interval corresponding to true anomalies between −130° and +130°, with the time-functions β(t) and v(t) described above. The advantage of the analytical code is that simulations can be made within reasonable computational time also for the large FOVs and emission times several orbital periods in the past as required for trail images. We consider the last seven perihelion passages, i.e. those contributing to the same trail after the last important orbit perturbation by Jupiter. When the Granada, Trieste and trail codes take as input the same dust environment (see Fig. 3), they always provide identical tail and coma fits. Figure 4 shows an example for TNG image (Table 2).
5. 67P dust environment
The free parameters of the model are the time-dependent emission speed and size distribution power index reported in panels c and d of Fig. 3, respectively. In panel c we show the dust ejection velocity from the inner coma (i.e. at about 20 nucleus radii) at the dust mass m0 = 10-6 kg: since the velocity depends on 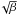 , the dust velocities of other masses m are obtained by multiplying the values in panel c by (m0/m)1/6; the two curves refer to two equivalent bulk densities of 102 and 103 kg m-3 (see Sect. 3). The emission speed at perihelion is constrained by the trail width, and by the position of the bright peak behind the nucleus observed from 2004 to 2006, as the trail shape around aphelion mainly depends on the perihelion activity. The velocities beyond 2 AU are constrained by the increasing width of the coma observed by VLT between 2008, June and October. A dust velocity function symmetric with respect to perihelion is consistent with all available images, although available data do not constrain post-perihelion velocities with the same accuracy as for pre-perihelion. When the dust velocity crosses the escape velocity, we get the minimum β for which grains escape the nucleus gravity field. Also in this case, this βmin has been converted into the largest escaping mass (panel a of Fig. 3) by adopting the two limit equivalent bulk densities of 102 and 103 kg m-3. At 3 AU (planned Rosetta Lander delivery), compact grains of 10 g leave the nucleus gravity field; at perihelion, compact grains with a mass of up to 10 kg may impact the Rosetta Orbiter; these masses become a factor 100 larger in case of fluffy grains.
, the dust velocities of other masses m are obtained by multiplying the values in panel c by (m0/m)1/6; the two curves refer to two equivalent bulk densities of 102 and 103 kg m-3 (see Sect. 3). The emission speed at perihelion is constrained by the trail width, and by the position of the bright peak behind the nucleus observed from 2004 to 2006, as the trail shape around aphelion mainly depends on the perihelion activity. The velocities beyond 2 AU are constrained by the increasing width of the coma observed by VLT between 2008, June and October. A dust velocity function symmetric with respect to perihelion is consistent with all available images, although available data do not constrain post-perihelion velocities with the same accuracy as for pre-perihelion. When the dust velocity crosses the escape velocity, we get the minimum β for which grains escape the nucleus gravity field. Also in this case, this βmin has been converted into the largest escaping mass (panel a of Fig. 3) by adopting the two limit equivalent bulk densities of 102 and 103 kg m-3. At 3 AU (planned Rosetta Lander delivery), compact grains of 10 g leave the nucleus gravity field; at perihelion, compact grains with a mass of up to 10 kg may impact the Rosetta Orbiter; these masses become a factor 100 larger in case of fluffy grains.
 |
Fig. 4 Comparison of the Trieste (solid lines), Granada (dotted lines) and trail (dashed lines) codes modelling the TNG image on 2003, March 27 at 2.6 AU post-perihelion with isotropic dust ejection. The innermost isophote corresponds to Af = 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −x axis, scale in km. |
The second free parameter of the model is the time-dependent power index of the differential size distribution α: it is related to the power index ϵ of the β-distribution by α = −ϵ −4 (Fulle 1989). Fits of the trail constrain this power index to α = −4 (Agarwal et al. 2010). However, all the observed trail grains have β < 10-2, whereas all grains observed in 67P coma and tail have 10-4 < β < 1. Therefore, at β < 5 × 10-4 we assume α = −4 constant in time. For β > 5 × 10-4, fits of the neckline observed in the TNG image (Fulle et al. 2004) require perihelion-asymmetric α-values, from α = −3 before, to α < −4 after perihelion. The perihelion-asymmetry of the size distribution perfectly agrees with the observed increase in the degree of linear polarisation of the 67P dust coma from 2008 to 2009 (Levasseur-Regourd et al. 2009; Hadamcik et al. 2010). Therefore, the dust size distribution is assumed to have a knee at βk = 5 × 10-4, as shown in panel d of Fig. 3. This has important consequences for the data analysis of images collected both from ground and for those which will be collected by Orbiter cameras. Before perihelion, the dust mass depends on all the grains with β < βk, whereas the dust cross section (i.e. the coma brightness) has a peak at βk (i.e. at m = 7 × 10-6 kg if grains are compact, or m = 7 × 10-4 kg if they are fluffy), so that our assumption Qpr = 1 is fully justified. On the contrary, after perihelion, both the coma brightness and the mass-loss rate depend on the smallest ejected grains, so that our assumption Qpr = 1 may introduce errors in the conversion from β to the dust mass. Similarly, this has fundamental consequences for the dust deposition on the Rosetta Orbiter. If a surface with the dust sticking factor Kstick faces an isotropic flux at a distance R from the nucleus center, a single dust monolayer is accumulated after the time
where Afρ and the dust velocity v(β,t) characterise the dust coma. If 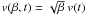 , the dust velocity at β = 5 × 10-4 is a factor 50 smaller than at β = 1. We conclude that at constant nucleus and heliocentric distances, the time to accumulate a dust monolayer is 50 times longer before perihelion than after.
, the dust velocity at β = 5 × 10-4 is a factor 50 smaller than at β = 1. We conclude that at constant nucleus and heliocentric distances, the time to accumulate a dust monolayer is 50 times longer before perihelion than after.
When we consider the Afρ data (Fig. 1), the dust velocity (panel c of Fig. 3) and the dust size distribution (panel d of Fig. 3), integrated over the dust mass range from about 10-15 kg (approximately corresponding to β = 1) to the largest escaping mass (panel a of Fig. 3), we obtain the dust mass-loss rate times the mean dust albedo Ap (see discussion in the previous section). The mass-loss rate shown in panel b of Fig. 3 was computed assuming a mean dust geometric albedo Ap = 0.04, taking into account the results of DID and OPE experiments onboard the Giotto spacecraft at comet 1P/Halley (Fulle et al. 2000); the mass-loss rate depends inversely on the Ap-value, and is independent of the assumed equivalent bulk density of the grains, i.e. on their fluffiness (Fulle 1989, 2004). Due to the perihelion-asymmetry of the dust size distribution, the dust mass-loss rates at pre-perihelion are higher than at post-perihelion, as opposed to to Afρ values, which are lower pre-perihelion. Since the pre-perihelion power index of the size distribution is −3, most of the mass ejected before perihelion is released in form of the largest grains; because we are assuming an upper limit of the escape velocity at the end of the gas drag, probably grains larger than those plotted in Fig. 3 may escape the nucleus gravity field, too; therefore, the pre-perihelion mass-loss rate should be considered a lower limit. On the other hand, since the post-perihelion power index of the size distribution is −4.2, a significant fraction of the mass ejected after perihelion is released in form of sub-micron grains, with masses smaller than the assumed minimum mass of about 10-15 kg; therefore, the post-perihelion mass-loss rates should also be considered lower limits.
 |
Fig. 5 Observed (solid lines) and computed (dashed lines) isophotes of the VLT image on 2008, June 1 at 2.99 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 8 × 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 107° counterclockwise from +y, scale in 106 km. |
 |
Fig. 6 Observed (solid lines) and computed (dashed lines) isophotes of the VLT image on 2008, September 4 at 2.29 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 10-, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 56° clockwise from +y, scale in 106 km. |
 |
Fig. 7 Observed (solid lines) and computed (dashed lines) isophotes of the VLT image on 2008, October 22 at 1.93 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 1.6 × 10-6, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 73° clockwise from +y, scale in 106 km. |
6. 67P nucleus seasons
 |
Fig. 8 Observed (solid lines) and computed (dashed lines) isophotes of IAA image on 2008, December 11 at 1.56 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 10-6, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 72° clockwise from +y, scale in 106 km. |
When we run the codes described above assuming isotropic dust ejection and the dust environment summarised in Fig. 3, at the observation times of VLT and IAA images (Table 2) we get the model comae and tails shown in the left panels of Figs. 5−8. Since the dust-loss rate was extracted from Afρ by assuming isotropic ejection, and taking into account the differences between observed Afρ values and the assumed interpolation in Fig. 1, we find an agreement within a factor two between observed and model Af values of the brightest isophote. However, the model predicts a perfectly circular coma, whereas observations show a very steep sunward coma with a well developed dust tail. The very steep sunward coma excludes a size distribution with power index lower than −3; indeed, sunward ejected grains must have a velocity even lower than that assumed in our model, and this suggests that the grains dominating the sunward coma brightness shall be even higher than assumed. We tested the tail and coma codes by adopting tens of different combinations of dust velocity and size distribution, but the coma shape did not change. The only possible explanation is that before perihelion the coma shape at heliocentric distances larger than 1.5 AU is dominated by strongly anisotropic dust ejection.
 |
Fig. 9 Spin orientation on the sky according to different models (adapted from Lamy et al. 2007). Black dot: this paper (the dot size is unrelated to model uncertainties). Grey region: Davidsson & Gutiérrez (2005). Symbol * : Chesley (2004). White dot: Schleicher (2006). Hatched region: Lamy et al. (2007). Dashed lines: obliquity of 50° or 130° (Weiler et al. 2004). |
In all VLT images, the dust tail is directed to north, or between the Sun and north directions. Physical models of comae (e.g. Crifo et al. 2004) have shown that the strongest coma anisotropies are driven by huge concavities in the nucleus shape. Since VLT images suggest a persistent coma anisotropy towards a constant direction, a possible scenario (of course not unique) is a huge concavity placed on the nucleus pole directed between the Sun and north directions, with the spin axis oriented in a way to expose that pole to Sun from 3.4 AU to 1.5 AU before perihelion. Taking into account our whole data set, we find that a spin axis with obliquity of 45° pointing to RA = 150°, δ = +70° (Fig. 9) is consistent with all observed coma anisotropies. Our scenario is independent of a prograde or retrograde spin, so that we simply define as north pole the pole pointing to the northern sky hemisphere. We cannot infer the uncertainty affecting the north pole coordinates (probably of the order of tens of degrees): only when the real 67P nucleus shape will be known, it will be possible to compute a physically consistent coma ejection pattern to be compared again with ground-based coma images. It is also possible that a persistent coma anisotropy is independent of the assumed spin axis orientation. The computer time required to explore this possibility is beyond present capabilities. A huge concavity on the north pole is consistent with the nucleus shape obtained by Lamy et al. 2007, which is poorly constrained at both poles. Our north pole position is consistent with the constraints derived by the analysis of non-gravitational forces affecting the 67P nucleus (Davidsson & Gutiérrez 2005). Models based on faint coma jets (Schleicher 2006) observed close to perihelion are much less reliable, because they assume that also the 67P neckline is a coma feature, whereas its formation is independent of actual dust anisotropy pattern (Fulle 2004).
In this paper we provide fits of all collected 67P dust images according to the dust environment shown in Fig. 3, with both isotropic ejection and seasonal ejection, the latter depending on the assumed spin orientation. We assume the northern heminucleus is in summer (sunlit north pole) before perihelion, at autumn equinox at true anomaly of −30°, and in winter after perihelion (sunlit south pole). This orientation of the nucleus spin axis offers a simple explanation of the strong perihelion-asymmetry of the dust size distribution (panel d in Fig. 3): the dust size distribution is different on the two hemi-nuclei, with very large grains in the North, and much smaller ones in the South. Age effects may explain such a non-uniform dust population: the surface on the south pole might be younger, giving off original sized grains, while the north pole surface might be older, releasing bigger mantle fragments (see e.g. De Sanctis et al. 2010, for more detailed analyses of the relationship between the nucleus obliquity and the comet activity). The degree of coma anisotropy is another model free parameter, tuned in order to get the best possible fit of each image. At this stage, it is impossible to compute how it should evolve, because the real nucleus shape is unknown. However, it is expected it must evolve, because the angle between the spin axis and the Sun direction is continuously changing. We assume an anisotropy pattern f(ω), depending on the solid angle direction ω: it has a strong peak on the direction of the assumed 67P north pole in summer, and of the south pole in winter. f is multiplied by another anisotropy pattern g(ω) peaked towards the Sun, in order to take into account that dust is mostly ejected from the subsolar point: around the equinox, the anisotropy pattern depends more on g than on f. Both the dust-loss rate and velocity are multiplied by f × g and normalised vs. ω, allowing us to obtain a much better fit of VLT and IAA images, and to conclude that coma and tail shapes in VLT and IAA images are indeed dominated by ejection anisotropy. Therefore, better fits of coma and tail features observed in 2008 have little sense before the real nucleus shape, topography, and spin state are fully determined.
7. Fit of 67P dust tail
 |
Fig. 10 Observed (solid lines) and computed (dashed lines) isophotes of the CARA image on 2009, January 25 at 1.31 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 1.7 × 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 68° clockwise from +y, scale in 106 km. |
In this section we apply the Trieste and Granada codes to all other 67P dust images; all the dust features observed from 2002 to 2006 (necklines and trails), and then at the 2009 perihelion, are independent of the dust ejection anisotropy, thus providing the best constraints to the 67P dust environment. We follow the data order of Table 2, according to 67P true anomaly at each observation. The CARA image taken close to the 2009 perihelion is very important, because a synchrone analysis shows that the prominent perspective sunward tail was ejected at 3 AU before perihelion. Since this feature has a surface brightness comparable to that of the antisunward tail ejected shortly before perihelion, this image strongly constrains models aimed to infer the time evolution of the 67P dust environment since its activity onset. In contrast to the VLT and IAA data, the tail fits are insensitive to the assumed ejection anisotropy (Fig. 10). In general, the models predict a sunward tail that is too faint with respect to the antisunward tail. We explored tens of combinations of different dust velocity and size distribution, but the fits did not improve. We conclude that the assumed interpolation of Afρ-values (Fig. 1) underestimates the loss rate beyond 2 AU before perihelion. In the next section we will discuss another dust environment based on an extrapolation of 67P Afρ data, better fitting the sunward tail in Fig. 10 and still consistent with all other 67P images.
In 2002 and 2003, many observers (e.g. Reach et al. 2003; Ishiguro 2008) reported the detection of a strong dust spike overlapped to the normal dust coma and tail. This feature was first interpreted as a trail, but its position angles proved it was actually a neckline (Fulle et al. 2004). This feature is very important, because it is composed of dust ejected beyond 2 AU before perihelion. Therefore, its surface brightness, compared to that of the dust coma and tail ejected months after perihelion, allows us to constrain the 67P dust environment over most of the comet orbit. Figure 11 confirms that the fits of this spike are independent of the assumed dust ejection anisotropy, and show that the dust environment in Fig. 3 is consistent with 67P neckline since its first apparition, when its signal was just above that of the background tail. On the contrary, the dust coma shows some asymmetry, less prominent than before perihelion, and directed to the South: the assumed anisotropy pattern based on the nucleus seasons described in the previous section well fits this coma asymmetry.
During 2003, many images of the 67P neckline were collected, but since all are similar in shape, we take into account only that with the best signal-to-noise ratio, the image taken at TNG on 2003, March 27. Here the spike reaches its most extended length and provides the strongest constraints to the dust size distribution over most of the orbit where the comet is active. Again, its fit is completely independent of dust ejection anisotropy (compare Fig. 4 to the left panel of Fig. 12); the assumed dust environment (Fig. 3) fits the spike along all its extension. This image allows us to show why a time-independent dust size distribution is inconsistent with 67P data. The right panel of Fig. 12 shows that a constant size distribution with power index α = −3.6 predicts a faint neckline, much shorter than the observed one. The same time-independent α = −3.6 provides a KISO image where the neckline disappears in the background tail. Other tests performed assuming other time-independent α-values provide poor data fits as well, a bit better than the right panel of Fig. 12 at α > −3.6, much worse at α < −3.6.
8. Constraints on the 67P dust-loss rate
In this section we discuss how the 67P dust-loss rate has to be modified in order to fit the sunward perspective tail observed around the 2009 perihelion. The interpolation of Afρ data plotted in Fig. 1 may underestimate the dust-loss rate times mean albedo A input of our tail codes, because these codes need the loss rate just where the dust drag by gas ends. Here, Afρ is surely higher than the upper limit of Afρ error bars, which always corresponds to ρ-values higher than the inner coma size (i.e. about 20 nucleus radii). This is particularly true beyond 1.5 AU before perihelion, when the observed coma slope is steeper. Indeed, the Af-value of model comae results on average a factor 2 lower than the observed one in VLT and IAA images (Figs. 5−8). In this section we adopt the Afρ curve shown in Fig. 13, in order to check if the Af-values of the model tail are still consistent with the observed ones, and if the sunward perspective tail in CARA image is better fit. With the Afρ-extrapolation shown in Fig. 13, the dust mass-loss rate shown in panel b of Fig. 3 becomes that shown in Fig. 14, whereas all other dust environment parameters remain the same of panels a, c, and d of Fig. 3.
Figure 15 shows the model tails for two sampled images output of the code when the extrapolated Afρ-values are taken in account. The sunward perspective tail in the CARA image is better fitted than in Fig. 10, because we are assuming a higher dust-loss rate beyond 1.5 AU before perihelion, when the dust composing that anti-tail was ejected. The shape of the model tails to be compared with the VLT images did not change: the only effect is that all Af-values increase by a factor 3, i.e. in average they become a factor 1.5 higher than the observed Af-values. This shows that the mass-loss rates plotted in Fig. 14 are probably upper limits, while those plotted in panel b of Fig. 3 are probably lower limits. These limits depend also on the uncertainties of the dust albedo, which are constrained by IR trail fits.
 |
Fig. 11 Observed (solid lines) and computed (dashed lines) isophotes of KISO image on 2002, December 2 at 1.72 AU post-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 5 × 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 65° counterclockwise from +y, scale in 106 km. |
 |
Fig. 12 Observed (solid lines) and computed (dashed lines) isophotes of TNG image on 2003, March 27 at 2.58 AU post-perihelion. Left panel: seasonal ejection with the time-dependent size distribution shown in panel d of Fig. 3, with a power index ranging from −3.0 before perihelion to −4.2 after; isotropic ejection provided very similar fits (Fig. 4). Right panel: constant size distribution index at −3.6. The innermost isophote corresponds to Af = 10-7, the outer isophotes decrease of a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 133° clockwise from +y, scale in 106 km. |
 |
Fig. 13 Afρdata of comet 67P (see Fig. 1 for symbol explanation). The solid line shows the Afρ curve better fitting the CARA image. |
 |
Fig. 14 Pre-perihelion dust mass loss rate computed assuming the Afρ extrapolation shown in Fig. 13 (solid line) and a geometric albedo Ap = 0.04. The post-perihelion mass-loss rate and all the other parameter values remain the same as shown in Fig. 3. |
9. Fit of 67P dust trail
We compare our model to three observations of the 67P dust trail obtained around aphelion between 2004 and 2006 (Agarwal et al. 2010). All grains in the fields of view of these observations had β < 10-2. Figure 16 shows the trail observed in 2004, April at optical wavelengths (without filter) at the ESO/MPG 2.2 m telescope. The trail close to the nucleus is better fit using the Afρ curve shown in Figs. 13 than by that in Fig. 1 (see panels a, c and d of Fig. 3 for the other environment parameters), while fits of the brightness far behind the nucleus and of the trail width are similar for both models. The model trail flux at the nucleus is 30% lower than the observed one: this confirms that the escape velocity at the end of the gas drag is probably lower than the assumed value of 0.5 m s-1. Figures 17 and 18 show our model and two observations of the trail in the thermal infrared (24 μm) made in 2005, August and 2006, April with Spitzer/MIPS. To model the infrared images, we used a colour temperature of 133 K and an emissivity ϵ = 0.5 at 24 μm, which is consistent with Sykes & Walker (1992), who measured ϵ/1 − AB) = 0.6 ± 0.2 in IRAS observations of the 67P trail, where AB is the visible Bond albedo. We assume AB = 0.18, converting the geometric albedo Ap = 0.04 according to the phase integral provided by Divine et al. (1986). The phase integral is ill constrained, but the uncertainty introduced thereby is low compared to that affecting the IRAS observations, because the IR flux depends only weakly on the Bond albedo. With the adopted parameters, the infrared flux in our model is 1.25 times higher than that of a blackbody with ϵ = 1 and AB = 0.18 at the same heliocentric distance. Since the grains in the trail have β < 10-2 (size larger than 60 μm for bulk densities ρ ≤ 103 kg m-3), we assume that the temperature does not depend on the grain size. In order to fit the two infrared observations (Figs. 17 and 18), we have first to convert the Af model surface brightness into a column density, assuming values of the geometric albedo Ap. We find that with Ap = 0.04 ± 0.02 the whole set of IR data lies between the environments defined by the curves in Figs. 1 and 13. The only disagreement regards the position of the peak dust brightness, which is at the nucleus position in the model, while the observations show a broader peak falling back behind the nucleus. The uncertainties affecting the dust emissivity and Bond albedo may change the IR trail flux up to ±30%, close to the correction factor needed to adapt the shape of our model flux to the observed one. The obtained value of the geometric albedo at zero phase angle is perfectly consistent with that found for the dust in the coma of comet 1P/Halley (Fulle et al. 2000).
The main differences between the current model and the best fit for the observations found by Agarwal et al. (2010) are the dependence of the emission speed on heliocentric distance, the introduction of the size distribution knee at β = 5 × 10-4 in this paper, and the absolute production rates. While the speed at perihelion is similar in both models, it decreases more steeply with heliocentric distance (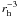 ) in Agarwal et al. (2010) than in the present model. The steeper decrease in speed flattens the peak close to the nucleus, but is inconsistent with all 67P dust coma and tail images. The fit in Agarwal et al. (2010) was achieved with a single-power law size distribution, however assuming that 67P was not ejecting dust with β > 10-2. For the same Afρ and for a given β value (except for the highest β values), the relative cross-section in the present model is higher than in the one used by Agarwal et al. (2010). When we compare the production rate of grains of a given β value, we find that around perihelion the rates in the present model (at Ap = 0.04) are about half of those giving the best fit in Agarwal et al. (2010). The shape and the falling back of the peak in the Spitzer images (but not in the ESO trail image, Fig. 16) are better reproduced with a large-grain size distribution exponent of −4.2 (Agarwal et al. 2010).
) in Agarwal et al. (2010) than in the present model. The steeper decrease in speed flattens the peak close to the nucleus, but is inconsistent with all 67P dust coma and tail images. The fit in Agarwal et al. (2010) was achieved with a single-power law size distribution, however assuming that 67P was not ejecting dust with β > 10-2. For the same Afρ and for a given β value (except for the highest β values), the relative cross-section in the present model is higher than in the one used by Agarwal et al. (2010). When we compare the production rate of grains of a given β value, we find that around perihelion the rates in the present model (at Ap = 0.04) are about half of those giving the best fit in Agarwal et al. (2010). The shape and the falling back of the peak in the Spitzer images (but not in the ESO trail image, Fig. 16) are better reproduced with a large-grain size distribution exponent of −4.2 (Agarwal et al. 2010).
 |
Fig. 15 Observed (solid lines) and computed (dashed lines, seasonal ejection) isophotes on the VLT image of 2008, September 4 (left panel) and of the CARA image on 2009, January 25 (right panel) according to the Afρ curve shown in Fig. 13. The innermost isophote corresponds to Af = 1.8 × 10-7 in the right panel, with a better fit of the sunward tail than in Fig. 10; and to Af = 3 × 10-6 in the left panel, a factor 3 higher than in Fig. 6. |
Since we have determined all ranges of dust parameters consistent with all coma, tail, and trail data, we can compute lower and upper limits of the 67P dust mass loss rate, provided in Tables 3 and 4 per mass bin at sampled heliocentric distances. These loss rates could still increase if the escape velocity where the gas drag on dust ends is lower than the assumed 0.5 m s-1.
10. Constraints on 67P gas-loss rates
In this section we discuss the most probable gas composition driving dust acceleration in 67P coma: water or more volatile species, namely CO or CO2. In Fig. 19 we plot all available data of water-loss rates from 67P: they do not show any evident perihelion asymmetry, and the range of heliocentric distances covered by observations is too low to extrapolate these data beyond 2 AU. In order to do that, and to infer which gas environment the Rosetta probe will face at its arrival at the comet, we must take into account models of water release from model nuclei, and CN observations, covering a much wider range of heliocentric distances. Available CN loss rates are plotted in Fig. 20: they show a very strong perihelion asymmetry. Before perihelion, CN was never detected beyond 2 AU: we plot the upper detection limits of four available VLT observations (Schulz, priv. comm.), already multiplied by a factor 103 in order to infer upper limits of water loss rate (assuming the canonical CN/water ratio of short period comets). Around perihelion, CN was widely observed, confirming a CN/water ratio close to 10-3. After perihelion, the CN loss rate remains almost constant up to 3 AU from the Sun. The nucleus seasons assumed in this paper offer a simple explanation of this behaviour: the northern 67P hemisphere is strongly depleted in CN with respect to the southern one, where the CN/water ratio is close to 10-3. This explanation has an important consequence on the water-loss rate beyond 2 AU before perihelion. The upper limits of water-loss rate plotted in Fig. 20 are valid only if water too is strongly depleted on the northern nucleus hemisphere, otherwise the CN abundance there cannot be used to infer the water-loss rate. That large grains are surely ejected beyond 2 AU (see the requirements to fit VLT images) suggests that water is uniformly distributed over both nucleus hemispheres, so that we must conclude CN observations do not provide reliable information on the water-loss rate during the Rosetta operations. In other words, available CN data show its distribution over 67P surface is surely highly inhomogeneous, but we have no reason now to assume that water follows the same non-homogeneous CN distribution.
 |
Fig. 16 Upper panel: observed (error bars) and computed (continuous lines: environment from Figs. 1 and 3; dashed lines: environment from Figs. 13 and 14) trail peak flux in 2004, April. Lower panel: trail half width inside (+ symbol) and outside (× symbol) the comet orbit, compared to predictions of the models. |
 |
Fig. 17 Upper panel: observed (error bars) and computed (continuous lines: environment from Figs. 1 and 3 with geometric albedo Ap = 0.06; dashed lines: environment from Figs. 13 and 14 with geometric albedo Ap = 0.02) trail peak flux in 2005, August. Lower panel: trail half width inside (+ symbol) and outside (× symbol) the comet orbit, compared to predictions of the models. |
 |
Fig. 18 Upper panel: observed (error bars) and computed (continuous lines: environment from Figs. 1 and 3 with geometric albedo Ap = 0.06; dashed lines: environment from Figs. 13 and 14 with geometric albedo Ap = 0.02) trail peak flux in 2006, April. Lower panel: trail half width inside (+ symbol) and outside (× symbol) the comet orbit, compared to predictions of the models. |
Therefore, the only way we have to infer the water-loss rate beyond 2 AU before perihelion is offered by models of water release from model nuclei. In Fig. 20 we plot two independent models, providing consistent results. The model by Gortsas et al. (2010) considers two possible heat conductivities in the nucleus material, much lower than that of compact ice or silicates, in order to take into account that probably nucleus material is highly porous. The results by De Sanctis et al. (2006) were rescaled in order to convert to 4% their assumed nucleus active area fraction of 50% (Gortsas et al. 2010, adopt 3%): with these similar active area fraction, both models perfectly fit available water-loss rates data at perihelion. To scale from an active area of 50% to 4%, we divide by 14 the water-loss rates computed by De Sanctis et al. (2006; note they assume a unit dust-to-gas ratio in all the nucleus: in case of a homogeneous nucleus, this is equivalent to an active area fraction of 50%). These authors assume the heat conductivity of compact ice, so that the water-loss rate curve beyond 2.5 AU must be much steeper than those obtained by Gortsas et al. (2010): therefore, beyond 2.5 AU, according to the real heat conductivity of nucleus material, the water-loss rate will be between the upper and lower plotted curves. When we take into account the mass dust-loss rate shown in panel b of Fig. 3 divided by 3, and then we convert the mass-loss rate values into water molecules per second, we get the continuous line in Fig. 20: this means that, above the active areas, a dust-to-gas ratio 3 constant in time perfectly fits all water data and model outputs at heliocentric distances closer than 2.5 AU. Beyond 2.5 AU, the water-loss rate curve inferred by the dust-loss rate is much steeper than any water curve provided by nucleus models. This is clearly due to the very steep increase of the mass of the largest ejected grain as 67P approaches the Sun (panel a in Fig. 3. CO or CO2 loss rates are expected to remain closely constant, or to continue to decrease as 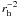 beyond 2.5 AU too. Were these species dominating the dust drag, a much less steep curve in panel a of Fig. 3 would be expected beyond 2.5 AU. The time evolution plotted in panel a of Fig. 3 strongly suggests water only is dragging all dust in 67P coma, irrespective of the heliocentric distance rh.
beyond 2.5 AU too. Were these species dominating the dust drag, a much less steep curve in panel a of Fig. 3 would be expected beyond 2.5 AU. The time evolution plotted in panel a of Fig. 3 strongly suggests water only is dragging all dust in 67P coma, irrespective of the heliocentric distance rh.
Lower limits of the dust mass-loss rate ṁr per mass bins and velocity vr at the heliocentric distances r (AU) before perihelion.
Upper limits of the dust mass-loss rate ṁr per mass bins and velocity vr at the heliocentric distances r (AU) before perihelion.
 |
Fig. 19 Observations of water-loss rates from 67P. Pre-perihelion data: triangle (Feldman 2004), diamond (Crovisier et al. 2002) and squares (Schleicher 2006). Post-perihelion data: symbols * (Hanner et al. 1985), + (Mäkinen 2004) and × (Schleicher 2006). |
 |
Fig. 20 Extrapolations beyond 2 AU of 67P pre-perihelion water-loss rates. Triangle, diamond and squares: observations (Fig. 19). Symbol × : post-perihelion CN-loss rates (Schleicher 2006 at sun distances lower than 2 AU, Schulz et al. 2004) beyond). Vertical error bars: upper limits of pre-perihelion CN-loss rate (Schulz, private communication) multiplied by 103. Solid line: water-loss rate obtained by the dust-loss rate assuming a constant dust-to-gas mass ratio of 3. Dotted lines: water-loss rate predicted by Gortsas et al. (2010) assuming an active area fraction of 3% and heat conductivities of 0.1 (lower line) and 10-3 W m-1 K-1 (upper line). Dashed line: water-loss rate predicted by De Sanctis et al. (2006) rescaled to 4% their assumed active area fraction of 50% (see text for discussion, assumed heat conductivity of 3 W m-1 K-1). |
11. Implications for GIADA instrument
The results discussed in previous sections and summarised in Tables 3 and 4 can be used to estimate the expected GIADA event rate and total number, i.e. to evaluate the capabilities of the GIADA instrument to produce statistically meaningful data on the dust environment of the target comet 67P. An instrument model (GIADA Performance Simulation Tool, PST) has been realised to obtain the expected rate of events detected by the GDS+IS system and the expected cumulative mass deposited on the MBSs, depending on the adopted operative scenario and considering GIADA detection limits (see Table 1).
A consolidated status of the Rosetta Mission Analysis has been presented by Rodriguez Canabal et al. (2003), and the mission profile up to the comet encounter in 2014 has been defined. After a matching manoeuvre when 67P will be at 4.0 AU from the Sun, on its inbound orbital branch, the near-nucleus operations (including the approach, a comet mapping phase, possibly close observations, and the delivery of the Rosetta Lander) will last until around 445 days after rendez-vous with the comet, but the exact timing and sequence of scientific operations at the comet is still under discussion. There will be several phases at the comet (Close Observation Phase, SSP (Surface Science Package) Delivery and Relay Phase, Extended Monitoring Phase ...), in which the distance of the spacecraft from the nucleus will vary, possibly between less than 2 RN and 200 RN, where RN is the nucleus mean radius. Therefore, for the purpose of this discussion, only a sample operation scenario will be adopted to obtain an estimate of the GIADA scientific capabilities and expected performances (conversely, the GIADA PST can be used to give instrument constraints on orbit type and orientation, pointing, operation sequence for the operation profile, in the framework of the GIADA Dust Model results). The adopted scenario is that of a circular orbit around a spherical nucleus of radius RN = 2 km (Lamy et al. 2009), with GIADA continuously operating for ~300 days (from rh = 3.4 to rh = 1.3 AU), and a spacecraft distance from the nucleus surface varying with the comet heliocentric distance as summarised in Table 5. For the purpose of this simulation, the dust production rates reported in Tables 3 and 4 are considered constant during the related phase duration in the adopted mission scenario (Table 5). Our computations cannot take into account the effect due to still undefined coma anisotropies. In other words, we are considering orbits around the nucleus sampling both most and least dense coma regions. This will be accomplished by an orbit e.g. crossing the subsolar point, but not by so-called terminator orbits.
Sample operative scenario (circular orbit) adopted to estimate GIADA capabilities at the comet.
Number of detections of single carbon grains (both compact and fluffy) and deposited mass (coming from nucleus-pointing direction) expected during a sample GIADA operative scenario at comet 67P, for GIADA continuously operating from rh = 3.4 to rh = 1.3 AU.
 |
Fig. 21 Expected GIADA GDS+IS events vs. heliocentric distance. The bars represent the lower-to-upper limit of expected events (measurement of scattering cross section, momentum, mass, and velocity) of single carbon grains (both compact and fluffy) detected by the GDS+IS according to the scenario described in Table 5. |
Figure 21 summarises the results of the GIADA PST for the GDS+IS system in the adopted sample operative scenario for compact and fluffy grains. Values in Tables 3 and 4 have been used to compute a lower-to-upper limit bar for the expected number of events (measurement of scattering cross section, momentum, mass, and velocity of single grains) detected by the GDS+IS, and to derive the expected deposited mass on the MBS sensor surface (for the device pointing directly towards the nucleus). In the adopted sample scenario of Table 5, the GIADA capabilities during the considered part of mission (from rh = 3.4 to rh = 1.3 AU, approximately corresponding to the time range between rendez-vous and approach to comet perihelion) are summarised in Table 6. The total number of events (in the example of carbon grains) ranges from about 5 × 103 to 4.4 × 104 for events between the detection and the saturation limits, i.e. events from which the full set of dynamical parameters of the detected grain can be derived. Other events giving only partial information due to saturation of one or both GDS and IS do not contribute to these numbers and increase the total number of events. For nucleus-pointing MBS, the expected total deposited mass is slightly above the saturation limit. This means that we will be able to measure the deposition rate of small grains along the whole mission, using the entire sensor dynamic range, with the possibility to have sensor saturation close to perihelion. The signal evolution from the other four MBSs (oriented at about 90° with respect to the nucleus-pointing one) cannot be estimated on the basis of the assumptions of the adopted model. Due to the wide dynamic range, it is expected that the mass deposition rate will be detectable, giving information on non-radial small dust grains of mass m < 10-13 kg. Considering the adopted observation scenario that will be refined in view of mission operations, the number of events from GDS+IS and deposited mass detected by MBS allow GIADA to reach all planned objectives.
12. Conclusions
Our main results can be summarised as follows:
-
The 67P dust environment discussed in this paper is defined outof the inner coma (of size of about20 nucleus radii) where dust is dragged out by gas:only in situ data will constrain the environmentcloser to the nucleus surface.
-
67P dust activity repeats regularly during each orbit: the GIADA Dust Environment Model (Fig. 3) fits dust coma, tail, and trail observations covering several perihelion passages.
-
The GIADA instrument will provide an experimental conversion from the radiation pressure coefficient β to the dust mass, updating that provided here by GIADA calibration.
-
67P activity cannot onset closer than the heliocentric distance of 3.4 AU (constraint coming from fits of dust coma observed by VLT on 2008, June at 3 AU inbound).
-
The dust ejection velocity of 1 mg compact grains ranges from 0.7 m s-1 at 3.3 AU to 5 m s-1 at 2.5 AU and to 7 m s-1 at perihelion (fluffy grains have values three times higher).
-
The pre-perihelion dust size distribution is well approximated by a power law with a knee at β = 5 × 10-4, with power index −3 for smaller grains, and −4 for larger ones.
-
Before perihelion, the dust cross section is dominated by grains of β ≈ 5 × 10-4, i.e. mass between 10-5 and 10-3 kg; their mass by grains of β ≤ 5 × 10-4.
-
IR trail fits provide the geometric dust albedo Ap = 0.04 ± 0.02.
-
If the escape velocity is 0.5 m s-1 where gas drag on dust ends, compact grains of 10-7 kg escape the nucleus gravity at 3.4 AU, of 10-2 kg at 3.0 AU, and of 10 kg at perihelion, respectively (fluffy grains have masses 100 times higher).
-
The mass-loss rate of compact or fluffy grains increases from 0.1 kg s-1 at 3.4 AU to 10−40 kg s-1 at 3.0 AU and to 500 kg s-1 at perihelion, respectively, taking into account Ap = 0.04.
-
VLT dust coma observations in 2008 suggest a strongly anisotropic dust ejection towards the direction RA = 150°, δ = +70°, possibly close to the nucleus spin axis.
-
Comparisons with available gas-loss rate data show 67P has a dust-to-gas ratio of 3 at perihelion.
-
Comparisons with available models of water release from 67P nucleus suggest 67P dust-to-gas ratio is constant at 3 above active areas from 2.5 AU inbound to perihelion.
-
67P activity depends on nucleus seasons, with the northern heminucleus active pre-perihelion: it is CN-depleted and is populated by grains much larger than the southern one.
-
The steep increase of the largest ejected mass from 3.4 AU to 2.5 AU inbound suggests water is the gas actually dragging dust in the inner coma since the activity onset.
-
From the activity onset up to 3.3 AU inbound, the GIADA instrument will detect some tens low-albedo grains orbiting at 20 km from the nucleus center.
-
During the whole Rosetta mission, the GIADA instrument is expected to collect more than 104 grains with a complete characterisation of mass and scalar velocity.
Acknowledgments
We gratefully acknowledge funding from the Italian Space Agency (ASI) under contracts I/032/05/0 and I/062/08/0 and from the Spanish Ministry of Education and Science (MEC). The GIADA project is carried out by an international consortium (I, E, UK, F, D, USA). The flight hardware has been developed and built in Italy, with contribution from Spain responsible for the Main Electronics design and production. The industrial partners are Galileo Avionica (Florence – I) and Sener (Madrid – E), for the Italian and Spanish teams, respectively. The Spanish participation was supported by The MICINN project AYA2009-08190. This work is partly based on observations made with the MPG/ESO 2.2 m telescope at the La Silla Observatory under programme ID 072.A-9011(A), and with the Spitzer Space Telescope under programme ID 20235. Spitzer is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This research was partly based on observations made with the European Southern Observatory telescopes obtained from the ESO/ST-ECF Science Archive Facility; and on data obtained at the Observatorio de Sierra Nevada, which is operated by the Instituto de Astrofísica de Andalucía, CSIC. We are grateful to the Sierra Nevada Observatory staff, and the telescope operators Francisco J. Aceituno, Victor Casanova, and Alfredo Sota for the image acquisition in service mode. We thank CARA observers kindly providing their Afρ observations of 67P, namely: W. Borghini, D. Carosati, S. Garro, V. Gonano, E. Guido, H. Mikuz, G. Muler, M. Nicolini, C. Perrella, J. A. Henriquez Santana, G. Sostero and D. Tirelli; and R. Trabatti for the design of CARA software. We thank A. C. Levasseur-Regourd for significant improvements to the previous version of the paper.
References
- Agarwal, J., Müller, M., Reach, W. T., et al. 2010, Icarus, 207, 992 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Schleicher, D. G., Feldman, P. D., Millis, R. L., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2005, Science, 310, 258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bohren, C. F., & Huffmann, D. 1983, Absorption and scattering of light by small particles (New York: Wiley) [Google Scholar]
- Brownlee, D. E., Tsou, P., Aléon, J., et al. 2006, Science, 314, 1711 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R. 2004, Bull. Am. Astron. Soc. 36, 1118 [Google Scholar]
- Churyumov, K. 2004, Discovery, observations and investigations of comet 67P in Kiyv, in The new Rosetta Targets, ed. L. Colangeli, E. Mazzotta Epifani, & P. Palumbo (Kluwer), 1 [Google Scholar]
- Colangeli, L., Lopez Moreno, J. J., Palumbo, P., et al. 2009, The GIADA instrument, in Rosetta. ESA’s mission to the Origin of the Solar System, ed. R. Schulz, C. Alexander, H. Boehnhardt, & K. H. Glassmeier (Springer), 243 [Google Scholar]
- Crifo, J. F., Fulle, M., Kömle, N. I., & Szego, K. 2004, Nucleus-coma structural relationships: lessons from physical models, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press) 471 [Google Scholar]
- Crovisier, J., Colom, P., Gérard, E., Bockelée-Morvan, D., & Bourgois, G. 2002, A&A 393, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davidsson, B. J. M., & Gutiérrez, P. J. 2005, Icarus, 176, 453 [NASA ADS] [CrossRef] [Google Scholar]
- De Sanctis, M. C., Capria, M. T., & Coradini, A. 2006, Adv. Space Res., 38, 1906 [NASA ADS] [CrossRef] [Google Scholar]
- De Sanctis, M. C., Lasue, J., Capria, M. T., et al. 2010, Icarus, 207, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Divine, N., Fecthig, H., Gombosi, T., et al. 1986, Space Sci. Rev., 43, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1988, ApJ, 328, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M., Levison, H., & Dones, L. 2004, in Comets II, ed. M. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 193 [Google Scholar]
- Esposito, F., Colangeli, L., Della Corte, V., Palumbo, P., & the International GIADA Team 2002, Adv. Space Res., 29, 1159 [NASA ADS] [CrossRef] [Google Scholar]
- Farinella, P., & Davis, D. 1996, Science, 273, 938 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Feldman, P. D., A’Hearn, M. F., & Festou, M. C. 2004, Observations of comet 67P with IUE at perihelion, in The new Rosetta Targets, ed. L. Colangeli, E. Mazzotta Epifani, & P. Palumbo (Kluwer Academic Publisher), 47 [Google Scholar]
- Fernández, J. A. 1980, MNRAS, 192, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M. 1989, A&A, 217, 283 [NASA ADS] [Google Scholar]
- Fulle, M. 2004, Motion of cometary dust, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 565 [Google Scholar]
- Fulle, M., Levasseur-Regourd, A. C., McBride, N., & Hadamcik, E. 2000, AJ, 119, 1968 [Google Scholar]
- Fulle, M., Barbieri, C., Cremonese, G., et al. 2004, A&A, 422, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glassmeier, K.-H., Boehnhardt, H., Koschny, D., Kuehrt, E., & Richter, I. 2009, in Rosetta. ESA’s mission to the Origin of the Solar System, ed. R. Schulz, C. Alexander, H. Boehnhardt, & K. H. Glassmeier (Springer), 1 [Google Scholar]
- Gortsas, N., Kührt, E., & Motschmann, U. 2010, Icarus, in press [Google Scholar]
- Hadamcik, E., Sen, A. K., Levasseur-Regourd, A. C., Gupta, R., & Lasue, J. 2010, A&A, 517, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanner, M. S., Giese, R. H., Weiss, K., & Zerull, R. 1981, A&A, 104, 42 [Google Scholar]
- Hanner, M. S., Tedesco, E., Tokunaga, A. T., et al. 1985, Icarus, 64, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ishiguro, M. 2008, Icarus, 193, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kelley, M. S., Reach, W. T., & Lien, D. J. 2008, Icarus, 193, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Kelley, M. S., Wooden, D. H., Tubiana, C., et al. 2009, AJ, 137, 4633 [NASA ADS] [CrossRef] [Google Scholar]
- Lamy, P., Toth, I., Davidsson, B. J. R., et al. 2007, SSR, 128, 23 [Google Scholar]
- Lamy, P., Toth, I., Davidsson, B. J. R., et al. 2009, in Rosetta. ESA’s mission to the Origin of the Solar System, ed. R. Schulz, C. Alexander, H. Boehnhardt, & K. H. Glassmeier (Springer), 21 [Google Scholar]
- Levasseur-Regourd, A. C., Hadamcik, E., Sen, A. K., Gupta, R., & Lasue, J. 2009, Recent polarimetric observations of comet 67P/Churyumov-Gerasimenko, in Proceedings of the International Astronomical Union, Icy Bodies of the Solar System, Rio de Janeiro, August, ed. J. A. Fernández, D. Lazzaro, D. Prialnik, & R. Schulz (Cambridge University Press), IAU Symp. S263, 5, 259, 2010 [Google Scholar]
- Mäkinen, J. T. 2004, Water production rate of comet 67P, in The new Rosetta Targets, ed. L. Colangeli, E. Mazzotta Epifani, & P. Palumbo (Kluwer Academic Publisher), 61 [Google Scholar]
- Marsden, B. G. 2009, PSS, 57, 1098 [Google Scholar]
- Mazzotta Epifani, E., Bussoletti, E., Colangeli, L., et al. 2002, Adv. Space Res., 29, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, G., Szabó, G., Sostero, G., et al. 2008, Icarus, 191, 517 [CrossRef] [Google Scholar]
- Morbidelli, A. 2005, Origin and dynamical evolution of comets and their reservoirs, Lectures on comet dynamics and outer solar system formation at the 35th Saas-Fee advanced course [Google Scholar]
- Moreno, F. 2009, ApJS, 183, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Lara, L. M., Muñoz, O., López-Moreno, J. J., & Molina, A. 2004, ApJ, 613, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Palomba, E., Colangeli, L., Palumbo, P., et al. 2002, Adv. Space Res., 29, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhard, R. 1986, Nature, 321, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Reach, W. T., Hicks, M. D., Gillam, S., et al. 2003, A&AS, DPS 35, 30.07 [Google Scholar]
- Rodriguez Canabal, J., Sánchez Pérez, J. M., & Yanez Otero, A. 2003, Rosetta: Consolidated Report on Mission Analysis, I 5, RO-ESC-RP-5500 [Google Scholar]
- Sagdeev, R. Z., Saabo, F., Avanesov, G. A., et al. 1986, Nature, 321, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G. 2006, Icarus, 181, 442 [CrossRef] [Google Scholar]
- Schulz, R. 2009, SoSyR, 43, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, R., Stüwe, J. A., & Boehnhardt, H. 2004, A&A, 422, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulz, R., Alexander, C., Boehnhardt, H., & Glassmeier, K. H. 2009, ESA’s Mission to the Origin of the Solar System (Springer) [Google Scholar]
- Soderblom, L. A., Becker, T. L., Bennett, G., et al. 2002, Science, 296, 1087 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sykes, M. V., & Walker, R. G. 1992, Icarus, 95, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, G. P., Boehnhardt, H., Licandro, J., et al. 2009, AAS/DPS, 41, 37 [Google Scholar]
- Wallis, M. K. 1982, Dusty gas-dynamics in real comets, in Comets, ed. L. L. Wilkening (Tucson: University of Arizona Press), 357 [Google Scholar]
- Weiler, M., Rauer, H., & Helbert, J. 2004, A&A, 414, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whipple, F. 1950, ApJ, 111, 375 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Sensitivity and upper limits of quantities measured by GIADA sub-systems (actual grain sizes depend on the chemical composition, we show the values of silicate and carbon grains, respectively).
Lower limits of the dust mass-loss rate ṁr per mass bins and velocity vr at the heliocentric distances r (AU) before perihelion.
Upper limits of the dust mass-loss rate ṁr per mass bins and velocity vr at the heliocentric distances r (AU) before perihelion.
Sample operative scenario (circular orbit) adopted to estimate GIADA capabilities at the comet.
Number of detections of single carbon grains (both compact and fluffy) and deposited mass (coming from nucleus-pointing direction) expected during a sample GIADA operative scenario at comet 67P, for GIADA continuously operating from rh = 3.4 to rh = 1.3 AU.
All Figures
 |
Fig. 1 Afρdata of comet 67P. Squares: pre-perihelion measurements on 2008 VLT images (this paper); Triangles: pre-perihelion measurements of the CARA 2008 campaign (http://cara.uai.it); Diamonds: post-perihelion measurements available in the Lowell Comet Database related to 1982 and 1983, and in the CARA Archive related to 1996. All measurements refer to the seeing-disc (upper error bar) and outermost (lower error bar) coma visible in the images. The interpolations (solid line: pre-perihelion; dashed line: post-perihelion) are the input to the dust environment model discussed in this paper. |
| In the text | |
 |
Fig. 2 Results of the calibration of the GIADA GDS+IS sub-system. The thin solid line was computed by the Mie theory applied to carbon spheres. The thick lines provide the geometric cross section of spheres of a bulk density of 102 (left) and 103 (right) kg m-3. |
| In the text | |
 |
Fig. 3 Dust environment of comet 67P. Panel a): maximum mass escaping the 67P inner coma (of size of about 20 nucleus radii) for compact (solid line) and fluffy (dotted line) grains. Panel b): pre-perihelion (solid line) and post-perihelion (dashed line) dust mass-loss rate provided by the interpolated values of Afρ (see Fig. 1), the dust velocity (panel c)), the differential size distribution (panel d)), and the assumed value of the geometric albedo Ap = 0.04: the mass-loss rate values are inversely proportional to Ap. Panel c): dust ejection velocity from the inner coma for compact (solid line) and fluffy (dotted line) grains; its intersection with the assumed escape velocity (dot-dashed line) provides the sun distance where 1 mg grains are able to escape the inner coma (panel a)). Panel d): pre-perihelion (solid line) and post-perihelion (dashed line) power index of the differential dust size distribution for grains of β > 5 × 10-4; two-dot-dashed line: power index of the dust distribution for grains of β < 5 × 10-4. |
| In the text | |
 |
Fig. 4 Comparison of the Trieste (solid lines), Granada (dotted lines) and trail (dashed lines) codes modelling the TNG image on 2003, March 27 at 2.6 AU post-perihelion with isotropic dust ejection. The innermost isophote corresponds to Af = 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −x axis, scale in km. |
| In the text | |
 |
Fig. 5 Observed (solid lines) and computed (dashed lines) isophotes of the VLT image on 2008, June 1 at 2.99 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 8 × 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 107° counterclockwise from +y, scale in 106 km. |
| In the text | |
 |
Fig. 6 Observed (solid lines) and computed (dashed lines) isophotes of the VLT image on 2008, September 4 at 2.29 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 10-, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 56° clockwise from +y, scale in 106 km. |
| In the text | |
 |
Fig. 7 Observed (solid lines) and computed (dashed lines) isophotes of the VLT image on 2008, October 22 at 1.93 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 1.6 × 10-6, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 73° clockwise from +y, scale in 106 km. |
| In the text | |
 |
Fig. 8 Observed (solid lines) and computed (dashed lines) isophotes of IAA image on 2008, December 11 at 1.56 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 10-6, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 72° clockwise from +y, scale in 106 km. |
| In the text | |
 |
Fig. 9 Spin orientation on the sky according to different models (adapted from Lamy et al. 2007). Black dot: this paper (the dot size is unrelated to model uncertainties). Grey region: Davidsson & Gutiérrez (2005). Symbol * : Chesley (2004). White dot: Schleicher (2006). Hatched region: Lamy et al. (2007). Dashed lines: obliquity of 50° or 130° (Weiler et al. 2004). |
| In the text | |
 |
Fig. 10 Observed (solid lines) and computed (dashed lines) isophotes of the CARA image on 2009, January 25 at 1.31 AU pre-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 1.7 × 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 68° clockwise from +y, scale in 106 km. |
| In the text | |
 |
Fig. 11 Observed (solid lines) and computed (dashed lines) isophotes of KISO image on 2002, December 2 at 1.72 AU post-perihelion. Left panel: isotropic ejection; right panel: seasonal ejection. The innermost isophote corresponds to Af = 5 × 10-7, the outer isophotes decrease by a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 65° counterclockwise from +y, scale in 106 km. |
| In the text | |
 |
Fig. 12 Observed (solid lines) and computed (dashed lines) isophotes of TNG image on 2003, March 27 at 2.58 AU post-perihelion. Left panel: seasonal ejection with the time-dependent size distribution shown in panel d of Fig. 3, with a power index ranging from −3.0 before perihelion to −4.2 after; isotropic ejection provided very similar fits (Fig. 4). Right panel: constant size distribution index at −3.6. The innermost isophote corresponds to Af = 10-7, the outer isophotes decrease of a factor 2 in Af. The Sun direction is along the −y axis; the north direction is in PA = 133° clockwise from +y, scale in 106 km. |
| In the text | |
 |
Fig. 13 Afρdata of comet 67P (see Fig. 1 for symbol explanation). The solid line shows the Afρ curve better fitting the CARA image. |
| In the text | |
 |
Fig. 14 Pre-perihelion dust mass loss rate computed assuming the Afρ extrapolation shown in Fig. 13 (solid line) and a geometric albedo Ap = 0.04. The post-perihelion mass-loss rate and all the other parameter values remain the same as shown in Fig. 3. |
| In the text | |
 |
Fig. 15 Observed (solid lines) and computed (dashed lines, seasonal ejection) isophotes on the VLT image of 2008, September 4 (left panel) and of the CARA image on 2009, January 25 (right panel) according to the Afρ curve shown in Fig. 13. The innermost isophote corresponds to Af = 1.8 × 10-7 in the right panel, with a better fit of the sunward tail than in Fig. 10; and to Af = 3 × 10-6 in the left panel, a factor 3 higher than in Fig. 6. |
| In the text | |
 |
Fig. 16 Upper panel: observed (error bars) and computed (continuous lines: environment from Figs. 1 and 3; dashed lines: environment from Figs. 13 and 14) trail peak flux in 2004, April. Lower panel: trail half width inside (+ symbol) and outside (× symbol) the comet orbit, compared to predictions of the models. |
| In the text | |
 |
Fig. 17 Upper panel: observed (error bars) and computed (continuous lines: environment from Figs. 1 and 3 with geometric albedo Ap = 0.06; dashed lines: environment from Figs. 13 and 14 with geometric albedo Ap = 0.02) trail peak flux in 2005, August. Lower panel: trail half width inside (+ symbol) and outside (× symbol) the comet orbit, compared to predictions of the models. |
| In the text | |
 |
Fig. 18 Upper panel: observed (error bars) and computed (continuous lines: environment from Figs. 1 and 3 with geometric albedo Ap = 0.06; dashed lines: environment from Figs. 13 and 14 with geometric albedo Ap = 0.02) trail peak flux in 2006, April. Lower panel: trail half width inside (+ symbol) and outside (× symbol) the comet orbit, compared to predictions of the models. |
| In the text | |
 |
Fig. 19 Observations of water-loss rates from 67P. Pre-perihelion data: triangle (Feldman 2004), diamond (Crovisier et al. 2002) and squares (Schleicher 2006). Post-perihelion data: symbols * (Hanner et al. 1985), + (Mäkinen 2004) and × (Schleicher 2006). |
| In the text | |
 |
Fig. 20 Extrapolations beyond 2 AU of 67P pre-perihelion water-loss rates. Triangle, diamond and squares: observations (Fig. 19). Symbol × : post-perihelion CN-loss rates (Schleicher 2006 at sun distances lower than 2 AU, Schulz et al. 2004) beyond). Vertical error bars: upper limits of pre-perihelion CN-loss rate (Schulz, private communication) multiplied by 103. Solid line: water-loss rate obtained by the dust-loss rate assuming a constant dust-to-gas mass ratio of 3. Dotted lines: water-loss rate predicted by Gortsas et al. (2010) assuming an active area fraction of 3% and heat conductivities of 0.1 (lower line) and 10-3 W m-1 K-1 (upper line). Dashed line: water-loss rate predicted by De Sanctis et al. (2006) rescaled to 4% their assumed active area fraction of 50% (see text for discussion, assumed heat conductivity of 3 W m-1 K-1). |
| In the text | |
 |
Fig. 21 Expected GIADA GDS+IS events vs. heliocentric distance. The bars represent the lower-to-upper limit of expected events (measurement of scattering cross section, momentum, mass, and velocity) of single carbon grains (both compact and fluffy) detected by the GDS+IS according to the scenario described in Table 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.