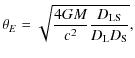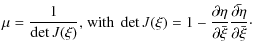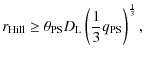| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/200913844 | |
| Published online | 05 October 2010 | |
Detectability of extrasolar moons as gravitational microlenses
C. Liebig - J. Wambsganss
Astronomisches Rechen-Institut, Zentrum
für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120
Heidelberg, Germany
Received 10 December 2009 / Accepted 25 April 2010
Abstract
We evaluate gravitational lensing as a technique for the detection of
extrasolar moons. Since 2004 gravitational microlensing has been
successfully applied as a detection method for extrasolar planets. In
principle, the method is sensitive to masses as low as an Earth mass or
even a fraction of it. Hence it seems natural to investigate the
microlensing effects of moons around extrasolar planets. We explore the
simplest conceivable triple lens system, containing one star, one
planet and one moon. From a microlensing point of view, this system can
be modelled as a particular triple with hierarchical mass ratios very
different from unity. Since the moon orbits the planet, the planet-moon
separation will be small compared to the distance between planet and
star. Such a configuration can lead to a complex interference of
caustics. We present detectability and detection limits by comparing
triple-lens light curves to best-fit binary light curves as caused by a
double-lens system consisting of host star and planet - without moon.
We simulate magnification patterns covering a range of mass and
separation values using the inverse ray shooting technique. These
patterns are processed by analysing a large number of light curves and
fitting a binary case to each of them. A chi-squared criterion is used
to quantify the detectability of the moon in a number of selected
triple-lens scenarios. The results of our simulations indicate that it
is feasible to discover extrasolar moons via gravitational microlensing
through frequent and highly precise monitoring of anomalous Galactic
microlensing events with dwarf source stars.
Key words: gravitational lensing: micro - planets and satellites: general - methods: numerical - methods: statistical
1 Introduction
By now hundreds of extrasolar planets have been
detected![]() . For all we know, none of
the
newly discovered extrasolar planets offers physical conditions
permitting any form of life. But the search for planets potentially
harbouring life and the search for indicators of habitability is
ongoing. One of these indicators might be the presence of a large
natural satellite - a moon - which stabilises the rotation axis of
the planet and thereby the surface climate (Benn
2001). It has
also been suggested that a large moon itself might be a good candidate
for offering habitable conditions (Scharf
2006). In the solar
system, most planets harbour moons. In fact, the moons in the solar
system outnumber the planets by more than an order of magnitude. No
moon has yet been detected around an extrasolar planet.
. For all we know, none of
the
newly discovered extrasolar planets offers physical conditions
permitting any form of life. But the search for planets potentially
harbouring life and the search for indicators of habitability is
ongoing. One of these indicators might be the presence of a large
natural satellite - a moon - which stabilises the rotation axis of
the planet and thereby the surface climate (Benn
2001). It has
also been suggested that a large moon itself might be a good candidate
for offering habitable conditions (Scharf
2006). In the solar
system, most planets harbour moons. In fact, the moons in the solar
system outnumber the planets by more than an order of magnitude. No
moon has yet been detected around an extrasolar planet.
The majority of known exoplanets has been discovered through radial velocity measurements, with the first successful finding reported by Mayor & Queloz (1995). This method is not sensitive to satellites of those planets, because the stellar ``Doppler wobble'' is only affected by the orbital movement of the barycentre of a planet and its satellites, though higher-order effects could play a role eventually. Here we consider Galactic microlensing, which has led to the discovery of several relatively low-mass exoplanets since the first report of a successful detection by Bond et al. (2004), as a promising technique for the search for exomoons.
As early as 1999, it has been suggested that extrasolar moons
might be
detectable through transit observations (Sartoretti
& Schneider 1999), either
through direct observation of lunar occultation or through transit
timing variations, as the moon and planet rotate around their common
barycentre, causing time shifts of the transit ingress and egress
(cf. also Holman & Murray
2005). In their simulations of space-based
gravitational microlensing Bennett
& Rhie (2002) mention the possibility
of discovering extrasolar moons similar to our own Moon. Later that
year, Han & Han (2002)
performed a detailed feasibility study whether
microlensing offers the potential to discover an Earth-Moon analogue,
but concluded that finite source effects would probably be too severe
to allow detections. Williams
& Knacke (2004) published the quite original
suggestion to look for spectral signatures of Earth-sized moons in the
absorption spectra of Jupiter-sized planets. Cabrera
& Schneider (2007)
proposed a sophisticated transit approach using ``mutual event
phenomena'', i.e. photometric variation patterns due to different
phases of occultation and light reflection of planet and
satellite. Han (2008)
undertook a new qualitative study of a
number of triple-lens microlensing constellations finding
``non-negligible'' light curve signals to occur in the case of an
Earth-mass moon orbiting a 10 Earth-mass planet, ``when the
planet-moon separation is similar to or greater than the Einstein
radius of the planet''. Lewis
et al. (2008) analysed pulsar
time-of-arrival signals for lunar signatures. Kipping (2009a,b)
refined and extended the transit timing models of
exomoons to include transit duration variations, and
Kipping et al. (2009)
examined transit detectability of exomoons with
Kepler-class photometry and concluded that in optimal cases moon
detections down to ![]() should be possible.
should be possible.
We cover here several new aspects concerning the microlensing search for exomoons, extending the work of Han (2008). First, the detectability of lunar light curve perturbations is determined with a statistical significance test that does not need to rely on human judgement. Second, all parameters of the two-dimensional three-body geometry, including the position angle of the moon with respect to the planet-star axis, are varied. Third, an unbiased extraction of light curves from the selected scenarios enables a tentative prediction of the occurrence rate of detectable lunar light curve signals. A more detailed account of this study is available as Liebig (2009).
The paper is structured as follows: in Sect. 2, we recall the fundamental equations of gravitational microlensing relevant to our work. Our method for quantifying the detection rates for extrasolar moons in selected lensing scenarios is presented in Sect. 3. In Sect. 4, we discuss the astrophysical implications of the input parameters of the simulations. Our results are presented in Sect. 5, together with a first interpretation and a discussion of potential problems of our method.
2 Basics of gravitational microlensing
The deflection of light by massive bodies is a consequence of the theory of general relativity (Einstein 1916) and has been experimentally verified since 1919 (Dyson et al. 1920), see Paczynski (1996) for an introduction to the field or Schneider et al. (2006) for a comprehensive review.
The typical scale of angular separations in gravitational
lensing is
the Einstein radius ![]() ,
the
angular radius of the ring of formally infinite image magnification
that appears when a source at a distance
,
the
angular radius of the ring of formally infinite image magnification
that appears when a source at a distance ![]() ,
a lens of mass Mat a distance
,
a lens of mass Mat a distance ![]() ,
and the observer are perfectly aligned:
,
and the observer are perfectly aligned:
where G denotes the gravitational constant, c the speed of light.
Here we focus on the triple lens case with host star (S),
planet
(P) and moon (M), see
Fig. 1
for
illustration. The lens equation can be expressed using complex
coordinates, where ![]() shall denote the angular source position and
shall denote the angular source position and
![]() the image
positions, cf. choice of notation in Witt
(1990)
and Gaudi et al. (1998).
the image
positions, cf. choice of notation in Witt
(1990)
and Gaudi et al. (1998).
![]() stands for
the angular position of the
lensing body i. qij
is the mass ratio between lenses i and
j (
stands for
the angular position of the
lensing body i. qij
is the mass ratio between lenses i and
j (
![]() ).
The lens equation gets the following
form, if the primary lens, the host star S, has
unit mass and is
placed in the origin of the lens plane,
).
The lens equation gets the following
form, if the primary lens, the host star S, has
unit mass and is
placed in the origin of the lens plane,
This is a mapping from the lens plane to the source plane, which maps the images of a source star to its actual position in the source plane. As pointed out in Rhie (1997), and explicitly calculated in Rhie (2002), the triple-lens equation is a tenth-order polynomial equation in
In microlensing, the images cannot be resolved. Detectable is
only the
transient change in magnitude of the source star, when lens and source
star are in relative motion to each other. The total
magnification ![]() of the base flux is obtained as the inverse of the determinant
of the Jacobian of the mapping Eq. (2),
of the base flux is obtained as the inverse of the determinant
of the Jacobian of the mapping Eq. (2),
Gravitational lensing changes the apparent solid angle of a source, not the surface brightness. The magnification
For a status report of the past, present and prospective future of planet searching via Galactic microlensing the recent white papers of 2008/2009 are a good source of reference (Gaudi et al. 2009; Beaulieu et al. 2008; Dominik et al. 2008; Bennett et al. 2009).
3 Method
The simplest gravitational lens system incorporating an extrasolar moon is a triple-lens system consisting of the lensing star, a planet and a moon in orbit around that planet, as sketched in Fig. 1. Most likely, lunar effects will first show up as noticeable irregularities in light curves that have been initially observed and classified as light curves with planetary signatures. To measure the detectability of a given triple-lens system among binary lenses, we have to determine whether the provided triple-lens light curve differs statistically significantly from binary-lens light curves.
| Figure 1:
Geometry of our triple-lens scenario, not to scale. Five parameters
have to be fixed: the mass ratios |
|
| Open with DEXTER | |
To clarify the terminology: We investigate light curves that show a
deviation from the single-lens case due to the presence of the
planetary caustic, i.e. which would be modelled as a star-plus-planet
system in a first approximation. We call lunar detectability
the
fraction of those light curves which display a significant deviation
from a star-plus-planet lens model due to the presence of the moon.
We measure the difference between a given triple-lens light curve
(which is taken to be the ``true'' underlying light curve of the
event) and its best-fit binary-lens counterpart. The best-fit
binary-lens light curve is found by a least-square fit. We then employ
![]() -statistics
to see whether the triple-lens light curve could
be explained as a normal fluctuation within the error boundaries of
the binary-lens light curve. If this is not the case, the moon is
considered detectable.
-statistics
to see whether the triple-lens light curve could
be explained as a normal fluctuation within the error boundaries of
the binary-lens light curve. If this is not the case, the moon is
considered detectable.
Detection and characterisation are two separate problems in the search for extrasolar planets or moons, though, and we do not make statements about the latter. When characterising an observed light curve with clear deviations from the binary model, it is still possible that ambiguous solutions - lunar and non-lunar - arise. This does not reflect on our results. We simply give the fraction of triple-lens light curves significantly deviating from binary-lens light curves, without exploring whether they can be uniquely characterised.
A qualitative impression of the lunar influence on the caustic structure can be gained from the magnification patterns in Fig. 2. Extracted example light curves are presented in Fig. 3. Going beyond the qualitative picture, in this paper we quantify the detectability of an extrasolar moon in gravitational microlensing light curves in selected scenarios.
![\begin{figure}
\par\includegraphics[height=22cm,width=16.5cm,clip]{13844fg02.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg58.png)
|
Figure 2:
Details of the analysed triple-lens magnification maps for an example
mass/separation scenario with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=22cm,width=16.5cm,clip]{13844fg03.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg60.png)
|
Figure 3:
Sample of triple-lens light curves corresponding to the source
trajectories depicted in Fig. 2. The solid
light curves were extracted with an assumed solar source size, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg04.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg62.png)
|
Figure 4:
Magnification pattern displaying the planetary caustic of a triple-lens
system with mass ratios |
| Open with DEXTER | |
3.1 Ray shooting
The triple-lens Eq. (2) is
analytically
solvable, but Han & Han (2002)
pointed out that numerical noise in the
polynomial coefficients caused by limited computer precision was too
high (
![]() )
when solving the polynomial numerically for the
very small mass ratios of moon and star (
)
when solving the polynomial numerically for the
very small mass ratios of moon and star (
![]() ). To avoid
this, we employ the inverse ray-shooting technique, which has the
further advantage of being able to account for finite source sizes and
non-uniform source brightness profiles more easily. It also gives us
the option of incorporating additional lenses (further planets or
moons) without increasing the complexity of the calculations. This
technique was developed by Schneider
& Weiß (1986), Kayser
et al. (1986)
and Wambsganss
(1990,1999)
and already applied to
planetary microlensing in Wambsganss
(1997).
). To avoid
this, we employ the inverse ray-shooting technique, which has the
further advantage of being able to account for finite source sizes and
non-uniform source brightness profiles more easily. It also gives us
the option of incorporating additional lenses (further planets or
moons) without increasing the complexity of the calculations. This
technique was developed by Schneider
& Weiß (1986), Kayser
et al. (1986)
and Wambsganss
(1990,1999)
and already applied to
planetary microlensing in Wambsganss
(1997).
Inverse ray-shooting means that light rays are traced from the
observer back to the source plane. This is equivalent to tracing rays
from the background source star to the observer plane. The influence
of all masses in the lens plane on the light path is calculated. In
the thin lens approximation, the deflection angle is just the sum of
the deflection angles of every single lens. After deflection, all
light rays are collected in pixel bins of the source plane. Thus a
magnification pattern is produced (e.g. Fig. 4).
Lengths in this map can be translated to angular separations or,
assuming a constant relative velocity between source and lens, to time
intervals. The number of collected light rays per pixel is
proportional to the magnification ![]() of a background source with
pixel size at the respective position in the source plane. The
resolution in magnification of these numerically produced patterns is
finite and depends on the total number of rays shot.
of a background source with
pixel size at the respective position in the source plane. The
resolution in magnification of these numerically produced patterns is
finite and depends on the total number of rays shot.
3.2 Light curve simulation
We obtain simulated microlensing light curves with potential
traces of
a moon by producing magnification maps (Fig. 4) of
triple-lens scenarios with mass ratios very different from unity. A
light curve is then obtained as a one-dimensional cut through the
magnification pattern, convolved with the luminosity profile of a
star. Only a few more assumptions are necessary to simulate
realistic, in principle observable, light curves: angular source size,
relative motion of lens and source, and lens mass. As a first
approximation to the surface brightness profiles of stars we use a
profile with radius ![]() and constant surface
brightness (ignoring limb-darkening effects). The light curve is
sampled at equidistant intervals. In Sect. 4.7 we
discuss physical implications of the sampling frequency. In order to
be able to make robust statistical statements about the detectability
of a moon in a chosen setting, i.e. a certain magnification pattern,
we analyse a grid of source trajectories that delivers about two
hundred light curves, see also Fig. 5. To
have an unbiased sample, the grid is chosen independently of lunar
caustic features, but all trajectories are required to show pronounced
deviations from the single-lens light curve due to the planet.
and constant surface
brightness (ignoring limb-darkening effects). The light curve is
sampled at equidistant intervals. In Sect. 4.7 we
discuss physical implications of the sampling frequency. In order to
be able to make robust statistical statements about the detectability
of a moon in a chosen setting, i.e. a certain magnification pattern,
we analyse a grid of source trajectories that delivers about two
hundred light curves, see also Fig. 5. To
have an unbiased sample, the grid is chosen independently of lunar
caustic features, but all trajectories are required to show pronounced
deviations from the single-lens light curve due to the planet.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg05.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg67.png)
|
Figure 5:
Illustration of how the magnification pattern of a given
star-planet-moon configuration is evaluated. In order to have an
unbiased statistical sample, the source trajectories are chosen
independently of the lunar caustic features, though all light curves
are required to pass through or close to the planetary caustic. This is
realised through generating a grid of source trajectories that is only
oriented at the planetary caustic. In the actual evaluation a
10 times denser grid than shown here was used. The
magnification map has to be substantially larger than the caustic to
ensure an adequate baseline for the light curve fitting. The side
length of this pattern is |
| Open with DEXTER | |
3.3 Fitting
For each triple-lens scenario, we produce an additional magnification pattern of a corresponding binary-lens system, where the mass of the moon is added to the planetary mass. As a first approximation, one can compare two light curves with identical source track parameters, see Fig. 6a. Numerically big differences can occur without a significant topological difference, because the additional third body not only introduces additional caustic features, it also slightly moves the location of the double-lens caustics.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg06.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg68.png)
|
Figure 6: Triple-lens light curve (solid line) extracted from the magnification pattern in Fig. 4, compared with a light curve extracted from the corresponding binary-lens magnification map (dashed line), with no third body and the planet mass increased by the previous moon mass. The difference of the two light curves is plotted as the dotted line. The central peak of the triple-lens light curve is caused by lunar caustic perturbations, that cannot easily be reproduced with a binary lens. In a), identical source trajectory parameters are used to extract the binary-lens light curve and large residuals remain that can be avoided with a different source trajectory. In b), the best-fit binary-lens light curve is shown (dashed) in comparison with the triple-lens light curve (solid). Here, the residuals can be attributed to the moon. If the deviation is significant, the moon is detectable in the triple-lens light curve. A source with solar radius at a distance of 8 kpc is assumed. |
| Open with DEXTER | |
3.4 Light curve comparison
We want to use the properties of the ![]() -distribution for a test
of significance of deviation between the two simulated light curves of
the triple lens and the corresponding binary lens.
-distribution for a test
of significance of deviation between the two simulated light curves of
the triple lens and the corresponding binary lens.
Most commonly, the ![]() -distribution is used to test
the
goodness-of-fit of a model to experimental data. To compare two
simulated curves instead, as in our case, one possible approach is to
randomly generate artificial data around one of them and then
consecutively fit the two theoretical curves to the artificial data
with some free parameters. Two ``
-distribution is used to test
the
goodness-of-fit of a model to experimental data. To compare two
simulated curves instead, as in our case, one possible approach is to
randomly generate artificial data around one of them and then
consecutively fit the two theoretical curves to the artificial data
with some free parameters. Two ``![]() -values'' Q21
and Q22will
result. Their difference,
-values'' Q21
and Q22will
result. Their difference, ![]() can then
be calculated and a threshold value
can then
be calculated and a threshold value ![]() is
chosen. The condition for reported detectability of the deviation is
then
is
chosen. The condition for reported detectability of the deviation is
then ![]() .
A detailed description
of the algorithm and its application to microlensing was presented by
Gaudi & Sackett (2000).
.
A detailed description
of the algorithm and its application to microlensing was presented by
Gaudi & Sackett (2000).
We decided to use a different approach here: In particular,
we were led to consider other possible techniques by the wish to avoid
``feeding'' our knowledge of the data distribution to a random number
generator in order to get an unbiased and random ![]() -distributed
sample of Q2, when at the
same time we have all the necessary
information to calculate a much more representative
-distributed
sample of Q2, when at the
same time we have all the necessary
information to calculate a much more representative ![]() -value.
We have developed a method to quantify significance of deviations
between two theoretical functions that avoids the steps of data
simulation and subsequent fitting.
-value.
We have developed a method to quantify significance of deviations
between two theoretical functions that avoids the steps of data
simulation and subsequent fitting.
Put simply, we calculate the mean ![]() of all
``
of all
``![]() -values''
that would result, if data with a Gaussian scatter
drawn from a triple-lens light curve is fitted with a
binary light curve. If the triple-lens case and the best-fit
binary-lens case are indistinguishable, then Q2
will be
-values''
that would result, if data with a Gaussian scatter
drawn from a triple-lens light curve is fitted with a
binary light curve. If the triple-lens case and the best-fit
binary-lens case are indistinguishable, then Q2
will be
![]() -distributed
and
-distributed
and ![]() will lie at or very
close to
will lie at or very
close to ![]() ,
the mean of the
,
the mean of the ![]() probability density function. If
the triple-lens light curve and the binary-lens light curve differ
significantly, then Q2 is
not
probability density function. If
the triple-lens light curve and the binary-lens light curve differ
significantly, then Q2 is
not ![]() -distributed
and
-distributed
and ![]() in particular will lie outside the expected range for
in particular will lie outside the expected range for
![]() -distributed
random variables. In the latter case, the moon is
detectable. This approach is presented in mathematical
detail in Appendix A.
-distributed
random variables. In the latter case, the moon is
detectable. This approach is presented in mathematical
detail in Appendix A.
4 Choice of scenarios
This section presents the assumptions that we use for our simulations. We discuss the astrophysical parameter space that is available for simulations of a microlensing system consisting of star, planet and moon. By choosing the most probable or most pragmatic value for each of the parameters, we create a standard scenario, summarised in Table 1 and visualised in Fig. 10, that all other parameters are compared against during the analysis.
The observational search for microlensing events caused by
extrasolar
planets is carried out towards the Galactic bulge, currently limited
to the fields of the wide-field surveys OGLE (Udalski
et al. 1992) and
MOA (Muraki et al. 1999).
This leads to some natural assumptions for the
involved quantities. The source stars are typically close to the
centre of the Galactic bulge at a distance of ![]() kpc,
where the surface density of stars is very high. For the distance to
the lens plane we adopt a value of
kpc,
where the surface density of stars is very high. For the distance to
the lens plane we adopt a value of ![]() kpc.
We assume our primary lens mass to be an M-dwarf star with a mass of
kpc.
We assume our primary lens mass to be an M-dwarf star with a mass of
![]() ,
because that is the most
abundant type, cf. Fig. 5 of Dominik
et al. (2008). Direct lens mass determination is
only possible if additional observables, such as parallax, can be
measured, cf. Gould (2009).
We derive the corresponding Einstein radius of
,
because that is the most
abundant type, cf. Fig. 5 of Dominik
et al. (2008). Direct lens mass determination is
only possible if additional observables, such as parallax, can be
measured, cf. Gould (2009).
We derive the corresponding Einstein radius of
![]() ms.
ms.
Five parameters describe our lens configuration, cf.
Fig. 1:
they are the mass ratios between
planet and star ![]() and between moon and planet
and between moon and planet ![]() ,
the
angular separations
,
the
angular separations ![]() between planet and star and
between planet and star and
![]() between moon and planet, and as the last parameter
between moon and planet, and as the last parameter
![]() ,
the position angle of the moon with respect to the planet-star
axis. These parameters are barely constrained by the physics of a
three-body system, even if we do require mass ratios very different
from unity and separations that allow for stable orbits.
,
the position angle of the moon with respect to the planet-star
axis. These parameters are barely constrained by the physics of a
three-body system, even if we do require mass ratios very different
from unity and separations that allow for stable orbits.
The apparent source size ![]() and the sampling rate
and the sampling rate
![]() affect the shape of the simulated light curves. We
have to define an observational uncertainty
affect the shape of the simulated light curves. We
have to define an observational uncertainty ![]() for the
significance test in the final analysis of the light curves.
for the
significance test in the final analysis of the light curves.
4.1 Mass ratio of planet and star q
We are interested in planets (and not binary stars). Accordingly, we
want a small value for the mass ratio of planet and star ![]() .
Our standard value will be
10-3 which is the mass ratio of Jupiter and Sun,
or a Saturn-mass
planet around an M-dwarf of
.
Our standard value will be
10-3 which is the mass ratio of Jupiter and Sun,
or a Saturn-mass
planet around an M-dwarf of ![]() .
At a given
projected separation between star and planet, this mass ratio
determines the size of the planetary caustic, with a larger
.
At a given
projected separation between star and planet, this mass ratio
determines the size of the planetary caustic, with a larger ![]() leading to a
larger caustic.
leading to a
larger caustic. ![]() is varied to also examine
scenarios with mass ratios corresponding to a Jovian mass around an
M-dwarf and to a Saturn mass around the Sun.
Summarised: for the mass ratio between planet and star we use the
three values
is varied to also examine
scenarios with mass ratios corresponding to a Jovian mass around an
M-dwarf and to a Saturn mass around the Sun.
Summarised: for the mass ratio between planet and star we use the
three values ![]() .
.
4.2 Mass ratio of moon and planet q

To be classified as a moon, the tertiary body must have a mass
considerably smaller than the secondary. The standard case in our
examination corresponds to the Moon/Earth mass ratio of
![]() .
We are generous
towards the higher mass end, and include a mass ratio of 10-1
in
our analysis, corresponding to the Charon/Pluto system. Both examples
are singular in the solar system, but we argue that a more massive
moon is more interesting, since it can effectively stabilise the
obliquity of a planet, which is thought to be favouring the
habitability of the planet (Benn 2001).
At the low mass end of
our analysis we examine
.
We are generous
towards the higher mass end, and include a mass ratio of 10-1
in
our analysis, corresponding to the Charon/Pluto system. Both examples
are singular in the solar system, but we argue that a more massive
moon is more interesting, since it can effectively stabilise the
obliquity of a planet, which is thought to be favouring the
habitability of the planet (Benn 2001).
At the low mass end of
our analysis we examine ![]() .
In
Fig. 7,
three different caustic interferences
resulting from the three adopted mass ratios are shown. Summarised:
For the mass ratio between moon and planet we use the three values
.
In
Fig. 7,
three different caustic interferences
resulting from the three adopted mass ratios are shown. Summarised:
For the mass ratio between moon and planet we use the three values
![]() .
.
4.3 Angular separation of planet and star 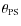
The physical separation of a planet and its host star, i.e. the
semi-major axis ![]() ,
is not directly measurable in gravitational
lensing. Only the angular separation
,
is not directly measurable in gravitational
lensing. Only the angular separation ![]() can directly be
inferred from an observed light curve, where
can directly be
inferred from an observed light curve, where ![]() is valid for a given physical separation
is valid for a given physical separation ![]() at a lens
distance
at a lens
distance ![]() .
The angular separation
.
The angular separation ![]() of a binary will
evoke a certain topology of caustics, illustrated e.g. in
Fig. 1 of
Cassan (2008). They
gradually evolve from the close separation
case with two small triangular caustics on the far side of the star
and a small central caustic at the star position, to a large central
caustic for the intermediate case, when the planet is situated near
the stellar Einstein ring,
of a binary will
evoke a certain topology of caustics, illustrated e.g. in
Fig. 1 of
Cassan (2008). They
gradually evolve from the close separation
case with two small triangular caustics on the far side of the star
and a small central caustic at the star position, to a large central
caustic for the intermediate case, when the planet is situated near
the stellar Einstein ring,
![]() .
This is also
called the ``resonant lensing'' case, as described in
Wambsganss (1997). If
the planet is moved further out, one
obtains a small central caustic and a larger isolated, roughly
kite-shaped planetary caustic that is elongated towards the primary
mass in the beginning, but becomes more and more symmetric and
diamond-shaped if the planet is placed further outwards.
.
This is also
called the ``resonant lensing'' case, as described in
Wambsganss (1997). If
the planet is moved further out, one
obtains a small central caustic and a larger isolated, roughly
kite-shaped planetary caustic that is elongated towards the primary
mass in the beginning, but becomes more and more symmetric and
diamond-shaped if the planet is placed further outwards.
| Figure 7:
Caustic topology with different lunar mass ratios. From left
to right, the lunar mass ratio increases from |
|
| Open with DEXTER | |
In analogy, a ``lunar resonant lensing zone'' can be defined, when
measuring the angular separation of moon and planet in units of
planetary Einstein radii ![]() .
Viewing our solar
system as a gravitational lens system at
.
Viewing our solar
system as a gravitational lens system at ![]() kpc
and with
kpc
and with ![]() kpc,
Jupiter's Einstein radius in physical lengths would be
0.11 AU in the lens plane, that is almost 10 times the
semi-major
axis of Callisto. However, the smaller moons of Jupiter cover the
region out to 2 Jovian Einstein radii. If there is a moon at an
angular separation of the planet of
kpc,
Jupiter's Einstein radius in physical lengths would be
0.11 AU in the lens plane, that is almost 10 times the
semi-major
axis of Callisto. However, the smaller moons of Jupiter cover the
region out to 2 Jovian Einstein radii. If there is a moon at an
angular separation of the planet of
![]() ,
it will show its influence
in any of the caustics topologies. But we focus our study on the
wide-separation case for the following reasons:
regarding the close-separation triangular caustics, we argue that the
probability to cross one of them is vanishingly small and,
furthermore, the magnification substantially decreases as they move
outwards from the star.
The intermediate or resonant caustic is well ``visible'' because it
is always located close to the peak of the single-lens curve. But all
massive bodies of a given planetary system affect the central caustic
with minor or major perturbations and deformations
(Gaudi et al. 1998).
There is no reason to expect that extrasolar
systems are generally less densely populated by planets or moons than
the solar system. Since we are looking for very small
deviations, identifying the signature of the moon among multiple
features caused by low-mass planets and possibly more moons would be
increasingly complex.
The wide-separation case is most favourable, because the planetary
caustic is typically caused by a single planet and interactions due to
the close presence of other planets are highly unlikely
(Bozza 2000,1999).
Any observed interferences can therefore
be attributed to satellites of the planet. Planets with only one
dominant moon are at least common in the solar system (Saturn &
Titan, Neptune & Triton, Earth & Moon). Such a system
would be the
most straightforward to detect in real data.
,
it will show its influence
in any of the caustics topologies. But we focus our study on the
wide-separation case for the following reasons:
regarding the close-separation triangular caustics, we argue that the
probability to cross one of them is vanishingly small and,
furthermore, the magnification substantially decreases as they move
outwards from the star.
The intermediate or resonant caustic is well ``visible'' because it
is always located close to the peak of the single-lens curve. But all
massive bodies of a given planetary system affect the central caustic
with minor or major perturbations and deformations
(Gaudi et al. 1998).
There is no reason to expect that extrasolar
systems are generally less densely populated by planets or moons than
the solar system. Since we are looking for very small
deviations, identifying the signature of the moon among multiple
features caused by low-mass planets and possibly more moons would be
increasingly complex.
The wide-separation case is most favourable, because the planetary
caustic is typically caused by a single planet and interactions due to
the close presence of other planets are highly unlikely
(Bozza 2000,1999).
Any observed interferences can therefore
be attributed to satellites of the planet. Planets with only one
dominant moon are at least common in the solar system (Saturn &
Titan, Neptune & Triton, Earth & Moon). Such a system
would be the
most straightforward to detect in real data.
This makes a strong case for concentrating on the
wide-separation
planetary caustic. As the standard we choose a separation of
![]() and also test a
scenario with
and also test a
scenario with ![]() .
For
comparison: the maximum projected separation of Jupiter at the chosen
distances
.
For
comparison: the maximum projected separation of Jupiter at the chosen
distances ![]() and
and ![]() corresponds to 1.5 solar Einstein radii.
Summarised: for the angular separation between planet and star we use
the two values
corresponds to 1.5 solar Einstein radii.
Summarised: for the angular separation between planet and star we use
the two values ![]() .
.
4.4 Angular separation of moon and planet 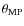
As the moon by definition orbits the planet, there is an upper
limit
to the semi-major axis of the moon ![]() .
It must not exceed the
distance between the planet and its inner Lagrange point. This
distance is called Hill radius and is calculated as
.
It must not exceed the
distance between the planet and its inner Lagrange point. This
distance is called Hill radius and is calculated as
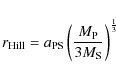
for circular orbits, with the semi-major axis
because for a physical distance
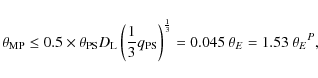
which leads to
We focus on configurations with strong interferences of
planetary and
lunar caustic, what one might call the ``resonant case of lunar
lensing'', examples of which are displayed in Fig. 8.
Therefore, our standard case will have an
angular separation of moon and planet of one planetary Einstein
radius. In total, we evaluate four settings: ![]() ,
in the chosen
setting (Table 1),
this corresponds to
physical projected separations from 0.5 to 0.8 AU.
,
in the chosen
setting (Table 1),
this corresponds to
physical projected separations from 0.5 to 0.8 AU.
| Figure 8:
Magnification patterns with side lengths of |
|
| Open with DEXTER | |
4.5 Position angle of moon 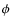
The fifth physical parameter for determining the magnification
patterns is the position angle of the moon ![]() with respect to
planet-star axis, as depicted in Fig. 1. It is
the only parameter that is not fixed in our standard
scenario. Instead, we evaluate this parameter in its entirety by
varying it in steps of
with respect to
planet-star axis, as depicted in Fig. 1. It is
the only parameter that is not fixed in our standard
scenario. Instead, we evaluate this parameter in its entirety by
varying it in steps of ![]() to complete a full circular orbit of
the moon around the planet. By doing this, we are aiming at getting
complete coverage of a selected mass/separation scenario.
Figure 2
visualises how the position of the moon affects
the planetary caustic. It is not to be expected that we will ever have
an exactly frontal view of a perfectly circular orbit, but it serves
well as a first approximation. Summarised: we choose 12 equally spaced
values for the position angle
to complete a full circular orbit of
the moon around the planet. By doing this, we are aiming at getting
complete coverage of a selected mass/separation scenario.
Figure 2
visualises how the position of the moon affects
the planetary caustic. It is not to be expected that we will ever have
an exactly frontal view of a perfectly circular orbit, but it serves
well as a first approximation. Summarised: we choose 12 equally spaced
values for the position angle ![]() of the moon relative to the
planet-star axis, and the results for the various parameter sets are
averaged over these 12 geometries.
of the moon relative to the
planet-star axis, and the results for the various parameter sets are
averaged over these 12 geometries.
4.6 Source size R

The source size strongly influences the amplitudes of the light curve
fluctuations and the ``time resolution''. Larger sources blur out
finer caustic structures, compare Fig. 9.
For our source star assumptions, we have to take into account not only
stellar abundances, but also the luminosity of a given stellar
type. Main sequence dwarfs are abundant in the Galactic bulge, but
they are faint, with apparent magnitudes of ![]() 15 mag to 25 mag at
15 mag to 25 mag at
![]() kpc. In the crowded
microlensing fields, they are difficult
to observe with satisfying photometry by ground-based telescopes, even
if they are lensed and magnified. Giant stars, with apparent baseline
magnitudes
kpc. In the crowded
microlensing fields, they are difficult
to observe with satisfying photometry by ground-based telescopes, even
if they are lensed and magnified. Giant stars, with apparent baseline
magnitudes ![]() 13 mag
to 17 mag, are more likely to allow precise
photometric measurements from ground and, therefore, today's follow-up
observations are biased towards these source stars.
13 mag
to 17 mag, are more likely to allow precise
photometric measurements from ground and, therefore, today's follow-up
observations are biased towards these source stars.
The finite source size constitutes a serious limitation to the
discovery of extrasolar moons. In fact, Han
& Han (2002) stated that
detecting satellite signals in the lensing light curves will be close
to impossible, because the signals are smeared out by the severe
finite-source effect. They tested various source sizes (and
planet-moon separations) for an Earth-mass planet with a Moon-mass
satellite. They find that even for a K0-type source star
(
![]() )
any light curve
modifications caused by the moon are washed out. Han
(2008)
increased lens masses and by assuming a solar source size
)
any light curve
modifications caused by the moon are washed out. Han
(2008)
increased lens masses and by assuming a solar source size
![]() ,
he finds that
``non-negligible satellite signals occur'' in the light curves of
planets of 10 to 300 Earth masses, ``when the planet-moon
separation
is similar to or greater than the Einstein radius of the planet'' and
the moon has the mass of Earth. We use a solar sized source as our
standard case, and present results for four more source radii:
,
he finds that
``non-negligible satellite signals occur'' in the light curves of
planets of 10 to 300 Earth masses, ``when the planet-moon
separation
is similar to or greater than the Einstein radius of the planet'' and
the moon has the mass of Earth. We use a solar sized source as our
standard case, and present results for four more source radii: ![]() .
In terms of stellar Einstein radii this corresponds to five different
source size settings from
.
In terms of stellar Einstein radii this corresponds to five different
source size settings from
![]() to
to
![]() .
.
The ability to monitor smaller sources - dwarfs, low-mass main sequence stars - with good photometric accuracy is one of the advantages of space-based observations. Hence a satellite mission is the ideal tool for this aspect of microlensing, routine detections of moons around planets can be expected with a space-based monitoring program on a dedicated satellite.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg9.eps}
\vspace*{-2.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg120.png)
|
Figure 9:
Illustration of the increasing source radius, compare Fig. 6b:
a)
|
| Open with DEXTER | |
4.7 Sampling rate f
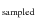
Typical exposure times for the microlensing light curves are 10 to
300 s at a 1.5 m telescope. The frequency of
observations of
an individual interesting event varies between once per 2 h to
once every few minutes, for a single observing site only limited by
exposure time and read-out time of the instrument. One example of this
is the peak coverage of MOA-2007-BLG-400, see Dong
et al. (2009),
where frames were taken every six minutes. Higher observing frequency
equals better coverage of the resulting light curve. A normal
microlensing event is seen as a transient brightening that can last
for a few days to weeks or even months. A planet will alter the light
curve from fraction of a day to about a week; the effect of a low-mass
planet or a moon will only last for a few hours or shorter, see
e.g. Beaulieu et al.
(2006). This duration is inversely proportional to
the transverse velocity ![]() with which the lens moves relative
to the line of sight or the relative proper motion
with which the lens moves relative
to the line of sight or the relative proper motion ![]() between
the background source and the lensing system. We fix this at a typical
between
the background source and the lensing system. We fix this at a typical
![]() km s-1
for
km s-1
for ![]() kpc or
kpc or
![]() .
.
For the simulations, a realistic, non-continuous observing
rate is
mimicked by evaluating the simulated light curve at intervals that
correspond to typical frequencies, but allowing for a constant
sampling rate, which in practise is often prohibited by observing
conditions. We sample the triple-lens light curve in equally sized
steps. With the assumed
constant relative velocity, this translates to equal spacing in
time. Aiming for a rate of ![]() ,
we choose a step size of
,
we choose a step size of
![]() .
To see the effect
of a decreased sampling rate, we have also examined the standard
scenario (see Table 1) with
sampling rates of
factors of 1.5 and 2 longer. Summarised: we use three different
sampling rates,
.
To see the effect
of a decreased sampling rate, we have also examined the standard
scenario (see Table 1) with
sampling rates of
factors of 1.5 and 2 longer. Summarised: we use three different
sampling rates, ![]() min,
1/22 min, 1/30 min.
min,
1/22 min, 1/30 min.
4.8 Assumed photometric uncertainty 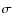
The standard error ![]() of a data point in a microlensing light
curve can vary significantly. Values between 5 and
100 mmag seem
realistic, see, e.g., data plots in the recent event analyses of
Gaudi et al. (2008)
or Janczak et al. (2009).
The photometric uncertainty
directly enters the statistical evaluation of each light curve as
described in Appendix A. We have
drawn results
for an (unrealistically) broad
of a data point in a microlensing light
curve can vary significantly. Values between 5 and
100 mmag seem
realistic, see, e.g., data plots in the recent event analyses of
Gaudi et al. (2008)
or Janczak et al. (2009).
The photometric uncertainty
directly enters the statistical evaluation of each light curve as
described in Appendix A. We have
drawn results
for an (unrealistically) broad ![]() -range from 0.5 mmag
to
500 mmag. An error as small as
-range from 0.5 mmag
to
500 mmag. An error as small as ![]() mmag
for a V=12.3star has recently been reached with
high-precision photometry of an
exoplanetary transit event at the Danish 1.54 m telescope at
ESO La
Silla (Southworth
et al. 2009), which is one of the telescopes
presently used for Galactic microlensing monitoring observations, but
this low uncertainty cannot be transferred to standard microlensing
observations, where crowded star fields make e.g. the use of
defocussing techniques impossible. In our discussion, we regard only
the more realistic range from
mmag
for a V=12.3star has recently been reached with
high-precision photometry of an
exoplanetary transit event at the Danish 1.54 m telescope at
ESO La
Silla (Southworth
et al. 2009), which is one of the telescopes
presently used for Galactic microlensing monitoring observations, but
this low uncertainty cannot be transferred to standard microlensing
observations, where crowded star fields make e.g. the use of
defocussing techniques impossible. In our discussion, we regard only
the more realistic range from ![]() to 100 mmag. We adopt
an ideal scenario with a fixed
to 100 mmag. We adopt
an ideal scenario with a fixed ![]() -value for all sampled points
on the triple-lens light curve and set
-value for all sampled points
on the triple-lens light curve and set ![]() mmag
to be our
standard for the comparison of different mass and separation
scenarios. Summarised: we explore 5 values as photometric
uncertainty:
mmag
to be our
standard for the comparison of different mass and separation
scenarios. Summarised: we explore 5 values as photometric
uncertainty: ![]() ,
10, 20, 50, 100 mmag.
,
10, 20, 50, 100 mmag.
Table 1: Parameter values of our standard scenario.
| Figure 10:
Visualisation of the approximate lunar resonance zone (dark-grey ring),
where planetary and lunar caustic overlap and interact. Also depicted
is the planet lensing zone (light grey), which is the area of planet
positions for which the planetary caustic(s) lie within the stellar
Einstein radius. Distances and caustic inset are to scale. The physical
scale depends not only on the masses of the lensing bodies, but also on
the distances to the lens system and the background star. In our
adopted standard scenario, cf. Table 1, the
Einstein radius |
|
| Open with DEXTER | |
5 Results: detectability of extrasolar moons in microlensing light curves
The numerical results of our work are presented and a first interpretation is made. We start by considering the result for a single magnification pattern in Sect. 5.1. We then present results that cover specific physical triple-lens scenarios (Sect. 5.2). We also evaluate the parameter dependence of the detectability rate, by varying each parameter separately.
5.1 Evaluation of a single magnification pattern
As described in Sect. 3,
all magnification maps are
evaluated by taking a large sample of
unbiased![]() light curves and
then determining the fraction of light curves with significant lunar
signals. The results for a single magnification map (here the pattern
from Fig. 5),
are displayed in Table 2.
light curves and
then determining the fraction of light curves with significant lunar
signals. The results for a single magnification map (here the pattern
from Fig. 5),
are displayed in Table 2.
Table 2: Detectability of the third mass in the magnification pattern of Fig. 5, for different assumed photometric uncertainties.
The percentages can be interpreted as the ``detection probability'' of the moon in a random observed light curve displaying a signature of the planetary caustic - ignoring the possible complication to fully characterise the signal. In this map, the detectability of the moon is about one third, provided we have an observational uncertainty of5.2 Results for selected scenarios
In order to be able to make general statements about a given
planetary/lunar system, we average the results for
12 magnification
patterns representing a full lunar orbit with ![]() .
.
5.2.1 Variation of the photometric uncertainty
The scenario described in Table 1 is evaluated for different photometric uncertainties by analysing the 12 magnification maps shown in Fig. 2. The results are displayed in Table 3.
Table 3: Detectability of the moon in our standard scenario as a function of assumed photometric uncertainty.
For an photometric uncertainty of- the host planet of the satellite has been detected;
- a small source size, up to a few solar radii, is required;
- the moon is massive compared to satellites in the solar system;
- we have assumed light curves with a constant sampling rate of one frame every 15 min for about 50 to 70 h.
5.2.2 Changing the angular separation of planet and moon
Table 4
lines up the changing detectability for
different values of the projected planet-moon separation
![]() ,
with all other parameters as in standard scenario
(Table 1).
,
with all other parameters as in standard scenario
(Table 1).
Table 4: Detectability of the moon as a function of the planet-moon separation for our standard scenario.
With the chosen range from5.2.3 Variation of the moon mass
Table 5
shows the changing detectability for a
varying mass ratio ![]() of lunar and planetary mass, with all other
parameters as in our standard scenario (Table 1).
of lunar and planetary mass, with all other
parameters as in our standard scenario (Table 1).
Table 5: Detectability of the moon depending on moon-planet mass ratio.
Over the range of the moon-planet mass ratio,5.2.4 Changing the planetary mass ratio
Table 6
lists the changing detectability for a
varying mass ratio between planet and star ![]() .
.
Table 6: Dependence of lunar detectability as a function of the planet-star mass ratio, all other parameters as in our standard scenario.
We adjusted the parameters of the grid of source trajectories, so that the grid spacing scales with the total caustic size. For a decreasing mass of the planet, the apparent source size increases relative to the caustic size, so finer features will be blurred out more in the case of a smaller planet. Also the absolute change in magnification scales with the planetary mass. As expected, the detection efficiency is roughly proportional to the planetary caustic size.5.2.5 Different sampling rates
Table 7 presents the changing lunar detectability for different sampling rates.
Table 7: Detectability of the moon depending on the sampling rate of the simulated light curves.
A lower sampling frequency lowers the detection probability, but the effect is less pronounced than expected. This means it may be favourable to monitor a larger number of planetary microlensing events with high sampling frequency, rather than a very small number of them with ultra-high sampling. Our assumed sampling rates can easily be met by follow-up observations, as they are presently performed for anomalous Galactic microlensing events.5.2.6 Source size variations
We analysed simulated light curves of the standard scenario with five
different source star radii. They cover the range between a star the
size of our Sun and a small giant star with ![]() at
at ![]() kpc.
kpc.
Table 8: Detectability of the moon depending on the size of the source star, all other parameters as in our standard scenario.
A larger source blurs out all sharp caustic-crossing features
of a
light curve, compare Fig. 9. We
see from our
results in Table 8 that
the discovery of a
moderately massive moon (see standard scenario assumptions in
Table 1)
is impossible for a source
star size of ![]() or larger within
our assumptions.
or larger within
our assumptions.
5.2.7 Increased separation between star and planet
For reasons given above in Sect. 4.3, we did not
vary the
separation between star and planet significantly, but stayed in the
outer ranges of the planet lensing zone, corresponding to a
well-detectable, wide-separation planetary caustic. For
![]() ,
we get a
detectability of 33.3%, which is similar to our standard case
(
,
we get a
detectability of 33.3%, which is similar to our standard case
(
![]() )
with 30.6%.
)
with 30.6%.
6 Conclusion and outlook
In this work we provide probabilities for the detection of
moons
around extrasolar planets with gravitational lensing. We showed that
massive extrasolar moons can principally be detected and identified
via the technique of Galactic microlensing. From our results it can be
concluded that the detection of an extrasolar moon - under favourable
conditions - is within close reach of available observing
technology. The unambiguous characterisation of observed lunar
features however will be challenging. The examined lens scenarios
model realistic triple-lens configurations. An observing rate of
about one frame per 15 min is desirable, which is high, but
well
within the range of what is now regularly performed in microlensing
follow-up observations of anomalous events. Similarly, an
observational uncertainty of about 20 mmag can be met with
today's
ground-based telescopes and photometric reduction techniques for
sufficiently bright targets. Bright microlensing targets are mostly
giant stars, which is an impediment to the detection of moons: Bulge
giants with radii of order 10 ![]() or larger smooth out any lunar
caustic feature. Therefore, in order to find moons, it is crucial to
be able to perform precise photometry on small sources with angular
sizes of the order of 10-3 Einstein radii,
corresponding to a few
solar radii or smaller at a distance of 8 kpc. This means
dwarf stars
rather than giants need to be monitored in order to identify moons in
the intervening planetary systems. Some improvement in resolution can
be gained with the lucky-imaging technique on medium-sized ground
telescopes (Grundahl
et al. 2009). Under very favourable circumstances,
exomoons might already be detectable from ground. However, future
space-based telescopes, such as ESA's proposed
Euclid
or larger smooth out any lunar
caustic feature. Therefore, in order to find moons, it is crucial to
be able to perform precise photometry on small sources with angular
sizes of the order of 10-3 Einstein radii,
corresponding to a few
solar radii or smaller at a distance of 8 kpc. This means
dwarf stars
rather than giants need to be monitored in order to identify moons in
the intervening planetary systems. Some improvement in resolution can
be gained with the lucky-imaging technique on medium-sized ground
telescopes (Grundahl
et al. 2009). Under very favourable circumstances,
exomoons might already be detectable from ground. However, future
space-based telescopes, such as ESA's proposed
Euclid![]() mission
(cf. Réfrégier et al.
2010, Chapter 17) or the dedicated Microlensing
Planet Finder (MPF) mission proposed to NASA
(cf. Bennett et al. 2009),
will surely have the potential to find
extrasolar moons through gravitational lensing.
mission
(cf. Réfrégier et al.
2010, Chapter 17) or the dedicated Microlensing
Planet Finder (MPF) mission proposed to NASA
(cf. Bennett et al. 2009),
will surely have the potential to find
extrasolar moons through gravitational lensing.
We thank our referee, Jean-Philippe Beaulieu, for his constructive comments, which helped to improve the manuscript. C.L. would like to thank Sven Marnach for his helpful input on the significance test. This research has made use of NASA's Astrophysics Data System and the arXiv e-print service operated by Cornell University.
Appendix A Significance of deviation
This section explains the method that we use to determine the significance of deviation between the two simulated light curves of the triple lens and the best-fit binary lens model.
When we want to decide whether real observational data is
better
described with a triple-lens or with a binary-lens model, we can fit
both models to the data and use the ![]() -test to assess the
significance of the deviation between the data and the models and pick
the model with the better fit.
-test to assess the
significance of the deviation between the data and the models and pick
the model with the better fit.
We do not have observational data, but numerically computed
light
curves. If we observed one of the simulated triple-lens systems, we
would expect the data points to have a Gaussian distribution around
the theoretical values. We could produce artificial data by randomly
scattering the simulated triple-lens light curve data points around
their theoretical values and then fit a binary-lens model and the
triple-lens model to this artificial data set, as described in
Sect. 3.4.
This approach allows us to use the
usual ![]() -test,
but is computationally intensive, because the
models have to be fitted numerous times to get a statistically sound
sample of
-test,
but is computationally intensive, because the
models have to be fitted numerous times to get a statistically sound
sample of ![]() -values.
In our approach, we directly calculate the
-values.
In our approach, we directly calculate the
![]() -value which
is the expectation value of the above method.
-value which
is the expectation value of the above method.
We hypothesise, every simulated point on our triple-lens light
curve
is in fact the mean ![]() of the distribution of a random variable
Xi that is
distributed according to the Gaussian probability
density function fi(xi)
with a standard deviation of
of the distribution of a random variable
Xi that is
distributed according to the Gaussian probability
density function fi(xi)
with a standard deviation of
![]() .
.
![]() is the variance of the
distribution
is the variance of the
distribution![]() .
.
We now want to examine whether the Xi
could be described equally
well with a binary-lens model ![]() .
We introduce the new
.
We introduce the new
![]() -distributed
-distributed![]() random variable
random variable
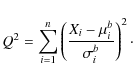
At this step, we could simulate data Xi in order to find a somewhat representative, randomly drawn value of Q2, but instead we simply calculate what the mean value of all possible Q2 would be. We use the definitions, to find
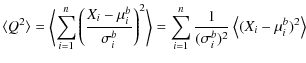
|
Here, we keep in mind that, in general,
| |
= | 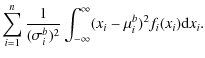
|
|
| = | 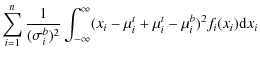
|
||
| = | 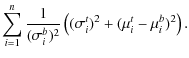
|
We used the definitions of
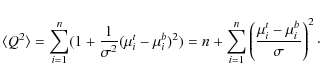
This is the mean of all Q2 possibly resulting, when comparing the simulated binary-lens light curve to randomly scattered triple-lens light curve points. It shall be our measure of deviation. Fortunately, we can provide all remaining parameters:
- n
- is the number of degrees of freedom, equal to the number of compared data points.
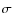
- is the assumed standard deviation or photometric uncertainty of observations.
-
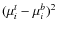
- equals the difference between the two compared light curves squared, which we already use for our least square fit.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13844fgA1.eps}
\vspace*{-4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg189.png)
|
Figure A.1:
The |
| Open with DEXTER | |
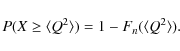
This probability is just the integral of the
We say we have a significant deviation between our two curves,
if the
mean value ![]() is so high that the probability Pfor any random
variable X being larger or equally large is
less than
1%. We interpret this to say, only if the probability for a given
triple lens light curve with independent, normally distributed data
points to be random fluctuation of the compared binary-lens light
curve is less than 1%, we consider it to be principally
detectable.
is so high that the probability Pfor any random
variable X being larger or equally large is
less than
1%. We interpret this to say, only if the probability for a given
triple lens light curve with independent, normally distributed data
points to be random fluctuation of the compared binary-lens light
curve is less than 1%, we consider it to be principally
detectable.
There are two known sources for overestimating the detection
rate
coming with our method. First, systematic errors are not accounted
for. A possible solution could be to add a further term to ![]() as in
as in ![]() ,
where
,
where ![]() can be assumed to lie in the few percent region for real data.
Secondly,
we avoid refitting the binary-lens model light curve and always
compare to the one we got as best-fit to the exact (simulated)
triple-lens model light curve. This overestimation effect vanishes for
can be assumed to lie in the few percent region for real data.
Secondly,
we avoid refitting the binary-lens model light curve and always
compare to the one we got as best-fit to the exact (simulated)
triple-lens model light curve. This overestimation effect vanishes for
![]() and is negligible for a sufficiently large n.
The high sampling frequency we use, ensures that the number of data
points is always large enough (n > 250 in all
cases).
and is negligible for a sufficiently large n.
The high sampling frequency we use, ensures that the number of data
points is always large enough (n > 250 in all
cases).
While we cannot exactly quantify the uncertainty of the results, we know that they pose strict upper limits for the lunar detectability in the various scenarios. This knowledge would enable us to infer a tentative census of extrasolar moons, once the first successful microlensing detections have been achieved.
References
- Beaulieu, J.-P., Albrow, M., Bennett, D. P., et al. 2006, Nature, 439, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Beaulieu, J.-P., Kerins, E., Mao, S., et al. 2008, ESA white paper, submitted [arXiv:0808.0005v1] [Google Scholar]
- Benn, C. R. 2001, Earth, Moon and Planets, 85, 61 [Google Scholar]
- Bennett, D. P., & Rhie, S. H. 2002, ApJ, 574, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D. P., Anderson, J., Beaulieu, J.-P., et al. 2009, white paper, submitted [arXiv:0902.3000v1] [Google Scholar]
- Bond, I. A., Udalski, A., Jaroszynski, M., et al. 2004, ApJ, 606, L155 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bozza, V. 1999, A&A, 348, 311 [NASA ADS] [Google Scholar]
- Bozza, V. 2000, A&A, 355, 423 [NASA ADS] [Google Scholar]
- Cabrera, J., & Schneider, J. 2007, A&A, 464, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassan, A. 2008, A&A, 491, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Domingos, R. C., Winter, O. C., & Yokoyama, T. 2006, MNRAS, 373, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M., Jørgensen, U. G., Horne, K., et al. 2008, ESA white paper, submitted [arXiv:0808.0004v1] [Google Scholar]
- Dong, S., Bond, I. A., Gould, A. P., et al. 2009, ApJ, 698, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Dyson, F. W., Eddington, A. S., & Davidson, C. 1920, R. Soc. London Phil. Trans. Ser. A, 220, 291 [Google Scholar]
- Einstein, A. 1916, Ann. Phys., 354, 769 [Google Scholar]
- Gaudi, B. S., & Sackett, P. D. 2000, ApJ, 528, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Gaudi, B. S., Naber, R. M., & Sackett, P. D. 1998, ApJ, 502, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Gaudi, B. S., Bennett, D. P., Udalski, A., Gould, A., et al. 2008, Science, 319, 927 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gaudi, B. S., Beaulieu, J.-P., Bennett, D. P., et al. 2009, white paper, [arXiv:0903.0880v1] [Google Scholar]
- Gould, A. P. 2009, in ASP Conf. Ser., ed. K. Z. Stanek, 403, 86 [Google Scholar]
- Grundahl, F., Christensen-Dalsgaard, J., Kjeldsen, H., et al. 2009, The Stellar Observations Network Group - the Prototype [arXiv:0908.0436v1] [Google Scholar]
- Han, C. 2008, ApJ, 684, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., & Han, W. 2002, ApJ, 580, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hunter, R. B. 1967, MNRAS, 136, 245 [NASA ADS] [Google Scholar]
- Janczak, J., Fukui, A., Dong, S., et al. 2010, ApJ, 711, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Kayser, R., Refsdal, S., & Stabell, R. 1986, A&A, 166, 36 [NASA ADS] [Google Scholar]
- Kipping, D. M. 2009a, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009b, MNRAS, 396, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M., Fossey, S. J., & Campanella, G. 2009, MNRAS, 400, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, K. M., Sackett, P. D., & Mardling, R. A. 2008, ApJ, 685, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Liebig, C. 2009, Diploma thesis, Universität Heidelberg [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Muraki, Y., Sumi, T., Abe, F., et al. 1999, Progress of Theoretical Physics Supplement, 133, 233 [Google Scholar]
- Paczynski, B. 1996, Ann. Rev. A&A, 34, 419 [CrossRef] [Google Scholar]
- Réfrégier, A., Amara, A., Kitching, T. D., et al. 2010, Euclid Imaging Consortium Science Book [arXiv:1001.0061v1] [Google Scholar]
- Rhie, S. H. 1997, ApJ, 484, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Rhie, S. H. 2002, How Cumbersome is a Tenth Order Polynomial? The Case of Gravitational Triple Lens Equation [arXiv:astro-ph/0202294v1] [Google Scholar]
- Sartoretti, P., & Schneider, J. 1999, A&AS, 134, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharf, C. A. 2006, ApJ, 648, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., & Weiß, A. 1986, A&A, 164, 237 [NASA ADS] [Google Scholar]
- Schneider, P., Kochanek, C. S., & Wambsganss, J. 2006, Gravitational Lensing: Strong, Weak and Micro, Saas-Fee Advanced Courses 33 (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Southworth, J., Hinse, T. C., Jørgensen, U. G., et al. 2009, MNRAS, 396, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymanski, M., Ka▯uzny, J., Kubiak, M., & Mateo, M. 1992, Acta Astron., 42, 253 [NASA ADS] [Google Scholar]
- Wambsganss, J. 1990, Ph.D. Thesis, Ludwig-Maximilians-Universität München [Google Scholar]
- Wambsganss, J. 1997, MNRAS, 284, 172 [NASA ADS] [Google Scholar]
- Wambsganss, J. 1999, J. Comput. Appl. Math., 109, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. M., & Knacke, R. F. 2004, Astrobiology, 4, 400 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Witt, H. J. 1990, A&A, 236, 311 [NASA ADS] [Google Scholar]
Footnotes
- ...
detected
![[*]](/icons/foot_motif.png)
- exoplanet.eu
- ...
unbiased
![[*]](/icons/foot_motif.png)
- I.e. independent of lunar features, but required to pass close to or through the planetary caustic.
- ...
Euclid
![[*]](/icons/foot_motif.png)
- http://sci.esa.int/euclid
- ...
distribution
![[*]](/icons/foot_motif.png)
- We recall the definitions of mean and
variance. For the random variable X with probability density
function f(x), they are in general
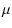
= 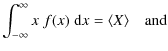
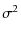
= 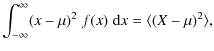
where we also introduce the notation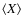 for the
expectation value of X.
for the
expectation value of X.
- ...
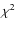 -distributed
-distributed![[*]](/icons/foot_motif.png)
- The
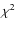 -distribution can be applied
to the sum of n independent, normally distributed random
variables Zi with the mean
-distribution can be applied
to the sum of n independent, normally distributed random
variables Zi with the mean 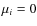 and the
standard deviation
and the
standard deviation
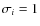 for all i,
for all i,
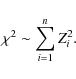
See any standard book with an introduction to calculus of probability. - ...
Library
![[*]](/icons/foot_motif.png)
- http://www.gnu.org/software/gsl/
All Tables
Table 1: Parameter values of our standard scenario.
Table 2: Detectability of the third mass in the magnification pattern of Fig. 5, for different assumed photometric uncertainties.
Table 3: Detectability of the moon in our standard scenario as a function of assumed photometric uncertainty.
Table 4: Detectability of the moon as a function of the planet-moon separation for our standard scenario.
Table 5: Detectability of the moon depending on moon-planet mass ratio.
Table 6: Dependence of lunar detectability as a function of the planet-star mass ratio, all other parameters as in our standard scenario.
Table 7: Detectability of the moon depending on the sampling rate of the simulated light curves.
Table 8: Detectability of the moon depending on the size of the source star, all other parameters as in our standard scenario.
All Figures
| |
Figure 1:
Geometry of our triple-lens scenario, not to scale. Five parameters
have to be fixed: the mass ratios |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=22cm,width=16.5cm,clip]{13844fg02.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg58.png)
|
Figure 2:
Details of the analysed triple-lens magnification maps for an example
mass/separation scenario with |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[height=22cm,width=16.5cm,clip]{13844fg03.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg60.png)
|
Figure 3:
Sample of triple-lens light curves corresponding to the source
trajectories depicted in Fig. 2. The solid
light curves were extracted with an assumed solar source size, |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg04.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg62.png)
|
Figure 4:
Magnification pattern displaying the planetary caustic of a triple-lens
system with mass ratios |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg05.eps}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg67.png)
|
Figure 5:
Illustration of how the magnification pattern of a given
star-planet-moon configuration is evaluated. In order to have an
unbiased statistical sample, the source trajectories are chosen
independently of the lunar caustic features, though all light curves
are required to pass through or close to the planetary caustic. This is
realised through generating a grid of source trajectories that is only
oriented at the planetary caustic. In the actual evaluation a
10 times denser grid than shown here was used. The
magnification map has to be substantially larger than the caustic to
ensure an adequate baseline for the light curve fitting. The side
length of this pattern is |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg06.eps}
\vspace*{-3mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg68.png)
|
Figure 6: Triple-lens light curve (solid line) extracted from the magnification pattern in Fig. 4, compared with a light curve extracted from the corresponding binary-lens magnification map (dashed line), with no third body and the planet mass increased by the previous moon mass. The difference of the two light curves is plotted as the dotted line. The central peak of the triple-lens light curve is caused by lunar caustic perturbations, that cannot easily be reproduced with a binary lens. In a), identical source trajectory parameters are used to extract the binary-lens light curve and large residuals remain that can be avoided with a different source trajectory. In b), the best-fit binary-lens light curve is shown (dashed) in comparison with the triple-lens light curve (solid). Here, the residuals can be attributed to the moon. If the deviation is significant, the moon is detectable in the triple-lens light curve. A source with solar radius at a distance of 8 kpc is assumed. |
| Open with DEXTER | |
| In the text | |
| |
Figure 7:
Caustic topology with different lunar mass ratios. From left
to right, the lunar mass ratio increases from |
| Open with DEXTER | |
| In the text | |
| |
Figure 8:
Magnification patterns with side lengths of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{13844fg9.eps}
\vspace*{-2.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg120.png)
|
Figure 9:
Illustration of the increasing source radius, compare Fig. 6b:
a)
|
| Open with DEXTER | |
| In the text | |
| |
Figure 10:
Visualisation of the approximate lunar resonance zone (dark-grey ring),
where planetary and lunar caustic overlap and interact. Also depicted
is the planet lensing zone (light grey), which is the area of planet
positions for which the planetary caustic(s) lie within the stellar
Einstein radius. Distances and caustic inset are to scale. The physical
scale depends not only on the masses of the lensing bodies, but also on
the distances to the lens system and the background star. In our
adopted standard scenario, cf. Table 1, the
Einstein radius |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13844fgA1.eps}
\vspace*{-4mm}
\end{figure}](/articles/aa/full_html/2010/12/aa13844-09/Timg189.png)
|
Figure A.1:
The |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.