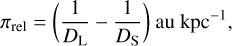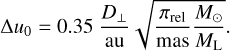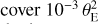| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202140351 | |
| Published online | 22 August 2022 | |
Euclid-Roman joint microlensing survey: Early mass measurement, free floating planets, and exomoons
1
Sorbonne Universités, CNRS, UMR 7095, Institut d’Astrophysique de Paris,
98 bis bd Arago,
75014
Paris, France
e-mail: etibachelet@gmail.com
2
Jodrell Bank Centre for Astrophysics, The University of Manchester,
Manchester
M13 9PL, UK
3
Department of Astronomy, The Ohio State University,
140 West 18th Avenue,
Columbus, OH
43210, USA
4
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg (ZAH),
69120
Heidelberg, Germany
5
National Astronomical Research Institute of Thailand,
260 Moo 4, T. Donkaew, A. Maerim,
Chiangmai
50180, Thailand
6
School of Physical Sciences, University of Tasmania,
Private Bag 37 Hobart,
Tasmania
7001, Australia
7
Las Cumbres Observatory,
6740 Cortona Drive, Suite 102,
93117
Goleta, CA, USA
8
University of St Andrews, Centre for Exoplanet Science, SUPA School of Physics & Astronomy,
North Haugh, St Andrews
KY16 9SS, UK
9
School of Physics and Astronomy, Tel Aviv University,
Tel Aviv
69978, Israel
10
Department of Physics, The University of Texas at Dallas,
800 W Campbell Road,
Richardson, TX
75080, USA
11
Department of Mathematics and Physics, University of Salento,
via per Arnesano,
73100
Lecce, Italy
12
INFN, Sezione di Lecce,
Via per Arnesano,
CP-193,
73100
Lecce, Italy
13
INAF, Sezione di Lecce,
Via per Arnesano,
CP-193,
73100
Lecce, Italy
14
Astronomical Observatory, University of Warsaw,
Al. Ujazdowskie 4,
00-478
Warsaw, Poland
15
Jet Propulsion Laboratory, California Institute of Technology,
4800 Oak Grove Drive,
Pasadena, CA
91109, USA
16
Institut UTINAM CNRS UMR6213, Université Bourgogne Franche-Comté, OSU THETA Franche-Comté Bourgogne, Observatoire de Besançon,
BP1615,
25010
Besançon Cedex, France
Received:
15
January
2021
Accepted:
21
February
2022
As the Kepler mission has done for hot exoplanets, the ESA Euclid and NASA Roman missions have the potential to create a breakthrough in our understanding of the demographics of cool exoplanets, including unbound, or free-floating, planets (FFPs). Roman will dedicate part of its core survey program to the detection of cool exoplanets via microlensing, while Euclid may undertake a microlensing program as an ancillary science goal. In this study, we demonstrate the complementarity of the two missions and propose two joint surveys to better constrain the mass and distance of microlensing events. We first demonstrate that an early brief Euclid survey (~7 h) of the Roman microlensing fields will allow the measurement of at least 30% of the events’ relative proper motions µrel and 42% of the lens magnitudes. This survey would place strong constraints on the mass and distance on thousands of microlensing events observed by Roman just after the first year of observation. Then, we study the potential of simultaneous observations by Roman and Euclid to enable the measurement of the microlensing parallax for the shortest microlensing events and, ultimately, obtain a direct measurement of the masses, distances, and transverse motions of FFPs. Using detailed simulations of the joint detection yield we show that within one year Roman-Euclid observations will be at least an order of magnitude more sensitive than current ground-based measurements. The recent tentative detection of an excess of short-duration events by the OGLE survey is consistent with a scenario of up to ten Earth-mass FFPs per Galactic star. For such a scenario a joint Roman-Euclid campaign should detect around 130 FFP events within a year, including 110 with measured parallax that strongly constrain the FFP mass, and around 30 FFP events with direct mass and distance measurements. The ability of the joint survey to completely break the microlens mass-distance-velocity degeneracy for a significant subset of events provides a unique opportunity to verify unambiguously the FFP hypothesis or else place abundance limits for FFPs between Earth and Jupiter masses that are up to two orders of magnitude stronger than provided by ground-based surveys. Finally, we study the capabilities of the joint survey to enhance the detection and characterization of exomoons, and find that it could lead to the detection of the first exomoon.
Key words: gravitational lensing: micro / planetary systems
© E. Bachelet et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Our understanding of exoplanet demographics has progressed enormously thanks to advances in exoplanet detection techniques that have led to the rapid growth of confirmed candidates1. A total of 3484 of the 4909 confirmed exoplanets discovered to date have come from primary transit observations, with around 2300 of these coming from the Kepler space mission alone1. The ability to observe from space has enabled robust large-scale regular and homogeneous photometric observations that are crucial for extending exoplanet sensitivity down to the Earth-size regime, or even sub-Earth-size regime. While the list of confirmed exoplanets now extends into the thousands, our knowledge of their demographics still suffers from severe incompleteness. Many of the current candidates are relatively massive and on short-period orbits compared to planets in our own Solar System. We have incomplete knowledge of the full extent of multi-planet systems, particularly for those systems, like our own Solar System, that host planets beyond the ice line. Understanding the planet population beyond the ice line is critical for understanding planet formation. Population synthesis simulations show that, unlike massive planets, low-mass planets that form beyond the ice line are not strongly affected by migration as their accretion timescales are short compared to the migration timescale (Mordasini 2018). This implies that cool low-mass planets provide key tracers of in situ planet formation. Studying the present-day demographics of cool low-mass planets can, uniquely, provide a direct test of planet formation models that is largely unaffected by complex planet migration histories.
Gravitational microlensing remains the only available method able to access the cool low-mass exoplanet regime. Ground-based microlensing surveys have so far detected over 100 planets1. Microlensing data have been used to show that the distribution of planet-to-host mass ratios exhibits a universal profile, and therefore may be a more primary diagnostic of planet formation than the planet mass function (Suzuki et al. 2016; Pascucci et al. 2018). Ground-based microlensing data have also tentatively indicated the existence of a significant population of planets that are isolated or very distant (i.e., ≥15 AU) from any host star (Sumi et al. 2011; Mróz et al. 2017, 2019a), often referred to as free-floating planets (FFPs). The first FFPs candidates were discovered two decades ago in star-forming regions (Oasa et al. 1999; Zapatero Osorio et al. 2000; Luhman et al. 2005; Burgess et al. 2009; Marsh et al. 2010) and are predicted by planet formation models (Veras & Raymond 2012; Ma et al. 2016). The existence of FFPs is also implicated by infrared surveys of nearby star-forming regions (Zapatero Osorio et al. 2017). In particular, Miret-Roig et al. (2022) recently found a ~5% relative abundance of FFPs (with a mass range of 4–13 MJup) in their survey of the Upper Scorpius and Ophiuchus regions. However, their Galactic abundance and typical mass scale remains uncertain. Because it does not rely on the measurement of the light emitted by the lens, microlensing is a powerful technique for discovering these objects (Sumi et al. 2011; Mróz et al. 2017, Mróz et al. 2019a). Whether FFPs form in isolation or exist as a consequence of being ejected from their hosts through dynamical exchanges with other planets remains unknown. Clearly, it is important to pin down the nature and abundance of FFPs in order to answer this question and to inform planet formation models. Microlensing is the only method available for studying FFPs over Galactic distance scales.
The primary observable, the Einstein radius crossing time tE, not only depends on the lens mass and distance from the observer, but also on the relative proper motion and relative parallax between lens and source (Gould 2000). The characterization of the lens mass and distance is therefore challenging and requires the measurements of some extra parameters, such as the microlensing parallax (Gould 1994), finite-source effects in the light curve (Witt & Mao 1994), the source and lens relative proper motion, and/or the lens flux (see, e.g., Vandorou et al. 2020). So far, it has been done only for about half of the bound microlensing planets. One example is OGLE-2015-BLG-0966Lb (Street et al. 2016), a lens system consisting of a 0.4 M⊙ M dwarf, orbited by a cold Neptune. It was simultaneously observed from the ground and with the Spitzer Space Telescope to obtain a direct planet mass measurement with a 10% precision. Ground- and space-based observations have also been used to directly image the lensing host star several years after an event has occurred. The host lens flux can then be used to convert the planet-to-host mass ratio, obtained from the microlensing light curve, to a planet mass (Yee 2015; Beaulieu 2018).
Due to the intrinsic rarity of microlensing, surveys must target highly crowded stellar fields toward the Galactic bulge. As a result, their sensitivity is severely affected by the combination of stellar crowding effects and seeing limitations caused by Earth’s atmosphere. As with the transit method, substantial sensitivity improvements can therefore be achieved by observing from space (Bennett & Rhie 1996; Penny et al. 2013, 2019). For microlensing, the primary signal is a time-dependent magnification of a background source whose light is deflected by the gravitational field of a foreground object. Because the gravitational lensing cross section (the Einstein ring radius) of the lens scales with the square root of its mass, the event duration is a function of the lens mass, up to several years for a ~10 M⊙ isolated mass black hole (Wyrzykowski et al. 2016) and down to few hours for a FFP (Mróz et al. 2020). If the angular Einstein ring radius θE is small compared to the angular size of the background source star θ*, the magnification averaged over the face of the source may be too small to be detected. A major benefit of observing from space is the ability to access large numbers of resolved main sequence stars (i.e., not blended with other stars) as from the ground most of the non-blended stars are the larger bulge giants. The more compact main sequence stars extend microlensing sensitivity down to around the mass of the Moon (Dominik et al. 2007; Penny et al. 2019).
In the next decade, both NASA and ESA will be launching facilities that could undertake high-precision exoplanet microlensing surveys. The NASA Nancy Grace Roman Space Telescope (formerly WFIRST and hereafter referred to as Roman; Spergel et al. 2015) core missions include a dark energy survey and a substantial microlensing program. The ESA Euclid mission’s (Laureijs et al. 2011) primary objective is to constrain the nature of dark energy, although the original mission definition included the possibility of undertaking a microlensing survey as an additional goal (Penny et al. 2013). Both telescopes are scheduled to be located in halo orbits at the Earth-Sun L2 point, with a potential separation between them of up to 600 000 km. Microlensing simulations have shown that both telescopes are ideal for microlensing, and have the potential to detect thousands of planets across a broad range of masses and semi-major axes (Penny et al. 2013, 2019). Johnson et al. (2020) predicts that Roman alone will detect ~250 FFPs, including ~60 planets less massive than the Earth, in good agreement with the estimation of Ban et al. (2016). Johnson et al. (2020) also forecast that a significant fraction of the FFP events detected by Roman will display finite-source effects. This implies that θE will be measured for most of these events because θ*, will be almost systematically known for events detected by Roman. On the other hand, Bachelet & Penny (2019) show that the microlensing parallax will not be detected by Roman alone for events with tE ≤ 3 days (i.e., outside of the FFP regime). However, the authors show that simultaneous observation from the Euclid mission would constrain the microlensing parallax down to the FFP regime if the separation between the two mission is sufficiently large. This was confirmed by the independent analysis of Ban (2020), that demonstrates that the parallax will be measurable for a large fraction of events due to FFP.
In this paper we argue that the Roman and Euclid missions should coordinate their observations to undertake a combined survey to enhance the characterization of the lensing systems. The paper is laid out as follows. In Sect. 2 we overview the
Roman and Euclid missions and their respective survey timelines, pointing out the options for a simultaneous observing program. In Sect. 3 we visit the theory behind precision mass measurements of microlensing events. In Sect. 4 we consider the potential of an early Euclid survey of the Roman microlensing fields for the measurements of the lens fluxes as well as the relative proper motions. In Sect. 5 we present a statistical study that details the unique constraints that offer a Euclid and Roman joint survey on the detection and characterization of microlensing events due to FFP. Section 6 considers the ability of a joint survey to detect exomoons. We conclude with a summary in Sect. 7.
2 Roman and Euclid missions
2.1 Timelines
Roman is a NASA flagship mission scheduled for launch in late 2025. Roman has three primary science goals: dark energy investigations using galaxy clustering, weak gravitational lensing, and Type Ia supernovae; exoplanet demographics via microlensing; and infrared surveys for a wide range of astrophysics applications, executed via a competitive General Observer (GO) program (Spergel et al. 2015). Additionally, Roman will carry a coronagraph instrument (CGI) technology demonstration that will be premiered in space; it will have a number of new techniques that will advance the state-of-the-art in coronagraphy by three orders of magnitude in star/planet contrast ratio. Additional surveys are possible within the primary mission, and via the GO program and a possible five-year extension.
Euclid is an ESA-led medium-class mission with significant technical and scientific contributions from NASA. Euclid is designed to map the universe with two distinct probes, galaxy clustering, and weak gravitational lensing, in order to study the nature of dark matter and dark energy (Laureijs et al. 2011). Euclid will perform these surveys with two instruments: VIS will do visible photometry in a single very wide band, and the NISP instrument will perform near-infrared photometry and grism spectroscopy in the range 1–2μm Euclid is scheduled to launch in late 2022 for a six-year primary mission. As the Euclid mission progresses, there will be increasing gaps in the cosmology survey that could be filled with microlensing observations. The Euclid NISP instrument is expected to be fully functional after the six-year primary survey and therefore microlensing observations using NISP could be viable. The VIS CCDs will likely suffer from increasing charge-transfer-efficiency (CTE) degradation throughout the mission, with a commensurate degradation of the VIS capabilities. While this may impact their suitability for weak lensing measurements, it is unlikely that increased CTE would dramatically degrade VIS’s ability to perform microlensing photometry. A full analysis of the effects of detector degradation on VIS microlensing measurements after the Euclid prime mission is beyond the scope of this paper.
2.2 Relevant instruments
The Roman Wide Field Instrument (WFI) consists of 18 4 k × 4 k Hawaii H4RG-10 HgCdTe detectors with a pixel scale of 0.11″, giving a 0.28 deg2 field of view (Spergel et al. 2015). In addition to a grism and prism, the instrument will have six broadband filters with central wavelengths spanning from 0.62 to 2.13 µm (R062, Z087, Y106, J129, H158, F184, K213) as well as an extremely wide 0.92-2.00 µm filter, W146, that will be used by the Galactic exoplanet survey. WFI delivers diffraction-limited imaging for the 2.4m Roman telescope in all but the shortest wavelength filter. Roman is able to slew to and settle on an adjacent field in about 60 s using reaction wheels for maneuvers.
Euclid uses a 1.2 m telescope that delivers light to two instruments that simultaneously observe the same field through a dichroic element (Laureijs et al. 2011). The VIS instrument has 36 4 k × 4 k e2v CCD273-84 CCD detectors with 0.10″ pixels, giving a 0.47 deg2 field of view. VIS provides diffraction-limited imaging in an extremely wide optical light bandpass of 0.550.90 µm (Cropper et al. 2018). The NISP instrument images the same field as VIS with 16 H2RG-18 HgCdTe detectors with a pixel scale of 0.30″ (Maciaszek et al. 2016). NISP can select from four grisms or three broadband filters with central wavelengths of 1.05, 1.37, and 1.77µm Euclid’s primary observing modes will allow VIS imaging to be captured simultaneously with NISP grism observations, but in principle it should be possible for VIS and NISP to both perform imaging observations simultaneously. Similarly, the number of VIS and NISP exposure time modes that are commissioned may be limited. Euclid uses cold gas thrusters to maneuver, which results in relatively long ~350 s slew and settle times to move to an adjacent field (Gómez-Alvarez et al. 2018).
2.3 Planned bulge surveys
Roman will conduct the Roman Galactic Exoplanet Survey, which will nominally consist of six seasons of continuous observations lasting 72 days each (Penny et al. 2019). The seasons will be spaced six months apart, surrounding the vernal and autumnal equinoxes when Roman can point toward the bulge. During this time Roman will observe ~2 deg2 of the Galactic bulge every 15 min in its wide W146 filter, and at least once every 12 h in at least one of the broadband filters, currently planned to be Z087.
Euclid will not conduct bulge observations as part of its primary mission, but we consider here two scenarios where bulge observations would be minimally disruptive to the Euclid primary mission: a short observing campaign of pre-imaging of the Roman bulge fields shortly after launch, and more extensive observations simultaneously with Roman late in the Euclid mission. Euclid can point toward the bulge in a narrower ~30-day window while maintaining thermal stability that is fully enclosed within the 72-day Roman seasons.
2.4 Orbital elements
Both telescopes will orbit around the L2 Sun-Earth Lagrangian point. While the exact orbital elements are not known yet, it is safe to assume that the orbits will be comparable to the current orbit of the Gaia telescope, with an orbital radius R ~ 300000 km and a period of ~180 days. Using these parameters, Bachelet & Penny (2019) show that simultaneous observations from the two telescopes unlock the parallax measurement down to the FFP regime if the telescope’s separation is at least ≥100 000 km. We use these parameters for the rest of this work.
3 Measurement of the masses and distances of microlenses
A microlensing event occurs when a lens object at a distance DL crosses the line of sight between the observer and a source at a further distance DS. When the angular distance between the source and the lens is sufficiently small (a few θE, see below), the gravity field of the lens modifies the pathway of the photons and creates several images of the source. The images are distributed around the lens and separated by few Einstein ring radius θE (Gould 2000)
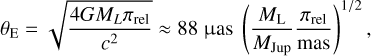 (1)
(1)
and ML is the lens mass, G is the gravitational constant, and c the speed of light in vacuum. As long as no finite source effects are measured, there is only a single measurable parameter that depends on the lens mass, namely the Einstein radius crossing time:
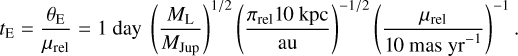 (3)
(3)
Worse still, tE also depends on the relative lens-source proper motion, µrel, giving rise to a three-parameter degeneracy between ML, µrel, and πre1. The physical mass and distance to the lens system can be estimated via a Bayesian analysis using a Galactic model to define the priors on πre1 and µrel (Han & Gould 1995, 2003; Bennett et al. 2014). Since these priors are rather broad toward the Galactic bulge, while the planet-to-host mass ratio is often well determined, absolute values of the physical parameters may not be well constrained. Fortunately, there are a number of ways to break the microlensing parameter degeneracy through combinations of high-precision photometry, high-resolution imaging follow-up, and simultaneous observations from well-separated observatories. We briefly review the methods that could be employed by Roman.
3.1 Mass-distance relation from finite source effects
The Einstein radius, θE, can be measured if a light curve shows evidence of finite source size effects (e.g., when the source approaches caustics of the lensing system). For a single lens this occurs when the angular separation separation β between the source and the lens becomes comparable to the angular size of the source star θ* (i.e., β ≲ θ*). This is also a common situation for microlensing events that involve a planetary lens, and it results in a differential magnification across the source face that is observable as a deviation of the microlensing light curve from the point-source model. The effect essentially allows the source angular size to be used as a standard ruler to measure θE via
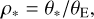 (4)
(4)
where ρ* is the angular size of the background source star in units of θE, a parameter that can be determined from a fit of a light curve exhibiting finite source effects. The source angular size, θ*, can be determined reliably via the infrared surface brightness relation (Yoo et al. 2004; Boyajian et al. 2013), determining θE through Eq. (4). This in turn yields a measurement of µrel through Eq. (3). Once θE has been measured, the microlens degeneracy reduces to a mass-distance relation
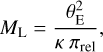 (5)
(5)
with κ ≡ 8.144 mas 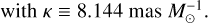 .
.
Roman will provide dense high-precision photometry on planetary microlensing events. Since a large fraction of these systems are expected to exhibit finite-source effects (either from low-mass FFP light curves or from bound planets detected via caustic crossings by the source), this type of mass-distance relation will be obtained routinely.
3.2 Mass-distance relation from lens flux
With observations at high enough angular resolution it is possible to disentangle the aligned source and lens stars from field stars at the subarcsec scale. Modeling of the photometric light curve allows the flux of the source star to be estimated accurately. In principle, we can then measure the excess flux aligned with the source star, and try to determine if some or all of this excess flux can be attributed the planetary host star. A complication at this point is that there might be contaminants, for example chance-aligned field stars, a companion to the source star, or another stellar companion to the host. These possibilities must be evaluated via a Bayesian analysis (Koshimoto et al. 2020). The resulting lens magnitude mL(λ) can be combined with an empirical mass-luminosity relation (Delfosse et al. 2000) or with stellar isochrones (Bertelli et al. 2008) to get a mass-distance constraint of the form
![$\matrix{ {{m_{\rm{L}}}\left( \lambda \right) = } \hfill & {10 + 5\,\log \left( {{D_{\rm{L}}}/kpc} \right) + {A_{\rm{L}}}\left( \lambda \right)} \hfill \cr {} \hfill & { + {M_{{\rm{isochrone}}}}\left( {\lambda ,{M_{\rm{L}}},{\rm{age}},\left[ {{\rm{Fe/H}}} \right]} \right),} \hfill \cr } $](/articles/aa/full_html/2022/08/aa40351-21/aa40351-21-eq7.png) (6)
(6)
where Misochrone is the absolute magnitude of the star at wavelength λ. If several bands can be used in concert, the constraints on the mass and distance of the lens, as well as the extinction along the line of sight, become stronger (Batista et al. 2015). As soon as the lens and the source are sufficiently separated (i.e., when the separation is ≳0.5 FWHM), generally several years after the event peak, the exact nature of the lens is known to very high precision (Vandorou et al. 2020; Bhattacharya et al. 2021). This is also the case for stellar remnants lenses because the high-resolution images can rule out the main sequence lens scenario (Blackman et al. 2021). This measurement is extremely challenging, if not impossible, for the faintest components, such as FFPs or stellar remnants lenses.
3.3 Mass-distance relations from lens-source relative proper motion
The lens-source relative proper motion introduced in Eq. (3) is typically on the order of ~ 5 mas yr−1 and generally in the range ~1 −10 mas yr−1. With the very stable point spread function (PSF) of Roman, it is possible to measure the centroid variations, even if the source and the lens are not fully resolved from each other, to constrain their flux ratio (as described in the previous subsection) and relative proper motion. Observing the microlensing event in several bands significantly increases the precision of the method, often referred to as color-dependent centroid shift. This has already been achieved, for example using the Hubble Space Telescope (Bhattacharya et al. 2018). The measurement of the proper motion, especially coupled with the measurement of the lens flux, provides strong constraints on microlensing models. This is particularly useful for breaking fundamental degeneracies that can arise in the light curve modeling, especially the ecliptic degeneracy (Skowron et al. 2011). Again, this method is almost impossible to use for the faintest lenses of the Milky Way.
3.4 Mass-distance relations from microlensing parallax
While measurements of tE and µrel (or, equivalently, θE) break some of the microlensing parameter degeneracy, we require an additional mass-sensitive measurement to fully resolve the degeneracy. The reward is not just the lens mass, but also its distance and transverse velocity, both of which are of physical interest. The relative lens-source parallax πrel introduced in Eq. (5) can be measured if tE is long enough to observe a subtle shift in the photometric light curve due to the Earth’s orbital motion (the annual parallax; Gould 2004) or if two observatories observe the event simultaneously (the satellite parallax; Refsdal 1966). In this case, microlensing parallax vector is approximately given by (Calchi Novati et al. 2015)
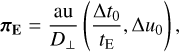 (7)
(7)
where D⊥ is the projected separation between the two observatories along the direction of the event, and Δu0 and Δt0 are respectively the differences in impact parameter and epoch of maximum magnification recorded by the two observatories. This leads again to the mass-distance relation of Eq. (5), but recast in the form
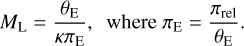 (8)
(8)
The switch from πrel to πE highlights that the key to detecting microlensing parallax is to obtain measurements of the light curve from positions that are separated over distances that, when projected onto the lens plane, span a sufficient fraction of the lens Einstein radius.
Recently, it has been demonstrated that the Roman observations from the Earth-Sun L2 point will be sufficient to detect parallax for microlensing events with tE ≳ 5 days, due to the orbit of the L2 point around the Sun (Bachelet & Penny 2019). This will ensure strong constraints on the mass and distance of the ~1500 bound planets expected to be detected by Roman (Penny et al. 2019). FFP microlensing events, however, are generally expected to have timescales of less than a few days. Measurements of parallax for such short tE events from surveys such as Roman or Euclid operating alone will be extremely challenging. Hamolli et al. (2016) find a relatively high efficiency for parallax measurement when events can be detected down to peak magnifications of 1.001, irrespective of signal-to-noise ratio (S/N). Hamolli et al. (2016) also determine parallax detection based on a comparison of the model residuals for the same event, with and without parallax, rather than between the best-fit parallax model and a best-fit model without parallax. Without very high S/N observations, we consider such a low detection threshold to be unreliable for secure false-positive rejection. For more robust selection criteria based on an event’s S/N, and a comparison of best-fit models with and without parallax, we would not expect either survey to be highly efficient to FFP parallax detection when observing alone.
However, simultaneous observations from Euclid and Roman are ideal for measuring the parallax for such events (Bachelet & Penny 2019). This is of particular interest because, as noted, FFPs are expected to produce short events on timescales of hours to days (Eq. (3)). For a typical FFP lens of 1 MJup, located at DL = 4 kpc and a source at DS = 8 kpc, the projected Einstein ring radius 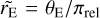 (Gould 2000) is about 0.25 au. For an orbital radius around L2 of ~300 000 km, the maximum separation between Euclid and Roman can be on the order of ~0.005 au, a range that allows the measurement of the parallax of FFP events. Rewriting Eq. (7) gives
(Gould 2000) is about 0.25 au. For an orbital radius around L2 of ~300 000 km, the maximum separation between Euclid and Roman can be on the order of ~0.005 au, a range that allows the measurement of the parallax of FFP events. Rewriting Eq. (7) gives
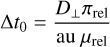 (9)
(9)
Assuming µrel = 4 mas yr−1, the previous configuration leads to Δt0 ~ 1 h and Δu0 ~ 0.02, offsets that should be measurable given the cadence and photometric precision of the surveys. Similarly, Yee (2013) and Bennett et al. (2018) described how simultaneous observation from Roman and ground-based telescopes would constrain the mass of FFP lenses. However, it is inevitable that the lower cadence and photometric precision of observation collected from the ground make these measurements more challenging.
4 Direct planet host mass measurements with early Euclid observations
In the case that the lens hosts a secondary object, the mass ratio q and the projected separation s have to be accounted for in the modeling of the microlensing light curve. These parameters will be precisely measured for planets down to the mass of Mars by the Roman microlensing survey (Penny et al. 2019). However, as previously presented, additional measurements are required to accurately derive the host and planet masses. In this section we demonstrate that an early epoch of imaging of the Roman microlensing fields can potentially improve lens mass measurements, including those for planet hosts, by increasing the time baseline over which the lens and source separation can be observed (Yee et al. 2014). Currently, launch dates of 2022 and 2026 are expected for Euclid and Roman, respectively, meaning that an epoch of imaging early in Euclid’s mission could extend the baseline by up to four years relative to the Roman microlensing survey’s expected 3.5–4.5 year baseline. Bennett et al. (2007) estimate that the precision of both lens flux and source-lens relative proper motion measurements will scale inversely with the square root of the number of photons (N−1/2), but as the inverse cube of the lens-source separation, or proper motion baseline (Δt−3). Therefore, a relatively short program to observe the Roman microlensing fields using a few hours of exposure time with Euclid could provide competitive, if not superior lens mass measurements for at least a subset of Roman’s expected ~1500 exoplanet discoveries, despite the almost ~100 h of exposure time Roman will collect in each field each season. In this section we use a simulation of Euclid images to demonstrate this possibility.
4.1 Description of simulations
We simulated an early Euclid image of a starfield containing microlensing events that Roman will observe. We used the image simulation component of the GULLS microlensing simulator (Penny et al. 2013, 2019). A 1.83′×1.83′ starfield was produced by drawing stars from the BGM1307 version of the Besançon model, which closely matches that detailed in Awiphan et al. (2015). From a sample of 1691 simulated Roman microlensing events with detectable planets from Penny et al. (2019), the brightest 432 (26%) microlensing events with lenses
brighter than W149 = 22.5 were added to the images; the W149 and VIS magnitude distributions of these samples are shown in Fig. 1. The full sample of events2 is a representative draw from the fiducial Roman simulations, with stellar properties (e.g., proper motion, magnitude) drawn from an earlier version of the Besançon model, BGM1106, as described in detail by Penny et al. (2013, 2019).The positions of all stars in the image were chosen randomly at a time t = 0 (corresponding to the Roman launch date), and their positions at other times determined by their proper motion. Source stars were placed randomly in the image, but lens stars were placed such that they would recreate the parameters of the simulated microlensing events given the relative proper motion of source and lens. Euclid VIS magnitudes were assumed to be equal to Z087 magnitudes from Roman, and the simulated source and lens magnitudes were calculated by integrating over an interpolation of the stellar spectral energy distribution output by the Besançon model in the R, I, Z, J, and H bands, plus the magnitudes of a blackbody with the same temperature, radius, distance, and extinction for the K and L bands.
We set the Euclid observations at t = −1800 days (i.e., about 5 years prior to the Roman launch), and generated a set of 16 1.83′ × 1.83′ images at the native resolution of the VIS instrument. Each of the 16 images was dithered by a set of randomly chosen offsets between 0 and 10 pixels in the X and Y directions. The 16 images at each epoch were stacked using the drizzle algorithm (Fruchter & Hook 2002) to refine the resolution to 0.0275 arcsec pixel−1.
 |
Fig. 1 Distribution of host star (lens) magnitudes from a sample of simulated planetary microlensing events injected in the Euclid image. The gray histogram shows the W149 (left) and VIS (right) magnitude distribution of all hosts in a sample of 1691 planetary microlensing events drawn from simulations presented in Penny et al. (2019), and the black histogram shows the distribution of 432 events brighter than W149 < 22.5, which were injected into our simulated image. The red histogram shows the distribution of magnitudes for the sources of the 432 events with bright lenses. |
4.2 Modeling process and results
We first estimated an empirical and flux-calibrated point spread function (PSF) of the drizzled images by modeling isolated stars, and we assumed a constant PSF. In practice, the PSF varies across the field but is extremely well characterized. Assuming that the lenses and sources are resolved when the separation is ≳0.25 FWHM (i.e., 1.8 pixels in this case), 64% of events are resolved at the time of the simulated Euclid observation. However, with a median separation of 2.1 pixels, many events are just at the limit of separation. We rejected three events from the analysis because they were too close to the image edges. We then fit the 429 remaining simulated events, assuming that the light present in small stamps around the event location (estimated for the event coordinates at t0) is solely due to the lens, the source, and a constant background. The fit parameters are the total flux ft = fs + f≳, where fs and fl are the source and lens fluxes, the flux ratio q = fs/ft, the proper motion of the source and the lens, and the background level. We used the first image from Euclid to estimate the potential of early Euclid observations.
The results of the fits are presented in the Fig. 2. We find µrel to be constrained, to better than 10% (relative), for 29% of the fits. We also find that the magnitude of the lens is reconstructed at better than 0.1 mag for 42% of our sample; 15% of the events are reconstructed within the two preceding constraints, and 85% of them are resolved (with a median separation of 3.5 pixels). For this subset of events, the properties of the lens will be reconstructed with high fidelity according to Eqs. (6) and (3). While the mass and distance degeneracy can persist for the lightest lenses (Yee 2015), Bachelet & Penny (2019) demonstrate that the parallax will be constrained for most events. Scaled to the 30 000 events expected from the Roman mission, this indicates that early Euclid observations can constrain the properties of over 2000 lenses, increasing our knowledge of the microlens distribution by several orders of magnitudes.
The analysis presented is relatively CPU intensive, and this was the primary motivation to limit the sample to lenses with W149 < 22.5 mag. While this sample is not exactly representative, we note that the distribution of the source magnitudes is much broader (with W149 < 26 mag). We did not find any significant trends in the fit results that depend on the source magnitudes, indicating that our fits would also be reliable for fainter lenses since the problem is symmetric. We note however that our fitting approach, while generally accurate, is suboptimal for a significant fraction of the events. This is mainly due to the presence of unrelated stars near to the line of sight, but this problem can be tackled by a more in-depth analysis such as that done by Bhattacharya et al. (2017). This can also result from a large difference in the lens and source brightness, coupled with a small lens-source proper motion. A complete understanding of
the fitting performance (for example the accuracy of the PRF and the noise models of drizzle images) is beyond the scope of this study, as our goal here is to highlight the potential of early Euclid observation. However, by studying each event individually, as would be the case with real data, it is likely that the performance could be significantly improved. The results presented here can therefore be considered conservative.
To conclude, a single Euclid observation prior to the Roman mission will place strong constraints on the mass and distance for thousands of lenses for a relatively small observational cost. Assuming that the microlensing Roman fields will be of 2 deg2 (Penny et al. 2019), it would take about four pointings of Euclid to cover the region of interest. Using the observing strategy presented in the previous section (16 dither images, each with a 300 s exposure time), this represents 7 h of Euclid telescope time with overheads. This strategy, coupled with the parallax measurements from the Roman light curve (see Sect. 3.4 and Bachelet & Penny 2019), will provide unprecedented constraints on masses and distances of thousands of lenses, ultimately placing exquisite constraints on the Galactic demographics of planets (Calchi Novati et al. 2015). It will also permit a direct measurement of the masses and distances of the earliest Roman microlensing events without needing to wait for the end of the Roman mission.
 |
Fig. 2 Distribution of fit residuals, defined as Δ = fit − true, as a function of µrel(top) and VIS lens magnitude L (bottom). The orange triangles are events meeting both criteria: |Δµrel| < 0.1µrel and |ΔL| < 0.1 mag. The left column gives the results for all 432 events, while the right column shows a zoomed-in image for events with |Δµrel| < 2.5 mas yr−1 and |ΔL| < 0.1 mag. |
5 Simulating joint Roman-Euclid observations of free-floating planets
5.1 Examples of joint observations
Planetary-mass lenses (assumed here as M ≤ 13 MJup) have extremely small Einstein radii, and therefore microlensing events due to such lenses can display strong finite-source effects (i.e., ρ* ≥ u0 from Eq. (4)), allowing the measurement of ρ*, and therefore θE. Obtaining parallax parameters (πE or πrel) for FFPs therefore means that the FFP mass and distance can be directly measured. It is worth noting that such microlensing measurements would yield not just the FFP mass, but also most of the FFP’s full phase space (with the exception of velocity along the line of sight). This may provide vital information on the mode of FFP formation.
To illustrate such measurements, we simulated three examples of simultaneous observations made by Roman W149 and Euclid NISP (H), assuming a phase separation of ~ π/4 between the orbits of the telescopes around the Earth-Sun L2. The photometric precision was similar for both telescopes, while the cadence of Euclid and Roman were set to 30 min and 15 min, respectively. We used the pyLIMA software to simulate and fit the light curve (Bachelet et al. 2017), and used the Gaia ephemerides around the Earth-Sun L2 to obtain realistic orbits. For each case, we modeled the event with and without including the parallax effect. We derived the log-likelihood ratio Δχ2 associated with a p-value p, indicating if the fit including parallax is statistically more significant than the simpler model. We ran two sets of fits: one including both telescopes and one using only Roman data. The results are presented in Fig. 3. We derived the lens masses and errors assuming θE to be known to within 10%. This implies ρ to be measured, and therefore we also force u0 ≤ ρ. We assumed a linear limb-darkening law and using Γ = 0.5 (Yoo et al. 2004).
5.2 Simulation of joint observations
In this section we explore, in a statistical sense, the capabilities offered by a Roman and Euclid joint survey for detecting and characterizing microlensing events due to FFPs. Therefore, this work is related to the previous works from Johnson et al. (2020) and Ban (2020), but, as detailed below, implements several refinements that can play a significant role in the characterization of events (i.e., the mass measurement). To list
a few, they include the consideration of limb-darkening for a more accurate magnification estimation, an updated version of the Besançon model calibrated to Hubble Space Telescope and compared to the OGLE-IV observations, and the use of time-integrated selection cuts that are more reliable to ensure the ability to measure finite-source effects and parallax, to ultimately better characterize events.
To assess the number of FFPs where such mass constraints could be obtained, we used a specially modified version of the MaBµlS-2 simulator3 (Specht et al. 2020) to allow for FFPs and to consider simultaneous parallax by separated observatories. MaBµ/lS-2 employs a synthetic population of microlensing lenses and source stars seeded from version 1307 of the Besançon Galactic model (BGM; Robin et al. 2012, 2014). MaBµ/lS-2 has been demonstrated by Specht et al. (2020) to provide an accurate match to the 8000-event sample from the OGLE-IV survey (Mróz et al. 2019b). Using the BGM, MaBµ/lS-2 simulates the microlensing event rate from the synthetic stellar catalogues produced.
The BGM divides the Galaxy into four components: the thin disk, bulge (Robin et al. 2012), thick disk, and halo (Robin et al. 2014), each with its own stellar initial mass functions, density laws, and kinematics. It also includes a 3D extinction model from Marshall et al. (2006). FFPs of various mass are injected to replace stars as lenses. The FFP mass functions that were considered included two Dirac delta functions, one peaked at Earth mass witha normalization often FFPs permain sequence star, as suggested by Mróz et al. (2019a), and another peaked at Jupiter mass with a normalization of two FFPs per main sequence star, as suggested by Sumi et al. (2011).
Finally, FFPs inherit the kinematics of the stars they replace in the synthetic catalogue. The overall procedure for computing the microlensing rate, optical depth, and average timescale follows the formalism detailed in Specht et al. (2020) with a few differences. First, S/Nselectioninvolves a time-averaged statistic
rather than the S/N at peak used in Specht et al. (2020). Specifically, we demand a Δχ2 between the synthetically generated microlens light curve and a best-fit constant flux model of at least 125, with at least six points reaching 3σ above the baseline.
In addition, the joint detection of space-based parallax between the Roman and Euclid light curves is required to be at least 5σ, following the Fisher matrix analysis of Bachelet & Penny (2019), with modifications to account for the BGM formalism. A detection of finite source effects is also demanded, with a minimum Δχ2 between a point-source point-lens (PSPL) and finite source model (FSPL) of 100. We apply a maximum impact parameter threshold value ut = 3 for umax, corresponding to a minimum required peak magnification of 1.017, following the formalism for umax from Specht et al. (2020). The properties of each filter used in this simulation are shown in Table 1.
The value of the maximum detectable impact parameter, umax, for each simulated event is obtained separately for the S/N criterion (uS/N), the parallax criterion (uplx), and the finite
source criterion (uFS), with the final value taken as umax = min(uS/N, uplx, uFS). In each case multi-dimensional linear interpolation is performed on a pre-computed umax look-up table to reduce computation time and prevent the necessity of performing expensive finite source calculations at runtime. The S/N look-up table was three-dimensional, with umax depending on the source magnitude, the cadence normalized to the event timescale x, and the normalized source radius ρ*. The parallax look-up table was six-dimensional, depending on the source magnitudes in the Roman W146 filter mW and the Euclid filter (either the VIS RIz filter or the NISP H-band filter mE), tE, ρ*, πE, and the angle between the projected baseline vector and the µrel vector ϕ. Finally, the finite source look-up table was also three-dimensional, depending on the same input parameters as the S/N table. The parameters and grid resolutions for each of the three umax grids are shown in Table 2.
Calculating the Euclid VIS and Roman W146 magnitudes for each source star was achieved by using approximations based on Johnson-Cousins filters. For VIS we used the Johnson-Cousins R band, which most closely mimics the VIS wavelength coverage and the wavelength of peak transmission. For W146, a weighted composite of the Johnson-Cousins J and H bands was used; shown in Fig. 4 are the transmission curves for J, H, and W146 for comparison. The resulting W146 magnitude mW146 is given by
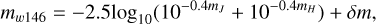 (11)
(11)
where δm accounts for the difference in the transmission integrals of W146 and the combination of J and H.
The results of the simulation, which used approximately 1.5 × 1011 unique lens-source pairs, were compiled into microlensing event rate maps over Galactic coordinates l ≤ 2.5°, l ≥ 358.5° and −2.5° ≤ b ≤ 0°, which covers the Roman Cycle-7 field locations proposed by Penny et al. (2019). Four Euclid fields were then added with dimensions 0.76° × 0.72° (Penny et al. 2013). Since the relative field rotation between the two is as yet unknown, an unoptimized scenario of field alignments was considered, where the Cycle-7 fields were aligned with the Galactic coordinate system, while the Euclid fields were aligned with the ecliptic coordinate system. Hence, the numbers provided in this work for total rates are deemed conservative. The Euclid field placements were optimized to maximize the joint Roman-Euclid detection rate in the Euclid NISP (H) filter for the Mróz model, using Nelder-Mead maximization that samples the
rate maps only in the overlap region between the two surveys. These field locations were then used for all other rate maps, with results shown in Fig. 5. An extra condition was applied requiring that the Euclid fields be contiguous and non-overlapping. To illustrate the fraction of events with µrel > 〈µrel〉min and for source stars brighter than H < Hmax, complimentary cumulative rate fraction plots were generated (see Fig. 6).
Predicted joint detection rates are displayed in Table 3. The numbers indicate that a joint survey would have parallax sensitivity down to Earth-mass FFPs. In our simulation, the parallax was measurable for 91% of events with a Jupiter-mass lens and 85% for events due to a Earth lens. Therefore, almost all FFP events observed by the joint Euclid-Roman survey will have at least one mass-distance relation constrained. The detection of finite-source effects occurs for 4% of Jupiter FFPs events and 21% of Earth events. For this smaller fraction, the mass and distance of the FFP will be known with high precision.
A comparison can be made to the parallax detection rates from Ban (2020), who used different methods to determine the event selection criteria along with microlensing calculations based on an earlier version of MaBµ/lS. Ban (2020) considers a single line of sight at (l, b) = (1.0°, −1.75°) for various telescope combinations (including the Vera Rubin Observatory, formerly LSST). Differences in calculation methodology make direct comparison difficult. Ban (2020) does not require a detection of finite source effects (although finite source effects without limb-darkening are taken into consideration when calculating simulated light curve photometry) and uses a S/N at peak selection (with S/N ≥ 50), as opposed to the time-integrated S/N used in the present study. This difference in S/N selection drives the main difference between results, with a rate per square degree per 60 days of observation of ΓEarth = 5.2 for this work and ΓEarth = 4.9 for Ban (2020), with a larger discrepancy for the rates of Jupiter-mass FFPs of ΓJupiter = 104 for this work and ΓJupiter = 31for Ban (2020), attributable to the effect of using a time integrated S/N selection on events of longer timescales. Similarly, we can compare the fraction of FFP events with finite-source effects found in this study with the fraction estimated in Johnson et al. (2020). The criterion for the detection of finite-source used in this work (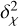 ≥ 100 between a FSPL and a PSPL model) can be approximated as ρ ≳ u0. Reading the fraction of detected events with ρ > u0 in Fig. 9 of Johnson et al. (2020) returns a small percentage for Jupiter-mass FPPs and
≥ 100 between a FSPL and a PSPL model) can be approximated as ρ ≳ u0. Reading the fraction of detected events with ρ > u0 in Fig. 9 of Johnson et al. (2020) returns a small percentage for Jupiter-mass FPPs and
~15% for the Super-Earth case (i.e., 10 M⊕), in good agreement with the estimated fraction presented in this work (4 and 21% respectively). We note an even better agreement if the same criterion used by Johnson et al. (2020) is chosen for detectable finite-source effects (i.e., ρ ≥ 0.5 u0).
It is clear from Table 3 that even a single-season Roman-Euclid joint campaign has the potential to detect and verify the existence of FFPs down to Earth mass, or to begin placing strong limits on their abundance, limits more than five times stronger than current limits (Mróz et al. 2017). With a multi-season joint campaign the sensitivity increases proportionately. If FFPs have an abundance comparable to one per Galactic star, then a joint campaign can obtain direct mass, distance, and kinematic measurements for a significant sample, providing a high-precision test of FFP formation models.
 |
Fig. 3 Three examples of simulated microlensing events due to FFP lenses as seen by Euclid and Roman. Shown are (from left to right) the case of a super-Jupiter lens, a Saturn-like lens, and a super-Earth lens. The distance of the source Ds is set at 8 kpc and the true mass Mtrue and distance Dtrue of the lenses, as well as the best-fit parameters, are indicated for each case. Those based only on Roman data are presented in brown, while the best-fit solutions using both datasets are shown in black. Using Roman data only, the mass of the lens can be reconstruct accurately only for the longer events. The magnitudes are artificially aligned to the Roman system for the plotting. |
Assumed sensitivities for the Roman W146 and Euclid VIS and NISP-H band passes used in our simulations.
Input parameters for each of the umax grids are shown, with the parameter ranges shown in square brackets.
 |
Fig. 4 Transmission curves for the Roman W146 and Johnson-Cousins J and H filters. Data for the W146 transmission is available at https://roman.gsfc.nasa.gov/science/Roman_Reference_Information.html |
 |
Fig. 5 FFP rate maps, in units of events per square degree per year, for events jointly detected by the Roman W146 filter and Euclid VIS filters (top two rows) and by the NISP filter (bottom two rows). Rows 1 and 3 use the Mróz model of ten Earth-mass FFPs per main sequence star, while rows 2 and 4 use the Sumi model of two Jupiter-mass FFPs per main sequence star. The left column shows rate maps constrained only by the S/N criterion, while the right column shows the equivalent rate maps with all selection criteria present, including parallax and finite source effects. |
6 Exomoons
The approach of combining Roman and Euclid observations not only provides the opportunity to detect planetary events of lunar mass (Penny et al. 2019), but would in tandem increase the chances of discovering extrasolar moons. Microlensing detections of exomoons has been suggested by Han & Han (2002) and simulated by Liebig & Wambsganss (2010). Exomoons are effectively described by triple point-mass lens models. As such, the number of caustic curve topologies and the respective variety
of light curves increases substantially, compared to binary lenses (Danek & Heyrovsky 2015). In most cases we can expect that the mass ratio of the lunar companion with respect to the host star is below 10−7 (the mass ratio of Ganymede relative to the Sun is q ~ 7.5 × 10−8), and thus will lead to a perturbed magnification pattern lasting a few hours at maximum. Although earlier works have emphasized detecting exomoons, from the source tracks shown in Fig. 7, it is clear that the separation of the tracks is comparable to the perturbation induced in the caustic curve, which could double the probability of detecting exomoons in an optimistic scenario.
To simulate the two source trajectories, we assume that both Euclid and Roman will have orbital elements similar to those of Gaia, and therefore we used the Gaia ephemeris to simulate the observations. Ideally, the detection of exomoons would require an armada of space telescopes simultaneously probing planetary caustics, which is well beyond the scope of the present concept. Even then, characterizing an exomoon would remain challenging, and securing a second light curve covering the exo-lunar caustic perturbation is essential to place a constraint on the exo-lunar mass ratio and separation from the planet.
As we are dealing with an uncharted region of the observable exo-lunar mass and semi-major axis parameter space, it is hard to estimate the number of detections. Given the frequency with which moons occur around Solar System planets4, it is highly likely that at least some of the ~1500 cool-orbit exoplanets that Roman will discover will host exomoons and that by combining data from Roman and Euclid we will be able to confirm the objects’ status as exomoons and establish in a statistically significant sense if exomoons are common.
In order to put the exomoon detection probability into context, one can introduce an exomoon lensing signature into the binary models of the full sample of microlensing exoplanets discovered to date. Little is known about the distribution of exomoons but based on the microlensing exoplanets and deriving exomoon properties known to date (mass and orbital radius) based on the distribution of moons in the Solar System, we can estimate the detection zone on a simulated magnification pattern under the following assumptions: the ratio of the exomoon mass to the host star mass q2 ∈ [10−5,10−2] is log-uniform distributed. The angular separation s2 between host planet and exomoon similarly was log-uniform distributed and is expressed in units of θE for a range of s2 e [10−3,10−1]. In addition, each exomoon should be uniformly distributed on a sphere around the exoplanet. The detection zone is shown in Fig. 8, and for randomly oriented tracks and lensed events (i.e., within 1 θE), a detection zone area of 10−3 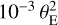 would correspond to a detection probability of ≈3%.
would correspond to a detection probability of ≈3%.
In order to corroborate such a heuristic approach and to reach a more conservative estimate, we can simulate the parallax of microlensing events based on the range of lensing parameters for all events documented in the NASA exoplanet archive and analyze those parts of the light curve with a magnification µ > 1.34, which represents the lensing zone. For a planet in the lensing zone with q1 = 10−3, s1 = 1 we find that for simulated exomoons and simulated tracks we obtain 0.9% detectable events for a detection threshold of 0.5% photometric accuracy, which is in agreement with the integrated detection zone shown earlier. Within this work, both missions are supposed to have a similar sampling rate closer to the Roman observing strategy. This leads us to the estimate that more than 0.8% of exomoons are detectable for host planet parameter ranges in the control region of 1og10(s1) ∈ [−0.15, 0.15] and log10(q1) ∈ [−3, −2]. Less than 10% of all expected extrasolar planets will be in that range, and thus our final assessment will include a representative sample of the s1, q1 parameter space shown in Fig. 8. Most events are covered by both missions and with a similar baseline of time series photometry, in which case the number of detected exomoons would modestly increase. In total 40 000 triple lens maps were simulated for the exomoon comparison with actual tracks. We find that 281 would be detected with both missions. The Roman mission alone would contribute 25 more events and Euclid (with a Roman-like cadence) would contribute another 25. That means the total number of exomoons would only decrease by less then 10% if Roman and Euclid were not combined. The main impact is the improved characterization of individual exomoon events, as indicated in Fig. 7.
If the number of exoplanets is as high as predicted (Penny et al. 2019) and exomoons are distributed in the aforementioned way, the first exomoon detections could become feasible and would certainly justify a more detailed study of that subject. For this purpose we use the original detection zone map and convert it to a detection probability evaluated for a representative sample of Penny et al. (2019) for the host planet parameters s and q. The respective value would be three, and thus on the order of one given the underlying assumptions. Finally, we would like to highlight that the orbital motion was not simulated as a second-order effect. In the following we assess the impact of the orbital motion by looking at a sample of simulated exomoons for the known default model of NASA’s exoplanet archive. Since we are relying on distributions based on actual planetary detections, we can extract the orbital periods of the exomoons. This also enables us to express the period in terms of tE as show in Fig. 9. The mode of the distribution of periods is ≈10tE, which could contribute to the characterization and would lead to a detectable change in orbital motion.
 |
Fig. 6 Cumulative rate fraction for a maximum H-band magnitude and minimum 〈µrel〉 is shown in both the Roman W146 and Euclid VIS filters (top two rows) and the NISP filter (bottom two rows). Rows 1 and 3 use the Mróz model of ten Earth-mass FFPs per main sequence star, while rows 2 and 4 use the Sumi model of two Jupiter-mass FFPs per main sequence star. The left column shows rate fraction constrained only by the S/N criterion, while the right column shows the equivalent rate fraction with all selection criteria present, including parallax and finite source effects. The 0.5, 0.75, and 0.9 contours are shown for reference. |
Predicted joint Roman-Euclid FFP microlensing detection rates per annual observing season, consisting of two 30-day Galactic bulge observing windows per season.
 |
Fig. 7 Simulated example of an exomoon event (a triple-lens caustic) observed from both Roman and Euclid. The top row displays the event geometry centered on the planetary caustic. The right column is a zoom-in on the time of the exomoon caustic crossing. The expected separation of the source tracks is comparable in scale to the perturbation induced on the caustic by the exomoon. The planet, with mass ratio q1 = 10−3, is at separation s1 = 1.3, and the moon has q2 = 10−2 and s2 = 0.032 relative to the planet. The Einstein timescale is tE = 47 days. The middle row is for a normalized source radius ρ = 0.00033, while the bottom row is for ρ = 0.001. |
7 Summary
In this paper we assessed the benefits of Euclid observations of Roman microlensing fields. After recalling the different methods used to estimate the mass and distance of the lenses, we studied the possibility of an early Euclid imaging campaign (about 5 yr prior to Roman launch). We simulated Euclid and Roman images of 432 microlensing events and modeled the proper motions and magnitudes of the sources and the lenses. Because of the larger separations between the sources and lenses at the time of the early Euclid images, we were able to reconstruct 29% of the simulated relative proper motions µrel to better than 10%, using the Euclid early image. Similarly, we demonstrated that it is possible to reconstruct 42% of lens magnitudes with a precision of 0.1 mag in the VIS band. We therefore conclude that the early imaging of the Roman fields by Euclid will allow a precise measurement of mass and distance for a large fraction of events that will be detected by Roman, for a modest telescope time investment of about 7 h, and this would be immediately available after the first year of Roman observations.
We further studied the potential of a joint simultaneous observing campaign, especially for constraining the microlensing parallax. We first show that this strategy allows the estimation of lens masses down to Earth-mass FFPs, a regime not achievable with Roman alone. We simulated billions of microlensing events with two FFP populations to estimate event rate maps toward the Roman microlensing fields. Based on these maps and assuming three detection criteria, we found that hundred of events due to FFPs will be detected every year. Moreover, the combination of the two datasets will constraint the parallax for more than 80% of the events. For about 20% of these events, finite-source effects will also be detectable and therefore the mass and distance of these objects will be known to high precision. We considered two different FFP population, constructed as Dirac delta functions, one peaked at Earth mass and normalized to ten FFPs per main sequence star (Mróz et al. 2019b) and the second peaked at Jupiter mass and normalized to two FFPs per main sequence star (Sumi et al. 2011). Our results indicate that 490 Jupiter-mass FFPs and 130 Earth-mass FFPs could be detected per year. Johnson et al. (2020) used different hypotheses; they considered the full observing season windows of Roman (~72 days) and one FFP per main
sequence star in the galaxy, but their results are in good agreement with our estimation. After correction of the hypothesis for the shorter Euclid observing seasons, the detection rate reported by Johnson et al. (2020) are 123 Earth-mass FFPs and about 550 Jupitermass FFPs per year. Ban (2020) also assumed one FFP per main sequence star and studied three Dirac delta populations peaking at Jupiter, Neptune, and Earth mass (Ban et al. 2016). By applying the same correction, their estimations scaled to with 152 Jupiter-mass and 123 Earth-mass FFPs detected every year. We note that the discrepancy in the rate of Jupiter-mass FFPs is mostly attributable to the difference in the detection criteria between the two studies. Our results are therefore compatible with these previous studies and reinforce the claim that a joint Roman-Euclid survey will detect hundreds of FFPs, depending on the exact population of these objects. This is a unique opportunity for studying the FFP population in great detail, especially to improve the picture of the abundance of FFPs, and to place strong constraints on FFP formation models.
Finally, we also studied the potential of the joint survey to detect exomoons. Using the distribution of moons in the Solar System and the planet distribution that Roman is expected to detect, we simulated 40000 triple lens events to estimate that about 1% of these moons should be detectable, and we therefore conclude that this survey could lead to the first detection of an exomoon. In this scenario the combination of the two datasets will be extremely valuable for the characterization of the lensing system because the projected separation between Roman and Euclid is on the same order as the caustic size induced by the presence of the moon.
 |
Fig. 8 Simulated detection zone areas converted to assess probability for exomoons around host stars (red dots) assuming a detection threshold of 0.5%, corresponding to 5 mmag accuracy for unblended events, well within the expectation of the Roman telescopes. In order to account for the sampling interval consecutive points should be within 10−3tE to be detectable. For more massive planets (green) the detection zone is expected to cover 10−3 |
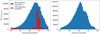 |
Fig. 9 Histogram of two million simulated exomoons for the default model of known microlensing exoplanets shown on NASA’s exoplanet archive. For illustrative purposes a rescaled histogram of planetary satellites6 and their orbital periods are indicated. To assess the impact and the orbital motion, the period is also shown with respect to the Einstein time. |
Acknowledgements
E.B. gratefully acknowledge support from NASA grant 80NSSC19K0291. The work of D.S. is funded by a UK Science and Technology Facilities Council (STFC) PhD studentship. E.K. also acknowledges support from the STFC. E.B., J.P.B. and C.R.’s work was carried out within the framework of the ANR project COLD-WORLDS supported by the French National Agency for Research with the reference ANR-18-CE31-0002. J.P.B. was supported by the University of Tasmania through the UTAS Foundation, ARC grant DP200101909 and the endowed Warren Chair in Astronomy. J.R. was supported by NASA ROSES grant 12-EUCLID12-0004, the Nancy Grace Roman Telescope, and JPL, which is run by Caltech under a contract for NASA. R.P. was supported by the Polish National Agency for Academic Exchange via Polish Returns 2019 grant. D.M. acknowledges support by the European Research Council (ERC) under the European Union’s FP7 Programme, Grant No. 833031. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
References
- Awiphan, S., Kerins, E., & Robin, A. C. 2015, MNRAS, 456, 1666 [Google Scholar]
- Bachelet, E., & Penny, M. 2019, ApJ, 880, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Bachelet, E., Norbury, M., Bozza, V., & Street, R. 2017, AJ, 154, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Ban, M. 2020, MNRAS, 494, 3235 [NASA ADS] [CrossRef] [Google Scholar]
- Ban, M., Kerins, E., & Robin, A. C. 2016, A&A, 595, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batista, V., Beaulieu, J. P., Bennett, D. P., et al. 2015, ApJ, 808, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Beaulieu, J.-P. 2018, Universe, 4, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D. P., & Rhie, S. H. 1996, ApJ, 472, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, D. P., Anderson, J., & Gaudi, B. S. 2007, ApJ, 660, 781 [Google Scholar]
- Bennett, D. P., Batista, V., Bond, I. A., et al. 2014, ApJ, 785, 155 [Google Scholar]
- Bennett, D. P., Akeson, R., Anderson, J., et al. 2018, ArXiv e-prints [arXiv:1803.08564] [Google Scholar]
- Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhattacharya, A., Bennett, D. P., Anderson, J., et al. 2017, AJ, 154, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, A., Beaulieu, J. P., Bennett, D. P., et al. 2018, AJ, 156, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, A., Bennett, D. P., Beaulieu, J. P., et al. 2021, AJ, 162, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Blackman, J. W., Beaulieu, J. P., Bennett, D. P., et al. 2021, Nature, 598, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2013, ApJ, 771, 40 [Google Scholar]
- Burgess, A. S. M., Moraux, E., Bouvier, J., et al. 2009, A&A, 508, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calchi Novati, S., Gould, A., Udalski, A., et al. 2015, ApJ, 804, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Cropper, M., Pottinger, S., Azzollini, R., et al. 2018, SPIE Conf. Ser., 10698, 1069828 [NASA ADS] [Google Scholar]
- Daněk, K., & Heyrovský, D. 2015, ApJ, 806, 99 [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Dominik, M., Rattenbury, N. J., Allan, A., et al. 2007, MNRAS, 380, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez-Alvarez, P., Dupac, X., Buenadicha, G., et al. 2018, SPIE Conf. Ser., 10707, 1070712 [Google Scholar]
- Gould, A. 1994, ApJ, 421, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A. 2000, ApJ, 542, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A. 2004, ApJ, 606, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Hamolli, L., Hafizi, M., De Paolis, F., & Nucita, A. A. 2016, Ap&SS, 361, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., & Gould, A. 1995, ApJ, 447, 53 [Google Scholar]
- Han, C., & Gould, A. 2003, ApJ, 592, 172 [Google Scholar]
- Han, C., & Han, W. 2002, ApJ, 580, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, S. A., Penny, M., Gaudi, B. S., et al. 2020, AJ, 160, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Koshimoto, N., Bennett, D. P., & Suzuki, D. 2020, AJ, 159, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Liebig, C., & Wambsganss, J. 2010, A&A, 520, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L., Adame, L., D’Alessio, P., et al. 2005, ApJ, 635, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, S., Mao, S., Ida, S., Zhu, W., & Lin, D. N. C. 2016, MNRAS, 461, L107 [Google Scholar]
- Maciaszek, T., Ealet, A., Jahnke, K., et al. 2016, SPIE Conf. Ser., 9904, 99040T [NASA ADS] [Google Scholar]
- Marsh, K. A., Plavchan, P., Kirkpatrick, J. D., et al. 2010, ApJ, 719, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miret-Roig, N., Bouy, H., Raymond, S. N., et al. 2022, Nat. Astron., 6, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C. 2018, Planetary Population Synthesis, eds. H. J. Deeg, & J. A. Belmonte (Cham: Springer International Publishing), 2425 [Google Scholar]
- Mróz, P., Udalski, A., Skowron, J., et al. 2017, Nature, 548, 183 [Google Scholar]
- Mróz, P., Udalski, A., Bennett, D. P., et al. 2019a, A&A, 622, A201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mróz, P., Udalski, A., Skowron, J., et al. 2019b, ApJS, 244, 29 [Google Scholar]
- Mróz, P., Poleski, R., Han, C., et al. 2020, AJ, 159, 262 [CrossRef] [Google Scholar]
- Oasa, Y., Tamura, M., & Sugitani, K. 1999, ApJ, 526, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Mulders, G. D., Gould, A., & Fernandes, R. 2018, ApJ, 856, L28 [CrossRef] [Google Scholar]
- Penny, M. T., Kerins, E., Rattenbury, N., et al. 2013, MNRAS, 434, 2 [CrossRef] [Google Scholar]
- Penny, M. T., Gaudi, B. S., Kerins, E., et al. 2019, ApJS, 241, 3 [CrossRef] [Google Scholar]
- Refsdal, S. 1966, MNRAS, 134, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Marshall, D. J., Schultheis, M., & Reylé, C. 2012, A&A, 538, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robin, A. C., Reylé, C., Fliri, J., et al. 2014, A&A, 569, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Skowron, J., Udalski, A., Gould, A., et al. 2011, ApJ, 738, 87 [Google Scholar]
- Specht, D., Kerins, E., Awiphan, S., & Robin, A. C. 2020, MNRAS, 498, 2196 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Baltay, C., et al. 2015, ArXiv e-prints [arXiv:1503.03757] [Google Scholar]
- Street, R. A., Udalski, A., Calchi Novati, S., et al. 2016, ApJ, 819, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Sumi, T., Kamiya, K., Bennett, D. P., et al. 2011, Nature, 473, 349 [Google Scholar]
- Suzuki, D., Bennett, D. P., Sumi, T., et al. 2016, ApJ, 833, 145 [Google Scholar]
- Vandorou, A., Bennett, D. P., Beaulieu, J.-P., et al. 2020, AJ, 160, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Veras, D., & Raymond, S. N. 2012, MNRAS, 421, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, H. J., & Mao, S. 1994, ApJ, 430, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., Kostrzewa-Rutkowska, Z., Skowron, J., et al. 2016, MNRAS, 458, 3012 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, J. C. 2013, ApJ, 770, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, J. C. 2015, ApJ, 814, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, J. C., Albrow, M., Barry, R. K., et al. 2014, ArXiv e-prints [arXiv:1409.2759] [Google Scholar]
- Yoo, J., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [Google Scholar]
- Zapatero Osorio, M. R., Béjar, V. J. S., Martín, E. L., et al. 2000, Science, 290, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Zapatero Osorio, M. R., Béjar, V. J. S., & Peña Ramírez, K. 2017, ApJ, 842, 65 [CrossRef] [Google Scholar]
According to The Exoplanet Encyclopedia (http://www.exoplanet.eu) accessed 3 January 2022.
Available at https://github.com/mtpenny/wfirst-ml-figures
For instance, there are 212 satellites on NASA’s list of planetary satellites https://ssd.jpl.nasa.gov/sats/elem/
All Tables
Assumed sensitivities for the Roman W146 and Euclid VIS and NISP-H band passes used in our simulations.
Input parameters for each of the umax grids are shown, with the parameter ranges shown in square brackets.
Predicted joint Roman-Euclid FFP microlensing detection rates per annual observing season, consisting of two 30-day Galactic bulge observing windows per season.
All Figures
 |
Fig. 1 Distribution of host star (lens) magnitudes from a sample of simulated planetary microlensing events injected in the Euclid image. The gray histogram shows the W149 (left) and VIS (right) magnitude distribution of all hosts in a sample of 1691 planetary microlensing events drawn from simulations presented in Penny et al. (2019), and the black histogram shows the distribution of 432 events brighter than W149 < 22.5, which were injected into our simulated image. The red histogram shows the distribution of magnitudes for the sources of the 432 events with bright lenses. |
| In the text | |
 |
Fig. 2 Distribution of fit residuals, defined as Δ = fit − true, as a function of µrel(top) and VIS lens magnitude L (bottom). The orange triangles are events meeting both criteria: |Δµrel| < 0.1µrel and |ΔL| < 0.1 mag. The left column gives the results for all 432 events, while the right column shows a zoomed-in image for events with |Δµrel| < 2.5 mas yr−1 and |ΔL| < 0.1 mag. |
| In the text | |
 |
Fig. 3 Three examples of simulated microlensing events due to FFP lenses as seen by Euclid and Roman. Shown are (from left to right) the case of a super-Jupiter lens, a Saturn-like lens, and a super-Earth lens. The distance of the source Ds is set at 8 kpc and the true mass Mtrue and distance Dtrue of the lenses, as well as the best-fit parameters, are indicated for each case. Those based only on Roman data are presented in brown, while the best-fit solutions using both datasets are shown in black. Using Roman data only, the mass of the lens can be reconstruct accurately only for the longer events. The magnitudes are artificially aligned to the Roman system for the plotting. |
| In the text | |
 |
Fig. 4 Transmission curves for the Roman W146 and Johnson-Cousins J and H filters. Data for the W146 transmission is available at https://roman.gsfc.nasa.gov/science/Roman_Reference_Information.html |
| In the text | |
 |
Fig. 5 FFP rate maps, in units of events per square degree per year, for events jointly detected by the Roman W146 filter and Euclid VIS filters (top two rows) and by the NISP filter (bottom two rows). Rows 1 and 3 use the Mróz model of ten Earth-mass FFPs per main sequence star, while rows 2 and 4 use the Sumi model of two Jupiter-mass FFPs per main sequence star. The left column shows rate maps constrained only by the S/N criterion, while the right column shows the equivalent rate maps with all selection criteria present, including parallax and finite source effects. |
| In the text | |
 |
Fig. 6 Cumulative rate fraction for a maximum H-band magnitude and minimum 〈µrel〉 is shown in both the Roman W146 and Euclid VIS filters (top two rows) and the NISP filter (bottom two rows). Rows 1 and 3 use the Mróz model of ten Earth-mass FFPs per main sequence star, while rows 2 and 4 use the Sumi model of two Jupiter-mass FFPs per main sequence star. The left column shows rate fraction constrained only by the S/N criterion, while the right column shows the equivalent rate fraction with all selection criteria present, including parallax and finite source effects. The 0.5, 0.75, and 0.9 contours are shown for reference. |
| In the text | |
 |
Fig. 7 Simulated example of an exomoon event (a triple-lens caustic) observed from both Roman and Euclid. The top row displays the event geometry centered on the planetary caustic. The right column is a zoom-in on the time of the exomoon caustic crossing. The expected separation of the source tracks is comparable in scale to the perturbation induced on the caustic by the exomoon. The planet, with mass ratio q1 = 10−3, is at separation s1 = 1.3, and the moon has q2 = 10−2 and s2 = 0.032 relative to the planet. The Einstein timescale is tE = 47 days. The middle row is for a normalized source radius ρ = 0.00033, while the bottom row is for ρ = 0.001. |
| In the text | |
 |
Fig. 8 Simulated detection zone areas converted to assess probability for exomoons around host stars (red dots) assuming a detection threshold of 0.5%, corresponding to 5 mmag accuracy for unblended events, well within the expectation of the Roman telescopes. In order to account for the sampling interval consecutive points should be within 10−3tE to be detectable. For more massive planets (green) the detection zone is expected to cover 10−3 |
| In the text | |
 |
Fig. 9 Histogram of two million simulated exomoons for the default model of known microlensing exoplanets shown on NASA’s exoplanet archive. For illustrative purposes a rescaled histogram of planetary satellites6 and their orbital periods are indicated. To assess the impact and the orbital motion, the period is also shown with respect to the Einstein time. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.