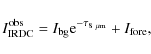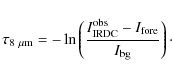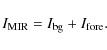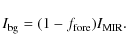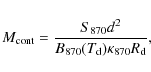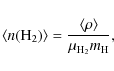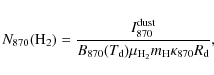| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/200913662 | |
| Published online | 08 October 2010 | |
LABOCA mapping of the infrared dark cloud
MSXDC G304.74+01.32![[*]](/icons/foot_motif.png)
O. Miettinen - J. Harju
Department of Physics, PO Box 64, 00014 University of Helsinki, Finland
Received 13 November 2009 / Accepted 18 March 2010
Abstract
Context. Infrared dark clouds (IRDCs) likely
represent very early stages of high-mass star/star cluster formation.
Aims. The aim is to determine the physical
properties and spatial distribution of dense clumps in the IRDC MSXDC
G304.74+01.32 (G304.74), and bring these characteristics into relation
to theories concerning the origin of IRDCs and their fragmentation into
clumps and star-forming cores.
Methods. G304.74 was mapped in the 870 ![]() m dust
continuum with the LABOCA bolometer on APEX. The 870
m dust
continuum with the LABOCA bolometer on APEX. The 870 ![]() m map was
compared with the 1.2 mm continuum map of the cloud by Béltran
et al. (2006, A&A, 447, 221). Archival
MSX and IRAS infrared data were used to study the
nature and properties of the submillimetre clumps within the cloud. The
H2 column densities were estimated using both
the 870
m map was
compared with the 1.2 mm continuum map of the cloud by Béltran
et al. (2006, A&A, 447, 221). Archival
MSX and IRAS infrared data were used to study the
nature and properties of the submillimetre clumps within the cloud. The
H2 column densities were estimated using both
the 870 ![]() m
dust emission and the MSX 8
m
dust emission and the MSX 8 ![]() m extinction data. The obtained values were
compared with near-infrared extinction which could be estimated along a
few lines of sight. We compared the clump masses and their spatial
distribution in G304.74 with those in several other recently studied
IRDCs.
m extinction data. The obtained values were
compared with near-infrared extinction which could be estimated along a
few lines of sight. We compared the clump masses and their spatial
distribution in G304.74 with those in several other recently studied
IRDCs.
Results. Twelve clumps were identified from the
870 ![]() m
dust continuum map. Three of them are associated with the
MSX and IRAS point sources. Moreover, one of the
clumps (SMM 6) is associated with two MSX 8
m
dust continuum map. Three of them are associated with the
MSX and IRAS point sources. Moreover, one of the
clumps (SMM 6) is associated with two MSX 8 ![]() m point-like
sources. Thus, there are 8 clumps within G304.74
which are not associated with mid-infrared (MIR) emission. The H2
column densities derived from the dust continuum and extinction data
are similar. The comparison suggests that the dust temperature may be
elevated (20-30 K) near the southern end of the cloud, whereas the
starless clumps in the centre and in the north are cool (
m point-like
sources. Thus, there are 8 clumps within G304.74
which are not associated with mid-infrared (MIR) emission. The H2
column densities derived from the dust continuum and extinction data
are similar. The comparison suggests that the dust temperature may be
elevated (20-30 K) near the southern end of the cloud, whereas the
starless clumps in the centre and in the north are cool (
![]() K). There is a high
likelihood that the clump mass distributions in G304.74 and in several
other IRDCs represent the samples of the same parent distribution. In
most cases the spatial distributions of clumps in IRDCs do not deviate
significantly from random distributions.
K). There is a high
likelihood that the clump mass distributions in G304.74 and in several
other IRDCs represent the samples of the same parent distribution. In
most cases the spatial distributions of clumps in IRDCs do not deviate
significantly from random distributions.
Conclusions. G304.74 contains several massive clumps
that are not associated with MIR emission. On statistical
grounds it is likely that some of them are or harbour high-mass
starless cores (HMSCs). The fact that the clump mass distributions
(resembling the high-mass stellar IMF), and in some cases also the
random-like spatial distributions, seem to be comparable between
different IRDCs, is consistent with the idea that the origin of IRDCs,
and their further sub-fragmentation down to scales of clumps is caused
by supersonic turbulence in accordance with results from giant
molecular clouds.
Key words: stars: formation - ISM: clouds - ISM: structure - radio continuum: ISM - submillimeter: ISM
1 Introduction
1.1 Infrared dark clouds
The so-called infrared dark clouds (IRDCs) were discovered by the
Infrared Space Observatory (ISO; Pérault
et al. 1996) and the Midcourse Space Experiment
(MSX; Egan et al. 1998);
the clouds were detected as dark absorption objects against the bright
mid-infrared (MIR) Galactic background radiation. Based on the
MSX 8 ![]() m
data of the Galactic plane from
m
data of the Galactic plane from
![]() and
and
![]() ,
Simon et al. (2006a) identified almost 11 000 IRDC
candidates. Recently, Peretto & Fuller (2009) used Spitzer
satellite data to extract about 9000 new IRDC candidates.
,
Simon et al. (2006a) identified almost 11 000 IRDC
candidates. Recently, Peretto & Fuller (2009) used Spitzer
satellite data to extract about 9000 new IRDC candidates.
Molecular line and dust continuum studies of IRDCs have shown
that they are
cold (T<25 K), dense (
![]() cm-3,
cm-3,
![]() cm-2),
and massive (
cm-2),
and massive (![]()
![]() )
structures with sizes of
)
structures with sizes of ![]() 1-15 pc (e.g., Carey et al. 1998; Simon et al. 2006b; Rathborne et al. 2006,
hereafter RJS06; Du & Yang 2008;
Vasyunina et al. 2009).
Most IRDCs are filamentary (e.g., Peretto
& Fuller 2009), and contain density enhancements, or
clumps
1-15 pc (e.g., Carey et al. 1998; Simon et al. 2006b; Rathborne et al. 2006,
hereafter RJS06; Du & Yang 2008;
Vasyunina et al. 2009).
Most IRDCs are filamentary (e.g., Peretto
& Fuller 2009), and contain density enhancements, or
clumps![]() , that are visible in
(sub)millimetre dust continuum maps (e.g., Carey
et al. 2000; Garay
et al. 2004; Ormel
et al. 2005; RJS06). The cold clumps (i.e., clumps
unassociated with MSX 8
, that are visible in
(sub)millimetre dust continuum maps (e.g., Carey
et al. 2000; Garay
et al. 2004; Ormel
et al. 2005; RJS06). The cold clumps (i.e., clumps
unassociated with MSX 8 ![]() m emission) identified by RJS06 have typical
sizes and masses of
m emission) identified by RJS06 have typical
sizes and masses of ![]() 0.5 pc
and
0.5 pc
and ![]()
![]() ,
respectively. Because IRDCs have clumpy structures, they are likely to
be in an early stage of fragmentation (e.g., RBG09 and references
therein).
,
respectively. Because IRDCs have clumpy structures, they are likely to
be in an early stage of fragmentation (e.g., RBG09 and references
therein).
The radial galactocentric distribution of IRDCs peaks at
![]() kpc
in
the 1st Galactic quadrant, and at
kpc
in
the 1st Galactic quadrant, and at
![]() kpc
in the 4th quadrant, which correspond to the location of the
Scutum-Centaurus spiral arm (see Simon
et al. 2006b; and Jackson
et al. 2008). This, together with the fact that
IRDCs have sizes
and masses similar to those of warm massive cluster-forming regions
(e.g., Lada & Lada 2003;
Motte et al. 2003),
has led to the suggestion
that IRDCs represent the very early stages of high-mass star/star
cluster formation. Indeed, several studies have found signs of ongoing
star formation within IRDCs. These include CH3OH
and H2O masers (Beuther
et al. 2002b; Pillai
et al. 2006a; Wang
et al. 2006; Ellingsen
2006), outflow signatures (Beuther
et al. 2005; Beuther
& Sridharan 2007; Sakai
et al. 2008), and associated infrared sources (e.g.,
Rathborne et al. 2005;
Beuther & Steinacker
2007; Chambers
et al. 2009; RBG09). Cold, dense clumps are
suggested to host/represent precursors of
hot molecular cores, i.e., high-mass starless cores
(HMSCs; e.g.,
Sridharan et al. 2005;
Beuther et al. 2007).
A few hot cores have been found
within IRDCs (Rathborne
et al. 2007, 2008), but it is important to increase
the
sample in order to study the sequence of events. It should be noted
that the
formation of hot cores may not be universal in IRDCs - some of them
seem to
form only low- to intermediate-mass stars (e.g., van der Wiel
& Shipman 2008).
kpc
in the 4th quadrant, which correspond to the location of the
Scutum-Centaurus spiral arm (see Simon
et al. 2006b; and Jackson
et al. 2008). This, together with the fact that
IRDCs have sizes
and masses similar to those of warm massive cluster-forming regions
(e.g., Lada & Lada 2003;
Motte et al. 2003),
has led to the suggestion
that IRDCs represent the very early stages of high-mass star/star
cluster formation. Indeed, several studies have found signs of ongoing
star formation within IRDCs. These include CH3OH
and H2O masers (Beuther
et al. 2002b; Pillai
et al. 2006a; Wang
et al. 2006; Ellingsen
2006), outflow signatures (Beuther
et al. 2005; Beuther
& Sridharan 2007; Sakai
et al. 2008), and associated infrared sources (e.g.,
Rathborne et al. 2005;
Beuther & Steinacker
2007; Chambers
et al. 2009; RBG09). Cold, dense clumps are
suggested to host/represent precursors of
hot molecular cores, i.e., high-mass starless cores
(HMSCs; e.g.,
Sridharan et al. 2005;
Beuther et al. 2007).
A few hot cores have been found
within IRDCs (Rathborne
et al. 2007, 2008), but it is important to increase
the
sample in order to study the sequence of events. It should be noted
that the
formation of hot cores may not be universal in IRDCs - some of them
seem to
form only low- to intermediate-mass stars (e.g., van der Wiel
& Shipman 2008).
1.2 Infrared dark cloud MSXDC G304.74+1.32
The IRDC studied in this paper was designated as
MSXDC G304.74+1.32 (hereafter, G304.74) by Simon
et al. (2006a). G304.74 was observed by Beltrán
et al. (2006) with the SIMBA bolometer array on SEST at
1.2 mm. Beltrán et al. (2006) identified eight
millimetre clumps within the cloud, out of which four were found to be
associated with MSX point sources. The distance to the cloud,
2.4 kpc, is a kinematic distance estimated
from the velocity of the CS line observed by Fontani et al.
(2005).
The galactocentric distance is ![]() 7.4 kpc.
7.4 kpc.
G304.74 was chosen for the present study because its relatively close distance allows for reasonably good spatial resolution in order to study its substructure. Moreover, a relatively high number of clumps (8) were already identified from the cloud (see above), and thus it was considered an appropriate object for studying IRDC fragmentation.
In this paper, we present the results of our 870 ![]() m dust
continuum mapping of G304.74. The paper pays special attention to the
clumpy
structure of the cloud, and the clump mass distribution, and thereby
addresses
the fragmentation of IRDCs. The observations and data-reduction
procedures are
described in Sect. 2. The observational results are presented
in Sect. 3. The MSX 8
m dust
continuum mapping of G304.74. The paper pays special attention to the
clumpy
structure of the cloud, and the clump mass distribution, and thereby
addresses
the fragmentation of IRDCs. The observations and data-reduction
procedures are
described in Sect. 2. The observational results are presented
in Sect. 3. The MSX 8 ![]() m optical thicknesses toward the submm peaks are
derived in Sect. 4. In Sect. 5, we describe the
methods used to derive the physical properties of the observed clumps.
In Sect. 6, we discuss the results
of our study, and in Sect. 7, we summarise our main
conclusions.
m optical thicknesses toward the submm peaks are
derived in Sect. 4. In Sect. 5, we describe the
methods used to derive the physical properties of the observed clumps.
In Sect. 6, we discuss the results
of our study, and in Sect. 7, we summarise our main
conclusions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13662fg1.ps}\hspace*{4mm}
\includegraphics[width=7.7cm,clip]{13662fg2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg30.png)
|
Figure 1:
Left: LABOCA map of the 870 |
| Open with DEXTER | |
Table 1: Submillimetre clumps identified by the clumpfind algorithm in the IRDC G304.74.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{13662fg3.ps}\hspace*{4mm}
\includegraphics[width=7.8cm,clip]{13662fg4.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg44.png)
|
Figure 2:
Left: wide-field (
|
| Open with DEXTER | |
2 Observations and data reduction
2.1 Submillimetre dust continuum
The 870 ![]() m
dust continuum observations toward G304.74 were carried out on
25-27 April 2009 with the 295 channel
bolometer array LABOCA (Large APEX Bolometer Camera) on APEX.
The central frequency of the instrument is 345 GHz,
and the bandwidth is 60 GHz. The half-power beam
width (HPBW) of the telescope is
m
dust continuum observations toward G304.74 were carried out on
25-27 April 2009 with the 295 channel
bolometer array LABOCA (Large APEX Bolometer Camera) on APEX.
The central frequency of the instrument is 345 GHz,
and the bandwidth is 60 GHz. The half-power beam
width (HPBW) of the telescope is
![]() (
(![]() 0.22 pc
at 2.4 kpc) at the frequency used. The total field of
view (FoV) of LABOCA is
0.22 pc
at 2.4 kpc) at the frequency used. The total field of
view (FoV) of LABOCA is
![]() .
The instrument and its observing modes are described in Siringo
et al. (2009).
.
The instrument and its observing modes are described in Siringo
et al. (2009).
Absolute flux calibration was achieved through observations of
the planets Mars, Uranus, and Neptune (the primary calibrators for
LABOCA), and the star CW Leo as secondary calibrator. The uncertainty
due to flux calibration was estimated to be ![]()
![]() .
The telescope focus and pointing were checked using the
planet Saturn, the star
.
The telescope focus and pointing were checked using the
planet Saturn, the star ![]() Carinae, and the H2O maser source B13134
(305.80-00.24).
The submm zenith opacity was determined using the sky-dip method and
the values varied from 0.20 to 0.38, with a median
value of 0.30. The observations were thus conducted in fair
weather conditions.
Carinae, and the H2O maser source B13134
(305.80-00.24).
The submm zenith opacity was determined using the sky-dip method and
the values varied from 0.20 to 0.38, with a median
value of 0.30. The observations were thus conducted in fair
weather conditions.
The observations were made using the on-the-fly (OTF) mapping
mode with
a scanning speed of ![]() s-1.
The size of the OTF map is
s-1.
The size of the OTF map is
![]() .
This was achieved by 204 subscans of
.
This was achieved by 204 subscans of
![]() in length (parallel with the
RA axis), spaced by
in length (parallel with the
RA axis), spaced by
![]() .
The area was
mapped five times, with a total observing time
of 5.2 h. In this manner, a uniform rms noise level
of
.
The area was
mapped five times, with a total observing time
of 5.2 h. In this manner, a uniform rms noise level
of
![]() Jy beam-1
was reached in the
central
Jy beam-1
was reached in the
central ![]()
![]() area
which covers the target source.
area
which covers the target source.
The data reduction was performed using the BoA (Bolometer
Array Analysis
Software) software package according to guidelines in the BoA User and
Reference Manual (2007)![]() .
The data reduction included flat-fielding, flagging bad/dark channels
and data
according to telescope speed and acceleration, correcting for the
atmospheric
opacity, division into subscans, baseline subtractions and median-noise
removal (correction for sky noise), despiking, and filtering-out of the
low frequencies of the 1/f-noise. Finally, the five
individual maps were
coadded.
.
The data reduction included flat-fielding, flagging bad/dark channels
and data
according to telescope speed and acceleration, correcting for the
atmospheric
opacity, division into subscans, baseline subtractions and median-noise
removal (correction for sky noise), despiking, and filtering-out of the
low frequencies of the 1/f-noise. Finally, the five
individual maps were
coadded.
We note that even the source model was iteratively used in the
reduction process, the resulting final map (Fig. 1, left
panel) has negative artefacts (``holes'') around regions of bright
emission. The depths of these negative holes are ![]()
![]() (
(![]()
![]() on average) of
the nearest peak object brightness, and thus they are likely to
introduce additional uncertainty in the source flux densities. We
estimate that the total flux density uncertainty due to calibration and
negative artefacts is in the range
on average) of
the nearest peak object brightness, and thus they are likely to
introduce additional uncertainty in the source flux densities. We
estimate that the total flux density uncertainty due to calibration and
negative artefacts is in the range ![]()
![]() .
These uncertainties are not, however, taken into account in the
analyses presented in this paper.
.
These uncertainties are not, however, taken into account in the
analyses presented in this paper.
2.2 Complementary near-, mid-, and far-infrared data
The target source (
![]() ,
,
![]() )
is not included in the GLIMPSE
(3.6, 4.5, 5.8, 8.0
)
is not included in the GLIMPSE
(3.6, 4.5, 5.8, 8.0 ![]() m)
and MIPSGAL (24 and 70
m)
and MIPSGAL (24 and 70 ![]() m) surveys of Spitzer
which cover the Galactic latitudes
m) surveys of Spitzer
which cover the Galactic latitudes
![]() .
We have used the near-infrared 2MASS (J, H,
and
.
We have used the near-infrared 2MASS (J, H,
and ![]() )
survey data
archive (Skrutskie
et al. 2006), data products from the
MSX survey
(Price et al. 2001;
Egan et al. 2003),
and the IRAS (Infrared Astronomical Satellite)
MIR and far-infrared (FIR) observations.
)
survey data
archive (Skrutskie
et al. 2006), data products from the
MSX survey
(Price et al. 2001;
Egan et al. 2003),
and the IRAS (Infrared Astronomical Satellite)
MIR and far-infrared (FIR) observations.
3 Observational results
3.1 Clump identification
The obtained LABOCA map is presented in the left panel of Fig. 1.
The cloud has a filamentary appearance and extends over about 13
![]() 2, i.e.,
about 9.2 pc at the cloud's distance. In order to
identify clumps in the LABOCA map, we employed the two-dimensional
clumpfind algorithm, clfind2d,
developed by Williams et al. (1994). The clfind2d
routine determines the peak position, the FWHM
(full width at half maximum) size (not corrected for beam size), and
the peak and total integrated flux density of clump based on specified
contour levels. The algorithm requires two input parameters:
1) the intensity threshold, i.e., the lowest contour level,
which determines the minimum emission to be included into clumps; and
2) the stepsize which determines the required ``contrast''
between two clumps to be considered as different objects. We set both
the intensity threshold and the stepsize to
2, i.e.,
about 9.2 pc at the cloud's distance. In order to
identify clumps in the LABOCA map, we employed the two-dimensional
clumpfind algorithm, clfind2d,
developed by Williams et al. (1994). The clfind2d
routine determines the peak position, the FWHM
(full width at half maximum) size (not corrected for beam size), and
the peak and total integrated flux density of clump based on specified
contour levels. The algorithm requires two input parameters:
1) the intensity threshold, i.e., the lowest contour level,
which determines the minimum emission to be included into clumps; and
2) the stepsize which determines the required ``contrast''
between two clumps to be considered as different objects. We set both
the intensity threshold and the stepsize to ![]() of the background noise level. With these settings, G304.74 divides
into 12 clumps.
of the background noise level. With these settings, G304.74 divides
into 12 clumps.
We note that the total number and size of clumps identified by
clumpfind is quite sensitive to the selected
contour levels.
The selected ![]() contour levels turned out to give the best agreement with the
identification by eye. This selection is also
recommended by Williams et al. (1994). See also Pineda
et al. (2009) for a recent discussion of clump identification
with clumpfind.
Pineda et al. (2009) concluded that small changes in the
threshold and/or stepsize values can lead to important changes in the
number of identified clumps.
contour levels turned out to give the best agreement with the
identification by eye. This selection is also
recommended by Williams et al. (1994). See also Pineda
et al. (2009) for a recent discussion of clump identification
with clumpfind.
Pineda et al. (2009) concluded that small changes in the
threshold and/or stepsize values can lead to important changes in the
number of identified clumps.
3.2 Observed properties of the clumps
Table 2: MSX point sources in the IRDC G304.74.
All the clumps have a peak flux density >The left panel of Fig. 2 shows the
wide-field MSX 8 ![]() m image (extracted from the MSX Galactic
Plane Survey images
m image (extracted from the MSX Galactic
Plane Survey images![]() )
towards G304.74. The MSX 8
)
towards G304.74. The MSX 8 ![]() m image zooming to the dark cloud with LABOCA
contours is shown in the right panel of Fig. 2.
There is a good agreement between the morphologies of
the 870
m image zooming to the dark cloud with LABOCA
contours is shown in the right panel of Fig. 2.
There is a good agreement between the morphologies of
the 870 ![]() m
continuum emission and the 8
m
continuum emission and the 8 ![]() m extinction visible as a
dark lane in the MSX image. The resolution of the
MSX image,
m extinction visible as a
dark lane in the MSX image. The resolution of the
MSX image,
![]() ,
is similar to that of the 870
,
is similar to that of the 870 ![]() m LABOCA map.
m LABOCA map.
Three of the submm clumps are associated with sources both
from the MSX and IRAS point source catalogues
(within ![]()
![]() and
and ![]()
![]() from
the dust peak position, respectively; see Fig. 1, left).
These are designated according to the IRAS names. The
remaining nine clumps are named SMM 1, SMM 2, etc.
One of the submm clumps, SMM 6, appears to be associated with
two 8
from
the dust peak position, respectively; see Fig. 1, left).
These are designated according to the IRAS names. The
remaining nine clumps are named SMM 1, SMM 2, etc.
One of the submm clumps, SMM 6, appears to be associated with
two 8 ![]() m
sources from the MSX catalogue. The stronger 8
m
sources from the MSX catalogue. The stronger 8 ![]() m source is
located at
m source is
located at ![]()
![]() from
the dust peak position (0.46 Jy beam-1),
whereas the weaker one is located at
from
the dust peak position (0.46 Jy beam-1),
whereas the weaker one is located at ![]()
![]() from
the closest dust emission peak (0.41 Jy beam-1)
within SMM 6. Furthermore, the eastern edge of SMM 4
is bright
in 8
from
the closest dust emission peak (0.41 Jy beam-1)
within SMM 6. Furthermore, the eastern edge of SMM 4
is bright
in 8 ![]() m
as the MSX source associated with IRAS 13037-6112
extends about 55
m
as the MSX source associated with IRAS 13037-6112
extends about 55
![]() west. Thus there are seven
clumps which are completely dark in the
MIR.
west. Thus there are seven
clumps which are completely dark in the
MIR.
The flux densities at MIR and FIR wavelengths
retrieved from the MSX (8.28, 12.13, 14.65, 21.34 ![]() m) and
IRAS (12, 25, 60, 100
m) and
IRAS (12, 25, 60, 100 ![]() m) archives for all the IRAS sources and
for the two 8
m) archives for all the IRAS sources and
for the two 8 ![]() m
point sources associated with SMM 6 are listed in
Tables 2
and 3,
respectively.
m
point sources associated with SMM 6 are listed in
Tables 2
and 3,
respectively.
4 IRDC
extinction and the 8  m
optical thicknesses
m
optical thicknesses
4.1 Principle
The observed 8 ![]() m
intensity towards an IRDC,
m
intensity towards an IRDC,
![]() ,
can be written as (e.g., Bacmann
et al. 2000)
,
can be written as (e.g., Bacmann
et al. 2000)
where
Following the notation of Bacmann et al. (2000) and Peretto & Fuller (2009), the observed MIR intensity around the IRDC is
To obtain an estimate for the value of
Table 3: IRAS point sources in the IRDC G304.74.
We note that the total size of the image used in the filtering process was4.2 Background and foreground estimation
To estimate the contribution of
![]() and
and
![]() to
the value of
to
the value of ![]() (Eq. (3),
and Fig. 3),
we used the similar analysis as used by Butler & Tan (2009,
their Sect. 3.1). We assumed that the radial distribution of
Galactic 8
(Eq. (3),
and Fig. 3),
we used the similar analysis as used by Butler & Tan (2009,
their Sect. 3.1). We assumed that the radial distribution of
Galactic 8 ![]() m
PAH (polycyclic aromatic hydrocarbon) emission has the same exponential
form as the radial distribution of molecular gas surface density
in the Galaxy (the radial scale length is
m
PAH (polycyclic aromatic hydrocarbon) emission has the same exponential
form as the radial distribution of molecular gas surface density
in the Galaxy (the radial scale length is
![]() kpc;
Williams & McKee 1997).
We note that this distribution is similar to that of the Galactic
surface density of OB associations (McKee
& Williams 1997), which was used by Butler &
Tan (2009, their Eq. (3)). The assumption that the radial
distribution of PAHs follows the molecular gas is supported
by the results of Mattila et al. (1999) who found that the UIR
(unidentified
infrared) emission band intensities in the disk of the galaxy
NGC 891 closely
follow those of the CO emission and 1.3 mm dust continuum
emission. However, UIR band intensities were found to be quite
different from that of the H
kpc;
Williams & McKee 1997).
We note that this distribution is similar to that of the Galactic
surface density of OB associations (McKee
& Williams 1997), which was used by Butler &
Tan (2009, their Eq. (3)). The assumption that the radial
distribution of PAHs follows the molecular gas is supported
by the results of Mattila et al. (1999) who found that the UIR
(unidentified
infrared) emission band intensities in the disk of the galaxy
NGC 891 closely
follow those of the CO emission and 1.3 mm dust continuum
emission. However, UIR band intensities were found to be quite
different from that of the H![]() emission (see Fig. 5 of Mattila et al. 1999).
Moreover, Kahanpää et al. (2003) found strong correlation
between the Galactic UIR bands and CO emission.
To estimate the vertical distribution of PAH emission, we used the
Galactic
vertical distribution of CO emission and adopted the scale
length
emission (see Fig. 5 of Mattila et al. 1999).
Moreover, Kahanpää et al. (2003) found strong correlation
between the Galactic UIR bands and CO emission.
To estimate the vertical distribution of PAH emission, we used the
Galactic
vertical distribution of CO emission and adopted the scale
length ![]() pc
(Dame et al. 1987; Bronfman et al. 1988;
Malhotra 1994).
pc
(Dame et al. 1987; Bronfman et al. 1988;
Malhotra 1994).
![\begin{figure}
\par\includegraphics[angle=270,width=8cm,clip]{13662fg5.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg92.png)
|
Figure 3:
Median filter estimate of |
| Open with DEXTER | |
We first calculated the
so-called ``foreground intensity ratio'', ![]() ,
which is defined as the ratio of the column of PAH emission
between the observer and the cloud and the total column through the
Galaxy
along the same line of sight, up to the galactocentric distance
16 kpc.
For G304.74, we obtained
,
which is defined as the ratio of the column of PAH emission
between the observer and the cloud and the total column through the
Galaxy
along the same line of sight, up to the galactocentric distance
16 kpc.
For G304.74, we obtained ![]() ,
where the uncertainty represents the mimimum-maximum error based on the
uncertainties in the scale lengths (see above). The distance of the Sun
from
the Galactic Centre was assumed to be 8.5 kpc in this
calculation. The intensity of the background emission is then given by
,
where the uncertainty represents the mimimum-maximum error based on the
uncertainties in the scale lengths (see above). The distance of the Sun
from
the Galactic Centre was assumed to be 8.5 kpc in this
calculation. The intensity of the background emission is then given by
The resulting values are
The observed 8 ![]() m intensities toward the submm dust continuum
peak positions, and the 8
m intensities toward the submm dust continuum
peak positions, and the 8 ![]() m optical thicknesses calculated from
Eq. (2),
are listed in Cols. (2) and (3) of Table 4. The
formal error in
m optical thicknesses calculated from
Eq. (2),
are listed in Cols. (2) and (3) of Table 4. The
formal error in
![]() was
calculated by propagating the errors
in
was
calculated by propagating the errors
in ![]() and
and ![]() .
In order to determine
.
In order to determine
![]() values
in the submm peak positions, the MSX image
was gridded with
values
in the submm peak positions, the MSX image
was gridded with
![]() pixels,
i.e., the LABOCA pixel size. We also estimated the possibility
that part of the observed 8
pixels,
i.e., the LABOCA pixel size. We also estimated the possibility
that part of the observed 8 ![]() m intensity originates from the bright
surroundings of a MIR dark clump. The measured point spread
function (PSF) in the MSX image is a
Gaussian with a FWHM of
m intensity originates from the bright
surroundings of a MIR dark clump. The measured point spread
function (PSF) in the MSX image is a
Gaussian with a FWHM of
![]() .
Convolution with this PSF reduces the
breadths of dark filaments, and, for the narrowest of them, increases
the minimum intensity in the middle. We estimate that for a
completely opaque source with a diameter of
.
Convolution with this PSF reduces the
breadths of dark filaments, and, for the narrowest of them, increases
the minimum intensity in the middle. We estimate that for a
completely opaque source with a diameter of ![]()
![]() ,
the MIR
radiation ``leakage'' from the surroundings amounts to
,
the MIR
radiation ``leakage'' from the surroundings amounts to ![]()
![]() of the
background level. This contribution was, however, neglected in the
above
analysis which uses only the peak (minimum) 8
of the
background level. This contribution was, however, neglected in the
above
analysis which uses only the peak (minimum) 8 ![]() m
intensities. Also, most of the MIR dark clumps are larger
than
m
intensities. Also, most of the MIR dark clumps are larger
than
![]() (see
Table 1,
Cols. (6) and (7)).
(see
Table 1,
Cols. (6) and (7)).
4.3 Dust temperature estimates
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13662fg6.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg103.png)
|
Figure 4:
MSX 8 |
| Open with DEXTER | |
where
The uncertainties of the ![]() estimates are very large in the southern part (SMM 1,
SMM 2; in the case of SMM 3 and SMM 4 no
reasonable estimate could be obtained because of the large error in
estimates are very large in the southern part (SMM 1,
SMM 2; in the case of SMM 3 and SMM 4 no
reasonable estimate could be obtained because of the large error in ![]() ). On the
other hand, the estimates with moderate formal errors in the central
and
northern part of the cloud suggest low temperatures of slightly above
10 K. It should be noted, however, that there are large uncertainties
concerning the dust opacities and the determination of the
). On the
other hand, the estimates with moderate formal errors in the central
and
northern part of the cloud suggest low temperatures of slightly above
10 K. It should be noted, however, that there are large uncertainties
concerning the dust opacities and the determination of the ![]() .
This
issue will be raised again in Sect. 6.2.
.
This
issue will be raised again in Sect. 6.2.
In view of these uncertainties, dust temperatures
estimated above should be compared with previous temperature
determinations from molecular lines. Observations towards several
other IRDC clumps (H2CO, Carey
et al. 1998; CH3CCH, Teyssier et al. 2002;
NH3, Pillai
et al. 2006b; Sakai
et al. 2008) provide gas kinetic
temperatures of ![]() K. The assumption that
K. The assumption that
![]() is
probably valid in dense clouds (
is
probably valid in dense clouds (
![]() cm-3;
e.g., Goldsmith & Langer
1978). Based on these considerations, we assume in what
follows that in general
cm-3;
e.g., Goldsmith & Langer
1978). Based on these considerations, we assume in what
follows that in general ![]() K.
Exceptions are made in the cases of
two IRAS sources, for which temperatures can be derived from
the
spectral energy distributions (SEDs). We will also separately consider
the possibility that
K.
Exceptions are made in the cases of
two IRAS sources, for which temperatures can be derived from
the
spectral energy distributions (SEDs). We will also separately consider
the possibility that ![]() is elevated in the four southern clumps SMM 1-4.
is elevated in the four southern clumps SMM 1-4.
Table 4:
The observed 8 ![]() m
intensity, the peak optical thickness, and the dust temperature toward
the submm peak positions.
m
intensity, the peak optical thickness, and the dust temperature toward
the submm peak positions.
5 Physical parameters of the clumps
5.1 Spectral energy distributions of the IRAS sources
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13662fg7.ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{13662fg8.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg126.png)
|
Figure 5:
Best-fit SEDs of IRAS 13037-6112 and IRAS 13039-6108.
MSX data points are shown by circles, IRAS data
points are shown by diamonds, and LABOCA and SIMBA (sub)mm data points
are indicated by squares. Upper limits are indicated by arrows. The
solid lines in both plots represent the sum of two (cold+hot)
components (see Cols. (4) and (5) of Table 5). The
absorption features appearing at |
| Open with DEXTER | |
Table 5: Results of the SED fits.
The MSX, IRAS, LABOCA, and SIMBA data
were used to fit the spectral energy distributions (SEDs) of
IRAS 13037-6112 and IRAS 13039-6108.
The SIMBA 1.2 mm flux densities of these sources are
0.89 and 1.36 Jy,
respectively (Beltrán
et al. 2006; Table 2 therein). Note that
there is not enough data points for IRAS 13042-6105 in order
to construct a reasonable SED (e.g., most of its IRAS flux
densities
are only upper limits, see Table 3). The derived
SEDs are shown in Fig. 5.
The least-squares fitting routine used in the derivation of the SED![]() minimises the sum
minimises the sum ![]() ,
where N
is the number of data points (7 and 8 for
IRAS 13037-6112 and 13039-6108, respectively),
,
where N
is the number of data points (7 and 8 for
IRAS 13037-6112 and 13039-6108, respectively), ![]() is the observed flux density, and
is the observed flux density, and ![]() is the model flux density.
In both cases, the data were fitted by a two-temperature composite
model. It was assumed that both components at different temperatures
emit as a blackbody modified by the wavelength-dependent dust opacity,
is the model flux density.
In both cases, the data were fitted by a two-temperature composite
model. It was assumed that both components at different temperatures
emit as a blackbody modified by the wavelength-dependent dust opacity, ![]() (see below). The best-fit model SEDs overestimate
the flux densities at
(see below). The best-fit model SEDs overestimate
the flux densities at ![]() 12-20
12-20 ![]() m, but
underestimate them at
m, but
underestimate them at ![]() 8and 25
8and 25 ![]() m. It should
be noted that the flux densities included in the SEDs are measured
using telescopes with different beam sizes. Thus the flux densities
obtained for extended sources are not fully comparable, and this can in
part explain discrepancies between MSX (
m. It should
be noted that the flux densities included in the SEDs are measured
using telescopes with different beam sizes. Thus the flux densities
obtained for extended sources are not fully comparable, and this can in
part explain discrepancies between MSX (
![]() )
and IRAS (
)
and IRAS (![]()
![]() at 12
at 12 ![]() m
to
m
to ![]()
![]() at 100
at 100 ![]() m)
fluxes at 12 and
m)
fluxes at 12 and ![]() 20-25
20-25 ![]() m.
On the
other hand, SIMBA and LABOCA flux densities at
m.
On the
other hand, SIMBA and LABOCA flux densities at ![]() mm
and 0.87 mm refer to clump areas (
mm
and 0.87 mm refer to clump areas (
![]() is typically
is typically ![]()
![]() )
derived by clumpfind.
)
derived by clumpfind.
![]() values
are similar for both IRAS 13037-6122 and
IRAS 13039-6108 (
values
are similar for both IRAS 13037-6122 and
IRAS 13039-6108 (![]()
![]() or
or ![]() 0.35-0.47 pc).
Assuming that the emission in the IRAS bands is confined in
the region of the submm
clump, the characteristic spatial scale associated with the SEDs
is
0.35-0.47 pc).
Assuming that the emission in the IRAS bands is confined in
the region of the submm
clump, the characteristic spatial scale associated with the SEDs
is ![]() 0.5 pc.
0.5 pc.
We have adopted a dust-to-gas mass ratio of
![]() ,
a value which has often been used in the IRDC studies (e.g., RJS06; Vasyunina et al. 2009;
Parsons et al. 2009).
However, this value can differ from 1/100. For instance, Draine
et al. (2007)
determined a value of
,
a value which has often been used in the IRDC studies (e.g., RJS06; Vasyunina et al. 2009;
Parsons et al. 2009).
However, this value can differ from 1/100. For instance, Draine
et al. (2007)
determined a value of
![]() based
on observed depletions
of heavy elements in the Galaxy. Dust opacities we have adopted
correspond
to a MRN size distribution with thick ice mantles
based
on observed depletions
of heavy elements in the Galaxy. Dust opacities we have adopted
correspond
to a MRN size distribution with thick ice mantles![]() at a gas density of
at a gas density of ![]() cm-3
(OH94).
The resulting SED parameters are given in Table 5.
The total (cold+hot) mass and the integrated bolometric luminosity are
given
in Cols. (2) and (3) of Table 5, respectively.
The temperatures of the two components are listed
in Cols. (4) and (5). In Cols. (6)
and (7), we give the mass and luminosity fractions of the cold
component versus the total mass and luminosity. Column (8)
lists the mass-to-luminosity ratio,
cm-3
(OH94).
The resulting SED parameters are given in Table 5.
The total (cold+hot) mass and the integrated bolometric luminosity are
given
in Cols. (2) and (3) of Table 5, respectively.
The temperatures of the two components are listed
in Cols. (4) and (5). In Cols. (6)
and (7), we give the mass and luminosity fractions of the cold
component versus the total mass and luminosity. Column (8)
lists the mass-to-luminosity ratio,
![]() ,
which is an evolutionary indicator of the clump as
it is expected to decrease with time. The envelope mass decreases
during the star formation process, and the luminosity of the embedded
star or stellar
cluster rises (e.g., Sridharan
et al. 2002). We note that the adopted dust opacity
model (corresponding to particles coated with thick ice mantles) is not
likely to be appropriate for hot dust, and therefore the total
bolometric luminosity for the hot component should be taken with
caution. The MIR spectral features (such as PAH emission) also
cause the fit to the hot
component being more uncertain than the fit to the cold part of
the spectrum. However, this should not alter the fact that for both
IRAS
sources the mass of the hot component is negligible (
,
which is an evolutionary indicator of the clump as
it is expected to decrease with time. The envelope mass decreases
during the star formation process, and the luminosity of the embedded
star or stellar
cluster rises (e.g., Sridharan
et al. 2002). We note that the adopted dust opacity
model (corresponding to particles coated with thick ice mantles) is not
likely to be appropriate for hot dust, and therefore the total
bolometric luminosity for the hot component should be taken with
caution. The MIR spectral features (such as PAH emission) also
cause the fit to the hot
component being more uncertain than the fit to the cold part of
the spectrum. However, this should not alter the fact that for both
IRAS
sources the mass of the hot component is negligible (![]()
![]() ),
and thus the bulk of the material is cold (
),
and thus the bulk of the material is cold (
![]() ).
The bolometric temperature of IRAS 13039-6108 (
).
The bolometric temperature of IRAS 13039-6108 (
![]() K)
is in good agreement with the rotation temperature
of 18 K derived from C17O by
Fontani et al. (2005).
K)
is in good agreement with the rotation temperature
of 18 K derived from C17O by
Fontani et al. (2005).
5.2 Linear sizes, masses, and H2 number densities
The clump linear radii were computed from the effective radii listed in
Col. (7) of Table 1.
The clump masses (gas+dust mass,
![]() )
were calculated
from their integrated 870
)
were calculated
from their integrated 870 ![]() m flux density, S870
(Table 1,
Col. (5)), assuming that the thermal dust emission
is optically thin (Hildebrand
1983):
m flux density, S870
(Table 1,
Col. (5)), assuming that the thermal dust emission
is optically thin (Hildebrand
1983):
where d
is the source distance. For
IRAS 13037-6112 and 13039-6108,
we assumed the dust temperatures to be the same as their bolometric
temperatures, ![]() K,
resulting from SED fits (see Table 5,
Col. (4)). For all the other clumps (SMM 1,
SMM 2,..., and IRAS 13042-6105),
it was assumed that
K,
resulting from SED fits (see Table 5,
Col. (4)). For all the other clumps (SMM 1,
SMM 2,..., and IRAS 13042-6105),
it was assumed that ![]() K
(Sect. 4.3). We assumed that
K
(Sect. 4.3). We assumed that ![]() m2 kg-1.
This value is interpolated from OH94, see Sect. 5.1. As in the
SED fits, the value 1/100 is adopted for
m2 kg-1.
This value is interpolated from OH94, see Sect. 5.1. As in the
SED fits, the value 1/100 is adopted for ![]() .
.
The volume-averaged H2 number
densities, ![]() ,
were calculated assuming a spherical geometry for the clumps, using the
formula
,
were calculated assuming a spherical geometry for the clumps, using the
formula
where
Table 6: Linear radii, masses, and H2 column and volume-averaged number densities of the submm clumps within the IRDC G304.74.
Table 7: Reddened 2MASS point sources within the IRDC G304.74.
5.3 H2 column densities
The H2 column densities,
![]() ,
towards the submm peaks were estimated using 1) the
dust emission at 870
,
towards the submm peaks were estimated using 1) the
dust emission at 870 ![]() m,
and 2) the dust extinction at 8
m,
and 2) the dust extinction at 8 ![]() m. In the
first method, the LABOCA intensities were converted to
m. In the
first method, the LABOCA intensities were converted to
![]() using
the equation
using
the equation
where
The MSX 8 ![]() m optical thicknesses (Table 4,
Col. (3)) were used to estimate the peak H2
column densities by applying
the formula
m optical thicknesses (Table 4,
Col. (3)) were used to estimate the peak H2
column densities by applying
the formula
where
5.4 Extinction estimates with 2MASS
We examined if
extinctions estimated from the ![]() photometry of
2MASS stars lying in the region can be used to calibrate the H2
column
densities derived above
photometry of
2MASS stars lying in the region can be used to calibrate the H2
column
densities derived above![]() .
A rarefaction of 2MASS point sources can be discerned in the cloud
region and its immediate vicinity, and it is not
possible to derive an extinction map of such detail that a comparison
between the LABOCA map would be meaningful.
Altogether 14 2MASS point sources with good
photometric quality in all three bands lie within the LABOCA contour
0.1 Jy beam-1. Three of them
show J-H
and
.
A rarefaction of 2MASS point sources can be discerned in the cloud
region and its immediate vicinity, and it is not
possible to derive an extinction map of such detail that a comparison
between the LABOCA map would be meaningful.
Altogether 14 2MASS point sources with good
photometric quality in all three bands lie within the LABOCA contour
0.1 Jy beam-1. Three of them
show J-H
and ![]() colours characteristic of giant stars reddened by substantial columns
of interstellar dust. This judgement is based on their locations near
the standard reddening line on the J-H
vs.
colours characteristic of giant stars reddened by substantial columns
of interstellar dust. This judgement is based on their locations near
the standard reddening line on the J-H
vs. ![]() plot, and on the fact that their
plot, and on the fact that their ![]() excesses, EJ-K,
are larger than 0.6 (see below).
The three stars are the 2MASS PSC objects 13064180-6128529,
13064266-6128213, and 13070908-6124303 (see Table 7 and
Fig. 6).
The first
two lie near the clump SMM 4 and are likely to represent
background K or M giants. The third is found very
close (
excesses, EJ-K,
are larger than 0.6 (see below).
The three stars are the 2MASS PSC objects 13064180-6128529,
13064266-6128213, and 13070908-6124303 (see Table 7 and
Fig. 6).
The first
two lie near the clump SMM 4 and are likely to represent
background K or M giants. The third is found very
close (![]()
![]() )
to IRAS 13039-6108
and is somewhat too bright for a class III giant in view of the
distance and
extinction. Because its NIR colours (
)
to IRAS 13039-6108
and is somewhat too bright for a class III giant in view of the
distance and
extinction. Because its NIR colours (
![]() ,
,
![]() )
are consistent with an YSO (young stellar object) candidate with NIR
excess (Matsuyanagi
et al. 2006), the source is possibly a NIR
counterpart of IRAS 13039-6108.
)
are consistent with an YSO (young stellar object) candidate with NIR
excess (Matsuyanagi
et al. 2006), the source is possibly a NIR
counterpart of IRAS 13039-6108.
![\begin{figure}
\par\includegraphics[width=8.2cm,height=8.2cm,clip]{13662fg9.ps}\vspace*{-1.5mm}\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg235.png)
|
Figure 6: LABOCA dust continuum map (contours) with 2MASS point sources (plus signs). The heavily reddened 2MASS stars within the cloud boundaries are marked with diamonds. The contour levels go from 0.1 to 0.6 by 0.1 Jy beam-1. |
| Open with DEXTER | |
The H2 column density ranges given in
Col. (7) of
Table 7
are derived using intrinsic colours for K0 III-M3 III giants (Bessell & Brett 1988),
and the relationship
![]() (Bohlin et al. 1978; Mathis 1990; Harjunpää & Mattila 1996).
The colour
excesses, EJ-K,
measure the total amount of dust in front of the
stars, so they are affected by dust in the foreground, and possibly
also in the background of the cloud. Therefore, the
(Bohlin et al. 1978; Mathis 1990; Harjunpää & Mattila 1996).
The colour
excesses, EJ-K,
measure the total amount of dust in front of the
stars, so they are affected by dust in the foreground, and possibly
also in the background of the cloud. Therefore, the
![]() values
are
upper limits for the contribution of the cloud itself. A
nearby line of sight (
values
are
upper limits for the contribution of the cloud itself. A
nearby line of sight (
![]() ,
,
![]() )
has been included in the
investigation of 3-D distribution of the extinction by Marshall
et al. (2006). Their results suggest a foreground
extinction of
)
has been included in the
investigation of 3-D distribution of the extinction by Marshall
et al. (2006). Their results suggest a foreground
extinction of ![]() (
(
![]() ;
Marshall et al. 2006;
Mathis 1990) up to the
cloud's distance 2.4 kpc.
;
Marshall et al. 2006;
Mathis 1990) up to the
cloud's distance 2.4 kpc.
The LABOCA 870 ![]() m intensities in the directions of
13064180-6128529,
13064266-6128213, and 13070908-6124303 are 0.49, 0.31, and
m intensities in the directions of
13064180-6128529,
13064266-6128213, and 13070908-6124303 are 0.49, 0.31, and
![]() Jy beam-1,
respectively. The conversion to the H2 column
densities using Eq. (8)
with
Jy beam-1,
respectively. The conversion to the H2 column
densities using Eq. (8)
with ![]() K gives
K gives
![]() ,
,
![]() ,
and
,
and ![]() cm-2.
The first two values are not consistent with the upper limits derived
from
EJ-K
(see Table 7,
Col. (9)).
In the case of 13064180-6128529, the H2 column
density derived from LABOCA
870
cm-2.
The first two values are not consistent with the upper limits derived
from
EJ-K
(see Table 7,
Col. (9)).
In the case of 13064180-6128529, the H2 column
density derived from LABOCA
870 ![]() m
data can be brought down to conform with 2MASS estimate by increasing
the dust temperature to
m
data can be brought down to conform with 2MASS estimate by increasing
the dust temperature to ![]() K,
whereas for the location
of 13064266-6128213 an increase to
K,
whereas for the location
of 13064266-6128213 an increase to
![]() K
would be sufficient. The latter value is in good agreement with the
bolometric temperature of IRAS 13037-6112 (
K
would be sufficient. The latter value is in good agreement with the
bolometric temperature of IRAS 13037-6112 (
![]() K,
see Table 5,
Col. (4)) which lies (in the plane of the sky) quite close to
13064266-6128213.
The 8
K,
see Table 5,
Col. (4)) which lies (in the plane of the sky) quite close to
13064266-6128213.
The 8 ![]() m
intensities in the directions of 13064180-6128529 and 13064266-6128213
are
m
intensities in the directions of 13064180-6128529 and 13064266-6128213
are ![]() and
and ![]() W m-2 sr-1,
respectively. These correspond to 8
W m-2 sr-1,
respectively. These correspond to 8 ![]() m optical thicknesses of
m optical thicknesses of
![]() and
0.02 (here the associated error is larger than the value),
respectively (see Eq. (2)).
Using Eq. (9),
the corresponding H2 column densities become
and
0.02 (here the associated error is larger than the value),
respectively (see Eq. (2)).
Using Eq. (9),
the corresponding H2 column densities become
![]() and
and
![]() cm-2,
respectively. The first value is consistent with the 2MASS estimate,
whereas the latter value is much lower.
cm-2,
respectively. The first value is consistent with the 2MASS estimate,
whereas the latter value is much lower.
The above results clearly show that it is important to know
the dust temperature in order to accurately determine the H2
column density from the
submm dust continuum emission (Eq. (8)). On the other
hand, the MIR absorption and 2MASS extinction methods require
several uncertain assumptions, such as the dust model and the
corresponding dust extinction cross-section, contribution of the
foreground
emission, and the relation between
![]() and
EJ-K.
Moreover, as the 2MASS extinction could be estimated only along a few
lines of sight, the present statistics is very poor. Thus, the data
presented here do not offer a firm conclusion about the most reliable
method to determine the H2 column
densities. We note that the empirical
relationship between
and
EJ-K.
Moreover, as the 2MASS extinction could be estimated only along a few
lines of sight, the present statistics is very poor. Thus, the data
presented here do not offer a firm conclusion about the most reliable
method to determine the H2 column
densities. We note that the empirical
relationship between ![]() and AJ
derived by Vuong et al. (2003) in
and AJ
derived by Vuong et al. (2003) in ![]() Oph,
used recently by Marshall et al. (2009), implies
Oph,
used recently by Marshall et al. (2009), implies
![]() cm
cm
![]() .
This would make the H2 column densities about
13% smaller than those estimated above.
.
This would make the H2 column densities about
13% smaller than those estimated above.
6 Discussion
6.1 Estimating the background and foreground MIR emission
The average MIR emission around the cloud,
![]() W m-2 sr-1,
was estimated in Sect. 4 by using median filtering. Vasyunina
et al. (2009)
estimated
W m-2 sr-1,
was estimated in Sect. 4 by using median filtering. Vasyunina
et al. (2009)
estimated ![]() in the vicinity of several IRDCs
directly from the 8
in the vicinity of several IRDCs
directly from the 8 ![]() m
images. They pointed out that it is difficult to
control the process of median filtering if large (
m
images. They pointed out that it is difficult to
control the process of median filtering if large (![]()
![]() )
filters
are needed. On the other hand, if the filter is too small (comparable
to the
cloud size), the value of
)
filters
are needed. On the other hand, if the filter is too small (comparable
to the
cloud size), the value of ![]() will be underestimated because it will be affected by the cloud itself (Butler & Tan 2009).
Because the largest diameter of G304.74 is
will be underestimated because it will be affected by the cloud itself (Butler & Tan 2009).
Because the largest diameter of G304.74 is ![]()
![]() ,
we tried
the direct method by choosing manually MIR emission patches
(free of strong
MIR emission sources) in the close vicinity of the IRDC. We
used three different patches with angular sizes of
,
we tried
the direct method by choosing manually MIR emission patches
(free of strong
MIR emission sources) in the close vicinity of the IRDC. We
used three different patches with angular sizes of
![]() ,
,
![]() ,
and
,
and
![]() .
The mean and standard deviation of the 8
.
The mean and standard deviation of the 8 ![]() m intensity within these regions
were
m intensity within these regions
were ![]() ,
,
![]() ,
and
,
and ![]() W m-2 sr-1,
respectively.
The mean and standard deviation of these three are
W m-2 sr-1,
respectively.
The mean and standard deviation of these three are
![]() W m-2 sr-1.
This result is in excellent
agreement with the value obtained from median filtering.
W m-2 sr-1.
This result is in excellent
agreement with the value obtained from median filtering.
Based on the observed anti-correlation between the
850 ![]() m
and 8
m
and 8 ![]() m
intensities (cf. Fig. 4),
Johnstone et al. (2003) and Ormel et al. (2005) found
that
m
intensities (cf. Fig. 4),
Johnstone et al. (2003) and Ormel et al. (2005) found
that ![]() in the case of
IRDC G11.11-0.12 and the W51 IRDC, respectively. Peretto &
Fuller (2009) constrained
in the case of
IRDC G11.11-0.12 and the W51 IRDC, respectively. Peretto &
Fuller (2009) constrained ![]() by the
requirement that both MIR absorption
and 1.2 mm emission should
give the same
by the
requirement that both MIR absorption
and 1.2 mm emission should
give the same ![]() .
In this method, it is assumed that the true
8
.
In this method, it is assumed that the true
8 ![]() m
opacity can be calculated from the millimetre emission (see
Eq. (3) of Peretto & Fuller 2009). Then, the value of
m
opacity can be calculated from the millimetre emission (see
Eq. (3) of Peretto & Fuller 2009). Then, the value of
![]() can
be calculated in terms of
can
be calculated in terms of ![]() (see our Eq. (2)).
Peretto & Fuller (2009) also showed that on the average the
background
emission is approximately equal to the foreground emission (their
Eq. (5)). The drawback in this approach is the uncertainty in
the ratio of the mass absorption coefficients at MIR and
(sub)mm wavelengths (
(see our Eq. (2)).
Peretto & Fuller (2009) also showed that on the average the
background
emission is approximately equal to the foreground emission (their
Eq. (5)). The drawback in this approach is the uncertainty in
the ratio of the mass absorption coefficients at MIR and
(sub)mm wavelengths (
![]() in Eq. (3) of Peretto
& Fuller 2009). In the present
study, we estimated the contributions of background and foreground
emission using the foreground intensity ratio (Sect. 4.2). We
also ended up with the result that
in Eq. (3) of Peretto
& Fuller 2009). In the present
study, we estimated the contributions of background and foreground
emission using the foreground intensity ratio (Sect. 4.2). We
also ended up with the result that
![]() .
Butler & Tan (2009) and RBG09 estimated that
.
Butler & Tan (2009) and RBG09 estimated that
![]() (
(
![]() -method) and
-method) and
![]() (850-8
(850-8 ![]() m
anti-correlation)
for their samples of IRDCs, respectively.
m
anti-correlation)
for their samples of IRDCs, respectively.
6.2 Comparison of H2 column densities determined from dust continuum emission and extinction data
The H2 column densities derived from submm
emission and
MIR absorption are mostly in good agreement (within a factor
of ![]() 2;
Table 6,
Cols. (4) and (5)). This suggests that the dust
parameters used in Eqs. (8)
and (9)
are reasonable.
The dust temperature,
2;
Table 6,
Cols. (4) and (5)). This suggests that the dust
parameters used in Eqs. (8)
and (9)
are reasonable.
The dust temperature, ![]() ,
is likely to show spatial variations, and
this causes uncertainties to column density estimates based on
submm emission (Eq. (8)),
but does not affect the 8
,
is likely to show spatial variations, and
this causes uncertainties to column density estimates based on
submm emission (Eq. (8)),
but does not affect the 8 ![]() m absorption method (Eq. (9)). The
greatest differences between
the two
m absorption method (Eq. (9)). The
greatest differences between
the two ![]() values are found toward positions with the highest
values are found toward positions with the highest
![]() values.
These are SMM 1, 3, and 4, where the
values.
These are SMM 1, 3, and 4, where the
![]() ratios are
ratios are ![]() ,
,
![]() ,
and
,
and ![]() ,
respectively (Col. (6) of Table 6). Some
of these discrepancies could (in part)
be remedied, e.g., by increasing the dust temperature
(cf. footnote in Table 6). It
seems possible that
the dust temperature is higher than 15 K in the four
clumps (SMM 1-4)
near southwestern tip of the cloud. On the other hand, Vasyunina
et al. (2009) showed that the extinction method becomes
unreliable at very high column densities, but this should happen only
at
,
respectively (Col. (6) of Table 6). Some
of these discrepancies could (in part)
be remedied, e.g., by increasing the dust temperature
(cf. footnote in Table 6). It
seems possible that
the dust temperature is higher than 15 K in the four
clumps (SMM 1-4)
near southwestern tip of the cloud. On the other hand, Vasyunina
et al. (2009) showed that the extinction method becomes
unreliable at very high column densities, but this should happen only
at ![]() cm-2.
cm-2.
However, there are also uncertainties in deriving
![]() ,
in particular related to the contamination by the foreground emission
(here
done by using the foreground intensity ratio, see Sect. 4),
and the dust
extinction cross-section (reliable only within a factor of
,
in particular related to the contamination by the foreground emission
(here
done by using the foreground intensity ratio, see Sect. 4),
and the dust
extinction cross-section (reliable only within a factor of ![]() 2, e.g.,
Ragan et al. 2006).
Also, the value of
2, e.g.,
Ragan et al. 2006).
Also, the value of
![]() ,
needed in the calculation of
,
needed in the calculation of
![]() (Eq. (8))
has an uncertainty
similar to that of
(Eq. (8))
has an uncertainty
similar to that of
![]() .
The dust-to-gas mass ratio could also differ from the adopted value
1/100 as mentioned in Sect. 5.1. Thus, the direct comparison
of
.
The dust-to-gas mass ratio could also differ from the adopted value
1/100 as mentioned in Sect. 5.1. Thus, the direct comparison
of ![]() derived from dust continuum and
extinction data should be taken with caution. We note that Parsons
et al. (2009) found for their
sample of IRDCs that
derived from dust continuum and
extinction data should be taken with caution. We note that Parsons
et al. (2009) found for their
sample of IRDCs that ![]() (MSX) and
(MSX) and ![]() (SCUBA)
agree within an order of magnitude. The moderate correspondence may be
partly
explained by the omission of the foreground emission.
(SCUBA)
agree within an order of magnitude. The moderate correspondence may be
partly
explained by the omission of the foreground emission.
6.3 Nature of submm clumps
The MSX 8 ![]() m
emission associated with molecular clumps suggests the presence of
protostars. By combining the submm LABOCA and
MIR MSX
data one can distinguish between candidate starless and star-forming
clumps.
Of the twelve clumps in G304.74, four are likely to be associated with
newly
born stars. In addition to the three IRAS (and MSX) sources,
the clump SMM 6
is associated with two MSX 8
m
emission associated with molecular clumps suggests the presence of
protostars. By combining the submm LABOCA and
MIR MSX
data one can distinguish between candidate starless and star-forming
clumps.
Of the twelve clumps in G304.74, four are likely to be associated with
newly
born stars. In addition to the three IRAS (and MSX) sources,
the clump SMM 6
is associated with two MSX 8 ![]() m point sources. The remaining eight
MIR
dark clumps are either starless or contain low-luminosity (low-mass)
YSOs falling under the detection limit of the MSX (cf. Parsons et al. 2009).
For instance, the Spitzer/GLIMPSE survey with better sensitivity and
resolution compared to that of MSX, revealed that some IRDC clumps
previously thought to be starless do contain MIR sources
(e.g., Chambers et al.
2009). Moreover, Chambers et al. (2009) detected H2O
masers towards some MIR dark clumps, which is a clear
indication of star
formation activity in them. On the other hand, starless clumps may be
either
prestellar or just unbound structures that will eventually disperse.
m point sources. The remaining eight
MIR
dark clumps are either starless or contain low-luminosity (low-mass)
YSOs falling under the detection limit of the MSX (cf. Parsons et al. 2009).
For instance, the Spitzer/GLIMPSE survey with better sensitivity and
resolution compared to that of MSX, revealed that some IRDC clumps
previously thought to be starless do contain MIR sources
(e.g., Chambers et al.
2009). Moreover, Chambers et al. (2009) detected H2O
masers towards some MIR dark clumps, which is a clear
indication of star
formation activity in them. On the other hand, starless clumps may be
either
prestellar or just unbound structures that will eventually disperse.
The extremely short lifetime of starless IRDC clumps (
103-104 yr,
i.e., ![]() half of the
time spent in the protostellar phase) derived
by Parsons et al. (2009) does not support the idea that all of
the
eight dark clumps in G304.74 could be starless. If gravitationally
bound, these clumps with masses in the range
half of the
time spent in the protostellar phase) derived
by Parsons et al. (2009) does not support the idea that all of
the
eight dark clumps in G304.74 could be starless. If gravitationally
bound, these clumps with masses in the range ![]()
![]() (Table 6,
Col. (3)) are capable of forming high-mass stars (Thompson et al. 2006),
and some of them could represent/contain HMSCs
(cf. Chambers et al. 2009).
The peak column densities of the clumps do not reach the minimum column
density threshold of 1 g cm-2,
i.e.,
(Table 6,
Col. (3)) are capable of forming high-mass stars (Thompson et al. 2006),
and some of them could represent/contain HMSCs
(cf. Chambers et al. 2009).
The peak column densities of the clumps do not reach the minimum column
density threshold of 1 g cm-2,
i.e., ![]() cm-2,
proposed by Krumholz & McKee (2008) for the formation of
high-mass stars. However, it is possible that the clumps host cores
where such a high
cm-2,
proposed by Krumholz & McKee (2008) for the formation of
high-mass stars. However, it is possible that the clumps host cores
where such a high ![]() values can be reached (e.g., Hennemann
et al. 2009).
values can be reached (e.g., Hennemann
et al. 2009).
The presence of high-luminosity (![]()
![]() )
IRAS
sources indicates that intermediate to high-mass star formation is
going on
in other parts of the cloud. In fact these luminosities
suggest intermediate-mass stars as high-mass protostellar objects
(HMPOs)
are often found in the range
)
IRAS
sources indicates that intermediate to high-mass star formation is
going on
in other parts of the cloud. In fact these luminosities
suggest intermediate-mass stars as high-mass protostellar objects
(HMPOs)
are often found in the range ![]()
![]() (e.g.,
Sridharan et al.
2002; Fazal
et al. 2008; Grave
& Kumar 2009). On the other hand, the envelope masses
of these sources (
(e.g.,
Sridharan et al.
2002; Fazal
et al. 2008; Grave
& Kumar 2009). On the other hand, the envelope masses
of these sources (![]()
![]() ,
see Col. (2) of Table 5) are
sufficiently large for high-mass star formation (Beuther & Steinacker 2007).
For comparison, majority of the low-mass protostars in nearby (
,
see Col. (2) of Table 5) are
sufficiently large for high-mass star formation (Beuther & Steinacker 2007).
For comparison, majority of the low-mass protostars in nearby (![]() pc)
molecular clouds have luminosites
pc)
molecular clouds have luminosites
![]() ,
the highest observed values being
,
the highest observed values being ![]()
![]() in only a few cases (e.g., Evans
et al. 2009). IRAS 13037-6112 and
IRAS 13039-6108 have similar SED parameters (see Fig. 5 and
Table 5),
suggesting that they probably represent the same evolutionary stage.
Based on its IRAS [25-12] and [60-12] colours (0.61
and 1.55, respectively), IRAS 13037-6112 belongs to the
so-called High sources,
and could potentially be associated with ultra-compact (UC) HII region (e.g., Wood & Churchwell 1989; Palla et al. 1991; Molinari et al. 1996).
However, the M/L ratio of
IRAS 13037-6112 (0.04) is more typical of sources younger than
UC HII regions (Sridharan et al. 2002).
IRAS 13039-6108 has a [25-12] colour index of 0.27,
settling it to the so-called Low sources. Moreover,
Fontani et al. (2005) found that the C17O
and CS linewidths in IRAS 13039-6108 are significantly smaller
than those typically observed in massive clumps associated with
UC HII regions
(e.g., Cesaroni et al.
1991; Hofner
et al. 2000). This further supports the idea that
both IRAS 13037-6112 and IRAS 13039-6108 represent
the same evolutionary stage (earlier than UC HII). Using the assumption of an
isothermal sphere with
in only a few cases (e.g., Evans
et al. 2009). IRAS 13037-6112 and
IRAS 13039-6108 have similar SED parameters (see Fig. 5 and
Table 5),
suggesting that they probably represent the same evolutionary stage.
Based on its IRAS [25-12] and [60-12] colours (0.61
and 1.55, respectively), IRAS 13037-6112 belongs to the
so-called High sources,
and could potentially be associated with ultra-compact (UC) HII region (e.g., Wood & Churchwell 1989; Palla et al. 1991; Molinari et al. 1996).
However, the M/L ratio of
IRAS 13037-6112 (0.04) is more typical of sources younger than
UC HII regions (Sridharan et al. 2002).
IRAS 13039-6108 has a [25-12] colour index of 0.27,
settling it to the so-called Low sources. Moreover,
Fontani et al. (2005) found that the C17O
and CS linewidths in IRAS 13039-6108 are significantly smaller
than those typically observed in massive clumps associated with
UC HII regions
(e.g., Cesaroni et al.
1991; Hofner
et al. 2000). This further supports the idea that
both IRAS 13037-6112 and IRAS 13039-6108 represent
the same evolutionary stage (earlier than UC HII). Using the assumption of an
isothermal sphere with ![]() K
and a density profile of the form
K
and a density profile of the form
![]() ,
which is typical of high-mass star-forming clumps
(e.g., Beuther et al.
2002a), the C17O(2-1) linewidth
of 0.93 km s-1
observed by Fontani et al. (2005) implies a virial mass
of
,
which is typical of high-mass star-forming clumps
(e.g., Beuther et al.
2002a), the C17O(2-1) linewidth
of 0.93 km s-1
observed by Fontani et al. (2005) implies a virial mass
of ![]()
![]() for IRAS 13039-6108 (
for IRAS 13039-6108 (
![]() ,
,
![]() ,
i.e., the virial parameter defined by Bertoldi & McKee (1992)
is
,
i.e., the virial parameter defined by Bertoldi & McKee (1992)
is
![]() )
(see, e.g., Eqs. (1) and (2) of Chen et al. 2008). Thus
the clump is near virial equilibrium. IRAS 13042-6105 in the
northern part of the cloud is probably in an earlier stage of evolution
than the other two IRAS sources because it is not as bright at
FIR wavelengths (see Table 3).
)
(see, e.g., Eqs. (1) and (2) of Chen et al. 2008). Thus
the clump is near virial equilibrium. IRAS 13042-6105 in the
northern part of the cloud is probably in an earlier stage of evolution
than the other two IRAS sources because it is not as bright at
FIR wavelengths (see Table 3).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{13662fg10.ps} .
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg285.png)
|
Figure 7:
Normalised cumulative mass functions,
|
| Open with DEXTER | |
6.4 Clump mass distribution
The mass distribution of clumps/cores is important parameter concerning the cloud fragmentation mechanism. Our sample of clumps is, however, so small (12 in total, 8 MIR dark) that it is not reasonable to study their mass distribution directly. Therefore, we only compared it with the mass distributions derived for other, larger IRDC clump samples, using the results of Sridharan et al. (2005), RJS06, Vasyunina et al. (2009), and RBG09.
Figure 7
presents the observed cumulative mass functions,
which include clumps of mass less than M, i.e.,
![]() ,
for G304.74 and for a sample of cold clumps from RJS06 and RBG09.
We note that the IRDC clump mass functions in RJS06 and in our work are
constructed by removing the MIR bright clumps from the samples
(in the case of G304.74, this means the three IRAS sources and
SMM 6). From the sample of Sridharan et al. (2005),
we excluded the high temperature clump No. 9, because its
temperature (32.7 K) was much higher than the rest of the
sample. From the the sample of RBG09, we removed the clumps associated
with YSOs, and the clumps possibly contaminated by foreground (or
background) stars. Thus, the mass functions include only those clumps
that initially have all their mass available for star formation.
,
for G304.74 and for a sample of cold clumps from RJS06 and RBG09.
We note that the IRDC clump mass functions in RJS06 and in our work are
constructed by removing the MIR bright clumps from the samples
(in the case of G304.74, this means the three IRAS sources and
SMM 6). From the sample of Sridharan et al. (2005),
we excluded the high temperature clump No. 9, because its
temperature (32.7 K) was much higher than the rest of the
sample. From the the sample of RBG09, we removed the clumps associated
with YSOs, and the clumps possibly contaminated by foreground (or
background) stars. Thus, the mass functions include only those clumps
that initially have all their mass available for star formation.
The previous studies taken into this comparison used slightly
different assumptions about the dust temperature and opacity.
We scaled all the clump masses included in the cumulative mass
functions
to correspond to a uniform dust temperature of
![]() K,
and an opacity
that is consistent with our
K,
and an opacity
that is consistent with our
![]() m2 kg-1.
RBG09 derived clump masses from the total hydrogen column
densities,
m2 kg-1.
RBG09 derived clump masses from the total hydrogen column
densities, ![]() ,
as estimated from the 8
,
as estimated from the 8 ![]() m optical thicknesses,
m optical thicknesses, ![]() .
For the dust extinction cross-section per H nucleus at 8
.
For the dust extinction cross-section per H nucleus at 8 ![]() m,
m, ![]() ,
they used the value
,
they used the value ![]() cm2,
based on the Weingartner & Draine (2001) dust model. According
to the model we have used (Ossenkopf
& Henning 1994), the corresponding number is
cm2,
based on the Weingartner & Draine (2001) dust model. According
to the model we have used (Ossenkopf
& Henning 1994), the corresponding number is
![]() cm2
per H nucleus (see Sect. 5.3). In their mass
formula, RBG09 used a factor of 1.16 as the ratio of the total gas mass
(including He) and the hydrogen
mass. In our calculations this ratio has been 1.4 (Sect. 5.3).
These
differences have been accounted for by scaling the masses from RBG09
by 0.8 in the comparison with our results.
cm2
per H nucleus (see Sect. 5.3). In their mass
formula, RBG09 used a factor of 1.16 as the ratio of the total gas mass
(including He) and the hydrogen
mass. In our calculations this ratio has been 1.4 (Sect. 5.3).
These
differences have been accounted for by scaling the masses from RBG09
by 0.8 in the comparison with our results.
Table 8: K-S test results between different IRDC clump mass distributions.
To determine whether our clump masses and those from other
studies are derived from the same clump mass distribution, we carried
out the two-sample Kolmogorov-Smirnov (K-S) test. For this test, the
mass scales
were matched, i.e., the comparison was done within the range of common
mass
interval. The K-S test results are shown in Table 8. The columns of
this table are: (1) the survey used in the
comparison; (2) number of clumps included; (3) the maximum vertical
difference
between the cumulative mass distributions (![]() ); (4) the probability for the
null hypothesis that the two functions are drawn form the same parent
distribution (the significance level of the K-S statistic).
); (4) the probability for the
null hypothesis that the two functions are drawn form the same parent
distribution (the significance level of the K-S statistic).
The highest number statistic is provided by the study of
RBG09, and when compared with this study, the K-S test yields a
probability of 99.8% that the clump mass distributions in G304.74 and
the other IRDCs
are drawn from the same parent distribution. This probability drops
significantly when smaller samples are used in the test (Table 8,
Col. (4)). Moreover, according to the K-S test,
there is a 100% probability (
![]() )
that the RBG09 and RJS06 clump
masses represent the subsamples of the same underlying parent
distribution. For this test, clump masses from RBG09 were also
multiplied by 0.8 to compare with the RJS06 masses which were
based on the value
)
that the RBG09 and RJS06 clump
masses represent the subsamples of the same underlying parent
distribution. For this test, clump masses from RBG09 were also
multiplied by 0.8 to compare with the RJS06 masses which were
based on the value
![]() m2 kg-1.
m2 kg-1.
For the clump masses between ![]() 30 and 3000
30 and 3000 ![]() ,
RBG09
derived an IRDC clump mass spectrum with a slope of
,
RBG09
derived an IRDC clump mass spectrum with a slope of
![]() ,
which is consistent with the mass functions
derived for high-mass star-forming regions, and also resembles the mass
function of Galactic stellar clusters (see RBG09 and references
therein).
Note, however, that RBG09 merged all their clumps into a single mass
function,
whereas we have used only starless clumps in deriving the cumulative
mass functions. RJS06 found a Salpeter-like (
,
which is consistent with the mass functions
derived for high-mass star-forming regions, and also resembles the mass
function of Galactic stellar clusters (see RBG09 and references
therein).
Note, however, that RBG09 merged all their clumps into a single mass
function,
whereas we have used only starless clumps in deriving the cumulative
mass functions. RJS06 found a Salpeter-like (
![]() ;
Salpeter 1955)
mass function for their cold IRDC clumps (
;
Salpeter 1955)
mass function for their cold IRDC clumps (
![]() at
at
![]() ).
The IRDC clump mass spectra derived by RJS06 and RBG09 are comparable
to those predicted by turbulent fragmentation models (see
Sect. 6.7 and references therein).
).
The IRDC clump mass spectra derived by RJS06 and RBG09 are comparable
to those predicted by turbulent fragmentation models (see
Sect. 6.7 and references therein).
6.5 Clump spatial distribution
In addition to the clump mass distribution, it is also useful to
determine how clumps are spatially distributed within the cloud in
order to unveil the presence of a possible preferred length-scale of
fragmentation (e.g., Muñoz
et al. 2007).
For this purpose, we determined the clump-separation distributions and
the number distributions of the projected separation distance between
nearest neighbours![]() in G304.74, and in nine other IRDCs for comparison.
We chose those IRDCs from the sample of RJS06 which contain the largest
number of clumps, i.e., MSXDC G023.60+00.00, G024.33+00.11,
G028.37+00.07, G028.53-00.25, G031.97+00.07, G033.69-00.01,
G034.43+00.24, and G035.39-00.33. Moreover, we determined the spatial
distribution of YSOs in the IRDC MSXDC G048.65-00.29 studied by van der
Wiel
& Shipman (2008). For these analyses, we selected only those
sources that are clearly associated (in the plane of the sky) with
their parental dark
cloud (e.g., clumps that lie within the dark filaments). Thus, we
excluded the millimetre clumps MM 1, 3, and 5 from
G023.60+00.00,
MM 2, 5, and 7 from G024.33+00.11, MM 3, 5, 7, 8, 12,
13, 18 from G028.37+00.07, MM 1 and 2 from G035.39-00.33, and
YSOs S4, 10, 17, 18, 19,
and 20 from G048.65-00.29. In addition to the observed spatial
distributions, we also determined the distributions expected from
random positions of the same number of objects as the observed samples
have. The areas over which the objects were randomly distributed were
chosen so that they approximate the observed dark cloud areas; the IRDC
areas were estimated by rectangles which just cover the observed dark
clouds. When needed, these rectangles were rotated with respect to the
in G304.74, and in nine other IRDCs for comparison.
We chose those IRDCs from the sample of RJS06 which contain the largest
number of clumps, i.e., MSXDC G023.60+00.00, G024.33+00.11,
G028.37+00.07, G028.53-00.25, G031.97+00.07, G033.69-00.01,
G034.43+00.24, and G035.39-00.33. Moreover, we determined the spatial
distribution of YSOs in the IRDC MSXDC G048.65-00.29 studied by van der
Wiel
& Shipman (2008). For these analyses, we selected only those
sources that are clearly associated (in the plane of the sky) with
their parental dark
cloud (e.g., clumps that lie within the dark filaments). Thus, we
excluded the millimetre clumps MM 1, 3, and 5 from
G023.60+00.00,
MM 2, 5, and 7 from G024.33+00.11, MM 3, 5, 7, 8, 12,
13, 18 from G028.37+00.07, MM 1 and 2 from G035.39-00.33, and
YSOs S4, 10, 17, 18, 19,
and 20 from G048.65-00.29. In addition to the observed spatial
distributions, we also determined the distributions expected from
random positions of the same number of objects as the observed samples
have. The areas over which the objects were randomly distributed were
chosen so that they approximate the observed dark cloud areas; the IRDC
areas were estimated by rectangles which just cover the observed dark
clouds. When needed, these rectangles were rotated with respect to the
![]() -coordinate
system. The random distributions were generated a hundred times per
cloud and the resulting averaged histograms were used in comparisons
with observed spatial distributions.
-coordinate
system. The random distributions were generated a hundred times per
cloud and the resulting averaged histograms were used in comparisons
with observed spatial distributions.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{13662fg11.ps}\par\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{13662fg12.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg301.png)
|
Figure 8: Top: observed clump-separation distribution (solid line) compared with the expected distribution for random distribution of the same number of clumps as the observed sample over rectangular area which approximate the area of the IRDC (dashed line). Bottom: observed nearest-neighbour distribution (solid line) compared with the expected distribution for random distribution (dashed line). |
| Open with DEXTER | |
Figure 8
(top) shows the observed clump-separation distribution
in G304.74, and the distribution expected for the same number of
randomly positioned clumps over minimum rectangular area which encloses
the dark cloud (![]() 29.8 arcmin2).
The mean and its standard deviation, and median of the clump
separations in G304.74 are
29.8 arcmin2).
The mean and its standard deviation, and median of the clump
separations in G304.74 are ![]() (
(
![]() AU)
and
AU)
and ![]() (
(
![]() AU),
respectively.
These values are similar to those of randomly positioned clumps, for
which the mean and median are
AU),
respectively.
These values are similar to those of randomly positioned clumps, for
which the mean and median are ![]() and
and ![]() (see Table 9).
The latter two values and their
(see Table 9).
The latter two values and their ![]() -errors quoted represent the average values and
their standard deviations derived from
the 100 generated random distributions. According to the K-S
test, the probability that the observed distribution and the generated
random distribution represent the same underlying distribution is 100%.
Statistics of the clump-separation distributions in other IRDCs studied
by RJS06 and van der Wiel & Shipman (2008)
are listed in Table 9. The
columns of this table are the following: (1) IRDC name; (2)
number of clumps used in the analysis (see above);
(3) distance; (4) area used to create the random distributions
(see above); (5) and (6) mean and median of the observed
clump-separation distribution (
-errors quoted represent the average values and
their standard deviations derived from
the 100 generated random distributions. According to the K-S
test, the probability that the observed distribution and the generated
random distribution represent the same underlying distribution is 100%.
Statistics of the clump-separation distributions in other IRDCs studied
by RJS06 and van der Wiel & Shipman (2008)
are listed in Table 9. The
columns of this table are the following: (1) IRDC name; (2)
number of clumps used in the analysis (see above);
(3) distance; (4) area used to create the random distributions
(see above); (5) and (6) mean and median of the observed
clump-separation distribution (
![]() and
and
![]() );
(7) and (8) mean and median of the
corresponding random distribution (
);
(7) and (8) mean and median of the
corresponding random distribution (
![]() and
and
![]() );
(9) and (10) ratios between the observed and random mean and median
separations (quoted errors are propagated from the standard deviations
of
);
(9) and (10) ratios between the observed and random mean and median
separations (quoted errors are propagated from the standard deviations
of ![]() and
and ![]() );
(11) probability given by the K-S test that the
observed and random distributions are drawn from the same
underlying distribution. The observed clump separations are mostly
similar to those expected from random distributions. This is evident
from the ratios
);
(11) probability given by the K-S test that the
observed and random distributions are drawn from the same
underlying distribution. The observed clump separations are mostly
similar to those expected from random distributions. This is evident
from the ratios ![]() and
and ![]() which are close to unity, and from the K-S probabilities which are high
(
which are close to unity, and from the K-S probabilities which are high
(![]()
![]() )
except for three cases (G035.39, G028.37, G024.33; see
Cols. (9)-(11) of Table 9).
)
except for three cases (G035.39, G028.37, G024.33; see
Cols. (9)-(11) of Table 9).
Figure 8
(bottom) compares the observed nearest-neighbour distribution in
G304.74 with the distribution for
randomly positioned clumps. The mean and median of the
nearest-neighbour distribution in G304.74 are
![]() (
(
![]() AU)
and
AU)
and
![]() (
(
![]() AU), respectively.
Again, these values are comparable to those of randomly positioned
clumps, for which the mean and median are
AU), respectively.
Again, these values are comparable to those of randomly positioned
clumps, for which the mean and median are
![]() and
and
![]() ,
respectively (see Table 10).
According to the K-S test, there is about 90% probability that the
observed and random nearest-neighbour distributions are samples of the
same underlying distribution. We note that the minimum observable
separation corresponds to the beam size, i.e,
,
respectively (see Table 10).
According to the K-S test, there is about 90% probability that the
observed and random nearest-neighbour distributions are samples of the
same underlying distribution. We note that the minimum observable
separation corresponds to the beam size, i.e,
![]() or
or ![]()
![]() AU (
AU (
![]() )
at 2.4 kpc. Statistics of the nearest-neighbour distributions
in other IRDCs are given in Table 10.
Table 10
have the same meaning as in Table 9, except
now for nearest neighbour separations. The observed nearest-neighbour
distances are similar to those expected from random distributions. This
is evident from the ratios
)
at 2.4 kpc. Statistics of the nearest-neighbour distributions
in other IRDCs are given in Table 10.
Table 10
have the same meaning as in Table 9, except
now for nearest neighbour separations. The observed nearest-neighbour
distances are similar to those expected from random distributions. This
is evident from the ratios
![]() and
and
![]() which are
(within the erros) about 1,
and by the high K-S probabilities (
which are
(within the erros) about 1,
and by the high K-S probabilities (![]()
![]() )
in every other case except G031.97, where this probability is
still
)
in every other case except G031.97, where this probability is
still ![]()
![]() (see Cols. (6)-(8) of Table 10).
(see Cols. (6)-(8) of Table 10).
In summary, the average projected separations between clumps
in the
studied IRDCs range from about
![]() AU
to
AU
to ![]() AU (i.e., the
minimum and maximum lie within a factor of five), and the average
projected distances between the nearest neighbours range from
AU (i.e., the
minimum and maximum lie within a factor of five), and the average
projected distances between the nearest neighbours range from
![]() AU
to
AU
to
![]() AU (i.e., the
changes are within a factor of six). For
most clouds, the distributions of projected separations and distances
between the nearest neighbours can be mimicked by clumps placed
randomly into the same projected area as occupied by the cloud.
Assuming that the vectors connecting clump pairs are randomly oriented,
the average projection factor is
AU (i.e., the
changes are within a factor of six). For
most clouds, the distributions of projected separations and distances
between the nearest neighbours can be mimicked by clumps placed
randomly into the same projected area as occupied by the cloud.
Assuming that the vectors connecting clump pairs are randomly oriented,
the average projection factor is
![]() ,
where
,
where ![]() is the angle between the line of sight and the vector pointing from
clump i to clump j. Correcting
for this projection effect, the grand averages of the separations and
distances between the nearest neighbours are about
is the angle between the line of sight and the vector pointing from
clump i to clump j. Correcting
for this projection effect, the grand averages of the separations and
distances between the nearest neighbours are about
![]() AU
(3.1 pc) and
AU
(3.1 pc) and ![]() AU
(1.1 pc), respectively.
AU
(1.1 pc), respectively.
Table 9: Statistics of the clump-separation distributions in IRDCs.
Table 10: Statistics of the number distributions of the projected separation distance between nearest neighbours in IRDCs.
6.6 Fragmentation of IRDCs
One plausible scenario for the origin of filamentary clouds is that they are formed in shocks occurring in converging flows driven by large-scale turbulence (e.g., Klessen et al. 2000; Padoan et al. 2001). The chaotic process can give rise to randomly positioned density peaks within filaments, and these can become centres of gravitational collapse. On the other hand, supposing that compression leads to an equilibrium structure, a filament can fragment through the Jeans instability.
The critical wavelength,
![]() ,
of perturbations leading
to gravitational instability depends on both the gas
kinetic tempeture,
,
of perturbations leading
to gravitational instability depends on both the gas
kinetic tempeture, ![]() ,
and the density,
,
and the density, ![]() :
:
![]() ,
or, in terms of the
surface density,
,
or, in terms of the
surface density, ![]() :
:
![]() ,
where
,
where ![]() is the sound speed, and G is the
gravitational constant (e.g., Larson
1985; Hartmann 2002).
is the sound speed, and G is the
gravitational constant (e.g., Larson
1985; Hartmann 2002).
The determination of the ``Jeans length'' is not quite
straightforward
in a study based on dust emission because the cloud mass and therefore
also the average density and surface density depend on the assumed dust
temperature, ![]() .
Furthermore, in the case of G304.74, there is no independent estimate
of
.
Furthermore, in the case of G304.74, there is no independent estimate
of ![]() ,
but it is assumed to be equal to
,
but it is assumed to be equal to ![]() .
.
The assumption ![]() K
yields a total mass of
K
yields a total mass of ![]()
![]() and an average surface density
of 0.05 g cm-2
for G304.74 (within the LABOCA contour
0.1 Jy beam-1). In these
circumstances, the critical wavelength in an isothermal equilibrium
filament is
and an average surface density
of 0.05 g cm-2
for G304.74 (within the LABOCA contour
0.1 Jy beam-1). In these
circumstances, the critical wavelength in an isothermal equilibrium
filament is
![]() pc
or 40 000 AU (Hartmann
2002; Larson 1985),
and the corresponding mass is
pc
or 40 000 AU (Hartmann
2002; Larson 1985),
and the corresponding mass is
![]() .
The comparison between dust emission at 870
.
The comparison between dust emission at 870 ![]() m,
8
m,
8 ![]() m
absorption,
and the visual extinction from 2MASS suggests an elevated temperature
in the southern part of the cloud (Table 4,
Col. (4)).
By assuming
m
absorption,
and the visual extinction from 2MASS suggests an elevated temperature
in the southern part of the cloud (Table 4,
Col. (4)).
By assuming ![]() K,
one
would obtain a total cloud mass of
K,
one
would obtain a total cloud mass of ![]()
![]() ,
and an average
surface density of
,
and an average
surface density of ![]() g cm-2.
These values of
temperature and surface density imply
g cm-2.
These values of
temperature and surface density imply
![]() pc
or
pc
or
![]() AU, and
AU, and
![]() .
The critical wavelength,
.
The critical wavelength, ![]() ,
is not expected to determine a uniform length scale of fragmentation.
According to the analysis of Stodólkiewicz (1963;
see also Curry 2000, and
references therein), the fastest growing
perturbations have a length scale of roughly twice
,
is not expected to determine a uniform length scale of fragmentation.
According to the analysis of Stodólkiewicz (1963;
see also Curry 2000, and
references therein), the fastest growing
perturbations have a length scale of roughly twice
![]() .
Nevertheless, the fragmentation of a homogenous cloud is likely to
result in a preferred length scale and a quasi-periodic structure, as
opposed to a random distribution of clumps.
.
Nevertheless, the fragmentation of a homogenous cloud is likely to
result in a preferred length scale and a quasi-periodic structure, as
opposed to a random distribution of clumps.
The projected distances between the nearest neighbours in
G304.74 lie
in the range ![]() AU.
They are comparable to the
characterics length scales indicated above. However, the clump masses
in the cool northern part (
AU.
They are comparable to the
characterics length scales indicated above. However, the clump masses
in the cool northern part (![]()
![]() )
are about ten times
larger than Jeans masses at 15 K and the surface
density implied by
this temperature. Either the Jeans instability has occurred when the
cloud has been warmer, i.e.
)
are about ten times
larger than Jeans masses at 15 K and the surface
density implied by
this temperature. Either the Jeans instability has occurred when the
cloud has been warmer, i.e. ![]() 30 K, and the clumps
have cooled
during the contraction, or the dense filament is a result of strong
compression by external forces. We note that the filament is thinner
at the northeastern end (cross-sectional diameter
30 K, and the clumps
have cooled
during the contraction, or the dense filament is a result of strong
compression by external forces. We note that the filament is thinner
at the northeastern end (cross-sectional diameter
![]() pc)
than in the southwest (
pc)
than in the southwest (
![]() pc). Moreover, the
filament can
have accumulated mass through gravitational inflow from the
surrounding cloud (Heitsch
et al. 2009).
pc). Moreover, the
filament can
have accumulated mass through gravitational inflow from the
surrounding cloud (Heitsch
et al. 2009).
The present average mass line density in G304.74, ![]()
![]() pc-1
exceeds the critical value for a non-magnetic, self-gravitating
isothermal cylinder in equilibrium (
pc-1
exceeds the critical value for a non-magnetic, self-gravitating
isothermal cylinder in equilibrium (![]()
![]() pc-1
at 15 K, the critical line density directly
proportional to
pc-1
at 15 K, the critical line density directly
proportional to
![]() ;
Ostriker 1964; Curry 2000). For comparison, in
several
filamentary IRDCs studied by Rathborne et al. (2006; G025.04,
G028.53,
G028.53, G031.97, G033.69, G034.43, and G035.39), the line densities
are in the range
;
Ostriker 1964; Curry 2000). For comparison, in
several
filamentary IRDCs studied by Rathborne et al. (2006; G025.04,
G028.53,
G028.53, G031.97, G033.69, G034.43, and G035.39), the line densities
are in the range ![]()
![]() pc-1.
Supercritical line densities seem to be a common feature in filamentary
IRDCs, and they are likely to fragment into smaller cores. Our
observations cannot resolve the
possible fragments in G304.74, but the process is manisfest in
presence of (intermediate- to high-mass) protostars, i.e., the two
IRAS
sources. On the other hand, the recent interferometric studies of
G28.34 (Zhang et al. 2009)
and IRDC 19175 (Beuther &
Henning 2009)
have provided direct evidence for sub-fragmentation of IRDC clumps.
The two studies offer, however, contradictory views of the nature of
the underlying instability (turbulent fragmentation vs. Jeans
instability).
pc-1.
Supercritical line densities seem to be a common feature in filamentary
IRDCs, and they are likely to fragment into smaller cores. Our
observations cannot resolve the
possible fragments in G304.74, but the process is manisfest in
presence of (intermediate- to high-mass) protostars, i.e., the two
IRAS
sources. On the other hand, the recent interferometric studies of
G28.34 (Zhang et al. 2009)
and IRDC 19175 (Beuther &
Henning 2009)
have provided direct evidence for sub-fragmentation of IRDC clumps.
The two studies offer, however, contradictory views of the nature of
the underlying instability (turbulent fragmentation vs. Jeans
instability).
6.7 The origin of IRDCs and substructures within them
IRDCs are the densest parts of molecular cloud complexes. Several
observational facts and modelling results suggest that turbulence has
an important role in the formation of IRDCs and their fragmentation
into clumps. 1) On large scales, molecular clouds have highly
supersonic linewidths. In general, these are considered to imply
turbulent motions (e.g., Elmegreen
& Scalo 2004; McKee
& Ostriker 2007). However, large linewidths in dense
clouds can also be
explained by collapsing motions towards local gravitational centres
(Heitsch et al. 2009).
2) The filamentary shapes of IRDCs, and molecular
clouds in general, are consistent with cloud morphologies predicted by
numerical models of supersonic turbulence driven on large scales
(e.g., Klessen 2000,
2001; Jappsen et al. 2005).
In this
model, a dense filament can form where converging flows meet. Also
the mass surface density distribution observed in IRDCs have been
found to correspond to expectations from numerical simulations of
turbulent clouds (Butler &
Tan 2009). 3) The high-mass end of the mass
distiribution of a large sample of IRDCs studied by Marshall
et al.
(2009) follows a power-law (
![]() )
which can be
reproduced by density fluctuations induced by turbulence. 4) The mass
spectrum of the high-mass clumps within the extensive IRDC sample of
RJS06 can be fitted with a power-law (
)
which can be
reproduced by density fluctuations induced by turbulence. 4) The mass
spectrum of the high-mass clumps within the extensive IRDC sample of
RJS06 can be fitted with a power-law (
![]() ).
This power-law agrees with fragmentation due to supersonic turbulence
in
self-gravitating clouds (Klessen
2001). 5) Finally, the spatial
distributions of clumps within IRDCs (cf. Sect. 6.5) show no
clear
deviation from a random distribution. This is what can be expected if
fragmentation is driven by a stochastic process.
).
This power-law agrees with fragmentation due to supersonic turbulence
in
self-gravitating clouds (Klessen
2001). 5) Finally, the spatial
distributions of clumps within IRDCs (cf. Sect. 6.5) show no
clear
deviation from a random distribution. This is what can be expected if
fragmentation is driven by a stochastic process.
The filamentary stuctures of IRDCs and the fact that star formation in them takes place in clusters suggest that turbulence is driven on large scales (e.g., Klessen 2001). The most likely driving agent for large-scale turbulence is provided by supernova explosions, with an important contribution of density fluctuations caused by older remnants (e.g., Korpi et al. 1998; Joung et al. 2009 and references therein). The Galactic distribution of IRDCs peak in the 5-kpc molecular ring (Simon et al. 2006a; Marshall et al. 2009), where most of the Galactic supernova remnants are found (e.g., Jackson et al. 2008).
The role of turbulence in the fragmention of IRDC clumps into dense cores is less evident. The observed spectral linewidths in clumps are broader than expected from thermal broadening (e.g., Ragan et al. 2006; Sakai et al. 2008; Gibson et al. 2009), but this does not inevitably imply that the gas is turbulent (Heitsch et al. 2009). As discussed in Sect. 6.6, high-resolution studies have revealed some regular stuctures within clumps (Zhang et al. 2009; Beuther & Henning 2009) which point towards gravitational or fluid dynamical instabilities. In any case, self-gravity of shock-compressed clumps or filaments is inherent also in the models of turbulent fragmentation.
7 Summary and conclusions
We have mapped IRDC G304.74 in the 870 ![]() m dust continuum emission
with the APEX telescope. The submm dust continuum observations have
been used
together with 1.2 mm data from Beltrán
et al. (2006), and archival MSX
and IRAS infrared data to derive the physical characteristics
of the clumps within the cloud. Besides the dust continuum we used dust
extinction data from MSX and 2MASS to derive the H2
column densities, and the mass distribution in the cloud. The results
obtained via different methods are in reasonable agreement with each
other taking into account the uncertain nature of some of the dust
properties and the relation between the H2
column density and extinction. However, the agreement can be improved
by assuming an elevated temperature in four clumps near the
southwestern end of the cloud, and the possibility of a temperature
gradient from about 15 K
in the north and centre to about 20-30 K in the south cannot
be ruled out.
m dust continuum emission
with the APEX telescope. The submm dust continuum observations have
been used
together with 1.2 mm data from Beltrán
et al. (2006), and archival MSX
and IRAS infrared data to derive the physical characteristics
of the clumps within the cloud. Besides the dust continuum we used dust
extinction data from MSX and 2MASS to derive the H2
column densities, and the mass distribution in the cloud. The results
obtained via different methods are in reasonable agreement with each
other taking into account the uncertain nature of some of the dust
properties and the relation between the H2
column density and extinction. However, the agreement can be improved
by assuming an elevated temperature in four clumps near the
southwestern end of the cloud, and the possibility of a temperature
gradient from about 15 K
in the north and centre to about 20-30 K in the south cannot
be ruled out.
The filamentary cloud G304.74 contains 12 submm clumps. Star
formation has already started in the cloud as three of the clumps are
associated with both MSX and IRAS point sources. The
SEDs of the two IRAS sources indicate bolometric luminosities
in the range ![]()
![]() .
These are likely to be intermediate- or high-mass protostars.
In addition, one of the clumps (SMM 6) is associatied with two
MSX 8
.
These are likely to be intermediate- or high-mass protostars.
In addition, one of the clumps (SMM 6) is associatied with two
MSX 8 ![]() m
point sources. The remaining eight submm clumps are MIR dark.
The masses of these clumps (
m
point sources. The remaining eight submm clumps are MIR dark.
The masses of these clumps (![]()
![]() )
are sufficiently large to enable high-mass star formation, or
alternatively, they can represent the cold precursors of
proto-clusters. Thus, some of the candidate starless clumps in G304.74
could represent/harbour the so-called high-mass starless cores (HMSCs,
e.g., Beuther et al. 2007).
Further studies of these high-mass starless clump/core
candidates are important in order to constrain the initial conditions
of high-mass star and star cluster formation.
)
are sufficiently large to enable high-mass star formation, or
alternatively, they can represent the cold precursors of
proto-clusters. Thus, some of the candidate starless clumps in G304.74
could represent/harbour the so-called high-mass starless cores (HMSCs,
e.g., Beuther et al. 2007).
Further studies of these high-mass starless clump/core
candidates are important in order to constrain the initial conditions
of high-mass star and star cluster formation.
The clump masses in G304.74 were compared with the clump mass
spectra
from more extensive surveys of IRDCs. We found that IRDC clump masses
from the present work, and those from Rathborne et al. (2006)
and Ragan
et al. (2009) probably represent subsamples of the same parent
distribution. Also, average distances between a clump and its nearest
neighbour in
different IRDCs are comparable (within a factor of ![]() 6),
suggesting that the fragmentation length-scale does not vary much from
cloud
to cloud. Moreover, in most IRDCs, clumps seem to be randomly
distributed within the cloud area.
These characteristics, and the fact the star formation in IRDCs
predominantly
occurs in the cluster mode, agree with models where fragmentation is
driven by large-scale turbulence. It is not clear, yet, how effectual
turbulence is for the fragmentation of IRDC clumps into dense cores.
High spatial resolution studies, like the ones presented in Zhang
et al. (2009) and Beuther & Henning (2009) have
recently started to throw light on scales where gravity is likely to
dominate.
6),
suggesting that the fragmentation length-scale does not vary much from
cloud
to cloud. Moreover, in most IRDCs, clumps seem to be randomly
distributed within the cloud area.
These characteristics, and the fact the star formation in IRDCs
predominantly
occurs in the cluster mode, agree with models where fragmentation is
driven by large-scale turbulence. It is not clear, yet, how effectual
turbulence is for the fragmentation of IRDC clumps into dense cores.
High spatial resolution studies, like the ones presented in Zhang
et al. (2009) and Beuther & Henning (2009) have
recently started to throw light on scales where gravity is likely to
dominate.
The authors thank the referee for comments and suggestions which significantly improved the paper. We would like to thank the APEX staff in Chile for performing the LABOCA observations. We acknowledge M. Hennemann for providing the SED fitting tool originally written by J. Steinacker. Furthermore, M. T. Beltrán, P. Bergman, M. J. Butler, J. Kainulainen, H. Linz, and K. Mattila are thanked for useful discussions and suggestions. The authors acknowledge support from the Academy of Finland through grants 117206 and 132291. This research made use of data products from the Midcourse Space Experiment. Processing of the MSX data was funded by the Ballistic Missile Defense Organization with additional support from the NASA Office of Space Science. In addition, this publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory/California Institute of Technology, under contract with NASA, the NASA Astrophysics Data System, and the VizieR Catalogue access tool (CDS, Strasbourg, France).
References
- Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A, 361, 555 [NASA ADS] [Google Scholar]
- Ballesteros-Paredes, J., Klessen, R. S., Mac Low, M.-M., & Vázquez-Semadeni, E. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: Univ. of Arizona Press), 63 [Google Scholar]
- Beltrán, M. T., Brand, J., Cesaroni, R., et al. 2006, A&A, 447, 221 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., & Henning, Th. 2009, A&A, 503, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., & Sridharan, T. K. 2007, ApJ, 668, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., & Steinacker, J. 2007, ApJ, 656, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002a, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Walsh, A., Schilke, P., et al. 2002b, A&A, 390, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Sridharan, T. K., & Saito, M. 2005, ApJ, 634, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Churchwell, E. B., McKee, C. F., & Tan, J. C. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: Univ. of Arizona Press), 165 [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bronfman, L., Cohen, R. S., Alvarez, H., May, J., & Thaddeus, P. 1988, ApJ, 324, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, M. J., & Tan, J. C. 2009, ApJ, 696, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Clark, F. O., Egan, M. P., et al. 1998, ApJ, 508, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Feldman, P. A., Redman, R. O., et al. 2000, ApJ, 543, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Walmsley, C. M., Koempe, C., & Churchwell, E. 1991, A&A, 252, 278 [NASA ADS] [Google Scholar]
- Chambers, E. T., Jackson, J. M., Rathborne, J. M., & Simon, R. 2009, ApJS, 181, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Launhardt, R., Bourke, T. L., Henning, Th., & Barnes, P. J. 2008, ApJ, 683, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Curry, C. L. 2000, ApJ, 541, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Du, F., & Yang, J. 2008, ApJ, 686, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Egan, M. P., Shipman, R. F., Price, S. D., et al. 1998, ApJ, 494, L199 [NASA ADS] [CrossRef] [Google Scholar]
- Egan, M. P., Price, S. D., Kraemer, K. E., et al. 2003, VizieR Online Data Catalog, 5114, 0 [Google Scholar]
- Ellingsen, S. P. 2006, ApJ, 638, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fazal, F. M., Sridharan, T. K., Qiu, K., et al. 2008, ApJ, 688, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Fontani, F., Beltrán, M. T., Brand, J., et al. 2005, A&A, 432, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garay, G., Faúndez, S., Mardones, D., et al. 2004, ApJ, 610, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, D., Plume, R., Bergin, E., Ragan, S., & Evans, N. 2009, ApJ, 705, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1978, ApJ, 222, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Grave, J. M. C., & Kumar, M. S. N. 2009, A&A, 498, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harjunpää, P., & Mattila, K. 1996, A&A, 305, 920 [NASA ADS] [Google Scholar]
- Hartmann, L. 2002, ApJ, 578, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Ballesteros-Paredes, J., & Hartmann, L. 2009, ApJ, 704, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Hennemann, M., Birkmann, S. M., Krause, O., et al. 2009, ApJ, 693, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hofner, P., Wyrowski, F., Walmsley, C. M., & Churchwell, E. 2000, ApJ, 536, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Finn, S. C., Rathborne, J. M., et al. 2008, ApJ, 680, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Jappsen, A.-K., Klessen, R. S., Larson, R. B., et al. 2005, A&A, 435, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, D., Fiege, J. D., Redman, R. O., et al. 2003, ApJ, 588, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Joung, M. R., Mac Low, M.-M., & Bryan, G. L. 2009, ApJ, 704, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kahanpää, J., Mattila, K., Lehtinen, K., Leinert, C., & Lemke, D. 2003, A&A, 405, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S. 2001, ApJ, 556, 837 [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Durán-Rojas, C. 2005, ApJ, 620, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Korpi, M. J., Brandenburg, A., & Tuominen, I. 1998, in Proceedings of the 5th International Workshop ``Planetary and Cosmic Dynamos'' (Czech Republic: Trest Studia Geoph. et Geod.), 42, 410 [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2008, Nature, 451, 1082 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1985, MNRAS, 214, 379 [NASA ADS] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, S. 1994, ApJ, 433, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, D. J., Joncas, G., & Jones, A. P. 2009, ApJ, 706, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1990, ARA&A, 28, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuyanagi, I., Itoh, Y., Sugitani, K., et al. 2006, PASJ, 58, L29 [NASA ADS] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Williams, J. P. 1997, ApJ, 476, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Brand, J., Cesaroni, R., & Palla, F. 1996, A&A, 308, 573 [NASA ADS] [Google Scholar]
- Motte, F., Schilke, P., & Lis, D. C. 2003, ApJ, 582, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz, D. J., Mardones, D., Garay, G., et al. 2007, ApJ, 668, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Shipman, R. F., Ossenkopf, V., & Helmich, F. P. 2005, A&A, 439, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, Th. 1994, A&A, 291, 943 (OH94) [NASA ADS] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Padoan, P., Juvela, M., Goodman, A. A., & Nordlund, Å 2001, ApJ, 553, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Palla, F., Brand, J., Comoretto, G., Felli, M., & Cesaroni, R. 1991, A&A, 246, 249 [NASA ADS] [Google Scholar]
- Parsons, H., Thompson, M. A., & Chrysostomou, A. 2009, MNRAS, 1235 [Google Scholar]
- Pérault, M., Omont, A., Simon, G., et al. 1996, A&A, 315, L165 [NASA ADS] [Google Scholar]
- Peretto, N., & Fuller, G. A. 2009, A&A, 505, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Wyrowski, F., Menten, K. M., & Krügel, E. 2006a, A&A, 447, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Wyrowski, F., Carey, S. J., et al. 2006b, A&A, 450, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillai, T., Wyrowski, F., Hatchell, J., et al. 2007, A&A, 467, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineda, J. E., Rosolowsky, E. W., & Goodman, A. A. 2009, ApJ, 699, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Price, S. D., Egan, M. P., Carey, S. J., et al. 2001, AJ, 121, 2819 [NASA ADS] [CrossRef] [Google Scholar]
- Ragan, S. E., Bergin, E. A., Plume, R., et al. 2006, ApJS, 166, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Ragan, S. E., Bergin, E. A., & Gutermuth, R. A. 2009, ApJ, 698, 324 (RBG09) [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., Chambers, E. T., et al. 2005, ApJ, 630, L181 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., & Simon, R. 2006, ApJ, 641, 389 (RJS06) [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Simon, R., & Jackson, J. M. 2007, ApJ, 662, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Jackson, J. M., Zhang, Q., & Simon, R. 2008, ApJ, 689, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, T., Sakai, N., Kamegai, K., et al. 2008, ApJ, 678, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Simon, R., Jackson, J. M., Rathborne, J. M., & Chambers, E. T. 2006a, ApJ, 639, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, R., Rathborne, J. M., Shah, R. Y., et al. 2006b, ApJ, 653, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sridharan, T. K., Beuther, H., Schilke, P., et al. 2002, ApJ, 566, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Sridharan, T. K., Beuther, H., Saito, M., et al. 2005, ApJ, 634, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Stodólkiewicz, J. S. 1963, Acta Astron., 13, 30 [NASA ADS] [Google Scholar]
- Teyssier, D., Hennebelle, P., & Pérault, M. 2002, A&A, 382, 624 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, M. A., Hatchell, J., Walsh, A. J., et al. 2006, A&A, 453, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Wiel, M. H. D., & Shipman, R. F. 2008, A&A, 490, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasyunina, T., Linz, H., Henning, Th., et al. 2009, A&A, 499, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vuong, M. H., Montmerle, T., Grosso, N., et al. 2003, A&A, 408, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., Zhang, Q., Rathborne, J. M., et al. 2006, ApJ, 651, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & McKee, C. F. 1997, ApJ, 476, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989, ApJS, 69, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Wang, Y., Pillai, T., & Rathborne, J. 2009, ApJ, 696, 268 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ...
MSXDC G304.74+01.32
![[*]](/icons/foot_motif.png)
- This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX). APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory.
- ...
clumps
![[*]](/icons/foot_motif.png)
- We prefer to use the term ``clump'' according to e.g.,
Ragan
et al. (2009, hereafter RBG09), rather than the term ``core''
which was used
by e.g., RJS06. Clumps have masses and sizes (radii) of
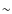
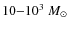 and
and 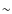 0.1-1 pc,
respectively (e.g., Bergin
& Tafalla 2007).
0.1-1 pc,
respectively (e.g., Bergin
& Tafalla 2007).
- ... (2007)
![[*]](/icons/foot_motif.png)
- http://www.astro.uni-bonn.de/boawiki/Boa
- ...
images
![[*]](/icons/foot_motif.png)
- http://irsa.ipac.ipac.caltech.edu
- ...
8.8
![[*]](/icons/foot_motif.png)
- Note, for the MSX band A filter the 50% cutoffs
are at 6.8 and 10.8
 m
(central wavelength is 8.8
m
(central wavelength is 8.8  m), whereas the isophotal central wavelength of
the filter is 8.28
m), whereas the isophotal central wavelength of
the filter is 8.28  m.
m.
- ...
SED
![[*]](/icons/foot_motif.png)
- The SED fitting routine was originally written by J. Steinacker.
- ...
mantles
![[*]](/icons/foot_motif.png)
- In cold, dense interiors of the IRDCs, dust grains are supposed to be coagulated and covered by icy mantles (e.g., Peretto & Fuller 2009, and references therein). This is supported by e.g., the observed depletion of H2CO (Carey et al. 1998, 2000), CO (Pillai et al. 2007; Zhang et al. 2009), and CS (Beuther & Henning 2009) in IRDCs. Moreover, Butler & Tan (2009) found some evidence for dust opacity changes within IRDCs, which could be caused by ice mantle formation and grain growth.
- ... above
![[*]](/icons/foot_motif.png)
- The 2MASS All-Sky Point Source Catalog (PSC) used here have been made available at http://irsa.ipac.caltech.edu/
- ... neighbours
![[*]](/icons/foot_motif.png)
- If the number of clumps in the cloud is
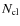 ,
then the number of clump-separations is
,
then the number of clump-separations is  ,
whereas the number of distances between an individual clump and its
nearest neighbour is equal to
,
whereas the number of distances between an individual clump and its
nearest neighbour is equal to  .
.
All Tables
Table 1: Submillimetre clumps identified by the clumpfind algorithm in the IRDC G304.74.
Table 2: MSX point sources in the IRDC G304.74.
Table 3: IRAS point sources in the IRDC G304.74.
Table 4:
The observed 8 ![]() m
intensity, the peak optical thickness, and the dust temperature toward
the submm peak positions.
m
intensity, the peak optical thickness, and the dust temperature toward
the submm peak positions.
Table 5: Results of the SED fits.
Table 6: Linear radii, masses, and H2 column and volume-averaged number densities of the submm clumps within the IRDC G304.74.
Table 7: Reddened 2MASS point sources within the IRDC G304.74.
Table 8: K-S test results between different IRDC clump mass distributions.
Table 9: Statistics of the clump-separation distributions in IRDCs.
Table 10: Statistics of the number distributions of the projected separation distance between nearest neighbours in IRDCs.
All Figures
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{13662fg1.ps}\hspace*{4mm}
\includegraphics[width=7.7cm,clip]{13662fg2.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg30.png)
|
Figure 1:
Left: LABOCA map of the 870 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{13662fg3.ps}\hspace*{4mm}
\includegraphics[width=7.8cm,clip]{13662fg4.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg44.png)
|
Figure 2:
Left: wide-field (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8cm,clip]{13662fg5.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg92.png)
|
Figure 3:
Median filter estimate of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13662fg6.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg103.png)
|
Figure 4:
MSX 8 |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{13662fg7.ps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{13662fg8.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg126.png)
|
Figure 5:
Best-fit SEDs of IRAS 13037-6112 and IRAS 13039-6108.
MSX data points are shown by circles, IRAS data
points are shown by diamonds, and LABOCA and SIMBA (sub)mm data points
are indicated by squares. Upper limits are indicated by arrows. The
solid lines in both plots represent the sum of two (cold+hot)
components (see Cols. (4) and (5) of Table 5). The
absorption features appearing at |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.2cm,height=8.2cm,clip]{13662fg9.ps}\vspace*{-1.5mm}\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg235.png)
|
Figure 6: LABOCA dust continuum map (contours) with 2MASS point sources (plus signs). The heavily reddened 2MASS stars within the cloud boundaries are marked with diamonds. The contour levels go from 0.1 to 0.6 by 0.1 Jy beam-1. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{13662fg10.ps} .
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg285.png)
|
Figure 7:
Normalised cumulative mass functions,
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{13662fg11.ps}\par\vspace*{2mm}
\includegraphics[width=7.5cm,clip]{13662fg12.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa13662-09/Timg301.png)
|
Figure 8: Top: observed clump-separation distribution (solid line) compared with the expected distribution for random distribution of the same number of clumps as the observed sample over rectangular area which approximate the area of the IRDC (dashed line). Bottom: observed nearest-neighbour distribution (solid line) compared with the expected distribution for random distribution (dashed line). |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.