| Issue |
A&A
Volume 520, September-October 2010
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 20 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/200911831 | |
| Published online | 29 September 2010 | |
The VIMOS-VLT deep survey: the group
catalogue![[*]](/icons/foot_motif.png)
O. Cucciati1,2 - C. Marinoni3 - A. Iovino1 - S. Bardelli4 - C. Adami2 - A. Mazure2 - M. Scodeggio5 - D. Maccagni5 - S. Temporin6 - E. Zucca4 - G. De Lucia7 - J. Blaizot8 - B. Garilli5 - B. Meneux9,10 - G. Zamorani4 - O. Le Fèvre2 - A. Cappi4 - L. Guzzo1 - D. Bottini5 - V. Le Brun2 - L. Tresse2 - G. Vettolani11 - A. Zanichelli11 - S. Arnouts12,2 - M. Bolzonella4 - S. Charlot13,14 - P. Ciliegi4 - T. Contini15 - S. Foucaud16 - P. Franzetti5 - I. Gavignaud17 - O. Ilbert2 - F. Lamareille15 - H. J. McCracken14,18 - B. Marano19 - R. Merighi4 - S. Paltani20,21 - R. Pellò15 - A. Pollo22,23 - L. Pozzetti4 - D. Vergani5 - E. Pérez-Montero24
1 - INAF-Osservatorio Astronomico di Brera, via Brera 28, 20021 Milan,
Italy
2 - Laboratoire d'Astrophysique de Marseille, Université de Provence,
CNRS, 38 rue Frederic Joliot-Curie, 13388 Marseille Cedex 13,
France
3 - Centre de Physique Théorique, UMR 6207, CNRS-Université de
Provence, 13288 Marseille, France
4 - INAF-Osservatorio Astronomico di Bologna, via Ranzani 1, 40127
Bologna, Italy
5 - IASF-INAF, via Bassini 15, 20133 Milano, Italy
6 - Institute of Astro- and Particle Physics,
Leopold-Franzens-University Innsbruck, Technikerstraße 25, 6020
Innsbruck, Austria
7 - INAF - Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143
Trieste, Italy
8 - Université de Lyon, 69003 Lyon, France; Université Lyon 1,
Observatoire de Lyon, 9 avenue Charles André, Saint-Genis Laval, 69230,
France; CNRS, UMR 5574, Centre de Recherche Astrophysique de Lyon;
École Normale Supérieure de Lyon, 69007 Lyon, France
9 - Max Planck Institut für Extraterrestrische Physik (MPE),
Giessenbachstrasse 1, 85748 Garching bei München, Germany
10 - Universitätssternwarte München, Scheinerstrasse 1, 81679 München,
Germany
11 - IRA-INAF, via Gobetti 101, 40129 Bologna, Italy
12 - Canada France Hawaii Telescope corporation, Mamalahoa Hwy,
Kamuela, 96743, USA
13 - Max Planck Institut für Astrophysik, 85741 Garching, Germany
14 - Institut d'Astrophysique de Paris, UMR 7095, 98 bis Bvd Arago,
75014 Paris, France
15 - Laboratoire d'Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 14 Av. E. Belin, 31400 Toulouse, France
16 - School of Physics & Astronomy, University of Nottingham,
University Park, Nottingham, NG72RD, UK
17 - Astrophysical Institute Potsdam, An der Sternwarte 16, 14482
Potsdam, Germany
18 - Observatoire de Paris, LERMA, 61 Avenue de l'Observatoire, 75014
Paris, France
19 - Università di Bologna, Dipartimento di Astronomia, via Ranzani 1,
40127 Bologna, Italy
20 - Integral Science Data Centre, ch. d'Écogia 16, 1290 Versoix,
Switzerland
21 - Geneva Observatory, ch. des Maillettes 51, 1290 Sauverny,
Switzerland
22 - The Andrzej Soltan Institute for Nuclear Studies, ul. Hoza 69,
00-681 Warszawa, Poland
23 - Astronomical Observatory of the Jagiellonian University, ul Orla
171, 30-244 Kraków, Poland
24 - Instituto de Astrofísica de Andalucía - CSIC. Apdo. de correos
3004, 18080 Granada, Spain
Received 11 February 2009 / Accepted 7 May 2010
Abstract
Aims. We present a homogeneous and complete
catalogue of optical galaxy groups identified in the purely
flux-limited (
![]() )
VIMOS-VLT deep redshift Survey (VVDS).
)
VIMOS-VLT deep redshift Survey (VVDS).
Methods. We use mock catalogues extracted from the
Millennium Simulation, to correct for potential systematics that might
affect the overall distribution as well as the individual properties of
the identified systems. Simulated samples allow us to forecast the
number and properties of groups that can be potentially found in a
survey with VVDS-like selection functions. We use them to correct for
the expected incompleteness and, to asses in addition, how well galaxy
redshifts trace the line-of-sight velocity dispersion of the underlying
mass overdensity. In particular, on these mock catalogues we train the
adopted group-finding technique i.e., the Voronoi-Delaunay Method
(VDM). The goal is to fine-tune its free parameters, recover in a
robust and unbiased way the redshift and velocity dispersion
distributions of groups (n(z) and
![]() ,
respectively), and maximize, at the same time, the level of
completeness and purity of the group catalogue.
,
respectively), and maximize, at the same time, the level of
completeness and purity of the group catalogue.
Results. We identify 318 VVDS groups with at least 2
members in the range ![]() ,
among which 144 (/30) with at least 3 (/5) members. The sample has an
overall completeness of
,
among which 144 (/30) with at least 3 (/5) members. The sample has an
overall completeness of ![]() 60%
and a purity of
60%
and a purity of ![]() 50%.
Nearly 45% of the groups with at least 3 members are still
recovered if we run the algorithm with a particular parameter set that
maximizes the purity (
50%.
Nearly 45% of the groups with at least 3 members are still
recovered if we run the algorithm with a particular parameter set that
maximizes the purity (![]() 75%)
of the resulting catalogue. We use the group sample to explore the
redshift evolution of the fraction
75%)
of the resulting catalogue. We use the group sample to explore the
redshift evolution of the fraction ![]() of blue galaxies (
of blue galaxies (
![]() )
in the redshift range
)
in the redshift range ![]() .
We find that the fraction of blue galaxies is significantly lower in
groups than in the global population (i.e. in the whole ensemble of
galaxies irrespective of their environment). Both of these quantities
increase with redshift, the fraction of blue galaxies in groups
exhibiting a marginally significant steeper increase. We also
investigate the dependence of
.
We find that the fraction of blue galaxies is significantly lower in
groups than in the global population (i.e. in the whole ensemble of
galaxies irrespective of their environment). Both of these quantities
increase with redshift, the fraction of blue galaxies in groups
exhibiting a marginally significant steeper increase. We also
investigate the dependence of ![]() on group richness: not only we confirm that, at any redshift, the blue
fraction decreases in systems with increasing richness, but we find
that this result continues to hold towards fainter luminosities.
on group richness: not only we confirm that, at any redshift, the blue
fraction decreases in systems with increasing richness, but we find
that this result continues to hold towards fainter luminosities.
Key words: galaxies: clusters: general - large-scale structure of Universe - galaxies: high-redshift - galaxies: evolution - galaxies: statistics
1 Introduction
Galaxy groups and clusters are the largest and most massive
gravitationally bound systems in the universe. Because of this, they
are very useful cosmological probes. For example, the evolution of
either their abundance or baryon fraction provides insights into the
value of fundamental cosmological parameters (e.g.,
Ettori
et al. 2009,2003; Zhang et al. 2006;
Newman
& Davis 2002; Allen et al. 2002; Borgani
et al. 1999), their mass and luminosity functions
fix
the amplitude of the power spectrum on cluster scales (e.g. Rosati
et al. 2002; Finoguenov et al. 2010),
while their optical
mass-to-light ratio allows us to constrain the matter density
parameter ![]() (e.g. Girardi
et al. 2000; Marinoni & Hudson 2002;
Sheldon
et al. 2009). Groups and clusters are also ideal
laboratories for
astrophysical studies. Several interesting physical processes are
indeed triggered on scales characterized by these extreme density
conditions. Their analysis is crucial in particular to understanding
the effects of local environment on galaxy formation and evolution
(e.g. Garilli
et al. 1999; Dressler et al. 1997;
Treu
et al. 2003; Oemler 1974; Poggianti
et al. 2006; Postman & Geller 1984;
Dressler
1980).
(e.g. Girardi
et al. 2000; Marinoni & Hudson 2002;
Sheldon
et al. 2009). Groups and clusters are also ideal
laboratories for
astrophysical studies. Several interesting physical processes are
indeed triggered on scales characterized by these extreme density
conditions. Their analysis is crucial in particular to understanding
the effects of local environment on galaxy formation and evolution
(e.g. Garilli
et al. 1999; Dressler et al. 1997;
Treu
et al. 2003; Oemler 1974; Poggianti
et al. 2006; Postman & Geller 1984;
Dressler
1980).
1.1 The detection of galaxy groups and clusters
A whole arsenal of algorithms allows us to identify and reconstruct galaxy systems. They range from the very first pioneering methods based on visual identification on photometric plates (Zwicky et al. 1968; Abell 1958) to more recent techniques which exploit various physical properties of the systems as a guide for identification. For example, the thermal bremsstrahlung emission from the hot intracluster gas trapped inside the cluster gravitational potential allows us to spot them by means of X-ray band observations. On the opposite side of the spectrum, in the centimetre regime, cluster detection is made possible thanks to the Sunyaev-Zeldovich effect (SZE, Sunyaev & Zeldovich 1980,1972). The hot intracluster gas, by means of inverse-Compton scattering the photons of the cosmic microwave background (CMB), leaves a characteristic imprint on the CMB spectrum, which can be exploited as a useful signature for identification. A cluster potential well can also be detected from the strong gravitational lensing or the cosmic shear induced by weak gravitational lensing (Morandi et al. 2010; Richard et al. 2010; Gavazzi et al. 2009; Limousin et al. 2009; Kneib et al. 2003; Limousin et al. 2010). Clusters identification can be based also on the properties of the member galaxies. Cluster cores are found to host typically red galaxies, among which there are the brightest cluster galaxies (BCG). Thus, a cluster center can be identified as a RA-dec concentration of galaxies with typical red colours (see for example the Red-Sequence Cluster Survey, Gladders & Yee 2000, the first cluster survey based on this method), in some cases also adding the constraint of a high luminosity (e.g. the maxBCG method, Hansen et al. 2005; Koester et al. 2007).
An orthogonal approach, based on geometrical algorithms, consists of identifying systems from the 3D spatial distribution properties of their members. These algorithms vary from the earlier hierarchical method (Materne 1978; Tully 1980) and the widely used ``friend of friend'' (FOF) method (Huchra & Geller 1982), to the 3D adaptive matched filter method (Kepner et al. 1999), the ``C4'' method (Miller et al. 2005), and the Voronoi-Delaunay Method (VDM, Marinoni et al. 2002). Finally, group-finding algorithms have been developed that use information extracted from photometric redshifts (e.g. Mazure et al. 2007; Adami et al. 2005).
The availability of several identification protocols is not
only
useful for confirming cluster detections by an a posteriori
cross-correlation of various independent catalogues, but it is also
crucial for anticipating systematics that might affect individual
detection techniques. For example, it was shown by the first joint
X-ray/optical survey (Donahue
et al. 2002) that only ![]() 20%
of optically selected clusters appeared to be identifiable in X-rays,
while
20%
of optically selected clusters appeared to be identifiable in X-rays,
while ![]() 60% of the
X-ray clusters were included in the optical
sample. Understanding the possible selection effects hidden behind the
different survey strategies is crucial to explain the small size of
the overlap between the two different cluster catalogues (see for
example Gilbank
et al. 2004; Ledlow et al. 2003).
Moreover,
using the RASS-SDSS galaxy cluster catalogue, Popesso et al. (2004)
show that a distinct class of ``X-ray underluminous Abell clusters''
does exist, with an X-ray luminosity
60% of the
X-ray clusters were included in the optical
sample. Understanding the possible selection effects hidden behind the
different survey strategies is crucial to explain the small size of
the overlap between the two different cluster catalogues (see for
example Gilbank
et al. 2004; Ledlow et al. 2003).
Moreover,
using the RASS-SDSS galaxy cluster catalogue, Popesso et al. (2004)
show that a distinct class of ``X-ray underluminous Abell clusters''
does exist, with an X-ray luminosity ![]() that is one order of
magnitude fainter than that expected for their mass according to the
typical
that is one order of
magnitude fainter than that expected for their mass according to the
typical ![]() -mass
relation (Popesso et al.
2007a). This supports the
concern of Donahue
et al. (2002) about the possible existence of
biases in catalogues selected in different wavebands.
-mass
relation (Popesso et al.
2007a). This supports the
concern of Donahue
et al. (2002) about the possible existence of
biases in catalogues selected in different wavebands.
A major challenge that we face is to extend cluster searches to high redshift. Most of the methods described above are affected by major problems when applied to this regime. Both the X-ray apparent surface brightness and the gravitational lensing cross-section of clusters decrease very rapidly with redshift. As a consequence, only very massive clusters can be detected at high z. In contrast, the SZE detection efficiency does not depend on redshift, but large SZ survey are yet to be completed. When detecting clusters using the spatial distribution of members, we emphasize the difference between photometric and spectroscopic galaxy data sets. Several methods have been proposed to detect clusters with photometric data, mainly exploiting galaxy colours in different bands. On the one side, this method has been successfully used both for surveys (see for example the above-mentioned Red-Sequence Cluster Survey, Gladders & Yee 2000) and single detections (e.g. Andreon et al. 2009). On the other hand, the selection of red galaxies, however, is biased towards older structures, where galaxies have lived enough time to be affected by the physical processes typical of the group environment (see for example the discussion in Gerke et al. 2007). Moreover, the depth required in photometric surveys to identify high-z groups and clusters increases the number of foreground and background contaminant galaxies, as the object surface number density is increased by the faint flux limit. This limits the effectiveness of 2D identifications at high-z. Knowledge of the third dimension is thus imperative if we wish to mitigate projection effects in an efficient way. Nonetheless, the uncertainty in the line-of-sight (l.o.s.) position of galaxies may be a concern when it is larger (or even far larger) than the typical velocity dispersion of group galaxies, as is typically the case for photometric redshifts.
1.2 This work and existing group and cluster samples
To date, many local, optically selected group catalogues are available
in literature. A review can be found in Eke
et al. (2004), where one of
the largest catalogue of galaxy groups detected in redshift space from
the Two Degree Field Galaxy Redshift Survey (2dFGRS) is presented. In
addition, several group catalogues have been extracted from the Sloan
Digital Sky Survey data (e.g. Weinmann et al. 2006; Miller
et al. 2005; Berlind et al. 2006).
Systematic searches of groups in redshift space have
also been undertaken at intermediate redshift (e.g. within the CNOC2
survey, up to redshift z=0.55, Carlberg et al. 2001).
The
compilation of optically selected and complete samples of groups up to
![]() and beyond
has become possible only recently thanks to
the completion of large and deep spectroscopic surveys, such as the
DEEP2 Galaxy Redshift Survey (Davis
et al. 2003), the VIMOS-VLT deep
survey (Le Fèvre et al.
2005), and the zCOSMOS survey
(Lilly
et al. 2007,2009).
and beyond
has become possible only recently thanks to
the completion of large and deep spectroscopic surveys, such as the
DEEP2 Galaxy Redshift Survey (Davis
et al. 2003), the VIMOS-VLT deep
survey (Le Fèvre et al.
2005), and the zCOSMOS survey
(Lilly
et al. 2007,2009).
Gerke et al.
(2005) present the first DEEP2 group catalogue, which
contains 899 groups with two or more members identified in the
redshift range ![]() with the VDM method. The DEEP2
sample reaches a limiting magnitude of
with the VDM method. The DEEP2
sample reaches a limiting magnitude of ![]() ,
and its galaxies
were pre-selected in colour before being targeted for spectroscopic
observations, to reduce the number of galaxies at
,
and its galaxies
were pre-selected in colour before being targeted for spectroscopic
observations, to reduce the number of galaxies at ![]() .
The first zCOSMOS group catalogue (Knobel
et al. 2009)
comprises
.
The first zCOSMOS group catalogue (Knobel
et al. 2009)
comprises ![]() 800 groups
with at least 2 members, covering the
redshift range
800 groups
with at least 2 members, covering the
redshift range ![]() .
The parent galaxy sample is
purely flux limited (
.
The parent galaxy sample is
purely flux limited (
![]() ),
and groups were
detected with the FOF method, combined with the VDM.
),
and groups were
detected with the FOF method, combined with the VDM.
In this work, we use the VIMOS-VLT deep survey (VVDS,
Le Fèvre et al. 2005)
to compile a homogeneous optically-selected
group catalogue in the redshift range 0.2<z<1.0.
We executed the
VDM code for a sample containing more than 6000 flux-limited galaxies
(
![]() )
for which reliable spectroscopic
redshifts had been measured. Particular care was taken to optimally
tune the parameters of the group-finding algorithm using VVDS-like
mock catalogues. The selection function of the sample, which
compensates only for the flux limitedness of the survey, is simple and
mostly insensitive to possibly uncontrolled biases such as those
affecting colour-selected samples. Moreover, the magnitude depth of
the VVDS allows us to select a galaxy population that is fainter in
luminosity than that currently probed by other flux-limited surveys of
the deep universe.
)
for which reliable spectroscopic
redshifts had been measured. Particular care was taken to optimally
tune the parameters of the group-finding algorithm using VVDS-like
mock catalogues. The selection function of the sample, which
compensates only for the flux limitedness of the survey, is simple and
mostly insensitive to possibly uncontrolled biases such as those
affecting colour-selected samples. Moreover, the magnitude depth of
the VVDS allows us to select a galaxy population that is fainter in
luminosity than that currently probed by other flux-limited surveys of
the deep universe.
The paper is organized as follows. In Sect. 2, the data sample and the mock catalogues are described. The reliability of the virial l.o.s. velocity dispersion estimated using galaxies is discussed in Sect. 3. In Sect. 4, we review the basics of the VDM group-finding algorithm, while the strategy followed to ascertain an optimal set of parameters is presented in Sect. 5. In Sect. 6, we describe the properties of the VVDS group catalogue. The redshift evolution of the U-B colour of group galaxies is analyzed in Sect. 7. Conclusions are drawn in Sect. 8.
We frame our analysis in the context of a ![]() Cold Dark Matter
model (
Cold Dark Matter
model (![]() CDM)
specified by the parameters
CDM)
specified by the parameters ![]() ,
,
![]() ,
and H0=70 km s-1 Mpc-1.
Magnitudes are expressed in the AB system.
,
and H0=70 km s-1 Mpc-1.
Magnitudes are expressed in the AB system.
2 Data sample and mock catalogues
2.1 The VVDS-02h sample
The VIMOS-VLT deep survey (VVDS) is a large spectroscopic survey whose primary aim is to study galaxy evolution and large-scale structure formation. The survey strategy and goals are described in detail by Le Fèvre et al. (2005). The VVDS is complemented by ancillary deep photometric data that have been collected at the CFHT telescope (BVRI, McCracken et al. 2003; Le Fèvre et al. 2004), at the NTT telescope (JK, Iovino et al. 2005; Temporin et al. 2008), and at the MPI telescope (U, Radovich et al. 2004). In addition, u*, g', r', i', and z'-band data are available as part of the CFHT Legacy Survey. The full suite of spectroscopic and photometric data provides a superb database to address across a wide redshift range many open questions of modern observational cosmology.
In this paper, we use data collected for the VVDS-0226-04 deep
field
(from now on ``VVDS-02h field''), for which the spectroscopic
observations targeted objects in the magnitude range ![]() .
In this range, the parent photometric sample is complete
and free of surface brightness selection effects
(McCracken et al. 2003),
resulting in a deep and purely flux-limited
spectroscopic sample. Spectroscopic observations (the so-called
``first epoch'' data) in the VVDS-02h field were carried out at the
ESO-VLT with the VIsible Multi-Object Spectrograph (VIMOS), a
4-channel imaging spectrograph, each channel (a quadrant)
covering
.
In this range, the parent photometric sample is complete
and free of surface brightness selection effects
(McCracken et al. 2003),
resulting in a deep and purely flux-limited
spectroscopic sample. Spectroscopic observations (the so-called
``first epoch'' data) in the VVDS-02h field were carried out at the
ESO-VLT with the VIsible Multi-Object Spectrograph (VIMOS), a
4-channel imaging spectrograph, each channel (a quadrant)
covering ![]()
![]() arcmin2
for a total field of view (a
pointing) of
arcmin2
for a total field of view (a
pointing) of ![]() 218 arcmin2.
The observations used 1 arcsec wide slits and the LRRed grism,
covering the spectral range
5500 Å
218 arcmin2.
The observations used 1 arcsec wide slits and the LRRed grism,
covering the spectral range
5500 Å
![]() 9400 Å. The
resulting effective spectral
resolution is
9400 Å. The
resulting effective spectral
resolution is ![]() ,
while the rms accuracy of the
redshift measurements is
,
while the rms accuracy of the
redshift measurements is ![]() 275 km s-1
(Le Fèvre et al. 2005).
275 km s-1
(Le Fèvre et al. 2005).
The VVDS-02h field covers a total sky area of ![]() deg2,
targeted by 1, 2, or 4 spectrograph passes. This strategy
produces an uneven target sampling rate as shown in Fig. 1. The
multiple-pass strategy ensures that
there is no serious undersampling of the denser regions, at least in
the
deg2,
targeted by 1, 2, or 4 spectrograph passes. This strategy
produces an uneven target sampling rate as shown in Fig. 1. The
multiple-pass strategy ensures that
there is no serious undersampling of the denser regions, at least in
the ![]() 80% of the
field covered by two or more spectrograph
passes. We note that some quadrants were discarded because of their
poor quality and not all the regions of the field covered by the same
number of passes have the same sampling rate. On average, spectra
were obtained for a total of 22.8% of the parent photometric
catalogue. Owing to the low signal-to-noise ratio and/or to the
absence of useful spectral features, redshifts are available for only
80% of the
field covered by two or more spectrograph
passes. We note that some quadrants were discarded because of their
poor quality and not all the regions of the field covered by the same
number of passes have the same sampling rate. On average, spectra
were obtained for a total of 22.8% of the parent photometric
catalogue. Owing to the low signal-to-noise ratio and/or to the
absence of useful spectral features, redshifts are available for only
![]() 80% of these
targeted objects, giving an overall sampling rate
of
80% of these
targeted objects, giving an overall sampling rate
of ![]() 18% (
18% (![]() 33%
considering only the area covered by 4 passes).
33%
considering only the area covered by 4 passes).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f1.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg46.png)
|
Figure 1:
Uneven spectrograph coverage in VVDS-02h field. The grey-scale from the
lightest to the darkest grey indicates the sampling rate, with
corresponding values shown in the label.
The grid used for the colour-code had steps of
|
| Open with DEXTER | |
The VVDS-02h field first epoch sample probes a comoving volume (up to
z = 1.5) of
nearly ![]() h-3 Mpc3
in a standard
h-3 Mpc3
in a standard
![]() CDM
cosmology. This volume has transversal dimensions
CDM
cosmology. This volume has transversal dimensions ![]()
![]() h-1 Mpcat
z = 1.5 and
extends over 3060 h-1 Mpcin
the radial
direction.
h-1 Mpcat
z = 1.5 and
extends over 3060 h-1 Mpcin
the radial
direction.
The collected sample contains 6615 galaxies and AGNs with
secure redshifts, i.e. ,
redshift determined with a quality flag = 2, 3, 4,
and 9 (6058 with ![]() ).
We refer the reader to Le Fèvre
et al. (2005) for
further details about redshift quality flags. By comparing
spectroscopic redshifts of objects observed
twice in independent observations, we note only that redshifts with
flag = 2(/3/4) are correctly estimated with a
likelihood of
81(/97/>99)%. We assigned a flag = 9 to a
spectrum with only a single secure spectral feature in emission. Given
the spectral range covered by
observations and the flux limits of the survey, this emission line is
typically [OII]3727Å or H
).
We refer the reader to Le Fèvre
et al. (2005) for
further details about redshift quality flags. By comparing
spectroscopic redshifts of objects observed
twice in independent observations, we note only that redshifts with
flag = 2(/3/4) are correctly estimated with a
likelihood of
81(/97/>99)%. We assigned a flag = 9 to a
spectrum with only a single secure spectral feature in emission. Given
the spectral range covered by
observations and the flux limits of the survey, this emission line is
typically [OII]3727Å or H![]() (in very rare cases
Ly
(in very rare cases
Ly![]() ). Thus
flag = 9 redshifts have a probability of being
correct
of
). Thus
flag = 9 redshifts have a probability of being
correct
of ![]() 50%, being
based on the choice between the two most probable
emission lines. We double-check the robustness of the likelihood
assigned to flag = 2 and
flag = 9 objects, by comparing their
spectroscopic and photometric redshifts. Photometric redshifts were
computed as described in Ilbert
et al. (2006), but using the more
recent T0005 release of CFHTLS data (u*,
g', r', i', z'
filters) and the latest data available from WIRCAM (J,
H and K filters, Bielby
et al. in prep.). According to the comparison of
the two types of redshift, flag = 2(/9) redshifts are
correctly inferred
with a likelihood of 78(/59)%, a figure that is in good agreement
with the independent determination discussed above.
50%, being
based on the choice between the two most probable
emission lines. We double-check the robustness of the likelihood
assigned to flag = 2 and
flag = 9 objects, by comparing their
spectroscopic and photometric redshifts. Photometric redshifts were
computed as described in Ilbert
et al. (2006), but using the more
recent T0005 release of CFHTLS data (u*,
g', r', i', z'
filters) and the latest data available from WIRCAM (J,
H and K filters, Bielby
et al. in prep.). According to the comparison of
the two types of redshift, flag = 2(/9) redshifts are
correctly inferred
with a likelihood of 78(/59)%, a figure that is in good agreement
with the independent determination discussed above.
We note also that the conclusions of our work are unaffected by our including or not flag = 9 low quality redshifts in our analysis. As a matter of fact, these objects constitute a small fraction (<3%) of the whole sample. Moreover, the effect of possible biases induced by incorrect redshift estimates is weakened by the existence of the galaxy correlation on small scales: if a galaxy with flag = 2 is located close (on the sky) to other galaxies with similar (but more secure) redshifts, the likelihood that it shares the same redshift actually increases with respect to the probability determined on the basis of our analysis.
2.2 Mock catalogues
We made extensive use of mock catalogues, both to test the potential
for group searches of the VVDS-02h field data and to tune the
parameters of the group-finding algorithm for optimal detection.
Before introducing any particular group-finding algorithm, one needs to test the limits to group reconstruction imposed by the specific characteristics of the VVDS survey design. Using mock catalogues that mimic the VVDS-02h field, we were able to explore which groups are lost irretrievably due to the survey sparse galaxy sampling. Furthermore, we were able to assess how our measurement of the l.o.s. velocity dispersion of group galaxies is degraded by both the sampling rate and the non-negligible VVDS redshift measurement error. After exploring these limits, we then moved to test and optimize the group-finding algorithm, within the ranges in redshift and velocity dispersion where we found that VVDS-02h data allow a reliable group reconstruction.
Mock catalogues were obtained by applying the semi-analytic
prescriptions of De Lucia
& Blaizot (2007) to the dark matter halo
merging trees extracted from the Millennium
Simulation![]() (Springel et al. 2005).
The simulation contains N
= 21603particles of mass
(Springel et al. 2005).
The simulation contains N
= 21603particles of mass ![]() within a
comoving box of size 500 h-1 Mpc
on a side. The cosmological model
is a
within a
comoving box of size 500 h-1 Mpc
on a side. The cosmological model
is a ![]() model with
model with ![]() ,
,
![]() ,
h = 0.73,
,
h = 0.73, ![]() ,
n = 1, and
,
n = 1, and ![]() .
The positions and velocities of all simulated particles were stored at
63 snapshots, spaced approximately logarithmically from z=20
to the
present day. Dark matter halos were identified using a standard
friends-of-friends (FOF) algorithm with a linking length
of 0.2 in
units of the mean particle separation.
.
The positions and velocities of all simulated particles were stored at
63 snapshots, spaced approximately logarithmically from z=20
to the
present day. Dark matter halos were identified using a standard
friends-of-friends (FOF) algorithm with a linking length
of 0.2 in
units of the mean particle separation.
In this simulation, group galaxies were assumed to be those in the same FOF halo, identified with a unique ID. For each simulated group, a wealth of physical information are available: galaxy membership, virial mass (computed directly using the simulated particles), virial radius, and virial velocity dispersion (both inferred from the virial mass, by means of scaling laws and the virial theorem). The virial mass is evaluated within the radius where the halo has an overdensity 200 times the critical density of the simulation.
We note that the model used to construct light-cones from the Millennium Simulation has been shown to be quite successful in reproducing several basic properties of our real data set. The most important are the average redshift distribution n(z)(Meneux et al. 2008) and the global luminosity function (LF) (Zucca et al., in prep.), which are in good agreement with the real VVDS-02h n(z) and LF, the only exception being a slight excess of galaxies in the n(z) mock samples for z<0.5. This small difference in n(z) does not affect the completeness and purity values (see Sect. 5.1) of our group catalogue, as we specifically tested using separately the mocks with the most similar and the most different n(z). Moreover, Meneux et al. (2008) demonstrated that the galaxy clustering in the Millennium Simulation light cones is consistent with that measured using the VVDS-02h sample.
From the database compiled from the Millennium Simulation
(Lemson & Virgo
Consortium 2006), we selected 10 ![]() deg2independent
Millennium light cones (generated with the code MoMaF,
Blaizot et al. 2005),
from which we extracted several kinds of
mocks, according to our purposes. First of all, we extracted
deg2independent
Millennium light cones (generated with the code MoMaF,
Blaizot et al. 2005),
from which we extracted several kinds of
mocks, according to our purposes. First of all, we extracted ![]() deg2
flux-limited samples with the same flux limits as VVDS-02h
sample (
deg2
flux-limited samples with the same flux limits as VVDS-02h
sample (
![]() ).
These catalogues each have a 100% sampling rate, and no
redshift measurement error has been
added. We called these catalogues M(100,0), the
first number in
brackets indicating the sampling rate and the second the redshift
error. We then randomly depopulated these catalogues to obtain subsets
with 33%, 17%, and 10% sampling rates, mimicking
roughly the
sampling rate of the 4 pass, 2 pass and 1 pass areas of the
VVDS-02h
field. These catalogues are called M(33,0), M(17,0),
and M(10,0)respectively. With these mock catalogues
and taking advantage of the
known group membership, we were able to determine the extent to which
a group catalogue is depopulated when the sampling rate is decreased
to values typical of those of VVDS-02h field.
).
These catalogues each have a 100% sampling rate, and no
redshift measurement error has been
added. We called these catalogues M(100,0), the
first number in
brackets indicating the sampling rate and the second the redshift
error. We then randomly depopulated these catalogues to obtain subsets
with 33%, 17%, and 10% sampling rates, mimicking
roughly the
sampling rate of the 4 pass, 2 pass and 1 pass areas of the
VVDS-02h
field. These catalogues are called M(33,0), M(17,0),
and M(10,0)respectively. With these mock catalogues
and taking advantage of the
known group membership, we were able to determine the extent to which
a group catalogue is depopulated when the sampling rate is decreased
to values typical of those of VVDS-02h field.
As an additional step, we added redshift measurement errors to
the 33% sampling rate mocks, randomly chosen from a Gaussian
distribution
centered on 0 with ![]() km s-1.
In this way, we took account of
the mean redshift measurement error in our true data. We called these
mock catalogues M(33,275). With these mock
catalogues, we were able
to test how well we can determine group virial velocity dispersion
when the survey has flux limits, sampling rate, and redshift
measurement errors mimicking those of the 4 pass areas of the
VVDS-02h
field.
km s-1.
In this way, we took account of
the mean redshift measurement error in our true data. We called these
mock catalogues M(33,275). With these mock
catalogues, we were able
to test how well we can determine group virial velocity dispersion
when the survey has flux limits, sampling rate, and redshift
measurement errors mimicking those of the 4 pass areas of the
VVDS-02h
field.
As a last step, we needed mock catalogues to test how effective the group-finding algorithm that we adopted is in identifying groups surviving in a sample such as VVDS-02h. To test the efficiency of our algorithm, we used 20 ``VVDS-like'' mocks extracted from the Millennium Simulation. These mocks have the same flux limits, geometry, uneven sampling rate, and redshift error measurement as the VVDS-02h sample (see Pollo et al. 2005; and Meneux et al. 2008, for the preparation of these mocks). Subtler effects, such as those introduced by a slit positioning bias, were also included, because the same slit positioning tool used for the VVDS-02h sample was used, with the same optimization criteria, to generate the VVDS-like mocks. The areas masked in the true photometric catalogue because of either bright stars and a beam of scattered light were also masked in the VVDS-like mocks.
For the sake of clarity, we emphasize that whenever we refer to the ``FOF'' or ``simulated'' groups in all the above-mentioned mock catalogues, we mean the sets of galaxies within the same original FOF halo provided by the simulation itself, before any depopulating process: we never executed any FOF algorithm on mocks after extracting M(100,0), M(33,0), M(17,0), M(10,0), M(33,275), and ``VVDS-like'' mocks from simulations.
3 Preliminary tests
3.1 Testing the effects of VVDS survey strategy on groups
We explored how closely a group catalogue extracted from a VVDS-like survey represents the group population of an ideal survey that is purely flux-limited. In a real flux-limited galaxy survey with a sampling rate lower than 100%, most groups have a smaller number of members and some even go undetected. We wish to assess the fraction of groups that ``survive'' as such (i.e. with at least 2 members) in a survey with a sampling rate similar to that of VVDS-02h. To identify groups, in both the full flux-limited and the various ``observed'' catalogues, we used at this phase the identification number of FOF groups in the Millennium database. In other words, we consider only the limitations introduced by the survey strategy, neglecting for the moment additional complications introduced by the incompleteness/failures of the specific group finding algorithm that we used.
In Fig. 2,
we plot the fraction of groups in
mock catalogues that are flux-limited at ![]() ,
surviving after applying a sampling rate corresponding to that
of the 1/2/4 pass regions (i.e. 10%, 17% and 33%,
respectively) as
indicated by different lines. In practice, we plot the ratio of the
number of groups in M(10,0), M(17,0)
and M(33,0) catalogues to
the number of groups in M(100,0) catalogues. This
ratio was computed
in non-independent running redshift bins of
,
surviving after applying a sampling rate corresponding to that
of the 1/2/4 pass regions (i.e. 10%, 17% and 33%,
respectively) as
indicated by different lines. In practice, we plot the ratio of the
number of groups in M(10,0), M(17,0)
and M(33,0) catalogues to
the number of groups in M(100,0) catalogues. This
ratio was computed
in non-independent running redshift bins of ![]() :
continuous
lines are fits along all the bins, while for reference the ratios
corresponding to the M(33,0) catalogues are also
shown for each
redshift bin as red diamonds. We note that the number of groups with
:
continuous
lines are fits along all the bins, while for reference the ratios
corresponding to the M(33,0) catalogues are also
shown for each
redshift bin as red diamonds. We note that the number of groups with
![]() km s-1
is quite low, mainly because of the small
field of view, thus the fraction of survived groups at
km s-1
is quite low, mainly because of the small
field of view, thus the fraction of survived groups at ![]() fluctuates about a mean value that we use to fit a straight
line. These fluctuations, however, are as high as 10% only in
the
worst cases. This is also true for the M(10,0) and M(17,0)catalogues,
for which we do not plot single points to avoid crowding
the figure. The horizontal dashed line at a fraction value equal
to 50% is shown for reference. The three panels correspond to
different
cuts in the virial l.o.s. velocity dispersion (
fluctuates about a mean value that we use to fit a straight
line. These fluctuations, however, are as high as 10% only in
the
worst cases. This is also true for the M(10,0) and M(17,0)catalogues,
for which we do not plot single points to avoid crowding
the figure. The horizontal dashed line at a fraction value equal
to 50% is shown for reference. The three panels correspond to
different
cuts in the virial l.o.s. velocity dispersion (
![]() )
quoted
in the mocks, as indicated by the label (from now onwards all velocity
dispersions quoted are l.o.s. velocity dispersions).
)
quoted
in the mocks, as indicated by the label (from now onwards all velocity
dispersions quoted are l.o.s. velocity dispersions).
Figure 2
shows that in 2 and 4 pass areas we can
recover the majority (![]()
![]() )
of groups to
)
of groups to ![]() km s-1
in the full redshift range below z=1.0. Going to
higher
values of
km s-1
in the full redshift range below z=1.0. Going to
higher
values of ![]() obviously allows us to extend the redshift
range. This lower limit to
obviously allows us to extend the redshift
range. This lower limit to ![]() agrees with that implied by
the non-negligible redshift measurement error of VVDS survey. As we
see in the next paragraph, our measurements of velocity dispersion for
groups with
agrees with that implied by
the non-negligible redshift measurement error of VVDS survey. As we
see in the next paragraph, our measurements of velocity dispersion for
groups with ![]() km s-1
are quite unreliable.
km s-1
are quite unreliable.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f2.ps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg66.png)
|
Figure 2:
The fraction, as a function of redshift, of ``surviving''
groups when the sampling rate is decreased from that of a purely
flux-limited
simulated sample |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.3cm]{11831f3a.ps}\includegraph...
...th=5.3cm]{11831f3e.ps}\includegraphics[width=5.3cm]{11831f3f.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg67.png)
|
Figure 3:
Comparison of l.o.s. velocity dispersion
|
| Open with DEXTER | |
3.2 Estimating group virial l.o.s. velocity dispersion
A robust determination of the l.o.s. velocity dispersion of galaxies
in group is essential to obtaining a reliable group mass. When group
members are sparsely sampled, as in the case of VVDS-02h data, the
``gapper method'', originally suggested by Beers
et al. (1990), has
proved to be the most robust velocity dispersion estimator (see
also Girardi
et al. 1993). This method measures velocity
dispersion
by analyzing the velocity gaps in the given velocity distribution of
galaxies, using the formula
where the l.o.s. velocities vi
are sorted into
ascending order. Beers
et al. (1990) show in their Table II that this
method reliably estimates the velocity dispersion with an efficiency
>90% for groups with ![]() 5-10 elements,
thanks to its
robustness in recovering the dispersion in a distribution even in the
more general case of a contaminated Gaussian distribution. We
emphasize that this range of group members is well suited to the study
we present in this work. On the one hand, we consider the velocity
dispersion reliably measurable only for groups with at least
5 members, and on the other hand the vast majority of groups
surviving in ``VVDS-like'' mocks have
5-10 elements,
thanks to its
robustness in recovering the dispersion in a distribution even in the
more general case of a contaminated Gaussian distribution. We
emphasize that this range of group members is well suited to the study
we present in this work. On the one hand, we consider the velocity
dispersion reliably measurable only for groups with at least
5 members, and on the other hand the vast majority of groups
surviving in ``VVDS-like'' mocks have ![]() 10 members.
10 members.
Hereafter, when discussing ``measured'' velocity dispersions
(
![]() )
we refer to velocity dispersions obtained by applying the gapper method
to the members of the given group. Of
course, we corrected this velocity dispersion by taking into account
the
scaling between redshift and velocity, using
)
we refer to velocity dispersions obtained by applying the gapper method
to the members of the given group. Of
course, we corrected this velocity dispersion by taking into account
the
scaling between redshift and velocity, using
where z is the redshift of the group.
We wish to test whether our measurement of the l.o.s velocity
dispersion ![]() is a reliable estimate of the virial
velocity dispersion
is a reliable estimate of the virial
velocity dispersion ![]() (as listed in the mock
catalogues). For this comparison, we used M(100,0),
M(33,0), and
M(33,275). We called the value of
(as listed in the mock
catalogues). For this comparison, we used M(100,0),
M(33,0), and
M(33,275). We called the value of ![]() measured for
these three kinds of catalogues
measured for
these three kinds of catalogues ![]() ,
,
![]() ,
and
,
and
![]() ,
respectively. In the case of a non-zero redshift
measurement error, such as in M(33,275) mock
catalogues, we took the
error itself into account when computing
,
respectively. In the case of a non-zero redshift
measurement error, such as in M(33,275) mock
catalogues, we took the
error itself into account when computing ![]() ,
by
subtracting the error (
,
by
subtracting the error (
![]() )
in quadrature as
)
in quadrature as
where
Figure 3
shows the comparison of
![]() with
with ![]() ,
,
![]() ,
and
,
and
![]() ,
respectively in the first, second, and third
columns. The first row is for the redshift bin 0.2<z<0.6,
and the
second for 0.6<z<1.0. In each plot,
the upper panel shows
isodensity contours in the plane
,
respectively in the first, second, and third
columns. The first row is for the redshift bin 0.2<z<0.6,
and the
second for 0.6<z<1.0. In each plot,
the upper panel shows
isodensity contours in the plane ![]() versus
versus ![]() for groups
with at least 5 members. Blue triangles are the median (on
x axis) and mean (on y axis)
values of single points grouped in
bins of
for groups
with at least 5 members. Blue triangles are the median (on
x axis) and mean (on y axis)
values of single points grouped in
bins of ![]() ,
with vertical error bars being the rms
of mean values. As a reference, purple squares are the same as
triangles but for groups with at least 8 members. The lower
panel in each plot shows the systematic offset of the
relation in the
upper panel; the offset is expressed as a percentage error (with its
rms) computed to be
,
with vertical error bars being the rms
of mean values. As a reference, purple squares are the same as
triangles but for groups with at least 8 members. The lower
panel in each plot shows the systematic offset of the
relation in the
upper panel; the offset is expressed as a percentage error (with its
rms) computed to be
where
Results graphically shown in Fig. 3 can be summarized as follows:
- 1)
- Effects of the VVDS-02h flux limit. The
plots in the
first column show that even in the ideal case of purely flux-limited
mock catalogues with 100% sampling rate and zero redshift measurement
error, the measured velocity dispersion
 systematically
underestimates
systematically
underestimates  .
This systematic offset, shown in the
lower part of the plots, is always below 20%, and its scatter
decreases with increasing
.
This systematic offset, shown in the
lower part of the plots, is always below 20%, and its scatter
decreases with increasing  and is lower in the lower
redshift bin. This offset can be easily understood by noting that in
a flux-limited survey, even with a 100% sampling rate, higher
redshift groups will progressively lose the fainter members that
lie outside the selected flux range. As a consequence the measured
velocity dispersion will underestimate the true virial velocity
dispersion, because the detectable galaxies will be the brighter, that
usually are found in group cores.
and is lower in the lower
redshift bin. This offset can be easily understood by noting that in
a flux-limited survey, even with a 100% sampling rate, higher
redshift groups will progressively lose the fainter members that
lie outside the selected flux range. As a consequence the measured
velocity dispersion will underestimate the true virial velocity
dispersion, because the detectable galaxies will be the brighter, that
usually are found in group cores.
- 2)
- Effects of the lower sampling rate introduced by
VVDS-02h strategy. The plots in the second column show that
if we
decrease the sampling rate from 100% to 33%, our ability to
recover
 decreases as well, as expected. The systematic offset
is not significantly worse than in mocks with 100% sampling
rate, but
the scatter about the systematic offset is larger, especially for low
decreases as well, as expected. The systematic offset
is not significantly worse than in mocks with 100% sampling
rate, but
the scatter about the systematic offset is larger, especially for low
 .
.
- 3)
- Effects of the VVDS redshift measurement error.
Finally, the plots in the third column illustrate that when we add
275 km s-1 of a redshift
error, low
 are very difficult to
recover, while, for
are very difficult to
recover, while, for  km s-1,
the systematic offset
and its rms remain below 25% with a slightly higher scatter
for
the higher redshift bin.
km s-1,
the systematic offset
and its rms remain below 25% with a slightly higher scatter
for
the higher redshift bin.
When considering
Our analysis globally suggests that we can use VVDS-02h data as a suitable sample for extracting high-z groups.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f4a.ps}\par\includegraphics[width=7cm,clip]{11831f4b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg84.png)
|
Figure 4:
As the plots in the last column of Fig. 3, but
with exchanged axes. In this case, the binning is made according to |
| Open with DEXTER | |
4 The group-finding algorithm
Several geometrical algorithms have been proposed to identify groups and clusters from the 3-dimensional distribution of galaxies, that is by optically identifying them within spectroscopic redshift surveys (see Sect. 1).
In this work we identified groups using the Voronoi-Delaunay method (VDM, Marinoni et al. 2002), which combines information about the three-dimensional Voronoi diagram and its dual, the Delaunay triangulation. The Voronoi diagram (Voronoi 1908) is a polyhedral partition of 3D space, each polyhedron surrounding a galaxy and defining the unique volume containing all the points that are closer to that galaxy than to any other galaxy in the sample. The Delaunay complex (Delaunay 1934) also contains proximity information. It is defined by the tetrahedra whose vertices are sets of four galaxies that have the property that the unique sphere that circumscribe them does not contain any other galaxy. The center of the sphere is a vertex of a Voronoi polyhedron, and each face of a Voronoi polyhedron is the bisector plane of one of the segments that link galaxies according to the Delaunay complex.
The basics of the VDM code are as follows. The denser the environment in which a galaxy lives, the smaller its associated Voronoi volume. Therefore the Voronoi partition performs a straightforward identification of the central regions of structures. In addition, the Delaunay triangulation assigns galaxy members to the identified core. We note that a crucial difference between the VDM and other methods is that, since it preliminarily identifies group centers, group membership reconstruction proceed radially outward, from the densest cores towards the outskirts of the structures.
An advantage offered by the Voronoi-Delaunay method is that it exploits the natural clustering of the galaxies in the sample. For example, the dimension of the volume assigned to each galaxy depends locally on the number density of the objects surrounding the galaxy itself. It is thus adaptively and unparametrically rescaled and not predefined on the basis of some fixed length parameter. Moreover, galaxies that are Delaunay connected to the central cores are processed with cylindrical windows whose dimensions are locally scaled on the basis of physical relations observed in simulated (and real) samples of groups and clusters. The specific set of VDM parameters is thus designed to provide the maximum amount of flexibility in selecting groups according to the a priori physical information we have about their structure. As a consequence, a fine-tuned VDM algorithm has been proven to be very efficient in reconstructing intrinsic characteristics of groups, such as for example the l.o.s. velocity dispersion of their members (Marinoni et al. 2002).
The Voronoi-Delaunay method was specifically designed to avoid some known drawbacks characterizing standard group-finding algorithms such as for example the FOF and the hierarchical methods. These methods are based on user-specified parameters (the FOF linking length, the ``affinity'' threshold in the hierarchical method) that do not depend on the true distribution of galaxies. One of the negative consequences is that spatially closed but unrelated structures often merge to form a single system. Moreover, some dynamical properties of clusters are very sensitive to the adopted group-finding algorithm: for example, the velocity dispersion of groups identified by the FOF algorithm is found to be systematically higher (by nearly 30%) than that of groups found by the hierarchical algorithm, even when both algorithms are optimized for the same galaxy sample (Giuricin et al. 2001).
We briefly describe here the VDM, although detailed accounts can be found in Marinoni et al. (2002) and Gerke et al. (2005) (from which we adopted some technical improvements).
The algorithm first computes the Voronoi-Delaunay mesh
following the
prescriptions in Barber
et al. (1996) and Mirtich
(1996). It
then searches for groups using a 3-step procedure. At each step, new
group members are identified by means of a cylindrical window (of
radius R and half-length L),
which is used to scan
Delaunay-connected galaxies and decide whether or not they are cluster
members. Phase I involves the 3-D identification of group seeds. In
Phase II, the algorithm determines group central richness, and
finally
in Phase III an adaptive scaling based on the N-![]() relation is
used to rescale the cylinder dimensions depending on the group
richness measured in Phase II. A detailed explanation of each of these
three steps is given in Sects. 4.1, 4.2, and 4.3.
relation is
used to rescale the cylinder dimensions depending on the group
richness measured in Phase II. A detailed explanation of each of these
three steps is given in Sects. 4.1, 4.2, and 4.3.
The radius and the half-length of the cylinders in both
Phase I
(
![]() and
and ![]() )
and of Phase II
(
)
and of Phase II
(
![]() and
and ![]() ),
in addition to r and l,
the scaling factors used to determine respectively the radius and
the half-length of the cylinder of Phase III (
),
in addition to r and l,
the scaling factors used to determine respectively the radius and
the half-length of the cylinder of Phase III (
![]() and
and
![]() ),
are free parameters of the algorithm. They need
to be optimized using physical information about clusters.
),
are free parameters of the algorithm. They need
to be optimized using physical information about clusters.
The choice of a cylindrical shape for the search window is physically motivated by the gravitational field of galaxy overdensities inducing peculiar velocities whose effect is to make the galaxy distribution appear elongated in the redshift direction. The only way to take this into account is by using a search window with a radial extension much longer than the transversal dimension, in order not to miss group members. We note that we also use a cylindrical window during our Phase I, while in Marinoni et al. (2002) the Phase I search window had a spherical shape. The original choice of a spherical window during the first phase was physically motivated by the finding that galaxies residing in the highest density peaks, i.e. the central cores of groups and clusters, are expected to have smaller peculiar velocities. However, we verified that for less rich systems, i.e. loose groups such as those we expect to recover in the VVDS sample, the optimal choice is a cylindrical window. The survey's quite large redshift measurement error and the sparse sampling rate were particularly important in deciding our choice.
As we wish the length of search cylinders to correspond
roughly to the
peculiar velocity of the galaxies in the group, we have to consider
that the mapping between redshift interval and peculiar velocity
changes with redshift, and thus, following Gerke et al. (2005),
our algorithm automatically rescales cylinder lengths ![]() as a
function of z, using the equation
as a
function of z, using the equation
| (6) |
where z0 is a reference redshift (see Sect. 4.2 for details) and
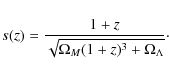
|
(7) |
This scaling is applied as a function of redshift to all
4.1 Phase I
During Phase I, galaxies are ranked according to the increasing size
of their Voronoi volume. A cylinder of radius ![]() and
half length
and
half length ![]() is then centered on the galaxy with the
smallest Voronoi volume. All galaxies inside the cylinder and
Delaunay-connected with the central galaxy are considered group
members and called first-order Delaunay neighbours.
The central
galaxy and its first-order Delaunay neighbours are assumed to be a
group seed. When no other galaxies are in the cylinder, the central
galaxy is rejected as a potential seed. Thus, the choice of
is then centered on the galaxy with the
smallest Voronoi volume. All galaxies inside the cylinder and
Delaunay-connected with the central galaxy are considered group
members and called first-order Delaunay neighbours.
The central
galaxy and its first-order Delaunay neighbours are assumed to be a
group seed. When no other galaxies are in the cylinder, the central
galaxy is rejected as a potential seed. Thus, the choice of
![]() and
and ![]() determines the final number of
identified groups. At the end of this Phase the barycenter of the
seed is computed using the positions of the central galaxy and its
first-order Delaunay neighbours.
determines the final number of
identified groups. At the end of this Phase the barycenter of the
seed is computed using the positions of the central galaxy and its
first-order Delaunay neighbours.
The algorithm then processes the full sequence of Phases for the found seed. After Phases II and III are complete, the whole procedure is reiterated by selecting from the sorted list the first galaxy not yet assigned to a group.
4.2 Phase II
In the second phase a different cylindrical window with
radius
![]() and half length
and half length ![]() is centered on
the barycenter determined in Phase I, and used to determine
the
central richness of the group. All galaxies within the
Phase II
cylinder and connected to the first-order Delaunay neighbours are
called second-order Delaunay neighbours, and are
considered to
be additional group members. The total number of group members after
this phase (the central galaxy plus first- and second-order
neighbours) is assumed to be the central richness
is centered on
the barycenter determined in Phase I, and used to determine
the
central richness of the group. All galaxies within the
Phase II
cylinder and connected to the first-order Delaunay neighbours are
called second-order Delaunay neighbours, and are
considered to
be additional group members. The total number of group members after
this phase (the central galaxy plus first- and second-order
neighbours) is assumed to be the central richness ![]() of the
group.
of the
group.
A reliable estimate of ![]() is important because it controls the
adaptive search window used during Phase III (see below). On the one
hand, considering only Delaunay-connected galaxies minimizes the
inclusion of interlopers in
is important because it controls the
adaptive search window used during Phase III (see below). On the one
hand, considering only Delaunay-connected galaxies minimizes the
inclusion of interlopers in ![]() .
On the other hand, in a
flux-limited survey such as VVDS, the
.
On the other hand, in a
flux-limited survey such as VVDS, the ![]() distribution varies as
a function of redshift, because of the variation in the luminosity
limit with redshift. To ensure a uniform group population,
distribution varies as
a function of redshift, because of the variation in the luminosity
limit with redshift. To ensure a uniform group population, ![]() must be
corrected as a function of z:
must be
corrected as a function of z:
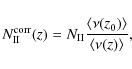
|
(8) |
where z0 is the redshift
zero point considered as
reference, and ![]() is the comoving number density,
which we calculated by smoothing the redshift distribution of the
galaxy sample, and then dividing it by the differential comoving
volume element at the considered redshift. In
Gerke et al. (2005),
z0 is the lower limit to the
DEEP2 galaxy
redshift distribution n(z), i.e.
z0=0.7. For the VVDS-02h
sample,
the lower limit to n(z) is z=0.2,
but at this redshift the volume
covered by the VVDS-02h is small. Because of this,
is the comoving number density,
which we calculated by smoothing the redshift distribution of the
galaxy sample, and then dividing it by the differential comoving
volume element at the considered redshift. In
Gerke et al. (2005),
z0 is the lower limit to the
DEEP2 galaxy
redshift distribution n(z), i.e.
z0=0.7. For the VVDS-02h
sample,
the lower limit to n(z) is z=0.2,
but at this redshift the volume
covered by the VVDS-02h is small. Because of this, ![]() can be poorly constrained. Moreover,
can be poorly constrained. Moreover, ![]() decreases very rapidly from z=0.2 to z=1.0.
Thus
we chose z0=0.7 as a
compromise between high statistics (it is
roughly the peak of our n(z)
distribution) and not yet so large
survey volume.
decreases very rapidly from z=0.2 to z=1.0.
Thus
we chose z0=0.7 as a
compromise between high statistics (it is
roughly the peak of our n(z)
distribution) and not yet so large
survey volume.
At the end of Phase II, the barycenter position is
readjusted using all ![]() members.
members.
4.3 Phase III
During Phase III, the algorithm reconstructs the full set of group members, using a new search window centered on the group barycenter determined at the end of Phase II with dimensions determined according to the following basic scaling relations.
Assuming that groups are singular isothermal spheres, at any
given
distance r from the center the mass density
distribution is related
to the velocity dispersion by the equation ![]() (Binney & Tremaine
1988). Since
(Binney & Tremaine
1988). Since ![]() ,
and when defining
,
and when defining ![]() to be the radius of a spherical volume
within which the mean density is
to be the radius of a spherical volume
within which the mean density is ![]() times the critical density
at the considered redshift, we find that
times the critical density
at the considered redshift, we find that ![]() ,
where
,
where ![]() is the virial mass. The virial theorem
implies that
is the virial mass. The virial theorem
implies that ![]() .
By applying the
correlation between velocity dispersion and central richness,
confirmed for loose groups up to massive clusters (for example,
see Bahcall 1981),
we obtain the chain of relations
.
By applying the
correlation between velocity dispersion and central richness,
confirmed for loose groups up to massive clusters (for example,
see Bahcall 1981),
we obtain the chain of relations
![]() .
.
Accordingly, we used the
central richness ![]() of each group to define both the
radius and the length of the cylindrical search window:
of each group to define both the
radius and the length of the cylindrical search window:


where, r and l are normalization parameters to be optimized using simulations. We note that the adaptive search window of Phase III differs from group to group and that all galaxies enclosed within the cylinder are assumed to be additional group members, irrespectively of the order of their Delaunay connections. From now on, we call richness N the final number of members assigned to each group at the end of Phase III.
5 Optimizing the group-finding algorithm
5.1 Success criteria
In this section we describe the optimization strategy that we devised to reconstruct groups in the most reliable and unbiased way, using VVDS-like mock catalogues. We applied the VDM algorithm to these catalogues, and compared the groups found by the algorithm with the groups present in the mocks identified by the same FOF identification number (see Sect. 2.2). From now on, we refer to FOF groups in the mocks as ``fiducial'' groups, while groups reconstructed by our algorithm are called ``reconstructed'' groups, or simply ``VDM'' groups.
There are two levels of success we are interested in: 1) success in finding groups, i.e. to establish the level of contamination by interlopers and fake groups, the percentage of missed galaxies and missed groups, and other statistics of this kind; 2) success in reproducing group properties, i.e. accurately measuring group properties on a group-by-group basis, and reproducing their statistical distribution as accurately as possible.
To test the VDM algorithm success in finding the fiducial groups present in the VVDS-like mocks, we used the following quality estimators (see also Marinoni et al. 2002; and Gerke et al. 2005, for more details):
- -
- galaxy success rate
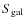 :
fraction of galaxies
belonging to fiducial groups that are identified members of
reconstructed groups;
:
fraction of galaxies
belonging to fiducial groups that are identified members of
reconstructed groups;
- -
- interlopers fraction
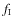 : fraction of
galaxies
identified by the algorithm as members of reconstructed groups that
are, however, interlopers;
: fraction of
galaxies
identified by the algorithm as members of reconstructed groups that
are, however, interlopers;
- -
- completeness C: fraction of fiducial groups that are ``successfully'' identified in the reconstructed catalogue;
- -
- purity P: fraction of reconstructed groups that ``correspond'' to fiducial groups.
Hence, we need to quantitatively determine whether a fiducial group is detected ``successfully'' and a reconstructed group ``corresponds'' to a fiducial one. We consider a detection to be successful when more than half of a fiducial group's members are detected in the same VDM group. In contrast, a VDM group corresponds to a fiducial one when more than half of its members belongs to that fiducial group. In general, these two conditions can be verified independently. These general cases are called one-way matches from one group catalogue to the other (from fiducial to VDM or in the opposite direction). But when these conditions are verified simultaneously involving the same fiducial and VDM group in both directions, we have a two-way match. We can therefore have a one-way completeness (C1) and a one-way purity (P1) when we consider only one-way matches in both the fiducial and the reconstructed group catalogue, respectively. A two-way completeness (C2) and a two-way purity (P2) can however also be defined when considering two-way matches.
On the one hand, knowing the absolute value of completeness
and purity
will help us to optimize the algorithm. On the other hand comparing,
C1 with C2
and P1 with P2
we can establish the kind of
errors in the reconstructed group catalogue. When ![]() ,
it
means that some fiducial groups are one-way
successes but not
two-way matches, and thus these fiducial groups
contain a low
fraction of the members of their reconstructed associated group. This
is an indication that the VDM algorithm tends to overmerge separated
groups to larger reconstructed groups, or to assign to reconstructed
groups too many interlopers. On the other hand, when
,
it
means that some fiducial groups are one-way
successes but not
two-way matches, and thus these fiducial groups
contain a low
fraction of the members of their reconstructed associated group. This
is an indication that the VDM algorithm tends to overmerge separated
groups to larger reconstructed groups, or to assign to reconstructed
groups too many interlopers. On the other hand, when ![]() we
know that VDM algorithm is affected by the opposite problem, i.e. the
reconstructed groups are highly fragmented with respect to the
fiducial ones.
we
know that VDM algorithm is affected by the opposite problem, i.e. the
reconstructed groups are highly fragmented with respect to the
fiducial ones.
We decided to use these indicators to search for the optimal
parameter
set for our algorithm following some guide lines. The basic idea is to
obtain as high as possible values of C1
and C2, while keeping
P1 and P2
at least above 50%. We also attempted to produce
neither a highly overmerged (
![]() )
or a highly fragmented
(
)
or a highly fragmented
(
![]() )
catalogue, and therefore we tried to ensure that
)
catalogue, and therefore we tried to ensure that ![]() and
and ![]() .
.
5.2 Algorithm optimization
We applied the VDM algorithm to 20 VVDS-like mocks, obtaining group
catalogues for the full redshift range ![]() ,
but for
the reasons discussed in Sect. 3.1
we
implemented the optimization strategy only in the range
,
but for
the reasons discussed in Sect. 3.1
we
implemented the optimization strategy only in the range ![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm]{11831f5a.ps}\includegraphics[width=7cm]{11831f5b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg113.png)
|
Figure 5:
C1 and C2
statistics as a function of ``fiducial''
group members (on the left) and P1
and P2 statistics as a
function of ``reconstructed'' group members (on the right).
One-way
statistics are shown as blue squares, and two-way statistics as red
crosses. C and P have been
computed separately in each mock:
in these plots, points are C and P
values averaged over all mocks,
while error bars are their rms. On the x axis,
we grouped the
number of elements in the following way: [N=2],[N=3,
4], [N=5, 6], and [ |
| Open with DEXTER | |
With a trial and error approach, we explored the flexibility of the 6
VDM parameters in recovering groups in a robust way. We allowed each
parameter to vary across a comprehensive range. In particular, 1) we
allowed ![]() and
and ![]() to increase to 1 h-1 Mpc,
with no lower limit: this was because we defined the
radii to span projected dimensions up to typical central radius of
massive clusters (Bahcall
1981). 2) We allowed r to
span the range
to increase to 1 h-1 Mpc,
with no lower limit: this was because we defined the
radii to span projected dimensions up to typical central radius of
massive clusters (Bahcall
1981). 2) We allowed r to
span the range ![]() ,
as we wished the radius of the
last search cylinder to be equal or larger than small group typical
size (
,
as we wished the radius of the
last search cylinder to be equal or larger than small group typical
size (![]() 0.5 h-1 Mpc,
see Borgani et al. 1997
and references
therein) and smaller than an Abell radius (
0.5 h-1 Mpc,
see Borgani et al. 1997
and references
therein) and smaller than an Abell radius (![]() 1.5 h-1 Mpc,
see
Borgani et al. 1997).
3) We defined
1.5 h-1 Mpc,
see
Borgani et al. 1997).
3) We defined ![]() ,
,
![]() ,
and l to vary from 4 to 20 h-1 Mpc,
to
include clusters with velocity dispersions as high as
2000 km s-1 also
at high redshift (
,
and l to vary from 4 to 20 h-1 Mpc,
to
include clusters with velocity dispersions as high as
2000 km s-1 also
at high redshift (![]() ).
In this case, the lower limit is
determined mainly by our redshift measurement error, which has to be
added to peculiar velocities. We imposed on
).
In this case, the lower limit is
determined mainly by our redshift measurement error, which has to be
added to peculiar velocities. We imposed on ![]() and
and
![]() the same limits applied to r and l.
Nevertheless, we also checked the performances of the algorithm
when no limits are applied to
the same limits applied to r and l.
Nevertheless, we also checked the performances of the algorithm
when no limits are applied to ![]() and
and
![]() ,
and we verified that, with the exception of very
few cases,
,
and we verified that, with the exception of very
few cases, ![]() and
and ![]() ``behave well'',
as we expected because the whole algorithm is based on physical scales
and scaling laws.
``behave well'',
as we expected because the whole algorithm is based on physical scales
and scaling laws.
Exploring the 6D parameter space, we found the parameter set that kept C1 and C2 as high as possible and P1 and P2 at least above 50%, while we monitored the behavior of the group properties, both on a group-by-group basis and from a statistical point of view. We then moved slightly around these chosen values in smaller steps, to search for a possible finer tuning.
At the end of this finer search, we found the following parameter set, from now on called the best set of parameters
- -
-
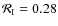 h-1 Mpc
h-1 Mpc
- -
-
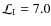 h-1 Mpc
h-1 Mpc
- -
-
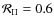 h-1 Mpc
h-1 Mpc
- -
-
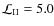 h-1 Mpc
h-1 Mpc
- -
- r=0.55 h-1 Mpc
- -
- l=14.0 h-1 Mpc.
Values of the quality parameters C1,
C2, P1,
P2, ![]() and
and ![]() can be found in Table 1.
We note that, to
test the quality of the algorithm as a function of redshift, we
separately considered two redshift bins (
can be found in Table 1.
We note that, to
test the quality of the algorithm as a function of redshift, we
separately considered two redshift bins (
![]() and
and
![]() ).
).
We also analyzed completeness and purity as a function of
group
richness. Figure 5
shows C1 and C2
as a function of
``fiducial'' group members and P1
and P2 as a function of
``reconstructed'' group members. One-way statistics are shown as blue
squares, and two-way statistics are shown as red crosses. The
parameters C and P
were computed separately in each mock. In Fig. 5, we plot C
and P values averaged over all mocks, while
error bars are their rms. The differences between C1
and C2 and
between P1 and P2
indicate that our group catalogue is
completely free from neither overmerging nor fragmentation.
Figure 6
also indicates that, while the galaxy success rate
![]() does not vary much as a function of N, the
interloper
fraction
does not vary much as a function of N, the
interloper
fraction ![]() decreases by a factor of
decreases by a factor of ![]() 2
from
2
from ![]() to
to
![]() .
.
Table 1:
Quality statistics (C1, C2,
P1, P2,
![]() ,
and
,
and
![]() ,
see text for details) of the reconstructed group catalogue,
for two different redshift bins and the whole redshift range.
,
see text for details) of the reconstructed group catalogue,
for two different redshift bins and the whole redshift range.
![\begin{figure}
\par\includegraphics[width=7cm]{11831f6.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg154.png)
|
Figure 6:
Interlopers fraction |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.cm,clip]{11831f7.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg155.png)
|
Figure 7: Mean distribution of fiducial groups as a function of redshift (continuous line), computed as the average over 20 VVDS-like mocks. The mean distribution of VDM-reconstructed groups over the same 20 mocks is over plotted as black points. |
| Open with DEXTER | |
5.3 Tests on recovered group properties
As discussed above, the comparison between group properties in both the fiducial and the reconstructed catalogue is an important way of verifying that the VDM algorithm is not only able to recover real groups, but also to maintain their characteristics. This means that when we compare the two catalogues on a group-by-group basis, the fractions of interlopers and missing galaxies modify group properties only below some tolerance level. The same has to hold also for the fiducial and reconstructed statistical distributions of these properties, when considering that the reconstructed catalogue contains fake groups and it fails to detect some groups. In this section, we show the properties of the redshift and velocity dispersion distributions for both the fiducial and reconstructed group catalogue.
5.3.1 The n(z) distribution
We analyzed how well the ``fiducial'' groups redshift
distribution
![]() is recovered by the distribution
is recovered by the distribution ![]() of the
groups found by the algorithm. We averaged the
of the
groups found by the algorithm. We averaged the ![]() distribution
over 20 independent VVDS-like mocks to obtain its mean
value, which is plotted as a continuous line in Fig. 7. In this
figure, the mean
distribution
over 20 independent VVDS-like mocks to obtain its mean
value, which is plotted as a continuous line in Fig. 7. In this
figure, the mean ![]() for the same
20 independent mocks is shown as black points, the vertical
bars being
the rms for the 20 mocks. The plot shows that the difference
between
for the same
20 independent mocks is shown as black points, the vertical
bars being
the rms for the 20 mocks. The plot shows that the difference
between ![]() and
and ![]() ,
despite the presence of fake
and/or missing groups in the VDM catalogue, is within the errors. A
,
despite the presence of fake
and/or missing groups in the VDM catalogue, is within the errors. A
![]() test between
the two mean distributions infers that
test between
the two mean distributions infers that ![]() .
We therefore conclude that the two n(z)
distributions are
statistically consistent with each other, even if there is a tendency
for there to be more VDM reconstructed groups at low redshift. We
repeated the same test using only groups with at least
5 members and
with
.
We therefore conclude that the two n(z)
distributions are
statistically consistent with each other, even if there is a tendency
for there to be more VDM reconstructed groups at low redshift. We
repeated the same test using only groups with at least
5 members and
with ![]() km s-1,
which are those groups for which we are
sure we can compute a reliable velocity dispersion, and we also found
in this case that
km s-1,
which are those groups for which we are
sure we can compute a reliable velocity dispersion, and we also found
in this case that ![]() and
and ![]() are consistent with
each other.
are consistent with
each other.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f8.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg160.png)
|
Figure 8: Comparison between virial (y axis) and VDM reconstructed (x axis) group velocity dispersion. Only two-way matches are considered in this plot. The upper panel shows the scatter plot, the lower shows the percentage error. Green and blue triangles are groups with at least 5 members, orange and purple squares groups with at least 8 members; green and orange points are single groups, while blue and purple symbols are the median (on x axis) and mean (on y axis) values in bins of the property on the x axis. Vertical error bars are rms of mean values. |
| Open with DEXTER | |
5.3.2 Velocity dispersion
For each VDM group, we measured the velocity dispersion ![]() of its
galaxies using Eq. (1),
correcting it as
indicated in Eq. (3).
Figure 8
compares the velocity dispersion in the
reconstructed groups (
of its
galaxies using Eq. (1),
correcting it as
indicated in Eq. (3).
Figure 8
compares the velocity dispersion in the
reconstructed groups (
![]() )
with the virial velocity
dispersion (
)
with the virial velocity
dispersion (
![]() quoted in the simulations) of the fiducial
groups in VVDS-like mocks on a group-by-group basis. Only two-way
matches are considered. The figure is divided into two panels
as in Fig. 4:
the upper part shows the
scatter plot, the lower the percentage error, computed as in
Fig. 4.
Green and blue triangles are
groups with at least 5 members, and both orange and purple
squares
represent groups with at least 8 members; green and orange
points are
single groups, while blue and purple symbols are the median (on x axis)
and mean (on y axis) values in bins of the
property on the x axis. Vertical error
bars are the rms of the mean values.
quoted in the simulations) of the fiducial
groups in VVDS-like mocks on a group-by-group basis. Only two-way
matches are considered. The figure is divided into two panels
as in Fig. 4:
the upper part shows the
scatter plot, the lower the percentage error, computed as in
Fig. 4.
Green and blue triangles are
groups with at least 5 members, and both orange and purple
squares
represent groups with at least 8 members; green and orange
points are
single groups, while blue and purple symbols are the median (on x axis)
and mean (on y axis) values in bins of the
property on the x axis. Vertical error
bars are the rms of the mean values.
This scatter plot shows the following: on a group-by-group
basis, for
![]() km s-1,
close to the intrinsic limit set by the
flux-limited nature of the VVDS catalogue, the correlation between
km s-1,
close to the intrinsic limit set by the
flux-limited nature of the VVDS catalogue, the correlation between
![]() and
and ![]() is such that
is such that ![]() overestimates
overestimates
![]() ,
but on average always by
,
but on average always by ![]() 30%
for groups with at least 5 members, while this overestimate is on
average
30%
for groups with at least 5 members, while this overestimate is on
average ![]() 10%
for groups with at least 8 members. As shown
in Sect. 3.2,
the velocity dispersion
10%
for groups with at least 8 members. As shown
in Sect. 3.2,
the velocity dispersion ![]() that one can
measure in groups within a VVDS-like data sample is not a
reliable estimator of
that one can
measure in groups within a VVDS-like data sample is not a
reliable estimator of ![]() for
for ![]() km s-1.
km s-1.
Besides the group-by-group comparison, it is also interesting
to
analyze the velocity dispersion distributions, thus including
unrecovered and fake groups in the fiducial and reconstructed
catalogues, respectively. Figure 9
compares
the ![]() and
and ![]() distributions (the solid
line and the black diamonds, respectively). The values on the y axis
are averaged over 20 VVDS-like mocks. The vertical bars
associated
with the
distributions (the solid
line and the black diamonds, respectively). The values on the y axis
are averaged over 20 VVDS-like mocks. The vertical bars
associated
with the ![]() points represent their rms over the 20 mocks. We note that the
areas below the two distributions differ. This
is mainly because for the
points represent their rms over the 20 mocks. We note that the
areas below the two distributions differ. This
is mainly because for the ![]() distribution we excluded
groups for which we were unable to measure
distribution we excluded
groups for which we were unable to measure ![]() ,
i.e. groups for
which we decided that
,
i.e. groups for
which we decided that ![]() .
This comparison indicates that
the two distribution agree for
.
This comparison indicates that
the two distribution agree for ![]() km s-1,
as confirmed by
a
km s-1,
as confirmed by
a ![]() test
between the two mean distributions for
test
between the two mean distributions for ![]() km s-1.
km s-1.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f9.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg167.png)
|
Figure 9:
Mean distribution of virial l.o.s. velocity dispersion (continuous
line), computed as the average over 20 VVDS-like mocks. The
mean
distribution of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f10.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg168.png)
|
Figure 10:
Normalized mean distribution of
|
| Open with DEXTER | |
As an additional test of the accuracy of the recovered ![]() distribution,
we compared it with the
distribution,
we compared it with the ![]() in mock
catalogues with the same flux limits as the VVDS-02h sample but
with 100% sampling rate (the M(100,0)
catalogues presented in Sect. 2.2), and
the
in mock
catalogues with the same flux limits as the VVDS-02h sample but
with 100% sampling rate (the M(100,0)
catalogues presented in Sect. 2.2), and
the ![]() of mock catalogues
with no flux limits (the complete light cones from which the
M(100,0) catalogues were extracted). In
Fig. 10,
we show the normalized mean
of mock catalogues
with no flux limits (the complete light cones from which the
M(100,0) catalogues were extracted). In
Fig. 10,
we show the normalized mean
![]() (black diamonds) for
(black diamonds) for ![]() km s-1.
It is
the same distribution as in Fig. 9,
but is
normalized by the total numbers of groups with
km s-1.
It is
the same distribution as in Fig. 9,
but is
normalized by the total numbers of groups with ![]() km s-1.
Overplotted green triangles represent the normalized mean
km s-1.
Overplotted green triangles represent the normalized mean
![]() of fiducial groups in M(100,0) mock catalogues,
and the orange crosses are the normalized mean
of fiducial groups in M(100,0) mock catalogues,
and the orange crosses are the normalized mean ![]() distribution
of fiducial groups in complete light cones of the
Millennium Simulation. For each distribution, the redshift range
considered is
distribution
of fiducial groups in complete light cones of the
Millennium Simulation. For each distribution, the redshift range
considered is ![]() .
For these normalized
distributions with
.
For these normalized
distributions with ![]() km s-1,
a
km s-1,
a ![]() test between the
test between the
![]() and the
and the ![]() for M(100,0) catalogues
implies that the two distributions are statistically in agreement. We
obtain the same result when we apply the same test to
for M(100,0) catalogues
implies that the two distributions are statistically in agreement. We
obtain the same result when we apply the same test to
![]() and
and ![]() for the complete
catalogues. This means that the
for the complete
catalogues. This means that the ![]() of the groups
reconstructed by our algorithm is unbiased with respect to the
of the groups
reconstructed by our algorithm is unbiased with respect to the
![]() of groups in the complete light cones.
of groups in the complete light cones.
We repeated the tests shown in Figs. 9 and 10 also using only groups with at least 5 members, and we found similar results.
As discussed in Sect. 4, one of the
primary goals
of the VDM is to be able to recover the virial l.o.s. velocity
dispersion of group galaxies, at least above some minimum
threshold. This is not achieved, for example, by other commonly used
group-finding algorithms, such as the FOF method (see Sect. 4). The
comparisons between the ![]() distributions of reconstructed
and fiducial groups presented in this
section show that this aim has been successfully obtained in a deep
redshift survey such as VVDS, at least up to z=1.
Moreover, the VVDS
redshift measurement error and sampling rate imposed an
a priori
lower limit to a reliable measurement of the l.o.s. velocity
dispersion of group galaxies (
distributions of reconstructed
and fiducial groups presented in this
section show that this aim has been successfully obtained in a deep
redshift survey such as VVDS, at least up to z=1.
Moreover, the VVDS
redshift measurement error and sampling rate imposed an
a priori
lower limit to a reliable measurement of the l.o.s. velocity
dispersion of group galaxies (
![]() km s-1,
see
Sect. 3.2).
We demonstrate in
Figs. 9
and 10
that the finding group algorithm that we used can not only recover a
reliable
km s-1,
see
Sect. 3.2).
We demonstrate in
Figs. 9
and 10
that the finding group algorithm that we used can not only recover a
reliable ![]() distribution above some minimum
distribution above some minimum ![]() ,
but
also does not worsen the minimum
,
but
also does not worsen the minimum ![]() threshold imposed by the
survey strategy itself. This result was achieved thanks to the
flexibility of the 6 VDM parameters. Each of them has a
specific role
in determining the choice of the group members, by means of an
intuitive localization of group barycenters (Phase I), a
reliable
estimate of the central richness (Phase II), and an
appropriate use of
group scaling laws (Phase III).
threshold imposed by the
survey strategy itself. This result was achieved thanks to the
flexibility of the 6 VDM parameters. Each of them has a
specific role
in determining the choice of the group members, by means of an
intuitive localization of group barycenters (Phase I), a
reliable
estimate of the central richness (Phase II), and an
appropriate use of
group scaling laws (Phase III).
5.4 Sampling rate
As we applied the algorithm to the VVDS-like mocks, we
optimized it
for the whole observed area (![]() 0.5 deg2
each), irrespective of
the varying sampling rate across the field. Nevertheless, we also
tested how both completeness and purity change if computed separately
in areas with very different sampling rate, covered by 1, 2,
or 4 passes of the spectrograph (hereafter called ``1p'',
``2p'', and ``4p''
areas). For this test, we assigned each group to the 1p, 2p, or 4p
area according to its RA-Dec position (computed as the median
value of RA and Dec of the member galaxies), even if it
extends over an area with either a sudden decrease or increase in the
sampling rate. Considering the whole redshift range
0.5 deg2
each), irrespective of
the varying sampling rate across the field. Nevertheless, we also
tested how both completeness and purity change if computed separately
in areas with very different sampling rate, covered by 1, 2,
or 4 passes of the spectrograph (hereafter called ``1p'',
``2p'', and ``4p''
areas). For this test, we assigned each group to the 1p, 2p, or 4p
area according to its RA-Dec position (computed as the median
value of RA and Dec of the member galaxies), even if it
extends over an area with either a sudden decrease or increase in the
sampling rate. Considering the whole redshift range ![]() ,
in the 4p area we find that
,
in the 4p area we find that ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() ,
while in
the (1+2)p areas
,
while in
the (1+2)p areas ![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() .
.
While the changes in C2,
P1, and P2
are within the error
bars, we measure a larger difference in C1
when we decrease the
number of spectrograph passes, i.e., the sampling rate. Analyzing the
dependence of C and P on group
richness, we can add that in the 4p
area completeness is higher even for ![]() .
We also note that in
4p area there is a higher overmerging, especially for
.
We also note that in
4p area there is a higher overmerging, especially for ![]() ,
while in the (1+2)p area fragmentation is increased
for
,
while in the (1+2)p area fragmentation is increased
for ![]() .
.
5.5 High purity parameters
With the best set of parameters, we can obtain from
VVDS-02h
data a group catalogue with high completeness, even though it has been
shown that only ![]() 50%
of groups is pure. This means that each
group identified by the algorithm has, on average, only a 50%
probability of being a real group. It may be useful to identify the
subsample of groups that has an even higher probability of being
real. Thus, we optimized the group-finding algorithm a second time, in
this case maximizing purity (but paying attention not to reduce the
new recovered group catalogue to a few ``super-secure'' groups). The
so-called high-purity parameter set was found to be
50%
of groups is pure. This means that each
group identified by the algorithm has, on average, only a 50%
probability of being a real group. It may be useful to identify the
subsample of groups that has an even higher probability of being
real. Thus, we optimized the group-finding algorithm a second time, in
this case maximizing purity (but paying attention not to reduce the
new recovered group catalogue to a few ``super-secure'' groups). The
so-called high-purity parameter set was found to be
- -
-
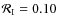 h-1 Mpc
h-1 Mpc
- -
-
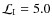 h-1 Mpc
h-1 Mpc
- -
-
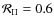 h-1 Mpc
h-1 Mpc
- -
-
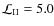 h-1 Mpc
h-1 Mpc
- -
- r=0.55 h-1 Mpc
- -
- l=14.0 h-1 Mpc.
Table 2
shows C and P for the
high-purity parameter set. Necessarily, C
is very low, but now
each group identified by the algorithm has ![]() 70% of probability
of being real, and the interlopers fraction fI
decreases from
70% of probability
of being real, and the interlopers fraction fI
decreases from ![]() 40%
to
40%
to ![]() 25% with
respect to the one obtained with the best set of
parameters (see Table 1).
25% with
respect to the one obtained with the best set of
parameters (see Table 1).
Table 2:
Quality statistics (C1, C2,
P1, P2,
![]() ,
and
,
and ![]() ,
see text for details) of the group catalogue reconstructed by the
algorithm with the high-purity parameter
set, for two different redshift bins and the whole redshift
range, considering groups with
,
see text for details) of the group catalogue reconstructed by the
algorithm with the high-purity parameter
set, for two different redshift bins and the whole redshift
range, considering groups with ![]() .
.
6 VVDS-02h field group catalogue
We applied the group-finding algorithm to the VVDS-02h sample
described in Sect. 2.1,
using the best set of
parameters. We defined the redshift and the position in the RA-Dec
plane of each group as the median values of redshift, right
ascension and declination of the group members. Figure 11 shows the
redshift distribution of the identified
groups, with different line styles for different cuts in group
richness, as indicated in the figure. It is clear that beyond ![]() there is a significant drop in the number of recovered groups,
irrespective of their richness, as expected from
Fig. 2.
This drop in the redshift distribution
may be partly related also to the choice of optimizing the algorithm
only up to z=1 (see Sect. 5.2).
We also
applied the VDM to our galaxy sample using the high-purity
set
of parameters. With the best set of parameters, the
algorithm
identified 318 groups with 2 or more members in the
redshift range
there is a significant drop in the number of recovered groups,
irrespective of their richness, as expected from
Fig. 2.
This drop in the redshift distribution
may be partly related also to the choice of optimizing the algorithm
only up to z=1 (see Sect. 5.2).
We also
applied the VDM to our galaxy sample using the high-purity
set
of parameters. With the best set of parameters, the
algorithm
identified 318 groups with 2 or more members in the
redshift range
![]() ,
one third of them having also been detected
with the high-purity set. The identified groups
comprise
,
one third of them having also been detected
with the high-purity set. The identified groups
comprise ![]() 19%
of the galaxies in our sample. Comparing this percentage with
the fraction of galaxies that reside in groups in VVDS-like mock
catalogues, we found that it is consistent with both the fraction of
galaxies residing in fiducial groups (
19%
of the galaxies in our sample. Comparing this percentage with
the fraction of galaxies that reside in groups in VVDS-like mock
catalogues, we found that it is consistent with both the fraction of
galaxies residing in fiducial groups (![]() 20%) and the
percentage of galaxies residing in reconstructed
groups (
20%) and the
percentage of galaxies residing in reconstructed
groups (![]() 22%).
22%).
Table 3:
Number of VVDS-02h groups reconstructed by the
algorithm using the best set of parameters in
VVDS-02h field,
for ![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f11.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg198.png)
|
Figure 11: The redshift distribution of groups in the VVDS-02h sample, found using the best set of parameters. Different line styles are for different cuts in group richness, as indicated. The total number of groups with the corresponding richness is quoted in the labels, for two different redshift ranges. |
| Open with DEXTER | |
For each group, we estimated the l.o.s. velocity dispersion ![]() .
We used the gapper method, as described in
Sect. 3.2,
and we corrected it for the redshift
measurement error by subtracting it in quadrature as in
Eq. (3).
We set
.
We used the gapper method, as described in
Sect. 3.2,
and we corrected it for the redshift
measurement error by subtracting it in quadrature as in
Eq. (3).
We set ![]() km s-1
for those groups
with a measured
km s-1
for those groups
with a measured ![]() (from Eq. (1))
lower than
the redshift error.
(from Eq. (1))
lower than
the redshift error. ![]() 25%
of groups with
25%
of groups with ![]() km s-1
were detected by the algorithm also with the high-purity
parameter set.
km s-1
were detected by the algorithm also with the high-purity
parameter set.
Given the small value of the parameter r, we note that, when driving the projected dimension of the search cylinder in Phase III (see Sect. 4.3), the typical projected radius within which the full set of group members is selected is always <1 h-1 Mpc.
Detailed group catalogue statistics are shown in Table 3. The number of groups found in VVDS-02h field is quoted. Different rows represent different values of velocity dispersion, different columns corresponding to different richnesses. The numbers in brackets indicate the number of groups that have been identified by the algorithm also with the high-purity set of parameters (even if with fewer members).
We tested the reliability of the reconstructed catalogue by recomputing the groups excluding galaxies with flag = 2 and 9, i.e. using only galaxies whose redshift has a high likelihood (>95%) of being correct. With respect to our original group catalogue, we verified that 80% (/77%/75%) of the groups with at least 5 (/4/3) members are still recovered. This implies that for these recovered groups the galaxies with flag = 2 and 9 were not in the seed of the group, i.e. in the first set of galaxies recovered in Phase I of the algorithm (see Sect. 4.1).
Table 4
lists all the groups identified
in the redshift window ![]() .
We note that the quoted
number of members has to be assumed to be a lower limit to the true
richness, as the sampling rate of our survey is not 100%. The
groups
labeled with a star near their ID are those also recovered when using
only galaxies with flag = 3 and 4. We apply
this label only to groups
with at least 3 members. The group members are presented in
Table 5.
We note that the galaxy ID is the
same used to identify galaxies in the public VVDS
release
.
We note that the quoted
number of members has to be assumed to be a lower limit to the true
richness, as the sampling rate of our survey is not 100%. The
groups
labeled with a star near their ID are those also recovered when using
only galaxies with flag = 3 and 4. We apply
this label only to groups
with at least 3 members. The group members are presented in
Table 5.
We note that the galaxy ID is the
same used to identify galaxies in the public VVDS
release![]() .
.
In Fig. 12, we present the two-dimensional VVDS galaxy distribution, with galaxy positions projected in both RA and redshift. Each plot represents a different redshift bin, as indicated on the y axis. Black dots are field galaxies, while coloured dots are group members (blue dots are pair members, green are triplet members, orange are quartet members and red dots are galaxies included in groups of 5 or more members).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f12a.ps}\par\includegraphics[width=8cm,clip]{11831f12b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg200.png)
|
Figure 12:
Two-dimensional VVDS galaxy distribution as a function of
Right Ascension and redshift (points are compressed on the Declination
dimension). Each plot shows a different redshift bin (
|
| Open with DEXTER | |
Table 4:
List of groups recovered in the VVDS-02h field in the range ![]() .
(This table is available in electronic form at the CDS).
.
(This table is available in electronic form at the CDS).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f13.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg201.png)
|
Figure 13: As in Fig. 9, but in this case the velocity dispersion distribution of VVDS-02h field groups is also shown with red triangles. |
| Open with DEXTER | |
Table 5: List of group galaxies belonging to the groups listed in Table 4. (This table is available in electronic form at the CDS).
6.1 L.o.s. velocity dispersion of group galaxies
It is interesting to verify that the real universe is similar to the simulated one. Now we compare the VVDS catalogue with the Millennium-based mock catalogues.
We compared the ![]() distributions of real and simulated
groups. Figure 13
shows the
distributions of real and simulated
groups. Figure 13
shows the ![]() distribution
for all VVDS-02h groups in the redshift range
distribution
for all VVDS-02h groups in the redshift range ![]() (red triangles) and the
(red triangles) and the ![]() distribution for
VVDS-like mock catalogues. As in Fig. 9,
the continuous line is the distribution of
distribution for
VVDS-like mock catalogues. As in Fig. 9,
the continuous line is the distribution of ![]() for fiducial groups, while black points represent
the mean distribution
for reconstructed groups, vertical bars being the
rms of
the 20 mock catalogues. In this plot, we consider the
for fiducial groups, while black points represent
the mean distribution
for reconstructed groups, vertical bars being the
rms of
the 20 mock catalogues. In this plot, we consider the ![]() measured
with the gapper method (for both mocks and real data) and not
the virial velocity dispersion. We exclude groups
with measured
measured
with the gapper method (for both mocks and real data) and not
the virial velocity dispersion. We exclude groups
with measured
![]() equal
to 0, because this value indicates that we have not
been able to measure it due to the redshift measurement error (see
Eq. (3)).
This is the reason why the area under
equal
to 0, because this value indicates that we have not
been able to measure it due to the redshift measurement error (see
Eq. (3)).
This is the reason why the area under
![]() in the plot is larger than the area under the other
distributions. In this figure, we note the consistency between the
in the plot is larger than the area under the other
distributions. In this figure, we note the consistency between the
![]() distributions
of true and mock group catalogues, at least
for
distributions
of true and mock group catalogues, at least
for ![]() km s-1.
km s-1.
The relatively large number of groups for which the velocity
dispersion estimated using Eq. (3) is
formally
negative is probably caused by our not taking into account possible
dependences of the mean redshift error on the properties of the
galaxies (i.e. magnitude, presence of emission lines etc.). It is most
likely that for many of these groups the redshift error associated
with their galaxy members is somewhat smaller than the adopted average
value (275 km s-1).
Nevertheless, we are reassured by none of the groups
with ![]() having
having ![]() .
.
6.2 Comparison with other group catalogues in the same field
Several group catalogues have already been compiled from different types of observations and with different methods in the sky area covered by the VVDS-02h field. For example, X-ray clusters have been identified from XMM-Newton images and then spectroscopically confirmed (Willis et al. 2005b; Pierre et al. 2006; Andreon et al. 2005; Bremer et al. 2006; Andreon et al. 2004b; Valtchanov et al. 2004; Willis et al. 2005a). The matched-filter technique has also been used (Olsen et al. 2007) in addition to a weak lensing search (Gavazzi & Soucail 2007) and structure identification using photometric redshifts (Mazure et al. 2007). All of these latter methods have been applied to photometric data from CFHTLS.
Among the X-ray clusters of the XMM-LSS, only 8 clusters fall
in the
VVDS-02h field area in the redshift bin ![]() :
XLSSC
005, XLSSC 013, and XLSSC 025 from the C1 catalogue, XLSSC 038 from
the C2 catalogue and then the clusters a, b, c, and
d
from the C3 catalogue (see Table 3 in Pierre
et al. 2006). We find
that both clusters b and c have
a counterpart in our VDM
catalogue (with 6 and 8 detected members,
respectively) with an almost
perfect match in their barycenters. Clusters XLSSC 013 and
XLSSC 025
have possible counterparts at the same z
(with 4 and 3 members,
respectively), but their barycenters in RA-Dec have a shift of
:
XLSSC
005, XLSSC 013, and XLSSC 025 from the C1 catalogue, XLSSC 038 from
the C2 catalogue and then the clusters a, b, c, and
d
from the C3 catalogue (see Table 3 in Pierre
et al. 2006). We find
that both clusters b and c have
a counterpart in our VDM
catalogue (with 6 and 8 detected members,
respectively) with an almost
perfect match in their barycenters. Clusters XLSSC 013 and
XLSSC 025
have possible counterparts at the same z
(with 4 and 3 members,
respectively), but their barycenters in RA-Dec have a shift of
![]() 200 h-1 kpc.
Inspecting these two groups in more detail, we
find that the possible XLSSC 025 counterpart is dominated by a
massive
galaxy distant from the XLSSC 025 barycenter
200 h-1 kpc.
Inspecting these two groups in more detail, we
find that the possible XLSSC 025 counterpart is dominated by a
massive
galaxy distant from the XLSSC 025 barycenter ![]() 100 h-1 kpc,
which indicates that a closer match would have been obtained if we had
computed a mass-weighted barycenter. In contrast, for a XLSSC 013
counterpart we do not identify any dominant galaxy. This shift of
100 h-1 kpc,
which indicates that a closer match would have been obtained if we had
computed a mass-weighted barycenter. In contrast, for a XLSSC 013
counterpart we do not identify any dominant galaxy. This shift of
![]() 200 h-1 kpc
could also be caused by the distribution the
distances between the barycenters of VDM groups and their
corresponding fiducial groups being a Gaussian centered at
200 h-1 kpc
could also be caused by the distribution the
distances between the barycenters of VDM groups and their
corresponding fiducial groups being a Gaussian centered at ![]() 0
with a scatter of
0
with a scatter of ![]() 200 h-1 kpc.
Finally, we do not find
counterparts for XLSSC 005, XLSSC 038, a,
and d in our
catalogue. They fall inside our low sampling rate areas (i.e., those
covered only by 1 or 2 passes of the spectrograph),
and an additional
inspection confirmed that the sampling rate in those regions does not
allow our algorithm to find at least two galaxies inside the volume
enclosed by the Phase I cylinder.
200 h-1 kpc.
Finally, we do not find
counterparts for XLSSC 005, XLSSC 038, a,
and d in our
catalogue. They fall inside our low sampling rate areas (i.e., those
covered only by 1 or 2 passes of the spectrograph),
and an additional
inspection confirmed that the sampling rate in those regions does not
allow our algorithm to find at least two galaxies inside the volume
enclosed by the Phase I cylinder.
We concluded this comparison with XMM-LSS detections by
inspecting the
relation between optical and X-ray properties of the four groups for
which there exists a (possible) XMM counterpart. In particular, we
considered the relation between the X-ray luminosity ![]() presented
in Table 5 of Pierre
et al. (2006) and the velocity dispersions
presented
in Table 5 of Pierre
et al. (2006) and the velocity dispersions ![]() that we
measured. We verified that groups XLSSC 013, b and c
have
a
that we
measured. We verified that groups XLSSC 013, b and c
have
a ![]() -
-![]() relation in close agreement with the linear fit in
the plane
relation in close agreement with the linear fit in
the plane ![]() -
-![]() presented in Fig. 13 of
Popesso et al. (2005).
For group XLSSC 025, we measure a
presented in Fig. 13 of
Popesso et al. (2005).
For group XLSSC 025, we measure a ![]() that would be too low for its
quoted
that would be too low for its
quoted ![]() ,
according to the
indicated relation, but as its
,
according to the
indicated relation, but as its ![]() is of the order of 200 km s-1
it
does not reside in the
is of the order of 200 km s-1
it
does not reside in the ![]() range
that we consider to be reliably
measured.
range
that we consider to be reliably
measured.
We note that our richest groups (10 groups with at
least 7 members) do not correspond well to XMM-LSS clusters,
except one that is the
counterpart of the X-ray selected group c. There
are at least
three reasons why an optical group may not have been detected in
X-rays: a) it may fall on the boundaries of a XMM-LSS pointing, thus
in a region where the X-ray detector is affected by vignetting;
b) it may have a redshift much higher than the mean z
reachable by
the performed X-ray observations; c) it may have a low surface
brightness, corresponding to a shallow potential well of the mass
distribution, thus making X-ray detection more difficult. We inspected
our richest groups, and found that all of them fall in at least one of
these three categories. In particular, we verified that the N(z)distribution
of all X-ray clusters in the above-cited works is peaked
at ![]() ,
while the N(z) distribution of
our richest groups is
quite flat and reaches
,
while the N(z) distribution of
our richest groups is
quite flat and reaches ![]() ,
there being 5 groups at
,
there being 5 groups at
![]() .
At least half of our richest groups also do not have a
dominant member, that is a galaxy with luminosity and/or stellar mass
much higher than the others. The VVDS-02h field sampling rate could be
enough to explain this lack of dominant galaxies, but in principle we
can not reject the hypothesis that a dominant galaxy in (some of)
these groups may not exist, thus that these groups have a low X-ray
surface brightness.
.
At least half of our richest groups also do not have a
dominant member, that is a galaxy with luminosity and/or stellar mass
much higher than the others. The VVDS-02h field sampling rate could be
enough to explain this lack of dominant galaxies, but in principle we
can not reject the hypothesis that a dominant galaxy in (some of)
these groups may not exist, thus that these groups have a low X-ray
surface brightness.
We compared our group catalogue with those of Gavazzi & Soucail (2007), Olsen et al. (2007), and Mazure et al. (2007).
Among the about 20 clusters in Olsen
et al. (2007) inside the sky area
and redshift range that we have explored, roughly half fall inside
regions with too low sampling rate for our Phase I cylinder to be able
to detect at least a pair; two of them (ID 30 and 42) fall
very near
in redshift to two wide structures at ![]() and
and ![]() ,
within which our algorithm detects (possibly fragmenting them) a few
groups. Finally, considering the depth of the redshift bins in which
Olsen's groups can reside (
,
within which our algorithm detects (possibly fragmenting them) a few
groups. Finally, considering the depth of the redshift bins in which
Olsen's groups can reside (
![]() )
due to the use of
photometric redshifts, we find that for 5 groups in Olsen's
catalogue
there exists a counterpart in our catalogue.
)
due to the use of
photometric redshifts, we find that for 5 groups in Olsen's
catalogue
there exists a counterpart in our catalogue.
Among the about 30 structures detected by Mazure et al. (2007)
in the
redshift range 0.2<z<1.0, we find that
about 20 fall inside regions
with too low a sampling rate for our finding group algorithm (13 of
which are in the 1 pass area); a few of them reside in redshift slices
(![]() ,
,
![]() ,
and
,
and ![]() )
where a wide (in RA-Dec)
structure is also present, which has possibly been fragmented by our
algorithm, producing in our catalogue more than one
counterpart. Finally, three of the structures detected by
Mazure et al. (2007)
have a possible direct counterpart in our catalogue
(general ID 5, 19 and 21, see Table 3 in Mazure et al. 2007).
)
where a wide (in RA-Dec)
structure is also present, which has possibly been fragmented by our
algorithm, producing in our catalogue more than one
counterpart. Finally, three of the structures detected by
Mazure et al. (2007)
have a possible direct counterpart in our catalogue
(general ID 5, 19 and 21, see Table 3 in Mazure et al. 2007).
Finally, the 3 structures detected by Gavazzi & Soucail (2007) that fall inside the VVDS-02h field are in very low sampling rate areas, thus in regions where our algorithm did not detect any group.
In this comparison, we also took into account that in the
CFHTLS data
used in the three above-mentioned works there are masked sky regions
that have not been used for group finding, as shown for example in
Fig. 1 in Mazure
et al. (2007) and Fig. 9 in Olsen et al. (2007). We
find
that ![]() 5% of our
groups in the range
5% of our
groups in the range ![]() fall
in those regions. Moreover, we observe that roughly half of this
masked area falls inside the region that in the VVDS-02h field has the
highest sampling rate (the central area highlighted in Fig. 1), and
that this higher-sampling region covers
only
fall
in those regions. Moreover, we observe that roughly half of this
masked area falls inside the region that in the VVDS-02h field has the
highest sampling rate (the central area highlighted in Fig. 1), and
that this higher-sampling region covers
only ![]() 25% of the
VVDS-02h field. Thus, the percentage of our
groups falling in the masked areas increases to
25% of the
VVDS-02h field. Thus, the percentage of our
groups falling in the masked areas increases to ![]() 8% for groups
with at least 3 members and to 20% for our
10 richest groups (those
with at least 7 members).
8% for groups
with at least 3 members and to 20% for our
10 richest groups (those
with at least 7 members).
7 The U - B colour of group galaxies
After producing a catalogue of groups at high z, we
wish to apply it
to study the dependence of galaxy properties on environment and its
evolution with cosmic time. More specifically, we investigate whether
the physical properties of group galaxies differ from those of all
galaxies, up to ![]() .
Are the relations that we see in groups at
low redshift already present at
.
Are the relations that we see in groups at
low redshift already present at ![]() ? Is there any unambiguous
signature of time evolution in known scaling relations characterizing
galaxies in cluster environments? In this paper, we do not carry on
an exhaustive analysis of this topic, which is possibly the goal of
future work. The main aim of this paper is to present the VVDS-02h
field group catalogue and discuss its reliability. In this section, we
show how our group catalogue can be used for studies related to
environmental effects on galaxy properties on group scales.
? Is there any unambiguous
signature of time evolution in known scaling relations characterizing
galaxies in cluster environments? In this paper, we do not carry on
an exhaustive analysis of this topic, which is possibly the goal of
future work. The main aim of this paper is to present the VVDS-02h
field group catalogue and discuss its reliability. In this section, we
show how our group catalogue can be used for studies related to
environmental effects on galaxy properties on group scales.
As we wish to investigate the redshift evolution of the
properties of
group galaxies, we study a group sample that is homogeneous at
all z. We thus require that the groups we
use for this analysis have at
least two members brighter than a luminosity limit that allows us to
be complete up to z=1. This luminosity limit
evolves with redshift.
Following roughly the evolution of M*,
the characteristic
magnitude of the luminosity function (Ilbert
et al. 2005), we set this
limit to be ![]() .
Our ``group galaxy'' sample consists
of galaxies brighter than this limit, in groups with at least two
members brighter than this limit itself. Moreover, we define a
``total'' galaxy sample considering all galaxies brighter than this
limit (including those also in groups).
.
Our ``group galaxy'' sample consists
of galaxies brighter than this limit, in groups with at least two
members brighter than this limit itself. Moreover, we define a
``total'' galaxy sample considering all galaxies brighter than this
limit (including those also in groups).
After defining the sample, as a first step we studied the
fraction of
``blue'' galaxies (![]() from now on) in both the group and total
samples, in the range
from now on) in both the group and total
samples, in the range ![]() .
The general blueing of
cluster galaxy population for increasing redshift, first shown by
Butcher & Oemler (1978)
and Butcher & Oemler (1984)
and known as the Butcher-Oemler
effect, has been widely confirmed by subsequent studies (see for
example Margoniner
et al. 2001; Gerke et al. 2007;
De
Propris et al. 2003). Nevertheless, nowadays there
is no full
agreement about the origin of this blueing. It may be related to
environmental effects (e.g. Dressler
et al. 1997), but has also been
proposed to be consistent with the overall ageing of all galaxies,
irrespective of their environment (Andreon et al. 2004a,2006).
.
The general blueing of
cluster galaxy population for increasing redshift, first shown by
Butcher & Oemler (1978)
and Butcher & Oemler (1984)
and known as the Butcher-Oemler
effect, has been widely confirmed by subsequent studies (see for
example Margoniner
et al. 2001; Gerke et al. 2007;
De
Propris et al. 2003). Nevertheless, nowadays there
is no full
agreement about the origin of this blueing. It may be related to
environmental effects (e.g. Dressler
et al. 1997), but has also been
proposed to be consistent with the overall ageing of all galaxies,
irrespective of their environment (Andreon et al. 2004a,2006).
According to our criteria, a galaxy is ``blue'' if it has a
colour ![]() .
This threshold has been chosen because it roughly corresponds
to the minimum (i.e. the green valley) in the bimodal U-B colour
distribution. This colour cut was kept constant at all redshifts
because we found that the green valley colour does not evolve much in
the z range considered. For the computation of the U-
and B-band
absolute magnitudes, we refer the reader to Ilbert
et al. (2005).
.
This threshold has been chosen because it roughly corresponds
to the minimum (i.e. the green valley) in the bimodal U-B colour
distribution. This colour cut was kept constant at all redshifts
because we found that the green valley colour does not evolve much in
the z range considered. For the computation of the U-
and B-band
absolute magnitudes, we refer the reader to Ilbert
et al. (2005).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f14.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg212.png)
|
Figure 14:
Fraction of
blue galaxies (
|
| Open with DEXTER | |
Since our goal is to study ![]() as a function of redshift, we
first verified that the failure rate in redshift measurement does not
depend on redshift for specific galaxy colours. We assigned a
``photometric type'' to each galaxy according to the scheme proposed by
Zucca et al. (2006).
The classification is carried out by fitting
the spectral energy distribution (SED) of galaxies to six templates
(four
observed spectra, Coleman
et al. 1980, and two starburts SEDs,
Bruzual & Charlot 1993).
We then proceeded as in Franzetti
et al. (2007), by
performing a bimodal classification. We considered E/S0 and early
spirals as ``early type'', and late-type spirals, irregular and
starburst types as ``late-type''. The relation between this
classification scheme and the colour U-B
that we used to compute
as a function of redshift, we
first verified that the failure rate in redshift measurement does not
depend on redshift for specific galaxy colours. We assigned a
``photometric type'' to each galaxy according to the scheme proposed by
Zucca et al. (2006).
The classification is carried out by fitting
the spectral energy distribution (SED) of galaxies to six templates
(four
observed spectra, Coleman
et al. 1980, and two starburts SEDs,
Bruzual & Charlot 1993).
We then proceeded as in Franzetti
et al. (2007), by
performing a bimodal classification. We considered E/S0 and early
spirals as ``early type'', and late-type spirals, irregular and
starburst types as ``late-type''. The relation between this
classification scheme and the colour U-B
that we used to compute ![]() is monotonic, bluer colours
being associated with ``late type''
templates. In particular, our ``early type'' population constitutes
>90% of the galaxies with U-B>1.
We computed the ``late type''
galaxy fraction in both our spectroscopic sample and in the
photometric parent catalogue, in three redshift bins in the range
is monotonic, bluer colours
being associated with ``late type''
templates. In particular, our ``early type'' population constitutes
>90% of the galaxies with U-B>1.
We computed the ``late type''
galaxy fraction in both our spectroscopic sample and in the
photometric parent catalogue, in three redshift bins in the range
![]() (using photometric redshifts for the parent
catalogue, see Sect. 2.1
for their determination). As
already found by Franzetti
et al. (2007), who carried out a similar
analysis on wider redshift intervals up to
(using photometric redshifts for the parent
catalogue, see Sect. 2.1
for their determination). As
already found by Franzetti
et al. (2007), who carried out a similar
analysis on wider redshift intervals up to ![]() ,
the ``late type''
fraction is 3% higher in the spectroscopic sample and this
increment does not depend on redshift. This result implies that any
trend of
,
the ``late type''
fraction is 3% higher in the spectroscopic sample and this
increment does not depend on redshift. This result implies that any
trend of ![]() with redshift is not caused by a measurement bias in
our sample.
with redshift is not caused by a measurement bias in
our sample.
Figure 14
shows ![]() for the group galaxies
(blue triangles) in three different redshift bins:
for the group galaxies
(blue triangles) in three different redshift bins: ![]() ,
,
![]() ,
and
,
and ![]() .
The vertical
error bars are the
.
The vertical
error bars are the ![]() confidence levels associated with
confidence levels associated with ![]() ,
computed with the usual approximation of the formula for binomial
statistics given in Gehrels
(1986) of
,
computed with the usual approximation of the formula for binomial
statistics given in Gehrels
(1986) of ![]() ,
where
,
where ![]() and n is the total number of galaxies in the
redshift bin.
and n is the total number of galaxies in the
redshift bin.
As reference, we plot the linear fit of the three points as a
blue
line, while the upper black line is the linear fit for ![]() computed
within the ``total'' sample. The fraction
computed
within the ``total'' sample. The fraction ![]() is clearly lower in
groups than in the total sample. The slopes of the two fits and their
is clearly lower in
groups than in the total sample. The slopes of the two fits and their
![]() confidence
levels are
confidence
levels are ![]() and
and ![]() for the group and total
sample, respectively. Although they both
differ significantly from zero, and the group slope is steeper, they
are compatible with each other, the group sample slope being steeper
only at a
for the group and total
sample, respectively. Although they both
differ significantly from zero, and the group slope is steeper, they
are compatible with each other, the group sample slope being steeper
only at a ![]() significance level. At this stage of the
investigation, we are only able to confirm the different overall value
of
significance level. At this stage of the
investigation, we are only able to confirm the different overall value
of ![]() between group galaxies and the total sample, but not their
possible different evolution. We verified that these results are
insensitive to any variation in the U-B
threshold adopted to define
blue galaxies (by
between group galaxies and the total sample, but not their
possible different evolution. We verified that these results are
insensitive to any variation in the U-B
threshold adopted to define
blue galaxies (by ![]() 0.05 mag).
We also found that they did not
change significantly when we implemented a colour cut that depends on
luminosity, following the mild dependence on magnitudes of the green
valley locus. Although we did not detect any redshift dependence of
the green valley locus up to z=1, we also allowed
the colour cut to
vary by 0.1 mag redward for any redshift decrease of dz=1.0
(as
suggested by Blanton 2006
and adopted by
Gerke et al. 2007).
Even in this case, the two slopes
differ appreciably from zero, and the difference between them is
significant at the
0.05 mag).
We also found that they did not
change significantly when we implemented a colour cut that depends on
luminosity, following the mild dependence on magnitudes of the green
valley locus. Although we did not detect any redshift dependence of
the green valley locus up to z=1, we also allowed
the colour cut to
vary by 0.1 mag redward for any redshift decrease of dz=1.0
(as
suggested by Blanton 2006
and adopted by
Gerke et al. 2007).
Even in this case, the two slopes
differ appreciably from zero, and the difference between them is
significant at the ![]()
![]() level.
level.
We compared our results with those presented by
Gerke et al.
(2007), who studied the fraction of blue galaxies
in both groups and the field within different subsamples extracted
from the DEEP2 data set. In their sample I, that with a selection most
similar to ours, they found that ![]() is lower in groups than in the
field, but they detected significant evolution in
is lower in groups than in the
field, but they detected significant evolution in ![]() with z in
neither groups nor the field. In all cases, evolutionary effects are
much more difficult to quantify in that sample since the redshift
range as well as the luminosity range covered is narrower with respect
to that explored in this study.
with z in
neither groups nor the field. In all cases, evolutionary effects are
much more difficult to quantify in that sample since the redshift
range as well as the luminosity range covered is narrower with respect
to that explored in this study.
Our results agree with those presented by Iovino et al. (2010),
who
studied the evolution of ![]() in groups and the field within the
zCOSMOS-10k sample (see also, for completeness, the analysis of
Kovac et al. 2010,
concerning the fraction of early-type
galaxies in groups). This agreement is based on the comparison with
their Sample II, that with a luminosity cut most similar to ours, and
it holds for both the group and the total sample. Interestingly,
Iovino et al. (2010)
find that in their luminosity limited sample
galaxy colour still depends on environment at
in groups and the field within the
zCOSMOS-10k sample (see also, for completeness, the analysis of
Kovac et al. 2010,
concerning the fraction of early-type
galaxies in groups). This agreement is based on the comparison with
their Sample II, that with a luminosity cut most similar to ours, and
it holds for both the group and the total sample. Interestingly,
Iovino et al. (2010)
find that in their luminosity limited sample
galaxy colour still depends on environment at ![]() (with a trend
similar to what we find in this work), but at the same redshift they
do not converge to the same conclusion when the blue fraction is
recovered from a (stellar) mass limited sample (
(with a trend
similar to what we find in this work), but at the same redshift they
do not converge to the same conclusion when the blue fraction is
recovered from a (stellar) mass limited sample (
![]() ).
They explain this result by suggesting that red galaxies of
these stellar masses, already in place at
).
They explain this result by suggesting that red galaxies of
these stellar masses, already in place at ![]() ,
may be produced by
internal mechanisms of evolution, on which environment has no
influence. We refer the reader to Iovino
et al. (2010) for more
details.
,
may be produced by
internal mechanisms of evolution, on which environment has no
influence. We refer the reader to Iovino
et al. (2010) for more
details.
Cucciati et al.
(2006) carried on a similar analysis using the same
VVDS-02h data set that we use in this work. They studied the
colour-density relation up to z=1.5, with the local
density computed
within Gaussian filters with ![]() h-1 Mpc.
They found that
the colour-density relation becomes weaker for increasing redshift
(the evolution of
h-1 Mpc.
They found that
the colour-density relation becomes weaker for increasing redshift
(the evolution of ![]() being faster in high densities), and that at
being faster in high densities), and that at
![]() no
significant colour-density relation is detected, for
galaxies with
no
significant colour-density relation is detected, for
galaxies with ![]() (that is equivalent to the threshold we
use in this work). Taken at face value, our results are not compatible
with these previous findings, as we find that at
(that is equivalent to the threshold we
use in this work). Taken at face value, our results are not compatible
with these previous findings, as we find that at ![]() ,
,
![]() still
differs between groups and the total sample. This difference can be
explained by our exploring higher densities/smaller scales
(<1 h-1 Mpc,
see Sect. 6).
For example,
several studies in the literature propose that environmental effects
on large scales are only a weaker residual of those acting on smaller
scales (e.g. Blanton
et al. 2006; Kauffmann et al. 2004).
The same hypothesis
is suggested by Cooper
et al. (2007), when comparing the
colour-density relation found in the DEEP2 data set with the one
presented in Cucciati
et al. (2006). They still find a colour-density
relation at
still
differs between groups and the total sample. This difference can be
explained by our exploring higher densities/smaller scales
(<1 h-1 Mpc,
see Sect. 6).
For example,
several studies in the literature propose that environmental effects
on large scales are only a weaker residual of those acting on smaller
scales (e.g. Blanton
et al. 2006; Kauffmann et al. 2004).
The same hypothesis
is suggested by Cooper
et al. (2007), when comparing the
colour-density relation found in the DEEP2 data set with the one
presented in Cucciati
et al. (2006). They still find a colour-density
relation at ![]() ,
but on smaller scales than those investigated by
Cucciati et al. (2006).
,
but on smaller scales than those investigated by
Cucciati et al. (2006).
A direct comparison of results obtained on the basis of
heterogeneous
definitions of the local environment (as for example density field
maxima as opposed to groups) is not straightforward.
Cooper et al. (2007)
showed, for example, that the evolution of
the colour-density relation is continuous in the range 0.4<z<1.3,
while Gerke
et al. (2007), who used the same DEEP2 data set
but a different definition of environment based on groups, found that
the evolution of ![]() in groups is flat in the range 0.7<z<1.0,
and
steepens for 1.0<z<1.3. Nevertheless,
the two works agree that at
in groups is flat in the range 0.7<z<1.0,
and
steepens for 1.0<z<1.3. Nevertheless,
the two works agree that at
![]() the
colour-density relation seems to disappear. No need to
emphasize that the physics associated with different environments has
still to be fully understood.
the
colour-density relation seems to disappear. No need to
emphasize that the physics associated with different environments has
still to be fully understood.
A direct comparison of our results with those presented in
other works
up to ![]() is not trivial. Interpretation is hampered by the the
non-homogeneity of group catalogues selected according to different
selection criteria. As a consequence, the picture emerging from these
studies is complex and sometimes even contradictory. As we intend only
to provide a general idea of the kind of studies that can be
potentially carried out with our group sample, we do not enter into
detail. We rather refer the reader to Poggianti
et al. (2006) and
Andreon et al. (2006)
for a more in-depth discussion about the status of
the art and the problems related to uncontrolled selection effects.
is not trivial. Interpretation is hampered by the the
non-homogeneity of group catalogues selected according to different
selection criteria. As a consequence, the picture emerging from these
studies is complex and sometimes even contradictory. As we intend only
to provide a general idea of the kind of studies that can be
potentially carried out with our group sample, we do not enter into
detail. We rather refer the reader to Poggianti
et al. (2006) and
Andreon et al. (2006)
for a more in-depth discussion about the status of
the art and the problems related to uncontrolled selection effects.
As a second step, we examined the behavior of ![]() in groups
characterized by different degrees of richness. There is still no
agreement in the literature about the dependence of
in groups
characterized by different degrees of richness. There is still no
agreement in the literature about the dependence of ![]() on cluster
properties. For example,
on cluster
properties. For example, ![]() is found to both depend on cluster
richness (Margoniner
et al. 2001; Goto et al. 2003), or
be independent of
it, as well as of l.o.s. velocity dispersion and mass
(Goto 2005;
Popesso
et al. 2007b; De Propris et al. 2004).
To address this
issue, we associated each group with the number of members found by
the algorithm. Nevertheless, due to the survey characteristics
(sampling rate, spectra signal to noise ratio, etc.), the observed
number has to be corrected to recover the real number of members
within the flux limit of the survey (
is found to both depend on cluster
richness (Margoniner
et al. 2001; Goto et al. 2003), or
be independent of
it, as well as of l.o.s. velocity dispersion and mass
(Goto 2005;
Popesso
et al. 2007b; De Propris et al. 2004).
To address this
issue, we associated each group with the number of members found by
the algorithm. Nevertheless, due to the survey characteristics
(sampling rate, spectra signal to noise ratio, etc.), the observed
number has to be corrected to recover the real number of members
within the flux limit of the survey (
![]() ). We did this by
weighting each galaxies with the ``target sampling rate'' and the
``spectroscopic success rate'' of the survey (see
Ilbert et al. 2005).
We then modulated this mean weight with a finer
correction taking into account that the sampling rate is not uniform
in the field. This was done by using the
). We did this by
weighting each galaxies with the ``target sampling rate'' and the
``spectroscopic success rate'' of the survey (see
Ilbert et al. 2005).
We then modulated this mean weight with a finer
correction taking into account that the sampling rate is not uniform
in the field. This was done by using the ![]() selection
function described in Cucciati
et al. (2006). For each group,
we computed a corrected richness (
selection
function described in Cucciati
et al. (2006). For each group,
we computed a corrected richness (![]() ), which is the sum of the
weights of those galaxies brighter than the evolving luminosity limit
described above. In Fig. 14,
green
diamonds, orange squares, and red stars show
), which is the sum of the
weights of those galaxies brighter than the evolving luminosity limit
described above. In Fig. 14,
green
diamonds, orange squares, and red stars show ![]() within groups with
within groups with
![]() ,
14, and 20. In the plot, we can see a general trend
of decreasing
,
14, and 20. In the plot, we can see a general trend
of decreasing ![]() for increasing
for increasing ![]() ,
at any redshift explored.
Given the error bars, this decrement is not significant when
considering single steps in
,
at any redshift explored.
Given the error bars, this decrement is not significant when
considering single steps in ![]() ,
but the overall tendency is
clear. Nevertheless, the
,
but the overall tendency is
clear. Nevertheless, the ![]() redshift evolution does not appear to
differ for different values of
redshift evolution does not appear to
differ for different values of ![]() .
These results are in
agreement with those found by Iovino
et al. (2010) in their
analysis of the zCOSMOS-10k group sample, but we have extended them to
fainter magnitudes. It would be indeed interesting to study the
dependence on
.
These results are in
agreement with those found by Iovino
et al. (2010) in their
analysis of the zCOSMOS-10k group sample, but we have extended them to
fainter magnitudes. It would be indeed interesting to study the
dependence on ![]() of other galaxy properties, as done for example
for star formation rate (SFR) and specific SFR (see for example
Popesso et al. 2007b).
This could provide insight into how
different galaxies properties are affected by different
environments. We defer this study to a future work.
of other galaxy properties, as done for example
for star formation rate (SFR) and specific SFR (see for example
Popesso et al. 2007b).
This could provide insight into how
different galaxies properties are affected by different
environments. We defer this study to a future work.
8 Summary and conclusions
We have compiled a homogeneous catalogue of optical groups
identified
in the VVDS-02 field by means of the VDM algorithm, in the range ![]() .
.
We used mock catalogues simulating the VVDS survey to optimize the performances of the group-finding algorithm (maximizing the completeness and the purity of the resulting group catalogue) as well as to minimize possible selection effects. Our main results are:
- -
- Using the mock catalogues, we verified that the VVDS-02h
survey sampling rate allows us to recover at least 50% of the
groups (with a virial l.o.s. velocity dispersion
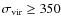 km s-1)
that are potentially present in the parent photometric
catalogue up to z=1.
km s-1)
that are potentially present in the parent photometric
catalogue up to z=1.
- -
- We tested how well
 of the halo mass particles
can be estimated using sparsely sampled galaxy velocities. We verified
that with this method, given the characteristics of our survey (flux
limit, sampling rate, redshift measurement error) we are able to
recover a sensible value of
of the halo mass particles
can be estimated using sparsely sampled galaxy velocities. We verified
that with this method, given the characteristics of our survey (flux
limit, sampling rate, redshift measurement error) we are able to
recover a sensible value of  for
for 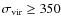 km s-1.
km s-1.
- -
- Applying the optimized algorithm to the VVDS real data set,
we obtained a catalogue of 318 groups of galaxies (with at least two
members) in the range
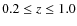 .
Among these groups, 63 have a measured l.o.s. velocity dispersion
greater than 350 km s-1. The
group catalogue is characterized by an overall completeness of
.
Among these groups, 63 have a measured l.o.s. velocity dispersion
greater than 350 km s-1. The
group catalogue is characterized by an overall completeness of
 60% and a
purity of
60% and a
purity of 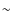 50%.
Nearly 19% of the total
population of galaxies live in these systems.
50%.
Nearly 19% of the total
population of galaxies live in these systems.
- -
- The number density distribution as a function of both
redshift (n(z)) and velocity
dispersion (
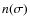 )
of the VVDS
groups with
)
of the VVDS
groups with 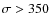 km s-1
scales in qualitative agreement with the
analogous statistics recovered from the mock catalogues.
km s-1
scales in qualitative agreement with the
analogous statistics recovered from the mock catalogues.
- -
- We studied the fraction
 of blue galaxies (
of blue galaxies (
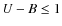 )
in the range
)
in the range 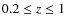 .
We used a luminosity-limited
subsample of galaxies extracted from our data (
.
We used a luminosity-limited
subsample of galaxies extracted from our data (
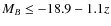 ),
complete up to z=1. We found that
),
complete up to z=1. We found that  is significantly lower
in groups than in the global galaxy population. Moreover,
is significantly lower
in groups than in the global galaxy population. Moreover,  increases as
a function of redshift irrespective of the environment,
with marginal evidence of a higher growth rate in groups. We also
analyzed how
increases as
a function of redshift irrespective of the environment,
with marginal evidence of a higher growth rate in groups. We also
analyzed how  varies as a function of group richness, finding
that, at any redshift explored,
varies as a function of group richness, finding
that, at any redshift explored,  decreases in systems with
increasing richness.
decreases in systems with
increasing richness.
Further explorations of the properties of VVDS groups is left to future work. We only anticipate that the high degree of completeness of the catalogue can be potentially exploited for extracting cosmological information via, for example, cluster count techniques. The high level of purity also makes the VVDS group sample ideal for astrophysical analyses studying various physical properties of galaxies as a function of local density and environment. We also note that the cross-correlation studies of our optically-selected catalogue with samples inferred in the same field with independent techniques will help us to gain insights not only into cluster selection biases but also the physics at work within these extreme environments.
AcknowledgementsO.C. thanks Stefano Andreon for stimulating discussions. We thank the referee for helpful comments. This research has been developed within the framework of the VVDS consortium and it has been partially supported by the CNRS-INSU and its Programme National de Cosmologie (France), by the Italian Ministry (MIUR) grants COFIN2000 (MM02037133) and COFIN2003 (num.2003020150) and by PRIN-INAF 2005 (CRA 1.06.08.10). The VLT-VIMOS observations have been carried out on guaranteed time (GTO) allocated by the European Southern Observatory (ESO) to the VIRMOS consortium, under a contractual agreement between the Centre National de la Recherche Scientifique of France, heading a consortium of French and Italian institutes, and ESO, to design, manufacture and test the VIMOS instrument. A. Pollo also acknowledges financial support from the Polish Ministry of Science, grant PBZ/MNiSW/07/2006/34A. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l'Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory.
References
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Adami, C., Mazure, A., Ilbert, O., et al. 2005, A&A, 443, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, S. W., Schmidt, R. W., & Fabian, A. C. 2002, MNRAS, 334, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Lobo, C., & Iovino, A. 2004a, MNRAS, 349, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Willis, J., Quintana, H., et al. 2004b, MNRAS, 353, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Valtchanov, I., Jones, L. R., et al. 2005, MNRAS, 359, 1250 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Quintana, H., Tajer, M., Galaz, G., & Surdej, J. 2006, MNRAS, 365, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Maughan, B., Trinchieri, G., & Kurk, J. 2009, A&A, 507, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bahcall, N. A. 1981, ApJ, 247, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Barber, C. B., Dobkin, D. P., & Huhdanpaa, H. 1996, ACM Transactions on Mathematical Software, 22, 469 [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., Frieman, J., Weinberg, D. H., et al. 2006, ApJS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1988, Galactic Dynamics (Princeton Univiversity Press) [Google Scholar]
- Blaizot, J., Wadadekar, Y., Guiderdoni, B., et al. 2005, MNRAS, 360, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R. 2006, ApJ, 648, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., & Zehavi, I. 2006, ApJ, 645, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Borgani, S., Gardini, A., Girardi, M., & Gottlober, S. 1997, New Astron., 2, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Borgani, S., Girardi, M., Carlberg, R. G., Yee, H. K. C., & Ellingson, E. 1999, ApJ, 527, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Bremer, M. N., Valtchanov, I., Willis, J., et al. 2006, MNRAS, 371, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, A. G., & Charlot, S. 1993, ApJ, 405, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, Jr., A. 1978, ApJ, 226, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Butcher, H., & Oemler, A. 1984, ApJ, 285, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., Yee, H. K. C., Morris, S. L., et al. 2001, ApJ, 552, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. D., Wu, C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., & Coil, A. L. 2007, MNRAS, 376, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Iovino, A., Marinoni, C., et al. 2006, A&A, 458, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, M., Faber, S. M., Newman, J., et al. 2003, in Discoveries and Research Prospects from 6- to 10-Meter-Class Telescopes II, Guhathakurta, Puragra, ed. P. Guhathakurta, Proc. SPIE, 4834, 161 [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., & Dickinson, M. 2003, ApJ, 598, 20 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Colless, M., Peacock, J. A., et al. 2004, MNRAS, 351, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Delaunay, B. 1934, Bull. Acad. Sci. USSR, 7, 793 [Google Scholar]
- Donahue, M., Scharf, C. A., Mack, J., et al. 2002, ApJ, 569, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Oemler, A. J., Couch, W. J., et al. 1997, ApJ, 490, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2004, MNRAS, 348, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Tozzi, P., & Rosati, P. 2003, A&A, 398, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., Morandi, A., Tozzi, P., et al. 2009, A&A, 501, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finoguenov, A., Watson, M. G., Tanaka, M., et al. 2010, MNRAS, 403, 2063 [NASA ADS] [CrossRef] [Google Scholar]
- Franzetti, P., Scodeggio, M., Garilli, B., et al. 2007, A&A, 465, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garilli, B., Maccagni, D., & Andreon, S. 1999, A&A, 342, 408 [NASA ADS] [Google Scholar]
- Gavazzi, R., & Soucail, G. 2007, A&A, 462, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, R., Adami, C., Durret, F., et al. 2009, A&A, 498, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, B. F., Newman, J. A., Davis, M., et al. 2005, ApJ, 625, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, B. F., Newman, J. A., Faber, S. M., et al. 2007, MNRAS, 376, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Gilbank, D. G., Bower, R. G., Castander, F. J., & Ziegler, B. L. 2004, MNRAS, 348, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Biviano, A., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1993, ApJ, 404, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Borgani, S., Giuricin, G., Mardirossian, F., & Mezzetti, M. 2000, ApJ, 530, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Giuricin, G., Samurovic, S., Girardi, M., Mezzetti, M., & Marinoni, C. 2001, ApJ, 554, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., & Yee, H. K. C. 2000, AJ, 120, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T. 2005, MNRAS, 356, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Okamura, S., Yagi, M., et al. 2003, PASJ, 55, 739 [NASA ADS] [Google Scholar]
- Hansen, S. M., McKay, T. A., Wechsler, R. H., et al. 2005, ApJ, 633, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iovino, A., McCracken, H. J., Garilli, B., et al. 2005, A&A, 442, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iovino, A., Cucciati, O., Scodeggio, M., et al. 2010, A&A, 509, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kepner, J., Fan, X., Bahcall, N., et al. 1999, ApJ, 517, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J., Hudelot, P., Ellis, R. S., et al. 2003, ApJ, 598, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Kovac, K., Lilly, S. J., Knobel, C., et al. 2010, ApJ, 718, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Mellier, Y., McCracken, H. J., et al. 2004, A&A, 417, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ledlow, M. J., Voges, W., Owen, F. N., & Burns, J. O. 2003, AJ, 126, 2740 [NASA ADS] [CrossRef] [Google Scholar]
- Lemson, G., & Virgo Consortium, T. 2006 [arXiv:astro-ph/0608019] [Google Scholar]
- Lilly, S. J., Fèvre, O. L., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., LeBrun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Limousin, M., Cabanac, R., Gavazzi, R., et al. 2009, A&A, 502, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Ebeling, H., Ma, C., et al. 2010, MNRAS, 474 [Google Scholar]
- Margoniner, V. E., de Carvalho, R. R., Gal, R. R., & Djorgovski, S. G. 2001, ApJ, 548, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Marinoni, C., & Hudson, M. J. 2002, ApJ, 569, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Marinoni, C., Davis, M., Newman, J. A., & Coil, A. L. 2002, ApJ, 580, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Materne, J. 1978, A&A, 63, 401 [NASA ADS] [Google Scholar]
- Mazure, A., Adami, C., Pierre, M., et al. 2007, A&A, 467, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCracken, H. J., Radovich, M., Bertin, E., et al. 2003, A&A, 410, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneux, B., Guzzo, L., Garilli, B., et al. 2008, A&A, 478, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, C. J., Nichol, R. C., Reichart, D., et al. 2005, AJ, 130, 968 [Google Scholar]
- Mirtich, B. 1996, Journal of graphics tools, 1, 31 [Google Scholar]
- Morandi, A., Pedersen, K., & Limousin, M. 2010, ApJ, 713, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, J. A., & Davis, M. 2002, ApJ, 564, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, A. J. 1974, ApJ, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, L. F., Benoist, C., Cappi, A., et al. 2007, A&A, 461, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierre, M., Pacaud, F., Duc, P.-A., et al. 2006, MNRAS, 372, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., von der Linden, A., De Lucia, G., et al. 2006, ApJ, 642, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Pollo, A., Meneux, B., Guzzo, L., et al. 2005, A&A, 439, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Böhringer, H., Brinkmann, J., Voges, W., & York, D. G. 2004, A&A, 423, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., Romaniello, M., & Voges, W. 2005, A&A, 433, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Biviano, A., Böhringer, H., & Romaniello, M. 2007a, A&A, 461, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Biviano, A., Romaniello, M., & Böhringer, H. 2007b, A&A, 461, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., & Geller, M. J. 1984, ApJ, 281, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Radovich, M., Arnaboldi, M., Ripepi, V., et al. 2004, A&A, 417, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, J., Smith, G. P., Kneib, J., et al. 2010, MNRAS, 313 [Google Scholar]
- Rosati, P., Borgani, S., & Norman, C. 2002, ARA&A, 40, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Sheldon, E. S., Johnston, D. E., Masjedi, M., et al. 2009, ApJ, 703, 2232 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Sunyaev, R. A., & Zeldovich, I. B. 1980, ARA&A, 18, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Temporin, S., Iovino, A., Bolzonella, M., et al. 2008, A&A, 482, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., Ellis, R. S., Kneib, J.-P., et al. 2003, ApJ, 591, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B. 1980, ApJ, 237, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Valtchanov, I., Pierre, M., Willis, J., et al. 2004, A&A, 423, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voronoi, G. F. 1908, J. Reine Angew. Math., 134, 198 [CrossRef] [Google Scholar]
- Weinmann, S. M., van den Bosch, F. C., Yang, X., & Mo, H. J. 2006, MNRAS, 366, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Willis, J. P., Pacaud, F., Valtchanov, I., et al. 2005a, MNRAS, 363, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Willis, J. P., Pacaud, F., Valtchanov, I., et al. 2005b, MNRAS, 364, 751 [NASA ADS] [Google Scholar]
- Zhang, Y., Böhringer, H., Finoguenov, A., et al. 2006, A&A, 456, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwicky, F., Herzog, E., & Wild, P. 1968, Catalogue of galaxies and of clusters of galaxies (Pasadena: California Institute of Technology (CIT), 1961-1968) [Google Scholar]
Footnotes
- ... catalogue
![[*]](/icons/foot_motif.png)
- Complete Tables 4 and 5 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/520/A42
- ...
Simulation
![[*]](/icons/foot_motif.png)
- http://www.mpa-garching.mpg.de/galform/virgo/millennium/
- ...
release
![[*]](/icons/foot_motif.png)
- http://cencosw.oamp.fr
All Tables
Table 1:
Quality statistics (C1, C2,
P1, P2,
![]() ,
and
,
and
![]() ,
see text for details) of the reconstructed group catalogue,
for two different redshift bins and the whole redshift range.
,
see text for details) of the reconstructed group catalogue,
for two different redshift bins and the whole redshift range.
Table 2:
Quality statistics (C1, C2,
P1, P2,
![]() ,
and
,
and ![]() ,
see text for details) of the group catalogue reconstructed by the
algorithm with the high-purity parameter
set, for two different redshift bins and the whole redshift
range, considering groups with
,
see text for details) of the group catalogue reconstructed by the
algorithm with the high-purity parameter
set, for two different redshift bins and the whole redshift
range, considering groups with ![]() .
.
Table 3:
Number of VVDS-02h groups reconstructed by the
algorithm using the best set of parameters in
VVDS-02h field,
for ![]() .
.
Table 4:
List of groups recovered in the VVDS-02h field in the range ![]() .
(This table is available in electronic form at the CDS).
.
(This table is available in electronic form at the CDS).
Table 5: List of group galaxies belonging to the groups listed in Table 4. (This table is available in electronic form at the CDS).
All Figures
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f1.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg46.png)
|
Figure 1:
Uneven spectrograph coverage in VVDS-02h field. The grey-scale from the
lightest to the darkest grey indicates the sampling rate, with
corresponding values shown in the label.
The grid used for the colour-code had steps of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f2.ps}\vspace*{-1.5mm}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg66.png)
|
Figure 2:
The fraction, as a function of redshift, of ``surviving''
groups when the sampling rate is decreased from that of a purely
flux-limited
simulated sample |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.3cm]{11831f3a.ps}\includegraph...
...th=5.3cm]{11831f3e.ps}\includegraphics[width=5.3cm]{11831f3f.ps} }\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg67.png)
|
Figure 3:
Comparison of l.o.s. velocity dispersion
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f4a.ps}\par\includegraphics[width=7cm,clip]{11831f4b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg84.png)
|
Figure 4:
As the plots in the last column of Fig. 3, but
with exchanged axes. In this case, the binning is made according to |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm]{11831f5a.ps}\includegraphics[width=7cm]{11831f5b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg113.png)
|
Figure 5:
C1 and C2
statistics as a function of ``fiducial''
group members (on the left) and P1
and P2 statistics as a
function of ``reconstructed'' group members (on the right).
One-way
statistics are shown as blue squares, and two-way statistics as red
crosses. C and P have been
computed separately in each mock:
in these plots, points are C and P
values averaged over all mocks,
while error bars are their rms. On the x axis,
we grouped the
number of elements in the following way: [N=2],[N=3,
4], [N=5, 6], and [ |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm]{11831f6.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg154.png)
|
Figure 6:
Interlopers fraction |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.cm,clip]{11831f7.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg155.png)
|
Figure 7: Mean distribution of fiducial groups as a function of redshift (continuous line), computed as the average over 20 VVDS-like mocks. The mean distribution of VDM-reconstructed groups over the same 20 mocks is over plotted as black points. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f8.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg160.png)
|
Figure 8: Comparison between virial (y axis) and VDM reconstructed (x axis) group velocity dispersion. Only two-way matches are considered in this plot. The upper panel shows the scatter plot, the lower shows the percentage error. Green and blue triangles are groups with at least 5 members, orange and purple squares groups with at least 8 members; green and orange points are single groups, while blue and purple symbols are the median (on x axis) and mean (on y axis) values in bins of the property on the x axis. Vertical error bars are rms of mean values. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f9.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg167.png)
|
Figure 9:
Mean distribution of virial l.o.s. velocity dispersion (continuous
line), computed as the average over 20 VVDS-like mocks. The
mean
distribution of |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f10.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg168.png)
|
Figure 10:
Normalized mean distribution of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f11.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg198.png)
|
Figure 11: The redshift distribution of groups in the VVDS-02h sample, found using the best set of parameters. Different line styles are for different cuts in group richness, as indicated. The total number of groups with the corresponding richness is quoted in the labels, for two different redshift ranges. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f12a.ps}\par\includegraphics[width=8cm,clip]{11831f12b.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg200.png)
|
Figure 12:
Two-dimensional VVDS galaxy distribution as a function of
Right Ascension and redshift (points are compressed on the Declination
dimension). Each plot shows a different redshift bin (
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{11831f13.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg201.png)
|
Figure 13: As in Fig. 9, but in this case the velocity dispersion distribution of VVDS-02h field groups is also shown with red triangles. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11831f14.ps}
\end{figure}](/articles/aa/full_html/2010/12/aa11831-09/Timg212.png)
|
Figure 14:
Fraction of
blue galaxies (
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



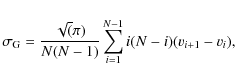
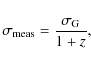
![\begin{displaymath}\displaystyle
\sigma(33,275)^2 = \frac{{\rm max}[0, \sigma(33,275)_{\rm G}^2-v_{\rm err}^2]}{(1+z)^2},
\end{displaymath}](/articles/aa/full_html/2010/12/aa11831-09/img74.png)
![\begin{displaymath}\displaystyle
{\rm err}.\% = \frac{[\sigma_{\rm meas}-\sigma_{\rm vir}]}{\sigma_{\rm vir}} \times 100,
\end{displaymath}](/articles/aa/full_html/2010/12/aa11831-09/img78.png)
![\begin{displaymath}\displaystyle
{\rm err}.\% = \frac{[\sigma(33,275)-\sigma_{\rm vir}]}{\sigma(33,275)} \times 100.
\end{displaymath}](/articles/aa/full_html/2010/12/aa11831-09/img81.png)