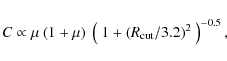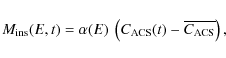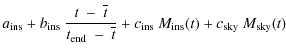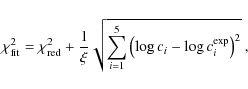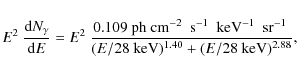EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 512 (March-April 2010) A&A, 512 (2010) A49 Full HTML
Free Access
Issue
A&A
Volume 512, March-April 2010
Article Number A49
Number of page(s) 13
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200913072
Published online 31 March 2010
A&A 512, A49 (2010)

INTEGRAL hard X-ray spectra of the cosmic X-ray background and Galactic ridge emission

M. Türler1,2 - M. Chernyakova3 - T. J.-L. Courvoisier1,2 - P. Lubinski1,4 - A. Neronov1,2 - N. Produit1,2 - R. Walter1,2

1 - ISDC Data Centre for Astrophysics, ch. d'Ecogia 16, 1290 Versoix, Switzerland
2 - Geneva Observatory, University of Geneva, ch. des Maillettes 51, 1290 Sauverny, Switzerland
3 - Dublin Institute for Advanced Studies, 31 Fitzwilliam Place, Dublin 2, Ireland
4 - Nicolaus Copernicus Astronomical Center, Bartycka 18, 00-716 Warszawa, Poland

Received 5 August 2009 / Accepted 4 January 2010

Abstract
Aims. We derive the spectra of the cosmic X-ray background (CXB) and of the Galactic ridge X-ray emission (GRXE) in the $\sim $20-200 keV range from the data of the IBIS instrument aboard the INTEGRAL satellite obtained during the four dedicated Earth-occultation observations in early 2006.
Methods. We analyze the modulation of the IBIS/ISGRI detector counts induced by the passage of the Earth through the field of view of the instrument. Unlike previous studies, we do not fix the spectral shape of the various contributions, but model instead their spatial distribution and derive for each of them the expected modulation of the detector counts. The spectra of the diffuse emission components are obtained by fitting the normalizations of the model lightcurves to the observed modulation in different energy bins. Because of degeneracy, we guide the fits with a realistic choice of the input parameters and a constraint for spectral smoothness.
Results. The obtained CXB spectrum is consistent with the historic HEAO-1 results and falls slightly below the spectrum derived with Swift/BAT. A 10% higher normalization of the CXB cannot be completely excluded, but it would imply an unrealistically high albedo of the Earth. The derived spectrum of the GRXE confirms the presence of a minimum around 80 keV with improved statistics and yields an estimate of $\sim $0.6  $M_{{\rm\odot}}$ for the average mass of white dwarfs in the Galaxy. The analysis also provides updated normalizations for the spectra of the Earth's albedo and the cosmic-ray induced atmospheric emission.
Conclusions. This study demonstrates the potential of INTEGRAL Earth-occultation observations to derive the hard X-ray spectra of three fundamental components: the CXB, the GRXE and the Earth emission. Further observations would be extremely valuable to confirm our results with improved statistics.

Key words: earth - Galaxy: disk - galaxies: active - diffuse radiation - X-rays: diffuse background - X-rays: general

1 Introduction

Although the cosmic X-ray background (CXB) was discovered before the cosmic microwave background (Giacconi et al. 1962), it is known in much less detail and its spectral shape and normalization are still subjects of debate. This diffuse emission is thought to be mainly due to unresolved active galactic nuclei (AGN) extending to cosmological distances with a contribution from type Ia supernovae in the low-energy gamma-rays (Zdziarski 1996). Evidence for the AGN origin of the CXB at energies below 10 keV comes from various X-ray mirror telescopes - in particular Chandra and XMM-Newton - that were able to resolve up to 80% of the diffuse emission into point sources (e.g. Gilli et al. 2007; Brandt & Hasinger 2005). The amount of resolved sources decreases rapidly with energy though so that only 2.5% of the diffuse background is resolved by the deepest survey yet in the 20-60 keV range, at the peak of the CXB emission (Paltani et al. 2008). The characterization of the actual spectral shape and normalization around this emission bump is crucial to estimate the fraction of heavily absorbed Compton-thick AGN thought to contribute significantly in this hard X-ray spectral range (Ueda et al. 2003; Sazonov et al. 2008; Treister et al. 2009; Gilli et al. 2007).

The High Energy Astronomical Observatory 1 (HEAO-1) is hitherto the only satellite which had a dedicated mechanism to disentangle the CXB from the instrumental background. By using a movable CsI crystal with a thickness of 5 cm to cover part of the field of view (FoV), the HEAO-1 observations of the mid-1970s are still the most accurate and reliable measurements of the CXB spectral shape in the hard X-rays (Gruber et al. 1999; Marshall et al. 1980; Kinzer et al. 1997). Without such a masking mechanism in recent space missions, a practical way to study this diffuse hard X-ray emission is to use the Earth as a screen occulting part of the background sky. For pointing satellites in low orbits around the Earth, our planet often crosses part of the field of view during normal operations. Such events can be analyzed in detail to evaluate the CXB spectrum. This was done by Frontera et al. (2007) for the BeppoSAX mission and by Ajello et al. (2008) for the data of the Burst Alert Telescope (BAT) aboard the Swift spacecraft.

\begin{figure} \par\includegraphics[width=6cm]{13072f1a.eps}\includegraphics[width=6cm]{13072f1b.eps} \end{figure} Figure 1:

Model IBIS/ISGRI images of the sky with ( right) and without ( left) instrumental vignetting effects (see Fig. 2). They show the geometry and relative intensity (on a logarithmic scale from dark and blue to red and bright areas) of the various components during the first EO at IJD = 2216.04 as derived for channel 3 ($\sim $27 keV). The bluish circle shows emission of the Earth occulting the diffuse sky background (purple), the Galactic ridge (red strip), and the point sources (bright dots). The instrumental background is ignored for clarity. The images extend over the partially coded FoV ( $28.8^\circ \times 29.2^\circ $). Point sources are convolved with a circular Gaussian typical for the instrumental resolution ( $\sigma = 0.1^\circ $).

Open with DEXTER

With its eccentric three-days orbit, the INTEGRAL satellite (Winkler et al. 2003) is close to the Earth only during the perigee passage when the instruments are not operating because of excessive background in the radiation belts. In order to study the X-ray background, a series of four dedicated observations were performed in January and February 2006. The Earth was allowed to pass through the FoV of the instruments shortly after radiation-belt exit while the spacecraft was aimed to point towards a fixed position in the sky. Churazov et al. (2007) described these observations by all four instruments aboard INTEGRAL in great detail and studied how the passage of the Earth modulates the detector counts by occulting part of the CXB.

The difficulty of using the Earth to shield the CXB comes from the fact that the Earth is not dark in the hard X-rays. The emission from the Earth in the 20-200 keV range consists of two major contributions: the reflection of the CXB by the atmosphere and its Compton emission under the bombardment by cosmic rays (CR). Disentangling the CXB occultation from the Earth emission is challenging. Churazov et al. (2007) assumed the spectral shape of the CXB and of the two Earth emission components and fitted their normalizations to the observed amplitude of the Earth modulation in the data. The studies of the BeppoSAX/PDS measurements (Frontera et al. 2007) and the Swift/BAT observations (Ajello et al. 2008) also relied on a priori assumptions on the spectral shape of the CXB and the Earth emission.

We present here a completely different approach for the analysis of the same INTEGRAL observations as were used by Churazov et al. (2007), but only focusing on the data of the IBIS/ISGRI instrument (Ubertini et al. 2003). Instead of fixing the spectral shapes of the CXB and the Earth emission components, we aim to derive them based on a detailed modeling of the spatial distribution of these components and of all instrumental effects. If the Earth surface brightness differs significantly from the uniform CXB occultation, it is possible to disentangle these components based on the recorded modulation when the Earth is crossing the FoV. This has the potential to simultaneously derive the spectral shape of the CXB and of the Earth emission from the observations.

Another difficulty of the analysis is the presence of the Galactic plane in the border of the wide FoV of IBIS (see Fig. 1). An empty extragalactic field would have been ideal to study the CXB, but this was not possible due to various scheduling constraints. This complication is however an opportunity to study in addition the diffuse Galactic ridge X-ray emission (GRXE) (e.g. Revnivtsev et al. 2006; Bouchet et al. 2008; Krivonos et al. 2007), which is also occulted by the passage of the Earth.

The observational material and the analysis method are described in Sects. 2 and 3, respectively. We present the obtained spectra in Sect. 4 and discuss them in comparison to previous results in Sect. 5, before concluding in Sect. 6. Unless otherwise stated, the quoted errors are 1-$\sigma$ uncertainties, i.e. at the 68% confidence level (CL).

2 Data

The data used here are the four Earth-occultation observations (EOs) conducted by INTEGRAL in January and February 2006 at the start of satellite revolutions number 401, 404, 405 and 406. We refer the reader to the detailed description of these observations in Churazov et al. (2007). We focus our analysis on the data of the IBIS/ISGRI gamma-ray imager that is best suited to study the emission in the $\sim $20-200 keV range.

Our work is based on the analysis of the modulation in full detector lightcurves induced by the passage of the Earth through the FoV. These lightcurves are obtained with the latest version of the ii_light executable that will be included in a forthcoming release of the Off-line Scientific Analysis (OSA) software package provided by the INTEGRAL Science Data Centre (ISDC, Courvoisier et al. 2003). They are corrected for instrumental dead time and the effect of dead and noisy pixels, which amount to typically 5% of all ISGRI pixels. For each of the four similar observations, we extracted detector lightcurves with a time binning of 300 s in a series of 16 energy bins (see Table 2), carefully chosen to isolate instrumental emission features, in particular the broad lines at 26 and 31 keV from CdTe and the narrow lines at 59 keV from W, 75-77 keV from Pb and 82-84 keV from Bi (Terrier et al. 2003).

The detector lightcurves originally expressed in units of count cm-2 s-1 were multiplied by 0.5 ( $128\times 0.4$ cm)2 = 1310.72 cm2, which is the area of the detector assumed by the standard ISGRI ancillary response file (ARF), describing the energy dependence of the effective area of the instrument. The factor 0.5 refers to the fraction of open coded mask elements, and 0.4 cm is the size of the $128 \times 128$ ISGRI detector elements. Apart from this change of unit to have full detector lightcurves, the only other manipulation of the data was a cleaning of the lightcurves. This was done by removing points with uncertainties of more than twice the average uncertainty and by iteratively removing a few isolated outstanding points lying more than 3$\sigma$ away from the smoothed lightcurve with a smoothing window of 30 min (i.e. 6 time bins).

Table 1:   List of point sources detected in at least one of the four EOs.

In order to subtract from the lightcurves the contribution of point sources in the FoV, we performed an image analysis separately for the four Earth observations. This was possible since the drift of the satellite was moderate despite the absence of star trackers during the pointings. The image analysis was done in a standard way with the default background maps of OSA 7.0. We searched for all sources previously detected by ISGRI including the new source IGR J17062-6143 already reported by Churazov et al. (2007). We then selected all sources that were detected with a significance of more than 2$\sigma$ in the 22-60 keV band. We chose this low significance threshold to minimize the contribution of the known point sources to the GRXE and the CXB. Sources with even less significance are more likely to be spurious and their global contribution will mostly cancel out with fake negative sources. We tested both a simple powerlaw and a bremsstrahlung model to fit the data. We found that for most sources the bremsstrahlung model gives a better phenomenological description of the data than a powerlaw because many sources have a convex spectral shape in this energy range. The fluxes derived for the brightest (>3$\sigma$) sources in our sample are listed in Table 1.

3 Method

The detector lightcurves described above were modulated by the passage of the Earth through the FoV of IBIS. Our approach was to model these observations in detail to derive the expected modulation of the detector counts for each emission component on the sky. This resulted in a series of model lightcurves in different energy bins for each emission component and each of the four EOs. We then fitted the normalizations of these model lightcurves to the observed detector counts to derive the actual contribution of the diffuse emission components.

This method requires the knowledge of the spacecraft position and attitude with respect to the Earth and to the background sky at any time, a description of the spatial distribution on the sky of the various emission components and also an accurate description of the IBIS/ISGRI instrumental characteristics. These aspects are described in the three subsections below. The generation of the model lightcurves is described in Sect. 3.4, whereas the actual spectral fitting procedure is the subject of Sect. 3.5.

Table 2:   Numerical values of the obtained spectra shown in Fig. 6.

3.1 Satellite position and attitude

To construct the images of the sky corresponding to each of the four Earth observations as illustrated in Fig. 1, we needed to know the exact attitude of the satellite and its distance to the Earth at any time. This information can be extracted from auxiliary files provided by the mission operation centre (MOC) in Darmstadt. It was used to compute the position of the Earth center, the position of the geographic and magnetic poles, and the apparent radius of the Earth as a function of time, all expressed in degrees, using the IBIS/ISGRI instrument coordinates (Y,Z). The spacecraft was close enough to the Earth at the beginning of the observation for the planet's sphericity to slightly affect its apparent radius. This was properly taken into account, as well as the $\sim $100 km of obscuring atmosphere in the hard X-rays mentioned by Churazov et al. (2007). The magnetic pole in the Northern hemisphere is set to its 2005 position of 82.7$^\circ$ N, 114.4$^\circ$ W.

3.2 Spatial distribution of components

Although we were only interested in the temporal modulation of counts on the full detector area, we needed a sufficiently precise description of the spatial distribution of the emission components. We chose to define all of them by analytical functions that are described below and are illustrated in Fig. 1.

The simplest component is the CXB that we assumed to be uniform on the sky. Although there is evidence that the CXB has some large-scale intensity variations (e.g. Boughn et al. 2002; Revnivtsev et al. 2008), they are small in amplitude ($\lesssim$2%) and it would be very difficult to evaluate and account for a possible non-uniformity so close to the Galactic bulge.

The GRXE was modeled with two perpendicular Lorentzian functions aligned with the Galactic coordinates. The full-width at half maximum (FWHM) of the Lorentzians are of $21\hbox{$^\circ$ }$ (Krivonos et al. 2007, Fig. 7) and $1.2^\circ$(Revnivtsev et al. 2006, Fig. 5) respectively along the Galactic longitude, l, and latitude, b. The Lorentzian's maximum are at the Galactic center with a slight latitude displacement of $b=-0.15^\circ$ as measured by Revnivtsev et al. (2006). As shown by Krivonos et al. (2007), this distribution matches well the COBE/DIRBE map at 4.9 $\mu$m, which was used by Bouchet et al. (2008) as a template for the GRXE below 120 keV.

We took special care to define the spatial distribution of the Earth's emission. There are two distinct components to be taken into account: the CXB reflection by the Earth (Churazov et al. 2008) and the CR-induced atmospheric emission (Sazonov et al. 2007). The authors of these studies performed Monte-Carlo simulations to derive both the spectrum and the surface brightness of the Earth emission. We used the latter results as a precise determination of the expected image of the Earth at hard X-rays.

Churazov et al. (2008) found that the X-ray albedo of the Earth is limb-darkened at lower energies and limb-brightened at higher energies. At energies below $\sim $100 keV - where this component dominates the Earth emission - the emission is found to be limb-darkened, but slightly less than for a sphere emitting black-body radiation. Such an object would have a linear dependence of the flux with $\mu \equiv \cos{\theta}$, where $\theta$ is the zenith angle, i.e. the angle between the line-of-sight and the normal to the surface. For the Earth albedo below $\sim $100 keV they instead found an angular dependence of the reflected flux that can be approximated by $F(\mu)\propto \mu~(1{-}0.5~\mu)$. We used this equation to define the Earth albedo component.

We modeled the CR-induced emission of the Earth's atmosphere according to Sazonov et al. (2007, Eq. (7)). By setting the solar modulation potential to $\phi = 0.5$ - corresponding to the solar minimum during the EOs of 2006 - we can simplify this equation as:

\begin{displaymath} C\propto \mu~(1+\mu)~\left(~1+(R_{{\rm cut}}/3.2)^2~\right)^{-0.5}, \end{displaymath} (1)

where $\mu$ is as defined above and $R_{{\rm cut}}$ is the geomagnetic cut-off rigidity. In the dipole approximation of the Earth's magnetic field, the latter depends mainly on the geomagnetic latitude $\lambda_{{\rm m}}$ as $R_{{\rm cut}}\simeq 14.5~\cos^4{\lambda_{{\rm m}}}$ GV (Smart & Shea 2005). The resulting atmospheric emission of the Earth is a combination of relatively strong limb-darkening from the $\mu$-dependence in Eq. (1) with enhanced emission at the magnetic poles from the $\lambda_{{\rm m}}$-dependence.

We note that we took into account for both Earth emission components the distortion of the surface brightness related to the fact that only a portion of the Earth's hemisphere can be seen when the spacecraft is relatively close to the planet.

\begin{figure} \par\includegraphics[bb=16 150 430 700,clip,width=9cm]{13072f2.eps} \end{figure} Figure 2:

Surfaces representing the five IBIS/ISGRI vignetting effects that affect the incoming radiation until it reaches the detector plane. The effects are those corresponding to channel 12 ($\sim $72 keV) and are: a) the IBIS tube transparency to off-axis radiation, b) the energy independent exposure map, c) the effective coded-mask transparency, d) the transmission of the Nomex structure supporting the mask, and e) the absorption of the ISGRI spider beams. The total vignetting effect is the product of the effects b) to e) with the addition of effect a), which extends well outside the partially coded FoV.

Open with DEXTER

3.3 Instrumental characteristics

As we wanted to fit real detector lightcurves with model lightcurves we needed to take into account the instrumental characteristics of the telescope in the modeling. This does not include detector responses, but all effects attenuating the incoming photon field on its path from outside the telescope until reaching the detector plane. We identified five effects that affected the detector illumination depending on the direction of the incoming radiation and sometimes on its energy. The most obvious effect is the attenuation due to the coded-mask elements which block out about half of the incoming radiation. The second effect is the non-uniform exposure map which is caused by a partial illumination of the detector for a source outside of the fully coded FoV. Another vignetting effect is induced by the Nomex honeycomb structure that supports the coded mask. The two last effects are due to the IBIS/ISGRI spider beams separating the eight detector modules and to the lead shielding of the IBIS telescope tube. The aluminum spider results in opacity at the lowest energies, and the lead shielding of the tube becomes transparent at the highest energies.

The five effects mentioned above are included in the standard IBIS/ISGRI software for image reconstruction and spectral extraction, but as we worked directly with the detector lightcurves, we needed to account for these effects independently. Their modeling as used in this work is described below and is illustrated in Fig. 2, while the overall vignetting effect is shown in Fig. 1.

The coded-mask transparency is ideally of 0.5 since there are as many elements open as closed. This is, however, only true at the center of the FoV. For off-axis sources there is an additional attenuation due to the thickness of 16 mm of the mask elements, which project a wider shadow on the detector for increasing off-axis angles. As the elements are made of tungsten - a strongly absorbing material - it is fair to assume the elements to be completely opaque in the energy range considered here. As we were only interested in the net effect over the full detector plane and in a simple analytical description we approximated the mask pattern as a giant chessboard of 46 equally-sized square elements on a side of 1064 mm. We then properly computed the additional shadow from radiation that crossed the border of the mask elements and did not fall onto the shadow of other elements.

The exposure map of IBIS/ISGRI is basically very simple with a value of 1 in the fully coded FoV and a linear decrease to zero in the partially coded FoV, except in the corners of the image where the decrease is quadratic. When we modeled this, we properly took into account the disposition of the eight modules of the IBIS/ISGRI detector and the two-pixel wide space between them.

The Nomex structure supporting the coded mask of IBIS is absorbing part of the incoming photons. This is corrected for in the OSA software by off-axis efficiency maps depending on energy. In 2006, at the time of the EOs, these maps were still an approximation with only a dependence on the off-axis angle. We used the new maps introduced in the OSA 6.0 release that do include an additional azimuthal dependence due to the alignment of the walls of the hexagonal tubes that the honeycomb structure is made of and also a correction for the tubes pointing $\sim $ $0.5\hbox{$^\circ$ }$ away from the center of the FoV; a misalignment likely due to on-ground manipulations of the spacecraft. We note that the attenuation by the cosine of the off-axis angle is included in these maps.

The eight IBIS/ISGRI detector modules are separated by an aluminum structure called the ISGRI spider. It is made of one beam along the Z axis and three perpendicular beams. According to the IBIS experiment interface document part B (EID-B) the beams have a trapezoidal section with a height of 48 mm a base of 9.5 mm and a wall angle of $4\hbox{$^\circ$ }$ resulting in an upper width of 2.8 mm. The wall angle ensures that the spider is not casting a shadow in the fully coded FoV. However, in the partially coded FoV, the spider can mask up to two rows of ISGRI pixels. We modeled this effect in detail for each energy bin based on the corresponding attenuation length of Al. We found that for some specific off-axis directions, the ISGRI spider can result in an attenuation of the radiation on the detector plane of up to $\sim $5% in the lower energy bins.

The last instrumental effect we considered is the IBIS telescope tube transparency. At higher energies, the tube becomes transparent to radiation from outside the fully coded FoV, giving an additional contribution to the detector lightcurves. The tube is made of two vertical walls perpendicular to the Y axis and of two walls inclined with an angle of $3.47\hbox{$^\circ$ }$ transverse to the Z axis. The walls are shielded with glued lead foils. The thickness of the Pb sheets for each wall is reported in Table 3.2.8.1 of the EID-B (issue 7.0). We used the values for the four upper sheets of the wall that are relevant for the calculation of the tube transparency for an off-axis angle up to about 45$^\circ$. The calculation was done carefully, avoiding radiation further blocked by other parts of the ISGRI collimating system: the 1 mm thick W shield of the ISGRI hopper and the 1.2 mm thick W-strips of the side shielding of the mask. The tube transparency is neglectable at the lower energies, but reaches $\sim $1% in channel 12 (see Fig. 2) near the Pb attenuation length edge at about 75-80 keV and $\sim $6% in the last energy bin. Although this might seem unrelevant, the cumulated effect on the detector plane from a wide region outside the FoV is actually far from negligible at these energies.

\begin{figure} \par\includegraphics[width=9cm]{13072f3.eps} \end{figure} Figure 3:

Model lightcurves of each component for channel 3 ($\sim $27 keV) of the first EO. The detector count rate values are the effective contribution of the point sources (orange stars). The other components are the sky background (red circles), the GRXE (blue squares), and the Earth CXB reflection (cyan triangles, long-dashed) and the CR-induced emission (magenta triangles, short-dashed). For these diffuse components the detector count rate corresponds to an incident radiation of 40 count s-1 sr-1. For the instrumental background (black diamonds) we show the relative modulation, $M_{{\rm ins}}(t)/\overline {M_{{\rm ins}}}$, derived from the SPI/ACS corresponding to a detector count rate of 10 count s-1.

Open with DEXTER

3.4 Construction of model lightcurves

The next step was to construct model lightcurves describing the modulation of the radiation of each component described in Sect. 3.2 as induced by the passage of the Earth through the IBIS/ISGRI FoV. A complete set of model lightcurves is shown in Fig. 3.

3.4.1 Extended components

For the diffuse components - the CXB, the GRXE and the two different Earth emission components - we constructed the model lightcurves by generating a series of images of the sky at different times based on the attitude of the spacecraft and the position of the Earth in the FoV (see Sect. 3.1). For each individual component, we considered only its own contribution and the instrumental vignetting effects (see Sect. 3.3) attenuating the count rates on the detector plane. The sum of the pixels in the images generated for different times during the Earth occultation defines the model lightcurve for a given component. Because the instrumental attenuation is energy dependent, we constructed these model lightcurves for each energy bin and for each of the four EOs because of the slightly different pointing directions with respect to the Galactic ridge and Earth positions. As high-energy radiation from outside the field of view also contributes to the detector counts (see Sect. 3.3), the simulated images were defined on a wide area extending 30$^\circ$ outside of the actual FoV of IBIS/ISGRI ( $\vert Y\vert<44.4^\circ$ and $\vert Z\vert<44.6^\circ$).

The normalization of the diffuse components in the input images - without vignetting effects - was set to 10 count s-1 sr-1. For the Earth emission components, this is the average intensity over the Earth disk, while it is the average in the area defined by $320^\circ < l < 340 ^\circ$ and $\vert b\vert < 5^\circ$ for the GRXE. After attenuation by the instrumental effects described in Sect. 3.3 the actual detector count rate was typically reduced by an order of magnitude (see Fig. 3).

3.4.2 Point sources

In addition to the lightcurves constructed for the extended components we also generated one lightcurve in each energy bin for the point sources in the FoV. The time modulation is step-like in this case due to the abrupt disappearance of a source when it gets occultated by the Earth. The count rate used for each source detected with a significance of more than 2$\sigma$ was derived from a bremsstrahlung fit to its observed IBIS/ISGRI spectrum (see Sect. 2) divided by the fraction of time during which the source was not occulted. These counts were then assigned to the corresponding source position in the simulated sky images, and detector counts were obtained by summing-up the image pixels after application of the instrumental vignetting effects. We did this at different times during the passage of the Earth through the FoV to get model detector lightcurves. As the set of model lightcurves for point sources at different energies was based on the actual data collected during each EO, they were considered as a fix contribution to the detector lightcurves.

3.4.3 Instrumental background

The last but the dominant contributor to the observed detector lightcurves is the instrumental background. The time variability of this component depends on the cosmic particle environment and the induced radioactive decay of the spacecraft's material. The particle environment is well monitored by the anti-coincidence shield (ACS) of the spectrometer SPI, the other gamma-ray instrument of INTEGRAL (Vedrenne et al. 2003). We found good evidence that the IBIS/ISGRI detector lightcurves are indeed following the variations recorded by the SPI ACS. To estimate the actual relationship between the count rates in the ACS and in the IBIS/ISGRI detector in each of the considered spectral bins, we used the extragalactic observations of revolution 342 (Her X-1 and XMM LSS). These observations, away from bright hard X-ray sources, were taken about six months before the EOs and have the particularity of including a solar flare at the start of the revolution, resulting in important correlated variations in the SPI ACS and the ISGRI detector counts during the 12-h decay of the flare between INTEGRAL Julian dates (IJD = JD $-\ 2~451~544.5$) of 2040.0 and 2040.5. This relationship is characterized by the slope $\alpha$of a linear fit of the ISGRI counts versus the SPI/ACS counts. This slope is likely to change from one observation to the other because the orientation of the spacecraft with respect to the solar radiation and particle flux will change the effective areas of both the SPI/ACS and the IBIS/ISGRI detectors in a complex manner. However, the energy dependence of the slope $\alpha(E)$ for different ISGRI energy bins is expected to be rather stable. We used this energy dependence of $\alpha$ as an indication of the amount of SPI/ACS modulation expected in the ISGRI detector lightcurves of the EOs. The model lightcurve for the variations of the instrumental background was thus constructed based on those of the SPI/ACS as:

\begin{displaymath} M_{{\rm ins}}(E,t) = \alpha(E)~\left( C_{{\rm ACS}}(t)-\overline{ C_{{\rm ACS}}} \right), \end{displaymath} (2)

where $C_{{\rm ACS}}(t)$ is the SPI/ACS count rate lightcurve measured during the EOs.

3.5 Spectral fitting

We described above the construction of the model lightcurves Mi(t) shown in Fig. 3 for each component i, which are the SPI/ACS-related variations of the instrumental background (ins), the sky background (sky), the GRXE (gal), the Earth's albedo (alb), the atmospheric CR-induced emission (atm), and the point sources (src) in the FoV. The next step is to adjust these model lightcurves to the observed detector lightcurve D(t) in a given energy band with a least-square fit. This is done by the following linear relation:

                              D(t) $\textstyle \approx$ $\displaystyle a_{{\rm ins}} + b_{{\rm ins}}~\frac{t~-~\overline{t}}{t_{{\rm end... ...\overline{t}} + c_{{\rm ins}}~M_{{\rm ins}}(t) + c_{{\rm sky}}~M_{{\rm sky}}(t)$  
  $\textstyle \quad +$ $\displaystyle c_{{\rm gal}}~M_{{\rm gal}}(t) + c_{{\rm alb}}~M_{{\rm alb}}(t) + c_{{\rm atm}}~M_{{\rm atm}}(t) + M_{{\rm src}}(t),$ (3)

where $a_{{\rm ins}}$, $b_{{\rm ins}}$ and the five ci are the seven free parameters of the fit, scaling the model lightcurves Mi(t) to best match the observations D(t). The $a_{{\rm ins}}$ parameter describes the average value of the instrumental background, whereas the $b_{{\rm ins}}$ and $c_{{\rm ins}}$parameters model its variations. The parameter $b_{{\rm ins}}$ allows us to account for a linearly increasing or decreasing trend of the instrumental background during the observation, centered on a time $\overline{t}$ and ending at a time $t_{{\rm end}}$. This turned out to have an important effect at energies above 60 keV (see Sect. 5.4). Short-term variations of the instrumental background $M_{{\rm ins}}(t)$ are derived from the simultaneous SPI/ACS lightcurve according to Eq. (2) and are scaled by the parameter $c_{{\rm ins}}$. The four other ci parameters are the count rates of the various diffuse emission components on the sky, already corrected for instrumental vignetting effects. Finally, the model lightcurve for the point sources in the FoV, $M_{{\rm src}}(t)$, was not scaled as it already represents effective count rates in the detector.

By fitting the observed lightcurves D(E,t) in different energy bands E, one derives count rate spectra ci(E) for the five components i. When we did this independently for each of the 16 energy bins, we obtained quite noisy spectra with a divergence towards non-plausible values in some channels. This is due to significant degeneracy between the various components that we discuss in Sect. 5.4. A way to overcome this problem was to include a link in the fitting between the values obtained in one energy bin and in some others. We did this by adding an additional constraint to the $\chi ^2$ minimization of the fit so that the fitted parameter value ci would not be too far from an expected value $c_i^{{\rm exp}}$ according to:

\begin{displaymath} \chi_{{\rm fit}}^2 = \chi_{{\rm red}}^2 + \frac{1}{\xi}\sqrt... ..._{i=1}^{5}{\left(\log{c_i}-\log{c_i^{{\rm exp}}}\right)^2} }~, \end{displaymath} (4)

where $\chi_{{\rm red}}^2 \equiv \chi^2/\mbox{d.o.f.}$ is the $\chi ^2$ divided by the number of degrees of freedom (d.o.f.) and $\xi$ is a factor to be chosen to get an appropriate balance between the quality of the fit and additional constraints. We calculated the difference with respect to the expected value on a logarithmic scale to avoid a dependence on the actual count rate values from one component to the other.

The choice of the expected values $c_i^{{\rm exp}}$ in this constraint fit can of course have strong implications on the results. We therefore took great care to define them without including wrong assumptions and systematic effects. For the parameter $c_{{\rm ins}}$, the expected value was set to be the mean value obtained over the 16 energy bins. This was motivated by our discussion in Sect. 3.4.3, where we concluded that this factor can differ from unity, but is expected to be rather constant from one energy bin to the other. For the four other ci parameters, we defined the expected value based on the assumption that the final, unfolded spectrum of each component is supposed to be smooth. For each component spectrum, ci(E), the expected count rate in a given channel, $c_i^{{\rm exp}}$, was set to be the linear interpolation between the values in the two adjacent energy bins corrected for the effects of different energy widths of the channels and of the detector response[*]. For the first and last energy bins, the spectral smoothness was similarly constrained, by setting the expected value to the linear extrapolation of the two closest channels. We note that we did not constrain the spectrum of the instrumental background level $a_{{\rm ins}}$ and its increasing or decreasing trend with time, $b_{{\rm ins}}$, because both can change rapidly from one energy bin to the other due to the presence of narrow emission lines (see Sect. 2). For the five other parameters, the introduced interdependence of the values obtained in adjacent energy bins typically reduces the number of free parameters of the fit by a factor of 2. This was taken into account when calculating the d.o.f. of the fit.

The actual fitting began with a set of input spectra and minimized the modified $\chi ^2$ of Eq. (4), one channel after the other. We then reran this process up to four times until the overall $\chi ^2$ - computed on the lightcurves in all energy bins - did not significantly improve anymore. This iterative spectral fitting was done independently for each of the four Earth-observation datasets, and we combined the results to get the final spectra.

An issue in the fitting process is the choice of the parameter $\xi$that defines the strength of the additional constraint on the fit in Eq. (4). If $\xi$ is low the spectral smoothness constraint becomes important and it then does not leave enough freedom to fit the actual data, whereas if $\xi$ is too high, the fit might diverge in some energy bins towards unrealistic values. We tested different values and chose $\xi = 15$, which leaves a lot of freedom to the fit, while limiting strong divergence to only a few energy bins in one of the four EOs, namely EO 3 in the 70-100 keV range (see Fig. 4).

Another important issue is the choice of the input parameters, since we experienced that they can have a significant influence on the final results. This is due to degeneracy between some components that we discuss in Sect. 5.4. It is therefore safe to start with values corresponding roughly to the expectations for the CXB and also for one of the two Earth emission components. We chose the analytical formula of Gruber et al. (1999) as the basis for the input CXB spectrum. A first guess of the spectral values of the other components was obtained by doing a fit with the input CXB spectrum fixed and imposing equal contributions for the two Earth emission components. We obtained a global Earth emission that is much lower at the highest energies than derived by Churazov et al. (2007). As the CR-induced emission of the Earth is the dominant component at these energies, this suggests that its normalization has to be scaled down by a factor of $\sim $0.4 (see Fig. 13). The final set of unperturbated input spectra was obtained by fitting the lightcurves again, but this time with fixed values for both the CXB and the CR-induced Earth emission. For the latter, the spectrum was defined by the analytical formula proposed by Sazonov et al. (2007, Eq. (1)) with a normalization C of 13.2 keV cm-2 s-1 sr-1, i.e. 0.4 times that derived by Churazov et al. (2007).

\begin{figure} \par\includegraphics[width=9cm]{13072f6.eps} \end{figure} Figure 4:

IBIS/ISGRI count rate spectra of each model component derived from the detector lightcurves of the INTEGRAL EOs. The values are vignetting-corrected count rates per channel in units of 10 count s-1 sr-1, except for the instrumental background (black diamonds) for which they are actual detector count rates in count s-1. For the CXB (red circles), the GRXE (blue squares) and the total Earth emission (green triangles), the dotted lines of the same color show the average spectra obtained for the four independent EOs. The relative contributions to the Earth emission from the CXB reflection (cyan triangles, long-dashed) and the CR scattering in the atmosphere (magenta triangles, short-dashed) are also shown.

Open with DEXTER

\begin{figure} \par\mbox{\includegraphics[width=6cm]{13072f5a.eps}\includegraphi... ...5b.eps}\includegraphics[width=6cm]{13072f5c.eps} } \vspace*{-1.5mm} \end{figure} Figure 5:

Examples of detector lightcurve fits ( upper panels) and associated residuals ( lower panels) for the first EO at three representative energies: $\sim $27 keV (channel 3), $\sim $52 keV (channel 9) and $\sim $112 keV (channel 15), from left to right. The reduced $\chi ^2$ value of the best-fit curve (red line) is 0.97, 1.08 and 1.06 respectively. The contribution of different components is shown by different colors with the same coding as in Figs. 3 and 4. From bottom to top we add to the instrumental background (grey) - modulated by the SPI/ACS lightcurve and a possible trend with time - the sky background (red), the GRXE (blue), the albedo (cyan) and atmospheric (magenta) Earth emissions, and the fixed contribution from point sources (orange).

Open with DEXTER

To smear-out the dependence of the final results on these input spectra and to estimate the uncertainties, we made a series of fits with different input parameter values. We did this by perturbating each channel value of the initial spectra by a random deviation following a Gaussian distribution with a $\sigma$ of 30%. This was done independently for all five component spectra, namely the CXB, the GRXE, the two Earth emission components and the average level of the instrumental background. We performed the whole fitting process described above starting from 30 different sets of perturbated input spectra. For the four EOs, this resulted in 120 spectral fits. Instead of taking the average on the obtained values, we took the median in each energy bin as a robust estimator of the mean. This has the advantage to be independent of the use of the actual results or of their logarithm and is not influenced by outstanding values. We estimated the 1-$\sigma$ (68% CL) statistical uncertainties on the median taking the two results at $\pm34\%/\sqrt{4} = \pm17\%$ in rank order away from the median, where the factor of four stands for the four EOs being independent measurements.

4 Results

Table 3:   Spectral fit parameters for the CXB, the GRXE and the Earth emission.

The count rate spectra and uncertainties obtained with the iterative spectral fitting process described in Sect. 3.5 are shown in Fig. 4. We note that the large scatter from one EO to the other is clearly dominating the uncertainties, which suggests that performing additional EOs in the future will allow us to significantly improve the statistics of the results. We obtained overall average reduced $\chi ^2$ values of $\chi_{{\rm red}}^2$ = 1.20, 1.11, 1.15 and 1.13 for EO 1 to EO 4, respectively. These values only slightly above unity show that we get a fair description of all the lightcurves, without overinterpreting the data by using too many free parameters. As an example we show the match between the model corresponding to the final results for EO 1 and the observed lightcurves in three representative channels in Fig. 5.

The count rate spectra ci(E) shown in Fig. 4 correspond to the values before entering the telescope, i.e. they are corrected for the instrumental vignetting effects described in Sect. 3.3. We could thus directly use them for spectral fitting with XSpec to get unfolded spectra in physical units. We did the spectral fitting with the standard IBIS/ISGRI ARF and RMF detector response files distributed with OSA 7.0. We did not consider Galactic hydrogen absorption in the fit because even along the galactic plane the hydrogen column density is small enough - $N_{{\rm H}} \approx 2\times 10^{22}$ cm-2 at Galactic coordinates of (l,b) = (330$^\circ$, 0$^\circ$) - to have only a negligible effect. The spectral fit parameters are given in Table 3 and the resulting unfolded spectra are shown in Fig. 6 with the numerical values given in Table 2.

\begin{figure} \par\includegraphics[width=9cm]{13072f4.eps} \end{figure} Figure 6:

Unfolded IBIS/ISGRI spectra of the sky background (red circles), the earth emission (green triangles) and the GRXE (blue squares) with their best fit (dashed lines) and the more physical (dotted lines) spectral models (see Tables 2 and 3). The contribution of the sum of the considered point sources averaged over the four EOs is also shown (orange stars).

Open with DEXTER

The CXB spectrum is best fitted by a broken powerlaw model with a break energy at $E_{{\rm b}} = 28.7$ keV and a high-energy photon index of $\Gamma_2 = 2.42 \pm 0.09$, giving a reduced chi-squared of $\chi_{{\rm red}}^2 = 0.51$ for 12 d.o.f. A more physical model for the CXB emission - considered as the superimposition of the emission of unresolved Seyfert galaxies - is to take a cut-off powerlaw model. The degeneracy between spectral slope and cut-off energy was solved by fixing the photon index to the value of $\Gamma = 1.95$ derived by Beckmann et al. (2009) on average for all Seyfert galaxies detected by INTEGRAL. We then obtained a good description of the CXB spectrum $\chi_{{\rm red}}^2/\mbox{d.o.f.} = 0.85/14$ with a cut-off energy of $E = 127 \pm 20$ keV, at slightly higher energy than E = 86 keV derived for Seyfert 1 galaxies (Beckmann et al. 2009).

We found that the GRXE spectrum was best fitted by a cut-off powerlaw plus a second powerlaw to account for the hard tail at energies above $\sim $80 keV. As the indices of the powerlaws are poorly constrained, we fixed their values to $\Gamma_1 = 0.0$ for the cut-off powerlaw and to $\Gamma_2 = 1.55$for the hard tail, as derived by Bouchet et al. (2008). This gives a very good description of the data with a $\chi_{{\rm red}}^2 = 0.25$ for 13 d.o.f. According to Revnivtsev et al. (2006), the main population contributing to the low-energy part of the GRXE are intermediate polar cataclysmic variables. The accretion column onto the magnetic poles of such types of accreting white dwarfs is emitting optically thin thermal emission. The best fit for this more physical bremsstrahlung model is almost undistinguishable from the cut-off powerlaw (see Fig. 6) and gives a typical average temperature of $kT = 14.7\pm1.4$.

The spectrum of the total Earth emission is best fitted by a broken powerlaw with a break at $E = 49.4\pm4.9$ keV and a high-energy photon index of $\Gamma_2 = 1.78 \pm 0.13$. This break energy is slightly higher than derived by the recent analysis of the Swift/BAT data by Ajello et al. (2008), while the obtained spectral slope is in remarkable agreement with their result of  $\Gamma_2 = 1.72 \pm 0.08$ (90% CL errors). We found a different normalization of the Earth emission spectrum however, which we discuss in Sect. 5.3, where we also discuss the separate spectra obtained for the albedo and the CR-induced emission.

The spectrum of the sum of all point sources detected at more than 2$\sigma$ on average among the 4 EOs is added in Fig. 6 for comparison. The impression that point sources contribute much less than the GRXE is misleading. This is related to the arbitrary area we chose for the normalization of the GRXE. If we had normalized it to the area actually covered by the partially coded FoV of IBIS, we would have had a GRXE spectrum scaled down by a factor of $\sim $4, depending a bit on the EO. This would then lead to a higher contribution of the point sources compared to the GRXE in qualitative agreement with the SPI results by Bouchet et al. (2008).

5 Discussion

The spectra in the $\sim $20-200 keV range presented above will now be compared to previously published INTEGRAL results and to spectra obtained by other satellites. In the subsections below, we discuss this separately for the CXB spectrum, the GRXE and the Earth emission.

5.1 Sky background spectrum

It is interesting to compare the CXB spectrum obtained by the thorough analysis of the IBIS/ISGRI detector lightcurves presented here with the INTEGRAL results previously published by Churazov et al. (2007). The comparison is shown in Fig. 7. Our approach could significantly increase the useful energy range of the IBIS/ISGRI data towards higher energies. The new results fall slightly below the previous IBIS/ISGRI spectrum, while we get a good agreement with the SPI results of Churazov et al. (2007), except possibly for the first energy bin.

\begin{figure} \par\includegraphics[width=8.5cm,clip]{13072f7.eps} \end{figure} Figure 7:

Comparison of the IBIS/ISGRI CXB spectrum obtained here (red circles) with the previous INTEGRAL results of IBIS/ISGRI (black diamonds), JEM-X (blue squares) and SPI (green triangles) published by Churazov et al. (2007).

Open with DEXTER

\begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f8.eps} \end{figure} Figure 8:

Comparison of the CXB spectrum obtained by INTEGRAL - JEM-X measurements (blue squares) from Churazov et al. (2007) and our IBIS/ISGRI results (red circles) - with the HEAO-1 spectra and analytical model by Gruber et al. (1999) (error bars and dashed line). The data of the A-4 instrument of HEAO-1 are shown in green with original normalization, while we show in orange the spectrum of the A-2 instrument and of the model, both increased by 10% in intensity.

Open with DEXTER

\begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f9.eps} \end{figure} Figure 9:

Comparison of the INTEGRAL IBIS/ISGRI (red circles, this work) and JEM-X (magenta diamonds, Churazov et al. 2007) spectra with the other recent CXB measurements by Swift and BeppoSAX. The Swift/XRT error box (orange shaded area) and the Swift/BAT results (green triangles) are from Moretti et al. (2009) and Ajello et al. (2008), respectively. The best-fit model of Moretti et al. (2009) for the combined Swift dataset is shown with a black line and grey uncertainty area. The original BeppoSAX/PDS measurements of Frontera et al. (2007) were scaled by +13% in intensity (blue squares) to correct for the difference in Crab normalization with respect to INTEGRAL. The analytical model we propose in Eq. (5) is shown as a purple dashed line.

Open with DEXTER

As shown in Fig. 8, the slightly lower emission we obtain now with IBIS/ISGRI is consistent with the HEAO-1 measurements and its analytical approximation by Gruber et al. (1999). The flux scaling of the HEAO-1 spectrum by +10% as suggested by Churazov et al. (2007) is actually not required anymore in the IBIS/ISGRI energy range. The discrepancy appears only below 20 keV for the INTEGRAL/JEM-X data that indicate a higher CXB intensity than the HEAO-1 measurements. It seems therefore that a simple scaling in intensity of the historic HEAO-1 spectrum is not able to consistently adjust the combined CXB measurements of INTEGRAL, both below and above the turnover.

However, as illustrated in Fig. 8, there is some freedom within the uncertainties to scale up by $\sim $10% the intensity of the spectrum of the A-2 instrument of HEAO-1 without changing that of the A-4 experiment. This would better match the JEM-X measurements and other results by recent X-ray instruments, which all suggest a higher intensity below 20 keV than obtained by HEAO-1/A-2 (e.g. Gilli et al. 2007, Fig. 15). The net effect would be a broadening of the CXB hump and a slight shift of its maximum towards lower energies. The expected qualitative consequence for an AGN population synthesis of the CXB would be a reduction of the contribution of the most highly obscured AGN, in particular the Compton-thick ones (e.g. Treister et al. 2009). Alternatively, it could also indicate a slightly stronger contribution from a population of distant (redshifted) luminous AGN compared to the local population (e.g. Treister & Urry 2005).

Another consistency check of our results is to compare them to the recent Swift and BeppoSAX measurements. This is illustrated in Fig. 9 where the Swift/XRT and the Swift/BAT spectra are from Moretti et al. (2009) and Ajello et al. (2008), respectively. Our data are consistent with the Swift/BAT results and the combined XRT-BAT spectral model proposed by Moretti et al. (2009), although they tend to be at a significantly lower intensity. Our data agree very well with the BeppoSAX/PDS data (Frontera et al. 2007, Fig. 6 Bottom) provided that they are scaled by a factor of 1.13 in intensity to account for the difference in the Crab normalization in the 20-50 keV band between BeppoSAX/PDS (Frontera et al. 2007, $F_{{\rm Crab}} = 9.22 \times 10^{-9}$erg cm-2 s-1) and INTEGRAL (Churazov et al. 2007, $F_{{\rm Crab}} = 10.4\!\times\!10^{-9}$erg cm-2 s-1). We note that the latter estimation for INTEGRAL is fully consistent with the value obtained with OSA 7.0. The measured fluxes are $F_{{\rm Crab}} = 10.30 \times 10^{-9}$erg cm-2 s-1 and $10.46 \times 10^{-9}$erg cm-2 s-1 for the Crab observations of revolutions 365 and 422, respectively. The obtained spectrum seems to be also very consistent in the peak region with the recent CXB synthesis model by Treister et al. (2009). It thus gives additional evidence for a small Compton-thick AGN fraction in the CXB spectrum, close to 9% instead about 30-40% postulated before (e.g. Treister & Urry 2005). Our data cannot constrain a possible hardening of the CXB spectrum above 100 keV, but are consistent with an additional contribution of flat-spectrum radio quasars, which have been found to dominate the CXB in the MeV range (Ajello et al. 2009).

Based on the considerations above, we can tentatively suggest a slight adaptation of the analytical description of the CXB proposed by Moretti et al. (2009, Eq. (4)), as:

\begin{displaymath} E^2~\frac{{\rm d}N_{\gamma}}{{\rm d}E}=E^2~\frac{0.109~\mbox... ...$^{-1}$ }}{(E/28~\mbox{keV})^{1.40}+(E/28~\mbox{keV})^{2.88}}, \end{displaymath} (5)

where the only difference - but a correction of a typo in the units - is a change of the break energy from 29 keV to 28 keV. The corresponding spectral shape is at the lower limit of the uncertainty area of the Swift model as shown in Fig. 9.

5.2 Galactic ridge emission

\begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f10.eps} \end{figure} Figure 10:

Comparison of the obtained GRXE spectrum (blue squares) with recent other determinations, all renormalized to the central radian of the Milky Way defined by $\vert l\vert < 30^\circ $ and $\vert b\vert < 15^\circ $. The previous INTEGRAL/IBIS data (red circles) and the RXTE/PCA measurements (black diamonds) are from Krivonos et al. (2007, Fig. 14). The INTEGRAL/SPI spectrum (green triangles) is from Bouchet et al. (2008, Fig. 9).

Open with DEXTER

It is not easy to compare results on the GRXE from one publication to the other, because the emission is often defined in different regions of the Galaxy. As the region covered by our observations is away from the Galactic bulge where most determinations have been made, we have to rescale them to a more commonly used area. We choose the central radian of the Milky Way defined in Galactic longitude l and latitude b by $\vert l\vert\leq 30^\circ$ and $\vert b\vert\leq 15^\circ$ as the reference area for a comparison of the various measurements. As we do have an analytical model of the GRXE (see Sect. 3.2), it is possible to determine the scaling factor from any region in the Galaxy to the chosen area. The resulting renormalized spectra are compared in Fig. 10. Our measurements had to be scaled by a factor of 0.16 to correspond to the chosen area. The INTEGRAL/IBIS spectrum from Krivonos et al. (2007, Fig. 14) corresponding to the IBIS FoV area centered on the Galactic bulge was multiplied by a calculated factor of 2.77. We used the same factor for the RXTE/PCA data that have been scaled by Krivonos et al. (2007) to match the IBIS measurement at 20 keV. For the INTEGRAL/SPI spectrum of Bouchet et al. (2008, Fig. 9) that correspond already to the area chosen here, we just had to convert the units.

In general, Fig. 10 shows a good agreement between the results of the various instruments. This is quite remarkable for data that were not arbitrarily renormalized, but were rescaled based on our very simple double-Lorentzian model of the GRXE. This suggests that the model provides a fair description of the overall emission of the inner Galaxy in the hard X-ray range. All three independent INTEGRAL measurements reveal a minimum at about 80 keV. This was only suggested by the 2-$\sigma$ upper limits of Krivonos et al. (2007), but is confirmed now by our Earth occultation results and the latest SPI results of Bouchet et al. (2008). Our IBIS/ISGRI results do, however, suggest that the minimum is shallower than previously found. The diffuse GRXE below 80 keV is thought to be due to a population of accreting white dwarfs too faint to be resolved into discrete sources in the hard X-rays (Revnivtsev et al. 2006; Krivonos et al. 2007). It is only at energies of $\sim $6-7 keV that the diffuse emission could finally be resolved using deep Chandra observations (Revnivtsev et al. 2009). The bremsstrahlung temperature of $kT = 14.7\pm1.4$ that we derived in Sect. 4 for the accretion column onto the pole of the white dwarfs agrees well with the measurements of individual intermediate polar systems detected by Swift/BAT (Brunschweiger et al. 2009). Based on Table 2 in the latter publication, we note that this temperature would correspond to a typical white dwarf mass of $M_{{\rm wd}} \simeq 0.60\pm0.05~M_{\odot}$ according to the model of Suleimanov et al. (2005). This estimate is just slightly above the expected average mass of white dwarfs in the Galaxy ( $\overline{M_{{\rm wd}}} \sim 0.5~M_{\odot}$) that was found to agree well with the previous IBIS/ISGRI results on the GRXE (Krivonos et al. 2007, and references therein).

\begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f11.eps} \end{figure} Figure 11:

Comparison of the obtained GRXE spectrum (blue error bars and long-dashed line) with the higher-energy emission of the Galactic ridge in the region defined by $\vert l\vert < 30^\circ $ and $\vert b\vert < 15^\circ $ as observed by INTEGRAL/SPI (green triangles) from Bouchet et al. (2008, Fig. 9) and by CGRO/COMPTEL (black diamonds) and CGRO/EGRET (red error bars). The CGRO data are from Porter et al. (2008, Fig. 3), which is based on the analysis by Strong et al. (2004,1999). The green solid line shows the model fitting the SPI observations above 100 keV (Bouchet et al. 2008). It is the sum of a powerlaw continuum (green dotted line), the positronium continuum (short-dashed line) and a narrow electron-positron annihilation line at 511 keV. A scaling by 20% of the high-energy powerlaw is indicated by the blue dotted-line.

Open with DEXTER

Above 80 keV the GRXE spectrum is likely dominated by inverse-Compton emission from the interstellar medium (Porter et al. 2008). We derived an intensity at the level of the 2-$\sigma$ upper limits of Krivonos et al. (2007), in excellent agreement with the latest SPI observations (Bouchet et al. 2008). The photon index of the high-energy powerlaw derived by these authors ( $\Gamma = 1.55$) also agrees very well with our results, although it is too poorly constrained by our data alone to be fitted independently.

The overall shape of the high-energy spectrum of the GRXE including the observations of the Compton gamma-ray observatory (CGRO) up to 10 GeV is shown in Fig. 11. As our data are scaled from a region at $320^\circ < l < 340 ^\circ$ lying outside the galactic bulge where the bulk of the positronium annihilation is emitted, they should be almost unaffected by the positronium continuum. This implies that the $\sim $20% higher normalization of the high-energy powerlaw suggested by our data should be intrinsic. This would agree well with the discussion of Porter et al. (2008) concerning a possible higher normalization of up to 40% for this powerlaw.

5.3 Earth emission

\begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f12.eps} \end{figure} Figure 12:

Comparison of the obtained Earth emission spectrum (green triangles) with previous determinations by various missions. The thin grey line is the INTEGRAL spectrum of Churazov et al. (2007) as described in Fig. 13. The obtained IBIS/ISGRI spectrum lies well between the OSO-3 (black diamonds) and the Swift/BAT (red circles) measurements of Schwartz & Peterson (1974) and Ajello et al. (2008), respectively. The values of the BeppoSAX/PDS measurements of Frontera et al. (2007) were increased by 13% (blue squares) to be consistent with Fig. 9.

Open with DEXTER

Before discussing the relative contributions of the two Earth emission components, we first compare, in Fig. 12, the obtained spectrum of the Earth with other determinations. The Earth emission is found to be very consistent with the spectra obtained previously, although there is a big scatter among the various determinations. This is at least partially due to the modulation of the Earth emission by the solar cycle and a dependence of the observed flux on the spacecraft altitude and the geomagnetic latitude (Sazonov et al. 2007). For instance, the difference in normalization between the Swift/BAT spectrum and our determination can be related to INTEGRAL drifting towards an almost polar orbit, while Swift has a more equatorial orbit. The difference by roughly a factor of two depending on the energy is consistent with the difference found by the polar-orbiting satellite 1972-076B between the equatorial and the polar regions (Imhof et al. 1976). We did not include these spectra here for the sake of clarity, but they would be compatible with the other determinations provided that they are corrected for unsubtracted CXB emission as shown by Ajello et al. (2008, Figs. 15 and 16).

A discrepancy we cannot ascribe to a different observation epoch or a different viewpoint is the inconsistency of our results with the spectrum derived from the same INTEGRAL observations by Churazov et al. (2007). We derive a higher Earth emission at low energies and a lower intensity at high energies. The discrepancy at the highest energies could somehow be due to the fact that our results are based on IBIS data and their results on SPI, although both instruments are well cross-calibrated. It is also possible that the difference comes from our more detailed modeling of several instrumental effects described in Sect. 3.3. At the lowest energies, the neglection of point source emission by Churazov et al. (2007) is a likely cause of the discrepancy, since for a given CXB we need more Earth emission to compensate for the occultation of point sources.

\begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f13.eps} \vspace*{6mm} \end{figure} Figure 13:

Resulting spectrum of the total Earth emission (green triangles, solid line) with separated contributions from the Earth reflection of the CXB (cyan triangles, short-dashed line) and the CR-induced atmospheric emission (magenta triangles, long-dashed line). The thin grey curves are normalized as derived by Churazov et al. (2007), whereas the thick colored lines are normalized to match our measurements.

Open with DEXTER

To better characterize the difference between the two determinations of the Earth spectrum, we show in Fig. 13 the decomposition of the overall Earth emission in the two distinct components considered in both studies. Those are the reflection of the CXB by the Earth - the albedo - and the emission induced by CR interactions in the atmosphere. The spectra of both components can be described by analytical functions fitted to the results of Monte-Carlo simulations published by Churazov et al. (2008) for the albedo, and by Sazonov et al. (2007) for the atmospheric emission. In order to fit the overall spectrum of the Earth with these two components, we need to increase the albedo component by $\sim $40% and decrease the atmospheric emission by $\sim $60% compared to the normalizations suggested by Churazov et al. (2007). We thus get a normalization of the atmospheric emission (Sazonov et al. 2007, Eq. (1)) of $13.2~\mbox{keV~cm$^{-2}$ ~s$^{-1}$ ~sr$^{-1}$ }$ at the break energy of E = 44 keV, instead of $32.9~\mbox{keV~cm$^{-2}$ ~s$^{-1}$ ~sr$^{-1}$ }$ as derived by Churazov et al. (2007). This difference in normalization is much more important than the few percent of likely overestimation mentioned by Sazonov et al. (2007) related to the inclusion of the Compton-scattering from particles that would have intersected the surface of the Earth. Further speculations on the origin of this discrepancy are beyond the scope of this paper.

Concerning the albedo, we note that the increase by a factor 1.4 we derive here is not on the Earth reflection expected for the HEAO-1 analytic approximation of Gruber et al. (1999), but on this spectrum already scaled by a factor of 1.1 according to the results of Churazov et al. (2007). As the CXB spectrum obtained here agrees well with the original HEAO-1 spectrum, our results suggest a reflection efficiency of the Earth atmosphere $\sim $50% higher than obtained by the Monte-Carlo simulations of Churazov et al. (2008). According to these authors, the shape of the input CXB spectrum has only a very limited effect on the reflected spectrum, especially at energies below $\sim $30 keV, so there must be another reason for the important difference we observe. One possibility is related to the delicate modeling of the composition of the atmosphere. Could the presence of clouds have a significant effect by increasing the amount of hydrogen atoms in the upper atmosphere, resulting in a more ``Sun-like'' albedo with more reflection at the lower energies (see Churazov et al. 2008, Fig. 6)? Another possibility would be the presence of another Earth emission component emerging at the lowest energies, in particular the potentially strong X-ray emission of aurorae (e.g. Østgaard et al. 2001). We note that Churazov et al. (2007) found clear evidence for auroral emission in the INTEGRAL/JEM-X data during EO 2 and EO 3.

Finally, it is fair to mention that the almost perfect agreement we show in Fig. 13 between the data and the model for the two distinct Earth emission components is mainly due to the choice of the input spectrum for the atmospheric emission (see Sect. 3.5). The strong degeneracy between the two Earth emission components discussed in Sect. 5.4 does not allow us to get such a good distinction of the two components when starting from an arbitrary set of input parameters. We would just get a tendency for the CR-induced emission to dominate at the higher energies and vice-versa at low energy.

5.4 Degeneracy issues

Degeneracy is the reason why it is so difficult to determine the CXB spectrum with Earth-occultation data. The basic problem is that a spatially uniform Earth emission cannot be distinguished from the CXB occultation when the instrumental background level is unknown. It is because of this that all previous studies using the Earth as occultator had to assume a priori the spectrum of the CXB and to a large extend also that of the Earth emission (see Ajello et al. 2008; Frontera et al. 2007; Churazov et al. 2007). Here, we tried to solve the degeneracy issue by fixing the spatial distribution of the Earth emission components rather than its spectral shape and by introducing a spectral smoothness constraint as explained in Sect. 3.5. However, because of the noise in the data and a possible deviation of the actual instrumental background variations compared to those assumed based on the SPI/ACS lightcurve (see Sect. 3.4.3) it is not possible to completely solve the degeneracy issues.

To overcome this problem, we had also to incorporate some a priori assumptions on the spectral shape of the CXB and of one of the two Earth emission components, chosen to be the atmospheric CR-induced emission because of its strong drop at low energies that cannot be easily determined otherwise. As explained in Sect. 3.5, this is however only used to define the set of input spectra that we then perturbate randomly before fitting the parameters to the data. Despite this, we still keep a dependence on the input parameters in the results. This is very obvious for the two Earth emission components that are strongly degenerated (see Sect. 5.3).

Another important degeneracy is between the instrumental background and the sum of the sky background plus Earth emission. A higher instrumental background will imply lower sky background and Earth emission, and vice-versa. Actually, the data do primarily constrain the difference between the Earth and the CXB emissions. This difference is basically the height of a bump in the lightcurve in case the Earth emission dominates or, alternatively, the depth of a trough, when the sky background occultation dominates (see Fig. 5). To test the effect of this degeneracy on our results, we fitted the data with the same procedure as explained in Sect. 3.5, but with an input spectrum for the CXB increased by 10%. This resulted in a CXB spectrum with a similar shape, but a higher normalization by about the same factor. However, to compensate this, the Earth albedo is then found to be higher than derived by Churazov et al. (2007) by a factor of $\sim $2, instead of $\sim $1.4 (see Sect. 5.3). Although this cannot be completely excluded, the discrepancy on the normalization of the albedo is judged to be unrealistically high. We thus favor the more conservative results obtained with the original normalization of the CXB for the input parameters.

The presence of the GRXE in the observed region of the sky can also add some degeneracy, but its location to the side of the FoV was actually rather optimal as its maximal occultation effect occurred earlier in the lightcurves than for the CXB (see Fig. 3). We only noted a slight degeneracy between the GRXE and the sum of the CXB and the polar-enhanced atmospheric emission.

We identified an instrumental effect that affects the results of both the GRXE and of the Earth emission at energies above $\sim $60 keV. By ignoring the possibility of an increasing or decreasing trend of the instrumental background in addition to the SPI/ACS modulation (see Eq. (3)), we obtained a high-energy drop of the Earth emission together with an unrealistically steep rise of the GRXE spectrum. This behavior aims at compensating a decreasing trend of the instrumental counts in the spectral region of the emission lines of W, Pb and Bi (60-80 keV, see Sect. 2) and an increasing trend of the counts at even higher energies. This is likely due to radioactive decay at the exit of the radiation belts and illustrates the sensitivity of the method on a very accurate description of all instrumental effects.

Finally, we note that an underestimation of the contribution of the point sources will tend to increase both the GRXE and the CXB intensity because point sources are distributed all over the FoV with increased density in the galactic plane.

6 Conclusion

We presented the results of an original analysis of the four consecutive Earth-occultation observations by the IBIS/ISGRI instrument aboard the INTEGRAL satellite. Our approach is complementary to the previous study of these data by Churazov et al. (2007), because instead of fixing the spectral shape of the CXB and fitting its normalization, we attempt to derive the complete spectral information from the observed detector lightcurves in different energy bins. This requires a deep understanding of the instrumental effects and a careful modeling of the spatial distribution of the various contributions from the Galaxy, the Earth and point sources. Despite inherent degeneracy issues that forced us to fit the data with an additional spectral smoothness constraint and adequate input parameters, the approach used here results in a coherent set of spectra for the CXB, the GRXE and the Earth emission.

The obtained IBIS/ISGRI results for the CXB are consistent with the historic HEAO-1 spectrum, without any scaling in intensity. The scaling by +10% in intensity proposed by Churazov et al. (2007) is not incompatible with the actual dataset, but is disfavored as it implies a CXB reflection by the Earth twice as strong than the one derived by the Monte-Carlo simulations of Churazov et al. (2008). The obtained spectrum also agrees well with recent Swift and BeppoSAX determinations. We propose a slight adaptation of the CXB model spectrum suggested by Moretti et al. (2009), which is based on Swift data alone, that implies a reduced fraction of strongly absorbed AGN, compared to the HEAO-1 spectrum of Gruber et al. (1999).

The spectrum of the Earth emission is very well described by the contribution of two distinct components: the reflection of the CXB that is dominant at lower energies, and the CR-induced atmospheric emission. The derived normalizations for these two components is however found to be very different from what was suggested by the study of Churazov et al. (2007).

With a total observation time of only about a day, these special types of INTEGRAL observations yield a spectrum of the GRXE with comparable statistics as obtained by combining all available INTEGRAL/SPI observations. This allows us to observationally estimate the average mass of white dwarfs in the Galaxy. Conducting similar observations in different regionsof the Galactic plane would be useful to characterize the longitudinal distribution of the GRXE.

However, it would be even more important to conduct Earth observations away from the Galactic plane to lift any degeneracy related to the presence of the GRXE and point sources. This would lead to a determination of the CXB with improved statistics and less systematics and thus fully exploit INTEGRAL's unique capability to observe the entire Earth from a high-altitude orbit.

Acknowledgements
Based on observations with INTEGRAL, an ESA mission with instruments and science data centre funded by ESA member states (especially the PI countries: Denmark, France, Germany, Italy Switzerland, Spain), Czech Republic and Poland, and with the participation of Russia and the USA. P.L. has been supported in part by the Polish MNiSW grants NN203065933 and 362/1/N-INTEGRAL/2008/09/0, and the Polish Astroparticle Network 621/E-78/BWSN-0068/2008.

References

  1. Ajello, M., Greiner, J., Sato, G., et al. 2008, ApJ, 689, 666 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ajello, M., Costamante, L., Sambruna, R. M., et al. 2009, ApJ, 699, 603 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101,17 [Google Scholar]
  4. Beckmann, V., Soldi, S., Ricci, C., et al. 2009, A&A, 505, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bouchet, L., Jourdain, E., Roques, J.-P., et al. 2008, ApJ, 679, 1315 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boughn, S. P., Crittenden, R. G., & Koehrsen, G. P. 2002, ApJ, 580, 672 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brandt, W. N., & Hasinger, G. 2005, ARA&A, 43, 827 [Google Scholar]
  8. Brunschweiger, J., Greiner, J., Ajello, M., et al. 2009, A&A, 496, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Churazov, E., Sunyaev, R., Revnivtsev, M., et al. 2007, A&A, 467, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Churazov, E., Sazonov, S., Sunyaev, R., et al. 2008, MNRAS, 385, 719 [NASA ADS] [CrossRef] [Google Scholar]
  11. Courvoisier, T. J.-L., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Frontera, F., Orlandini, M., Landi, R., et al. 2007, ApJ, 666, 86 [NASA ADS] [CrossRef] [Google Scholar]
  13. Giacconi, R., Gursky, H., Paolini, F. R., et al. 1962, Phys. Rev. Lett., 9, 439 [NASA ADS] [CrossRef] [Google Scholar]
  14. Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Gruber, D. E., Matteson, J. L., Peterson, L. E., et al. 1999, ApJ, 520, 124 [NASA ADS] [CrossRef] [Google Scholar]
  16. Imhof, W. L., Nakano, G. H., & Reagan, J. B. 1976, J. Geophys. Res., 81, 2835 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kinzer, R. L., Jung, G. V., Gruber, D. E., Matteson, J. L., & Peterson, L. E. 1997, ApJ, 475, 361 [NASA ADS] [CrossRef] [Google Scholar]
  18. Krivonos, R., Revnivtsev, M., Churazov, E., et al. 2007, A&A, 463, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Marshall, F. E., Boldt, E. A., Holt, S. S., et al. 1980, ApJ, 235, 4 [NASA ADS] [CrossRef] [Google Scholar]
  20. Moretti, A., Pagani, C., Cusumano, G., et al. 2009, A&A, 493, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Østgaard, N., Stadsnes, J., Bjordal, J., et al. 2001, J. Geophys. Res., 106, 26081 [NASA ADS] [CrossRef] [Google Scholar]
  22. Paltani, S., Walter, R., McHardy, I. M., et al. 2008, A&A, 485, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Porter, T. A., Moskalenko, I. V., Strong, A. W., Orlando, E., & Bouchet, L. 2008, ApJ, 682, 400 [NASA ADS] [CrossRef] [Google Scholar]
  24. Revnivtsev, M., Sazonov, S., Gilfanov, M., Churazov, E., & Sunyaev, R. 2006, A&A, 452, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Revnivtsev, M., Molkov, S., & Sazonov, S. 2008, A&A, 483, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Revnivtsev, M., Sazonov, S., Churazov, E., et al. 2009, Nature, 458, 1142 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  27. Sazonov, S., Churazov, E., Sunyaev, R., et al. 2007, MNRAS, 377, 1726 [NASA ADS] [CrossRef] [Google Scholar]
  28. Sazonov, S., Krivonos, R., Revnivtsev, M., Churazov, E., & Sunyaev, R. 2008, A&A, 482, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Schwartz, D. A., & Peterson, L. E. 1974, ApJ, 190, 297 [NASA ADS] [CrossRef] [Google Scholar]
  30. Smart, D. F., & Shea, M. A. 2005, Advances in Space Research, 36, 2012 [Google Scholar]
  31. Strong, A. W., Bloemen, H., Diehl, R., Hermsen, W., & Schönfelder, V. 1999, Astrophys. Lett. Comm., 39, 209 [Google Scholar]
  32. Strong, A. W., Moskalenko, I. V., & Reimer, O. 2004, ApJ, 613, 962 [NASA ADS] [CrossRef] [Google Scholar]
  33. Suleimanov, V., Revnivtsev, M., & Ritter, H. 2005, A&A, 435, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Terrier, R., Lebrun, F., Bazzano, A., et al. 2003, A&A, 411, L167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Treister, E., & Urry, C. M. 2005, ApJ, 630, 115 [NASA ADS] [CrossRef] [Google Scholar]
  36. Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Ueda, Y., Akiyama, M., Ohta, K., et al. 2003, ApJ, 598, 886 [NASA ADS] [CrossRef] [Google Scholar]
  39. Vedrenne, G., Roques, J.-P., Schönfelder, V., et al. 2003, A&A, 411, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Winkler, C., Courvoisier, T. J.-L., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Zdziarski, A. A. 1996, MNRAS, 281, L9 [NASA ADS] [Google Scholar]

Footnotes

... response[*]
To take into account the effect of the ISGRI detector response, we used XSpec (Arnaud 1996) with the standard ISGRI ARF and redistribution matrix file (RMF) of OSA 7.0 to derive the relative strength of the instrumental modulation of a powerlaw model spectrum from one channel to the other. 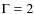This modulation follows basically that of the ARF, with some additional smoothing and distortion towards lower energies due to the RMF, with only a slight dependence on the photon index taken to be typically of $\Gamma = 2$.
Copyright ESO 2010

All Tables

Table 1:   List of point sources detected in at least one of the four EOs.

Table 2:   Numerical values of the obtained spectra shown in Fig. 6.

Table 3:   Spectral fit parameters for the CXB, the GRXE and the Earth emission.

All Figures

  \begin{figure} \par\includegraphics[width=6cm]{13072f1a.eps}\includegraphics[width=6cm]{13072f1b.eps} \end{figure} Figure 1:

Model IBIS/ISGRI images of the sky with ( right) and without ( left) instrumental vignetting effects (see Fig. 2). They show the geometry and relative intensity (on a logarithmic scale from dark and blue to red and bright areas) of the various components during the first EO at IJD = 2216.04 as derived for channel 3 ($\sim $27 keV). The bluish circle shows emission of the Earth occulting the diffuse sky background (purple), the Galactic ridge (red strip), and the point sources (bright dots). The instrumental background is ignored for clarity. The images extend over the partially coded FoV ( $28.8^\circ \times 29.2^\circ $). Point sources are convolved with a circular Gaussian typical for the instrumental resolution ( $\sigma = 0.1^\circ $).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=16 150 430 700,clip,width=9cm]{13072f2.eps} \end{figure} Figure 2:

Surfaces representing the five IBIS/ISGRI vignetting effects that affect the incoming radiation until it reaches the detector plane. The effects are those corresponding to channel 12 ($\sim $72 keV) and are: a) the IBIS tube transparency to off-axis radiation, b) the energy independent exposure map, c) the effective coded-mask transparency, d) the transmission of the Nomex structure supporting the mask, and e) the absorption of the ISGRI spider beams. The total vignetting effect is the product of the effects b) to e) with the addition of effect a), which extends well outside the partially coded FoV.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{13072f3.eps} \end{figure} Figure 3:

Model lightcurves of each component for channel 3 ($\sim $27 keV) of the first EO. The detector count rate values are the effective contribution of the point sources (orange stars). The other components are the sky background (red circles), the GRXE (blue squares), and the Earth CXB reflection (cyan triangles, long-dashed) and the CR-induced emission (magenta triangles, short-dashed). For these diffuse components the detector count rate corresponds to an incident radiation of 40 count s-1 sr-1. For the instrumental background (black diamonds) we show the relative modulation, $M_{{\rm ins}}(t)/\overline {M_{{\rm ins}}}$, derived from the SPI/ACS corresponding to a detector count rate of 10 count s-1.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{13072f6.eps} \end{figure} Figure 4:

IBIS/ISGRI count rate spectra of each model component derived from the detector lightcurves of the INTEGRAL EOs. The values are vignetting-corrected count rates per channel in units of 10 count s-1 sr-1, except for the instrumental background (black diamonds) for which they are actual detector count rates in count s-1. For the CXB (red circles), the GRXE (blue squares) and the total Earth emission (green triangles), the dotted lines of the same color show the average spectra obtained for the four independent EOs. The relative contributions to the Earth emission from the CXB reflection (cyan triangles, long-dashed) and the CR scattering in the atmosphere (magenta triangles, short-dashed) are also shown.

Open with DEXTER
In the text

  \begin{figure} \par\mbox{\includegraphics[width=6cm]{13072f5a.eps}\includegraphi... ...5b.eps}\includegraphics[width=6cm]{13072f5c.eps} } \vspace*{-1.5mm} \end{figure} Figure 5:

Examples of detector lightcurve fits ( upper panels) and associated residuals ( lower panels) for the first EO at three representative energies: $\sim $27 keV (channel 3), $\sim $52 keV (channel 9) and $\sim $112 keV (channel 15), from left to right. The reduced $\chi ^2$ value of the best-fit curve (red line) is 0.97, 1.08 and 1.06 respectively. The contribution of different components is shown by different colors with the same coding as in Figs. 3 and 4. From bottom to top we add to the instrumental background (grey) - modulated by the SPI/ACS lightcurve and a possible trend with time - the sky background (red), the GRXE (blue), the albedo (cyan) and atmospheric (magenta) Earth emissions, and the fixed contribution from point sources (orange).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=9cm]{13072f4.eps} \end{figure} Figure 6:

Unfolded IBIS/ISGRI spectra of the sky background (red circles), the earth emission (green triangles) and the GRXE (blue squares) with their best fit (dashed lines) and the more physical (dotted lines) spectral models (see Tables 2 and 3). The contribution of the sum of the considered point sources averaged over the four EOs is also shown (orange stars).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{13072f7.eps} \end{figure} Figure 7:

Comparison of the IBIS/ISGRI CXB spectrum obtained here (red circles) with the previous INTEGRAL results of IBIS/ISGRI (black diamonds), JEM-X (blue squares) and SPI (green triangles) published by Churazov et al. (2007).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f8.eps} \end{figure} Figure 8:

Comparison of the CXB spectrum obtained by INTEGRAL - JEM-X measurements (blue squares) from Churazov et al. (2007) and our IBIS/ISGRI results (red circles) - with the HEAO-1 spectra and analytical model by Gruber et al. (1999) (error bars and dashed line). The data of the A-4 instrument of HEAO-1 are shown in green with original normalization, while we show in orange the spectrum of the A-2 instrument and of the model, both increased by 10% in intensity.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f9.eps} \end{figure} Figure 9:

Comparison of the INTEGRAL IBIS/ISGRI (red circles, this work) and JEM-X (magenta diamonds, Churazov et al. 2007) spectra with the other recent CXB measurements by Swift and BeppoSAX. The Swift/XRT error box (orange shaded area) and the Swift/BAT results (green triangles) are from Moretti et al. (2009) and Ajello et al. (2008), respectively. The best-fit model of Moretti et al. (2009) for the combined Swift dataset is shown with a black line and grey uncertainty area. The original BeppoSAX/PDS measurements of Frontera et al. (2007) were scaled by +13% in intensity (blue squares) to correct for the difference in Crab normalization with respect to INTEGRAL. The analytical model we propose in Eq. (5) is shown as a purple dashed line.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f10.eps} \end{figure} Figure 10:

Comparison of the obtained GRXE spectrum (blue squares) with recent other determinations, all renormalized to the central radian of the Milky Way defined by $\vert l\vert < 30^\circ $ and $\vert b\vert < 15^\circ $. The previous INTEGRAL/IBIS data (red circles) and the RXTE/PCA measurements (black diamonds) are from Krivonos et al. (2007, Fig. 14). The INTEGRAL/SPI spectrum (green triangles) is from Bouchet et al. (2008, Fig. 9).

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f11.eps} \end{figure} Figure 11:

Comparison of the obtained GRXE spectrum (blue error bars and long-dashed line) with the higher-energy emission of the Galactic ridge in the region defined by $\vert l\vert < 30^\circ $ and $\vert b\vert < 15^\circ $ as observed by INTEGRAL/SPI (green triangles) from Bouchet et al. (2008, Fig. 9) and by CGRO/COMPTEL (black diamonds) and CGRO/EGRET (red error bars). The CGRO data are from Porter et al. (2008, Fig. 3), which is based on the analysis by Strong et al. (2004,1999). The green solid line shows the model fitting the SPI observations above 100 keV (Bouchet et al. 2008). It is the sum of a powerlaw continuum (green dotted line), the positronium continuum (short-dashed line) and a narrow electron-positron annihilation line at 511 keV. A scaling by 20% of the high-energy powerlaw is indicated by the blue dotted-line.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f12.eps} \end{figure} Figure 12:

Comparison of the obtained Earth emission spectrum (green triangles) with previous determinations by various missions. The thin grey line is the INTEGRAL spectrum of Churazov et al. (2007) as described in Fig. 13. The obtained IBIS/ISGRI spectrum lies well between the OSO-3 (black diamonds) and the Swift/BAT (red circles) measurements of Schwartz & Peterson (1974) and Ajello et al. (2008), respectively. The values of the BeppoSAX/PDS measurements of Frontera et al. (2007) were increased by 13% (blue squares) to be consistent with Fig. 9.

Open with DEXTER
In the text

  \begin{figure} \par\includegraphics[bb=16 144 600 510,clip,width=9cm]{13072f13.eps} \vspace*{6mm} \end{figure} Figure 13:

Resulting spectrum of the total Earth emission (green triangles, solid line) with separated contributions from the Earth reflection of the CXB (cyan triangles, short-dashed line) and the CR-induced atmospheric emission (magenta triangles, long-dashed line). The thin grey curves are normalized as derived by Churazov et al. (2007), whereas the thick colored lines are normalized to match our measurements.

Open with DEXTER
In the text

Copyright ESO 2010

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.