EDP Sciences
Home All issues Volume 508 / No 3 (December IV 2009) A&A, 508 3 (2009) 1173-1191 Full HTML
Free Access
Issue
A&A
Volume 508, Number 3, December IV 2009
Page(s) 1173 - 1191
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/200810644
Published online 27 October 2009

A&A 508, 1173-1191 (2009)

Photometric redshifts and cluster tomography in the ESO Distant Cluster Survey[*],[*]

R. Pelló1 - G. Rudnick2 - G. De Lucia3,18 - L. Simard4 - D. I. Clowe5 - P. Jablonka6,7 - B. Milvang-Jensen8,19 - R. P. Saglia9 - S. D. M. White3 - A. Aragón-Salamanca10 - C. Halliday11,20 - B. Poggianti12 - P. Best13 - J. Dalcanton14 - M. Dantel-Fort15 - B. Fort15 - A. von der Linden3 - Y. Mellier15 - H. Rottgering16 - D. Zaritsky17

1 - Laboratoire d'Astrophysique de Toulouse-Tarbes, CNRS, Université de Toulouse, 14 avenue Édouard Belin, 31400 Toulouse, France
2 - Leo Goldberg Fellow, National Optical Astronomical Observatory, 950 North Cherry Avenue, Tucson, AZ 85721, USA
3 - Max-Planck-Institut für Astrophysik, Karl-Schwarschild-Str. 1, Postfach 1317, 85741 Garching, Germany
4 - Herzberg Institute of Astrophysics, National Research Council of Canada, Victoria, BC V9E 2E7, Canada
5 - Department of Physics and Astronomy, Ohio University, Athens, OH 45701, USA
6 - Observatoire de Genève, Laboratoire d'Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), 1290 Sauverny, Switzerland
7 - GEPI, CNRS-UMR8111, Observatoire de Paris, section de Meudon, 5 place Jules Janssen, 92195 Meudon Cedex, France
8 - Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
9 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, Postfach 1312, 85741 Garching, Germany
10 - School of Physics and Astronomy, University of Nottingham, University Park, Nottingham NG7 2RD, UK
11 - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
12 - Osservatorio Astronomico, vicolo dell'Osservatorio 5, 35122 Padova, Italy
13 - SUPA, Institute for Astronomy, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ, UK
14 - Astronomy Department, University of Washington, Box 351580, Seattle, WA 98195, USA
15 - Institut d'Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
16 - Sterrewacht Leiden, PO Box 9513, 2300 RA, Leiden, The Netherlands
17 - Steward Observatory, University of Arizona, 933 North Cherry Avenue, Tucson, AZ 85721
18 - INAF - Astronomical Observatory of Trieste, via G.B. Tiepolo 11, 34143 Trieste, Italy
19 - The Royal Library/Copenhagen University Library, Research Dept., Box 2149, 1016 Copenhagen K, Denmark
20 - Department of Physics and Astronomy, University of Glasgow, Glasgow G12 8QQ, UK

Received 21 July 2008 / Accepted 16 October 2009

Abstract
Context. This paper reports the results obtained on the photometric redshifts measurement and accuracy, and cluster tomography in the ESO Distant Cluster Survey (EDisCS) fields.
Aims. We present the methods used to determine photometric redshifts to discriminate between member and non-member galaxies and reduce the contamination by faint stars in subsequent spectroscopic studies.
Methods. Photometric redshifts were computed using two independent codes both based on standard spectral energy distribution (SED) fitting methods ( ${\it Hyperz}$and Rudnick's code). Simulations were used to determine the redshift regions for which a reliable determination of photometric redshifts was expected. The accuracy of the photometric redshifts was assessed by comparing our estimates with the spectroscopic redshifts of $\sim $1400 galaxies in the $0.3\le z\le 1.0$ domain. The accuracy expected for galaxies fainter than the spectroscopic control sample was estimated using a degraded version of the photometric catalog for the spectroscopic sample.
Results. The accuracy of photometric redshifts is typically $\sigma(\Delta z/(1+z))\sim 0.05 \pm 0.01$, depending on the field, the filter set, and the spectral type of the galaxies. The quality of the photometric redshifts degrades by a factor of two in $\sigma (\Delta z/(1+z))$ between the brightest ($I\la 22$) and the faintest ($I\sim 24$-24.5) galaxies in the EDisCS sample. The photometric determination of cluster redshifts in the EDisCS fields using a simple algorithm based on $z_{\rm phot}$ is in excellent agreement with the spectroscopic values, such that $\delta z \sim$0.03-0.04 in the high-z sample and $\delta z \sim 0.05$ in the low-z sample, i.e. the $z_{\rm phot}$ cluster redshifts are at least a factor $\sim $(1+z) more accurate than the measurements of $z_{\rm phot}$ for individual galaxies. We also developed a method that uses both photometric redshift codes jointly to reject interlopers at magnitudes fainter than the spectroscopic limit. When applied to the spectroscopic sample, this method rejects $\sim $$50{-}90\%$ of all spectroscopically confirmed non-members, while retaining $\gtrsim$90% of all confirmed members.
Conclusions. Photometric redshifts are found to be particularly useful for the identification and study of clusters of galaxies in large surveys. They enable efficient and complete pre-selection of cluster members for spectroscopy, allow accurate determinations of the cluster redshifts based on photometry alone, and provide a means of determining cluster membership, especially for bright sources.

Key words: galaxies: clusters: general - galaxies: distances and redshifts - galaxies: photometry - galaxies: evolution

1 Introduction

Photometric redshifts are becoming an important tool in cosmological studies based on large and/or deep photometric surveys. Different studies have been devoted to the detailed analysis of photometric redshift accuracy in different contexts (e.g. Ilbert et al. 2006; Feldmann et al. 2006; Mobasher et al. 2007; Banerji et al. 2008; Margoniner & Wittman 2008; Hildebrandt et al. 2008; Ilbert et al. 2009). The robust evaluation of the accuracy reached by photometric redshifts requires homogeneous deep photometric data and a large dataset of spectroscopic redshifts for the same field. Simulations can be used to achieve uniform coverage in parameter spaces beyond the limits of spectroscopic surveys, in particular when missing information about certain redshift domains and/or spectroscopic types of galaxies.

Several papers used a recalibration between data and template models to improve the precision of photometric redshifs (e.g. Coe et al. 2006; Ilbert et al. 2006; Feldmann et al. 2006; Mobasher et al. 2007; Capak et al. 2007; Ilbert et al. 2009), a method that requires a large and representative training set of spectroscopic redshifts. However, model templates, optimized to achieve the highest possible accuracy in a given catalog/field, are not necesarily optimal in all cases because systematic problems in the catalog photometry could remain unrecognized during the template calibration process. A more robust estimate of photometric redshifts accuracy can be achieved for large datasets acquired in different independent fields. This is the approach used in this paper.

The ESO Distant Cluster Survey (hereafter EDisCS) is an ESO Large Programme designed to study the evolution of cluster galaxies over a significant fraction of cosmic time (White et al. 2005). The 20 clusters included in the EDisCS sample were selected from the Las Campanas Distant Cluster Survey (LCDCS, Gonzalez et al. 2001) with redshifts ranging between $\sim $0.4 and 1. More details about the survey and the cluster selection procedure can be found in the paper by White et al. (2005), and the EDisCS website[*]. The EDisCS programme includes homogeneous and deep photometry with ESO VLT and NTT (optical and near-IR; White et al. 2005; Aragón-Salamanca et al. in preparation) and multi-object spectroscopy with ESO VLT (Halliday et al. 2004; Milvang-Jensen et al. 2008), as well as other follow-up observations with HST/ACS (Desai et al. 2007), narrowband H$\alpha$ imaging (Finn et al. 2005) and XMM data (Johnson et al. 2006).

This paper is also intended to be the reference for the photometric redshifts and the cluster membership criteria adopted by the EDisCS collaboration, and used in the different EDisCS papers dealing with cluster membership and related quantities (e.g. De Lucia et al. 2004; White et al. 2005; Clowe et al. 2006; Poggianti et al. 2006; De Lucia et al. 2007; Desai et al. 2007; Rudnick et al. 2009). Photometric redshifts are particularly useful when used with cluster/structure finding algorithms, because they help to ensure that time-consuming spectroscopic observations are optimized (e.g. Li & Yee 2008).

The paper is organized as follows. In Sect. 2, we summarize the characteristics of the relevant photometric and spectroscopic data. A technical description of the photometric redshift methods and related procedures is provided in Sect. 3. The photometric redshift accuracy in the EDisCS survey is addressed in Sect. 4 using three different approaches: 1) simulations are used to determine the redshift regions for which a reliable determination of photometric redshifts is expected; 2) the actual quality achieved in this survey is estimated by direct comparison between the photometric and spectroscopic redshifts; and 3) the accuracy expected for galaxies fainter than the spectroscopic control sample is estimated using a degraded version of the spectroscopic sample catalog. Section 5 presents the comparison between spectroscopic and photometric determinations of cluster redshifts, as well as the results obtained on cluster tomography in the EDisCS fields. The photometric cluster membership criteria adopted by the EDisCS collaboration is introduced and discussed in Sect. 6. Discussion and conclusions are given in Sect. 7. The following cosmological parameters are adopted throughout this paper: $\Omega_{\Lambda}=0.7$, $\Omega_{\rm m}=0.3$, and $H_{0}=70~\rm km~ s^{-1}~ Mpc^{-1}$. Magnitudes are given in the Vega system.

2 Photometric and spectroscopic data

We use the ground-based photometric catalogs and spectroscopic redshifts obtained by the EDisCS collaboration for 20 clusters of galaxies with redshifts ranging between 0.4 and 1.0 (White et al. 2005). Although the final redshift distribution of this sample is found to be fairly uniformly distributed within this redshift interval, the original filter set was designed to bracket the relevant wavelength domain at $z\sim 0.5$ (low-z sample) and $z\sim 0.8$ (high-zsample). Photometric redshifts and related quantities depend strongly on the wavelength domain covered by the photometric Spectral Energy Distributions (hereafter SED), i.e. the filter set. Throughout the paper, we therefore retain the original division of the clusters into the ``low-z'' and the ``high-z'' samples.

Deep optical photometric data was acquired with FORS2 at the VLT, in BVI and VRI bands for the low-z and the high-z cluster samples, respectively. The photometric depth (5$\sigma $ in 1 $^{\prime\prime}$ radius aperture) is typically 26.4(B), 26.2(V) and 24.8(I) in the low-z sample, and 26.5(V), 26.0(R) and 25.2(I) in the high-z sample (see also White et al. 2005, Table 1). The field of view covered by these data is 6.5$^\prime$ $\times$ 6.5$^\prime$. Seeing conditions were excellent during all imaging observations, ranging typically between 0.5 $^{\prime\prime}$ and 0.8 $^{\prime\prime}$ (see White et al. 2005 for details). Deep near-IR images were also obtained for almost all clusters with SOFI at the NTT, in $K_{\rm s}$ and $JK_{\rm s}$ for the low-z and the high-zsamples, respectively (details are provided by Aragón-Salamanca et al. 2009, in preparation). The photometric depth (5$\sigma $) is typically 22.8 in J and 21.5 in $K_{\rm s}$. These data cover a field of $4.2\hbox{$^\prime$ }\times 6.0\hbox{$^\prime$ }$ at low-z, and $4.2\hbox{$^\prime$ }\times 5.4\hbox{$^\prime$ }$ at high-z. Photometry was performed on seeing-matched images using SExtractor v.2.2.2 (Bertin & Arnouts 1996). Table 3 summarizes the filter set used to compute photometric redshifts for each cluster in the EDisCS sample.

Spectroscopic data in the EDisCS fields were obtained during three observing runs with FORS2 at VLT, using the 600RI+19 grism. The wavelength domain covered by our observations ranged between $\sim $5300 and 9000 Å. More details can be found in the reference papers by Halliday et al. (2004) and Milvang-Jensen et al. (2008). The total number of good quality spectra acquired per field ranged between $\sim $60 and 100 for the low-z sample, and was around $\sim $100 for the high-z sample. There are typically 30-50 confirmed members in every cluster. We use objects with either secure spectroscopic redshifts (hereafter type 1) or medium quality, slightly tentative redshifts (hereafter type 2) to characterize the behavior of photometric redshifts and cluster-membership criteria. Objects with tentative redshifts ($\sim $50% secure, type 3) represent less than 2% of the total sample and are mostly used for illustration pusposes. The total number of spectroscopic redshifts available is 637(977) in the low-z(high-z) samples, from which the total number of secure (secure + slightly tentative, i.e. type 1+2) redshifts in the $0.3\le z\le 1.0$ domain are 544(564) and 854(885) respectively for the low-z and high-z samples (see also Table 4).

An important issue when deriving photometric redshifts for a given galaxy is to construct its SED using magnitudes and corresponding fluxes derived for identical aperture sizes in each of the bandpass images. Photometric SEDs were obtained from seeing-matched images according to the following scheme. For ``isolated'' objects (SExtractor flag = 0), photometric redshifts were derived from isophotal magnitudes measured within the reference I-band isophotal region corresponding to 1.5$\sigma $ of the local background noise. In the case of ``crowded'' objects (SExtractor flag $\ge$ 0), we used magnitudes computed within 1 $^{\prime\prime}$ radius apertures. This scheme enabled us to improve the SED determination in crowded regions, while increasing the S/N for isolated galaxies.

We did not use the standard SExtractor errors because these are known to underestimate the error for dithered data where adjacent pixels are correlated. We determined our errors instead by means of a set of empty aperture simulations as described in White et al. (2005). The accurate determination of the errors is important because photometric redshifts are sensitive to photometric errors.

A correction for Galactic extinction was also included for each cluster field according to the E(B-V) derived from Schlegel et al. (1998) for the center of the cluster. The E(B-V) corrections in the EDisCS fields typically ranged between 0.03 and 0.08 mag (see Table 3).

Bright unsaturated stars were used as secondary standards to check the consistency of our photometric system for deriving photometric redshifts and, when required, to introduce small zero-point corrections in the photometric catalogs. In practice, we compared the color-color diagrams of observed stars in our fields with the expected positions derived using the Pickles library (Pickles 1998). Stars at this stage are objects selected with SExtractor stellarity index $\ge$0.95 that belong to the stellar sequence in the I-band isophotal-radius versus aperture-magnitude diagrams. This procedure was particularly useful during the first photometric runs to correct near-IR imaging data for the effects of non-photometric conditions. Due to the addition of high-quality observations, the zero-point corrections improved successively during the lifetime of the project, in addition to the quality of the photometric catalogs and related quantities, such as photometric redshifts. The results presented here were obtained with the final version of the photometric catalogs, for which the zero-point corrections are negligible, apart from two cases: Cl1138-1133 ( $\Delta V=0.10$ and $\Delta J=-0.15$), and Cl1232-1250 ( $\Delta J=-0.20$).

All the results published by the EDisCS collaboration since 2004 were obtained with the current and final version of the photometric catalogs used in this paper, publically available from the EDisCS website[*]. The last version of EDisCS photometric redshifts was obtained in April 2006. The quality of this final version with respect to the previous ones (since 2004) is about the same in terms of accuracy (i.e. systematic offsets, dispersion and catastrophic failures; see criteria in Sect. 4). The main differences come from the related quantities which are provided in addition to photometric redshifts (e.g. absolute magnitudes, photometric classification of galaxies, ...).

3 Photometric redshifts

Photometric redshifts (hereafter $z_{\rm phot}$ ) were computed using two different codes: a modified version of the public code Hyperz[*] (Bolzonella et al. 2000), and the code of Rudnick et al. (2001), with the modifications introduced by Rudnick et al. (2003) (hereafter GR code). The two codes use different approaches based on SED fitting procedures, as summarized below. The reader is referred to the reference papers for a more detailed description of the codes themselves. Here we summarize only the main relevant settings and modifications.

Hyperz results were initially used by the EDisCS collaboration for three main purposes: to determine a first guess for each cluster redshift, to help in spectroscopic pre-selection, and to reduce the contamination by faint stars during spectroscopic observations. Subsequently, the two codes were jointly used to establish cluster membership in magnitude-limited samples using their respective normalized probability distributions (see Sect. 6).

We used 14 galaxy templates with Hyperz:

  • eight evolutionary synthetic SEDs computed with the 2003 version of the Bruzual & Charlot code (Bruzual & Charlot 1993, 2003), spanning a grid of ages between 0.0001 and 13.5 Gyr, with Chabrier (2003) IMF and solar metallicity (a delta burst -SSP-, a constant star-forming system, and 6 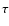$\tau$-models with exponentially decaying SFR);

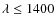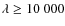  • a set of 4 empirical SEDs compiled by Coleman et al. (1980) (hereafter CWW) to represent the local population of galaxies, with fixed age, extended to wavelengths $\lambda \le 1400$ Å and $\lambda \ge 10~000$ Å using the equivalent Bruzual & Charlot spectra;

  • two starburst galaxies (SB1 and SB2) from the Kinney et al. (1996) template library.

The internal reddening law is taken from Calzetti (2000), and considered as a free parameter with AV ranging between 0 and 1.5 mag (E(B-V) between 0 and $\sim $0.45 mag). When an object is not detected in a given filter, the flux in this filter is set to zero with an error bar corresponding to the limiting magnitude that corresponds to a S/N ratio $\sim $1 in this filter. Absolute magnitudes MB for galaxies were allowed between $-24 \le M_B \le -11$, which imposed a relatively weak prior on $z_{\rm phot}$ while preventing obvious catastrophic identifications in the case of degenerate solutions. P(z) were normalized within the permitted redshift interval according to this restriction.

The GR code is based on the non-negative linear combination of redshifted galaxy templates, for which:

  • the set of 4 CWW empirical templates described above;

  • the starburst galaxies SB1 and SB2 from the Kinney et al. (1996);

  • a 10 Myr old, single stellar population burst obtained from the 1999 version of the Bruzual & Charlot (1993) code with Salpeter (1955) IMF and solar metallicity.

The 4 CWW and starburst templates were extended from their published short-wavelength limits (1400 and 1232 Å  respectively) by a power-law fit to the 1400-1800 and 1240-1740 Å wavelength ranges, respectively, using Bruzual & Charlot (2003) spectra.

There are no limitations on absolute magnitude in the GR code, and the direct flux measurements were used for all galaxies, even when an object was not formally detected.

Hyperz $z_{\rm phot}$ were computed in the range $0 \le z \le 6$, whereas GR ones span the $0 \le z \le 2$ range. The upper limit had a negligible impact on the $z_{\rm phot}$ value itself and related quantities, except in the normalization of the $z_{\rm phot}$ probability distribution (P(z)). When deriving the cluster membership criteria presented in Sect. 6, P(z) computed with the two codes were normalized within the $0 \le z \le 2$ interval, and Hyperz $z_{\rm phot}$ were also restricted to this interval.

3.1 Photometric discrimination between galaxies, stars and quasars

The method used to discriminate photometrically between galaxies, stars, and quasars, was based on Hyperz, and closely followed the developments presented in Hatziminaoglou et al. (2000). For stars, it was based on a standard SED fitting minimization about $z \sim 0$ using the complete library of stellar templates by Pickles (1998). The galactic E(B-V) correction was considered as a free parameter, ranging between 0 and the corresponding value for the field given in Table 3. For quasars, we used a library of synthetic spectra similar to Hatziminaouglou et al. (2000), and the same prescriptions as for galaxies, apart from the absolute magnitude limitation.

In practice, the usual Hyperz $z_{\rm phot}$ for galaxies and quasars, and the best fit with the stellar library were computed for each object, and three classification parameters were given to quantify the goodness of the best fit as a galaxy/star/quasar (respectively NG, N* and NQ). The object was ``rejected'' as a galaxy/star/quasar when its $\chi^2$ excluded it at higher than the 95% confidence level (N=0). The object was ``fully compatible'' when the probability associated with the reduced $\chi^2$ exceeded 90% (N=2). The object was ``undetermined'' (N= 1) in all the other intermediate cases. This classification allowed us to define different samples of objects in these fields, either galaxies (with $N_G \ge 1$, irrespective of the star type) or stars (with N* > 1 and NG<1). These classification criteria were used during the spectroscopic runs to lower the contamination due to faint and red stars to values below $\sim $$10\%$ (Halliday et al. 2004; Milvang-Jensen et al. 2008), and they are also used below in Sect. 5.3. The quasar classification was not considered for the spectroscopic preselection. Johnson et al. (2006) used this classification to identify possible AGNs detected in X-rays in these fields.

3.2 Photometric classification of galaxies

Galaxies were classified into five different spectral types, corresponding to their rest-frame photometric SED: (1) E/S0, (2) Sbc, (3) Scd, (4) Im, and (5) SB (starbursts). These types correspond to the simplest empirical templates given above, namely the four SEDs compiled by CWW for the local galaxies, plus the Kinney starbursts. This classification corresponds to the best fit templates for the GR code. In the case of Hyperz, it is the best fit of the rest-frame SED at $z_{\rm phot}$. The classification obtained with the two codes is in perfect agreement, excepted for catastrophic identifications. We use this classification in Sect. 4 to address the $z_{\rm phot}$ accuracy as a function of the spectral type.

3.3 Photometric redshift catalogs

Photometric redshifts for EDisCS catalogs computed with the two different codes are publically available from the EDisCS website[*].

EDisCS online catalogs also include an optimized flag for the discrimination between galaxies and stars, based on the combination between the above Hyperz criterion, a similar fit using the GR code (flag $_{\rm GR}=1$ when the object is well fit as a star) (1), the SExtractor stellarity flag (flag $_{\rm SEx}$) (2), and the size for bright objects (3), i.e.

1.
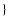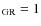
$\{$ N* >1 AND NG < 1 $\}$ OR flag $_{\rm GR}=1$

2.
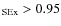
flag $_{\rm SEx} > 0.95$

3.
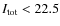
rh(I) < $r_{\rm thresh}$ if $I_{\rm tot} < 22.5$

where rh(I) is the half-light radius in the I band, and $r_{\rm thresh}$ is the threshold radius determined from the stellar locus in the corresponding rh versus total I magnitude.

4 Determination of the photometric redshift accuracy

The expected accuracy of $z_{\rm phot}$ as a function of redshift depends strongly on the photometric accuracy and the filter set used to derive the photometric SEDs. As explained in Sect. 2 and in White et al. (2005), we introduced an accurate determination of photometric errors to address the former issue. The filter set used by EDisCS contains a relatively small number of filters because it was designed originally to cover the relevant wavelength domain in the rest frame of low $z\sim 0.5$ and high $z\sim 0.8$ clusters. In particular, they bracketed the 4000 Å break for the relevant redshift intervals, but they were not designed to explore the full redshift domain. For this reason, we address the $z_{\rm phot}$ accuracy in three different ways described below. Using simulations, we first determine the redshift ranges for which we expect a reliable estimate of $z_{\rm phot}$ for the low and high-z filter sets, and the ideal (maximum) accuracy expected from simple SED fitting. Secondly, the quality of EDisCS $z_{\rm phot}$ achieved is estimated by direct comparison with the spectroscopic redshifts. In a third subsection, we determine the $z_{\rm phot}$ accuracy expected for galaxies fainter than the spectroscopic control sample.

The following quantities were computed to quantify the $z_{\rm phot}$  accuracy, where $z_{\rm spec}$ stands for both ``spectroscopic'' and ``model'' redshifts:

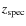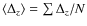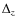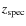  • the systematic deviation between $z_{\rm phot}$ and $z_{\rm spec}$, $\left<\Delta_z \right>=\sum \Delta_z /N$, given by the mean difference between these two quantities, where $\Delta_z$ =  $z_{\rm spec}$ - $z_{\rm phot}$ and N is the total number of galaxies;

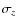
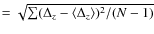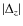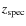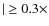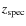  • the standard deviation $\sigma_z$ $ = \sqrt{\sum (\Delta_z-\left<\Delta_z \right>)^2/(N-1)}$, excluding catastrophic identifications, defined here in a conservative way for those galaxies with $ \vert \Delta_z \vert $ = | $z_{\rm spec}$ - $z_{\rm phot}$  $\vert \ge 0.3 \times $(1 +  $z_{\rm spec}$);

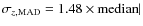
  • the median absolute deviation 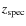$\sigma_{z,\rm MAD} = 1.48 \times {\rm median} \\ Vert$ $z_{\rm spec}$  -  $z_{\rm phot}$ |, which is less sensitive to outliers;

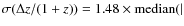
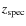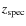  • the normalized median absolute deviation defined as $\sigma(\Delta z/(1+z)) = 1.48 \times {\rm median} (\vert$ $z_{\rm spec}$ - $z_{\rm phot}$ |/(1+ $z_{\rm spec}$));

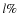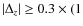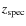  • the percentage of catastrophic identifications ($l\%$), i.e. galaxies ``lost'' from their original spectroscopic redshift bin, with $\vert \Delta_z \vert \ge 0.3 \times (1$ +  $z_{\rm spec}$);

  • the percentage of galaxies included in a given photometric redshift interval that are catastrophic identifications (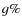$g\%$), i.e. galaxies that contaminate the sample because they are incorrectly assigned to the redshift bin.

4.1 Expected accuracy from simulations

Photometric redshift determinations are based on the detection of strong spectral features, such as the 4000 Å break, Lyman break or strong emission lines. In general, broad-band filters allow only detection of strong breaks and are insensitive to the presence of emission lines, apart from when the contribution of a line to the total flux in a given filter is higher than or similar to the photometric errors, as happens in the case of AGNs (Hatziminaoglou et al. 2000).

To determine the redshift domains where a reliable measurement of $z_{\rm phot}$ can be obtained given the filter sets used in the low and high-z samples, we completed a series of simulations assuming a homogeneous redshift distribution in the redshift interval $0 \le z \le 2$. These simulations were performed using Hyperz related software, and $z_{\rm phot}$ computed with both Hyperz and the GR code, but the results should be representative of the general behavior of pure SED-fitting $z_{\rm phot}$ codes. Synthetic catalogs contain 105 galaxies within this redshift interval, for each filter set, spanning all the basic spectral types defined in Sect. 3.2, with uniform redshift distribution. Photometric errors in the different filters were assigned following a Gaussian distribution with $\sigma $ scaled to magnitudes according to $\Delta m \simeq 2.5 \log~ [1+1/(S/N)]$, where S/N is the signal-to-noise ratio, which is a function of apparent magnitude. Here we used the mean S/N achieved in the different filters for the spectroscopic (bright) sample, i.e. for objects ranging between I=18.5(19.0) and 22.0 in the low-z(high-z) sample, and the same settings used for $z_{\rm phot}$  computation on real catalogs. In this way, the results obtained from simulations should be considered to be ``ideal'' but still consistent with those derived in Sect. 4.2. Because of the limited scope of these simulations, we do not intend to explore all possible domains of parameter space, but focus instead on studying the main systematics introduced by the photometric system.

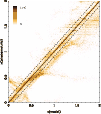
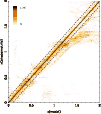
\begin{figure} \par\psfig{file=10644f1.eps,width=8.8cm} \end{figure} Figure 1:

Photometric versus model redshifts retrieved from ${\it BVIK}_{\rm s}$ SEDs (low-z sample), for 105 simulated galaxies uniformly distributed between $0 \le z \le 2$. The diagram displays the number density of galaxies in linear scale.

Open with DEXTER

\begin{figure} \par\psfig{file=10644f2.eps,width=8.8cm} \end{figure} Figure 2:

Photometric versus model redshifts retrieved from ${\it VRIJK}_{\rm s}$ SEDs (high-z sample), for 105 simulated galaxies uniformly distributed between $0 \le z \le 2$. The diagram displays the number density of galaxies in linear scale.

Open with DEXTER

\begin{figure} {% \leavevmode \psfig{file=10644f3.ps,angle=270,width=8.8cm}\newline \psfig{file=10644f4.ps,angle=270,width=8.8cm} } \vspace*{6mm} \end{figure} Figure 3:

These figures present the expected $z_{\rm phot}$ accuracy derived from simulations, for galaxies with photometric quality similar to the spectroscopic sample. The top panel displays the systematic deviation $\langle \Delta_z \rangle \pm \sigma_z$, the standard deviation excluding catastrophic identifications, for the ${\it BVIK}_{\rm s}$ (low-z, black dots) and ${\it VRIJK}_{\rm s}$ (high-z, open/red dots) filter sets, within the relevant redshift domain. The botton panel displays a plot of $\sigma (\Delta z/(1+z))$ as a function of redshift for the same filter combinations.

Open with DEXTER
Figures 1 and 2 display the photometric versus model redshifts retrieved from ${\it BVIK}_{\rm s}$ (low-zsample) and ${\it VRIJK}_{\rm s}$ (high-z sample), respectively. Figure 3 and Table 1 summarize the quality of $z_{\rm phot}$ in the simulations using Hyperz, within the relevant redshift domain. The same results are presented in Table 9 for the GR code.

Some systematic trends are clearly visible in Figs. 1-3. The high-z filter combination provides a higher quality and smaller systematic deviations than the low-z one. This trend was expected because of the more complete and contiguous spectral coverage of the high-z set. The lack of an R filter for the low-z sample introduces a systematic trend in $\Delta_z$ $\sim $ 0.05-0.08 at $z \ga 0.3$; the highest $z_{\rm phot}$ quality for this sample is expected to be around $\sigma(\Delta z/(1+z)) \la 0.06$ at $0.4 \la z \la 0.6$, i.e. within the sensitive redshift domain. Because of the lack of B-band photometry for the high-z sample, the highest quality results are expected at $z \ga 0.4$. This trend is indeed observed in the simulations. However, the quality achived for high-zsimulated data at $z \la 0.4$ with Hyperz is expected to be overestimated with respect to real data, because templates and models are drawn from the same parent set. This is a general criticism of simulations used in assessing the realistic performance of $z_{\rm phot}$ quality. Also  $z_{\rm phot}$  quality depends on the spectral type of galaxies. With respect to the average quality presented in Fig. 3 for a uniform distribution of types, early types exhibit up to a $\sim $50% improvement in $\sigma (\Delta z/(1+z))$ with Hyperz in the redshift domains where the filter sets bracket the 4000 Å break.

The results for the GR code in Table 9 are similar in average to Hyperz's ones. The quality tend to be slightly better for the bluest spectral types, whereas it is worse for early types. This trend can be explained by the broad paramer space spanned by the simulations, the same used by Hyperz for $z_{\rm phot}$ determinations, as compared to the GR code. The noise for late-type galaxies in Hyperz tend to be dominated by degeneracies, whereas the GR code cannot properly fit highly-reddened E-Sbc galaxies. Note that the uniform distribution in redshift and types in these simulations does not represent a realistic population of galaxies.

4.2 Comparison with spectroscopic redshifts

The $z_{\rm phot}$ accuracy achieved for EDisCS was estimated by direct comparison with its 1449 spectroscopic redshifts in the $0.3 \le z \le 1$ interval (type 1+2). Although spectroscopic targets in our sample were strongly biased in favor of cluster members with $z_{\rm phot}$ within the interval $z_{\rm cluster} \pm 0.2$(see Halliday et al. 2004; Milvang-Jensen et al. 2008, and Sect. 5.1), the geometrical configuration of slits in one hand, and the need for reference field galaxies on the other hand, ensured that non-member galaxies were also targeted during the spectroscopic runs. In principle, these field galaxies should allow us to extend the present study to the 0 $\le$  $z_{\rm spec}$  $\le$ 1 interval, according to the restrictions imposed by the set of filters (see Sect. 4.1).

Table 3 presents the $z_{\rm phot}$ accuracy obtained with Hyperz and Rudnick's (GR) code for the different low-z and high-zclusters, based on the direct comparison with the spectroscopic sample, excluding stars. Only type 1 objects, i.e. objects with secure spectroscopic redshifts, were taken into account. In Table 3, systematic deviations and $\sigma_z$ were computed over all the $0.3 \le z_{\rm spec} \le 1$ interval. In the low-z bin, the two clusters with only BVI photometry were excluded from the sample when computing the average $z_{\rm phot}$ quality over the cluster sample. In the high-z bin, we excluded Cl1122-1136 from the cluster statistics, because of the small number of $z_{\rm spec}$ available in this field.

Our main result is that there is no significant systematic shift, neither in the $\langle \Delta_z \rangle \pm \sigma_z$ nor in the $\sigma (\Delta z/(1+z))$ results, with respect to the values expected from simulations in Sect. 4.1, with some field-to-field differences discussed below. The accuracy of $z_{\rm phot}$ ranges usually between $\sigma(\Delta z/(1+z))\sim0.05$ for Hyperz and $\sim $0.06 for GR, both for the low-z and the high-z samples. This result is in good agreement with the highest possible accuracy expected from ideal simulations in the low-z case, it is $\sim $25% worse than ideal expectations in the high-z case for Hyperz, and compatible with GR results for late type galaxies (early-type errors were overestimated, as mentioned in Sect. 4.1). The differential trend between low and high-z samples with respect to simulations in both codes can be explained because of the different population of ``bright'' galaxies in these fields, low-z and high-z samples containing a smaller and larger fraction of late-type galaxies respectively, compared to the uniform average population in simulated data (e.g. De Lucia et al. 2007). This effect is clearly seen in Table 4. The fraction of objects lost from (or spuriously assigned to) the relevant redshift interval according to the definitions given above ($l\%$ and $g\%$), is negligible in the low-z sample and typically below 5% for the high-z one.

Table 4 summarizes the results obtained for the entire low-zand high-z samples, for both type 1 (secure) and type 1 + type 2 (both secure and slightly tentative redshifts) spectroscopic data. The results are similar in both cases. In the high-z bin, $z_{\rm phot}$  accuracy improves slightly when the sample is restricted to the $0.45 \le z_{\rm spec} \le 1$ interval, where both Hyperz and GR codes yield the same $\sigma(\Delta z/(1+z))\sim0.052$. This effect is easily understood because at $z \la 0.45$ the rest-frame 4000 Å break is found shortward of the V-band filter. Table 4 also summarizes the $z_{\rm phot}$ accuracy achieved for the different spectral types of galaxies in the entire sample, i.e. all type 1, 2 and 3 spectra. Tentative type 3 galaxies represent less than 2% of the total sample, and the results remain unchanged whith respect to type 1+2. The number of galaxies as a function of the spectral type given in this table correspond to Hyperz. Excepted for catastrophic identifications, the classification obtained with the two codes is in perfect agreement. The lowest quality $\sigma (\Delta z/(1+z))$ values are measured as expected for the bluest galaxy types (SB), for both the Hyperz and GR codes. Early types display the highest quality results with Hyperz, whereas GR code has lower quality results for early types in the high-z sample. This trend may indicate that the CWW templates provide an inappropriate description of the SEDs of early types at intermediate redshifts.

The comparison between the Hyperz and GR codes, either on a cluster-by-cluster basis or as a function of the filter combination, yields similar results, even though these codes are based on different approaches and have different strengths/weaknesses. In general, Hyperz results are found to be of slightly higher accuracy than GR's ones (by $\la$20% in $\sigma (\Delta z/(1+z))$), but both are in close agreement with the expectations under ``ideal'' conditions. An interesting trend is that the quality of both codes is highly correlated, in the sense that the highest and the lowest quality results (in terms of $\sigma (\Delta z/(1+z))$ and systematics) are found for the same clusters. Given the homogeneous photometry of the EDisCS project, this trend can hardly be explained by the use of an incomplete or imperfect template set (as suggested by Ilbert et al. 2006), because in such a case we would expect the same systematic behavior in all fields, given a certain filter set, as is observed in Sect. 4.1 with Hyperz. In contrast, different systematic trends are observed for different clusters, which are then found to be almost identical for the two independent $z_{\rm phot}$  codes. This behavior suggests strongly that the origin of the systematics is more likely to be the input photometric catalog rather than the $z_{\rm phot}$ codes and templates. In particular, we cannot exclude small remaining zero-point shifts in our data, approximately equal to or less than $\sim $0.05 mag, because we are limited by the accuracy of the stellar templates (see Sect. 2).

A brief discussion of particular aspects of $z_{\rm phot}$ accuracy in the low-z and high-z samples is given below.

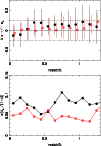
4.2.1 Low-z cluster fields

Figure 4 displays a direct comparison between the spectroscopic and the photometric redshifts for the low-z clusters in the EDisCS sample. Hyperz was used to derive $z_{\rm phot}$ in this figure, but the results with the GR code are very similar, as discussed above. Error bars in $z_{\rm phot}$ correspond to a 1$\sigma $confidence level in the photometric redshift probability distribution P(z), i.e. to the 68% confidence level computed through the $\Delta \chi^2$ increment for a single parameter (Avni 1976). Figure 16 shows the comparison between spectroscopic and photometric redshifts for the entire low-z sample, obtained with Hyperz and GR codes, as well as the $z_{\rm spec} - z_{\rm phot}$ distribution.

The $z_{\rm phot}$ quality in this sample ranges usually between $0.04 \la \sigma(\Delta z/(1+z)) \la 0.07$ with both Hyperz and GR codes, with some exceptions. On the one hand, Cl1119-1129 and Cl1238-1144 were only observed in BVI, which produces lower quality $z_{\rm phot}$ and a higher fraction of catastrophic identifications. These two clusters were not included when deriving the mean values in Table 3. On the other hand, Cl1232-1250 was observed in J in addition to BVIK, and this provides a more accurate $z_{\rm phot}$ estimate with respect to average with Hyperz, although there is no clear improvement with the GR code. Compared to simulations, the systematic trend $\Delta_z \sim 0.05$-0.08 at $z \ga 0.3$ is far smaller in real data, whereas $\sigma (\Delta z/(1+z))$ is in agreement with ideal results.

Table 1:   $z_{\rm phot}$ accuracy from simulations for galaxies in the spectroscopic sample, based on Hyperz.

Table 2:   $z_{\rm phot}$ accuracy expected for the faintest galaxies in the EDisCS sample, in the low-z and high-z fields, based on Hyperz.

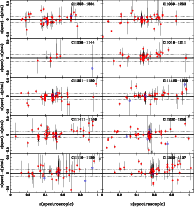
4.2.2 High-z cluster fields

Figure 5 displays a direct comparison between the spectroscopic and the photometric redshifts for the high-z clusters in the EDisCS sample. Error bars in $z_{\rm phot}$ correspond to 1$\sigma $confidence level in the photometric redshift probability distribution P(z). Figure 17 shows the comparison between spectroscopic and photometric redshifts for the whole high-z sample, obtained with Hyperz and GR codes, as well as the $z_{\rm spec} - z_{\rm phot}$ distribution.

The $z_{\rm phot}$ quality in this sample usually ranges between $0.05 \la \sigma(\Delta z/(1+z)) \la 0.08$ with both Hyperz and GR codes, with some exceptions. The statistics in Cl1122-1136 is based on a small number of spectroscopic redshifts, hence we exclude this cluster when deriving the mean values in Table 4. Two out of the ten clusters in the high-z sample are actually in a redshift range typical of the low-z sample. Indeed, in the case of Cl1037-1243a and Cl1138-1133, the low redshift of the cluster implies that B-band photometry is required to ensure that an accurate $z_{\rm phot}$ measurement is achieved, although the quality of their $z_{\rm phot}$ measurements is close to average. As seen in Fig. 5, individual error bars are larger in these two fields than in the other high-z clusters. Compared to simulations, there is no systematic trend in $\Delta_z$ as expected, whereas $\sigma (\Delta z/(1+z))$ is in agreement with ideal results.

Table 3:   Summary of $z_{\rm phot}$ accuracy achieved for the individual low-z and high-z clusters.

Table 4:   Summary of $z_{\rm phot}$ accuracy achieved for the whole low-z and high-z samples with Hyperz and GR codes.

4.3 Expected accuracy for galaxies fainter than the spectroscopic sample

We determine the $z_{\rm phot}$ accuracy expected for galaxies fainter than the spectroscopic control sample used in Sect. 4.2, i.e. galaxies with magnitudes typically ranging between I=18.5(19.0) and 22.0 in the low-z (high-z) sample, in particular for the faintest galaxies in the EDisCS sample. The concept is to derive $z_{\rm phot}$ on a degraded version of the photometric catalog for the spectroscopic sample (in terms of S/N), using the same recipes and settings as the main catalogs. This method was preferred instead of simulations because it uses the observed SEDs of the control sample instead of an arbitrary mixture of spectral types at a given redshift.

Degradated catalogs were generated from the original (spectroscopic) ones, to reproduce the photometric properties of the faintest galaxies in the EDisCS sample. The mean I magnitude was set to be $\langle I\rangle=24.00$(24.5) for the low-z(high-z) cluster fields, corresponding to a $S/N \sim 5$. For all the other j filters, magnitudes were scaled according to the original SEDs, i.e. keeping colors unchanged: $m_{\rm new}(j)= m(j) + [24.0/24.5 - I]$Photometric errors as a function of apparent magnitudes were introduced and assigned as in Sect. 4.1. In this case, $\Delta m_{\rm new}^2(j) = [2.5 \log [1+1/(S/N)]]^2 - \Delta^2 m(j) $, where $\Delta m(j)$ is the catalog error corresponding to m(j), and $S/N = S/N(m(j)) 10^{-0.4(m_{\rm new}(j)-m(j))}$. This procedure conserves globally the colors of galaxies. The main caveat is the fact that this noisy population does not necessarily match the true color distribution of the faintest galaxies in the sample. However, it is useful to estimate the degradation expected in $z_{\rm phot}$ accuracy between the brightest and the faintest galaxies because of the lowered S/N. Because $z_{\rm phot}$ quality is quite insensitive to spectroscopic quality, we added the type 1 + type 2 spectroscopic catalogs.

Table 2 and 10 summarize the results obtained for the faintest galaxies using Hyperz and the GR code respectively. These tables can be compared directly with Table 4. The quality of photometric redshifts degrades typically by a factor of two in $\sigma (\Delta z/(1+z))$ between the brightest ($I\la 22$) and the faintest ($I\sim 24$-24.5) galaxies in the EDisCS sample. Most of the trends observed in Table 4 for the spectroscopic sample are found in the Table 2 for the simulations of the faintest sample, in particular the lack of systematics in $\Delta_z$, and the higher quality results in the high-z bin. The fraction of catastrophic identifications increases, but remains typically below $\sim $5%. The difference in $z_{\rm phot}$ quality between early and late types is smaller for the faintest galaxy sample. In this case, the simulation results with the GR code are found to be of slightly higher accuracy than Hyperz's ones (by $\la$20% in $\sigma (\Delta z/(1+z))$). In Sect. 6.3, we comment on the implications that this results will have for the calculation of membership using the photometric redshifts.

5 Photometric determination of cluster redshifts

5.1 Spectroscopic sample preselection

Before the first spectroscopic runs, cluster redshifts were estimated from the first $z_{\rm phot}$ catalogs using Hyperz. Spectroscopic targets were selected mainly to have $z_{\rm phot}$ within the interval $z_{\rm cluster} \pm 0.2$, or absolute $P(z_{\rm cluster})$ $\ge$ 0.5, and according to the magnitude selection (see Halliday et al. 2004). Although the results discussed in this section were obtained with Hyperz, they should be representative of the general behavior of all SED-fitting $z_{\rm phot}$ codes.

Table 5:   Comparison between spectroscopic ( $z_{\rm cl}$) and photometric determinations of cluster redshifts in the low and high-z samples.

The photometic cluster redshifts were computed from the photometric redshift distribution by comparing the N(z) obtained in the center of the field with the equivalent one over a wider region of the same area, obtained under the same conditions from the $z_{\rm phot}$ point of view (same effective exposure time and number of filters), and used as a blank field. A real cluster or other structure should have appeared as an excess of galaxies in the central region in comparison to the outer parts. In this exercise, we considered only objects with $N_G \ge 1$ i.e. objects that could not be excluded as galaxies without applying a cut in magnitude. Figure 6 displays the results found for the different fields.The histograms in this Figure display the difference between the redshift distribution within a $\sim $140 $^{\prime\prime}$ radius region centered on the center of the image ( $N_{\rm in}(z)$, black solid line), and the distribution within an outer ring, $140\hbox{$^{\prime\prime}$ }\le r \le 200\hbox{$^{\prime\prime}$ }$, ( $N_{\rm out}(z)$, dashed black lines). Red solid lines show the positive difference between the two histograms, $N_{\rm in}(z) - N_{\rm out}(z)$. Histograms were obtained with a $\delta z =0.05$ sampling step and smoothed with a $\delta z =0.15$ sliding window. This window corresponded approximately to the $1\sigma$ uncertainty in the $z_{\rm phot}$  estimate for the faintest galaxies in the catalog.

Where there was a distinct peak in $N_{\rm in}(z) - N_{\rm out}(z)$distribution, we used this value to represent the ``cluster redshift''. We also computed 2D number density maps and cluster tomography (see Sect. 5.3 below) to emphasize the reality of the clusters, in particular for the uncertain cases. A summary of these results was provided in White et al. (2005). We note that the efficiency of the cluster-finding algorithm could be enhanced if the central region was centered on the cluster centroid instead of the center of the image. This ideal situation could be achieved in wider surveys.

\begin{figure} \par\psfig{file=10644f5.ps,width=17cm}\vspace{1mm} \vspace{2mm} \end{figure} Figure 4:

( $z_{\rm spec}$ - $z_{\rm phot}$ ) versus spectroscopic redshift for the low-z clusters in the EDisCS sample. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Error bars in $z_{\rm phot}$  correspond to 1$\sigma $. Dot-dashed lines display $z_{\rm spec}$ - $z_{\rm phot}$  = $\pm 0.1$ to guide the eye. (See text for details.)

Open with DEXTER

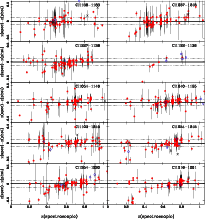
\begin{figure} {% \leavevmode \psfig{file=10644f6.ps,angle=270,width=18cm} } \vspace{3mm} \end{figure} Figure 5:

( $z_{\rm spec}$ - $z_{\rm phot}$ ) versus spectroscopic redshift for the high-z clusters in the EDisCS sample. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Error bars in  $z_{\rm phot}$  correspond to 1$\sigma $ Dot-dashed lines display $z_{\rm spec}$ - $z_{\rm phot}$  = $\pm $ 0.1 to guide the eye. (See text for details.)

Open with DEXTER
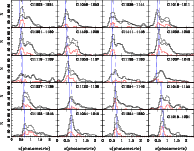
\begin{figure} \par\psfig{file=10644f7.ps,width=17cm} \end{figure} Figure 6:

Photometric redshift distributions in the EDisCS fields, with the cluster redshift increasing from top to bottom and from left to right, for the low-z and high-z samples (first and second series respectively). The histograms display the following redshift distributions: $N_{\rm in}(z)$ (black thick solid lines), $N_{\rm out}(z)$ (thin black lines), and the positive difference between $N_{\rm in}(z) - N_{\rm out}(z)$ (lowest histograms, thick red lines). A real cluster or other structure corresponds to a positive excess in the lower (red) histogram. Histograms were obtained with a $\delta z =0.05$ sampling step, smoothed by a $\delta z =0.15$ sliding window. Vertical solid and dashed lines indicate the spectroscopic and photometric values, respectively, adopted for the cluster redshift. All vertical scales are identical in the number of galaxies/ $\Delta z = 0.05$, from N(z)=0 to 100, apart from Cl1216-1201, for which the range is 0 to 115.

Open with DEXTER

5.2 Spectroscopic versus photometric cluster redshifts

Figure 6 summarizes the comparison between the $z_{\rm phot}$ and spectroscopic redshifts for the different cluster fields. The photometric cluster redshift can be defined in different ways. Here we have adopted two different definitions, which are reported in Table 5: (1) the mean weighted value, computed from the excess peak, and (2) the redshift corresponding to the maximum value in the $N_{\rm in}(z) - N_{\rm out}(z)$ histogram. Table 5 provides a comparison between spectroscopic and photometric determinations of cluster redshifts for the low and high-zsamples. Cluster redshifts in Table 5 and Fig. 6 correspond to the most prominent cluster identification when several clusters were present in the field (Milvang-Jensen et al. 2008). Five fields were excluded when computing the systematic deviation and dispersion: Cl1119-1129 and Cl1238-1144 in the low-zsample, because of incomplete photometry; and Cl1122-1136, Cl1037-1243a and Cl1138-1133 in the high-z sample, the first because of the lack of a clear cluster in the field, and the two others because their low cluster redshifts implied that B-band photometry was required to achieve an accurate $z_{\rm phot}$ (see also Milvang-Jensen et al. 2008). We note however the accurate photometric identification of the Cl1037-1243a cluster, for which a poor determination was expected.

In general, the differences between photometric and spectroscopic values are small, ranging from $\delta z \sim0.03$-0.04 at high-z to $\delta z \sim 0.05$ at low-z. The dispersion is much lower than the approximate cut introduced by the spectroscopic preselection ( $z_{\rm cluster} \pm 0.2$). Therefore, there is no reason why a cluster should have been ``missed'' within the relevant redshift interval due to $z_{\rm phot}$ preselection. The systematic trend of lower quality in $z_{\rm phot}$ for the low-z sample was expected from the simulations presented in Sect. 4.1, and also observed in the comparison with the spectroscopic sample in Sect. 4.2.

5.3 Cluster tomography

We present results about cluster tomography along the line-of-sight in the different EDisCS fields. This highlights the capability of $z_{\rm phot}$  in identifying and studying clusters of galaxies in deep photometric surveys.

A local density estimate was derived at each point in the field using a grid with $\delta x= \delta y = 1$ $^{\prime\prime}$. The density estimator was defined, according to the formalism introduced by Dressler (1980), to equal $\Sigma_{20}=20/(\pi d_{20}^2)$, where d20 was the projected linear distance to the 20th closest neighbor. Photometric redshift slices of $\Delta z= 0.1$ were used to cover the redshift range $0\le z \le 1.4$. Close neighbors were selected within $z_{\rm phot}$  $\pm $ 0.1, centered on the redshift bin. The arbitrary choices of $\Sigma_n$ and n=20 were justified by the typical richnesses of clusters and the $z_{\rm phot}$ accuracy. We tested other values of n ranging between 5 and 20 and achieved similar results for the cluster detection. Edge effects were corrected by using external fields in the main eight directions (i.e. X+, Y+, X-, Y-, X+Y+, X+Y-, X-Y+, X-Y-), containing different realizations of the same $z_{\rm phot}$ slice with xycoordinates randomly sorted. The density maps were smoothed with a Gaussian kernel of $\sigma=5\hbox{$^{\prime\prime}$ }$.

Figures 7 and 8 display the projected number density maps obtained with this method, for the low and high-zsamples, respectively. In these figures, clusters are presented with $z_{\rm cluster}$ increasing from top to bottom. Projected number densities are displayed on a linear scale, for an arbitrary redshift step $\Delta z= 0.1$, with isopleths corresponding to increasing number density bins, equally spaced with $\Delta \Sigma_{20}= \langle \Sigma_{20}\rangle$, starting at the mean $\Sigma _{20}$ within the redshift slice. The presence of a cluster along the line-of-sight is clearly seen in most cases, at least in all cases where a cluster was clearly detected in the field. We note that the $\langle \Sigma_{20}\rangle$ value is affected by the presence of a cluster in the corresponding redshift bin. The most significant contrast in the density map is found usually for the $z_{\rm cluster} \pm 0.1$ redshift slice (rightmost column of Figs. 7 and 8). The position of the BCG (White et al. 2005; Milvang-Jensen et al. 2008; Whiley et al. 2008; displayed by a blue cross in these figures) coincides usually with the maximum contrast in the density map for the most prominent clusters in a given field. The comparison between this maximum-contrast slice and the tomography with fixed arbitrary step (e.g. $\Delta z= 0.1$, the step used in Figs. 7 and 8) suggests that the optimal redshift step for detection of clusters along the line-of-sight should be close to the typical difference between photometric and spectroscopic $z_{\rm cluster}$, in this case $\Delta z \sim 0.05$. Structures separated by less than $\Delta z \sim 0.05$ in redshift space cannot be distinguished by $z_{\rm phot}$ tomography (e.g. clusters Cl1138 (z=0.48) and Cl1138a (z=0.45) in the 1138.2-1133 field, and Cl1227 (z=0.63) and Cl1227a (z=0.58) in the 1227.9-1138 field; Milvang-Jensen et al. 2008).

For all clusters clearly identifiable in this sample (i.e. all clusters except Cl1059-1253, Cl1202-1224 and Cl1119-1129), the maximum contrast is found to be at least $\sim $ $ 3{-}4 \times \langle \Sigma_{20}\rangle$ about $z_{\rm cluster} \pm 0.1$. All clusters in our sample exhibit a significant $\gtrsim$$3\sigma$ overdensity around $z_{\rm cluster} \pm 0.1$, defined to be $\Sigma_{20}-\langle \Sigma_{20}\rangle / \sigma(z)$, where $\sigma(z)$ represents the standard deviation in the projected number density within the redshift bin. For all apart from the three aforementioned clusters, the detection level exceeds $4\sigma $, and ranges between 6 and $9\sigma$ for Cl1216-1201, Cl1227-1138, Cl1411-1148, Cl1420-1236, Cl1040-1155, Cl1054-1245, Cl1138-1133, Cl1018-1211, and Cl1054-1146. No other significant overdensities are found along the line-of-sight of density peaks exceeding $3 \times \langle \Sigma_{20}\rangle$, which are typical values for rich clusters in this sample. However, several overdensities are found with slightly smaller values, around $\sim $ $2{-}3 \times \langle\Sigma_{20}\rangle$, and detection levels exceeding $4\sigma $. These structures are identified by circles in Figs. 7 and 8 (see below). Their reliability is difficult to assess with the presently available data.

Several fields deserve further comment. More information concerning the spectroscopic identification of clusters in these fields can be found in the reference papers by Halliday et al. (2004) and Milvang-Jensen et al. (2008):

  • Cl1301-1139: The two clusters identified in this field with z(spectroscopic) = 0.397 (Cl1301a) and 0.482 (Cl1301) are consistent with the two different 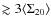$\gtrsim 3 \langle\Sigma_{20}\rangle$ peaks observed by our tomography.

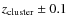  • Cl1037-1243: The most distinct $\sim $ $3 \langle \Sigma_{20}\rangle$ overdensity in this field corresponds to the ``a'' component at z(spectroscopic) = 0.425, whereas the first identification was given at z(spectroscopic) = 0.578 ( $z_{\rm cluster} \pm 0.1$ in Fig. 8). Both structures are seen by tomography.

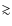
  • Cl1354-1230: the two clusters Cl1354 and Cl1354a (z=0.762 and z=0.595 respectively) are consistent with overdensities at the 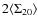$\gtrsim$ $ 2 \langle \Sigma_{20}\rangle$ level.

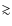
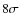  • Cl1103-1245: The prominent cluster detected in this field at z=0.96 is clearly visible ($\gtrsim$$8\sigma$ level) both in the density map and the $z_{\rm phot}$ distribution (Fig. 6). The two components Cl1103a (z=0.626) and Cl1103b (z=0.703) can hardly be separated by tomography.

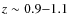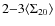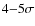  • Other secondary peaks at $z\sim 0.9{-}1.1$ are seen in the N( $z_{\rm phot}$ ) distribution of Cl1018-1211, Cl1301-1139, Cl1420-1236, Cl1054-1245, and Cl1040-1155 (Fig. 6). All can be associated with spatial overdensities of $2{-}3 \langle\Sigma_{20}\rangle$ at the $4{-}5\sigma$ level, apart from in the field of Cl1040-1155, where no significant overdensity is found.

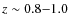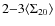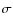  • Several additional overdensities/structures at $z\sim 0.8{-}1.0$ are found in Cl1411-1148, Cl1119-1129, Cl1238-1144, and Cl1216-1201, with $2{-}3 \langle\Sigma_{20}\rangle$ and detection levels ranging between 4 and 6$\sigma $. Given the limited photometric coverage of Cl1119-1129 and Cl1238-1144, the detected overdensities in these fields are rather dubious.

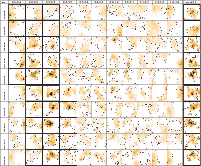
\begin{figure} \par\psfig{file=10644f8.ps,angle=270,width=18cm} \end{figure} Figure 7:

Projected number density maps for the low-z sample, for different redshift slices with $z_{\rm cluster}$ increasing from top to bottom. Projected number densities are displayed in a linear scale. Isopleths correspond to increasing number density bins with $\Delta \Sigma_{20}= \langle \Sigma_{20}\rangle$, starting at the mean  $\Sigma _{20}$ within the redshift slice. Thick frames highlight the redshift slices encompassing $z_{\rm cluster} \pm 0.1$. The rightmost column displays the density map for the $z_{\rm cluster} \pm 0.1$ redshift slice, where the maximum contrast in the density peak is usually reached. The position of the BCG for the most prominent clusters in the field are displayed by a blue cross. For Cl1059-1253, Cl1202-1224, and Cl1119-1129, only two isopleths are displayed corresponding to 1 and $1.5 \langle \Sigma_{20}\rangle$. Additional overdensities along the line of sight with detection levels exceeding $4\sigma $ are displayed by circles.

Open with DEXTER

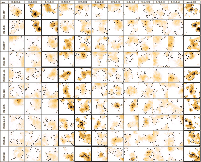
\begin{figure} \par\psfig{file=10644f9.ps,angle=270,width=18cm} \end{figure} Figure 8:

Projected number density maps for the high-z sample, for different redshift slices. Same comments as in Fig. 7. There is no clear BCG identified in Cl1122-1136.

Open with DEXTER

6 Cluster membership criteria

The most unambiguous way to determine cluster membership is by means of accurate spectroscopic redshifts. Unfortunately, it is far too time-consuming to obtain high spectroscopic completeness in cluster member observations, even to relatively bright limits of I< 22-23. For this reason, it is necessary to develop membership criteria that rely solely on photometric data. To achieve many EDisCS science goals, such as study of luminosity functions and cluster substructure, any method should: 1) retain >90% of cluster members; 2) reject an optimal number of non-members; and 3) measure a probability that a given galaxy is a cluster member. The first two criteria should be implemented so that there is little dependence on the galaxy color, e.g. for Butcher-Oemler-type studies. While traditional methods of statistical subtraction using ``field'' surveys of comparable depth offer a viable method to satisfy the first two criteria, they do not satisfy the third. For this reason, we developed an alternative method for membership determination based on our photometric redshifts estimates.

We present below how we use the photometric redshift probability distribution P(z) to reject non-members from each cluster field. We describe the method that we developed and its calibration based on EDisCS spectroscopic redshifts. We discuss how this method can be extended to the entire magnitude-limited sample for a given cluster and outline its limitations.

6.1 The method

Traditionally, $z_{\rm phot}$-based methods for determining cluster membership were based on a simple cut in redshift, such that a galaxy was considered to be a member if $\vert z_{\rm phot} - z_{\rm clust}\vert < \Delta z_{\rm thresh}$. One disadvantage of this method is that $\Delta z_{\rm thresh}$ can be as high as 0.3 (e.g. Toft et al. 2004), causing considerable field contamination to enter into the cluster sample. An additional disadvantage of the method is that it uses only the best-fit redshift in determining membership and ignores the information contained in the full redshift probability distribution P(z).

Brunner & Lubin (2000) suggested an improved technique that used P(z) in determining galaxy membership. They assumed a Gaussian P(z) of width calculated from the comparison with $z_{\rm spec}$, and defined the quantity

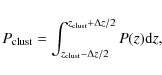
\begin{displaymath}P_{\rm clust} = \int^{z_{\rm clust}+\Delta z/2}_{z_{\rm clust}-\Delta z/2}P(z){\rm d}z, \end{displaymath} (1)

where $\Delta z$ was an interval defined around $z_{\rm clust}$ that reflected the dispersion in the $z_{\rm phot}$ versus $z_{\rm spec}$ diagram, and $z_{\rm clust}$ was the spectroscopic redshift of the cluster. In Sect. 6.2 we explain in detail the method we used to calibrate a threshold value for $P_{\rm clust}$, $P_{\rm thresh}$, below which a galaxy would be considered to be a non-member. However, in reality, P(z) can be highly non-Gaussian, with multiple maxima and extended tails at large distances from the most likely solution. For this reason, it may not be optimal to assume the Gaussian approximation. We therefore extended the Brunner & Lubin method to use the full P(z) dataset calculated directly from the two $z_{\rm phot}$ codes. We tested the accuracy of our P(z) by comparing the confidence intervals derived from P(z) with the disagreement between $z_{\rm spec}$ and $z_{\rm phot}$ (see Figs. 4 to 17 in Sect. 4). The $z_{\rm spec}$ fell within the 68% confidence limits on $z_{\rm phot}$for $\sim $$ 68\%$ of the galaxies and many of the galaxies with large $\vert z_{\rm phot}-z_{\rm spec}\vert$ also had correspondingly large 68% confidence intervals. This gave us assurance that P(z) was accurate enough for our purposes.

6.2 Calibrating from the spectroscopic sample

We adopt the large and uniform EDisCS spectroscopic sample (Halliday et al. 2004; Milvang-Jensen et al. 2008) to calibrate the $P_{\rm thresh}$ that we use to reject non-members.

We show in Figs. 9 and 10 the $P_{\rm clust}$ versus $z_{\rm phot}$- $z_{\rm clust}$ for all galaxies with secure $z_{\rm spec}$ measurements in our clusters, for the low and high redshift samples, respectively. Results presented here were obtained for the GR code, but they are similar for Hyperz. As seen in Sect. 4, the $z_{\rm phot}$ accuracy as well as the fraction of catastrophic identifications in a given field depend on the spectral type of galaxies, although the difference between early and late types is smaller for the faintest galaxies in our sample. Therefore, we have studied the reliability of the membership criteria for both early and late SED types using a cut in the restframe color which splits the sample into two equal halves of red (early) and blue (late) type galaxies. The color cuts are found to be $(B-V)_{\rm rest}$ = 0.79 and 0.67 for the low-z and high-z samples respectively. The left and right-hand panels in Figs. 9 and 10 provide results for objects of different spectral types.

We note that the ratio of members to non-members increases as a function of $P_{\rm clust}$. There are also few galaxies with $z_{\rm phot}$ $\approx$  $z_{\rm spec}$ and very low $P_{\rm clust}$ values. This implies that there are not many members that would be rejected because their faint magnitudes correspond to broad P(z) and lead to their rejection even if $z_{\rm phot}$ $\approx$  $z_{\rm spec}$. It is important to consider, however, that the spectroscopic sample consists of the brightest galaxies of probably the tightest P(z) values and that this behavior might not be similar at fainter magnitudes (see Sect. 6.3).

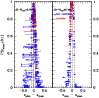
\begin{figure} \par\psfig{file=10644f10.eps,width=9cm} \end{figure} Figure 9:

The integrated probability of being at $z_{\rm clust}$ $\pm $ 0.1 vs. $z_{\rm phot}$ -  $z_{\rm clust}$ for the low-z clusters. All galaxies with secure spectroscopic redshifts were included. The different panels represent the blue and red halves of the sample in $(B-V)_{\rm rest}$. The typically lower values of blue galaxies is due to their broader probability distributions. The solid vertical line indicates $z_{\rm phot}$ =  $z_{\rm clust}$ and the dashed lines indicate $\pm $0.1 in redshift. Horizontal error bars correspond to 68% confidence intervals.

Open with DEXTER

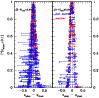
\begin{figure} \par\psfig{file=10644f11.eps,width=9cm} \end{figure} Figure 10:

Same as Fig. 9 but for the high-z clusters.

Open with DEXTER

For the GR code, Figs. 11 and 12 demonstrate how the retained fraction of members and rejected fraction of non-members depends on the $P_{\rm clust}$ threshold $P_{\rm thresh}$ for the low-z and high-z samples, respectively. In both cases, it is possible to define a $P_{\rm thresh}$ value such that >90% of confirmed cluster members are retained with little dependence on rest-frame (or observed) color.

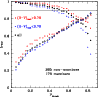
\begin{figure} \par\psfig{file=10644f12.eps,width=9cm} \end{figure} Figure 11:

The fraction of retained members and rejected non-members as a function of the $P_{\rm thresh}$ and as a function of $(B-V)_{\rm rest}$. This plot was created using all galaxies with secure $z_{\rm spec}$ measurements in clusters with BVIK photometry. clusters. Open symbols represent the fractions of rejected non-members, while solid points are the fractions of retained members. The color and shape of the points indicate the $(B-V)_{\rm rest}$ cut applied. The solid horizontal line at 0.9 is included to guide the eye. This figure only shows the results for the GR code, as an illustration of the technique. It is not directly comparable to the numbers quoted in Tables 6 and 7, which utilize the combination of both the GR code and Hyperz.

Open with DEXTER

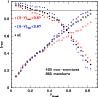
\begin{figure} \par\psfig{file=10644f13.eps,width=9cm} \end{figure} Figure 12:

Same as Fig. 11 but for clusters with VRIJK photometry.

Open with DEXTER

Since the performance is similar using Hyperz, we use both codes jointly to provide the most efficient rejection. In Figs. 18 and 19, we plot $P_{\rm clust}({\rm GR})$ versus $P_{\rm clust}({\rm Hyperz})$. While there is a large scatter, there is a definite correlation between the two probabilities, such that the majority of objects with low $P_{\rm clust}$ for one code also have a low $P_{\rm clust}$ with the other code. A Spearman's Rank Correlation test on the distribution of $P_{\rm clust}({\rm GR})$vs. $P_{\rm clust}({\rm Hyperz})$ shows that there is higher than 99.9% probability that these two variables are correlated. The same result is found for the low and high-z samples, when using the full magnitude-limited samples or other subsamples restricted to the brightest galaxies. This implies that a joint rejection is feasible. After extensive tests, we decided to reject galaxies if $P_{\rm clust}$ <  $P_{\rm thresh}$ for either code; in these tests, the $P_{\rm thresh}$ values for each code were determined separately, such that the highest rejection, independent of rest-frame color, was possible, while retaining >90% of the confirmed members. The adopted thresholds are summarized in Table 6 and the performance of these thresholds is summarized in Table 7.

Table 6:   Rejection thresholds.

Table 7:   Retained and rejected fraction in spectroscopic sample

Because P(z) is broader for galaxies without NIR data, $P_{\rm clust}$ is also systematically lower and the $P_{\rm thresh}$, determined for galaxies with NIR data, is no longer be applicable. To calibrate $P_{\rm thresh}$ for galaxies without NIR data, we re-derived $z_{\rm phot}$ for the entire spectroscopic sample, excluding the NIR filters. We recalibrate $P_{\rm thresh}$ and summarize the performance and adopted cuts in Tables 6 and 7. It is important to note that the performance of the rejection is different in areas with and without NIR data and the retained member population differs in the two regions. For this reason, we limit all studies using the photometric redshifts to those areas with NIR data.

We checked how the effectiveness of the adopted $P_{\rm thresh}$ varied across the sample. Because of the limited numbers of spectroscopically observed objects per cluster, this was not possible on a cluster-by-cluster basis. Instead we split each of the high-z and low-z samples into two subsamples each and examined how the accepted and rejected fractions differed. The retained fractions of members ranges from 87-98% and the rejected fractions of non-members ranges from 50-60%.

6.3 P clust threshold performance in magnitude limited samples

We examine how applicable our adopted $P_{\rm thresh}$, calibrated using the spectroscopic subsample, is to the full magnitude-limited sample. In Fig. 13, we show the apparent magnitude distribution of the spectroscopic sample and the total photometric sample with the same magnitude limit, for two clusters in each redshift range with the widest spectroscopic coverage. It is clear from these plots that we are not spectroscopically complete at any magnitude and that the spectroscopic sample, as expected, is biased towards brighter magnitudes.

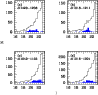
\begin{figure} \par\psfig{file=10644f14.eps,width=8.8cm} \end{figure} Figure 13:

The apparent magnitude histograms for the spectroscopic sample (solid blue histogram) versus the total sample of the same limiting magnitude (open black). For both samples at low-z (a and b) and high-z (c and d), two of the clusters with the most complete spectroscopic coverage are displayed. We note that the spectroscopic sample, even for clusters with the most extensive spectroscopy, is not complete at any magnitude limit and is biased towards brighter magnitudes. The magnitudes correspond to the I-band AUTO magnitudes from SExtractor.

Open with DEXTER

The spectroscopic target lists were not only constructed with a magnitude limit in mind, but also with an eye towards reducing the number of galaxies that had low probabilities of being at the cluster redshift, in addition to including some galaxies that were not formally present about $z_{\rm clust}$. We examine in general how this preselection causes the $P_{\rm clust}$ distributions of the spectroscopic sample to differ from those in a magnitude-limited photometric sample. In Fig. 20, we compare the histogram of the $P_{\rm clust}$ values for the spectroscopic samples with those for the entire sample down to the same magnitude limits. The spectroscopic preselection manifests itself as an excess of high $P_{\rm clust}$ values and a deficit of low $P_{\rm clust}$ for the spectroscopic sample with respect to the photometric sample. Within the precision of our numerical routine, a KS-test gives 0% probability that these two distributions are drawn from the same parent distribution. This inherent bias implies that a certain $P_{\rm thresh}$ removes a higher fraction of galaxies in the photometric sample than was the case in the spectroscopic subsample.

We examine how the spectroscopically calibrated $P_{\rm clust}$ rejection operates when applied to a magnitude-limited sample. We illustrate these results using the GR code, but the conclusions would be equivalent using Hyperz. In Figs. 14, 21, 15, and 22, we plot the $P_{\rm clust}$ versus $z_{\rm phot}$ for two high-zand two low-z clusters. Each figure has panels that show how this distribution changes with apparent magnitude. As we move to fainter magnitude limits, many galaxies appear at all $P_{\rm clust}$ values. Those at high $P_{\rm clust}$ do indeed fall close to $z_{\rm clust}$, as predicted by the spectroscopic studies. Encouragingly, the galaxies with low $P_{\rm clust}$ values fall systematically away from $z_{\rm clust}$. In fact, even at the faintest magnitudes, there are very few galaxies within $z_{\rm clust}$ $\pm $ 0.1 that have $P_{\rm clust}$ < 0.2. We recall that this must not be the case: galaxies with $z_{\rm phot}$ $\approx$  $z_{\rm clust}$ but broad P(z) distributions will have low probabilities of being at the cluster redshift, even though their best value lies around $z_{\rm clust}$. This self-consistency implies that $P_{\rm clust}$ is, in fact, providing us with a real indication of whether these faint objects are at the cluster redshift. This effect would be difficult to reproduce by systematic errors in the photometric redshifts because it appears for all clusters, regardless of their redshift range or presence of NIR data. Nonetheless, there are some faint galaxies with $z_{\rm phot}\sim z_{\rm clust}$ that may be rejected because of a broad P(z). Also, the tests presented in Sect. 4.3 demonstrate that the photometric redshift accuracy is expected to be lower for fainter galaxies, implying that there will be galaxies who are truly at $z_{\rm cluster}$ but are scattered away from the cluster redshift. In Rudnick et al. (2009), we discuss how these effects may differ for red and blue galaxies and we present the implications for the study of the cluster galaxy luminosity function.

The total fraction of galaxies rejected for each cluster as a function of I magnitude are presented in the Cols. 3-6 of Table 8. When our rejection criteria is applied, we reject 55-82% of the galaxies at I<22 and 75-93% at I<24.5.

\begin{figure} \par\psfig{file=10644f15.eps,width=9cm} \end{figure} Figure 14:

A plot of $P_{\rm clust}$ vs. $z_{\rm phot}$ for Cl1018-1211 that compares the spectroscopic sample with the magnitude-limited sample. Each tile corresponds to a different magnitude limit for the photometric sample. The full photometric sample is indicated by black dots. The spectroscopically confirmed cluster members are indicated by solid red triangles and the non-members by open blue squares. The solid vertical line indicates $z_{\rm phot}$ =  $z_{\rm clust}$ and the dashed lines indicate the intervals $\pm $0.1 in redshift. We note that, at fainter magnitudes, the galaxies with low $P_{\rm clust}$ values do not lie at $z_{\rm phot}\sim z_{\rm clust}$ in large numbers, but rather are at different redshifts.

Open with DEXTER

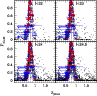
\begin{figure} \par\psfig{file=10644f16.eps,width=9cm} \end{figure} Figure 15:

Same as Fig. 14 except for Cl1216-1201.

Open with DEXTER

Table 8:   Total fraction of galaxies rejected as cluster members as a function of the I magnitude (Cols. 3 to 6 for $I\ge 22$, 23, 24 and 24.5 respectively).

7 Discussion and conclusions

We have used two independent codes to compute photometric redshifts: Hyperz and GR code. In general, the two codes yield rather similar results, either on a cluster-by-cluster basis or as a function of the filter set and spectral type, of typically $\sigma(\Delta z/(1+z))\sim0.05$ to 0.06. Hyperz results are found to be slightly more accurate than GR's ones in general, by $\la$20% in $\sigma (\Delta z/(1+z))$. The quality achieved by both codes is consistent with the expectations derived from ``ideal'' simulations. An interesting trend is that the quality of both codes is highly correlated, in the sense that the highest and lowest quality results, in terms of $\sigma (\Delta z/(1+z))$, and systematics are found for the same clusters. This trend cannot be due to the use of an incomplete or imperfect template set, as suggested by other authors (Ilbert et al. 2006), because in such a case, we should expect the same systematic behavior in all fields, given a filter set, as discussed in Sect. 4.1. In contrast, different systematics are observed in the different fields, which are found to be almost equal for the two independent $z_{\rm phot}$ codes. This behavior suggests that the origin of the systematic errors is more likely to be associated with small residuals in the input photometry rather than the $z_{\rm phot}$  templates and codes. Indeed, small zero-point shifts of $\la$0.05 mag cannot be excluded, in particular for the near-IR data.

Photometric redshifts are found to be particularly useful in the identification and study of galaxy clusters in large surveys. The determination of cluster redshifts in the EDisCS fields using a simple algorithm based on $z_{\rm phot}$ is highly accurate. Indeed, the differences between photometric and spectroscopic values are found to be small, typically ranging between $\delta z \sim$0.03-0.04 in the high-zsample and $\delta z \sim 0.05$ in the low-z sample. This is at least a factor $\sim(1+z)$ more accurate than the determination of $z_{\rm phot}$ for individual galaxies. The accuracy is more sensitive to the filter set used rather than the redshift of the cluster. The systematic lower quality results for the low-z sample was somewhat expected from the simulations presented in Sect. 4.1. Tomography based on $z_{\rm phot}$ could be used in searches for clusters along the line-of-sight, using redshift steps optimized to be close in value to the typical difference between photometric and spectroscopic $z_{\rm cluster}$ to maximize the contrast between members and non-member galaxies (in this case, $\Delta z \sim 0.05$).

The cluster membership criterion presented in Sect. 6 has been used to extend the spectroscopic studies of cluster galaxies to fainter limits in magnitude (e.g. De Lucia et al. 2004; White et al. 2005; Clowe et al. 2006; Poggianti et al. 2006; De Lucia et al. 2007; Desai et al. 2007; Rudnick et al. 2009).

In conclusion, photometric redshifts are useful tools for studying galaxy clusters. They enable efficient and complete pre-selection of cluster members for spectroscopy, allow accurate determinations of the cluster redshifts based on photometry alone, provide a means of determining cluster membership, especially for bright sources, and can be used to search for galaxy clusters.

Acknowledgements
Part of this work was supported by the French Centre National de la Recherche Scientifique, by the French Programme National de Cosmologie (PNC) and the Programme National Galaxies (PNG). The Dark Cosmology Centre is funded by the Danish National Research Foundation.

References

Online Material

Table 9:   $z_{\rm phot}$ accuracy derived from simulations for galaxies in the spectroscopic sample, based on the GR code.

Table 10:   $z_{\rm phot}$ accuracy expected for the faintest galaxies in the EDisCS sample, based on the GR code.

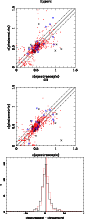
\begin{figure} {\hspace*{6mm}\psfig{file=10644f17.ps,angle=270,width=6.2cm}\hsp... ...pace*{6mm}} \par {\psfig{file=10644f19.ps,angle=270,width=7.4cm} }\end{figure} Figure 16:

Comparison between spectroscopic and photometric redshifts for the low-z sample, obtained with Hyperz ( top panel) and GR ( central panel) codes. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Dot-dashed lines display $z_{\rm spec}$  =  $z_{\rm phot}$  $\pm $ 0.1 to guide the eye. The bottom panel displays the $z_{\rm spec} - z_{\rm phot}$ distribution obtained for this sample with Hyperz (solid black line) and GR (dotted red line). Vertical lines indicate the mean $\langle \Delta_z \rangle$.

Open with DEXTER

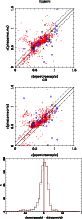
\begin{figure} {\hspace*{5mm}\psfig{file=10644f20.ps,angle=270,width=6.2cm}\hsp... ...pace*{5mm}} \par {\psfig{file=10644f22.ps,angle=270,width=7.2cm} }\end{figure} Figure 17:

(Comparison between spectroscopic and photometric redshifts for the high-z sample, obtained with Hyperz ( top panel) and GR ( central panel) codes. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Dot-dashed lines display $z_{\rm spec}$  =  $z_{\rm phot}$  $\pm $ 0.1 to guide the eye. The bottom panel displays the $z_{\rm spec} - z_{\rm phot}$ distribution obtained for this sample with Hyperz (solid black line) and GR (dotted red line). Vertical lines indicate the mean $\langle \Delta_z \rangle$.

Open with DEXTER

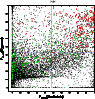
\begin{figure} \par\psfig{file=10644f23.eps,width=9cm} \end{figure} Figure 18:

A comparison of $P_{\rm clust}$ computed by the two different photometric redshift codes for the clusters with BVIK photometry. The black open circles represent all galaxies with I<24.5. The solid red squares are spectroscopically confirmed members and the solid green triangles are spectroscopically confirmed non-members. There is a broad correlation of $P_{\rm clust}$ between the two codes, such that the overwhelming number of galaxies have low $P_{\rm clust}$ for both methods with a smooth distribution of higher $P_{\rm clust}$ galaxies extending to the upper right, coincident with the confirmed members. The blue lines indicate the $P_{\rm thresh}$ values for each code that were determined to reject jointly the largest number of non-members, while retaining at least $90\%$ of the confirmed members. Objects to the left of the vertical blue line or beneath the horizontal blue line are flagged as interlopers.

Open with DEXTER

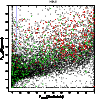
\begin{figure} \par\psfig{file=10644f24.eps,width=9cm} \end{figure} Figure 19:

Same as Fig. 18 but for the clusters with VRIJK photometry.

Open with DEXTER

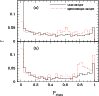
\begin{figure} \par\psfig{file=10644f25.eps,width=8.8cm} \end{figure} Figure 20:

The histogram of $P_{\rm clust}$ values for the photometric sample (solid line) versus that of the spectroscopic sample (dotted line). Panel  a) is for the high-z sample at I<22.5 and panel  b) is for the low-z sample at I<22. In each case, the histograms represent the fraction of the total number of objects over all $P_{\rm clust}$.

Open with DEXTER

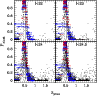
\begin{figure} \par\psfig{file=10644f26.eps,width=9cm} \end{figure} Figure 21:

Same as Fig. 14 except for Cl1420-1236.

Open with DEXTER

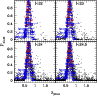
\begin{figure} \par\psfig{file=10644f27.eps,width=9cm} \end{figure} Figure 22:

Same as Fig. 14 except for Cl1040-1155.

Open with DEXTER

Footnotes

... Survey[*]
Based on observations collected at the European Southern Observatory, Paranal and La Silla, Chile, as part of the ESO LP 166.A-0162.
...[*]
Figures 16-22, Tables 9 and 10 are only available in electronic form at http://www.aanda.org
... website[*]
http://www.mpa-garching.mpg.de/galform/ediscs
... website[*]
http://www.mpa-garching.mpg.de/galform/ediscs
... Hyperz[*]
http://webast.ast.obs-mip.fr/hyperz/
... website[*]
http://www.mpa-garching.mpg.de/galform/ediscs

All Tables

Table 1:   $z_{\rm phot}$ accuracy from simulations for galaxies in the spectroscopic sample, based on Hyperz.

Table 2:   $z_{\rm phot}$ accuracy expected for the faintest galaxies in the EDisCS sample, in the low-z and high-z fields, based on Hyperz.

Table 3:   Summary of $z_{\rm phot}$ accuracy achieved for the individual low-z and high-z clusters.

Table 4:   Summary of $z_{\rm phot}$ accuracy achieved for the whole low-z and high-z samples with Hyperz and GR codes.

Table 5:   Comparison between spectroscopic ( $z_{\rm cl}$) and photometric determinations of cluster redshifts in the low and high-z samples.

Table 6:   Rejection thresholds.

Table 7:   Retained and rejected fraction in spectroscopic sample

Table 8:   Total fraction of galaxies rejected as cluster members as a function of the I magnitude (Cols. 3 to 6 for $I\ge 22$, 23, 24 and 24.5 respectively).

Table 9:   $z_{\rm phot}$ accuracy derived from simulations for galaxies in the spectroscopic sample, based on the GR code.

Table 10:   $z_{\rm phot}$ accuracy expected for the faintest galaxies in the EDisCS sample, based on the GR code.

All Figures

  \begin{figure} \par\psfig{file=10644f1.eps,width=8.8cm} \end{figure} Figure 1:

Photometric versus model redshifts retrieved from ${\it BVIK}_{\rm s}$ SEDs (low-z sample), for 105 simulated galaxies uniformly distributed between $0 \le z \le 2$. The diagram displays the number density of galaxies in linear scale.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f2.eps,width=8.8cm} \end{figure} Figure 2:

Photometric versus model redshifts retrieved from ${\it VRIJK}_{\rm s}$ SEDs (high-z sample), for 105 simulated galaxies uniformly distributed between $0 \le z \le 2$. The diagram displays the number density of galaxies in linear scale.

Open with DEXTER
In the text

  \begin{figure} {% \leavevmode \psfig{file=10644f3.ps,angle=270,width=8.8cm}\newline \psfig{file=10644f4.ps,angle=270,width=8.8cm} } \vspace*{6mm} \end{figure} Figure 3:

These figures present the expected $z_{\rm phot}$ accuracy derived from simulations, for galaxies with photometric quality similar to the spectroscopic sample. The top panel displays the systematic deviation $\langle \Delta_z \rangle \pm \sigma_z$, the standard deviation excluding catastrophic identifications, for the ${\it BVIK}_{\rm s}$ (low-z, black dots) and ${\it VRIJK}_{\rm s}$ (high-z, open/red dots) filter sets, within the relevant redshift domain. The botton panel displays a plot of $\sigma (\Delta z/(1+z))$ as a function of redshift for the same filter combinations.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f5.ps,width=17cm}\vspace{1mm} \vspace{2mm} \end{figure} Figure 4:

( $z_{\rm spec}$ - $z_{\rm phot}$ ) versus spectroscopic redshift for the low-z clusters in the EDisCS sample. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Error bars in $z_{\rm phot}$  correspond to 1$\sigma $. Dot-dashed lines display $z_{\rm spec}$ - $z_{\rm phot}$  = $\pm 0.1$ to guide the eye. (See text for details.)

Open with DEXTER
In the text

  \begin{figure} {% \leavevmode \psfig{file=10644f6.ps,angle=270,width=18cm} } \vspace{3mm} \end{figure} Figure 5:

( $z_{\rm spec}$ - $z_{\rm phot}$ ) versus spectroscopic redshift for the high-z clusters in the EDisCS sample. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Error bars in  $z_{\rm phot}$  correspond to 1$\sigma $ Dot-dashed lines display $z_{\rm spec}$ - $z_{\rm phot}$  = $\pm $ 0.1 to guide the eye. (See text for details.)

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f7.ps,width=17cm} \end{figure} Figure 6:

Photometric redshift distributions in the EDisCS fields, with the cluster redshift increasing from top to bottom and from left to right, for the low-z and high-z samples (first and second series respectively). The histograms display the following redshift distributions: $N_{\rm in}(z)$ (black thick solid lines), $N_{\rm out}(z)$ (thin black lines), and the positive difference between $N_{\rm in}(z) - N_{\rm out}(z)$ (lowest histograms, thick red lines). A real cluster or other structure corresponds to a positive excess in the lower (red) histogram. Histograms were obtained with a $\delta z =0.05$ sampling step, smoothed by a $\delta z =0.15$ sliding window. Vertical solid and dashed lines indicate the spectroscopic and photometric values, respectively, adopted for the cluster redshift. All vertical scales are identical in the number of galaxies/ $\Delta z = 0.05$, from N(z)=0 to 100, apart from Cl1216-1201, for which the range is 0 to 115.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f8.ps,angle=270,width=18cm} \end{figure} Figure 7:

Projected number density maps for the low-z sample, for different redshift slices with $z_{\rm cluster}$ increasing from top to bottom. Projected number densities are displayed in a linear scale. Isopleths correspond to increasing number density bins with $\Delta \Sigma_{20}= \langle \Sigma_{20}\rangle$, starting at the mean  $\Sigma _{20}$ within the redshift slice. Thick frames highlight the redshift slices encompassing $z_{\rm cluster} \pm 0.1$. The rightmost column displays the density map for the $z_{\rm cluster} \pm 0.1$ redshift slice, where the maximum contrast in the density peak is usually reached. The position of the BCG for the most prominent clusters in the field are displayed by a blue cross. For Cl1059-1253, Cl1202-1224, and Cl1119-1129, only two isopleths are displayed corresponding to 1 and $1.5 \langle \Sigma_{20}\rangle$. Additional overdensities along the line of sight with detection levels exceeding $4\sigma $ are displayed by circles.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f9.ps,angle=270,width=18cm} \end{figure} Figure 8:

Projected number density maps for the high-z sample, for different redshift slices. Same comments as in Fig. 7. There is no clear BCG identified in Cl1122-1136.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f10.eps,width=9cm} \end{figure} Figure 9:

The integrated probability of being at $z_{\rm clust}$ $\pm $ 0.1 vs. $z_{\rm phot}$ -  $z_{\rm clust}$ for the low-z clusters. All galaxies with secure spectroscopic redshifts were included. The different panels represent the blue and red halves of the sample in $(B-V)_{\rm rest}$. The typically lower values of blue galaxies is due to their broader probability distributions. The solid vertical line indicates $z_{\rm phot}$ =  $z_{\rm clust}$ and the dashed lines indicate $\pm $0.1 in redshift. Horizontal error bars correspond to 68% confidence intervals.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f11.eps,width=9cm} \end{figure} Figure 10:

Same as Fig. 9 but for the high-z clusters.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f12.eps,width=9cm} \end{figure} Figure 11:

The fraction of retained members and rejected non-members as a function of the $P_{\rm thresh}$ and as a function of $(B-V)_{\rm rest}$. This plot was created using all galaxies with secure $z_{\rm spec}$ measurements in clusters with BVIK photometry. clusters. Open symbols represent the fractions of rejected non-members, while solid points are the fractions of retained members. The color and shape of the points indicate the $(B-V)_{\rm rest}$ cut applied. The solid horizontal line at 0.9 is included to guide the eye. This figure only shows the results for the GR code, as an illustration of the technique. It is not directly comparable to the numbers quoted in Tables 6 and 7, which utilize the combination of both the GR code and Hyperz.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f13.eps,width=9cm} \end{figure} Figure 12:

Same as Fig. 11 but for clusters with VRIJK photometry.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f14.eps,width=8.8cm} \end{figure} Figure 13:

The apparent magnitude histograms for the spectroscopic sample (solid blue histogram) versus the total sample of the same limiting magnitude (open black). For both samples at low-z (a and b) and high-z (c and d), two of the clusters with the most complete spectroscopic coverage are displayed. We note that the spectroscopic sample, even for clusters with the most extensive spectroscopy, is not complete at any magnitude limit and is biased towards brighter magnitudes. The magnitudes correspond to the I-band AUTO magnitudes from SExtractor.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f15.eps,width=9cm} \end{figure} Figure 14:

A plot of $P_{\rm clust}$ vs. $z_{\rm phot}$ for Cl1018-1211 that compares the spectroscopic sample with the magnitude-limited sample. Each tile corresponds to a different magnitude limit for the photometric sample. The full photometric sample is indicated by black dots. The spectroscopically confirmed cluster members are indicated by solid red triangles and the non-members by open blue squares. The solid vertical line indicates $z_{\rm phot}$ =  $z_{\rm clust}$ and the dashed lines indicate the intervals $\pm $0.1 in redshift. We note that, at fainter magnitudes, the galaxies with low $P_{\rm clust}$ values do not lie at $z_{\rm phot}\sim z_{\rm clust}$ in large numbers, but rather are at different redshifts.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f16.eps,width=9cm} \end{figure} Figure 15:

Same as Fig. 14 except for Cl1216-1201.

Open with DEXTER
In the text

  \begin{figure} {\hspace*{6mm}\psfig{file=10644f17.ps,angle=270,width=6.2cm}\hsp... ...pace*{6mm}} \par {\psfig{file=10644f19.ps,angle=270,width=7.4cm} }\end{figure} Figure 16:

Comparison between spectroscopic and photometric redshifts for the low-z sample, obtained with Hyperz ( top panel) and GR ( central panel) codes. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Dot-dashed lines display $z_{\rm spec}$  =  $z_{\rm phot}$  $\pm $ 0.1 to guide the eye. The bottom panel displays the $z_{\rm spec} - z_{\rm phot}$ distribution obtained for this sample with Hyperz (solid black line) and GR (dotted red line). Vertical lines indicate the mean $\langle \Delta_z \rangle$.

Open with DEXTER
In the text

  \begin{figure} {\hspace*{5mm}\psfig{file=10644f20.ps,angle=270,width=6.2cm}\hsp... ...pace*{5mm}} \par {\psfig{file=10644f22.ps,angle=270,width=7.2cm} }\end{figure} Figure 17:

(Comparison between spectroscopic and photometric redshifts for the high-z sample, obtained with Hyperz ( top panel) and GR ( central panel) codes. Solid (red) circles, open (blue) circles, and crosses correspond to objects with good (type 1), medium (type 2) and tentative (type 3) spectroscopic redshift determinations, respectively. Dot-dashed lines display $z_{\rm spec}$  =  $z_{\rm phot}$  $\pm $ 0.1 to guide the eye. The bottom panel displays the $z_{\rm spec} - z_{\rm phot}$ distribution obtained for this sample with Hyperz (solid black line) and GR (dotted red line). Vertical lines indicate the mean $\langle \Delta_z \rangle$.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f23.eps,width=9cm} \end{figure} Figure 18:

A comparison of $P_{\rm clust}$ computed by the two different photometric redshift codes for the clusters with BVIK photometry. The black open circles represent all galaxies with I<24.5. The solid red squares are spectroscopically confirmed members and the solid green triangles are spectroscopically confirmed non-members. There is a broad correlation of $P_{\rm clust}$ between the two codes, such that the overwhelming number of galaxies have low $P_{\rm clust}$ for both methods with a smooth distribution of higher $P_{\rm clust}$ galaxies extending to the upper right, coincident with the confirmed members. The blue lines indicate the $P_{\rm thresh}$ values for each code that were determined to reject jointly the largest number of non-members, while retaining at least $90\%$ of the confirmed members. Objects to the left of the vertical blue line or beneath the horizontal blue line are flagged as interlopers.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f24.eps,width=9cm} \end{figure} Figure 19:

Same as Fig. 18 but for the clusters with VRIJK photometry.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f25.eps,width=8.8cm} \end{figure} Figure 20:

The histogram of $P_{\rm clust}$ values for the photometric sample (solid line) versus that of the spectroscopic sample (dotted line). Panel  a) is for the high-z sample at I<22.5 and panel  b) is for the low-z sample at I<22. In each case, the histograms represent the fraction of the total number of objects over all $P_{\rm clust}$.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f26.eps,width=9cm} \end{figure} Figure 21:

Same as Fig. 14 except for Cl1420-1236.

Open with DEXTER
In the text

  \begin{figure} \par\psfig{file=10644f27.eps,width=9cm} \end{figure} Figure 22:

Same as Fig. 14 except for Cl1040-1155.

Open with DEXTER
In the text

Copyright ESO 2009

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.