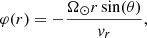| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A257 | |
| Number of page(s) | 11 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202451005 | |
| Published online | 19 November 2024 | |
Magnetic connectivity from the Sun to the Earth with MHD models
I. Impact of the magnetic modelling on connectivity validation
1
AIM/DAp – CEA Paris-Saclay, Université Paris-Saclay, Université Paris-Cité, Gif-sur-Yvette, France
2
Centre for Mathematical Plasma-Astrophysics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
3
Institute of Physics, University of Maria Curie-Skłodowska, Pl. Marii Curie-Skłodowska 5, 20-031 Lublin, Poland
⋆ Corresponding author; barbara.perri@cea.fr
Received:
5
June
2024
Accepted:
30
September
2024
Context. The magnetic connectivity between the Sun and the Earth is crucial to our understanding of the solar wind and space weather events. However, establishing this connectivity is challenging because of the lack of direct observations, which explains the need for reliable simulations.
Aims. The method most often used to make such measurements over the last few years is the two-step ballistic method, but it has many free parameters that can affect the final result. Thus, we want to provide a connectivity method based on self-consistent magnetohydrodynamics (MHD) models.
Methods. To this end, we combined the COCONUT coronal model with the EUHFORIA heliospheric model to compute the magnetic field lines from the Earth to the Sun. We then developed a way to quantify both the spatial and temporal uncertainty associated with this computation. To validate our method, we selected four cases already studied in the literature and associated with high-speed-stream events coming from unambiguous coronal holes visible on the disk.
Results. We always find a partial overlap with the assumed CH of origin. The extent of this overlap is 19% for event 1, 100% for event 2, 45% for event 3, and 100% for event 4. We looked at the polarity at Earth over the full Carrington rotation to better understand these results. We find that, on average, MHD simulations provide a very good polarity estimation, showing 69% agreement with real data for event 1, 36% for event 2, 68% for event 3, and 69% for event 4. For events 1 and 3, we can then explain the mixed results by the spatial and temporal uncertainty. An interesting result is that, for MHD models, minimum-activity cases appear to be more challenging because of the multiple recurrent crossings of the HCS, while maximum-activity cases appear easier because of the latitudinal extent of the HCS. A similar result was also found with Parker Solar Probe data in another study.
Conclusions. We demonstrate that it is possible to use MHD models to compute magnetic connectivity and that this approach provides results of equal quality to those from the two-step ballistic method, with additional possibilities for improvements as the models integrate more critical physics.
Key words: magnetohydrodynamics (MHD) / Sun: corona / Sun: magnetic fields / solar wind
© ESO 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Space weather forecasting can be described as the ability to anticipate the most energetic events from the Sun and their corresponding impact on our planet (Schrijver et al. 2015). Such events include, for example, solar particles accelerated to a relativistic speed by flares, that is, solar energetic particles (SEPs) or large clouds of coronal matter ejected in the interplanetary medium by magnetic reconnection, known as coronal mass ejections (CMEs) (Temmer 2021). These events can have a strong impact on the Earth’s environment by disrupting the magnetosphere’s magnetic field and enhancing the radiation in the van Allen belts (Pulkkinen 2007). These consequences are significant for our heavily technology-dependent society, as they can jeopardise astronaut equipment, satellite lifetimes, communication efficiency, aviation crew safety, and even ground-based large-scale electrical installations (Lanzerotti 2001). However, connecting these solar events with their geo-effective counterpart is far from trivial (Zhang et al. 2021): this is due to the dynamics of the interplanetary medium, which is shaped by the continuous ejection of particles that is the solar wind (Parker 1958). The latter can slow down or even deflect events (Lavraud & Rouillard 2014), and even cause disturbances by itself through its fastest component, high-speed streams (HSSs) (Verbanac et al. 2011). When the solar wind becomes highly dynamic (e.g., close to maximum activity), it then becomes especially challenging to produce reliable space-weather forecasts (Riley et al. 2018).
One tool to connect solar observations with those at L1 is to use the interplanetary magnetic field (Owens & Forsyth 2013). This field is generated inside the Sun through the dynamo effect, which is the ability of a magnetised fluid to sustain and amplify a large-scale magnetic field against Ohmic dissipation (Moffatt 1978; Parker 1993). This dynamo-generated magnetic field is variable in time, with an 11-year cycle of activity for sunspots and a 22-year cycle for polarity reversal (Hathaway 2015). This large-scale magnetic field expands across the solar surface and bathes the entire Solar System. It then interacts with the solar wind, creating complex dynamics where the particles follow the field lines in the lower corona. In contrast, further away from the Sun, the frozen magnetic field traces the path of the plasma. Energetic particles emitted during specific events such as SEPs are also sensitive to the influence of magnetic field and tend to gyrate around field lines (Heber & Potgieter 2006). Knowledge of the interplanetary magnetic field can therefore be used to build a map of the Sun–Earth connectivity. A well-known example of this complex connectivity is the Parker spiral. Due to the Sun’s rotation, magnetic field lines are twisted to an angle that reaches 45° at the Earth (Parker 1958), and hence western-limb events tend to be more geo-effective on average than events close to the central meridian (Cid et al. 2012). However, this method is still challenging to use, as there are no direct observations of the interplanetary magnetic field (only punctual local in situ measurements or indirect proxies, such as white-light polarized brightness images) (Owens & Forsyth 2013). Most methods thus rely on models, but these usually do not consider the perturbations created by turbulence, waves, shears, shocks, or magnetic reconnection.
One of the first examples of computation of the magnetic connectivity was presented by Nolte & Roelof (1973), with the extrapolated quasi-radial hypervelocity (ERQH) approximation. This method is based on the Parker spiral with a constant solar wind speed along the trajectory and was used to trace the origin of an HSS (Krieger et al. 1973) and SEP events back to the solar surface (Roelof & Krimigis 1973). This method was later labeled the ballistic back-mapping method, as mapping starts from the planet or spacecraft and the solar wind trajectory is computed from there. Neugebauer et al. (1998) presented a follow-up study, computing the connectivity of the WIND and Ulysses spacecraft, and exploring new semi-empirical models such as the potential field source surface extrapolation (PFSS; see Schatten et al. 1969) and current sheet models (Schatten 1971). These new methods were labeled magnetic mappings, starting from the solar magnetic field and focusing on the extension of the field lines. More recent studies using the Parker Solar Probe (PSP) data have shown that these methods alone have limitations (Macneil et al. 2022) and that the best way to compute the magnetic connectivity is to use both methods one after the other, which is now known as two-step ballistic mapping (Peleikis et al. 2017). Such methods are used to compute the connectivity for solar missions such as Solar Orbiter (Rouillard et al. 2020). There is ongoing research on how to improve both the two-step ballistic method and the computation of its corresponding uncertainties (Koukras et al. 2022; da Silva et al. 2023; Dakeyo et al. 2024).
However, these empirical models tend to have many free parameters that strongly impact the connectivity forecast (Badman et al. 2020). Magnetohydrodynamics (MHD) models are more self-consistent but until recently have not been used for space-weather applications as they tend to be too slow for operational use. However, the situation has now changed, with new models such as EUHFORIA (Pomoell & Poedts 2018), COCONUT (Perri et al. 2022), and ICARUS (Verbeke et al. 2022), which are specifically designed and optimised for operational forecasts. This forecasting time can even be improved through the architecture of forecasting facilities, which allows the coupling of coronal and heliospheric models (Poedts et al. 2020). Through this chain of models, we can also derive the magnetic connectivity and then test the advantages and limitations of this new method compared to existing ones. Such a comparison was made by Neugebauer et al. (1998), who tested these coupled models against the “magnetohydrodynamic algorithm outside a sphere” (MAS) from Linker & Mikić (1997). This work was completed by Riley et al. (2006), who found that the topology of PFSS and MHD models is usually similar. More recently, Badman et al. (2023) studied the connectivity between the Sun and PSP using many different models, including MHD models such as MAS but also MS-FLUKSS (Singh et al. 2022). Badman et al. (2023) also found similar results for Encounters 4 and 10 of the PSP mission in terms of connectivity estimations made with PFSS or MHD models. However, such a systematic comparison has not been conducted recently for the connectivity to Earth.
The structure of this paper is as follows. In Sect. 2, we provide more information about the 3D MHD models used (COCONUT for the corona and EUHFORIA for the heliosphere), how we connect the two to compute the magnetic connectivity, and the alternative way of computing the connectivity using PFSS and ballistic back-mapping, which we used for comparison. In Sect. 3, we present the different validation cases selected. In Sect. 4, we compute the magnetic connectivity for the chosen cases and compare the results with those using traditional connectivity methods. In Sect. 5, we discuss the quality of these results and explain their differences using in situ data. Finally, in Sect. 6 we summarise all of our results and offer future perspectives.
2. Computation of the magnetic connectivity
As explained above, this study is unique in that it uses only MHD models to compute the magnetic connectivity.
2.1. MHD models
2.1.1. MHD coronal model: COCONUT
COCONUT (COolfluid COroNa UnsTructured) is a 3D MHD data-driven coronal model that uses implicit numerical methods. A full description of the model can be found in Perri et al. (2022); here we only describe its main characteristics. The model is based on the COOLFluid framework for fluid mechanics (Lani et al. 2013). It solves the ideal MHD equations written in their conservative form in Cartesian coordinates and dimensionless form. It uses a time-implicit backward Euler scheme for finite volume methods to reach operational running times (Perri et al. 2022) and runs on an unstructured grid to avoid polar singularities (Brchnelova et al. 2022a). The default mesh uses a sixth-level subdivision of the geodesic polyhedron with 20 480 surface elements, resulting in a grid with 3.9M elements. To ensure the divergence constraint ∇ ⋅ B = 0, we use the artificial compressibility analogy (Chorin 1997), which is very similar to the hyperbolic divergence cleaning (HDC) method initially developed by Dedner et al. (2002). COCONUT neglects some elements to speed up the calculations, such as the Hall term in the induction equation. Also, the Coriolis force or centrifugal forces are neglected in the momentum equation. Hence, the solar rotation is not considered, as it does not influence the result below 20 solar radii (Perri et al. 2022). COCONUT takes as input a synoptic magnetic map of the Sun as the inner boundary condition for the radial magnetic field. The map is projected onto spherical harmonics and is reconstructed using the first 30 modes. It has been validated both at minimum (Perri et al. 2023) and maximum activity (Kuźma et al. 2023) by comparison with various solar datasets. More specifically, the validation was done during total solar eclipse events using white-light polarized brightness images. That way, the coronal magnetic field structure could be inferred and compared with the numerically obtained magnetic field.
This version of the COCONUT model uses a polytropic relation between the density and the pressure as an approximation of coronal heating. Indeed, by stating that the corona is almost isothermal (with a polytropic index of 1.05), we simulate a constant input of energy to accelerate the wind. However, with this assumption, only a slow or fast solar wind is considered, and not both simultaneously. The model was run with the same parameters as those described in Perri et al. (2023), which means ρ⊙ = 1.67 × 10−16 g/cm3 and T⊙ = 1.9 × 106 K for fixed-value Dirichlet conditions of density and pressure. The pressure at the inner boundary follows from the solar surface temperature by application of the ideal gas law: P⊙ = 4.15 × 10−2 dyn/cm2. All other quantities of the magnetic field have zero-gradient conditions. This means that ∂Bθ/∂r = ∂Bφ/∂r = 0. Regarding the velocity, it is aligned with the magnetic field in order to limit surface currents, as explained in Brchnelova et al. (2022b). The frame used in COCONUT is the same as the input map. As we explain below, we used SDO/HMI synoptic maps in the Carrington frame for this study. We demonstrated in Perri et al. (2023) that these maps yield the most realistic results for the base parameters of COCONUT.
2.1.2. MHD heliospheric model: EUHFORIA
EUHFORIA (EUropean Heliospheric FORecasting Information Asset) is a model for forecasting the solar wind in the inner heliosphere and the potential CME evolution within (Pomoell & Poedts 2018). The complete model contains a coronal part (up to 21.5 solar radii) and a heliospheric part (up to Mars’ orbit). However, we replaced the coronal part with COCONUT to provide the solar wind radial speed, temperature, density, and radial magnetic field at the interface. The heliospheric part is a 3D magneto-hydrodynamics model in which the ideal MHD equations are solved with gravity included. These equations are solved in the heliocentric Earth equatorial HEEQ coordinate system. We use a finite volume method combined with a constrained transport approach to solve the MHD equations. We use an approximate Riemann solver with standard piece-wise linear reconstruction (Kissmann & Pomoell 2012; Pomoell & Vainio 2012) to obtain a robust and second-order accurate scheme. At the outer radial boundary, we use open boundary conditions implemented via a simple extrapolation, whereas at the latitudinal boundaries, we use symmetric reflection boundary conditions. Although the chosen frame is not inertial, we choose to omit the Coriolis and centrifugal terms, which should be the result of Earth’s orbital motion, as their contribution is negligible compared to the other plasma forces and timescales due to the slow rotation of the Sun. A value of 1.5 is selected for the polytropic index, as in Odstrcil et al. (2004). The default setup has a 2° angular resolution. We did not include any CMEs in this project.
2.2. Magnetic connectivity using MHD models
This section now explains how we compute the magnetic connectivity from the Sun to the Earth with the outputs of the two previously described MHD models. As explained previously, the two models have different frames (Carrington for COCONUT, HEEQ for EUHFORIA), which we must adjust to make the physical quantities continuous. The equivalent of the HEEQ frame for the coronal part is the Stonyhurst heliographic coordinate frame (Thompson 2006; Beck 2010). We thus compute the longitude of the Carrington longitude in this frame and proceed to rotate the COCONUT data accordingly.
We can start tracing the magnetic field lines once the two models are in the same reference frame. We use the PyVista Python package (Sullivan & Kaszynski 2019), which reads in the COCONUT and EUHFORIA 3D datasets and traces streamlines using a Runge-Kutta 2 integrator. The streamlines of a magnetic vector field are what we call magnetic field lines. We start from the position of the Earth, which is always located in the heliospheric part, and so the data from EUHFORIA are used first. From the magnetic field computed by EUHFORIA, we trace the field lines down to ∼0.1 AU. The endpoint of the field line in the heliospheric part for EUHFORIA gives the starting seed for the field line in the coronal part for COCONUT. We finally trace the second magnetic field line from this interface point until the inner boundary of COCONUT, which corresponds to the inner corona close to the solar surface. This second streamline’s endpoint is then Earth’s connectivity point on the solar surface. The resulting magnetic connectivity can be seen in Fig. 1. The Earth is depicted as a gray sphere to show the initial seed of the magnetic field line. Then, we have a first field line computed in EUHFORIA in the heliospheric part (shown as a white flux tube). The interface between the coronal and heliospheric parts (COCONUT and EUHFORIA) is shown via a transparent sphere at 0.1 AU. Finally, inside the coronal part, we show the second magnetic field line computed using COCONUT results (white flux tube inside the transparent sphere). In summary, for each date, we can provide the magnetic connectivity point at the surface of the Sun that is magnetically connected to the Earth. This procedure is used here only for the connectivity between the Earth and the Sun, but the same principle could be applied to other satellites.
 |
Fig. 1. Example of magnetic connectivity computed between the Earth and the Sun using COCONUT and EUHFORIA models. The Earth is depicted as a gray sphere to show the initial seed of the magnetic field line. Then, we have a first field line computed in EUHFORIA in the heliospheric part (shown as a white flux tube). The interface between the coronal and heliospheric parts (COCONUT and EUHFORIA) is shown via a transparent sphere at 0.1 AU. Finally, inside the coronal part, we show the second magnetic field line computed using COCONUT results (white flux tube inside the transparent sphere). |
A complementary approach is to use the velocity streamlines as another indicator of connectivity in addition to the magnetic field lines: because of the frozen-in theorem, magnetic and velocity streamlines should coincide most of the time. However, we cannot be certain that this is always the case: in the case of magnetic reconnection in particular, magnetic field lines may become discontinuous, but velocity streamlines may not, which simplifies the complexity of certain events. The use of velocity streamlines will be examined more thoroughly in a future study.
Because we work with realistic field lines, they are not always continuous. This can be caused by numerical reconnection in the current sheet due to the resolution, or by shocks and discontinuities that form naturally in the numerical domain. We developed specific procedures to exclude these exceptions and only compute the field lines that extend between the two models. This means that we exclude field lines in EUHFORIA that do not reach the interface at ∼0.1 AU, and we also exclude field lines in COCONUT that do not reach the inner boundary condition at one solar radius.
We performed an event-based study to test the accuracy of our connectivity estimates. The events and how they were chosen can be seen in Sect. 3. To assess the robustness of our results, we computed uncertainties associated with each event. First, we took into account a temporal uncertainty: this comes from the fact that the solar wind takes four days to travel from the Sun to the Earth on average, but this is a statistical approximation obtained for HSSs produced by coronal holes (CHs) (Vršnak et al. 2007). In practice, the solar wind speed can vary along the trajectory and thus impact the propagation time (Koukras et al. 2022). To take this into account, when we are trying to derive the magnetic connectivity at an event seen at Earth for a specific date, we average the connectivity points we find over the past few days before the event to get an idea of the temporal evolution of the magnetic connectivity over the propagation phase of the solar wind. However, we specify that this temporal variation is made solely by rotation of the simulation by assuming that the magnetic field configuration does not vary over the studied period (which is not always the case at maximum activity). Second, we also take into account spatial uncertainty: as explained above, the magnetic field lines can be discontinuous, or they can also be very divergent locally, which means that we cannot rely upon a single field line for the magnetic connectivity estimate. This spatial uncertainty also includes the possible deviation of a few degrees induced by the neglect of the effect of rotation. To improve our estimation of the uncertainty, we thus compute several field lines for the Earth connectivity, each starting from a seed point separated from Earth by an angle of between 5 and 10° in latitude and/or longitude. Ultimately, we use nine points around the Earth’s position and thus compute between one and nine field lines, depending on their continuity. Thus, we can ultimately get several dozen points for the magnetic connectivity estimate. We take the mean value of the points’ positions and compute the standard deviation to provide a magnetic connectivity zone instead of a magnetic connectivity point. As a general rule, if the difference in latitude exceeds 20°, the zone is split into two different subzones.
2.3. Alternative way of computing connectivity for validation
To validate our magnetic connectivity estimation, we compare it with other studies such as Reiss et al. (2021) and Koukras et al. (2022). The first study is purely observational, focusing on an HSS case where the connected coronal hole could be easily identified (as described in more detail in the following section). The second study uses a modified back-mapping method, replacing the ballistic part with a two-part Parker solution approximation. In contrast, the PFSS part is based on GONG magnetograms. We also compare our MHD connectivity estimate with a more traditional one based on the usual back-mapping method. We describe this method as implemented here, using the two steps of ballistic mapping and magnetic mapping.
Ballistic mapping is where the solar wind is traced from a point in the inner heliosphere to the source surface using the Parker spiral corresponding to the solar wind speed vr measured in situ and assuming it is constant with distance (Krieger et al. 1973; Peleikis et al. 2017). For a spiral of heliographic colatitude θ, the heliographic longitude φ(r) of the spiral as a function of heliocentric distance (r) relative to its starting longitude is given by:
where Ω⊙ is the angular velocity of the Sun. Strictly speaking, the radial dependency should be (r − rss), where rss is the source surface height in order to be self-consistent with the PFSS condition that field lines are radial at the outer boundary, but we assume this correction to be small enough so that we can neglect it.
The second concept used together with the Parker spiral for validation is the PFSS extrapolation (Altschuler & Newkirk 1969; Schatten et al. 1969; Schrijver & De Rosa 2003). This model focuses on the structure of the coronal magnetic field in its minimum-energy state. This simplistic model assumes that the coronal magnetic field is potential, that is, that the rotation of B is zero, so that it cannot capture twisted structures. The PFSS extrapolation uses a photospheric magnetogram as the inner boundary condition for the magnetic field potential, which satisfies the Laplace equation. The magnetic field is assumed to be purely radial starting from the source surface (usually around 2.5 solar radii; see Hoeksema et al. 1983). This method is very efficient for estimating the magnetic field geometry in the solar atmosphere and is therefore commonly used in space-weather forecasting (Lee et al. 2011; Pomoell & Poedts 2018). To implement this technique, the Python package pfsspy was used, which is an open-source code fully integrated into the sunkit-magex package1 within sunpy (Stansby et al. 2020). For the latter calculations, a 3D spherical grid is used, with 50, 360 and 720 grid points. For each case, a source surface radius of 2 was chosen by comparing the HCS from PFSS with the one simulated with the MHD model, and then by selecting the best match. A summary of the two different methods used for the magnetic connectivity estimations of this paper can be found in Fig. 2.
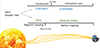 |
Fig. 2. Illustration of the two different chains of models used to compute the magnetic connectivity in this paper. The first chain is our combination of MHD models, COCONUT and EUHFORIA. The second one is the traditional back-mapping chain with the PFSS extrapolation coupled with the ballistic mapping. |
3. Description of the validation cases
To measure the quality of our magnetic connectivity estimation, we need reference cases so that we can validate our results against observations. However, establishing the magnetic connectivity between the Sun and the Earth is challenging due to the lack of direct measurements of the interplanetary magnetic field. The only available information related to the magnetic connectivity pertains to the ion charge and elemental measurements (Landi et al. 2012). Indeed, composition abundances tend to be frozen in the solar wind, and therefore, in theory, we can connect spectroscopic and in situ measurements with the same ion charge states (oxygen or carbon ratio). Baker et al. (2023) and Yardley et al. (2024) provide two examples where remote sensing and in situ data were combined to obtain the magnetic connections. However, this technique has not yet been applied systematically, which means that very few validation cases have been identified unambiguously. Therefore, we used another method as a proxy to determine the magnetic connectivity between the Sun and the Earth, which is to track high-speed stream (HSS) events. HSSs are fast solar wind streams detected at Earth (Snyder et al. 1963; Grandin et al. 2019). Studying these events is relatively straightforward because their identification can often be unambiguous, since they are characterized by a shock and jump from 400 km/s to 700 km/s) and can easily be connected to the solar surface. Indeed, the sources of the fast solar wind are currently better understood than those of the slow solar wind (Cranmer et al. 2017) and have been determined to be the central regions of CHs (Krieger et al. 1973; McComas et al. 2000; Kohl et al. 2006). CHs are low-density patches in the solar corona due to open magnetic field lines, resulting in a darker region in extreme ultraviolet (EUV), which can also be easily identified (Zirker 1977). By assuming that the magnetic field lines are frozen in the solar wind, we can use these events to validate the magnetic connectivity.
In particular, we use four cases previously identified and studied in the literature (see Fig. 3). The CHs that are possible sources can be found in Fig. 4. The first one is from Reiss et al. (2021) and corresponds to an HSS reaching Earth on the 1 June 2018 (event 1; top left panel). The other three cases are from Koukras et al. (2022) and correspond to various HSSs on 22 December 2020 (event 2; top right panel), 4 August 2018 (event 3; bottom left panel), and 13 April 2012 (event 4; bottom right panel). In the selected cases, only pure fast solar wind events were chosen in order to avoid the perturbations induced by compression regions. We display the in situ measurements of the mean solar wind velocity and the radial magnetic field. These data come from the satellite ACE (Advanced Composition Explorer) at Lagrange point L1. Three cases are during a solar minimum (events 1, 2 and 3) and one is during a solar maximum (event 4). The solar maximum case is expected to be more challenging because solar activity can affect the accuracy of the magnetic connectivity.
 |
Fig. 3. In situ data for events 1 to 4 (left to right, then top to bottom). For each event, we show the mean velocity of the solar wind in km/s (top subpanel) and the radial magnetic field in nanoTesla (bottom subpanel). The ACE data, measured in situ, help us to identify the HSS corresponding to the CH event and indicate the polarity at Earth. The red and blue squares indicate the specific period of the event where a positive and negative polarity is expected, respectfully. |
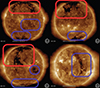 |
Fig. 4. AIA (193 Å) images from SDO for events 1 to 4 (left to right, then top to bottom). The CHs are the darker regions visible and marked in the EUV wavelengths. The red and blue squares indicate the specific CH where a positive and negative polarity is expected, respectfully. The figures are made with Helioviewer (Helioviewer Project 2023). More information about the events can be found in Table 1. |
The radial-magnetic-field component indicates the polarity of the interplanetary magnetic field. A positive value corresponds to a positive polarity (field line going away from the Sun), while a negative value indicates a negative polarity (field line going towards the Sun). Please note that ACE does not directly provide Br, but instead provides the GSE frame coordinates2, and we assume that Br ∼ −BGSE, x. The implications of the polarity are discussed in more detail in Sect. 5.
The in situ data for our events can be seen in Fig. 3. For the first event in 2018 (top left panel), we show the data between 31 May 2018 and 5 June 2018. The polarity for that event is clearly negative (marked by a blue rectangle). For the second event in 2020 (top right panel), we see that the polarity changes a lot between 22 and 23 December 2020, but is primarily positive (marked by a red rectangle). For the third event in 2017 (bottom left panel), we can see that the polarity goes from negative to positive and remains positive during the HSS. For the last event in 2012 during a solar maximum (bottom right panel), the overall magnetic polarity is negative.
As we also have access to the CHs polarity at the surface of the Sun, this gives us a tool with which to more precisely pinpoint the CH that is responsible for the observed HSS of the same polarity. With this approach, we can complement the in situ data from Fig. 3 with remote-sensing data in Fig. 4. This figure displays the Sun in EUV (193 Å from SDO/AIA), which allows us to see the CHs responsible for the fast solar wind as darker regions. We have marked the largest CHs with rectangles, the color of which denotes their polarity (red for positive, blue for negative). Returning to the in situ data, we can then assume that for event 1 (top left panel), the HSS observed at Earth originates from the central CH (which is what was found in Reiss et al. 2021) or the southern CH. Similarly, event 2 originates from the northern CH, event 3 also originates from the northern CH, and finally event 4 originates from the equatorial CH.
With the HSS events well identified at Earth, we performed the corresponding coronal and heliospheric numerical simulations to reproduce them. To do so, we used a magnetic map as input that covers the period before the event. Indeed, as solar wind can take 2 to 5 days, on average, to reach the Earth, we cannot select a single magnetic map at a specific date to reproduce the exact solar configuration that triggered the HSS. Instead, we use HMI Carrington maps that accumulate observations over the full Carrington rotation for both the MHD model and the back-mapping method. These maps have also been shown to give the best results for the COCONUT model (Perri et al. 2023). The most realistic way to model the magnetic connectivity would of course be to have a time-dependent model (Lionello et al. 2023). Still, this feature is not available yet for the COCONUT and EUHFORIA models and is thus outside the scope of this paper. The relevant information about the validation events, including the corresponding arrival of the solar wind at Earth and the period covered by the magnetic map of the Sun for the four cases studied, can be found in Table 1.
Arrival times of solar wind on Earth and period covered by the magnetogram at the Sun.
4. Validation of the magnetic connectivity
We now compare our magnetic connectivity MHD estimations with results from previous studies and the traditional two-step ballistic mapping. The results for all four events are plotted together in Fig. 5: event 1 (2018) is on the top left, event 2 (2020) is on the top right, event 3 (2017) is on the bottom left, and event 4 (2012) on the bottom right. We show the location at the surface of the Sun that is the most likely to be connected to Earth during the corresponding HSS event.
 |
Fig. 5. Validation of the MHD connectivity estimation for the four cases selected. We show the location at the surface of the Sun that is most likely to be connected to Earth during the corresponding HSS event. The MHD connectivity estimate is shown in bright blue, the two-step ballistic estimate is shown in pink, and the magnetic connectivity estimate from other studies (Reiss et al. 2021 for event 1 and Koukras et al. 2022 for other events) is shown with a purple rectangle. The area covered by the magnetic connectivity estimate represents the spatial and temporal uncertainties. We also show the HCS (red line) and CHs to explain these results better. The red and dark blue patches indicate respectively the positive and negative polarity regions of open magnetic field lines in the COCONUT simulation, while the gray areas indicate the CHs extracted from the SDO Carrington EUV maps using the EZSEG algorithm for events 1−3 (Caplan et al. 2016). |
 |
Fig. 6. Validation of the global Earth magnetic connectivity using in situ polarity. Each line corresponds to one of the studied events (event 1 for line 1, and so forth). For the left column, we plot the Earth’s latitude for each date over the simulated period and indicate the corresponding in situ polarity measured by ACE with a colored box (blue for negative, and red for positive). We put this in perspective with the simulated HCS at Earth’s orbit (black line). The middle column is essentially the same plot, except that this time, the polarity at Earth positions comes from the MHD simulations. Finally, the right column quantifies the agreement between in situ and simulated polarity for each date (in green when there is agreement, and in red otherwise). These plots were inspired by the work of Badman et al. (2022). |
For the first event (top left panel), the simulation shows three potential MHD connectivity points. One magnetic connection is in the northern CH, with a positive polarity; another is connected to a negative-polarity southern CH, and the last is in an equatorial CH, which also has a negative polarity. The two-step ballistic mapping method yields a mean magnetic connectivity point located around the equatorial CH, which has a negative polarity.
In the simulation, the Earth is mainly located beneath the HCS, and so it is more likely that the magnetic connection is with the equatorial or the southern CH, which have the same polarity as that seen in the in situ data and the two-step ballistic mapping. For this event, it was previously determined that the correct magnetic connection is with the equatorial CH (see Reiss et al. 2021 for more details). The results of EUHFORIA and COCONUT also support this outcome but with more uncertainty than the back-mapping method. This could be attributed to the simulation parameters (the equatorial CH is smaller in the simulation compared to the observations, which can lead to a less spatially and temporally extended HSS) or the complexity of the field line configurations (which could explain the incursion of a positive-polarity patch in this region). A summary of the polarity for all cases can be found in Table 2.
Magnetic polarity from COCONUT and EUHFORIA, and the two-step ballistic mapping method.
Mean values of the magnetic connectivity locations for the four studied events.
If we then look at event 2 (top right panel), we see that the MHD simulation gives a result around the northern CH with a positive polarity, similar to the result obtained in the study of Koukras et al. (2022). However, the two-step ballistic method gives a mean value around the equator with a negative polarity. In this case, the result obtained with COCONUT can be assumed to be correct because it has the same magnetic polarity as seen in the in situ data. This shows that MHD simulations can provide an accurate estimate of the magnetic connectivity even in complex cases, as here, the event corresponds to a very patchy CH located close to active regions (i.e., closed field lines very close to open field lines).
For event 3 (bottom left panel), the MHD simulations produced three different results: a magnetic connection point at a southern CH with a negative polarity, a magnetic connection point at a northern CH with a positive polarity, and a magnetic connection point at an equatorial CH also with a negative polarity. This last point is difficult to see because of the minor uncertainties. The back-mapping method also gave a result around the CH in the north with a positive polarity, which is consistent with the result obtained by Koukras et al. (2022). Therefore, it is more likely that the actual magnetic connection is at the northern CH, where both the simulation and the in situ data have a positive polarity.
Finally, for event 4 (bottom right panel), we can see that all the results of the different approaches are located around the equator, and all with a negative polarity. The HCS from the simulation (red line) is far more complex and less flat than in the previous cases, which seems to provide more precise results. The results obtained with COCONUT and EUHFORIA are located in a CH close to the CH found by Koukras et al. (2022). We do not have the observations needed to confirm which CH is correct (Koukras et al. 2022 assumed it was the largest one).
The coordinates of the connectivity estimates derived using the MHD models and the two-step ballistic mapping are summarized in Table 3. Latitudes are in degrees, and longitudes are in degrees in the Carrington frame. The table’s last column indicates the overlap between the results obtained from COCONUT and EUHFORIA and those obtained by Reiss et al. (2021) and Koukras et al. (2022). The percentage of overlap was calculated by dividing the total number of magnetic connections to the right CH throughout the entire period by the total number of connections obtained during that period.
What is very surprising here is that the most difficult cases (event 2 because of patchy CH and event 4 because of maximum activity) are the ones where the connectivity is better estimated. Events 1 and 3 yield some overlap (respectively 19 and 45%), and so the MHD connectivity is only partly correct. This can be explained for event 1 by the small opening of the equatorial CH, but is more difficult to explain for event 3. To understand these results further, we look more precisely at the polarity variations in the following section.
5. Discussion: Polarity estimation
To understand why certain events provide good magnetic connectivity while others do not, we can explore the magnetic configuration on a larger scale and compute the polarity seen at Earth over the full Carrington rotation in our simulations. Indeed, if the in situ polarity is not correct at the date of the event, we cannot recover the proper CH connectivity. This would indicate that the cause of the error is more complex and linked to a mistake in the HCS position. The work of Badman et al. (2022) inspired this analysis; these authors performed a similar study on solar wind simulations for comparison with PSP data.
The corresponding analysis can be found in Fig. 6. Each line corresponds to one of the studied events (event 1 for line 1, and so forth). For the left column, we plot the Earth’s latitude for each date over the simulated time and indicate the corresponding in situ polarity measured by ACE (blue for negative, red for positive). The latitude of the Earth is determined using the SpiceyPy Python package (Annex et al. 2020). Each date is obtained by rotating the steady-state simulation to the corresponding Carrington longitude. The in situ data are the same as shown in Fig. 3. We put this in perspective with the simulated HCS at Earth’s orbit (black line). We use EUHFORIA data to compute the HCS location at 1 AU by separating positive and negative polarities. We unfortunately do not have a way to measure the HCS position around Earth (it is possible to determine its shape at around 4 solar radii using SOHO/LASCO data – see Poirier et al. 2021 –, but not further without using theoretical assumptions). However, we can check whether the crossings between Earth’s orbit and the HCS correspond to polarity switches. Our HCS positioning is erroneous during this period if it does not correspond to a switch between polarities in the observations. To better illustrate this potential mismatch, the middle column is almost the same plot, except that this time, the polarity at Earth positions comes from the MHD simulations. It can then be directly compared to the measured in situ polarity showcased by the colored box to see whether they match (which means that they have the same color). Finally, the right column quantifies the agreement between in situ and simulated polarity for each date (in green when there is agreement, and in red otherwise). From this final plot, we can compute a percentage of agreement between data and simulations, quantifying the quality of our global polarity estimate and thus our chances of obtaining an accurate determination of the magnetic connectivity for an event during this period.
Using the latter, we can determine that we have a 69% agreement for event 1, a 36% agreement for event 2, a 68% agreement for event 3, and a 69% agreement for event 4. This shows that our MHD simulations are consistent, and that for most of these cases we are recovering the right connectivity for 70% of the dates. Interestingly, even though event 2 has the lowest score for the HCS agreement, we still recover the correct magnetic connectivity with positive polarity. In contrast, events 1 and 3 have good scores for the polarity match despite lower scores for CH connectivity. We can then look at the left column of Fig. 6 to understand these results further.
For event 1 (top line), the explanation is relatively straightforward: we can see on the left panel that the negative polarity (in blue) was measured at Earth sooner than in our simulations. This slight delay of 24 hours explains why we have residual connectivity to the northern CH. Then, it is impossible to distinguish between the contributions of the equatorial and southern CH, which have the same polarity. The fact that the equatorial CH is smaller than observed is likely the main explanation for this confusion.
For event 2 (second line), we can see that the polarity around the event in the simulations is positive (in red), as it should be, which explains why the connectivity estimation is correct. However, immediately after the event, we switch early to a negative polarity (in blue) due to the crossing of the HCS. This switch is close to what is observed in the data, where this patchy CH leads to rapid switches between positive and negative polarities. In this case, the uncertainty of the simulation is accentuated by the fact that we are close to the end of the Carrington rotation, which can cause discrepancies in the simulation results. Hence, this confirms that it was a very difficult case but that we could still recover the global trends.
For event 3 (third line), we can see that the HCS positioning for the blue negative polarity between 31 July and 4 August in our simulation does not match the observations, with the blue positive polarity starting too early on 1 August. This should help us recover the right CH polarity which is positive. However, we still get some magnetic field lines from the negative southern CH. This means that because of the large extended northern CH, field lines are more twisted and thus some isolated positive field lines may be close to the Earth’s location in our simulation. This means that, in this case, we do recover an accurate determination of the magnetic connectivity at the exact location of the Earth. Still, the surrounding uncertainty is high.
For event 4 (bottom line), the HSS event happens during a long period of negative polarity, which is well reproduced in our simulation. Because of the larger latitudinal amplitude of the HCS (between −30 and 60° here, compared to −10 and 15° in previous cases), it may be easier to recover the right polarity for MHD simulations. This could mean that the maximum number of activity cases may be more reliable than the minimum number of activity cases, because the crossing of the HCS is better defined and happens less often for the Earth’s location. This conclusion is consistent with the findings by Badman et al. (2023) for PSP data. This explains why we recover the right polarity. We cannot then distinguish between the various negative CHs.
In conclusion, with this additional analysis we can quantify that, on average, our MHD simulations provide an accurate description of the magnetic polarity with an almost 70% accuracy rate for the studied periods. We can explain uncertainties in our results because of errors in the HCS positioning (event 1). We can also proceed to a more in-depth analysis and show that the polarity estimate does not guarantee perfect magnetic connectivity: event 2 is a very difficult case and still provides a good result, while event 3 should have been easy and generated mixed results. This analysis shows that the cases where there is maximum activity may be easier to compute for MHD simulations due to the more extended shape of the HCS. Cases at minimum activity indeed show more polarity switches, requiring higher resolution and perhaps the perfect capture of a greater number of physical (non-ideal MHD for the reconnection) and numerical (time-dependent simulations) features.
6. Conclusions
This study follows recent developments surrounding the determination of the Sun–Earth magnetic connectivity, which is crucial for understanding solar wind events and anticipating space-weather events. Traditionally, the solar magnetic connectivity is determined using a two-step ballistic mapping, combining a PFSS extrapolation close to the Sun with a Parker spiral approximation close to Earth. However, this method uses many free parameters that can significantly influence the final result. Here, we aim to use another approach based on MHD simulations, which are more self-consistent, have a more solid basis in physics, and can now run on an operational scale. To do so, we combined the coronal model COCONUT with the heliospheric model EUHFORIA and traced the magnetic field lines from the Earth to the Sun. We can define spatial uncertainty by probing locations close to Earth and temporal uncertainty by computing the magnetic connectivity averaged over a few days before the event. Using the model’s default parameters, we checked whether we can recover the correct magnetic connectivity for various standard events. Four cases were chosen: three during a solar minimum and one during a solar maximum, already investigated in Reiss et al. (2021) and Koukras et al. (2022). These cases correspond to HSS events, for which we can obtain the most reliable magnetic connectivity validation possible, as there are no direct observations of the magnetic connectivity.
For all four selected events, we always find at least partial overlap with the assumed CH of origin (19% for event 1, 100% for event 2, 45% for event 3, and 100% for event 4). This is better than the two-step ballistic method, where event 2 leads to an entirely incorrect connection. The fact that we also include other CHs is related to the spatial and temporal uncertainty. We looked at the global polarity of the simulation for Earth over the full Carrington rotation to understand these results better. We find that, on average, MHD simulations provide a very good polarity estimation (69% agreement with real data for event 1, 36% for event 2, 68% for event 3, and 69% for event 4). For event 1, it is the temporal uncertainty that yields mixed results due to a delay of 24 hours for the HCS crossing, while for event 3 it is the spatial uncertainty that yields mixed results due to a complex open magnetic structure. Challenging cases still provide good results: event 2, despite being a complex case with a patchy CH and challenging magnetic connectivity; event 4, despite being a maximum activity case. This helps us find the benefits and limits of this method of computation for the connectivity: minimum activity cases appear to be more challenging because of multiple recurrent crossings of the HCS, which are difficult to reproduce accurately for ideal MHD simulations; maximum activity cases appear easier for MHD models because of the latitudinal extent of the HCS. Of course, more statistics are required to confirm the trends we find in our analysis, and so we need more confirmed connectivity events for validation.
In conclusion, we demonstrate that we can use MHD models to compute the magnetic connectivity between the Sun and the Earth. The accuracy of the connectivity estimation relies on the good match between the simulation and observations (which calls for more automated validation techniques for both coronal and heliospheric simulations). Still, even with default parameters for four different dates between 2012 and 2020, we find at least a partial overlap with the correct CH for all cases. The method we present here performs similarly well to the thoroughly fine-tuned two-step ballistic method, yet it yields more information about the global magnetic field polarity configuration (which can help provide feedback on improving the simulation), does not require any adjustment, and offers significant room for improvement by developing better models. A more self-consistent inclusion of the solar rotation for example could be added to reduce the spatial and temporal uncertainty of our estimations. The COCONUT model has already been enhanced with the inclusion of multiple fluids (Brchnelova et al. 2023), while the EUHFORIA model has been upgraded to AMR features with its new version ICARUS (Verbeke et al. 2022; Baratashvili & Poedts 2024). In particular, MHD models would need to have a better spatial resolution to get more small-scale changes in the HCS and include non-ideal MHD effects to be able to more accurately describe the reconnection in the HCS in terms of the underlying physics. Ideally, models should even be time-dependent to remove the need for temporal uncertainty (Lionello et al. 2023). Studies with other MHD models could be carried out to confirm these trends. The next step of this study will focus on sources of uncertainty for connectivity other than the models themselves; in particular, we will look at the impact of the input magnetic map on the quality of our final estimates.
More information can be found here: https://github.com/sunpy/sunkit-magex
More information about the various ACE coordinate systems can be found here: https://izw1.caltech.edu/ACE/ASC/coordinate_systems.html
Acknowledgments
The authors thank Rui Pinto, Predictive Science Inc. and the ISWAT S2-05 team for valuable discussions. SK and SP acknowledge support from the projects C14/19/089 (C1 project Internal Funds KU Leuven), G0B5823N and G002523N (WEAVE) (FWO-Vlaanderen), 4000145223 (SIDC Data Exploitation (SIDEX2), ESA Prodex), and Belspo project B2/191/P1/SWiM. We used the VSC – Flemish Supercomputer Center infrastructure for the computations, funded by the Hercules Foundation and the Flemish Government – department EWI. HMI data are courtesy of the Joint Science Operations Center (JSOC) Science Data Processing team at Stanford University. We thank the ACE SWEPAM instrument team and the ACE Science Center for providing the ACE data.
References
- Altschuler, M. D., & Newkirk, G. 1969, Sol. Phys., 9, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Annex, A. M., Pearson, B., Seignovert, B., et al. 2020, J. Open Source Softw., 5, 2050 [CrossRef] [Google Scholar]
- Badman, S. T., Bale, S. D., Martínez Oliveros, J. C., et al. 2020, ApJS, 246, 23 [Google Scholar]
- Badman, S. T., Brooks, D. H., Poirier, N., et al. 2022, ApJ, 932, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Badman, S. T., Riley, P., Jones, S. I., et al. 2023, J. Geophys. Res.: Space Phys., 128, e2023JA031359 [NASA ADS] [CrossRef] [Google Scholar]
- Baker, D., Démoulin, P., Yardley, S. L., et al. 2023, ApJ, 950, 65 [CrossRef] [Google Scholar]
- Baratashvili, T., & Poedts, S. 2024, A&A, 683, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, J. 2010, HMI& WCS Coordinates, Projections and Arrays for Dummies [Google Scholar]
- Brchnelova, M., Zhang, F., Leitner, P., et al. 2022a, J. Plasma Phys., 88, 905880205 [NASA ADS] [CrossRef] [Google Scholar]
- Brchnelova, M., Kuźma, B., Perri, B., Lani, A., & Poedts, S. 2022b, ApJS, 263, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Brchnelova, M., Kuźma, B., Zhang, F., Lani, A., & Poedts, S. 2023, A&A, 678, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caplan, R. M., Downs, C., & Linker, J. A. 2016, ApJ, 823, 53 [CrossRef] [Google Scholar]
- Chorin, A. J. 1997, J. Comput. Phys., 135, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Cid, C., Cremades, H., Aran, A., et al. 2012, J. Geophys. Res.: Space Phys., 117, A11102 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., Gibson, S. E., & Riley, P. 2017, Space Sci. Rev., 212, 1345 [Google Scholar]
- Dakeyo, J. B., Badman, S. T., Rouillard, A. P., et al. 2024, A&A, 686, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Silva, D. E., Wallace, S., Arge, C. N., & Jones, S. Space 2023, Weather, 21, e2023SW003554 [NASA ADS] [CrossRef] [Google Scholar]
- Dedner, A., Kemm, F., Kröner, D., et al. 2002, J. Comput. Phys., 175, 645 [Google Scholar]
- Grandin, M., Aikio, A. T., & Kozlovsky, A. 2019, J. Geophys. Res.: Space Phys., 124, 3871 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H. 2015, Liv. Rev. Sol. Phys., 12, 4 [Google Scholar]
- Heber, B., & Potgieter, M. S. 2006, Space Sci. Rev., 127, 117 [Google Scholar]
- Helioviewer Project 2023, Helioviewer: Solar and Heliospheric Image Browser, https://www.helioviewer.org [Google Scholar]
- Hoeksema, J. T., Wilcox, J. M., & Scherrer, P. H. 1983, J. Geophys. Res., 88, 9910 [CrossRef] [Google Scholar]
- Kissmann, R., & Pomoell, J. 2012, SIAM J. Sci. Comput., 34, A763 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., Noci, G., Cranmer, S. R., & Raymond, J. C. 2006, A&ARv, 13, 31 [Google Scholar]
- Koukras, A., Dolla, L., & Keppens, R. 2022, SHINE 2022 Workshop, 68 [Google Scholar]
- Krieger, A. S., Timothy, A. F., & Roelof, E. C. 1973, Sol. Phys., 29, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Kuźma, B., Brchnelova, M., Perri, B., et al. 2023, ApJ, 942, 31 [CrossRef] [Google Scholar]
- Landi, E., Gruesbeck, J. R., Lepri, S. T., & Zurbuchen, T. H. 2012, ApJ, 750, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Lani, A., Villedieu, N., Bensassi, K., et al. 2013, COOLFluiD: An Open Computational Platform for Multi-physics Simulation [Google Scholar]
- Lanzerotti, L. J. 2001, Geophys. Monogr. Ser., 125, 11 [NASA ADS] [Google Scholar]
- Lavraud, B., & Rouillard, A. 2014, in Nature of Prominences and their Role in Space Weather, eds. B. Schmieder, J. M. Malherbe, & S. T. Wu, 300, 273 [NASA ADS] [Google Scholar]
- Lee, C. O., Luhmann, J. G., Hoeksema, J. T., et al. 2011, Sol. Phys., 269, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Linker, J. A., & Mikić, Z. 1997, Geophys. Monogr. Ser., 99, 269 [NASA ADS] [Google Scholar]
- Lionello, R., Downs, C., Mason, E. I., et al. 2023, ApJ, 959, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Macneil, A. R., Owens, M. J., Finley, A. J., & Matt, S. P. 2022, MNRAS, 509, 2390 [NASA ADS] [Google Scholar]
- McComas, D. J., Barraclough, B. L., Funsten, H. O., et al. 2000, J. Geophys. Res., 105, 10419 [Google Scholar]
- Moffatt, H. K. 1978, Cambridge Monographs on Mechanics and Applied Mathematics (Cambridge: University Press) [Google Scholar]
- Neugebauer, M., Forsyth, R. J., Galvin, A. B., et al. 1998, J. Geophys. Res., 103, 14587 [NASA ADS] [CrossRef] [Google Scholar]
- Nolte, J. T., & Roelof, E. C. 1973, Sol. Phys., 33, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Odstrcil, D., Riley, P., & Zhao, X. P. 2004, J. Geophys. Res.: Space Phys., 109, A02116 [NASA ADS] [CrossRef] [Google Scholar]
- Owens, M. J., & Forsyth, R. J. 2013, Liv. Rev. Sol. Phys., 10, 5 [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Parker, E. N. 1993, ApJ, 408, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Peleikis, T., Kruse, M., Berger, L., & Wimmer-Schweingruber, R. 2017, A&A, 602, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perri, B., Leitner, P., Brchnelova, M., et al. 2022, ApJ, 936, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Perri, B., Kuźma, B., Brchnelova, M., et al. 2023, ApJ, 943, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Poedts, S., Kochanov, A., Lani, A., et al. 2020, J. Space Weather Space Clim., 10, 14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poirier, N., Rouillard, A. P., Kouloumvakos, A., et al. 2021, Front. Astron. Space Sci., 8, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Pomoell, J., & Poedts, S. 2018, J. Space Weather Space Clim., 8, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pomoell, J., & Vainio, R. 2012, ApJ, 745, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Pulkkinen, T. 2007, Liv. Rev. Sol. Phys., 4, 1 [Google Scholar]
- Reiss, M. A., Muglach, K., Möstl, C., et al. 2021, ApJ, 913, 28 [Google Scholar]
- Riley, P., Linker, J. A., Mikić, Z., et al. 2006, ApJ, 653, 1510 [Google Scholar]
- Riley, P., Mays, M. L., Andries, J., et al. 2018, Space Weather, 16, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Roelof, E. C., & Krimigis, S. M. 1973, J. Geophys. Res., 78, 5375 [NASA ADS] [CrossRef] [Google Scholar]
- Rouillard, A. P., Pinto, R. F., Vourlidas, A., et al. 2020, A&A, 642, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schatten, K. H. 1971, Cosmic Electrodyn., 2, 232 [NASA ADS] [Google Scholar]
- Schatten, K. H., Wilcox, J. M., & Ness, N. F. 1969, Sol. Phys., 6, 442 [Google Scholar]
- Schrijver, C. J., & De Rosa, M. L. 2003, Sol. Phys., 212, 165 [Google Scholar]
- Schrijver, C. J., Kauristie, K., Aylward, A. D., et al. 2015, Adv. Space Res., 55, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, T., Kim, T. K., Pogorelov, N. V., & Arge, C. N. 2022, ApJ, 933, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, C. W., Neugebauer, M., & Rao, U. R. 1963, J. Geophys. Res., 68, 6361 [NASA ADS] [CrossRef] [Google Scholar]
- Stansby, D., Yeates, A., & Badman, S. T. 2020, J. Open Source Softw., 5, 2732 [Google Scholar]
- Sullivan, C., & Kaszynski, A. 2019, J. Open Source Softw., 4, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Temmer, M. 2021, Liv. Rev. Sol. Phys., 18, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, W. T. 2006, A&A, 449, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbanac, G., Vršnak, B., Veronig, A., & Temmer, M. 2011, A&A, 526, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbeke, C., Baratashvili, T., & Poedts, S. 2022, A&A, 662, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vršnak, B., Temmer, M., & Veronig, A. M. 2007, Sol. Phys., 240, 331 [Google Scholar]
- Yardley, S. L., Brooks, D. H., D’Amicis, R., et al. 2024, Nat. Astron., 8, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Temmer, M., Gopalswamy, N., et al. 2021, Progr. Earth Planet. Sci., 8, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Zirker, J. B. 1977, Rev. Geophys. Space Phys., 15, 257 [CrossRef] [Google Scholar]
All Tables
Arrival times of solar wind on Earth and period covered by the magnetogram at the Sun.
Magnetic polarity from COCONUT and EUHFORIA, and the two-step ballistic mapping method.
All Figures
 |
Fig. 1. Example of magnetic connectivity computed between the Earth and the Sun using COCONUT and EUHFORIA models. The Earth is depicted as a gray sphere to show the initial seed of the magnetic field line. Then, we have a first field line computed in EUHFORIA in the heliospheric part (shown as a white flux tube). The interface between the coronal and heliospheric parts (COCONUT and EUHFORIA) is shown via a transparent sphere at 0.1 AU. Finally, inside the coronal part, we show the second magnetic field line computed using COCONUT results (white flux tube inside the transparent sphere). |
| In the text | |
 |
Fig. 2. Illustration of the two different chains of models used to compute the magnetic connectivity in this paper. The first chain is our combination of MHD models, COCONUT and EUHFORIA. The second one is the traditional back-mapping chain with the PFSS extrapolation coupled with the ballistic mapping. |
| In the text | |
 |
Fig. 3. In situ data for events 1 to 4 (left to right, then top to bottom). For each event, we show the mean velocity of the solar wind in km/s (top subpanel) and the radial magnetic field in nanoTesla (bottom subpanel). The ACE data, measured in situ, help us to identify the HSS corresponding to the CH event and indicate the polarity at Earth. The red and blue squares indicate the specific period of the event where a positive and negative polarity is expected, respectfully. |
| In the text | |
 |
Fig. 4. AIA (193 Å) images from SDO for events 1 to 4 (left to right, then top to bottom). The CHs are the darker regions visible and marked in the EUV wavelengths. The red and blue squares indicate the specific CH where a positive and negative polarity is expected, respectfully. The figures are made with Helioviewer (Helioviewer Project 2023). More information about the events can be found in Table 1. |
| In the text | |
 |
Fig. 5. Validation of the MHD connectivity estimation for the four cases selected. We show the location at the surface of the Sun that is most likely to be connected to Earth during the corresponding HSS event. The MHD connectivity estimate is shown in bright blue, the two-step ballistic estimate is shown in pink, and the magnetic connectivity estimate from other studies (Reiss et al. 2021 for event 1 and Koukras et al. 2022 for other events) is shown with a purple rectangle. The area covered by the magnetic connectivity estimate represents the spatial and temporal uncertainties. We also show the HCS (red line) and CHs to explain these results better. The red and dark blue patches indicate respectively the positive and negative polarity regions of open magnetic field lines in the COCONUT simulation, while the gray areas indicate the CHs extracted from the SDO Carrington EUV maps using the EZSEG algorithm for events 1−3 (Caplan et al. 2016). |
| In the text | |
 |
Fig. 6. Validation of the global Earth magnetic connectivity using in situ polarity. Each line corresponds to one of the studied events (event 1 for line 1, and so forth). For the left column, we plot the Earth’s latitude for each date over the simulated period and indicate the corresponding in situ polarity measured by ACE with a colored box (blue for negative, and red for positive). We put this in perspective with the simulated HCS at Earth’s orbit (black line). The middle column is essentially the same plot, except that this time, the polarity at Earth positions comes from the MHD simulations. Finally, the right column quantifies the agreement between in situ and simulated polarity for each date (in green when there is agreement, and in red otherwise). These plots were inspired by the work of Badman et al. (2022). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.