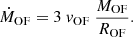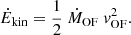| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 25 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202347756 | |
| Published online | 12 December 2023 | |
Investigating the impact of quasar-driven outflows on galaxies at z ∼ 0.3–0.4
1
Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
e-mail: kiherse@gmail.com
2
Instituto de Astrofísica de Canarias, Calle Vía Láctea, s/n, 38205 La Laguna, Tenerife, Spain
3
Department of Physics & Astronomy, University of Sheffield, S3 7RH Sheffield, UK
Received:
18
August
2023
Accepted:
14
September
2023
Aims. We present a detailed study of the kinematics of 19 type 2 quasars (QSO2s) with redshifts in the range 0.3 < z < 0.41 and [OIII] luminosities of L[OIII] > 108.5 L⊙. We aim to advance our understanding of the active galactic nucleus (AGN) feedback phenomenon by correlating outflow properties with (i) young stellar populations (YSPs) with ages < 100 Myr, (ii) the optical morphology and the environment of the galaxies, and (iii) the radio luminosity.
Methods. We characterized the ionized gas kinematics using the [OIII]λ5007 Å emission line profiles detected in intermediate spectral resolution (R ∼ 1500–2500) optical spectra of the QSO2s. To do this, we employed three different outflow detection methods: multicomponent parametric, flux-weighted nonparametric, and peak-weighted nonparametric.
Results. We detect ionized outflows in 18 of the 19 QSO2s using the parametric analysis, and in all of them using the nonparametric methods. We find higher outflow masses using the parametric analysis (average log MOF(M⊙) = 6.47 ± 0.50), and higher mass rates and kinetic powers with the flux-weighted nonparametric method (MOF = 4.0 ± 4.4 M⊙ yr−1 and Ekin = 41.9 ± 0.6 erg s−1). However, when we use the parametric method and the maximum outflow velocities (vmax), we measure the highest outflow mass rates and kinetic energies (MOF = 23 ± 35 M⊙ yr−1 and log(Ekin) = 42.9 ± 0.6 erg s−1). We do not find any significant correlation between the outflow properties and the previously mentioned AGN and galaxy-wide properties.
Conclusions. Four of the five QSO2s without a YSP of age < 100 Myr show highly disturbed kinematics, whereas only 5 out of the 14 QSO2s with YSPs show similarly asymmetric [OIII] profiles. Despite the small sample size, this might be indicative of negative feedback. The lack of a correlation between the outflow properties and the galaxies optical morphologies might be due to their different dynamical timescales (millions of years in the case of the outflows versus billions of years in the case of galaxy mergers). Last, the small radio luminosity range covered by our sample, log(L5 GHz) = [22.1, 24.7] W Hz−1, may impede the detection of any correlation between radio emission and outflow properties.
Key words: galaxies: nuclei / galaxies: evolution / galaxies: interactions / galaxies: kinematics and dynamics / ISM: jets and outflows
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
All galaxies, or at least the most massive ones, are thought to experience short episodes of nuclear activity, of ≤100 Myr (Martini 2004; Novak et al. 2011; Schawinski et al. 2015). These nuclear activity phases are considered key drivers of galaxy evolution because they can potentially regulate black hole and galaxy growth (Di Matteo et al. 2005; Harrison 2017).
Cosmological simulations require active galactic nucleus (AGN) feedback to quench star formation and to prevent galaxies from becoming overmassive (Di Matteo et al. 2005; Dubois et al. 2016), thereby reproducing the observed galaxy-halo mass relations (Silk & Rees 1998; Croton et al. 2006; Moster et al. 2010). Furthermore, observational studies have found plenty of evidence of this feedback on different scales, from the central tens to hundreds of parsecs (García-Burillo et al. 2021; Ramos Almeida et al. 2022) to hundreds of kiloparsecs (Rupke et al. 2019; Martín-Navarro et al. 2021).
Multiphase outflows of molecular, neutral, and ionized gas (Rupke & Veilleux 2013; Cicone et al. 2018; Herrera-Camus et al. 2020; Fluetsch et al. 2021) are one of the primary AGN feedback mechanisms that can quench star formation by heating up, disrupting, and ultimately removing the surrounding gas that is available to form stars. However, AGN-driven outflows have also been found to have the opposite effect, often referred to as “positive feedback”, as they can promote star formation by pressurizing the gas and enhancing fragmentation (Klamer et al. 2004; Cresci et al. 2015; Cresci & Maiolino 2018; Carniani et al. 2016; Bessiere & Ramos Almeida 2022). Hence, we still need to advance in our understanding of their actual impact on star formation.
The drivers of these multiphase outflows have also been subject of study, with radio jets or AGN-winds as the main potential candidates (Mukherjee et al. 2018; Fischer et al. 2019). For example, jetted Seyfert galaxies (Whittle 1992; García-Burillo et al. 2014, 2019; Morganti et al. 2015) have been found to show higher outflow velocities than those without jets, suggesting an influence of these jets in launching and/or accelerating the outflows (Wylezalek & Morganti 2018; Jarvis et al. 2019). Furthermore, even in the case of lower radio-power Seyferts and radio-quiet quasars, recent studies have found evidence that compact and modest radio jets might induce nuclear outflows (Aalto et al. 2016; Audibert et al. 2019, 2023; Fernández-Ontiveros et al. 2020; García-Bernete et al. 2021; Speranza et al. 2022). The influence of jets on the ionized gas kinematics has been also studied using low angular resolution data, such as from the Sloan Digital Sky Survey (SDSS): Mullaney et al. (2013) and Zakamska & Greene (2014) found that the higher the radio luminosity, the more disrupted the [OIII] kinematics. However, it has also been claimed that this correlation disappears if the influence of the host galaxy gravitational potential is taken into account (see Ayubinia et al. 2023 and references therein).
Mergers and interactions have long been known as a mechanism that triggers AGN (Canalizo & Stockton 2001; Hopkins et al. 2008; Ramos Almeida et al. 2011, 2012; Bessiere et al. 2012; Satyapal et al. 2014; Goulding et al. 2018; Pierce et al. 2023). Since mergers can simultaneously enhance nuclear star formation and nuclear activity (e.g., Satyapal et al. 2014), it might be possible that outflow incidence and properties depend on galaxy morphology and/or environment. For example, some of the most powerful outflows in the local Universe are found in ultra-luminous infrared galaxies (ULIRGs; Cicone et al. 2014; Rose et al. 2018; Lamperti et al. 2022), which are almost uniquely associated with major mergers. In addition, the merger-induced gas flows may also provide a rich ISM with plenty of cool gas for the radiation-driven winds and any jets to interact with, thus increasing the coupling with the hosts and facilitating the detection of the outflows.
The properties of AGN-driven outflows have been shown to depend on AGN luminosity because they tend to be faster and more powerful as the AGN luminosity increases (Zakamska & Greene 2014; Fiore et al. 2017). However, recent works showed that other factors such as nuclear gas concentration and coupling between the winds and/or jets and the galaxy disks might also play a key role (Ramos Almeida et al. 2012; Audibert et al. 2023). Type 2 quasars (QSO2s) in the local Universe are ideal laboratories for characterizing outflows and studying their impact on the host galaxies: The outflows are easier to identify than the lower-velocity outflows of Seyfert galaxies, and the high obscuration (either nuclear or galaxy wide; Ramos Almeida & Ricci 2017) blocks the emission from the broad-line region and the AGN continuum, avoiding dilution of the emission line and stellar absorption features.
The most widely studied gas outflow phase is the warm ionized phase (T ∼ 104 K) because it emits strong forbidden emission lines in the infrared and optical range, of which the [OIII]λ5007 Å is one of the strongest. QSO2s are commonly found to present complex emission line profiles, showing strong blue asymmetries and deviations from Gaussianity (Greene et al. 2011; Liu et al. 2013; Villar-Martín et al. 2011, 2014; Harrison et al. 2014; Ramos Almeida et al. 2017, 2019), indicating highly disrupted kinematics. The overall majority of AGN outflow studies characterized the ionized gas kinematics following a parametric approach (Holt et al. 2011; Greene et al. 2011; Villar-Martín et al. 2011; Arribas et al. 2014), considering that each gaseous component that contributes to the kinematics can be described by a Gaussian distribution. They have the advantage of making it possible to characterize the properties of different gas components, but for objects with highly disrupted kinematics, it becomes difficult to ascribe a physical meaning to each component (Bessiere & Ramos Almeida 2022). Hence, other studies implemented a nonparametric analysis based on measuring emission line velocities at fixed fractions of the peak intensity or the cumulative line flux function (Whittle 1985; Harrison et al. 2014; Zakamska & Greene 2014; Speranza et al. 2021; Bessiere & Ramos Almeida 2022). Nonparametric methods are better suited for characterizing spectra with low signal-to-noise ratios and complex emission line profiles. Although they do not allow us to separate different gaseous contributions, they can easily identify high-velocity gas in tail ends of emission line wings. Despite the large number of works that use parametric and nonparametric methods to characterize AGN-driven outflows, to the best of our knowledge, no comparison between their results has been performed for a common sample of objects.
Considering this, we use three different outflow detection methods (parametric, flux-weighted nonparametric, and the peak-weighted nonparametric method from Speranza et al. 2021) for characterizing the ionized gas kinematics of 19 QSO2s with redshifts in the range 0.3 < z < 0.41 and [OIII] luminosities of L[OIII] > 108.5 L⊙. Furthermore, with the aim of advancing in our understanding of the AGN feedback phenomenon, we study potential correlations between the outflow properties of the QSO2s and different AGN and host galaxy properties, including (i) young stellar populations (YSPs) with ages < 100 Myr, (ii) the optical morphology and environment, and (iii) the AGN and radio luminosity.
In Sect. 2 we describe the QSO2 sample and the spectroscopic data used here, as well as the previously studied AGN and host galaxy properties. In Sect. 3 we explain the three different methods we used to analyze the ionized gas kinematic and present the results. Section 4 describes the physical properties of the outflows derived through each of the three methods. In Sect. 5 we evaluate the possible correlations between the outflow properties and different AGN and host galaxy properties. In Sect. 6 we discuss the results, and finally, in Sect. 7 we summarize the findings of our work. Throughout this paper, we assume a cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7.
2. Sample and data
Our QSO2 sample is based on the sample studied by Bessiere et al. (2012), which is a subset of the narrow-line AGN catalog of Zakamska et al. (2003), selected from SDSS (York et al. 2000) using emission line ratio diagnostic diagrams. We specifically selected this QSO2 sample because several host galaxy properties, including the stellar populations, optical morphologies, and environments, were already characterized (Bessiere et al. 2012, 2017; Ramos Almeida et al. 2013), allowing us to investigate potential correlations between them and the outflow properties that we report in this work.
Bessiere et al. (2012) selected the 20 QSO2s with right ascension (RA) in the range 23 < RA < 10 h, declination (δ) of δ < +20°, redshifts in the range 0.3 < z < 0.41, and emission line luminosities of L[OIII] > 108.5 L⊙. The luminosity cut is equivalent to an absolute magnitude of MB < −23 mag, which is the classical definition of quasar. Subsequent updates to the [OIII] luminosities were reported for these QSO2s in Reyes et al. (2008); they are included in Table 1. These updated luminosities implied that six objects from the original selection fall marginally below the quasar L[OIII] cut, but Bessiere et al. (2012) chose to retain the original sample of 20 objects. In a more recent work, Bessiere et al. (2017) reported deep optical spectroscopic observations for 19 of the 20 QSO2s. SDSS J015911+143922 (J0159+1439) was excluded from their analysis because they were unable to obtain spectroscopic data of sufficient quality to model the stellar populations. This sample of 19 QSO2s is then 95% complete, and it constitutes our QSO2 sample. Table 1 includes the AGN bolometric luminosities of the QSO2s, which range from log LBOL = 44.9 to 46.7 erg s−1, with a median value of 45.5 erg s−1. These luminosities were calculated from the extinction-corrected [OIII] luminosities from Kong & Ho (2018) and using the correction factor of 454 from Lamastra et al. (2009).
Main properties of the QSO2s.
2.1. Spectroscopic data
The optical spectroscopic data used in this work, described in Bessiere et al. (2017), were mainly obtained using the Gemini Multi-Object Spectrograph (GMOS-S) mounted on the Gemini South telescope at Cerro Pachón, Chile. Long-slit spectra were taken for 16 objects during semesters 2010B and 2011B using a relatively wide slit of 1.5 arcsec in both the B600 and the R400 gratings. The observations consisted of 4 × 675 s exposures using the B600 grating and 3 × 400 s exposures using the R400 grating. The average spectral resolutions measured from the sky lines were 7.2 and 11.4 Å for the blue and red wavelength ranges, respectively. However, because all the observations but one (J2358-00) have a seeing full width at half maximum (FWHM) smaller than the slit width, the actual spectral resolutions range from 4.0–8.2 Å for the different spectra.
Different spectroscopic observations were compiled for the other three QSO2s in the sample, either because no GMOS-S observations were obtained (J0217–00 and J0114+00), or because [OIII] was not covered by the GMOS-S spectrum (J0142+00, for which only the blue range was observed). J0217–00 was observed with the Gran Telescopio Canarias (GTC) at the Roque de los Muchachos Observatory, La Palma, Spain. The Optical System for Imaging and low-Intermediate-Resolution Integrated Spectroscopy (OSIRIS) instrument was used in long-slit spectroscopy mode, using a slit of 1.23 arcsec width. The target was observed with the R2000B and R2500R grisms (spectral resolutions of 4 and 5 Å respectively), with integration times of 3 × 1800 s and 3 × 1200 s. Finally, the spectra of J0114+00 and J0142+00 were obtained from the SDSS, which uses a standard 3 arcsec fiber covering an observed wavelength range of 3800–9200 Å, with a spectral resolution (R) varying from R ∼ 1500 at 3800 Å to R ∼ 2500 at 9000 Å. This spectral resolution corresponds to an FWHM = 2.78 Å at 7000 Å.
We used the reduced and flux-calibrated data from Bessiere et al. (2017), where further details can be found. Large extraction apertures of 1.5–2 arcsec (≈8 kpc) were used there with the aim of performing stellar population modeling of the QSO2s host galaxies. Because our goal is to study the nuclear gas kinematics, we extracted the spectra using a diameter determined by the size of the seeing of each observation. The seeing was measured from the FWHM of the stars detected in the corresponding acquisition images of the QSO2s (0.53–1.13 arcsec ≈ 2.7–6.1 kpc; see Table 1), with the exception of J2358–00, for which we used an aperture of 8.5 kpc because the seeing of 1.58 arcsec exceeds the slit width. To extract these nuclear 1D spectra from the reduced and calibrated 2D spectra, we used the task apall within the IRAF package twodspec. First, we summed the flux contribution for the wavelengths centered around the ionized [OIII]λ5007 emission line. Then, by plotting this flux against the spatial axis, we located the maximum of the emission, and extracted a seeing-sized aperture centered at this position. In the case of the two QSO2s with SDSS data, the spectra correspond to physical sizes 15.8 kpc, set by the size of the fiber. We chose the [OIII] emission line to perform the kinematic analysis of the ionized gas because it is intense and AGN-dominated in the case of QSO2s, and it is not blended with other emission lines. In the case of the targets for which the [OIII] line was detected in both the red and the blue GMOS-S spectra, we used the blue because its spectral resolution is higher.
2.2. Galaxy properties
The selected sample was previously studied by Bessiere et al. (2012, 2017) and Ramos Almeida et al. (2013). From these works, we can obtain information about multiple properties of the QSO2s and their host galaxies, including the presence of YSPs, optical morphologies, environments, and radio emission (see Table 1). One of our goals is to search for correlations between these AGN and galaxy properties and those of the ionized outflows that we characterize here, for the first time in these QSO2s.
Bessiere et al. (2017) presented a detailed study of the stellar populations of the host galaxies of the 19 QSO2s in our sample plus another 2 QSO2s. Their study was based on the modeling of the spectra described in Sect. 2.1. To fit the spectra, they used a combination of up to two stellar population models that are representative of viable star formation histories, and a power law of varying spectral index to account for the contribution from scattered AGN light. Based on this analysis, Bessiere et al. (2017) concluded that 71% of the 21 QSO2 host galaxies require the inclusion of a YSP with an age < 100 Myr to correctly model the stellar features detected in the optical range. Of the sample of 19 QSO2s studied here, 14 host galaxies (74%) need the inclusion of this YSP (see Table 1). In the following, we just focus on the detection or nondetection of these YSPs in the QSO2s because their ages are comparable with the current phase of quasar activity and the outflows that it drives (Martini 2004; Hickox et al. 2014).
A full analysis of the optical morphologies of our QSO2 sample was presented in Bessiere et al. (2012). They visually inspected deep optical broadband images that were also observed with the GMOS-S instrument on the Gemini South telescope. They claimed that 15 of the 19 QSO2s (79% of the sample) show signs of galaxy interactions in the form of tails, shells, fans, irregular features, amorphous halos, and/or double nuclei. Based on the presence or absence of these structures, Bessiere et al. (2012) classified the host galaxies into four categories that correspond to different stages of the interaction between two galaxies: (1) galaxy pair in tidal interaction, (2) galaxies presenting other signs of morphological disturbance such as fans, shells, and/or tails, (3) galaxies with multiple nuclei, separated by ≤10 kpc, and (4) isolated galaxies without signs of morphological disturbance.
Bessiere et al. (2012) also reported the 5 GHz radio luminosities of the QSO2s, which are listed in Table 1. They were calculated using the integrated flux at 1.4 GHz, obtained either from the FIRST or NVSS surveys, assuming a spectral index of α = −0.75 when unknown. These 5 GHz luminosities range from 22.1 to 24.7 W Hz−1, with a median value of 22.35 W Hz−1, excluding the six QSO2s with upper limits (< 22.6 W Hz−1).
Last, Ramos Almeida et al. (2013) characterized and quantified the environment of the QSO2s by means of the angular clustering amplitude, Bgq, and using the deep GMOS-S optical imaging data from Bessiere et al. (2012). The spatial clustering amplitude measures the excess in the number of galaxies around the target as compared with the expected number of background galaxies, assuming that the galaxy clustering is spherically symmetric around each target. Both the neighbors and the background galaxies were counted as the total number of galaxies surrounding the QSO2 (or its corresponding position in the offset fields) within a projected distance of a 170 kpc radius and with magnitudes between m − 1 and m + 2, where m is the magnitude of a generic galaxy at the redshift of the target. More information about the procedure can be found in Ramos Almeida et al. (2013). In Table 1 we show the values of 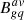 , calculated using all the offset fields (i.e., without the QSO2) to determine the average number of background galaxies. Most of the QSO2s have low values of
, calculated using all the offset fields (i.e., without the QSO2) to determine the average number of background galaxies. Most of the QSO2s have low values of 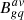 , corresponding to low-density environments. The average value reported by Ramos Almeida et al. (2013) for the QSO2s is 151 ± 76, and for comparison, values of
, corresponding to low-density environments. The average value reported by Ramos Almeida et al. (2013) for the QSO2s is 151 ± 76, and for comparison, values of 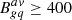 are typical of cluster environments. Ramos Almeida et al. (2013) compared the values of
are typical of cluster environments. Ramos Almeida et al. (2013) compared the values of 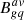 obtained for the QSO2s and for a control sample of quiescent early-type galaxies and did not find significant difference between them.
obtained for the QSO2s and for a control sample of quiescent early-type galaxies and did not find significant difference between them.
3. Kinematic analysis
We analyzed the nuclear [OIII]λλ4959,5007 Å profiles in order to investigate the kinematic properties of our sample, especially the possible presence of outflows. As explained in Sect. 2.1, we extracted a nuclear spectrum of each source by choosing an aperture comparable to the seeing of each observation (see Table 1). These apertures correspond to physical sizes of ∼3–6 kpc, except for J2358–00, whose size is 8.5 kpc. For the two QSO2s for which only SDSS spectra are available, J0114+00 and J0142+00, the fiber size corresponds to ∼15.8 kpc.
To characterize the ionized gas kinematics, the main methods applied in the literature are based either on a parametric or on a nonparametric approach. At every spatial location, different gaseous components with different kinematics can contribute to the flux and modify the shape of the line profiles: gas in the narrow-line region (NLR), outflowing gas, contributions from companion objects, and so on. Parametric methods are based on the assumption that the different kinematic components can be described as a Gaussian distribution. They have the advantage of enabling us to characterize the properties of the different kinematic components, including density and reddening (Holt et al. 2011; Villar-Martín et al. 2014; Arribas et al. 2014). The challenge is that in some objects with disrupted kinematics, it is difficult to ascribe a physical meaning to all the fitted kinematic components (Bessiere & Ramos Almeida 2022). On the other hand, the nonparametric analysis consists of measuring emission line velocities at various fixed fractions of the peak intensity (Speranza et al. 2021) or the line cumulative flux function (Whittle 1985; Harrison et al. 2014). This method is most appropriate for characterizing gas properties in galaxies with multiple kinematic components because it permits us to easily identify high-velocity gas in tail ends of emission line wings. However, nonparametric methods do not allow us to characterize the relative contribution of the different gaseous components at play.
Considering the previous, here we adopted both parametric and nonparametric methods to characterize the ionized gas kinematics of the QSO2s. In this way, we can investigate the dependence of the outflow properties, when present, on the method that is employed to measure them. First, we modeled the [OIII]λλ4959,5007 Å emission line profiles using a parametric method (i.e., fitting Gaussians to the line profiles). Second, taking advantage of the parametric fit of the [OIII]λ5007 Å, we used both flux-weighted and peak-weighted nonparametric methods to characterize the line profile. In Sect. 4 we compare the results we obtained with the different methods that we describe below.
3.1. Parametric method
We fit the [OIII]λλ4959,5007 profiles with multiple Gaussian components using a PYTHON program that we developed based on the Specutils and the Astropy packages. Initially, before fitting the emission lines, the underlying continuum was subtracted by linearly interpolating the spectrum between two line-free regions close to the [OIII] doublet, redward and blueward (see the left panel of Fig. 1). To select the number of Gaussians that were fit to each of the QSO2s, we added new components until the increment of the reduced χ2 (Δχ2) of the residuals was lower than 10%, following Bessiere & Ramos Almeida (2022). We also imposed that any component must be broader than the instrumental width (see Sect. 2.2), and its corresponding parameters larger than their associated uncertainties. An example of a fit including two Gaussians is shown in the right panel of Fig. 1.
 |
Fig. 1. Parametric fit of the [OIII] doublet for the QSO2 J0924+01. The left panel shows the line-free regions (in blue) that we selected to fit the underlying continuum (orange solid line). The right panel shows the two kinematic components we fit in the case of this QSO2. The residuals are included in the inset at the bottom. The green shaded region in the residuals corresponds to the region that is affected by atmospheric absorption. |
Each kinematic component that was fit to the [OIII] doublet corresponds to a set of two Gaussians that were fit simultaneously (i.e., that share the same width and velocity shift relative to systemic), with a fixed wavelength separation (taking the cosmological spread of the wavelength shift between the two lines into account) and an amplitude ratio of [OIII]λ4959/[OIII]λ5007 = 1/3 (Dimitrijević et al. 2007). It is noteworthy that the GMOS-S spectra reduced and analyzed by Bessiere et al. (2017) have residual atmospheric absorption around the spectral region 6863–6913Å. When this residual absorption lies on top of or close to one of the emission lines, as is the case of the QSO2s J0114+00, J0142+14, J0217–01, J0218–00, J0320+00, and J0923+01, we first fit just the unaffected [OIII] line, and then used the corresponding parameters to force the fit of the affected line. In the case of J0924+01, where the atmospheric absorption lies between the two emission lines, the affected wavelength range was masked before we fit the emission line profiles (see the right panel of Fig. 1).
All the fits and corresponding parameters derived from them (number of Gaussians, flux, FWHM, velocity shift from systemic, luminosity, and percentage luminosity of each component relative to the total luminosity of the line) are shown in Fig. A.1 and Table A.1. We note that the values of the FWHM have not been corrected for instrumental width, with the aim of keeping them comparable with W80 (see Sect. 3.2). Nevertheless, the individual instrumental FWHMs are listed in Table A.1. The uncertainties of the parameters were computed through a Monte Carlo simulation, for which we created 1000 mock spectra by varying the flux at each wavelength and adding random values from a normal distribution with an amplitude given by the noise of the continuum. The errors were then computed as the 1σ of each parameter distribution generated from the mock spectra.
Following the method described above, we fit n Gaussian components to the [OIII] profiles of the QSO2s and classified them as narrow (n) when FWHM < 800 km s−1, intermediate (i) for 800 km s−1 ≤ FWHM ≤ 2000 km s−1, and broad (b) when FWHM > 2000 km s−1.
We used these values to ascribe a physical meaning to the different kinematic components. We assumed that the narrow components are associated with gas in the NLR, whose emission lines typically present FWHMs ∼ 400–600 km s−1 (Netzer 1990; Groves 2007). The intermediate components are broader than the typical NLR FWHMs, but narrower than the broad components from the BLR, which have FWHM > 2000 km s−1. We note, however, that the broad components that we measured for the [OIII] emission lines cannot be associated with the BLR because they are forbidden lines. Thus, the intermediate and broad components would be most likely associated with turbulent outflowing ionized gas. With this is mind, the velocity shifts reported in Table A.1 were computed relative to the narrow component, or to the centroid of the multiple narrow components when present. We consider these velocity shifts as the outflow velocities relative to the average kinematics of the NLR. Because these are conservative estimates, we also calculated the outflow maximum velocities as vmax = vs + 2σ (Rupke & Veilleux 2013), where σ is FWHM/2.355.
In addition to the (n), (i), and (b) components, the fits of the QSO2s J0217–01 and J0320+00 also include a narrow and redshifted (r) component (see Table A.1), which although it does not meet all the criteria described at the beginning of this section, was necessary to successfully reproduce the [OIII] profiles. However, these red components are not included in the outflow analysis.
We found intermediate and broad components in 18 of the 19 QSO2s, which implies an outflow incidence rate of ∼95%. The only QSO2 without intermediate or broad components is J0218–00. The outflow components that we measured for the other 18 QSO2s present an average FWHM of 1800 km s−1, with a standard deviation of 1100 km s−1. They are mainly blueshifted, with an average value of vs = −370 km s−1, a standard deviation of 400 km s−1 (see Table 2), and a maximum velocity of vmax = −1800 ± 1400 km s−1.
Average and median outflow properties from the parametric and nonparametric methods.
We find that 14 of the QSO2s (74% of the sample) require the inclusion of more than two Gaussian components (2 QSO2s with four and 12 with three Gaussians) to correctly model the emission line profiles. The remaining 5 QSO2s (26% of the sample) are well fit with just two Gaussian components. This diversity of detected kinematic components in the [OIII] lines is common in QSO2s (Villar-Martín et al. 2011, 2016; Harrison et al. 2014; McElroy et al. 2015). However, the heterogeneous results from our parametric analysis make it difficult to characterize the outflow properties of the sample. For this reason, and taking advantage of the parametric analysis described here, we performed a nonparametric analysis of the emission line profiles. This analysis, described in Sect. 3.2, provides a more homogeneous set of results, which allowed us to easily evaluate possible correlations between the outflow and host galaxy properties (see Sect. 5).
3.2. Nonparametric analysis
We used two different nonparametric methods for characterizing the [OIII]λ5007 Å emission line: the flux-weighted and peak-weighted method. They require a noiseless isolated emission line profile, and we therefore used the models resulting from the parametric method described in Sect. 3.1 (i.e., the sum of the Gaussian components used to fit the [OIII]λ5007 Å emission line of each QSO2; see the right panel of Fig. 1 for an example).
3.2.1. Flux-weighted nonparametric analysis
We first used a flux-weighted nonparametric approach (Heckman et al. 1981; Harrison et al. 2014; Zakamska & Greene 2014) to describe the kinematic properties of the modeled [OIII]λ5007 Å emission line. The velocities v05, v10, v90, and v95 are defined as the velocities at the 5th, 10th, 90th, and 95th percentiles of the normalised cumulative function of the emission line flux. Other quantities that we use hereafter are the peak velocity (vp), that corresponds to the peak flux of the emission line and it is representative of the narrow component(s) fit in Sect. 3.1, and the median velocity (vmed), defined as the 50th percentile of the velocity and also representative of gas in the NLR. We also measured W80, defined as the width of the line containing 80% of the total emission line flux (W80 = v90–v10), and Δv = (v05 + v95)/2, that is the velocity offset of any blueshifted or redshifted component relative to the systemic velocity (i.e., the peak velocity, vp). Finally, we measured the asymmetry, a = ∣v90 − vmed ∣ − ∣ v10 − vmed∣, with negative (positive) values indicating a blue (red) tail in the line profiles.
In the following, we consider that only the gas with velocities higher than v05 and v95 is outflowing, and we define the corresponding outflow velocities (vOF) as the median velocity (v50) of the blueshifted and redshifted wings (blue and red areas in Fig. 2). In the example shown in Fig. 2, the median velocity of the blue wing is −1926 ± 37 km s−1, and 789 ± 21 km s−1 for the red wing. For the whole sample, we measure vOF = −1120 ± 510 km s−1 for the blue wing and 680 ± 200 km s−1 for the red. All the parameters and figures derived using this method are shown in Appendix B. As in the case of the parametric method, the uncertainties were computed as the 1σ of each parameter distribution generated with a Monte Carlo simulation of 1000 mock spectra.
 |
Fig. 2. Example of the flux-weighted nonparametric method. The solid blue line is the parametric fit to the [OIII]λ5007 Å emission line shown in Fig. 1 for J0924+01, without the continuum. The nonparametric velocity definitions included in this figure are the median velocity (vmed), the velocities at the 5, 10, 90, and 95% points of the normalized cumulative function of the emission line flux (v05, v10, v90, and v95), and the width of the line containing 80% of the total flux (W80 = v90 − v10). The gray region corresponds to the area containing 80% of the total flux (i.e., between v10 and v90), and the blue and red regions correspond to high-velocity gas, which we consider to be outflowing. |
We find a wide range of emission line widths, with an average W80 = 940 ± 280 km s−1. Twelve of the 19 QSO2s present broad [OIII] line profiles, with W80 > 800 km s−1. Regardless of this, we considered that all the QSO2s have outflows of ionized gas because by definition, every emission line profile will include velocities higher than v05 and v95. The average values of the asymmetry, v05, and v95 are −120 ± 130 km s−1, −820 ± 320 km s−1, and 530 ± 140 km s−1. All the QSO2s show negative asymmetry values, except for J0227+01. These negative values are related to the blue tails in the profiles (see Fig. B.1 and Table B.1). Blueshifted wings are more commonly detected than redshifted wings because we usually see the bulk of the outflowing gas that approaches us, and the receding side is partly hidden behind the host galaxy. When the outflows subtend a small angle relative to the galaxy disks, it is possible to detect both the blueshifted and redshifted outflow components, or depending on the galaxy inclination, a dominant redshifted component. This might be the case of J0227+01. Last, it should be mentioned that the quasar J0218–00, which did not need the inclusion of an intermediate or broad component in the parametric model, presents low values of the asymmetry and the velocity offset.
3.2.2. Peak-weighted nonparametric analysis
As described in Sect. 3.2.1, the flux-weighted nonparametric method likely overestimates the outflow mass because by definition, a certain proportion of the gas is outflowing, both blueshifted and redshifted. In addition, Speranza et al. (2021) argued that v05 might still be representative of rotating gas, which generally constitutes most of the emission line flux, and hence may not be fully representative of outflowing gas. Consequently, Speranza et al. (2021) proposed a different nonparametric analysis based on the detection of asymmetries in the emission lines (see Fig. 3 for an example) to measure the outflow properties.
 |
Fig. 3. Same as in Fig. 2, but using the peak-weighted nonparametric method from Speranza et al. (2021). The solid black line on the blue side of the emission line corresponds to the mirror image of the red side. The gray area is the core of the line, defined as the region between the peak and one-third of the peak flux. The orange area is the result of subtracting the black from the blue line outside the core region, which is what we consider to be outflowing gas using this method. The vertical dashed black and gray lines are the peak and outflow velocities (vp and vOF). |
For this method, we also use the model of the [OIII]λ5007 Å emission line profile from the parametric method. The core of the emission line was defined as the region between the peak of the line and one-third of the peak (i.e., the region that corresponds to ∼90% of the total flux of the line considering a Gaussian profile). By subtracting a mirror image of the less prominent from the most prominent wing, we removed the symmetric component of the emission line, and only the asymmetric wing was left. This residual is associated with outflowing gas (orange area in Fig. 3). To characterize the outflow, we used two parameters: the median velocity of the residual, vOF (the 50th percentile of its total flux), and the flux of the residual wing Fw. As in Sect. 3.2.1, the uncertainties were estimated as 1σ of each parameter distribution from 1000 mock spectra. All the plots and parameters derived from the peak-weighted nonparametric analysis are shown in Fig. C.1 and Table C.1.
Using this method, we find that all the QSO2s in the sample show ionized outflows in the form of asymmetric wings. Eighteen of the 19 QSO2s, including those with low values of W80, such as J0218–00, present blue wings. J0227+01 instead presents a red wing, which agrees with its positive asymmetry value. The average value of the outflow velocity computed using this method, considering the 18 QSO2s with blue wings, is vOF = −840 ± 260 km s−1, while for J0227+01, we obtain a value of 676 ± 21 km s−1 (see Tables 2 and C.1).
4. Physical properties of the outflows
In Sect. 3 we described the three methods we used to characterize the ionized outflows of the QSO2s, and the corresponding results. The parameters derived from these fits are direct measurements (e.g., FWHM, W80, a, and vmed), but we can use them to derive physical properties, such as the outflow mass, outflow mass rate, and kinetic power. These are key quantities for investigating the outflow impact on the surrounding environment. First, we calculated the mass of the ionized outflows using Eq. (1) (Osterbrock & Ferland 2006; Carniani et al. 2015; Fiore et al. 2017),
where ne is the electronic gas density, C is the condensation factor, L[OIII] is the outflowing gas luminosity and O/H = [O/H] – [O/H]⊙ is the oxygen abundance ratio relative to solar, with [O/H]⊙ ∼ 8.86 (Centeno & Socas-Navarro 2008). For the whole sample, we assumed that the gas clouds have the same electron density, leading to 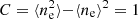 , and solar metallicity as in Bessiere et al. (2017), hence O/H = 0.
, and solar metallicity as in Bessiere et al. (2017), hence O/H = 0.
For ionized outflows, an important source of uncertainty is the electron density (Harrison et al. 2018; Holden & Tadhunter 2023). The outflow mass is inversely proportional to the gas density, which can be estimated from the ratio of the [SII]λλ6716,6731 doublet, from the [OIII]/Hβ and [NII]/Hα ratios, or using the fainter trans-auroral lines. The latter technique uses the flux ratios of the [SII]λλ6716,6731 and [O II]λλ3726,3729 doublets as well as of the trans-auroral [O II]λλ7319,7331 and [SII]λλ4068,4076 lines. The trans-auroral ratios have the advantage of being sensitive to higher-density gas than the classical [SII] ratio (Holt et al. 2011; Rose et al. 2018; Ramos Almeida et al. 2019). Using [SII], Harrison et al. (2014) reported densities in the range 200–1000 cm−3 for a sample of 16 QSO2s at z < 0.2, and Singha et al. (2022) measured outflow densities of ∼1900 for type 1 AGN at 0.01 < z < 0.06. Using the trans-auroral lines, Rose et al. (2018) measured outflow densities in the range 2500 < ne (cm−3) < 20 000 for ULIRGS with 0.06 < z < 0.15. Finally, using optical line ratios, Baron & Netzer (2019) reported densities of ∼30 000 cm−3 for a sample of 234 nearby type 2 AGN. Because our spectra do not cover the [SII] doublet, the trans-auroral lines, or the [NII] and Hα emission lines, we adopted a gas density of ne = 200 cm−3 for all the QSO2s, as in Fiore et al. (2017) and Speranza et al. (2021). Therefore, the derived outflow masses most likely are upper limits.
To estimate the total ionized gas mass of the outflows, we assume that it is three times the [OIII] outflow mass (MOF = 3 × M[OIII]; Fiore et al. 2017). The outflow mass rate represents the instantaneous rate of outflowing gas at the edge of the wind. Assuming a spherical sector (Fiore et al. 2017; Lutz et al. 2020), it can be defined as three times the total [OIII] mass divided by the time required to push this mass through a spherical surface of radius ROF,
As there are no integral field observations that we can use to constrain the outflow radius (ROF), it might be possible to do this using averaged spatial slices of the broad-line wings detected in the long-slit spectra, as in Rose et al. (2018) and Ramos Almeida et al. (2019). However, this procedure is not straightforward in the case of the [OIII] lines because the blueshifted wing of [OIII]λ5007 is blended with [OIII]λ4959, and the blueshifted wing of the latter is much fainter. Moreover, because we measure a median seeing of 0.83 arcsec (∼3.8 kpc at the average redshift of the sample, z ∼ 0.366) for the GMOS-S spectra, the ionized outflows are most likely unresolved according to other studies of QSO2s at similar redshifts (Villar-Martín et al. 2011, 2016; Karouzos et al. 2016; Ramos Almeida et al. 2017, 2019; Speranza et al. 2021). Early studies of quasar-driven outflows based on optical integral field observations of local QSO2s reported ionized outflows extending up to ∼10–15 kpc (Liu et al. 2013; Harrison et al. 2014; McElroy et al. 2015). However, later works claimed that these sizes were overestimated because of seeing smearing effects (Husemann et al. 2016; Karouzos et al. 2016; Harrison et al. 2018) or selection biases (Villar-Martín et al. 2016). More recent studies reported ionized outflows with sizes of ∼1–3.4 kpc for local QSO2s (Karouzos et al. 2016; Ramos Almeida et al. 2017, 2019; Speranza et al. 2022). Hence, we assumed an outflow radius of 1 kpc for all the QSO2s in our sample. If the radii exceed this value, our mass outflow rates are upper limits, although more compact outflows have been reported for nearby ULIRGs and AGN (Tadhunter et al. 2018, 2021; Singha et al. 2022; Winkel et al. 2023).
The outflow velocity (vOF) that we used to compute the outflow mass rate depends on the method: In the case of the parametric analysis, we considered both vs and vmax (see Table A.1). vs is the velocity of the intermediate and/or broad components relative to the narrow component(s), and vmax = vs + 2σ (see Sect. 3.1). We computed the outflow mass rate associated with each of the intermediate and/or broad components and then added them to compute the total outflow rate (see Table A.2).
For the flux-weighted nonparametric analysis, we used as outflow velocities, vOF, the v50 of the red and blue areas shown in Figs. 2 and B.1. Then, we computed two separate outflow rates for each QSO2, red and blue, which we finally added to compute the total outflow mass rate (see Table B.2). Finally, for the peak-weighted nonparametric analysis, we used the 50th velocity percentile of the residual wings (orange areas in Figs. 3 and C.1) to calculate the outflow mass rates (see Table C.1).
After we estimated the outflow mass rates using Eq. (2), we calculated the kinetic power as
The outflow masses, outflow mass rates, and kinetic powers measured with the three different methods are shown in Tables A.2, B.2, and C.1, and in Fig. 4. The uncertainties were computed using propagation of errors.
 |
Fig. 4. Histograms of the outflow masses, mass rates, and kinetic powers computed through the three different methods: parametric (considering either vs or vmax as the outflow velocities), flux-weighted, and peak-weighted nonparametric. To facilitate comparison of the values, we omitted the highest values of 57 and 151 M⊙ yr−1 in the outflow mass rate histograms that were obtained for J0923+01 and J0142+14 using vmax in the parametric method. |
The outflow masses computed through the parametric, flux-weighted, and peak-weighted nonparametric methods have average values of log(MOF) = 6.47 ± 0.50, 6.03 ± 0.30, and 5.75 ± 0.32 M⊙, and the medians are 6.46, 5.93, and 5.75 M⊙, respectively (see Table 2). From these results, and from the outflow mass histograms shown in Fig. 4, we conclude that the highest outflow masses are derived using the parametric method. This is because with this method we consider the integrated flux of the intermediate and/or broad Gaussian components as outflowing gas, while in the case of the nonparametric methods we just use the flux that is included in the tails of the emission lines.
The average outflow mass rates measured from the parametric, flux-weighted, and peak-weighted nonparametric methods are 2.8 ± 2.6, 4.0 ± 4.4, and 1.9 ± 1.8 M⊙ yr−1, and the medians are 1.8, 2.5, and 1.3 M⊙ yr−1 (see Table 2). The flux-weighted nonparametric method results in higher outflow mass rates because blueshifted and redshifted gas (see Sect. 3.2.1) with high velocities are always included. However, all the values measured from the three methods are between 0.2 and 9 M⊙ yr−1, except for J0142+14, which has an outflow rate of 20 M⊙ yr−1 measured from the flux-weighted nonparametric method. When we consider the parametric vmax values, we obtain the highest outflow mass rates (average value of 23 ± 35 M⊙ yr−1, with a median value of 11 M⊙ yr−1; see the middle panel of Fig. 4 and Table 2).
Focusing on the kinetic powers, we measure average values of log(Ėkin) = 40.5 ± 1.2, 41.9 ± 0.6, and 41.4 ± 0.5 erg s−1 using the three methods. The median values are 40.3, 41.9, and 41.4 erg s−1 (see Table 2). In this case, the lowest values of the kinetic power are those measured with the parametric method. This is because it depends on 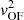 , which is higher in the case of the nonparametric methods (see Tables A.1, B.2, and C.1). By using the velocity shift of the broad and/or intermediate components (vs) relative to the narrow component(s) as outflow velocity, we derive lower kinetic powers than when we consider the mean velocities (v50) of the high-velocity tails considered in the nonparametric methods. If instead of vs we use vmax, as is commonly done in the literature (McElroy et al. 2015; Fiore et al. 2017), the kinetic powers are larger than the nonparametric ones (average of 42.9 ± 0.6 erg s−1 and median of 42.9 erg s−1; see Table 2). Finally, the average values of the coupling efficiencies (Ėkin/LBOL) derived from for the parametric, flux-weighted, and peak-weighted nonparametric methods are (0.014 ± 0.032)%, (0.080 ± 0.16)%, and (0.020 ± 0.025)%, with medians of 0.001%, 0.02%, and 0.01%. These values are one order of magnitude lower than those reported by other studies of ionized outflows in AGN that have followed similar considerations (Fiore et al. 2017; Baron & Netzer 2019; Davies et al. 2020; Speranza et al. 2021). However, in the case of the parametric method using vmax (as in Fiore et al. 2017), we obtain much higher values, with an average of (1.2 ± 3.0)%, and a median of 0.22%. The high value of the average and its dispersion come from three QSO2s with coupling efficiencies higher than one: J0142+14, J0332–00, and J0948+00 (see Table A.2). In this case, the median value is more representative of the whole sample.
, which is higher in the case of the nonparametric methods (see Tables A.1, B.2, and C.1). By using the velocity shift of the broad and/or intermediate components (vs) relative to the narrow component(s) as outflow velocity, we derive lower kinetic powers than when we consider the mean velocities (v50) of the high-velocity tails considered in the nonparametric methods. If instead of vs we use vmax, as is commonly done in the literature (McElroy et al. 2015; Fiore et al. 2017), the kinetic powers are larger than the nonparametric ones (average of 42.9 ± 0.6 erg s−1 and median of 42.9 erg s−1; see Table 2). Finally, the average values of the coupling efficiencies (Ėkin/LBOL) derived from for the parametric, flux-weighted, and peak-weighted nonparametric methods are (0.014 ± 0.032)%, (0.080 ± 0.16)%, and (0.020 ± 0.025)%, with medians of 0.001%, 0.02%, and 0.01%. These values are one order of magnitude lower than those reported by other studies of ionized outflows in AGN that have followed similar considerations (Fiore et al. 2017; Baron & Netzer 2019; Davies et al. 2020; Speranza et al. 2021). However, in the case of the parametric method using vmax (as in Fiore et al. 2017), we obtain much higher values, with an average of (1.2 ± 3.0)%, and a median of 0.22%. The high value of the average and its dispersion come from three QSO2s with coupling efficiencies higher than one: J0142+14, J0332–00, and J0948+00 (see Table A.2). In this case, the median value is more representative of the whole sample.
From this comparison, we conclude that the three adopted methods provide different physical properties of the outflows as a result of the particular considerations and procedure of each one. However, these differences are consistent within the uncertainties considering that we did not account for those associated with the electron density and outflow radius. In Fig. 5 we plot the outflow mass rates and kinetic powers derived from each method as a function of the bolometric luminosity. The values from the compilation of Fiore et al. (2017) are also shown for comparison. They also considered a fixed density of ne = 200 cm−3, an outflow radius of ROF = 1 kpc, and the same outflow geometry as we assumed here. We find that the flux-weighted nonparametric results lie within the lower values of the outflow rates and kinetic powers measured by Fiore et al. (2017) for AGN of similar luminosities, while the peak-weighted and the parametric results are smaller. However, the parametric results using vmax are the most similar to Fiore et al. (2017), as expected, because they also used vmax to calculate the physical properties of the outflows.
 |
Fig. 5. Outflow mass rate and kinetic power as a function of the bolometric luminosity of the AGN. Light and dark blue squares correspond to the values derived from the parametric method using vs and vmax, respectively. Green and orange circles are the values from the flux-weighted and peak-weighted nonparametric methods. The values from Fiore et al. (2017) are shown as gray triangles for comparison. |
5. Correlations between outflow properties and galaxy properties
As previously mentioned, in addition to determining the outflow demographics and corresponding properties of our QSO2 sample, our goal is to evaluate possible correlations with different AGN and galaxy properties. These properties, available from Bessiere et al. (2012, 2017) and Ramos Almeida et al. (2013), include the presence or absence of stellar populations younger than 100 Myr (YSP), of mergers (including interaction stage), the density of the large-scale environment (Bgq), and the radio luminosity (L5 GHz).
To do this, we evaluated the matrix correlation, shown in Fig. 6, between the outflow properties derived from the flux-weighted nonparametric analysis (see Sects. 3.2.1 and 4) and the AGN and host galaxy properties (see Sect. 2.2). From the direct outflow measurements, we selected W80, v05, v95, vmed, and a; and from the physical properties of the outflows, we chose MOF, ṀOF, and Ėkin.
 |
Fig. 6. Correlation matrix between the QSO2 outflow properties derived from the [OIII] emission line and using the flux-weighted nonparametric method, and their AGN and host galaxies properties. The Spearman rank correlation coefficients (ρ) are shown in the top right half of the matrix (blue and red), and the corresponding p-values are plotted in the bottom left half (gray). |
In order to quantify the degree of correlation among all the properties, we computed the Spearman rank correlation coefficient (ρ) for each variable pair, which is a nonparametric measurement of the strength and direction of the statistical dependence that exists between two variables. Unlike the Pearson correlation coefficient (r), the Spearman rank correlation coeffient does not assume that the data sets are normally distributed, and it assesses how well the relation between both can be described using a monotonic function. Hence, values of ρ equal to −1 or 1 imply an exact monotonic relation. Positive values indicate that as the X variable increases, Y increases as well, while negative values imply that as X increases, Y decreases. In general, absolute values of ρ in the range 0–0.39 are regarded as a weak or nonexistent correlation, 0.40–0.59 as a moderate, 0.6–0.79 as a strong, and 0.8–1 as a very strong correlation. The ρ values found for our sample are shown in the top right half of Fig. 6, where darker colors indicate stronger correlations.
We also performed a p-value test to verify the strength of the correlations, which is shown in the lower left half of the matrix shown in Fig. 6. The p-value measures the probability of observing a correlation coefficient as extreme or more extreme than the one observed from two datasets of uncorrelated properties, that is, it quantifies the probability of observing this correlation purely by chance. Seeking for a 90% confidence in our results, we set a significance level of α = 0.1 (100%-confidence level). This would imply that if the p-value ≤0.1, we can be confident at the 90% level that the correlation between two properties is genuine. In contrast, if the p-value > 0.1, the correlation could have arisen by chance, and hence we cannot conclude that it is significant.
As a sanity check, we first confirmed that correlations between certain outflow properties exist. For example, W80 shows strong correlations with the outflow projected velocities, v05 and v95 (ρ = −0.91 and ρ = 0.81, respectively). The reason is that broader emission line profiles have faster velocities associated with the wings. Similarly, v05 is also strongly correlated with the asymmetry, a, with ρ = 0.86. This is not the case for v95 (ρ = −0.23) because most of the asymmetries in our sample are associated with blueshifted gas. These direct outflow measurements also show strong correlations with some of the physical properties of the outflows, especially with the outflow mass rates and kinetic powers.
Focusing on the possible correlations between the AGN properties and the outflow measurements, we only find moderate correlations between the bolometric luminosity of the AGN and the outflow mass and outflow mass rate, both with ρ = 0.52, respectively (p-values of 0.021 and 0.023). This implies that more luminous AGN have more massive ionized outflows and also higher outflow mass rates (Cicone et al. 2014; Hainline et al. 2014; Fiore et al. 2017; Revalski et al. 2018). We did not find any significant correlations between the outflow properties and the host galaxy properties. Regarding the presence or absence of YSPs, 4 out of the 5 quasars (80%; J0114+00, J0234-07, J0332-00, and J0948+00) that do not require an YSP to reproduce their optical spectra show high asymmetry values |a|> 100. In contrast, only 5 of the 14 QSO2s with a YSP (36%) have |a|> 100. Because stronger asymmetries are associated with more disrupted gas and faster outflows, this result, despite the small sample size, might indicate that recent star formation is supressed more efficiently in the QSO2s with the most disrupted kinematics. Nevertheless, as we noted above, some QSO2s with disrupted kinematics also show YSPs.
For the optical morphologies of the QSO2s, we found that three out of the four galaxies that do not show any evidence of mergers or interactions (75%; J0332–00, J0234–07, J0114+00, and J0948+00) show |a|> 100. For the merging QSO2s (15/19), we do not find any trend between the outflow properties and the stage of the interaction either (i.e., precoalescence or postcoalescence; Ramos Almeida et al. 2011; Bessiere et al. 2012). This would imply that, on the spatial scales that our spectra probe, the outflowing gas and/or disrupted kinematics are AGN-driven instead of merger-driven. Considering this, it is not surprising that we do not find any correlation between the outflow properties and the large-scale environment either. In particular, we considered the spatial clustering amplitudes (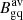 ) from Ramos Almeida et al. (2013). The QSO2s with the most disrupted kinematics do not show any preference for either denser or sparser environments.
) from Ramos Almeida et al. (2013). The QSO2s with the most disrupted kinematics do not show any preference for either denser or sparser environments.
Finally, we also considered possible correlations between the outflow properties and the radio luminosity of the QSO2s. Mullaney et al. (2013) and Zakamska & Greene (2014) found a connection between the width of the [OIII] profiles and L1.4GHz. The radio luminosity can be associated with star formation and/or nuclear activity (Jarvis et al. 2021; Bessiere et al., in prep.). For our QSO2s, we do not find any correlation between L5 GHz and any of the outflow properties here considered. We used the integrated luminosities at 5 GHz from Bessiere et al. (2012), measured from 5 arcsec resolution FIRST data, and we also checked that the results are the same when we instead use peak luminosities. The lack of a correlation might be due to the limited range of radio luminosities that our sample probes: 22.1–24.7 erg s−1, with an average value of 22.80 ± 0.80 erg s−1 and a median of 22.35 erg s−1 (see Table 1 and Sect. 6.2).
6. Discussion
We characterized the ionized outflow properties of a sample of 19 QSO2s at redshift 0.3 < z < 0.41 using three different analysis methods. We compared the results, and searched for correlations between the outflow properties and various AGN and galaxy properties. We now discuss these results and place them in context with others from the literature.
6.1. Demographics and energetics of ionized outflows
We found signatures of ionized outflows in 18 of the 19 QSO2s using the parametric method (Sect. 3.1), based on the detection of at least one Gaussian component with FWHM > 800 km s−1, generally blueshifted, as in Villar-Martín et al. (2011, 2016). Using the peak-weighted nonparametric method, we find that all the QSO2s have signatures of outflowing gas: 18 in the form of blueshifted asymmetries, and one redshifted asymmetry. This implies an outflow incidence rate of ∼95–100%, similar to the results found in other QSO2s studies (Villar-Martín et al. 2011, 2016; Fischer et al. 2018; Dall’Agnol de Oliveira et al. 2021) and higher than those generally reported for low-to-intermediate luminosity AGN (see e.g., Riffel et al. 2023 and references therein).
Some of the QSO2s show extreme [OIII] kinematics, for example, J0924+01 (see Figs. 1–3). From the flux-weighted nonparametric analysis of all the QSO2s, we find emission line widths ranging from 530 to 1645 km s−1 (average W80 = 940 ± 280 km s−1) and asymmetry values ranging from −235 to 50 km s−1 (average a = −120 ± 130 km s−1). The fastest outflow velocities come from the flux-weighted parametric method (average vOF = −1120 ± 510 km s−1) and from the parametric method when we compute the maximum velocity (average vmax = −1800 ± 1400 km s−1). These velocities are typical of AGN-driven ionized outflows detected in quasars with these bolometric luminosities (Mullaney et al. 2013; Zakamska & Greene 2014).
We computed the physical properties of the outflows, such as the outflow mass, outflow mass rate, and kinetic rates, from the direct outflow measurements derived through each kinetic analysis method (see Sect. 3). These quantities are key for investigating the outflow impact on the surrounding environment of their hosts. From the definition of these quantities (see Sect. 4), it is clear that both the electron density and the outflow radius play a critical role in their determination, along with the outflow flux and velocity derived via each method. Because we cannot constrain either ne or ROF with our data, we assumed a gas density of ne = 200 cm−3 and a radius of 1 kpc for all the QSO2s, as in Fiore et al. (2017). By assuming these values, we can just focus on the differences that are inherent to the method used to measure the outflow flux and velocity.
From our analysis of the outflow energetics using the three different methods we find that on average, the parametric method results in the highest outflow masses (log MOF(M⊙) = 6.47 ± 0.50) because it considers the integrated flux of the broad and intermediate components. The flux-weighted nonparametric method produces higher outflow mass rates and kinetic powers (MOF = 4.0 ± 4.4 M⊙ yr−1 and Ekin = 41.9 ± 0.6 erg s−1) than the peak-weighted nonparametric method and the parametric method using vs (see Fig. 4 and Table 2) because by definition, it always includes a contribution from both the blue and red emission line wings. This effect is more pronounced in the kinetic powers because 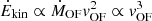 . Nevertheless, we find the highest values of the outflow mass rate and kinetic power when we use the parametric method and vmax instead of vs (MOF = 23 ± 35 M⊙ yr−1 and log(Ekin) = 42.9 ± 0.6 erg s−1).
. Nevertheless, we find the highest values of the outflow mass rate and kinetic power when we use the parametric method and vmax instead of vs (MOF = 23 ± 35 M⊙ yr−1 and log(Ekin) = 42.9 ± 0.6 erg s−1).
The comparison between the mass outflow rates and kinetic powers derived from the three methods and the values reported by Fiore et al. (2017) for a sample of 94 AGN is shown in Fig. 5. The values derived from the parametric vmax method are fully consistent with those of Fiore et al. (2017), as expected, because they used the same velocity definition to measure the physical properties of the outflows. However, we argue that these maximum velocities are not representative of outflowing gas because they only trace the highest-velocity gas instead of the bulk of the outflowing gas mass. This biases the results towards high values of the physical properties. Other works using higher electron densities for the winds and/or lower outflow velocities such as vs report outflow properties that are lower by one to three orders of magnitude (Holt et al. 2011; Villar-Martín et al. 2016; Rose et al. 2018; Spence et al. 2018; Davies et al. 2020; Holden et al. 2023). In addition, Davies et al. (2020) pointed out that the relatively low scatter reported by Fiore et al. (2017) for the data shown in Fig. 5 is partly due to the adoption of common values of the outflow density and radius.
The median coupling efficiencies that we measure for the outflows using the three methods are 0.001%, 0.02%, and 0.01%, and when we use the parametric method and vmax, this increases to 0.22%. The former three values are lower than those reported in the recent literature (Fiore et al. 2017; Baron & Netzer 2019; Speranza et al. 2021), while the parametric vmax value is similar. For example, both Fiore et al. (2017) and Speranza et al. (2021) reported a coupling efficiency of ∼0.2% for a sample of AGN at z < 0.5 and log(LBOL) ∼ 45.5 erg s−1, and of 3CR radio galaxies at z < 0.3 with log(LBOL) = 42–46 erg s−1, respectively. Again, this is a consequence of using maximum outflow velocities and assuming a low density value.
6.2. Lack of correlations between the nuclear ionized outflow properties and galaxy properties
To evaluate the outflow impact on star formation and their possible relation with other AGN and/or host galaxy properties, we investigated in Sect. 5 the correlation matrix using results from the flux-weighted nonparametric method. We only found moderate correlations between the bolometric luminosity of the AGN and the outflow masses and mass rates, both with a Spearman coefficient of ρ = 0.52. More massive and powerful outflows are usually found in luminous AGN galaxies (Hainline et al. 2014; Fiore et al. 2017; Revalski et al. 2018). Because we considered bolometric luminosities of the AGN derived from the extinction-corrected [OIII] luminosities, it is not surprising to find correlations, albeit weak, with the outflow masses measured from the [OIII] emission line. Likewise, high outflow mass rates are expected for luminous AGN (Fiore et al. 2017), although here we only find a modest correlation. This can be a consequence of the relatively small luminosity range probed by our sample, which is log(LBOL) = 44.9–46.7 erg s−1.
We did not find any significant correlations between the outflow and the host galaxies properties here considered. Because we assumed fixed values of the outflow density and radius for all the targets, the outflow physical quantities are not precise. Therefore, the different correlations that we evaluated here might change if individual radii and densities were measured. This is not the case for the direct outflow measurements, such as the velocity, W80, or asymmetry. The outflow density has one of the strongest impacts on the derived outflow physical quantities. The outflow mass rate and kinetic power vary by one order of magnitude when we assume a density of 2000 cm−3 instead of 200 cm−3. However, we find the same lack of a correlation between the outflow properties derived from the flux-weighted nonparametric method and different AGN and host galaxy properties when precise density measurements are used for the individual targets in the QSOFEED sample of QSO2s (Bessiere et al., in prep.).
Focusing on the potential impact that outflows might have on recent star formation, we find that 4 of the 5 QSO2s lacking a YSP with age < 100 Myr (Bessiere et al. 2017) present disturbed kinematics with high asymmetry values (|a|> 100). On the other hand, only 5 of the 14 QSO2s with a YSP present high asymmetry values. Despite the small size of our sample, these results might indicate that recent star formation (i.e., having the same dynamical timescales as the outflows) is suppressed more efficiently in the QSO2s with most disrupted kinematics. Nevertheless, there are also QSO2s with disrupted kinematics that have YSPs. This could be due either to positive feedback (Klamer et al. 2004; Gaibler et al. 2012; Zubovas et al. 2013; Cresci et al. 2015), to the different spatial scales considered for the stellar population analysis (∼8 kpc) and for the outflow measurements (∼3.9 kpc), and/or to the time that the winds might need to suppress star formation. Using integral-field spectroscopic data of the QSO2 Mrk 34, Bessiere & Ramos Almeida (2022) showed that both positive and negative feedback can occur simultaneously in different parts of the same galaxy, depending on the amount of energy and turbulence that the outflows inject in the ISM. This illustrates the complexity of the outflow-ISM interplay, and it shows the importance of using spatially resolved studies of AGN to evaluate the impact of feedback.
Because interactions between galaxies disrupt the stellar and gas content of the galaxies involved, we could expect higher gas turbulence in mergers than in undisturbed galaxies. However, we do not find any trend between the [OIII] kinematics and the optical morphologies of the QSO2s or with their environment. This is most likely due to the different timescales involved: 1–3 Gyr for the mergers (Conselice et al. 2003), and 1–100 Myr for the AGN-driven outflows (Zubovas & King 2016). A major or minor merger can efficiently transport gas toward the center of the galaxy during hundreds of millions of years, and this gas supply can be intermittent, leading to different phases of nuclear activity (King & Nixon 2015). This makes it challenging to search for correlations between the large-scale galaxy morphology and the AGN-driven outflows.
Finally, we investigated the role of jets in driving or contributing to drive outflows in our QSO2s. We do not find any significant correlation between the outflow properties and either the integrated or peak 5 GHz luminosities from FIRST. Using spectra from SDSS, Mullaney et al. (2013) concluded that the width of the [OIII]λ5007 line shows a maximum in AGN with radio luminosities of log(L1.4 GHz) = 23–25 W Hz−1, that is, moderate radio luminosities such as those of our QSO2s. The lack of a correlation between these parameters is probably due to the small radio luminosity range probed by our QSO2s, which is 22.1–24.7 W Hz−1. However, the dominant origin of this radio emission is still a matter of ongoing debate (Zakamska & Greene 2014), as it might be produced by nonthermal AGN emission (Jarvis et al. 2019), star formation (Bessiere et al., in prep.), and/or shocks induced by the quasar winds or outflows (Fischer et al. 2023).
7. Conclusions
We characterized the ionized gas kinematics and energetics of a sample of 19 QSO2s at 0.3 < z < 0.41 using three different methods, parametric and nonparametric, to analyze the nuclear (∼3.9 kpc) [OIII] emission-line profiles. The main conclusions of the work are listed below.
-
We detect ionized gas outflows in the form of asymmetric and broad emission line profiles in 95–100% of the sample using the three methods. Eighteen of the 19 QSO2s show [OIII] profiles with blueshifted wings, and the other one shows a redshifted wing.
-
The average physical properties of the outflows (e.g., outflow mass, mass rate, and kinetic energy) that we derived from the three methods are consistent within the errors. The parametric method results in the highest outflow masses, and the flux-weighted nonparametric and especially the parametric method using vmax provide the highest mass outflow rates and kinetic powers.
-
We measure outflow mass rates ranging between 0.2 and 20 M⊙ yr−1 and kinetic powers between 38.3 and 42.9 erg s−1 for the QSO2s. For the parametric method using vmax, the highest values reach 151 M⊙ yr−1 and 44.0 erg s−1. These values are most likely upper limits, considering that we assumed fixed values of 200 cm−3 and 1 kpc for the outflow density and radius, respectively.
-
We find a modest correlation between the bolometric luminosity of the AGN and the outflow mass and mass rate, but we do not find any correlation with the host galaxy properties here considered.
-
Four of the 5 QSO2s lacking a YSP with age < 100 Myr present disturbed kinematics with high asymmetry values (|a|> 100). On the other hand, only 5 of the 14 QSO2s with a YSP present large asymmetry values. Despite the small sample size, these results might indicate that recent star formation is suppressed more efficiently in the QSO2s with the most disrupted kinematics.
In this work we showed for the first time a comparison between outflow measurements using three different methods that are commonly used in the literature. By assuming a fixed outflow density and radius, it becomes possible to just focus on the differences associated with the flux and velocity calculations. We conclude that although the average physical properties derived for the outflow from the three methods are consistent within the errors, the commonly adopted parametric measurements using maximum outflow velocities provide the highest values, which are not representative of the average outflow velocity. Finally, we argue that the lack of correlations between the outflow and the AGN and galaxy properties considered here is most likely due to the small luminosity ranges probed by our sample, and to the different timescales of the outflows and galaxy-wide properties.
Acknowledgments
C.R.A. and G.S. acknowledge financial support from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement No. 860744 (BiD4BESt). C.R.A.., G.S., J.A.P., and P.S.B. acknowledge the project “Feeding and feedback in active galaxies”, with reference PID2019-106027GB-C42, funded by MICINN-AEI/10.13039/501100011033. C.R.A. also acknowledges the project “Quantifying the impact of quasar feedback on galaxy evolution”, with reference EUR2020-112266, funded by MICINN-AEI/10.13039/501100011033 and the European Union NextGenerationEU/PRTR. C.R.A. thanks the Kavli Institute for Cosmology of the University of Cambridge for their hospitality while working on this paper, and the IAC Severo Ochoa Program for the corresponding financial support. The authors thank the anonymous referee for useful and constructive suggestions.
References
- Aalto, S., Costagliola, F., Muller, S., et al. 2016, A&A, 590, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arribas, S., Colina, L., Bellocchi, E., Maiolino, R., & Villar-Martin, M. 2014, A&A, 568, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audibert, A., Combes, F., García-Burillo, S., et al. 2019, A&A, 632, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audibert, A., Ramos Almeida, C., García-Burillo, S., et al. 2023, A&A, 671, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ayubinia, A., Woo, J.-H., Rakshit, S., & Son, D. 2023, ApJ, 954, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, D., & Netzer, H. 2019, MNRAS, 486, 4290 [Google Scholar]
- Bessiere, P. S., & Ramos Almeida, C. 2022, MNRAS, 512, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Bessiere, P., Tadhunter, C. N., Ramos Almeida, C., & Villar Martín, M. 2012, MNRAS, 426, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Bessiere, P. S., Tadhunter, C. N., Ramos Almeida, C., Villar Martín, M., & Cabrera-Lavers, A. 2017, MNRAS, 466, 3887 [NASA ADS] [CrossRef] [Google Scholar]
- Canalizo, G., & Stockton, A. 2001, ApJ, 555, 719 [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2015, A&A, 580, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2016, A&A, 591, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centeno, R., & Socas-Navarro, H. 2008, ApJ, 682, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Brusa, M., Ramos Almeida, C., et al. 2018, Nat. Astron., 2, 176 [Google Scholar]
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [CrossRef] [Google Scholar]
- Cresci, G., & Maiolino, R. 2018, Nat. Astron., 2, 179 [Google Scholar]
- Cresci, G., Marconi, A., Zibetti, S., et al. 2015, A&A, 582, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Agnol de Oliveira, B., Storchi-Bergmann, T., Kraemer, S. B., et al. 2021, MNRAS, 504, 3890 [CrossRef] [Google Scholar]
- Davies, R., Baron, D., Shimizu, T., et al. 2020, MNRAS, 498, 4150 [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitrijević, M., Popović, L., Kovačević, J., Dačić, M., & Ilić, D. 2007, MNRAS, 374, 1181 [CrossRef] [Google Scholar]
- Dubois, Y., Peirani, S., Pichon, C., et al. 2016, MNRAS, 463, 3948 [Google Scholar]
- Fernández-Ontiveros, J., Dasyra, K., Hatziminaoglou, E., et al. 2020, A&A, 633, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, T. C., Kraemer, S. B., Schmitt, H. R., et al. 2018, ApJ, 856, 102 [Google Scholar]
- Fischer, T., Smith, K. L., Kraemer, S., et al. 2019, ApJ, 887, 200 [Google Scholar]
- Fischer, T. C., Johnson, M. C., Secrest, N. J., Crenshaw, D. M., & Kraemer, S. B. 2023, ApJ, 953, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2021, MNRAS, 505, 5753 [NASA ADS] [CrossRef] [Google Scholar]
- Gaibler, V., Khochfar, S., Krause, M., & Silk, J. 2012, MNRAS, 425, 438 [NASA ADS] [CrossRef] [Google Scholar]
- García-Bernete, I., Alonso-Herrero, A., García-Burillo, S., et al. 2021, A&A, 645, A21 [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [Google Scholar]
- García-Burillo, S., Combes, F., Almeida, C. R., et al. 2019, A&A, 632, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Alonso-Herrero, A., Ramos Almeida, C., et al. 2021, A&A, 652, A98 [NASA ADS] [CrossRef] [Google Scholar]
- Goulding, A. D., Greene, J. E., Bezanson, R., et al. 2018, PASJ, 70, S37 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Zakamska, N. L., Ho, L. C., & Barth, A. J. 2011, ApJ, 732, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. 2007, in The Central Engine of Active Galactic Nuclei, eds. L. C. Ho, & J. W. Wang, ASP Conf. Ser., 373, 511 [NASA ADS] [Google Scholar]
- Hainline, K. N., Hickox, R. C., Greene, J. E., et al. 2014, ApJ, 787, 65 [Google Scholar]
- Harrison, C. 2017, Nat. Astron., 1, 1 [Google Scholar]
- Harrison, C., Alexander, D., Mullaney, J., & Swinbank, A. 2014, MNRAS, 441, 3306 [CrossRef] [Google Scholar]
- Harrison, C., Costa, T., Tadhunter, C., et al. 2018, Nat. Astron., 2, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Miley, G. K., van Breugel, W. J., & Butcher, H. R. 1981, ApJ, 247, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Camus, R., Janssen, A., Sturm, E., et al. 2020, A&A, 635, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickox, R. C., Mullaney, J. R., Alexander, D. M., et al. 2014, ApJ, 782, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Holden, L. R., & Tadhunter, C. N. 2023, MNRAS, 524, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Holden, L. R., Tadhunter, C. N., Morganti, R., & Oosterloo, T. 2023, MNRAS [Google Scholar]
- Holt, J., Tadhunter, C., Morganti, R., & Emonts, B. 2011, MNRAS, 410, 1527 [NASA ADS] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš, D. 2008, ApJS, 175, 356 [Google Scholar]
- Husemann, B., Scharwächter, J., Bennert, V. N., et al. 2016, A&A, 594, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarvis, M., Harrison, C., Thomson, A., et al. 2019, MNRAS, 485, 2710 [NASA ADS] [CrossRef] [Google Scholar]
- Jarvis, M. E., Harrison, C. M., Mainieri, V., et al. 2021, MNRAS, 503, 1780 [NASA ADS] [CrossRef] [Google Scholar]
- Karouzos, M., Woo, J.-H., & Bae, H.-J. 2016, ApJ, 819, 148 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., & Nixon, C. 2015, MNRAS, 453, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Klamer, I. J., Ekers, R. D., Sadler, E. M., & Hunstead, R. W. 2004, ApJ, 612, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, M., & Ho, L. C. 2018, ApJ, 859, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Lamastra, A., Bianchi, S., Matt, G., et al. 2009, A&A, 504, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamperti, I., Pereira-Santaella, M., Perna, M., et al. 2022, A&A, 668, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, G., Zakamska, N. L., Greene, J. E., Nesvadba, N. P., & Liu, X. 2013, MNRAS, 430, 2327 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Sturm, E., Janssen, A., et al. 2020, A&A, 633, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín-Navarro, I., Pillepich, A., Nelson, D., et al. 2021, Nature, 594, 187 [CrossRef] [Google Scholar]
- Martini, P. 2004, in Coevolution of Black Holes and Galaxies, ed. L. C. Ho, (Cambridge: Cambridge University Press) 169 [Google Scholar]
- McElroy, R., Croom, S. M., Pracy, M., et al. 2015, MNRAS, 446, 2186 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R., Oosterloo, T., Oonk, J. R., Frieswijk, W., & Tadhunter, C. 2015, A&A, 580, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moster, B. P., Somerville, R. S., Maulbetsch, C., et al. 2010, ApJ, 710, 903 [Google Scholar]
- Mukherjee, D., Wagner, A. Y., Bicknell, G. V., et al. 2018, MNRAS, 476, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J., Alexander, D., Fine, S., et al. 2013, MNRAS, 433, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 1990, Active Galactic Nuclei (Springer), 57 [Google Scholar]
- Novak, G. S., Ostriker, J. P., & Ciotti, L. 2011, ApJ, 737, 26 [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics Of Gas Nebulae and Active Galactic Nuclei (University Science Books) [Google Scholar]
- Pierce, J., Tadhunter, C., Ramos Almeida, C., et al. 2023, MNRAS, 522, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., & Ricci, C. 2017, Nat. Astron., 1, 679 [Google Scholar]
- Ramos Almeida, C., Tadhunter, C. N., Inskip, K., et al. 2011, MNRAS, 410, 1550 [Google Scholar]
- Ramos Almeida, C., Bessiere, P., Tadhunter, C., et al. 2012, MNRAS, 419, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Bessiere, P., Tadhunter, C., et al. 2013, MNRAS, 436, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Piqueras López, J., Villar-Martín, M., & Bessiere, P. S. 2017, MNRAS, 470, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Acosta-Pulido, J. A., Tadhunter, C. N., et al. 2019, MNRAS, 487, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Bischetti, M., García-Burillo, S., et al. 2022, A&A, 658, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Revalski, M., Dashtamirova, D., Crenshaw, D. M., et al. 2018, ApJ, 867, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Reyes, R., Zakamska, N. L., Strauss, M. A., et al. 2008, AJ, 136, 2373 [Google Scholar]
- Riffel, R. A., Storchi-Bergmann, T., Riffel, R., et al. 2023, MNRAS, 521, 1832 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, M., Tadhunter, C., Ramos Almeida, C., et al. 2018, MNRAS, 474, 128 [Google Scholar]
- Rupke, D. S., & Veilleux, S. 2013, ApJ, 768, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., Coil, A., Geach, J. E., et al. 2019, Nature, 574, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Satyapal, S., Ellison, S. L., McAlpine, W., et al. 2014, MNRAS, 441, 1297 [Google Scholar]
- Schawinski, K., Koss, M., Berney, S., & Sartori, L. F. 2015, MNRAS, 451, 2517 [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Singha, M., Husemann, B., Urrutia, T., et al. 2022, A&A, 659, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spence, R., Tadhunter, C., Rose, M., & Rodríguez Zaurín, J. 2018, MNRAS, 478, 2438 [NASA ADS] [CrossRef] [Google Scholar]
- Speranza, G., Balmaverde, B., Capetti, A., et al. 2021, A&A, 653, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Speranza, G., Almeida, C. R., Acosta-Pulido, J., et al. 2022, A&A, 665, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tadhunter, C., Rodríguez Zaurín, J., Rose, M., et al. 2018, MNRAS, 478, 1558 [NASA ADS] [CrossRef] [Google Scholar]
- Tadhunter, C., Patel, M., & Mullaney, J. 2021, MNRAS, 504, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- Villar-Martín, M., Humphrey, A., Delgado, R. G., Colina, L., & Arribas, S. 2011, MNRAS, 418, 2032 [CrossRef] [Google Scholar]
- Villar-Martín, M., Emonts, B., Humphrey, A., Cabrera Lavers, A., & Binette, L. 2014, MNRAS, 440, 3202 [CrossRef] [Google Scholar]
- Villar-Martín, M., Arribas, S., Emonts, B., et al. 2016, MNRAS, 460, 130 [Google Scholar]
- Whittle, M. 1985, MNRAS, 213, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Whittle, M. 1992, ApJ, 387, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Winkel, N., Husemann, B., Singha, M., et al. 2023, A&A, 670, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wylezalek, D., & Morganti, R. 2018, Nat. Astron., 2, 181 [Google Scholar]
- York, D., Adelman, J., Anderson, J., Jr, et al. 2000, MNRAS, 414, 940 [Google Scholar]
- Zakamska, N. L., & Greene, J. E. 2014, MNRAS, 442, 784 [Google Scholar]
- Zakamska, N. L., Strauss, M. A., Krolik, J. H., et al. 2003, AJ, 126, 2125 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & King, A. 2016, MNRAS, 462, 4055 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., Nayakshin, S., King, A., & Wilkinson, M. 2013, MNRAS, 433, 3079 [Google Scholar]
Appendix A: Parametric analysis
In Figure A.1 we include all the fits we performed using the parametric method (except for the one shown in Figure 1), which is described in full in Section 3.1. The parameters of the kinematic components fit to the [OIII] lines are listed in Table A.1, and the physical properties of the outflows are listed in Table A.2.
 |
Fig. A.1. Parametric fits of the [OIII] doublet for the whole QSO2 sample. The figures are identical to the example case in Figure 1. |
 |
Fig. A.1. continued |
 |
Fig. A.1. continued |
Results from the parametric fits of the [OIII]λ5007 line.
Physical properties of the outflows resulting from the parametric method.
Appendix B: Flux-weighted nonparametric analysis
In Figure B.1 we include all the fits performed using the flux-weighted nonparametric method (except for the one shown in Figure 2), which is described in full in Section 3.2.1. The corresponding parameters from the fits of the [OIII] line are listed in Table B.1, and the physical properties of the outflows are listed in Table B.2.
 |
Fig. B.1. Flux-weighted nonparametric fits of the [OIII]λ5007 Å emission line shown for the whole sample. The figures are identical to the example in Figure 2. |
 |
Fig. B.1. continued |
Results from the flux-weighted nonparametric fits of the [OIII]λ5007 line.
Physical properties of the outflows resulting from the flux-weighted nonparametric method.
Appendix C: Peak-weighted nonparametric analysis
In Figure C.1 we include all the fits we performed using the peak-weighted nonparametric method from Speranza et al. 2021 (except for the one shown in Figure 3), which is described in full in Section 3.2.2. The corresponding outflow velocities derived from the fits of the [OIII] line and the physical properties of the outflows are listed in Table C.1.
 |
Fig. C.1. Peak-weighted nonparametric fits of the [OIII]λ5007 Å emission line shown for the whole sample. The figures are identical to the example in Figure 3. |
 |
Fig. C.1. continued |
Physical properties of the outflows derived from the peak-weighted nonparametric fits of the [OIII]λ5007 line.
All Tables
Average and median outflow properties from the parametric and nonparametric methods.
Physical properties of the outflows resulting from the flux-weighted nonparametric method.
Physical properties of the outflows derived from the peak-weighted nonparametric fits of the [OIII]λ5007 line.
All Figures
 |
Fig. 1. Parametric fit of the [OIII] doublet for the QSO2 J0924+01. The left panel shows the line-free regions (in blue) that we selected to fit the underlying continuum (orange solid line). The right panel shows the two kinematic components we fit in the case of this QSO2. The residuals are included in the inset at the bottom. The green shaded region in the residuals corresponds to the region that is affected by atmospheric absorption. |
| In the text | |
 |
Fig. 2. Example of the flux-weighted nonparametric method. The solid blue line is the parametric fit to the [OIII]λ5007 Å emission line shown in Fig. 1 for J0924+01, without the continuum. The nonparametric velocity definitions included in this figure are the median velocity (vmed), the velocities at the 5, 10, 90, and 95% points of the normalized cumulative function of the emission line flux (v05, v10, v90, and v95), and the width of the line containing 80% of the total flux (W80 = v90 − v10). The gray region corresponds to the area containing 80% of the total flux (i.e., between v10 and v90), and the blue and red regions correspond to high-velocity gas, which we consider to be outflowing. |
| In the text | |
 |
Fig. 3. Same as in Fig. 2, but using the peak-weighted nonparametric method from Speranza et al. (2021). The solid black line on the blue side of the emission line corresponds to the mirror image of the red side. The gray area is the core of the line, defined as the region between the peak and one-third of the peak flux. The orange area is the result of subtracting the black from the blue line outside the core region, which is what we consider to be outflowing gas using this method. The vertical dashed black and gray lines are the peak and outflow velocities (vp and vOF). |
| In the text | |
 |
Fig. 4. Histograms of the outflow masses, mass rates, and kinetic powers computed through the three different methods: parametric (considering either vs or vmax as the outflow velocities), flux-weighted, and peak-weighted nonparametric. To facilitate comparison of the values, we omitted the highest values of 57 and 151 M⊙ yr−1 in the outflow mass rate histograms that were obtained for J0923+01 and J0142+14 using vmax in the parametric method. |
| In the text | |
 |
Fig. 5. Outflow mass rate and kinetic power as a function of the bolometric luminosity of the AGN. Light and dark blue squares correspond to the values derived from the parametric method using vs and vmax, respectively. Green and orange circles are the values from the flux-weighted and peak-weighted nonparametric methods. The values from Fiore et al. (2017) are shown as gray triangles for comparison. |
| In the text | |
 |
Fig. 6. Correlation matrix between the QSO2 outflow properties derived from the [OIII] emission line and using the flux-weighted nonparametric method, and their AGN and host galaxies properties. The Spearman rank correlation coefficients (ρ) are shown in the top right half of the matrix (blue and red), and the corresponding p-values are plotted in the bottom left half (gray). |
| In the text | |
 |
Fig. A.1. Parametric fits of the [OIII] doublet for the whole QSO2 sample. The figures are identical to the example case in Figure 1. |
| In the text | |
 |
Fig. A.1. continued |
| In the text | |
 |
Fig. A.1. continued |
| In the text | |
 |
Fig. B.1. Flux-weighted nonparametric fits of the [OIII]λ5007 Å emission line shown for the whole sample. The figures are identical to the example in Figure 2. |
| In the text | |
 |
Fig. B.1. continued |
| In the text | |
 |
Fig. C.1. Peak-weighted nonparametric fits of the [OIII]λ5007 Å emission line shown for the whole sample. The figures are identical to the example in Figure 3. |
| In the text | |
 |
Fig. C.1. continued |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} M_{\rm [OIII]} = 4 \times 10^7 M_{\odot } \left(\frac{C}{10^\mathrm{O/H}}\right) \left(\frac{L_{\rm [OIII]}}{10^{44}}\right) \left(\frac{10^{3}}{\langle n_{\rm e} \rangle }\right) ,\end{aligned} $$](/articles/aa/full_html/2023/12/aa47756-23/aa47756-23-eq6.gif)