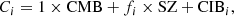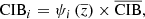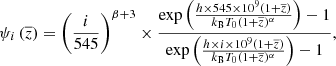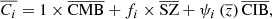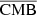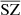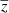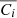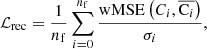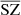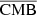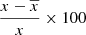EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A91 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A91
Number of page(s) 10
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202245624
Published online 31 May 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The first light ever propagated in our Universe, namely the cosmic microwave background (CMB), is still detectable today and remains a major probe in observational cosmology. Its spatial anisotropies have been observed and analysed over recent decades by many instruments such as COBE (Smoot et al. 1992; Mather et al. 1994), Boomerang (Lange et al. 2001), and WMAP (Bennett et al. 2003). The most up-to-date full-sky picture of the CMB was observed in the 2010s by the Planck satellite (Planck HFI Core Team 2011), while more detailed CMB features are being observed nowadays in smaller portions of the sky by ground-based experiments such as ACT (Fowler et al. 2010), Advanced ACTPol (Henderson et al. 2016), SPT (Carlstrom et al. 2011), and SPTpol (Austermann et al. 2012). All these instruments have led to unprecedented precision on the computation of the six cosmological parameters of the concordance ΛCDM model, which include ΩM and σ8 (Planck Collaboration VI 2020; Aiola et al. 2020; Aylor et al. 2017). In the coming years, other experiments with even greater spatial resolution, such as the Simons Observatory (SO, Ade et al. 2019) and CMB-S4 (Abazajian et al. 2016), will provide a huge amount of new data and will lead to exciting times for data analysis and cosmology with the CMB.

In the submillimetre frequencies, where the CMB is observable, other sources of emission are also present, which makes it difficult to disentangle the different components. Some are emissions from objects between our detectors and the CMB; these are the so-called foregrounds, containing for example dust from our galaxy, radio emission, molecular gas emission (CO), and the integrated diffuse infrared emission from all galaxies: the cosmic infrared background (CIB, Dole et al. 2006). Other components are distortions of the CMB itself due to its interaction with the objects within the path of the photons; one such distortion is the Sunyaev–Zel’dovich effect (SZ, Sunyaev & Zeldovich 1970). The known spectral signatures of the different components can potentially be used to separate them, within limitations.

Over recent decades, several algorithms have been developed to separate the different components or clean the CMB; for example, the spectral matching independent component analysis (SMICA, Delabrouille et al. 2003; Cardoso et al. 2008) and the generalized morphological component analysis (GMCA, Bobin et al. 2007), as well as the sparsity-based algorithms (Bobin et al. 2008, 2013), Commander (Eriksen et al. 2008), needlet internal linear combination (NILC, Delabrouille et al. 2009), generalized needlet internal liner combination (GNILC, Remazeilles et al. 2011), spectral estimation via expectation maximisation (SEVEM, Leach et al. 2008; Fernández-Cobos et al. 2012), modified internal linear combination algorithm (MILCA, Hurier et al. 2013), and reduced wavelet scattering transform (RWST, Allys et al. 2019). These have been successfully applied in order to separate the CMB (e.g., Planck Collaboration I 2020), but have also been used to differentiate between components, such as the SZ effect, in different experiments; for example, in Planck (Planck Collaboration XXI 2016; Tanimura et al. 2022a), ACT (Madhavacheril et al. 2020), SPT (Bleem et al. 2022), and a combination of them such as Planck+ACT (PACT, Aghanim et al. 2019; Naess et al. 2020) and SPT+Planck for CMB lensing (Omori et al. 2017). However, for the reconstruction of the SZ effect in particular, one of the main challenges is to confront the contamination from the CIB (e.g., Hurier et al. 2013; Planck Collaboration XIV 2016). The CIB signal at high frequencies often leaks in SZ spectral filters and can potentially induce extra power at small scales in SZ power spectra, and vice versa. This is an important effect to take into account when computing cosmological parameters with the SZ power spectrum (e.g., Salvati et al. 2018; Douspis et al. 2022; Gorce et al. 2022; Tanimura et al. 2022a). Another important source of contamination in any CMB component-separation analysis is the galactic dust and the CIB in polarisation data, specifically when aiming to detect the B-mode in polarization (Allys et al. 2019; Lenz et al. 2019; Regaldo-Saint Blancard et al. 2020), which is the main future challenge in CMB data analysis.

Deep learning networks, and especially UNets (Ronneberger et al. 2015), are very sensitive to both spectral and morphological information and can capture highly non-Gaussian distributions (such as some of the components in CMB frequency maps). This makes those networks particularly suited to studying CMB data and indeed they have been applied with increasing frequency over recent years for different purposes, such as galaxy cluster detection via the SZ signal (e.g., Bonjean 2020; Lin et al. 2021), inpainting of the CMB signal (e.g., Puglisi & Bai 2020; Montefalcone et al. 2021), detection of the kinetic SZ (kSZ) effect (e.g., Tanimura et al. 2022a), galaxy cluster mass estimations in CMB frequency maps (e.g., Gupta & Reichardt 2020; de Andres et al. 2022), and even foreground cleaning or component separation (e.g., Caldeira et al. 2019; Grumitt et al. 2020; Petroff et al. 2020; Lin et al. 2021; Hurier et al. 2021; Li et al. 2022; Wang et al. 2022); also, see Dvorkin et al. (2022) for a review. In some cases of machine learning applications, the networks can perform very well (even better than standard methods or than a human) with the condition that very robust, balanced, and well-labelled data is available. Without any known labels – as in our case, where the exact different component maps (SZ, CIB, CMB) are not familiar to us –, self-supervised learning can be used instead. In this kind of machine learning approach, the output Y is reconstructed from the input X without any need for human labelling. Component separation in CMB data is very similar to, for example, transparency separation, dehazing, or mixture images, to which the above-mentioned self-supervised deep learning networks have recently been successfully applied (e.g., Gandelsman et al. 2018).

In this paper, we perform component separation of all components of the extragalactic sky simultaneously and in an unsupervised way (specifically, in a self-supervised way). The network, the design of which is inspired by techniques used in transparency separation applied on images (Gandelsman et al. 2018), does not rely on known, labelled data for training and could be trained either on numerical simulations to check the performance or directly on real data. Here we apply our algorithm to high-resolution numerical simulations of the extragalactic submillimetre sky from WebSky (Stein et al. 2020). Maps are input and reconstructed in HEALPIX format (Górski et al. 2005), with nside = 4096. Contrary to the methods developed to work in the HEALPIX 1D vector (Perraudin et al. 2019; Krachmalnicoff & Tomasi 2019), we perform the training on small projected patches in two dimensions. We are able to efficiently and simultaneously recover all the input signals (CMB, CIB, and SZ), without any strong contamination from the other components. In this proof-of-concept paper, we demonstrate the potential of this method by applying it to an ideal case of numerical simulation and by comparing the results – when possible – with a state-of-the-art traditional method, MILCA (used to construct the Planck y maps; Hurier et al. 2013; Planck Collaboration XXI 2016; Tanimura et al. 2022b, described in Sect. 2.4).

Our paper is organised as follows: in Sect. 2, we present the component maps from the WebSky simulations that we used and describe how we constructed mock maps of the total submillimetre emission at different frequencies, together with MILCA. In Sect. 3, we present the method, the network architecture, and the training procedure in detail. We present our results in Sect. 4, performing different kinds of comparison between the reconstructed component and the original ones, first visually, and then in more quantitative ways, analysing full-sky power spectra, cross-spectra, and SZ fluxes from clusters. In Sect. 5, we discuss our results and present our conclusions and perspectives for future studies.

2. Data

In this section, we describe the data used in the present study, that is, the WebSky extragalactic simulation maps from Stein et al. (2020) and the derived frequency emission maps.

2.1. WebSky extragalactic component maps

The WebSky extragalactic simulation full-sky maps are a modelisation of the extragalactic components of the submillimetre sky in HEALPIX format, with nside = 4096. They include maps of the infrared emission (CIB) from dusty star-forming galaxies from z = 0 to z = 4.6, a map of the thermal SZ emission from groups and clusters of galaxies, a map of the kinetic SZ effect (kSZ) produced by the Doppler boosting by Thomson scattering of the CMB by bulk flows, and a map of weak gravitational lensing of primary CMB anisotropies by the large-scale distribution of matter in the Universe. The maps are constructed based on a light-cone projection on the full sky of a simulation of halos computed with ellipsoidal collapse dynamics and Lagrangian perturbation theory in the redshift range 0 < z < 4.6 (with a volume of ∼600 (Gpc h−1)3 resolved with ∼1012 resolution elements). The distribution of halos is then converted into intensity maps of the different components using models based on existing observations and on hydrodynamical simulations (see Stein et al. 2020 for details). The WebSky maps and halo catalogues are publicly available1. The WebSky collaboration also provides the conversion factors to apply to the CIB maps and to the SZ map in order to reconstruct the full modelisation of the three components (SZ, CIB, and CMB) on the sky per frequency in units of μKCMB. These latter authors modelled the components in 12 frequencies in total from SO and Planck High Frequency Instrument (HFI), that is, at 27, 39, 93, 100, 143, 145, 217, 225, 280, 353, 545, and 857 GHz. In our study, we discard the frequencies where the radio emission or the dust emission from extragalactic objects are dominant, and so we focus on nine frequencies between 93 GHz and 545 GHz (see e.g., Fig. 4 in Planck Collaboration I 2020). We use the maps of the different components (here SZ, CMB, and CIB) to model the extragalactic submillimetre sky at each frequency in Sect. 2.2, and we use the catalogue of halos to construct a pixel weight map w in Sect. 2.3.

2.2. Mock submillimetre sky maps

In this study, we focus on extragalactic signals. Therefore, all emissions from our galaxy (i.e., CO, galactic dust, and synchrotron) are not taken into account to model the total emission maps per frequency. We do not take into account either the noise or the effects of beams of the instruments. These effects will be addressed in a future paper. We thus use the components of the WebSky extragalactic simulation maps, namely CMB, SZ, and CIB, at 93, 100, 143, 145, 217, 225, 280, 353, and 545 GHz. The observed maps Ci at frequency i can then be expressed in μKCMB as

C i = 1 × CMB + f i × SZ + CIB i , $$ \begin{aligned} {C}_i = 1\times \mathrm{CMB} + f_i \times \mathrm{SZ} + \mathrm{CIB}_i, \end{aligned} $$(1)

where fi are the frequency-dependent weights of the SZ effect and CIBi is the CIB in the ith frequency. As mentioned in Sect.1, all the maps are constructed in HEALPIX format with nside = 4096.

2.3. Weight map from bright clusters

We focus in particular on the SZ effect and on its correlation with the CIB. As the SZ effect is mainly produced from galaxy clusters, the coverage on the sky is very small; that is, only a very small percentage of the pixels of the HEALPIX maps actually contain a significant SZ signal. As the error on the reconstruction in the case of a UNet approach is based on the mean of all the pixels, we rebalance the statistics of the pixels by constructing a map of weights, w, in order to emphasise the regions associated with galaxy clusters. A catalogue of the coordinates on the sky of the halos from the numerical simulations of WebSky was also delivered by Stein et al. (2020), together with some physical properties, such as the redshift z and the mass M200. We use this catalogue to compute the SZ flux for all clusters in the WebSky SZ map and select only the ones with an SZ flux detected with more than 5σ from a distribution of fluxes computed at random positions on the sky. We select only the brightest ones in order to apply a strategy that could also be applied in real data (in which we would have only the brightest SZ clusters with which to apply weights). We construct the weight map w in HEALPIX, with 1 at the position of the approximately 13 000 selected clusters, and put 0 otherwise. We then convolved the map with an FWHM of 5 arcmin (chosen arbitrarily; we further checked that changing this value does not affect the results), and squared the weight-map to further emphasise the central pixels of clusters. We divided by the sum of the pixels so that the average of the map on the pixels is equal to 1, as in the case of a uniform weight map. By weighting the pixels is this way, the very central regions of the clusters account for about 50%, and the remaining 50% are associated with the external regions. We later show that this weighting procedure simply helps the network to converge faster but is not dependent on the catalogue of clusters for which we weight the pixels. As all the clusters in the real sky are not known, this is a very important statement, and subsequently allows us to apply this self-supervised method to real data.

2.4. MILCA maps

We use MILCA-based reconstructed maps of SZ and CMB applied in the WebSky submillimetre maps as a reference comparison in our study. MILCA (Hurier et al. 2013; Tanimura et al. 2022b) is based on the internal linear combination (ILC) approach, which preserves an astrophysical component given the known spectrum by minimising the variance in the reconstructed signal. In MILCA, extra degrees of freedom are used to null-out other components (such as CMB for SZ) and minimize noises using noise maps estimated from split maps such as half-mission maps. This approach was used to extract the SZ signal using Planck data (Planck Collaboration XXI 2016; Tanimura et al. 2022b) and Planck+ACT data (Aghanim et al. 2019). However, the correlation between SZ and CIB is known to induce a certain level of contamination in the resulting y-map (Planck Collaboration XIV 2016), especially at small scales, and causes a large uncertainty in astrophysical (Vikram et al. 2017) and cosmological analyses (Hill & Spergel 2014; Planck Collaboration XXI 2016; Tanimura et al. 2022b).

3. Method

In this section, we explain our model of the submillimetre extragalactic sky, the architecture of the network used, and the construction of the training set we use.

3.1. Model

The aim of the study is to separate the CMB, the SZ, and the CIB emissions as efficiently as possible using both frequency and spatial morphologies. Unlike the CMB or the SZ emissions, the weights of the CIB spectrum are different at each line of sight, meaning that there should be as many CIB maps as frequencies used. To perfectly recover all the components, one should then recover (i) the CMB, (ii) the SZ y map, and (iii) the CIB at all the frequencies used, which gives 2 + n components (where n is the number of frequency used, here n = 9); meaning a total of 11 in our case. However, it is impossible to recover more components than the number of maps in inputs because of the important degeneracies between solutions. 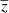Hence, we assume that the CIB in the different frequencies, CIBi, can be approximated by one CIB map fixed at one frequency CIB ¯ $ \overline{\mathrm{CIB}} $ (here the maximum frequency f = 545 GHz) weighted by the values ψi(z), which represent a modified black body per pixel at a mean redshift z ¯ $ \overline{z} $. 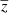This enables the frequency dependency of the weights, and both the maps CIB ¯ $ \overline{\mathrm{CIB}} $ and z ¯ $ \overline{z} $ to be learned at the same time during the training. The model can be written as

CIB i = ψ i ( z ¯ ) × CIB ¯ , $$ \begin{aligned} \mathrm{CIB}_i = \psi _i\left(\overline{z}\right) \times \overline{\mathrm{CIB}}, \end{aligned} $$(2)

with

ψ i ( z ¯ ) = ( i 545 ) β + 3 × exp ( h × 545 × 10 9 ( 1 + z ¯ ) k B T 0 ( 1 + z ¯ ) α ) − 1 exp ( h × i × 10 9 ( 1 + z ¯ ) k B T 0 ( 1 + z ¯ ) α ) − 1 , $$ \begin{aligned} \psi _i\left(\overline{z}\right) = \left(\frac{i}{545}\right)^{\beta + 3} \times \frac{\mathrm{exp}\left(\frac{h\times 545\times 10^9 (1+\overline{z})}{k_{\rm B}{T}_0 (1+\overline{z})^\alpha }\right)-1}{\mathrm{exp}\left(\frac{h\times i\times 10^9 (1+\overline{z})}{k_{\rm B}{T}_0 (1+\overline{z})^\alpha }\right)-1}, \end{aligned} $$(3)

where β is the slope of the power law of the modified black body, T0 is the effective dust temperature, α is the parameter for the redshift dependency of the dust temperature, h is the Planck constant, and kB is the Boltzmann constant. In this study, we fixed β = 1.6, T0 = 20.7 K, and α = 0.2 following Stein et al. (2020). While it is a rough approximation to consider the CIB as a modified black body with a fixed β per pixel (i.e., per line of sight), it is still a reasonable approximation for this work. In a forthcoming analysis, we will consider more realistic models of the spectrum of the CIB using for example the Taylor expansion of the modified black body proposed in Chluba et al. (2017).

Merging Eqs. (1) and (2), the maps Ci can then be modelled by

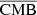C i ¯ = 1 × CMB ¯ + f i × SZ ¯ + ψ i ( z ¯ ) CIB ¯ , $$ \begin{aligned} \overline{{C}_i} = 1\times \overline{\mathrm{CMB}} + f_i \times \overline{\mathrm{SZ}} + \psi _i\left(\overline{z}\right) \overline{\mathrm{CIB}}, \end{aligned} $$(4)

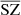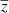where CMB ¯ $ \overline{\mathrm{CMB}} $ is the extracted CMB component, SZ ¯ $ \overline{\mathrm{SZ}} $ is the reconstructed SZ component, CIB ¯ $ \overline{\mathrm{CIB}} $ is the extracted CIB component at 545 GHz, and z ¯ $ \overline{z} $ is the spatially dependent map of the mean redshift of the modified black body of the CIB per pixel. 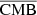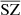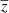Here, we simultaneously fit the four components CMB ¯ $ \overline{\mathrm{CMB}} $, SZ ¯ $ \overline{\mathrm{SZ}} $, CIB ¯ $ \overline{\mathrm{CIB}} $, and z ¯ $ \overline{z} $, still allowing nine different CIBs.

3.2. Network architecture

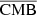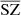In this study, we use a combination of specific architectures of deep convolutional neural networks (CNNs), the so-called ResUNets – which have been shown to be very efficient in image regression (Zhang et al. 2018) –, to reconstruct the three components CMB ¯ $ \overline{\mathrm{CMB}} $, SZ ¯ $ \overline{\mathrm{SZ}} $, and CIB ¯ $ \overline{\mathrm{CIB}} $ directly from the input maps Ci. Our approach is based on transparency separation for dehazing of images developed in Gandelsman et al. (2018). Indeed, in this domain, they have a very similar goal; they are all designed to reconstruct a blurred image by decomposing it into a dehazed image and an image of the haze. Another application is the recovery of two images that are superposed on each other, or the removal of water droplet marks on the camera lens and seen in pictures. This technique is quite simple: the goal is to output two images from one, reconstructed by two different networks in parallel (allowing the non-correlation between the two images as each network is independent from the other), and by adding a term in the loss function that minimises the cross-correlation between the two reconstructed images. This technique has shown surprisingly good results, especially in the domain of dehazing images (Gandelsman et al. 2018; Feng et al. 2021; Ge et al. 2021; Miao et al. 2022). This is somewhat similar to separation techniques for emission in submillimetre. 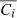We apply our knowledge of the physics concerning the frequency dependency of the components to the outputs of the ResUNets in parallel (that are images) in order to construct a final combined output C i ¯ $ \overline{C_i} $ (given by Eq. (4)) that has to match the input maps. We apply a loss function ℒrec between the final outputs 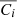C i ¯ $ \overline{C_i} $ and the inputs Ci, and the component is extracted by the outputs of each ResUNet. We can put different priors by modifying the activation function on the different outputs of each network. Doing this helps the networks to converge faster to the accurate solution and helps avoid degeneracies. For 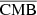CMB ¯ $ \overline{\mathrm{CMB}} $, we choose an activation function that is a Sigmoid between −1000 and +1000 μKCMB. For CIB ¯ $ \overline{\mathrm{CIB}} $, we choose a Softmax function that outputs only positive numbers (CIB being a positive luminosity). For the redshift of CIB 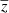z ¯ $ \overline{z} $, we choose a Sigmoid function between 0 and 5. For 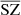SZ ¯ $ \overline{\mathrm{SZ}} $, we choose a Softmax function removing −20 × 106 so that y > −20 × 106. Although we know the y Compton parameter cannot be negative, forcing it to be positive only leads to a non-Gaussian error on the reconstruction map. This effect produces a bias in all the mean values of the different components in an attempt to reproduce Gaussian noise in the total reconstruction of the frequency maps (characteristics of the MSE loss function). A diagram of our architecture is shown in Fig. 1.

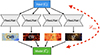thumbnail Fig. 1.

Diagram of our architecture. Four ResUNets are used to construct CMB ¯ $ \overline{\mathrm{CMB}} $, SZ ¯ $ \overline{\mathrm{SZ}} $, CIB ¯ $ \overline{\mathrm{CIB}} $, and z ¯ $ \overline{z} $ directly from the input Ci, and a reconstruction loss ℒrec is applied between the inputs Ci and the models C i ¯ $ \overline{C_i} $ obtained with Eq. (4).

We define the reconstruction loss ℒrec as the sum of the weighted mean squared errors (wMSE) in the different frequencies i divided by the standard deviation of the maps σi, namely

L rec = 1 n f ∑ i = 0 n f wMSE ( C i , C i ¯ ) σ i , $$ \begin{aligned} \mathcal{L} _{\rm rec} = \frac{1}{n_{\rm f}}\sum _{i = 0}^{n_{\rm f}} \frac{\mathrm{wMSE}\left({C}_i, \overline{\mathrm{C}_i}\right)}{\sigma _i}, \end{aligned} $$(5)

where nf is the number of frequencies (here, nf = 9), 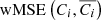wMSE ( C i , C i ¯ ) $ \mathrm{wMSE}\left({C}_i, \overline{{C}_i}\right) $ is the MSE in the ith frequency weighted by the weight map w, and σi is the standard deviation of the map Ci.

3.3. Training set

Our network architecture is applied to sets of 2D patches projected on the sky. We extracted n = 100 000 multi-channel 2D patches from the Ci maps, with the nine frequencies from 93 to 545 GHz. The images are 64 × 64 pixels with a resolution of θpix ∼ 0.8 arcmin (giving a field of view of ∼0.8° × ∼ 0.8°).

The dimensions of the input data are thus 100 000 × 64 × 64 × 9 pixels. As in Bonjean (2020), we train our network on 90% of the sky and leave 10% of the sky completely unseen by the network (as commonly done in machine learning applications). We also tried a ratio of 80%–20% and checked that this choice was not affecting the results. In this first application, the 10% unseen fraction of the sky is randomly selected on the sphere. One could however use a clean area of the sky (away from galaxy contamination) for a study including dust and radio emission. In this configuration, we can compute global properties of the different extracted components at each epoch of the training, such as the means and the variances, and compare them to the expected values. When those values converge into a good solution and reach a plateau together with the loss value on this very same 10% unseen area, we consider that the network has reached convergence and stop it. With the trained models, we subsequently reconstruct the full-sky HEALPIX maps entirely by estimating projected patches on the full sky and averaging the pixels, at nside = 4096, for the different components.

4. Results

In this section, we present the results and compare the reconstructed HEALPIX maps of the different extracted components to the original one from WebSky in several ways.

First, we visually inspect the maps by showing projections of the components centred on the brightest SZ cluster to quickly check the contrasts and the non-Gaussian aspects of the pixel distributions of the different fields. We then present further quantitative statistical comparisons and show the power spectra and the PDF of the pixels of the full-sky maps for all the components. We also compare the cross power spectra with the original components. For the case of the SZ effect, we also compare with the outputs of a traditional but state-of-the-art method, MILCA (Hurier et al. 2013; Planck Collaboration XXI 2016; Tanimura et al. 2022b). We compute the cross spectra between all the different components to study the contamination of the maps coming from the leakage from other components. Finally, we put particular emphasis on the regions around galaxy clusters, and perform an SZ flux comparison between those extracted from the reconstructed components and those from the WebSky maps.

4.1. Frequency settings

First, we explore the impact of the choice of the frequency setting on the results and for this we define two combinations of frequencies: one with seven frequencies, from 93 to 280 GHz, and another combination adding the 353 and 545 GHz frequency maps in which the CIB is dominant. We compared the global properties of the components in the unseen area for each of the epochs and for the different combinations. The means and variances of the reconstructed components for the two frequency combinations are shown in Fig. 2. We directly see that the configuration with seven frequencies is not evolving into an expected solution (shown by the dashed lines), but rather shows biases in the mean values of all components and a lack of variance for the CIB. In the other configuration, the mean and variances are well recovered, except for the variance of SZ, which is expected as SZ is a very weak signal and hence some reconstruction noise is expected, adding extra variance. This is due to the spectral dependencies of the SZ and the CIB in the range 100–250 GHz, which are too similar, making it difficult to break the degeneracy between the two components. Instead of learning a lower redshift 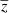z ¯ $ \overline{z} $ of the CIB at the position of the clusters as we expect (as CIB at the positions of clusters is dominated by the galaxies from the galaxy clusters itself), it does the opposite and tends to learn a higher redshift. This produces a lower bias in the SZ flux to balance the total emission and the model hence converges to an inaccurate solution. For these reasons, considering our model, we must take into account the higher frequency maps at 353 and 545 where the CIB is dominant and where the spectral dependencies of the two components SZ and CIB start to differ one from another. In the following, our results are thus obtained in the configuration with nine frequencies, including the 353 and 545 GHz maps. We also note that in Fig. 2, the values of the means and variances of the CIB are not the same for seven and nine frequencies, as we are computing the CIB at 280 GHz for the first case and the CIB at 545 GHz for the second case.

thumbnail Fig. 2.

Evolution of the different statistical quantities of the extracted components in the unseen area of the sky. Top: evolution of the means of the components on the left for the seven-frequency configuration and on the right for the nine-frequency configuration. Bottom: evolution of the variances of the components on the left for the seven-frequency configuration and on the right for the nine-frequency configuration. Dashed lines represent the expected values. The values for the CIB are not the same for the seven and the nine frequencies models, as we are computing the CIB at 280 GHz for the first case and the CIB at 545 GHz for the second case. Units are different for each map: SZ ¯ $ \overline{\mathrm{SZ}} $ and z ¯ $ \overline{z} $ are without units (y and redshift), CMB ¯ $ \overline{\mathrm{CMB}} $ is in μK, and CIB ¯ $ \overline{\mathrm{CIB}} $ is in MJy sr−1.

4.2. Visual inspection

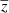We trained our network with nine frequencies and reconstructed the HEALPIX maps of the four extracted components: CMB ¯ $ \overline{\mathrm{CMB}} $, SZ ¯ $ \overline{\mathrm{SZ}} $, CIB ¯ $ \overline{\mathrm{CIB}} $, and z ¯ $ \overline{z} $. The training lasted six days on a Tesla V100 GPU. A first comparison can be made visually to qualitatively check the ranges of pixel values, contrasts, and the non-Gaussian distribution of the pixels of the fields. We present an example in Fig. 3, where we show the projection of the different maps on a 5° ×5° patch centred around the position of the brightest SZ cluster. 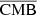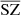The left column shows the WebSky maps of CMB, SZ, and CIB; the middle column shows the reconstructed maps CMB ¯ $ \overline{\mathrm{CMB}} $, SZ ¯ $ \overline{\mathrm{SZ}} $, and CIB ¯ $ \overline{\mathrm{CIB}} $, and the right column shows the residuals between the true and reconstructed components. The reconstructed components appear, visually, to be in good agreement with the WebSky original components, with clusters well recovered, and without any significant features seen in the residual images.

thumbnail Fig. 3.

Projection in a 5° ×5° patch of the HEALPIX maps of the different components around the brightest SZ cluster. Left column: from top to bottom, the SZ, CMB, and CIB from WebSky simulation maps. Middle column: from top to bottom, the reconstructed SZ ¯ $ \overline{\mathrm{SZ}} $, CMB ¯ $ \overline{\mathrm{CMB}} $, and CIB ¯ $ \overline{\mathrm{CIB}} $. Right column: residuals between the WebSky component and the reconstructed ones. Very good agreement is seen visually between the reconstructed maps and the expected map, without structures in the residuals.

4.3. PDF comparison

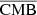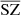We pursue our comparison by checking the PDF of the pixels for the different components. In Fig.4, we show the distribution of the pixels for the CMB ¯ $ \overline{\mathrm{CMB}} $, SZ ¯ $ \overline{\mathrm{SZ}} $, and CIB ¯ $ \overline{\mathrm{CIB}} $, where we compare to the original distributions from WebSky maps. For the case of SZ, we also compare to the distribution of pixels from the SZ maps reconstructed with MILCA. We see a very good match between the distributions of pixels for CMB and CIB, while the distribution is more flattened for the recovered SZ maps from our method and from MILCA. This indicates a noisy reconstruction of the SZ signal, which is expected considering the very low amplitude of the SZ effect compared to CMB or CIB, which are the dominant signals in some frequencies. However, the variance of the reconstructed SZ map with our method seems larger than that of the map obtained with MILCA, which is also expected as our model contains a greater number of free parameters than MILCA (simultaneously constraining CMB, SZ, z, and CIB). This is discussed in more detail when comparing cross-spectra and contamination from other components below.

thumbnail Fig. 4.

PDF comparison between the reconstructed components and the WebSky ones. Left: case for the CMB. Middle: case for the SZ. Right: case for the CIB.

4.4. Power-spectra comparison

We computed the auto power spectra for all the recovered components and compared them to the power spectra of the original WebSky components. For each component, we also compare the cross power spectra between the recovered components and the original ones to check whether or not the signal is fully recovered when removing the reconstructed noise of the estimated components. In Fig. 5, we show the resulting power spectra for the CMB in the left panel, SZ in the middle one, and CIB on the right. We also show the 𝒞ℓ residuals as a percentage at the bottom of each plot. For the case of CMB, we recover the signal very well, with reconstructed noise dominating from ℓ > 1000. Removing the reconstructed noise in the cross spectrum with the WebSky CMB leads to very good recovery of the CMB signal, with below 1% error up to ℓ = 2500. For the CIB, we see very good agreement between the two power spectra, with less than 3% error and a bias of below 2% up to ℓ = 2500. The cross spectrum between CIB ¯ $ \overline{\mathrm{CIB}} $ and CIB also shows a good recovery of the signal. 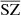For the SZ reconstructed maps, the power spectra are above the expected signal for both MILCA and our method SZ ¯ $ \overline{\mathrm{SZ}} $, especially at small scales. This indicates the presence of additional signal – for example, noise –, which is in good agreement with the effect seen in the distributions of the PDF in Sect. 4.3 (greater noise for 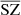SZ ¯ $ \overline{\mathrm{SZ}} $ than for MILCA). By performing the cross spectra with the SZ WebSky map, interesting observations can be made. At all ℓ, we see a lack of signal in the cross spectrum between MILCA and the true SZ emission from WebSky (MILCAxSZ), leading to a bias of between 10% and 25% within 10 < ℓ < 2500, which is not seen in the cross-spectrum 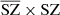SZ ¯ × SZ $ \overline{\mathrm{SZ}} \times \mathrm{SZ} $. This effect is due to the contamination of the CIB in the MILCA SZ map, itself attributable to the correlation between SZ and CIB. The residuals of the cross-spectrum 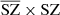SZ ¯ × SZ $ \overline{\mathrm{SZ}}\times \mathrm{SZ} $ indicate a good recovery of the signal within an error of 5% up to ℓ = 2500 and with a bias of below 3% at all ℓ. We confirm this result in the following section, where we demonstrate how we compute the cross-spectra between all the components to study the contamination.

thumbnail Fig. 5.

Power spectra of the components, the recovered components, and the cross power spectra between the two. 𝒞ℓ residuals as a percentage are also shown in the bottom of each plot, where residuals are defined as x − x ¯ x × 100 $ \frac{x-\overline{x}}{x}\times100 $ for the quantity x. Left: case for the CMB. Middle: case for the SZ. MILCA is also shown in this plot. Right: case for the CIB.

4.5. Cross-spectra between components

We computed the cross-power spectra between all the components CMB × SZ, CMB × CIB, and CIB × SZ. In each case, we cross correlated all combinations between the original WebSky components and the reconstructed ones, either from MILCA or with our method for the cases where SZ is involved. Figure 6 shows the results for all the different components. We detail the different cases hereafter.

thumbnail Fig. 6.

Cross power spectra between the different components. Left: case for CMBxCIB. Middle: case for CIBxSZ. MILCA is also considered in this plot. Right: case for CMBxSZ.

4.5.1. CMB × CIB

For the CMB × CIB case (left panel of Fig. 6), where there is no correlation expected (blue line), we did not find any correlation between the different combinations, except for 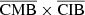CMB ¯ × CIB ¯ $ \overline{\mathrm{CMB}} \times \overline{\mathrm{CIB}} $. This means that the reconstructed CMB is not contaminated by the CIB, and that the reconstructed CIB is not contaminated by the CMB. On the other hand, the correlation between 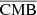CMB ¯ $ \overline{\mathrm{CMB}} $ and CIB ¯ $ \overline{\mathrm{CIB}} $ is expected (but not necessarily problematic), as this correlation is coming from the correlated reconstructed noise between the two components, which is not expected to be independent, as the two components are reconstructed at the same time.

4.5.2. CIB × SZ

For the CIB × SZ case (middle panel of Fig. 6), there is an expected correlation between the two components (shown in blue) (Planck Collaboration XIV 2016; Stein et al. 2020). This correlation comes from the fact that the dominant part of the CIB in clusters, which is where the SZ signal is dominant, is generated from the dust emission of galaxies in these very same clusters. This correlation is a bias in the SZ reconstruction (e.g., Planck Collaboration XIV 2016) that we recover in 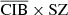CIB ¯ × SZ $ \overline{\mathrm{CIB}} \times \mathrm{SZ} $ (in red), indicating that the reconstructed CIB is not contaminated by the SZ. However, CIB × MILCA (in green) is below the correlation line, indicating that the MILCA SZ map is perturbed by the CIB and might lack flux. This translates into a lack of SZ power at small scales, which is also seen in the SZ auto power spectra in Sect. 4.4. However, the cross-spectrum 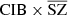CIB × SZ ¯ $ \mathrm{CIB}\times\overline{\mathrm{SZ}} $ (in orange) is closer to the expected correlation in blue, indicating a weaker contamination from the CIB in the 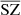SZ ¯ $ \overline{\mathrm{SZ}} $ reconstructed map. In conclusion, the reconstructed 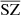SZ ¯ $ \overline{\mathrm{SZ}} $ map is noisier than that produced with MILCA (with noise coming from the reconstruction method and larger than that produced by MILCA, as our model contains a greater number of free parameters, as it simultaneously constrains CIB, SZ, z, and CIB; this would also be the case for MILCA (noise would increase if we increase the number of constraints), albeit less contaminated by the CIB. Having a noisier SZ map might be a disadvantage if we use auto power spectra or maps, but this is not an issue if we want to cross-correlate the maps with other tracers (e.g., galaxy densities or weak lensing maps) and we should prioritise maps that are less biased by CIB. For example, the extra SZ power coming from CIB contamination is a potential source of bias for the study of the cosmological parameters from the SZ angular power spectrum (Komatsu & Seljak 2002; Horowitz & Seljak 2017; Douspis et al. 2022; Tanimura et al. 2022b), and is reduced in our method compared to MILCA, at the cost of slightly poorer precision.

4.5.3. CMB × SZ

For the CMB × SZ case (right panel of Fig. 6), no correlation is expected (blue line). We do not find any correlation, either with the recovered components – indicating that there is no contamination from CMB in the reconstructed SZ map – or with the SZ in the reconstructed CMB map. This is also the case for the SZ map derived by MILCA; we do not see any correlation with CMB, as expected.

4.6. SZ fluxes from clusters

After studying the statistics and contamination of the recovered component maps, we focus on the SZ fluxes from galaxy clusters. For each of the SZ maps, that is, WebSky, MILCA, and 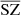SZ ¯ $ \overline{\mathrm{SZ}} $, we computed the SZ fluxes around a selection of the most massive low-redshift clusters (M200 > 4 × 1014 M⊙ and z < 1) in the exact same way – using aperture photometry – from the numerical simulation (SZ fluxes for lower masses or higher redshift clusters become too low and noisy). We compare the SZ fluxes in Fig. 7, showing those from MILCA in green and those from 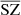SZ ¯ $ \overline{\mathrm{SZ}} $ in orange and red. The fluxes displayed in orange are obtained in the training region of the sky while the fluxes displayed in red are obtained in the unseen area of the sky. The very good consistency between all the fluxes indicates a very good recovery of the SZ fluxes for this selection of clusters with all methods, meaning that the network can recover the SZ fluxes well, even in the unseen area, and with an error of the same order of magnitude as that for the fluxes obtained with the traditional state-of-the-art method MILCA. The dashed blue line in the figure indicates the SZ flux beyond which the clusters have been enhanced in the weight map w used to rebalance the weight of the pixels inside clusters. We see a good correlation even before the vertical line, meaning that even clusters that have not been enhanced are very well recovered. This indicates that the weight map w is helping the network to learn the SZ spectral and spatial features faster but does not bias the results to the typical objects for which w are input (otherwise, we would see a good agreement only beyond the vertical flux limit and no correlation before). In the right panel of Fig. 7, we compare the residuals of the SZ fluxes for MILCA and 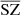SZ ¯ $ \overline{\mathrm{SZ}} $. We see that the fluxes computed in 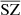SZ ¯ $ \overline{\mathrm{SZ}} $ have an error on the same order of magnitude as that for the fluxes computed with MILCA, with a standard deviation of percentage residuals of σ = 40.44% and σ = 42.9%, respectively. However, we obtain biased fluxes, which is due to the contamination of CIB. The biases are quite important in MILCA, with 4.97% bias, while the biases are reduced significantly in the case of 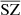SZ ¯ $ \overline{\mathrm{SZ}} $, with a bias of 1.39%. These biases obtained with MILCA should be investigated in a more detailed study and confirmed with other standard methods, as they might be an important source of contamination in cosmological analyses using SZ fluxes or SZ spectra.

thumbnail Fig. 7.

Comparison of the SZ fluxes computed with aperture photometry in the exact same way in the SZ WebSky map, in the SZ ¯ $ \overline{\mathrm{SZ}} $ map, and in the MILCA SZ map. Left: fluxes on the reconstructed maps as a function of the SZ WebSky fluxes. The blue dashed line represents the SZ flux have been enhanced in the weight map w. Right: histograms of the residuals. The dashed lines show the median values of the distributions.

5. Discussion and summary

We explored a new way of performing component separation using machine learning networks in a self-supervised way. Focusing on the extragalactic submillimetre sky, this method allows us to extract CMB, CIB, and SZ effect maps, and can already be applied to the clean part of the sky (free from foreground emissions), for example to some of the cleanest regions (at very high Galactic latitudes) of the Planck frequency maps. Being self-supervised, this method has the potential to be applied directly to data without the need for known labels (the model that is trained here on numerical simulations will not be the one applied to real data). In this paper, we show how we applied our new method to numerical simulations from WebSky and achieved good results when focusing on the power spectra and cross spectra of the different reconstructed components, as well as interesting results regarding the contamination from other components. Our method still has some limitations, which will be investigated in future studies. For example, we did not include a model of the foreground galactic emissions; that is, dust, radio, and CO sources. These emissions could be accounted for by adding other ResUNets in parallel, allowing the reconstruction of these very same components all at once. We also did not include models of either noise or the effect of the instrumental beams, as the aim of this study is to investigate the theoretical response of these networks in an ideal case and to compare this with the results of a traditional but state-of-the-art method (here, MILCA). Focusing on the individual results for each component: for the CMB case, we obtain a very good reconstruction of the signal, albeit slightly noisy. When we cross-match with the CMB from WebSky, we obtain a very good reconstruction of the signal up to ℓ = 2500 at least. We obtain a very good reconstructed CIB, within a 3% error and a bias of below 2% up to ℓ = 2500. For the SZ, we also very nicely recover the signal, with both an advantage and a disadvantage compared to the result obtained with MILCA. Two things can be said about SZ: first, the signal retrieved using our new method is less contaminated by the CIB than that obtain with MILCA. This aspect has very important consequences for the ability to perform cosmology using the SZ signal or to compute cluster masses, and is particularly emphasised in this study. Second, this lower contamination comes with the price of a higher variance, coming from the reconstruction noise that is higher than that obtained with MILCA. Indeed, our method simultaneously constrains CMB, CIB, z, and SZ, and therefore entails a greater number of free parameters than MILCA, which constrains only SZ and removes the CMB. This produces a larger variance in the reconstructed maps at the end. Neither of the reconstructed components, CMB or CIB, is contaminated by other components, as seen in the cross power spectra, and the contamination from CIB in the SZ reconstructed maps is lower than in MILCA, as seen in Fig. 6. To completely remove the contamination of the CIB, our spectral CIB model could be improved to take into account the fact that the emission of the CIB is not a power law but rather the sum of a power law, which could be modelled in greater detail (e.g., in Taylor expansion, Chluba et al. 2017; Vacher et al. 2023, 2022), but the modelling and reconstruction of the CIB represent a significant challenge, especially for the dust–CIB separation for the detection of the B-modes (e.g., Remazeilles et al. 2011; Remazeilles 2018; Allys et al. 2019; Aylor et al. 2021; Regaldo-Saint Blancard et al. 2021). For example, Allys et al. (2019, 2020) developed an algorithm of wavelet scattering transform (WST, Allys et al. 2019; Regaldo-Saint Blancard et al. 2020) similar to convolutional neural networks. The main difference is that the filters of the layers of convolution are fixed instead of learned, and the statistics of the CIB within this transform can later be input as a prior for the extraction of the CIB in component separation.

Compared to other methods using a deep learning network to extract components from CMB data (e.g., Caldeira et al. 2019; Grumitt et al. 2020; Li et al. 2022; Wang et al. 2022; Petroff et al. 2020; Lin et al. 2021), in our approach we estimate all components simultaneously. This allows a less biased reconstruction, taking into account the dependencies and the correlations with the other components during the training.

The lower effect of the CIB contamination in the power spectra, especially in the reconstruction of the SZ effect, could decrease a potential bias in the computation of the cosmological parameters using the SZ power spectra (Salvati et al. 2018; Douspis et al. 2022; Gorce et al. 2022; Tanimura et al. 2022b). Going a step further, and modelling the polarisation, this method could be used in the future for the detection of the B-mode by combining the data of Planck, ACT2, SPT, SO (Ade et al. 2019), and CMB-S4 (Abazajian et al. 2019).

Acknowledgments

The authors thank the anonymous referee for her/his useful comments that helped increasing the quality of the publication. The authors thank useful discussions with Marc Huertas-Company, and with all the members of the ByoPiC project. We also thank Stephane Caminade and IDOC for using the IDOC computing facilities. Part of this research has been supported by the funding for the ByoPiC project from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement ERC-2015-AdG 695561. T.B. acknowledges funding from the French government under management of Agence Nationale de la Recherche as part of the “Investissements d’avenir” program, reference ANR-19-P3IA-0001 (PRAIRIE 3IA Institute). The sky simulations used in this paper were developed by the WebSky Extragalactic CMB Mocks team, with the continuous support of the Canadian Institute for Theoretical Astrophysics (CITA), the Canadian Institute for Advanced Research (CIFAR), and the Natural Sciences and Engineering Council of Canada (NSERC), and were generated on the Niagara supercomputer at the SciNet HPC Consortium (cite https://arxiv.org/abs/1907.13600). SciNet is funded by: the Canada Foundation for Innovation under the auspices of Compute Canada; the Government of Ontario; Ontario Research Fund – Research Excellence; and the University of Toronto.

References

  1. Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, arXiv e-prints [arXiv:1610.02743] [Google Scholar]
  2. Abazajian, K., Addison, G., Adshead, P., et al. 2019, arXiv e-prints [arXiv:1907.04473] [Google Scholar]
  3. Ade, P., Aguirre, J., Ahmed, Z., et al. 2019, J. Cosmol. Astropart. Phys., 2019, 056 [Google Scholar]
  4. Aghanim, N., Douspis, M., Hurier, G., et al. 2019, A&A, 632, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Aiola, S., Calabrese, E., Maurin, L., et al. 2020, J. Cosmol. Astropart. Phys., 2020, 047 [Google Scholar]
  6. Allys, E., Levrier, F., Zhang, S., et al. 2019, A&A, 629, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Allys, E., Marchand, T., Cardoso, J. F., et al. 2020, Phys. Rev. D, 102, 103506 [Google Scholar]
  8. Austermann, J. E., Aird, K. A., Beall, J. A., et al. 2012, in Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI, eds. W. S. Holland, & J. Zmuidzinas, SPIE Conf. Ser., 8452, 84521E [NASA ADS] [CrossRef] [Google Scholar]
  9. Aylor, K., Hou, Z., Knox, L., et al. 2017, ApJ, 850, 101 [NASA ADS] [CrossRef] [Google Scholar]
  10. Aylor, K., Haq, M., Knox, L., Hezaveh, Y., & Perreault-Levasseur, L. 2021, MNRAS, 500, 3889 [Google Scholar]
  11. Bennett, C. L., Halpern, M., Hinshaw, G., et al. 2003, ApJS, 148, 1 [Google Scholar]
  12. Bleem, L. E., Crawford, T. M., Ansarinejad, B., et al. 2022, ApJS, 258, 36 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bobin, J., Starck, J.-L., Fadili, J., & Moudden, Y. 2007, IEEE Trans. Image Process., 16, 2662 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bobin, J., Moudden, Y., Starck, J. L., Fadili, J., & Aghanim, N. 2008, Stat. Methodol., 5, 307 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bobin, J., Starck, J. L., Sureau, F., & Basak, S. 2013, A&A, 550, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bonjean, V. 2020, A&A, 634, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Caldeira, J., Wu, W. L. K., Nord, B., et al. 2019, Astron. Comput., 28, 100307 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cardoso, J.-F., Le Jeune, M., Delabrouille, J., Betoule, M., & Patanchon, G. 2008, IEEE J. Selec. Topics Signal Process., 2, 735 [NASA ADS] [CrossRef] [Google Scholar]
  19. Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [CrossRef] [Google Scholar]
  20. Chluba, J., Hill, J. C., & Abitbol, M. H. 2017, MNRAS, 472, 1195 [NASA ADS] [CrossRef] [Google Scholar]
  21. de Andres, D., Cui, W., Ruppin, F., et al. 2022, Eur. Phys. J. Web Conf., 257, 00013 [CrossRef] [EDP Sciences] [Google Scholar]
  22. Delabrouille, J., Cardoso, J. F., & Patanchon, G. 2003, MNRAS, 346, 1089 [NASA ADS] [CrossRef] [Google Scholar]
  23. Delabrouille, J., Cardoso, J. F., Le Jeune, M., et al. 2009, A&A, 493, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Dole, H., Lagache, G., Puget, J. L., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Douspis, M., Salvati, L., Gorce, A., & Aghanim, N. 2022, A&A, 659, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Dvorkin, C., Mishra-Sharma, S., Nord, B., et al. 2022, arXiv e-prints [arXiv:2203.08056] [Google Scholar]
  27. Eriksen, H. K., Jewell, J. B., Dickinson, C., et al. 2008, ApJ, 676, 10 [Google Scholar]
  28. Feng, T., Wang, C., Chen, X., et al. 2021, Appl. Soft Comput., 102, 106884P [CrossRef] [Google Scholar]
  29. Fernández-Cobos, R., Vielva, P., Barreiro, R. B., & Martínez-González, E. 2012, MNRAS, 420, 2162 [Google Scholar]
  30. Fowler, J. W., Acquaviva, V., Ade, P. A. R., et al. 2010, ApJ, 722, 1148 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gandelsman, Y., Shocher, A., & Irani, M. 2018, arXiv e-prints [arXiv:1812.00467] [Google Scholar]
  32. Ge, W., Lin, Y., Wang, Z., Wang, G., & Tan, S. 2021, IEICE Trans. Inf. Syst., E104.D, 2218 [CrossRef] [Google Scholar]
  33. Gorce, A., Douspis, M., & Salvati, L. 2022, A&A, 662, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [Google Scholar]
  35. Grumitt, R. D. P., Jew, L. R. P., & Dickinson, C. 2020, MNRAS, 496, 4383 [NASA ADS] [CrossRef] [Google Scholar]
  36. Gupta, N., & Reichardt, C. L. 2020, ApJ, 900, 110 [NASA ADS] [CrossRef] [Google Scholar]
  37. Henderson, S. W., Allison, R., Austermann, J., et al. 2016, J. Low Temp. Phys., 184, 772 [NASA ADS] [CrossRef] [Google Scholar]
  38. Hill, J. C., & Spergel, D. N. 2014, J. Cosmol. Astropart. Phys., 2014, 030 [CrossRef] [Google Scholar]
  39. Horowitz, B., & Seljak, U. 2017, MNRAS, 469, 394 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hurier, G., Macías-Pérez, J. F., & Hildebrandt, S. 2013, A&A, 558, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Hurier, G., Aghanim, N., & Douspis, M. 2021, A&A, 653, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Komatsu, E., & Seljak, U. 2002, MNRAS, 336, 1256 [NASA ADS] [CrossRef] [Google Scholar]
  43. Krachmalnicoff, N., & Tomasi, M. 2019, A&A, 628, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Lange, A. E., Ade, P. A., Bock, J. J., et al. 2001, Phys. Rev. D, 63, 042001 [NASA ADS] [CrossRef] [Google Scholar]
  45. Leach, S. M., Cardoso, J. F., Baccigalupi, C., et al. 2008, A&A, 491, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Lenz, D., Doré, O., & Lagache, G. 2019, ApJ, 883, 75 [Google Scholar]
  47. Li, P., Ilayda Onur, I., Dodelson, S., & Chaudhari, S. 2022, arXiv e-prints [arXiv:2205.07368] [Google Scholar]
  48. Lin, Z., Huang, N., Avestruz, C., et al. 2021, MNRAS, 507, 4149 [NASA ADS] [CrossRef] [Google Scholar]
  49. Madhavacheril, M. S., Hill, J. C., Næss, S., et al. 2020, Phys. Rev. D, 102, 023534 [Google Scholar]
  50. Mather, J. C., Cheng, E. S., Cottingham, D. A., et al. 1994, ApJ, 420, 439 [Google Scholar]
  51. Miao, Y., Zhao, X., & Kan, J. 2022, Signal Image Video Process., 16 [Google Scholar]
  52. Montefalcone, G., Abitbol, M. H., Kodwani, D., & Grumitt, R. D. P. 2021, J. Cosmol. Astropart. Phys., 2021, 055 [CrossRef] [Google Scholar]
  53. Naess, S., Aiola, S., Austermann, J. E., et al. 2020, J. Cosmol. Astropart. Phys., 2020, 046 [Google Scholar]
  54. Omori, Y., Chown, R., Simard, G., et al. 2017, ApJ, 849, 124 [NASA ADS] [CrossRef] [Google Scholar]
  55. Perraudin, N., Defferrard, M., Kacprzak, T., & Sgier, R. 2019, Astron. Comput., 27, 130 [NASA ADS] [CrossRef] [Google Scholar]
  56. Petroff, M. A., Addison, G. E., Bennett, C. L., & Weiland, J. L. 2020, ApJ, 903, 104 [Google Scholar]
  57. Planck Collaboration XIV. 2016, A&A, 594, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Planck Collaboration XXII. 2016, A&A, 594, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Planck Collaboration I. 2020, A&A, 641, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Planck HFI Core Team 2011, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Puglisi, G., & Bai, X. 2020, ApJ, 905, 143 [Google Scholar]
  63. Regaldo-Saint Blancard, B., Levrier, F., Allys, E., Bellomi, E., & Boulanger, F. 2020, A&A, 642, A217 [EDP Sciences] [Google Scholar]
  64. Regaldo-Saint Blancard, B., Allys, E., Boulanger, F., Levrier, F., & Jeffrey, N. 2021, A&A, 649, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Remazeilles, M. 2018, arXiv e-prints [arXiv:1806.01026] [Google Scholar]
  66. Remazeilles, M., Delabrouille, J., & Cardoso, J.-F. 2011, MNRAS, 410, 2481 [Google Scholar]
  67. Ronneberger, O., Fischer, P., & Brox, T. 2015, arXiv e-prints [arXiv:1505.04597] [Google Scholar]
  68. Salvati, L., Douspis, M., & Aghanim, N. 2018, A&A, 614, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Smoot, G. F., Bennett, C. L., Kogut, A., et al. 1992, ApJ, 396, L1 [Google Scholar]
  70. Stein, G., Alvarez, M. A., Bond, J. R., van Engelen, A., & Battaglia, N. 2020, JCAP, 2020, 012 [CrossRef] [Google Scholar]
  71. Sunyaev, R. A., & Zeldovich, Y. B. 1970, Ap&SS, 7, 20 [Google Scholar]
  72. Tanimura, H., Aghanim, N., Bonjean, V., & Zaroubi, S. 2022a, A&A, 662, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Tanimura, H., Douspis, M., Aghanim, N., & Salvati, L. 2022b, MNRAS, 509, 300 [Google Scholar]
  74. Vacher, L., Aumont, J., Montier, L., et al. 2022, A&A, 660, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Vacher, L., Chluba, J., Aumont, J., Rotti, A., & Montier, L. 2023, A&A, 669, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Vikram, V., Lidz, A., & Jain, B. 2017, MNRAS, 467, 2315 [NASA ADS] [Google Scholar]
  77. Wang, G.-J., Shi, H.-L., Yan, Y.-P., et al. 2022, ApJS, 260, 13 [NASA ADS] [CrossRef] [Google Scholar]
  78. Zhang, Z., Liu, Q., & Wang, Y. 2018, IEEE Geosci. Remote Sens. Lett., 15, 749 [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Diagram of our architecture. Four ResUNets are used to construct CMB ¯ $ \overline{\mathrm{CMB}} $, SZ ¯ $ \overline{\mathrm{SZ}} $, CIB ¯ $ \overline{\mathrm{CIB}} $, and z ¯ $ \overline{z} $ directly from the input Ci, and a reconstruction loss ℒrec is applied between the inputs Ci and the models C i ¯ $ \overline{C_i} $ obtained with Eq. (4).
In the text
thumbnail Fig. 2.

Evolution of the different statistical quantities of the extracted components in the unseen area of the sky. Top: evolution of the means of the components on the left for the seven-frequency configuration and on the right for the nine-frequency configuration. Bottom: evolution of the variances of the components on the left for the seven-frequency configuration and on the right for the nine-frequency configuration. Dashed lines represent the expected values. The values for the CIB are not the same for the seven and the nine frequencies models, as we are computing the CIB at 280 GHz for the first case and the CIB at 545 GHz for the second case. Units are different for each map: SZ ¯ $ \overline{\mathrm{SZ}} $ and z ¯ $ \overline{z} $ are without units (y and redshift), CMB ¯ $ \overline{\mathrm{CMB}} $ is in μK, and CIB ¯ $ \overline{\mathrm{CIB}} $ is in MJy sr−1.
In the text
thumbnail Fig. 3.

Projection in a 5° ×5° patch of the HEALPIX maps of the different components around the brightest SZ cluster. Left column: from top to bottom, the SZ, CMB, and CIB from WebSky simulation maps. Middle column: from top to bottom, the reconstructed SZ ¯ $ \overline{\mathrm{SZ}} $, CMB ¯ $ \overline{\mathrm{CMB}} $, and CIB ¯ $ \overline{\mathrm{CIB}} $. Right column: residuals between the WebSky component and the reconstructed ones. Very good agreement is seen visually between the reconstructed maps and the expected map, without structures in the residuals.
In the text
thumbnail Fig. 4.

PDF comparison between the reconstructed components and the WebSky ones. Left: case for the CMB. Middle: case for the SZ. Right: case for the CIB.
In the text
thumbnail Fig. 5.

Power spectra of the components, the recovered components, and the cross power spectra between the two. 𝒞ℓ residuals as a percentage are also shown in the bottom of each plot, where residuals are defined as x − x ¯ x × 100 $ \frac{x-\overline{x}}{x}\times100 $ for the quantity x. Left: case for the CMB. Middle: case for the SZ. MILCA is also shown in this plot. Right: case for the CIB.
In the text
thumbnail Fig. 6.

Cross power spectra between the different components. Left: case for CMBxCIB. Middle: case for CIBxSZ. MILCA is also considered in this plot. Right: case for CMBxSZ.
In the text
thumbnail Fig. 7.

Comparison of the SZ fluxes computed with aperture photometry in the exact same way in the SZ WebSky map, in the SZ ¯ $ \overline{\mathrm{SZ}} $ map, and in the MILCA SZ map. Left: fluxes on the reconstructed maps as a function of the SZ WebSky fluxes. The blue dashed line represents the SZ flux have been enhanced in the weight map w. Right: histograms of the residuals. The dashed lines show the median values of the distributions.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.