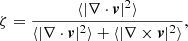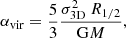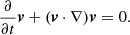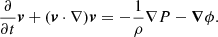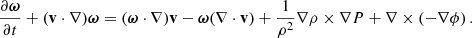EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A193 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A193
Number of page(s) 12
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202245491
Published online 20 April 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Gas in galaxies is supersonically turbulent (see the review by Elmegreen & Scalo 2004; Hennebelle & Falgarone 2012). The turbulent energy decays on a timescale that is much shorter than the time for which molecular clouds are turbulent. Thus, there must be a mechanism that continuously provides turbulent energy to molecular clouds.

Processes suggested so far have been shear from galactic rotation (Fleck 1981), mass transport (Krumholz & Burkhart 2016; Krumholz et al. 2018), stellar feedback (see e.g., Mac Low & Klessen 2004 Ostriker & Shetty 2011; Faucher-Giguère et al. 2013; Padoan et al. 2016; Hayward & Hopkins 2017), gravitational instabilities (see e.g., Bournaud et al. 2010), and gas accretion (Klessen & Hennebelle 2010; Goldbaum et al. 2015, 2016; Ginzburg et al. 2022; Forbes et al. 2022). However, distinguishing their respective roles is difficult.

For instance, Krumholz & Burkhart (2016) developed an analytical prediction for the dependence of the gas velocity dispersion on star formation rate in galaxies with gravity- and feedback-dominated turbulence injection. They found that observational data are best fitted by gravity-dominated injection for high-redshift galaxies, but the low-redshift case is less clear. The predictions of the two models are very close to each other for the low-redshift case (see also Varidel et al. 2020; Girard et al. 2021; Yu et al. 2021). Using numerical simulations with self-gravity and stellar feedback, Bournaud et al. (2010) found that the characteristic length of a turbulent cascade for a Large Magellanic Cloud-type galaxy model is set by the Jeans length, and that gravity dominates turbulence injection. Using simulations of 1 kpc3 sized regions of galaxies with turbulent forcing, Brucy et al. (2020) showed that turbulence injection via feedback may be sufficient to regulate star formation for gas surface densities typical of z ≃ 0, but stronger driving becomes necessary at higher gas surface densities. These theoretical studies thus suggested that gravitational instabilities may be the most important injection mechanism, while others suggested that stellar feedback remains dominant, at least for z ≃ 0 (see e.g., Orr et al. 2020).

On the observational side, galaxy-wide velocity dispersions are reported to be well correlated to their star formation rates, thus implying a connection between turbulence and star formation feedback (e.g., Green et al. 2010; Lehnert et al. 2013). However, some giant molecular clouds (GMC) are seen to be turbulent even without star formation (see e.g., Poidevin et al. 2013). For instance, observing 272 GMCs in CO(1-0) in the Large Magellanic Cloud, Kawamura et al. (2009) did not find a different line width between clouds without massive star formation, clouds with HII regions, and clouds with HII regions and young clusters. Furthermore, observations of gas-rich local galaxies (Fisher et al. 2017) and z ≃ 2 galaxies (see e.g., Übler et al. 2019) found that both categories of galaxies are marginally Toomre (1964) stable, suggesting a predominant role of gravity in their elevated velocity dispersion. It is thus necessary to study these two processes independently to better understand their respective roles.

However, the turbulent injection process is likely to have evolved among cosmic times. In particular, the high gas fraction observed in z ≃ 2 galaxies should change the morphology and internal dynamics of galaxies drastically compared to galaxies in the local Universe, which tend to have low gas fractions (see Fensch & Bournaud 2021, and references therein). Gravity-driven turbulence and its cascade down to scales of star formation regions may thus be a function of gas fraction.

In this study, we propose to answer this question by following the turbulent cascade generated purely by gravitational instabilities and galactic dynamics for gas-poor and gas-rich disks under the simplifying assumptions of an isothermal equation of state and no star formation or stellar feedback. Thus, except for the isothermal equation of state, our numerical methods do not include sub-grid models. Our purpose is to characterise the gravity-generated turbulence cascade and to investigate whether this cascade changes with the gas fraction of the galaxy. The study of the interplay between gravity and star formation feedback will be presented in a forthcoming publication.

The numerical methods and simulation sample are presented in Sect. 2. Results are described in Sect. 3. The discussion and conclusions are presented in Sects. 4 and 5, respectively. The appendix presents the study of the robustness of the different results with respect to the chosen numerical methods. In what follows, the number density n is defined as the number density of hydrogen nuclei, which is assumed to have a mass fraction of 0.76, and ρ is defined as the total mass density, including both hydrogen and helium. Pressure is derived from temperature using the ideal gas law and hydrogen and helium densities, with a mean molecular weight given by the ionisation state of the gas.

2. Simulation code and disk models

2.1. Numerical methods

We used the simulation code RAMSES (Teyssier 2002). RAMSES uses adaptive mesh refinement (AMR), solves the hydrodynamics equations using a second-order Godunov method (MUSCL scheme), and solves the Poisson equation using a conjugate gradient method. We used an isothermal equation of state for gas denser than 10−3 cm−3, with temperatures of 236 K or 104 K, depending on the galaxy models described in the following subsection. Gas less dense than n = 10−3 cm−3 was set to the virial temperature T = 4 × 106(n/10−3 cm−3)2/3 K (Bournaud et al. 2010) to maintain the halo gas in gravothermal equilibrium. We used a simple isothermal equation of state because we study purely gravitational and not thermal instabilities. The effect of a full cooling model is discussed in Sect. 4.2.

Cells were refined whenever they contained more than 50 initial condition particles, their mass (gas plus particles) exceeded 5 × 104 M⊙, or when the Jeans length was less than four cells wide. The box size was 100 kpc3. The coarsest cells had a width of 781 pc (level 7), and refinement was allowed to a width of 6 pc (level 14). For gas at the maximum resolution for which the local Jeans length is less than four cells wide, we increased the temperature of the cell following a polytrope equation, with T ∝ ρ providing a pressure floor preventing artificial fragmentation, which we refer to as the Truelove et al. (1997) criterion (see Teyssier et al. 2010, for details).

After 100 Myr of evolution, we chose an over-density region in each simulation by eye at approximately the same galactocentric radius of 3 kpc, and we stored its orbit. The region was a sphere of 1 kpc diameter, which we call the zoomed region hereafter. We repeated the simulation and this time allowed more refinement in the zoomed region that followed the stored orbit. We note that the additional refinement in the zoomed region is only seen by the gas and not by the particles, which only see refinement up to the previous 6 pc resolution to prevent over-sampling their gravity. The refinement was allowed to AMR level 20, that is, down to 0.095 pc. The refinement strategy followed the same criteria as above, but the refinement was also triggered whenever the local Jeans length is less than 30 cells wide, which is the convergence criterion for resolving the solenoidal motions of the turbulence presented by Federrath et al. (2011). Furthermore, a maximum cell width of 3 pc was imposed for all cells less than 500 pc from the centre of the zoomed region.

To avoid numerical artefacts due to the refinement timescale, for example the creation of spurious shocks if the gas does not have time to settle at the new resolution limit, we activated a new level of refinement every one million years. This is far longer than the timescale for convergence found by Seifried et al. (2017).

Furthermore, in order to prevent collapse of the gas entering the zoomed region, we used a target strategy: level 15 (corresponding to a cell width of 3 pc) was triggered only within 600 pc from the centre of the zoomed region, level 16 within 550 pc, and so on, up to level 20 within 350 pc. To prevent any jump in the pressure floor (see above), it evolved linearly such that the Jeans length always exceeded a four cell width at the highest resolution. At the maximum level, the Jeans polytrope was activated for densities above 106 H cm−3 and 3.5 × 107 H cm−3 for isothermal temperatures of 236 K and 104 K, respectively. The density-temperature diagrams, corresponding to the zoomed regions, are shown in Fig. 1. In the zoomed regions presented in this paper, we reached up to 26 million leaf cells (i.e. cells that are not split into sub-cells).

thumbnail Fig. 1.

Density-temperature diagrams for the zoomed regions, 10 Myr of evolution after the activation of level 20. The dashed lines show the minimum pressure floor to satisfy the Truelove et al. (1997) criterion for levels 15–20, from left to right. This pressure floor is smoothly reduced towards the centre of the zoom (see text).

We stress that we did not extract the region in the zoom for a new simulation, as is often done in the literature (see e.g., Van Loo et al. 2013; Bonnell et al. 2013; Butler et al. 2015; Dobbs et al. 2022, but see Smith et al. 2020, with an analytical background gravitational potential). Instead, the full galaxy was simulated self-consistently in our setup, along with the zoomed region, in order to retain shear and large-scale gravity.

2.2. Simulation set

We used the G2 galaxy model from Perret et al. (2014), which is based on the MASSIV sample of z ∼ 1.5 galaxies (Contini et al. 2012). The parameters of the simulations are described in Table 1. We studied two disk galaxies, F10 and F65, with the same total mass distribution, thus the same rotation curve. The gaseous and stellar disks were initialised with an initial Toomre Q parameter of 1 and 1.7, respectively. The two galaxies differ in two ways. First, the F10 (F65) galaxy had a gas mass fraction of 10% (65%). The gas fraction is defined as the gas mass over the sum of the stellar and gas masses. Second, the value of the constant temperature was chosen to obtain a similar Qgas in both cases. We chose to do this to isolate the effect of changing the gas fraction. Because the shear curve was set to be the same, that the sound speed cs evolves with the square root of the temperature, and that the gas surface density is 6.5 times higher in the F65 case, we set TF10 = TF65/6.52. We chose TF65 = 104 K (see e.g., Behrendt et al. 2016), and thus TF10 = 236 K.

Table 1.

Characteristics of the simulated galaxies.

2.3. Disk model characteristics

The gas and stellar density maps of the simulations before starting the zoom procedure are shown in Fig. 2. The F10 model develops a spiral morphology, both in its gaseous and stellar components, and has a gas disk height of around 100 pc. The F65 model develops a clumpy morphology both in its gaseous and stellar components, and has a gas disk height of around 1 kpc. This is similar to what has been obtained for other isothermal gas-rich disk simulations (see e.g., Behrendt et al. 2016).

thumbnail Fig. 2.

Gas density of the F10 (left) and F65 (right) runs. The white circles show the location of the zoomed region.

In Fig. 3 we show the density probability density functions (PDF) in the simulations on the snapshots illustrated in Fig. 2. From turbulence theory, the density PDF of isothermal fluids with supersonic turbulence is expected to be well represented by a log-normal form (see e.g., Kritsuk et al. 2007; Federrath et al. 2008, 2010). We resolve densities up to a few 104 and 106 H/cc for F10 and F65, respectively.

thumbnail Fig. 3.

Normalised gas density PDFs for the F10 and F65 runs at the time shown in Fig. 2, i.e. before the refinement in the zoomed-in region is triggered. Local maxima in the density PDF correspond to density thresholds for refinement.

In Fig. 4 we show the three velocity component power spectra for both the F10 and F65 simulations, from the snapshots shown in Fig. 2. These power spectra are measured from 2D maps at the highest resolution. Thus, low-resolution regions are interpolated. In the appendix, we present power spectra with an increasingly coarse resolution limit, down to the uniform grid limit. It is shown that this interpolation to higher resolution does not change the results. Several features are visible in Fig. 4. First, on large scales, vertical and planar velocities are decorrelated. Second, n small scales, the three velocity components follow the same power-law, which differs between the F10 and F65 models.

thumbnail Fig. 4.

Power spectra of the three velocity components from face-on mass-weighted velocity projection maps. The spectra are compensated by k3. The F65 model is shown with bold lines, and the F10 model is plotted with thin lines. The F10 power spectra are shifted down by 3 dex for clarity. The spikes seen at the small spatial scales are due to oversampling because of the AMR grid out of which the Fourier transform was performed. These spectra show that the injection scale of turbulence is indeed different in the two models, and corresponds roughly to the disk scale height.

The decorrelation between the vertical and the planar velocities has also been obtained in previous works (see e.g., Bournaud et al. 2010) and observations (see e.g., Grisdale et al. 2017). It was interpreted as being due to the injection scale for turbulence, which is thought to be similar to the disk height. We reproduce this result here: the transition occurs approximately at their disk scale height: 100 pc and 1 kpc for the F10 and F65 models, respectively.

We fit power laws to the velocity power spectra. As was done in the literature, we defined the exponent of the power law with respect to the norm of the wave vector k, which is the inverse of the spatial scale l: k = 1/l. The two power-law exponents for small scales differ between the two models. For the radial, tangential, and altitudinal velocity components, we obtain exponents −3.4, −3.3, and −3.0 for F10 and −4.4, −4.5, and −4.2 for F65. We note that the inertial range, which is defined as the range in spatial scales for which the velocity power spectrum is well fit by a single power law, is quite short for the F10 simulation, around 1 dex. A power law with an index equal to −3 corresponds to the scaling expected for a 2D power spectrum in Burgers (1948) turbulence, compared to an index equal to −2.6 for Kolmogorov (1941) turbulence.

3. Results: Turbulence cascade down to sub-parsec

In this section, we present the effect of large-scale gravitational instabilities on the structure of the interstellar medium (ISM) in the encapsulated zoomed region. If not stated otherwise, the analysis was performed on a single snapshot of the simulation 10 Myr after the activation of the final level of refinement (level 20), if not indicated otherwise.

3.1. Gas distribution

Gas density maps in the zoomed region after 10 Myr are shown in Fig. 5. The gas fragments into very dense, n > 107 H cm−3, gas clumps. The gas density PDFs in the zoomed regions of each galaxy are shown in Fig. 6. In the F65 simulation, gas reaches densities of a few 1010 H cm−3, almost three orders of magnitude above the highest densities reached in F10. In order to study the evolution of the gas density distribution after the activation of level 20, we show the ratio of the gas density PDF at different times with respect to the last snapshot, 10 Myr after the activation of level 20 in Fig. 7. For both models, the high-density end of gas density PDF increases progressively with time, and after ≃7 Myr, the gas density PDFs do not differ by more than a factor of 2 per density bin.

thumbnail Fig. 5.

Zoomed regions in both galaxies. Left panels: gas density maps. Right panels: maximum level of refinement along the line of sight. Top panels: zoom in the F10 simulation, seen face-on. Lower panels: zoom in the F65 simulation seen face-on.

thumbnail Fig. 6.

Normalised gas density PDF in the zoomed regions in the F10 (black) and F65 (red) models 10 Myr of evolution after the activation of level 20.

thumbnail Fig. 7.

Evolution of the ratio between the gas density PDF to the final gas density PDF. The top (bottom) panel shows the F10 (F65) simulation.

This convergence of the gas density PDF only occurs as a result of the pressure support from the Jeans polytrope. Without this pressure floor at high density, gas would continue to collapse under the effect of its own gravity. Inclusion of this Jeans polytrope thus allows us to freeze the collapse of gas onto pressure-supported sub-structures, analogous to hot cores in observed molecular clouds.

3.2. Gas turbulence

We measured the 3D velocity dispersion σ3D in the zoomed region at the uniform resolution of 3 pc (level 15) by mass-weighting the variances obtained in each parent cell at level 14, containing 23 cells at level 15. We obtained 3D velocity dispersions of 11.4 km s−1 and 103.0 km s−1 for the F10 and F65 models, respectively. These velocity dispersion are of the same order as those observed in galaxies with a corresponding gas fraction (see the review by Förster Schreiber & Wuyts 2020) and correspond to supersonic gas, relative to the ambient isothermal sound speed: 1.8 km s−1 and 11.7 km s−1 for a mean molecular weight of 0.6 and a temperature of 236 K and 104 K, respectively.

The evolution of σ3D after the last level activation is shown in Fig. 8. It evolves towards a stabilised value after ≃6 Myr in each simulation. This convergence time is similar to the convergence time of the gas density PDF presented in the previous sub-section.

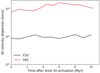thumbnail Fig. 8.

Evolution of the 3D velocity dispersion in F10 and F65 after the activation of level 20.

We then studied how these turbulent motions are structured. In Fig. 9 we show the compressive ratio ζ, defined as (see e.g., Kida & Orszag 1990; Kritsuk et al. 2007)

ζ = ⟨ | ∇ · v | 2 ⟩ ⟨ | ∇ · v | 2 ⟩ + ⟨ | ∇ × v | 2 ⟩ , $$ \begin{aligned} \zeta = \frac{ \langle |\nabla \cdot \boldsymbol{v}|^2\rangle }{ \langle |\nabla \cdot \boldsymbol{v}|^2\rangle + \langle |\nabla \times \boldsymbol{v}|^2\rangle } , \end{aligned} $$(1)

thumbnail Fig. 9.

Evolution of the compressive ratio ζ after the activation of level 20 in F10 (black) and F65 (red). The dashed grey line shows the locus of energy equipartition: ζ = 30%.

where the average are is weighted by mass, to obtain energy ratios. Following the convergence criterion of Renaud et al. (2013), we computed this ratio for cells and parent cells that are larger than eight times the highest-resolution cells, that is, above or equal to level 17 (see Grisdale et al. 2017). This was done to correctly capture solenoidal motions, which need more resolution elements to be resolved than compressive motions (Federrath et al. 2011).

The evolution of this ratio is rather noisy, typically between 20 and 40%, with rapid variation between snapshots. At energy equipartition, we expect ζ = 33% from a dimensional argument (compressive motions are along one direction, whereas solenoidal motions are along two dimensions; see e.g., Hennebelle & Falgarone 2012). During the first 10 Myr after the activation of level 20, ζ is typically above that value in F10 and below it in F65. However, given the noise in the measurements, the data do not allow us to conclude that compressive motions are stronger in either of the simulations.

3.3. Velocity structure

Energy transfer from large to small scales via turbulence is imprinted into the velocity power spectrum. In Fig. 10 we show the velocity power spectra for the three velocity components and their evolution after the activation of level 20. The power spectra are well fitted by power laws between the spatial scales of 100 pc and 1 pc. Below this range, the power spectra steepen. This is discussed in Sect. 4.1. Moreover, the power spectrum of vz flattens for the F10 run at a spatial scale of 100 pc. This is similar to what was observed in Fig. 4 and is interpreted as the transition between 2D and 3D turbulence at the disk scale height.

thumbnail Fig. 10.

Velocity power spectra for the two simulations. Top panel: 2D power spectrum of the three velocity components 10 Myr after the activation of level 20. The curves are compensated by k3. Curves from to the F65 run are plotted in bold, and the thin lines show the F10 run. The F10 power spectra are shifted down by 3 dex for the sake of clarity. Bottom panel: evolution of the power-law index of the fit of the velocity power spectra. Curves related to the F65 run are shown in bold.

We fit power laws to the 2D velocity power spectrum. The fits were performed between 1 pc and 100 pc for F10 and 1 kpc for F65. For the radial, tangential, and altitudinal velocity components, we obtain exponents −3.1, −3.2, and −3.1 for F10 and −3.0, −3.1, and −2.9 for F65. They are similar for each galaxy model and close to the value of −3, which is the scaling of Burgers’ turbulence. In the F65 simulation, the injection scale is around 1 kpc, that is, the disk scale height, seen as a transition in Fig. 4, and we followed the same power law down to scales of around 1 pc. Thus our setup is able to resolve a turbulent inertial range over three orders of magnitude in spatial scales, which is more than the largest supersonic turbulence simulations so far (see e.g., Federrath et al. 2021, with an inertial range of 2 orders of magnitude).

In Fig. 10 the vz power spectrum for the F10 simulation lies between 0.5 and 1 dex below the vr and vθ power spectra. The vz power spectrum for the F65 also lies below the vr and vθ power spectra, but only by 0.3 dex at most. This effect is also shown in Fig. 4 to a lesser extent. This is interpreted as a consequence of the stronger anisotropy of the velocity field between in-plane and vertical motions in the F10 galaxy: in the zoomed region maps used to compute the power spectra, the standard deviation of the vz distribution is about three times lower than that of vr and vθ in the F10 galaxy, but only up to 50% lower in the F65 galaxy. These different anisotropies could have originated from the fact that the gas in the F10 simulation is dominated by the gravity of the stellar background, while in the F65 galaxy, the self-gravity of the gas is dominant. In the zoomed region, the gas mass fraction is 14% and 87% in the F10 and F65 galaxies, respectively. A detailed study of the anisotropy of the velocity field and its origin is beyond the scope of this paper.

3.4. Gas structure

Turbulence creates structures in the gas. The question is whether these structures differ with the gas fraction. For instance, both analytical (Saichev & Woyczynski 1996) and numerical simulations of compressible non-gravitating gas (Kim & Ryu 2005; Kritsuk et al. 2007; Konstandin et al. 2016) find density power spectra following power laws with indices going from −2 for sub-sonic turbulence to 0 at the infinite Mach number limit. In Fig. 11 we show the power spectra of the gas surface density in the zoomed region for each simulation. The power spectra are strikingly similar, despite the large differences in the density maps seen in Fig. 5. In particular, at spatial scales higher than one parsec, the power spectra are well fitted by a power law with exponent of ≃ − 0.7. We note that this power law is a good fit during the full 10 Myr of evolution after the activation of level 20. Furthermore, both power spectra become steeper at scales smaller than 1 pc, similar to the velocity power spectra shown in Fig. 10. This result is rather surprising because several studies have shown a dependence of the power-law exponent on the Mach number, combined with the fact that the Mach number is different in the two simulations (from 6.5 to 9, see Sect. 3.2). These studies did not include self-gravity.

thumbnail Fig. 11.

Surface density power spectra for the two simulations. Top panel: surface density power spectra for F10 and F65, 10 Myr after the activation of level 20. The curves are compensated by k0.7. Bottom panel: evolution of the power law of the fit of the velocity power spectra.

To study the density structure inside the zoomed region further, we used the Python package ASTRODENDRO1 to detect bound sub-structures. We detected all structures with a peak density above 104 H cm−3 and with an area of at least 20 pixels square on the density map, that is, 0.18 pc2. We note that this density threshold is lower than the threshold at which cells are affected by the pressure support from the Jeans polytrope (see Sect. 2.1). We then computed the virial parameter αvir of each clump, defined as (see e.g., Bertoldi & McKee 1992)

α vir = 5 3 σ 3 D 2 R 1 / 2 G M , $$ \begin{aligned} \alpha _\mathrm{vir} = \frac{5}{3} \frac{\sigma _\mathrm{3D} ^2 \ R_{1/2}}{\mathrm{G} M} , \end{aligned} $$(2)

where R1/2 is the half-mass radius of the clump, M is its gas mass, and σ3D is its internal 3D velocity dispersion. In order to account for the non-homogeneity and non-sphericity of the clumps, we used the half-mass radius instead of the detection radius, and we consider that a clump was gravitationally bound if αvir <  2. The following results are not qualitatively affected by using αvir <  1 or αvir <  5, as we describe in the following. Examples of gravitationally bound clumps in both simulations are shown in Fig. 12.

thumbnail Fig. 12.

Substructures in the zoomed regions. Left panel: gas density maps in the central regions in the zoom. The origin is the centre of the zoomed region. Right panel: gravitationally bounds clumps (with αvir <  2, see text). The top and bottom panels show the F10 and F65 runs, respectively.

There are several hundred such clumps in each simulation. The typical clump size is about 1 pc, which corresponds to the spatial scale of the breaks of power spectra seen in Figs. 10 and 11, both of which are steeper for smaller scales. We stress that the physics of the gas for our clumps is not realistic in the sense that we stopped the isothermal collapse by introducing a pressure floor, and we did not remove the gas into star formation, and thus have a continuous accretion of matter onto our sub-structures, which affects the clump sizes. The mass spectra of the clumps are shown in Fig. 13. For the F65 simulation, the number and masses of the gravitationally bound clumps are not significantly modified by edge-on or face-on maps. The last two dex of the high-mass end of the mass spectra are well fitted by power laws with an index close to −1.8. These power laws vary by less than 3% around these values when the selection criterion is changed to αvir <  1 or αvir <  5. The hierarchy of structures in a turbulent field without gravity produces a mass spectrum with an index −2 (Elmegreen 2009), whereas numerical studies by Hennebelle & Audit (2007) and Audit & Hennebelle (2010), which did include different gas cooling functions or equations of state, but not self-gravity, found a similar slope of −1.7. This exponent −1.8 is the same as that of CO clump mass distributions (in, Hennebelle & Falgarone 2012, see Sect. 4.3). This scaling therefore appears to be universal for any turbulent medium, regardless of the nature of the drivers.

thumbnail Fig. 13.

Mass spectrum of the substructures for the two simulations. Top panel: mass spectrum of the bound structures in the zoom (αvir <  2). The pink histogram and fit are obtained for a detection performed on the edge-on density map. The power slopes are parametrised by dN/dM ∝ M−β. Bottom panel: evolution of the slope of the power-law fit to the high-mass end of the mass spectrum. The dashed grey line shows the location of the −1.8 exponent.

4. Discussion

4.1. Origin of Burgers’ turbulence scalings

In Sect. 3.3 we obtained 2D velocity power spectra that were well fitted by a power law with an index of about −3, which is similar to the Burgers turbulence scaling. Burgers turbulence is a model in which the transfer of energy to small scales is achieved via shocks. This is different from the Kolmogorov turbulence model, which applies to incompressible fluids and for which the transfer of energy to small scales is achieved via eddies. In this model, the 2D velocity power spectrum follows a power law with an index of −8/3 (Kolmogorov 1941).

The inviscid 3D Burgers equation is pure advection and reads

∂ ∂ t v + ( v · ∇ ) v = 0 . $$ \begin{aligned} \frac{\partial }{\partial t} \boldsymbol{v} + (\boldsymbol{v} \cdot \nabla ) \boldsymbol{v} = 0 . \end{aligned} $$(3)

Our simulation uses an isothermal equation of state up to 106 and 107.5 H cm−3 at the resolution limit for F10 and F65, respectively. The regions affected by this pressure floor are mainly located in the gravitationally bound sub-structures (see above). Thus our effective Euler equation reads outside regions affected by the pressure floor, and where ϕ is the gravitational potential,

∂ ∂ t v + ( v · ∇ ) v = − 1 ρ ∇ P − ∇ ϕ . $$ \begin{aligned} \frac{\partial }{\partial t} \boldsymbol{v} + (\boldsymbol{v} \cdot \nabla ) \boldsymbol{v} = -\frac{1}{\rho } \nabla P - \boldsymbol{\nabla }\phi . \end{aligned} $$(4)

In the supersonic case, where pressure does not affect the motions strongly, the velocity power spectrum is expected to follow the scalings of Burgers turbulence for 1D and 2D turbulence (see e.g., Boldyrev 2002). In 3D, the scaling might change because vorticity is generated (see also Hennebelle & Audit 2007; Padoan et al. 2016; Iffrig & Hennebelle 2017).

Without viscosity and with gravity as the only external force, the evolution of the vorticity ω = ∇ × v reads

∂ ω ∂ t + ( v · ∇ ) ω = ( ω · ∇ ) v − ω ( ∇ · v ) + 1 ρ 2 ∇ ρ × ∇ P + ∇ × ( − ∇ ϕ ) . $$ \begin{aligned} \frac{\partial \boldsymbol{\omega }}{\partial t} + (\mathbf v \cdot \nabla ) \boldsymbol{\omega }= (\boldsymbol{\omega }\cdot \nabla ) \mathbf v - \boldsymbol{\omega }(\nabla \cdot \mathbf v ) + \frac{1}{\rho ^2}\nabla \rho \times \nabla P + \nabla \times \left( - \nabla \phi \right). \end{aligned} $$(5)

In our isothermal setup, ∇P ∝ ∇ρ, and as the gravitational force is a conservative force, it does not generate vorticity. This is also shown in Fig. 9, where the compressive ratio remains close to equipartition during the full 10 Myr of the simulation. Furthermore, the Jeans polytrope mainly affects gravitationally bound substructures with a typical size of 1 pc. This explains why the 2D velocity power spectra are well fitted by power laws with an exponent close to −3 for scales between the injection scale and the start of the pressure support, as shown in Fig. 10. We note that this scaling is not likely to be found in observations if the velocity field is impacted by forces generating vorticity.

4.2. Importance of other physics

Our numerical setup only accounts for hydrodynamics and self-gravity. In particular, we imposed a constant temperature (except in the highest density cells). The change effected when more physics, such as cooling, magnetic fields, or star formation and its feedback, were introduced remains to be defined.

4.2.1. Cooling

First, if a full cooling and heating model was implemented, we would have pressure gradients in the Euler equation. For non-barotropic fluids, the term ∇ρ × ∇P would not necessarily vanish and could induce vorticity. A deviation from Burgers’ scaling would then be possible (see e.g., Hennebelle & Audit 2007; Padoan et al. 2016).

There are two stable phases at pressure equilibrium in the ISM: the warm neutral medium at T ≃ 104 K, and the cold neutral medium at T ≃ 100 K. The transition between these two stable phases is a thermal instability due to an elevation of the local density. Thus it occurs at a characteristic spatial scale, depending on the average gas density and metal content of galaxies. This process might then leave its imprint in the turbulent cascade. This characteristic scale depends on the average gas density in galaxies and may vary with the gas fraction, unlike the gravity-driven turbulence presented above.

4.2.2. Magnetic fields

Magnetic fields may affect the turbulence cascade in two ways. First, magnetic fields act as a source term in the vorticity equation. In the presence of a magnetic field, Eq. (5) has an additional term on the right-hand side that corresponds to the rotational of the Lorentz force: ∇ × (J × B)/ρ, with J and B the current and the magnetic field, respectively. This creation of vorticity may impact the transfer of energy by creating eddies, and thus may change the velocity power spectrum (see e.g., Hennebelle & Audit 2007; Padoan et al. 2016).

Second, magnetic fields may also induce turbulence via the magneto-rotational instability (see e.g., Kim et al. 2003; Piontek & Ostriker 2007). This instability occurs in disks in the presence of a poloidal component of the magnetic field in a region where the angular velocity decreases with galactocentric radius, which for instance occurs in the flat velocity rotation part of galaxies.

Thus, magnetic fields might in principle leave their imprint on the isothermal turbulence cascade in galactic disks. Dedicated numerical simulations would be required to study them.

4.2.3. Star formation and feedback

First, enabling star formation would allow gas depletion in the densest cell. In the long term, star formation should reduce the gas fraction of the galaxy. However, we have seen that the characteristics of the turbulent cascade do not change with the decrease of gas fraction, thus we do not expect significant changes in our results if we formed stars instead of using the Jeans polytrope to stop the fragmentation at the limit of resolution.

Second, star formation feedback, in the form of heating and radiative pressure from HII regions and supernovae (SN) explosions, would also inject energy at a given scale, likely around 50 pc to 100 pc with a dependence on SN – and thus star formation – clustering, but also ambient density gas (Padoan et al. 2016; Iffrig & Hennebelle 2017; Ostriker & Kim 2022). The fraction and spatial scale of energy deposited in the ISM may also be a function of disk scale height and thus gas fraction (Orr et al. 2022a,b). By releasing kinetic energy at a characteristic spatial scale, star formation feedback may thus leaves an imprint on the turbulent cascade.

Several works on turbulence in the ISM either focussed on galaxy scales, without forcing (see e.g., Bournaud et al. 2010; Falceta-Gonçalves et al. 2015; Grisdale et al. 2017; Körtgen et al. 2021; Bieri et al. 2022), or on ISM boxes of typically 1 kpc3, thus without the self-consistent energy injection from large scales (see e.g., Iffrig & Hennebelle 2017; Brucy et al. 2020; Hu et al. 2022; Rathjen et al. 2021). In either case, inclusion of a thermodynamical model and star formation feedback gives velocity power spectrum scalings between that of Burgers and Kolmogorov (1941), which was primarily obtained for incompressible turbulence.

Thus, the inclusion of both cooling and star formation and its feedback may leave an imprint of their characteristic scales on the turbulent cascade. This scale may depend on the gas fraction of the galaxy. In a forthcoming paper, we include these processes to quantify their effects on the turbulent cascade.

4.3. Comparison to observations

Observations of the gas and velocity structure in the atomic ISM are mostly achieved via the 21 cm HI line. Because it is difficult, the Fourier analysis of the gas structure is achieved only for the surface density and not for the line-of-sight velocity (see e.g., Elmegreen et al. 2001; Dutta et al. 2008; Grisdale et al. 2017). The velocity power spectrum for galaxies may be achieved using other tracers, such as ionised gas, or stars in the solar neighbourhood (Bovy et al. 2015).

Grisdale et al. (2017) computed the 2D power spectra of HI gas in six galaxies from the THINGS survey (Walter et al. 2008) and compared them to their simulations, which included gas cooling and star formation. They observed HI power spectra that are much steeper than ours: they awere fitted with power laws with slopes varying from −1.6 to −2.8, agreeing with their simulations, whereas we have found an universal isothermal slope of −0.7. Theory and simulations predict power laws with slopes between 0 and −2 for isothermal sub-sonic to supersonic compressible non-gravitating gas (see Sect. 3.4).

The analysis of the observational data was limited by the large beam size, between 100 and 300 pc, which is the same order of magnitude as the disk scale height. At these scales, turbulence acts on two dimensions, instead of three as in our setup, which might change the index of the power spectrum. However, the resolution limit of the simulations was much lower (4.6 pc), and their surface density power spectra were measured down to ≃50 pc. We note that their fits are all steeper than ours, even for their shallower power spectra, which were obtained when they did not have stellar feedback. Gas cooling and star formation feedback may therefore be the cause of the steepening of HI power spectra. This will be studied in a forthcoming paper.

5. Conclusions

The aim of this paper was to study the characteristics of isothermal gravity-driven turbulence in galaxies with two different gas fractions. We followed the turbulence cascade from its injection scale (100 pc to 1 kpc, depending on the galaxy model) down to the resolution limit of 0.095 pc, using a zoom-in method on a gas overdensity. This method allowed us to self-consistently probe the self-generated turbulence cascade over three orders of magnitude in spatial scales, and over 10 Myr.

As expected, the difference in gas fraction triggers different types of instabilities, and thus galaxy morphologies. The F10 model develops spiral arms, while the F65 disk fragments into many massive gas clumps. Despite very different morphologies in the gas distribution and structure, and despite the difference in the spatial scale of turbulence generation, which is about an order of magnitude, we find that the turbulence and gas structure cascade follow the same scalings laws in both setups.

In particular, the velocity power spectrum follows the Burgers scaling, the surface gas density power spectrum has a power-law slope of −0.7 and gravitationally bound substructures follow a mass distribution with −1.8 slope, similar to that of CO clumps.

We note that the turbulent velocity and density fields reach steady-state after ≃6 Myr. This timescale is shorter than the lifetime of giant molecular clouds, a few tens of million years (see the review by Chevance et al. 2022), in particular, shorter than the time it takes internal feedback to have a significant effect. Thus, this setup provides insights into plausible initial conditions for isothermal and non-magnetic star-forming clouds (see also Lane et al. 2022).

These simulations thus suggest that gravity-driven isothermal turbulent cascade are universal in galaxies across cosmic times. Our encapsulated zoomed method is a promising tool for studying the interplay between turbulence injection processes at widely different spatial scales.

1

Accessible at this address: https://github.com/dendrograms/astrodendro/

Acknowledgments

We thank the anonymous referee for their careful reading and detailed comments which improved the paper. We thank Eva Ntormousi and Elliot Lynch for very stimulating discussions. Simulations were produced using PRACE (grant 2020225366) and GENCI allocations (grants A0090411111 and A0110411111). We gratefully acknowledge support from the PSMN (Pôle Scientifique de Modélisation Numérique) of the ENS de Lyon for the computing resources. JF, FB, NB and PH acknowledge support from PNCG. NB and PH acknowledge financial support from the European Research Council (ERC) via the ERC Synergy Grant ‘ECOGAL: Understanding our Galactic ecosystem – From the disk of the Milky Way to the formation sites of stars and planets’ (grant 855130). We made use of Astropy (Astropy Collaboration 2013), with heavy usage of the Python packages NumPy (van der Walt et al. 2011), iPython (Perez & Granger 2007), SciPy (Jones et al. 2001), matplotlib (Hunter 2007). We would thus like to thank all who designed and contributed to these excellent pieces of software, and most importantly made them available to the community. This research made use of astrodendro, a Python package to compute dendrograms of Astronomical data (http://www.dendrograms.org/).

References

  1. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Audit, E., & Hennebelle, P. 2010, A&A, 511, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Behrendt, M., Burkert, A., & Schartmann, M. 2016, ApJ, 819, L2 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bieri, R., Naab, T., Geen, S., et al. 2022, MNRAS, submitted, [arXiv:2209.06842] [Google Scholar]
  6. Boldyrev, S. 2002, ApJ, 569, 841 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bonnell, I. A., Dobbs, C. L., & Smith, R. J. 2013, MNRAS, 430, 1790 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bournaud, F., Elmegreen, B. G., Teyssier, R., Block, D. L., & Puerari, I. 2010, MNRAS, 409, 1088 [CrossRef] [Google Scholar]
  9. Bovy, J., Bird, J. C., García Pérez, A. E., et al. 2015, ApJ, 800, 83 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brucy, N., Hennebelle, P., Bournaud, F., & Colling, C. 2020, ApJ, 896, L34 [NASA ADS] [CrossRef] [Google Scholar]
  11. Burgers, J. 1948, Adv. Appl. Mech., 1, 171 [CrossRef] [Google Scholar]
  12. Butler, M. J., Tan, J. C., & Van Loo, S. 2015, ApJ, 805, 1 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chevance, M., Krumholz, M. R., McLeod, A. F., et al. 2022, ArXiv e-prints [arXiv:2203.09570] [Google Scholar]
  14. Contini, T., Garilli, B., Le Fèvre, O., et al. 2012, A&A, 539, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Dobbs, C. L., Bending, T. J. R., Pettitt, A. R., & Bate, M. R. 2022, MNRAS, 509, 954 [Google Scholar]
  16. Dutta, P., Begum, A., Bharadwaj, S., & Chengalur, J. N. 2008, MNRAS, 384, L34 [NASA ADS] [Google Scholar]
  17. Elmegreen, B. G. 2009, in The Galaxy Disk in Cosmological Context, eds. J. Andersen, B. Nordströara, & J. Bland-Hawthorn, 254, 289 [NASA ADS] [Google Scholar]
  18. Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [Google Scholar]
  19. Elmegreen, B. G., Kim, S., & Staveley-Smith, L. 2001, ApJ, 548, 749 [NASA ADS] [CrossRef] [Google Scholar]
  20. Falceta-Gonçalves, D., Bonnell, I., Kowal, G., Lépine, J. R. D., & Braga, C. A. S. 2015, MNRAS, 446, 973 [CrossRef] [Google Scholar]
  21. Faucher-Giguère, C.-A., Quataert, E., & Hopkins, P. F. 2013, MNRAS, 433, 1970 [Google Scholar]
  22. Federrath, C., Klessen, R. S., & Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
  23. Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M.-M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
  25. Federrath, C., Klessen, R. S., Iapichino, L., & Beattie, J. R. 2021, Nat. Astron., 5, 365 [NASA ADS] [CrossRef] [Google Scholar]
  26. Fensch, J., & Bournaud, F. 2021, MNRAS, 505, 3579 [CrossRef] [Google Scholar]
  27. Fisher, D. B., Glazebrook, K., Abraham, R. G., et al. 2017, ApJ, 839, L5 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fleck, R. C. Jr. 1981, ApJ, 246, L151 [NASA ADS] [CrossRef] [Google Scholar]
  29. Forbes, J. C., Emami, R., Somerville, R. S., et al. 2022, AAS J. submitted, [arXiv:2204.05344] [Google Scholar]
  30. Förster Schreiber, N. M. F., & Wuyts, S. 2020, ARA&A, 58, 661 [CrossRef] [Google Scholar]
  31. Ginzburg, O., Dekel, A., Mandelker, N., & Krumholz, M. R. 2022, MNRAS, 513, 6177 [NASA ADS] [CrossRef] [Google Scholar]
  32. Girard, M., Fisher, D. B., Bolatto, A. D., et al. 2021, ApJ, 909, 12 [NASA ADS] [CrossRef] [Google Scholar]
  33. Goldbaum, N. J., Krumholz, M. R., & Forbes, J. C. 2015, ApJ, 814, 131 [NASA ADS] [CrossRef] [Google Scholar]
  34. Goldbaum, N. J., Krumholz, M. R., & Forbes, J. C. 2016, ApJ, 827, 28 [NASA ADS] [CrossRef] [Google Scholar]
  35. Green, A. W., Glazebrook, K., McGregor, P. J., et al. 2010, Nature, 467, 684 [NASA ADS] [CrossRef] [Google Scholar]
  36. Grisdale, K., Agertz, O., Romeo, A. B., Renaud, F., & Read, J. I. 2017, MNRAS, 466, 1093 [CrossRef] [Google Scholar]
  37. Hayward, C. C., & Hopkins, P. F. 2017, MNRAS, 465, 1682 [Google Scholar]
  38. Hennebelle, P., & Audit, E. 2007, A&A, 465, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Hennebelle, P., & Falgarone, E. 2012, A&A Rev., 20, 1 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hu, Y., Federrath, C., Xu, S., & Mathew, S. S. 2022, MNRAS, 513, 2100 [NASA ADS] [CrossRef] [Google Scholar]
  41. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
  42. Iffrig, O., & Hennebelle, P. 2017, A&A, 604, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Jones, E., Oliphant, T., & Peterson, P. 2001, SciPy: Open Source Scientific Tools for Python [Google Scholar]
  44. Kawamura, A., Mizuno, Y., Minamidani, T., et al. 2009, ApJS, 184, 1 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kida, S., & Orszag, S. A. 1990, J. Sci. Comput., 5, 1 [NASA ADS] [CrossRef] [Google Scholar]
  46. Kim, J., & Ryu, D. 2005, ApJ, 630, L45 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kim, W.-T., Ostriker, E. C., & Stone, J. M. 2003, ApJ, 599, 1157 [NASA ADS] [CrossRef] [Google Scholar]
  48. Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
  50. Konstandin, L., Schmidt, W., Girichidis, P., et al. 2016, MNRAS, 460, 4483 [NASA ADS] [CrossRef] [Google Scholar]
  51. Körtgen, B., Pingel, N., & Killerby-Smith, N. 2021, MNRAS, 505, 1972 [CrossRef] [Google Scholar]
  52. Kritsuk, A. G., Norman, M. L., Padoan, P., & Wagner, R. 2007, ApJ, 665, 416 [NASA ADS] [CrossRef] [Google Scholar]
  53. Krumholz, M. R., & Burkhart, B. 2016, MNRAS, 458, 1671 [NASA ADS] [CrossRef] [Google Scholar]
  54. Krumholz, M. R., Burkhart, B., Forbes, J. C., & Crocker, R. M. 2018, MNRAS, 477, 2716 [CrossRef] [Google Scholar]
  55. Lane, H. B., Grudić, M. Y., Guszejnov, D., et al. 2022, MNRAS, 510, 4767 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lehnert, M. D., Le Tiran, L., Nesvadba, N. P. H., et al. 2013, A&A, 555, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [Google Scholar]
  58. Orr, M. E., Hayward, C. C., Medling, A. M., et al. 2020, MNRAS, 496, 1620 [NASA ADS] [CrossRef] [Google Scholar]
  59. Orr, M. E., Fielding, D. B., Hayward, C. C., & Burkhart, B. 2022a, ApJ, 924, L28 [NASA ADS] [CrossRef] [Google Scholar]
  60. Orr, M. E., Fielding, D. B., Hayward, C. C., & Burkhart, B. 2022b, ApJ, 932, 88 [NASA ADS] [CrossRef] [Google Scholar]
  61. Ostriker, E. C., & Kim, C.-G. 2022, ApJ, 936, 137 [NASA ADS] [CrossRef] [Google Scholar]
  62. Ostriker, E. C., & Shetty, R. 2011, ApJ, 731, 41 [Google Scholar]
  63. Padoan, P., Pan, L., Haugbølle, T., & Nordlund, Å. 2016, ApJ, 822, 11 [NASA ADS] [CrossRef] [Google Scholar]
  64. Perret, V., Renaud, F., Epinat, B., et al. 2014, A&A, 562, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
  66. Piontek, R. A., & Ostriker, E. C. 2007, ApJ, 663, 183 [NASA ADS] [CrossRef] [Google Scholar]
  67. Poidevin, F., Falceta-Gonçalves, D., Kowal, G., de Gouveia Dal Pino, E.& Mário Magalhães, A. 2013, ApJ, 777, 112 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rathjen, T.-E., Naab, T., Girichidis, P., et al. 2021, MNRAS, 504, 1039 [NASA ADS] [CrossRef] [Google Scholar]
  69. Renaud, F., Bournaud, F., Emsellem, E., et al. 2013, MNRAS, 436, 1836 [NASA ADS] [CrossRef] [Google Scholar]
  70. Saichev, A. I., & Woyczynski, W. A. 1996, SIAM J. Appl. Math., 56, 1008 [CrossRef] [Google Scholar]
  71. Seifried, D., Walch, S., Girichidis, P., et al. 2017, MNRAS, 472, 4797 [NASA ADS] [CrossRef] [Google Scholar]
  72. Smith, R. J., Treß, R. G., Sormani, M. C., et al. 2020, MNRAS, 492, 1594 [NASA ADS] [CrossRef] [Google Scholar]
  73. Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
  74. Teyssier, R., Chapon, D., & Bournaud, F. 2010, ApJ, 720, L149 [NASA ADS] [CrossRef] [Google Scholar]
  75. Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
  76. Truelove, J. K., Klein, R. I., McKee, C. F., et al. 1997, ApJ, 489, L179 [CrossRef] [Google Scholar]
  77. Übler, H., Genzel, R., Wisnioski, E., et al. 2019, ApJ, 880, 48 [Google Scholar]
  78. van der Walt, S., Colbert, S. C., Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [NASA ADS] [CrossRef] [Google Scholar]
  79. Van Loo, S., Butler, M. J., & Tan, J. C. 2013, ApJ, 764, 36 [NASA ADS] [CrossRef] [Google Scholar]
  80. Varidel, M. R., Croom, S. M., Lewis, G. F., et al. 2020, MNRAS, 495, 2265 [NASA ADS] [CrossRef] [Google Scholar]
  81. Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [Google Scholar]
  82. Yu, X., Bian, F., Krumholz, M. R., et al. 2021, MNRAS, 505, 5075 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Computing 2D power spectra on non-uniform grids

Throughout the paper, power spectra were measured on 2D maps at the highest resolution. Thus, low-resolution regions were interpolated. In this section, we present power spectra measured with coarser and coarser highest resolution, down to the uniform grid limit, at level 15. The results of the tests, both for altitudinal velocity and surface density power spectra, are shown in Fig. A.1. The slope of the compensated power spectra is not changed by the fact that we use cells with different resolutions.

thumbnail Fig. A.1.

Compensated power spectra computed with on 2D maps for the maps shown in Fig. 5. The upper and lower panels show altitudinal velocity and surface density power spectra, respectively. Each colour corresponds to a different highest resolution of the cells, varying from level 20 down to level 15, which corresponds to a uniform grid. Power spectra in bold and thin lines correspond to the F65 and F10 runs, respectively. The latter are all shifted down by 5 dex for clarity.

All Tables

Table 1.

Characteristics of the simulated galaxies.

In the text

All Figures

thumbnail Fig. 1.

Density-temperature diagrams for the zoomed regions, 10 Myr of evolution after the activation of level 20. The dashed lines show the minimum pressure floor to satisfy the Truelove et al. (1997) criterion for levels 15–20, from left to right. This pressure floor is smoothly reduced towards the centre of the zoom (see text).
In the text
thumbnail Fig. 2.

Gas density of the F10 (left) and F65 (right) runs. The white circles show the location of the zoomed region.
In the text
thumbnail Fig. 3.

Normalised gas density PDFs for the F10 and F65 runs at the time shown in Fig. 2, i.e. before the refinement in the zoomed-in region is triggered. Local maxima in the density PDF correspond to density thresholds for refinement.
In the text
thumbnail Fig. 4.

Power spectra of the three velocity components from face-on mass-weighted velocity projection maps. The spectra are compensated by k3. The F65 model is shown with bold lines, and the F10 model is plotted with thin lines. The F10 power spectra are shifted down by 3 dex for clarity. The spikes seen at the small spatial scales are due to oversampling because of the AMR grid out of which the Fourier transform was performed. These spectra show that the injection scale of turbulence is indeed different in the two models, and corresponds roughly to the disk scale height.
In the text
thumbnail Fig. 5.

Zoomed regions in both galaxies. Left panels: gas density maps. Right panels: maximum level of refinement along the line of sight. Top panels: zoom in the F10 simulation, seen face-on. Lower panels: zoom in the F65 simulation seen face-on.
In the text
thumbnail Fig. 6.

Normalised gas density PDF in the zoomed regions in the F10 (black) and F65 (red) models 10 Myr of evolution after the activation of level 20.
In the text
thumbnail Fig. 7.

Evolution of the ratio between the gas density PDF to the final gas density PDF. The top (bottom) panel shows the F10 (F65) simulation.
In the text
thumbnail Fig. 8.

Evolution of the 3D velocity dispersion in F10 and F65 after the activation of level 20.
In the text
thumbnail Fig. 9.

Evolution of the compressive ratio ζ after the activation of level 20 in F10 (black) and F65 (red). The dashed grey line shows the locus of energy equipartition: ζ = 30%.
In the text
thumbnail Fig. 10.

Velocity power spectra for the two simulations. Top panel: 2D power spectrum of the three velocity components 10 Myr after the activation of level 20. The curves are compensated by k3. Curves from to the F65 run are plotted in bold, and the thin lines show the F10 run. The F10 power spectra are shifted down by 3 dex for the sake of clarity. Bottom panel: evolution of the power-law index of the fit of the velocity power spectra. Curves related to the F65 run are shown in bold.
In the text
thumbnail Fig. 11.

Surface density power spectra for the two simulations. Top panel: surface density power spectra for F10 and F65, 10 Myr after the activation of level 20. The curves are compensated by k0.7. Bottom panel: evolution of the power law of the fit of the velocity power spectra.
In the text
thumbnail Fig. 12.

Substructures in the zoomed regions. Left panel: gas density maps in the central regions in the zoom. The origin is the centre of the zoomed region. Right panel: gravitationally bounds clumps (with αvir <  2, see text). The top and bottom panels show the F10 and F65 runs, respectively.
In the text
thumbnail Fig. 13.

Mass spectrum of the substructures for the two simulations. Top panel: mass spectrum of the bound structures in the zoom (αvir <  2). The pink histogram and fit are obtained for a detection performed on the edge-on density map. The power slopes are parametrised by dN/dM ∝ M−β. Bottom panel: evolution of the slope of the power-law fit to the high-mass end of the mass spectrum. The dashed grey line shows the location of the −1.8 exponent.
In the text
thumbnail Fig. A.1.

Compensated power spectra computed with on 2D maps for the maps shown in Fig. 5. The upper and lower panels show altitudinal velocity and surface density power spectra, respectively. Each colour corresponds to a different highest resolution of the cells, varying from level 20 down to level 15, which corresponds to a uniform grid. Power spectra in bold and thin lines correspond to the F65 and F10 runs, respectively. The latter are all shifted down by 5 dex for clarity.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.