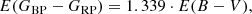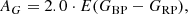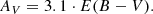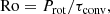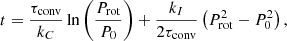| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202245441 | |
| Published online | 17 May 2023 | |
The rotation period distribution in the young open cluster NGC 6709⋆
1
Leibniz-Institute for Astrophysics Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: lizmcole@gmail.com
2
Space Science Institute, 4765 Walnut St STE B, Boulder, CO, 80301
USA
Received:
11
November
2022
Accepted:
28
February
2023
Open clusters serve as a useful tool for calibrating models of the relationship between mass, rotation, and age for stars with an outer convection zone due to the homogeneity of the stars within the cluster. Cluster-to-cluster comparisons are essential to determine whether the universality of spin-down relations holds. NGC 6709 is chosen as a more distant representative Pleiades-aged cluster for which no rotation periods of members have previously been obtained. This cluster is at a distance of over 1 kpc and has two red giant members. Isochrones place the age of the cluster at around 150 Myr, or approximately the same age as the Pleiades. Photometry is obtained over a multi-month observing season at the robotic observatory for STELLar Activity (STELLA). After basic processing, point-spread-function (PSF) photometry was derived using DAOPHOT II, and a suite of related software allowed us to create time series of relative magnitude changes for each star. Four time series analysis methods were then applied to these light curves to obtain rotation periods for members stars. We obtain, for the first time, rotation periods for 45 FGK cluster members of NGC 6709. We plot the Gaia DR3 colors of the member stars against their rotation periods and find a slow-rotating sequence with increasing rotation periods toward redder stars and a smaller clump of rapid rotators that have not yet joined this sequence. NGC 6709 has rotation periods very similar to those of another Pleiades-aged open cluster, NGC 2516.
Key words: stars: rotation / stars: solar-type / starspots / stars: variables: general / techniques: photometric / open clusters and associations: individual: NGC 6709
Table 5 and data for all stars found in the field of view are only available at the CDS via anonymous ftp to https://cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/673/A119.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The rotation periods of cool stars, both in open clusters and in the field, have attracted considerable attention in recent years. Not only does the rotation period provide the basic observable that governs the activity properties of cool stars, but it can also be measured very precisely. Furthermore, the rotation period distributions evince patterns (e.g., Barnes 2003) that inform us about internal processes in stars or even their ages (e.g., Skumanich 1972; Barnes 2007). Open clusters are particularly valuable as calibrating objects, or more generally because they offer us homogeneous samples of coeval stars of the same composition. This paper contributes to that effort by presenting a newly determined rotation period distribution for a hitherto unstudied young open cluster, NGC 6709.
The Sun is not unique as a star, and so the physics of the solar-wind and angular momentum of the Sun in studies by those such as Parker (1958) and Weber & Davis (1967) can be applied to other stars. A star after formation should spin down as angular momentum is lost from the interactions of the stellar winds with magnetic fields (e.g., Mestel 1968). This tendency for older stars to spin more slowly takes the form of Skumanich’s relationship for solar mass stars: v sin i ∝ t−1/2 (Skumanich 1972). This relationship has been generalized to one where the rotation period depends on both the mass (or, equivalently, color) and age of a star. If such a relationship actually exists, it can be inverted to provide the age of a star from its measured rotation period and color, a procedure that is called gyrochronology (Barnes 2003).
Early measurements of stellar rotation predating large-format CCDs used v sin i measurements from spectroscopy (e.g., Gaige 1993). Modern observing techniques allow more precise and unambiguous measurements of the rotation period via photometric changes. Thus, the most efficient way of observing the rotation rates of stars is through changes in brightness in a time series of observations of an object. Kron (1947) initially observed periodic changes in light curves due to large, cool star spots. FGKM stars have an outer convection zone, and the suppression of convection from the magnetic field causes a cool spot to form, analogous to the sunspots. As these spots rotate across the line of sight, a dip in the stellar brightness may be observed (e.g., Chugainov 1966; Bopp & Evans 1973; Rodono et al. 1986; Strassmeier 2009). Since star spots are thought to last at least the order of a few months, the stellar rotation can then be extracted from a time series of observations of a star’s brightness.
Open clusters provide a rich laboratory for observing stellar rotation. Cluster members can be considered largely homogeneous in chemical composition and age (e.g., De Silva et al. 2006), and so observing the rotation rates of the FGK stars (and M dwarfs where possible) can provide information about the dependence of rotation periods on mass. Furthermore, the age of the open cluster can be determined by other independent methods such as isochrones (e.g., Sandage & Eggen 1969) and measurements of the chromospheric flux (e.g., Mamajek & Hillenbrand 2008). Open clusters can therefore serve to calibrate the age-mass-rotation relationship essential to gyrochronology. This method of using individual open clusters as snapshots of stellar rotation at a single age only holds if all clusters of a similar age and metallicity show similar distributions in rotation periods. Cluster-to-cluster comparisons become essential to this theory.
One benchmark candidate for young open clusters around the age of 125 Myr is the well-studied Pleiades at a distance of 133 pc (e.g., van Leeuwen et al. 1987; Hartman et al. 2010; Rebull et al. 2016). This cluster, along with Hyades (e.g., Radick et al. 1987; Delorme et al. 2011; Douglas et al. 2019), was used to derive Skumanich’s relationship for the evolution of rotation for solar-type stars. Fritzewski et al. (2020, hereafter F20) compared the rotation rates of members of four other Pleiades-age clusters and find that all measured ones behave similarly.
NGC 6709 was chosen as a significantly more distant representative of Pleiades-age clusters with no previous observations of rotation rates of member stars. Several membership studies are available the in literature relying on either spectroscopic or proper motion membership determination methods (Hakkila et al. 1983; Tadross 2001; Dias et al. 2001, 2014; Kharchenko et al. 2004, 2013; Vande Putte et al. 2010; Sampedro et al. 2017; Cantat-Gaudin et al. 2018). It has two red giant members (Lindoff 1968; Sears & Sowell 1997; Ahumada & Lapasset 2007; Mermilliod et al. 2008), possible Be stars (Schild & Romanishin 1976; Subramaniam & Sagar 1999), and possible blue stragglers (Ahumada & Lapasset 2007). One of the red giants is a spectroscopic binary (Mermilliod et al. 2007) and the other is a possible member of a quadruple star system (Smiljanic et al. 2018).
The above-1000 pc distance and consequent faintness of the cluster has led to some disparity in adopted parameters due to the difficulty in observing the cluster, although with the advent of Gaia, these values have been more in agreement in recent publications. Values for the EB − V color excess range from 0.28−0.35 (Johnson et al. 1961; Becker 1963; Burki 1975; Mermilliod 1981; Subramaniam & Sagar 1999; Tadross 2001; Lata et al. 2002; Ahumada & Lapasset 2007; Piskunov et al. 2007; Kharchenko et al. 2013; Joshi et al. 2016; Sampedro et al. 2017). Distance estimates range from 930−1253 pc (Johnson et al. 1961; Hoag & Applequist 1965; Lindoff 1968; Burki 1975; Mermilliod 1981; Hakkila et al. 1983; Barkhatova et al. 1987; Lynga & Palous 1987; Leisawitz 1988; Subramaniam & Sagar 1999; Dias et al. 2001; Tadross 2001; Loktin & Beshenov 2003; Kharchenko et al. 2005; Cantat-Gaudin et al. 2018).
Age estimates based on various methods of isochrone fitting in literature have ranged from 65 Myr to 320 Myr. Earlier studies of NGC 6709 tend to obtain ages of less than 80 Myr (Lindoff 1968; Burki 1975; Mermilliod 1981; Barkhatova et al. 1989) or older than 200 Myr (Barbaro et al. 1969; Sagar & Subramaniam 1999; Subramaniam & Sagar 1999), possibly due to instrument limitations at the time and the distance to NGC 6709. More recent studies place the age around 100−190 Myr (Tadross 2001; Lata et al. 2002; Chen et al. 2003; Kharchenko et al. 2005; Ahumada & Lapasset 2007; Wu et al. 2009; Vande Putte et al. 2010; Smiljanic et al. 2018; Bossini et al. 2019; Cantat-Gaudin et al. 2020).
Radial velocity measurements have only been obtained for a few member stars, including the red giant members. Hence, there is some degree of uncertainty, and published values range from −7 to −13 km s−1 (Lynga & Palous 1987; Kharchenko et al. 2005, 2013; Vande Putte et al. 2010; Conrad et al. 2017; Soubiran et al. 2018). Metallicity is not well-measured for this cluster, but spectroscopy from UVES members from Gaia-ESO data places the cluster near solar values (Magrini et al. 2021).
This work is part of the Stellar activity Open Cluster Survey (SOCS). The survey observes multiple open clusters over periods of several months to obtain rotation periods using the STELLar Activity (STELLA) robotic telescope. The objective is to establish the similarities between open clusters of similar ages as well as to track the evolution of rotation periods over time with clusters of different ages (e.g., Fügner et al. 2011; Barnes et al. 2015).
2. Methods
To derive rotation periods for stars in NGC 6709, we observed the field over several months – a comparatively long baseline that is permitted by our robotic observing – determined which stars in the field belong to the cluster, and obtained their corresponding colors from literature. We then constructed light curves for each star from the collection of frames and performed time-series analyses to obtain rotation periods and error estimates for each member star.
2.1. Data acquisition and reduction
The observations were carried out using the 1.2 m telescope STELLA-I at the Izaña Observatory in Tenerife, Spain from May 2015 until September 2016. This is part of the STELLA robotic observatory, which also includes the 1.2 m spectroscopic telescope STELLA-II. The observatory operates robotically each night via in-house custom-built software (Granzer 2004), provided conditions are suitable for observing targets determined by a program with user-defined priorities. For more information about STELLA operations, we invite the reader to consult Strassmeier et al. (2004, 2010), and Weber et al. (2016).
The CCD resolution for the wide-field imager WiFSIP V2.0 is 4066 × 4064 pixels, or 22′×22′. A single field was used to observe NGC 6709 due to its relatively small angular size. This field contains over two-thirds of the member stars when centered on the cluster. Observations were acquired in the Johnson V band with exposure times of 24 s, 120 s, and 300 s to retain sensitivity to as wide a range of bright (bluer) and faint (redder) stars as was practicable.
Table 1 summarizes the dates and total number of successful observations available for each exposure time, after discarding any unusable frames due to bad seeing, poor weather conditions, lunar proximity, and tracking errors. Significant numbers of such frames are a typical consequence of robotic observations. With the 24 s exposures, visits to the target happened up to ten times per night, although typically usable frames on any successful night were in the range of three to seven. For the longer exposures of 120 s, this dropped to a maximum of seven times per night, with typical values below six. And for the longest exposure time, the range was up to four times per night for the target. The maximum time baseline of observations for each exposure group is under six months in order to observe multiple theoretical variability cycles. This dataset exceeds our minimum requirement of 50 usable frames for each exposure time and the minimum acceptable time baseline of 60 days to preserve our sensitivity to the longer rotation periods.
Observations and exposure times.
2.2. Membership
We adopted the membership study of Cantat-Gaudin et al. (2018, hereafter CG18) and define member stars as all those given a membership probability by CG18 of 0.5 or higher. This study makes use of the recent high-precision Gaia observations and includes many dimmer members that previous studies were unable to observe likely due to instrument limitations (e.g., Hakkila et al. 1983; Kharchenko et al. 2013; Dias et al. 2014). According to CG18, the mean proper motion of NGC 6709 is μRA = 1.414 mas yr−1 and μDec = −3.532 mas yr−1, and the distance is 1064 pc. The properties we adopted for NGC 6709 and their references are listed in Table 2. The study by CG18 with our membership criteria provides 299 open cluster members in total.
Properties of open cluster NGC 6709.
Figure 1 shows the location of all stars with a membership probability ≥0.5 and the stars used in this study. Our field of observation covers the denser cluster center, and so we have observations for 210 of the cluster members. CG18 was limited to stars with mG < 18 due to the increase in errors at higher apparent magnitudes. This effectively limits the determination of membership for stars of NGC 6709 to K stars or bluer due to the distance and reddening of the cluster. We searched for possible additional members not included in CG18 using the Gaia DR3 proper motion data and the asymmetric membership described in Wu et al. (2002). We used the proper motion errors provided by Gaia for individual stars for the ϵRA and ϵDec, and the dispersion for the cluster is from CG18, listed in Table 2. For the dispersion of the field stars, we filtered the data for stars with proper motion errors < 0.1 and fit Gaussian distributions in the right ascension and declination separately to obtain values of σRA, f = 3.3 and σDec, f = 4.3. From these results, we further filtered for parallaxes between 0.83 and 1.11 mas, corresponding to distances of 0.9−1.2 kpc. We searched for additional members beyond the mG < 18 cutoff or members with suitable proper motions and parallaxes as determined by the Gaia DR3 data that were not included in CG18 (which used the Gaia DR2 data). These additional stars are listed in Table 3 and are represented by the circled diamonds in Fig. 1. Radial velocity measurements for cluster members are sparse, with measurements mainly obtained from the red giants and a few other bright members (e.g., Subramaniam & Sagar 1999; Mermilliod et al. 2008; Kharchenko et al. 2013; Soubiran et al. 2018) and so membership through radial velocity measurements is not possible with existing surveys.
 |
Fig. 1. NGC 6709 members. The field of observation is centered on the dense center of the cluster and encompasses approximately two-thirds of the members. Stars used in this study are encircled, and our field of view is indicated by the square. Additional stars used as members in this study are shown as green diamonds. |
Additional cluster members.
2.2.1. Catalogs
Supporting data for observations in standard pass bands are taken from the literature by cross-referencing the coordinates of stars in our field with widely used catalogs. The coordinates were obtained by converting pixel coordinates to sky coordinates using WCSTOOLS (Mink 1997) and then matched to catalogs with ASTROPY (Astropy Collaboration 2018). We used the UCAC4 catalog for measurements in the B and V pass bands (Zacharias et al. 2013) and the Gaia DR3 catalog for G, GBP, and GRP (Gaia Collaboration 2016, 2020) pass bands. We find some improvement in the Gaia colors with the DR3 catalog over the DR2 values given in CG18.
We primarily utilized the Gaia DR3 colors for this work as it is the most complete catalog to date with photometry for almost all of the stars in our field. Observations in the B and V pass bands only exist for the brighter stars and hence are available for only a fraction of our cluster members. In order to facilitate a comparison with studies performed in B − V colors, we used the equations in Appendix A of Gruner & Barnes (2020) to calculate values for B − V from GBP − GRP when no such values can be found in the UCAC4 catalog. The conversions between the two are piece-wise empirical functions fit to, among others, the Pleiades, and so they should be reasonable for NGC 6709.
2.2.2. Open cluster parameters of NGC 6709
Values for reddening are selected based on literature values and adjusted by fitting isochrones. Literature values fall in the relative range from 0.28 (Kharchenko et al. 2013) to 0.35 (Subramaniam & Sagar 1999) for E(B − V). We used the following relations from Gruner & Barnes (2020):
and
Gaia DR3 measured parallaxes for each star are used for the distance modulus calculation rather than a single value for the entire cluster.
We used a fit to solar-metallicity PARSEC isochrones for 150 Myr to determine a good reddening value for this work (Bressan et al. 2012). This is based on the oft-cited age of NGC 6709 of about 150 Myr, although the main-sequence turnoff does not fit this isochrone and the cluster is quite probably older than said value. We selected solar metallicity based on the spectroscopic analysis of Smiljanic et al. (2018) for the red giant member BD+10 3697 (Gaia DR3 4311559274405377280), where [Fe/H] = −0.01. This isochrone also provides a good fit for the two red giants in the membership study of CG18. The CMDs corrected with the values in Table 4 are shown in Fig. 2 for (B − V)0 versus MV and (GBP − GRP)0 versus MG. We also include the 200 Myr isochrone as this provides a slightly better fit for the main-sequence turn-off in Gaia colors. Where measurements are lacking for mB and mV, we instead used the conversion Eqs. (A.3) and (A.7) of Gruner & Barnes (2020) to convert the Gaia colors to Johnson colors and fill in the lower right section of the main sequence displayed in the upper panel, as well as a few brighter members that also lack observations in both the B and V bands. Also shown are the PARSEC isochrones. Possible binaries in the lower panel are either determined by their location above the main sequence or by the corresponding Gaia re-normalized unit weight error (RUWE) measurements, where RUWE < 1.4 indicates a good astrometric solution and hence single star, and values above this indicate a possible multistar system (Gaia Collaboration 2016). Possible photometric binaries are defined as stars that lie 0.25 mag above the main sequence line. We show possible binary members and indicate whether these are due to RUWE values in the bottom panel of Fig. 2.
 |
Fig. 2. Color magnitude diagrams for NGC 6709 in B − V (above), and Gaia color (below). PARSEC isochrones for 150 Myr and 200 Myr are also displayed. The line-of-sight extinction is calculated for each star using individual stellar parallaxes as measured by Gaia instead of the mean cluster distance. Calculated (B − V)0 from Gaia colors are shown by small gold dots (above). Possible photometric binaries are indicated in blue and RUWE-value binaries are indicated by orange triangles (below). |
Adopted parameters used for NGC 6709.
2.3. Construction of light curves
The light curves for individual stars are constructed using DAOPHOT II (Stetson 1987; Stetson et al. 1990). First, one master frame for each exposure time was selected from all the usable observations. We selected frames from the following dates: 9 Jul. 2016 for 24 s, 31 May 2016 for 120 s, and 17 Jul. 2015, for 300 s. These frames were selected based on low levels of light contamination, the goodness of the instrument focus, the lack of artifacts, and the low ellipticity of the stars. In order to use point-spread-function (PSF) photometry, suitable stars had to be selected from all possibilities found by DAOPHOT II. Approximately 300 sources were selected for PSF photometry from the suggested PSF stars found by the program and individually checked for counts comfortably between the background and saturation level and a minimum distance from other light sources of at least 15″. Furthermore, a cross-section examination of pixel values across these stars should have a single peak and the star circular. As a final step, any stars located near bad pixels were discarded.
Once the stars for PSF photometry were selected, ALLSTAR was used to find instrumental magnitudes for all sources in each frame using the stars assigned for the PSF photometry as a reference point. The magnitudes from each of these frames were then assembled as light curves using DAOMATCH and DAOMASTER. DAOMATCH first pinpointed each source possible in every frame by taking the 30 brightest stars in each separate frame, matched triangles with the master frame, and derived a coordinate transformation for use from frame to frame. DAOMASTER then refined those transformations and applied them to all sources and assigned each source its own identifier across all frames. Each source was then outputted with its pixel location on the master frame and measured magnitudes from each frame, forming a time series for each star.
Figure 3 shows the standard deviation σx found by Daophot versus the magnitude mG from the Gaia DR3 catalog. Magnitude differences are detectable down to the millimag regime. It can be seen that the fainter stars exhibit more uncertainty overall and that the field contains some highly variable stars. The final step in producing the light curves was to remove outliers using the sigma clipping function in SCIPY (Jones et al. 2001; Virtanen et al. 2020).
 |
Fig. 3. Standard deviation versus magnitude for all stars with light curves. |
2.3.1. Time series analysis
To analyze the light curves, four methods were selected with the criteria of applicability to randomly spaced observations. The phase dispersion minimization (PDM) method from Stellingwerf (1978) tests for periods that minimize the dispersion when the data are phased to the test periods. No a priori knowledge of the shape of the light curve is required for this method, and so possible spot structure should not affect the results. The string length (SL) method of Dworetsky (1983) phases the data with a test period and calculates a total “string length” between the data points, seeking periods that minimize this string length. Similarly to the PDM method, this one utilizes phase folding and seeks a minimum in the periodogram. This method is chosen as an alternative method to the PDM to examine the dispersion present in a phase-folded light curve.
The generalized Lomb-Scargle (GLS) method of Zechmeister & Kürster (2009) is a frequency analysis method that accounts for errors and offsets of the dataset. The GLS method can handle unevenly sampled data and fits the light curves to a combination of sine and cosine waves. We additionally used the CLEAN method of Roberts et al. (1987), which also samples frequencies but removes artifacts from unevenly sampled data such as the one-day alias. This serves as a complementary method to GLS in that it may amplify the true signal when more than one period is present in the data or there is noise contribution. Periods obtained via these methods appear as maxima in the periodograms.
2.3.2. Period selection
After obtaining periodograms with the four methods, we selected a period based on the criteria as follows. Firstly, there should be agreement within 0.1 d between a primary dip in the PDM method and primary peak in the GLS method, and there should also be similar evidence of a minimum or maximum in the periodograms for either or both of the SL and CLEAN methods. Secondly, the magnitude variations should be higher than the noise from constant stars of similar magnitudes. Thirdly, the phase-folded data should have a single maximum and minimum to avoid selecting a higher harmonic of the period. Finally, the fit should be valid across most of the time series and there should be a suitable density of observations. Each criterion was given one point, and only periods that have three or four points total for at least one exposure time were selected as candidate periods for the stars.
The light curve and the selected period are visually inspected for each of the three exposure times independently. This system of determining periods tends to err on the side of caution in assigning a rotation period since each individual method does not always successfully recover the true rotation period and depends on factors such as the signal-to-noise ratio, object brightness, and sampling (e.g., Graham et al. 2013). 186 out of the 204 cluster member stars were found in more than one exposure batch, and so the selected periods at different exposure times for the same star are compared. In most cases, the discrepancy is less than 0.1 day and the few exceptions are harmonics or subharmonics.
From the cases where a star has more than one possible period due to the multiple exposure times, we selected whichever fulfilled more criteria, had the clearest peaks or dips in the periodograms, and had the most observations, in that order, as our period. In some cases, a period is not recovered at a different exposure time, either because the exposure time was too short to capture the magnitude changes and variability, or the exposure time was too long and reached saturation.
2.3.3. Uncertainties in the period
Error bars for periods are obtained from Gaussian fits to the corresponding period minimum in the PDM. Fits are made for PDMs with minima ≤0.6, although exceptions are made for those with a minimum between 0.6 and 0.8 that show a strong single peak in the GLS periodogram. We used the standard deviation σ of the Gaussian distribution as an indication of the uncertainties in the periods so that wide peaks corresponded to a larger uncertainty than narrow peaks. We only used the error associated with the exposure from which the final period was selected. Because this is selected via Gaussian distributions fit to the PDM periodogram, this σ is accordingly only associated with the PDM method. The SL method does not provide clear minima in most cases, and the GLS and CLEAN methods use a grid in frequency space and thus skew the errors when translated to the period space.
3. Results
Each exposure time group was analyzed independently in DAOPHOTII. This allowed for confirmation of rotation periods among stars that appeared in more than one exposure group. Of the 210 cluster members mentioned in Sect. 2.2, we constructed light curves for 187 probable members. Of these, 182 are FGK stars and five are A stars. From these, we find periods for 45 FGK cluster members and for two of the A stars. All rotation periods found and the Gaia DR3 designations along with catalog and calculated colors are shown in Table 5. Final periods were selected via the method outlined in Sect. 2.3.2. Stars either showed agreement between different exposure times within a few percent, or the harmonic or subharmonic periods produced a stronger signal at a different exposure. The phased light curves and results from the period analysis methods for all member stars with rotation periods are shown in Fig. A.1. All possible binary stars with strong period signals are photometric, with RUWE values between 0.86 and 1.13. In most cases, the selected period shows agreement between the PDM, CLEAN, and GLS methods, but in a few cases the noise level is higher than the magnitude changes and the minima with the PDM methods are weak, and so we selected our periods from the CLEAN and GLS methods. The SL method is primarily useful for confirming a period in the PDM of less than three days. With each phased light curve, we subtracted the mean. Our methods are best suited to finding rotation periods greater than one day due to the sampling rate per night and the dominance of the one-day alias.
Results for NGC 6709 FGK member stars with Prot.
Our color-period diagram (CPD) is shown in Fig. 4 for both (B − V)0 and (GBP − GRP)0. We show the (B − V)0 for comparison with other literature studies of rotation rates versus colors, but as can be seen here, the sequence demonstrates more spread than for (GBP − GRP)0 because the uncertainties in these colors are greater. The CPD shows a sequence of increasing rotation periods toward redder stars. Below this sequence, there is a small clump of rapidly rotating K stars, which is to be expected for a cluster that is younger than ≈200 Myr. The photometric binaries lie below the slow rotator sequence, although these also have longer periods toward the cooler stars. NGC 6709, due to observational limits, lacks observations for the M dwarfs. Above the slow rotator sequence, there is at least one probable binary with a much slower rotation period and a membership probability of 0.6. There are also two bright A stars that had periodic brightening and dimming, but whether these are the result of being multiple star systems or some other phenomenon occurring in the line of sight is unknown. The rotation periods for these two stars only appeared in the 24 s exposure due to saturation at longer exposure times, but the periodic magnitude change is significant enough that a signal was found in multiple time-series analysis methods.
 |
Fig. 4. Periods versus (B − V)0 (top) and (GBP − GRP)0 (bottom). Error bars are the σ value of the Gaussian fit to the minimum at the period in the PDM periodogram. Squares in (B − V)0 indicate magnitudes calculated from (GBP − GRP)0, while circles show magnitudes found in the UCAC4 and Gaia DR3 catalogs (top and bottom, respectively). Possible binaries are indicated in blue. |
4. Discussion
Due to the faintness of NGC 6709, we used the GBP and GRP color system from the Gaia DR3 survey to avoid the necessity of converting the colors for the fainter stars that lack observations in other pass bands. We used the conversion from Gruner & Barnes (2020) to convert between Gaia colors and Johnson colors. The two bluest stars with rotation periods from NGC 6709 are omitted from the discussion as these are A stars and lack a convection zone, considered a critical component for the dynamo type that supports the formation of star spots (e.g., Berdyugina 2005). Thus, their periodicity is likely the result of being members of a multiple star system and actual rotation rate is unknown. For a more in-depth discussion of the behavior of these models including M dwarfs, which are not present in our sample, the reader is referred to F20.
4.1. Stellar spin-down models
We compare the results with several models of stellar rotation and age. These models are semi-empirical and use a theoretical framework built on the mechanisms thought to be responsible for stellar spin-down and are calibrated to observations of, for example, the Sun, or well-studied clusters such as the Hyades. We selected the models of Barnes & Kim (2010, hereafter B10), Matt et al. (2015, hereafter M15), Amard et al. (2019, hereafter A19), and Spada & Lanzafame (2020, hereafter S20) to derive theoretical isochrones for the estimated age of NGC 6709.
The isochrones from the models are plotted against the rotation periods found for NGC 6709 in Fig. 5. All four stellar spin-down models have the same basic premise: a zero-age main sequence star with some initial rotation rate P0 will begin to spin down due to coupling of the magnetic field with the stellar wind. The spin-down rate depends on the Rossby number
 |
Fig. 5. Rotation periods versus (GBP − GRP)0 for cluster members and comparison to models. A19 refers to the model by Amard et al. (2019), where both the sequences for initially slow and fast rotators are shown by solid and dashed lines, respectively. M15 is the model of Matt et al. (2015) with the unsaturated and saturated regimes indicated by solid and dotted lines, respectively. B10 is the model of Barnes & Kim (2010), with the solid and dashed lines again denoting initially slow and fast rotators. S20 is the model of Spada & Lanzafame (2020). |
where τconv is the convective turnover time. The selected models differ in some of the physical constraints and free parameters, but all reproduce the observed rotational behavior to some degree.
4.1.1. The Barnes & Kim (2010) model
The B10 model is a dimensionless description of period evolution over time. The equation combines the evolution of both the fast (C) and slow (I) sequences so that the period evolution equation is
where t is the stellar age, kC and kI are dimensionless constants derived from observations, Prot is the rotation period at stellar age, and P0 is the initial rotation period. In order to be consistent with previous work, τconv is the global τc from Table 1 of Barnes & Kim (2010), which is converted to color using the corresponding columns for B and V colors and transformed using the equations of Gruner & Barnes (2020) to (GBP − GRP)0. The constants kC and kI are 0.646 d Myr−1 and 452 Myr d−1, respectively. The initial rotation of the fast sequence is P0 = 0.12 d, and for the slow sequence, P0 = 3.4 d. These are based on observations of the extrema of initial rotation periods of young cluster members. The C and I sequences that emerge from these equations provide limiting cases.
The B10 model is shown in Fig. 5 for an age of 150 Myr with initial rotation periods of 3.4 d and 0.12 d as the solid and dotted blue lines, respectively, to recreate the limits of the I and C sequences. This model results in rotation periods that are too slow for F stars and too fast for the K stars when compared to the observed rotation periods of NGC 6709 for the I sequence. There are no cluster members with rotation periods shorter than the limit created by the C sequence, which corresponds to stars with an initial rotation period of 0.12 d; this is near the break-up speed for FGK stars. The rapid rotators are not well-populated, at least partially due to the lack of observations for M stars. Barnes et al. (2016) noted that this model does not account for evolution of pre-main sequence stars and works better for clusters and stars between 400 Myr and 2.5 Gyr. The model appears to have a spin-down that is too aggressive for solar or hotter young stars, and not aggressive enough for cooler young stars. The G stars fit the model moderately well, which is not a surprise as the constants for this model were calibrated using the solar age and rotation period.
4.1.2. The Matt et al. (2015) model
The M15 model examines the changes in the torque over time on a star and the relationship with Ro. Stellar activity is divided into two regimes, saturated and unsaturated, based on whether magnetic activity indicators have approached some saturated values independent of Ro. The saturated and unsaturated regimes correspond to rapid and slow rotators, respectively. We modeled the limit of the saturated and unsaturated regimes, Eqs. (10) and (11), respectively, in M15, and input an age of 150 Myr. The moment of inertia is from the stellar tracks of Baraffe et al. (2015) and the convective turnover time is based on the empirical relation given in Cranmer & Saar (2011), as the model is calibrated to these values for τ. For the saturated limit, we used an initial rotation period of P0 = 0.2 d. Using the adopted parameters provided in Table 1 in the Erratum which are adjusted to recreate solar values at a solar age, we show the model in Fig. 5 with the solid line indicating the limit from the unsaturated regime and the dotted line the limit from the saturated regime.
The model provides a pretty good description of the G stars and our few K stars along the slow branch. Our F stars show rotation periods where the model predicts either very rapid rotation or none at all. The saturated limit for the torque is similar to the lower limit of the most rapid rotators from the B10 model, although it allows for slightly more rapid rotation in the solar regime. Few cluster members actually lie near this limit, but instead occupy the space between.
4.1.3. The Amard et al. (2019) model
The rotation periods of A19 are based on models calculated using the STAREVOL v3.40 code. The models follow structural and rotational evolution and include the disk-coupling timescale and wind braking. To match our cluster, we used the models for solar metallicity (Z = 0.0134) and an age of log T = 8.2, or 158 Myr. We show the models for both the slow and rapid rotators in Fig. 5 as solid and dotted gold lines, respectively. This corresponds to initial rotation rates of 1.6 days (2.3 days for stars with M > 1.2 M⊙) for the rapid rotators and 9.0 days for the slow rotators.
It can be seen from the figure that this model does not fit well, and a younger isochrone for the cluster would likely fit better as this one has an all-around too aggressive spin-down for stars compared to the other models. This model, however, does reproduce the rotation rates of our few F stars better. The lower limit for the rapid rotators matches fairly closely with the corresponding saturated limit of the M15 model for the GK stars. This is not entirely surprising as the torque at the surface uses the M15 formulation for the change in angular momentum.
4.1.4. The Spada & Lanzafame (2020) model
We also show the model of S20 in Fig. 5 in violet. Unlike the previous models, this model only has the slow rotator sequence. The model scales rotational coupling and stellar wind braking with mass to explain the lack of low-mass stars that have reached the slow rotator sequence for clusters younger than 1 Gyr. We used the isochrones from Table A.1 in the work of S20 for 150 Myr and the relation from Gruner & Barnes (2020) to convert (B − V)0 to (GBP − GRP)0. This model does reproduce the rotation periods for the K stars and the hotter G stars fairly well, but the spin-down is not aggressive enough for the solar-type and cooler stars, and the resulting rotation periods are too rapid compared to what has been observed for our cluster members.
4.2. Comparison to other open clusters
We compare the CPD of NGC 6709 to the similarly aged clusters detailed in F20. It can be seen in Fig. 6 from overlaying NGC 6709 with NGC 2516, the benchmark cluster from that work, that although NGC 6709 is fainter and has a few giant members, it exhibits almost identical rotational behavior. F20 also compared their open cluster with other similarly aged open clusters such as M 35, the Pleiades, M 50, and Blanco I in their Fig. 17 and noted the near-identical structure of the rotation periods versus color. Our cluster is no exception, and it fits in well with the age group of Pleiades-like open clusters.
 |
Fig. 6. Overlay of CPD of NGC 6709 on that of NGC 2516 from F20. The two distributions appear to be nearly identical in the region of overlap. |
The slow rotator sequence of NGC 6709 is very similar to that of NGC 2516. The slow-sequence for NGC 6709 is slightly above that of NGC 2516, and so this cluster should accordingly be slightly older. This matches with the evidence from Fig. 2 where the main-sequence turnoff does not match the isochrone, indicating a cluster age older than 150 Myr. There is an outlier with a much longer rotation period than expected (≈12.5 d), but similar outliers are observed for M 35, the Pleiades, and M 50. NGC 6709 also exhibits the gap between stars on the rapid rotator sequence and stars that have evolved onto the slow rotator sequence. The rapid rotators for NGC 6709 all have color values of (GBP − GRP)0 < 1.4, and so a comparison of the structure of the rapid rotators that have not yet joined the slow rotator sequence is not possible.
5. Conclusions
We observed the open cluster NGC 6709 over multiple observing seasons to obtain, for the first time, two-to-four-month-long photometric light curves using DAOPHOT II. Member FGK stars were identified and analyzed using four different methods (PDM, SL, GLS, and CLEAN) to find periodicities. By comparing the results from these four methods, we obtain rotation periods for 47 member stars within our field. We calculate the uncertainty of these rotation periods from the FWHM of the peak from the PDM method.
Using Gaia colors, we constructed a color-period diagram of cluster members. This CPD has a sequence of slow rotators with increasing rotation periods toward the redder stars and a small clump of rapidly rotating stars that have not yet converged onto the aforementioned slow sequence. The six possible photometric binary members show no significant difference and follow the same pattern as other member stars. We compare isochrones from theoretical, empirical, and semi-empirical models for stellar rotation and evolution to our CPD and estimate the cluster age to be about 150 Myr. This is within the range of ages estimated from literature based on isochrones from color-magnitude comparisons. The models that best fit the CPD of NGC 6709 are those of M15 and S20.
The rotation periods follow a similar behavior to that observed in other open clusters of similar ages and characteristics. We compared this cluster’s CPD to NGC 2516 in the work of F20 and find that the rotation period distribution for NGC 6709 matches that of NGC 2516. F20 also compares NGC 2516 to four more open clusters of similar ages, the Pleiades, M 35, M 50, and Blanco I. This further supports the notion that the mechanisms driving the star formation and subsequent spin-down for stars with similar parameters are the same for open clusters with sufficiently similar parameters of age and metallicity.
Acknowledgments
We thank the anonymous referee for their insightful and useful comments. E.C.K. gratefully acknowledges funding from the Deutsche Forschungs-Gemeinschaft (DFG project 4535/1-1B). STELLA was made possible by funding through the State of Brandenburg (MWFK) and the German Federal Ministry of Education and Research (BMBF) and is run collaboratively with the IAC in Tenerife, Spain. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research made use of Astropy (https://www.astropy.org), a community-developed core Python package for Astronomy.
References
- Ahumada, J. A., & Lapasset, E. 2007, A&A, 463, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amard, L., Palacios, A., Charbonnel, C., et al. 2019, A&A, 631, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbaro, G., Dallaporta, N., & Fabris, G. 1969, Ap&SS, 3, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Barkhatova, K. A., Kutuzov, S. A., & Osipkov, L. P. 1987, AZh, 64, 956 [NASA ADS] [Google Scholar]
- Barkhatova, K. A., Ossipkov, L. P., & Kutuzov, S. A. 1989, AZh, 66, 1154 [NASA ADS] [Google Scholar]
- Barnes, S. A. 2003, ApJ, 586, 464 [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [Google Scholar]
- Barnes, S. A., & Kim, Y.-C. 2010, ApJ, 721, 675 [Google Scholar]
- Barnes, S. A., Weingrill, J., Granzer, T., Spada, F., & Strassmeier, K. G. 2015, A&A, 583, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, S. A., Spada, F., & Weingrill, J. 2016, Astron. Nachr., 337, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, W. 1963, ZAp, 57, 117 [NASA ADS] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Bopp, B. W., & Evans, D. S. 1973, MNRAS, 164, 343 [CrossRef] [Google Scholar]
- Bossini, D., Vallenari, A., Bragaglia, A., et al. 2019, A&A, 623, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Burki, G. 1975, A&A, 43, 37 [NASA ADS] [Google Scholar]
- Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantat-Gaudin, T., Anders, F., Castro-Ginard, A., et al. 2020, A&A, 640, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, L., Hou, J. L., & Wang, J. J. 2003, AJ, 125, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Chugainov, P. F. 1966, Inf. Bull. Var. Stars, 122, 1 [NASA ADS] [Google Scholar]
- Conrad, C., Scholz, R. D., Kharchenko, N. V., et al. 2017, A&A, 600, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [Google Scholar]
- Delorme, P., Collier Cameron, A., Hebb, L., et al. 2011, MNRAS, 413, 2218 [Google Scholar]
- De Silva, G. M., Sneden, C., Paulson, D. B., et al. 2006, AJ, 131, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Lépine, J. R. D., & Alessi, B. S. 2001, A&A, 376, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dias, W. S., Monteiro, H., Caetano, T. C., et al. 2014, A&A, 564, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douglas, S. T., Curtis, J. L., Agüeros, M. A., et al. 2019, ApJ, 879, 100 [Google Scholar]
- Dworetsky, M. M. 1983, MNRAS, 203, 917 [NASA ADS] [Google Scholar]
- Fritzewski, D. J., Barnes, S. A., James, D. J., & Strassmeier, K. G. 2020, A&A, 641, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fügner, D., Granzer, T., & Strassmeier, K. G. 2011, ASP Conf. Ser., 448, 863 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2020, A&A, 649, A1 [Google Scholar]
- Gaige, Y. 1993, A&A, 269, 267 [NASA ADS] [Google Scholar]
- Graham, M. J., Drake, A. J., Djorgovski, S. G., et al. 2013, MNRAS, 434, 3423 [NASA ADS] [CrossRef] [Google Scholar]
- Granzer, T. 2004, Astron. Nachr., 325, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Gruner, D., & Barnes, S. A. 2020, A&A, 644, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hakkila, J., Sanders, W. L., & Schroeder, R. 1983, A&AS, 51, 541 [NASA ADS] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Kovács, G., & Noyes, R. W. 2010, MNRAS, 408, 475 [Google Scholar]
- Hoag, A. A., & Applequist, N. L. 1965, ApJS, 12, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., Hoag, A. A., Iriarte, B., Mitchell, R. I., & Hallam, K. L. 1961, Lowell Obs. Bull., 5, 133 [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open Source Scientific Tools for Python, http://www.scipy.org [Google Scholar]
- Joshi, Y. C., Dambis, A. K., Pandey, A. K., & Joshi, S. 2016, A&A, 593, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R. D. 2004, Astron. Nachr., 325, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R. D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R. D. 2013, A&A, 558, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kron, G. E. 1947, PASP, 59, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Lata, S., Pandey, A. K., Sagar, R., & Mohan, V. 2002, A&A, 388, 158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leisawitz, D. 1988, NASA Ref. Publ., 1202, 1 [NASA ADS] [Google Scholar]
- Lindoff, U. 1968, Arkiv for Astronomi, 5, 1 [NASA ADS] [Google Scholar]
- Loktin, A. V., & Beshenov, G. V. 2003, Astron. Rep., 47, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Lynga, G., & Palous, J. 1987, A&A, 188, 35 [NASA ADS] [Google Scholar]
- Magrini, L., Lagarde, N., Charbonnel, C., et al. 2021, A&A, 651, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [Google Scholar]
- Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [Google Scholar]
- Mermilliod, J. C. 1981, A&AS, 44, 467 [NASA ADS] [Google Scholar]
- Mermilliod, J. C., Andersen, J., Latham, D. W., & Mayor, M. 2007, A&A, 473, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J. C., Mayor, M., & Udry, S. 2008, A&A, 485, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mestel, L. 1968, MNRAS, 138, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Mink, D. J. 1997, ASP Conf. Ser., 125, 249 [NASA ADS] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Piskunov, A. E., Schilbach, E., Kharchenko, N. V., Röser, S., & Scholz, R. D. 2007, A&A, 468, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radick, R. R., Thompson, D. T., Lockwood, G. W., Duncan, D. K., & Baggett, W. E. 1987, ApJ, 321, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Stauffer, J. R., Bouvier, J., et al. 2016, AJ, 152, 113 [Google Scholar]
- Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 [Google Scholar]
- Rodono, M., Cutispoto, G., Pazzani, V., et al. 1986, A&A, 165, 135 [NASA ADS] [Google Scholar]
- Sagar, R. 1987, Bull. Astron. Soc. India, 15, 193 [NASA ADS] [Google Scholar]
- Sagar, R., & Subramaniam, A. 1999, in Revista Mexicana de Astronomia y Astrofisica Conference Series, eds. N. I. Morrell, V. S. Niemela, & R. H. Barbá, 8, 93 [NASA ADS] [Google Scholar]
- Sampedro, L., Dias, W. S., Alfaro, E. J., Monteiro, H., & Molino, A. 2017, MNRAS, 470, 3937 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Eggen, O. J. 1969, ApJ, 158, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Schild, R., & Romanishin, W. 1976, ApJ, 204, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Sears, R. L., & Sowell, J. R. 1997, AJ, 113, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [Google Scholar]
- Smiljanic, R., Donati, P., Bragaglia, A., Lemasle, B., & Romano, D. 2018, A&A, 616, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soubiran, C., Cantat-Gaudin, T., Romero-Gómez, M., et al. 2018, A&A, 619, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spada, F., & Lanzafame, A. C. 2020, A&A, 636, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [Google Scholar]
- Stetson, P. B., Davis, L. E., & Crabtree, D. R. 1990, ASP Conf. Ser., 8, 289 [NASA ADS] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2004, Astron. Nachr., 325, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 970306 [CrossRef] [Google Scholar]
- Subramaniam, A., & Sagar, R. 1999, AJ, 117, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Tadross, A. L. 2001, New Astron., 6, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Vande Putte, D., Garnier, T. P., Ferreras, I., Mignani, R. P., & Cropper, M. 2010, MNRAS, 407, 2109 [Google Scholar]
- van Leeuwen, F., Alphenaar, P., & Meys, J. J. M. 1987, A&AS, 67, 483 [NASA ADS] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
- Weber, E. J., & Davis, L., Jr. 1967, ApJ, 148, 217 [Google Scholar]
- Weber, M., Granzer, T., & Strassmeier, K. G. 2016, SPIE Conf. Ser., 9910, 99100N [NASA ADS] [Google Scholar]
- Wu, Z. Y., Tian, K. P., Balaguer-Núñez, L., et al. 2002, A&A, 381, 464 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Z.-Y., Zhou, X., Ma, J., & Du, C.-H. 2009, MNRAS, 399, 2146 [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Phased light curves for FGK member stars with rotation periods
 |
Fig. A.1. Phased light curves and results of period analysis methods. An asterisk after the Gaia designation and blue phased light curve indicates a possible binary. The vertical dotted line marks the found period. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.7. continued. |
 |
Fig. A.1. continued. |
All Tables
All Figures
 |
Fig. 1. NGC 6709 members. The field of observation is centered on the dense center of the cluster and encompasses approximately two-thirds of the members. Stars used in this study are encircled, and our field of view is indicated by the square. Additional stars used as members in this study are shown as green diamonds. |
| In the text | |
 |
Fig. 2. Color magnitude diagrams for NGC 6709 in B − V (above), and Gaia color (below). PARSEC isochrones for 150 Myr and 200 Myr are also displayed. The line-of-sight extinction is calculated for each star using individual stellar parallaxes as measured by Gaia instead of the mean cluster distance. Calculated (B − V)0 from Gaia colors are shown by small gold dots (above). Possible photometric binaries are indicated in blue and RUWE-value binaries are indicated by orange triangles (below). |
| In the text | |
 |
Fig. 3. Standard deviation versus magnitude for all stars with light curves. |
| In the text | |
 |
Fig. 4. Periods versus (B − V)0 (top) and (GBP − GRP)0 (bottom). Error bars are the σ value of the Gaussian fit to the minimum at the period in the PDM periodogram. Squares in (B − V)0 indicate magnitudes calculated from (GBP − GRP)0, while circles show magnitudes found in the UCAC4 and Gaia DR3 catalogs (top and bottom, respectively). Possible binaries are indicated in blue. |
| In the text | |
 |
Fig. 5. Rotation periods versus (GBP − GRP)0 for cluster members and comparison to models. A19 refers to the model by Amard et al. (2019), where both the sequences for initially slow and fast rotators are shown by solid and dashed lines, respectively. M15 is the model of Matt et al. (2015) with the unsaturated and saturated regimes indicated by solid and dotted lines, respectively. B10 is the model of Barnes & Kim (2010), with the solid and dashed lines again denoting initially slow and fast rotators. S20 is the model of Spada & Lanzafame (2020). |
| In the text | |
 |
Fig. 6. Overlay of CPD of NGC 6709 on that of NGC 2516 from F20. The two distributions appear to be nearly identical in the region of overlap. |
| In the text | |
 |
Fig. A.1. Phased light curves and results of period analysis methods. An asterisk after the Gaia designation and blue phased light curve indicates a possible binary. The vertical dotted line marks the found period. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.7. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.