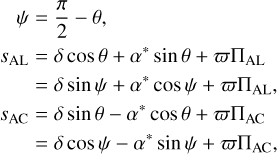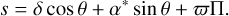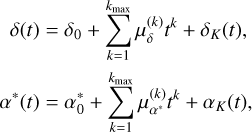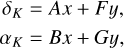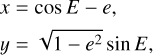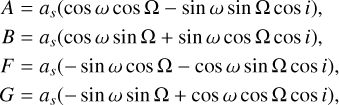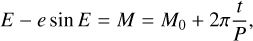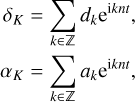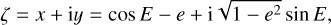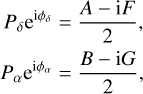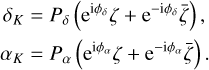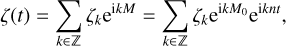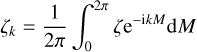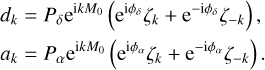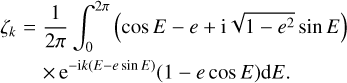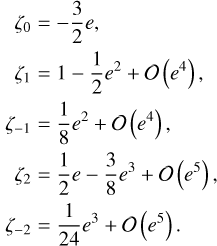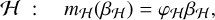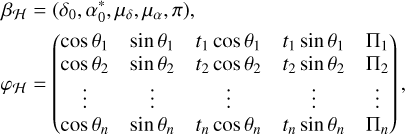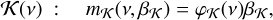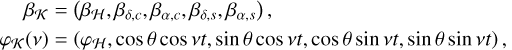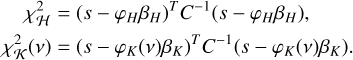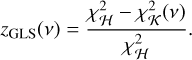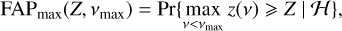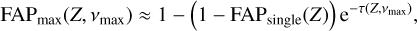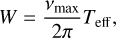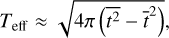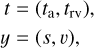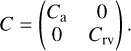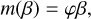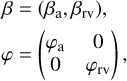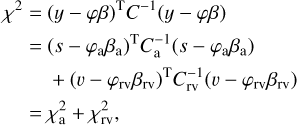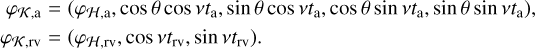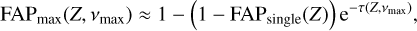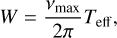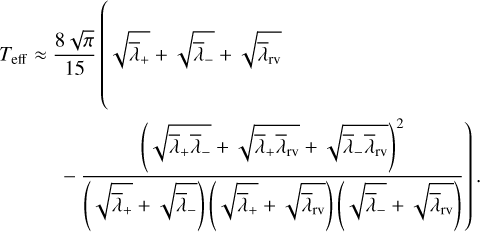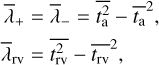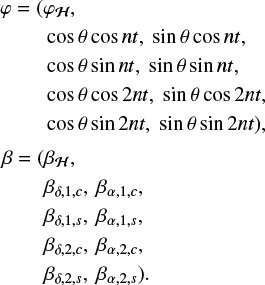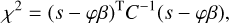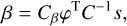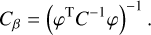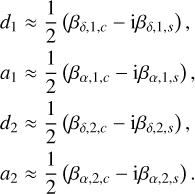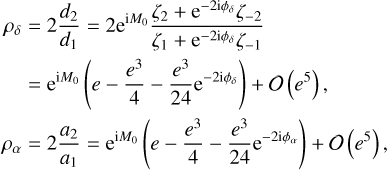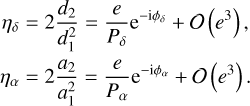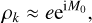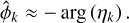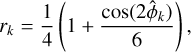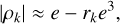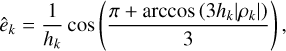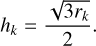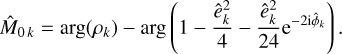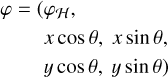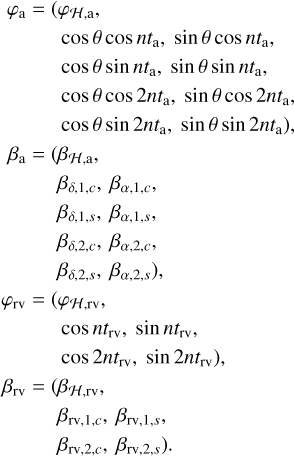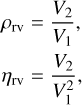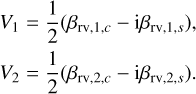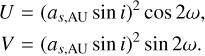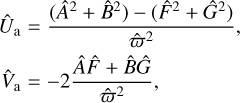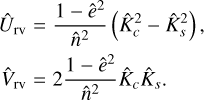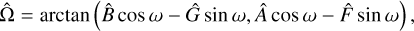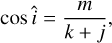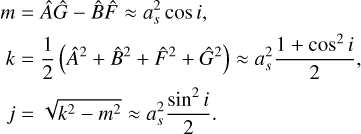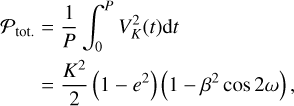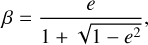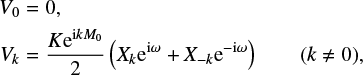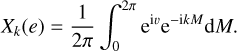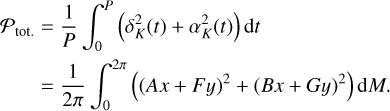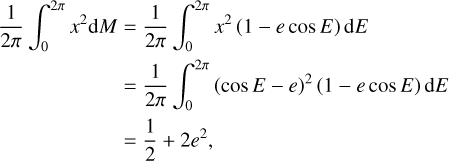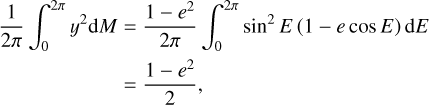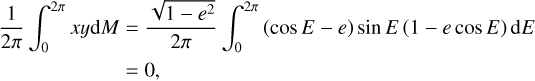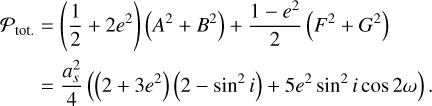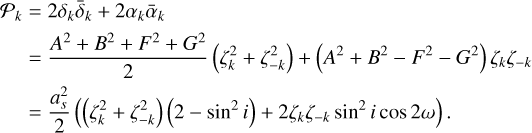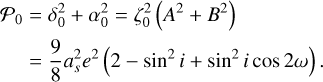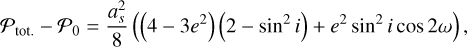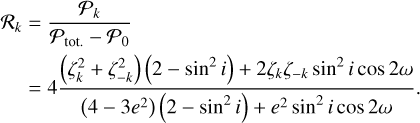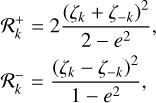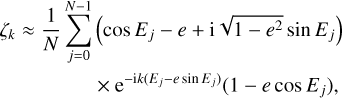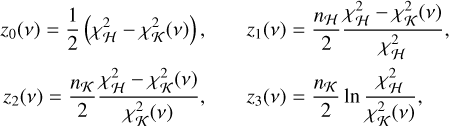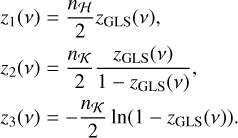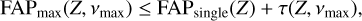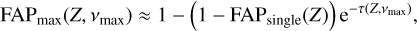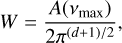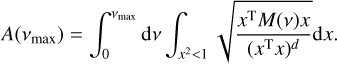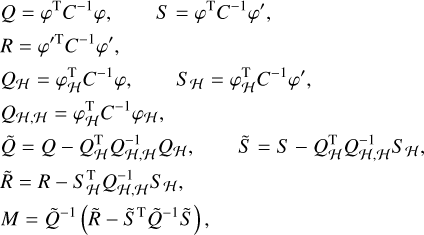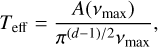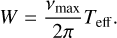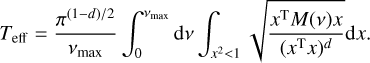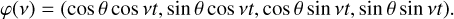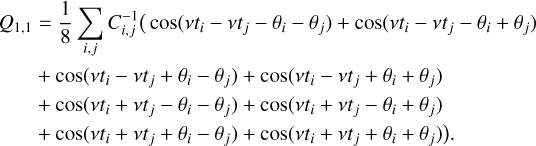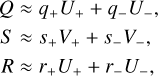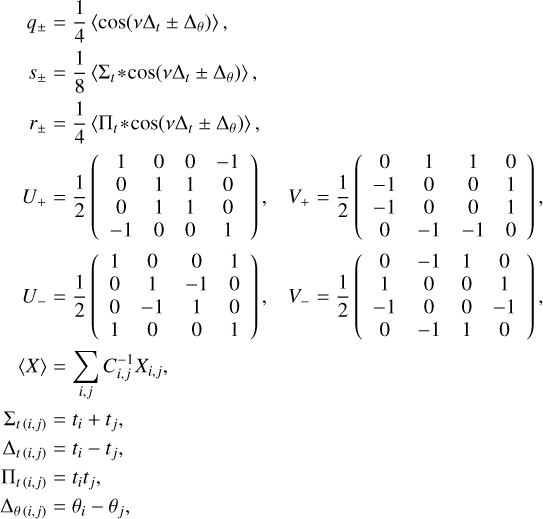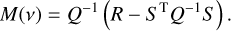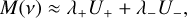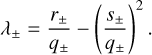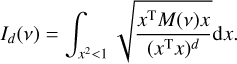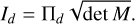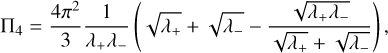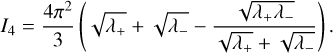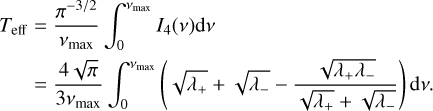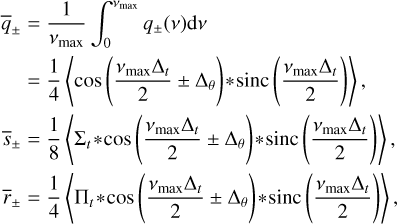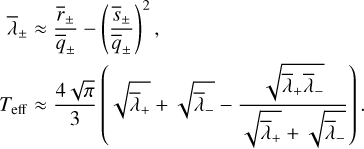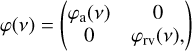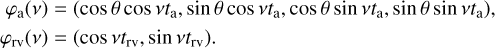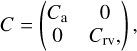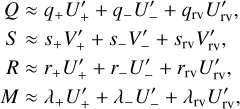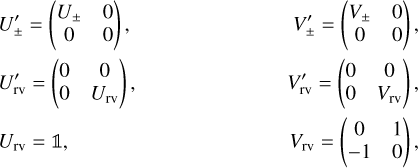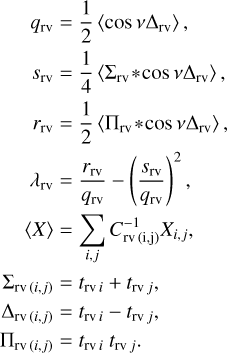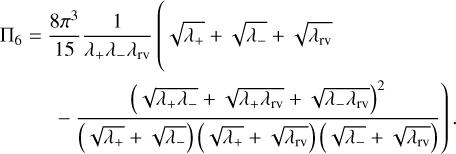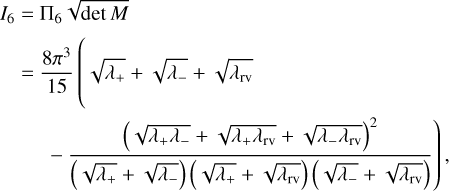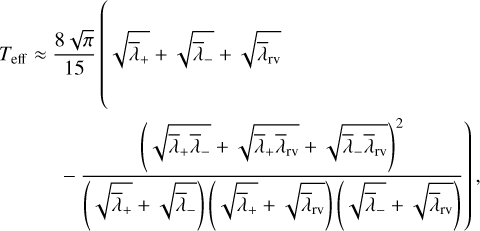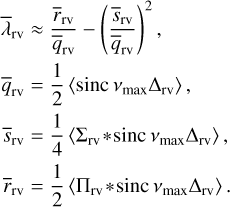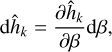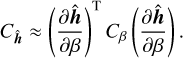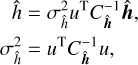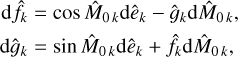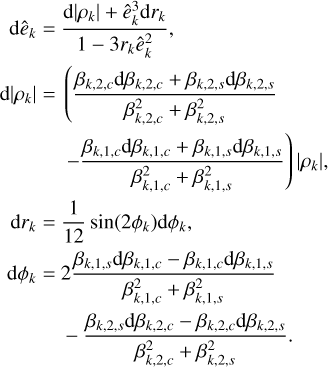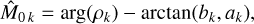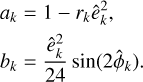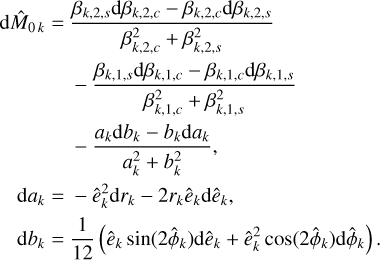| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A172 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202244018 | |
| Published online | 29 November 2022 | |
Analytical determination of orbital elements using Fourier analysis
II. Gaia astrometry and its combination with radial velocities★
Département d’astronomie, Université de Genève,
chemin Pegasi 51,
1290
Versoix, Switzerland
e-mail: jean-baptiste.delisle@unige.ch
Received:
13
May
2022
Accepted:
13
September
2022
The ESA global astrometry space mission Gaia has been monitoring the position of a billion stars since 2014. The analysis of such a massive dataset is challenging in terms of the data processing involved. In particular, the blind detection and characterization of single or multiple companions to stars (planets, brown dwarfs, or stars) using Gaia astrometry requires highly efficient algorithms. In this article, we present a set of analytical methods to detect and characterize companions in scanning space astrometric time series as well as via a combination of astrometric and radial velocity time series. We propose a general linear periodogram framework and we derive analytical formulas for the false alarm probability (FAP) of periodogram peaks. Once a significant peak has been identified, we provide analytical estimates of all the orbital elements of the companion based on the Fourier decomposition of the signal. The periodogram, FAP, and orbital elements estimates can be computed for the astrometric and radial velocity time series separately or in tandem. These methods are complementary with more accurate and more computationally intensive numerical algorithms (e.g., least-squares minimization, Markov chain Monte-Carlo, genetic algorithms). In particular, our analytical approximations can be used as an initial condition to accelerate the convergence of numerical algorithms. Our formalism has been partially implemented in the Gaia exoplanet pipeline for the third Gaia data release. Since the Gaia astrometric time series are not yet publicly available, we illustrate our methods on the basis of Hipparcos data, together with on-ground CORALIE radial velocities, for three targets known to host a companion: HD 223636 (HIP 117622), HD 17289 (HIP 12726), and HD 3277 (HIP 2790).
Key words: planets and satellites: general / methods: analytical / astrometry / techniques: radial velocities
We provide an open-source implementation of the methods presented in this article: the kepmodel python package, installable with pip or conda. The sources are available at https://gitlab.unige.ch/jean-baptiste.delisle/kepmodel.
© J.-B. Delisle and D. Ségransan 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The Gaia mission started its nominal operations in 2014 to monitor the positions of a billion stars. The amount of data generated by the spacecraft is massive and their calibration and analysis represent a vast processing challenge. In this context, the computing time dedicated to the analysis of each target is necessarily limited and efficient analysis methods have to be developed. In this article, we present efficient analytical methods for detecting and characterizing companions (planets, brown dwarfs, or stars) in astrometric time series as well as via a combination of astrometric and radial velocity time series. This study is part of an effort to improve the Gaia exoplanet detection pipeline and, more specifically, the MIKS-GA1 algorithms (Holl et al. 2022). The methods presented here have been partially integrated in MIKS-GA for the third Gaia data release (DR3).
The least-squares or Lomb-Scargle (LS) periodogram (Lomb 1976; Scargle 1982) and subsequent generalizations (e.g., Ferraz-Mello 1981; Zechmeister & Kürster 2009) are powerful tools in the search for periodicities in uneven time series and widely used in many branches of astronomy. In the context of two-dimensional (2D) astrometry (i.e., when both sky coordinates are measured at once, with a similar level of precision), the LS periodogram has also been used to search for periodicities on each coordinate independently (e.g., Black & Scargle 1982) or jointly (e.g., Catanzarite et al. 2006). More sophisticated periodograms have also been developed in the case of 2D astrometry, for instance, the phase distance correlation periodogram (Zucker 2019). However, to our knowledge, these approaches have not been extended to the case of scanning space astrometric missions, such as Hipparcos and Gaia. Here, we propose a general linear periodogram framework to efficiently locate the periods of candidate companions among scanning space astrometric time series alone and among astrometric and radial velocity time series combined. We additionally derive an analytical false alarm probability (FAP) criterion to assess the significance of the candidates. This periodogram and FAP framework builds on the previous works of Baluev (2008) and Delisle et al. (2020a), which were primarily focused on the analysis of radial velocity time series.
Once a companion is detected and its period is known, the next step is to determine the complete set of parameters describing its orbit. This is usually achieved using numerical methods, such as least-squares minimization (or likelihood maximization) algorithms, or Markov chain Monte-Carlo. However these numerical methods can be expensive in terms of computing time, especially if the initialization of the parameters is far from the solution. Here, we propose an analytical method that can efficiently determine approximate orbital elements, which may be used as the initial conditions for numerical methods. it relies on the Fourier decomposition of the time series. indeed, for an eccentric orbit, the signature of the companion has some power at the orbital period, but also at the harmonics of the orbital period. In particular, the amplitude at the first harmonics is approximately proportional to the eccentricity. We used such properties to derive all the orbital parameters from a linear least-square fit with sinusoids at the orbital period and its first harmonics. Similar methods have been developed in the context of astrometry with the cancelled space interferometry mission (SIM), (Konacki et al. 2002) and radial velocities (Correia 2008; Delisle et al. 2016). In this work, we extend the method proposed in Delisle et al. (2016) to the case of scanning space astrometry as well as to the case where astrometry and radial velocities are combined.
This article is organized as follows. In Sect. 2, we present the scanning space astrometric method and the expected astrometric signature of an unseen companion orbiting a star. Then, we define in Sect. 3 a general linear periodogram for an astrometric time series and its combination with radial velocities and we derive analytical approximations of the corresponding FAp. We obtain in Sect. 4 analytical formulas to derive an approximation of all the orbital parameters once the period is known. We illustrate our methods in Sect. 5 to reanalyze the astrometric and radial velocity time series of three stars known to host companions. While our methods have been developed in view of analyzing Gaia data, we had to fall back to illustrating them on the basis of Hipparcos data, since Gaia astrometric time series will not be publicly available before DR4. Finally, we discuss in Sect. 6 the possible uses of these methods.
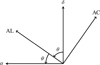 |
Fig. 1 Scan angle convention for Gaia (θ) and Hipparcos (ψ). |
2 Scanning space astrometry and Keplerian motion
2.1 Coordinates and scan-angle
Scanning space astrometric missions such as Hipparcos or Gaia do not directly measure the instantaneous declination (δ) and right-ascension (α) of a star in the ICRS frame. They instead measure the abscissa, sAL, of the star along a scan direction with great precision, while the perpendicular coordinate, sAC, is determined with a much lower precision. The measured coordinates (sAL, sAC) depend on the scanning direction which is represented with a different convention between Gaia and Hipparcos (see Fig. 1). The Gaia scan angle θ is the angle between the north (increasing δ) and the along-scan direction (increasing sAL), while the Hipparcos scan angle ψ is the angle between the along-scan direction and the East (increasing α). We thus have:
where α* = α cos δ is the modified right-ascension, ϖ is the parallax, and ∏AL, ∏AC are the parallax factors. Across scan observations can actually be treated the same way as along scan observations by defining θ′ = θ − π/2 and ψ′ = ψ + π/2. in the following, we assume that all the observations (Gaia or Hipparcos, along or across scan) are converted to follow the Gaia along-scan convention
The instantaneous coordinates of the star (δ, α*) evolve due to the proper motion of the system barycenter and to potential companions. The proper motion can be expressed as a polynomial expansion over time, so the coordinates follow
where 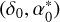 is the position of the system barycenter at the reference epoch (t = 0), kmax is the degree of the expansion of the proper motion,
is the position of the system barycenter at the reference epoch (t = 0), kmax is the degree of the expansion of the proper motion, 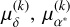 are the coefficients of this expansion, and (δK, αK) is the Keplerian part of the signal (due to companions). in most cases, only a linear proper motion is accounted for (kmax = 1), and we simplify the notations as
are the coefficients of this expansion, and (δK, αK) is the Keplerian part of the signal (due to companions). in most cases, only a linear proper motion is accounted for (kmax = 1), and we simplify the notations as 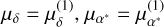
2.2 Keplerian astrometric signal
Here, we consider a star that is orbited by a single companion, assuming that the orbit is Keplerian. This Keplerian motion is given by
where
with e as the eccentricity, E the eccentric anomaly, and A, B, F, G the Thiele-Innes coefficients
where ω, Ω, and i are the argument of periastron, longitude of ascending node, and inclination of the orbit, respectively, and as is the semi-major axis of the orbit of the star around the center of mass of the system, expressed in mas. The eccentric anomaly is implicitly expressed as a function of time through the Kepler equation
where M is the mean anomaly, M0 is the mean anomaly at the reference epoch, and P is the orbital period.
2.3 Fourier decomposition of a Keplerian astrometric signal
The Keplerian part of the astrometric signal is P-periodic and can be decomposed as a discrete Fourier series
with n = 2π/P as the planet mean-motion. We introduce the complex coordinate,
and the complex coefficients,
such that
We then write the Fourier decomposition of ζ in the following form:
where
are functions of the eccentricity only. The coefficients dk and ak are then easily expressed as functions of the coefficients ζk
The coefficients ζk can be computed numerically (see Appendix A). They can also be computed analytically as power series of the eccentricity. We go on to rewrite Eq. (13) as an integral over the eccentric anomaly, E,
This expression can then straightforwardly be developed in power series of the eccentricity and integrated over E. We obtain for the first terms:
At low eccentricity, the leading Fourier coefficients of δ and α are found at the orbital period. The amplitude of the first harmonics (half the orbital period) terms is proportional to the eccentricity. Higher order harmonics have a much lower amplitude (higher powers of the eccentricity). In the following, we aim to detect the presence of a companion using a linear periodogram approach where we approximate the Keplerian signal with the fundamental frequency only. Then, once the companion is detected and its orbital period is known, we estimate the remaining parameters by approximating the Keplerian signal using the fundamental and the first harmonics. These two approximations remain valid for low to moderate eccentricity. In order to assess the domain of validity of this approach, we estimated the fraction of the signal power that lies in the fundamental and in the first harmonics. We show, in Fig. 2, these power fractions as a function of the eccentricity. As a comparison, we also provide the same fractions in the case of a radial velocity Keplerian signal. The details of these derivations are presented in Appendix A. As expected, we see in Fig. 2 that at low eccentricity, the power of the signal is concentrated in the fundamental frequency both for a radial velocity signal and an astrometric signal. However, the behavior of both kinds of signal differs at higher eccentricity. For the radial velocities, the power fraction in the fundamental drops to zero when the eccentricity reaches 1. Therefore, for a radial velocity signal, the linear periodogram approach (with a single frequency) has a significant loss of sensitivity for high eccentricity signals (see also Baluev 2015). To circumvent this issue, more complex periodogram definitions have been proposed in the literature (e.g., Baluev 2013, 2015; Zucker 2018). In the case of astrometry, the power fraction in the fundamental also decreases with eccentricity, but it always remains above about 80 %. Therefore, the linear periodogram approach remains fairly sensitive even for highly eccentric orbits, and a more complex periodogram approach would probably be less beneficial than in the radial velocity case.
While a high power fraction in the fundamental improves the detection sensitivity of the linear periodogram, it also reduces the ability to characterize the companion’s eccentricity and argument of periastron. Indeed, the fundamental frequency alone does not contain sufficient information to derive these parameters. Therefore, one can only derive the eccentricity and argument of periastron with good precision for a signal that has significant power in the harmonics. This applies in particular to our analytical method (Sect. 4) but, more generally, independently of the method, we expect the eccentricity and argument of periastron to be characterized with less precision using astrometry than using radial velocities, for a similar signal to noise ratio (S/N).
 |
Fig. 2 Fraction of the signal power in the fundamental and in the first harmonics for a radial velocity time series and an astrometric time series. |
3 Periodogram and false alarm probability
3.1 General linear periodogram
Here, we adopt a periodogram approach to detect the signature of a companion and estimate its orbital period. Following Baluev (2008); Delisle et al. (2020a), we define a general linear periodogram by comparing the χ2 of the residuals of a linear base model, H, with p parameters and enlarged linear model, K, of p + d parameters, further parameterized by the angular frequency, v. The linear base model, H, follows:
where βH is the vector of size p of the model parameters, φH is a n × p matrix, and n is the number of points in the time series. Typically, this base model includes five linear parameters, including the position, the proper motion, and the parallax (see Eqs. (2), (3)):
but any additional linear parameters might be included. For instance, a quadratic proper motion can be accounted for by adding the columns t2 cos θ, t2 sin θ in φH.
The enlarged model K(v) follows
where βK = (βH,β) is the vector of the p + d linear parameters, and φK(v) is the n × (p + d) matrix whose p first columns are the columns of φH, and whose d last columns are functions of the angular frequency, v.
In the case of radial velocities (see Baluev 2008; Delisle et al. 2020a), we would typically have d = 2, with the additional columns of cos vt and sin vt, to account for any possible phase of the potential companion. This definition implicitly assumes that the signature of the companion is dominated by the fundamental frequency (see Sect. 2.3). In the astrometric case, the same approximation is achieved with the d = 4 additional columns: cos θ cos vt, sin θ cos vt, cos θ sin vt, and sin θ sin vt. These four terms allow us to account for any possible phase and for the projection of the orbit over both axes (see Eqs. (2), (3)). Thus, we typically use
where βK is the vector of the p + 4 parameters, and φK is the (n × (p + 4)) matrix obtained by horizontal concatenation of φH and the four additional columns.
We denote by 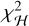 and
and 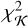 the χ2 of the residuals after a linear least squares fit with a covariance matrix C of the models H and K(v), respectively:
the χ2 of the residuals after a linear least squares fit with a covariance matrix C of the models H and K(v), respectively:
The covariance matrix, C, may account for all sources of correlated and uncorrelated noise, and in particular the instrument systematics.
In the general case, the periodogram is a function 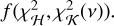 . A general linear periodogram z is thus defined by the models, H and K(v), and the function f. For instance, the widespread GLS periodogram (see Ferraz-Mello 1981; Zechmeister & Kürster 2009) is defined as
. A general linear periodogram z is thus defined by the models, H and K(v), and the function f. For instance, the widespread GLS periodogram (see Ferraz-Mello 1981; Zechmeister & Kürster 2009) is defined as
Baluev (2008) proposed four alternative definitions of the periodogram. In the following, we focus on the GLS periodogram since it is more widely used, but similar derivations can be found in Appendix B for these alternative definitions.
3.2 False alarm probability
Once the periodogram is computed, it is useful to compute the p-value of the highest peak (FAP), defined as:
where Z is the value of the maximum peak of the periodogram computed on the data. In this section, we provide analytical approximations of the FAP for the GLS periodogram of Eq. (22). Similar approximations for the alternative periodogram definitions and their precise derivation is provided in Appendix B.
The model H is defined as in Eq. (17), where the n × p matrix φH is user-defined, and the model K is defined as in Eq. (20). The periodogram is computed in the range of frequencies ]0, vmax] (i.e., 0 excluded and vmax included). The FAP is approximated by (see Baluev 2008):
where analytical expressions for FAPsingle and τ(Z, vmax) are given in Table 1 (d = 4). These expressions depend on the rescaled frequency bandwidth, W, defined as
where Teff is the effective time series length. We provide in Appendix B analytical estimates of Teff in the general case of correlated noise. In the simplest case of white noise, that is, for a diagonal covariance matrix C = diag(σ2), the effective time series length can be approximated by
where 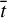 and
and 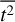 are weighted means with weights
are weighted means with weights 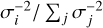 . This expression is proportional to the weighted standard deviation of the measurement times.
. This expression is proportional to the weighted standard deviation of the measurement times.
The FAP estimate that we obtain here rely on the correct estimation of the power, Z, of the highest peak in the considered range of angular frequency ]0, vmax]. When computing the periodogram, we should thus sample v with a sufficiently small step size to determine Z with a good precision. Moreover, it is also important for the following steps to correctly identify the period of the highest peak, which also requires for the periodogram to be correctly sampled. The width of periodogram peaks is typically 2π/Teff (in angular frequency). Each peak should be sampled with a sufficient number of points to obtain a good estimation of the peak height. A standard procedure in the literature is to sample the angular frequency linearly with a step size of 2π/noT where T is the total time span of the observations (which is a proxy for Teff), and no > 10 is the oversampling factor. The maximum angular frequency vmax, or equivalently the minimum period Pmin, is user-defined. By increasing the size of the frequency range, we increase the probability of obtaining a higher peak by chance (null hypothesis), which is why the FAP estimate takes into account the maximum frequency, vmax, through the rescaled frequency bandwidth, W.
False alarm probability for the GLS periodogram (see Eq. (22)) following the method of Baluev (2008).
3.3 Combining astrometric and radial velocity time series
We now consider the case where both astrometric and radial velocity time series are available for a source. We extend to this case the periodogram and analytical FAP approach described above. In the following, we assume that the calendars of astrometric and radial velocity observations are independent and that the noise affecting both time series is independent.
The general linear periodogram framework described above is compatible with heterogeneous time series (such as astrometry and radial velocities). We define the full dataset as a concatenation of the astrometric and radial velocity datasets:
where ta and trv are the astrometric and radial velocities calendars respectively, s is the time series of astrometric abscissa, and v is the radial velocity time series. Vectors t and y both have length n = na + nrv. Since we assumed the noise affecting both time series to be independent, the full covariance matrix is block-diagonal:
Considering the linear models ma(βa) = φaβa for the astrometric time series and mrv(βrv) = φrvβrv for the radial velocity time series, the corresponding full linear model is written as
with
and the corresponding χ2 is written as:
since φ and C are block-diagonal.
The base model H can thus be defined completely independently for the astrometry and the radial velocities. As mentioned in Sect. 3.1, for the astrometry, the base model typically includes five linear parameters (see Eq. (18)). In the radial velocity case, the base model typically includes instruments offsets and might additionally take into account drift terms (typically linear, quadratic, or cubic trends) or activity indicators (R′HK, FWHM, etc.).
The enlarged model K(v) includes four additional linear predictors for the astrometry and two additional predictors for the radial velocities:
We thus have d = 6 additional parameters in the model K(v), compared to H. The periodogram z(v) is then computed according to the definition of Eq. (22), or one of the alternative definitions of Appendix B. The FAP approximation is very similar to the case of astrometry alone (Sect. 3.2) or radial velocities alone (see Baluev 2008; Delisle et al. 2020a). Furthermore, we have:
where analytical expressions for FAPsingle and τ(Z, vmax) are given in Table 1 (d = 6). The rescaled frequency bandwidth, W, is still defined as (see Eq. (25))
but the effective time series length Teff is now approximated as (see Appendix B):
The expressions of 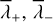 , and
, and 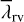 are provided in Appendix B in the general case of correlated noise. In the white noise case (diagonal covariance matrices
are provided in Appendix B in the general case of correlated noise. In the white noise case (diagonal covariance matrices 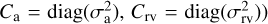 , we find:
, we find:
where 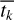 and
and 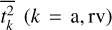 are weighted means with weights
are weighted means with weights 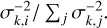 . The expression for the effective time series length is thus a combination of the weighted standard deviations of the measurement times of both time series.
. The expression for the effective time series length is thus a combination of the weighted standard deviations of the measurement times of both time series.
4 Analytical determination of orbital parameters
Once a significant peak has been identified in the periodogram, we may attribute this peak to the presence of a companion. The periodogram peak provides an estimate of the companion period and the next step is usually to derive the other parameters. This step is usually performed using numerical algorithms (local minimization methods, MCMC, genetic algorithms, etc.). In order to improve the performances of such methods, a good initial guess of the parameters is very valuable. We thus adapt the method we developed for the radial velocities (see Delisle et al. 2016) to the case of an astrometric signal (Sect. 4.1) and to the combination of astrometry and radial velocities (Sect. 4.2). An analogous method was developed in the case of interferometric astrometry by Konacki et al. (2002). The principle of the method is to deduce the orbital parameters from the amplitudes and phases of the signal at the period and first harmonics of the planet. For instance, the amplitude of the k-th harmonics scales as ek, so the ratio between the amplitudes of the first harmonics and the fundamental period provides insights into the eccentricity.
4.1 Astrometric time series
We assume here that the orbital period of the companion has been correctly determined with the periodogram approach. We define a new linear model similar to the one used for the periodogram (Eq. (20)) but including both the mean motion n = 2π/P and the first harmonics 2n:
The corresponding χ2 is written as
and is minimized for
where Cβ is the covariance matrix of the parameters
By definition, we have (see Eq. (8)):
We then define (see Eqs. (14), (16)):
and
These expressions are very similar to the radial velocity case (see Delisle et al. 2016). We thus follow the same lines to deduce the planet’s orbital parameters. At first order in eccentricity, we find (see Eq. (42)):
so the eccentricity e and mean anomaly M0 could be directly deduced from the amplitude and phase of ρk. However, a better precision can be achieved by taking into account the terms of order 3 in eccentricity. Following Delisle et al. (2016), we first determine a crude approximation of ϕk:
Then, defining the coefficients rk as:
we obtain the same cubic equation for e as in the radial velocity case (see Eq. (42) and Delisle et al. 2016):
whose unique solution in the interval [0, 1] is given by (see Delisle et al. 2016):
with
Then, the mean anomaly M0 can be deduced using (see Eq. (42)):
With this method, we obtain two estimates for e and M0 − one corresponding to the motion against the declination and one corresponding to the motion against the right ascension. We then need to combine these estimates. A simple average could be used, however, depending on the scanning law, one of the estimates could be much more precise than the other. We would thus rather perform a weighted average, with weights computed by propagating the errorbars of the linear fit. The details of this error propagation and weighting method are detailed in Appendix C. in order to test the accuracy of our analytical estimate of e and M0, we generated sets of orbital parameters and provided to our algorithm the exact values of the Fourier decomposition of the corresponding astrometric signal: d1, d2, a1, a2. We then compared the eccentricity, e, and mean anomaly, M0, estimated from these Fourier coefficients using our algorithm, with the true parameters e and M0. We show in Fig. 3 the results of this comparison as a function of the true eccentricity, e, and argument of periastron, ω. For each couple, e, ω, we generated a grid of inclination, i, and longitude of the node, Ω, and plotted the maximum deviations over this grid in Fig. 3. We see that the analytical estimates of e and M0 remain very close to the true values even at high eccentricity, with a maximum deviation of about 0.05 for the eccentricity and 1 deg for the mean anomaly at e = 0.95. The method could be further refined by using a Newton-Raphson correcting algorithm, as proposed in Delisle et al. (2016). However, in practice, the accuracy of the method is mainly limited by the precision of the determination of the Fourier coefficients d1, d2, a1, a2, which we neglected in this test.
Once P, e and M0 are known, the orbit is then fully characterized by computing the Thiele-Innes coefficients, which are linear parameters (see Eqs. (4)-(6)). We first solve the Kepler equation (Eq. (7)) to compute the eccentric anomaly E. Then we compute the vectors x, y according to Eq. (5), and solve the linear problem (see Eq. (4)):
to obtain estimates for A, B, F, and G.
 |
Fig. 3 Accuracy of our analytical estimates of e and M0 (see Sect. 4.1) assuming the Fourier decomposition of the signal to be perfectly known. We plot the range of deviations from the true eccentricity (top) and mean anomaly (bottom) as a function of the argument of periastron, ω, and the true eccentricity, e. |
4.2 Combining astrometric and radial velocity time series
The method described in Sect. 4.1 to derive an estimate of the eccentricity, e, and of the mean anomaly at reference epoch, M0, can be extended to the case of a combination of astrometric and radial velocity time series in a straightforward way. We still assume that the orbital period of the companion has been correctly determined with the periodogram approach and we define a linear model including the fundamental frequency (mean motion n = 2π/P) and the first harmonics (2n), for both time series:
We obtain the best-fitting parameters βa, βrv, as well as the covariance matrices 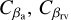 by minimizing the corresponding χ2. We derive the values of ρδ, ρα, ηδ, ηα (see Eqs. (42)-(41)) from the astrometric parameters βa. We also derive (see Delisle et al. 2016):
by minimizing the corresponding χ2. We derive the values of ρδ, ρα, ηδ, ηα (see Eqs. (42)-(41)) from the astrometric parameters βa. We also derive (see Delisle et al. 2016):
with
We then use the method described in Delisle et al. (2016) and Sect. 4.1 to obtain the estimates êk and 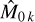 from the values of ρk and ηk (k = δ, α, rv). These three estimates are finally combined to obtain ê and
from the values of ρk and ηk (k = δ, α, rv). These three estimates are finally combined to obtain ê and 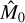 , using the error propagation and weighting method detailed in Appendix C.
, using the error propagation and weighting method detailed in Appendix C.
Following the same line as in Sect. 4.1, we performed a linear fit of the astrometric time series to obtain estimates of the Thiele-Innes coefficients (A, B, F, and G). Similarly, we performed a linear fit of the radial velocity time series to obtain estimates of Kc = K cos ω and Ks = K sin ω. These estimates should again be combined to obtain a set of four parameters describing the orbit, in addition to the three parameters already determined (P, e, M0).
The astrometry is sensitive to all the orbital parameters but has a degeneracy between two symmetric solutions for the argument of periastron ω and the longitude of the node Ω (ω′ = ω + π, Ω′ = Ω + π). On the contrary, the radial velocities are not sensitive to the inclination, i, and the longitude of the node, Ω, but allow us to break the degeneracy by providing an estimate of the argument of periastron, ω. To combine the parameters obtained from astrometry and radial velocities, we introduce the following parameters:
These parameters can be derived both from the astrometric parameters,
and the radial velocity parameters,
We followed the same approach as in Appendix C to propagate the covariance matrices of the linear fits and performed a weighted average of the two estimates of U and V. From the weighted estimates Û, 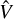 it is straightforward to derive estimates for as sin i and ω. For the argument of periastron, ω, two solutions are actually possible since U and V depend on 2ω, but we chose the one that is closest to the radial velocity estimate (obtained from
it is straightforward to derive estimates for as sin i and ω. For the argument of periastron, ω, two solutions are actually possible since U and V depend on 2ω, but we chose the one that is closest to the radial velocity estimate (obtained from 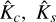 ). The two remaining parameters only depend on the astrometry and can be chosen arbitrarily. For instance, Ω can be estimated with
). The two remaining parameters only depend on the astrometry and can be chosen arbitrarily. For instance, Ω can be estimated with
and cos i can be estimated using (e.g., Popovic & Pavlović 1995):
with
5 Applications
We go on to illustrate our methods with a reanalysis of the astrometric and radial velocity time series of three stars known to host a companion: HD 223636 (HIP 117622), HD 17289 (HIP 12726), and HD 3277 (HIP 2790). We used Hipparcos data (with the reduction of van Leeuwen 2007) for the astrometry and CORALIE data for the radial velocities. We binned Hipparcos data over one-day intervals and excluded the bins with a resulting uncertainty larger than 2.5 mas.
An upgrade of CORALIE was performed in 2007 to improve the overall transmission of the instrument. This upgrade affected the instrumental zero point and the overall instrument stability (Ségransan et al. 2010). We thus actually considered the data taken before and after the upgrade as coming from two different instruments (COR98 before and COR07 after). We modeled the noise as the quadratic sum of the individual measurements errors, as provided by the instruments reduction pipelines, and an additional instrumental jitter: 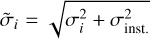 . Such a modeling process allows us to account for both stellar and instrumental noises that are not already modeled by the reduction pipelines. We thus defined three jitter terms: σHIP for Hipparcos data and then σCOR98 and σCOR07 for CORALIE data. We initially set the default values σCOR98 = 5 m s−1 and σCOR07 = 8 m s−1, which correspond to the observed scatter of a set of bright and stable solar type stars monitored on a regular basis with CORALIE since 1998. For Hipparcos, we used a default value of σHIP = 0 mas. We let the three jitter values vary at the end of the analysis to adapt to the specificity of each dataset.
. Such a modeling process allows us to account for both stellar and instrumental noises that are not already modeled by the reduction pipelines. We thus defined three jitter terms: σHIP for Hipparcos data and then σCOR98 and σCOR07 for CORALIE data. We initially set the default values σCOR98 = 5 m s−1 and σCOR07 = 8 m s−1, which correspond to the observed scatter of a set of bright and stable solar type stars monitored on a regular basis with CORALIE since 1998. For Hipparcos, we used a default value of σHIP = 0 mas. We let the three jitter values vary at the end of the analysis to adapt to the specificity of each dataset.
We applied a similar procedure for each target, using our open source python package kepmodel2. We analyzed the astrometric and radial velocity time series both independently and jointly. We computed the periodogram and associated FAP according to Delisle et al. (2020a) (radial velocities) and Sect. 3 (astrometry and joint analysis). All the periodograms were computed using the normalized power of Eq. (22) and by sampling the angular frequency linearly in the range [2π/50 000, 2π/0.9] (rad day−1) with 50 000 values, such that the oversampling factor is always above 10. We then extracted from the periodogram the period corresponding to the highest peak and applied our analytical methods to estimate the other orbital parameters, using Delisle et al. (2016; radial velocities) and Sect. 4 (astrometry and joint analysis). We then adjusted the values of all the parameters by performing a local maximization of the likelihood ℒ using the L-BFGS-B algorithm provided by the scipy python package. This algorithm makes use of the partial derivatives of the likelihood with respect to the parameters, which we computed analytically. We estimated errorbars on the parameters by extracting the diagonal of the inverse of the Hessian matrix of the likelihood. We then repeated the fitting procedure but additionally adjusting the values of the instrumental jitter terms. Finally, we computed the periodograms and FAP of the residuals of the joint model, considering the astrometric and radial velocity time series independently or jointly.
 |
Fig. 4 Periodogram of the Hipparcos astrometric time series of HD 223636. |
Fit parameters for HD 223636.
5.1 HD 223636
We first considered HD 223636 (HIP 117622), which was found to host a companion at about 1008 days by Goldin & Makarov (2007), based on an analysis of the Hipparcos time series. No radial velocities are available for this target and we thus only reanalyzed the Hipparcos time series. The periodogram of the astrometric data is shown in Fig. 4, where we clearly see a very significant peak (FAP = 3 × 10−5) around 1050 days.
We show in Table 2 the parameters obtained using our analytical estimation method (initial guess), after a local maximization of the likelihood and after a second fit, including the jitter term. We observe that the initial guess of the parameters is very close to the maximum likelihood estimate. When adjusting the jitter, we obtain a value of about 0.64 mas, while the average Hipparcos errorbar (over one day bins) is about 0.93 mas. Accounting for this jitter significantly increases the uncertainties on all the parameters, and allows to have a better assessment of the actual precision on these parameters. We note that the final uncertainty on the argument of periastron, ω, is large (29 deg), while the other angles have errorbars below 5 deg. The set of parameters is chosen as to avoid strong correlations between these angles. In particular, the phase of the planet on its orbit is modeled using the mean argument at the reference epoch M0 + ω instead of the mean anomaly M0 (which is anti-correlated with ω) or the mean longitude λ0 = M0 + ω + Ω (which is correlated with Ω). The astrometric orbit corresponding to the maximum likelihood parameters (including jitter), is shown in Fig. 5 superimposed with Hipparcos measurements. The periodogram of the residuals is shown in Fig. 6, where no significant peak is found (FAP = 0:89).
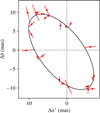 |
Fig. 5 Astrometric orbit of HD 223636. |
 |
Fig. 6 Periodogram of Hipparcos astrometric residuals of HD 223636 after fitting for its companion. |
5.2 HD 17289
The second target, HD 17289 (HIP 12726), was also found to host a companion by Goldin & Makarov (2007) using Hipparcos astrometry alone. The companion was later confirmed and better characterized by Sahlmann et al. (2011) using both Hipparcos astrometry and CORALIE radial velocities. This system is actually a binary star, with a mass ratio of about 2 between the primary and the companion, leading to a contrast of about 1 : 180 in the visible, which slightly affects the radial-velocity measurements. This issue is discussed in details in Sahlmann et al. (2011) and is beyond the scope of our study. Here, we use the same Hipparcos and CORALIE data as Sahlmann et al. (2011). The CORALIE data consist of 29 measurements (22 COR98 and 7 COR07).
We show in Fig. 7 the periodogram of the astrometric data alone, the radial velocities alone, as well as the joint periodogram. In the three cases, a significant peak is detected around 570 days. Since the time span of CORALIE measurements (11.3 yr) is much longer than the time span of Hipparcos measurements (3.2 yr), the radial velocity peak is much narrower. The joint periodogram shows a very similar shape as the radial velocity periodogram, but provides stronger evidence for the existence of a companion (FAP = 3 × 10−8 and 10−3, respectively).
Table 3 provides the parameters obtained at the different steps of our procedure using astrometry alone, radial velocities alone, and both datasets together. In all three cases, our analytical method provides a good initial guess of the parameters. When using the radial velocities alone, the provided value for the semi-major axis, as, is actually the minimum semi-major axis (as sin i), which is equivalent to assuming an inclination of 90 deg. Since the actual inclination is about 174 deg (sin i ≈ 0.1), this explains the factor of 10 difference with regard to the astro-metric or joint value. The other parameters show coherent values between astrometry and radial velocities. When using astrometric data alone, the parameters ω and Ω present two degenerated solutions (ω, Ω) and (ω + π, Ω + π). In order to ease the comparisons, we chose the solution that is the closest to the value of ω obtained with radial velocities. However, it should be kept in mind that there is no way to break this degeneracy using astrometry alone. We observe that while the inclination, i, and longitude of the node Ω are not constrained by radial velocities, we obtain a much higher precision on these parameters with the joint fit than using astrometry alone. This is because of the correlations between these two parameters and the other orbital parameters, which are much better constrained by the radial velocities than the astrometry.
The astrometric orbit corresponding to the maximum likelihood parameters (including jitter), superimposed with Hipparcos measurements, is shown in Fig. 8, while the phase-folded radial velocity model, superimposed with CORALIE measurements, is shown in Fig. 9. Finally, the periodograms of the residuals are shown in Fig. 10, where no significant peak is found (FAP > 0.66).
Fit parameters of HD 17289.
 |
Fig. 7 Periodograms of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint periodogram (bottom) of HD 17289. |
5.3 HD 3277
The last system we analyzed is HD 3277 (HIP 2790). It was first listed by Tokovinin et al. (2006) as an uncertain spectroscopic binary based on few CORALIE measurements and Sahlmann et al. (2011) confirmed the presence of a companion using additional CORALIE measurements as well as Hipparcos data. The primary component is a G8 star while the companion is an M-dwarf. We analyzed the same data as in Sahlmann et al. (2011), namely, Hipparcos data and 14 CORALIE measurements (10 COR98 and 4 COR07).
The periodograms and FAP of the astrometric and radial velocity time series are shown in Fig. 11. We observe a nonsignificant peak around 46 days in the radial velocities periodogram (FAP = 0.16). This high FAP value can be explained by the poor sampling of the radial velocity time series, which consists of only 14 points split among two instruments. To test this hypothesis, we recomputed the periodogram and FAP of the radial velocity time series but assuming the offset between COR98 and COR07 to be negligible, and found a more significant FAP of 0.015. A peak is also visible in the astrometric periodogram at the same period, but it is not the highest one, and the FAP is very high (0.73). The joint periodogram is very similar in shape to the radial velocities periodogram but the associated FAP is significantly lower (5 × 10−8).
Since the 46 days signal is not detected using astrometry alone, we only applied our procedure to the radial velocities and the joint model. The parameters we obtained are shown in Table 4. As for previous systems, our analytical method provides a good initial guess of the parameters, which is then refined by maximizing the likelihood. The most challenging parameter is the inclination, which is only constrained by the astrometry, for which the initial guess is within 40 deg of the maximum likelihood value. This slight discrepancy is not surprising considering the low S/N of the signal in the astrometric time series (high FAP, other more significant peaks in the periodogram). The maximum likelihood astrometric and radial velocity models, superimposed with the corresponding data, are shown in Figs. 12 and 13. The periodograms of the residuals are shown in Fig. 14, where no significant peak is found (FAP > 0.77).
 |
Fig. 8 Astrometric orbit of HD 17289. |
 |
Fig. 9 Phase-folded RV time series of HD 17289. |
 |
Fig. 10 Periodograms of the residuals of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint peri-odogram (bottom) of HD 17289, after fitting for its companion. |
 |
Fig. 11 Periodograms of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint periodogram (bottom) of HD 3277, after fitting for its companion. |
Fit parameters of HD 3277.
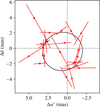 |
Fig. 12 Astrometric orbit of HD 3277. |
 |
Fig. 13 Phase-folded RV time series of HD 3277. |
6 Discussion
In this work, we present a set of methods to detect and characterize companions (planets, brown dwarfs, and stars) in astrometric or radial velocity time series, or both. We propose a general linear periodogram framework with an analytical method to compute the associated FAP. We additionally provide an analytical method to obtain an estimate of the orbital parameters once the period of the companion has been determined (from the periodogram approach). These methods can be applied to astrometric data alone, radial velocities alone, but also when combining both detection techniques.
Being based on analytical approximations, our methods are very efficient in terms of computational cost. This is of particular interest in the context of the Gaia space mission, considering the amount of generated data. It should be noted that these approximate analytical methods are complementary with more precise numerical methods. For instance, in Sect. 5, we use our analytical estimate of the orbital parameters as a starting point for a likelihood maximization algorithm. More generally, both the periodogram-FAP approach and the orbital parameters approximation can be used to improve the convergence speed of numerical algorithms, such as Markov chain Monte-Carlo, genetic algorithms, and so on. In particular, our analytical estimate of orbital parameters has been implemented in the genetic algorithm of the official Gaia pipeline for the detection of planets (MIKS-GA, see Holl et al. 2022).
Indeed, a primary objective of this article is to provide building blocks for the detection and characterization of planets using Gaia astrometry alone as well as in combination with on-ground radial velocities. Since the Gaia collaboration will not publish astrometric time series before DR4, we were not able to illustrate our methods on Gaia sources hosting planetary companions. We instead chose to reanalyze the Hipparcos astrometric time series of three stars known to host a stellar companion: HD 223636 (HIP 117622), HD 17289 (HIP 12726), and HD 3277 (HIP 2790). Using Hipparcos astrometry and publicly available CORALIE radial velocities, we obtained results similar to the literature. In these examples, we found that the joint periodograms (astrometry + radial velocities) were very similar to the periodogram of the radial velocity alone. This is because the S/N of the companion is much higher in CORALIE radial velocities than in Hipparcos astrometry. Therefore, a combined periodogram might not actually appear necessary to find the companion period in these cases. However, since Gaia will provide much higher precision astrometric time series and with a much longer time span than Hipparcos, the contribution of astrometry and radial velocities will be more balanced.
Finally, it should be noted that while we assume white noise in our illustrations (Sect. 5), our methods are derived in the more general case of correlated noise. Indeed, radial velocities are known to be affected by stellar activity, which is often modeled using Gaussian processes (i.e., correlated noise models). Other sources of noise, such as the spectrograph calibration noise, can also introduce correlated noise in the radial velocity time series (e.g., Delisle et al. 2020b). In the case of astrometric data, the stellar activity signature is expected to be much smaller than for radial velocities (Lagrange et al. 2011). However, the attitude calibration of the satellite might introduce correlated noise in the astrometric time series. In the case of Gaia, the correlated noise contribution remains to be investigated and characterized, but once this is done, our framework is readily equipped to account for it.
 |
Fig. 14 Periodograms of the residuals of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint periodogram (bottom) of HD 3277, after fitting for its companion. |
Acknowledgements
We thank the anonymous referee for their very constructive feedback that helped to improve this manuscript. We acknowledge financial support from the Swiss National Science Foundation (SNSF). This work has, in part, been carried out within the framework of the National Centre for Competence in Research PlanetS supported by SNSF.
Appendix A Power fraction in the fundamental and harmonics
In this appendix, we compute the power fraction that is found in the fundamental and in the harmonics for a radial velocity (Appendix A.1) and an astrometric Keplerian signal (Appendix A.2).
A.1 Radial velocity signal
We follow Baluev (2015) to define the total power of a Keplerian radial velocity signal VK(t) = K(cos(v(t) + ω) + e cos ω) as:
where
and v is the true anomaly. The Fourier expansion of this signal is (e.g., Delisle et al. 2016):
where Xk is the Hansen coefficient 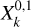 which only depends on the eccentricity e and is defined has
which only depends on the eccentricity e and is defined has
The power in the harmonics are thus:
Finally the power fraction in the k-th harmonics (k > 0) is:
As shown by Baluev (2015), the ratio R1 is linked with the detection efficiency of the classical periodogram (which only uses the fundamental frequency) compared to a more complex Keplerian periodogram (which uses the full information contained in the signal).
The power fraction Rk depends on the eccentricity and (weakly) on the argument of periastron. For a given eccentricity, the extrema of the power fraction correspond to 2ω = 0 or π. We define
such that Rk is always between 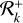 and
and 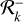 (the order depending on k and e). In Fig. 2, we plot the possible range of values of Rk as a function of the eccentricity, for k = 1,2 (fundamental and first harmonics). For this plot, we evaluated the Hansen coefficients by numerical integration over the eccentric anomaly (see Delisle et al. 2016, Appendix A).
(the order depending on k and e). In Fig. 2, we plot the possible range of values of Rk as a function of the eccentricity, for k = 1,2 (fundamental and first harmonics). For this plot, we evaluated the Hansen coefficients by numerical integration over the eccentric anomaly (see Delisle et al. 2016, Appendix A).
A.2 Astrometric signal
Here, we follow the same approach as in the radial velocity case. Since the astrometric signal has two dimensions, we define the total power of the signal as the sum of powers along both directions:
We have
thus:
The Fourier expansion of δK and αK is provided in Eqs. (8), (14), from which we deduce the power in the k-th harmonics (k > 0):
In contrast to the case of radial velocities, the Keplerian astro-metric signal is not centered, which implies that the power ofthe constant part (k = 0) is not zero, that is,
In practice, the constant part does not contain any information about the companion because the reference position of the primary always needs to be adjusted at the same time as the orbit. Therefore, in the following, we normalize the power in the harmonics by the useful total power:
which is equivalent to re-centering the Keplerian astrometric model. We then define the power fraction as
This fraction depends on e, ω and i. For a given eccentricity, the extrema of the fraction appears for 2ω = 0, π and i = π/2. We thus define
such that Rk is always between 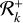 and
and 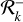 . We then need to evaluate the coefficients ζk to compute these fractions. We use the same method as for the Hansen coefficient (Appendix A.1). We estimate the integral of Eq. (15) numerically by sampling E in [0, 2π],
. We then need to evaluate the coefficients ζk to compute these fractions. We use the same method as for the Hansen coefficient (Appendix A.1). We estimate the integral of Eq. (15) numerically by sampling E in [0, 2π],
with Ej = 2π j/N. A very good precision is achieved using N = 100 (see Delisle et al. 2016), which is the value we use to compute the fractions shown in Fig. 2.
Appendix B Periodogram definitions and computation of the FAP
In this appendix, we provide details on the computation of the periodogram FAP in the case of astrometric data alone and in the case of a combination of astrometric and radial velocity time series. The FAP computation takes into account correlated noise. Our approach is very similar to the one used in Delisle et al. (2020a) for radial velocity time series. It is an extension to the correlated noise case of the method of Baluev (2008), which assumed white noise.
In addition to GLS periodogram defined in Eq. (22), Baluev (2008) proposed four alternative periodogram definitions:
where nH = n − p and nK = n − (p + d). The definitions z1,2,3 are actually related to each other and to the GLS periodogram. Indeed, we have:
False alarm probability for the two definitions (Eqs. (22), (B.1)) of the periodogram power (see Baluev 2008).
In the following, we only consider the GLS (Eq. (22)) and the definition z0 (Eq. (B.1)) of the periodogram, but all the results on the GLS also apply to z1,2,3 (using Eq. (B.2)).
The FAP can be bounded by (see Baluev 2008, Eq. (5))
and approximated by (see Baluev 2008, Eq. (6))
where Z is the maximum periodogram power, FAPsingle(Z) is the FAP in the case in which the angular frequency v of the putative additional signal is fixed, τ(Z, vmax) is the expectation of the number of up-crossings of the level Z by the periodogram (see Baluev 2008). Computing FAPsingle(Z) and τ(Z, vmax) requires us to specify the definition of the periodogram z(v). Baluev (2008) proposed several definitions and derived the corresponding formulas for FAPsingle(Z) and τ(Z, vmax). These results are summarized in Table B.1, for the definitions of the periodogram of Eqs. (22), (B.1). The only quantity left to compute is the factor W, which is the rescaled frequency bandwidth, defined as (see Baluev 2008)
where
The d × d matrix M(ν) is defined as follows (see Delisle et al. 2020a)
where x′ = ∂x/∂v. Baluev (2008) also defined the effective time series length as
such that
From Eqs. (B.6) and (B.8), we obtain
In the following we derive analytical approximations for Teff in the case of astrometric data alone (Appendix B.1) and in the case of astrometric and radial velocity data (Appendix B.2). The case of radial velocities alone was already treated in Delisle et al. (2020a).
B.1 Astrometric time series
In the case of astrometric data alone, we have d = 4 and
We thus replace this expression in the definitions of O, S, and R (Eq. (B.7)). As an example, for Q11 we obtain
We follow Baluev (2008); Delisle et al. (2020a) and neglect aliasing effects. In this approximation all the terms in Q, S, and R that contain a sine or cosine of vti + vtj ± θi ± θj average out when summing over i, j. Similarly, the terms containing a sine or cosine of θi + θj ± vti ± vtj average out. Finally, the terms containing sin(vti − vtj ± (θi − θj)) can also be neglected. Indeed, in the low frequency limit (|vti − vtj ± (θi − θj)| ≪ 1), the sine vanishes, while in the high frequency limit (|vti − vtj ± (θi − θj)| ≫ 1), the sine average out. Using these approximations, we obtain
with
and * denotes the Hadamard (or elementwise) product.
Following Baluev (2008); Delisle et al. (2020a), we additionally assume that 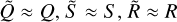 , and
, and
Replacing Eq. (B.13) in Eq. (B.15), we find
with
The eigenvalues of M are thus λ±, both with a multiplicity of 2.
In order to determine the effective time series length Teff (Eq. (B.10)) we then need to evaluate the integral
As shown by Baluev (2008), for a matrix M with eigenvalues λi (i = 1, …, d), the integral I is linked to the surface-area ∏d of the d-dimensional ellipsoid with semi-axes 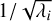 , through
, through
Moreover, since in our case the eigenvalues have even multiplicities, the surface area can be expressed in terms of elementary functions (see Tee 2005). Following the method described in Tee (2005), we obtain
and
The effective time series length is thus (see Eq. (B.10)):
Finally, following Delisle et al. (2020a), we approximate the integral over the angular frequency v by replacing q±, s±, and r± by their average over the range ]0, vmax]. We have:
and we make the following approximations
B.2 Astrometric and radial velocity time series
In the case of a periodogram taking into account both astrometric and radial velocity time series, we have d = 6 and:
with
Assuming the covariance matrix, C, to also be block diagonal,
the contributions of the astrometry and radial velocities in the matrix Q, S, R, and M are completely separated and these matrices are also block diagonal. Neglecting aliasing effects as in Baluev (2008); Delisle et al. (2020a), and Appendix B.1, we find
where
q±, s±, r±, and λ± are defined according to Eqs. (B.14), (B.17), and (see Delisle et al. 2020a)
The eigenvalues of M are thus λ+, λ−, and λrv, each with multiplicity 2. Following the same steps as in Appendix B.1, we compute the surface-area ∏6 of the 6D ellipsoid with semi-axes 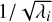 using the method of Tee (2005) and find:
using the method of Tee (2005) and find:
We deduce
and approximate the effective time series length as
with 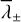 defined as in Eq. (B.24) and
defined as in Eq. (B.24) and
Appendix C Error propagation and weighted average for the eccentricity and the mean anomaly
In this appendix, we provide details on the error propagation method used to combine the estimates of the eccentricity and mean anomaly at reference epoch obtained in Sect. 4.1 (astrometry alone) or Sect. 4.2 (astrometry and radial velocities). We actually rather combine the estimates of f = e cos M0 and g = e sin M0. For each estimate, we first linearize the problem in the form
where h = f, g and k = δ, α (astrometry alone) or k = δ, α, rv (astrometry and radial velocities). The vector β is the complete set of parameters obtained after a linear fit (β = βa or β = (βa, βrv) depending on the considered case). Then, we propagate the covariance matrix of the linear parameters to approximate the covariance matrix 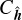 of
of 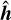
Finally, we compute the weighted average as
with u = (1 , 1), or (1 , 1 , 1), depending on the considered case
The partial derivatives 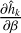 needed to apply this method can be derived from Eqs (42)–(50) We have
needed to apply this method can be derived from Eqs (42)–(50) We have
with
Moreover, we have (see Eq (50))
with
We thus derive:
References
- Arsenault, R., Alonso, J., Bonnet, H., et al. 2003, SPIE Conf. Ser., 4839, 174 [NASA ADS] [Google Scholar]
- Barrell, K., & Pask, C. 1979, Optica Acta, 26, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J.-L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brogi, M., & Line, M. R. 2019, AJ, 157, 114 [Google Scholar]
- Brogi, M., Snellen, I., De Kok, R., et al. 2013, ApJ, 767, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Coudé du Foresto, V., Maze, G., & Ridgway, S. 1993, in Astronomical Society of the Pacific Conference Series, Fiber Optics in Astronomy II, ed. P.M. Gray, 37, 285 [Google Scholar]
- Coudé du Foresto, V. 1994, in Very High Angular Resolution Imaging, eds. J.G. Robertson, & W.J. Tango, 158, 261 [CrossRef] [Google Scholar]
- Crepp, J. R. 2014, Science, 346, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Crepp, J. R., Johnson, J. A., Fischer, D. A., et al. 2012, ApJ, 751, 97 [Google Scholar]
- de Kok, R. J., Brogi, M., Snellen, I. A., et al. 2013, A&A, 554, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delorme, J.-R., Jovanovic, N., Echeverri, D., et al. 2021, J. Astron. Telescopes Instrum. Syst., 7, 035006 [NASA ADS] [Google Scholar]
- Dorn, R. J., Follert, R., Bristow, P., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, International Society for Optics and Photonics, 9908, 99080I [Google Scholar]
- Fusco, T., Rousset, G., Sauvage, J.-F., et al. 2006, Opt. Express, 14, 7515 [NASA ADS] [CrossRef] [Google Scholar]
- Ghasempour, A., Kelly, J., Muterspaugh, M. W., & Williamson, M. H. 2012, in Modern Technologies in Space-and Ground-based Telescopes and Instrumentation II, International Society for Optics and Photonics, 8450, 845045 [NASA ADS] [Google Scholar]
- Gibson, R. K., Oppenheimer, R., Matthews, C. T., & Vasisht, G. 2020, J. Astron. Telescopes Instrum. Syst., 6, 011002 [NASA ADS] [Google Scholar]
- Guyon, O., Pluzhnik, E., Kuchner, M. J., Collins, B., & Ridgway, S. 2006, ApJS, 167, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Jeunhomme, L. B. 1983, Single-mode Fiber Optics. Principles and Applications [Google Scholar]
- Jovanovic, N., Martinache, F., Guyon, O., et al. 2015, PASP, 127, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Jovanovic, N., Cvetojevic, N., Schwab, C., et al. 2016, SPIE Conf. Ser., 9908, 99080R [NASA ADS] [Google Scholar]
- Jovanovic, N., Schwab, C., Guyon, O., et al. 2017, A&A, 604, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, SPIE Conf. Ser., 5492, 1218 [NASA ADS] [Google Scholar]
- Kasper, M., Cerpa Urra, N., Pathak, P., et al. 2021, The Messenger, 182, 38 [Google Scholar]
- Kotani, T., Kawahara, H., Ishizuka, M., et al. 2020, in Adaptive Optics Systems VII, International Society for Optics and Photonics, 11448, 1144878 [Google Scholar]
- Lovis, C., Snellen, I., Mouillet, D., et al. 2017, A&A, 599, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyot, B. 1933, J. R. Astron. Soc. Canada, 27, 265 [NASA ADS] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Natl. Acad. Sci. U.S.A., 111, 12661 [Google Scholar]
- Mawet, D., Pueyo, L., Lawson, P., et al. 2012, in Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, eds. M.C. Clampin, G.G. Fazio, H.A. MacEwenJr., & J.M.O., International Society for Optics and Photonics (SPIE), 8442, 62 [Google Scholar]
- Mawet, D., Ruane, G., Xuan, W., et al. 2017, ApJ, 838, 92 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- McLean, I. S., Becklin, E. E., Bendiksen, O., et al. 1998, in Infrared Astronomical Instrumentation, International Society for Optics and Photonics, 3354, 566 [NASA ADS] [CrossRef] [Google Scholar]
- N’Diaye, M., Dohlen, K., Cuevas, S., et al. 2010, A&A, 509, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- N’Diaye, M., Dohlen, K., Cuevas, S., et al. 2012, A&A, 538, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- N’Diaye, M., Dohlen, K., Fusco, T., & Paul, B. 2013, A&A, 555, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neumann, E.-G. 1988, in Single-Mode Fibers (Springer), 210 [CrossRef] [Google Scholar]
- Otten, G., Vigan, A., Muslimov, E., et al. 2021, A&A, 646, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paul, B., Mugnier, L., Sauvage, J.-F., Dohlen, K., & Ferrari, M. 2013, Opt. Express, 21, 31751 [NASA ADS] [CrossRef] [Google Scholar]
- Piso, A.-M.A., Pegues, J., & Öberg, K.I. 2016, ApJ, 833, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Pourcelot, R., Vigan, A., Dohlen, K., et al. 2021, A&A, 649, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riaud, P., & Schneider, J. 2007, A&A, 469, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Service, M., Lu, J. R., Campbell, R., et al. 2016, PASP, 128, 095004 [NASA ADS] [CrossRef] [Google Scholar]
- Shaklan, S., & Roddier, F. 1988, Appl. Opt., 27, 2334 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A., De Kok, R. J., De Mooij, E. J., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A., Brandl, B. R., De Kok, R. J., et al. 2014, Nature, 509, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I., de Kok, R., Birkby, J. L., et al. 2015, A&A, 576, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soummer, R., Aimé, C., & Falloon, P. 2003a, A&A, 397, 1161 [CrossRef] [EDP Sciences] [Google Scholar]
- Soummer, R., Dohlen, K., & Aime, C. 2003b, A&A, 403, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soummer, R., Ferrari, A., Aime, C., & Jolissaint, L. 2007, ApJ, 669, 642 [Google Scholar]
- Vigan, A., Bonnefoy, M., Ginski, C., et al. 2016, A&A, 587, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigan, A., Otten, G., Muslimov, E., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, International Society for Optics and Photonics, 10702, 1070236 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wang, J., Mawet, D., Ruane, G., Hu, R., & Benneke, B. 2017, AJ, 153, 183 [Google Scholar]
- Wildi, F. P., Michaud, B., Crausaz, M., et al. 2010, SPIE Conf. Ser., 7735, 77352V [NASA ADS] [Google Scholar]
- Yelda, S., Lu, J. R., Ghez, A. M., et al. 2010, ApJ, 725, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Zurlo, A., Vigan, A., Mesa, D., et al. 2014, A&A, 572, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zurlo, A., Vigan, A., Galicher, R., et al. 2016, A&A, 587, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
False alarm probability for the GLS periodogram (see Eq. (22)) following the method of Baluev (2008).
False alarm probability for the two definitions (Eqs. (22), (B.1)) of the periodogram power (see Baluev 2008).
All Figures
 |
Fig. 1 Scan angle convention for Gaia (θ) and Hipparcos (ψ). |
| In the text | |
 |
Fig. 2 Fraction of the signal power in the fundamental and in the first harmonics for a radial velocity time series and an astrometric time series. |
| In the text | |
 |
Fig. 3 Accuracy of our analytical estimates of e and M0 (see Sect. 4.1) assuming the Fourier decomposition of the signal to be perfectly known. We plot the range of deviations from the true eccentricity (top) and mean anomaly (bottom) as a function of the argument of periastron, ω, and the true eccentricity, e. |
| In the text | |
 |
Fig. 4 Periodogram of the Hipparcos astrometric time series of HD 223636. |
| In the text | |
 |
Fig. 5 Astrometric orbit of HD 223636. |
| In the text | |
 |
Fig. 6 Periodogram of Hipparcos astrometric residuals of HD 223636 after fitting for its companion. |
| In the text | |
 |
Fig. 7 Periodograms of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint periodogram (bottom) of HD 17289. |
| In the text | |
 |
Fig. 8 Astrometric orbit of HD 17289. |
| In the text | |
 |
Fig. 9 Phase-folded RV time series of HD 17289. |
| In the text | |
 |
Fig. 10 Periodograms of the residuals of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint peri-odogram (bottom) of HD 17289, after fitting for its companion. |
| In the text | |
 |
Fig. 11 Periodograms of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint periodogram (bottom) of HD 3277, after fitting for its companion. |
| In the text | |
 |
Fig. 12 Astrometric orbit of HD 3277. |
| In the text | |
 |
Fig. 13 Phase-folded RV time series of HD 3277. |
| In the text | |
 |
Fig. 14 Periodograms of the residuals of the Hipparcos time series (astrometry, top), CORALIE time series (RV, middle), and joint periodogram (bottom) of HD 3277, after fitting for its companion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.