| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 21 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202039674 | |
| Published online | 10 March 2021 | |
Toward the true number of flaring giant stars in the Kepler field
Are their flaring specialities associated with their being giant stars?
1
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences,
Budapest,
Hungary
e-mail: Olah@konkoly.hu
2
Department of Physics, and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology,
Cambridge,
MA
02139,
USA
3
Max-Planck-Institut für Sonnensystemforschung,
Göttingen,
Germany
4
Eötvös Loránd University, Department of Astronomy,
Budapest,
Hungary
Received:
14
October
2020
Accepted:
7
January
2021
Aims. We aim to give a reliable estimate of the number of flaring giant stars in the Kepler field. By analyzing the flaring activity of these stars, we explored their flare statistics and the released flare energies. The role of oscillation in suppressing magnetic activity was also investigated. We searched for flaring specialities that may be associated with the giant nature across a sample of flaring giant stars.
Methods. We searched for flares using the ≈4 yr long Kepler data on a sample of 706 stars compiled from two lists of flaring giants (log g ≤ 3.5) found in the literature. To lessen the probability of false positives two different pipelines are used independently for flare detection. Tests are carried out to correct the detection bias at low flare energies for a subsample of 19 further studied, frequently flaring stars. For these 19 stars flare energy distributions and flare frequency diagrams (FFDs) are constructed. For comparison purposes KIC 2852961 is re-analyzed with our present approach.
Results. From the 706 Kepler flaring giant candidates, we ruled out those where oscillations or pulsations were misclassified and those that turned out to be dwarf stars. Finally, we confirm only 61 stars as flaring giants. Among these 61 flaring giants, we found only six that also show oscillations; we suggest that a large fraction of the 61 flaring giants are members of spectroscopic binaries, which has already been proven for 11 of them. The number of detected flares on giant stars correlate only weakly with the rotational periods. The FFDs for the 19 most flaring stars were fit by power-law functions. Regarding log–log representation, the slopes of the individual fits lead to an average α = 2.01 ± 0.16 power-law index, but the ranges of flare energies scatter within almost two orders, showing the inherent heterogeneity of the sample of flaring giants. Broken power-law fits are applied for two giant stars that have similar flare energy ranges; however, the energy at the breakpoints of the power laws are different, unveiling possible differences in the magnetic field strengths and atmospheric structures of these stars. The average power-law index of α ≈ 2 is the same for the flaring giants, the (super)flaring G-dwarfs, and dwarf stars between spectral types M6 and L0.
Conclusions. The 61 confirmed flaring giant stars make up only ≈0.3% of the entire giant star population in the Kepler database, which is in contrast with previous estimates of about an order higher percentage. We found that most of the false positives are in fact oscillating red giants. No strong correlation was found between the stellar properties and the flaring characteristics. The majority of the flaring specialities are hardly related to the giant nature, if at all. This, together with the finding that the observed flare durations correlate with flare energies, regardless of the flare energy level and stellar luminosity class, suggests common background physics in flaring stars, or in other words, a general scaling effect behind the flares on different stars.
Key words: stars: activity / stars: flare / stars: late-type
© ESO 2021
1 Introduction
Magnetism accompanies stars from cradle to grave, and magnetic fields play a crucial role from the formation of stars to the end of their existence. Most stars at a certain stage of stellar evolution exhibit enhanced magnetic activity, showing phenomena like the most easily observable flares. Stellar flares are sudden eruptions of energy through magnetic reconnection that occur mostly (but not exclusively) on late-type stars. The incidence of flaring stars among different types of stars, including solar-type stars, cool dwarfs, active giants, and even early-type stars, marks the presence and strength of the magnetic field, and thus has a serious impact on the study of the evolution of such stars in general (Cantiello et al. 2016). Therefore, knowing their true number is essential. Magnetically active red giant stars with strong flares gather on the red giant branch (RGB) of the Hertzsprung−Russell diagram (HRD). This is an exciting episode of stellar evolution. Depending on their mass, the stars spend only a short period of their life on the RGB, with continuously expanding atmospheres and basic changes in their inner structure and energy production.
Flares on stars (including the Sun) originate through magnetic reconnection in emerging flux tubes. Shibata & Magara (2011) reviewed theoretical descriptions of the magnetohydrodynamic processes based on data of the only star for which flares are directly observable, the Sun. For a flare eruption, a working magnetic dynamo originating from the counteraction of the differential rotation and convective motions in the stellar envelope is needed. A comprehensive review of solar-stellar magnetism was recently presented by Brun & Browning (2017). These works, however, deal mostly with late-type dwarf stars. The role of the magnetic field in the activity of giant stars is seldom studied and not well understood. To our knowledge, no more recent studies of emerging (and trapped) magnetic flux tubes causing the observable magnetic features like spots or flares exist than the one by Holzwarth & Schüssler (2001).
The existence of the magnetic field is the basis of the flare activity on giant stars as well as on dwarfs; however, measuring it is not an easy task. The interested reader can find a summary of magnetic field measurements on stars in Reiners (2012). Indirect evidence of magnetic activity on giant stars is the rotational modulation of brightness caused by starspots, which has been monitored using photometry for decades on a few active giants (Oláh et al. 2009, for example) and was studied more recently by Doppler imaging e.g., Kővári et al. (2017, see their Table 1), while a summary of the observables of cool star dynamos, including giant stars, is presented by Kővári & Oláh (2014). Recently, spots on giant stars’ surfaces were even directly imaged (Roettenbacher et al. 2016).
Before the era of space-borne photometry, observations of flares on giant stars were restricted to very few studies. The reason behind this is the fact that flares on giants are hardly observable from the ground: (i) the day-night period on the Earth generally restricts the continuous monitoring of stars. With rotational periods over about one day to weeks, even one single rotation cannot be fully covered – except in the polar regions of the Earth with only a few instruments. As an example, we invite the reader to consult the results of a continuous 10.15 day BV R photometry with a 155 s cadence for the RS CVn active binary V841 Cen (and the non-radially pulsating δ Scuti star V1034 Cen) from the Antarctica by Strassmeier et al. (2008); (ii) the signal-to-noise (S/N) of the ground-based photometry is limited by atmospheric effects and weather conditions; (iii) due to the high luminosity of giant stars, the flares appear on a luminous background, resulting in only a small amplitude brightness increase relative to the star. Figure 1 shows a flare lasting a few hours on an active giant star with a long period and high amplitude rotational modulation. This flare would be barely (or even not at all) observable from the ground.
Among the very few flares observed on giant stars from the ground, there is a remarkable six-day-long event. This huge eruption, observed in Hα by Catalano & Frasca (1994), occurred on HK Lac, a close binary with an active giant component. The flare released 1.28 × 1037 erg total in Hα, and it was correlated with the appearance of a new active region on the star (Oláh et al. 1991). Another interesting example is an almost ten-day longflare event lasting for about one stellar rotation on YY Men, an FK Com-type K1III giant star, observed photometrically in 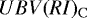 broadband colors by Cutispoto et al. (1992) and obtaining one data point per night. The total released energy in the optical passbands was about 1.8 × 1039 erg (Cutispoto et al. 1992).
broadband colors by Cutispoto et al. (1992) and obtaining one data point per night. The total released energy in the optical passbands was about 1.8 × 1039 erg (Cutispoto et al. 1992).
Continuous monitoring of stars by space instruments in optical wavelengths (Kepler, TESS), both in 2-min and 30-min cadence immediately initiated studies of the incidence of flaring objects among stars with different stellar parameters such as their spectral type, mass, effective temperature, and so on. A number of different algorithms have been developed to find flares in the enormous photometric datasets provided by the satellites (to the order of 105 − 106 stars from each instrument). At the same time, the question of how trustful the algorithms are arose, considering that flares can be mixed up with several real and erroneous features like stellar oscillations or photometric errors. Of course, false positive detections are probably unavoidable, but the goal is to minimize their number.
Davenport (2016) investigated the available Kepler data from Quarters 0–17 and cataloged 4041 flare stars, but they did not list their luminosity classes. Van Doorsselaere et al. (2017, hereafter D17) analyzed the long-cadence Kepler data from Quarter 15 and tabulated the flaring stars by spectral type. They gave a list of 695 flaring giant stars out of the 21 875 analyzed giants yielding a 3.18% flare incidence, slightly higher than the rate for the G-stars. These cited results used fully automatic pipelines for flare detection, which resulted in a high number of false positives. The possible origin of the detected false positives in Davenport (2016) was explained by Davenport et al. (2019) in their own results; namely, the earlier version of the appaloosa code was insufficient in treating the periodic signals in the data, leaving sharp or peaked structures in the residuals that then were recognized as flares.
Finally, applying all Kepler long-cadence DR 25 data, Yang & Liu (2019, hereafter YL19) discussed in detail the origin of the high number of false positive flare detections in the earlier studies and summarized the characteristics of all previous flare-finding techniques together with their own approach, which included the possibility of visually checking the results. In their Table 3, YL19 compared the flare incidences published by different authors with their own results, and, specifically, they found a 0.33% flare incidence for the giant stars. From the final dataset of 3420 flaring stars of YL19, the published stellar parameters made it possible for us to select the giant flaring stars of the paper for our present study.
In this paper, we revise the earlier detections of D17 and YL19 on the incidence of flaring stars among the giants in the Kepler field and give details about the flare characteristics of the confirmed flaring giants. Recently, we studied KIC 2852961, a giant star in the Kepler field, and discussed its flaring properties in Kővári et al. (2020, hereafter Paper I), entitled “Superflares on the late-type giant KIC 2852961”. Upon studying dozens of flaring giants, a perhaps naive question arises: what does “superflare” actually mean? Since superflares are commonly defined by energies log Ebol > 32.0 [erg], all detectable flares on giant stars would automatically be classified as superflares. However, this definition is only an energy scale; the environments in which the flares originate are different on ultracool dwarfs (full convection, high gravity), on main-sequence G-, K-, and M-dwarfs (convective shell, high gravity), and on giants (convective shell, low gravity). This question is discussed in Sect. 5.5.
The outline of the paper is as follows: the applied data are summarized in Sect. 2, and the descriptions of the applied methods are found in Sect. 3. In Sect. 4 and Sect. 5, the results are given and discussed, and these are summarized in Sect. 6.
 |
Fig. 1 One flare on KIC 6861498 (from the 16 observed) lasting about five hours with negligible amplitude compared to the rotational modulation of ≈89 days long. Top: whole dataset. Bottom left: flare on the descending branch of the rotational modulation. Bottom right: flare enlarged. |
2 Data
To check the flaring events in giant stars, we used a set of 706 stars compiled from the lists of D17 with radii of under 30 solar radius (666 stars) and from YL19 (80 stars in this paper; 40 stars are common in the two lists). The stars in the aforementioned lists were selected taking logg ≤ 3.5 as well. Both these studies originally used the stellar parameters from the Kepler Input Catalog (KIC) database; D17 used KIC DR10, while YL19 used KIC DR25. However, Berger et al. (2018) recently revised the radii of the Kepler stars and used the Teff values from Mathur et al. (2017) supplemented with information from other sources. The Revised TESS Input Catalog (Stassun et al. 2019, hereafter TICv8) contains most of the stars we planned to study. Thus, it is timely to revise the flaring giant statistics in light of the revised stellar parameters.
To decide the most useful catalog to represent stellar parameters for our study, in Fig. 2 we plot the Teff and radii of those 77 flaring stars from the resulting 86 (see Sect. 4, Table B.1) that have values in all of the following catalogs: KIC, Gaia DR2, TICv8, and that of Berger et al. (2018). The result shows that, with regard to the KIC data, the radii of the stars strongly deviate from the values compared to the other three sources; data from Berger et al. (2018), Gaia DR2, and TICv8 agree well with each other. The temperature values of Berger et al. (2018) and KIC have a small, on average ≈100 K systematic difference compared to the Gaia DR2 and TICv8 data. The mean effective temperature of the 77 stars from the Gaia DR2 and TIC catalogs are 4831 ± 305 and 4872 ± 428; whereas from Berger et al. (2018) and KIC, they are 4977 ± 366 and 5018 ± 312, respectively.We note that the temperature values in Gaia DR2, and TIC catalogs, and similarly the KIC and Berger catalogs are mostly of the same origin, as is also shown by these averages. For the full D17+YL19 sample of giants used in this paper, comparisons of the temperatures, radii and distances (which are important for the radius determinations) are compared in Appendix A on Figs. A.1–A.3.
In this work, we used the long-cadence Kepler pre-search data conditioning (PDC) light curves from DR25 with the help of various facilities of the NASA Exoplanet Archive. Finally, Teff and the radii of the stars in the tables of results of the present paper are taken from TICv8 (Stassun et al. 2019). If they were unavailable, then they were taken from Gaia DR2 and KIC DR25, in this order.
3 Methods
To identify the flaring giant stars, we used a combination of conventional (visual inspection) and automated pipeline searches. The first approach to check if the stars were indeed flaring in D17 and YL19 was simply to inspect their light curves one by one visually. First, we kept the seemingly truly flaring and the questionable cases and obtained a list of stars that were good candidates as veritable flaring giants.
Next, a flare search made use of an automated pipeline accompanied by a visual inspection. To this end, we ran an updated version of the flare detection algorithm from Günther et al. (2020) on the detrended Kepler light curves.First, we computed a Lomb-Scargle periodogram to identify (semi-) periodic modulation caused by stellar variability or rotation. Then, we removed the dominating periodic signal using a cubic spline with knots spaced at one tenth of this period. During this step, we also identified and masked all outlier data points at 3σ by sigma clipping the data residuals. We repeated this entire process two more times, or until no new periods were found. Finally, from the collected list of all outliers, we considered those to be flare-like events that contained a series of at least three subsequent 3σ outliers.
These candidates were then visually inspected to decide if they should be declared a flare or a false positive. For this, we used the prior knowledge of typical M-dwarf flare profiles in white light, which typically show a rapid rise followed by exponential decay. However, we also identified and recorded various shapes that were clearly distinct from the stellar variability, but did not match the classical rapid rise and exponential decay profile exactly. These might have been altered by quasi-period oscillations, scatter, instrumental effect, multiple flare events – or a different physical process leading to the flare origin.
We cross-matched the lists from the two approaches (purely visual, and automated pipeline combined with visual inspection) and checked the questionable cases again. Those stars that show brightenings that we considered unlikely to be flares were deleted from the list. This way, we obtained a final list of 86 flaring stars.
Next, we ran the pipeline FLATW’RM (FLAre deTection With Ransac Method) of Vida & Roettenbacher (2018)1 for each target of the final list of 86 flaring stars for independent automated flare detections. Finally, the individual flare detections carried out by the two independent pipelines from Günther et al. (2020) and FLATW’RM of Vida & Roettenbacher (2018) were cross-matched, and a flare was considered real when it appeared as a result from both pipelines.
The observed flare duration is the time difference between the last and first data points of the flares which are above the 3σ detection limit, and, due to the long (30 min) cadence, this underestimates the true flare duration especially for shorter flares. To calculate the εf relative flare energies (i.e. the flare energies relative to the quiescent star), we also made use of the program FLATW’RM (Vida & Roettenbacher 2018). To run FLATW’RM, we set the minimum number of flare points to two, and the detection level to 3σ. This way, we were able to minimize the number of false positives at the cost of missing some smaller events. As a template, a simple “classical” flare shape was used (Davenport et al. 2014); we discuss the effect of this simplification in the flare energy calculations of complex flares in Sect. 5.1. From the εf relative flare energies, the Ef absolute flare energies were derived by multiplying εf values by the L⋆Kep base luminosity of the quiescent flare-hosting star. Base luminosities in most cases are obtained using stellar effective temperatures and radii from TICv8 (if not available, then from Gaia DR2 and KIC DR25, see Table B.1) and assuming black-body radiation through the Kepler filter. For more details on flare energy calculations, we invite the reader to consult Paper I (Sect. 6). Finally, rotational periods of the flaring stars were calculated using the Lomb-Scargle algorithm provided by the NASA Exoplanet Archive Kepler Stellar Table.
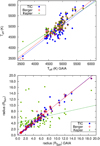 |
Fig. 2 Comparison of effective temperature and radius values of 77 flaring stars from the resulting 86 using TICv8, Berger (Berger et al. 2018), Kepler, and Gaia DR2 databases. See the text for more details. |
4 Results
4.1 The confirmed flaring giant stars
Among the 706 giant stars that we compiled from the lists of D17 and YL19, we confirm the detection of flares in 86 cases, and we do not measure any significant flare signal in the rest of the sample. We also confirm the detection of flares for 53 of the 80 flaring red giants that were found by YL19.
As already mentioned in the Introduction, according to Davenport et al. (2019) the false positive flare detections in Davenport (2016) originated from the earlier version of the appaloosa code, which left sharp or peaked pseudo-structures in the residuals from the periodic signals. Such a failure might also occur when using automated search for flares in other, earlier codes. When discussing what kind of variability was behind the false positives in D17, YL19 mentioned pulsating stars but did not giveany further details (see their Sects. 2.2 and 3.2). The origin of the high number of false positive flare detections has finally been unveiled with the help of the recent papers by Hon et al. (2019) and Gaulme et al. (2020).
Cross-matching the 666 stars from the D17 flaring giant sample with the results of Hon et al. (2019), we found 577 common stars, meaning that these could in fact be oscillating giants. These 577 oscillating stars by Hon et al. (2019) include the 310 brighter ones (Kpmag < 12.5) from Gaulme et al. (2020), which were detected independently. Visualizing these results, the HRD of the studied sample and our results are shown in Fig. 3, where the brighter subsample of the oscillating giants derived by Gaulme et al. (2020) is plotted with light blue crosses. In Fig. B.1, an enlarged version of the dense part of Fig. 3 is found to also include the oscillating stars from Hon et al. (2019) cross-matched with our sample. Taking this evidence into account, we can conclude that the vast majority of the false positive flaring giants we found are in fact oscillating stars. Of course, the co-adding and cross-matching of samples of many stars from different sources may result in a few misclassifications, but we are confident that this number is very small. It turns out that flaring stars also show oscillations (e.g., the Sun), but we found only a few among our verified flaring giants. We discuss the incidence of oscillations in flaring giants in Sect. 4.3.2.
The stellar parameters from the TICv8 (if not available, then from Gaia DR2 and KIC DR25), the rotational periods calculated using the Lomb-Scargle algorithm provided by the NASA Exoplanet Archive Kepler Stellar Table, and the number of detected flares, are given in Table B.1. We note that the luminosity classes reported in the TICv8 indicate that 17 of the 86 flaring stars are actually dwarfs, and another eight stars are not found in the TICv8, thus no evolutionary status is given for these. Therefore, the number of flaring giants we confirm is at best 69 – only confirming a tenth of the originally claimed discoveries of D17. Figure 3 shows a clear main sequence with the position of the Sun marked; this is drawn by the polluting flaring dwarfs.
There are 17 stars in the combined sample of 706 flaring giant candidates from D17+YL19 that we find difficult to classify as flaring giants for various reasons; for example, they have too short or no measured rotational periods, or are blended by other stars, or demonstrate a possible oscillating or pulsating nature of variability. They are listed Table B.2 with explanations; six stars in the table are considered as dwarfs in TICv8.
The distributions of effective temperatures and stellar radii of both the full sample and the confirmed flaring giants are displayed in Fig. 4. The two panels show that only 10–12% of the giants of the D17+YL19 candidates do exhibit flares. The histogram of effective temperatures shows that the distribution of the confirmed flaring stars is very similar to that of the whole sample. On the contrary, the distribution of radii is significantly different: the whole sample peaks at about 10 R⊙, whereas the distribution of confirmed flaring stars peaks between 3 and 7 R⊙. This is well in line with the finding of Gaulme et al. (2020, Fig. 9, upper part of the bottom panel), showing that highest number of the radii of active giants on the RGB is around 5–6 R⊙. The part of the sample with the smaller radii mostly consists of dwarf stars (dark red color in Fig. 4), which contaminate the sample according to TICv8.
The stellar radii versus temperature are shown in Fig. 5. In the upper panel, we show the whole investigated sample, while in the lower panel we show the most dense part, which contains all the resulted flaring stars. The dense group of false positive flaring giant stars (gray dots) with radii between 6–14 R⊙ in temperatures ranging from 4500–5200 K are mostly oscillating red giants, as is suggested by our cross-matching results detailed above.
Magnetic fields are measured in 29 single G-K giant stars via the Zeeman-effect by Aurière et al. (2015, Fig. 5) depicting a well-defined “magnetic strip” on the HRD indicating the maximum convective turnover time (τc) on the tracks and presenting a Rossby-number (ratio of the rotational period and the convective turnover time, Ro = Prot∕τc) of the studied stars. The origin of these fields is thought to be working α − Ω dynamos, whose existence is predicted by Charbonnel et al. (2017, Fig. 6, upper-right panel) showing that low Rossby numbers, which are essential to the generation of the magnetic field, are characteristic of the segments of the theoretical evolutionary tracks where the giant stars with the measured magnetic fields are found (Aurière et al. 2015). The location of the “magnetic strip” drawn both by observations and theory agrees well with the position of the flaring giant stars shown in Fig. 3 (confirmed in this paper).
 |
Fig. 3 Locations of D17+YL19 giant sample in the HRD. Symbols: gray dots: D17+YL19 giant sample; big red dots: flaring giants verified in the present paper; small red dots: contaminating dwarfs and stars with unknown evolutionary status. Light blue crosses mark the oscillating giant stars from Gaulme et al. (2020) for stars brighter than Kpmag = 12.5 which coincide with the stars in our D17+YL19 sample overlapping them on the figure. The orange star marks the location of the Sun. See the text and Fig. B.1 for more details. |
 |
Fig. 4 Distribution of effective temperatures (top) and radii (bottom) of the full sample (originally identified as flaring giants by D17 and YL19) and the number of stars we found as flaring giants plotted in gray and red, respectively. Dark red marks the stars classified as dwarfs by TICv8. We note that the histogram of radii does not exceed 20 solar radius (18 stars) for better visibility, since no flaring star is found above this limit. |
 |
Fig. 5 Radii of the flaring giants. Top: entire investigated sample. Bottom: enlarged region of radii. Gray dots represent the D17+YL19 giant sample, big red dots mark the flaring giants that are verified in the present paper, while small red dots represent the contaminating dwarfs and stars with unknown evolutionary status. |
 |
Fig. 6 Number of flares at different rotational periods (top) and rotational velocities (bottom). Light blue crosses mark the flaring red giants that also show oscillations (see Sect. 4.3.2). |
4.2 Activity and rotation
We plotted the number of flares as a function of the rotational periods and rotational velocities in Fig. 6. Looking at the upper panel of the figure, one can see that flaring giant stars with the shortest rotational periods and those of up to 30–40 days can produce both higher and lower numbers of flares. There are 15 stars in Fig. 6 with rotational periods longer than 35 days and flare numbers below 65: all of them are giants, and they constitute about one quarter of the confirmed flaring giantpopulation (minimum 61 stars). From the lower panel of Fig. 6, no real distinction of flare numbers between stars with lower and higher rotational velocities is seen, though a slight decrease in flares with a higher rotational velocity may be present. However, due to the low number of stars with higher rotational velocities, this change is not significant. The investigation of the connection (if any) between the rotational properties and flare numbers of giant stars requires detailed knowledge of the physical parameters of these giants and goes beyond the scope of the present paper.
4.3 Binarity and oscillations among the flaring red giants
4.3.1 Binarity
Gaulme et al. (2020) searched for the incidence of binary systems among the red giants that show photometric rotational modulation. They obtained multi-epoch spectroscopic observations for a subsample of 85 stars. Among these 85 stars, 14 belong to the 61 flaring giants studied in the present paper (see Table B.1). Of these 14 stars, one is a subgiant (or a small red giant) spectroscopic binary (KIC 11551404), nine are clear red giants in spectroscopic binaries with no oscillations, one is an oscillating (weak oscillations) red giant in a spectroscopic trinary (KIC 8515227), one is a single fast rotating red giant (KIC 11087027), and two are fast rotators (KICs 5821762 and 8749284) for which the spectroscopic signal is too noisy to assess any radial-velocity variability (Fig. 7 and Table B.1). Even though only a complete spectroscopic survey would be needed, this information confirms that close binary systems are likely to compose a large fraction of the sample: 11 SBs represent 18% of the 61 giants.
We also computed the photometric index Sph (percent) for each target. This parameter is the mean standard deviation of the time series computed over five rotational periods (Mathur et al. 2014). It is commonly used as a proxy of magnetic activity in photometric time series: the larger Sph, the larger the surface magnetic field. Figure 7 shows this parameter of all 86 stars from Table B.1 as a function of the rotational period. No particular trend is visible, but it is worth noting that its value is always higher than 0.2% for all the flaring giants, whereas regular inactive red giants have Sph < 0.1% (Gaulme et al. 2020). In addition, a large fraction of the targets display values of Sph larger than 1%. According to the spectroscopic study of 85 red giants with activity in Gaulme et al. (2020), red giants with 0.1 ≤ Sph ≤ 1% are fast single rotators, whereas the vast majority of red giants with Sph ≥ 1% belong to close binary systems (see their Fig. 12). We can therefore rightly suspect that a large fraction of our flaring giants do belong to close binary systems.
 |
Fig. 7 Photometric index Sph (percent) as a function of rotation period Prot (days) for the 86 flaring stars from Table B.1. Both axes are in logarithmic scale. The blue and red symbols indicate the non-oscillating and oscillating giant stars, respectively. The orange markers indistinctly indicate dwarf and subgiant stars. The upward-pointing triangles are confirmed close spectroscopic binaries including at least one red giant, and the circles identify RV-stable red giant stars (Gaulme et al. 2020). The orange diamond with black edges is a confirmed subgiant belonging to a close binary system (KIC-11551404, Gaulme et al. 2020). The gray background reflects the distribution of Sph of the regular inactive red giant stars (the darker, the higher) according to Gaulme et al. (2020). |
4.3.2 Oscillations
Red giants are known to display oscillations in the vast majority of cases (≥99% Gaulme et al. 2020). The only situation where oscillations are not detectable corresponds to red giants in close binary systems: more than 85% of the red giants with no oscillations are in close binaries (Gaulme et al. 2020). The presence of oscillations is thus a parameter that is complementary to large values of Sph to indicate the presence of close binary systems. We therefore looked for oscillations in all the 86 targets of the sample. We note that we could not search for oscillations of main-sequence or subgiant stars of the sample because the sampling of the Kepler light curves (30-minute cadence) is not fast enough to access stars with a frequency of a maximum amplitude larger than about 300 μHz.
Despite the fact that 20 targets were already listed in Gaulme et al. (2020) and 24 in Hon et al. (2019, the same plus four), we thoroughly restudied them one by one. Indeed, light curves with flares are tedious to deal with, as a single uncorrected flare event is able to ruin the power spectrum of the light curve, which is where we search for oscillations. Hon et al. (2019) reported the detection of oscillations for the 24 stars that are common to our list. On the contrary, Gaulme et al. (2020) report the detection of oscillations in only four red giants of the same list. We reprocessed the light curves one by one thanks to the flare date and duration produced by the flare automatic pipeline. We systematically cut the flares and bridged them with a smoothing of the light curves during the gaps. We also manually removed a few remaining flares that were not selected by the algorithms. Except for the removal of the flares, we processed the data in the same way as Gaulme et al. (2020), and we refer the reader to this paper for more details.
Of the 86 flaring stars, we detect red-giant oscillations in seven of them (KIC 4680688, 5286780, 5808398, 6445442, 7363468, 8515227, and 8951096) and rule out all of the others. The discrepancies with the results of Hon et al. (2019) are explainable by the fact that they make use of an automatic pipeline based on machine learning that deals with almost all of the Kepler red giants observed by Kepler. Individual errors can happen sporadically, and it is not surprising that this occurred on light curves with large flares, which are a terrible source of systematic noise in the Fourier domain. The oscillating stars are indicated in Fig. 7 in the form of red symbols. We also detect a γ Doradus–δ Scuti-type oscillator in the sample.
It has been observed that red giants in close eclipsing binary (EB) systems have peculiar photometric properties (Gaulme et al. 2014). Among the 35 Kepler red giants that are confirmed to belong to EBs, 18 display regular solar-like oscillations – with their amplitudes matching the empirical expectations (e.g., Kallinger et al. 2014) – and no rotational modulation. All of the remaining systems display rotational modulation, seven with partially suppressed oscillations, and ten with no detectable oscillations (Benbakoura et al. 2021; Gaulme et al. 2014, 2016). Gaulme et al. (2016) showed that the non-detection of oscillations is not an observational bias. This is observed in the closest systems, where most orbits are circularized, and rotation periods are either synchronized or in a spin-orbit resonance. Such a configuration is observed for systems whose orbital periods are shorter than about Porb ~ 150 days. Gaulme et al. (2014) suggested that the surface activity and its concomitant mode suppression originate from tidal interactions. During the red giant branch, close binary systems reach a tidal equilibrium, where stars are synchronized and orbits circularized (e.g., Verbunt & Phinney 1995; Beck et al. 2018). Red giant stars are spun up during synchronization, which leads to the development of a dynamo mechanism inside the convective envelope, leading to surface spots. The magnetic field in the envelope likely reduces the turbulent excitation of pressure waves by partially inhibiting convection. Since spots can also absorb acoustic energy, these two effects lead to the suppression of oscillations.
A summary of the results on the binarity and oscillations of the flaring red giants is plotted in Fig. 8. The list of six giant stars plus one of an unknown evolutionary status, all of which are flaring and show oscillations, and one γ Dor/δ Sct-type star, is given in Table 1. The star without a given evolutionary status (KIC 5286781) seems to be a dwarf star concerning its position in the HRD, see Fig. 8. The flaring rate of the six giant stars with oscillations in Table 1 (16 flares on average) is much lower than the average flare number of the 61 giants (52 flares on average), which is clearly seen in Fig. 6, where the oscillating red giants are marked with light blue crosses. This fact is in line with the result of Gaulme et al. (2016) showing that the presence of oscillations suggests weaker activity. Finally, we added the four non-oscillating red giants (KIC 3955867, 4569590, 7943602, 9291629) that belong to eclipsing binary systems studied by Gaulme et al. (2016), which are also observed to display flares. Their parameters are known from dynamical analysis, that is, a combination of high-resolution spectroscopy and eclipse photometry.
 |
Fig. 8 Locations of the flaring giants (big red dots, present paper), dwarfs or stars with an unknown evolutionary status (small red dots, present paper), possible binaries from Table B.1 by Gaulme et al. (2020, dark blue dots), and eclipsing giants with oscillations (light blue dots) oractivity (pink dots) from Gaulme et al. (2016) and Benbakoura et al. (2021) in the Hertzsprung−Russell-diagram. Light blue cross-over red dots mark the flaring and oscillating stars from the present paper. The orange star marks the location of the Sun. |
4.3.3 The case of KIC 5080290
We list KIC 5080290 in Table 1 as γ Dor / δ Sct hybrid without a derived rotational period. This star was first identified as a δ Sct star by Uytterhoeven et al. (2011), who listed four independent δ Sct-type frequencies. However, this star had at least six unambiguous flares concerning our cross-matched results with logarithmic energies between 35.7 ≤ logEKp ≤ 37.2 [erg]. KIC 5080290 is a bright star of 9.51 mag in the G-band, with neighboring stars not even coming close at several magnitudes fainter.
Just recently however, Zwintz et al. (2020) showed that β Cas, an F2III δ Sct-type pulsator with only three p-mode frequencies of low amplitude, has a complex magnetic field very possibly of dynamo origin. β Cas is a terminal-age main-sequence (TAMS) star with logg = 3.53 ± 0.58 and Teff = 6920 ± 140 K, which is rotating very quickly with Prot = 0.898 d, which probably helps to maintain the dynamo even at such a high temperature (Zwintz et al. 2020). Thus, KIC 5080290 could be another example of a pulsating star with magnetic activity.
The mass of β Cas is about 2.1 M⊙ (or 1.91 ± 0.02 as given in Che et al. 2011) and is already moving away from the TAMS. Its age is 1.18 ± 0.05 Gyr according to Che et al. (2011). We may suppose that a star such as β Cas could be a progenitor of the flaring giant stars investigated in this paper. Specifically, KIC 2852961, with the highest energy flares among the flaring giants confirmed in this paper, has a mass of 1.7 ± 0.3 M⊙, and its age is about 1.7 Gyr. As discussed in Paper I, it is conceivable that the progenitor of KIC 2852961 was an A5-F0-type star.
Flaring stars from the 86 of Table B.1 with oscillations derived by Gaulme et al. (2020, G+20) and in the present paper (pp).
5 Discussion of flares
5.1 Reliability of the derived flare numbers and their energies
To test the performance of the cross-matched results of flare recoveries from the D17+YL19 sample by the pipeline from Günther et al. (2020) and FLATW’RM of Vida & Roettenbacher (2018), we compared the flare list of KIC 2852961 from the present paper with the visually located and checked flares published in Paper I, Table 3. From the 59 flares in Paper I, our automated detection found 51. Of the missing eight flares, seven belong to the low-energy regime log EKp < 36.6 [erg] (equivalent to εf ≈1-min relative energy) or less, where the probability of detecting a flare starts to diverge noticeably from 100%, according to the test results presented in Paper I (see Sect. 7 of that paper). One non-detection belongs to a complex flare. However, the total number of automatically detected flares of KIC 2852961 in this paper is, coincidentally, also 59, due to the detection of complex events with multiple peaks as series of single events by the pipelines. This comparison shows that we successfully avoid false positives at the cost of missing some real, mostly small energy flares, and the overall picture of the detected flare numbers and energies are not misleading.
We compared the derived flare energies of 51 flares of KIC 2852961, which are available both in Paper I and the present paper. From these flares, 24 are complex and 27 are simple events. Since we used a simple flare template to automatically derive the flare energies by FLATW’RM (Vida & Roettenbacher 2018), we also checked how this simplification affected the resulting flare energies. The simple mean of the difference between the two approaches (in the sense of energies from the present paper minus those of Paper I) is (−0.326 ± 1.481) × 1037, showing that there is a small shift between the results due to the different L⋆Kep used in the two sources. Separately from the complex and simple flares, the results are (−0.293 ± 1.941) × 1037 and (−0.355 ± 0.940) × 1037, respectively,which is only a small difference. The higher standard deviation of the mean of the complex flares points toward a slightly higher average scatter of the resulting flare energies when using the simple template for calculating the energies of complex events, but this does not modify the FFDs noticeably as is shown in Fig. 13 (see Sect. 5.3).
5.2 Distribution of flare energies
In Fig. 9, flare energy distributions of the 17 dwarfs (light blue), 61 giants (dark blue), and KIC 2852961 (red) from Table B.1 are compared. Missing are those eight stars for which no evolutionary status is given. The differences in the mean flare energies between dwarfs and giants are clear. The extended tail of the flare energy distributions of giants is mostly made up by the excess high energy flares of KIC 2852961.
On the histogram of the dwarfs (light blue) a small secondary maximum is found toward higher energy. This hump is mostly due to two stars listed as dwarfs in TICv8, KIC 9116222 (260 flares) and KIC 11515713 (186 flares), which have approximately one order higher energy flares than the rest of the dwarfs. The common energy distribution of these two stars is marked with slanted blue lines in Fig. 9. These dwarfs could be G-type superflaring stars, and both of them have effective temperatures of about 5500 K (see also Shibayama et al. 2013, their Fig. 8). On the other hand, the radii are 2.7 and 2.8 R⊙ (Table B.1), and the logg values from LAMOST2 are 3.69 and 3.88 for KIC 9116222 and KIC 11515713, respectively, suggesting a slightly evolved, subgiant evolutionary status of these stars. In the LAMOST catalog, 45 stars out of the 86 from Table B.1 have spectra, and the LAMOST parameters (Teff, log g and [Fe/H]) of these stars are given in Table B.3 as supplementary information.
From the final results of the 86 stars in Table B.1, we selected 19 giant stars with the highest number of observed flares in order to compare their flare energy distributions. The basic stellar parameters (Teff, R⊙, Prot), quiescent stellar luminosity values in the Kepler bandpass, average flare energies, equivalent times (=relative flare energies), histogram skews, and remarks as to whether the star is a member of a binary system, are given in Table 2. Comparing these stars with that of KIC 2852961 (Table 2, bottom line) we find that the latter has on average much higherenergy flares than the selected 19 flaring giants. The flare energy distribution of KIC 2852961 mostly reveals high-energy flares (Paper I, Fig. 15) opposite to the ones observed for the selected 19 stars, which all show declining number of flares toward higher energies. The low energy parts of the histograms are affected by the recovery bias.
The individual flare energy distribution histograms of the 19 stars are plotted in Appendix C, Fig. C.1 together with that of KIC 2852961. Most of the histograms of Fig. C.1 are approximately symmetric or moderately positively skewed (skewness is less than 0.5, or from 0.5–1.0, respectively), except two cases with highly positive skew. Only the histogram for KIC 2852961 shows a small negative skew, meaning that the mean flare energy is smaller than the peak of the distribution, that is, the high-energy flares dominate. The comparison of the distribution between 2188 individual flare energies of 19 stars together, and that of KIC 2852961 in Fig. 10, depicts the striking difference in the energy distributions in one figure.
One can see from Table 2 that the flare characteristics of the two confirmed spectroscopic binaries (both SB2) are not different to the rest of the stars, therefore the binarity itself cannot be the ultimate cause of thedifference between the flaring nature of the 19 stars and KIC 2852961. It has already been shown by Strassmeier et al. (1990, 1994) from observations of chromospheric activity at CaII H&K and Hα that, contrarily to MS active stars in binaries, in the case of evolved stars binarity does not play a crucial role in the activity level.
Basic stellar parameters, average flare energies (Ef, in the Kepler bandpass), and equivalent times (teq) of the 19 most flaring stars, and characteristics of the flare distributions.
 |
Fig. 9 Comparison of distribution of flare energies in the Kepler bandpass observed on 17 dwarfs (light blue), 61 giants (dark blue),and KIC 2852961 (red). A part of the dwarf star’s light blue histogram striped with dark blue lines are occupied by the flares of two, possibly subgiant stars. See the text for more information. |
 |
Fig. 10 Comparison of combined distribution of flare energies in the Kepler bandpass of the most flaring 19 giants (dark blue columns) and that of KIC 2852961 (red columns; see also Fig. C.1). |
 |
Fig. 11 Flare recovery rate in the function of relative flare energy (equivalent time in s). The recovery rates (dots) were derived from a recovery test using artificial flares injected into the original 20 data files. The test results were generalized using a parameterized hyperbolic tangent function (blue line). The inset shows the details below 50 s of equivalent time. See the text for more information. |
5.3 Flare recovery completeness
We carried out flare recovery tests for the 19 most flaring giant stars and for KIC 2852961 to compare the results of the present paper with those of Paper I, using the code allesfitter (Günther & Daylan 2019, 2020). We note that the tests were done and used only for long-cadence, 30-min time-resolution Kepler data according tothe method described in detail in Paper I, Sect. 7. The photometric precision of the 20 stars with Kp magnitudes from 10.2–14.0 are similar3, so the effect of S/N has no, or very minor, influence of the test results.
The recovered flare rates for 20 stars (19 most flaring giants plus KIC 2852961) were plotted together in the function of the relative flare energies of the injected flares in Fig. 11. The shapes of the individual test results proved to be very similar, so we tried to use the test as a single recovery application by fitting the test results with an arbitrarily chosen parameterized hyperbolic tangent (tanh) function tracking the envelope of the test results. This generalized function makes it possible to automatically correct the detection bias of the cumulative number of flare frequencies toward lower energies for all stars at the same time. However, there are deviating points in Fig. 11 between 50 ≤ εf ≤ 300 s relative flare energies (≡ teq equivalent times), but most of these come from the recovery tests of three stars (out of 20) only. Figure 12 shows the difference between applying the common recovery correction and the one realized for the star only in the most deviating case of KIC 5480528. The very small difference between the slopes of the fits to the cumulative number of flare frequencies proves that the use of a common correction function for all stars is appropriate.
The inset of Fig. 11 shows the lowest part of the relative flare energies of the test. The total number of flares to be corrected for recovery bias is 2247, and from these only 30 flares fall below 10 s of equivalent time (1.3%), where the applied function does not follow the envelope of the test results well. We note that at the lowest relative flare energies (i.e., below εf ≈ 5 s), the test gave quite uncertain results, because at this range the data noise exceeds the lowest flare amplitudes. The other reason could be thelimited (30-min) time resolution of the observing data.
Finally, from the generalized tanh recovery function, we derived correction factors (multiplicative inverses) to estimate the real flare numbers significant only at the low energy ranges. These correction factors were used to provide the detection bias-corrected cumulative flare-frequency diagrams (FFDs) in the following plots.
 |
Fig. 12 Largest deviation between application of the common recovery correction and the one realized for the star only (called own correction). The object is KIC 5480528; black, red, and blue colors mark the data and fits to the original data, own corrections, and common corrections, respectively. The difference between the slopes of the fits for the two different corrections (red and blue) is within two sigma. Flare energies are derived for the Kepler bandpass. (The five lowest energy data points were excluded from the fits.) |
 |
Fig. 13 Detection bias-corrected cumulative FFD for KIC 2852961 using the two different cross-matched, automatic flare-detection results introduced in the present paper. The original data points are plotted in gray, and the blue points show the detection-bias-corrected values. The orange crosses show the detection-bias-corrected results from Paper I. Flare energies are derived for the Kepler bandpass. |
5.4 Reliability of the flare frequency diagrams
A flare frequency diagram (FFD) was drawn for KIC 2852961, with the method described in detail in Paper I (Sect. 6). This time, we used the stellar parameters as given in TICv8, that is, everything was done in the same way for KIC 2852961 as for the selected most flaring 19 stars. The result is plotted in Fig. 13 using gray and blue points from the original data and from the corrected flare recovery, respectively. The bias-corrected recovery values from Paper I (Fig. 11) are plotted with orange crosses. The comparison with the blue points and orange crosses shows that the flares that were not detected by our method were mostly low-energy flares as discussed above in Sect. 5.2. A very small shift in the cumulative energy derived in the present paper toward the lower values is also seen due to the different base stellar flux calculated from the temperature and radius given in TICv8 and in Paper I. However, the two distributions are very similar.
The result for the fit to the lower energy range (red line) yields a power-law index of α = 1.31 ± 0.02, while the result in Paper I is α = 1.29 ± 0.02. Similarly, the fit for the high-energy range (green line) yields α = 2.65 ± 0.09, while the result in Paper I is α = 2.84 ± 0.06. From these very similar results, we conclude that the method we apply for the 19 frequent flaring giants gives reliable frequency diagrams and fits.
 |
Fig. 14 FFDs for KIC 2852961 (red) and the 19 most flaring giant stars (blue) of the Kepler field. Flare energies are derived for the Kepler bandpass. A simple linear fit is drawn to the plots, in the upper-right corner the slopes of the fits and their errors are indicated. |
5.5 Flare frequency diagrams of 19 giant stars
After correcting for the detection bias, FFDs were constructed for the 19 most flaring giants stars from Table B.1, plotted in Fig. 14 applying simple linear fits to the data. Most of the FFDs can be fit well with a single line, except KIC 11551404, whose FFD shows a continuous curvature. The slopes of the linear fits (without KIC 2852961) spread between −0.82 and −1.33 with errors between 0.02 and 0.05. The mean of the slopes translates to α = 2.01 ± 0.16 power-law index for the 19 giants (see Fig. 14).
For KIC 7676676 and KIC 9419002, the two-component linear fits shown in Fig. 15 look more appropriate. The breakpoints between the high- and low-energy parts of the FFDs are at log EKp = 35.75, 36.0, and 37.6 [erg] for KIC 7676676, KIC 9419002 (Fig. 15), and KIC 2852961 (Fig. 13), respectively.
Studying flare energy spectra of dwarf stars and those of the Sun with two distinct power-law regions, Mullan & Paudel (2018) showed that the breakpoint in an FFD appears at a certain critical energy E(c), which depends on the local magnetic field strength and the local density, thus it should not be the same for all stars. The energy range within which the flares are detectable on a given star depends on observational selection; for example, low-activity stars exhibit a smaller number of flares, and low-energy flares cannot be detected at high S/N. Thus, it is not necessary for the critical energy E(c) to lie inside the observable energy range of flares. If it is outside, no break appears in the FFD, as was suggested by Mullan & Paudel (2018). We may extend this important finding to FFDs of more evolved stars discussed in the present paper. The two FFDs plotted in Fig. 15 span about the same energy range, but the breakpoints of the power laws are different, suggesting different magnetic field strengths and densities of the atmospheres, which probably originate from different masses and evolutionarystages on the RGB.
An interesting question is to explore the changes of the flare activity during different strengths of the overall activity of stars (activity cycles). We already addressed this problem in Paper I (Fig. 13). From the 19 selected stars, KIC 7676676 shows a continuous increase of the light curve amplitude, suggesting an increasing activity level of the star. In Fig. 16, FFDs are plotted for the time intervals of the lower (blue, 35 flares) and higher (red, 51 flares) amplitude rotational modulation. While at low energies, the two distributions are nearly the same, from about log EKp = 35.7 [erg] the energies of the flares observed after day ≈700 (Kepler time, plotted in red) are significantly higher, together with the increased overall activity manifested in higher amplitude rotational modulation. At the highest energies, the number of flares is small, but it is interesting that the highest energy flare occurred near the end of the lower activity phase of the star.
Cumulative FFD for the 19 most flaring stars co-adding 2188 flares is shown in Fig. 17 with gray and black dots for the original and bias-corrected values. Red dots and bars show the means and error bars for 30 bins throughout the data. The error bars were calculated from the 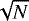 Poisson noise in each bin. Toward the low-energy parts, the individual FFDs bend at different energies, even after the correction for the recovery bias; therefore, when summing up all flares, a curvature on the overall FFD appears, ending around log EKp = 36 [erg]. Toward higher energies, the flare frequency is nearly linearly decreasing in all FFDs, and consequently in the common FFD, except for the highest energy part with a few flares only, where the decrease is faster. We note the similarity between our Fig. 17 and what is shown in Yang & Liu (2019, their Fig. 15). The FFD of KIC 2852961 is plotted separately into the cumulative FFD of the 19 giants (gray for the original data and blue for bias-corrected data and the fit). The high-energy part of the FFD of KIC 2852961 starts near the same energy (log EKp = 37.60 [erg]) where the highest energy flare of the 19 giants (logEKp = 37.56 [erg]) appears, meaning that in the high-energy range all flares of KIC 2852961 are more powerful than any flare from the 19 frequently flaring giantstars.
Poisson noise in each bin. Toward the low-energy parts, the individual FFDs bend at different energies, even after the correction for the recovery bias; therefore, when summing up all flares, a curvature on the overall FFD appears, ending around log EKp = 36 [erg]. Toward higher energies, the flare frequency is nearly linearly decreasing in all FFDs, and consequently in the common FFD, except for the highest energy part with a few flares only, where the decrease is faster. We note the similarity between our Fig. 17 and what is shown in Yang & Liu (2019, their Fig. 15). The FFD of KIC 2852961 is plotted separately into the cumulative FFD of the 19 giants (gray for the original data and blue for bias-corrected data and the fit). The high-energy part of the FFD of KIC 2852961 starts near the same energy (log EKp = 37.60 [erg]) where the highest energy flare of the 19 giants (logEKp = 37.56 [erg]) appears, meaning that in the high-energy range all flares of KIC 2852961 are more powerful than any flare from the 19 frequently flaring giantstars.
The recent works of Paudel et al. (2018), Shibayama et al. (2013), and the present paper allow an interesting comparison between the FFDs of a set of ultracool dwarfs, G-dwarfs, and flaring giants. The observations of ten ultracool dwarfs with spectral types from M6-L0 were made during the Kepler K2 mission, the flare recovery and the individual FFDs of their targets were calculated and presented in the same way as the giants in this paper. For a comparison, we invite the reader to consult Paudel et al. (2018, their Figs. 3 and 4) and Figs. 14 and 18 in this paper. The energy ranges of the flares on the ultracool dwarfs are between 29.0≤ log EKp ≤ 33.5 [erg], whereas thewhole energy range of the giants is outside this interval at higher energies, between 33.9≤ logEKp ≤ 38.7 [erg]. The average power-law index of the individual fits to the FFDs of the ten ultracool dwarfs (Paudel et al. 2018) and 20 flaring giants (present paper) is the same: α ≈ 2.0. Between theultracool dwarfs and flaring giants are the flare energies of the (super)flaring G-dwarf stars with bolometric 33.0≤ logE ≤ 36.0 [erg] energy studied by Shibayama et al. (2013, also from Kepler data), who found power-law indices α ≈2.0–2.2 for slowly rotating G-stars, and for all G-dwarfs together. The flare energy interval the Kepler passband for the G-dwarfs is about 32.2≤ logEKp ≤ 35.2 [erg] using the conversion form from Osten & Wolk (2015). Yang & Liu (2019) calculated FFDs for different spectral types of flaring stars (see their Fig. 3) and gave α =1.90 ± 0.10 power-law index especially for the giants and ≈2 as an average for all spectral types except the A-stars.
These results present a consistent view of magnetically active stars with flares from the smallest L0-stars through G- and M-dwarfs, to normal giants in a wide range of stellar masses, structures and ages. In this pool, all stars show flares of magnetic origin with similar shapes but of different timescales spanning a huge energy range of 29.0≤ logEKp ≤ 38.7 [erg]. The flares were observed with the same instrument (Kepler) and treated using the same or very similar methods. The FFDs of the different groups of stars run in the same way with a common power-law index of α ≈2.0. The different flare energies from an L0 to a giant star result from only a scaling effect depending on the details of the magnetic field, on the size of the active regions from where the flares originate, and on the conditions of the local environments, such as density and gravity. We discussed the details of the scaling effect in Paper I (Sect. 9.5).
A recent paper of Maehara et al. (2021, Fig. 14) compares the observed flare durations in the function of flare energies of the Sun, the flaring M-dwarf YZ CMi, G-dwarfs (Shibayama et al. 2013), and KIC 2852961 from Paper I. The slope of the relation is about 1/3, assuming constant magnetic filed strengths, and in this relation KIC 2852961 is on the same line as the Sun with B = 60 G (Maehara et al. 2021). The selected 19 most flaring stars of the present paper have observed flare durations from about 1–30 h (59–1766 min), and the energies are between 33.9 ≤ logEKp ≤ 37.6 [erg] occupying a region in the upper-right part of Fig. 14 in Maehara et al. (2021). The slope of the flare energy-duration power-law relation of KIC 2852961 from Paper I is 0.325 ± 0.026, while that from the present paper is higher, at 0.50 ± 0.04 as seen from Fig. C.2 (upper-left corner, red); however, the two results are within 3σ of each other. On this basis, we may suspect that the slopes of the relations of some from the other 19 individual stars, plotted in Fig. C.2, are probably also higher than the slope suggested by Maehara et al. (2021), due to the underestimation of the flare duration mostly for the shorter, lower energy flares (see Sect. 3 for an explanation). Nevertheless, all the slopes reveal positive correlation; they are different, but concerning the errors the difference is not significant.
Concerning the question we ask in the Introduction about the correct definition of the term “superflare”, we cannot give a definite answer. The flare energy ranges of stars embrace ≈1010 erg from the smallest flare on an ultracool dwarf to the most energetic one on a giant star. A specific, high-energy limit for flares to reach in order to be considered a “superflare” in an individual star could be estimated through the maximum available magnetic energies, as we did in Paper I (see Sect. 9.4) for KIC 2852961. However, this is a complicated task with many uncertainties, including the sizes of the active regions (through spot modeling), the magnetic field strengths (from measurements), and the flare loop sizes (from models). Perhaps the term “superflare” would be better reserved only for the Sun, where these parameters can directly be measured.
 |
Fig. 15 Two-component fits to the FFDs for KIC 7676676 and KIC 9419002. Black dots correspond to the original values, while red dots are bias corrected. We note the similar flare energy range and the different breakpoints of the fits for the two targets. Flare energies are derived for the Kepler bandpass. See the text for more details. |
 |
Fig. 16 FFDfor KIC 7676676 in two activity levels. The data points showing lower and higher amplitude rotational modulation are marked with blue and red dots in the inset, and the same colors mark the corresponding FFDs. The broken power-law fit (gray line) corresponds to all the data (gray dots) shown in Fig. 15, upper panel. The highest amplitude flare occurred near the end of the lower amplitude rotational modulation. Flare energy values are derived for the Kepler bandpass. |
 |
Fig. 17 Cumulative FFD for the 19 most flaring giant stars, co-adding their 2188 flares (gray and black dots show the original and bias-corrected values, respectively), with an estimate of the range of values in energy bins (blue dots and bars). The FFD ofKIC 2852961 and the two-component fit is added separately (gray and red dots and lines for original and corrected values). We note the difference in the high-energy range. Flare energies are derived for the Kepler bandpass. |
 |
Fig. 18 Fits and slopes of individual FFDs for the 19 most flaring giant stars from the Kepler database, together with their mean (thick black line). For three stars, broken power-law fits are also plotted. Flare energies are derived for the Kepler bandpass. |
6 Summary and conclusions
We confirmed 61 flaring giant stars in the Kepler field. This number could increase to 69 with the eight stars of unknown evolutionary status (Table B.1), and it could further increase by a few giants from the uncertain cases (Table B.2) once any of those proves to be the origin of the observed flares.
Throughout this paper, we use the recent study of KIC 2852961 (Paper I) to verify the new methods and results by re-analyzing this star with the more automatized approaches introduced in this paper. We show that the rotational periods of the flaring giants correlates only weakly with the number of flares, hence with this measure of the activity strength. No correlation was found between Sph and rotational periods, but the index was found to be significantly higher for all stars than for their inactive counterparts (Gaulme et al. 2020). We found only six giants that show both flares and oscillations, and on one pulsating star (a γ Dor-δ Sct hybrid) we identified a few significant flares.
Flare energies were calculated, and energy distributions in histograms were drawn for all flaring giants and contaminating dwarfs from Table B.1 with peak energies at log EKp = 35.6 [erg] and logEKp = 34.2 [erg], respectively.Most of the histograms have nearly symmetric shapes with longer tails toward higher energies.
We constructed FFDs for a subsample of the 19 most flaring stars from Table B.1 plus a new FFD for KIC 2852961 from Paper I for comparison purposes. The individual FFDs were fit first by a single power law. For two stars from this subsample, broken power-law approaches turned out to be more appropriate. These two stars have flares in the same energy range, but the breakpoints of their fits are at different energies, suggesting a difference between thelocal environments from which their flares originate. We also find that even the weakest flare from the high-energy part of the KIC 2852961 FFD is stronger than any flare erupted in the subsample of the 19 most flaring stars.
We find that the slopes of fits to the individual FFDs of the 19 most flaring stars are quite similar to each other, the average being α =2.01 ± 0.16, although the difference between the energy ranges of the individual stars is close to two orders (see Fig. 18). Positive flare energy-duration correlations were found for the subsample of the 19 most flaring giants with slopes somewhat higher than suspected due to the low sampling of the data (30 min cadence), since the observed flare durations were underestimated.
From the results summarized above we conclude that:
-
Only about 0.3% of the Kepler giant stars with logg ≤ 3.5 show flare activity, that is, about 10% of the result in D17, but this agrees well with the result of YL19.
-
No strong correlation was found between the stellar properties (rotation period, velocity, binarity) and the flaring characteristics. The wide scale of the flaring specialities points toward the heterogeneity of flaring giants.
-
On flaring giant stars, similar to flaring dwarfs, observed flare durations correlate with flare energies, suggesting similar background physics and a scaling effect behind the flares on different stars (see Paper I).
-
The flaring nature of KIC 2852961 with higher energy flares in excess is markedly different from the rest of the studied giants. The reason for the dissimilarity, probably specific to the stellar structure, needs further investigation.
-
A large fraction of the flaring red giants are likely to belong to close binary systems, given the levels of photometric variability, Sph, the general absence of oscillations, and the fact that 11 out of the 14 giants that have spectroscopic data are binaries.
Above all, the most important finding of our study is that the true number of flaring giant stars in the Kepler field should be much lower (only about 10%) than what was previously reported by D17. Also, we further confirm the hypothesis of Kővári et al. (2020) that flares of different energy levels emitted by different active stars across the Hertzsprung-Russell diagram are based on a similar physical background differing only in scale.
Acknowledgements
We thank an anonymous referee for useful comments which helped to express our results more clearly. This work was supported by the Hungarian National Research, Development and Innovation Office grant OTKA K131508 and by the Lendület Program of the Hungarian Academy of Sciences, project No. LP2018-7/2019. Authors from Konkoly Observatory acknowledge the financial support of the Austrian-Hungarian Action Foundation (95 öu3, 98öu5, 101öu13). B.S. was supported by the ÚNKP-19-3 New National Excellence Program of the Ministry for Innovation and Technology. M.N.G. acknowledges support from MIT’s Kavli Institute as a Torres postdoctoral fellow. P. Gaulme acknowledges funding from the German Aerospace Center (Deutsches Zentrum für Luft- und Raumfahrt) under PLATO Data Center grant 50OO1501. This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia DR2 data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. Guoshoujing Telescope (the Large Sky Area Multi-Object Fiber Spectroscopic Telescope LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. LAMOST isoperated and managed by the National Astronomical Observatories, Chinese Academy of Sciences.
Appendix A Comparison of temperature, radius, and distance values from different data sources
Figures A.1–A.3 compare the temperature and radius values, and the distances of all Kepler stars used throughout this paper originating from D17, YL19, and Hon et al. (2019) using temperature, radii, and distances from KIC DR25, TIC catalogs, and Berger et al. (2018).
 |
Fig. A.1 Left: comparison of distances of the flaring giant stars from D17 and YL19 and oscillating giant stars from Hon et al. (2019) using distances from different catalogs marked in the top right. The positions of the flaring stars verified in the present paper are also marked. Right: zoom-in on Fig. A.1. |
 |
Fig. A.2 Left: comparison of radii of the flaring giant stars from D17 and YL19 and oscillating giant stars from Hon et al. (2019) using radii from different catalogs marked in the top right. The positions of the flaring stars verified in the present paper are also marked. Right: zoom-in on Fig. A.2. |
 |
Fig. A.3 Left: comparison of temperatures of the flaring giant stars from D17 and YL19 and oscillating giant stars from Hon et al. (2019) using temperatures from different catalogs marked in the top right. The positions of the flaring stars verified in the present paper are also marked. Right: zoom-in on Fig. A.3. |
Appendix B Flaring giants and contaminating dwarfs in the Kepler field
Flaring giants and contaminating dwarfs in the Kepler field.
 |
Fig. B.1 Enlarged center of HRD showing locations of the D17+YL19 giant sample (gray dots) and the derived flaring stars from this sample in the present paper (red dots). Light blue crosses mark the oscillating giant stars from Gaulme et al. (2020) for stars brighter than Kpmag = 12.5, and black plusses stand for the results of oscillating giants by Hon et al. (2019), cross-matched with our D17+YL19 giant sample. |
Uncertain cases from the D17+YL19 sample.
Available LAMOST results.
Appendix C Flare energy distributions and flare energy−observed flare duration correlations of the 19 most flaring stars, and that of KIC 2852961
 |
Fig. C.1 Flare energy distributions of the 19 most flaring stars (blue), plus KIC 2852961 (red). |
 |
Fig. C.2 Flare energy−observed flare duration correlations of the 19 most flaring stars (blue), plus KIC 2852961 (red). |
References
- Aurière, M., Konstantinova-Antova, R., Charbonnel, C., et al. 2015, A&A, 574, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P. G., Mathis, S., Gallet, F., et al. 2018, MNRAS, 479, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Benbakoura, M., Gaulme, P., McKeever, J., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202037783 [Google Scholar]
- Berger, T. A., Huber, D., Gaidos, E., & van Saders, J. L. 2018, ApJ, 866, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., & Browning, M. K. 2017, Liv. Rev. Sol. Phys., 14, 4 [Google Scholar]
- Cantiello, M., Fuller, J., & Bildsten, L. 2016, ApJ, 824, 14 [CrossRef] [Google Scholar]
- Catalano, S., & Frasca, A. 1994, A&A, 287, 575 [NASA ADS] [Google Scholar]
- Charbonnel, C., Decressin, T., Lagarde, N., et al. 2017, A&A, 605, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Cutispoto, G., Pagano, I., & Rodono, M. 1992, A&A, 263, L3 [Google Scholar]
- Davenport, J. R. A. 2016, ApJ, 829, 23 [Google Scholar]
- Davenport, J. R. A., Hawley, S. L., Hebb, L., et al. 2014, ApJ, 797, 122 [Google Scholar]
- Davenport, J. R. A., Covey, K. R., Clarke, R. W., et al. 2019, ApJ, 871, 241 [Google Scholar]
- Frasca, A., Molenda-Żakowicz, J., De Cat, P., et al. 2016, A&A, 594, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaulme, P., Jackiewicz, J., Appourchaux, T., & Mosser, B. 2014, ApJ, 785, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Gaulme, P., McKeever, J., Jackiewicz, J., et al. 2016, ApJ, 832, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gaulme, P., Jackiewicz, J., Spada, F., et al. 2020, A&A, 639, A63 [EDP Sciences] [Google Scholar]
- Günther, M. N., & Daylan, T. 2019, Astrophysics Source Code Library [record ascl:1903.003] [Google Scholar]
- Günther, M. N., & Daylan, T. 2020, AAS J., submitted [arXiv:2003.14371] [Google Scholar]
- Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [CrossRef] [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2001, A&A, 377, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hon, M., Stello, D., García, R. A., et al. 2019, MNRAS, 485, 5616 [NASA ADS] [Google Scholar]
- Kallinger, T., De Ridder, J., Hekker, S., et al. 2014, A&A, 570, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kővári, Zs., & Oláh, K. 2014, Space Sci. Rev., 186, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Kővári, Zs., Oláh, K., Kriskovics, L., et al. 2017, Astron. Nachr., 338, 903 [Google Scholar]
- Kővári, Zs., Oláh, K., Günther, M. N., et al. 2020, A&A, 641, A83 [EDP Sciences] [Google Scholar]
- Maehara, H., Notsu, Y., Namekata, K., et al. 2021, PASJ, 73, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., Salabert, D., García, R. A., & Ceillier, T. 2014, J. Space Weather Space Clim., 4, A15 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Mathur, S., Huber, D., Batalha, N. M., et al. 2017, ApJS, 229, 30 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mosser, B., Benomar, O., Belkacem, K., et al. 2014, A&A, 572, L5 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Mullan, D. J., & Paudel, R. R. 2018, ApJ, 854, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., Hall, D. S., & Henry, G. W. 1991, A&A, 251, 531 [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osten, R. A., & Wolk, S. J. 2015, ApJ, 809, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Paudel, R. R., Gizis, J. E., Mullan, D. J., et al. 2018, ApJ, 858, 55 [Google Scholar]
- Reiners, A. 2012, Liv. Rev. Sol. Phys., 9, 1 [Google Scholar]
- Roettenbacher, R. M., Monnier, J. D., Korhonen, H., et al. 2016, Nature, 533, 217 [Google Scholar]
- Shibata, K., & Magara, T. 2011, Liv. Rev. Sol. Phys., 8, 6 [Google Scholar]
- Shibayama, T., Maehara, H., Notsu, S., et al. 2013, ApJS, 209, 5 [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
- Strassmeier, K. G., Fekel, F. C., Bopp, B. W., Dempsey, R. C., & Henry, G. W. 1990, ApJS, 72, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Handler, G., Paunzen, E., & Rauth, M. 1994, A&A, 281, 855 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Briguglio, R., Granzer, T., et al. 2008, A&A, 490, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Shariati, H., & Debosscher, J. 2017, ApJS, 232, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Verbunt, F., & Phinney, E. S. 1995, A&A, 296, 709 [NASA ADS] [Google Scholar]
- Vida, K., & Roettenbacher, R. M. 2018, A&A, 616, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vrard, M., Kallinger, T., Mosser, B., et al. 2018, A&A, 616, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, H., & Liu, J. 2019, ApJS, 241, 29 [CrossRef] [Google Scholar]
- Zwintz, K., Neiner, C., Kochukhov, O., et al. 2020, A&A 643, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Flaring stars from the 86 of Table B.1 with oscillations derived by Gaulme et al. (2020, G+20) and in the present paper (pp).
Basic stellar parameters, average flare energies (Ef, in the Kepler bandpass), and equivalent times (teq) of the 19 most flaring stars, and characteristics of the flare distributions.
All Figures
 |
Fig. 1 One flare on KIC 6861498 (from the 16 observed) lasting about five hours with negligible amplitude compared to the rotational modulation of ≈89 days long. Top: whole dataset. Bottom left: flare on the descending branch of the rotational modulation. Bottom right: flare enlarged. |
| In the text | |
 |
Fig. 2 Comparison of effective temperature and radius values of 77 flaring stars from the resulting 86 using TICv8, Berger (Berger et al. 2018), Kepler, and Gaia DR2 databases. See the text for more details. |
| In the text | |
 |
Fig. 3 Locations of D17+YL19 giant sample in the HRD. Symbols: gray dots: D17+YL19 giant sample; big red dots: flaring giants verified in the present paper; small red dots: contaminating dwarfs and stars with unknown evolutionary status. Light blue crosses mark the oscillating giant stars from Gaulme et al. (2020) for stars brighter than Kpmag = 12.5 which coincide with the stars in our D17+YL19 sample overlapping them on the figure. The orange star marks the location of the Sun. See the text and Fig. B.1 for more details. |
| In the text | |
 |
Fig. 4 Distribution of effective temperatures (top) and radii (bottom) of the full sample (originally identified as flaring giants by D17 and YL19) and the number of stars we found as flaring giants plotted in gray and red, respectively. Dark red marks the stars classified as dwarfs by TICv8. We note that the histogram of radii does not exceed 20 solar radius (18 stars) for better visibility, since no flaring star is found above this limit. |
| In the text | |
 |
Fig. 5 Radii of the flaring giants. Top: entire investigated sample. Bottom: enlarged region of radii. Gray dots represent the D17+YL19 giant sample, big red dots mark the flaring giants that are verified in the present paper, while small red dots represent the contaminating dwarfs and stars with unknown evolutionary status. |
| In the text | |
 |
Fig. 6 Number of flares at different rotational periods (top) and rotational velocities (bottom). Light blue crosses mark the flaring red giants that also show oscillations (see Sect. 4.3.2). |
| In the text | |
 |
Fig. 7 Photometric index Sph (percent) as a function of rotation period Prot (days) for the 86 flaring stars from Table B.1. Both axes are in logarithmic scale. The blue and red symbols indicate the non-oscillating and oscillating giant stars, respectively. The orange markers indistinctly indicate dwarf and subgiant stars. The upward-pointing triangles are confirmed close spectroscopic binaries including at least one red giant, and the circles identify RV-stable red giant stars (Gaulme et al. 2020). The orange diamond with black edges is a confirmed subgiant belonging to a close binary system (KIC-11551404, Gaulme et al. 2020). The gray background reflects the distribution of Sph of the regular inactive red giant stars (the darker, the higher) according to Gaulme et al. (2020). |
| In the text | |
 |
Fig. 8 Locations of the flaring giants (big red dots, present paper), dwarfs or stars with an unknown evolutionary status (small red dots, present paper), possible binaries from Table B.1 by Gaulme et al. (2020, dark blue dots), and eclipsing giants with oscillations (light blue dots) oractivity (pink dots) from Gaulme et al. (2016) and Benbakoura et al. (2021) in the Hertzsprung−Russell-diagram. Light blue cross-over red dots mark the flaring and oscillating stars from the present paper. The orange star marks the location of the Sun. |
| In the text | |
 |
Fig. 9 Comparison of distribution of flare energies in the Kepler bandpass observed on 17 dwarfs (light blue), 61 giants (dark blue),and KIC 2852961 (red). A part of the dwarf star’s light blue histogram striped with dark blue lines are occupied by the flares of two, possibly subgiant stars. See the text for more information. |
| In the text | |
 |
Fig. 10 Comparison of combined distribution of flare energies in the Kepler bandpass of the most flaring 19 giants (dark blue columns) and that of KIC 2852961 (red columns; see also Fig. C.1). |
| In the text | |
 |
Fig. 11 Flare recovery rate in the function of relative flare energy (equivalent time in s). The recovery rates (dots) were derived from a recovery test using artificial flares injected into the original 20 data files. The test results were generalized using a parameterized hyperbolic tangent function (blue line). The inset shows the details below 50 s of equivalent time. See the text for more information. |
| In the text | |
 |
Fig. 12 Largest deviation between application of the common recovery correction and the one realized for the star only (called own correction). The object is KIC 5480528; black, red, and blue colors mark the data and fits to the original data, own corrections, and common corrections, respectively. The difference between the slopes of the fits for the two different corrections (red and blue) is within two sigma. Flare energies are derived for the Kepler bandpass. (The five lowest energy data points were excluded from the fits.) |
| In the text | |
 |
Fig. 13 Detection bias-corrected cumulative FFD for KIC 2852961 using the two different cross-matched, automatic flare-detection results introduced in the present paper. The original data points are plotted in gray, and the blue points show the detection-bias-corrected values. The orange crosses show the detection-bias-corrected results from Paper I. Flare energies are derived for the Kepler bandpass. |
| In the text | |
 |
Fig. 14 FFDs for KIC 2852961 (red) and the 19 most flaring giant stars (blue) of the Kepler field. Flare energies are derived for the Kepler bandpass. A simple linear fit is drawn to the plots, in the upper-right corner the slopes of the fits and their errors are indicated. |
| In the text | |
 |
Fig. 15 Two-component fits to the FFDs for KIC 7676676 and KIC 9419002. Black dots correspond to the original values, while red dots are bias corrected. We note the similar flare energy range and the different breakpoints of the fits for the two targets. Flare energies are derived for the Kepler bandpass. See the text for more details. |
| In the text | |
 |
Fig. 16 FFDfor KIC 7676676 in two activity levels. The data points showing lower and higher amplitude rotational modulation are marked with blue and red dots in the inset, and the same colors mark the corresponding FFDs. The broken power-law fit (gray line) corresponds to all the data (gray dots) shown in Fig. 15, upper panel. The highest amplitude flare occurred near the end of the lower amplitude rotational modulation. Flare energy values are derived for the Kepler bandpass. |
| In the text | |
 |
Fig. 17 Cumulative FFD for the 19 most flaring giant stars, co-adding their 2188 flares (gray and black dots show the original and bias-corrected values, respectively), with an estimate of the range of values in energy bins (blue dots and bars). The FFD ofKIC 2852961 and the two-component fit is added separately (gray and red dots and lines for original and corrected values). We note the difference in the high-energy range. Flare energies are derived for the Kepler bandpass. |
| In the text | |
 |
Fig. 18 Fits and slopes of individual FFDs for the 19 most flaring giant stars from the Kepler database, together with their mean (thick black line). For three stars, broken power-law fits are also plotted. Flare energies are derived for the Kepler bandpass. |
| In the text | |
 |
Fig. A.1 Left: comparison of distances of the flaring giant stars from D17 and YL19 and oscillating giant stars from Hon et al. (2019) using distances from different catalogs marked in the top right. The positions of the flaring stars verified in the present paper are also marked. Right: zoom-in on Fig. A.1. |
| In the text | |
 |
Fig. A.2 Left: comparison of radii of the flaring giant stars from D17 and YL19 and oscillating giant stars from Hon et al. (2019) using radii from different catalogs marked in the top right. The positions of the flaring stars verified in the present paper are also marked. Right: zoom-in on Fig. A.2. |
| In the text | |
 |
Fig. A.3 Left: comparison of temperatures of the flaring giant stars from D17 and YL19 and oscillating giant stars from Hon et al. (2019) using temperatures from different catalogs marked in the top right. The positions of the flaring stars verified in the present paper are also marked. Right: zoom-in on Fig. A.3. |
| In the text | |
 |
Fig. B.1 Enlarged center of HRD showing locations of the D17+YL19 giant sample (gray dots) and the derived flaring stars from this sample in the present paper (red dots). Light blue crosses mark the oscillating giant stars from Gaulme et al. (2020) for stars brighter than Kpmag = 12.5, and black plusses stand for the results of oscillating giants by Hon et al. (2019), cross-matched with our D17+YL19 giant sample. |
| In the text | |
 |
Fig. C.1 Flare energy distributions of the 19 most flaring stars (blue), plus KIC 2852961 (red). |
| In the text | |
 |
Fig. C.2 Flare energy−observed flare duration correlations of the 19 most flaring stars (blue), plus KIC 2852961 (red). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


