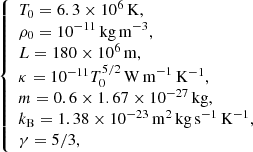| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201936072 | |
| Published online | 20 August 2019 | |
Damping of slow magnetoacoustic oscillations by the misbalance between heating and cooling processes in the solar corona
1
Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, CV4 7AL Coventry, UK
e-mail: d.kolotkov.1@warwick.ac.uk
2
St. Petersburg Branch, Special Astrophysical Observatory, Russian Academy of Sciences, 196140 St. Petersburg, Russia
3
Samara National Research University, Department of Physics, Samara 443086, Russia
4
Lebedev Physical Institute of Russian Academy of Sciences, Samara Branch, Department of Theoretical Physics, Russia
Received:
11
June
2019
Accepted:
16
July
2019
Context. Rapidly decaying slow magnetoacoustic waves are regularly observed in the solar coronal structures, offering a promising tool for a seismological diagnostics of the coronal plasma, including its thermodynamical properties.
Aims. The effect of damping of standing slow magnetoacoustic oscillations in the solar coronal loops is investigated accounting for field-aligned thermal conductivity and a wave-induced misbalance between radiative cooling and some unspecified heating rates.
Methods. The non-adiabatic terms were allowed to be arbitrarily large, corresponding to the observed values. The thermal conductivity was taken in its classical form, and a power-law dependence of the heating function on the density and temperature was assumed. The analysis was conducted in the linear regime and in the infinite magnetic field approximation.
Results. The wave dynamics is found to be highly sensitive to the characteristic timescales of the thermal misbalance. Depending on certain values of the misbalance, timescales three regimes of the wave evolution were identified, namely the regime of a suppressed damping, enhanced damping in which the damping rate drops down to observational values, and acoustic over-stability. The specific regime is determined by the dependences of the radiative cooling and heating functions on thermodynamical parameters of the plasma in the vicinity of the perturbed thermal equilibrium.
Conclusions. The comparison of the observed and theoretically derived decay times and oscillation periods allows us to constrain the coronal heating function. For typical coronal parameters, the observed properties of standing slow magnetoacoustic oscillations could be readily reproduced with a reasonable choice of the heating function.
Key words: Sun: oscillations / waves / radiation mechanisms: thermal
© ESO 2019
1. Introduction
The study of wave and oscillatory processes in the plasma of the solar corona is one of the most rapidly developing research topics of modern solar physics (e.g. De Moortel & Nakariakov 2012; Wang 2016). The interest in coronal oscillations is connected, in particular, with their seismological potential, i.e. with the use of the oscillations as natural probes of the plasma and physical processes operating there (e.g. Liu & Ofman 2014). Moreover, the striking similarity between the properties of oscillations detected in solar and stellar flares (see e.g. Cho et al. 2016) suggests interesting perspectives for the exploitation of the solar-stellar analogy.
Slow magnetoacoustic waves are often detected in coronal plasma non-uniformities, such as coronal loops, plumes, and interplume regions, as propagating periodic disturbances of extreme ultraviolet (EUV) emission (see e.g. De Moortel 2009; Banerjee & Krishna Prasad 2016, respectively). Another common manifestation of slow waves in the corona are standing waves in loops, detected as rapidly decaying periodic Doppler shifts of coronal emission lines (see e.g. Wang 2011). Standing slow waves are usually referred to as SUMER oscillations, after the instrument used in their first detection (Solar Ultraviolet Measurements of Emitted Radiation onboard Solar and Heliospheric Observatory (SoHO/SUMER); see Wang et al. 2002). An interpretation of this detection can be found in Ofman & Wang (2002). These SUMER oscillations still remain a subject of intensive studies. For example, standing slow waves in non-flaring fan loops, which have periods of 27 min, a damping time of about 45 min, and a phase speed corresponding to the plasma temperature of about 0.6 MK, have been studied by Pant et al. (2017). A 10 min periodicity has been identified in the time series of Doppler shift and line-integrated intensity of the Fe XXI emission line, soft X-ray flux, and EUV light curves (Li et al. 2017). A 2 min oscillation of the thermal component of the microwave emission of a solar flare has been interpreted in terms of the emission modulation by a standing slow wave. An 80 s oscillation of the X-ray and microwave emissions in a solar flare has been associated with the second harmonic of a standing slow wave in a flaring arcade (Kupriyanova et al. 2019). The 8–30 min periodic pulsations of the soft X-ray emission generated in an active region before a flare could also be associated with standing slow waves (Tan et al. 2016). Seismological applications of slow waves include the estimation of the polytropic index (Van Doorsselaere et al. 2011; Krishna Prasad et al. 2018), average magnetic field (Wang et al. 2007) in the oscillating loop, and transport coefficients (Wang et al. 2015, 2018). An important foundation of the interpretations and seismology is provided by forward modelling of imaging and spectroscopic observables (Yuan et al. 2015).
Recent theoretical studies of standing slow waves in coronal loops include accounting for weakly nonlinear effects that are found to manifest as an appearance of higher parallel harmonics (e.g. Kumar et al. 2016); full-MHD numerical simulations with various scenarios of transport processes, which aim at revealing the reason for the unexpected linear scaling of the observed damping time with the oscillation period (e.g. Wang et al. 2018); and the excitation mechanism (e.g. Provornikova et al. 2018).
An important physical process that should be taken into account in the modelling of compressive oscillations is the perturbation of thermal equilibrium by oscillation, i.e. the effect of the misbalance between radiative and, possibly, thermal conductive cooling, and an unspecified but definitely present heating. Similar effects are considered in the interstellar medium and molecular clouds, while mainly in the contexts of plasma condensation caused by thermal instability (e.g. Krasnobaev & Tagirova 2017), and basic theoretical studies of autowave regimes (e.g. Zavershinsky & Molevich 2013) and Alfvén wave amplification (e.g. Zavershinsky & Molevich 2014). In the coronal context, it has been shown that the effect of thermal misbalance can either strengthen the damping or suppress it (e.g. Nakariakov et al. 2017). However, this conclusion was reached in the limit of weak non-adiabaticity, using the assumption that the imaginary part of the oscillation frequency is much smaller than the real part. On the other hand, for example, the damping time of SUMER oscillations is known to be comparable with the oscillation period. This justifies the need to soften this assumption.
The aim of this paper is to develop a theory of linear standing slow magnetoacoustic oscillations in coronal loops with thermal misbalance. In Sect. 2 we describe the model and derive dispersion relations, which are analysed in Sect. 3. The findings are summarised and discussed in Sect. 4.
2. Governing equations, timescales, and dispersion relation
We consider the evolution of slow magnetoacoustic waves in the infinite magnetic field approximation, upon which the set of governing equations reduces to the usual hydrodynamic Euler equation, continuity equation, ideal gas state equation, and the energy equation (see Eqs. (1)–(4), respectively). This approximation is extensively used for modelling slow waves in the corona; see e.g. Nakariakov et al. (2000), Ofman & Wang (2002), De Moortel & Hood (2004), Verwichte et al. (2008), Ruderman (2013), and Kumar et al. (2016). Under this approximation, the waves are assumed to propagate strictly along the ambient infinitely stiff magnetic field lines, and hence do not perturb the field and the speed of the waves is independent of the field.
Accounting for the effects of the optically thin radiation, unspecified heating, and thermal conductivity, the governing equations are written as
where ρ, T, and P are the density, temperature, and pressure, respectively; Vz is the velocity component along the z-axis, which coincides with the magnetic field direction; kB is Boltzmann constant; m is the mean particle mass; CV = (γ − 1)−1kB/m is the specific heat capacity at constant volume with γ = 5/3 being the standard adiabatic index; κ is the field-aligned thermal conductivity; and the function Q(ρ, T) = L(ρ, T) − H(ρ, T) combines the effects of radiative losses L(ρ, T) and some unspecified heating H(ρ, T). For the energy equation in form (4), the heating/cooling function Q(ρ, T) is measured in W kg−1. For example, numerous observational studies have demonstrated that the temperature across and along the loop remains almost constant (see e.g. Reale 2014 for a detailed review of the coronal loop properties and Gupta et al. 2019 and references therein for the most recent results). Hence, we consider the plasma to be in a uniform isothermal equilibrium. Thus, in the equilibrium Q(ρ0, T0) = 0, where the index 0 indicates equilibrium quantities. In general, the equilibrium thermal structure of the loop is also determined by thermal conduction at the footpoints. But, as we consider waves in the coronal, almost isothermal part of an active region, this effect is omitted. For slow waves propagating upwards along loops and plumes this omission is naturally justified. For standing slow waves this omission could be justified by the structure of the pressure, density, and temperature perturbations along the loop. In contrast with the perturbations of the parallel velocity that have nodes at the footpoints, perturbations of thermodynamical parameters in standing slow waves have antinodes at the footpoints (e.g. Reale 2016; Wang et al. 2018). Hence, near the footpoints the derivative of the temperature perturbation in the wave with respect to the field-aligned coordinate could be taken as zero, thus suppressing the wave damping by the thermal conduction in these regions. Thus, in our analysis the chromosphere and transition region act only as the solid-wall perfectly reflecting boundaries for slow waves and are not involved in the wave evolution by any other means (see e.g. Ofman & Wang 2002; Selwa et al. 2005; Taroyan et al. 2007, where a similar approach was employed for the coronal slow wave modelling). In other words, our simple reflecting boundary conditions mimic a more realistic model of the transition region and the chromosphere used by, for example Nakariakov et al. (2004) or Reale (2016), in which slow waves are found to naturally reflect at the lower boundary because they hit the transition region. We need to stress that in the considered scenario the waves do not contribute to the heating, but perturb the physical parameters of the plasma that may affect the efficiency of the heating.
For the solar corona, the optically thin radiation loss function can be modelled as L(ρ, T) = χρTβ, whose temperature dependence is illustrated in Fig. 1, determined from the CHIANTI1 atomic database (Dere et al. 1997; Del Zanna et al. 2015). The function L(ρ, T) represents the radiative losses per unit mass (W kg−1), which is obtained from the radiative losses per unit volume (W m−3) divided by the plasma density ρ. Likewise, the unknown coronal heating function can be locally parametrised as H(ρ, T) = hρaTb (see e.g. Rosner et al. 1978; Ibanez & Escalona 1993; Dahlburg & Mariska 1988), where a certain combination of the power-law indices a and b could be associated with a specific heating mechanism. The proportionality coefficient h can in turn be determined applying the thermal equilibrium condition Q(ρ0, T0) = 0. More recent observational and theoretical works have suggested that the coronal heating function may also have an intermittent time-dependent component (see e.g. Klimchuk 2006; Reale 2016). Characteristic times of such a time-varying heating are shown to be predominantly short, i.e. shorter than a minute (e.g. Testa et al. 2014; Tajfirouze et al. 2016). On the timescales of the considered slow coronal waves (with periods from several minutes to several tens of minutes), the chosen form of the function H(ρ, T) thus represents a time-averaged steady heating, sustaining the oscillating loop at approximately the same mean temperature. Thus, we determine a misbalance between the heating and cooling processes in the solar corona, caused by slow waves, through different dependences of the functions L(ρ, T) and H(ρ, T) on the plasma density and temperature perturbed by the wave. As a specific heating scenario has not been revealed yet, the power-law indices a and b in the parametric dependence of the heating function are treated as free parameters.
 |
Fig. 1. Left: piecewise dependence of the optically thin radiation losses per unit mass L(ρ, T) = χρTβ on temperature, where the specific values of the parameters χ and β are determined from the CHIANTI atomic database v. 8.0.7 for the plasma concentration 1016 m−3 and vary with the temperature interval considered. Right: variation of τ1 (red) and τ2 (blue) determined by Eq. (6) with temperature, for the radiative cooling shown in the left-hand panel and a heating model with the density and temperature power indices a = −0.5 and b = −3, respectively. The green dashed lines indicate the SUMER observational channels 6.3 MK and 8.9 MK. |
We linearise the governing equations around the initial equilibrium, obtaining energy Eq. (4) in the form
where the symbol “∼” indicates the linear perturbations, and
are characteristic timescales of the thermal misbalance, fully determined by the parameters of the equilibrium and by the rates of change of the heating/cooling function Q(ρ, T) with density, Qρ ≡ (∂Q/∂ρ)T, and temperature QT ≡ (∂Q/∂T)ρ. In the following analysis, we consider only positive values of both τ1 and τ2, thus focussing on the effect of the slow wave (isentropic) damping or over-stability (see Field 1965, for details). Typical values of the misbalance timescales τ1 and τ2 for the radiative cooling determined by CHIANTI and a guessed heating function (determined by the specific values of the density and temperature power indices a and b) in a dense loop (Reale 2014) are illustrated in the right-hand panel of Fig. 1. For example, for the temperatures associated with SUMER oscillations, 6.3 MK and 8.9 MK, we obtain τ1 ≈ 37 min and τ2 ≈ 12 min, and τ1 ≈ 65 min and τ2 ≈ 19 min, respectively, for a = −0.5 and b = −3. This example is provided for the illustrative purposes only, while a more comprehensive analysis of the behaviour of τ1 and τ2 with a and b and their effect on the slow wave dynamics are given in Sect. 3. No further assumptions on the values of the characteristic times τ1 and τ2 are made in the following analysis, implying the non-adiabatic terms on the right-hand side of energy Eq. (5) are allowed to be arbitrarily large; this is in contrast with Kumar et al. (2016) and Nakariakov et al. (2017) where the effect of the thermal misbalance on slow waves is investigated under the assumption of a weak non-adiabaticity. We would also like to stress that in contrast to previous works (e.g. De Moortel & Hood 2004), investigating the effects of radiative cooling on the damping of slow waves keeping the heating term constant, i.e. not affected by the perturbations of the plasma parameters by a wave and hence not contributing into the wave dynamics, we account for the variation of both heating and radiative cooling by the wave. Therefore, the heating/cooling misbalance times τ1, 2 (Eq. (6)) are not associated with the corresponding timescales of the cooling or heating processes considered separately of each other.
We seek a solution of the linearised set of governing equations in the form ei(kz − ωt), which yields the following dispersion relation between the cyclic frequency ω and the wavenumber k,
where the coefficients are
where 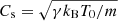 is a standard definition of the sound speed. We need to mention at this point that as the plasma gets perturbed by the wave, the condition of the initial isothermality discussed above is violated, allowing the plasma temperature to vary with both space and time. Thus, Cs is the sound speed in a non-isothermal medium with the adiabatic index γ = 5/3. Equation (7) is found to be asymmetric with respect to space and time, being a fourth- and third-order equation with respect to k and ω. Similar to De Moortel & Hood (2003), a wavelength-dependent term in the coefficients A(k) and C(k) could be associated with the characteristic timescale of the field-aligned thermal conductivity, so that
is a standard definition of the sound speed. We need to mention at this point that as the plasma gets perturbed by the wave, the condition of the initial isothermality discussed above is violated, allowing the plasma temperature to vary with both space and time. Thus, Cs is the sound speed in a non-isothermal medium with the adiabatic index γ = 5/3. Equation (7) is found to be asymmetric with respect to space and time, being a fourth- and third-order equation with respect to k and ω. Similar to De Moortel & Hood (2003), a wavelength-dependent term in the coefficients A(k) and C(k) could be associated with the characteristic timescale of the field-aligned thermal conductivity, so that
where λ = 2π/k is the wavelength. In the regime of a weak non-adiabaticity, i.e. assuming the parameters 1/ωτcond and 1/ωτ1, 2 are small, dispersion relation (7) reduces to
Weakly non-adiabatic dispersion relation (9) is a limiting case of Eq. (21) in Nakariakov et al. (2017) in neglecting the effects of the viscosity and oblique propagation. In the following analysis, we study full dispersion relation (7). Thus, we allow the imaginary part of the frequency to be of the same order of magnitude as the real part. This regime is motivated by the apparently high damping rates of the coronal slow oscillations usually observed (see Sect. 3 for references).
3. Stability analysis
Processes described by dispersion relation similar to Eq. (7) have been previously shown to affect both the phase speed and the damping/amplification length of propagating magnetoacoustic waves (Ibanez & Sanchez 1992; Ibanez & Escalona 1993). In this section we analyse these effects on standing slow magnetoacoustic waves in hot coronal loops (SUMER oscillations), addressing recent advances in observational detections of these waves (Wang 2011). In particular, SUMER oscillations are usually seen to damp rapidly and have a quality factor (q-factor) that is the ratio of the damping time to the oscillation period, which is less than 2–3 (Wang et al. 2003; Mariska 2006; Cho et al. 2016; Nakariakov et al. 2019).
Dictated by the observational properties of standing slow oscillations in the corona, we choose the following set of physical parameters:
where L is the loop length, and the chosen value of the temperature T0 corresponds to a typical detection of a SUMER oscillation (see Nakariakov et al. 2019, for the most recent review). The set of parameters (10) corresponds to the observations of dense loops (e.g. Nisticò et al. 2017), providing the sound speed ![$ C_{\mathrm{s}}\approx152\sqrt{T_0[\mathrm{MK}]}\approx 382 $](/articles/aa/full_html/2019/08/aa36072-19/aa36072-19-eq13.gif) km s−1, acoustic oscillation period P = 2L/Cs ≈ 15.7 min, and the characteristic timescale of the thermal conduction τcond ≈ 448 min (obtained by substituting the set of parameters (10) into Eq. (8) and taking λ = 2L). The ratio of the oscillation period to thermal conduction time, P/τcond ≈ 0.035, coincides by an order of magnitude with the estimation in, for example De Moortel & Hood (2003), for the chosen value of ρ0. Such a ratio of the oscillation period to the thermal conduction time justifies a non-isothermal nature of the discussed waves, implying that in the considered physical conditions (10) the thermal conduction mechanism is insufficient to smooth out the temperature perturbation on the wave period. However, in shorter and hotter loops the thermal conduction time could be significantly shorter, making the waves almost isothermal. In turn, the heating/cooling times τ1, 2 (Eq. (6)) are treated as free parameters in this analysis because they are mainly determined by the properties of an unknown heating function.
km s−1, acoustic oscillation period P = 2L/Cs ≈ 15.7 min, and the characteristic timescale of the thermal conduction τcond ≈ 448 min (obtained by substituting the set of parameters (10) into Eq. (8) and taking λ = 2L). The ratio of the oscillation period to thermal conduction time, P/τcond ≈ 0.035, coincides by an order of magnitude with the estimation in, for example De Moortel & Hood (2003), for the chosen value of ρ0. Such a ratio of the oscillation period to the thermal conduction time justifies a non-isothermal nature of the discussed waves, implying that in the considered physical conditions (10) the thermal conduction mechanism is insufficient to smooth out the temperature perturbation on the wave period. However, in shorter and hotter loops the thermal conduction time could be significantly shorter, making the waves almost isothermal. In turn, the heating/cooling times τ1, 2 (Eq. (6)) are treated as free parameters in this analysis because they are mainly determined by the properties of an unknown heating function.
 |
Fig. 2. Variation of ωI obtained for τ1 = 15 min, and τ2 = 8.2 min (green) and τ2 = 6 min (red), left; and τ1 = 10 min, and τ2 = 13 min (green) and τ2 = 22 min (red), right. The grey lines in both panels indicate |
We seek a solution to dispersion relation (7) in a standing wave form, i.e. assuming the cyclic frequency ω to be complex, ω = ωR + iωI, while the wavenumber k is real. Substituting this into Eq. (7), we solve the polynomial equation for ωI numerically using Maple 20162 environment. Variation of ωI with k is shown in Fig. 2 for different values of the heating/cooling times τ1, 2, including the case with τ1, 2 → ∞, which corresponds to the damping by thermal conduction only, 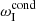 , and with τcond → ∞ indicating a pure thermal misbalance case,
, and with τcond → ∞ indicating a pure thermal misbalance case, 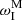 . Depending on the values of τ1, 2, the imaginary value
. Depending on the values of τ1, 2, the imaginary value 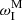 can contribute either positively or negatively into
can contribute either positively or negatively into 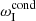 , revealing regimes of the enhanced damping (ωI <
, revealing regimes of the enhanced damping (ωI < 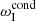 ) or suppressed damping (
) or suppressed damping (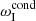 < ωI < 0) and over-stability (ωI > 0). These regimes have been discussed in, for example Kumar et al. (2016) and Nakariakov et al. (2017). However, in those works the non-adiabatic effects were weak, thus not describing the strong damping detected in observations (e.g. Wang et al. 2003; Mariska 2006; Cho et al. 2016; Nakariakov et al. 2019).
< ωI < 0) and over-stability (ωI > 0). These regimes have been discussed in, for example Kumar et al. (2016) and Nakariakov et al. (2017). However, in those works the non-adiabatic effects were weak, thus not describing the strong damping detected in observations (e.g. Wang et al. 2003; Mariska 2006; Cho et al. 2016; Nakariakov et al. 2019).
The left-hand panel of Fig. 3 illustrates regions of the damping enhancement, suppression, and over-stability in the two-dimensional parametric space (τ1, τ2) for the fundamental mode of the oscillation, i.e. with k = π/L. We treat the characteristic times τ1 and τ2 as free parameters. The damping enhancement occurs when τ1 > τ2 (see for example the last term on the right-hand side of Eq. (9)), where the q-factor drops down to the observational values of about 1–3 (e.g. Wang et al. 2003; Mariska 2006; Cho et al. 2016; Nakariakov et al. 2019). We calculate the values of the heating/cooling times τ1, 2 adapting four heating models from Ibanez & Escalona (1993) (see Table 1). For the chosen set of parameters (10), the obtained values of τ1, 2 for those heating models are found to be either of different signs or both negative, which would result into the development of thermal instabilities of a non-acoustic nature (see Field 1965). Therefore, neither of these is found to be suitable for the observational damping of SUMER oscillations.
 |
Fig. 3. Left: parametric regions of the wave damping enhancement (I), suppression (II), and thermal over-stability (III). Grey-shaded regions indicate the values of τ1, 2 where the q-factor is in between 1 (the green line) and 2 (the blue line, Ia), and in between 2 and 3 (the purple line, Ib). The red, green, and blue symbols indicate some arbitrary values of τ1, 2 chosen for the numerical solutions shown in Fig. 4. Right: heating/cooling times τ1, 2 (see Eq. (6), black and red contours, respectively) determined for the CHIANTI radiative cooling, and the heating function in the form H(ρ, T) ∝ ρaTb for the varying temperature and density power indices a and b. The grey-shaded areas indicate the values of a and b where 1 < q-factor < 2 (light grey) and 2 < q-factor < 3 (dark grey). The green, blue, and purple lines show q-factor equals 1, 2, and 3, respectively. |
Coronal heating functions modelled as H(ρ, T) ∝ ρaTb for Ohmic heating (1), constant heating per unit volume (2) and mass (3), and Alfvén waves/mode conversion (4) (see Ibanez & Escalona 1993); the corresponding τ1, 2 (Eq. (6)) in minutes, where the radiative cooling is determined by CHIANTI (see Fig. 1).
As τ1, 2 depend on the parameters a and b of the heating function (6), we calculate τ1, 2 for a and b both ranging from, for example −5 to 5 (see the right-hand panel of Fig. 3). The obtained values of τ1, 2 are seen to depend strongly on a and b, varying from several to a hundred of minutes and longer for the chosen values of the plasma density and temperature. Both τ1 and τ2 have the vertical asymptote at a ≈ 1 and b ≈ 0.4, above which they both become negative. The blank regions in the right-hand panel of Fig. 3 and where the contour lines do not intersect correspond to the negative or different signs of τ1, 2, respectively, which give rise to other thermal instabilities (see Field 1965) which are out of the scope of this study. We now compare this diagram to the values of τ1, 2, for which the oscillation q-factor was found to vary from 1 to 2 (see the left-hand panel of Fig. 3), constraining the heating functions which are able to reproduce the observational damping (see the grey-shaded area in the right-hand panel of Fig. 3). For lower plasma densities, the values of indices a and b, which give the misbalance times τ1, 2 about the observed periods, would be even lower.
We choose three different pairs of the heating/cooling times τ1 and τ2, which provide the q-factor to be lower than 1, from 1 to 2, and from 2 to 3. Using parameters (10), we then solve the linearised set of governing equations numerically in Maple 2016 in a closed resonator located between z = 0 and z = L and with the initial broadband Gaussian-shaped acoustic perturbation of the width w = 0.12L, shifted towards one of the boundaries. The cross-sections of the obtained standing solutions at z = L/2 are shown in the left-hand panel of Fig. 4. As expected from the dispersion relation (see Eq. (7) and Fig. 2), the higher harmonics decay faster, so that after about one cycle of the oscillation the initial broadband pulse develops into a pure fundamental mode which then also decays. This example illustrates how sensitive the damping of standing slow waves is to the parameters of the heating/cooling function, and it represents the rapidly decaying oscillations of the SUMER-oscillation type. In a more exotic case, when the values of τ1 and τ2 appear to be just near the boundary ωI = 0 (see for example the red line in the left-hand panel of Fig. 3), the damping could be highly suppressed by the thermal misbalance (see for example the apparently non-decaying oscillation observed in the Fe XV emission line in Fig. 3 of Mariska et al. 2008). Adapting the physical parameters corresponding to this observation, namely T0 = 106.32 K and L = 342 Mm, and choosing ρ0 = 10−12 kg m−3, we can reproduce the observed non-decaying oscillation within the developed model for, for example τ1 = 19.5 min and τ2 = 22.3 min.
 |
Fig. 4. Left: cross-sections of the perturbed velocity as a function of time, obtained for τ1 = 40 min and τ2 = 23 min (blue), τ1 = 61 min and τ2 = 11.5 min (red), and τ1 = 30 min and τ2 = 5 min (green). Right: similar to the left-hand panel, but for the set of physical parameters from Mariska et al. (2008) (see Sect. 3 for details) and with τ1 = 19.5 min and τ2 = 22.3 min. |
4. Summary and conclusions
We investigated the mechanism for the damping of linear standing slow magnetoacoustic waves in the solar corona through the misbalance of some heating and radiative cooling processes. We addressed the coronal part of a loop with an isothermal equilibrium. This is a standard approach for modelling slow waves in the corona. However, we consider the wave dynamics in the presence of a temperature- and pressure-dependent heating and radiative cooling and thermal conduction, addressing a misbalance of those processes caused by the waves. The wave dynamics was found to be highly sensitive to the parameters of the misbalance, expressed in terms of the characteristic times τ1, 2 of the heating/cooling function change with the plasma density and temperature perturbed by the wave (see Sect. 2). Depending upon the values of τ1, 2, we found three different regimes of the wave evolution, which are enhanced and suppressed damping (with respect to that caused by the field-aligned thermal conductivity), and thermal over-stability. Unlike the previous analytical works, we did not treat the non-adiabatic terms as small, which allowed us to obtain the enhanced damping rates matching those detected in observations.
Our findings allow us to reproduce the observed behaviour of SUMER oscillations, keeping the thermal conduction coefficient in its standard estimation, but accounting for the heating/cooling misbalance. For the set of physical parameters corresponding to the observations of SUMER oscillations (see Sect. 3), the characteristic timescale of the thermal conduction was found to be at least an order of magnitude longer than the oscillation period. This indicates a low efficiency of the field-aligned thermal conductivity in damping these oscillations. In turn, typical heating/cooling times τ1, 2 were found to be comparable to the observed periods of SUMER oscillations (from a few minutes to a few tens of minutes; see Fig. 3), for a sufficiently broad range of the heating function parameters and for the CHIANTI radiative cooling. For τ1 > τ2, this results in a domination of the damping by the heating/cooling misbalance over conductive damping. Moreover, the discussed effect persists even in the limiting case of isothermal waves, which are not subject to the damping by thermal conduction at all, occurring in the case of the dominant thermal conduction (De Moortel & Hood 2003). In this regime, the cooling and heating functions, and therefore their misbalance, are still affected by the perturbations of density in the wave and hence contribute to its damping.
Using the CHIANTI model for the radiative cooling and fixing other parameters of the equilibrium, the values of τ1, 2 become fully determined by the heating function. This suggests a new approach to the diagnostics of the coronal heating mechanism via damping of SUMER oscillations. For example, none of four heating models considered by Ibanez & Escalona (1993) (see Table 1) were found to reproduce the observed damping of SUMER oscillations. On the other hand, we determined the range of the power-law indices a and b, which give the observed damping times. Moreover, the developed theory could also address a more exotic case of an apparently non-decaying SUMER type oscillation detected by Mariska et al. (2008), by choosing the values of τ1 and τ2 which give ωI ≈ 0. In addition, acoustic over-stability could be considered as a mechanism for the excitation of 8–30 min oscillations of the soft X-ray emission generated in pre-flaring active region (Tan et al. 2016).
The need to comply with observational properties of coronal slow waves may put additional constraints on the empirical determination of the dependence of the heating function on the plasma parameters. This seismological information about the acceptable ranges of the parameters a and b, together with the information obtained by other methods, could be used to reveal the heating function. In particular, our study suggests that −2 ≲ a ≲ 2 and b ≲ 0 for the chosen values of the equilibrium density and temperature. Those intervals should be subject to a dedicated follow-up analysis. In particular, the effect of different parametric forms of the heating function dependence on the density and temperature, for example polynomial, should be considered. Likewise, the time-dependence of the coronal heating function, neglected in this study on the timescale of a slow wave, could be more important for shorter period coronal MHD waves, for instance fast waves with about 1-min periodicity. Also, this neglect does not allow us to address the transient events in which the loop is impulsively heated and rapidly cools down at the timescale comparable to the wave period (e.g. Reale et al. 2019), thus making the developed theory restricted to the loops sustained at approximately the same mean temperature during the whole wave evolution. In addition, future development of the theory needs to soften certain assumptions made in this paper. In particular, we neglect the effects of the oblique wave propagation, i.e. the departure of the slow wave speed from the sound speed in the case of finite β, and viscosity, which could bring additional timescales into the problem. This could be important if the coronal heating depends on the magnetic field (Hood 1992; Nakariakov et al. 2017). We also do not consider the effect of geometrical dispersion (Edwin & Roberts 1983; Yuan et al. 2015), which is usually weak for slow waves in coronal loops. Likewise, we do not account for nonlinear effects. Another interesting development of this study could be the inclusion of a chromosphere. Accounting for these effects should be addressed in a follow up study.
Acknowledgments
This work was supported by STFC consolidated grant ST/P000320/1 (V.M.N., D.Y.K.), and the Russian Foundation for Basic Research grant No. 18-29-21016 (V.M.N.). Calculations presented in the reported study were also funded by RFBR according to the research project No. 18-32-00344 (D.I.Z.). The study was supported in part by the Ministry of Education and Science of Russia under a public contract with educational and research institutions within the project 3.1158.2017/4.6. CHIANTI is a collaborative project involving George Mason University, the University of Michigan (USA) and the University of Cambridge (UK). Maple is a trademark of Waterloo Maple Inc.
References
- Banerjee, D., & Krishna Prasad, S. 2016, in Low-Frequency Waves in Space Plasmas, Geophys. Monograph Ser., 216, 419 [Google Scholar]
- Cho, I.-H., Cho, K.-S., Nakariakov, V. M., Kim, S., & Kumar, P. 2016, ApJ, 830, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlburg, R. B., & Mariska, J. T. 1988, Sol. Phys., 117, 51 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I. 2009, Space Sci. Rev., 149, 65 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2003, A&A, 408, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2004, A&A, 415, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Phil. Trans. R. Soc. London Ser. A, 370, 3193 [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, G. R., Del Zanna, G., & Mason, H. E. 2019, A&A, 627, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hood, A. W. 1992, Plasma Phys. Control. Fusion, 34, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Ibanez, S. M. H., & Escalona, T. O. B. 1993, ApJ, 415, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Ibanez, S. M. H., & Sanchez, D. N. M. 1992, ApJ, 396, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Krasnobaev, K. V., & Tagirova, R. R. 2017, MNRAS, 469, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Krishna Prasad, S., Raes, J. O., Van Doorsselaere, T., Magyar, N., & Jess, D. B. 2018, ApJ, 868, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, S., Nakariakov, V. M., & Moon, Y.-J. 2016, ApJ, 824, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Kupriyanova, E. G., Kashapova, L. K., Van Doorsselaere, T., et al. 2019, MNRAS, 483, 5499 [NASA ADS] [CrossRef] [Google Scholar]
- Li, D., Ning, Z. J., Huang, Y., et al. 2017, ApJ, 849, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., & Ofman, L. 2014, Sol. Phys., 289, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Mariska, J. T. 2006, ApJ, 639, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Mariska, J. T., Warren, H. P., Williams, D. R., & Watanabe, T. 2008, ApJ, 681, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Verwichte, E., Berghmans, D., & Robbrecht, E. 2000, A&A, 362, 1151 [NASA ADS] [Google Scholar]
- Nakariakov, V. M., Tsiklauri, D., Kelly, A., Arber, T. D., & Aschwanden, M. J. 2004, A&A, 414, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Afanasyev, A. N., Kumar, S., & Moon, Y.-J. 2017, ApJ, 849, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Kosak, M. K., Kolotkov, D. Y., et al. 2019, ApJ, 874, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Nisticò, G., Polito, V., Nakariakov, V. M., & Del Zanna, G. 2017, A&A, 600, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Wang, T. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Pant, V., Tiwari, A., Yuan, D., & Banerjee, D. 2017, ApJ, 847, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Provornikova, E., Ofman, L., & Wang, T. 2018, Adv. Space Res., 61, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F. 2014, Sol. Phys., 11, 4 [Google Scholar]
- Reale, F. 2016, ApJ, 826, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Reale, F., Testa, P., Petralia, A., & Graham, D. R. 2019, ApJ, accepted [arXiv:1907.02291] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2013, A&A, 553, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selwa, M., Murawski, K., & Solanki, S. K. 2005, A&A, 436, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tajfirouze, E., Reale, F., Petralia, A., & Testa, P. 2016, ApJ, 816, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, B., Yu, Z., Huang, J., Tan, C., & Zhang, Y. 2016, ApJ, 833, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Taroyan, Y., Erdélyi, R., Wang, T. J., & Bradshaw, S. J. 2007, ApJ, 659, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Testa, P., De Pontieu, B., Allred, J., et al. 2014, Science, 346, 1255724 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Wardle, N., Del Zanna, G., et al. 2011, ApJ, 727, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Haynes, M., Arber, T. D., & Brady, C. S. 2008, ApJ, 685, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. 2011, Space Sci. Rev., 158, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J. 2016, in Low-Frequency Waves in Space Plasmas, Geophys. Monograph Ser., 216, 395 [Google Scholar]
- Wang, T., Solanki, S. K., Curdt, W., Innes, D. E., & Dammasch, I. E. 2002, ApJ, 574, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Solanki, S. K., Curdt, W., et al. 2003, A&A, 406, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T., Innes, D. E., & Qiu, J. 2007, ApJ, 656, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Ofman, L., Sun, X., Provornikova, E., & Davila, J. M. 2015, ApJ, 811, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Ofman, L., Sun, X., Solanki, S. K., & Davila, J. M. 2018, ApJ, 860, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, D., Van Doorsselaere, T., Banerjee, D., & Antolin, P. 2015, ApJ, 807, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Zavershinsky, D. I., & Molevich, N. E. 2013, Tech. Phys. Lett., 39, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Zavershinsky, D. I., & Molevich, N. E. 2014, Tech. Phys. Lett., 40, 701 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Coronal heating functions modelled as H(ρ, T) ∝ ρaTb for Ohmic heating (1), constant heating per unit volume (2) and mass (3), and Alfvén waves/mode conversion (4) (see Ibanez & Escalona 1993); the corresponding τ1, 2 (Eq. (6)) in minutes, where the radiative cooling is determined by CHIANTI (see Fig. 1).
All Figures
 |
Fig. 1. Left: piecewise dependence of the optically thin radiation losses per unit mass L(ρ, T) = χρTβ on temperature, where the specific values of the parameters χ and β are determined from the CHIANTI atomic database v. 8.0.7 for the plasma concentration 1016 m−3 and vary with the temperature interval considered. Right: variation of τ1 (red) and τ2 (blue) determined by Eq. (6) with temperature, for the radiative cooling shown in the left-hand panel and a heating model with the density and temperature power indices a = −0.5 and b = −3, respectively. The green dashed lines indicate the SUMER observational channels 6.3 MK and 8.9 MK. |
| In the text | |
 |
Fig. 2. Variation of ωI obtained for τ1 = 15 min, and τ2 = 8.2 min (green) and τ2 = 6 min (red), left; and τ1 = 10 min, and τ2 = 13 min (green) and τ2 = 22 min (red), right. The grey lines in both panels indicate |
| In the text | |
 |
Fig. 3. Left: parametric regions of the wave damping enhancement (I), suppression (II), and thermal over-stability (III). Grey-shaded regions indicate the values of τ1, 2 where the q-factor is in between 1 (the green line) and 2 (the blue line, Ia), and in between 2 and 3 (the purple line, Ib). The red, green, and blue symbols indicate some arbitrary values of τ1, 2 chosen for the numerical solutions shown in Fig. 4. Right: heating/cooling times τ1, 2 (see Eq. (6), black and red contours, respectively) determined for the CHIANTI radiative cooling, and the heating function in the form H(ρ, T) ∝ ρaTb for the varying temperature and density power indices a and b. The grey-shaded areas indicate the values of a and b where 1 < q-factor < 2 (light grey) and 2 < q-factor < 3 (dark grey). The green, blue, and purple lines show q-factor equals 1, 2, and 3, respectively. |
| In the text | |
 |
Fig. 4. Left: cross-sections of the perturbed velocity as a function of time, obtained for τ1 = 40 min and τ2 = 23 min (blue), τ1 = 61 min and τ2 = 11.5 min (red), and τ1 = 30 min and τ2 = 5 min (green). Right: similar to the left-hand panel, but for the set of physical parameters from Mariska et al. (2008) (see Sect. 3 for details) and with τ1 = 19.5 min and τ2 = 22.3 min. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



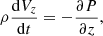
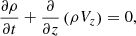
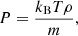
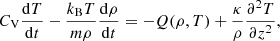
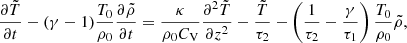
![$$ \begin{aligned} \tau _{1}={\gamma C_\mathrm{V} }/\left[{Q_{\rm T}-(\rho _0/T_0)Q_{\rho }}\right], \quad \tau _{2}={C_\mathrm{V} }/{Q_{\rm T}} \end{aligned} $$](/articles/aa/full_html/2019/08/aa36072-19/aa36072-19-eq6.gif)
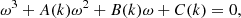
![$$ \begin{aligned} A=i\left[\frac{k^2\kappa }{\rho _0 C_\mathrm{V} }+\frac{1}{\tau _2}\right], B=-C_\mathrm{s} ^2k^2,C=-i\frac{k_\mathrm{B} T_0}{m}k^2 \left[\frac{k^2\kappa }{\rho _0 C_\mathrm{V} }+\frac{\gamma }{\tau _1}\right], \end{aligned} $$](/articles/aa/full_html/2019/08/aa36072-19/aa36072-19-eq8.gif)
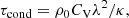
![$$ \begin{aligned} \omega ^2 = C_{\rm s}^2 k^2\left\{ 1-i\omega ^{-1}\left[\frac{\gamma - 1}{\gamma }\frac{4\pi ^2}{\tau _{\mathrm{cond}}}+\frac{\tau _1-\tau _2}{\tau _1\tau _2}\right]\right\} \cdot \end{aligned} $$](/articles/aa/full_html/2019/08/aa36072-19/aa36072-19-eq11.gif)