| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526003 | |
| Published online | 13 November 2015 | |
Online material
Appendix A: Calibration of QMS
The integrated ion current measured by a QMS corresponding to a mass fragment m/z of the molecules of a given species desorbed during ice irradiation experiments is proportional to the total number of molecules desorbed, and it can be calculated as follows: ![]() (A.1)where A(m/z) is the integrated area below the QMS signal of a given mass fragment m/z during photon-induced desorption, kQMS is the proportionality constant, σ+(mol) the ionization cross section for the first ionization of the species of interest and the incident electron energy of the mass spectrometer, N(mol) the total number of desorbed molecules in column density units, IF(z) the ionization factor, that is, the fraction of ionized molecules with charge z, FF(m) the fragmentation factor, that is, the fraction of molecules of the isotopolog of interest leading to a fragment of mass m in the mass spectrometer, and S(m/z) the sensitivity of the QMS to the mass fragment (m/z) (see Tanarro et al. 2007, and references therein).
(A.1)where A(m/z) is the integrated area below the QMS signal of a given mass fragment m/z during photon-induced desorption, kQMS is the proportionality constant, σ+(mol) the ionization cross section for the first ionization of the species of interest and the incident electron energy of the mass spectrometer, N(mol) the total number of desorbed molecules in column density units, IF(z) the ionization factor, that is, the fraction of ionized molecules with charge z, FF(m) the fragmentation factor, that is, the fraction of molecules of the isotopolog of interest leading to a fragment of mass m in the mass spectrometer, and S(m/z) the sensitivity of the QMS to the mass fragment (m/z) (see Tanarro et al. 2007, and references therein).
The measured ion current depends on the ionization cross section of the species (σ+(mol)), since only ionized molecules produce a signal in the QMS. The product IF(z)·FF(m) represents the fraction of desorbed molecules that leads to the monitored mass fragment m/z once they are ionized in the QMS. The sensitivity S(m/z) must be calibrated for every mass spectrometer. On the other hand, kQMS depends not only on the mass spectrometer, but on the configuration of the experimental setup, and, in particular, on the fraction of desorbed molecules that reach the QMS. This fraction in turn depends on the pumping speed for the different molecules. A brief study of the pumping speed of the setup described in Sect. 2 is presented in Muñoz Caro et al. (2010). In the following discussion we have assumed as a first approximation that this speed is the same for all the molecules, so that kQMS does not depend on the species. The same assumption has been used in previous works (see Fayolle et al. 2013; Fillion et al. 2014, and references therein). Both kQMS and, to a lesser extent, S(m/z) are subject to variations in the behavior of the QMS with time. Calibration of these two factors for our QMS is described below.
Appendix A.1: Calibration of proportionality constant kQMS
As we explained in Sect. 1, CO ice irradiation experiments under UHV conditions can be used as a reference to calibrate the QMS signal. Equation (A.1) can be rewritten as follows: 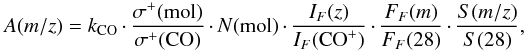 (A.2)where kCO is
(A.2)where kCO is 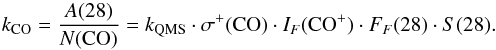 (A.3)Therefore, the problem of calibrating kQMS can be replaced by the problem of calculating kCO. To derive kCO for our experimental setup, we performed UV-irradiation experiments of a pure CO ice made by deposition of CO (gas, Praxair 99.998%), using the protocol described in Sect. 2. Since in the case of solid CO photon-induced chemistry accounts for only ~5% of the absorbed photons (Muñoz Caro et al. 2010), the area below the m/z = 28 signal detected with the QMS (A(28) in Eq. (A.3); left panel of Fig. A.1) practically corresponds to the loss of CO molecules in the ice (N(CO) in Eq. (A.3)), measured with the FTIR spectrometer (middle panel of Fig. A.1). The relation between A(28) and N(CO) (right panel of Fig. A.1) gives kCO = 1.32 × 10-10 A min ML-1, with 1 ML defined as 1015 molecules cm-2. This value is good for our setup by the time the experiments were performed.
(A.3)Therefore, the problem of calibrating kQMS can be replaced by the problem of calculating kCO. To derive kCO for our experimental setup, we performed UV-irradiation experiments of a pure CO ice made by deposition of CO (gas, Praxair 99.998%), using the protocol described in Sect. 2. Since in the case of solid CO photon-induced chemistry accounts for only ~5% of the absorbed photons (Muñoz Caro et al. 2010), the area below the m/z = 28 signal detected with the QMS (A(28) in Eq. (A.3); left panel of Fig. A.1) practically corresponds to the loss of CO molecules in the ice (N(CO) in Eq. (A.3)), measured with the FTIR spectrometer (middle panel of Fig. A.1). The relation between A(28) and N(CO) (right panel of Fig. A.1) gives kCO = 1.32 × 10-10 A min ML-1, with 1 ML defined as 1015 molecules cm-2. This value is good for our setup by the time the experiments were performed.
Appendix A.2: Calibration of the QMS sensitivity S (m/z)
The experimental protocol used to obtain S(m/z) was slightly different from the one described in Sects. 2 and A.1. The QMS ion current (I(m/z)), corresponding to a mass fragment m/z of the molecules of a given species present in the chamber at a given time, is proportional to the pressure measured for that species (Pmol), and can be calculated with an equation similar to Eq. (A.1), but with a different constant of proportionality: ![]() (A.4)In this case, the Bayard-Alpert ionization gauge (model IoniVac IM540) used as manometer in ISAC does not discriminate between different isotopologs of the same species, and P(mol) (once corrected for the gas correction factors provided by the gauge manufacturer) account for all of them. Therefore, an isotopic factor (IsF(m)) must be introduced to take into account only the isotopolog of mass m that is being measured by the QMS.
(A.4)In this case, the Bayard-Alpert ionization gauge (model IoniVac IM540) used as manometer in ISAC does not discriminate between different isotopologs of the same species, and P(mol) (once corrected for the gas correction factors provided by the gauge manufacturer) account for all of them. Therefore, an isotopic factor (IsF(m)) must be introduced to take into account only the isotopolog of mass m that is being measured by the QMS.
Since Eq. (A.2) uses the relative sensitivity of the QMS between any mass fragment and the mass fragment m/z = 28, it is not necessary to obtain the absolute sensitivity of the mass spectrometer. Instead we worked with 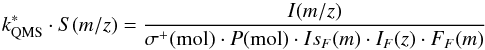 (A.5)for every mass fragment, since the ratio S(m/z)/S(28) is the same as the ratio
(A.5)for every mass fragment, since the ratio S(m/z)/S(28) is the same as the ratio ![]() /
/![]() .
.
To derive a relation between ![]() and m/z that could be used for mass fragments of any species, we introduced three nobel gases into the ISAC chamber: He (gas, Air Liquide 99.999%), Ne (gas, Air Liquide 99.995%), and Ar (gas, Praxair 99.997%) at different pressures. For every gas, the ratio between the QMS signal (I(m/z)) and the pressure of the gas (P(mol)) was corrected for the factors in Eq. (A.5) (Table A.1, except for the fragmentation factor, since noble gas atoms do not produce any fragments in the mass spectrometer), leading to a value of
and m/z that could be used for mass fragments of any species, we introduced three nobel gases into the ISAC chamber: He (gas, Air Liquide 99.999%), Ne (gas, Air Liquide 99.995%), and Ar (gas, Praxair 99.997%) at different pressures. For every gas, the ratio between the QMS signal (I(m/z)) and the pressure of the gas (P(mol)) was corrected for the factors in Eq. (A.5) (Table A.1, except for the fragmentation factor, since noble gas atoms do not produce any fragments in the mass spectrometer), leading to a value of ![]() for three different m/z values (m/z = 4 for He, m/z = 20 for Ne, and m/z = 40 for Ar). These values are plotted in Fig. A.2. An exponential fit leads to a sensitivity curve
for three different m/z values (m/z = 4 for He, m/z = 20 for Ne, and m/z = 40 for Ar). These values are plotted in Fig. A.2. An exponential fit leads to a sensitivity curve ![]() (A.6)in A mbar-1Å-2.
(A.6)in A mbar-1Å-2.
|
Fig. A.1
Left: evolution of the m/z = 28 QMS signal corresponding to the photodesorption of CO during UV irradiation of a pure CO ice. The ion current in the y-axis corresponds, approximately, to the partial pressure (mbar) in the main chamber. Dotted lines represent the baselines used to calculate A(28) in every irradiation period. Note that the y-axis is on a logarithmic scale. Middle: evolution of the C=O stretching mode of CO at 2139 cm-1 during UV irradiation of pure CO ice. Differences in the column densities after every period of irradiation correspond to N(CO) in Eq. (A.3). Right: relation between A(28) and N(CO). The solid line is a linear fit. |
|
| Open with DEXTER | |
 |
Fig. A.2
Relation between |
| Open with DEXTER | |
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


