| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525834 | |
| Published online | 22 June 2015 | |
Online material
Appendix A: Luminosity evolution scatter
The evolution-corrected luminosities of galaxies become increasingly uncertain with redshift. This is mainly due to the intrinsic variation in properties of the LRGs, as illustrated in the bottom panel of Fig. 2, where the difference between the e-correction curves increases with redshift for the different models.
To obtain a rough estimate of how intrinsic scatter in the (k + e)-corrected absolute magnitudes affects our results, we made a simple test. We started with randomly drawing 105 redshifts and (k + e)-corrected absolute magnitudes from the original distribution, that is, the distribution that is shown in the bottom panel of Fig. 3. We assumed that these magnitudes are the intrinsic ones. Next, we assigned a mass to each object using our nominal best-fit luminosity-to-halo mass relation from Table 2. Note that our conclusions do not sensitively depend on the choice of slope and offset. We computed an NFW profile for each object at 100 logarithmically spaced radial bins between 0.05 ![]() Mpc and 1
Mpc and 1 ![]() Mpc. We stacked the NFW profiles of objects that fall inside a lens bin as defined in Fig. 3, and fitted an NFW to the resulting profile using the mean redshift of these objects.
Mpc. We stacked the NFW profiles of objects that fall inside a lens bin as defined in Fig. 3, and fitted an NFW to the resulting profile using the mean redshift of these objects.
Next, we simulated the intrinsic scatter in absolute magnitude by assuming that it can be described by a Gaussian whose width increases as σ = 0.3z. This particular choice covers the range of e-correction curves of the SSP models that agree reasonably well with the colours of the LRGs, as shown in Fig. 2. We drew a random number from this Gaussian and added it to the “intrinsic” magnitudes: these are the “observed” magnitudes. We stacked the NFW profiles, but now using the “observed” magnitudes to select the lenses. Again, we fitted an NFW profile to the stacked profile using the mean redshift of the observed objects. The impact of intrinsic luminosity scatter was then estimated from the ratio of this “observed” mass to the intrinsic one. The mass typically changes by a few percent. The largest difference is found for the L3z4 bin, where the difference is ~10%. However, in all cases, the error is considerably smaller than the statistical errors. We therefore conclude that intrinsic scatter of the luminosities can be safely ignored.
Appendix B: Systematic tests
 |
Fig. B.1
Weighted mean of the lensing signal times the radius for a low-z and high-z LRG lens sample, measured with different source samples as indicated in the plot. For both lens samples, we find consistent results, suggesting that our measurement pipeline is robust and does not introduce a redshift-dependent bias. |
| Open with DEXTER | |
Since this work aims at measuring the redshift dependence of the lensing signal, we have to be particularly careful with systematic effects that mimic a redshift scaling. One problem that requires attention is computing the mean lensing efficiency. For example, if we miss the high-redshift tail of the source redshift distribution, the mean lensing efficiency would be biased increasingly low for higher lens redshifts, which would mimic a redshift dependence in the lensing signal. Motivated by the differences in mean lensing efficiency computed from the photometric redshift catalogue from Ilbert et al. (2009) and Ilbert et al. (2013) at high lens redshifts, we performed the following test.
We divided our source sample into six different samples, with magnitude cuts of 22 <mr′< 23, 23 <mr′< 24, and 22 <mr′< 22.5, 22.5 <mr′< 23, 23 <mr′< 23.5, 23.5 <mr′< 24. We split the LRGs into a low-redshift sample with 0.15 <z< 0.5 and a high-redshift sample with 0.5 <z< 0.8 and measured their lensing signals using each source sample. Note that for each source sample, we separately determined the shear signal around random points, the mean lensing efficiencies using the Ilbert et al. (2013) photometric redshift catalogues, the contamination of source galaxies around the lenses, and the noise bias correction. We measured the weighted mean of the lensing signal times the projected separation, as that is roughly a constant with radius, over the range ![]() Mpc. We show these values for the two LRG samples in Fig. B.1.
Mpc. We show these values for the two LRG samples in Fig. B.1.
The weighted mean of the lensing signal of each lens sample is consistent for the various source samples. Clearly, the measurements are correlated for the source samples that overlap in apparent magnitude, but the four bins of 0.5 mag width are more or less independent (not completely, because they are similarly affected by cosmic variance). This result strongly suggests that the measurement process is robust.
We have repeated this test using the photometric redshift catalogue of Ilbert et al. (2009) instead. For the 0.15 <z< 0.5 LRG sample the results are consistent, but for the high-z sample, some bins differ by 2–3σ. This indicates a problem with the source redshift distribution used to compute the lensing efficiencies. Since the photometric redshift catalogue of Ilbert et al. (2013) gives consistent results for the different source samples, even at high redshifts, this suggests that the source redshift distribution is sufficiently accurately determined with the latter, but not with the former (see also the discussion in Hoekstra et al. 2015).
Appendix C: Fitting methodology
We used Bayesian inference techniques to determine the posterior probability distribution ![]() of the model parameters λ, given the data
of the model parameters λ, given the data ![]() . According to Bayes’ theorem,
. According to Bayes’ theorem, 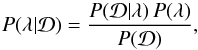 (C.1)where P(D | λ) is the likelihood of the data given the model parameters, P(λ) is the prior probability of these parameters, and
(C.1)where P(D | λ) is the likelihood of the data given the model parameters, P(λ) is the prior probability of these parameters, and 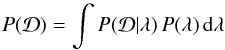 (C.2)is called the evidence. Since we do not intend to perform model selection, the evidence just acts as a normalisation constant that does not need to be calculated. Therefore, the posterior distribution P(λ | D) is given by
(C.2)is called the evidence. Since we do not intend to perform model selection, the evidence just acts as a normalisation constant that does not need to be calculated. Therefore, the posterior distribution P(λ | D) is given by 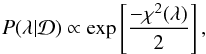 (C.3)where
(C.3)where 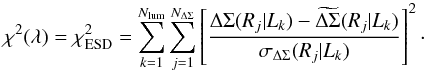 (C.4)
(C.4)![]() denotes the model prediction, σΔΣ is the corresponding error, Nlum = 3 and NΔΣ = 12,12,12,11 for the low- and high-redshift bins of the LOWZ and CMASS samples, respectively. For our fiducial model, the set of model parameters is λfid = (Mmean,σlog M,fconc), where
denotes the model prediction, σΔΣ is the corresponding error, Nlum = 3 and NΔΣ = 12,12,12,11 for the low- and high-redshift bins of the LOWZ and CMASS samples, respectively. For our fiducial model, the set of model parameters is λfid = (Mmean,σlog M,fconc), where
-
Mmean is the mean halo mass for the k-th luminosity bin;
-
σlog M is the scatter of ⟨ Nc | M ⟩;
-
fconc is the normalisation of the c(M) relation.
When exploring model variations (see Sect. 4.1), we employed λmiscen = (λfid,poff,Roff) and λsatfrac = (λfid,M1). For all model parameters, we adopted a flat, sufficiently wide prior such that the results are not biased.
We sampled the posterior distribution of our model parameters given the data using a Markov chain Monte Carlo (MCMC). In particular, we implemented the Metropolis-Hastings algorithm to construct the MCMC. At any point in the chain, a trial model is generated using a method specified below. The χ2 statistic for the trial model, ![]() , is calculated using Eq. (C.4). This trial model is accepted to be a member of the chain with a probability given by
, is calculated using Eq. (C.4). This trial model is accepted to be a member of the chain with a probability given by 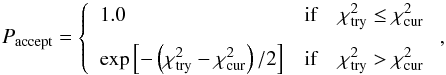 (C.5)where
(C.5)where ![]() denotes the χ2 for the current model in the chain. We initialized the chain from a random position in our multi-dimensional parameter space and obtained a chain of ~500 000 models. We discarded the first 10 000 models (the burn-in period) allowing the chain to sample from a more probable part of the distribution. We used this chain of models to estimate the confidence levels on the parameters and on the lensing signal, as shown in Fig. 4.
denotes the χ2 for the current model in the chain. We initialized the chain from a random position in our multi-dimensional parameter space and obtained a chain of ~500 000 models. We discarded the first 10 000 models (the burn-in period) allowing the chain to sample from a more probable part of the distribution. We used this chain of models to estimate the confidence levels on the parameters and on the lensing signal, as shown in Fig. 4.
A proper choice of the proposal distribution is very important to achieve fast convergence and a reasonable acceptance rate for the trial models. The posterior distribution in a multi-dimensional parameter space, such as the one we are dealing with, will have degeneracies and in general can be very difficult to sample from. We have adopted the following strategy to overcome these difficulties. During the first half of the burn-in stage, we chose an independent Gaussian proposal distribution for every model parameter, as is common for the Metropolis-Hastings
algorithm. Half-way through the burn-in stage, we performed a Fisher information matrix analysis at the best-fit model found thus far. The Fisher information matrix, given by 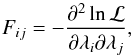 (C.6)is an Np × Np symmetric matrix, where Np denotes the number of parameters in our model, and ℒ ∝ e− χ2/ 2 is the likelihood. The inverse of the Fisher matrix gives the covariance matrix, C, of the posterior constraints on the model parameters. More importantly, the eigenvectors of the covariance matrix are an excellent guide to the degeneracies in the posterior distribution, and the corresponding eigenvalues set a scale for how wide the posterior ought to be in a given direction. Therefore, for the second half of the burn-in period, we used this information and a proposal distribution that is a multi-variate Gaussian centred on the current value of the parameters and with a covariance given by the aforementioned matrix. In practice, the trial model (λtry) can be generated from the current model (λcur) using
(C.6)is an Np × Np symmetric matrix, where Np denotes the number of parameters in our model, and ℒ ∝ e− χ2/ 2 is the likelihood. The inverse of the Fisher matrix gives the covariance matrix, C, of the posterior constraints on the model parameters. More importantly, the eigenvectors of the covariance matrix are an excellent guide to the degeneracies in the posterior distribution, and the corresponding eigenvalues set a scale for how wide the posterior ought to be in a given direction. Therefore, for the second half of the burn-in period, we used this information and a proposal distribution that is a multi-variate Gaussian centred on the current value of the parameters and with a covariance given by the aforementioned matrix. In practice, the trial model (λtry) can be generated from the current model (λcur) using ![]() (C.7)where x is a vector consisting of Np standard normal deviates, the matrix A is such that AAT = C, and ζ is a parameter that we have chosen to achieve an average acceptance rate of ~30%. We repeated the Fisher matrix analysis at the end of the burn-in period (using the best-fit model found thus far) and used the covariance matrix to define our proposal distribution to be used for the MCMC. This strategy has proven to be extremely efficient in sampling posterior distributions for similar studies (see e.g. Cacciato et al. 2013, 2014).
(C.7)where x is a vector consisting of Np standard normal deviates, the matrix A is such that AAT = C, and ζ is a parameter that we have chosen to achieve an average acceptance rate of ~30%. We repeated the Fisher matrix analysis at the end of the burn-in period (using the best-fit model found thus far) and used the covariance matrix to define our proposal distribution to be used for the MCMC. This strategy has proven to be extremely efficient in sampling posterior distributions for similar studies (see e.g. Cacciato et al. 2013, 2014).
Appendix D: k-corrected-only results
We have attempted to account for the evolution of the luminosities of LRGs by applying a luminosity evolution correction. Unfortunately, this correction is uncertain and will also add scatter to the corrected luminosities because LRGs cover a range of intrinsic properties such as formation age and metallicity, which complicates the interpretation of the results. Therefore, it is also interesting to apply only the k-correction to the absolute magnitudes. The resulting luminosities are closer to the real luminosities, meaning they have smaller scatter. Interpreting any trend in the luminosity-to-halo mass relation will be harder as both the luminosity and the halo mass may evolve simultaneously, but a comparison with simulations, for example, should be more straightforward.
Hence we divided the lens sample into bins of k-corrected absolute magnitude and redshift. Details of the lens samples can be found in Table D.1. The selection is also illustrated in Fig. 3. For each subsample, we stacked the lensing signal of all the lenses inside that bin and show the result in Fig. D.1. We fitted the halo model using the same set-up as before and show the best-fit models, together with the model uncertainties, in Fig. D.1. The corresponding effective masses and normalisations of the mass-concentration relation are listed in Table D.1.
Properties of the lens bins (after k-correction).
 |
Fig. D.1
Lensing signal ΔΣ of LOWZ (top two rows) and CMASS (bottom two rows) lenses as a function of projected separation for the five luminosity bins (after the k-correction is applied). The solid red lines show the best-fit halo model, the orange and yellow regions the 1 and 2σ model uncertainty, respectively. We fit the signal on scales between 0.05 and 2 |
| Open with DEXTER | |
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


